Disrupting the Myosin Converter-Relay Interface Impairs Drosophila Indirect Flight Muscle Performance

Abstract

Structural interactions between the myosin converter and relay domains have been proposed to be critical for the myosin power stroke and muscle power generation. We tested this hypothesis by mutating converter residue 759, which interacts with relay residues I508, N509, and D511, to glutamate (R759E) and determined the effect on Drosophila indirect flight muscle mechanical performance. Work loop analysis of mutant R759E indirect flight muscle fibers revealed a 58% and 31% reduction in maximum power generation (P_WL) and the frequency at which maximum power (f_WL) is generated, respectively, compared to control fibers at 15°C. Small amplitude sinusoidal analysis revealed a 30%, 36%, and 32% reduction in mutant elastic modulus, viscous modulus, and mechanical rate constant 2πb, respectively. From these results, we infer that the mutation reduces rates of transitions through work-producing cross-bridge states and/or force generation during strongly bound states. The reductions in muscle power output, stiffness, and kinetics were physiologically relevant, as mutant wing beat frequency and flight index decreased about 10% and 45% compared to control flies at both 15°C and 25°C. Thus, interactions between the relay loop and converter domain are critical for lever-arm and catalytic domain coordination, high muscle power generation, and optimal Drosophila flight performance.

Introduction

During muscular contraction, force and motion are generated by the myosin mechanoenzyme as a result of transduction of chemical energy stored in the terminal phosphate bond of MgATP to mechanical energy. A critical component of this energy transduction is the link between the release of hydrolysis products Pi and MgADP from myosin's active site to the power stroke motion of the lever arm (1). The active site and lever arm are not in direct contact, thus intervening domains and interfaces must help coordinate these enzymatic and conformational changes. One potential communication pathway proposed to be critical for lever arm movement involves the relay and converter domains (Fig. 1). This pathway is based on interpretations of atomic level crystal structures of various myosins with different nucleotide analogs in their active sites, allowing for visualization of some pre- and postpower stroke states of the actomyosin cross-bridge cycle (2–6). Molecular dynamic simulations have been used to predict transitions that occur between these states of the cycle (3). Release of the terminal MgATP phosphate has been proposed to trigger repositioning of switch-2. Switch-2 movement induces kinking and rotation of the relay helix, which changes the conformation of the relay loop. The change in conformation of the loop is hypothesized to induce movement of the converter region, which appears to move with the lever arm (5,7,8). Thus, relay conformational changes may drive movement of the lever arm, and conversely, the converter may provide stress and strain feedback to the active site through the relay domain (9–11). If this is the case, then disrupting interactions between the domains should have severe effects on myosin and muscle function.

Figure 1.

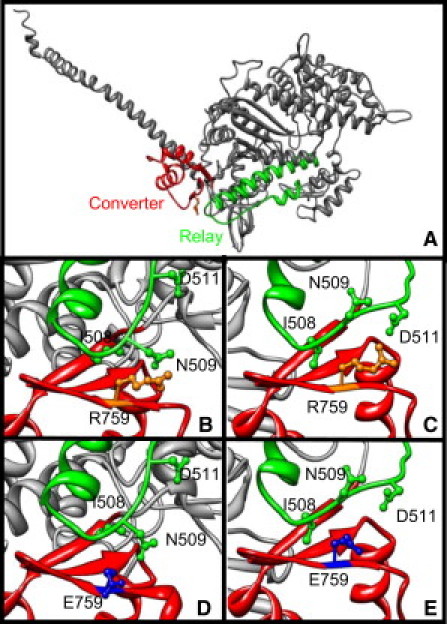
(A) Diagram of the mutant Drosophila IFM myosin heavy chain isoform (gray) showing the converter (red; residues 712–780 (12);) and relay (green; residues 469–525 (17)) domains in the prepower stroke state. (B) Close-up view of the wild-type, prepower stroke state of the relay and converter interface showing the three relay resides, I508, N509, and D511, with which converter residue R759 (gold) interacts (16,17). (C) Close-up view of the wild-type, postpower stroke state. (D) Close-up view of the mutant prepower stroke state showing the E759 converter mutation (blue). (E) Close-up view of the mutant postpower stroke state. Panels B–E are 90° counterclockwise rotated compared to panel A. Scallop myosin structures in the pre- and postpower stroke were used as templates and the Drosophila converter and relay amino acids substituted for the corresponding scallop residues (PDB codes 1QVI (4) and 1KK8 (6)). Molecular operating environment (MOE; http://www.chemcomp.com/software.htm) and UCSF CHIMERA (37) softwares were used to generate the figure.

In all currently available myosin crystal structures, the interface between the relay (residues 472–528; note that chicken skeletal muscle myosin numbering is used throughout the article) and converter (residues 712–779) domains appear to remain intact (5,12–14). Two Dictyostelium myosin II mutational studies indicate the importance of relay converter interdomain connectivity. Disulfide cross-linking of substituted cysteines at the Dictyostelium equivalents of myosin relay residue isoleucine 508 and converter residue arginine 759 minimally affected actin binding, MgATP-induced actin release, and actin-activated MgATPase (14). When the interface was weakened by a myosin relay loop point mutation in Dictyostelium, I508A, actin-activated MgATPase decreased and movement of actin in the motility assay was completely eliminated (15).

Recently, the importance of the interface between the converter and relay was studied in muscle myosin by mutating R759 to E759 in the converter domain of Drosophila indirect flight muscle (IFM) myosin (Fig. 1, A and B (16)). Molecular modeling suggests this mutation weakens the hydrophobic interactions of arginine 759 with relay residue isoleucine 508 and polar interactions with asparagine 509, especially in the prepower stroke state, and eliminates a salt bridge with the relay's negatively charged aspartate 511 in the postpower stroke state (16,17). Initial characterization of the effects of the R759E mutation found that it decreased basal and actin-activated MgATPase activity 60%, but did not alter the K_m for actin. In vitro actin motility was decreased by 35% and the intrinsic tryptophan fluorescence response to nucleotide was altered, suggesting an impact on lever arm movement (16).

However, the importance of the relay-converter connection has not been examined in a muscle fiber where the lever arm must operate under high loads to generate force and power. IFM fibers from Drosophila genetically engineered to express transgenic myosin are amenable to various mechanical measurements (18–20). Here we take advantage of this system to study the effects of disrupting the interface between the relay and converter domains. We used the large amplitude work loop technique and observed a decrease in maximum power output (P_WL) and its optimal frequency (f_WL) in mutant R759E fibers compared to control fibers at 15°C. Employing sinusoidal analysis, we measured substantial decreases in R759E complex modulus, elastic modulus (E_e), viscous modulus (E_v), and mechanical rate constant 2πb compared to control fibers. The reduced muscle performance caused decreased flight ability, as mutant wing beat frequency (WBF) and flight index decreased compared to control flies. These experiments demonstrate that the relay-converter pathway is critical for coordinating the catalytic and lever arm domains to enable power generation during Drosophila flight.

Methods

Transgenic lines

The control fly line, PwMhc2, which expresses wild-type myosin in a myosin IFM null background, Mhc¹⁰ (21), was generated using P element-mediated germline transformation (20). Two independent lines expressing the mutant R759E myosin, R759-1 and R759E-2 (originally named PwMhcR759E-V5 and PwMhcR759E-V8 (16)), were constructed using site-directed mutagenesis to replace arginine at myosin heavy chain position 759 with glutamic acid (16). The mutant lines were also crossed into the Mhc¹⁰ null background, which results in expression of only the mutant myosin in the IFM. SDS-PAGE confirmed that the mutant protein was expressed at 100% of wild-type levels in both the R759E-1 and R759E-2 lines (16).

Fly stocks were maintained at 18°C rather than a higher temperature to produce larger IFM fibers. Females were collected within 24 h of eclosion and transferred to fresh vials each day. After 48 h, these female flies were subjected to flight and wing beat assays or dissected to obtain IFM fibers for mechanical tests.

Flight assay and wing beat frequency

Flight assays were conducted on 2–3-day-old female flies at 15°C and 25°C. The flight phenotype was determined by observing whether each fly tested flew upward (U), horizontal (H), down (D), or displayed no flight (N) when released in a flight chamber (22) and quantified using a flight index equal to 6U/T + 4H/T + 2D/T + 0N/T, where T is the total number of flies tested (23). Wing beat frequency (WBF) was measured on 2–3-day-old female flies using an optical tachometer (24).

Fiber mechanics

In brief (detailed in Swank et al. (25)), a pair of IFM bundles containing six fibers each were dissected out of 2–3-day-old female fly thoraces and demembranated for 1 h at 4°C in skinning solution (5 mM ATP, 1 mM free Mg²⁺, 0.25 mM phosphate, 5 mM EGTA, 20 mM N, n-Bis (2-hydroxyethyl)-2-aminoethanesulfonic acid (BES) at pH 7.0, 1 mM dithreitol, 50% glycerol, and 0.5% Triton X-100; pCa = 8.0 and ionic strength = 175 mM adjusted with Na methane sulfonate). Tungsten wire probes were used to separate and split the individual fibers. An aluminum clip was wrapped around each end of the fiber preparation to grip and firmly contain all constituent myofibrils. The preparations were attached to a mechanical measurement apparatus and bathed in relaxing solution (5 mM ATP, 8 mM phosphate, 15 mM creatine phosphate, 300 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES at pH 7.0, 1 mM dithreitol; pCa = 8.0; ionic strength = 200 mM, adjusted with Na methane sulfonate). Fibers were stretched by 5% from resting length. Fibers were subjected to sinusoidal analysis (see below) in relaxing solution (pCa = 8.0) before a partial exchange with activating solution (same as relaxing solution but pCa adjusted to 4.0) in the chamber to bring the pCa to 5.0. The active fiber was further stretched (in 2% increments of fiber length between clips) until power generation was maximal. At this optimized length, different relaxing, activating, or rigor solutions were exchanged into the chamber and further sinusoidal analysis, work loop analysis, or tension measurements performed. Separate sets of fibers were used for the work loop study and the sinusoidal analysis study to ensure individual fibers were not fatigued. A standard work loop or sinusoidal analysis condition was run at the beginning and end of each experiment to ensure the fiber's performance did not decrease >10%.

Sinusoidal analysis and muscle mechanical rate constants

To measure muscle stiffness and mechanical rate constants of the fibers, sinusoidal analysis was performed as described previously (26) except the activating solution components were adjusted to 12.5 mM MgATP, 0 mM Pi, 30 mM creatine phosphate, 350 U/ml creatine phosphokinase with an ionic strength of 260 mM, based on the findings of Swank et al. (26), for optimal fiber performance. Briefly, a 0.125% muscle length (ML) peak-to-peak amplitude sine wave was applied to the fiber at 50 frequencies from 0.5 to 650 Hz. At each frequency the amplitude ratio and phase difference for force and length were calculated and this ratio was divided by the fiber cross-sectional area to obtain the complex, elastic, and viscous moduli.

The complex modulus from each fiber was fitted to a three-term equation. This is based on the equation originally developed by Kawai and Brandt (27) for sinusoidal analysis and has been slightly modified to be more suitable for IFM (26): Y(f) = A (2π if/α)^k – B if/(b +if) + C if/(c +if), where f is the applied frequency of oscillation (0.5–650 Hz), i is the square root of −1, α is defined as 1 Hz, and k is a unitless exponent (26). The first term (A) reflects the viscoelastic properties of passive structures within the fiber, whereas the second and third terms (B and C) reflect an outcome of transitions between cross-bridge states (changes in complex moduli due to the strain-sensitivity of cross-bridge rate constants) that are exponential in the time domain. Process B is primarily influenced by work-producing steps of the cross-bridge cycle whereas process C is influenced by work-absorbing steps before and including myosin detachment from actin (Fig. 2). Processes B and C appear as hemispheres in the Nyquist plot with characteristic frequencies b and c (26). In the time domain, these frequencies correspond to rate constants 2πb and 2πc. For a more detailed explanation, including information on the relationship between these rate constants and those derived from step analysis, see Kawai and Brandt (27).

Figure 2.

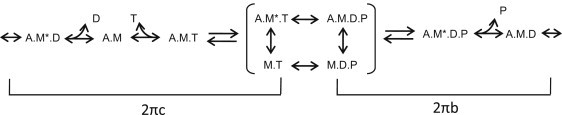
Cross-bridge scheme for sinusoidal analysis where M is myosin, A is actin, T is MgATP, D is MgADP, and P is phosphate. (Asterisk) Second conformational state. For conceptual purposes, the primary transitions that influence 2πb and 2πc when a myosin isomerization between Pi and ADP release is rate-limiting, are bracketed. See Swank et al. (26) for a full mathematical description of the elementary rate constant's relationship to 2πb and 2πc, and the derivation of 2πb and 2πc from small amplitude sinusoidal analysis.

Work loop analysis

Net work and power output were determined by subjecting the fibers to sinusoidal ML amplitudes up to 12-fold greater than those used for sinusoidal analysis. These greater strain amplitudes are likely used by Drosophila during flight (28). Strain amplitudes were 0.0625%, 0.25%, 0.5%, 0.75%, 1%, 1.25%, and 1.5% (peak to peak) of fiber resting length at sinusoidal oscillation frequencies of 50 Hz, 75 Hz, 100 Hz, 125 Hz, 150 Hz, 175 Hz, 200 Hz, and 225 Hz. The work loop results were analyzed using a different method than small amplitude sinusoidal analysis. Our small amplitude analysis assumes the resultant tension trace is also a nearly perfect sinusoid, which is true for strain amplitudes <∼0.25% ML (18). Above this, the force response becomes nonlinear with the length change. For work loops, 10 identical consecutive sinusoids were applied to the muscle and both tension and length traces recorded. Positive work (work produced by the muscle during shortening) and negative work (work absorbed by the muscle during lengthening) were determined by calculating the area under the tension curve during shortening and lengthening, respectively, for each half cycle. Negative work was subtracted from positive work to calculate net work, and net work was multiplied by oscillation frequency to calculate power. Data from the eighth length-change cycle were used, as the tension record reaches a stable state by the sixth or seventh cycle. The activation solution for work loop experiments was the same as the activation solution used for sinusoidal analysis except for the following increased concentrations: 18 mM MgATP, 37 mM creatine phosphate, and 450 units/ml creatine phosphokinase. These higher concentrations were used to ensure that fiber performance was not limited by MgATP diffusion into the fiber or MgADP buildup, as the fibers generate much higher power when run under work loop conditions than when subjected to small amplitude sinusoidal analysis.

Results

Flight assays

Two-to-three-day-old female mutant R759E-1 and R759E-2 flies exhibited impaired flight ability compared to control flies at 15°C and 25°C. Flight indices of both R759E-1 and R759E-2 were decreased by 45% compared to control values (Table 1), similar to the decrease at 25°C found in the initial study of the R759E flies (16). The mutant flies were able to take off appropriately; however, they were unable to remain airborne for more than a few seconds and landed promptly. WBF values for the mutant R759E-1 and R759E-2 lines were significantly decreased by 10% and 15% at 15°C and 25°C, respectively, compared to control flies (Table 1). About twice as many mutant as control flies either were unable or refused to beat their wings when flight tested. These flies were not included in the WBF calculations.

Table 1.

Flight characteristics

	Flight index		Wing beat frequency (Hz)
	15°C	25°C	15°C	25°C
Control	2.31 ± 0.10 (124)	4.31 ± 0.16 (102)	140 ± 2 (9)	174 ± 4 (10)
R759E-2	1.25 ± 0.09 (107)∗	2.38 ± 0.09 (110)∗	127 ± 3 (7)∗	144 ± 5 (10)∗
R759E-1	1.32 ± 0.08 (129)∗	2.40 ± 0.10 (130)∗	126 ± 3 (7)∗	149 ± 4 (10)∗

Flight index and wing beat frequency values obtained for the two independently generated mutant lines, R759E-1 and R759E-2, were not statistically different (p > 0.05). All values are mean ± SE. Numbers in parentheses indicate the number of flies tested.

^∗Statistically different from the control flies (Student's t-test, p < 0.05).

Work loop analysis of power generation

We performed muscle mechanics on just the R759E-2 line because all other results showed that the phenotypes of the two independently generated R759E lines were identical. The two lines yielded identical flight index and wing beat frequency values at both 15°C and 25°C (Table 1). Previous work showed normal myosin expression levels and no significant difference in myofibril ultrastructure, which was essentially normal with occasional minor disruption at two days of age (16).

To measure the effects of disrupting the converter relay interface on muscle power generation, we used the work loop technique (29) (Fig. 3 A). The optimal ML change amplitude for power generation was 0.75% ML for the control and mutant flies, but the optimum frequency of muscle oscillation (f_WL) was 31% lower in the mutant (Table 2). Power generation by the mutant was 58% less under optimal conditions for each line (Table 2 and Fig. 3 A). Comparing power generation at the same frequencies and amplitudes showed that over most conditions where positive power was generated, the mutation caused a significant decrease in power generation (Fig. 3, B and C). At an oscillation frequency of 150 Hz, the mutant did not produce as much power as the control fibers at amplitudes <1.0% (Fig. 3 B). At a ML change amplitude of 0.75%, frequencies 125 Hz and above showed significant decreases in power generation by the mutant compared to the control (Fig. 3 C). R759E fiber power was not reduced as much at lower oscillation frequencies. This observation, along with the decreased frequency at which maximum power was generated (f_WL, Table 2), revealed that the mutation slowed muscle kinetics.

Figure 3.

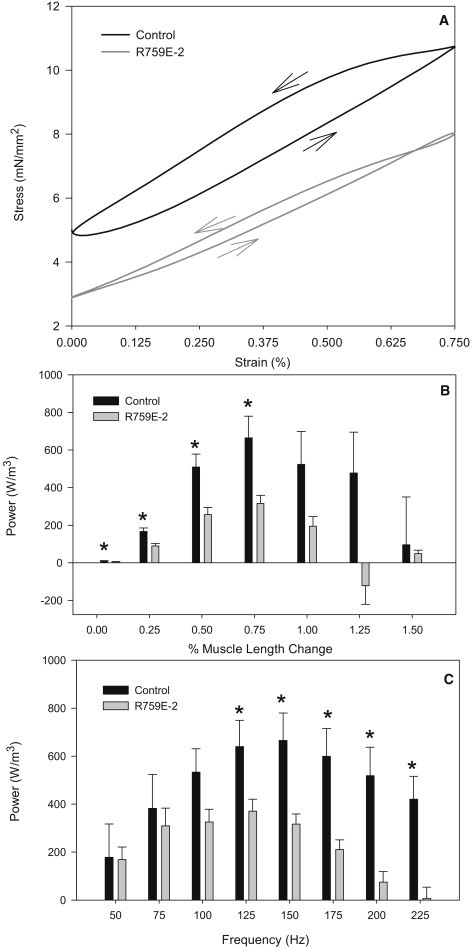
Work loop analysis. (A) Representative work loop traces. Control (solid) and R759E-2 (shaded) work loop traces from single fibers run under identical ML strain and frequency conditions, 0.75% ML and 150 Hz. Both loops generated net positive work (counterclockwise loops as indicated by the arrows) with the mutant loop generating a small clockwise subloop (work absorption) at the beginning of shortening. (B) Power as a function of sinusoidal ML change from 0.0625% to 1.5% ML (peak to peak) at a frequency of 150 Hz. (C) Power as a function of frequency at a ML change of 0.75%. Data are from control (N = 10) and mutant R759E-2 (N = 12) fibers. Mean ± SE. (Asterisk) Statistically different from control fibers (Student's t-test, p < 0.05). Experiments were performed at 15°C.

Table 2.

Dynamic properties from large amplitude work loops

	N	PWL(W/m3)	fWL(Hz)	W(J/m3)	W+(J/m3)	W−(J/m3)
Control	10	816 ± 55	152 ± 11	5.7 ± 0.9	44.4 ± 5.2	38.7 ± 3.6
R759E-2	12	347 ± 49∗	106 ± 10∗	2.9 ± 0.4∗	28.1 ± 3.7∗	25.2 ± 3.3∗

P_WL is the maximum power that the fiber type is capable of producing when strain amplitude and frequency are optimized for power production. f_WL is the frequency at which maximum power was produced. Work per cycle values were obtained under the same conditions, i.e., optimal f_WL and strain that generated P_WL. W is net work per cycle, W+ is the work generated during shortening, and W− is the work absorbed during lengthening. All values are mean ± SE. N is the number of fibers tested.

^∗Value is significantly different from control fibers (Student's t-test, p < 0.05).

The decrease in R759E fiber power was due, in part, to a decrease in work production at most frequencies and amplitudes tested. R759E net work per cycle was 49% lower than control fibers at conditions optimized for maximum power generation (Table 2 and Fig. 3 A). Work produced during shortening and work absorbed during lengthening were both reduced as a result of the mutation, by 37% and 35%, respectively (Table 2).

Isometric tension

No significant differences were observed for active, passive, or net tension (active tension minus passive tension, T_max) between the mutant R759E-2 fibers and control fibers (Table 3). The lack of difference in isometric tension along with the observation that less positive work is produced during the work loops suggests that the mutation only affects dynamic tension. Net rigor tension of R759E was reduced by 48% compared to the control (Table 3).

Table 3.

Isometric properties

	N	Active tension(mN/m2)	Passive tension(mN/m2)	Tmax(mN/m2)	Rigor tension(mN/m2)
Control	11	5.7 ± 0.8	3.4 ± 0.6	2.3 ± 0.5	4.4 ± 0.4
R759E-2	12	4.8 ± 0.6	3.0 ± 0.4	1.7 ± 0.3	2.3 ± 0.6∗

T_max = net active tension (active tension minus passive tension). Rigor tension = net rigor tension (gross rigor tension minus passive tension). All values are mean ± SE. N is the number of fibers tested.

^∗Statistically different from control fibers (Student's t-test, p < 0.05).

Sinusoidal analysis

To determine the effect of the mutation on muscle stiffness, we used small amplitude sinusoidal analysis. The complex stiffness is shown in a Nyquist plot in Fig. 4 A. In general, R759E complex stiffness was reduced as seen by the leftward shift and reduced absolute value of the viscous modulus amplitude. Complex stiffness is a composite parameter composed of two moduli, elastic (E_e) and viscous (E_v). The R759E E_e value was lowest (dip frequency) at 150 Hz (Fig. 4 B). At this frequency, R759E E_e was 56% lower than control E_e. Similarly, comparing dip frequency values (lowest value) between lines, the mutant's E_e was 30% lower than the control (Table 4). Overall, the R759E fibers were not as stiff as control fibers at frequencies <∼300 Hz (Fig. 4 B).

Figure 4.

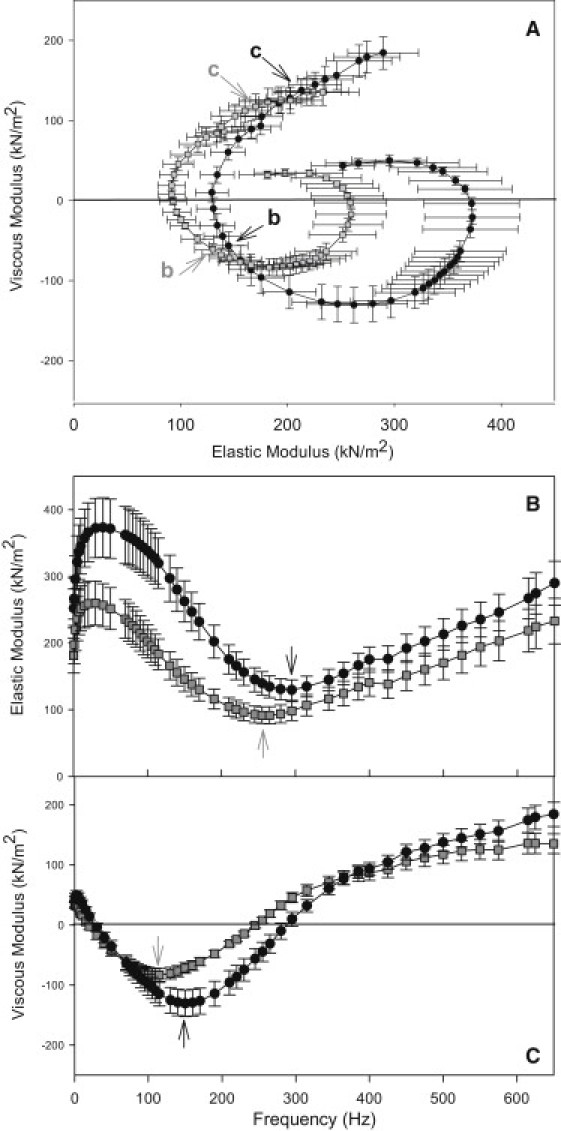
Effect of weakening the converter and relay interface on (A) complex stiffness displayed as a Nyquist plot, (B) elastic modulus, and (C) viscous modulus. The average b- and c-frequencies, derived from fitting the Nyquist plot with our three-term equation (see Methods), are indicated in panel A. Dip frequencies (Arrows, panels B and C). Data from mutant R759E-2 (N = 12; shaded squares) and control fibers (N = 11; solid circles). ML change is 0.125% peak to peak. Experiments were performed at 15°C. Mean ± SE.

Table 4.

Dynamic properties from small amplitude sinusoidal oscillations

	N	Complex stiffness(kN/m2)	Ee(kN/m2)	−Ev(kN/m2)	fEv(Hz)
Control	11	240 ± 27	206 ± 22	135 ± 21	148 ± 9
R759E-2	12	161 ± 20∗	143 ± 18∗	86 ± 11∗	116 ± 5∗

Average complex stiffness, elastic modulus (E_e), and viscous modulus (−E_v) minimum values were measured at the oscillation frequency (dip frequency) that produced the lowest value for each individual fiber. fE_v is the dip frequency for the viscous modulus. All values are mean ± SE. N is the number of fibers tested.

^∗Significantly different from control fibers (Student's t-test, p < 0.05).

The R759E viscous modulus plot does not dip as low as that of the control fibers, indicating less small amplitude work produced (Fig. 4 C). At frequencies >∼130 Hz and <∼300 Hz, which include Drosophila's WBF range, the mutant E_v was less negative than the control E_v. At the lowest E_v frequency (fE_v) for the control fibers, R759E E_v was 55% of the control fiber E_v value (Fig. 4 C). Comparing the lowest E_v values, the mutant was 36% of the control minimum E_v (Table 4). The kinetics of the fiber were slowed by the mutation; this is shown by the R759E fibers lowest E_v point being shifted to the left (Fig. 4 C), resulting in fE_v for R759E being 22% lower than fE_v of the control fibers (Table 4).

Mechanical rate constants

We determined the influence of the mutation on mechanical rate constants using the complex stiffness fitting method and equation that we have refined for Drosophila IFM (26). The mutation did not have a significant effect on A or k, but decreased B and C amplitudes by 67% and 65% (Table 5). The mutation decreased the mechanical rate constant for work production, 2πb, 32%, while having no effect on the rate constant for work absorption, 2πc (Table 5 and Fig. 4 A). Based on interpretations from previous studies using this analysis (27,30,31), these results indicate that there was no change in passive viscoelastic components of the muscle (A process), and that transition rates between work producing rather than work absorbing steps of myosin's cross bridge cycle are decreased by the mutation. The amplitude of work producing steps (B process) and absorbing steps (C process) of the cycle are both reduced, suggesting a decrease in the number of myosins producing force at any given time and/or cross-bridge stiffness during strongly bound steps of the cycle (Fig. 2).

Table 5.

Mechanical rate constants and amplitudes

	N	A (kN/m2)	k	B (kN/m2)	2πb (s−1)	C (kN/m2)	2πc (s−1)
Control	11	220 ± 27	0.11 ± 0.003	1731 ± 344	1558 ± 96	1611 ± 324	3180 ± 396
R759E-2	12	177 ± 24	0.10 ± 0.006	573 ± 94∗	1065 ± 108∗	573 ± 84∗	3225 ± 270

See Methods for a full description of the significance of these values. All values are mean ± SE. N is the number of fibers tested.

^∗Statistically different from control fibers (Student's t-test, p < 0.05).

Discussion

Our experiments, the first (to our knowledge) to probe the converter-relay interface in muscle fibers, demonstrate that this pathway is critical to muscle kinetics and mechanical performance. Weakening links between the relay and converter in the pre- and postpower stroke states, by mutating R759, decreased muscle power generation. Lower work production and slower kinetics were both responsible for the decrease in power. Decreased work production was observed in our work loop experiments and in the less negative viscous modulus during sinusoidal analysis. The decrease in work is likely from lower force generation during oscillatory work, because positive work generation during work loop measurements was lower than the control, but isometric tension was not statistically different. Slower muscle kinetics in mutant fibers is supported by the reduced frequencies for maximum work and power generation and the decrease in the dip frequencies for the dynamic, elastic, and viscous moduli. The slowing of muscle kinetics is due to cross-bridge steps that influence mechanical rate constant 2πb rather than 2πc (Fig. 2) (26,27,30,31). Kawai and Halvorson (32) demonstrated that 2πb is directly influenced by the force generation step.

We have developed hypotheses for the mechanism(s) behind the decreased fiber performance by evaluating our results in light of previous work on this Drosophila mutant by Kronert et al. (16) along with data from Sasaki et al. (15). Sasaki et al. (15) disrupted similar converter-relay linkages with the relay mutation I499A in Dictyostelium myosin II (I508A, chicken skeletal myosin numbering).

Our first hypothesis is that coordination of lever arm movement with conformational changes in the myosin catalytic domain has been impaired. Sasaki et al. (15), using intrinsic tryptophan fluorescence and fluorescence resonance energy transfer, suggested that disrupting the converter-relay link caused the myosin converter and lever arm to preferentially remain in the postpower stroke state, even when the MgATPase site was in the prepower stroke state. Similarly, Kronert et al. (16) found that the Drosophila R759E mutant showed less intrinsic tryptophan fluorescence upon MgATP addition compared to wild-type. A reduced probability of adopting the prestroke state (resetting the lever arm) that decreases the probability of actin binding and proceeding through the subsequent force generating transitions could explain the mutant fibers' slower kinetics, reduced 2πb, and decreased stiffness (fewer heads bound). It is also possible that some myosins fail to fully reset into the prepower stroke state, but still bind and proceed through the cycle without a power stroke or with a shorter or less effective power stroke. This could explain the mutant's decreased work production and process B amplitude, as the B process is primarily set by cross-bridge transitions related to actin binding and work producing steps of the cross-bridge cycle (30).

Our second hypothesis is that the interface between the relay and converter contributes to cross-bridge stiffness. The large decrease in E_e, C process amplitude (without a change in 2πc), and the significant decrease in rigor tension suggest that the mutation reduces cross-bridge stiffness when it is in strongly bound states after the power stroke. This would also imply that the interface is a main pathway of force transmission from the thick to thin filament. Alternatively or in addition, the R759E mutation could be decreasing the stiffness of the converter itself, as recent stiffness measurements of converter cardiomyopathy mutants have shown the converter is likely the most compliant myosin domain when myosin is arranged in a sarcomere (33,34).

Our third hypothesis is that the mutation interferes with strain or stress feedback from the lever arm to the nucleotide pocket. Our previous work with the Drosophila exon 9 series, which encodes alternative relay domains, suggests different versions of the relay domain alter myosin kinetics by differentially responding to strain or load (35). Altered response to imposed strain could also explain the large decrease in R759E tension during dynamic work loops, without a change in isometric tension.

A hypothesis proposed by Kronert et al. (16) is that the R759E mutation increases the time myosin spends attached to actin (t_on), which would contribute to the 35% decrease in actin motility velocity and the slower muscle kinetics. However, we found no change in 2πc that is primarily influenced by detachment related steps (26,27) and has recently been shown to strongly correlate with the inverse of t_on (31). Further, increased t_on would increase muscle stiffness as the number of heads bound would increase; yet, we observed a decrease in stiffness. Kronert et al. (16) also found that the R759E mutation slightly disrupted myofibril integrity; thus some of the decrease in stiffness, work, and power could be due to impaired tension transmission in the sarcomere. However, compared to our previous work with many other myosin mutants that showed various degrees of myofibril disruption (20,25,26,35), we estimate that this degree of disruption is likely to make a very minimal contribution to the change in muscle parameters.

Decreased flight ability

These alterations in muscle and myosin performance caused by the R759E mutation are physiologically relevant as seen by the decrease in flight index and wing beat frequency of 2-day-old R759E flies at both temperatures tested. The mutant wing beat frequency was significantly lowered, possibly as a result of decreased IFM stiffness and/or kinetics. However, it is currently thought that wing beat frequency is primarily set by the inertia of the wings and stiffness of the flight system, including cuticle and flight musculature. This facilitates the resonance required for wing beating, as the IFMs do not directly attach to the wings (hence the name “indirect flight muscle”), instead inserting into the cuticle and causing it to vibrate and move the wings through a hinge mechanism (36). Molloy et al. (36) modeled WBF of flies using a tuning fork equation: WBF = (1/2π) √k_m/I, where k_m = muscle stiffness and I = moment of inertia of the wings. Thus, we can estimate WBF by using a k_m value of 155 kNm⁻² and 280 kNm⁻² for the mutant and control lines, respectively, which we obtained from the elastic modulus measurements at an oscillation frequency of 140 Hz (the wing beat frequency for the control flies (Table 1)). The WBF of the mutant would be predicted to decrease by 7% of the control fly WBF, presuming there is no change in the moment of inertia, a theoretical WBF of 130 Hz for the mutant. This is within the standard error of the R759E WBF of 127 Hz (Table 1).

Work loop technique

We measured power from Drosophila R759E IFMs at ML strains greater than our usual 0.125%. We chose to use larger amplitude work loops for this study to evaluate the effect of the R759E mutation at larger, more physiologically relevant strains because the relay has been proposed to be a strain and load sensitive domain (35). In the past, we avoided larger strain amplitudes as it appeared that the IFM fibers developed a rigor core under these conditions. We presumed this was due to the increased MgATP consumption required for higher power output when undergoing larger amplitude length changes. However, we recently determined that the IFM's need for much higher [MgATP] compared to most other fiber types was primarily due to the lower affinity of IFM myosin for MgATP (26). We found that with an optimized creatine phosphate and creatine phosphokinase regeneration system, and [MgATP] ≥ 12 mM, power generation and muscle kinetics saturate (26). Thus, MgATP amount is not limiting, no rigor core developed, and we can use the work loop technique to measure power generation under conditions more closely mimicking IFM use during flight (28). We will continue to use small amplitude sinusoidal analysis to measure muscle stiffness and mechanical rate constants. Together with the genetic advantages of the Drosophila system, these two mechanics techniques revealed that the converter and relay domain pathway is critical for myosin function, optimal muscle power generation, and flight performance.