Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2011 Sep 7;101(5):1105–1113. doi: 10.1016/j.bpj.2011.07.017

Hysteresis-Based Mechanism for the Directed Motility of the Ncd Motor

Sirish Kaushik Lakkaraju †, Wonmuk Hwang †,‡,∗
PMCID: PMC3164182  PMID: 21889447

Abstract

Ncd is a Kinesin-14 family protein that walks to the microtubule's minus end. Although available structures show its α-helical neck in either pre- or post-stroke orientations, little is known about the transition between these two states. Using a combination of molecular dynamics simulations and structural analyses, we find that the neck sequentially makes intermediate contacts with the motor head along its mostly longitudinal path, and it develops a 24° twist in the post-stroke orientation. The forward (pre-stroke to post-stroke) motion has an ∼4.5 kBT (where kB is the Boltzmann constant, and T = 300 K) free-energy barrier and is a diffusion guided by the intermediate contacts. The post-stroke free-energy minimum is higher and is formed ∼10° before reaching the orientation in the post-stroke crystal structure, consistent with previous structural data. The importance of intermediate contacts correlates with the existing motility data, including those for mutant Ncds. Unlike the forward motion, the recovery stroke goes nearly downhill in free energy, powered in part by torsional relaxation of the neck. The hysteresis in the energetics of the neck motion arises from the mechanical compliance of the protein, and together with guided diffusion, it may be key to the directed motility of Ncd.

Introduction

All motor proteins in the kinesin family share a similar ATPase catalytic core (1,2). Different motility behaviors are achieved by modifying subdomains such as those that mediate track binding, force generation, and allosteric transduction of ATPase or mechanical events to other parts of the motor (3). A prime example is the direction reversal in Ncd compared to that in Kinesin-1 (4,5). Unlike Kinesin-1, which has the motor head (MH) at the N-terminal end, the MH of Ncd is at the C-terminal end (hence called a C-terminal kinesin) (2). Although they have nearly identical MH structures, the two kinesins differ mainly in the neck domain that connects the MH to the coiled-coil stalk (6). Instead of a flexible neck linker as in Kinesin-1, Ncd has an α-helical neck that continues from the stalk and connects directly to the MH (Fig. 1). Mutational studies show that directionality is partly determined by the neck domains: a chimeric Kinesin-1 with Ncd's neck showed microtubule (MT) minus-end-directed motility, whereas an Ncd with Kinesin-1's neck linker was plus-end-directed; motility was impaired in both cases (6–9). However, the underlying structural mechanism, particularly that for Ncd, is still not well understood.

Figure 1.

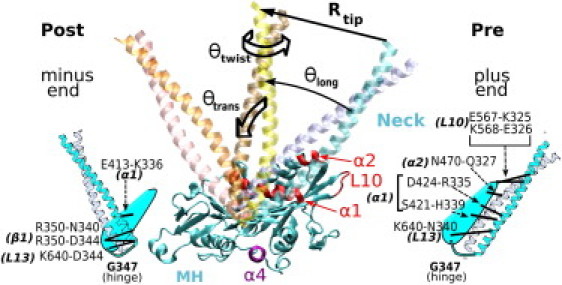
Figure 1

Open in a new tab

Major MH-neck contacts of Ncd in the pre- and post-stroke structures. Hydrophobic contacts (not shown) play a less specific role during the neck travel, and they are less conserved within the Kinesin-14 family (Table S2). We call the α-helical coiled-coil (α0) (A295-R346) the neck. The MT plus end is on the right. We measured the orientation of the neck using three angles, θlong, θtrans, and θtwist. Rtip is the distance of the tip of the neck (the S297 Cα atom) from its pre-stroke position. When the MH is bound to the MT, α1 is approximately parallel to the MT axis and guides the neck motion by forming intermediate contacts with it. The relay helix α4 mediates the nucleotide-dependent see-saw motion of the MH (Fig. S1) (52,53). Atomistic structures are rendered using VMD (59).

In the case of Kinesin-1, the neck linker is disordered when unbound, and it docks to the MH upon ATP binding (10). Recent computational (11) and experimental (12) studies showed that the N-terminal cover strand protruding from the MH is also crucial for force generation, where the folding of the cover strand and the neck linker into a β-sheet named the cover-neck bundle provides the necessary forward bias. In contrast to such an order-disorder transition, cryo-electron microscopy (cryo-EM) and x-ray studies indicate that the α-helical neck of Ncd rotates by ∼70°, more like a lever arm (13,14). However, the atomistic details of the rotation are unknown. In x-ray structures of Ncd in the pre- and post-stroke states, the neck makes contacts with the MH in respective orientations (Fig. 1 shows a list of contacts). Point mutations of these contacts have different effects on MT gliding velocities: some have near wild-type (WT) velocities, whereas others are significantly slower or even switch directionality (15,16). Despite detailed studies of the kinetics of Ncd (17–19), the nucleotide state in which the motion of the neck occurs is not clear (14,20,21). Single-molecule studies even suggest occasional plus-end directed stepping events (22,23), further supporting the need for an atomistic picture.

Here, we use molecular dynamics (MD) simulations and structural analyses to elucidate the motion of the Ncd neck between the pre- and post-stroke orientations. We find several intermediate contacts between the neck and the MH that are not seen in the x-ray structures for the end states. The neck moves along the α1 subdomain of the MH, which serves as a guide rail. The free-energy profile along the path of the neck (i.e., the potential of mean force (PMF)) shows an energy barrier in the forward motion, but lacking a strong directional bias, the neck moves mostly via diffusion guided by the intermediate contacts. In contrast, the PMF for the reverse motion (the recovery stroke) is very different and has no major energy barrier. This is due to the compliance of the protein, which causes the intermediate bond patterns to differ between the two directions of motion. Also, relaxation of the torsional strain of the neck in the post-stroke position partly drives the recovery stroke. The PMF profile is consistent with cryo-EM data showing a lower stability of the neck in the post-stroke position, and it explains a ∼10° mismatch in the orientation of the neck in x-ray and cryo-EM structures (14). The importance of residues in making the intermediate contacts correlates with the differences in MT gliding velocities of the corresponding mutants (15). We also find that the C-terminal tail of Ncd (20) may not play a direct role during the neck motion. The present results suggest that guided diffusion enables Ncd to walk under load, and the hysteresis in energetics provides directionality in the mechanochemical cycle of Ncd.

Simulation Method

Structures used

We used three x-ray structures of the Ncd dimer from the Protein Data Bank (PDB): 1CZ7 (24), 1N6M (13), and 3L1C (20). Both heads in PDB 1CZ7 have the neck in the pre-stroke orientation. In PDB 1N6M and 3L1C, the two heads of the dimer are in the pre- and post-stroke states, respectively. We used various combinations of these structures (see Section S1 and Table S1 in the Supporting Material), and the pathways of the neck between the two conformations were all very similar. We also tested 10 mutants of Ncd to elucidate their behavior in MT gliding experiments (15,16) (Table S1).

Overview of simulations and analyses

To find the pathways of the neck between the pre- and post-stroke orientations, we performed multiple restricted-perturbation targeted molecular dynamics (RP-TMD) simulations (25,26) (Table S1) and analyzed the trajectories statistically (Section S1 in the Supporting Material). To confirm that the observed features are not caused by the biasing potential of RP-TMD, for a representative trajectory, we performed explicit-water equilibrium simulations of the key intermediate structures without any bias (Section S2 in the Supporting Material). Additional structural analysis revealed that the pathway of the neck also provides a sterically plausible picture (explained in Results).

In addition to RP-TMD (25,26), we considered two other methods for characterizing the pathway of the neck: the normal-mode superposition model (27) and the minimum energy path (MEP) method (28,29). However, as in the case of the conformational changes in Kinesin-1 (30), normal modes were not directly linked to the transition of the neck. MEP was not effective either, possibly because the Ncd neck moves diffusively, whereas MEP is a zero-temperature method (25,31). A comparison of these methods can be found in Section S3 in the Supporting Material.

We used CHARMM (32) for simulations, except for some equilibrium simulations in explicit water, where we used GROMACS (33) for its speed (Section S1 and Section S2 in the Supporting Material). We used the param19 force field (34) for simulations with the ACE2 (35) and FACTS (36) implicit solvent models. For simulations in explicit water and the GBSW implicit solvent (37), we used the param27 force field (38). The simulation temperature was 300 K in all cases. BLASTP was used for sequence alignment (Table S2 in the Supporting Material) (39).

We quantified the orientation and elastic deformation of the neck during the transition by adopting methods we developed for the analysis of α-helical filaments (40,41) (Section S4 and Section S5 in the Supporting Material). To calculate the PMF along RP-TMD trajectories, we applied the tug-of-war sampling (TOWS) method that we previously used for the study of Kinesin-1 (11), with higher-order terms included for greater accuracy in the calculated force (free-energy gradient) (42) (Section S6 in the Supporting Material). We calculated the first passage time to diffuse over the PMF, which allowed comparison with experimentally measured stepping time of Ncd (22,23) (Section S7 in the Supporting Material).

Results

Two-step RP-TMD for Ncd conformational change

With suitable choices for parameters in RP-TMD (Section S1 in the Supporting Material), the neck moves between pre- and post-stroke structures. In Fig. 1, if the MH is treated as bound to the MT, the other, unbound head of the Ncd dimer (not shown) passively moves with the neck without affecting its interaction with the bound head (Movie S1 in the Supporting Material). This is consistent with the comparable MT gliding velocities of the monomeric and dimeric Ncd constructs (14). The results discussed below are thus obtained using a single head, as in Fig. 1.

TMD in general has a tendency to cause transitions to occur first in regions with large root-mean-square deviation (RMSD) between the initial and target structures (25). When RP-TMD is applied directly between pre- and post-stroke structures (we performed 50 such simulations under different conditions), the neck rotates first, followed by the MH rearrangement. In reality, however, when the neck is in the pre-stroke position, a chemical event such as ATP binding (14) or ADP release (13,20) would cause the MH to change conformation and trigger the neck motion. It would thus be more natural for the MH to make the pre → post conformational change, followed by the transition of the neck. To test this, we applied the biasing potential of the RP-TMD only to the MH to drive it to the post-stroke state, whereas the neck remained in the pre-stroke position. This caused the K325-E567 and E326-K568 bonds (Fig. 1) to break, weakening the MH-neck contact. The neck consequently became more mobile, with an increase in the range of thermal motion of the tip of the neck in the 1-ns MD simulation, from 9.3 Å (before) to 17.6 Å (after MH rearrangement). We show below, furthermore, that the motion of the neck after the MH rearrangement costs less free energy than the motion before rearrangement (Fig. S2 in the Supporting Material). Thus, the forward RP-TMD trajectories discussed below are obtained through two steps, so that the MH rearranges first and then the neck rotates to the post-stroke position (Movie S2 in the Supporting Material). For the reverse motion from post to pre-stroke state, we found that it is more likely for the neck to move first, followed by the MH rearrangement to the pre-stroke conformation (see below).

Substeps during the neck motion

For the forward motion of the neck, we performed 70 RP-TMD runs using two different implicit solvent models under different conditions and one explicit-water simulation (Table S1). We sought features that are common to these RP-TMD trajectories. Most notably, instead of a free swing, the neck forms and breaks a series of bonds with the MH. The main players on the neck are R335 and K336, which interact with E413, Q420, and D424 of α1. Closer to the G347 hinge, N340 and D344 interact with K640 in L13 and R350 in β1 (Fig. 1).

We recorded a bond-formation event as a function of the distance of the tip of the neck from its pre-stroke position, Rtip (Fig. 1). A sample trajectory is shown in Fig. 2 A: after partial breakage of the MH-neck contacts by the MH rearrangement, the Q327-N470 and H339-S421 bonds, as well as other hydrophobic contacts (between F329 and M333, and L471 and W473 (not shown)), break soon after the neck starts to move. At Rtip ≃ 25 Å, R335 breaks from D424 and forms a transient bond with Q420 until Rtip ≃ 51 Å. K336, which does not interact with the MH in the pre-stroke state, follows the neighboring R335 and sequentially forms and breaks bonds with D424 and Q420. At Rtip = 67 Å, K336 breaks away from Q420. Subsequently, at Rtip = 74 Å, the K336-E413 bond forms, followed by others in the post-stroke x-ray structure (Fig. 1). K640 switches contacts with N340 (pre) and D344 (post) in an overlapping manner (Fig. 2 A).

Figure 2.

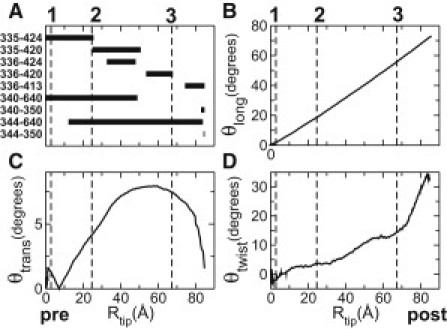
Figure 2

Open in a new tab

A representative forward trajectory of the neck with PDB 1CZ7 as the pre- and 1N6M as the post-stroke structure. The same trajectory was used for the forward case in Figs. 4 and 5. (A) Major bond pattern. (B, C, and D) Orientation angles defined in Fig. 1. Three vertical dashed lines numbered 1–3 mark the substep events noted in Fig. 5.

Since nearly all residues forming intermediate contacts participate in the pre- or post-stroke contacts (Fig. 1), intermediate contact formation is a natural consequence of the neck switching its binding partners between the two states. The order of forming the contacts is determined mainly by the geometric proximity between the residues of the moving neck and those of the MH (see Fig. 4 A for comparison), which should be overall preserved in different simulation trajectories. The probability of forming a bond as a function of Rtip indeed shows a common pattern (Fig. 3). The precise values of Rtip at which a given bond is formed or broken are likely to vary even among steps that Ncd actually makes. The only way the neck can avoid the intermediate contacts would be a large transverse motion away from the MH, which is unlikely.

Figure 4.

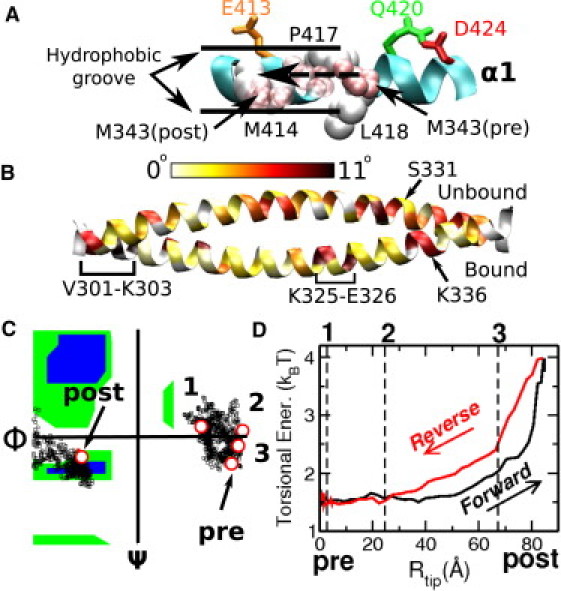
Figure 4

Open in a new tab

Guidance and conformational changes of the neck. (A) α1 as a guide rail. R335 and K336 of the neck sequentially form bonds with D424, Q420, and E413 (Fig. 2A), whereas M343 of the neck moves in the hydrophobic groove formed by M414, P417, and L418. (B) Distribution of torsional strains in the α-helices of the neck in the post- relative to the pre-stroke structure. (C) Ramachandran plot for the G347 hinge during the forward motion. Substeps 1–3 (see Figs. 2 and 5) are marked by circles. G347 becomes α-helical past substep 3. (D) Increase in the torsional energy of the neck in the post-stroke state, notably after substep 3, where the cumulative torsion increases (Fig. 2D and Fig. S3B). The reference structure for measuring the elastic energy is an isolated and equilibrated neck coiled-coil, which causes an ∼1.5 kBT basal energy when the neck is attached to the MH.

Figure 3.

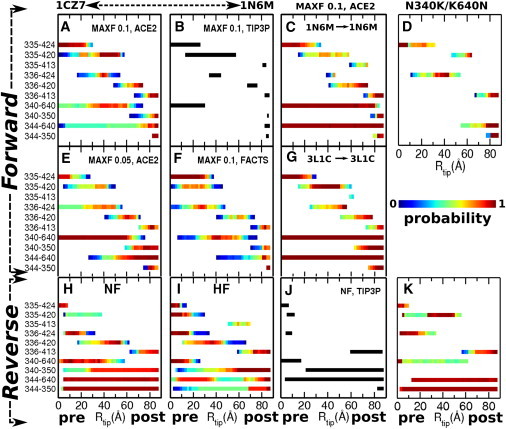
Figure 3

Open in a new tab

Probability of forming MH-neck contacts in RP-TMD under various conditions (Table S1 and Section S1 in the Supporting Material). Forward (A–G) and reverse (H–K) trajectories. The structures used are PDB 1CZ7 (pre-stroke) and 1N6M (post-stroke), except in the cases of C and G, where 1N6M and 3L1C are used for both pre- and post-stroke structures. In D and K, a double mutant N340K/K640N. The maximum perturbation allowed in RP-TMD (MAXF) is 0.1, except (E) MAXF = 0.05. The solvent model used is ACE2, except in F (FACTS) and B and J (explicit water). In H, J, and K, the biasing potential of RP-TMD is applied to the neck first (NF) whereas in I, it is applied to the MH first (HF) (cf., Fig. 5B). In B and J, bond patterns are for single explicit-water simulations. The R335-D424 bond persists over a wider range in forward than in reverse trajectories, which is responsible for the barrier at position 2 in the forward PMF (cf., Fig. 5B).

Although the above shows that intermediate contacts are sterically plausible, due to the biasing potential of RP-TMD, they might also be a result of poor relaxation of the system, because of the rapid neck motion, which lasts <200 ps (Table S1). To test whether they stay formed without the biasing potential, we took four structures from RP-TMD trajectories and performed regular explicit-water simulations at 300 K. The identified contacts persisted during the 2-ns simulation time (Section S2 in the Supporting Material). An exception was the N340-Y426 bond, which broke within 0.1 ns and hence was excluded from our analysis.

Aside from polar or charged residues that mediate intermediate contacts, hydrophobic residues M414, P417, and L418 at the N-terminal half of α1 form a groove through which M343 travels (Fig. 4 A), further highlighting its role as a guide rail. The same set of contacts was observed during the reverse travel (post → pre) in 61 RP-TMD runs (Fig. 3, H–J, and Table S1). The main difference from the forward travel is in the range of Rtip over which a given bond is present (see below).

Twist of the neck toward the post-stroke state

We quantified the orientation of the neck using the three angles shown in Fig. 1 (Section S4 in the Supporting Material). The longitudinal angle, θlong, grows monotonically to 73°, as in the x-ray structures (Fig. 2 B). The transverse angle, θtrans, for the motion of the neck away from the MH, grows no more than 7.9° (Fig. 2 C). This reflects that the neck maintains contact with α1 (Fig. 4 A), whose 7° bend is responsible for the bell-shaped profile of θtrans. Interestingly, θtwist, for the axial rotation of the neck, grows to 32.3° in the post-stroke position, which may indicate untwisting of the left-handed coiled-coil in the post-stroke state.

We further analyzed the distribution of angular strains in individual α-helices of the neck in the post-stroke relative to the pre-stroke structure (Fig. 4 B, and Section S5 in the Supporting Material). Bending angles are at most 2°, whereas torsional angles varied more: the α-helix of the neck belonging to the MT-bound head (Fig. 4 B, Bound) is strained in V301-L303 (11°), K325-E326 (9°), and K336 (7°). The second α-helix, extending into the unbound MH (Fig. 4 B, Unbound), is also strained, with a maximum strain at S331 (10°). Among these, only the K325-K336 region contains residues that interact with the MH (Fig. 1). Other domains may develop strains via a nonlocal response to perturbation in α-helical coiled-coils (43). Since the torsional angles in Fig. 4 are positive, the right-handed α-helices in the post-stroke state are over-twisted, which is consistent with unwinding of the coiled-coil, as the two have opposite chirality (44).

Distribution of torsional strains across the neck coiled-coil in the post-stroke structures had a similar trend with an overall positive twist (Fig. S3 A). The cumulative torsion on the tip of the neck is 24° (Fig. S3 B). The remaining ∼8° in θtwist (Fig. 2 D) is achieved by rigid-body axial rotation of the coiled-coil with G347 as a pivot (Section S4 in the Supporting Material). G347 becomes α-helical in the post-stroke state, as the Ramachandran plot shows (Fig. 4 C). Note that torsional strains (Fig. 4 B and Fig. S3 A) are present in the x-ray structures, and they are not outcomes of simulation. RP-TMD shows that the torsional strain increases more steeply for Rtip > 60 Å (Fig. S3 B), similar to θtwist (Fig. 2 D).

To find the strain energy, we measured the local elastic moduli of the coiled-coil by applying a fluctuation analysis method that we developed for studying the coiled-coil protein tropomyosin (Section S5 in the Supporting Material) (40). On average, its stiffnesses in two orthogonal bending directions are 8.28 × 10−28 N·m2 and 7.63 × 10−28 N·m2, and 4.96 × 10−28 N·m2 for torsion, approximately one-third of those for the leucine zipper (40,41). This is consistent with experiments showing a lower stability of the neck (45). Using these results, we found that the neck is ∼2.5 kBT higher in torsional energy in the post-stroke structure (Fig. 4 D).

Free energy changes during the forward transition

Existence of intermediate contacts suggests that the forward motion of the neck is not a free diffusion. To quantify its energetics, we used the TOWS simulation (Section S6 in the Supporting Material) (11,42). For a given RP-TMD trajectory, we selected snapshots in ∼2-Å intervals of Rtip. The number of snapshots varied between 45 and 57, depending on the trajectory used. For each snapshot, we applied a harmonic constraint to the tip and performed a 0.8-ns MD simulation while holding the MH. The positional fluctuation of the tip can be used to calculate the force generated at the center of the harmonic constraint (negative of the free-energy gradient) (42).

In contrast to the strong directional bias found for the cover-neck bundle of Kinesin-1 (11), the force vectors do not point in the post-stroke direction (Fig. 5 A). Their large axial components are due to the high extensional modulus of the neck coiled-coil (40,46), and they do not contribute to the rotation of the neck. The only relevant components are those along the direction of travel, which provide the PMF when integrated along the path (Fig. 5 B, circles). Using Rtip as a reaction coordinate allows us to compare PMFs for different RP-TMD trajectories where paths of the neck differ slightly. Upon the pre→post MH rearrangement and partial breakage of bonds with the MH, the PMF rises by ∼4 kBT. This energy is likely provided by an ATPase event in reality. We denote the MH rearrangement as the first substep (Figs. 2 and 5 B, 1). Next, a major 8.5-kBT energy barrier (4.5 kBT after the MH rearrangement) is imposed by the R335-D424 bond (Figs. 2 and 5 B, 2), the breakage of which marks the beginning of a downhill free-energy gradient until the K336-Q420 bond breaks (Figs. 2 and 5 B, 3). Finally, the PMF goes uphill as the neck reaches the post-stroke orientation. For comparison, we calculated the PMF for the case where the neck moves before the MH rearrangement (Fig. S2). Its energy barrier is higher by 1.4 kBT, and the PMF at the end of the transition is 7.5 kBT higher than the case where the MH rearrangement precedes the neck motion. Thus, the latter pathway is energetically more preferred.

Figure 5.

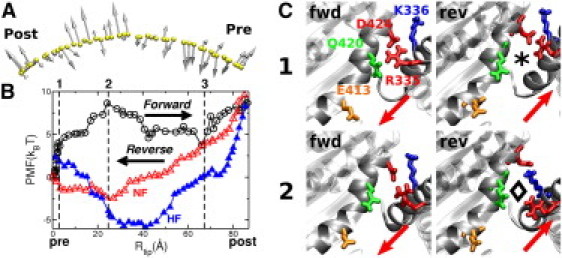
Figure 5

Open in a new tab

Energetics during neck travel. (A) Force vectors obtained using the TOWS simulation at the tip of the neck for the trajectory in Fig. 2. Forces range between 6 and 43 pN. Viewing direction is the same as in Fig. 1. (B) PMF curves obtained by integrating the components of the force vectors along the direction of travel, for forward (circles) and reverse (triangles) trajectories. Substeps marked 1–3 coincide with those in Fig. 2. For the reverse motion, two types of trajectories were used, with the MH rearranging before neck travel (HF; solid triangles), and with the neck moving first (NF; open triangles). (C) Comparison between forward and reverse trajectories at Rtip = 5 Å (near position 1) and 21 Å (before position 2). Arrows indicate the direction of travel. In the reverse trajectory, the R335-D424 bond is formed only when the neck has almost finished its travel (⋄ versus ⋆). (See Movie S3).

To ensure that our PMF calculation is robust, we verified the following (Section S6 in the Supporting Material): the PMFs calculated using two other RP-TMD trajectories, including one in explicit water, were all similar (Fig. S4 A), and the type and strength of constraints used in the TOWS had no major effect (Fig. S4, B and C). Quality of sampling was also good, as the PMFs obtained using the first and second halves of the 0.8-ns sampling time matched well (Fig. S4 D). Similar profiles of PMFs in these tests also suggest that the RP-TMD trajectories closely follow the minimum free-energy path.

The PMF is higher on the post-stroke side, which agrees with the higher mobility of the neck (14). An energetically favored post-stroke position is substep 3 in Fig. 5 B, not at the end of travel. This also agrees with the report where ∼10° rotation of the neck in PDB 1N6M gives a better fit to the cryo-EM density map (14). In 15% of the RP-TMD trajectories, the neck at sp 3 was further stabilized by another R335-E413 bond (Fig. 3, C and G). Nevertheless, the 3→ post transition may occur through thermal fluctuation, whereby the neck is captured and stabilized by the bonds with the MH.

We estimated the first passage time for the neck to diffuse across the PMF from the pre-stroke position (Section S7 in the Supporting Material). Assuming the neck to be a cylinder 15.3 Å in diameter and 75.4 Å long, its rotational diffusion coefficient with one end pivoted is 3.01 × 106 rad2/s (47,48). The first passage time (49) is then 2.32–8.25 μs for the pre→3 transition and another ∼1.92–11.53 μs for the 3→post transition (Fig. S5). By comparison, a single-molecule experiment of a full-length Ncd dimer estimates a 200–400 ms stepping time (22). This is likely an upper bound due to the 50-ms dynamic response time of their system and the large drag on the moving MT and the trapping beads while Ncd remains stationary in the three-bead assay. As in the experiment, if we regard the tip of the neck to be stationary and the MH translocates a 4.3-μm-long MT with two beads 1 μm in diameter attached, the estimated first passage time is 1.98–7.07 ms (pre → 3) and 1.64–9.88 ms (3→post), which would be even longer if the full-length stalk were used in simulations. On the other hand, the first passage time with a flat PMF is only 271 ns when the neck is assumed to move with a stationary MH, and 243 μs when the MT is translocated as in the single-molecule experiment. Therefore, the neck likely moves to the post-stroke position through a series of substeps driven by thermal fluctuations rather than by pure diffusion.

Hysteresis in the neck travel

As mentioned above, the MH rearrangement upon an ATPase event precedes the forward travel of the neck. In the reverse motion, if the MH takes the pre-stroke conformation before the recovery stroke of the neck (compare Fig. 6, D to E), the MH may rebind to the MT site from which it detached. It is thus more likely that the neck moves before the MH rearranges back to its pre-stroke state. To test, we performed two types of RP-TMD simulations of the reverse motion. In the first case, the neck moves ahead of the MH rearrangement to the pre-stroke state (Fig. 5 B, NF (neck first)). In the other case, the order is reversed and the MH rearranges first (Fig. 5 B, HF). The trajectories differ mainly in the values of Rtip at which a given bond is formed and broken (Fig. 3). However, the net free-energy change for the NF case matches better with that of the forward PMF than does that for the HF case, since the NF PMF ends at 0.1 kBT at Rtip = 0 Å (Fig. 5 B, open triangles), whereas the HF PMF ends at 3.0 kBT (solid triangles). Furthermore, the HF PMF is mostly uphill below Rtip ≃ 30 Å, as the R335-Q420 and K336-D424 bonds persist near the end of the motion and impede the return of the neck to the pre-stroke position (Fig. 3, H versus I). These results indicate that the recovery stroke of the neck precedes the MH rearrangement. Hence, we use the NF case for the analysis below.

Figure 6.

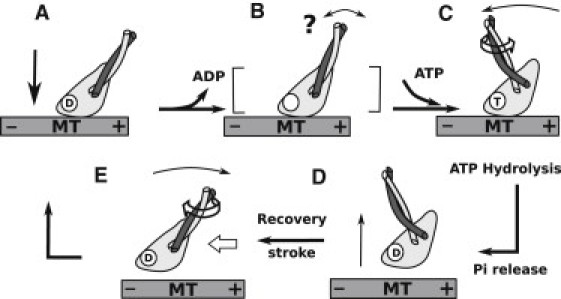
Figure 6

Open in a new tab

Possible Ncd mechanochemical cycle. (A) MH of an Ncd dimer in the ADP state binds to the MT (the unbound head is not shown). (B) ADP releases during or after binding to the MT (14). Whether the motion of the neck is initiated by the ADP release (21) or by ATP binding (14) is unclear (marked by “?”). (C) ATP binding leads to travel of the neck to the post-stroke side (14). (D) The MH detaches upon ATP hydrolysis or γ-phosphate release. (E) The unbound MH advances toward the minus end via recovery stroke driven by torsional relaxation and diffusion.

The forward and recovery strokes differ qualitatively, since there is no energy barrier in the latter. This difference originates from the compliance of the protein: during the forward motion, since the R335-D424 bond persists until substep 2, these residues become strained (Fig. 5 C, lower left). After the bond breaks, the distance between R335 and D424 rapidly increases as they relax. During the reverse motion, the bond can thus form again only near the end of the transition (Fig. 5 C, ⋄ to ⋆, and Movie S3). This can also be seen in explicit-water RP-TMD simulations (Fig. 3, B versus J). The strained state of the R335-D424 bond near substep 2 is not an outcome of the biasing force of RP-TMD, since it was also maintained during the TOWS simulation without any bias on the bond. Nor did it break during a 2-ns equilibrium simulation in explicit water (Section S2 in the Supporting Material). Although the R335-D424 bond may eventually break in longer simulations, its importance is consistent with a large reduction in the MT gliding velocity of a mutant without the bond (15) (see Concluding discussion).

Another notable feature of the reverse PMF is the nearly monotonic downhill gradient in the post→2 region. To see whether this is related to the torsional strain of the neck, we changed its conformation in the post-stroke orientation to that of the pre-stroke state. When the replacement includes G347, the extra α-helical turn at this position in the post-stroke state (Fig. 4 C) disappears. In either case, the calculated PMF does not decrease in the post → 3, but in 3→2, the PMF still decreases (Fig. S3 C), suggesting that the torsional strain of the neck affects the PMF in the 3→post region. The opposite trends of the forward and reverse PMFs between substeps 2 and 3 are likely collective results of multiple bonds involved in this region (Fig. 3).

Role of the C-terminal tail

Since available x-ray structures align reasonably well with cryo-EM maps (14), and the neck and α1 are spatially separated from the MT, the present results are unlikely to be affected by the presence of the MT (Movie S1). A domain that might have a potential influence is the C-terminal tail (C-tail; V666-K700), which is mostly invisible in available structures. We hypothesized earlier that it may play a dynamical role similar to the cover-neck bundle formation in Kinesin-1 (11). This is supported in the recently published PDB 3L1C (20): the C-tail is visible up to K674 and it points to the MT plus end, analogous to the neck linker of Kinesin-1 in the MH-docked state. In RP-TMD of 3L1C, K674 forms a bond with D344 of the neck after the MH rearrangement. However, this bond is unstable and breaks within 0.2 ns in an explicit water simulation, unlike the contacts between the MH and α1 that are present in all solvent models tested (Section S2 in the Supporting Material). Instead, the C-tail, being positively charged, may interact with the MT E-hook domain, which is negatively charged and mobile (50). We constructed a model of an MT-bound Ncd with the C-tail and E-hooks of the two tubulins added (Fig. S6). Regardless of the MH conformation, the C-tail made contact with the E-hook of β-tubulin. Considering the length of the two domains, their interaction may assist with the binding of Ncd to the MT. Indeed, a chimera without the C-tail fails to bind to MT (9,20).

The neck-linker-like conformation of the C-tail in 3L1C is coupled to the tilting of α4 out of the MH (Fig. S1 and Fig. S6). This see-saw motion occurs in many kinesin families to make room for the neck-linker docking in the ATP state (51–53). In Ncd, α4 does not interact with the neck, and its orientation does not affect the RP-TMD trajectory, as can be seen in our simulations with PDB 1N6M and 3L1C, which have α4 in orientations before and after the see-saw motion, respectively (Fig. 3, C and G). This may reflect the weaker coupling of the Ncd stepping event to the nucleotide state (23). In contrast, the C-tail is more clearly defined in x-ray structures of another Kinesin-14 motor, kinesin-like calmodulin binding protein (KCBP) (54–56). Its 52-residue C-tail consists of the 10-residue neck mimic that is homologous to the neck linker of Kinesin-1, a calmodulin binding helix, and the negatively charged C-terminal coil (56). In the ATP-like state, the neck mimic docks to the MH, similar to the neck linker of Kinesin-1 (54,55). However, Ncd and KCBP belong to different subfamilies, Kinesin-14A and 14B, respectively (2), and their C-tails have no sequence homology. It is thus unclear whether the two C-tails behave similarly. Other than mediating the MT binding, the C-tail of Ncd might interact with the neck at most for the initiation of the forward motion in the ATP state, as hypothesized for KCBP (54). In contrast to the lack of homology in the C-tail, key residues mediating the MH-neck contacts are conserved between Ncd and KCBP, and they have comparable MT gliding velocities (Table S2). Although more study of the C-tail is necessary, the MH-neck contacts likely play a more significant role in the motion of the neck.

Concluding Discussion

Validation of the RP-TMD result

Since RP-TMD uses a bias to drive conformational change, the resulting trajectories (see movies in the Supporting Material) do not represent the actual motion of the neck (25,26). They instead reveal the likely minimum free-energy path along which the neck performs diffusion. Since the full energy landscape is unknown, whether the trajectories indeed follow the minimum free-energy path should be validated by considering the possible effect of the bias in RP-TMD and also by considering whether they are physically and sterically plausible. As explained in Results, the common pattern of intermediate contacts over a large number of RP-TMD simulations (Fig. 3 and Table S1) suggests that they are unlikely to be artifacts of RP-TMD. This is further supported by their persistence in TOWS and other equilibrium simulations (Section S2 in the Supporting Material). The α1 guide rail assists with a longitudinal motion of the neck, and the intermediate contacts mainly follow the placement of residues in α1 (Fig. 4 A). In simulations of mutants without these contacts, the neck indeed swivels away from the MH (see below and Section S8 in the Supporting Material). Furthermore, RP-TMD has a tendency to select a path that is more accessible in the vicinity of the initial structure. The fact that the forward PMF starts with an energy barrier (Fig. 5 B) instead of following the downhill path of the reverse PMF near Rtip = 0 Å suggests that the hysteresis behavior represents a property inherent in the Ncd structure and not a consequence of using RP-TMD. Besides, the present results are consistent with a wide range of structural and motility data.

Ncd mechanochemical cycle

Combining the results presented here with those of previous experiments, a possible mechanochemical cycle of Ncd is proposed (Fig. 6). At the beginning, binding of the MH to the MT leads to the release of ADP (Fig. 6 A) (18,19). In the nucleotide-free state, the neck points to the MT plus end (14), and binding of an ATP leads to a conformational change that breaks the head-neck contacts, at least partially. It also has been suggested that ADP release leads to the rotation of the neck (Fig. 6 B, “?”) (20,21). Regardless of whether the neck rotation is initiated by ADP release or by ATP binding, in the ATP state, the mobile neck reaches the post-stroke position via guided diffusion (Fig. 6 C). The MH detaches from the MT upon ATP hydrolysis (14,17) or release of γ-phosphate (18) (Fig. 6 D). Finally, the recovery stroke advances the detached MH to the MT minus-end direction (Fig. 6 E). Since the moving neck interacts mainly with the α1 guide rail, whose conformation does not depend on the nucleotide state, the proposed mechanisms for the forward and recovery strokes of the neck (Fig. 6, B→C and D→E) are likely to hold regardless of which ATPase event initiates the transition. Furthermore, a recent single-molecule analysis indicates that the motion of the neck is not as strongly coupled to the nucleotide state as in Kinesin-1, since 30% of the stepping events were MT plus-end-directed (23).

Guided diffusion and hysteresis

Diffusion guided by intermediate contacts is an efficient strategy for generating unidirectional motion. Conformational relaxation after the breakage of the R335-D424 bond will make it difficult to re-form (Fig. 5 C). The neck instead forms other bonds after position 2, to reach substep 3 (Figs. 2 A and 3). A similar diffusion and binding mechanism may move the neck beyond substep 3 at the expense of an increased torsion. Compared to free diffusion, the intermediate contacts can reduce the burden imposed by external load during the forward travel. This scenario is also energetically plausible, since ADP release and ATP binding would provide a few to several kBT, respectively (44), which are comparable to the changes in the PMF of the neck (Fig. 5 B). Although the recovery stroke may be initially powered by the accumulated torsion of the neck, below Rtip ∼ 30 Å it may reach the pre-stroke position via diffusion without a bias (Fig. 5 B, NF). Since the recovery stroke occurs in the unbound Ncd (Fig. 6 E), it may not require as much tolerance to load. Single-molecule experiments suggest that the plus-end-directed stepping event of Ncd is slower and has a smaller step size (23), which is consistent with the profile of the reverse PMF and supports the idea that the neck moves differently in the two directions.

Comparison with mutants and other Kinesin-14 members

The role of the intermediate contacts can also be seen in the effects of mutations on motility. In a study where MT gliding velocities of several Ncd mutants were compared (15), a >50% reduction in velocity was observed in alanine mutations of key residues that are involved with intermediate contacts, including R335, K336, Q420, and K640. Blocking intermediate contacts would reduce velocity, because the neck has to diffuse over a wider range. By comparison, mutants of E567 and K568 that break bonds with the neck upon MH rearrangement in RP-TMD (Fig. 1) had 99% of the wild-type velocity. The Y426A mutant had 57% of the wild-type velocity, even though the N340-Y426 bond was not maintained in the explicit-water MD simulation (Section S2 in the Supporting Material). Y426 is at the border between α1 and β3 of the central β-sheet of the MH core, so it may be structurally important.

We performed RP-TMD simulations of 10 mutants taken from Sablin et al. (15) and Endow and Huguchi (16) (Fig. 3, D and K, and Section S8 and Table S1 in the Supporting Material) Under the assumption that these mutations do not affect the Ncd structure significantly, our results generally agree with the correlation between the loss of key intermediate contacts and the reduction in the MT gliding velocity. Comparing the sequences of the Kinesin-14 family and available MT gliding velocities (Table S2) also suggests that residues forming the intermediate contacts, such as R335, K336, N340, and D344 of the neck, and those in α1, L13, and β1 of the MH, are highly conserved. In contrast, residues that break contacts after the MH rearrangement in RP-TMD, as well as those that make hydrophobic contacts, show less conservation.

Implication for motor mechanism

In nonmotile enzymes, transition paths between different conformations may have less functional significance compared to the end-state conformations. However, since translocating motor proteins work out of equilibrium, hysteresis in conformational transitions may be required for directed motility. In the case of Kinesin-1, the cover-neck bundle formation drives the forward motion (11,12), whereas the neck linker unbinds likely through the see-saw motion of α4 in reverse (52,53). In myosin, power and recovery strokes occur in different nucleotide and actin-binding states (57). Likewise, Ncd's neck moves in two different phases of the mechanochemical cycle where the MH is in different conformational states (Fig. 6). The hysteresis is achieved by the compliance of the protein, which is similar in origin to the adhesion-energy hysteresis between macromolecular surfaces (58). Elucidating hysteresis in the motility cycle will be important for understanding other translocating motors as well.

Acknowledgments

We thank Sharyn Endow for helpful discussions and Martin Karplus for critical feedback on the manuscript. We used the Texas A&M Supercomputing Facility for simulations.

This work was supported by grant R01GM087677 from the National Institutes of Health (Bethesda, MD).

Supporting Material

Document S1. Additional sections, references, figures and tables
mmc1.pdf (1.8MB, pdf)
Movie S1. RP-TMD of the Ncd dimer
Download video file (1.4MB, mpg)
Movie S2. Two-step forward RP-TMD
Download video file (1.6MB, mpg)
Movie S3. Hysteresis in the neck motion
Download video file (4.3MB, mpg)

References

  • 1.Vale R.D. The molecular motor toolbox for intracellular transport. Cell. 2003;112:467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
  • 2.Miki H., Okada Y., Hirokawa N. Analysis of the kinesin superfamily: insights into structure and function. Trends Cell Biol. 2005;15:467–476. doi: 10.1016/j.tcb.2005.07.006. [DOI] [PubMed] [Google Scholar]
  • 3.Hwang W., Lang M.J. Mechanical design of translocating motor proteins. Cell Biochem. Biophys. 2009;54:11–22. doi: 10.1007/s12013-009-9049-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.McDonald H.B., Stewart R.J., Goldstein L.S.B. The kinesin-like ncd protein of Drosophila is a minus end-directed microtubule motor. Cell. 1990;63:1159–1165. doi: 10.1016/0092-8674(90)90412-8. [DOI] [PubMed] [Google Scholar]
  • 5.Walker R.A., Salmon E.D., Endow S.A. The Drosophila claret segregation protein is a minus-end directed motor molecule. Nature. 1990;347:780–782. doi: 10.1038/347780a0. [DOI] [PubMed] [Google Scholar]
  • 6.Wade R.H., Kozielski F. Structural links to kinesin directionality and movement. Nat. Struct. Biol. 2000;7:456–460. doi: 10.1038/75850. [DOI] [PubMed] [Google Scholar]
  • 7.Henningsen U., Schliwa M. Reversal in the direction of movement of a molecular motor. Nature. 1997;389:93–96. doi: 10.1038/38022. [DOI] [PubMed] [Google Scholar]
  • 8.Case R.B., Pierce D.W., Vale R.D. The directional preference of kinesin motors is specified by an element outside of the motor catalytic domain. Cell. 1997;90:959–966. doi: 10.1016/s0092-8674(00)80360-8. [DOI] [PubMed] [Google Scholar]
  • 9.Endow S.A., Waligora K.W. Determinants of kinesin motor polarity. Science. 1998;281:1200–1202. doi: 10.1126/science.281.5380.1200. [DOI] [PubMed] [Google Scholar]
  • 10.Rice S., Lin A.W., Vale R.D. A structural change in the kinesin motor protein that drives motility. Nature. 1999;402:778–784. doi: 10.1038/45483. [DOI] [PubMed] [Google Scholar]
  • 11.Hwang W., Lang M.J., Karplus M. Force generation in kinesin hinges on cover-neck bundle formation. Structure. 2008;16:62–71. doi: 10.1016/j.str.2007.11.008. [DOI] [PubMed] [Google Scholar]
  • 12.Khalil A.S., Appleyard D.C., Lang M.J. Kinesin's cover-neck bundle folds forward to generate force. Proc. Natl. Acad. Sci. USA. 2008;105:19247–19252. doi: 10.1073/pnas.0805147105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Yun M., Bronner C.E., Endow S.A. Rotation of the stalk/neck and one head in a new crystal structure of the kinesin motor protein, Ncd. EMBO J. 2003;22:5382–5389. doi: 10.1093/emboj/cdg531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Endres N.F., Yoshioka C., Vale R.D. A lever-arm rotation drives motility of the minus-end-directed kinesin Ncd. Nature. 2006;439:875–878. doi: 10.1038/nature04320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Sablin E.P., Case R.B., Fletterick R.J. Direction determination in the minus-end-directed kinesin motor ncd. Nature. 1998;395:813–816. doi: 10.1038/27463. [DOI] [PubMed] [Google Scholar]
  • 16.Endow S.A., Higuchi H. A mutant of the motor protein kinesin that moves in both directions on microtubules. Nature. 2000;406:913–916. doi: 10.1038/35022617. [DOI] [PubMed] [Google Scholar]
  • 17.Foster K.A., Correia J.J., Gilbert S.P. Equilibrium binding studies of non-claret disjunctional protein (Ncd) reveal cooperative interactions between the motor domains. J. Biol. Chem. 1998;273:35307–35318. doi: 10.1074/jbc.273.52.35307. [DOI] [PubMed] [Google Scholar]
  • 18.Pechatnikova E., Taylor E.W. Kinetics processivity and the direction of motion of Ncd. Biophys. J. 1999;77:1003–1016. doi: 10.1016/S0006-3495(99)76951-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Foster K.A., Mackey A.T., Gilbert S.P. A mechanistic model for Ncd directionality. J. Biol. Chem. 2001;276:19259–19266. doi: 10.1074/jbc.M008347200. [DOI] [PubMed] [Google Scholar]
  • 20.Heuston E., Bronner C.E., Endow S.A. A kinesin motor in a force-producing conformation. BMC Struct. Biol. 2010;10:19–31. doi: 10.1186/1472-6807-10-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Hallen M.A., Liang Z.Y., Endow S.A. Two-state displacement by the kinesin-14 Ncd stalk. Biophys. Chem. 2011;154:56–65. doi: 10.1016/j.bpc.2011.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.deCastro M.J., Fondecave R.M., Stewart R.J. Working strokes by single molecules of the kinesin-related microtubule motor ncd. Nat. Cell Biol. 2000;2:724–729. doi: 10.1038/35036357. [DOI] [PubMed] [Google Scholar]
  • 23.Butterfield A.E., Stewart R.J., Skliar M. Bidirectional power stroke by ncd kinesin. Biophys. J. 2010;99:3905–3915. doi: 10.1016/j.bpj.2010.10.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Kozielski F., De Bonis S., Wade R.H. The crystal structure of the minus-end-directed microtubule motor protein ncd reveals variable dimer conformations. Structure. 1999;7:1407–1416. doi: 10.1016/s0969-2126(00)80030-1. [DOI] [PubMed] [Google Scholar]
  • 25.van der Vaart A., Karplus M. Simulation of conformational transitions by the restricted perturbation-targeted molecular dynamics method. J. Chem. Phys. 2005;122:114903. doi: 10.1063/1.1861885. [DOI] [PubMed] [Google Scholar]
  • 26.van der Vaart A., Karplus M. Minimum free energy pathways and free energy profiles for conformational transitions based on atomistic molecular dynamics simulations. J. Chem. Phys. 2007;126:164106. doi: 10.1063/1.2719697. [DOI] [PubMed] [Google Scholar]
  • 27.Cecchini M., Houdusse A., Karplus M. Allosteric communication in myosin V: from small conformational changes to large directed movements. PLOS Comput. Biol. 2008;4:e1000129. doi: 10.1371/journal.pcbi.1000129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Fischer S., Karplus M. Conjugate peak refinement: an algorithm for finding reaction paths and accurate transition states in systems with many degrees of freedom. Chem. Phys. Lett. 1992;194:252–261. [Google Scholar]
  • 29.Fischer S., Windshügel B., Smith J.C. Structural mechanism of the recovery stroke in the myosin molecular motor. Proc. Natl. Acad. Sci. USA. 2005;102:6873–6878. doi: 10.1073/pnas.0408784102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Zheng W., Doniach S. A comparative study of motor-protein motions by using a simple elastic-network model. Proc. Natl. Acad. Sci. USA. 2003;100:13253–13258. doi: 10.1073/pnas.2235686100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Yu H., Ma L., Cui Q. Mechanochemical coupling in the myosin motor domain. II. Analysis of critical residues. PLOS Comput. Biol. 2007;3:e23. doi: 10.1371/journal.pcbi.0030023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Brooks B.R., Brooks C.L., 3rd, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Van Der Spoel D., Lindahl E., Berendsen H.J. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  • 34.Neria E., Fischer S., Karplus M. Simulation of activation free energies in molecular systems. J. Chem. Phys. 1996;105:1902–1921. [Google Scholar]
  • 35.Schaefer M., Bartels C., Karplus M. Effective atom volumes for implicit solvent models: comparison between Voronoi volumes and minimum fluctuation volumes. J. Comput. Chem. 2001;22:1857–1879. doi: 10.1002/jcc.1137. [DOI] [PubMed] [Google Scholar]
  • 36.Haberthür U., Caflisch A. FACTS: Fast analytical continuum treatment of solvation. J. Comput. Chem. 2008;29:701–715. doi: 10.1002/jcc.20832. [DOI] [PubMed] [Google Scholar]
  • 37.Im W., Lee M.S., Brooks C.L., 3rd Generalized born model with a simple smoothing function. J. Comput. Chem. 2003;24:1691–1702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
  • 38.MacKerell A.D., Jr., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  • 39.Altschul S.F., Gish W., Lipman D.J. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
  • 40.Lakkaraju S.K., Hwang W. Modulation of elasticity in functionally distinct domains of the tropomyosin coiled-coil. Cell Mol Bioeng. 2009;2:57–65. doi: 10.1007/s12195-009-0050-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Lakkaraju S.K., Hwang W. Critical buckling length versus persistence length: what governs biofilament conformation? Phys. Rev. Lett. 2009;102:118102. doi: 10.1103/PhysRevLett.102.118102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Hwang W. Calculation of conformation-dependent biomolecular forces. J. Chem. Phys. 2007;127:175104. doi: 10.1063/1.2784557. [DOI] [PubMed] [Google Scholar]
  • 43.Yogurtcu O.N., Wolgemuth C.W., Sun S.X. Mechanical response and conformational amplification in α-helical coiled coils. Biophys. J. 2010;99:3895–3904. doi: 10.1016/j.bpj.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Howard J. Sinauer; Sunderland, MA: 2001. Mechanics of Motor Proteins and the Cytoskeleton. [Google Scholar]
  • 45.Ito M., Morii H., Tanokura M. Coiled coil in the stalk region of ncd motor protein is nonlocally sustained. Biochemistry. 2006;45:3315–3324. doi: 10.1021/bi051480f. [DOI] [PubMed] [Google Scholar]
  • 46.Adamovic I., Mijailovich S.M., Karplus M. The elastic properties of the structurally characterized myosin II S2 subdomain: a molecular dynamics and normal mode analysis. Biophys. J. 2008;94:3779–3789. doi: 10.1529/biophysj.107.122028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Broersma S. Rotational diffusion constant of a cylindrical particle. J. Chem. Phys. 1960;32:1626–1631. [Google Scholar]
  • 48.Tracy M.A., Pecora R. Dynamics of rigid and semirigid rodlike polymers. Annu. Rev. Phys. Chem. 1992;43:525–557. [Google Scholar]
  • 49.Gardiner C.W. 4th ed. Springer; New York: 2009. Stochastic Methods: A Handbook for the Natural and Social Sciences. [Google Scholar]
  • 50.Löwe J., Li H., Nogales E. Refined structure of αβ-tubulin at 3.5 Å resolution. J. Mol. Biol. 2001;313:1045–1057. doi: 10.1006/jmbi.2001.5077. [DOI] [PubMed] [Google Scholar]
  • 51.Vale R.D., Milligan R.A. The way things move: looking under the hood of molecular motor proteins. Science. 2000;288:88–95. doi: 10.1126/science.288.5463.88. [DOI] [PubMed] [Google Scholar]
  • 52.Sindelar C.V., Budny M.J., Cooke R. Two conformations in the human kinesin power stroke defined by x-ray crystallography and EPR spectroscopy. Nat. Struct. Biol. 2002;9:844–848. doi: 10.1038/nsb852. [DOI] [PubMed] [Google Scholar]
  • 53.Sindelar C.V., Downing K.H. An atomic-level mechanism for activation of the kinesin molecular motors. Proc. Natl. Acad. Sci. USA. 2010;107:4111–4116. doi: 10.1073/pnas.0911208107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Vinogradova M.V., Reddy V.S., Fletterick R.J. Crystal structure of kinesin regulated by Ca2+-calmodulin. J. Biol. Chem. 2004;279:23504–23509. doi: 10.1074/jbc.M400741200. [DOI] [PubMed] [Google Scholar]
  • 55.Vinogradova M.V., Malanina G.G., Fletterick R.J. Structural dynamics of the microtubule binding and regulatory elements in the kinesin-like calmodulin binding protein. J. Struct. Biol. 2008;163:76–83. doi: 10.1016/j.jsb.2008.04.004. [DOI] [PubMed] [Google Scholar]
  • 56.Vinogradova M.V., Malanina G.G., Fletterick R.J. Structure of the complex of a mitotic kinesin with its calcium binding regulator. Proc. Natl. Acad. Sci. USA. 2009;106:8175–8179. doi: 10.1073/pnas.0811131106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Sweeney H.L., Houdusse A. Structural and functional insights into the Myosin motor mechanism. Annu. Rev. Biophys. 2010;39:539–557. doi: 10.1146/annurev.biophys.050708.133751. [DOI] [PubMed] [Google Scholar]
  • 58.Leckband D., Israelachvili J. Intermolecular forces in biology. Q. Rev. Biophys. 2001;34:105–267. doi: 10.1017/s0033583501003687. [DOI] [PubMed] [Google Scholar]
  • 59.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Additional sections, references, figures and tables
mmc1.pdf (1.8MB, pdf)
Movie S1. RP-TMD of the Ncd dimer
Download video file (1.4MB, mpg)
Movie S2. Two-step forward RP-TMD
Download video file (1.6MB, mpg)
Movie S3. Hysteresis in the neck motion
Download video file (4.3MB, mpg)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES