Abstract
Background/Aims
Population-based studies have successfully identified genes affecting common diseases, but have not provided a molecular mechanism. We describe an approach for alcohol dependence connecting a mechanistic model at the molecular level with disease risk at the population level, and investigate how this model implies statistical gene-gene interactions that affect disease risk.
Methods
We develop a pharmacokinetic model describing how genetic variations in ADH1B, ADH1C, ADH7, ALDH2, and TAS2R38 affect consumption behavior, and alcohol and acetaldehyde levels over time in various tissues of individuals with a particular genotype to predict their susceptibility to alcohol dependence.
Results
We show that there is good agreement between the observed genotype/haplotype frequencies and those predicted by the model among cases and controls. Based on this framework, we show that we expect to observe statistical interactions among these genes for a reasonably large sample size when logistic regression models are used to relate genotype effects and disease risk.
Conclusion
Our model exemplifies mechanistic modeling of how genes interact to influence an individual's susceptibility to alcohol dependence. We anticipate that this general approach could also be applied to study other diseases at the molecular level.
Key Words: Mechanistic model, Alcohol dependence, Pharmacokinetic models, Gene-gene interactions, Genetic association
Introduction
Through recent efforts involving numerous genome-wide association studies (GWAS), many genes and genomic regions have been implicated in common diseases. Although these results are promising and help lead to insights on biological pathways underlying these diseases, GWAS data only reveal statistical associations and do not offer a mechanistic explanation of how different genes interact with each other or how environmental risk factors affect an individual's disease susceptibility. Some research groups have explored possible interactions among the identified loci [1,2]. However, only statistical interactions were considered, although it is well known that statistical interactions depend both on the scale used to measure phenotypes and the models that relate phenotypes and genotypes. In contrast to statistical methods that are predominantly used to describe population-level associations between genes and diseases, many detailed mathematical models have been developed to describe disease pathogenesis at the molecular level [3,4,5]. However, there is little in the literature to relate the understanding at the molecular level to the genetic and phenotypic variation that is observed at the population level. This is partly due to the lack of a phenotype where good quality data are available at both molecular and population levels. In 2005, Lin et al. incorporated pharmacokinetic models into their approach to relate haplotype variation to drug response [6], and later extended their method to consider genetic interactions [7]. In their recent article, Ahn et al. [8] explain the utility of this general approach exemplified by Lin et al. [6,7], termed functional mapping, elucidating the detailed architecture of drug response. They argue that because all biological traits are dynamic or the result of a developmental process, mapping the underlying quantitative trait loci (QTL) is the most natural way to approach the genetics of such traits. In particular, they emphasize the importance of incorporating pharmacokinetic and pharmacodynamic models in this process. They describe the general theoretical framework and highlight the work of others conducted in this field, which each present variations of the model's implementation, applied to different drugs and diseases. Many of these example studies employed more complex, drug- and disease-specific pharmacokinetic/pharmacodynamic models than that by Lin et al. [6,7]. In a similar spirit, the goal of this article is to develop a general approach that relates molecular-level interactions to population-level observations, connecting genetic variation with disease risk. Rather than searching for causal genes, however, which is the main goal of functional mapping, we aim to integrate known information about how genetic variation within each gene affects disease risk individually at the molecular level to predict how these genes work together to affect disease risk. This approach can be used to identify the genes (and the haplotypes of these genes) that play the largest role at each point in time during the pathogenesis of a disease. Although such models are typically a simplistic representation of a complex reality, they offer a starting point to explain the observed population-level associations with molecular interactions, and may also allow us to assess the adequacy of the molecular-level models. Our approach can be used to study any disease where sufficient knowledge on the molecular mechanism is available; however, we demonstrate its use by studying alcohol dependence (AD), where a number of genes have been implicated in their associations with an individual's susceptibility to AD. In addition, there is a large body of literature on the metabolism of ethanol after it is consumed. In the following, we first review the genes that have been implicated in AD.
Metabolic Genes
The ADH (alcohol dehydrogenase) and ALDH (aldehyde dehydrogenase) genes are the key genes of the primary alcohol metabolism pathway [1,9]. Ethanol is first oxidized into acetaldehyde by ADH enzymes, which is subsequently oxidized into acetate by ALDH enzymes [1,9]. The intermediary, acetaldehyde, is a toxin [1,10]. Buildup of acetaldehyde causes unpleasant flushing effects which serve as a deterrent against drinking alcohol [1,10,11]. High ADH activity or low ALDH activity contributes to acetaldehyde buildup [1,10,11]. Thus, they affect the risk of AD by influencing further alcohol consumption [1,10,11].
There are several classes of ADH and ALDH genes, which are expressed at different levels in different tissues. The distinct kinetic parameters of their corresponding enzymes make each form more sensitive to, and more efficient at oxidizing, different alcohols and aldehydes [12]. Consequently, only a subset of ADH and ALDH is specifically relevant to ethanol and acetaldehyde metabolism, respectively.
The class I ADH genes – ADH1A, ADH1B, and ADH1C – have been the main focus of most previous studies on ADH and AD. Primarily expressed in the liver [13], they encode subunits that form a homo- or heterodimer [1], which accounts for 70% of hepatic ethanol oxidation [14,15]. ADH1B and ADH1C are polymorphic, with three and two alleles [16], respectively, defined by the amino acids encoded by single nucleotide polymorphisms (SNPs). For ADH1B, there are three alleles, ADH1B∗1, ADH1B∗2, and ADH1B∗3, jointly defined by the SNPs at Arg48His and Arg369Cys, where ADH1B∗1 corresponds to Arg and Arg at these two SNPs, ADH1B∗2 corresponds to His and Arg at these two SNPs, and ADH1B∗3 corresponds to Arg and Cys at these two SNPs, respectively. For ADH1C, there are two alleles, ADH1C∗1 and ADH1C∗2, jointly defined by the SNPs at Arg271Gln and Ile349Val, where ADH1C∗1 corresponds to Arg and Ile at these two SNPs, and ADH1C∗2 corresponds to Gln and Val at these two SNPs, respectively.
ADH1B∗2, ADH1B∗3, and ADH1C∗1 are thought to protect against AD because they encode faster forms of the enzyme [16], leading to buildup of acetaldehyde. ADH1B has been shown to alter susceptibility to AD [16]. ADH1C has also been associated with AD, but this may be an artifact due to its linkage disequilibrium with ADH1B [17].
ADH7, which is expressed in the gastric mucosa, is the first ADH to encounter ethanol and has the highest maximal activity [18]. Thus, ADH7 encodes the primary enzyme for gastric ethanol oxidation and is considered a prime candidate gene for AD. Many East Asians express little or no ADH7 [19,20]. Consequently, lack of ADH7 is thought to protect against AD in these populations. A few studies have found associations between non-coding ADH7 SNPs and AD [14,21], including an interaction with ADH1B∗48His[2]. However, these results have been inconsistent, so it is unclear which variant truly affects ADH7 expression, and whether it actually plays a significant role in AD.
ALDH2 has been the primary focus of studies on ALDH genes and AD because of its efficiency at oxidizing acetaldehyde [16,22]. It has two alleles defined by a single SNP, Glu487Lys: ALDH2∗1 has the amino acid Glu at this position, while ALDH2∗2 has Lys. These peptides form a homotetramer composed of a pair of dimers; however, ALDH2∗2 is dominant negative [11] because the heterodimer is unstable, thereby greatly reducing the number of active homotetramers that can form. Moreover, homozygotes for ALDH2∗2 have no ALDH2 activity. Thus, in both homozygotes and even heterozygotes, the absent/reduced activity leads to buildup of acetaldehyde. Like ADH1B, ALDH2 has been shown to alter susceptibility to AD [16].
Taste Receptor Genes
It has been posited that bitter-taste receptors modulate ethanol intake by mediating the perception of ethanol: those individuals who are very sensitive to bitterness perceive ethanol to be bitter, and thus drink little of it, since they are averse to its taste, while those who are not sensitive to bitterness perceive ethanol to be sweet, and drink more of it. One such bitter-taste receptor gene, TAS2R38, has two major alleles defined by three SNPs at Pro49Ala, Ala262Val, and Val296Ile jointly, where allele is defined by Pro, Ala, and Val at these three SNPs and AVI is defined by Ala, Val, and Ile at these three SNPs, respectively. Duffy et al. [23] showed that the TAS2R38 genotype is associated with the yearly ethanol intake (which is later discussed and shown in table 1), but because the study did not include alcoholic status, no direct association with AD could be made. Since an individual must use alcohol excessively in order to become an alcoholic, TAS2R38 is a promising candidate gene for AD.
Table 1.
Fixed parameters
| Parameter | Source | Reported units | Reported value | Reported margin of error |
|---|---|---|---|---|
| ADH1 km*B1-C1 | [12] | mmol/l | 0.13 | 0.04 |
| ADH1 km*B1-C2 | [12] | mmol/l | 0.11 | 0.04 |
| ADH1 km*B2-C1 | [12] | mmol/l | 1.6 | 0.1 |
| ADH1 km*B2-C2 | [12] | mmol/l | 1.7 | 0.1 |
| ADH1 km*B3-C1 | [12] | mmol/l | 9.8 | 3.7 |
| ADH1 km*B3-C2 | [12] | mmol/l | 15 | 5 |
| ADH1 vmax*B1-C1 | [12] | mmol/min/1.4 kg liver | 2.1 | 0.1 |
| ADH1 vmax*B1-C2 | [12] | mmol/min/1.4 kg liver | 1.7 | 0.1 |
| ADH1 vmax*B2-C1 | [12] | mmol/min/1.4 kg liver | 20 | 1 |
| ADH1 vmax*B2-C2 | [12] | mmol/min/1.4 kg liver | 19 | 1 |
| ADH1 vmax*B3-C1 | [12] | mmol/min/1.4 kg liver | 7.6 | 1.3 |
| ADH1 vmax*B3-C2 | [12] | mmol/min/1.4 kg liver | 8.2 | 1.4 |
| ADH7 km*l | [4] | mmol/l | 2,090 | none |
| ADH7 km*2 | none | mmol/l | NA | none |
| ADH7 vmax*l | [4] | mmol/min/kg0.75 | 0.0015 | none |
| ADH7 vmax*2 | none | mmol/min/kg0.75 | 0* | none |
| ALDH2 km*l | [5] | mmol/l | 0.4 | none |
| ALDH2 km*2 | none | mmol/l | NA | none |
| ALDH2 vmax*2 | none | mmol/min/kg liver | 0* | none |
| DPY TAS2R38*1/*1 | [23] | number of drinks per year | 132.90 | 21.98 |
| DPY TAS2R38*1/*2 | [23] | number of drinks per year | 180.49 | 29.32 |
| DPY TAS2R38*2/*2 | [23] | number of drinks per year | 285.16 | 55.82 |
Each parameter was fixed at the reported value. vmax values for ADH7 and ALDH2 isoforms reported to be inactive in the literature were not explicitly reported, but inferred to be zero (0*), in which case the corresponding km value was irrelevant or not applicable (NA).
Of the genes discussed above, only ADH1B and ALDH2 have been definitively linked with AD [16]. The evidence for ADH7 has been inconsistent, possibly due to its small marginal effects. The effect of TAS2R38 on AD still needs to be tested. However, if an individual never drinks alcohol because he/she dislikes the taste, this person cannot become an alcoholic, despite any metabolic predisposition for the disease that the person might have. Therefore, it seems likely that TAS2R38 might interact epistatically with the metabolic genes as well.
In this article, we specifically aim to develop a mathematical model at the molecular level involving all the genes discussed above and relate this model to an individual's susceptibility to AD. Our model is intended to be mechanistic in nature. Thus, it can be used to associate molecular pathways with statistical interactions among genes involved in a biological process, proving some links between biological and statistical interactions. A similar approach can be used to study other diseases.
Materials and Methods
Study Design and Data
Though our model has many layers, which are discussed in subsequent sections in greater detail, it is largely constructed by introducing the concept of genetic variation into pre-existing, experimentally determined, pharmacokinetic models of alcohol metabolism. Genetic variation functionally manifests itself in different ways. For enzyme genes, each haplotype corresponds to a variant of the same enzyme with a different set of values for the kinetic parameters. This is the case for ADH1B, ADH1C, ADH7, and ALDH2. For receptor genes, each haplotype corresponds to a variant of the same receptor with different properties. In the case of the taste receptor TAS2R38, this translates to receptor variants that confer a quantifiably stronger or weaker preference for alcohol. The form of the model is the same across all genotypes; however, by replacing the general, overall value for each parameter with the value corresponding to a specific genotype, we are essentially creating a unique submodel for each multilocus genotype. These submodels can be used to show how known functional differences, caused by genetic variation within each of these genes individually, lead to variation in susceptibility to AD and the relative importance of each gene in this process. The validity of the model is verified by incorporating genotype or haplotype frequencies for each of these genes from the literature. The model is used to predict the frequencies of alcoholics, using observed control frequencies as priors. A good agreement between predicted and observed frequencies for alcoholics indicates a good model fit.
The details of this process are described below. We mention each piece of data as it is incorporated into each step of our method. However, we first describe all data here, so that it is all in one place.
Some general ideas for our model were taken from the pharmacokinetic models of Wilkinson et al. [3], MacDonald et al. [4], and Umulis et al. [5]. Wilkinson et al. [3] used original time-series data on blood alcohol concentration, as it relates to the consumption of different doses of alcohol in white males, in order to study the nature of the kinetics of ethanol metabolism. They were one of the first groups to establish that this process exhibits Michaelis-Menten kinetics, and study the effects of alcohol on gastric emptying. MacDonald et al. [4] divided their model of ethanol metabolism into compartments, while Umulis et al. [5] added the metabolism of acetaldehyde into their model of ethanol metabolism. We would have ideally liked to use similar time-series data on individuals to validate our model, but without such data, we relied on the validity of these past models.
All data in our current work was taken from the literature. The kinetic parameters corresponding to the ADH1C-ADH1B combinatorial genotypes were estimated from a model by Lee et al. [12]. This was based on kinetic parameters that were experimentally determined for each haplotype of each gene individually in vitro [12]. The kinetic parameters for ADH7 and ALDH2 were estimated from pharmacokinetic models by MacDonald et al. [4] and Umulis et al. [5], respectively. The degree of preference for alcohol corresponding to each genotype of TAS2R38 is based on observations by Duffy et al. [23] on the average number of drinks per year (DPY) by individuals with each genotype (TAS2R38∗1/∗1 = PAV/PAV; TAS2R38∗1/∗2 = PAV/AVI; TAS2R38∗2/∗2 = AVI/AVI). These values, which link each genotype of each gene to their individual effect on some aspect of AD, are all shown in table 1.
Ideally, multilocus genotype frequencies across all five genes would have been collected from individual-level genotype data on alcoholics and controls. Since individual data were lacking, we resorted to the literature; however, such information was still difficult to find in a single population. Because East Asians are polymorphic for all five genes with the most complete data available, we chose to test our model in this population. Since the frequencies of all five genes had never been studied jointly, we were forced to obtain the frequencies for individual genes from different sources. We obtained joint ADH1C-ADH1B haplotype frequencies and ALDH2 genotype frequencies in alcoholics and controls from Chen et al. [1]. These were based on a sample of Han Chinese living in Taiwan, including 340 alcoholics and 545 controls [1]. The observed frequencies for controls and alcoholics are shown in table 2. TAS2R38 haplotype frequencies of 0.696 (PAV) and 0.304 (AVI) were obtained from the database ALFRED [7], which is publicly available. These frequencies were calculated from a sample of 50 Taiwanese Han living around Taipei, Taiwan (ALFRED UID SA000001B) [7]. Because we strove to capture the effects of differential ADH7 expression in our model, and because this differential gene expression has yet to be linked to a particular expression QTL (eQTL), our ADH7 frequencies are not actual genotype frequencies. Instead, they represent frequencies of varying degrees of ADH7 expression observed by Baraona et al. [19]. Using gel electrophoresis to examine the presence of the enzyme in stomach tissue isolated from subjects during various surgeries, they found that the enzyme was completely absent in 14, and ‘barely detectable’ in 3 of 21 Japanese individuals [19]. For simplification, we refer to these as the ‘genotype’ frequencies – 0.667 and 0.143 – of the artificial ‘genotypes’ ADH7–2/2 and ADH7–1/2, respectively. The remaining frequency, 0.190, corresponds to ADH7–1/1, which represents the standard expression of ADH7. Because the TAS2R38 and ADH7 frequencies are general and were not calculated for alcoholics specifically, they are only used as prior information in our method to test model fit.
Table 2.
Genetic frequencies
|
ADH1C-ADH1B haplotypes |
ALDH2 genotypes |
||||||
|---|---|---|---|---|---|---|---|
| ADH1C*1-ADH1B*1 | ADH1C*1-ADH1B*2 | ADH1C*2-ADH1B*1 | ADH1C*2-ADH1B*2 | ALDH2-1/1 | ALDH2-1/2 | ALDH2-2/2 | |
| Observed controls | 0.197 | 0.710 | 0.070 | 0.023 | 0.560 | 0.400 | 0.040 |
| Observed alcoholics | 0.377 | 0.447 | 0.162 | 0.015 | 0.830 | 0.170 | 0 |
| Predicted alcoholics | 0.383 | 0.446 | 0.155 | 0.016 | 0.830 | 0.155 | 0.015 |
Model and Assumptions
Our model has three components, with the first component modeling how ethanol is metabolized and how acetaldehyde is accumulated in an individual after a single dose of alcohol use, the second component modeling the drinking behavior of an individual, and the third component relating an individual's susceptibility to AD to the accumulated alcohol use. We describe these three components in detail in the following section.
Component 1: Ethanol Metabolism
This component models how ethanol is metabolized in an individual. To obtain an accurate model, ideally, we would like to monitor the alcohol level of an individual after ethanol consumption. However, such data are lacking, and we expand upon the models of Wilkinson et al. [3], MacDonald et al. [4], and Umulis et al. [5], which are estimated from this type of time-series data. Since ethanol is ingested orally and is distributed and metabolized in different parts of the body at different rates, we use a compartmental pharmacokinetic model for ethanol levels throughout the body, following ethanol consumption. Because blood acetaldehyde buildup has been shown to inversely affect further ethanol consumption, we include acetaldehyde in the model. This enables the modeling of consumption behavior, which is vital for modeling a disease that is contingent upon alcohol use. Genetics comes into play in two ways. The preference for ethanol use depends on the genotype for bitter-taste receptor genes, while the rate of metabolism depends on the genotypes of alcohol metabolism genes. The genotype-specific kinetic parameters will be introduced later in our discussion of the model. Thus, unlike previous studies which aimed to study the nature of the kinetics of ethanol metabolism and elimination from the body, we focus on how genetic variations affect ethanol metabolism and alcohol consumption, thereby affecting a person's risk for AD.
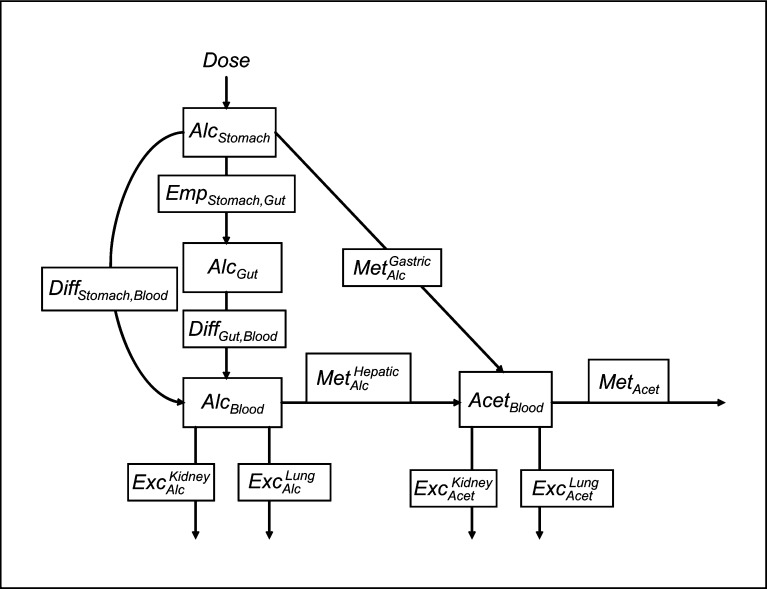
Figure 1 shows the compartmental model we use to describe how ethanol is metabolized in an individual, with the three compartments being the stomach, gut, and blood, in which it tracks the alcohol in the stomach, AlcStomach, the alcohol in the gut, AlcGut, the alcohol in the blood, AlcBlood, and the acetaldehyde in the blood, AcetBlood. This is a similar but abbreviated set of the compartments used by MacDonald et al. [4], with the addition of acetaldehyde, as in the model by Umulis et al. [5]. An individual is first given a particular Dose of alcohol. For simplification, we assume that the consumption of the entire dose of alcohol does not take any time, but that the entire dose enters the stomach instantaneously upon consumption, so that the stomach alcohol at time zero is the dose. From the stomach, the alcohol can go through three possible processes. It can be absorbed directly into the blood via simple diffusion, with a rate constant of DiffStomach, Blood. This absorption is modeled by MacDonald et al. [4] in a similar manner. It can also follow the digestive tract from the stomach into the gut at the stomach emptying rate, EmpStomach, Gut. It has been shown that stomach alcohol inhibits peristalsis [3]. Therefore, if the original dose is larger, alcohol will exit the stomach more slowly than the same amount of alcohol with a smaller original dose. Hence, this rate is not a constant, but is given by equation (1):
| (1) |
Fig. 1.
Model diagram.
This coefficient is directly adopted from the model by Wilkinson et al. [3]. Finally, the stomach alcohol can also be oxidized into acetaldehyde by ADH7, with a rate coefficient of MetGAlacstric. Since this occurs at the stomach lining, it is assumed that the resulting acetaldehyde does not flow back into the stomach cavity, but directly enters the bloodstream. Alcohol in the gut can only be absorbed into the blood via simple diffusion, with a rate constant of DiffGut, Blood, which is similarly modeled by MacDonald et al. [4]. Alcohol in the blood can be oxidized into acetaldehyde by ADH1B and ADH1C, with a rate coefficient of MetHAlecpatic. Blood acetaldehyde can leave the system through oxidation into acetate by ALDH enzymes, with a rate coefficient of MetAcet. Because ADH1B, ADH1C, ADH7, and ALDH2 are thought to operate under Michaelis-Menten kinetics, MetGAlacstric, MetHAlecpatic, and MetAcet are not constants, but are given by equations (2)–(4):
| (2) |
| (3) |
| (4) |
Such forms were used in all three previous models [3,4,5]. The kinetic parameters – km and vmax – for each metabolic gene (ADH7, ADH1B and ADH1C together, and ALDH2 alone) differ among individuals with different genotypes, and we will return to their values later.
Combining all the reactions discussed above, we obtain the following set of differential equations:
| (5) |
| (6) |
| (7) |
| (8) |
As discussed above, because ADH1B, ADH1C, and ALDH2 are polymorphic, each kinetic parameter may take on a number of different values, each corresponding to a specific genotype. Therefore, the model will produce different results for different genotypes. Since there are two ADH1C alleles and three ADH1B alleles, there are six possible joint ADH1C-ADH1B alleles, corresponding to six independent sets of values for kmADH1 and vmAaDxH1, determined by Lee et al. [12]. We assume the parameter values for each genotype are the average of the values corresponding to the component alleles. Since there are two ALDH2 alleles, there are two possible sets of values for kmALDH and vmAaLxDH. We assume the values for the active form correspond to parameters of acetaldehyde oxidation estimated by Umulis et al. [5], while vmAaLxDH is zero for the inactive form, in which case kmALDH is irrelevant. We also assume that the parameter values for homozygotes are the values of their component allele, while vmAaLxDHfor heterozygotes is one-sixteenth that of ALDH2∗1, with an identical kmALDH. Differential gene expression, rather than polymorphism, is important for ADH7. For simplification, however, we consider only two cases: expression of ADH7 at the ‘normal’ level versus no expression at all. Since a lack of ADH7 enzymes due to no gene expression is equivalent to an inactive enzyme, there are two possible sets of values for kmADH7 and vmAaLxD7 as well. We refer to the active and inactive forms by the artificial genotypes ‘ADH7–1/1’ and ‘ADH7–2/2’, respectively. We assume the values for the active form correspond to parameters of gastric ethanol oxidation estimated by MacDonald et al. [4], while vmAaDxH7 is zero for the inactive form, in which case kmADH7 is irrelevant. We also manufacture a ‘medium’ level of expression, which we call ‘ADH7–1/2’, with a vmAaDxH7 half that of the active form, with an identical kmADH7. These values are all shown in table 1.
Lastly, small amounts of alcohol and acetaldehyde in the blood can be excreted via the kidneys and the bladder through the urine, or exhaled by the lungs in the breath, with rate coefficients of ExcKAildcney and ExcLAulncg in equation (7), and ExcKAicdentey and ExcLAucnegt in equation (8), respectively. These rates are assumed to be the same across all genotypes. For lack of better data, we assume that these rates are a small percentage of the rates of hepatic alcohol metabolism for the reference genotype ADH1C–1/1-ADH1B–2/2 (equations (9) and (10)), and acetaldehyde metabolism for the reference genotype ALDH2–1/1 (equations (11) and (12)).
| (9) |
| (10) |
| (11) |
| (12) |
Component 2: Consumption Behavior
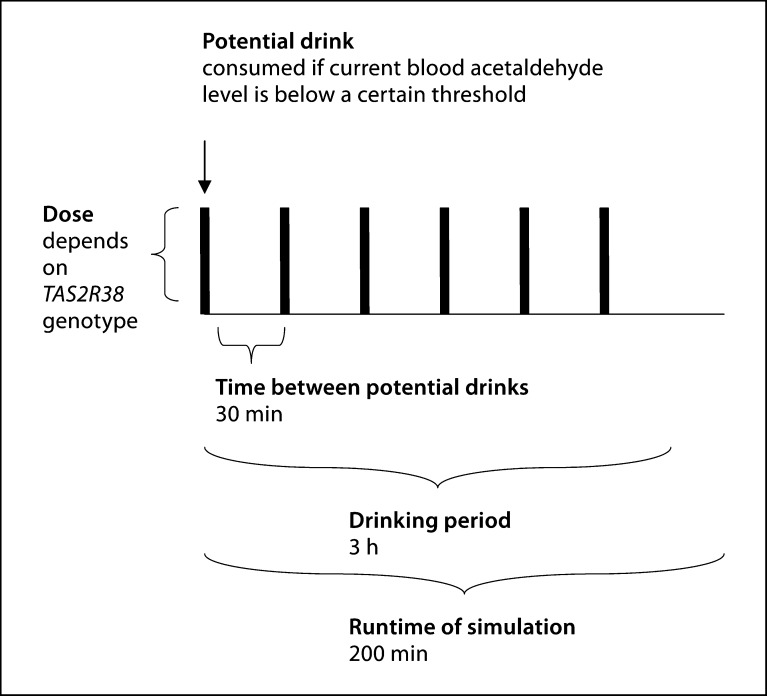
Since there are no robust data upon which to base a mathematical model of alcohol consumption behavior, we developed a simplified model and then subjected it to sensitivity analysis, which we describe later in this paper. In this simplified consumption scheme, illustrated in figure 2, we assume that drinking periods last 3 h, during which a maximum of six drinks can be taken, one every 30 min. Each time an opportunity for a drink arises during an episode, the drink will be taken if the current acetaldehyde level is below a certain threshold. The size of each drink depends on the TAS2R38 genotype. PAV homozygotes consume a standard drink containing 0.25 mol of ethanol. Individuals with the other two genotypes consume more ethanol with each drink, in proportion to the average yearly ethanol intake for their genotype in table 1[23].
Fig. 2.
Consumption scheme.
Based on components 1 and 2, we can infer the drinking behavior for an individual with a given set of genotypes at relevant genes. The dynamics of ethanol metabolism can be inferred based on the differential equations discussed above, and we use the fourth-order Runge-Kutta method to approximate solutions to the system of ordinary differential equations for 200 min. This is done in MATLAB. The trapezoidal rule is used to calculate the areas under the ethanol curve. Therefore, for each combination of genotypes, we can obtain a theoretical profile consisting of a time-course of ethanol and acetaldehyde levels in the stomach, gut, and blood, and the area under the blood alcohol curve throughout the 200-min period.
Component 3: Alcohol Dependence and Total Alcohol Consumption
Diagnosis of AD is largely based on excess alcohol use, either by drinking large amounts of alcohol, or by drinking over long periods of time [24]. The degree of alcohol use can thus be summarized by alcAUC, the area under the (blood) alcohol curve. Since alcohol metabolism and taste perception presumably influence this component of AD the most, we assume that the probability that an individual with multilocus genotype Gj is alcoholic (Y = 1) has the following functional form of alcAUC, which can be calculated based on the assumptions laid out in components 1 and 2.
| (13) |
This form involves three parameters, α, β, and γ, which have the following interpretations. β, which is the value of the function when alcAUC is zero, represents the baseline probability of being an alcoholic. The function approaches α as alcAUC tends to infinity. It represents the maximum possible probability that an individual with any one genotype is an alcoholic. Parameter γ controls the steepness of the curve.
Relating the Model to Observed Data
To evaluate how well the above proposed model explains the drinking behavior and susceptibility to AD of people with different genotypes, the ideal data would consist of ethanol metabolism within an individual, short-term and long-term drinking behavior, and disease diagnosis. However, these detailed individual-level data are not available, and we have limited information on each person's drinking patterns. Instead, data on disease status (alcoholic or not) and genotypes in a group of individuals are often available. If all the parameters in the above model are known, we can easily calculate the probability that a person becomes alcoholic for a given set of genotypes at relevant genes, P(Y ∣ G), where Y = 1 denotes that this person is an alcoholic and 0 that the person is not alcoholic, and G denotes the collection of genotypes across relevant genes. Therefore, we can derive the probability that a person has a specific genotype G conditional on this person's disease status using the simple Bayes rule:
| (14) |
Let Θ denote the set of parameter values in the model. We can compare how well the predicted genotype distributions among the cases and controls match the observed proportions. A good agreement between the predicted and observed proportions implies that the proposed model as well as the model parameters provide a plausible explanation for ethanol metabolism, drinking behavior, and susceptibility to AD. Such an agreement was obtained at the values reported in the literature for most of the parameters. For the parameters whose literature values may not be accurate, or for the parameters not reported in the literature at all, however, we can use the observed data to estimate the model parameters by the maximum likelihood estimates:
| (15) |
Ideally, we would have genetic marker data from all the genes at the individual level for cases and controls, so that we could calculate the genotype frequencies for each multilocus genotype. However, there is no published study in which all five genes were simultaneously studied. The best we could find in the literature was joint ADH1C-ADH1B haplotype frequencies in cases and controls [1], ALDH2 genotype frequencies in cases and controls [1], ADH7 ‘genotype’ frequencies in controls only [19], and TAS2R38 haplotype frequencies in controls only [25], all from different sources and East Asian populations, as we previously discussed in our section Study Design and Data. Consequently, P(Gj) can be evaluated as:
| (16) |
where GB denotes the genotype of ADH1B, GC denotes the genotype of ADH1C, G7 denotes the genotype of ADH7, GL denotes the genotype of ALDH2, and GT denotes the genotype of TAS2R38. Since these genes segregate essentially independently, with the exception of ADH1B and ADH1C, this decomposition is valid. The resulting P(Gj ∣ Y = 1) and P(Gj ∣ Y = 0) are the frequency values for the transformed theoretical case-control table.
Using a specific set of parameter values, we calculated marginal genotype frequencies for ADH7, ALDH2 and TAS2R38, and joint genotype frequencies for ADH1B and ADH1C, for the case and control groups separately by summing over all possible genotypes for the other genes. ADH1C-ADH1B haplotype frequencies were calculated using the EM algorithm, while TAS2R38 haplotype frequencies were calculated using Hardy-Weinberg equilibrium, in order to compare them with the empirical data. Because there are no empirical frequencies in alcoholics for ADH7 and TAS2R38, we could only compare the theoretical and empirical ALDH2 genotype frequencies for alcoholics and the theoretical and empirical ADH1C-ADH1B haplotype frequencies for alcoholics (table 2). We then used these values to calculate the log-likelihood of the data for this specific set of parameter values:
| (17) |
where Θ is again the set of model parameter values, and O and are the observed and predicted frequencies in alcoholics, respectively, for both ADH1C-ADH1B and ALDH2. We used the log-likelihood to compare different models and, ultimately, to find an optimized set of parameter values, within the margins of error reported in the literature for each parameter.
Numerically, we used the Nelder-Mead algorithm [26] to find the maximum likelihood estimators of these parameters. The parameters from the literature, listed in table 1, provide a good fit to the population-level data. The four observed ADH1C-ADH1B haplotype frequencies and the three observed ALDH2 genotype frequencies in table 2 gave us 5 d.f. to ultimately estimate the four remaining parameters, listed in table 3, using the initial values, and the lower and upper bounds shown in the table. Their optimized values are also shown. The parameters shown in table 1 were fixed at their reported values for this process, which we ultimately used in our analysis.
Table 3.
Optimized parameters
| Parameter | ALDH2*1vmax | α | β | γ |
|---|---|---|---|---|
| Source | [5] | none | none | none |
| Reported units | mmol/min/kg liver | none | none | none |
| Reported value | 2.2 | free | free | free |
| Reported margin of error | none | NA | NA | NA |
| Initial value | 2.2 | 0.25 | 1.00 × 10−5 | 0.3 |
| Lower bound | 0 | 1.00 × 10−5 | 1.00 × 4 10−5 | 0 |
| Upper bound | +∞ | 1 | 1 | +∞ |
| Optimized value | 3.8 | 2.00 × 10−5 | 1.69 × 10−5 | 6.03 × 10−1 |
α, β, and γ are free parameters of the sigmoid function, so they have no margin of error. The initial value, the lower bound and the upper bound are those values used as input to the Nelder-Mead algorithm.
NA = Not applicable.
Gene-Gene Interactions
We consider the use of a logistic regression model to relate disease status with genotypes at the candidate genes a standard approach in statistical genetics. In logistic regressions, both marginal and interaction effects can be studied. Genotypes at the genes analyzed can be coded in different ways to consider either additive or dominant effects. Under a logistic regression model, if the marginal effect for a gene is significant, then this gene is implicated. A statistically significant interaction term between two or more genes is often interpreted as possible biological interactions between these genes in pathways. In our analysis with the logistic regression model, there are two variables for each gene, representing its first and second alleles. The value of each variable is the number of copies of the corresponding allele in the multilocus genotype.
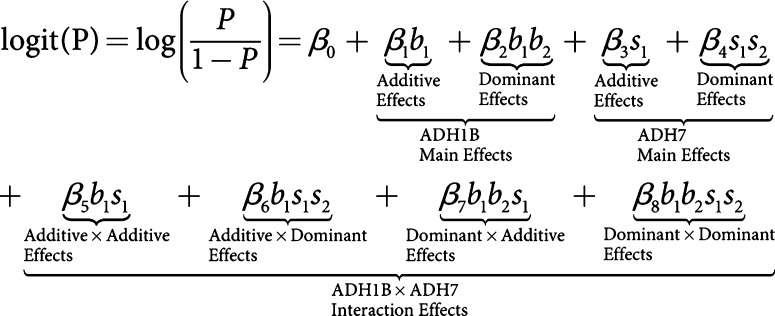
To be more general, we considered a general co-dominant model. Therefore, the logistic regression equation to test the marginal and interaction effects of ADH1B and ADH7, for example, can be written in the following form:
As opposed to the additive model, the co-dominant model contains extra terms measuring the dominant portion of the main effects for each gene and three extra sets of terms for the interaction effects. Therefore, a complete coding of the additive, dominant, and all pairwise interaction effects between these five genes totalled 50 terms.
First, we consider how the model might fit the observed data when the sample size is large (10,000 cases and 10,000 controls) and there is no deviation of the observed number of individuals for each genotype combination from that predicted by the model. This was achieved by first calculating the probability of each genotype conditional on alcoholic status, which can be easily derived from our model. For each of the 486 distinct multilocus genotypes, the probability of observing the specific genotype was multiplied by 10,000 and rounded to give the number of cases and controls for each genotype. Based on these calculated counts of genotypes for both the case and control groups, we used forward-backward stepwise logistic regression on the entire dataset to derive a model relating genotypes to disease risk.
In addition to this analysis under the very large sample scenario, we calculated the statistical power to detect a significant association between an individual term and disease risk in this model. This was done through the likelihood ratio test by comparing the full model to a reduced model formed by leaving the term out. For marginal terms, the full model consisted of the term as the single predictor, while the reduced model was the null model consisting of no predictors. For interaction terms between two genes, the reduced model consisted of all marginal terms of these genes, while the interaction term of interest was added for the full model.
Results
Model Parameter Inference
The values reported in the literature for the kinetic and yearly ethanol intake parameters provided a good model fit, with the exception of the vmax value for ALDH2∗1. These values are listed in table 1. The maximum likelihood estimates for ALDH2∗1 vmax and the sigmoid function parameters are shown in table 3. The optimized value for ALDH2∗1 vmax was 3.8, just under twice the reported value [4]. Because no margin of error was reported for ALDH2∗1 vmax, it is unclear whether this value is realistic.
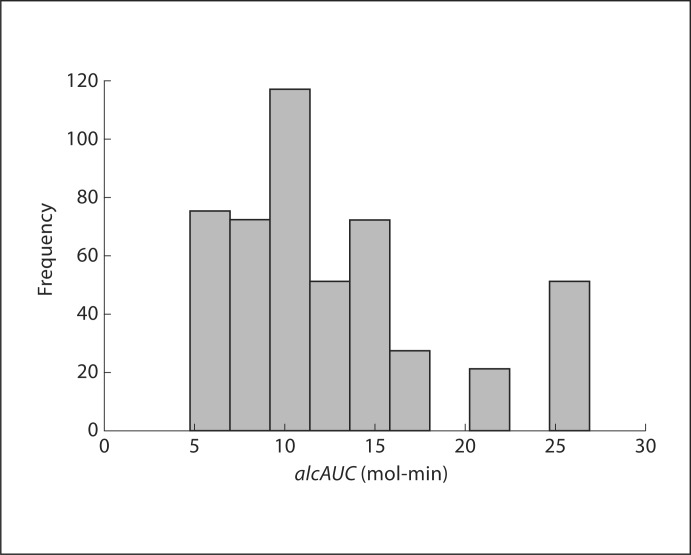
Figure 3 shows the distribution of alcAUC, predicted by the model in the population, if each genotype has the same probability of being observed, which ranges from 4.7698 mol-min to 26.8852 mol-min. Most genotypes have a lower alcAUC; however, some genotypes have a high alcAUC over 20 mol-min, while other genotypes have an even higher alcAUC with over 25 mol-min. We assume individuals with these genotypes are at a higher risk for developing AD.
Fig. 3.
alcAUC distribution in all multilocus genotypes.
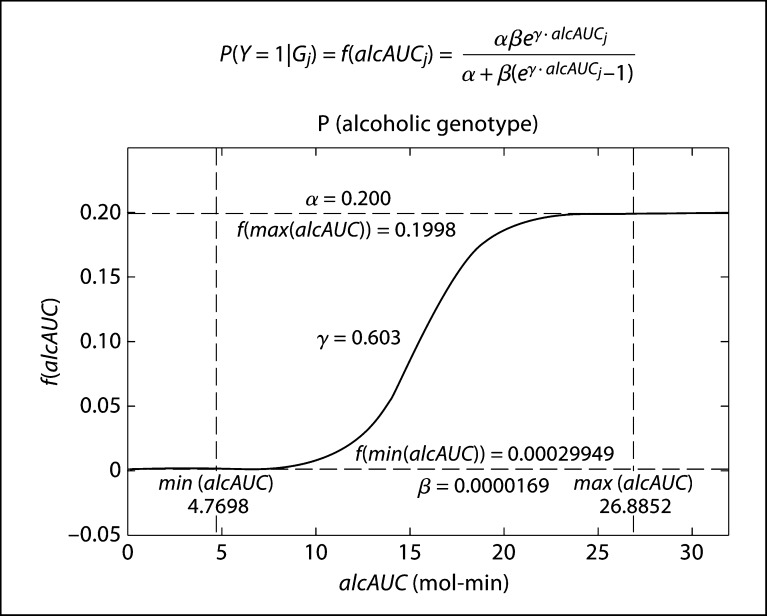
The optimized parameters for the sigmoid function (fig. 4) are α = 0.200, β = 1.69 × 10−5, and γ = 0.603. This can be intuitively interpreted such that the baseline probability of anyone becoming an alcoholic is close to zero, at 0.002%, while the maximum probability of a person with a certain genotype becoming an alcoholic is 20.0%. This model predicts that the probability of someone with the minimum alcAUC value of 4.7698 mol-min being an alcoholic is approximately 0.03%, while this probability rises to 19.98% for someone with the maximum alcAUC value of 26.8852 mol-min, for an overall prevalence of 1.18% in East Asians.
Fig. 4.
Sigmoid function.
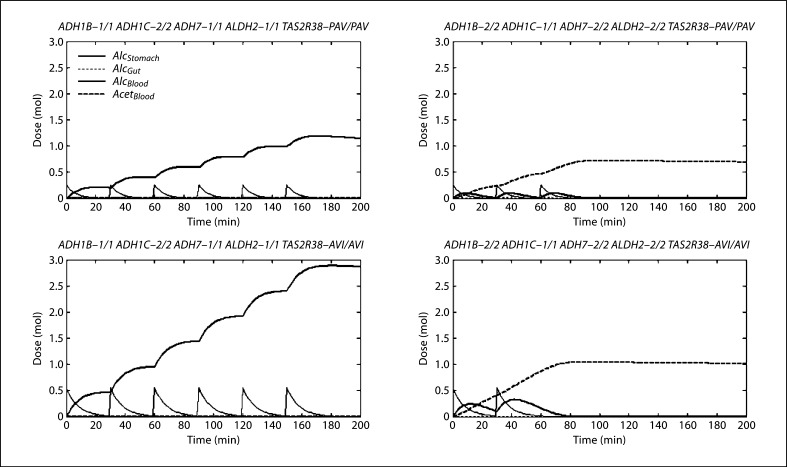
Figure 5 shows a few sample profiles during and after a 3-hour drinking period, which represent extreme genotypes. Although the magnitudes of each substance level are larger for larger drink portions, those with the non-protective form have similar profiles, characterized by rising blood alcohol levels throughout the drinking period with the maximum six drinks taken. Despite differences in magnitude, those with the protective form also have similar profiles; although blood acetaldehyde rises dramatically, the blood alcohol levels, resulting from both the standard and larger drink portions, are not as high as for the non-protective genotype. Fewer drinks were also taken. Therefore, it appears that the metabolic genes have a greater impact. However, while individuals taking larger drinks consumed more ethanol with each drink, they only took two total drinks, compared with three drinks in individuals with the same metabolic genotype taking standard drinks. A doubling of the drink portion does not correspond to a doubling in the area under the blood alcohol curve. Therefore, the model predicts that the taste receptor genes might interact with the metabolic genes to affect the risk of becoming an alcoholic.
Fig. 5.
Ethanol-acetaldehyde profiles. These profiles were chosen because they represent extreme genotypes. The left column represents the putative non-protective form of all the metabolism genes, while the right column represents the putative protective multilocus genotype. The top represents the ancestral TAS2R38 genotype, consuming standard drinks, while the bottom represents the derived TAS2R38 genotype, consuming larger drinks. Each spike in stomach alcohol represents the consumption of a drink.
Comparison between Predicted and Inferred Haplotype/Genotype Frequencies
The predicted ADH1C-ADH1B haplotype frequencies and the ALDH2 genotype frequencies based on the fitted model are very close to the observed frequencies in the literature (table 2), suggesting that the proposed mechanistic model provides a plausible biological interpretation for an individual's susceptibility to AD.
Logistic Regression-Based Analysis
For a very large sample size, i.e. 10,000 cases versus 10,000 controls, the fitted coefficients and the significance for each term in the final logistic regression model are shown in table 4. ADH1B, ALDH2, and TAS2R38 are all marginally significant, exhibiting both additive and dominant effects, although the additive effects are stronger for all three genes. ADH1B appears to have the greatest effect, followed by ALDH2, and then TAS2R38. The estimates for the additive effects of ADH1B and ALDH2 are positive, alluding to the fact that each copy of ADH1B∗1 and ALDH2∗1 increases the susceptibility to AD, while the estimate for the additive effect of TAS2R38 is negative, indicating the protective nature of the TAS2R38∗1 (PAV) allele. The estimates for the dominant effects of all three genes are all negative, indicating that the log-odds of AD for heterozygotes of these genes are less than predicted by additive effects alone. Therefore, the model predicts that the protective alleles (ADH1B∗2, ALDH2∗2, and TAS2R38∗1) are dominant for these genes.
Table 4.
Logistic regression results
| Term | β | SE | p value |
|---|---|---|---|
| Intercept | −0.94 | 0.08 | 1.69 × 10−35 |
| b1 | 1.84 | 0.16 | 2.20 × 10−30 |
| b1:b2 | −0.69 | 0.09 | 1.59 × 10−35 |
| 11 | 1.15 | 0.13 | 1.03 × 10−19 |
| l1:l2 | −0.72 | 0.09 | 8.69 × 10−17 |
| t1 | −0.95 | 0.03 | 3.51 × 10−201 |
| t1:t2 | −0.49 | 0.03 | 6.07 × 10−63 |
| b1:c1:c2 | −0.11 | 0.03 | 3.77 × 10−4 |
| b1:b2:c1 | −0.23 | 0.44 | 1.94 × 10−9 |
| b1:l1 | −0.77 | 0.11 | 1.09 × 10−11 |
| b1:l1:l2 | 0.32 | 0.07 | 8.39 × 10−7 |
| b1:b2:l1 | 0.67 | 0.06 | 6.41 × 10−32 |
| b1:t1 | −0.53 | 0.05 | 4.20 × 10−29 |
| b1:t1:t2 | 0.36 | 0.04 | 1.04 × 10−23 |
| b1:b2:t1:t2 | −0.19 | 0.02 | 1.31 × 10−19 |
| c1:c2:t1:t2 | 0.21 | 0.03 | 1.32 × 10−12 |
| l1:l2:t1:t2 | 0.16 | 0.04 | 4.75 × 10−5 |
The interaction effect, whose coefficient estimate is highest in magnitude, is in bold. All other terms with coefficient estimates greater in magnitude are also in bold.
Though less influential than the marginal effects, the model also predicts all possible pairwise interactions among these three genes. The interaction between ADH1B and ALDH2 appears to have the largest effect. Because multiple interaction terms are significant for each gene pair, the interpretation is somewhat complex: for ADH1B and ALDH2, while each copy of the susceptible allele increases the log-odds of AD, the combination of susceptible alleles at both genes is less severe than expected by considering the genes individually. Each copy of ALDH2∗1 further exacerbates the log-odds of disease for ADH1B heterozygotes, while each copy of ADH1B∗1 further exacerbates the log-odds of disease for ALDH2 heterozygotes. For ADH1B and TAS2R38, while the first alleles of these genes have competing effects, the protective effect of TAS2R38∗1 overtakes the susceptibility effect of ADH1B∗1, resulting in an overall protective effect beyond the individual effects of the two genes. Each copy of ADH1B∗1 further exacerbates the log-odds of disease for TAS2R38 heterozygotes, though the effect is less severe for double heterozygotes. For double heterozygotes of ALDH2 and TAS2R38, the log-odds of disease is slightly higher than expected by considering the two genes individually.
Although it is not marginally significant, the model predicts interaction effects between ADH1C and ADH1B and TAS2R38, the other two genes which affect alcohol levels. Being heterozygous for ADH1C seems to dampen the exacerbating effect of ADH1B∗1, while it further exacerbates the log-odds of AD for TAS2R38 heterozygotes. Each copy of ADH1C∗1 further protects against AD in ADH1B heterozygotes. The model predicts no marginal effects for ADH7, nor interactions with other genes.
The power to detect each term in various sample sizes is shown in online suppl. table 1 (for all online suppl. material, see www.karger.com/doi/10.1159/000317056). There is essentially no power (<30%) to detect marginal effects of ADH7 or interaction effects between ADH7 and the other genes in sample sizes up through 20,000, which is much higher than the sample sizes used in typical case-control studies. This suggests that the model does not predict these effects, which is consistent with our regression results, since none of these terms were found to be significant. All other terms with such low power were found to be insignificant in the regression results as well, with one exception, namely b1:c1:c2. Conversely, a few terms with high power (>80%) at a sample size of 20,000 were not significant in the regression results: b1:b2:c1:c2, b1:b2:l1:l2, b1:b2:t1, and l1:l2:t1. However, other interaction terms for ADH1B and ADH1C, ADH1B and ALDH2, ADH1B and TAS2R38, and ALDH2 and TAS2R38 remained significant, compensating for the previously mentioned insignificant terms, respectively, and suggesting pairwise interactions among these genes overall. The exact nature of these interactions merely remains unclear. Additionally, several ADH1C terms, including all marginal terms, all interaction terms with ALDH2, and all but one interaction term with TAS2R38, show high power at a sample size of 20,000, but were not significant in the logistic regression results. We suspect this is due to multicollinearity between ADH1C and ADH1B.
Overall, the additive component of TAS2R38 has the highest power at the lowest sample sizes of all the terms, followed by the additive component of ADH1B and both marginal terms for ALDH2. At mid-level sample sizes (2,000–5,000), typical of association studies, there is high power to detect these marginal terms and both marginal terms for ADH1C, while there is modest (>50%) power to detect the dominant components of ADH1B and TAS2R38. Of all the interaction terms, those between ADH1B and ALDH2 (ADH1B × ALDH2) have the highest power at the lowest sample sizes, with high power at sample sizes as low as 500. At this sample size, we start to have modest power to detect ADH1B × TAS2R38, followed by ALDH2 × TAS2R38, and ADH1C × TAS2R38, with small gains in sample size. With mid-level sample sizes, there is high power to detect all these interactions. ADH1C × ALDH2 and ADH1B × ADH1C are detectable, but only at very high sample sizes, while interactions with ADH7 are barely detectable at all. This suggests that in a typical association study of AD in East Asians, ADH1B, ADH1C, ALDH2, and TAS2R38 should be found marginally significant, while interactions between ADH1B and ALDH2, ADH1B and TAS2R38, ALDH2 and TAS2R38, and ADH1C and TAS2R38 should be found significant, if our model accurately describes the molecular mechanism of AD, and if dependencies among these genes are ignored.
Model Limitations
Although our model yielded a good fit to the observed data, it is clearly too simplistic to expect that this model appropriately models many complex biological processes leading to AD. For example, we did not include gender, weight, or the effects of food consumption in the model, primarily because we hoped to predict the phenotypic variation resulting from genetic variation in the metabolic and taste receptor genes, rather than from variations in other factors. Practically, many of the model components and parameter values which we borrowed from the literature were estimated based on a 70-kg fasting man. Therefore, we did not want to extrapolate our model to more general cases. Further factors we did not explore in the model were the diuretic effects of ethanol on the kidney, since doing so would have required a much more detailed account of the nephritic system. Additional components, such as the levels of vasopressin and a model of its relationship to ethanol, would have had to be included. This would have necessitate the inclusion of many more parameters, none of which we had. Furthermore, our limited gene frequency data would not have given us the d.f. to estimate these parameters, and such model complexity is hardly worthwhile for 5% of the ethanol, since approximately 95% of ingested ethanol is degraded by the liver.
Exploration of Alternative Models
Because our consumption scheme is somewhat arbitrary, we also explored alternative consumption schemes in three ways, which we define in online supplementary table 2. We first set out to determine whether the model could adequately fit the data by examining the differences in alcohol metabolism after the consumption of a single drink (scheme A). We tried two additional consumption schemes (schemes B) by varying the number of possible drinks per drinking episode and the time between these drinks: (1) three possible drinks, 60 min apart, and (2) 18 possible drinks, 10 min apart. In our original scheme, we used a blood acetaldehyde threshold of 0.5 mol; subjects will take a potential drink if their current blood acetaldehyde level is below this threshold, but will not take it if their current blood acetaldehyde level is above it. This threshold was chosen arbitrarily. However, it has been suggested that people start to experience unpleasant flushing effects and tachycardia at blood acetaldehyde levels as low as 0.0022 mol [27], and that 0.5 mol of toxic acetaldehyde in the blood (which is 226.7574 times this amount) could be fatal [28]. Therefore, we explored additional consumption schemes (schemes C) by varying this threshold for multiples of this baseline value (0.0022 mol). Preliminary analysis revealed a range of values to try. A multiple of 1 produced the highest threshold at which everybody consumed at most one drink. A multiple of 1,029 produced the lowest threshold at which everybody consumed all six drinks. Therefore, we tested these two thresholds, along with a third mid-level value closer to the original threshold: a multiple of 91, which produced the highest threshold at which everybody consumed less than six drinks.
We found the optimal set of parameters for each of these alternative consumption schemes and calculated the resulting AD prevalence and log-likelihood, which are also shown in online supplementary table 2. The frequencies for alcoholics, which are predicted by each model and form the basis for the log-likelihood, are shown in online supplementary table 3. Scheme A has the lowest log-likelihood and the poorest fit, with predicted alcoholic frequencies identical to the observed frequencies for controls. This indicates that one cannot accurately predict the alcoholic status from the genotype at these genes based on the consumption of a single drink, most likely because this leaves out the adaptive consumption mechanism by which these genes probably operate. Schemes B1 and B2, however, have almost identical log-likelihoods to the original consumption scheme, with predicted frequencies very close to those of the original consumption scheme and the observed frequencies of alcoholics. This suggests that our model captures the general relationship between AD susceptibility and alcohol metabolism regulated by a number of genes. In fact, the total area under the blood alcohol curve under these varying consumption schemes provides a good proxy for alcohol consumption, thus AD risk. Similarly, scheme C2, which includes a mid-level multiple of the acetaldehyde threshold closest to that of the original scheme, has a log-likelihood very close to that of the original consumption scheme, with similar predicted frequencies. Schemes C1 and C3, however, which have more extreme multiples of the acetaldehyde threshold, have lower log-likelihoods, with predicted frequencies that diverge from those of the original scheme and those that are observed for alcoholics. This suggests that a mid-range of the acetaldehyde threshold is more robust and supports the original scheme as an appropriate model.
Discussion
In this paper, we attempt to develop a mechanistic model to describe how an individual's genotype affect ethanol metabolism after alcohol consumption, preference for drinking, and drinking behavior over both short and long terms. This model can be used to predict the probability that people with a particular genotype combination tend to become alcoholics. With limited data, we were able to connect previous models of ethanol metabolism based on time-series data with genetic and kinetic information from the literature in order to formulate the pharmacokinetic component of our model. We have discussed the appropriateness of our consumption scheme, which, when combined with the pharmacokinetic component, predicts the interplay between drinking behavior, ethanol and acetaldehyde levels over time in different tissue components of the body in individuals with different genotypes.
Thus, our model is composed of two components: the behavioral component, illustrated by our consumption scheme, and the pharmacokinetic component, which can be subdivided further into the kinetics of individual enzymes and the flow of ethanol and acetaldehyde between tissues. A model with so many layers and parameters may appear complex, especially without substantial data of our own to justify it. Therefore, one might wonder whether simpler, alternative models would suffice.
For example, there are many different types of kinetic models. Reactions that proceed at a constant rate, for instance, are said to exhibit zero-order kinetics. Other reactions may proceed at a rate proportional to the concentration of reactants, under first-order kinetics. Higher-order models are more complex. Michaelis-Menten kinetics is another type of kinetics which specifically models enzyme kinetics. Under this model, an enzyme is able to catalyze a reaction more quickly if there is a greater concentration of substrate, similar to first-order kinetics, because there is a greater chance that a free enzyme molecule and a free substrate molecule will encounter each other and form the complex necessary for the reaction to take place. However, as more enzyme molecules leave the free state and bind to substrate molecules, additional free substrate molecules become decreasingly helpful at increasing the rate of the reaction, since less and less free enzyme is available. While the reaction still speeds up, it does so at a slower and slower rate, until the enzyme is completely saturated with substrate, at which point the enzyme has reached its maximal rate. Therefore, it is non-linear in nature. This may seem overly complicated; however, it is a standard model in the field of kinetics, and the simplest model of enzyme kinetics. Moreover, other researchers [4] have experimentally shown that ADH and ALDH2 enzymes operate under this model, which is why we have chosen to incorporate this one in particular.
The division of our model into separate compartments corresponding to different tissues adds another layer of complexity. Many biological phenomena are elegantly modeled by non-compartmental models which treat each tissue uniformly. The tissue specificity of the expression of ethanol metabolism genes and the differential distribution of ethanol and acetaldehyde among different tissues, however, necessitate the separation of key tissues. Therefore, we are unable to consolidate the tissues into a single compartment and simplify the model in this manner. This separation requires that we model the flow of ethanol and acetaldehyde between tissues. The rate of the flow of ethanol from the stomach and gut into the blood is specified by the conventional linear term to model simple diffusion, the simplest mode of liquid transport across a permeable membrane. The flow of ethanol from the stomach into the gut is considerably more complex; however, there is experimental support for this portion of the model, and without time-series data of our own to test simpler alternative models, we must trust the experts. The elimination rates of ethanol and acetaldehyde in the urine and breath are perhaps the most questionable. Although alternative models likely describe the underlying elimination mechanism more accurately, we do not know what these alternatives are, for we did not find any in the literature that specifically pertain to alcohol. Without pertinent data of our own, we cannot postulate alternatives ourselves. Therefore, we hope more experimental research will be done in this area to construct explicit mechanistic models of alcohol elimination. Due to the complexities of the nephritic system, however, we doubt that such alternative models would be simpler than the ones proposed here.
The consumption component of our model admittedly has the least amount of support in the literature, for while the interplay of behavior and genetics in the pathogenesis of disease is often qualitatively described, it is rarely explicitly modeled. For this reason, we thought it was necessary to analyze the sensitivity of our model to variation in consumption scheme parameters. As already mentioned in the Results, however, the sensitivity analysis showed that our original choice of parameters is most robust. Furthermore, it showed that a simpler consumption scheme of a single drink does not adequately describe the behavior mechanism, for it fails to incorporate the negative feedback loop of acetaldehyde buildup on further alcohol consumption. Consequently, our consumption scheme is not unnecessarily complicated for a model of something as complex as behavior.
In general, we emphasize that our model is not statistical but mechanistic. Although it may appear complex and certain details remain uncertain, as discussed above, we believe it is the simplest model that reasonably reflects the mechanism underlying the development of AD.
Our approach is strikingly similar to the method posed by Lin et al. [6,7], which exemplifies the functional mapping approach described by Ahn et al. [8] to examine the effects of genetic variation on drug response. Both methods attempt to relate haplotypes to the effect of a substance on quantitative traits. They also both try to offer some explanation for the mechanism behind the genetic interactions involved by incorporating similar, though distinct, kinetic models, whose parameters have different values for each haplotype. However, there are critical differences.
The sets of values which are known and unknown are contrary in the two methods. In their method, Lin et al. [6,7] observed the drug response profile for each subject and used it to estimate the values of the kinetic parameters for each diplotype in order to predict whether there are differences among the diplotypes in terms of their effect on drug response. The approach of using an observed dynamic trait profile to estimate genotype-specific parameter values, then test whether there are significant differences in these values, is characteristic of functional mapping in general [8]. In our method, we already know that there are differences among the haplotypes for each individual gene, for they encode enzymes or receptors with different properties. Variants of each enzyme metabolize ethanol or acetaldehyde at different rates, while variants of the taste receptor affect preference for alcohol, and thus affect consumption behavior. We also know the nature and the values (within a margin of error) of the parameters corresponding to each haplotype of each gene, which are based on previous experimental work by other researchers [4,5,12,23]. Consequently, we know exactly how different haplotypes are within the same gene in terms of their effect on the ethanol-acetaldehyde profile, when each gene is considered separately. Each gene functions as a separate unit (with the exception of ADH1B and ADH1C which form a heterodimer); however, their combined effect does not. Although we know that each joint haplotype among all the genes will have a different effect on the ethanol-acetaldehyde profile, we do not know what this effect will be, nor do we know the contribution of genetic variation within one gene, relative to another gene. Therefore, we use prior knowledge about how haplotype variation in each individual gene affects the ethanol-acetaldehyde profile separately to predict the ethanol-acetaldehyde profile which results from the interaction. Hence, our approaches are reversed to fulfill a different purpose.
Lin et al. [6,7] incorporated a kinetic model into their approach, which enabled them to give some mechanistic interpretation. However, it is still primarily a general statistical model that requires no information about the system it is applied to a priori, and is intended to detect statistical associations and interactions among genes at the haplotype level. The kinetic model is used because they believe drug response follows this pattern, much like a straight line is used in linear regression. Therefore, their ability to comment on pharmacokinetics is a side effect of the interpretation of the model parameters. Conversely, our model is mechanistic. It is not intended to predict whether genes interact statistically, but to illustrate how they interact biologically. Being mechanistic, it specifically reflects alcohol consumption, ethanol and acetaldehyde metabolism, and the genes involved. Thus, while our general approach can be applied to other dynamic phenotypes, the specific model must be changed. The approach of Lin et al. [6,7] is general, so it has the advantage that it can be applied blindly to any system without having to change it. However, the mechanistic information it provides is limited. In particular, when gene-gene interactions are considered in their approach, a single set of parameter values is estimated for each joint haplotype of the gene pair [7]. These kinetic values are informative if the peptides encoded by the two genes function together as a single unit. This happens to be the case for the adrenergic receptors β1AR and β2AR that Lin et al. [6,7] chose to apply their method to, as they heterodimerize. If they function as separate units, however, the kinetic values reflect the general joint effect, but not the biological basis of how they interact to produce this effect.
Thus, their approach [7] is extremely useful for detecting statistical interactions among (receptor) genes underlying dynamic quantitative traits such as drug response at the haplotype level. However, it may best be used as a first-pass approach to detect the existence of gene-gene interactions when nothing is known about a system, and to get a glimpse of the possible nature of these interactions. Our approach is best utilized when you know how individual genes function as separate units and how genetic variation within them affects their function, but want to explore how they interact to produce a joint effect on dynamic quantitative traits. The idea is not necessarily to predict statistical interactions, but to demonstrate the biological basis of these interactions. This enables us to identify which haplotypes of which genes have the largest relative effect at different points in a dynamic system, particularly during disease pathogenesis. To our knowledge, this is the first such report in the literature.
We also developed a method to relate this molecular-level information to population-level information, by incorporating observed gene frequencies of controls into the model and then comparing the predicted alcoholic gene frequencies to those observed in the literature. When our model is fitted to the observed case-control data for East Asians, we find a good agreement between the predicted and the observed haplotype/genotype frequencies available for ADH1C-ADH1B and ALDH2. The estimated kinetic parameters, which were assumed in this comparison, were all within the margins of error reported in the literature, with the exception of ALDH2∗1 vmax, for which no margin of error was reported. This suggests that our model describes a plausible mechanism for the development of AD in the East Asians in regard to ADH1B, ADH1C, and ALDH2. Due to the lack of frequency data on alcoholics for ADH7 and TAS2R38, it is inconclusive whether our model fits the data with respect to these genes.
Using our logistic regression-based analysis, we also showed that our model implicates genes in AD and predicts statistical interactions between them, and demonstrated their relative importance and our power to detect them. The model does not predict statistical interactions among these genes per se, nor is this its primary goal, as it is in the method by Lin et al. [7]. We conducted the logistic regression-based analysis merely to show how the biological interactions illustrated in the model correspond to, and imply, statistical interactions, which might be detected by a typical GWAS. A regression model very similar to the one used by Lin et al. [7] is used to describe the statistical nature – additive or dominant – of these effects. The model implicates ADH1B, ALDH2, and TAS2R38 as well as all pairwise interactions among them in AD. The marginal effects of ADH1B and ALDH2 are not surprising, since ADH1B∗2 and ALDH2∗2 are known to protect against AD; however, their predicted statistical interaction contradicts the widely held belief that their effects are independent. It is also the first time, to our knowledge, that interactions have been predicted between TAS2R38 and these genes. The nuances of these interactions are complex, due to the many significant interaction terms for each gene pair. Furthermore, their significance is sensitive to multicollinearity and the assumptions made about the kinetics of heterozygotes, so interpretations of the nature of these interactions remain unclear. However, it appears that the protective effect of TAS2R38∗1 somewhat overrides the risk conferred by ADH1B∗1, similar to our hypothesis; individuals are not likely to develop AD if they rarely drink, despite any metabolic predisposition they may have.
An interaction between ADH1B and ADH1C was found to be significant; however, this is undetectable at sample sizes typical of association studies. In general, we believe the lack of significance of ADH1C is due to dependency on ADH1B, and posit that linkage disequilibrium between the two genes is a likely factor.
The fact that our model does not predict any effects of ADH7 goes against claims that its expression levels are related to AD, or that it somehow interacts with ADH1B. It appears that, based on our model, the alcohol in the stomach simply empties too quickly for ADH7 to have much of an impact on alcohol or acetaldehyde levels and, by extension, on AD. This could be the case, but it may also be that this part of the model is flawed, or that we did not incorporate ADH7 into the model correctly. For instance, we did not have time-series data to validate the speed of gastric emptying, but instead relied on previous models. Also, we did not have gene expression data to include in the model. Lastly, we did not have ADH7 ‘genotype’ frequency information for alcoholics to verify the model fit for ADH7. For these reasons, we caution not to take our model, or the statistical interactions it predicts, as truth, but to accept it as a good starting point for such integrative analyses, considering the limited data available – a hint at what could be done in the future if more data were available. Due to these limitations, the significance of our work is not the specific model and its implications for AD we have offered, but the general approach we have presented.
Molecular-level phenomena are not separate from population-level observations, so we must relate the two. There are many different types of data generated: genotypes (including multilocus genotypes), gene expression data (many in time series) in different tissues, kinetic data, metabolite levels (also many in time series), other endophenotypes, and disease status. Therefore, it seems logical that we should integrate as many of these as we can in our analyses, utilizing as much information possible to gain a fuller understanding of a system. The problem is that all pertinent types of data are rarely available for the same system. These holes in the data, as we have already mentioned, posed the greatest challenge for our present analysis. The lack of frequency data on all of these genes, individually and jointly, for alcoholics reflects how little work has been done on gene-gene interactions in AD. Since AD is a complex disease, expected to be caused by the interaction of many genes which may contribute little to the disease individually, such frequency data should be generated and made more widely available. This would enable the inclusion of more genes in our model in the future and the estimation of more model parameters. In general, there should be more gene frequency information available for individuals with particular diseases to compare it with the frequency distribution of controls. Gene expression data, which could have easily been incorporated into our model, are also lacking for these genes. However, this information would be useful, since these genes are expressed at different levels in different tissues, especially for ADH7, whose gene expression level is thought to affect susceptibility to AD, although its differential gene expression has not been associated with a particular marker. Determining an eQTL for the expression of ADH7 would be a significant breakthrough in the study of AD and could be a major component of a future model. Finding all necessary kinetic parameters for our model was particularly difficult; they were often available only for a single (unspecified) allele, with no margins of error stated, while others were only described qualitatively as ‘inactive’, forcing us to infer the values. More work should be dedicated to determining the kinetic parameters associated with different genes, with a particular emphasis on the kinetic parameters for different alleles, since many genes encode enzyme subunits; thus, these kinetic values are the link for how genetic variation leads to phenotypic variation. It would also be useful to obtain overall kinetic estimates of heterozygotes and of multiple genes simultaneously, since subunits encoded by multiple genes may join to form a single enzyme. This would provide further insight into the mode of inheritance for each gene and the interaction among genes, rather than making assumptions about them. The generation and availability of such information would certainly aid in the improvement of our current model. However, the integration of these data into a single database would help facilitate this type of analysis for other diseases as well. We hope our current analysis serves as a prototype for such future analyses.
Supplementary Material
Supplemental Tables
Acknowledgements
We would like to acknowledge the ‘Yale University Biomedical High Performance Computing Center’ and NIH grant RR19895, which funded the instrumentation. This work was supported in part by NSF grant DMS-0714817 (to H.Z.) and NIH grants R01 AA009379 from the NIAAA (to K.K.K.), T15 LM07056 from the NLM (to P.M.), GM59507 (to H.Z.), and a pilot grant from the Yale Pepper Center P30AG021342 (to H.Z.).
References
- 1.Chen CC, Lu RB, Chen YC, Wang MF, Chang YC, Li TK, Yin SJ. Interaction between the functional polymorphisms of the alcohol-metabolism genes in protection against alcoholism. Am J Hum Genet. 1999;65:795–807. doi: 10.1086/302540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Osier MV, Lu RB, Pakstis AJ, Kidd JR, Huang SY, Kidd KK. Possible epistatic role of ADH7 in the protection against alcoholism. Am J Med Genet B Neuropsychiatr Genet. 2004;126B:19–22. doi: 10.1002/ajmg.b.20136. [DOI] [PubMed] [Google Scholar]
- 3.Wilkinson PK, Sedman AJ, Sakmar E, Kay DR, Wagner JG. Pharmacokinetics of ethanol after oral administration in the fasting state. J Pharmacokinet Biopharm. 1977;5:207–224. doi: 10.1007/BF01065396. [DOI] [PubMed] [Google Scholar]
- 4.MacDonald AJ, Rostami-Hodjegan A, Tucker GT, Linkens DA. Analysis of solvent central nervous system toxicity and ethanol interactions using a human population physiologically based kinetic and dynamic model. Regul Toxicol Pharmacol. 2002;35:165–176. doi: 10.1006/rtph.2001.1507. [DOI] [PubMed] [Google Scholar]
- 5.Umulis DM, Gürmen NM, Singh P, Fogler HS. A physiologically based model for ethanol and acetaldehyde metabolism in human beings. Alcohol. 2005;35:3–12. doi: 10.1016/j.alcohol.2004.11.004. [DOI] [PubMed] [Google Scholar]
- 6.Lin M, Aquilante C, Johnson JA, Wu R. Sequencing drug response with HapMap. Pharmacogenomics J. 2005;5:149–156. doi: 10.1038/sj.tpj.6500302. [DOI] [PubMed] [Google Scholar]
- 7.Lin M, Li H, Hou W, Johnson JA, Wu R. Modeling sequence-sequence interactions for drug response. Bioinformatics. 2007;23:1251–1257. doi: 10.1093/bioinformatics/btm110. [DOI] [PubMed] [Google Scholar]
- 8.Ahn K, Luo J, Berg A, Keefe D, Wu R: Functional mapping of drug response with pharmacodynamic-pharmacokinetic principles. Trends Pharmacol Sci 2010, Epub ahead of print. [DOI] [PubMed]
- 9.Edenberg H. Alcohol dehydrogenases. In: Guengerich F, editor. Comprehensive Toxicology. vol 3. New York: Pergamon; 1997. pp. 119–131. [Google Scholar]
- 10.Thomasson HR, Edenberg HJ, Crabb DW, Mai XL, Jerome RE, Li TK, Wang SP, Lin YT, Lu RB, Yin SJ. Alcohol and aldehyde dehydrogenase genotypes and alcoholism in Chinese men. Am J Hum Genet. 1991;48:677–681. [PMC free article] [PubMed] [Google Scholar]
- 11.Crabb DW, Edenberg HJ, Bosron WF, Li TK. Genotypes for aldehyde dehydrogenase deficiency and alcohol sensitivity. The inactive ALDH2(2) allele is dominant. J Clin Invest. 1989;83:314–316. doi: 10.1172/JCI113875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee SL, Chau GY, Yao CT, Wu CW, Yin SJ. Functional assessment of human alcohol dehydrogenase family in ethanol metabolism: significance of first-pass metabolism. Alcohol Clin Exp Res. 2006;30:1132–1142. doi: 10.1111/j.1530-0277.2006.00139.x. [DOI] [PubMed] [Google Scholar]
- 13.Ashmarin IP, Danilova RA, Obukhova MF, Moskvitina TA, Prosorovsky VN. Main ethanol metabolizing alcohol dehydrogenases (ADH I and ADH IV): biochemical functions and the physiological manifestation. FEBS Lett. 2000;486:49–51. doi: 10.1016/s0014-5793(00)02229-8. [DOI] [PubMed] [Google Scholar]
- 14.Edenberg HJ, Xuei X, Chen HJ, Tian H, Wetherill LF, Dick DM, Almasy L, Bierut L, Bucholz KK, Goate A, Hesselbrock V, Kuperman S, Nurnberger J, Porjesz B, Rice J, Schuckit M, Tischfield J, Begleiter H, Foroud T. Association of alcohol dehydrogenase genes with alcohol dependence: a comprehensive analysis. Hum Mol Genet. 2006;15:1539–1549. doi: 10.1093/hmg/ddl073. [DOI] [PubMed] [Google Scholar]
- 15.Edenberg HJ, Foroud T. The genetics of alcoholism: identifying specific genes through family studies. Addict Biol. 2006;11:386–396. doi: 10.1111/j.1369-1600.2006.00035.x. [DOI] [PubMed] [Google Scholar]
- 16.Dick DM, Foroud T. Candidate genes for alcohol dependence: a review of genetic evidence from human studies. Alcohol Clin Exp Res. 2003;27:868–879. doi: 10.1097/01.ALC.0000065436.24221.63. [DOI] [PubMed] [Google Scholar]
- 17.Osier M, Pakstis AJ, Kidd JR, Lee JF, Yin SJ, Ko HC, Edenberg HJ, Lu RB, Kidd KK. Linkage disequilibrium at the ADH2 and ADH3 loci and risk of alcoholism. Am J Hum Genet. 1999;64:1147–1157. doi: 10.1086/302317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Han Y, Oota H, Osier MV, Pakstis AJ, Speed WC, Odunsi A, Okonofua F, Kajuna SL, Karoma NJ, Kungulilo S, Grigorenko E, Zhukova OV, Bonne-Tamir B, Lu RB, Parnas J, Schulz LO, Kidd JR, Kidd KK. Considerable haplotype diversity within the 23kb encompassing the ADH7 gene. Alcohol Clin Exp Res. 2005;29:2091–2100. doi: 10.1097/01.alc.0000191769.92667.04. [DOI] [PubMed] [Google Scholar]
- 19.Baraona E, Yokoyama A, Ishii H, Hernandez-Munoz R, Takagi T, Tsuchiya M, Lieber CS. Lack of alcohol dehydrogenase isoenzyme activities in the stomach of Japanese subjects. Life Sci. 1991;49:1929–1934. doi: 10.1016/0024-3205(91)90295-m. [DOI] [PubMed] [Google Scholar]
- 20.Yin SJ, Liao CS, Wu CW, Li TT, Chen LL, Lai CL, Tsao TY. Human stomach alcohol and aldehyde dehydrogenases: comparison of expression pattern and activities in alimentary tract. Gastroenterology. 1997;112:766–775. doi: 10.1053/gast.1997.v112.pm9041238. [DOI] [PubMed] [Google Scholar]
- 21.Birley AJ, James MR, Dickson PA, Montgomery GW, Heath AC, Whitfield JB, Martin NG. Association of the gastric alcohol dehydrogenase gene ADH7 with variation in alcohol metabolism. Hum Mol Genet. 2008;17:179–189. doi: 10.1093/hmg/ddm295. [DOI] [PubMed] [Google Scholar]
- 22.Ramchandani VA, Bosron WF, Li TK. Research advances in ethanol metabolism. Pathol Biol (Paris) 2001;49:676–682. doi: 10.1016/s0369-8114(01)00232-2. [DOI] [PubMed] [Google Scholar]
- 23.Duffy VB, Davidson AC, Kidd JR, Kidd KK, Speed WC, Pakstis AJ, Reed DR, Snyder DJ, Bartoshuk LM. Bitter receptor gene (TAS2R38), 6-n-propylthiouracil (PROP) bitterness and alcohol intake. Alcohol Clin Exp Res. 2004;28:1629–1637. doi: 10.1097/01.ALC.0000145789.55183.D4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.American Academy of Family Physicians, American Psychiatric Association . Work Group on DSM-IV-PC.: Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition: Primary Care Version, ed 1. Washington, DC: American Psychiatric Association; 1995. [Google Scholar]
- 25.Cheung KH, Osier MV, Kidd JR, Pakstis AJ, Miller PL, Kidd KK. ALFRED: an allele frequency database for diverse populations and DNA polymorphisms. Nucleic Acids Res. 2000;28:361–363. doi: 10.1093/nar/28.1.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nelder JA, Mead R. A simplex method for function minimization. The Computer Journal. 1965;7:308–313. [Google Scholar]
- 27.Lindros KO. Human blood acetaldehyde levels: with improved methods, a clearer picture emerges. Alcohol Clin Exp Res. 1983;7:70–75. doi: 10.1111/j.1530-0277.1983.tb05414.x. [DOI] [PubMed] [Google Scholar]
- 28.Karch SB. Drug Abuse Handbook. ed 2. Boca Raton: CRC Press/Taylor & Francis; 2007. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Tables