Optimization Methods for Spiking Neurons and Networks

Abstract

Spiking neurons and spiking neural circuits are finding uses in a multitude of tasks such as robotic locomotion control, neuroprosthetics, visual sensory processing, and audition. The desired neural output is achieved through the use of complex neuron models, or by combining multiple simple neurons into a network. In either case, a means for configuring the neuron or neural circuit is required. Manual manipulation of parameters is both time consuming and non-intuitive due to the nonlinear relationship between parameters and the neuron’s output. The complexity rises even further as the neurons are networked and the systems often become mathematically intractable. In large circuits, the desired behavior and timing of action potential trains may be known but the timing of the individual action potentials is unknown and unimportant, whereas in single neuron systems the timing of individual action potentials is critical. In this paper, we automate the process of finding parameters. To configure a single neuron we derive a maximum likelihood method for configuring a neuron model, specifically the Mihalas–Niebur Neuron. Similarly, to configure neural circuits, we show how we use genetic algorithms (GAs) to configure parameters for a network of simple integrate and fire with adaptation neurons. The GA approach is demonstrated both in software simulation and hardware implementation on a reconfigurable custom very large scale integration chip.

I. Introduction

Since the seminal work of Hodgkin and Huxley [1] many neuronal models have been developed varying both, in biological accuracy and complexity. Biologically faithful models, such as the Hodgkin–Huxley [1] and Morris–Lecar [2] models, have complex sets of equations governing the conductances of voltage-gated ion channels within the neuron membrane. These models are used to understand neuron behavior at its most basic level. Biological accuracy can be traded for computational efficiency and smaller parameter spaces. The computationally simple integrate and fire model aims to capture the most basic behavior of the neuron in a biophysical fashion, while the Izhikevich model [3] sacrifices biophysically to achieve a large number of firing modalities in an efficient manner. Modifications, such as introducing spike-induced currents [4] and a variable threshold [5], can be made to the integrate and fire model to allow for more firing types (for a review see Izhikivich [3]). The use of these models ranges from attempting to understand neural behavior at its most fundamental level to modeling vision [6], [7], audition [8], neural prosthetics [9], and robotic locomotion controllers [10]–[12].

Implementing these models as single neurons or as a circuit of multiple individual neurons poses the problem of configuring model parameters in different contexts. For example, in single neuron applications it is often desired to have as biologically faithful a model as possible, resulting in a large number of parameters to configure for the single neuron. In neural circuits, a simpler abstraction allows many more neurons to be instantiated and assembled into networks, however, this results in many more synaptic weights or other neural properties to be tuned. While the basic task for both single neurons and networks is parameter estimation, the optimal approach to do so differs.

In the single neuron case, Paninski and Pillow [4] showed that with an appropriate neuron model choice, it is possible to develop a maximum likelihood (ML) technique to determine the optimal neuron parameters that match the model’s individual spike times to measured ones. They showed that the log-likelihood function for the general integrate and fire (GIF) neuron they used was concave in shape and consequently conventional optimization methods can be used to solve for the parameters. In this paper, we extend Paninski and Pillow’s method to the Mihalas–Niebur (M–N) neuron model [5]. This is a linear integrate and fire model with a voltage-dependent threshold and spike induced currents. The varying threshold allows the model to adopt more firing modalities than models with a fixed threshold and spike-induced currents [5]. The differential equations of the model are very similar to those of the basic leaky integrate and fire neuron, resulting in a computationally efficient model.

Circuits of many individual neurons quickly become mathematically intractable and require a different optimization approach. Genetic algorithms (GAs) provide a natural choice to optimize these networks as they require no knowledge of the underlying network. They simply seek to minimize a fitness function and their randomized searching methods ensure that a large portion of the parameter space is searched. The rate of convergence has been a problem when using GAs in the past. However, it was shown in [13] and in our previous work [14], [15] that the rate of convergence may be increased by using techniques such as “behavioral memory” developed by de Garis [16] and “staged evolution” developed by Lewis [17]. GAs have previously been used as learning rules for spiking neural networks acting as classifiers [18], [19]. The work presented in this paper differs in that GAs are used to configure the dynamics of pattern generator networks whose outputs are sustained rhythmic patterns. This is discussed in Section III. The term “learning” is not used in this paper, as we feel it is more suited to the updating of network parameters such that an input is mapped to an output as in [20] and [21]. We view our work as more similar to biological development in that we are not only tuning the weights of an established network, but also determining the topology of the network and the properties of the individual neurons. To make this distinction we use the term “configuration.”

While seemingly incompatible, ML methods and GAs are complementary to each other in that ML allows configuration of neurons at a very fine level while GAs provide configuration at a coarser granularity. This allows ML and GA to potentially be used together to provide fine tuning of neural circuit outputs. First the GA could be used to configure the overall network behavior, and then ML could be used to configure the parameters that are necessary for an individual neuron within the circuit to spike at specified times. This has parallels to neural development, e.g., during the development of the spinal cord circuitry of the mouse, the neural circuits responsible for locomotion are developed in two stages [22], with the second stage of development hypothesized to begin when the motor neurons axons reach their muscle contacts and more information (in the form of target derived signals) is available for development [23], [24].

The remainder of this paper is organized as follows. First, the likelihood equations for the M–N neuron model are derived. Next, an example validating this method is shown. Section III elaborates on our previous work in the application of GAs to configuring spiking neural network parameters in software and in silico and for the configuring of network topologies. As an example network, a central pattern generator (CPG), which is used for locomotion control, is configured. The results of the application of the GA are then presented and discussed.

II. ML Method for the M–N Neuron

A. M–N Neuron Model

The M–N model [5] is a linear integrate and fire model with a voltage-dependent threshold. The equations defining the model are as follows:

$$\begin{array}{l}\frac{{dI}_j(t)}{dt}=-k_j{I}_j(t);j=1,2\\ \frac{dV(t)}{dt}=\frac{1}{C}\left(I_{\mathit{ext}}+\sum _j{I}_j(t)-G(V(t)-V_{\mathit{leak}})\right)\\ \frac{d\mathrm{\Theta }(t)}{dt}=a(V(t)-V_{\mathit{leak}})-b(\mathrm{\Theta }(t)-{\mathrm{\Theta }}_{\infty })\end{array}$$ (1)

where V(t) is the membrane potential, Θ(t) is the threshold, Θ_∞ is the steady-state threshold value, I_j are internal currents, I_ext is the external current, G is the membrane conductance, V_leak is the leak potential, and a controls the dependance of the threshold on the membrane potential and b controls the dependence of the threshold on its current value. When V(t) = Θ(t), a spike occurs and the system is updated using the following rules:

$$\begin{array}{l}{I}_j(t^{+})\leftarrow R_j\times I_j(t^{-})+A_j\\ V(t^{+})\leftarrow V_{\mathit{reset}}\\ \mathrm{\Theta }(t^{+})\leftarrow \mathit{max}({\mathrm{\Theta }}_{\mathit{reset}},\mathrm{\Theta }(t^{-}))\end{array}$$ (2)

where t⁻ is the moment just before the neuron fires and t⁺ is the moment immediately after the neuron fires. V_reset is the membrane’s post-spike reset potential, Θ_reset is the minimum allowable threshold potential. R_j and A_j specify the manner in which the spike-induced currents are updated. For instance, if R_j is zero, then the current has a constant update function, it is independent of the value of the current before the spike. Parameters R_j, A_j, V_reset, and Θ_reset can be chosen freely providing Θ_reset > V_reset.

B. ML Estimation with the M–N Model

Given an input current I_ext and a set of spike times t₁, t₂, …, t_n, we wish to find the parameters X = {G, V_reset, A1, A2, a, b, Θ_reset} which cause the model to spike at the desired times. (The parameter space is reduced by assigning Θ_∞ = Θ_reset and V_leak = V_reset). The work done by Paninski and Pillow utilized the fact that the subthreshold dynamics of the GIF neuron’s membrane potential are linear. For the M–N model, the (noiseless) membrane potential can be computed analytically to be

$$V(t)=V_{\mathit{leak}}+\frac{1}{C}{I}_{\mathit{ext}}(t)\ast e^{-\frac{G}{C}t}+\sum _j\frac{I_{j0}{e}^{-k_{j}t}}{G-{Ck}_j}+\left(V_{\mathit{reset}}-V_{\mathit{leak}}-\sum _j\frac{I_{j0}}{G-{Ck}_j}\right)e^{-\frac{G}{C}t}.$$ (3)

I_j0 is the initial condition of current I_j over a given interspike interval. When t = 0 s, the neuron has yet to spike, and consequently there are no post-spike currents and I _j0 = 0. Once the neuron spikes at time t, then the initial conditions of the post-spike currents at time t⁺ are obtained using the update rule in (2). The post-spike currents evolve with time as

$$I_j(t)=I_{j0}{e}^{-k_{j}t}.$$ (4)

The noiseless threshold is computed as

$$\begin{array}{l}\mathrm{\Theta }(t)={\mathrm{\Theta }}_{\infty }+\frac{a}{C}{I}_{\mathit{ext}}(t)\ast e^{-\frac{G}{C}t}\ast e^{-bt}\\ +\sum _j\frac{{aI}_{j0}}{(b-k_j)(G-{Ck}_j)}{e}^{-k_{j}t}\\ +\frac{a}{b-\frac{G}{C}}\left(V_{\mathit{reset}}-V_{\mathit{leak}}-\sum _j\frac{I_{j0}}{G-{Ck}_j}\right)e^{-\frac{G}{C}t}\\ +({\mathrm{\Theta }}_0-{\mathrm{\Theta }}_{\infty }-\frac{a}{b-\frac{G}{C}}(V_{\mathit{reset}}-V_{\mathit{leak}}\\ -\sum _j\frac{I_{j0}}{C(b-k_j)}\left)\right)e^{-bt}\end{array}$$ (5)

where * denotes convolution. Θ₀ is the value of the threshold value immediately after a spike has occured. This value is determined by the update rule in (2). It is clear that both (3) and (5) have linear dynamics. Thus if Gaussian noise is added to either equation, it will assume a Gaussian probability density [25]. The threshold voltage is dependent on the value of the membrane potential and, consequently, if noise is added to V(t), then Θ(t) will be a random variable that depends on V(t). To avoid this dependence and simplify the calculations needed later, the noise is added into the threshold whose governing equation becomes

$$d\mathrm{\Theta }(t)=a(V(t)-V_{\mathit{leak}})-b(\mathrm{\Theta }(t)-{\mathrm{\Theta }}_{\infty })dt+\sigma {dW}_t$$ (6)

where dW_t is Gaussian noise with standard deviation 1.

Like Paninski, we will denote the induced Gaussian density as G(Θ(t)|X, I_ext). The mean of this density is the deterministic threshold shown in (5) and the variance is calculated to be

$$\mathit{VAR}[\mathrm{\Theta }(t)]=\frac{{\sigma }^2}{2b}\left(1-e^{-2bt}\right).$$ (7)

On a given interspike interval [t_i−1, t_i], the set

$$C_i=\underset{t_{i-1}\le t<t_i}{\cap }\{\mathrm{\Theta }(t)>V(t)\}\cap \{\mathrm{\Theta }(t_i)\le V(t_i)\}$$ (8)

describes the set of all possible paths the threshold may take such that a spike occurs during the time bin t_i. Thus the likelihood that the neuron spikes at time t_i, given that there was a spike at time t_i−1, is the probability of the event Θ(t) ∈ C_i, which is given by

$${\int }_{\mathrm{\Theta }(t)\in C_i}G(\mathrm{\Theta }(t)\mid \mathbf{X},I_{\mathit{ext}}).$$ (9)

When a spike occurs, the membrane potential and threshold are updated according to the rules in (2).

The initial distribution of G(Θ (t)|X, I_ext) over the inter-spike interval t ∈ [t_i, t_i+1] depends on the final distribution of G(Θ (t)|X, I_ext) at time t = t_i. That is, the interspike interval over t ∈ [t_i, t_i+1] is conditionally dependent on the previous interspike interval t ∈ [t_i−1, t_i]. To ensure conditional independence between interspike intervals, we make the assumption that the probability of Θ is reset using the deterministic value of Θ given in (5). The resulting system is a first-order nonhomogeneous Markov process and the likelihood of the entire spike train can be written as the multiplication of the conditional probabilities for each individual spike in the train [26]

$$Li(t_n,\dots ,t_1)=\prod _{i=1}^n{\int }_{\mathrm{\Theta }(t)\in C_i}G(\mathrm{\Theta }(t)\mid \mathbf{X},I_{\mathit{ext}}).$$ (10)

Neural data is stochastic in nature. If multiple recordings are made from the same neuron, under identical stimuli conditions, then there will be a slight variance between the recorded spike trains. This variance can be explicitly accounted for if the the ML optimization is performed across the multiple spike trains. Consider k spike trains recorded from the same neuron. It can be assumed that their likelihoods are independent and so the total likelihood across all the trials is simply

$${Li}_{\mathit{total}}=\prod _{j=1}^k{Li}^j(t_n,\dots ,t_1)$$ (11)

where Li ^j (t_n,…, t₁) is the likelihood of the j^th spike train.

C. Implementation

An efficient method is needed to calculate the likelihoods used in (11). Given X and t_i−1, we can make use of the fact that (6) is an Ito stochastic differential equation and thus the probability evolution of Θ (t) to t_i satisfies the Fokker–Planck equation [27], [4]

$$\frac{\partial P}{\partial t}=-\frac{\partial ([a(V(t)-V_{\mathit{leak}})-b(\mathrm{\Theta }(t)-{\mathrm{\Theta }}_{\infty })]P)}{\partial \mathrm{\Theta }}+\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}P}{\partial {\mathrm{\Theta }}^2}$$ (12)

where P is the probability of the threshold being above the neuron membrane potential (i.e., the probability that the neuron has not yet spiked). In the above, the first term describes the drift of probability due to the subthreshold neuron dynamics presented in (1) and the second term describes the outwards diffusion of probability due to the injected noise.

The boundary conditions for the system are

$$\begin{array}{l}P(\mathrm{\Theta }=max({\mathrm{\Theta }}_{\mathit{reset}},\mathrm{\Theta }(t_{i-1})),t=0)\\ =\delta (\mathrm{\Theta }-max({\mathrm{\Theta }}_{\mathit{reset}},\mathrm{\Theta }(t_{i-1})))\\ P(\mathrm{\Theta }=V,t)=0\forall t\ne t_i.\end{array}$$ (13)

The first boundary condition describes the resetting of probability to the deterministic value of the threshold. The second boundary condition is an absorbing condition that removes the probability of the neuron spiking from the evolution. It is easy to see that the absorbing boundary falls onto the neuron’s membrane potential, which is given in (3).

We can then calculate the likelihood of the neuron firing at a given time t_i as follows [4]. The cumulative distribution of no spike occurring at time t is given by

$$\int P(\mathrm{\Theta },t)d\mathrm{\Theta }.$$ (14)

Consequently

$$F(t)=1-\int P(\mathrm{\Theta },t)d\mathrm{\Theta }$$ (15)

is the cumulative distribution of a spike occurring at time t. The probability density function of a spike at time t is thus given by

$$\frac{dF(t)}{dt}=f(t)=-\frac{d}{dt}\int P(\mathrm{\Theta },t)d\mathrm{\Theta }$$ (16)

which is the likelihood of a spike occuring at time t. To calculate the likelihood for a given spike train, we make use of the conditional independence of the probability of interspike intervals and write

$$Li(t_n,\dots ,t_1)=\prod _{i=1}^{n}f(t_i).$$ (17)

D. Finite Difference Method

The simplest method to solve the partial differential equation in (12) is through the use of finite difference methods. Finite difference methods approximate the derivatives in the partial differential equation with finite difference equations. Special care must be taken in the discretization of the diffusion term. When the movement of probability due to drift is greater than that through diffusion (i.e., the probability evolution has a high Peclet number), then central difference methods become unstable. To circumvent this, upwind methods [28], where the derivative is approximated by either backward or forward difference equations depending on the direction of probability flow, were used at the cost of introducing numerical diffusion into the solution. This diffusion can be reduced using high-order upwind methods, however this also increases the size of the stencil needed. Central differences were used on the diffusion term, and the Crank–Nicolson method [29] was used to discretize time.

E. Application of Optimization Method to Configure Tonic Bursting

Parameters for tonic bursting were taken from [5] and used to simulate 250 ms of neural activity. The action potentials were extracted from the results and used as the desired spike times for the optimization. The initial parameters of the neuron were chosen at random and the results of the optimization are shown in Fig. 1(a). It can be seen that the predicted spike times match the desired spike times almost perfectly. Fig. 1(b) and (c) shows the probability evolution of the threshold. The resetting of the probability distribution after every spike ensures conditional independence between interspike intervals and, as (7) predicts, the variance of the distribution increases with time. The dotted line is the absorbing boundary condition and is responsible for removing the probability that the neuron has already spiked from the evolution. This removal of probability can be seen in Fig. 1(b) and (c), where the probability density at any time t is zero below the boundary.

Fig. 1.

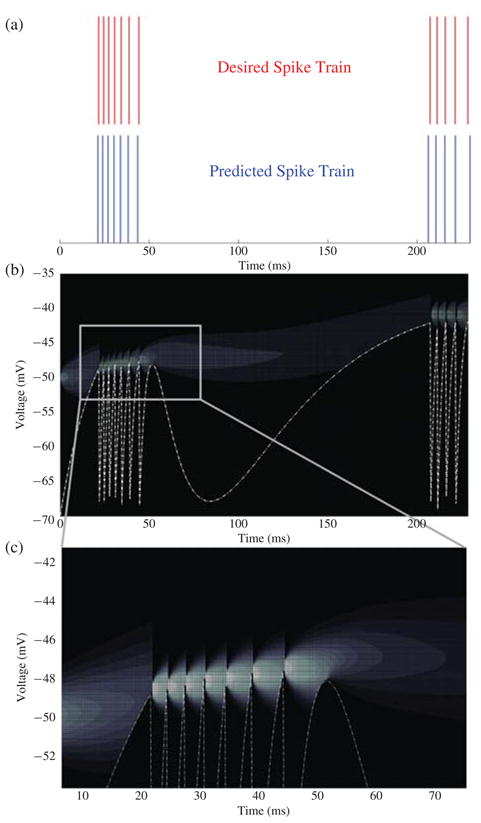
(a) Desired and predicted spike times. Both the desired and predicted spike trains were simulated without noise. If the model were to be used to predict real neural signals, noise could be added to account for the variability inherent in real neural data. (b) Threshold probability evolution for tonic bursting. The dispersion of probability with time is shown by the shading. The whiter the shading, the higher the probability. The dotted line is the boundary condition which coincides with the deterministically calculated membrane potential of the neuron. (c) Magnified view of the probability evolution during the first bursting cycle.

F. Application of Optimization Method to Real Neuron Data

To test the validity of the optimization method against real neural data, the ML method was used to configure the M–N neuron to predict 1 s of firing activity from a regular spiking L5 pyramidal cell. The data was taken from Challenge A in the International Neuroinformatics Coordinating Facility’s Quantitative Single-Neuron Modeling Challenge 2009 [30]. The dataset consists of 13 voltage recordings from the neuron responding to identical current stimuli. The spike times for each repetition were extracted by taking the times at which the voltage traces crossed 0 mV. The optimization was then performed across all 13 spike trains to account for the statistical nature inherent in neural data.

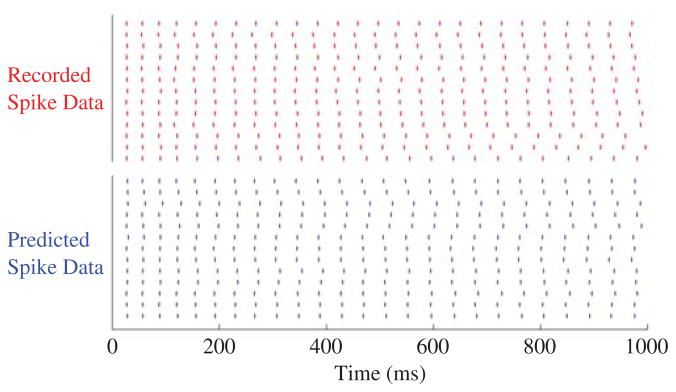
The results of the optimization along with the recorded spike times are shown in Fig. 2. On average, the length of the predicted interspike intervals differed by the recorded interspike intervals by 1.2 ms with a standard deviation of 1.12 ms. The average interspike interval of the recorded data is 39.4 ms. The average error between the recorded and predicted interspike intervals is thus 3%. This shows that the predicted spike times (bottom raster) closely agree with the desired spike times (top raster). Furthermore, by optimizing the noise between trials the variability between recordings has been included in the model. ML methods are a powerful tool for configuring the individual spike times of a neuron. However, in certain circumstances it is more appropriate to use a network of neurons than a single instantiation. In this scenario, the dynamics of the network quickly becomes mathematically intractable and an ML-based method is no longer applicable. GAs provide a good alternative as there is optimization based on the fitness of the network’s outputs without requiring information of the underlying dynamics. We now show how GAs can be used to configure both the parameters and topology of spiking neural networks.

Fig. 2.

Top raster: One second worth of spike data taken from the Quantitative Single-Neuron Modeling Competition 2009 [30]. Each row is a separate recording resulting from identical stimulation. Bottom raster: The predicted spike trains from the M–N neuron.

III. Configuring Spiking Neural Networks Using GAs

GAs have previously been used to train both single neurons [31] and neural networks [18], [19] to perform classification tasks. In the single neuron case, Northmore and Elias [31] used GA to set the synaptic weights of a single in silico neuron so that it would respond to coincident synaptic inputs. Oros et al. [18] used a GA to train a simulated two-wheeled robot and spiking neural network to perform chemotaxis. Jin et al. [19] used a Pareto-based multiobjective GA to optimize both classification performance and network connectivity of a spiking neural network. In this instance, each neuron in the network was allowed to fire just once per classification task. In [32], an alternative method to GAs is discussed for the training of spiking neural networks to perform visual recognition tasks. The network consisted of three layers. The first two layers are fixed and perform time-domain encoding and passive filtering, respectively. Learning occurs in the third layer, in which the synaptic weights and network connectivity are trained to recognize specific input classes. The learning algorithm is an online-incremental algorithm, and the details are given in [33]. The work presented in this paper differs in that it uses GAs to configure the internal state of the spiking neural network such that it behaves as a pattern generator—a network able to produce sustained rhythmic outputs [34].

The cyclic nature of a pattern generator’s outputs require a different training approach to that of spiking neural networks performing classification. In a classification network, the internal dynamics of the network are unimportant as long as the decision neuron fires correctly. In a pattern generator, the network outputs are a continuous periodic pattern of activation whose dynamics is important at all times. The neurons forming a pattern generator network fall into two classes: oscillator neurons and motor neurons. Oscillator neurons set the base frequency of the network using recurrent connections. The periodicity of the motor neurons’ outputs is controlled by the oscillator neurons. The summation of multiple motor neuron outputs generates the temporal pattern of activation of a robot’s actuators. This poses three design questions. What should the parameters be such that the oscillator neurons fire at the correct frequency? How many motor neurons are needed to realize a specific motor pattern? And, how should these neurons be connected to the oscillator neurons? In [14] and [15], the authors showed how GAs can be used to configure pattern generator networks. The following section presents those results in a more complete framework with special emphasis on answering the above questions and on the difficulties of configuring in silico networks. Specifically, we focus on the configuration of CPGs for bipedal robot locomotion.

A. CPGs

The CPG is a network of neurons able to endogenously produce sustained rhythmic outputs [34]. The outputs of CPGs are responsible for most rhythmic motor patterns such as walking, flying, swimming, and breathing. These networks have been used to control snake-like robots [11], [36], quadrupedal robots, hexapedal robots [17], [12], [37], [38], and bipedal robots [10], [35], [13], [14]. The network discussed in this paper is the canonical network developed by Lewis et al. [35] for the control of a bipedal robot and is shown in Fig. 3. To generate a successful gait, the hips should burst with a duty cycle of 50% and the knees must be 90° out of phase with the hips [35]. Both the software and hardware implementations of CPGs discussed here are comprised of integrate and fire with adaptation (IFA) neurons, although the actual model differs slightly between hardware and software as discussed in the relevant sections. IFA neurons were used as they are computationally efficient and have enough functionality to implement the desired networks. However, any neuron model that allows for adaptation can be used. The M–N neuron is a good alternative, as it is computationally efficient and its wide range of firing modalities (including adaptation) allows for greater flexibly during network design.

Fig. 3.

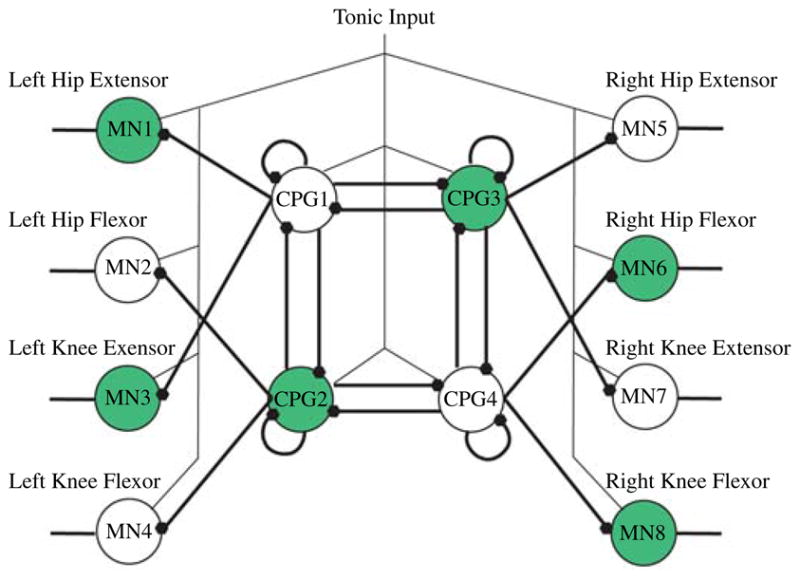
Canonical network used by Lewis et al. [35]. The shaded neurons are 180° out of phase from the non-shaded neurons. Filled dots denote inhibitory synapses. MN denotes motor neurons.

B. Description of the GA

Rate of convergence cannot be guaranteed when using a GA and is therefore of particular concern. To improve the rate of convergence, the concepts of behavioral memory [16] and staged evolution [17] were used. Behavioral memory entails guiding the search to the correct parameter space using two fitness functions: the first is more general and easily satisfied, while the second is more specific and used to fine-tune the solution. Staged evolution builds on this concept and involves breaking the problem into stages that are solved sequentially, thus guiding the algorithm toward the final solution. Staged evolution can increase the probability of finding a solution. Consider a CPG where the optimization process can be divided into finding neuron parameters and finding interneuron weights. There is a strong interdependence between these two parameter sets and thus both parameter sets must be correctly configured for the network to work properly. Furthermore interneuron parameters which may work for one set of neuron parameters may not work for another.

Let X be the random variable of correctly choosing a set of neuron parameters so that the CPG functions correctly and Y be the random variable of choosing interneuron weights so that the network functions correctly. The probability of choosing correct neuron parameters is P(X), the probability of choosing correct synaptic weights given a set of neuron parameters is P(Y|X), and the probability of simultaneously choosing both the correct neuron parameters and correct synaptic weights is P(X∩Y).

Consider staged evolution. The probability of choosing the correct neuron parameters in n attempts is P_n(X) = 1 −(1 − P(X))ⁿ. Given the correct neuron parameters, finding the interneuron weights in a further n attempts is P_n(Y |X) = 1− (1− P(Y|X))ⁿ. The probability of finding a correct solution using staged evolution in a total of 2n trials is thus

$$P_{2n}^{\mathit{staged}}(\mathit{CPG})=P_n(X)P_n(Y\mid X).$$ (18)

Now consider non-staged evolution. Again, using a total of 2n trials, the probability of finding a correct solution is

$$P_{2n}^{\mathit{non}-\mathit{staged}}(\mathit{CPG})=1-{(1-P(X\cap Y))}^{2n}$$ (19)

but P(X∩Y) = P(Y|X)P(X) and so

$$P_{2n}^{\mathit{non}-\mathit{staged}}(\mathit{CPG})=1-{(1-P(Y\mid X)P(X))}^{2n}.$$ (20)

The difference in probability between the two methods is

$$P_{2n}^{\mathit{difference}}=P_{2n}^{\mathit{staged}}(\mathit{CPG})-P_{2n}^{\mathit{non}\mathit{staged}}(\mathit{CPG}).$$ (21)

This difference is shown in Fig. 4 for P(X), P(Y |X) < 0.1, and n = 100. Note that this difference is always positive, indicating that $P_{2n}^{\mathit{staged}}(\mathit{CPG})\ge P_{2n}^{\mathit{non}\mathit{staged}}(\mathit{CPG})$ in this region. This shows the advantage of using staged evolution when P(X) and P(Y |X) are both small (a reasonable assumption in the case of a CPG). Thus staged evolution is more likely to converge quickly than non-staged evolution for small probabilities. Furthermore, for the CPG case, staged evolution saves time not only because fewer trial solutions need to be investigated, but also because trial solutions for individual neurons (stage 1) can be evaluated faster than those for an entire network (stage 2 or the non-staged approach). The reasons for this are discussed in Section III-D.2. In the work presented below, three stages of optimization are used, however, the above is easily extended to this scenario.

Fig. 4.

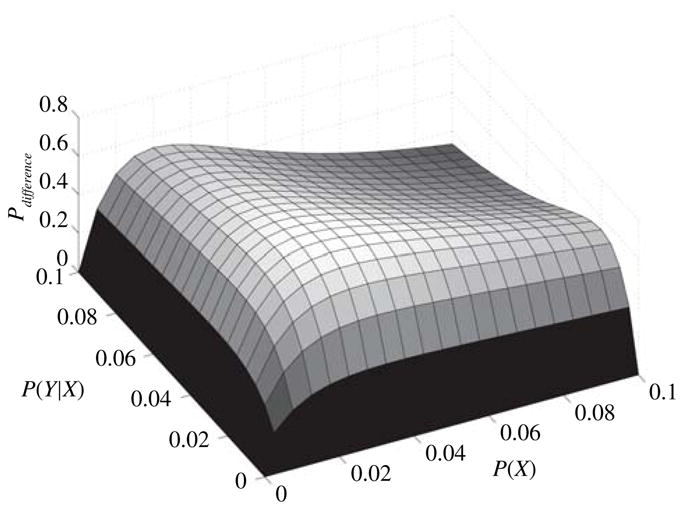
Increase in probability of finding a solution as a result of using staged evolution when P(X) and P(Y |X) are small and n = 100. P(X) is the probability of correctly choosing a set of neuron parameters such that the CPG will work. P(Y |X) is the probability of correctly choosing interneuron parameters given a set of neuron parameters.

Inada and Ishii [13] used a GA and a similar staged evolution approach to optimize parameters for a CPG-based controller (constructed from non-spiking neurons) of ankle, knee, hip, and pitching of the waist movements in a simulated biped. More recently, some of us used GAs to configure spiking neural networks, both in software and in silico, to control a biped robot [14], [15].

The GA used was based on FBGAMIN, a single goal optimizer, which falls into the class of an adaptive mutation breeder algorithm [39]. The adaptive mutation ensures that the mutation rate is always optimal, while elitism ensures the best solutions from each generation propagates through to the next generation thus guaranteeing that solutions remain the same or improve through generations. Breeder algorithms are well suited for the optimization of real-valued functions, and the adaptive mutation characteristic algorithm utilizes a simple feedback loop within the algorithm to ensure that the mutation rate is always optimal [14], [15].

Staged evolution was performed in three stages. In the first stage, each neuron was individually configured to spike at a specified frequency of 100 Hz with no interneuron connections present. In the second stage, interneuron connections were introduced and optimized to obtain the specified frequency and duty cycle. In the third and final stage, additional inhibitory coupling is introduced to control phase differences between the oscillator and motor neurons. The order in which interneuron connections were introduced differs between hardware and software as discussed in the respective sections. Solutions were stored in a lookup table which was used as a starting point for obtaining new solutions. The fitness functions for the three stages are given as

$$\begin{array}{l}{\mathit{err}}_f={(f_{\mathit{desired}}-f_{\mathit{measured}})}^2\\ {\mathit{err}}_{BL}({\mathit{CPG}}_x)={({BL}_{\mathit{desired}}-{BL}_{\mathit{measured}})}^2\\ {\mathit{error}}_{\phi }={({\phi }_{\mathit{desired}}-{\phi }_{\mathit{measured}})}^2\\ {\mathit{fitness}}_1={\mathit{err}}_f+V\\ {\mathit{fitness}}_2={\mathit{err}}_{BL}({\mathit{CPG}}_1)+{\mathit{err}}_{BL}({\mathit{CPG}}_2)+V\\ {\mathit{fitness}}_3=w\times {\mathit{err}}_{BL}+\alpha \times {\mathit{err}}_{\phi }+V.\end{array}$$ (22)

In the above equations, f refers to the spike frequency of a single isolated neuron. BL refers to “Burst Length” and is defined as the period over which a neuron fires. The period of oscillation of the half-centered oscillator is given by the sum of burst lengths for C PG₁ and C PG₂. By varying the ratio of B L(C PG₁) to B L(C PG₂), the duty cycle of oscillation can be varied. φ is used to denote phase difference between coupled neurons. In the fitness equation for stage 3, w is set to greater than 1 to increase the importance of frequency in the fitness function. α is a scaling factor used to convert the phase error to a magnitude similar to that of frequency and burst length. V is a validity term which is set arbitrarily large when invalid solutions are found. Invalid solutions are defined differently for each application and details of V are discussed in the relevant sections. During parameter configuration, the target frequencies of oscillation were chosen to lie between 1 and 3 Hz, which is approximately the natural locomotion frequency of animals with limb lengths of 30 cm (the leg length of the biped robot used to test the CPG outputs).

For all software implemented optimizations, the GA was configured with a population size of 200 where 1 chromosome was the suggested trial solution and the remaining 199 chromosomes were generated by multiplying each gene in the suggested solution by a uniformly distributed random number between 0 and 5. This ensured that the initial population searched a wide parameter space. Such a large population size was facilitated by the fact that simulations can run faster than real time. When the GA was used to optimize the parameters of in silico networks, it was configured in a similar manner, but with a reduced population size of 100. The trial solution for the first stage of optimization was obtained from trial and error and allowed for a single neuron to spike anywhere between 10 and 200 Hz. The trial solutions for the second and third stages of optimization were the results of the first and second stages, respectively.

C. Evolving CPG Parameters in Software

1) Network Description

The IFA neurons used in software simulations have a slight modification on the adaptation term. This modification causes the adaptation current to cease if the neuron does not spike for a specified period of time. The equations describing the i^th neuron in a network are given by

$$\begin{array}{l}{V}_i^{\prime }=\sum _{k=1}^n{I}_{k\to i}+a_i-b_i{V}_i+g_i(d_i-V_i)\\ \text{if}{V}_i\ge V_{\mathit{thresh}}\text{then}{V}_i=V_{\mathit{reset}}\\ g_i^{\prime }=\frac{e_i\delta (t)-g_i}{{\tau }_i}\\ \text{if}{t}_{\mathit{fire}}\ge t_{\mathit{thresh}}\text{then}{g}_i=0\end{array}$$ (23)

where V is the membrane potential, I_k→i is the coupling current from neuron k to i, a is the tonic input, and b is the membrane impedance. g, e, d, and τ describe the adaptation. V_reset is the reset potential of the neuron, t_{f ire} is the time since the neuron last fired, and t_thresh is the time a neuron can go without firing before its adaptation is reset.

Using this model, which has six parameters per neuron, the 12-neuron network of Fig. 3 will have 108 parameters, including the 36 interneuron connection weights. A key to successfully configuring these parameters is to identify manners in which the parameter space can be reduced. If we exploit symmetries such as allowing similar neuron types (e.g., central oscillator neurons, left/right hip motor neurons, and left/right knee motor neurons) to have similar properties, then the dimensionality of the network can be halved. The dimensionality of the problem can be further reduced if additional constraints are placed on the network (e.g., connections forming the main oscillator neurons are symmetric, left and right hips are 180° out of phase with each other and the knees are 90° out of phase). These constraints reduce the network in Fig. 3 to that in Fig. 5. In software, the fitness functions of (22) are simplified because err_BL (CPG₁) = err_BL (CPG₂) due to symmetry and the assumption of a 180° phase shift between left and right. The resulting simplified network is shown in Fig. 5. The constraints of symmetry can be relaxed later to find other network operation modes, however, careful choice of free variables as well as the use of staged evolution for more complicated modes is critical to good convergence.

Fig. 5.

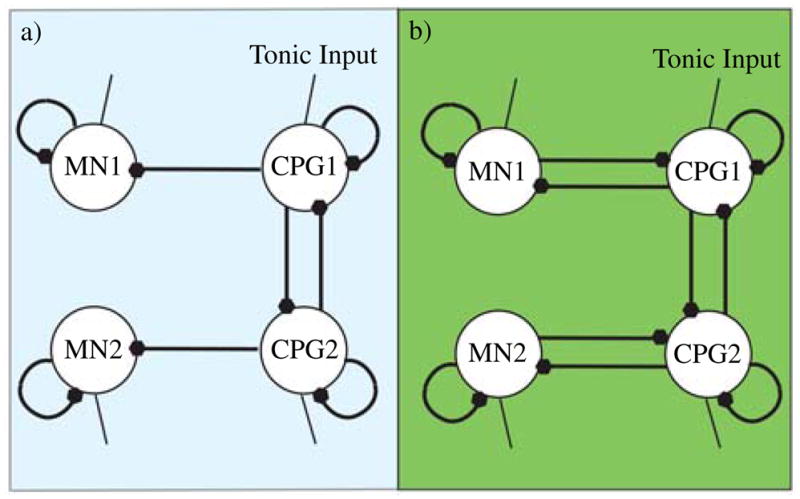
Reduced canonical network for (a) software simulations and (b) hardware simulations. Similarities and symmetries between neural outputs allow CPG1 and CPG2 to act as the half-centered oscillator as well as the hip extensors (CPG1-left hip, CPG2-right hip), and flexors (CPG1-right hip, CPG2-left hip). Further 180° symmetry between legs allows the motor neurons to function as both knee extensors (MN1-left knee, MN2-right knee) and flexors (MN1-right knee, MN2-left knee). The additional coupling between the motor and CPG neurons in the hardware implementation allows for greater flexibility and control of the gait. For nonsymmetric gaits, the network would be expanded to allow independent control of the left and right motor neurons.

2) Optimization

Hierarchal evolution was implemented on the reduced canonical network of Fig. 5(a) by first configuring individual neurons to spike at 100 Hz. Then mutual inhibition between CPG1 and CPG2 was introduced and the walking frequency parameters were optimized for oscillation frequencies from 0.5 to 3 Hz in steps of 0.25 Hz while maintaining a duty cycle of 50% for each neuron. Solutions that did not oscillate were marked as invalid and assigned an arbitrarily large error using the validity term. The results from the previous frequency evolution were used to seed the evolution of the next walking frequency. The following parameters were optimized in the second stage of evolution: { $V_{\mathit{thresh}}^{\mathit{CPG}1},a^{\mathit{CPG}1},b^{\mathit{CPG}1},e^{\mathit{CPG}1},d^{\mathit{CPG}1},{\tau }^{\mathit{CPG}1},I_{\mathit{CPG}1-\mathit{CPG}2},V_{\mathit{thresh}}^{\mathit{CPG}2},a^{\mathit{CPG}2},b^{\mathit{CPG}2},e^{\mathit{CPG}2},d^{\mathit{CPG}2},{\tau }^{\mathit{CPG}2}$ and I_CPG2-CPG1}. Once the parameters to allow walking at various frequencies were evolved, feedforward inhibition was introduced from CPG1 to MN1 and from CPG2 to MN2. In this stage, the validity term was used to eliminate solutions in which motor neurons begin firing less than 180° out of phase with the inhibiting oscillator neuron. The phase relationship between the hips and knees was configured during this stage. Parameters were found to cause phase shifts between 0° and 90°. Using the above method, parameters were found to walk at each specific frequency and gait (hip–knee phase relationship).

3) Implementation

Network parameters were obtained through implementation of the GA and neural network in MATLAB (The Mathworks Inc, Natick, MA, USA). Once the parameters had been determined, the network was implemented on a dsPIC30f4011 (Microchip, Chandler, AZ, USA) microcontroller and the network outputs were used to control servo motors on the Redbot [40] bipedal robot (Fig. 13). The servo motor angles were measured during operation and fed back to the PC to verify network operation. The system is capable of running without a PC, but inclusion of the PC allows updating of network parameters from a previously generated lookup table for gait modification on the fly.

Fig. 13.

Redbot [40] bipedal robot walking using the evolved network mimicking human joint angle profiles.

D. Evolving CPG Parameters In Silico

Computational limitations restrict the design of large real-time neural networks in software. It is desirable to take advantage of the real-time parallel nature of analog very large scale integration implementations. By decreasing the membrane capacitances used in the silicon neurons, it is even possible to run these large networks in faster than real time. Furthermore, these circuits are of low power and provide an important processing paradigm for the future. Unfortunately, while in silico implementation solves some problems, it introduces others. Previously, in software simulations we made use of network symmetry to reduce the parameter space. Configuring silicon neurons increases the parameter space because the assumption of symmetry no longer holds due to the “fixed pattern” noise introduced by transistor mismatch. An optimal set of parameters for a particular neuron will not necessarily be optimal for another neuron due to this noise. To demonstrate the use of GA on networks implemented in silico, we used a reconfigurable custom-designed chip to emulate a CPG network [40].

1) Network Description

Once again, IFA neurons were used. A circuit diagram of a silicon neuron is shown in Fig. 6. Adaptation was implemented externally to the chip using self feedback through an RC delay. The limited number of external inputs (four) restricts us to four IFA neurons. We implemented the reduced canonical network of Fig. 5(b). It is a slight modification of Fig. 5(a) in that it has additional feedback from the motor neurons to increase robustness in the face of electrical noise.

Fig. 6.

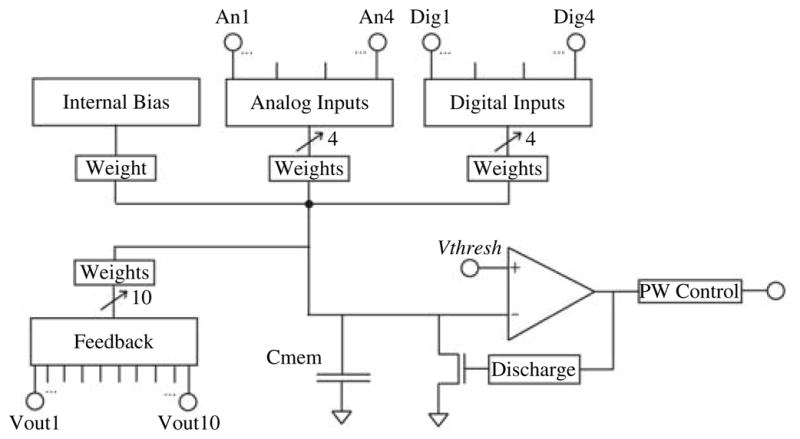
Circuit diagram for a single integrate and fire silicon neuron. PW control determines the pulsewidth of the output spikes, Discharge determines how long the membrane discharges for after a spike. Vthresh is the spike threshold. The weights each have an 8-bit programmable magnitude and a sign bit. Adaptation is implemented using an external RC circuit which filters the output and feeds the result back into one of the analog inputs. The Feedback inputs are internal to the chip and one is connected to the output of each neuron on chip.

2) Optimization

In order for the operation of the in silico neural network to be accurately simulated, special attention must be given to the effects of noise, transistor mismatch, and temperature of the circuit. This is not trivial and so parameters for the in silico network were found by applying the GA directly to the silicon network during optimization. This presents additional complexity, as the integrated circuit containing the spiking neural network needs to not only be interfaced with the host computer running the GA in real time but time must be allowed for the network to settle to a steady state when switching parameters and a possible solution must be evaluated over multiple periods of oscillation to ensure that it is a stable solution. In small networks, this may result in the optimization process taking longer than if an equivalent size network was simulated. However, for larger networks this in silico optimization will be substantially faster than the simulated version due to the parallel nature of the silicon network.

The fitness functions remain unchanged except for the validity term, but the interneuron connections implemented in each stage differ from software implementations. In the first stage of evolution, no connections are present, as was the case in software. The in silico neurons emit a fixed width pulse after every spike. If the interspike interval of the spikes of a single neuron are too small, then it is possible that the neuron will fire again before the output pulse for the previous spike has ended. If this occurs, then multiple spikes may be hidden under a single output envelope and they will be recorded as a single spike. The validity term was used to eliminate solutions in which this occurred. The minimum pulse width of a spike was constrained by the need to reliably detect each spike by the microcontroller.

In the second stage the CPG1/MN1 and CPG2/MN2, mutual inhibition is implemented to form two half-centered oscillators. These are optimized in parallel using f itness₂ to obtain specified frequency and duty cycle. The validity term was used to eliminate solutions which did not oscillate or in which bursts of less than five spikes occurred. The target frequency for the second stage was empirically chosen to be 1.5 times that of the final network because a reduction in frequency is expected during stage 3 of evolution. (The two oscillators are coupled together using inhibitory connections. Thus when coupled, additional time must be allowed from the neurons to recover from hyperpolarization and the network will slow down). In the third stage, the CPG1/CPG2 mutual inhibition is implemented and optimized for 180° phase shift between left and right sides. This connection also slows down the overall frequency of the network.

3) Implementation

As shown in Fig. 8, the dsPIC30f4011 was used to interface the PC and the silicon chip. The PC communicates network parameters with the microcontroller, which configures the silicon chip appropriately. The microcontroller records the spike times and communicates them back to the host PC, which runs the GA.

Fig. 8.

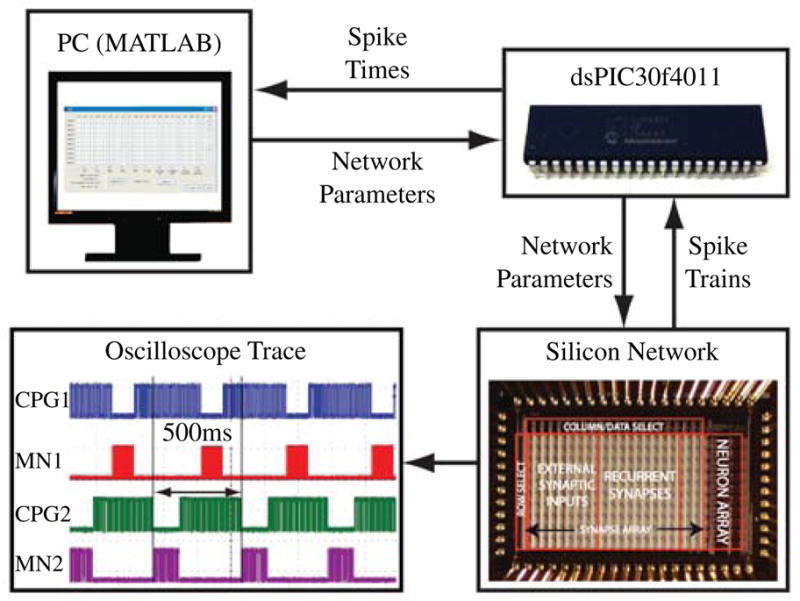
Hardware setup for silicon implementation of the CPG from Fig. 5. MATLAB code on the host PC runs the GA. Network parameters are communicated to a microcontroller which configures the neural chip appropriately. Neuron outputs are digitized by the microcontroller, which communicates them back to the PC where the fitness function is computed. The spiking output waveform was recorded from the silicon network once it had been optimized with target parameters of 2 Hz, 70% duty cycle, and 180° phase shift between the oscillators controlling the left and right side.

IV. Configuring Network Topology

Thus far we have only controlled the duty cycle, frequency, and phase of the network, but did not have any control over the actual shape of the joint angle profiles. The required shape of the joint angle profile is not always specified, but for cases in which it is known, such as when we want to impart human walking gaits to a robotic biped [41], an optional fourth stage of software optimization was developed. The complexity of achievable joint angle profiles is determined by the network topology. Simple sinusoidal joint angle pro-files may be possible with a much simpler network than is required to mimic human joint angle profiles. Having a different network for each case is desirable to ensure that additional neurons are not simulated unnecessarily. To achieve this, six feed forward neurons were initially added per joint (see Fig. 7). The motor neuron parameters were optimized to minimize a fitness function which was the mean square error between the resulting and desired joint angle profiles. The summation kernel consisted of a weighted summation of the motor neuron’s outputs. The sign and weight of each neuron’s output were determined during optimization. In the final stage, a loop ran in which the motor neuron with the smallest relative weighting in the summation kernel was removed until no more motor neurons could be removed without crossing above the specified error threshold, which was set to (15°)². The network was then re-optimized without the removed neurons.

Fig. 7.

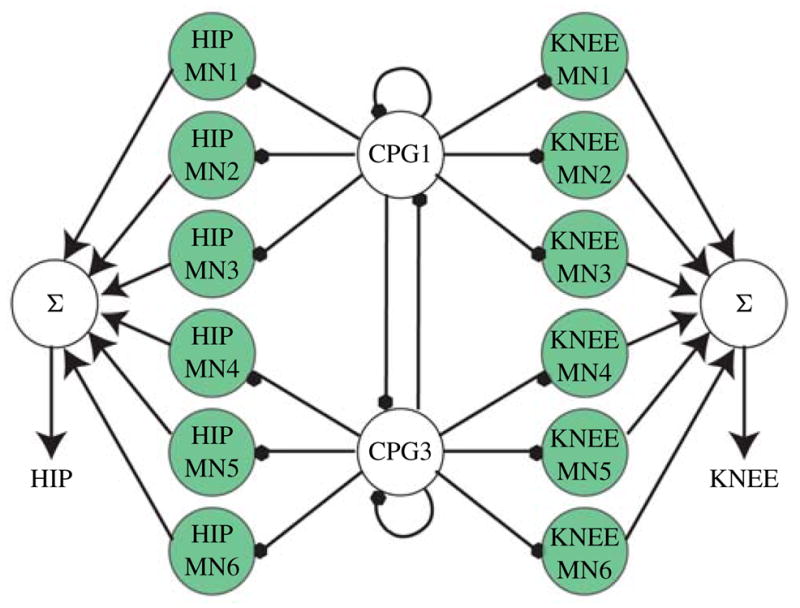
Initial topology used to control the shape of the joint angle profiles. To avoid clutter, only the motor neurons for the left side are shown. The circuit would look almost identical for the right side, except that CPG1 and CPG2 would be swapped around to cause a 180° phase shift. At the beginning of this stage of evolution, we introduce six motor neurons (shaded neurons) per joint. Motor neurons with little or no contribution (low summation weights) are later removed from the network to conserve computational resources. Each final summation weight can be positive or negative as determined by the optimization process.

V. Results

A. Evolving CPG Network Parameters in Software

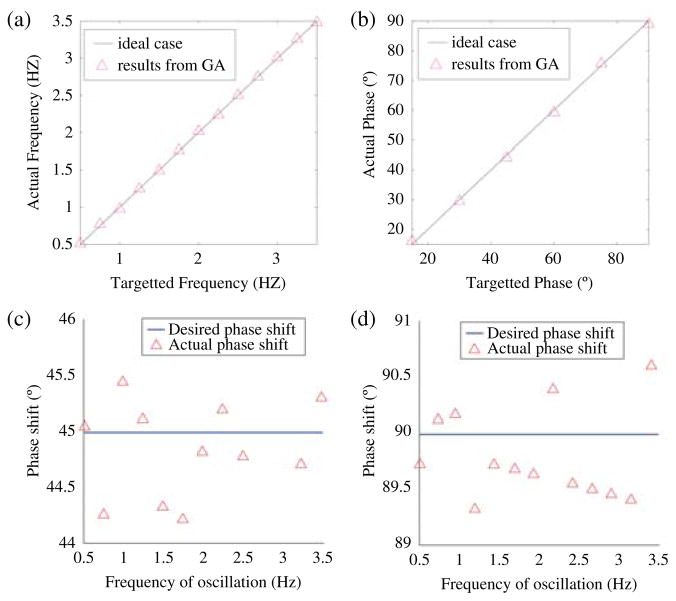
Parameters were easily found to cause the single neurons to fire at the desired 100 Hz. Fig. 9(a) shows the results of the second stage of optimization where the simulated network was configured to obtain walking frequencies from 0.5 to 3.5 Hz in 0.25-Hz increments. This stage of evolution converged to a solution within three generations for all target frequencies. The task was significantly simplified by imposing the constraint that the neurons in the central oscillator all have identical parameters due to symmetry. Fig. 9(b)–(d) shows the results of the third stage of optimization where parameters were found to cause phase shifts of 15° to 90°, in 15° increments, across all walking frequencies. Fig. 9(b) shows that parameters could accurately be found to cause all desired phase shifts at a walking frequency of 1 Hz. Fig. 9(c) and (d) shows that the desired phase shifts (45° and 90° in this case) could be found to an accuracy of within 1° across all walking frequences. Stage 3 of evolution also converged quickly, usually within two generations, because only a relatively simple hip–knee connection is optimized in this stage.

Fig. 9.

Results from software optimization of CPG parameters. Discussed under Section V-A. (a) Stage II optimization results where the simulated network was configured to oscillate at walking frequencies between 0.5 and 3.5 Hz. (b) Stage III optimization results where the network was configured for various phase differences between 10 and 90° at a walking frequency of 1 Hz. (c) Stage III results where the network was configured for a 45° phase difference across all walking frequencies. (d) Stage III results where the network was configured for a 90° phase difference across all walking frequencies.

Note that, due to the 180° phase shift between left and right, angles above 90° can be obtained by simply swapping the outputs for the left and right knees. In [14], we used this network to control walking in a bipedal robot with hip support. The joint angle profiles obtained from the network and used to control the biped are shown in Fig. 12(a).

Fig. 12.

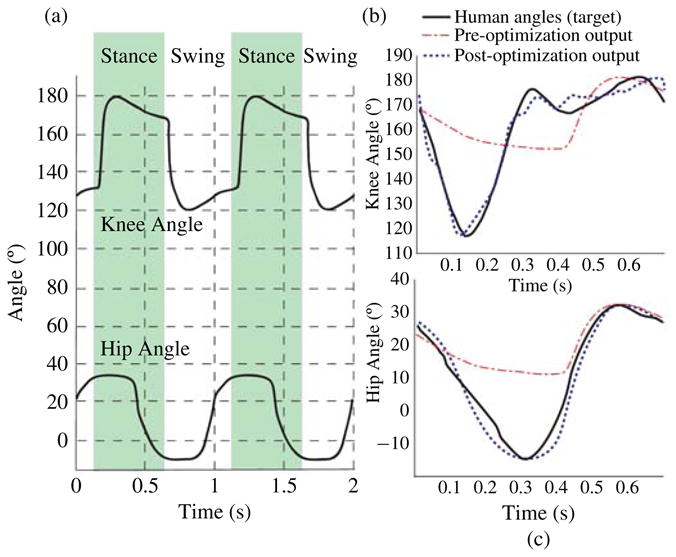
(a) Simulated network output once it has been optimized for a frequency of 1 Hz and with a phase shift of 90° between the hips and knees. (b) and (c) show the evolution of the knee and hip joint angle profiles, respectively, as they target the human data (solid line). The dashed lines show the joint angle profiles before optimization and the dotted lines show the post optimization joint angle profiles.

B. Evolving CPG Parameters In Silico

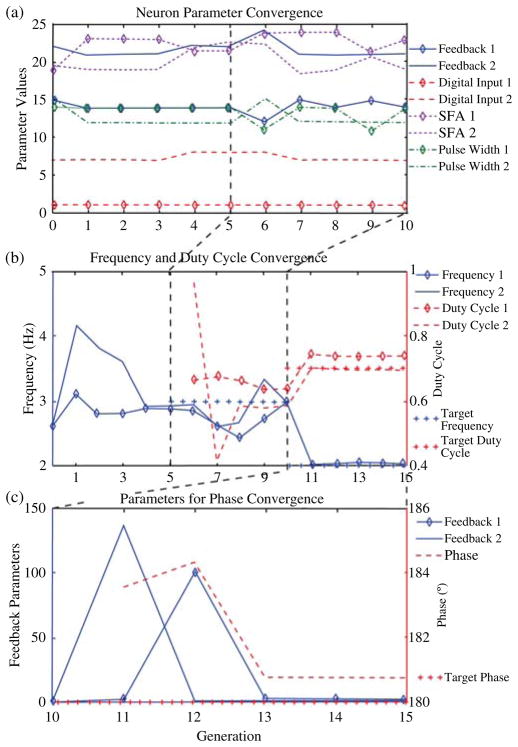
The silicon CPG was given a target walking frequency of 2 Hz with duty cycle of 70% and 180° phase shift between the left and right half-centered oscillator. Fig. 10 shows how the frequency, phase, and duty cycle evolve during optimization to successfully obtain the desired parameters. Note that the target frequency for the second stage is 3 Hz. This decreases and is optimized for 2 Hz during the final stage of optimization.

Fig. 10.

Evolution of parameters during optimization. Each stage of evolution runs for five generations. The transition between stages is shown by the dashed lines. Note that the target frequency varies between stages. (a) Results of neuron parameter evolution over stage 1 and stage 2. (b) Results of frequency and duty cycle convergence over stages 1–3. (c) Results of parameter evolution for phase convergence in stage 3.

C. Evolving Network Topology

Human walking data was obtained and the GA was used to evolve the parameters for the feedforward motor neurons as well as control the number of neurons required by the network to mimic the human joint angle profile (Fig. 11). The GA successfully configured the network to obtain human walking joint angle profiles and was able to achieve this with only 7 of original 12 motor neurons made available per joint. The relatively simple shape of the hip profiles required only three motor neurons, while the more complex shape of the knee angles required four motor neurons to stay below the specified maximum mean square error of (15°)². The final fitness of the hip network was (9.5°)² and the final fitness of the knee network was (13.2°)². The resulting joint angle profiles are shown in Fig. 12(b) and (c). Fig. 13 shows the robot walking with this controller.

Fig. 11.

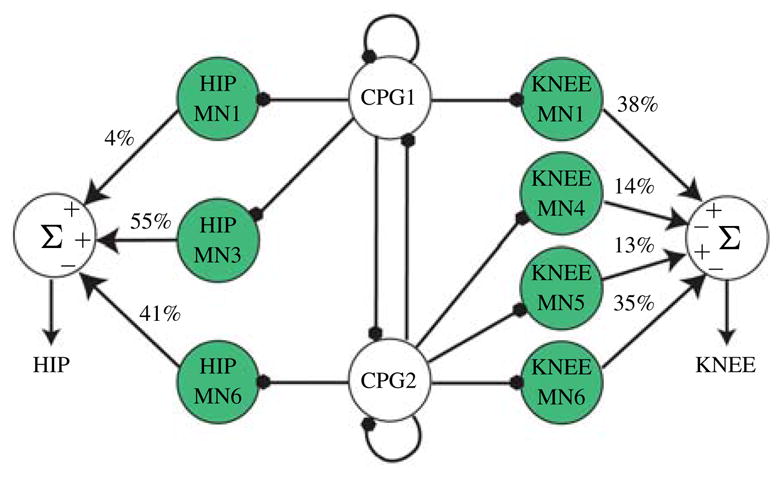
Network topology resulting from GA optimization. The relatively simple shape of the hip joint angle profile requires only three motor neurons to achieve the specified accuracy, while the more complex shape of the knee profile requires four motor neurons. The sign of each weight is indicated in the summation kernel. The percentage contribution of each neuron is also shown.

VI. Discussion

We have demonstrated how ML methods and GAs can be used to configure parameters of spiking neurons instantiated as both single models and in circuits. Specifically, we extended the work done by Paninski and Pillow [4] to the more powerful M–N neuron model. Kumar et al. [42] recently described a parameter estimation method for the Izikevich neuron, which like the M–N model is able to reproduce almost all spiking and bursting modalities of cortical neurons. Our work differs in that the M–N model is biophysically more plausible [5], its dynamics are simpler to understand, it is simpler to implement in complimentary metal-oxide-semiconductor [43], and it can be used in event-based simulations [5]. Furthermore, the stochastic nature of the ML method accounts for the statistical variability of spike timings, something not accounted for in Kumar et al. [42] method. In regards to neural circuits, we used a GA with staged evolution and behavioral memory to configure a CPG neural circuit in both software and hardware to produce the hip flexor and extensor signals required for a typical bipedal gait. This is just an example of how GAs can be used to configure neural circuits, and the approach can easily be adapted for use on other neural circuits. Our example allows the user to specify a walking frequency and phase shift between neurons in a known circuit topology or to use the GA to configure basic circuit topology and parameters for a given gait. The rate of convergence of the GA was dominated by the time necessary to simulate or record circuit behavior. The time taken to evaluate the network output and generate new solutions was negligible by comparison. This suggests that GAs are well suited to configuring parameters in neural circuits which operate at high frequencies.

In the methods section, a GA was used to configure an individual neuron to have an average spike rate of 100 Hz. However, if GAs were used to configure parameters for exact spike times in a single neuron, what fitness function would be appropriate? A spike distance-based metric such as that given by Victor and Purpura [44] is a choice, however, the penalties associated with missing or inaccurate spike times are almost arbitrary in meaning and the method cannot take into account the intrinsic variability in biological action potential times. ML methods, however, provide a meaningful measure of spike timings and easily take into account the statistical variability of spike times. Furthermore, ML and GA can work together to provide greater tuning of neural circuit outputs. Consider the canonical network shown in Fig. 3. Suppose the spike timings of MN1 were known. GA could be used to configure the behavior of the oscillator neurons CPG1–CPG4 and ML could then be used to tune the parameters of MN1 and the synaptic connection between CPG1 and MN1. The extension to the ML method is minimal and simply requires an additional current term to be added to the membrane potential of the neuron to account for the effect of CPG1 on MN1.

VII. Conclusion

Manual configuration of spiking neuron models and networks is a time-consuming task requiring an intricate knowledge of the system being configured. As the complexity of the model or neural circuit rises, it becomes increasingly unintuitive and difficult to control. The work presented in this paper illustrates two automated configuration methods tailored to suit the different demands of configuring individual spiking neuron models and spiking neural circuits.

Biographies

Alexander Russell received the B.Sc. degree in mechatronic engineering from the University of Cape Town, Rondebosch, South Africa, in 2006, and the M.S.E degree in electrical engineering from Johns Hopkins University, Baltimore, MD, in 2009. Currently he is pursuing the Ph.D. degree at the Computational Sensory-Motor Systems Laboratory, Johns Hopkins University.

His current research interests include optimization methods for spiking neurons and networks, mixed-signal very large scale integration design, and biofidelic sensory encoding algorithms.

Mr. Russell was a recipient of the Klaus-Jurgen Bathe Scholarship as well as the Manuel and Luby Washkansky Postgraduate Scholarship from the University of Cape Town, and the Paul V. Renoff Fellowship from Johns Hopkins University.

Garrick Orchard received the B.S. degree in electrical engineering from the University of Cape Town, Rondebosch, South Africa, and the M.S.E. degree in electrical engineering from Johns Hopkins University, Baltimore, MD, in 2006 and 2009, respectively.

He is currently a member of the Computational Sensory-Motor Systems Laboratory at Johns Hopkins University. His current research interests include mixed-signal very large scale integration design and intelligent compact sensors for mobile robotics.

Yi Dong received the B.S. degree in physics from Nanjing University, Nanjing, China, in 2003, and the Masters degree in physics from Johns Hopkins University, Baltimore, MD, in 2005. Currently he is pursuing the Ph.D. degree at the Computational Neuroscience Laboratory, Neuroscience Department, Johns Hopkins University, led by Dr. E. Niebur.

His current research interests include high-performance computation and the brain.

Ştefan Mihalaş received the B.S. degree in physics and the M.S. degree in differential geometry from West University, Timisoara, Romania, and the Ph.D. degree in physics from the California Institute of Technology, Pasadena.

He is currently a Post-Doctoral Fellow in computational neuroscience at Johns Hopkins University, Baltimore, MD.

Ernst Niebur received the Graduate degree and the M.S. degree (Diplom Physiker) from the Universität Dortmund, Dortmund, Germany. He received the Post-Graduate Diploma in artificial intelligence from the Swiss Federal Institute of Technology, Zurich, Switzerland, and the Ph.D. degree (Dr és sciences) in physics from the Universitè de Lausanne, Lausanne, Switzerland. His dissertation topic was computer simulation of the nervous system of the nematode C. elegans.

He was a Research Fellow and a Senior Research Fellow at the California Institute of Technology, Pasadena, and an Adjunct Professor at Queensland University of Technology, Brisbane, Australia. He is currently an Associate Professor of neurosciences in the School of Medicine and of Brain and Psychological Sciences, Krieger School of Arts and Sciences, Johns Hopkins University, Baltimore, MD. His current research interests include computational neuroscience.

Dr. Niebur was the recipient of the Seymour Cray (Switzerland) Award in Scientific Computation in 1988, the Alfred P. Sloan Fellowship in 1997, and the National Science Foundation CAREER Award in 1998.

Jonathan Tapson (M′05) received the B.Sc. degree in physics and in electrical engineering in 1986 and 1988, respectively, and the Ph.D. degree in 1994, all from the University of Cape Town, Rondebosch, South Africa.

He rejoined his alma mater in 1997 and was promoted to Professor of Instrumentation in 2003, after spells in industry and in a government research laboratory. His current research interests include smart sensors, networked instruments, and bio-inspired systems.

Dr. Tapson serves on the boards of three companies which have spun out of his research work. These operate in areas as diverse as web-based monitoring of industrial machinery and induction melting of platinum and precious metals in the jewelry industry. He is most proud of Cell-life, Inc., a not-for-profit corporation which uses GSM cellphone technology to provide IT solutions for the HIV/AIDS crisis in Africa, and which currently supports over 65 000 patients, including over 5000 children.

Ralph Etienne-Cummings (S′95–M′98–SM′08) received the B.Sc. degree in physics from Lincoln University, PA, in 1988. He obtained the M.S.E.E. and Ph.D. degrees in electrical engineering at the University of Pennsylvania, Philadelphia, in December 1991 and 1994, respectively.

He is currently a Professor of electrical and computer engineering, and computer science at Johns Hopkins University (JHU), Baltimore, MD. He is the former Director of Computer Engineering at JHU and the Institute of Neuromorphic Engineering, currently administered by the University of Maryland, College Park. He is also an Associate Director for Education and Outreach of the National Science Foundation (NSF) sponsored Engineering Research Centers on Computer Integrated Surgical Systems and Technology at JHU. His current research interests include mixed-signal very large scale integration systems, computational sensors, computer vision, neuromorphic engineering, smart structures, mobile robotics, legged locomotion, and neuroprosthetic devices.

Prof. Etienne-Cummings is the recipient of the NSF CAREER Award and the Office of Naval Research Young Investigator Program Award. In 2006, he was named a Visiting African Fellow and a Fulbright Fellowship Grantee for his sabbatical at the University of Cape Town, Rondebosch, South Africa. He was invited to be a Lecturer at the National Academies of Science Kavli Frontiers Program, held in November 2007.