Assessment of Transport Mechanisms Underlying the Bicoid Morphogen Gradient

Abstract

Morphogen gradients dictate the spatial patterning of multicellular organisms and are established via transport mechanisms. One of the best-characterized morphogens, Bicoid, acts as a polarity determinant in the Drosophila embryo through spatial-temporal control of gap gene expression. The prevailing model for establishment of the gradient has been localized anterior translation, subsequent diffusion, and spatially uniform degradation, consistent with the observed exponential anterior-posterior decay. However, a recent direct measurement of the Bicoid diffusion coefficient via fluorescence recovery after photobleaching (FRAP) resulted in a surprisingly low estimate, which challenged the prevailing model and led to more complicated active transport models. Here, we reassessed this conclusion using a detailed computational model of the FRAP experiment and analysis. In our model, we found disagreement between the input diffusion coefficient and the resulting estimated diffusion coefficient, as measured by previous methods. By using the model to reproduce the original data, we estimate that Bicoid’s mitotic diffusion coefficient is 3-fold larger than the originally reported value. Thus, the long-standing diffusive transport model still holds.

INTRODUCTION

In developing multicellular organisms, initially identical cells differentiate into a wide range of cell fates via position-dependent morphogen signaling. Morphogens are locally produced transcription factors or extracellular signaling molecules, which provide cells with spatial information in a concentration-dependent manner ^5,18. In many cases, the morphogen concentration gradient is established via transport away from a localized source, and the proper production of this gradient dictates the spatial patterning of the organism.

One of the best-characterized morphogen gradients is the Bicoid (Bcd) gradient. In early Drosophila melanogaster embryos, Bcd is translated from maternally deposited mRNA concentrated near the anterior pole of the embryo and mediates anterior-posterior patterning of the embryo. Early observations of the Bcd gradient showed that it forms an exponentially decaying, anterior to posterior concentration gradient ⁶. This observation led to the prevailing model of localized synthesis, with subsequent diffusion, and uniform degradation (SDD) for gradient establishment ^4,6,7,9.

This simple diffusive transport model, however, was challenged by the first direct measurement of the Bcd diffusion coefficient during mitosis 13 ⁹. By fitting a 3D diffusion equation ³ to fluorescence recovery after photobleaching (FRAP) data of fluorescently tagged Bcd, Bcd-eGFP, the mitotic diffusion coefficient of Bcd-GFP was estimated at 0.30 ± 0.09 μm²/s ⁹. This surprisingly low measurement could not explain the observed developmental timescale of the Bcd gradient by the generally accepted SDD model and therefore led to the subsequent development of more complicated active transport models ^9,10.

Alternative to active transport models, recent measurements of the Bcd mRNA gradient ¹⁷ along with computational modeling ¹⁶ suggest that the experimentally measured diffusion coefficient is sufficient to form the observed gradient if the characteristic length of the Bcd source is comparable to the characteristic length of the protein gradient. While the specific localization of Bcd production is not entirely clear, this model predicts that in the limit, if the Bcd gradient mirrors the mRNA gradient, then the Bcd diffusion coefficient should approach zero. If the diffusion coefficient were higher, then diffusive transport would contribute significantly to gradient formation.

A puzzling aspect of the estimated diffusion coefficient is a discrepancy between the low estimate and the relatively fast recovery ⁹. For pure diffusion, τ_1/2 = δ²/(2D), where δ=3.5 μm is the diffusion distance from the edge to the center of the photobleached area (from the short side of the 16 × 16 × 7 μm³ photobleach volume used by Gregor et al.⁹) and D = 0.30 μm²/s is the diffusion coefficient, the halftime to recovery, τ_1/2, is ~20s. This value is almost three times larger than the halftime to recovery of ~7s, which can be estimated from the published recovery curve ⁹. With this smaller halftime to recovery, we would expect the recovery curve to give a diffusion coefficient closer to 1.0 μm²/s.

As it is obvious that there is much controversy over the different Bcd gradient models, it is important to address the apparent discrepancies in the estimation of the Bcd diffusion coefficient to ultimately rule out the SDD or competing models ¹³. Also, as computational modeling, by integrating constituent protein dynamics with developmental assumptions and observations, continues to be a valuable tool in determining the efficacy of certain gradient formation models, it will be important to have accurate estimates of the protein kinetics within these models. Therefore, we sought to investigate the source of the apparent discrepancies within the Bcd diffusion estimate.

To begin to evaluate these discrepancies, we created a detailed computational model of the two-photon FRAP experiment performed by Gregor et al.⁹ Here, we demonstrate that there is a significant difference between the input diffusion coefficient used in the model and the measured diffusion coefficient, as it would be estimated by the procedure of Gregor et al.⁹, for a wide range of values. The discrepancy originates from the use of the analytical recovery model of Brown et al.³, which assumes nearly instantaneous bleaching, whereas the experiments of Gregor et al.⁹ required several seconds to complete the bleaching process. Since the bleaching time scale is comparable to the recovery time scale, significant recovery will occur before the bleaching scan in a two-photon system is complete. As a result, our model predicts that the mitotic Bcd diffusion coefficient is nearly three times larger than originally estimated ⁹. This revised estimate is within the range required for gradient establishment by the prevailing simple diffusive transport model (SDD). This result also demonstrates the value of integrating computational and experimental studies to more accurately estimate biomolecular transport properties.

RESULTS

The FRAP experiment, as performed by Gregor et al.⁹, consists of three aspects that our model simulates: 1) diffusion of Bcd-GFP within a defined volume, 2) photobleaching a 16 × 16 × 7 μm³ volume with a two-photon scanning laser, and 3) an observation period where photon counts within the photobleached volume are measured at 0.5 s intervals. In our model, we controlled the input Bcd diffusion coefficient (D_input) and then compared this to the measured diffusion coefficient (D_meas) obtained via fitting our simulated recovery curve to the 3D diffusion equation used by Gregor et al.⁹ (see Experimental Procedures). An example of the simulated experiment output is shown in Fig. 1a.

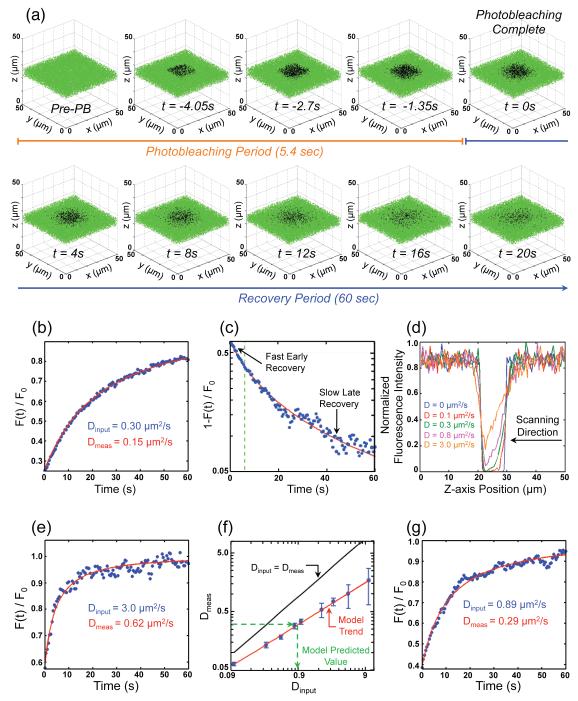
FIGURE 1.

(a) Representative example of simulated fluorescence recovery for molecules with a diffusion coefficient of D_input = 1.0 μm²/s. Green and black dots represent discrete fluorescent and photobleached molecules, respectively. Sequential images include progressive photobleach images (t<0) followed by images from 0-20 s post-bleach at 4 s intervals. Only a 7 μm wide slice from the 50 × 50 × 50 μm³ volume is shown so that the photobleached region in the center of the model volume may be more easily visualized. (b) Recovery curve for molecules with D_input = 0.30 μm²/s. Data points are calculated at 0.5 s intervals and are represented by blue dots. Red line represents the solution to the 3D diffusion equation³ yielding the corresponding diffusion coefficient (D_meas). (c) Log-linear plot of a typical recovery curve after instantaneous photobleaching (blue dots) and resulting fit from Brown et al.³ (red line) for molecules with D_input = 1.0 μm²/s. Diffusive fluorescence recovery rate changes over time. Early recovery is rapid, followed by a relatively slow sustained recovery. Green dashed line marks the end of the experimental photobleaching period (~6 s)⁹. To quantitatively characterize the recovery rate as a function of time, it was assumed that F(t)/F₀ = 1-e^−kt, and therefore the rate (k) is given by the slope of the curve on a log-linear scale. (d) Fluorescence intensity cross-section along the optical imaging axis of the bleach zone at t = 0 sec (photobleaching complete) for a range of D_input. D_input = 0 μm²/s (shown in blue) represents instantaneous photobleaching. Each cross-section trace is normalized to the maximum fluorescence reading of all five traces. (e) Recovery curve, similar to that shown in (b), for molecules with D_input = 3.0 μm²/s. (f) Log-log plot of D_meas versus D_input for a range of diffusion coefficients (blue dots ± SD). Red line represents a fit to the simulated data (blue dots), while black line represents the expected values (D_meas = D_input). The model predicted diffusion coefficient of D = 0.89 μm²/s was obtained through inverse prediction of the D_input that resulted in D_meas = 0.30 μm²/s, based on the model trend (red line). (g) Recovery curve, similar to that shown in (b) and (e), for molecules with D_input = 0.89 μm²/s. Recovery curve has similar recovery timescale and measured diffusion coefficient (D_meas) to that previously published⁹.

We started by first examining the previously reported diffusion coefficient of D = 0.30 μm²/s ⁹. With this value for D_input, the recovery curve did not reach steady state within the observation period and resulted in D_meas two fold lower than D_input (Fig. 1b). To insure that our result was not due to a discrepancy within our model, we used our computational model to simulate a spot-photobleaching two-photon FRAP experiment, thereby upholding the assumptions of the model derived by Brown et al.³ (see Experimental Procedures), for D_input values ranging from 0.1 – 10 μm²/s (data not shown). Regression analysis of the expected values (D_input) versus the measured values (D_meas) for the spot-photobleaching simulations resulted in a trend-line with a slope that was not significantly different than 1 (p = 0.62, Student’s T-test). This demonstrated that the previous difference between D_input and D_meas was not due to a discrepancy within our model, nor to an error in the diffusion equation of Brown et al.³, but instead must have been due to the inapplicability of the assumptions inherent within the equation derived by Brown et al.³ to a large volume pattern-photobleaching experiment. In particular, the equation of Brown et al.³ assumes that bleaching is nearly instantaneous compared to recovery, whereas in the experiment of Gregor et al.⁹, the timescale of bleaching (6 sec) was comparable to the timescale of recovery (7 sec).

As shown by a log-linear plot of a diffusion recovery curve (1-F(t)/F₀) after instantaneous photobleaching, simple diffusive recovery does not follow a single exponential (Fig. 1c). While the diffusion equation does not predict exponential recovery, it is important to note that the diffusive fluorescence recovery rate is not constant over time. In particular, initial recovery is fast, followed by a slower sustained recovery. An appreciable change in the rate of recovery occurs during the time period for photobleaching, and so subsequently observed fluorescence recovery is dominated by the slower sustained recovery (Fig. 1c). Examining the fluorescence distribution across the photobleached region when bleaching is complete (t = 0 sec) shows the predicted extent of recovery during the photobleaching period (Fig. 1d). Recovery during photobleaching is spatially asymmetric within the bleach zone with respect to the scanning direction of the two-photon laser and increases with increasing input diffusion coefficients (Fig. 1d). Because of the relatively long time for photobleaching (6 sec), substantial recovery occurs in the bleach zone prior to the recovery imaging when the diffusion coefficient is set to be at or above that previously estimated ⁹ (Fig. 1c,d). In the experimental setting, recovery during the time to bleach would result in a visible fluorescence gradient with respect to the laser scanning direction (e.g. z-axis in Fig. 1d).

This result led us to use our model to examine a range of values for D_input in order to determine what value for D_input best matched the data previously published ⁹. For each D_input, we found D_meas to be significantly different, with this difference increasing for greater values of D_input (Fig. 1e,f). This trend is not surprising considering that the amount of recovery during bleaching increases for greater values of D_input as well (Fig. 1d). By fitting this data to a log-log plot of D_meas versus D_input, our model predicts that D_input = 0.89 ± 0.06 μm²/s (mean ± SEM) will result in D_meas = 0.30 μm²/s (Fig. 1f). As seen in Fig. 1g, D_input = 0.89 μm²/s produced a recovery curve with a similar recovery timescale and estimated diffusion coefficient to that previously published ⁹. Simulation of an equal number of experiments as originally performed ⁹, with D_input equal to our predicted value (D_input = 0.89 μm²/s), resulted in an estimated Bcd diffusion coefficient equal to that originally estimated (D_meas = 0.30 ± 0.01 μm²/s, mean ± SEM) (p = 0.82, Student’s T-test). Using our predicted value in the halftime to recovery equation from above (τ_1/2 = δ²/(2D)) gives us τ_1/2 = 7 s, which is the halftime estimated from the published recovery curve ⁹. Therefore, we conclude that the mitotic Bcd diffusion coefficient is approximately 3-fold larger than the value reported previously ⁹.

DISCUSSION

Since the discovery of Bcd’s role in development, a major question has been: how does it establish the observed anterior to posterior gradient? Initially a simple synthesis, diffusion, and uniform degradation (SDD) model was generally accepted, however, the recently published diffusion coefficient of 0.30 μm²/s found in live embryos suggested the invalidity of the SDD model, since such a small diffusion coefficient would not be sufficient to establish the gradient in the observed developmental timescale ⁹. Upon reassessment of this measurement, we estimate the diffusion coefficient of Bcd-GFP to be closer to D = 0.89 ± 0.06 μm²/s (mean ± SEM).

We then asked whether our revised estimate was consistent with the minimum diffusion coefficient required for the SDD model. Previously, it was believed that a diffusion coefficient of D >> 2 μm²/s was needed to set up a 100 μm gradient that reached stability in 90 min via the SDD model ⁹. However, this conclusion only holds if stability in nuclear Bcd concentrations implies stability in the overall Bcd gradient, which is not necessarily true ^1,2. Therefore, to re-estimate the minimum necessary diffusion coefficient we used the overall Bcd gradient profiles at specific developmental time points (e.g. at 50 and 160 min post-oviposition). At 50 min, the Bcd concentration decays to 1/e by 20% of the total embryo length (EL), or 100 μm in a 500 μm embryo ⁹. At 160 min, the Bcd concentration decays to 1/e at 30% EL, or 150 μm ⁹. However, we note that the Bcd source is not necessarily at the anterior-most end of the embryo. Rather, when cortical Bcd levels are projected along the anterior-posterior axis, the concentration peak is ~40 μm from the anterior end of the embryo ¹¹. Therefore, we estimate that the decay lengths at 50 and 160 min post-oviposition are actually closer to 60 μm and 110 μm, respectively. In the absence of degradation, the minimum diffusion coefficient for establishing a decay of length λ in time. τ is given by D = λ²/(2τ). Therefore, a minimum diffusion coefficient of D > 0.6 μm²/s, in the absence of degradation, is sufficient to form the observed Bcd profile at early and late nuclear cycles. Based on this re-estimation, we conclude that the SDD model is not invalidated by our revised Bcd diffusion coefficient estimate (D = 0.89 ± 0.06 μm²/s).

It is important to note that our revised Bcd diffusion coefficient applies only to diffusion during mitosis 13, and that the value of the diffusion coefficient has yet to be measured during mitoses 1-12 and during each interphase. In the case of interphase, Bcd is dynamically exchanged between the nuclei and cytoplasm with a significant fraction of Bcd present in each domain ⁹, implying that the contributions of both domains to the net transport of Bcd need to be considered. Further, the estimated mitotic diffusion coefficient is more than 10-fold lower than measured for dextran of similar size ⁸, strongly suggesting that mitotic Bcd exists in complexes that are relatively large and slow to diffuse. To truly evaluate the SDD model, we need to estimate the spatially-temporally averaged Bcd diffusion coefficient. We estimate that the spatially-temporally averaged diffusion coefficient (D_eff) is given by

$${\mathrm{D}}_{\mathrm{eff}}={\mathrm{D}}_{\mathrm{mit}}{\mathrm{f}}_{\mathrm{mit}}+<{\mathrm{D}}_{\mathrm{int}}>{\mathrm{f}}_{\mathrm{int}}$$ [1]

where D_mit is the mitotic diffusion coefficient, < D_int > is the effective averaged interphase diffusion coefficient, f_mit is the fraction of time the embryo spends in mitosis, and f_int is the fraction of time the embryo spends in interphase. Because Bcd is not limited to one embryonic domain during interphase, < D_int > should be estimated from the long-standing Maxwell expression for diffusion in a biphasic medium ^12,14,16. This estimation is dependent on two assumptions, that Bcd diffuses faster in the cytoplasm compared to nuclei and that the nuclear volume fraction of Bcd is relatively small. While it is clear that the nuclear volume fraction is relatively small (0.03, 0.07, 0.09, 0.13, and 0.13 in nuclear cycles 10-14, respectively), further experiments are needed to compare the cytoplasmic and nuclear diffusion coefficients during interphase. However, even if the cytoplasmic and nuclear diffusion coefficients are equal, confining Bcd within the nucleus of a defined volume will effectively reduce the diffusion due to relatively long time constant for nuclear export ⁹. In summary, to test the SDD model, or any possible alternative models, it will be important to estimate both interphase and mitotic diffusion coefficients in space and time during development.

COMPUTATIONAL MODEL

All custom code was written for Monte Carlo simulations and curve fitting using MATLAB 7.6.0 (R2008a) (The MathWorks, Inc., Natick, MA).

General Description of the Model

Initially Bcd-GFP molecules are randomly distributed within a 50 × 50 × 50 μm³ volume. This model volume represents a subvolume from the anterior portion of the embryo and provides a source of fluorescent molecules to diffuse into the photobleached area during recovery. Diffusion within the volume is modeled as a stochastic process by taking a random step of size δ = (2Dt)^1/2, where D is the diffusion coefficient and t is the time step (3 ms during bleaching and 5 ms during recovery), in each of the three Cartesian coordinate directions. Considering that during the short experimental period (~1 minute), Bcd-GFP concentration should remain nearly constant, there is no net flux of molecules in or out of our modeled volume. To accomplish this, each boundary is treated as a reflective surface.

Photobleaching

The 16 × 16 × 7 μm³ photobleached volume is modeled as a 3D lattice in the center of our 50 × 50 × 50 μm³ model volume, where each point in the lattice is separated by 1 μm on each side. The lattice points represent the focal point of the two-photon laser at each time step as the laser moves through the photobleach volume. With a two-photon laser, excitation is confined to a small ellipsoidal volume where the photon flux is high enough to produce two-photon fluorescence excitation. The size and shape of the ellipsoid critically depends on the numerical aperture (NA) of the microscope’s objective lens ¹⁵. In the experiments of Gregor et al.⁹, a 0.8 NA objective lens is used, which produces a prolate excitation ellipsoid with estimated x and y radii of 0.5 μm and z radius of 1.5 μm ¹⁵. Because our model has a finite number of laser steps, each spaced 1 μm apart, an excitation ellipsoid with x and y radii equal to 0.5 μm would be tangential about the equator to each adjacent ellipsoid, thus creating empty space where molecules could potentially avoid bleaching. In order to compensate for this inability to model a continuous scan, we increased the ellipsoidal x and y radii to 0.75 μm to increase laser overlap between time steps. The two-photon laser steps through seven xy-planes, starting at the top and working down. The full laser scan takes 5.4 s with a time step of 3 ms. At each time step during the photobleaching period, the position of the ellipsoid is calculated, molecules within the ellipsoid are photobleached based on a 50% bleach efficiency, each molecule diffuses, and the ellipsoid is moved to the next lattice point.

Observation Period and Data Analysis

Immediately after photobleaching was completed, the number of fluorescent molecules within the 16 × 16 × 7 μm³ volume was counted at 0.5 sec intervals while diffusion events occurred at 5 ms time intervals. The number of molecules within the box at a given time point was assumed to be the fluorescence (F(t)). The fluorescence was normalized to a molecule count within the same 16 × 16 × 7 μm³ volume prior to photobleaching (F₀, the pre-bleach equilibrium fluorescence).

Simulated recovery curves were fit to the 3D diffusion equation, as described in Brown et al.³, using the embedded MATLAB function nlinfit. In the diffusion equation, w_r and w_z correspond to the dimensions of the photobleached region and are typically the two-photon 1/e² beam dimensions in a spot-bleaching experiment. Since this is not a spot-photobleaching experiment, however, the values of w_r and w_z come from the 16 × 16 × 7 μm³ volume, which is assumed to have radial and axial radii of 8 μm and 3.5 μm respectively. β is referred to as the “depth parameter,” and is related to the bleach depth, which is defined as [F₀ – F(t = 0)]/F₀. Essentially β is a measurement of the photobleaching efficiency, and it determines the starting value as well as the initial slope of the fit curve, but has little effect on the diffusion coefficient estimation ³. The value for β was constrained for each recovery curve by determining the value that corresponded to the normalized fluorescence at t =0 (<F(t =0)/F₀>).

Spot-photobleaching

During the spot-photobleaching simulations, an ellipsoid pulse of the same size as was used in our model photobleaching simulations was delivered for a period of 20 μs to the center of a 10 × 10 × 10 μm³ volume while diffusion occurred at 1 μs time intervals. Based on the 3D diffusion equation from Brown et al.³, complete recovery within our ellipsoid should occur within 0.3-0.5 s for molecules with a diffusion coefficient of D ~ 1.0 μm²/s. Therefore, photon counts within the volume of the ellipsoid were made at 2.5 ms intervals for a period of 0.3 s. Recovery curves were fit to a solution to the 3D diffusion equation ³, using the same method as described above, in order to estimate the measured diffusion coefficient.