Teaching Biology through Statistics: Application of Statistical Methods in Genetics and Zoology Courses

Abstract

Incorporation of mathematics into biology curricula is critical to underscore for undergraduate students the relevance of mathematics to most fields of biology and the usefulness of developing quantitative process skills demanded in modern biology. At our institution, we have made significant changes to better integrate mathematics into the undergraduate biology curriculum. The curricular revision included changes in the suggested course sequence, addition of statistics and precalculus as prerequisites to core science courses, and incorporating interdisciplinary (math–biology) learning activities in genetics and zoology courses. In this article, we describe the activities developed for these two courses and the assessment tools used to measure the learning that took place with respect to biology and statistics. We distinguished the effectiveness of these learning opportunities in helping students improve their understanding of the math and statistical concepts addressed and, more importantly, their ability to apply them to solve a biological problem. We also identified areas that need emphasis in both biology and mathematics courses. In light of our observations, we recommend best practices that biology and mathematics academic departments can implement to train undergraduates for the demands of modern biology.

INTRODUCTION

Biology and mathematics have been interconnected for a long time. In fact, many biological processes are described by mathematical equations and certain mathematical concepts have arisen directly from the need to describe interactions, relationships, and processes in living systems (Jungck, 1997; Cohen, 2004). This has led to the concept of interdisciplines such as biophysics, biostatistics, and bioinformatics, to mention a few. Modern technology allows researchers to rapidly generate a vast amount of data that are shared through virtual databases and, depending on how they are analyzed, can serve to answer a variety of questions. Examples are the field of genomics, which demands the need for mathematics and computer science to significantly contribute to modern biology (Ditty et al., 2010); or phylogenetic systematics, which requires mathematical algorithms and statistical tests to propose hypotheses regarding the evolutionary relationships of our biodiversity (Hedges et al., 2008). One specific example of the relevance of this integration is the work done by structural biologists (Tsai et al., 2007). These scientists use crystallography to study the three-dimensional structure of a protein, a process that applies geometry and physics. With the aid of computational models and statistics, structural biologists test several hypotheses to explain a protein's function based on its structure. Furthermore, they can use bioinformatics to trace the evolutionary history of a protein. Thus, now more than ever, biologists need to be proficient in mathematics and computer science to be able to acquire, analyze, and understand the significance of data (Gross, 2004).

Despite the anticipated demands for greater math emphasis in biology education, curricular reforms have not complied with the need to integrate mathematics and computational sciences into undergraduate biology courses (Bialek and Botstein, 2004; Klymkowsky, 2005). Most science and mathematics courses are taught to undergraduate students as a set of facts isolated from related fields, resulting in students with a shortsighted view of their own disciplines. Undergraduate students majoring in biology often question why they are required to take statistics and other mathematics. The problem becomes more evident when we as researchers have students working in our labs and discover that even bright students, who passed these math and statistics requirements, are incapable of applying the concepts to solve a biological question or as tools for analysis of data they generate in the lab. Therefore, incorporation of mathematics into the biology curriculum is critical to underscore for our students the importance and usefulness of mathematics in most fields of biology (National Research Council, 2003; Marsteller et al., 2010). The challenge is to determine how this can be accomplished. How do we help our students see the relevance of mathematics and statistics in biology? How do we offer our students the tools to confront the new interdisciplinary problems in biology?

At our institution, we have made significant changes to better integrate mathematics into the undergraduate biology curriculum. Curricular revision, implemented in 2008, included changes in the suggested course sequence and the addition of statistics and precalculus as prerequisites to core science courses such as genetics and zoology. In response to these efforts and a National Institutes of Health Minority Access to Research Careers (NIH-MARC)-funded initiative to improve mathematical skills among undergraduate biology students, we decided to modify the way we taught our genetics and zoology courses (Colon, 2010). We provided opportunities to apply statistical methods to solve biological problems based on real data, expecting these opportunities would help our students increase their understanding of fundamental concepts in statistics, see how statistics helped interpret biological patterns, and develop scientific process skills. In this article, we describe the activities developed to attain these goals and the assessment tools employed to measure improved learning in biology and statistics. In light of the current need for the integration of science and mathematics, this work describes a feasible way in which students can be engaged not just in learning about these fields but in valuing the need for computational literacy in biology. We present our efforts in two very different courses, genetics and zoology, as examples of how this can be done with diverse subject matter. Hopefully, students who learn the applicability of math to biology in this way will be better prepared to succeed in graduate studies and will contribute to the development of new ways in which the fields of math and biology can enhance knowledge (Miller and Walston, 2010).

The time—now—and place—Puerto Rico—chosen to implement efforts to improve mathematical skills among biology students is just right for several reasons. The University of Puerto Rico (UPR) has a history of National Science Foundation (NSF)-funded initiatives to improve teacher preparation in the sciences and mathematics (Scope Sequence and Coordination; Systemic Statewide Initiatives; Collaborative for Excellence in Teacher Preparation; Math and Science Partnerships). Despite these efforts, teachers are still deficient in quantitative skills and limited in their ability to show their students the connections between these disciplines (Quintero, 2006). Future math and biology teachers learn their science content in our courses together with science majors. Therefore, the learning activities we provide in the classroom have the potential to influence students further down on the educational ladder. In addition, the curricular reform in our biology department calls for student involvement in undergraduate research. Development of quantitative skills with relevance to biological problems, as modeled herein, will help these students to see the application of mathematics to bioinformatics, biotechnology, rates of change, and data analysis. Finally, the Puerto Rican government has proposed to improve the local economy by stimulating the biotechnology industry in what they have referred to as an “economy of knowledge” (INDUNIV Research Consortium, 2010). As a result, several consortia between industry and UPR have been developed to promote student training in biotechnology and development of scientific process skills (Potera, 2007). Undergraduate teaching initiatives that promote interdisciplinarity between math and science are key to achieving this goal.

STUDENT PROFILE AND TARGETED COURSES

The student populations in the genetics and zoology courses are similar, as they have already completed a year of introductory biology; however, while statistics is a prerequisite for genetics, not all students in zoology have taken it.

Description of Activities in the Genetics Course

Genetics is a 1.5-h lecture course taught twice weekly independent of the genetics laboratory. Students usually take the lab the semester after they take the lecture course. Most of the activities that emphasized development of quantitative skills in genetics were conducted in the first 6 wk of the semester. These activities involved solving genetic crosses; analyzing data describing the distribution of quantitative traits, and allelic, genotypic, and phenotypic frequencies; and genetic mapping of eukaryotic chromosomes. Typically, students allocated 30–40 min of the class period to solving and discussing problem sets in cooperative groups. Additional quantitative exercises with supplementary explanation modules were provided for students to solve at home and discuss later in the week in scheduled peer-tutoring sessions and/or office hours with the professor. The Blackboard (2011) academic online platform was used to distribute supplementary modules, practice exercises, and weekly quizzes that enforced student preparation. The supplementary statistics unit addressed concepts relevant to the analysis of genetics data, such as the basic laws of probability, binomial and chi-square probability distributions, defining a null hypothesis, and the application of the chi-square as a “goodness of fit” test between observed and expected genetic outcomes. The peer-tutoring walk-in sessions were an important component of this course, because they provided another opportunity for students to get help on the assigned problem sets. These peer mentors were volunteer undergraduate students who had passed the genetics course in previous semesters with an A or B. The genetics tutors held weekly meetings with the professor (M.C.B.) to discuss the material to be covered in class, clarify their own doubts, and conceive ways in which they would work with the students. As part of their training, tutors also took a weekly quiz through Blackboard that included content-related questions, as well as math–genetics exercises.

With the purpose of measuring the understanding of basic statistics concepts that students brought into the genetics course, and later, assessing the knowledge gained from curricular activities provided throughout the course, we implemented an assessment instrument in a pretest/posttest manner. For this, we translated and slightly modified a survey by Metz (2008) designed to measure knowledge of statistics among incoming students in general biology. The modified test instrument included two different surveys: a 12-item pretest and a 12-item posttest that shared only five identical questions. The other seven questions measured knowledge of the same concepts, but encouraged higher-level thinking skills by requiring application of the quantitative concepts discussed in class to solve genetics problems. The concepts assessed in this pretest/posttest manner included: basic probability, descriptive statistics, p value, r value, graph interpretations, and cause-and-effect relationships (Metz, 2008). Content validity was achieved by the critical examination of the test by three other genetics professors and two biology professors engaged in science education and math–biology integration. The pretest survey was administered on the first day of class, whereas the posttest was administered during the last week of the semester. Students were asked to voluntarily complete both surveys. Although the quantitative activities were offered to all the students in the course (n = 220), we report the learning results of only a small session taught by one of the authors (M.C.B.). Of 33 students registered for this session, only 16 students took both the pretest and the posttest. Analyses of the results for the 16 students taking the pretest and the posttest included a graphic view of the change in score distribution between the pretest and the posttest (Figure 1), and a chi-square test to determine whether the levels of achievement per concept were independent of the knowledge gained after instruction (pretest vs. posttest). All the class and assessment materials, including the pretests and posttests, are available upon request in Spanish and English (see Supplemental Material 1 and 2 or contact the corresponding author).

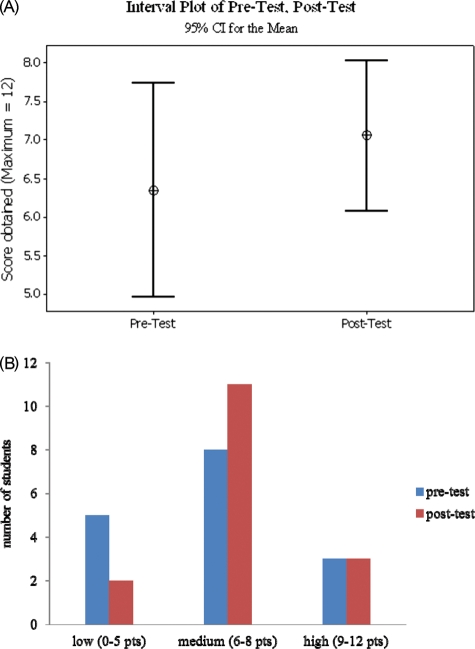
Figure 1.

(A) Interval plot for mean pretest and posttest scores in genetics, with 95% confidence intervals. (B) Change in levels of achievement throughout the genetics course as measured by the pretest and the posttest. Low achievement is equivalent to a score of 0–5 points; medium, 6–8 points; and high, 9–12 points out of a maximum of 12 available points for both tests.

Description of Activities in the Zoology Course

A total of 40 students were enrolled in the zoology course. During the semester, students undertook three projects requiring the application of some kind of computational skill to answer questions about animals. The first project aimed at developing simple bioinformatics skills by requiring consultation, analysis, and synthesis of data available in the International Union for Conservation of Nature website. The second project required the application of statistical methods to determine morphological patterns in bats. The third project involved the application of precalculus and calculus concepts to develop a model of sustainable yield for two valuable resources in an Amazonian forest. The projects were presented in class as biological problems, and the needed statistical or mathematical skills were discussed and explained in the context of the question. Students worked in pairs, and had 2 wk to turn in a five-page written report, which included appropriate tables and figures. Because we focus on the integration of statistics to biology in this paper, we limit our discussion to the second project, which dealt with bat morphology and statistics.

Students were given an Excel worksheet with data on the wingspan (cm), weight (g), and sex (male vs. female) of a neotropical bat, Artibeus jamaicensis, commonly known as the fruit bat because of its alimentary habits. The data were based on field observations (Rodriguez-Duran, 2005) but were artificially generated to ensure that they would meet all the assumptions of parametric statistics. In class, we discussed the ecology and reproductive biology of this bat, mentioning relevant details, such as the fact that Caribbean fruit bats reproduce twice a year and female fruit bats give birth to a single offspring, which they carry around, and lactate for 3–4 mo (Gannon et al., 2005). Students were expected to analyze the data by applying simple descriptive (mean, variance, SD, range) and parametric (t test and linear regression) statistics in order to answer the biological and statistical questions described in Table 1. Before analyzing the data, students were required to formulate a biological hypothesis for each question and to state the null and alternative hypotheses for each statistical test considered. Finally, students were expected to predict which sex was capable of carrying more weight during flight, and discuss what selective forces may have favored the evolution of the characteristics of body size and morphology observed in these bats.

Table 1.

Biological and statistical questions addressed by the students through the bat activity in zoology class

Biological questions	Statistical understanding questions
1. Do you expect to see differences in the wingspan and weight between male and female bats? Hypothesize.	1. Test for differences in wingspan and weight between sexes. State your null and alternative hypotheses. What does it mean to have statistical significance?
2. If there are differences, can they be appreciated graphically? Illustrate.	2. What probability value must be associated to a statistic in order to reject your null hypothesis? What does it mean to have a p > 0.05?
3. Do you expect to see a relationship between wingspan and weight for all bats? Predict how this relationship might be and justify.	3. What does it mean to have a significant Pearson product-moment correlation coefficient (r) between two variables?
4. If present, can this relationship be illustrated graphically?	4. What is the difference between a positive or negative r?
5. Does this relationship hold for males? For females? Explain.	5. What additional information can you get from a linear regression if you have already determined a significant positive r?

To assess the heterogeneity of the student population, we used clickers (InterWrite Personal Response System, GTCO Calcomp, Columbia, MD; Smith et al., 2011) to ask questions about their gender, ethnicity, year at the university, courses approved, research experience, and, more relevant to this project, their background in and attitude toward math/statistics. The effectiveness of the bat activity in promoting biological and statistical knowledge was assessed by their performance in their written reports, which was evaluated using a rubric that measured the level of achievement of the following goals: A) the biological hypotheses reflect knowledge on the biology, ecology, or physiology of the bats; B) the statistical hypotheses (H₀ and H_a) were correctly stated for every test applied; C) the p value associated with each statistic was properly reported and correctly interpreted biologically; D) the data were graphed in a way that would properly describe a pattern; E) the biological interpretation of the graph was accurate; and F–J) the answers to statistical concept questions (1–5) as described in Table 1 were correct. Students could score within a range of 1–4 for each of these learning objectives, where 4 = completely achieved, 3 = somewhat achieved, 2 = poorly achieved, and 1 = not achieved (see Table 2).

Table 2.

Results of rubric to assess learning gain after the zoology bat activity^a

	Achievement level score
Learning objective	4	3	2	1
A. The biological hypotheses reflect knowledge on the biology, ecology, or physiology of the bats	5 (25%)	6 (30%)	8 (40%)	1 (5%)
B. The statistical hypotheses (H0, and Ha) were correctly stated for every test applied	6 (30%)	3 (15%)	9 (45%)	2 (10%)
C. The p value associated with each statistic was properly reported and correctly interpreted biologically	3 (15%)	4 (20%)	6 (30%)	7 (35%)
D. The data were graphed in a way that would properly describe a pattern	14 (70%)	4 (20%)	2 (10%)	0 (0%)
E. The biological interpretation of the graph was accurate.	6 (30%)	6 (30%)	5 (25%)	3 (15%)
F. Understanding statistical significance	3 (15%)	4 (20%)	6 (30%)	7 (35%)
G. Understanding p value	3 (15%)	4 (20%)	6 (30%)	7 (35%)
H. Understanding applicability of Pearson product-moment correlation coefficient	6 (30%)	6 (30%)	5 (25%)	3 (15%)
I. Differentiating between positive and negative correlations	6 (30%)	7 (35%)	5 (25%)	2 (10%)
J. Understanding the added mathematical value of a linear regression	3 (15%)	3 (15%)	7 (35%)	7 (35%)

^a Students could score between 1 and 4 for each learning objective, where 4 = completely achieved, 3 = somewhat achieved, 2 = poorly achieved, and 1 = not achieved.

OUTCOMES

Genetics

The overall student achievement, evaluated by the distribution of student test scores, improved after instruction, in spite of the increase in complexity of some of the questions in the posttest (Figure 1A and Tables 3 and 4). When student performance was categorized by levels of achievement as low (0–5 points/12 available points), medium (6–8 points/12 points), or high (9–12 points/12 points), it was evident that the greatest change after instruction was among students improving from a low to a medium level (Figure 1B). In the pretest, close to 35% of the students scored poorly, while in the posttest more than one-half of these students improved to the medium level of achievement (Figure 1B).

Table 3.

Item analysis of identical questions in the pretest and posttest in genetics (n = 16)^a

		% Correct answers
Quantitative concept	Question	Pretest	Posttest
Basic probability	A bag has seven red balls and two white balls; what is the probability of drawing a white ball?	62.5	87.5
Probability applied to genetics	What combination of gametes is generated from an organism with genotype EeVv?	93.8	87.5
Probability applied to genetics	What percentage of EeVv organisms will result from the cross between EeVv and eevv?	56.3	75
Data interpretation	Given the number of individuals with blood types M, MN, and N in two different populations, determine the frequency of the M allele.	56.3	62.5
Data interpretation	Given the number of individuals with blood types M, MN, and N in two different populations, choose the best interpretation of the results.	37.5	50

^a The alternative choices for each of the questions can be obtained by requesting a copy of the tests from the authors.

Table 4.

Item analysis of different questions in the pretest and posttest in genetics (n = 16)^a

	Pretest				Posttest
General concept	Item number	Bloom's taxonomy	Question	% of correct answers	Item number	Bloom's taxonomy	Question	% of correct answers
Probability	2	Application	Two fertilization events are independent. What is the probability that a couple with two boys will have another boy?	81.3	1	Analysis	Using a mix with 60% adenine, 20% guanine, 10% cytosine, and 10% thymine to make an in vitro polymerization reaction, what is the probability of obtaining an adenine–cytosine–thymine triplet?	75
	6	Application	A bag has seven red balls and two white balls. What is the probability that when drawing two balls, both of them are white?	25	12	Analysis	What is the probability that two carriers for the recessive sickle cell trait have two kids, both affected or both normal?	25
Graph interpretation	3	Analysis	Which type of graph is used to evaluate the relationship between two quantitative variables?	62.5	2	Analysis	Which graph would you use to evaluate the relationship between the height of the plant and the weight of the fruit?	81.25
	4	Analysis	Which type of graph is used to evaluate the distribution of potato weights under certain conditions?	31.3	8	Evaluation	Given a graph with the frequencies of blood types A, B, AB, and O in two different populations, choose the sentence with an adequate interpretation of the data.	50
	11	Evaluation	Given two different graphs that plot the number of individuals with three different genotypes vs. weight, choose the sentence that better describes the data.	18.8	9	Evaluation	Given two different graphs that plot the number of individuals with three different genotypes vs. weight, choose the sentence that better describes the data.	68.75
Correlation coefficient	12	Evaluation	A table with three columns with data from cattle is shown: father weight (Z), mother weight (X), and progeny weight (Y). Interpret the r value.	18.8	3	Evaluation	Given data from height of the plant and weight of the fruit, r = 0.89, determine the association of the two traits.	62.5
p Value	5	Evaluation	Given the average peak size in two populations of Geospiza fortis, and the p value, determine if the differences between the two populations is significant.	56.3	7	Evaluation	Given a graph with the frequencies of blood types A, B, AB, and O in two different populations, choose the sentence with an adequate interpretation of the p value and its statistical significance.	37.5
					4	Creating	The chi-square analysis of a dihybrid cross determines that the differences between the observed and the expected frequencies in F2 are not significant. If the critical value is 0.5, find the associated p value.	25

^aThe alternative choices for each of the questions can be obtained by requesting a copy of the tests from the authors.

By looking at student performance on each of the 12 items, we were able to identify specific skills where students showed improvement in the posttest. Table 3 summarizes student outcomes on questions that were identical in the pretest and the posttest, considerable improvement was shown on most items. These questions included statistical concepts of basic probability, probability applied to genetics, and data interpretation, which were discussed during the first 6 wk of the course relevant to the topics of Mendelian genetics, population genetics, and quantitative genetics. The one item that showed no change, but was well achieved even in the pretest, asked students to predict the gametes involved in a cross between individuals of known genotype. This suggests that students understood this basic Mendelian concept, perhaps from studying it in their general biology course. The item in this group with the lowest correct answer rate dealt with interpretation of data comparing three blood groups of two different populations (Table 3; 10 in the pretest, eight in the posttest). In spite of instruction, only 50% of the students were able to determine allelic frequencies for blood groups, given the phenotypic and genotypic frequencies for two populations. This question was at the highest level of Bloom's taxonomy of learning domains (Bloom and Krathwohl, 1956), because it required comparison, evaluation, and formulation of a conclusion regarding the phenotypic, genotypic, and allelic frequencies of two populations. Overall, the identical pretest/posttest questions revealed that, while most students acquired knowledge in statistics that improved their ability to apply statistics to genetics, only a few students reached higher thinking levels requiring evaluation and synthesis (creation) of conclusions.

Table 4 summarizes student outcomes in the questions that were modified from the pretest and the posttest. All of these questions involved analysis of quantitative concepts in a biological context. Students improved mostly in skills that required interpretation of graphs and correlation coefficients. This outcome suggests that efforts to provide exercises where students had to discern scientific patterns from graphical data and calculate correlation coefficients in class proved beneficial (see item 12 in the pretest and 3 in the posttest in Table 4). However, the concept of probability did not show considerable improvement, perhaps because the questions were applied to difficult genetics concepts that required higher levels of analysis than the ones presented in the pretest. Questions dealing with interpretation of p value presented a decrease in correct responses in the posttest. The items testing knowledge and understanding of the p value (items 4 and 7) had different elements and distractors in the posttest that augmented the difficulty and the level of analysis required to answer the question. The decrease in scores observed for these items shows students had a very basic knowledge of the concept of p value before the genetics course, and our efforts to improve their understanding of it to a point where they could synthesize resulting data and create a conclusion were not enough.

Zoology

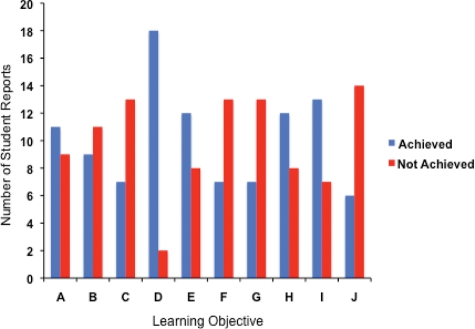
The population of students enrolled in this experimental zoology course was 100% Hispanic, 75% female, 65% upperclassmen (third year or greater), and, as far as their mathematical background, 100% had taken college precalculus and 65% had taken calculus, but only 52% of the students had taken a statistics course. When asked “Do you think that mathematics is very useful for biologists?” in a pre/postinstruction manner, the number of students agreeing increased at the end of the semester, and their responses were significantly associated with postinstruction (χ² = 22.789, degrees of freedom = 3, p = 0.000). Table 2 and Figure 2 summarize the learning gain in biology and statistics obtained by zoology students after working on the bat activity. The results show that learning objectives B, C, F, G, and J were not achieved by students, regardless of class instruction and the opportunity to work on a relevant biological problem requiring the application of statistical methods. Misconceptions were noted in the inability to formulate hypotheses and understanding of the significance of the probability that statistical tests associate to these hypotheses. For example, when obtaining a p value ≤ 0.05 for an f statistic of a regression equation between two variables, many students did not know whether they should reject the null hypothesis (H₀: there is no relationship between the variables; slope = 0) and accept the alternative (H_a: there is a linear relationship between the variables; slope ≠ 0), or vice versa. This suggests that students confused type I (α) and type II (β) errors and, as a consequence, often drew incorrect conclusions on their results. Although the concept of correlation between variables with sex was understood, as indicated by students being able to ascertain that bat weight and wingspan were associated with sex from calculating high Pearson product-moment correlation coefficients (r), students were unable to distinguish the added value of a regression analysis. Only 30% of the student reports showed complete or partial achievement of this objective (Table 2). This small group of students included at least two of the following critical elements in their answers: 1) a discussion of how regression can add information on rate of change by providing a slope for a line describing the relationship between the dependent (weight) and independent (wingspan) variables; 2) a description of how the linear model can serve to predict the wingspan of a bat with a particular weight; 3) an acknowledgment that regression might suggest a nonlinear association between the variables; and/or 4) a mention of the value of r² when discussing the fit of the data to the linear model. On the other hand, students were capable of stating informed biological hypotheses related to the physiology of the bats, had no trouble translating numbered data into graphs that adequately described a pattern, and could explain the biological meaning of these patterns (Figure 2).

Figure 2.

Number of students in zoology who achieved (scored 4–3 in rubric) or did not achieve (scored 2–1 in rubric) specific learning goals as described in Table 2, after the bat activity.

CONCLUSIONS AND RECOMMENDATIONS

This paper presents the results of two independent projects aimed at integrating statistical concepts into undergraduate biology courses—genetics and zoology—in two very different ways. In general, we found an increase of understanding of and ability to apply statistical concepts of correlation and association between variables to biology. We also saw improvement in students’ ability to use graphs to describe and interpret patterns in numerical data. In addition, students expressed their understanding of the relevance of statistics as a tool to analyze biological data and understand its significance. However, we identified other concepts for which students had more difficulty demonstrating knowledge gain despite in-class instruction and educational activities. Interestingly, although the instructional approach and the assessment instruments used were different, these two courses yielded similar results. We will discuss the implications of these results in light of the challenges we face in order to further integrate math and biology, and we provide some suggestions to meet the need for interdisciplinary teaching in these fields.

Areas That Need Emphasis

The lack of understanding of probability distributions, interpretation of the p value associated with statistics, and when to reject a null hypothesis was evident in both courses. This was observed in spite of the fact that more than 50% of our students had completed an introductory statistics course and received additional instruction in the statistical concepts relevant to biology in our classes. Mathematical concepts associated with linear relationships between two variables were also weak. Specific to the students in the zoology course was the inability to extrapolate the biological meaning of strong positive or negative slopes versus flat slopes describing the relationship between two variables, a concept that can be traced back to high school geometry and algebra. In both courses, we could see that students were able to distinguish the meaning of high or low correlation coefficients, but it was then difficult for them to synthesize a conclusion explaining the relationship between the variables involved, and to predict potential biological causation for the event described by the data.

How to Confront the Challenges

The challenges biology educators face today are multidimensional. First, biology courses generally do not emphasize the role of mathematical analysis in the description of biological data, a critical element in many major scientific discoveries. Second, most mathematics courses do not make a connection between mathematical concepts and applications to other fields of science (Robeva and Laubenbacher, 2009). The lack of connection between the general statistics course required for majors in biology and the content discussed in the biology courses is also evident (A’Brook and Weyers, 1996; Metz, 2008). Our observations underscore the need for interaction and collaboration to provide new alternatives to traditional math courses (Marsteller et al., 2010). It has been shown that a course integrating math and biology concepts does not hinder student learning in either of the two content areas, but rather may enhance interdisciplinary knowledge (Madlung et al., 2011). Thus, we suggest that professors of introductory courses in math, statistics, and biology convene to discuss these issues. Such collaboration could lead to new math courses or supplementary instruction involving biological examples in calculus and statistics courses. This can be done by sharing research data and/or discussing interdisciplinary papers dealing with computational biology and effectively planning ways to present this information in their classes (Robeva et al., 2010; Watkins, 2010). In addition, instructors may consider using or modifying the activities available from the BioQUEST Curriculum Consortium (2011) or resources from the National Institute of Mathematics and Biological Sciences (NIMBIOS; 2011).

The fact that students take math requirements at different points in the curriculum and come to biology courses with widely divergent quantitative skills is yet another challenge. To rectify this, we recommend that faculty members in biology departments reevaluate their undergraduate curricular sequence, so that students take calculus and basic statistics during their freshman year, when they are also taking their general biology courses. In this manner, they can move on to higher-level courses, such as genetics, microbiology, botany, zoology, and biotechnology, with basic concepts that will allow them to apply mathematical tools to data generated in laboratories, interpretation of graphics, and the understanding of modern scientific theory.

Student attitude is also a challenge, because students may resist learning more math than required for math courses and may tend to avoid the biology professors who incorporate math into their curricula. However, if a coordinated effort is developed among the departments, such that the true interdisciplinary nature between math and biology is highlighted in all courses across the curriculum, we would expect this feeling to be ameliorated with time, and students will value the opportunity to apply what they have learned throughout their career as they construct new knowledge. In fact, in the semesters following this study, we have observed a change in student attitude; students seem more receptive to the idea that they will do “a lot of math” in our courses. Specifically, for genetics, we have observed an improvement in student grades for exams one and two, which are mostly quantitative, compared with previous semesters. We will evaluate whether this improvement in grades and attitude is due to the curricular changes, or because a subset of students who are more advanced in math and in the curriculum in general are concentrated in our sections.

Finally, we must admit that professors of mathematics and biology are not always capable of bridging between these two subject areas with the best examples. This might be resolved by a summer workshop for biology professors given by a biostatistician or an expert in bioinformatics or mathematical ecology who has experience and interest in the teaching/learning processes. The idea of the workshop would be to work out specific problems where statistical methods and mathematical algorithms contribute to better understanding of biological processes. NIMBIOS offers a variety of investigative workshops that may provide professional development in this area (NIMBIOS, 2011).

The incorporation of math in biology is now an irrefutable need. As mentioned earlier, modern fields of biology require mathematical and computational analysis of large amounts of data that help to predict models and describe the function of biological processes at the ecological, organismal, and cellular level (Elser and Hamilton, 2007). Although modern fields like bioinformatics and biostatistics reflect the interdisciplinary nature of biological sciences today, the issue of the lack of emphasis of mathematical concepts in biology education is still evident. In this paper, we present alternative ways to incorporate into biology curricula the application of mathematical tools, specifically statistics, that help students see the advantage of developing quantitative skills in order to analyze different kinds of biological data and discover the patterns and processes occurring in that data. We expect our work to serve as an example for professors in different fields of biology on providing learning opportunities to bridge the gap between math and biology, identifying specific areas that need to be improved, and devising alternative ways to address the gap. The materials and assessment instruments used in this study are available upon request in Spanish and English. These materials will also be very useful for high school teachers interested in using activities that link math and biology. In the future, as our curriculum becomes more interdisciplinary, and we put in practice some of our own recommendations, we expect to adopt a case-based approach, where students design their own experiments, as exemplified by the BioQUEST Curriculum. In this way, we will encourage the development of higher-order thinking skills, while illustrating the relevance of math and computational skills to understanding biological processes.