Differentially Private Empirical Risk Minimization

Abstract

Privacy-preserving machine learning algorithms are crucial for the increasingly common setting in which personal data, such as medical or financial records, are analyzed. We provide general techniques to produce privacy-preserving approximations of classifiers learned via (regularized) empirical risk minimization (ERM). These algorithms are private under the ε-differential privacy definition due to Dwork et al. (2006). First we apply the output perturbation ideas of Dwork et al. (2006), to ERM classification. Then we propose a new method, objective perturbation, for privacy-preserving machine learning algorithm design. This method entails perturbing the objective function before optimizing over classifiers. If the loss and regularizer satisfy certain convexity and differentiability criteria, we prove theoretical results showing that our algorithms preserve privacy, and provide generalization bounds for linear and nonlinear kernels. We further present a privacy-preserving technique for tuning the parameters in general machine learning algorithms, thereby providing end-to-end privacy guarantees for the training process. We apply these results to produce privacy-preserving analogues of regularized logistic regression and support vector machines. We obtain encouraging results from evaluating their performance on real demographic and benchmark data sets. Our results show that both theoretically and empirically, objective perturbation is superior to the previous state-of-the-art, output perturbation, in managing the inherent tradeoff between privacy and learning performance.

1. Introduction

Privacy has become a growing concern, due to the massive increase in personal information stored in electronic databases, such as medical records, financial records, web search histories, and social network data. Machine learning can be employed to discover novel population-wide patterns, however the results of such algorithms may reveal certain individuals’ sensitive information, thereby violating their privacy. Thus, an emerging challenge for machine learning is how to learn from data sets that contain sensitive personal information.

At the first glance, it may appear that simple anonymization of private information is enough to preserve privacy. However, this is often not the case; even if obvious identifiers, such as names and addresses, are removed from the data, the remaining fields can still form unique “signatures” that can help re-identify individuals. Such attacks have been demonstrated by various works, and are possible in many realistic settings, such as when an adversary has side information (Sweeney, 1997; Narayanan and Shmatikov, 2008; Ganta et al., 2008), and when the data has structural properties (Backstrom et al., 2007), among others. Moreover, even releasing statistics on a sensitive data set may not be sufficient to preserve privacy, as illustrated on genetic data (Homer et al., 2008; Wang et al., 2009). Thus, there is a great need for designing machine learning algorithms that also preserve the privacy of individuals in the data sets on which they train and operate.

In this paper we focus on the problem of classification, one of the fundamental problems of machine learning, when the training data consists of sensitive information of individuals. Our work addresses the empirical risk minimization (ERM) framework for classification, in which a classifier is chosen by minimizing the average over the training data of the prediction loss (with respect to the label) of the classifier in predicting each training data point. In this work, we focus on regularized ERM in which there is an additional term in the optimization, called the regularizer, which penalizes the complexity of the classifier with respect to some metric. Regularized ERM methods are widely used in practice, for example in logistic regression and support vector machines (SVMs), and many also have theoretical justification in the form of generalization error bounds with respect to independently, identically distributed (i.i.d.) data (see Vapnik, 1998 for further details).

For our privacy measure, we use a definition due to Dwork et al. (2006b), who have proposed a measure of quantifying the privacy-risk associated with computing functions of sensitive data. Their ε-differential privacy model is a strong, cryptographically-motivated definition of privacy that has recently received a significant amount of research attention for its robustness to known attacks, such as those involving side information (Ganta et al., 2008). Algorithms satisfying ε-differential privacy are randomized; the output is a random variable whose distribution is conditioned on the data set. A statistical procedure satisfies ε-differential privacy if changing a single data point does not shift the output distribution by too much. Therefore, from looking at the output of the algorithm, it is difficult to infer the value of any particular data point.

In this paper, we develop methods for approximating ERM while guaranteeing ε-differential privacy. Our results hold for loss functions and regularizers satisfying certain differentiability and convexity conditions. An important aspect of our work is that we develop methods for end-to-end privacy; each step in the learning process can cause additional risk of privacy violation, and we provide algorithms with quantifiable privacy guarantees for training as well as parameter tuning. For training, we provide two privacy-preserving approximations to ERM. The first is output perturbation, based on the sensitivity method proposed by Dwork et al. (2006b). In this method noise is added to the output of the standard ERM algorithm. The second method is novel, and involves adding noise to the regularized ERM objective function prior to minimizing. We call this second method objective perturbation. We show theoretical bounds for both procedures; the theoretical performance of objective perturbation is superior to that of output perturbation for most problems. However, for our results to hold we require that the regularizer be strongly convex (ruling L₁ regularizers) and additional constraints on the loss function and its derivatives. In practice, these additional constraints do not affect the performance of the resulting classifier; we validate our theoretical results on data sets from the UCI repository.

In practice, parameters in learning algorithms are chosen via a holdout data set. In the context of privacy, we must guarantee the privacy of the holdout data as well. We exploit results from the theory of differential privacy to develop a privacy-preserving parameter tuning algorithm, and demonstrate its use in practice. Together with our training algorithms, this parameter tuning algorithm guarantees privacy to all data used in the learning process.

Guaranteeing privacy incurs a cost in performance; because the algorithms must cause some uncertainty in the output, they increase the loss of the output predictor. Because the ε-differential privacy model requires robustness against all data sets, we make no assumptions on the underlying data for the purposes of making privacy guarantees. However, to prove the impact of privacy constraints on the generalization error, we assume the data is i.i.d. according to a fixed but unknown distribution, as is standard in the machine learning literature. Although many of our results hold for ERM in general, we provide specific results for classification using logistic regression and support vector machines. Some of the former results were reported in Chaudhuri and Monteleoni (2008); here we generalize them to ERM and extend the results to kernel methods, and provide experiments on real data sets.

More specifically, the contributions of this paper are as follows:

• We derive a computationally efficient algorithm for ERM classification, based on the sensitivity method due to Dwork et al. (2006b). We analyze the accuracy of this algorithm, and provide an upper bound on the number of training samples required by this algorithm to achieve a fixed generalization error.

• We provide a general technique, objective perturbation, for providing computationally efficient, differentially private approximations to regularized ERM algorithms. This extends the work of Chaudhuri and Monteleoni (2008), which follows as a special case, and corrects an error in the arguments made there. We apply the general results on the sensitivity method and objective perturbation to logistic regression and support vector machine classifiers. In addition to privacy guarantees, we also provide generalization bounds for this algorithm.

• For kernel methods with nonlinear kernel functions, the optimal classifier is a linear combination of kernel functions centered at the training points. This form is inherently non-private because it reveals the training data. We adapt a random projection method due to Rahimi and Recht (2007, 2008b), to develop privacy-preserving kernel-ERM algorithms. We provide theoretical results on generalization performance.

• Because the holdout data is used in the process of training and releasing a classifier, we provide a privacy-preserving parameter tuning algorithm based on a randomized selection procedure (McSherry and Talwar, 2007) applicable to general machine learning algorithms. This guarantees end-to-end privacy during the learning procedure.

• We validate our results using experiments on two data sets from the UCI Machine Learning repositories (Asuncion and Newman, 2007) and KDDCup (Hettich and Bay, 1999). Our results show that objective perturbation is generally superior to output perturbation. We also demonstrate the impact of end-to-end privacy on generalization error.

1.1 Related Work

There has been a significant amount of literature on the ineffectiveness of simple anonymization procedures. For example, Narayanan and Shmatikov (2008) show that a small amount of auxiliary information (knowledge of a few movie-ratings, and approximate dates) is sufficient for an adversary to re-identify an individual in the Netflix data set, which consists of anonymized data about Netflix users and their movie ratings. The same phenomenon has been observed in other kinds of data, such as social network graphs (Backstrom et al., 2007), search query logs (Jones et al., 2007) and others. Releasing statistics computed on sensitive data can also be problematic; for example, Wang et al. (2009) show that releasing R²-values computed on high-dimensional genetic data can lead to privacy breaches by an adversary who is armed with a small amount of auxiliary information.

There has also been a significant amount of work on privacy-preserving data mining (Agrawal and Srikant, 2000; Evfimievski et al., 2003; Sweeney, 2002; Machanavajjhala et al., 2006), spanning several communities, that uses privacy models other than differential privacy. Many of the models used have been shown to be susceptible to composition attacks, attacks in which the adversary has some reasonable amount of prior knowledge (Ganta et al., 2008). Other work (Mangasarian et al., 2008) considers the problem of privacy-preserving SVM classification when separate agents have to share private data, and provides a solution that uses random kernels, but does provide any formal privacy guarantee.

An alternative line of privacy work is in the secure multiparty computation setting due to Yao (1982), where the sensitive data is split across multiple hostile databases, and the goal is to compute a function on the union of these databases. Zhan and Matwin (2007) and Laur et al. (2006) consider computing privacy-preserving SVMs in this setting, and their goal is to design a distributed protocol to learn a classifier. This is in contrast with our work, which deals with a setting where the algorithm has access to the entire data set.

Differential privacy, the formal privacy definition used in our paper, was proposed by the seminal work of Dwork et al. (2006b), and has been used since in numerous works on privacy (Chaudhuri and Mishra, 2006; McSherry and Talwar, 2007; Nissim et al., 2007; Barak et al., 2007; Chaudhuri and Monteleoni, 2008; Machanavajjhala et al., 2008). Unlike many other privacy definitions, such as those mentioned above, differential privacy has been shown to be resistant to composition attacks (attacks involving side-information) (Ganta et al., 2008). Some follow-up work on differential privacy includes work on differentially-private combinatorial optimization, due to Gupta et al. (2010), and differentially-private contingency tables, due to Barak et al. (2007) and Kasivishwanathan et al. (2010). Wasserman and Zhou (2010) provide a more statistical view of differential privacy, and Zhou et al. (2009) provide a technique of generating synthetic data using compression via random linear or affine transformations.

Previous literature has also considered learning with differential privacy. One of the first such works is Kasiviswanathan et al. (2008), which presents a general, although computationally inefficient, method for PAC-learning finite concept classes. Blum et al. (2008) presents a method for releasing a database in a differentially-private manner, so that certain fixed classes of queries can be answered accurately, provided the class of queries has a bounded VC-dimension. Their methods can also be used to learn classifiers with a fixed VC-dimension (Kasiviswanathan et al., 2008) but the resulting algorithm is also computationally inefficient. Some sample complexity lower bounds in this setting have been provided by Beimel et al. (2010). In addition, Dwork and Lei (2009) explore a connection between differential privacy and robust statistics, and provide an algorithm for privacy-preserving regression using ideas from robust statistics. Their algorithm also requires a running time which is exponential in the data dimension, which is computationally inefficient.

This work builds on our preliminary work in Chaudhuri and Monteleoni (2008). We first show how to extend the sensitivity method, a form of output perturbation, due to Dwork et al. (2006b), to classification algorithms. In general, output perturbation methods alter the output of the function computed on the database, before releasing it; in particular the sensitivity method makes an algorithm differentially private by adding noise to its output. In the classification setting, the noise protects the privacy of the training data, but increases the prediction error of the classifier. Recently, independent work by Rubinstein et al. (2009) has reported an extension of the sensitivity method to linear and kernel SVMs. Their utility analysis differs from ours, and thus the analogous generalization bounds are not comparable. Because Rubinstein et al. use techniques from algorithmic stability, their utility bounds compare the private and non-private classifiers using the same value for the regularization parameter. In contrast, our approach takes into account how the value of the regularization parameter might change due to privacy constraints. In contrast, we propose the objective perturbation method, in which noise is added to the objective function before optimizing over the space classifiers. Both the sensitivity method and objective perturbation result in computationally efficient algorithms for our specific case. In general, our theoretical bounds on sample requirement are incomparable with the bounds of Kasiviswanathan et al. (2008) because of the difference between their setting and ours.

Our approach to privacy-preserving tuning uses the exponential mechanism of McSherry and Talwar (2007) by training classifiers with different parameters on disjoint subsets of the data and then randomizing the selection of which classifier to release. This bears a superficial resemblance to the sample-and-aggregate (Nissim et al., 2007) and V-fold cross-validation, but only in the sense that only a part of the data is used to train the classifier. One drawback is that our approach requires significantly more data in practice. Other approaches to selecting the regularization parameter could benefit from a more careful analysis of the regularization parameter, as in Hastie et al. (2004).

2. Model

We will use ‖x‖, ‖x‖_∞, and ‖x‖_ℋ to denote the ℓ₂-norm, ℓ_∞-norm, and norm in a Hilbert space ℋ, respectively. For an integer n we will use [n] to denote the set {1,2,…,n}. Vectors will typically be written in boldface and sets in calligraphic type. For a matrix A, we will use the notation ‖A‖₂ to denote the L₂ norm of A.

2.1 Empirical Risk Minimization

In this paper we develop privacy-preserving algorithms for regularized empirical risk minimization, a special case of which is learning a classifier from labeled examples. We will phrase our problem in terms of classification and indicate when more general results hold. Our algorithms take as input training data 𝒟 = {(x_i,y_i) ∈ 𝒳 ×𝒴 : i = 1,2,…,n} of n data-label pairs. In the case of binary classification the data space 𝒳 = ℝ^d and the label set 𝒴 = {−1,+1}. We will assume throughout that 𝒳 is the unit ball so that ‖x_i‖₂ ≤ 1.

We would like to produce a predictor f : 𝒳 → 𝒴. We measure the quality of our predictor on the training data via a nonnegative loss function ℓ : 𝒴 × 𝒴 → ℝ.

In regularized empirical risk minimization (ERM), we choose a predictor f that minimizes the regularized empirical loss:

$$J(\mathbf{f},𝒟)=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\ell (\mathbf{f}({\mathbf{x}}_i),{\mathbf{y}}_i)+\mathrm{\Lambda }N(\mathbf{f}).$$ (1)

This minimization is performed over f in an hypothesis class ℋ. The regularizer N(·) prevents over-fitting. For the first part of this paper we will restrict our attention to linear predictors and with some abuse of notation we will write f(x) = f^Tx.

2.2 Assumptions on Loss and Regularizer

The conditions under which we can prove results on privacy and generalization error depend on analytic properties of the loss and regularizer. In particular, we will require certain forms of convexity (see Rockafellar and Wets, 1998).

Definition 1 A function H(f) over f ∈ ℝ^d is said to be strictly convex if for all α ∈ (0,1), f, and g,

$$H(\mathrm{\alpha }\mathbf{f}+(1-\mathrm{\alpha })\mathbf{g})<\mathrm{\alpha }H(\mathbf{f})+(1-\mathrm{\alpha })H(\mathbf{g}).$$

It is said to be λ-strongly convex if for all α ∈ (0,1), f, and g,

$$H(\mathrm{\alpha }\mathbf{f}+(1-\mathrm{\alpha })\mathbf{g})\le \mathrm{\alpha }H(\mathbf{f})+(1-\mathrm{\alpha })H(\mathbf{g})-\frac{1}{2}\mathrm{\lambda }\mathrm{\alpha }(1-\mathrm{\alpha }){\Vert \mathbf{f}-\mathbf{g}\Vert }_2^2.$$

A strictly convex function has a unique minimum (Boyd and Vandenberghe, 2004). Strong convexity plays a role in guaranteeing our privacy and generalization requirements. For our privacy results to hold we will also require that the regularizer N(·) and loss function ℓ(·, ·) be differentiable functions of f. This excludes certain classes of regularizers, such as the ℓ₁-norm regularizer N(f) = ‖f‖₁, and classes of loss functions such as the hinge loss ℓ_SVM(f^T x, y) = (1 − yf^T x)⁺. In some cases we can prove privacy guarantees for approximations to these non-differentiable functions.

2.3 Privacy Model

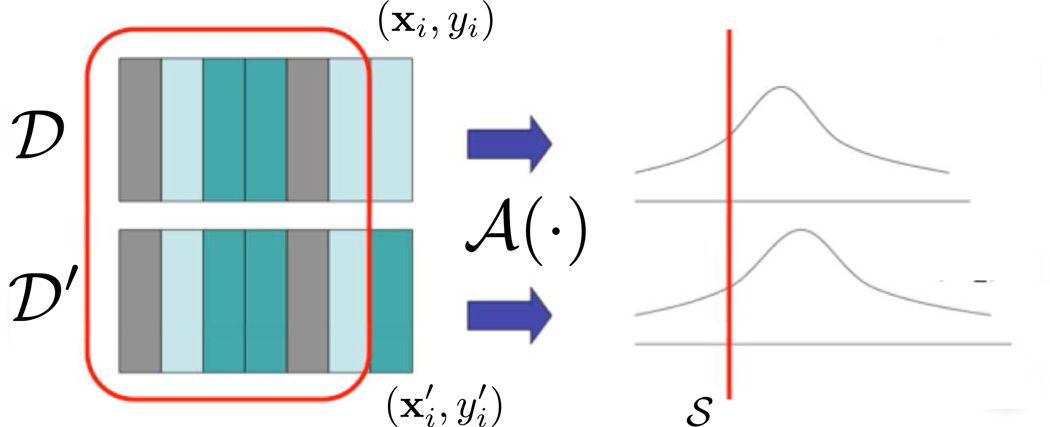
We are interested in producing a classifier in a manner that preserves the privacy of individual entries of the data set 𝒟 that is used in training the classifier. The notion of privacy we use is the ε-differential privacy model, developed by Dwork et al. (2006b) (see also Dwork (2006)), which defines a notion of privacy for a randomized algorithm 𝒜(𝒟). Suppose 𝒜(𝒟) produces a classifier, and let 𝒟′ be another data set that differs from 𝒟 in one entry (which we assume is the private value of one person). That is, 𝒟′ and 𝒟 have n − 1 points (x_i, y_i) in common. The algorithm 𝒜 provides differential privacy if for any set 𝒮, the likelihood that 𝒜(𝒟) ∈ 𝒮 is close to the likelihood 𝒜(𝒟′) ∈ 𝒮, (where the likelihood is over the randomness in the algorithm). That is, any single entry of the data set does not affect the output distribution of the algorithm by much; dually, this means that an adversary, who knows all but one entry of the data set, cannot gain much additional information about the last entry by observing the output of the algorithm.

The following definition of differential privacy is due to Dwork et al. (2006b), paraphrased from Wasserman and Zhou (2010).

Definition 2 An algorithm 𝒜(ℬ) taking values in a set 𝒯 provides ε_p-differential privacy if

$$\underset{𝒮}{\text{sup}}\underset{𝒟,𝒟\prime }{\text{sup}}\frac{\mu (𝒮|ℬ=𝒟)}{\mu (𝒮|ℬ=𝒟\prime )}\le e^{{\mathrm{\epsilon }}_p},$$ (2)

where the first supremum is over all measurable 𝒮 ⊆ 𝒯, the second is over all data sets 𝒟 and 𝒟′ differing in a single entry, and μ(·|ℬ) is the conditional distribution (measure) on 𝒯 induced by the output 𝒜(ℬ) given a data set ℬ. The ratio is interpreted to be 1 whenever the numerator and denominator are both 0.

Note that if 𝒮 is a set of measure 0 under the conditional measures induced by 𝒟 and 𝒟′, the ratio is automatically 1. A more measure-theoretic definition is given in Zhou et al. (2009). An illustration of the definition is given in Figure 1.

Figure 1.

An algorithm which is differentially private. When data sets which are identical except for a single entry are input to the algorithm 𝒜, the two distributions on the algorithm’s output are close. For a fixed measurable 𝒮 the ratio of the measures (or densities) should be bounded.

The following form of the definition is due to Dwork et al. (2006a).

Definition 3 An algorithm 𝒜 provides ε_p-differential privacy if for any two data sets 𝒟 and 𝒟′ that differ in a single entry and for any set 𝒮,

$$\text{exp}(-{\mathrm{\epsilon }}_p)\mathbb{P}(𝒜(𝒟\prime )\in 𝒮)\le \mathbb{P}(𝒜(𝒟)\in 𝒮)\le \text{exp}({\mathrm{\epsilon }}_p)\mathbb{P}(𝒜(𝒟\prime )\in 𝒮),$$ (3)

where 𝒜(𝒟) (resp. 𝒜(𝒟′)) is the output of 𝒜 on input 𝒟 (resp. 𝒟′).

We observe that an algorithm 𝒜 that satisfies Equation 2 also satisfies Equation 3, and as a result, Definition 2 is stronger than Definition 3.

From this definition, it is clear that the 𝒜(𝒟) that outputs the minimizer of the ERM objective (1) does not provide ε_p-differential privacy for any ε_p. This is because an ERM solution is a linear combination of some selected training samples “near” the decision boundary. If 𝒟 and 𝒟′ differ in one of these samples, then the classifier will change completely, making the likelihood ratio in (3) infinite. Regularization helps by penalizing the L₂ norm of the change, but does not account how the direction of the minimizer is sensitive to changes in the data.

Dwork et al. (2006b) also provide a standard recipe for computing privacy-preserving approximations to functions by adding noise with a particular distribution to the output of the function. We call this recipe the sensitivity method. Let g : (ℝ^m)ⁿ → ℝ be a scalar function of z₁,…, z_n, where z_i ∈ ℝ^m corresponds to the private value of individual i; then the sensitivity of g is defined as follows.

Definition 4 The sensitivity of a function g : (ℝ^m)ⁿ → ℝ is maximum difference between the values of the function when one input changes. More formally, the sensitivity S(g) of g is defined as:

$$S(g)=\underset{i}{\text{max}}\underset{z_1,\dots ,z_n,z_i^{\prime }}{\text{max}}|g(z_1,\dots ,z_{i-1},z_i,z_{i+1},\dots ,z_n)-g(z_1,\dots ,z_{i-1},z_1^{\prime },z_{i+1},\dots ,z_n)|.$$

To compute a function g on a data set 𝒟 = {z₁,…, z_n}, the sensitivity method outputs g(z₁,…,z_n) + η, where η is a random variable drawn according to the Laplace distribution, with mean 0 and standard deviation $\frac{S(g)}{{\mathrm{\epsilon }}_p}$. It is shown in Dwork et al. (2006b) that such a procedure is ε_p-differentially private.

3. Privacy-preserving ERM

Here we describe two approaches for creating privacy-preserving algorithms from (1).

3.1 Output Perturbation: The Sensitivity Method

Algorithm 1 is derived from the sensitivity method of Dwork et al. (2006b), a general method for generating a privacy-preserving approximation to any function A(·). In this section the norm ‖·‖ is the L₂-norm unless otherwise specified. For the function A(𝒟) = argminJ(f,𝒟), Algorithm 1 outputs a vector A(𝒟) + b, where b is random noise with density:

$$\mathrm{\nu }(\mathbf{b})=\frac{1}{\mathrm{\alpha }}{e}^{-\mathrm{\beta }\Vert \mathbf{b}\Vert },$$ (4)

where α is a normalizing constant. The parameter β is a function of ε_p, and the L₂-sensitivity of A(·), which is defined as follows.

Definition 5 The L₂-sensitivity of a vector-valued function is defined as the maximum change in the L₂ norm of the value of the function when one input changes. More formally,

$$S(A)=\underset{i}{\text{max}}\underset{z_1,\dots ,z_n,z_i^{\prime }}{\text{max}}\Vert A(z_1,\dots ,z_i,\dots )-A(z_1,\dots ,z_1^{\prime },\dots )\Vert .$$

The interested reader is referred to Dwork et al. (2006b) for further details. Adding noise to the output of A(·) has the effect of masking the effect of any particular data point. However, in some applications the sensitivity of the minimizer argminJ(f,𝒟) may be quite high, which would require the sensitivity method to add noise with high variance.

Algorithm 1.

ERM with output perturbation (sensitivity)

Inputs: Data 𝒟 = {zi}, parameters εp,Λ.

Output: Approximate minimizer fpriv.

Draw a vector b according to (4) with $\mathrm{\beta }=\frac{n\mathrm{\Lambda }{\mathrm{\epsilon }}_p}{2}$

Compute fpriv = argminJ(f,𝒟) + b.

3.2 Objective Perturbation

A different approach, first proposed by Chaudhuri and Monteleoni (2008), is to add noise to the objective function itself and then produce the minimizer of the perturbed objective. That is, we can minimize

$$J_{\text{priv}}(\mathbf{f},𝒟)=J(\mathbf{f},𝒟)+\frac{1}{n}{\mathbf{b}}^T\mathbf{f},$$

where b has density given by (4), with β = ε_p. Note that the privacy parameter here does not depend on the sensitivity of the of the classification algorithm.

Algorithm 2.

ERM with objective perturbation

Inputs: Data 𝒟 = {zi}, parameters εp, Λ, c.

Output: Approximate minimizer fpriv.

$\text{Let}{\mathrm{\epsilon }}_p^{\prime }={\mathrm{\epsilon }}_p-\text{log}(1+\frac{2c}{n\mathrm{\Lambda }}+\frac{c^2}{n^2{\mathrm{\Lambda }}^2})$.

$\text{if}{\mathrm{\epsilon }}_p^{\prime }>0,\text{then}\mathrm{\Delta }=0,\text{else}\mathrm{\Delta }=\frac{c}{n(e^{{\mathrm{\epsilon }}_p/4}-1)}-\mathrm{\Lambda },\text{and}{\mathrm{\epsilon }}_p^{\prime }={\mathrm{\epsilon }}_p/2$ .

Draw a vector b according to (4) with $\mathrm{\beta }={\mathrm{\epsilon }}_p^{\prime }/2$.

$\text{compute}{\mathbf{f}}_{\text{priv}}=\text{argmin}{J}_{\text{priv}}(\mathbf{f},𝒟)+\frac{1}{2}\mathrm{\Delta }{\Vert \mathbf{f}\Vert }^2$ .

The algorithm requires a certain slack, $\text{log}(1+\frac{2c}{n\mathrm{\Lambda }}+\frac{c^2}{n^2{\mathrm{\Lambda }}^2})$, in the privacy parameter. This is due to additional factors in bounding the ratio of the densities. The “If” statement in the algorithm is from having to consider two cases in the proof of Theorem 9, which shows that the algorithm is differentially private.

3.3 Privacy Guarantees

In this section, we establish the conditions under which Algorithms 1 and 2 provide ε_p-differential privacy. First, we establish guarantees for Algorithm 1.

3.3.1 PRIVACY GUARANTEES FOR OUTPUT PERTURBATION

Theorem 6 If N(·) is differentiable, and 1-strongly convex, and ℓ is convex and differentiable, with |ℓ′(z)| ≤ 1 for all z, then, Algorithm 1 provides ε_p-differential privacy.

The proof of Theorem 6 follows from Corollary 8, and Dwork et al. (2006b). The proof is provided here for completeness.

Proof From Corollary 8, if the conditions on N(·) and ℓ hold, then the L₂-sensivity of ERM with regularization parameter Λ is at most $\frac{2}{n\mathrm{\Lambda }}$. We observe that when we pick ‖b‖ from the distribution in Algorithm 1, for a specific vector b₀ ∈ ℝ^d, the density at b₀ is proportional to $e^{-\frac{n\mathrm{\Lambda }{\mathrm{\epsilon }}_p}{2}\Vert {\mathbf{b}}_{\mathbf{0}}\Vert }$. Let 𝒟 and 𝒟′ be any two data sets that differ in the value of one individual. Then, for any f,

$$\frac{g(\mathbf{f}|𝒟)}{g(\mathbf{f}|𝒟\prime )}=\frac{\mathrm{\nu }({\mathbf{b}}_1)}{\mathrm{\nu }({\mathbf{b}}_2)}=e^{-\frac{n\mathrm{\Lambda }\mathrm{\epsilon }p}{2}(\Vert {\mathbf{b}}_1\Vert -\Vert {\mathbf{b}}_2\Vert )},$$

where b₁ and b₂ are the corresponding noise vectors chosen in Step 1 of Algorithm 1, and g(f|𝒟) (g(f|𝒟′) respectively) is the density of the output of Algorithm 1 at f, when the input is 𝒟 (𝒟′ respectively). If f₁ and f₂ are the solutions respectively to non-private regularized ERM when the input is 𝒟 and 𝒟′, then, b₂ − b₁ = f₂ − f₁. From Corollary 8, and using a triangle inequality,

$$\Vert {\mathbf{b}}_1\Vert -\Vert {\mathbf{b}}_2\Vert \le \Vert {\mathbf{b}}_1-{\mathbf{b}}_2\Vert =\Vert {\mathbf{f}}_2-{\mathbf{f}}_1\Vert \le \frac{2}{n\mathrm{\Lambda }}.$$

Moreover, by symmetry, the density of the directions of b₁ and b₂ are uniform. Therefore, by construction, $\frac{\mathrm{\nu }({\mathbf{b}}_1)}{\mathrm{\nu }({\mathbf{b}}_2)}\le e^{{\mathrm{\epsilon }}_p}$. The theorem follows.

The main ingredient of the proof of Theorem 6 is a result about the sensitivity of regularized ERM, which is provided below.

Lemma 7 Let G(f) and g(f) be two vector-valued functions, which are continuous, and differentiable at all points. Moreover, let G(f) and G(f) + g(f) be λ-strongly convex. If f₁ = argmin_f G(f) and f₂ = argmin_f G(f) + g(f), then

$$\Vert {\mathbf{f}}_1-{\mathbf{f}}_2\Vert \le \frac{1}{\mathrm{\lambda }}\underset{\mathbf{f}}{\text{max}}\Vert \nabla g(\mathbf{f})\Vert .$$

Proof Using the definition of f₁ and f₂, and the fact that G and g are continuous and differentiable everywhere,

$$\nabla G({\mathbf{f}}_1)=\nabla G({\mathbf{f}}_2)+\nabla g({\mathbf{f}}_2)=\mathbf{0}.$$ (5)

As G(f) is λ-strongly convex, it follows from Lemma 14 of Shalev-Shwartz (2007) that:

$${(\nabla G({\mathbf{f}}_1)-\nabla G({\mathbf{f}}_2))}^T({\mathbf{f}}_1-{\mathbf{f}}_2)\ge \mathrm{\lambda }{\Vert {\mathbf{f}}_1-{\mathbf{f}}_2\Vert }^2.$$

Combining this with (5) and the Cauchy-Schwartz inequality, we get that

$$\Vert {\mathbf{f}}_1-{\mathbf{f}}_2\Vert ·\Vert \nabla g({\mathbf{f}}_2)\Vert \ge {({\mathbf{f}}_1-{\mathbf{f}}_2)}^T\nabla g({\mathbf{f}}_2)={(\nabla G({\mathbf{f}}_1)-\nabla G({\mathbf{f}}_2))}^T({\mathbf{f}}_1-{\mathbf{f}}_2)\ge \mathrm{\lambda }{\Vert {\mathbf{f}}_1-{\mathbf{f}}_2\Vert }^2.$$

The conclusion follows from dividing both sides by λ‖f₁ − f₂‖.

Corollary 8 If N(·) is differentiable and 1-strongly convex, and ℓ is convex and differentiable with |ℓ′(z)| ≤ 1 for all z, then, the L₂-sensitivity of J(f,𝒟) is at most $\frac{2}{n\mathrm{\Lambda }}$.

Proof Let 𝒟 = {(x₁,y₁),…, (x_n, y_n)} and $𝒟\prime =\{({\mathbf{x}}_1,y_1),\dots ,({\mathbf{x}}_n^{\prime },y_n^{\prime })\}$ be two data sets that differ in the value of the n-th individual. Moreover, we let G(f) = J(f,𝒟), g(f) = J(f,𝒟′) − J(f,𝒟), f₁ = argmin_fJ(f,𝒟), and f₂ = argmin_fJ(f,𝒟′). Finally, we set $g(\mathbf{f})=\frac{1}{n}(\ell (y_n^{\prime }{\mathbf{f}}^T{\mathbf{x}}_n^{\prime })-\ell (y_n{\mathbf{f}}^T{\mathbf{x}}_n))$ .

We observe that due to the convexity of ℓ, and 1-strong convexity of N(·), G(f) = J(f,𝒟) is Λ-strongly convex. Moreover, G(f) + g(f) = J(f,𝒟′) is also Λ-strongly convex. Finally, due to the differentiability of N(·) and ℓ, G(f) and g(f) are also differentiable at all points. We have:

$$\nabla g(\mathbf{f})=\frac{1}{n}(y_n\ell \prime (y_n{\mathbf{f}}^T{\mathbf{x}}_n){\mathbf{x}}_n-y_n^{\prime }\ell \prime (y_n^{\prime }{\mathbf{f}}^T{\mathbf{x}}_n^{\prime }){\mathbf{x}}_n^{\prime }).$$

As y_i ∈ [−1,1], |ℓ′(z)| ≤ 1, for all z, and ‖x_i‖ ≤ 1, for any f, $\Vert \nabla g(\mathbf{f})\Vert \le \frac{1}{n}(\Vert {\mathbf{x}}_n-{\mathbf{x}}_n^{\prime }\Vert )\le \frac{1}{n}(\Vert {\mathbf{x}}_n\Vert +\Vert {\mathbf{x}}_n^{\prime }\Vert )\le \frac{2}{n}$. The proof now follows by an application of Lemma 7.

3.3.2 PRIVACY GUARANTEES FOR OBJECTIVE PERTURBATION

In this section, we show that Algorithm 2 is ε_p-differentially private. This proof requires stronger assumptions on the loss function than were required in Theorem 6. In certain cases, some of these assumptions can be weakened; for such an example, see Section 3.4.2.

Theorem 9 If N(·) is 1-strongly convex and doubly differentiable, and ℓ(·) is convex and doubly differentiable, with |ℓ′(z)| ≤ 1 and |ℓ″(z)| ≤ c for all z, then Algorithm 2 is ε_p-differentially private.

Proof Consider an f_priv output by Algorithm 2. We observe that given any fixed f_priv and a fixed data set 𝒟, there always exists a b such that Algorithm 2 outputs f_priv on input 𝒟. Because ℓ is differentiable and convex, and N(·) is differentiable, we can take the gradient of the objective function and set it to 0 at f_priv. Therefore,

$$\mathbf{b}=-n\mathrm{\Lambda }\nabla N({\mathbf{f}}_{\text{priv}})-{\displaystyle \sum _{i=1}^n}{y}_i\ell \prime (y_i{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_i){\mathbf{x}}_i-n\mathrm{\Delta }{\mathbf{f}}_{\text{priv}}.$$ (6)

Note that (6) holds because for any f, ∇ℓ(f^T x) = ℓ′(f^T x)x.

We claim that as ℓ is differentiable and $J(\mathbf{f},𝒟)+\frac{\mathrm{\Delta }}{2}{\Vert \mathbf{f}\Vert }^2$ is strongly convex, given a data set 𝒟 = (x₁,y₁),…, (x_n, y_n), there is a bijection between b and f_priv. The relation (6) shows that two different b values cannot result in the same f_priv. Furthermore, since the objective is strictly convex, for a fixed b and 𝒟, there is a unique f_priv; therefore the map from b to f_priv is injective. The relation (6) also shows that for any f_priv there exists a b for which f_priv is the minimizer, so the map from b to f_priv is surjective.

To show ε_p-differential privacy, we need to compute the ratio g(f_priv|𝒟)/g(f_priv|𝒟′) of the densities of f_priv under the two data sets 𝒟 and 𝒟′. This ratio can be written as (Billingsley, 1995)

$$\frac{g({\mathbf{f}}_{\text{priv}}|𝒟)}{g({\mathbf{f}}_{\text{priv}}|𝒟\prime )}=\frac{\mu (\mathbf{b}|𝒟)}{\mu (\mathbf{b}\prime |𝒟\prime )}·\frac{{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}|𝒟))|}^{-1}}{{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}\prime |𝒟\prime ))|}^{-1}},$$

where J(f_priv → b|𝒟), J(f_priv → b|𝒟′) are the Jacobian matrices of the mappings from f_priv to b, and μ(b|𝒟) and μ(b|𝒟′) are the densities of b given the output f_priv, when the data sets are 𝒟 and 𝒟′ respectively.

First, we bound the ratio of the Jacobian determinants. Let b^(j) denote the j-th coordinate of b. From (6) we have

$${\mathbf{b}}^{(j)}=-n\mathrm{\Lambda }\nabla N{({\mathbf{f}}_{\text{priv}})}^{(j)}-{\displaystyle \sum _{i=1}^n}\ell \prime (y_i{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_i){\mathbf{x}}_i^{(j)}-n\mathrm{\Delta }{\mathbf{f}}_{\text{priv}}^{(j)}.$$

Given a data set 𝒟, the (j, k)-th entry of the Jacobian matrix J(f → b|𝒟) is

$$\frac{\mathrm{\partial }{\mathbf{b}}^{(j)}}{\mathrm{\partial }{\mathbf{f}}_{\text{priv}}^{(k)}}=-n\mathrm{\Lambda }{\nabla }^{2}N{({\mathbf{f}}_{\text{priv}})}^{(j,k)}-{\displaystyle \sum _i}{y}_i^2\ell \prime \prime (y_i{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_i){\mathbf{x}}_i^{(j)}{\mathbf{x}}_i^{(k)}-n\mathrm{\Delta }1(j=k),$$

where 1(·) is the indicator function. We note that the Jacobian is defined for all f_priv because N(·) and ℓ are globally doubly differentiable.

Let 𝒟 and 𝒟′ be two data sets which differ in the value of the n-th item such that 𝒟 = {(x₁,y₁),…, (x_n−1,y_n−1), (x_n,y_n)} and $𝒟\prime =\{({\mathbf{x}}_1,y_1),\dots ,({\mathbf{x}}_{n-1},y_{n-1}),({\mathbf{x}}_n^{\prime },y_n^{\prime })\}$. Moreover, we define matrices A and E as follows:

$$\begin{array}{cc}A\hfill & =n\mathrm{\Lambda }{\nabla }^{2}N({\mathbf{f}}_{\text{priv}})+{\displaystyle \sum _{i=1}^n}{y}_i^2\ell \prime \prime (y_i{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_i){\mathbf{x}}_i{\mathbf{x}}_i^T+n\mathrm{\Delta }{I}_d,\hfill \\ E\hfill & =-y_n^2\ell \prime \prime (y_n{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_n){\mathbf{x}}_n{\mathbf{x}}_n^T+{(y_n^{\prime })}^2\ell \prime \prime (y_n^{\prime }{\mathbf{f}}_{\text{priv}}^T\mathbf{x}{\prime }_n)\mathbf{x}{\prime }_n\mathbf{x}{\prime }_n^T.\hfill \end{array}$$

Then, J(f_priv → b|𝒟) = −A, and J(f_priv → b|𝒟′) = −(A + E).

Let λ₁(M) and λ₂(M) denote the largest and second largest eigenvalues of a matrix M. As E has rank at most 2, from Lemma 10,

$$\frac{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}|𝒟\prime ))|}{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}|𝒟))|}=\frac{|\text{det}(A+E)|}{|\text{det}A|}=|1+{\mathrm{\lambda }}_1(A^{-1}E)+{\mathrm{\lambda }}_2(A^{-1}E)+{\mathrm{\lambda }}_1(A^{-1}E){\mathrm{\lambda }}_2(A^{-1}E)|.$$

For a 1-strongly convex function N, the Hessian ∇²N(f_priv) has eigenvalues greater than 1 (Boyd and Vandenberghe, 2004). Since we have assumed ℓ is doubly differentiable and convex, any eigenvalue of A is therefore at least nΛ + nΔ; therefore, for $j=1,2,|{\mathrm{\lambda }}_j(A^{-1}E)|\le \frac{|{\mathrm{\lambda }}_j(E)|}{n(\mathrm{\Lambda }+\mathrm{\Delta })}$. Applying the triangle inequality to the trace norm:

$$|{\mathrm{\lambda }}_1(E)|+|{\mathrm{\lambda }}_2(E)|\le |y_n^2\ell \prime \prime (y_n{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_n)|·\Vert {\mathbf{x}}_n\Vert +|-{(y_n^{\prime })}^2\ell \prime \prime (y_n^{\prime }{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_n^{\prime })|·\Vert {\mathbf{x}}_n^{\prime }\Vert .$$

Then upper bounds on |y_i|, ‖x_i‖, and |ℓ″(z)| yield

$$|{\mathrm{\lambda }}_1(E)|+|{\mathrm{\lambda }}_2(E)|\le 2c.$$

Therefore, |λ₁(E)| · |λ₂(E)| ≤ c², and

$$\frac{|\text{det}(A+E)|}{|\text{det}(A)|}\le 1+\frac{2c}{n(\mathrm{\Lambda }+\mathrm{\Delta })}+\frac{c^2}{n^2{(\mathrm{\Lambda }+\mathrm{\Delta })}^2}={\left(1+\frac{c}{n(\mathrm{\Lambda }+\mathrm{\Delta })}\right)}^2.$$

We now consider two cases. In the first case, Δ = 0, and by definition, in that case, $1+\frac{2c}{n\mathrm{\Lambda }}+\frac{c^2}{n^2{\mathrm{\Lambda }}^2}\le e^{{\mathrm{\epsilon }}_p-{\mathrm{\epsilon }}_p^{\prime }}$. In the second case, Δ > 0, and in this case, by definition of Δ, ${(1+\frac{c}{n(\mathrm{\Lambda }+\mathrm{\Delta })})}^2=e^{{\mathrm{\epsilon }}_p/2}=e^{{\mathrm{\epsilon }}_p-{\mathrm{\epsilon }}_p^{\prime }}$.

Next, we bound the ratio of the densities of b. We observe that as |ℓ′(z)| ≤ 1, for any z and |y_i|, ‖x_i‖ ≤ 1, for data sets 𝒟 and 𝒟′ which differ by one value,

$$\mathbf{b}\prime -\mathbf{b}=y_n\ell \prime (y_n{\mathbf{f}}_{\text{priv}}^T{\mathbf{x}}_n){\mathbf{x}}_n-y_n^{\prime }\ell \prime (y_n{\mathbf{f}}_{\text{priv}}^T\mathbf{x}{\prime }_n)\mathbf{x}{\prime }_n.$$

This implies that:

$$\Vert \mathbf{b}\Vert -\Vert \mathbf{b}\prime \Vert \le \Vert \mathbf{b}-\mathbf{b}\prime \Vert \le 2.$$

We can write:

$$\frac{\mu (\mathbf{b}|𝒟)}{\mu (\mathbf{b}\prime |𝒟\prime )}=\frac{{\Vert \mathbf{b}\Vert }^{d-1}{e}^{-{\mathrm{\epsilon }}_p^{\prime }\Vert \mathbf{b}\Vert /2}·\frac{1}{\text{surf}(\Vert \mathbf{b}\Vert )}}{{\Vert \mathbf{b}\prime \Vert }^{d-1}{e}^{-{\mathrm{\epsilon }}_p^{\prime }\Vert \mathbf{b}\prime \Vert /2}·\frac{1}{\text{surf}(\Vert \mathbf{b}\prime \Vert )}}\le e^{{\mathrm{\epsilon }}_p^{\prime }(\Vert \mathbf{b}\Vert -\Vert \mathbf{b}\prime \Vert )/2}\le e^{{\mathrm{\epsilon }}_p^{\prime }},$$

where surf(x) denotes the surface area of the sphere in d dimensions with radius x. Here the last step follows from the fact that surf(x) = surf(1)x^d−1, where surf(1) is the surface area of the unit sphere in ℝ^d.

Finally, we are ready to bound the ratio of densities:

$$\frac{g({\mathbf{f}}_{\text{priv}}|𝒟)}{g({\mathbf{f}}_{\text{priv}}|𝒟\prime )}=\frac{\mu (\mathbf{b}|𝒟)}{\mu (\mathbf{b}\prime |𝒟\prime )}·\frac{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}|𝒟\prime ))|}{|\text{det}(\mathbf{J}({\mathbf{f}}_{\text{priv}}\to \mathbf{b}\prime |𝒟))|}=\frac{\mu (\mathbf{b}|𝒟)}{\mu (\mathbf{b}\prime |𝒟\prime )}·\frac{|\text{det}(A+E)|}{|\text{det}A|}\le e^{{\mathrm{\epsilon }}_p^{\prime }}·e^{{\mathrm{\epsilon }}_p-{\mathrm{\epsilon }}_p^{\prime }}\le e^{{\mathrm{\epsilon }}_p}.$$

Thus, Algorithm 2 satisfies Definition 2.

Lemma 10 If A is full rank, and if E has rank at most 2, then,

$$\frac{\text{det}(A+E)-\text{det}(A)}{\text{det}(A)}={\mathrm{\lambda }}_1(A^{-1}E)+{\mathrm{\lambda }}_2(A^{-1}E)+{\mathrm{\lambda }}_1(A^{-1}E){\mathrm{\lambda }}_2(A^{-1}E),$$

where λ_j(Z) is the j-th eigenvalue of matrix Z.

Proof Note that E has rank at most 2, so A⁻¹E also has rank at most 2. Using the fact that λ_i(I + A⁻¹E) = 1 + λ_i(A⁻¹E),

$$\frac{\text{det}(A+E)-\text{det}(A)}{\text{det}A}=\text{det}(I+A^{-1}E)-1=(1+{\mathrm{\lambda }}_1(A^{-1}E))(1+{\mathrm{\lambda }}_2(A^{-1}E))-1={\mathrm{\lambda }}_1(A^{-1}E)+{\mathrm{\lambda }}_2(A^{-1}E)+{\mathrm{\lambda }}_1(A^{-1}E){\mathrm{\lambda }}_2(A^{-1}E).$$

3.4 Application to Classification

In this section, we show how to use our results to provide privacy-preserving versions of logistic regression and support vector machines.

3.4.1 LOGISTIC REGRESSION

One popular ERM classification algorithm is regularized logistic regression. In this case, $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, and the loss function is ℓ_LR(z) = log(1 + e^−z). Taking derivatives and double derivatives,

$$\begin{array}{c}{\ell }_{\text{LR}}^{\prime }(z)=\frac{-1}{(1+e^z)},\hfill \\ {\ell }_{\text{LR}}^{″}(z)=\frac{1}{(1+e^{-z})(1+e^z)}.\hfill \end{array}$$

Note that ℓ_LR is continuous, differentiable and doubly differentiable, with $c\le \frac{1}{4}$. Therefore, we can plug in logistic loss directly to Theorems 6 and 9 to get the following result.

Corollary 11 The output of Algorithm 1 with $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, ℓ = ℓ_LR is an ε_p-differentially private approximation to logistic regression. The output of Algorithm 2 with $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2,c=\frac{1}{4}$, and ℓ = ℓ_LR, is an ε_p-differentially private approximation to logistic regression.

We quantify how well the outputs of Algorithms 1 and 2 approximate (non-private) logistic regression in Section 4.

3.4.2 SUPPORT VECTOR MACHINES

Another very commonly used classifier is L₂-regularized support vector machines. In this case, again, $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, and

$${\ell }_{\text{SVM}}(z)=\text{max}(0,1-z).$$

Notice that this loss function is continuous, but not differentiable, and thus it does not satisfy conditions in Theorems 6 and 9.

There are two alternative solutions to this. First, we can approximate ℓ_SVM by a different loss function, which is doubly differentiable, as follows (see also Chapelle, 2007):

$${\ell }_s(z)=\{\begin{array}{ccc}0\hfill & \text{if}\hfill & z>1+h\hfill \\ -\frac{{(1-z)}^4}{16h^3}+\frac{3{(1-z)}^2}{8h}+\frac{1-z}{2}+\frac{3h}{16}\hfill & \text{if}\hfill & |1-z|\le h\hfill \\ 1-z\hfill & \text{if}\hfill & z<1-h.\hfill \end{array}$$

As h → 0, this loss approaches the hinge loss. Taking derivatives, we observe that:

$${\ell }_s^{\prime }(z)=\{\begin{array}{ccc}0\hfill & \text{if}\hfill & z>1+h\hfill \\ \frac{{(1-z)}^3}{4h^3}-\frac{3(1-z)}{4h}-\frac{1}{2}\hfill & \text{if}\hfill & |1-z|\le h\hfill \\ -1\hfill & \text{if}\hfill & z<1-h.\hfill \end{array}$$

Moreover,

$${\ell }_s^{″}(z)=\{\begin{array}{ccc}0\hfill & \text{if}\hfill & z>1+h\hfill \\ -\frac{3{(1-z)}^2}{4h^3}+\frac{3}{4h}\hfill & \text{if}\hfill & |1-z|\le h\hfill \\ 0\hfill & \text{if}\hfill & z<1-h.\hfill \end{array}$$

Observe that this implies that $|{\ell }_s^{″}(z)|\le \frac{3}{4h}$ for all h and z. Moreover, ℓ_s is convex, as ${\ell }_s^{″}(z)\ge 0$ for all z. Therefore, ℓ_s can be used in Theorems 6 and 9, which gives us privacy-preserving approximations to regularized support vector machines.

Corollary 12 The output of Algorithm 1 with $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, and ℓ = ℓ_s is an ε_p-differentially private approximation to support vector machines. The output of Algorithm 2 with $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2,c=\frac{3}{4h}$, and ℓ = ℓ_s is an ε_p-differentially private approximation to support vector machines.

The second solution is to use Huber Loss, as suggested by Chapelle (2007), which is defined as follows:

$${\ell }_{\text{Huber}}(z)=\{\begin{array}{ccc}0\hfill & \text{if}\hfill & z>1+h\hfill \\ \frac{1}{4h}{(1+h-z)}^2\hfill & \text{if}\hfill & |1-z|\le h\hfill \\ 1-z\hfill & \text{if}\hfill & z<1-h.\hfill \end{array}$$ (7)

Observe that Huber loss is convex and differentiable, and piecewise doubly-differentiable, with $c=\frac{1}{2h}$. However, it is not globally doubly differentiable, and hence the Jacobian in the proof of Theorem 9 is undefined for certain values of f. However, we can show that in this case, Algorithm 2, when run with $c=\frac{1}{2h}$ satisfies Definition 3.

Let G denote the map from f_priv to b in (6) under ℬ = 𝒟, and H denote the map under ℬ = 𝒟′. By definition, the probability ℙ(f_priv ∈ 𝒮 | ℬ = 𝒟) = ℙ_b(b ∈ G(𝒮)).

Corollary 13 Let f_priv be the output of Algorithm 2 with ℓ = ℓ_Huber, $c=\frac{1}{2h}$, and $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }_2^2$. For any set 𝒮 of possible values of f_priv, and any pair of data sets 𝒟, 𝒟′ which differ in the private value of one person (x_n, y_n),

$$e^{-{\mathrm{\epsilon }}_p}\mathbb{P}(𝒮|ℬ=𝒟\prime )\le \mathbb{P}(𝒮|ℬ=𝒟)\le e^{{\mathrm{\epsilon }}_p}\mathbb{P}(𝒮|ℬ=𝒟\prime ).$$

Proof Consider the event f_priv ∈ 𝒮. Let 𝒯 = G(𝒮) and 𝒯′ = H(𝒮). Because G is a bijection, we have

$$\mathbb{P}({\mathbf{f}}_{\text{priv}}\in 𝒮|ℬ=𝒟)={\mathbb{P}}_{\mathbf{b}}(\mathbf{b}\in 𝒯|ℬ=𝒟),$$

and a similar expression when ℬ = 𝒟′.

Now note that ${\ell }_{\text{Huber}}^{\prime }(z)$ is only non-differentiable for a finite number of values of z. Let 𝒵 be the set of these values of z.

$$𝒞=\{\mathbf{f}:y{\mathbf{f}}^T\mathbf{x}=z\in 𝒵,(\mathbf{x},y)\in 𝒟\cup 𝒟\prime \}.$$

Pick a tuple (z, (x,y)) ∈ 𝒵 × (𝒟 ∪ 𝒟′). The set of f such that yf^T x = z is a hyperplane in ℝ^d. Since ∇N(f) = f/2 and ℓ′ is piecewise linear, from (6) we see that the set of corresponding b’s is also piecewise linear, and hence has Lebesgue measure 0. Since the measure corresponding to b is absolutely continuous with respect to the Lebesgue measure, this hyperplane has probability 0 under b as well. Since 𝒞 is a finite union of such hyperplanes, we have ℙ(b ∈ G(𝒞)) = 0.

Thus we have ℙ_b(𝒯 | ℬ = 𝒟) = ℙ_b(G(𝒮\𝒞) | ℬ = 𝒟), and similarly for 𝒟′. From the definition of G and H, for f ∈ 𝒮\𝒞,

$$H(\mathbf{f})=G(\mathbf{f})+y_n\ell \prime (y_n{\mathbf{f}}^T{\mathbf{x}}_n){\mathbf{x}}_n-y_n^{\prime }\ell \prime (y_n^{\prime }{\mathbf{f}}^T{\mathbf{x}}_n^{\prime }){\mathbf{x}}_n^{\prime }.$$

since f ∉ 𝒞, this mapping shows that if ℙ_b(G(𝒮 \ 𝒞) | ℬ = 𝒟) = 0 then we must have ℙ_b(H(𝒮 \ 𝒞) | ℬ = 𝒟) = 0. Thus the result holds for sets of measure 0. If 𝒮\𝒞 has positive measure we can calculate the ratio of the probabilities for f_priv for which the loss is twice-differentiable. For such f_priv the Jacobian is also defined, and we can use a method similar to Theorem 9 to prove the result.

Remark: Because the privacy proof for Algorithm 1 does not require the analytic properties of 2, we can also use Huber loss in Algorithm 1 to get an ε_g-differentially private approximation to the SVM. We quantify how well the outputs of Algorithms 1 and 2 approximate private support vector machines in Section 4. These approximations to the hinge loss are necessary because of the analytic requirements of Theorems 6 and 9 on the loss function. Because the requirements of Theorem 9 are stricter, it may be possible to use an approximate loss in Algorithm 1 that would not be admissible in Algorithm 2.

4. Generalization Performance

In this section, we provide guarantees on the performance of privacy-preserving ERM algorithms in Section 3. We provide these bounds for L₂-regularization. To quantify this performance, we will assume that the n entries in the data set 𝒟 are drawn i.i.d. according to a fixed distribution P(x,y). We measure the performance of these algorithms by the number of samples n required to acheive error L* + ε_g, where L* is the loss of a reference ERM predictor f₀. This resulting bound on ε_g will depend on the norm ‖f₀‖ of this predictor. By choosing an upper bound ν on the norm, we can interpret the result as saying that the privacy-preserving classifier will have error ε_g more than that of any predictor with ‖f₀‖ ≤ ν.

Given a distribution P the expected loss L(f) for a classifier f is

$$L(\mathbf{f})={𝔼}_{(\mathbf{x},y)~P}[\ell ({\mathbf{f}}^T\mathbf{x},y)].$$

The sample complexity for generalization error ε_g against a classifier f₀ is number of samples n required to achieve error L(f₀) + ε_g under any data distribution P. We would like the sample complexity to be low.

For a fixed P we define the following function, which will be useful in our analysis:

$$\overline{J}(\mathbf{f})=L(\mathbf{f})+\frac{\mathrm{\Lambda }}{2}\Vert \mathbf{f}{\Vert }^2.$$

The function J̄(f) is the expectation (over P) of the non-private L₂-regularized ERM objective evaluated at f.

For non-private ERM, Shalev-Shwartz and Srebro (2008) show that for a given f₀ with loss L(f₀) = L*, if the number of data points satisfies

$$n>C\frac{\Vert {\mathbf{f}}_0{\Vert }^2\text{log}(\frac{1}{\mathrm{\delta }})}{{\mathrm{\epsilon }}_g^2}$$

for some constant C, then the excess loss of the L₂-regularized SVM solution f_svm satisfies L(f_svm) ≤ L(f₀) + ε_g. This order growth will hold for our results as well. It also serves as a reference against which we can compare the additional burden on the sample complexity imposed by the privacy constraints.

For most learning problems, we require the generalization error ε_g < 1. Moreover, it is also typically the case that for more difficult learning problems, ‖f₀‖ is higher. For example, for regularized SVM, $\frac{1}{\Vert {\mathbf{f}}_0\Vert }$ is the margin of classification, and as a result, ‖f₀‖ is higher for learning problems with smaller margin. From the bounds provided in this section, we note that the dominating term in the sample requirement for objective perturbation has a better dependence on ‖f₀‖ as well as $\frac{1}{{\mathrm{\epsilon }}_g}$; as a result, for more difficult learning problems, we expect objective perturbation to perform better than output perturbation.

4.1 Output Perturbation

First, we provide performance guarantees for Algorithm 1, by providing a bound on the number of samples required for Algorithm 1 to produce a classifier with low error.

Definition 14 A function g(z) :ℝ → ℝ is c-Lipschitz if for all pairs (z₁, z₂) we have |g(z₁) − g(z₂)| ≤ c|z₁ − z₂|.

Recall that if a function g(z) is differentiable, with |g′(z)| ≤ r for all z, then g(z) is also r-Lipschitz.

Theorem 15 Let $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, and let f₀ be a classifier such that L(f₀) = L*, and let δ > 0. If ℓ is differentiable and continuous with |ℓ′(z)| ≤ 1, the derivative ℓ₀ is c-Lipschitz, the data 𝒟 is drawn i.i.d. according to P, then there exists a constant C such that if the number of training samples satisfies

$$n>C\text{max}(\frac{\Vert {\mathbf{f}}_0{\Vert }^2\text{log}(\frac{1}{\mathrm{\delta }})}{{\mathrm{\epsilon }}_g^2},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})c^{1/2}\Vert {\mathbf{f}}_0{\Vert }^2}{{\mathrm{\epsilon }}_g^{3/2}{\mathrm{\epsilon }}_p}),$$ (8)

where d is the dimension of the data space, then the output f_priv of Algorithm 1 satisfies

$$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-2\mathrm{\delta }.$$

Proof Let

$$\begin{array}{c}{\mathbf{f}}_{\text{rtr}}=\underset{\mathbf{f}}{\text{argmin}}\overline{J}(\mathbf{f}),\hfill \\ {\mathbf{f}}^{*}=\underset{\mathbf{f}}{\text{argmin}}J(\mathbf{f},𝒟),\hfill \end{array}$$

and f_priv denote the output of Algorithm 1. Using the analysis method of Shalev-Shwartz and Srebro (2008) shows

$$L({\mathbf{f}}_{\text{priv}})=L({\mathbf{f}}_0)+(\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}}))+(\overline{J}({\mathbf{f}}_{\text{rtr}})-\overline{J}({\mathbf{f}}_0))+\frac{\mathrm{\Lambda }}{2}\Vert {\mathbf{f}}_0{\Vert }^2-\frac{\mathrm{\Lambda }}{2}\Vert {\mathbf{f}}_{\text{priv}}{\Vert }^2.$$ (9)

We will bound the terms on the right-hand side of (9).

For a regularizer $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$ the Hessian satisfies ‖∇²N(f)‖₂ ≤ 1. Therefore, from Lemma 16, with probability 1 − δ over the privacy mechanism,

$$J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟)\le \frac{8d^2{\text{log}}^2(d/\mathrm{\delta })(c+\mathrm{\Lambda })}{{\mathrm{\Lambda }}^2{n}^2{\mathrm{\epsilon }}_p^2}.$$

Furthermore, the results of Sridharan et al. (2008) show that with probability 1 − δ over the choice of the data distribution,

$$\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}})\le 2(J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟))+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right).$$

The constant in the last term depends on the derivative of the loss and the bound on the data points, which by assumption are bounded. Combining the preceeding two statements, with probability 1 − 2δ over the noise in the privacy mechanism and the data distribution, the second term in the right-hand-side of (9) is at most:

$$\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}})\le \frac{16d^2{\text{log}}^2(d/\mathrm{\delta })(c+\mathrm{\Lambda })}{{\mathrm{\Lambda }}^2{n}^2{\mathrm{\epsilon }}_p^2}+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right).$$ (10)

By definition of f_rtr, the difference (J̄(f_rtr) − J̄(f₀)) ≤ 0. Setting $\mathrm{\Lambda }=\frac{{\mathrm{\epsilon }}_g}{{\Vert {\mathbf{f}}_0\Vert }^2}$ in (9) and using (10), we obtain

$$L({\mathbf{f}}_{\text{priv}})\le L({\mathbf{f}}_0)+\frac{16\Vert {\mathbf{f}}_0{\Vert }^4{d}^2{\text{log}}^2(d/\mathrm{\delta })(c+{\mathrm{\epsilon }}_g/\Vert {\mathbf{f}}_0{\Vert }^2)}{n^2{\mathrm{\epsilon }}_g^2{\mathrm{\epsilon }}_p^2}+O(\Vert {\mathbf{f}}_0{\Vert }^2\frac{\text{log}(1/\mathrm{\delta })}{n{\mathrm{\epsilon }}_g})+\frac{{\mathrm{\epsilon }}_g}{2}.$$

Solving for n to make the total excess error equal to ε_g yields (8).

Lemma 16 Suppose N(·) is doubly differentiable with ‖∇²N(f)‖₂ ≤ η for all f, and suppose that ℓ is differentiable and has continuous and c-Lipschitz derivatives. Given training data 𝒟, let f* be a classifier that minimizes J(f,𝒟) and let f_priv be the classifier output by Algorithm 1. Then

$${\mathbb{P}}_{\mathbf{b}}(J({\mathbf{f}}_{\text{priv}},𝒟)\le J({\mathbf{f}}^{*},𝒟)+\frac{2d^2(c+\mathrm{\Lambda }\mathrm{\eta }){\text{log}}^2(d/\mathrm{\delta })}{{\mathrm{\Lambda }}^2{n}^2{\mathrm{\epsilon }}_p^2})\ge 1-\mathrm{\delta },$$

where the probability is taken over the randomness in the noise b of Algorithm 1.

Note that when ℓ is doubly differentiable, c is an upper bound on the double derivative of ℓ, and is the same as the constant c in Theorem 9.

Proof Let 𝒟 = {(x₁,y₁),…, (x_n,y_n)}, and recall that ‖x_i‖ ≤ 1, and |y_i| ≤ 1. As N(·) and ℓ are differentiable, we use the Mean Value Theorem to show that for some t between 0 and 1,

$$J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟)={({\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*})}^T\nabla J(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})\le \Vert {\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*}\Vert ·\Vert \nabla J(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})\Vert ,$$ (11)

where the second step follows by an application of the Cauchy-Schwartz inequality. Recall that

$$\nabla J(\mathbf{f},𝒟)=\mathrm{\Lambda }\nabla N(\mathbf{f})+\frac{1}{n}{\displaystyle \sum _i}{y}_i\ell \prime (y_i{\mathbf{f}}^T{\mathbf{x}}_i){\mathbf{x}}_i.$$

Moreover, recall that ∇J(f*,𝒟) = 0, from the optimality of f*. Therefore,

$$\nabla J(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}},𝒟)=\nabla J({\mathbf{f}}^{*},𝒟)-\mathrm{\Lambda }(\nabla N({\mathbf{f}}^{*})-\nabla N(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}}))-\frac{1}{n}{\displaystyle \sum _i}{y}_i(\ell \prime (y_i{({\mathbf{f}}^{*})}^T{\mathbf{x}}_i)-\ell \prime (y_i{(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})}^T{\mathbf{x}}_i)){\mathbf{x}}_i.$$ (12)

Now, from the Lipschitz condition on ℓ, for each i we can upper bound each term in the summation above:

$$\Vert y_i(\ell \prime (y_i{({\mathbf{f}}^{*})}^T{\mathbf{x}}_i)-\ell \prime (y_i{(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})}^T{\mathbf{x}}_i)){\mathbf{x}}_i\Vert \le |y_i|·\Vert {\mathbf{x}}_i\Vert ·\ell \prime (y_i{({\mathbf{f}}^{*})}^T{\mathbf{x}}_i)-\ell \prime (y_i{(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})}^T{\mathbf{x}}_i)|\le |y_i|·\Vert {\mathbf{x}}_i\Vert ·c·|y_i(1-t){({\mathbf{f}}^{*}-{\mathbf{f}}_{\text{priv}})}^T{\mathbf{x}}_i|\le c(1-t)|y_i{|}^2·\Vert {\mathbf{x}}_i|{|}^2·\Vert {\mathbf{f}}^{*}-{\mathbf{f}}_{\text{priv}}\Vert \le c(1-t)\Vert {\mathbf{f}}^{*}-{\mathbf{f}}_{\text{priv}}\Vert .$$ (13)

The third step follows because ℓ′ is c-Lipschitz and the last step follows from the bounds on |y_i| and ‖x_i‖. Because N is doubly differentiable, we can apply the Mean Value Theorem again to conclude that

$$\Vert \nabla N(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})-\nabla N({\mathbf{f}}^{*})\Vert \le (1-t)\Vert {\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*}\Vert ·\Vert {\nabla }^{2}N(\mathbf{f}″){\Vert }_2$$ (14)

for some f″ ∈ ℝ^d.

As 0 ≤ t ≤ 1, we can combine (12), (13), and (14) to obtain

$$\Vert \nabla J(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}},𝒟)\Vert \le \Vert \mathrm{\Lambda }(\nabla N({\mathbf{f}}^{*})-\nabla N(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}}))\Vert +\Vert \frac{1}{n}{\displaystyle \sum _i}{y}_i(\ell \prime (y_i{({\mathbf{f}}^{*})}^T{\mathbf{x}}_i)-\ell \prime (y_i{(t{\mathbf{f}}^{*}+(1-t){\mathbf{f}}_{\text{priv}})}^T{\mathbf{x}}_i)){\mathbf{x}}_i\Vert \le (1-t)\Vert {\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*}\Vert ·(\mathrm{\Lambda }\mathrm{\eta }+\frac{1}{n}·n·c)\le \Vert {\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*}\Vert (\mathrm{\Lambda }\mathrm{\eta }+c).$$ (15)

From the definition of Algorithm 1, f_priv − f* = b, where b is the noise vector. Now we can apply Lemma 17 to ‖f_priv − f*‖, with parameters k = d, and $\mathrm{\theta }=\frac{2}{\mathrm{\Lambda }n{\mathrm{\epsilon }}_p}$. From Lemma 17, with probability 1 − δ, $\Vert {\mathbf{f}}_{\text{priv}}-{\mathbf{f}}^{*}\Vert \le \frac{2d\text{log}\left(\frac{d}{\mathrm{\delta }}\right)}{\mathrm{\Lambda }n{\mathrm{\epsilon }}_p}$. The Lemma follows by combining this with Equations 15 and 11.

Lemma 17 Let X be a random variable drawn from the distribution Γ(k,θ), where k is an integer. Then,

$$\mathbb{P}(X<k\mathrm{\theta }\text{log}(\frac{k}{\mathrm{\delta }}\left)\right)\ge 1-\mathrm{\delta }.$$

Proof Since k is an integer, we can decompose X distributed according to Γ(k, θ) as a summation

$$X=X_1+\dots +X_k,$$

where X₁,X₂,…,X_k are independent exponential random variables with mean θ. For each i we have ℙ(X_i ≥ θ log(k/δ)) = δ/k. Now,

$$\mathbb{P}(X<k\mathrm{\theta }\text{log}(k/\mathrm{\delta }))\ge \mathbb{P}(X_i<\mathrm{\theta }\text{log}(k/\mathrm{\delta })i=1,2,\dots ,k)={(1-\mathrm{\delta }/k)}^k\ge 1-\mathrm{\delta }.$$

4.2 Objective Perturbation

We now establish performance bounds on Algorithm 2. The bound can be summarized as follows.

Theorem 18 Let $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$, and let f₀ be a classifier with expected loss L(f₀) = L*. Let ℓ be convex, doubly differentiable, and let its derivatives satisfy |ℓ′(z)| ≤ 1 and |ℓ″(z)| ≤ c for all z. Then there exists a constantC such that for δ > 0, if the n training samples in 𝒟 are drawn i.i.d. according to P, and if

$$n>C\text{max}\left(\frac{{\Vert {\mathbf{f}}_0\Vert }^2\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g^2},\frac{c{\Vert {\mathbf{f}}_0\Vert }^2}{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p}\right),$$

then the output f_priv of Algorithm 2 satisfies

$$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-2\mathrm{\delta }.$$

Proof Let

$$\begin{array}{cc}{\mathbf{f}}_{\text{rtr}}\hfill & =\underset{\mathbf{f}}{\text{argmin}}\overline{J}(\mathbf{f}),\hfill \\ \hfill {\mathbf{f}}^{*}& =\underset{\mathbf{f}}{\text{argmin}}J(\mathbf{f},𝒟),\hfill \end{array}$$

and f_priv denote the output of Algorithm 1. As in Theorem 15, the analysis of Shalev-Shwartz and Srebro (2008) shows

$$L({\mathbf{f}}_{\text{priv}})=L({\mathbf{f}}_0)+(\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}}))+(\overline{J}({\mathbf{f}}_{\text{rtr}})-\overline{J}({\mathbf{f}}_0))+\frac{\mathrm{\Lambda }}{2}{\Vert {\mathbf{f}}_0\Vert }^2-\frac{\mathrm{\Lambda }}{2}{\Vert {\mathbf{f}}_{\text{priv}}\Vert }^2.$$ (16)

We will bound each of the terms on the right-hand-side.

If $n>\frac{c{\Vert {\mathbf{f}}_0\Vert }^2}{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p}\text{and}\mathrm{\Lambda }>\frac{{\mathrm{\epsilon }}_g}{4{\Vert {\mathbf{f}}_0\Vert }^2}$, than $n\mathrm{\Lambda }>\frac{c}{4{\mathrm{\epsilon }}_p}$, so from the definition of ${\mathrm{\epsilon }}_p^{\prime }$ in Algorithm 2,

$${\mathrm{\epsilon }}_p^{\prime }={\mathrm{\epsilon }}_p-2\text{log}(1+\frac{c}{n\mathrm{\Lambda }})={\mathrm{\epsilon }}_p-2\text{log}(1+\frac{{\mathrm{\epsilon }}_p}{4})\ge {\mathrm{\epsilon }}_p-\frac{{\mathrm{\epsilon }}_p}{2},$$

where the last step follows because log(1 + x) ≤ x for x ∈ [0,1]. Note that for these values of Λ we have ${\mathrm{\epsilon }}_p^{\prime }>0$.

Therefore, we can apply Lemma 19 to conclude that with probability at least 1 − δ over the privacy mechanism,

$$J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟)\le \frac{4d^2{\text{log}}^2(d/\mathrm{\delta })}{\mathrm{\Lambda }{n}^2{\mathrm{\epsilon }}_p^2}.$$

From Sridharan et al. (2008),

$$\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}})\le 2(J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟))+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right)\le \frac{8d^2{\text{log}}^2(d/\mathrm{\delta })}{\mathrm{\Lambda }{n}^2{\mathrm{\epsilon }}_p^2}+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right).$$

By definition of f*, we have J̄(f_rtr) − J̄(f₀) ≤ 0. If Λ is set to be $\frac{{\mathrm{\epsilon }}_g}{{\Vert {\mathbf{f}}_0\Vert }^2}$, then, the fourth quantity in Equation 16 is at most $\frac{{\mathrm{\epsilon }}_g}{2}$. The theorem follows by solving for n to make the total excess error at most ε_g.

The following lemma is analogous to Lemma 16, and it establishes a bound on the distance between the output of Algorithm 2, and non-private regularized ERM. We note that this bound holds when Algorithm 2 has ${\mathrm{\epsilon }}_p^{\prime }>0$, that is, when Δ = 0. Ensuring that Δ = 0 requires an additional condition on n, which is stated in Theorem 18.

Lemma 19 Let ${\mathrm{\epsilon }}_p^{\prime }>0$. Let f* = argminJ(f,𝒟), and let f_priv be the classifier output by Algorithm 2. If N(·) is 1-strongly convex and globally differentiable, and if ℓ is convex and differentiable at all points, with |ℓ′(z)| ≤ 1 for all z, then

$${\mathbb{P}}_{\mathbf{b}}\left(J({\mathbf{f}}_{\text{priv}},𝒟)\le J({\mathbf{f}}^{*},𝒟)+\frac{4d^2{\text{log}}^2(d/\mathrm{\delta })}{\mathrm{\Lambda }{n}^2{\mathrm{\epsilon }}_p^2}\right)\ge 1-\mathrm{\delta },$$

where the probability is taken over the randomness in the noise b of Algorithm 2.

Proof By the assumption ${\mathrm{\epsilon }}_p^{\prime }>0$, the classifier f_priv minimizes the objective function $J(\mathbf{f},𝒟)+\frac{1}{n}{\mathbf{b}}^T\mathbf{f}$, and therefore

$$J({\mathbf{f}}_{\text{priv}},𝒟)\le J({\mathbf{f}}^{*},𝒟)+\frac{1}{n}{\mathbf{b}}^T({\mathbf{f}}^{*}-{\mathbf{f}}_{\text{priv}}).$$

First, we try to bound ‖f* − f_priv‖. Recall that ΛN(·) is Λ-strongly convex and globally differentiable, and ℓ is convex and differentiable. We can therefore apply Lemma 7 with G(f) = J(f,𝒟) and $g(\mathbf{f})=\frac{1}{n}{\mathbf{b}}^T\mathbf{f}$ to obtain the bound

$$\Vert {\mathbf{f}}^{*}-{\mathbf{f}}_{\text{priv}}\Vert \le \frac{1}{\mathrm{\Lambda }}\Vert \nabla (\frac{1}{n}{\mathbf{b}}^T\mathbf{f})\Vert \le \frac{\Vert \mathbf{b}\Vert }{n\mathrm{\Lambda }}.$$

Therefore by the Cauchy-Schwartz inequality,

$$J({\mathbf{f}}_{\text{priv}},𝒟)-J({\mathbf{f}}^{*},𝒟)\le \frac{{\Vert \mathbf{b}\Vert }^2}{n^2\mathrm{\Lambda }}.$$

Since ‖b‖ is drawn from a $\mathrm{\Gamma }(d,\frac{2}{{\mathrm{\epsilon }}_p})$ distribution, from Lemma 17, with probability 1 − δ, $\Vert \mathbf{b}\Vert \le \frac{2d\text{log}(d/\mathrm{\delta })}{{\mathrm{\epsilon }}_p}$. The Lemma follows by plugging this in to the previous equation.

4.3 Applications

In this section, we examine the sample requirement of privacy-preserving regularized logistic regression and support vector machines. Recall that in both these cases, $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$.

Corollary 20 (Logistic Regression) Let training data 𝒟 be generated i.i.d. according to a distribution P and let f₀ be a classifier with expected loss L(f₀) = L*. Let the loss function ℓ = ℓ_LR defined in Section 3.4.1. Then the following two statements hold:

1. There exists a C₁ such that if

   $$n>C_1\text{max}\left(\frac{{\Vert {\mathbf{f}}_0\Vert }^2\text{log}(\frac{1}{\mathrm{\delta }})}{{\mathrm{\epsilon }}_g^2},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }}){\Vert {\mathbf{f}}_0\Vert }^2}{{\mathrm{\epsilon }}_g^{3/2}{\mathrm{\epsilon }}_p}\right),$$

   then the output f_priv of Algorithm 1 satisfies

   $$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-\mathrm{\delta }.$$
2. There exists a C₂ such that if

   $$n>C\text{max}\left(\frac{{\Vert {\mathbf{f}}_0\Vert }^2\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g^2},\frac{{\Vert {\mathbf{f}}_0\Vert }^2}{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p}\right),$$

   then the output f_priv of Algorithm 2 with $c=\frac{1}{4}$ satisfies

   $$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-\mathrm{\delta }.$$

Proof Since ℓ_LR is convex and doubly differentiable for any z₁, z₂,

$${\ell }_{\text{LR}}^{\prime }(z_1)-{\ell }_{\text{LR}}^{\prime }(z_2)\le {\ell }_{\text{LR}}^{″}(z^{*})(z_1-z_2)$$

for some z* ∈ [z₁,z₂]. Moreover, $|{\ell }_{\text{LR}}^{″}(z^{*})|\le c=\frac{1}{4}$, so ℓ′ is $\frac{1}{4}-\text{Lipschitz}$. The corollary now follows from Theorems 15 and 18.

For SVMs we state results with ℓ = ℓ_Huber, but a similar bound can be shown for ℓ_s as well.

Corollary 21 (Huber Support Vector Machines) Let training data 𝒟 be generated i.i.d. according to a distribution P and let f₀ be a classifier with expected loss L(f₀) = L*. Let the loss function ℓ = ℓ_Huber defined in (7). Then the following two statements hold:

1. There exists a C₁ such that if

   $$n>C_1\text{max}\left(\frac{{\Vert {\mathbf{f}}_0\Vert }^2\text{log}(\frac{1}{\mathrm{\delta }})}{{\mathrm{\epsilon }}_g^2},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }}){\Vert {\mathbf{f}}_0\Vert }^2}{h^{1/2}{\mathrm{\epsilon }}_g^{3/2}{\mathrm{\epsilon }}_p}\right),$$

   then the output f_priv of Algorithm 1 satisfies

   $$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-\mathrm{\delta }.$$
2. There exists a C₂ such that if

   $$n>C\text{max}\left(\frac{{\Vert {\mathbf{f}}_0\Vert }^2\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g^2},\frac{{\Vert {\mathbf{f}}_0\Vert }^2}{h{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p},\frac{d\text{log}(\frac{d}{\mathrm{\delta }})\Vert {\mathbf{f}}_0\Vert }{{\mathrm{\epsilon }}_g{\mathrm{\epsilon }}_p}\right),$$

   then the output f_priv of Algorithm 2 with $c=\frac{1}{4}$ satisfies

   $$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})\le L^{*}+{\mathrm{\epsilon }}_g)\ge 1-\mathrm{\delta }.$$

Proof The Huber loss is convex and differentiable with continuous derivatives. Moreover, since the derivative of the Huber loss is piecewise linear with slope 0 or at most $\frac{1}{2h}$, for any z₁, z₂,

$$|{\ell }_{\text{Huber}}^{\prime }(z_1)-{\ell }_{\text{Huber}}^{\prime }(z_2)|\le \frac{1}{2h}|z_1-z_2|,$$

so ${\ell }_{\text{Huber}}^{\prime }$ is $\frac{1}{2h}-\text{Lipschitz}$. The first part of the corollary follows from Theorem 15.

For the second part of the corollary, we observe that from Corollary 13, we do not need ℓ to be globally double differentiable, and the bound on |ℓ″(z)| in Theorem 18 is only needed to ensure that ${\mathrm{\epsilon }}_p^{\prime }>0$; since ℓ_Huber is double differentiable except in a set of Lebesgue measure 0, with $|{\ell }_{\text{Huber}}^{″}(z)|\le \frac{1}{2h}$, the corollary follows by an application of Theorem 18.

5. Kernel Methods

A powerful methodology in learning problems is the “kernel trick,” which allows the efficient construction of a predictor f that lies in a reproducing kernel Hilbert space (RKHS) ℋ associated to a positive definite kernel function k(·, ·). The representer theorem (Kimeldorf and Wahba, 1970) shows that the regularized empirical risk in (1) is minimized by a function f(x) that is given by a linear combination of kernel functions centered at the data points:

$${\mathbf{f}}^{*}(\mathbf{x})={\displaystyle \sum _{i=1}^n}{a}_{i}k(\mathbf{x}(i),\mathbf{x}).$$ (17)

This elegant result is important for both theoretical and computational reasons. Computationally, one releases the values a_i corresponding to the f that minimizes the empirical risk, along with the data points x(i); the user classifies a new x by evaluating the function in (17).

A crucial difficulty in terms of privacy is that this directly releases the private values x(i) of some individuals in the training set. Thus, even if the classifier is computed in a privacy-preserving way, any classifier released by this process requires revealing the data. We provide an algorithm that avoids this problem, using an approximation method (Rahimi and Recht, 2007, 2008b) to approximate the kernel function using random projections.

5.1 Mathematical Preliminaries

Our approach works for kernel functions which are translation invariant, so k(x,x′) = k(x − x′). The key idea in the random projection method is from Bochner’s Theorem, which states that a continuous translation invariant kernel is positive definite if and only if it is the Fourier transform of a nonnegative measure. This means that the Fourier transform K(θ) of translation-invariant kernel function k(t) can be normalized so that K̄(θ) = K(θ)/‖K(θ)‖₁ is a probability measure on the transform space Θ. We will assume K̄ (θ) is uniformly bounded over θ.

In this representation

$$k(\mathbf{x},\mathbf{x}\prime )={\displaystyle {\int }_{\mathrm{\Theta }}}\mathrm{\varphi }(\mathbf{x};\mathrm{\theta })\mathrm{\varphi }(\mathbf{x}\prime ;\mathrm{\theta })\overline{K}(\mathrm{\theta })d\mathrm{\theta },$$ (18)

where we will assume the feature functions ϕ(x;θ) are bounded:

$$|\mathrm{\varphi }(\mathbf{x};\mathrm{\theta })|\le \mathrm{\zeta }\forall \mathbf{x}\in 𝒳,\forall \mathrm{\theta }\in \mathrm{\Theta }.$$

A function f ∈ ℋ can be written as

$$\mathbf{f}(\mathbf{x})={\displaystyle {\int }_{\mathrm{\Theta }}}a(\mathrm{\theta })\mathrm{\varphi }(\mathbf{x};\mathrm{\theta })\overline{K}(\mathrm{\theta })d\mathrm{\theta }.$$

To prove our generalization bounds we must show that bounded classifiers f induce bounded functions a(θ). Writing the evaluation functional as an inner product with k(x, x′) and (18) shows

$$\mathbf{f}(\mathbf{x})={\displaystyle {\int }_{\mathrm{\Theta }}}({\displaystyle {\int }_{𝒳}}\mathbf{f}(\mathbf{x}\prime )\mathrm{\varphi }(\mathbf{x}\prime ;\mathrm{\theta })d\mathbf{x}\prime )\mathrm{\varphi }(\mathbf{x};\mathrm{\theta })\overline{K}(\mathrm{\theta })d\mathrm{\theta }.$$

Thus we have

$$\begin{array}{c}a(\mathrm{\theta })={\displaystyle {\int }_{𝒳}}\mathbf{f}(\mathbf{x}\prime )\mathrm{\varphi }(\mathbf{x}\prime ;\mathrm{\theta })d\mathbf{x}\prime \hfill \\ |a(\mathrm{\theta })|\le \text{Vol}(𝒳)·\mathrm{\zeta }·{\Vert \mathbf{f}\Vert }_{\mathrm{\infty }}.\hfill \end{array}$$

This shows that a(θ) is bounded uniformly over Θ when f(x) is bounded uniformly over 𝒳. The volume of the unit ball is $\text{Vol}(𝒳)=\frac{{\mathrm{\pi }}^{d/2}}{\mathrm{\Gamma }\left(\frac{d}{2}+1\right)}$ (see Ball, 1997 for more details). For large d this is ${(\sqrt{\frac{2\mathrm{\pi }e}{d}})}^d$ by Stirling’s formula. Furthermore, we have

$${\Vert \mathbf{f}\Vert }_{\mathscr{H}}^2={\displaystyle {\int }_{\mathrm{\Theta }}}a{(\mathrm{\theta })}^2\overline{K}(\mathrm{\theta })d\mathrm{\theta }.$$

5.2 A Reduction to the Linear Case

We now describe how to apply Algorithms 1 and 2 for classification with kernels, by transforming to linear classification. Given {θ_j}, let R : 𝒳 → ℝ^D be the map that sends x(i) to a vector v(i) ∈ ℝ^D where v_j(i) = ϕ(x(i);θ_j) for j ∈ [D]. We then use Algorithm 1 or Algorithm 2 to compute a privacy-preserving linear classifier f in ℝ^D. The algorithm releases R and f̃. The overall classifier is f_priv(x) = f̃(R(x)).

As an example, consider the Gaussian kernel

$$k(\mathbf{x},\mathbf{x}\prime )=\text{exp}(-\mathrm{\gamma }{\Vert \mathbf{x}-\mathbf{x}\prime \Vert }_2^2).$$

The Fourier transform of a Gaussian is a Gaussian, so we can sample θ_j = (ω,ψ) according to the distribution Uniform[−π,π] × 𝒩(0,2γI_d) and compute ν_j = cos(ω^T x + ψ). The random phase is used to produce a real-valued mapping. The paper of Rahimi and Recht (2008a) has more examples of transforms for other kernel functions.

Algorithm 3.

Private ERM for nonlinear kernels

Inputs: Data {(xi, yi) : i ε [n]}, positive definite kernel function k(·, ·), sampling function K̄(θ), parameters εp, Λ, D

Outputs: Predictor fpriv and pre-filter {θj : j ε [D]}.

Draw {θj : j = 1,2,…,D} iid according to K̄ (θ).

Set $\mathbf{v}(i)=\sqrt{2/D}{[\mathrm{\phi }(\mathbf{x}(i);{\mathrm{\theta }}_1)\cdots \mathrm{\phi }(\mathbf{x}(i);{\mathrm{\theta }}_D)]}^T$ for each i.

Run Algorithm 1 or Algorithm 2 with data {(v(i), y(i))} and parameters εp, Λ.

5.3 Privacy Guarantees

Because the workhorse of Algorithm 3 is a differentially-private version of ERM for linear classifiers (either Algorithm 1 or Algorithm 2), and the points {θ_j : j ∈ [D]} are independent of the data, the privacy guarantees for Algorithm 3 follow trivially from Theorems 6 and 9.

Theorem 22 Given data {(x(i),y(i)) : i = 1,2,…,n} with (x(i),y(i)) and ‖x(i)‖ ≤ 1, the outputs (f_priv,{θ_j : j ∈ [D]}) of Algorithm 3 guarantee ε_p-differential privacy.

The proof trivially follows from a combination of Theorems 6, 9, and the fact that the θ_j’s are drawn independently of the input data set.

5.4 Generalization Performance

We now turn to generalization bounds for Algorithm 3. We will prove results using objective perturbation (Algorithm 2) in Algorithm 3, but analogous results for output perturbation (Algorithm 1) are simple to prove. Our comparisons will be against arbitrary predictors f₀ whose norm is bounded in some sense. That is, given an f₀ with some properties, we will choose regularization parameter Λ, dimension D, and number of samples n so that the predictor f_priv has expected loss close to that of f₀.

In this section we will assume $N(\mathbf{f})=\frac{1}{2}{\Vert \mathbf{f}\Vert }^2$ so that N(·) is 1-strongly convex, and that the loss function ℓ is convex, differentiable and |ℓ′(z)| ≤ 1 for all z.

Our first generalization result is the simplest, since it assumes a strong condition that gives easy guarantees on the projections. We would like the predictor produced by Algorithm 3 to be competitive against an f₀ such that

$${\mathbf{f}}_0(\mathbf{x})={\displaystyle {\int }_{\mathrm{\Theta }}}{a}_0(\mathrm{\theta })\mathrm{\varphi }(\mathbf{x};\mathrm{\theta })\overline{K}(\mathrm{\theta })d\mathrm{\theta },$$ (19)

and |a₀(θ)| ≤ C (see Rahimi and Recht, 2008b). Our first result provides the technical building block for our other generalization results. The proof makes use of ideas from Rahimi and Recht (2008b) and techniques from Sridharan et al. (2008); Shalev-Shwartz and Srebro (2008).

Lemma 23 Let f₀ be a predictor such that |a₀(θ)| ≤ C, for all θ, where a₀(θ) is given by (19), and suppose L(f₀) = L*. Moreover, suppose that ℓ′(·) is c-Lipschitz. If the data 𝒟 is drawn i.i.d. according to P, then there exists a constant C₀ such that if

$$n>C_0·\text{max}(\frac{C^2\sqrt{\text{log}(1/\mathrm{\delta })}}{{\mathrm{\epsilon }}_p{\mathrm{\epsilon }}_g^2}·\text{log}\frac{C\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g\mathrm{\delta }},\frac{c{\mathrm{\epsilon }}_g}{{\mathrm{\epsilon }}_p\text{log}(1/\mathrm{\delta })}),$$ (20)

then Λ and D can be chosen such that the output f_priv of Algorithm 3 using Algorithm 2 satisfies

$$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})-L^{*}\le {\mathrm{\epsilon }}_g)\ge 1-4\mathrm{\delta }.$$

Proof Since |a₀(θ)| ≤ C and the K̄(θ) is bounded, we have (Rahimi and Recht, 2008b, Theorem 1) that with probability 1 − 2δ there exists an f_p ∈ ℝ^D such that

$$L({\mathbf{f}}_p)\le L({\mathbf{f}}_0)+O\left(\right(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{D}}\left)C\sqrt{\text{log}\frac{1}{\mathrm{\delta }}}\right),$$ (21)

We will choose D to make this loss small. Furthermore, f_p is guaranteed to have ‖f_p‖_∞ ≤ C/D, so

$${\Vert {\mathbf{f}}_p\Vert }_2^2\le \frac{C^2}{D}.$$ (22)

Now given such an f_p we must show that f_priv will have true risk close to that of f_p as long as there are enough data points. This can be shown using the techniques in Shalev-Shwartz and Srebro (2008). Let

$$\overline{J}(\mathbf{f})=L(\mathbf{f})+\frac{\mathrm{\Lambda }}{2}{\Vert \mathbf{f}\Vert }_2^2,$$

and let

$${\mathbf{f}}_{\text{rtr}}=\underset{\mathbf{f}\in {ℝ}^D}{\text{argmin}}\overline{J}(\mathbf{f})$$

minimize the regularized true risk. Then

$$\overline{J}({\mathbf{f}}_{\text{priv}})=\overline{J}({\mathbf{f}}_p)+(\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}}))+(\overline{J}({\mathbf{f}}_{\text{rtr}})-\overline{J}({\mathbf{f}}_p)).$$

Now, since J̄(·) is minimized by f_rtr, the last term is negative and we can disregard it. Then we have

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_p)\le (\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}}))+\frac{\mathrm{\Lambda }}{2}{\Vert {\mathbf{f}}_p\Vert }_2^2-\frac{\mathrm{\Lambda }}{2}{\Vert {\mathbf{f}}_{\text{priv}}\Vert }_2^2.$$ (23)

From Lemma 19, with probability at least 1 − δ over the noise b,

$$J({\mathbf{f}}_{\text{priv}})-J(\underset{\mathbf{f}}{\text{argmin}}J(\mathbf{f}))\le \frac{4D^2{\text{log}}^2(D/\mathrm{\delta })}{\mathrm{\Lambda }{n}^2{\mathrm{\epsilon }}_p^2}.$$ (24)

Now we can bound the term (J̄(f_priv) − J̄(f_rtr)) by twice the gap in the regularized empirical risk difference (24) plus an additional term (Sridharan et al., 2008, Corollary 2). That is, with probability 1 − δ:

$$\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}})\le 2(J({\mathbf{f}}_{\text{priv}})-J({\mathbf{f}}_{\text{rtr}}))+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right).$$ (25)

If we set $n>\frac{c}{4{\mathrm{\epsilon }}_p\mathrm{\Lambda }}$, then ${\mathrm{\epsilon }}_p^{\prime }>0$, and we can plug Lemma 19 into (25) to obtain:

$$\overline{J}({\mathbf{f}}_{\text{priv}})-\overline{J}({\mathbf{f}}_{\text{rtr}})\le \frac{8D^2{\text{log}}^2(D/\mathrm{\delta })}{\mathrm{\Lambda }{n}^2{\mathrm{\epsilon }}_p^2}+O\left(\frac{\text{log}(1/\mathrm{\delta })}{\mathrm{\Lambda }n}\right).$$ (26)

Plugging (26) into (23), discarding the negative term involving ${\Vert {\mathbf{f}}_{\text{priv}}\Vert }_2^2$ and setting Λ = ε_g/‖f_p‖² gives

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_p)\le \frac{8{\Vert {\mathbf{f}}_p\Vert }_2^2{D}^2{\text{log}}^2(D/\mathrm{\delta })}{n^2{\mathrm{\epsilon }}_p^2{\mathrm{\epsilon }}_g}+O\left(\frac{{\Vert {\mathbf{f}}_p\Vert }_2^2\text{log}\frac{1}{\mathrm{\delta }}}{n{\mathrm{\epsilon }}_g}\right)+\frac{{\mathrm{\epsilon }}_g}{2}.$$ (27)

Now we have, using (21) and (27), that with probability 1 − 4δ:

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_0)\le (L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_p))+(L({\mathbf{f}}_p)-L({\mathbf{f}}_0))\le \frac{8{\Vert {\mathbf{f}}_p\Vert }_2^2{D}^2{\text{log}}^2(D/\mathrm{\delta })}{n^2{\mathrm{\epsilon }}_p^2{\mathrm{\epsilon }}_g}+O\left(\frac{{\Vert {\mathbf{f}}_p\Vert }_2^2\text{log}(1/\mathrm{\delta })}{n{\mathrm{\epsilon }}_g}\right)+\frac{{\mathrm{\epsilon }}_g}{2}+O\left(\right(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{D}}\left)C\sqrt{\text{log}\frac{1}{\mathrm{\delta }}}\right),$$

Substituting (22), we have

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_0)\le \frac{8C^{2}D{\text{log}}^2(D/\mathrm{\delta })}{n^2{\mathrm{\epsilon }}_p^2{\mathrm{\epsilon }}_g}+O\left(\frac{C^2\text{log}(1/\mathrm{\delta })}{\mathit{\text{Dn}}{\mathrm{\epsilon }}_g}\right)+\frac{{\mathrm{\epsilon }}_g}{2}+O\left(\right(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{D}}\left)C\sqrt{\text{log}\frac{1}{\mathrm{\delta }}}\right).$$

To set the remaining parameters, we will choose D < n so that

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_0)\le \frac{8C^{2}D{\text{log}}^2(D/\mathrm{\delta })}{n^2{\mathrm{\epsilon }}_p^2{\mathrm{\epsilon }}_g}+O\left(\frac{C^2\text{log}(1/\mathrm{\delta })}{\mathit{\text{Dn}}{\mathrm{\epsilon }}_g}\right)+\frac{{\mathrm{\epsilon }}_g}{2}+O\left(\frac{C\sqrt{\text{log}(1/\mathrm{\delta })}}{\sqrt{D}}\right).$$

We set $D=O(C^2\text{log}(1/\mathrm{\delta })/{\mathrm{\epsilon }}_g^2)$ to make the last term ε_g/6, and:

$$L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_0)\le O\left(\frac{C^4\text{log}\frac{1}{\mathrm{\delta }}{\text{log}}^2\frac{C^2\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g^2\mathrm{\delta }}}{n^2{\mathrm{\epsilon }}_p^2{\mathrm{\epsilon }}_g^3}\right)+O\left(\frac{{\mathrm{\epsilon }}_g}{n}\right)+\frac{2{\mathrm{\epsilon }}_g}{3}.$$

Setting n as in (20) proves the result. Moreover, setting $n>\frac{c{\Vert {\mathbf{f}}_p\Vert }^2}{4{\mathrm{\epsilon }}_p{\mathrm{\epsilon }}_g}=C_0·\frac{c{\mathrm{\epsilon }}_g}{{\mathrm{\epsilon }}_p\text{log}(1/\mathrm{\delta })}$ ensures that $n>\frac{c}{4\mathrm{\Lambda }{\mathrm{\epsilon }}_p}$.

We can adapt the proof procedure to show that Algorithm 3 is competitive against any classifier f₀ with a given bound on ‖f₀‖_∞. It can be shown that for some constant ζ that |a₀(θ)| ≤ Vol(𝒳)ζ‖f₀‖_∞. Then we can set this as C in (20) to obtain the following result.

Theorem 24 Let f₀ be a classifier with norm ‖f₀‖_∞, and let ℓ′(·) be c-Lipschitz. Then for any distribution P, there exists a constant C₀ such that if

$$n>C_0·\text{max}(\frac{{\Vert {\mathbf{f}}_0\Vert }_{\mathrm{\infty }}^2{\mathrm{\zeta }}^2{(\text{Vol}(𝒳))}^2\sqrt{\text{log}(1/\mathrm{\delta })}}{{\mathrm{\epsilon }}_p{\mathrm{\epsilon }}_g^2}·\text{log}\frac{{\Vert {\mathbf{f}}_0\Vert }_{\mathbf{\infty }}\text{Vol}(𝒳)\mathrm{\zeta }\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g\mathrm{\delta }\mathrm{\Gamma }(\frac{d}{2}+1)},\frac{c{\mathrm{\epsilon }}_g}{{\mathrm{\epsilon }}_p\text{log}(1/\mathrm{\delta })}),$$ (28)

then Λ and D can be chosen such that the output f_priv of Algorithm 3 with Algorithm 2 satisfies ℙ(L(f_priv) − L(f₀) ≤ ε_g) ≥ 1 − 4δ.

Proof Substituting C = Vol(𝒳)ζ‖f₀‖_∞ in Lemma 23 we get the result.

We can also derive a generalization result with respect to classifiers with bounded ‖f₀‖_ℋ.

Theorem 25 Let f₀ be a classifier with norm ‖f₀‖_ℋ, and let ℓ′ be c-Lipschitz. Then for any distribution P, there exists a constant C₀ such that if,

$$n=C_0·\text{max}(\frac{{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^4{\mathrm{\zeta }}^2{(\text{Vol}(𝒳))}^2\sqrt{\text{log}(1/\mathrm{\delta })}}{{\mathrm{\epsilon }}_p{\mathrm{\epsilon }}_g^4}·\text{log}\frac{{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}\text{Vol}(𝒳)\mathrm{\zeta }\text{log}(1/\mathrm{\delta })}{{\mathrm{\epsilon }}_g\mathrm{\delta }\mathrm{\Gamma }(\frac{d}{2}+1)},\frac{c{\mathrm{\epsilon }}_g}{{\mathrm{\epsilon }}_p\text{log}(1/\mathrm{\delta })}),$$

then Λ and D can be chosen such that the output of Algorithm 3 run with Algorithm 2 satisfies ℙ (L(f_priv) − L(f₀) ≤ ε_g) ≥ 1 − 4δ.

Proof Let f₀ be a classifier with norm ${\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^2$ and expected loss L(f₀). Now consider

$${\mathbf{f}}_{\text{rtr}}=\underset{\mathbf{f}}{\text{argmin}}L(\mathbf{f})+\frac{{\mathrm{\Lambda }}_{\text{rtr}}}{2}{\Vert \mathbf{f}\Vert }_{\mathscr{H}}^2,$$

for some Λ_rtr to be specified later. We will first need a bound on ‖f_rtr‖_∞ in order to use our previous sample complexity results. Since f_rtr is a minimizer, we can take the derivative of the regularized expected loss and set it to 0 to get:

$${\mathbf{f}}_{\text{rtr}}(\mathbf{x}\prime )=\frac{-1}{{\mathbf{\Lambda }}_{\text{rtr}}}(\frac{\mathrm{\partial }}{\mathrm{\partial }\mathbf{f}}{\displaystyle {\int }_{𝒳}}\ell (\mathbf{f}(\mathbf{x}\prime ),y)\mathit{\text{dP}}(\mathbf{x},y))=\frac{-1}{{\mathrm{\Lambda }}_{\text{rtr}}}\left({\displaystyle {\int }_{𝒳}}\right(\frac{\mathrm{\partial }}{\mathrm{\partial }\mathbf{f}(\mathbf{x}\prime )}\ell (\mathbf{f}(\mathbf{x}),y))·(\frac{\mathrm{\partial }}{\mathrm{\partial }\mathbf{f}(\mathbf{x}\prime )}\mathbf{f}(\mathbf{x}))\mathit{\text{dp}}(\mathbf{x},y)),$$

where P(x,y) is a distribution on pairs (x,y). Now, using the representer theorem, $\frac{\mathrm{\partial }}{\mathrm{\partial }\mathbf{f}(\mathbf{x}\prime )}\mathbf{f}(\mathbf{x})=k(\mathbf{x}\prime ,\mathbf{x})$. Since the kernel function is bounded and the derivative of the loss is always upper bounded by 1, so the integrand can be upper bounded by a constant. Since P(x,y) is a probability distribution, we have for all x′ that |f_rtr(x′)| = O(1/Λ_rtr). Now we set ${\mathrm{\Lambda }}_{\text{rtr}}={\mathrm{\epsilon }}_g/{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^2$ to get

$${\Vert {\mathbf{f}}_{\text{rtr}}\Vert }_{\mathrm{\infty }}=O\left(\frac{{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^2}{{\mathrm{\epsilon }}_g}\right).$$

We now have two cases to consider, depending on whether L(f₀) < L(f_rtr) or L(f₀) > L(f_rtr).

Case 1: Suppose that L(f₀) < L(f_rtr). Then by the definition of f_rtr,

$$L({\mathbf{f}}_{\text{rtr}})+\frac{{\mathrm{\epsilon }}_g}{2}·\frac{{\Vert {\mathbf{f}}_{\text{rtr}}\Vert }_{\mathscr{H}}^2}{{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^2}\le L({\mathbf{f}}_0)+\frac{{\mathrm{\epsilon }}_g}{2}.$$

Since $\frac{{\mathrm{\epsilon }}_g}{2}·\frac{{\Vert {\mathbf{f}}_{\text{rtr}}\Vert }_{\mathscr{H}}^2}{{\Vert {\mathbf{f}}_0\Vert }_{\mathscr{H}}^2}\ge 0$, we have $L({\mathbf{f}}_{\text{rtr}})-L({\mathbf{f}}_0)\le \frac{{\mathrm{\epsilon }}_g}{2}$.

Case 2: Suppose that L(f₀) > L(f_rtr). Then the regularized classifier has better generalization performance than the original, so we have trivially that $L({\mathbf{f}}_{\text{rtr}})-L({\mathbf{f}}_0)\le \frac{{\mathrm{\epsilon }}_g}{2}$.

Therefore in both cases we have a bound on ‖f_rtr‖_∞ and a generalization gap of ε_g/2. We can now apply Theorem 24 to show that for n satisfying (28) we have

$$\mathbb{P}(L({\mathbf{f}}_{\text{priv}})-L({\mathbf{f}}_0)\le {\mathrm{\epsilon }}_g)\ge 1-4\mathrm{\delta }.$$

6. Parameter Tuning

The privacy-preserving learning algorithms presented so far in this paper assume that the regularization constant Λ is provided as an input, and is independent of the data. In actual applications of ERM, Λ is selected based on the data itself. In this section, we address this issue: how to design an ERM algorithm with end-to-end privacy, which selects Λ based on the data itself.

Our solution is to present a privacy-preserving parameter tuning technique that is applicable in general machine learning algorithms, beyond ERM. In practice, one typically tunes parameters (such as the regularization parameter Λ) as follows: using data held out for validation, train predictors f(·;Λ) for multiple values of Λ, and select the one which provides the best empirical performance. However, even though the output of an algorithm preserves ε_p-differential privacy for a fixed Λ (as is the case with Algorithms 1 and 2), by choosing a Λ based on empirical performance on a validation set may violate ε_p-differential privacy guarantees. That is, if the procedure that picks Λ is not private, then an adversary may use the released classifier to infer the value of Λ and therefore something about the values in the database.

We suggest two ways of resolving this issue. First, if we have access to a smaller publicly available data from the same distribution, then we can use this as a holdout set to tune Λ. This Λ can be subsequently used to train a classifier on the private data. Since the value of Λ does not depend on the values in the private data set, this procedure will still preserve the privacy of individuals in the private data.

If no such public data is available, then we need a differentially private tuning procedure. We provide such a procedure below. The main idea is to train for different values of Λ on separate subsets of the training data set, so that the total training procedure still maintains ε_p-differential privacy. We score each of these predictors on a validation set, and choose a Λ (and hence f(·;Λ)) using a randomized privacy-preserving comparison procedure (McSherry and Talwar, 2007). The last step is needed to guarantee ε_p-differential privacy for individuals in the validation set. This final algorithm provides an end-to-end guarantee of differential privacy, and renders our privacy-preserving ERM procedure complete. We observe that both these procedures can be used for tuning multiple parameters as well.

6.1 Tuning Algorithm

Algorithm 4.

Privacy-preserving parameter tuning

Inputs: Database 𝒟, parameters {Λ1,…, Λm}, εp.

Outputs: Parameter fpriv.

Divide 𝒟 into m + 1 equal portions 𝒟1,…, 𝒟m+1, each of size $\frac{|𝒟|}{m+1}$

For each i = 1,2,…,m, apply a privacy-preserving learning algorithm (for example Algorithms 1, 2, or 3) on 𝒟i with parameter Λi and εpto get output fi.

Evaluate zi, the number of mistakes made by fi on 𝒟m+1. Set fpriv = fi with probability

$q_i=\frac{e^{-{\mathrm{\epsilon }}_p{z}_i/2}}{{\displaystyle {\sum }_{i=1}^m}{e}^{-{\mathrm{\epsilon }}_p{z}_i/2}}$.

We note that the list of potential Λ values input to this procedure should not be a function of the private data set. It can be shown that the empirical error on 𝒟_{m + 1} of the classifier output by this procedure is close to the empirical error of the best classifier in the set {f₁,…,f_m} on 𝒟_m+1, provided |𝒟| is high enough.

6.2 Privacy and Utility

Theorem 26 The output of the tuning procedure of Algorithm 4 is ε_p-differentially private.

Proof To show that Algorithm 4 preserves ε_p-differential privacy, we first consider an alternative procedure ℳ. Let ℳ be the procedure that releases the values (f₁,…,f_m, i) where, f₁,…,f_m are the intermediate values computed in the second step of Algorithm 4, and i is the index selected by the exponential mechanism step. We first show that ℳ preserves ε_p-differential privacy.

Let 𝒟 and 𝒟′ be two data sets that differ in the value of one individual such that 𝒟 = 𝒟̄ ∪ {(x,y)}, and 𝒟′ = 𝒟̄ ∪ {(x′,y′)}.

Recall that the data sets 𝒟₁,…,𝒟_{m + 1} are disjoint; moreover, the randomness in the privacy mechanisms are independent. Therefore,

$$\mathbb{P}({\mathbf{f}}_1\in {𝒮}_1,\dots ,{\mathbf{f}}_m\in {𝒮}_m,i=i^{*}|𝒟)={\displaystyle {\int }_{{𝒮}_1\times \dots {𝒮}_m}}\mathbb{P}(i=i^{*}|{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m,{𝒟}_{m+1})\mu ({\mathbf{f}}_1,\dots ,{\mathbf{f}}_m|𝒟)d{\mathbf{f}}_1\cdots d{\mathbf{f}}_m={\displaystyle {\int }_{{𝒮}_1\times \dots {𝒮}_m}}\mathbb{P}(i=i^{*}|{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m,{𝒟}_{m+1}){\displaystyle \prod _{j=1}^m}{\mu }_j({\mathbf{f}}_j|{𝒟}_j)d{\mathbf{f}}_1\cdots d{\mathbf{f}}_m,$$ (29)

where μ_j(f) is the density at f induced by the classifier run with parameter Λ_j, and μ(f₁,…,f_m) is the joint density at f₁,…,f_m, induced by ℳ. Now suppose that (x,y) ∈ 𝒟_j, for j = m + 1. Then, ${𝒟}_k={𝒟}_k^{\prime }$, and ${\mu }_j({\mathbf{f}}_j|{𝒟}_j)={\mu }_j({\mathbf{f}}_j|{𝒟}_j^{\prime })$ for k ∈ [m]. Moreover, given any fixed set f₁,…,f_m,

$$\mathbb{P}(i=i^{*}|{𝒟}_{m+1}^{\prime },{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m)\le e^{{\mathrm{\epsilon }}_p}\mathbb{P}(i=i^{*}|{𝒟}_{m+1},{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m).$$ (30)

Instead, if (x,y) ∈ 𝒟_j, for j ∈ [m], then, ${𝒟}_k={𝒟}_k^{\prime }$, for k ∈ [m + 1], k ≠ j. Thus, for a fixed f₁,…,f_m,

$$\mathbb{P}(i=i^{*}|{𝒟}_{m+1}^{\prime },{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m)=\mathbb{P}(i=i^{*}|{𝒟}_{m+1},{\mathbf{f}}_1,\dots ,{\mathbf{f}}_m),$$ (31)

$${\mu }_k({\mathbf{f}}_k|{𝒟}_k)\le e^{{\mathrm{\epsilon }}_p}{\mu }_k({\mathbf{f}}_k|{𝒟}_k^{\prime }).$$ (32)

The lemma follows by combining (29)–(32).

Now, an adversary who has access to the output of ℳ can compute the output of Algorithm 4 itself, without any further access to the data set. Therefore, by a simulatibility argument, as in Dwork et al. (2006b), Algorithm 4 also preserves ε_p-differential privacy.

In the theorem above, we assume that the individual algorithms for privacy-preserving classification satisfy Definition 2; a similar theorem can also be shown when they satisfy a guarantee as in Corollary 13.

The following theorem shows that the empirical error on 𝒟_{K + 1} of the classifier output by the tuning procedure is close to the empirical error of the best classifier in the set {f₁,…,f_K}. The proof of this Theorem follows from Lemma 7 of McSherry and Talwar (2007).

Theorem 27 Let z_min = min_i z_i, and let z be the number of mistakes made on D_m+1 by the classifier output by our tuning procedure. Then, with probability 1 − δ,

$$z\le z_{\text{min}}+\frac{2\text{log}(m/\mathrm{\delta })}{{\mathrm{\epsilon }}_p}.$$

Proof In the notation of McSherry and Talwar (2007), the z_min = OPT, the base measure μ is uniform on [m], and S_t = {i : z_i < z_min + t}. Their Lemma 7 shows that

$$\mathbb{P}({\overline{S}}_{2t})\le \frac{\text{exp}(-{\mathrm{\epsilon }}_{p}t)}{\mu (S_t)},$$

where μ is the uniform measure on [m]. Using min $\mu (S_t)=\frac{1}{m}$ to upper bound the right side and setting it equal to δ we obtain

$$t=\frac{1}{{\mathrm{\epsilon }}_p}\text{log}\frac{m}{\mathrm{\delta }}.$$

From this we have

$$\mathbb{P}(z\ge z_{\mathit{\text{min}}}+\frac{2}{{\mathrm{\epsilon }}_p}\text{log}\frac{m}{\mathrm{\delta }})\le \mathrm{\delta },$$

and the result follows.

7. Experiments

In this section we give experimental results for training linear classifiers with Algorithms 1 and 2 on two real data sets. Imposing privacy requirements necessarily degrades classifier performance. Our experiments show that provided there is sufficient data, objective perturbation (Algorithm 2) typically outperforms the sensitivity method (1) significantly, and achieves error rate close to that of the analogous non-private ERM algorithm. We first demonstrate how the accuracy of the classification algorithms vary with ε_p, the privacy requirement. We then show how the performance of privacy-preserving classification varies with increasing training data size.

The first data set we consider is the Adult data set from the UCI Machine Learning Repository (Asuncion and Newman, 2007). This moderately-sized data set contains demographic information about approximately 47,000 individuals, and the classification task is to predict whether the annual income of an individual is below or above $50,000, based on variables such as age, sex, occupation, and education. For our experiments, the average fraction of positive labels is about 0.25; therefore, a trivial classifier that always predicts −1 will achieve this error-rate, and only error-rates below 0.25 are interesting.

The second data set we consider is the KDDCup99 data set (Hettich and Bay, 1999); the task here is to predict whether a network connection is a denial-of-service attack or not, based on several attributes. The data set includes about 5,000,000 instances. For this data the average fraction of positive labels is 0.20.

In order to implement the convex minimization procedure, we use the convex optimization library provided by Okazaki (2009).

7.1 Preprocessing

In order to process the Adult data set into a form amenable for classification, we removed all entries with missing values, and converted each categorial attribute to a binary vector. For example, an attribute such as (Male,Female) was converted into 2 binary features. Each column was normalized to ensure that the maximum value is 1, and then each row is normalized to ensure that the norm of any example is at most 1. After preprocessing, each example was represented by a 105-dimensional vector, of norm at most 1.

For the KDDCup99 data set, the instances were preprocessed by converting each categorial attribute to a binary vector. Each column was normalized to ensure that the maximum value is 1, and finally, each row was normalized, to ensure that the norm of any example is at most 1. After preprocessing, each example was represented by a 119-dimensional vector, of norm at most 1.

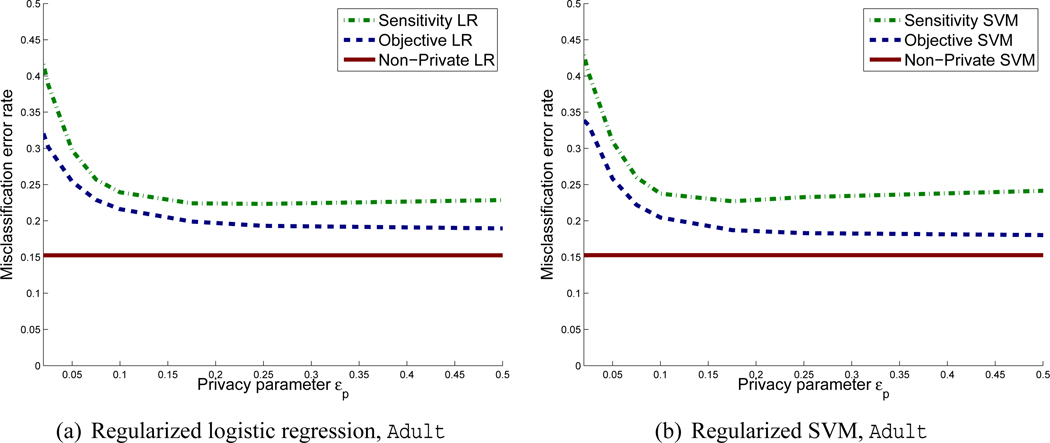
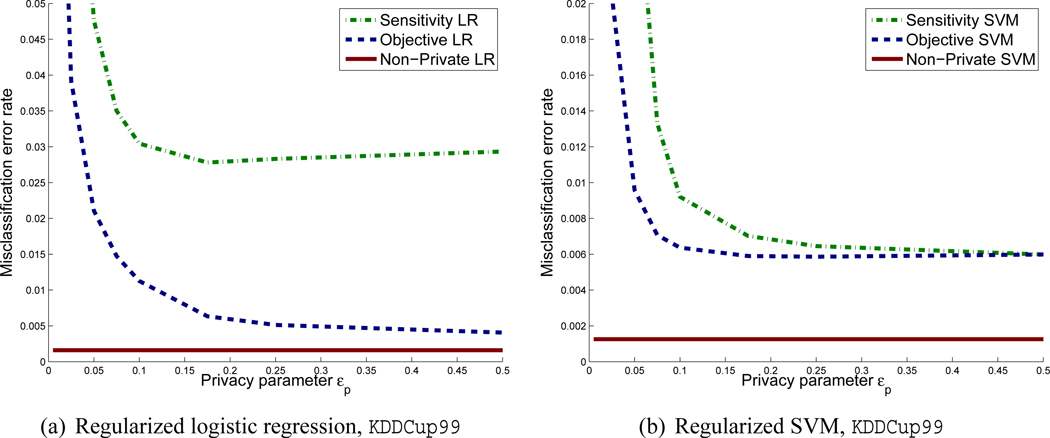
7.2 Privacy-Accuracy Tradeoff

For our first set of experiments, we study the tradeoff between the privacy requirement on the classifier, and its classification accuracy, when the classifier is trained on data of a fixed size. The privacy requirement is quantified by the value of ε_p; increasing ε_p implies a higher change in the belief of the adversary when one entry in 𝒟 changes, and thus lower privacy. To measure accuracy, we use classification (test) error; namely, the fraction of times the classifier predicts a label with the wrong sign.

To study the privacy-accuracy tradeoff, we compare objective perturbation with the sensitivity method for logistic regression and Huber SVM. For Huber SVM, we picked the Huber constant h = 0.5, a typical value (Chapelle, 2007).¹ For each data set we trained classifiers for a few fixed values of Λ and tested the error of these classifiers. For each algorithm we chose the value of Λ that minimizes the error-rate for ε_p = 0.1.² We then plotted the error-rate against ε_p for the chosen value of Λ. The results are shown in Figures 2 and 3 for both logistic regression and support vector machines.³ The optimal values of Λ are shown in Tables 1 and 2. For non-private logistic regression and SVM, each presented error-rate is an average over 10-fold cross-validation; for the sensitivity method as well as objective perturbation, the presented error-rate is an average over 10-fold cross-validation and 50 runs of the randomized training procedure. For Adult, the privacy-accuracy tradeoff is computed over the entire data set, which consists of 45,220 examples; for KDDCup99 we use a randomly chosen subset of 70,000 examples.

Figure 2.

Privacy-Accuracy trade-off for the Adult data set

Figure 3.

Privacy-Accuracy trade-off for the KDDCup99 data set

Table 1.

Error for different regularization parameters on Adult for ε_p = 0.1. The best error per algorithm is in bold.

Λ	10−10.0	10−7.0	10−4.0	10−3.5	10−3.0	10−2.5	10−2.0	10−1.5
Logistic
Non-Private	0.1540	0.1533	0.1654	0.1694	0.1758	0.1895	0.2322	0.2478
Output	0.5318	0.5318	0.5175	0.4928	0.4310	0.3163	0.2395	0.2456
Objective	0.8248	0.8248	0.8248	0.2694	0.2369	0.2161	0.2305	0.2475
Huber
Non-Private	0.1527	0.1521	0.1632	0.1669	0.1719	0.1793	0.2454	0.2478
Output	0.5318	0.5318	0.5211	0.5011	0.4464	0.3352	0.2376	0.2476
Objective	0.2585	0.2585	0.2585	0.2582	0.2559	0.2046	0.2319	0.2478

Table 2.

Error for different regularization parameters on KDDCup99 for ε_p = 0.1. The best error per algorithm is in bold.

Λ	10−9.0	10−7.0	10−5.0	10−3.5	10−3.0	10−2.5	10−2.0	10−1.5
Logistic
Non-Private	0.0016	0.0016	0.0021	0.0038	0.0037	0.0037	0.0325	0.0594
Output	0.5245	0.5245	0.5093	0.3518	0.1114	0.0359	0.0304	0.0678
Objective	0.2084	0.2084	0.2084	0.0196	0.0118	0.0113	0.0285	0.0591
Huber
Non-Private	0.0013	0.0013	0.0013	0.0029	0.0051	0.0056	0.0061	0.0163
Output	0.5245	0.5245	0.5229	0.4611	0.3353	0.0590	0.0092	0.0179
Objective	0.0191	0.0191	0.0191	0.1827	0.0123	0.0066	0.0064	0.0157

For the Adult data set, the constant classifier that classifies all examples to be negative acheives a classification error of about 0.25. The sensitivity method thus does slightly better than this constant classifier for most values of ε_p for both logistic regression and support vector machines. Objective perturbation outperforms sensitivity, and objective perturbation for support vector machines achieves lower classification error than objective perturbation for logistic regression. Non-private logistic regression and support vector machines both have classification error about 0.15.

For the KDDCup99 data set, the constant classifier that classifies all examples as negative, has error 0.19. Again, objective perturbation outperforms sensitivity for both logistic regression and support vector machines; however, for SVM and high values of ε_p (low privacy), the sensitivity method performs almost as well as objective perturbation. In the low privacy regime, logistic regression under objective perturbation is better than support vector machines. In contrast, in the high privacy regime (low ε_p), support vector machines with objective perturbation outperform logistic regression. For this data set, non-private logistic regression and support vector machines both have a classification error of about 0.001.

For SVMs on both Adult and KDDCup99, for large ε_p (0.25 onwards), the error of either of the private methods can increase slightly with increasing ε_p. This seems counterintuitive, but appears to be due the imbalance in fraction of the two labels. As the labels are imbalanced, the optimal classifier is trained to perform better on the negative labels than the positives. As ε_p increases, for a fixed training data size, so does the perturbation from the optimal classifier, induced by either of the private methods. Thus, as the perturbation increases, the number of false positives increases, whereas the number of false negatives decreases (as we verified by measuring the average false positive and false negative rates of the private classifiers). Therefore, the total error may increase slightly with decreasing privacy.

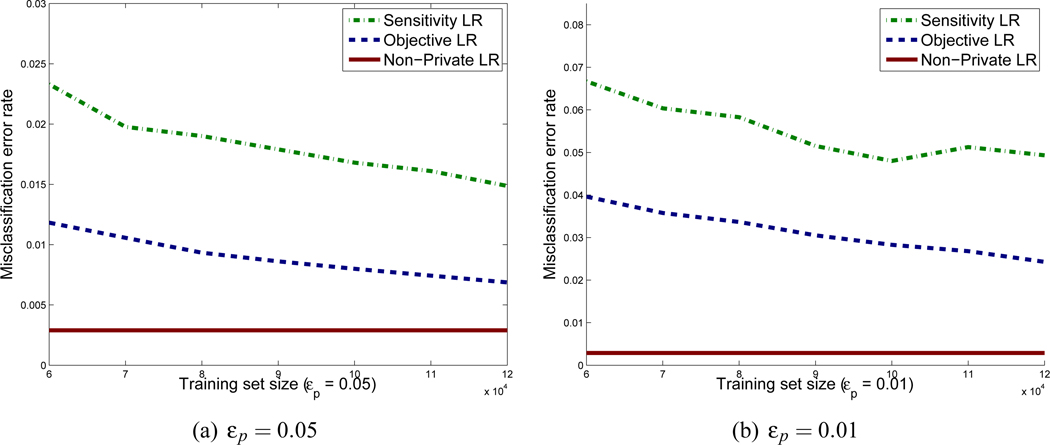
7.3 Accuracy vs. Training Data Size Tradeoffs

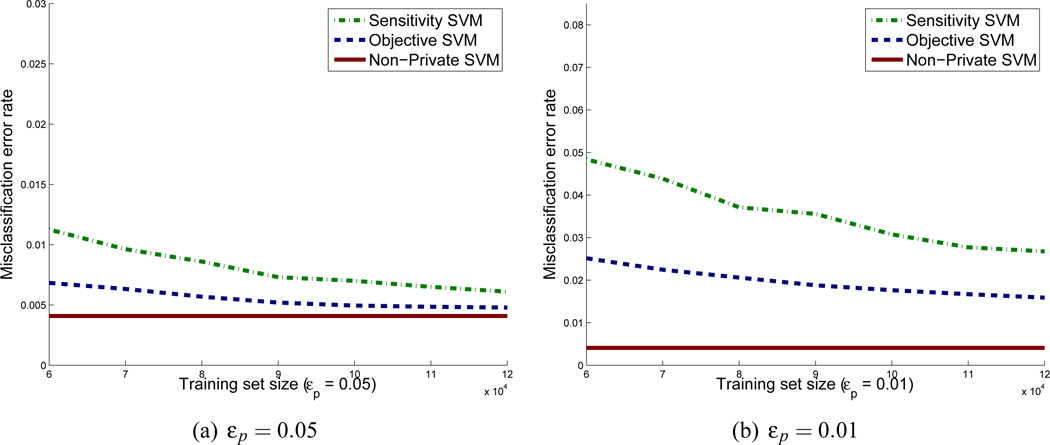
Next we examine how classification accuracy varies as we increase the size of the training set. We measure classification accuracy as the accuracy of the classifier produced by the tuning procedure in Section 6. As the Adult data set is not sufficiently large to allow us to do privacy-preserving tuning, for these experiments, we restrict our attention to the KDDCup99 data set.

Figures 4 and 5 present the learning curves for objective perturbation, non-private ERM and the sensitivity method for logistic loss and Huber loss, respectively. Experiments are shown for ε_p = 0.01 and ε_p = 0.05 for both loss functions. The training sets (for each of 5 values of Λ) are chosen to be of size n = 60,000 to n = 120,000, and the validation and test sets each are of size 25,000. Each presented value is an average over 5 random permutations of the data, and 50 runs of the randomized classification procedure. For objective perturbation we performed experiment in the regime when ${\mathrm{\epsilon }}_p^{\prime }>0$, so Δ = 0 in Algorithm 2.⁴

Figure 4.

Learning curves for logistic regression on the KDDCup99 data set

Figure 5.

Learning curves for SVM on the KDDCup99 data set

For non-private ERM, we present result for training sets from n = 300,000 to n = 600,000. The non-private algorithms are tuned by comparing 5 values of Λ on the same training set, and the test set is of size 25,000. Each reported value is an average over 5 random permutations of the data.

We see from the figures that for non-private logistic regression and support vector machines, the error remains constant with increasing data size. For the private methods, the error usually decreases as the data size increases. In all cases, objective perturbation outperforms the sensitivity method, and support vector machines generally outperform logistic regression.

8. Discussions and Conclusions

In this paper we study the problem of learning classifiers with regularized empirical risk minimization in a privacy-preserving manner. We consider privacy in the ε_p-differential privacy model of Dwork et al. (2006b) and provide two algorithms for privacy-preserving ERM. The first one is based on the sensitivity method due to Dwork et al. (2006b), in which the output of the non-private algorithm is perturbed by adding noise. We introduce a second algorithm based on the new paradigm of objective perturbation. We provide bounds on the sample requirement of these algorithms for achieving generalization error ε_g. We show how to apply these algorithms with kernels, and finally, we provide experiments with both algorithms on two real data sets. Our work is, to our knowledge, the first to propose computationally efficient classification algorithms satisfying differential privacy, together with validation on standard data sets.

In general, for classification, the error rate increases as the privacy requirements are made more stringent. Our generalization guarantees formalize this “price of privacy.” Our experiments, as well as theoretical results, indicate that objective perturbation usually outperforms the sensitivity methods at managing the tradeoff between privacy and learning performance. Both algorithms perform better with more training data, and when abundant training data is available, the performance of both algorithms can be close to non-private classification.

The conditions on the loss function and regularizer required by output perturbation and objective perturbation are somewhat different. As Theorem 6 shows, output perturbation requires strong convexity in the regularizer and convexity as well as a bounded derivative condition in the loss function. The last condition can be replaced by a Lipschitz condition instead. However, the other two conditions appear to be required, unless we impose some further restrictions on the loss and regularizer. Objective perturbation on the other hand, requires strong convexity of the regularizer, convexity, differentiability, and bounded double derivatives in the loss function. Sometimes, it is possible to construct a differentiable approximation to the loss function, even if the loss function is not itself differentiable, as shown in Section 3.4.2.

Our experimental as well as theoretical results indicate that in general, objective perturbation provides more accurate solutions than output perturbation. Thus, if the loss function satisfies the conditions of Theorem 9, we recommend using objective perturbation. In some situations, such as for SVMs, it is possible that objective perturbation does not directly apply, but applies to an approximation of the target loss function. In our experiments, the loss of statistical efficiency due to such approximation has been small compared to the loss of efficiency due to privacy, and we suspect that this is the case for many practical situations as well.

Finally, our work does not address the question of finding private solutions to regularized ERM when the regularizer is not strongly convex. For example, neither the output perturbation, nor the objective perturbation method work for L₁-regularized ERM. However, in L₁-regularized ERM, one can find a data set in which a change in one training point can significantly change the solution. As a result, it is possible that such problems are inherently difficult to solve privately.

An open question in this work is to extend objective perturbation methods to more general convex optimization problems. Currently, the objective perturbation method applies to strongly convex regularization functions and differentiable losses. Convex optimization problems appear in many contexts within and without machine learning: density estimation, resource allocation for communication systems and networking, social welfare optimization in economics, and elsewhere. In some cases these algorithms will also operate on sensitive or private data. Extending the ideas and analysis here to those settings would provide a rigorous foundation for privacy analysis.

A second open question is to find a better solution for privacy-preserving classification with kernels. Our current method is based on a reduction to the linear case, using the algorithm of Rahimi and Recht (2008b); however, this method can be statistically inefficient, and require a lot of training data, particularly when coupled with our privacy mechanism. The reason is that the algorithm of Rahimi and Recht (2008b) requires the dimension D of the projected space to be very high for good performance. However, most differentially-private algorithms perform worse as the dimensionality of the data grows. Is there a better linearization method, which is possibly data-dependent, that will provide a more statistically efficient solution to privacy-preserving learning with kernels?

A final question is to provide better upper and lower bounds on the sample requirement of privacy-preserving linear classification. The main open question here is to provide a computationally efficient algorithm for linear classification which has better statistical efficiency.

Privacy-preserving machine learning is the endeavor of designing private analogues of widely used machine learning algorithms. We believe the present study is a starting point for further study of the differential privacy model in this relatively new subfield of machine learning. The work of Dwork et al. (2006b) set up a framework for assessing the privacy risks associated with publishing the results of data analyses. Demanding high privacy requires sacrificing utility, which in the context of classification and prediction is excess loss or regret. In this paper we demonstrate the privacy-utility tradeoff for ERM, which is but one corner of the machine learning world. Applying these privacy concepts to other machine learning problems will lead to new and interesting tradeoffs and towards a set of tools for practical privacy-preserving learning and inference. We hope that our work provides a benchmark of the current price of privacy, and inspires improvements in future work.