Abstract
Exploiting the experimental information from small-angle x-ray solution scattering (SAXS) in conjunction with structure prediction algorithms can be advantageous in the case of ribonucleic acids (RNA), where global restraints on the 3D fold are often lacking. Traditional usage of SAXS data often starts by attempting to reconstruct the molecular shape ab initio, which is subsequently used to assess the quality of model Here, an alternative strategy is explored whereby the models from a very large decoy set are directly sorted according to their fit to the SAXS data is developed. For rapid computation of SAXS patterns, the method developed here makes use of a coarse-grained representation of RNA. It also accounts for the explicit treatment of the contribution to the scattering of water molecules and ions surrounding the RNA. The method, called Fast-SAXS-RNA, is first calibrated using a transfer RNA (tRNA-val) and then tested on the P4-P6 fragment of group I intron (P4-P6). Fast-SAXS-RNA is then used as a filter for decoy models generated by the MC-Fold and MC-Sym pipeline, a suite of RNA 3D all-atoms structure algorithms that encode and exploit RNA 3D architectural principles. The ability of Fast-SAXS-RNA to discriminate native folds is tested against three widely used RNA molecules in molecular modeling benchmarks: the tRNA, the P4-P6, and a synthetic hairpin suspected to assemble into a homodimer. For each molecule, a large pool of decoys are generated, scored, and ranked using Fast-SAXS-RNA. The method is able to identify low-RMSD models among top ranking structures, for both tRNA and P4-P6. For the hairpin, the approach correctly identifies the dimeric state as the solution structure over the monomeric state and alternative secondary structures. The method offers a powerful strategy for recognizing native RNA conformations as well as multimeric assemblies and alternative secondary structures, thus enabling high-throughput RNA structure determination using SAXS data.
Introduction
Small-angle x-ray solution scattering (SAXS) is an experimental method that can provide low-resolution structural information about macromolecules in solution.1–7 The method is powerful because it allows for structural characterization of biomolecular complexes in various solution conditions, without the need of growing ordered crystals as in X-ray crystallography. Ribonucleic acids (RNA), given their key role in living cells, are often the subject of such SAXS analysis.8,9
SAXS data can be exploited in three different ways to advance our knowledge of RNA structures. For example, one can attempt to determine an ab initio molecular shape capable to reproduce the experimental SAXS profile;10 The goodness of fit of a RNA three-dimensional (3D) model structure is then measured by performing a rigid-body docking of the model into this shape (shape-models comparison). Ab initio molecular shapes are generally constructed from a collection of beads, and are obtained at a high computational cost. One concern is that different ab initio shapes can yield similar scattering profiles, giving rise to the problem of non-uniqueness of the solution. Furthermore, current ab initio shape generators have been designed often for globular proteins, and may not be appropriate for RNA characterization with their branch-like shapes. An alternative strategy consists in deriving a real-space pair-density distribution function P(r) from the SAXS profile, which can then be interpreted as the probability of observing a pair-wise distance r of two particles. The goodness of fit of a model structure is then measured by comparing its P(r) distribution to the experimentally-derived one. Difficulties arise from the fact that the calculation of P(r) requires extra assumptions about the value of Dmax the maximum pairwise distance within the macromolecule. In other words, although P(r) is related to the Fourier transform of the SAXS profile I(q) (where q is a scattering distance in reciprocal space, q = 2π/d, and d is the Bragg spacing), its accurate determination requires such a prior Dmax value (e.g., see ref.1), which might be non-trivial to obtain for macromolecules such as flexible multidomain protein complexes. Another difficulty is that the derived P(r), because of the scattering contribution of hydration in I(q), includes the contribution not only from the macromolecular itself but also from the surrounding hydration layer. Both the shape-reconstruction and the P(r) approaches seek to transform the SAXS profile into a real-space quantity to measure the goodness of fit of an RNA 3D model, and thus attempt to solve the “inverse” problem of converting I(q) to P(r). However, the inverse problem encounters difficulties in the introduction of the aforementioned assumption on Dmax as well as the completeness of the SAXS spectrum needed for the Fourier transform, which ultimately limit and undermine the full use of SAXS data. To circumvent those difficulties, one can use a “forward” approach by generating putative 3D structures and then test them directly for their goodness of fit to the raw SAXS data.8,11–13 This approach has the clear advantage of avoiding any extra assumptions in the interpretation of the experimental data that are required to solve the inverse scattering problem.
Several RNA 3D structure prediction methods are now available, ranging from simplified bead models to atomistically-detailed models.14–20 In this context, a rapid computational method for calculating the theoretical scattering profile from a given RNA model for a direct comparison with experimental SAXS profile offers clear advantages. Any given model is attributed a score, χ2, which allows sorting, filtering and subsequent identification of the native fold among a pool of decoys. In this scenario, it is mandatory to develop a computational method that is capable of computing SAXS profiles from a given RNA model in an efficient and accurate fashion. Existing approaches to calculate SAXS profiles treat macromolecules at the atomic level, while the contribution from the solvent at the molecular surface is taken into account implicitly.21 These approaches are too slow as well as insufficiently accurate. Given the low-resolution nature of SAXS, coarse-graining both solvent molecules and the solute macromolecule is more efficient. With this strategy, a Fast-SAXS method has been previously developed for protein scattering,22 resulting in a significant reduction of computational costs without comprising any accuracy. In this paper, we extend the Fast-SAXS method to RNA scattering calculations.
Methods
Theoretical Background
X-ray scattering from proteins and nucleic acids in solution essentially measures the electron density contrast between the macromolecules and bulk solvent. The scattering profile, I(q), is determined from the scattering of macromolecular samples after the subtraction of the background buffer contribution.1 Theoretically, the scattering intensity from dilute samples is proportional to the spherically averaged scattering of a single molecule, minus the excluded volume contributions and plus the excess electron density in the hydration layer,3
| (1) |
where the amplitude of the wavevector transfer q = |q| = 2π/d = 4π sinθ/λ (d is the Bragg spacing, θ is half of the scattering angle, and λ is the x-ray wavelength). Am(q) is the scattering amplitude from the macromolecule in vacuum, As(q) is from the solvent with an excluded volume displaced by the macromolecule, and Ab(q) is from the shell of bound waters reflected in the density excess (Δρb) relative to the bulk phase.23 The brackets 〈 · · · (Ω) stands for an average over all possible orientations of the macromolecule. Eq. (1) provides the theoretical basis for solution scattering.
Similar to the Fast-SAXS method for protein,22 a coarse-grained method is developed and applied on a given RNA conformation where the scattering contribution arises from the RNA molecule itself in vacuum, the excluded volume of solvent displaced by the RNA, and the excess electron density at the RNA surface. These three aspects are briefly described as follows. First, the scattering I(q) from the RNA itself is calculated using the Debye formula,
| (2) |
where fi are atomic form factors (i = 1, · · ·, n, where n is the number of atoms), analytically provided by the Cromer-Mann scattering-factor coefficients.24 At the limit of q = 0, fi is the electron number of atom i, and ri j is the distances between atoms i and j. Second, the excluded solvent effect can be incorporated into the scattering factors by assigning a Gaussian sphere approximated for the atoms,25
| (3) |
where vi are the observed atomic volumes from experiments.25 Therefore, the scattering from the macromolecule, taking into account the excluded volume, is given by,
| (4) |
where are the scattering factors after the consideration of the excluded volume effect as in Eq. (3). Third, the excess electron density in the solution layer at the RNA surface also contributes to the total scattering.23,26–28 This excess density gives rise to the third term in the total scattering of I(q) in Eq. (1). An explicit solvent treatment is implemented into Fast-SAXS calculations, as described below.
Coarse-Grained Representation
The low-resolution intrinsic to SAXS data allows us to simplify each nucleotide into a two-particle model, where one particle represents the sugar-phosphatase backbone group and the other represents the base sidechain group. The positions of the particles are taken from the coordinates of the atoms which are closest to the center-of-scattering (RCOS) of each group, as defined by,
| (5) |
where is the solvent-corrected atomic scattering factor at q = 0 and ri is the position of atom i.
One also has to replace the atomic scattering factors with an effective structure factors that account for the internal details of individual nucleic electron densities, in a similar fashion to amino acids in protein scattering.22,29–32 For each nucleotide, two effective structure factors FCG(q) defined for their backbone and sidechain groups, are derived from a set of high-resolution nucleic atomic coordinates, using the Debye formula,33
| (6) |
where m is the number of atoms within each group. The brackets 〈 · · · 〉PDB indicate that the scattering factor is averaged over a set of backbone conformers and sidechain rotamers taken from the Protein Data Bank.
Explicit Solvent Representation
In Fast-SAXS calculations, a layer of explicit water molecules is placed around the RNA surface to account for the excess electron density. For a TIP3P water molecule,34 an effective scattering factor has already been derived,22
| (7) |
where ri j is the distance between water particles i and j. In practice, these water molecules are represented by dummy atoms centered at the oxygen positions, in bulk solvent density (ρs = 0.334 e/Å3 at 20°C). These dummy atoms are taken from a pre-equilibrated TIP3P waterbox if their positions are within 3.5 to 6.5 Å away from the RNA coarse-grained particles. To effectively model the excess electron density in the hydration layer, the scattering factor of dummy water molecules is assigned a proper weight w by
| (8) |
The optimal value of the weighting factor w for RNA is calibrated using the experimental SAXS data of tRNA-Val.35 With this strategy, the total scattering of a given RNA structure is conveniently and accurately represented by its 2N nucleic two-particle plus the surrounding M explicit dummy water molecules. Therefore, the total calculated scattering corresponding to the Fast-SAXS-RNA method is given by the following Debye formula,
| (9) |
where are the effective coarse-grained scattering factors for both nucleic two-particle and dummy water molecules (Eq. (6) and Eq. (8)). The parameters N and M are the number of nucleotides and water molecules, respectively.
RNA Conformational Sampling
RNA conformational sampling is performed using the recently introduced MC-Fold and MC-Sym pipeline.16 The conformational sampling via MC-Sym is enhanced by the use of NCMs,16,36,37 which makes it possible to build structures for RNA sequences of up to 120 nucleotides. The advantage of MC-Sym is to build all-atom models with proper excluded volumes and electronic densities. Two RNA molecules with available experimental SAXS data, the Escherichia coli tRNA-VAL (tRNA)35 and the P4-P6 domain of Tetrahymena thermophila group I intron (P4-P6),38 are used. Interestingly, these two RNA molecules belong to two different structural classes: coplanar for the tRNA and bipolar for the P4-P6.39 Additional tests include a RNA dimer which is suspected to form a dimeric complex in solution.40
For tRNA, two sets of 9999 decoys were made: tRNA_high and tRNA_low. The tRNA_low set was produced using knowledge of the secondary structure, in-stem-only non-canonical base pairs (14–21, 26–44, 54–58), and local 3D motifs such as the T-loop41,42 and the anticodon loop,43 thus without any explicit long-range distance information. The single-stranded acceptor terminator, nucleotides 73–76, is assumed to be in the A-RNA conformation. Furthermore, the coaxial stacking of the four helical domains was used in the tRNA sampling. The tRNA_high set is to identify the rough global L-shape of the tRNA fold. The tRNA_high set was produced with the knowledge of tRNA_low, in addition to long-range interactions: 15–48, 18–55, 19–56, and base triples: 8-14-21, 9-23-12, 22-46-13, as predicted from multiple-sequence analysis.44,45 The purpose of this tRNA_high set is to test the SAXS approach to identify high-resolution three-dimensional models among closely related L-shaped structures.
For P4-P6, two sets of decoy models were made: the P4-P6_low set (9999 decoys) and the P4-P6_high set (8867 decoys). The P4-P6_high set was generated by assembling stems/hairpins with the knowledge of a long-range contact between the tip of the P5b stem, a GNRA tetraloop, and it’s receptor in the P6 stem. This interaction was predicted by Murphy and Cech (MC),46 and later confirmed in the crystal structure of the P4-P6 domain.47 Here, the stems are sampled in the context of the crystal structure, with the distance constraint imposed by the MC contact. The group I domain is assembled by coaxially stacking the stems P6, P4 and P5 in axis 1, and the stems P5b on P5a in axis 2. The two axes are put relative to one another via an explicit Sugar/Sugar base pair relation (LW nomenclature48) between nucleotides 153 and 250. Final modeling steps link the two axes (Supplementary Figure 11, magenta). The P4-P6_low set was generated by arranging the stems into coaxially stacked axes, and by connecting the two axes via the 123–125/197–198 junctions. Because the distance constraint imposed by the MC contact was not imposed, the two axes are free to move in any directions to generate a broad range of model structures, such as the native U-shape, but also L-shapes and fully extended conformations.
For the RNA dimeric complex, we built various decoy sets representing different multimeric states and secondary structures. RNA hairpin monomers were first built using NCMs (Supplementary Figure 12, set #1). The receptor module was taken from PDB file 1GID.38 Then, the pairs of monomers were assembled into dimers in 3D space by using a Sugar-Sugar base pair edge interaction (LW nomenclature) between nucleotides A23 of monomer A and G8 of monomer B (Supplementary Figure 12, set #2). The symmetric docking of nucleotide A23 of monomer B into nucleotide G8 of monomer A was achieved by using two distance constraints which simulate a Sugar-Sugar edge base pair interaction. This produces homodimers which are doubly-docked. Another set was made in which the symmetric docking is not enforced. Only one tetraloop-receptor is modeled explicitly (Supplementary Figure 12, set #4). This produces singly-docked configurations, but doubly-docked ones can occur fortuitously.
The last decoy set was made by using the MC-Fold computer program to generate alternative secondary structures from a tandem repeat of the monomer sequences X and Y, attached by an UUCG linker and to yield a 5′-X-UUCG-Y-3′ sequence. The linker is used to coax the sequence into a long extended hairpin. From MC-Fold, the UUCG linker is subtracted and further checked. Additional alternative secondary structures forming a 4-way junction were obtained (Supplementary Figure 12; set #3). Interestingly, the extended duplex was not found in the top 20 MC-Fold solutions, as it features too many non-canonical base pairs to compete against more potent structures. However, this possibility still had to be explored, as RNA hairpins in solution can hybridize to one another to form extended double-helices.49 The alternative fold, which comprise a 4-way junction, is made up of two monomer units in which the basal stem would unzip up to just after the tetraloop receptor, hence unfolding it, then hybridize with complementary strands from another partially unzipped monomer (notice that the basal stems of monomers A and B in Supplementary Figure 12 set #3 is made of two different colors or units). Similar to the tRNA fold, these four branches were organized into two main axes by coaxially stacking two stems, on their 5′ sides. The 3D models of both axes were first built using MC-Sym, then assembled into complete structures in a second step.
All 3D models were refined using the Tinker molecular modeling package version 4.2.50 A steepest-descent minimization algorithm, combined with the Amber99 force field51 in a gas phase, was used until a gradient RMS of 5.0 kcal/(mol · Å) or a maximum of 200 steps was reached. Nucleobase atom positions were kept fixed using a spring constant of 1001 kcal/(mol · Å). Sugar pucker in the C3′-endo anti configuration is enforced using a spring constant of 0.025 kcal/(mol °C) on the torsion angle 〈 C3′ C4′, O4′, C1′〉 with mean 22.2°C degrees and standard deviation 4.3 4.3°C.
SAXS-based χ2 Scoring
A ranking score, χ2, is used to measure the similarity between the experimental SAXS data and its theoretically-computed Fast-SAXS-RNA profile,
| (10) |
where qmin and qmax are the lower and upper limits of the q-range from the experimental scattering profile Iexp(q), δ Ilog(q) are the experimental uncertainties on logIexp(q). The value of Δ is the offset between the theoretical and experimental SAXS profiles (logIcal and log Iexp) at q = qmin.
Results
Coarse-Grained Representation
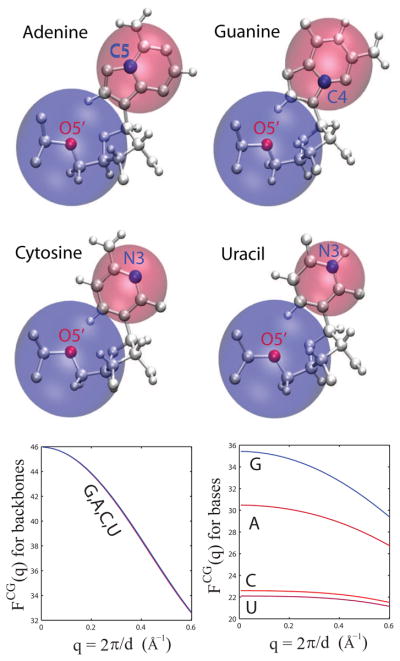
Recognizing the intrinsic low-resolution nature of SAXS data, the goal is to develop a coarse-grained approach for computing RNA scattering profiles. The coarse-graining development is built upon the theoretical basis of SAXS, as described in the Methods section. The nucleic units of RNA (Adenine, Guanine, Cytosine, and Uracil) are simplified into a two-particle model, each representing the scattering of the sugar-phosphate group of the backbone and the sidechain group of the base. Figure 1a shows the schematics of the two-particle representation for the four nucleotides. Subsequently, effective scattering structure factors for the resulting eight pseudo-particles are derived according to Eq. (6), based on their atomistically-detailed representations. In practice, the effective scattering is obtained by averaging a set of high-resolution RNA atomistic coordinates, such as those deposited in the Protein Data Bank, to account for nucleotide conformational heterogeneity. The averaging converges when a set of one hundred nucleotide coordinates are used. Therefore, these effective structure factors are derived by taking advantage of the low-resolution nature of SAXS. In the derived effective structure factors, an excluded volume effect for each atom is taken into account by assigning a Gaussian sphere (Eq. (3)) such that it effectively accounts for the electron density contrast between RNA molecules and the bulk solvent.25 Figure 1b shows that the effective structure factors for sugar-phosphate backbone groups are nearly identical for the four RNA nucleotide units, but are quite different for the sidechain groups to the bases.
Figure 1.
Two-particle model of RNA for SAXS computing. (top) Schematic representation of the four RNA nucleic units: Adenine (A), Guanine (G), Cytosine (C) and Uracil (U). Each nucleotide is simplified into a two-particle model, where one particle accounts for the scattering of the phosphate and sugar groups, the backbone group, and the other for the sidechain group. The location of the site is determined by the position of the atom closest to the center-of-scattering. Backbone positions are highlighted by red dots, and sidechain ones in blue. The relative sizes of these particles are drawn approximately proportional to their scattering intensity at q = 0. (bottom) Derived structure factors. On the left are shown the structure factors for the backbone groups and on the right are the structure factors for the sidechain groups.
Eq. (5) is used to determine the optimal placement of the pseudo-particles. The site placement is determined by the proximity to the group center of effective electron density, or center-of-scattering. It results in selecting the positions of O5′ atoms for the backbone groups. The positions selected for the sidechain groups are C5 for Adenine, C4 for Guanine, and N3 for both Cytosine and Uracil. Figure 1 depicts the placement of the pseudo-particles. The different positioning for the sidechain groups between Adenine and Guanine is simply due to the different location of the amine group of the base; close to C5 in Adenine but close to C4 in Guanine. It is shown below that the reduced representation is sufficient to reproduce the scattering curves of solved RNA structures. It is noteworthy that a reduced representation with one particle per residue was found sufficient for the scattering of proteins.10,22,52
Explicit Solvent Representation
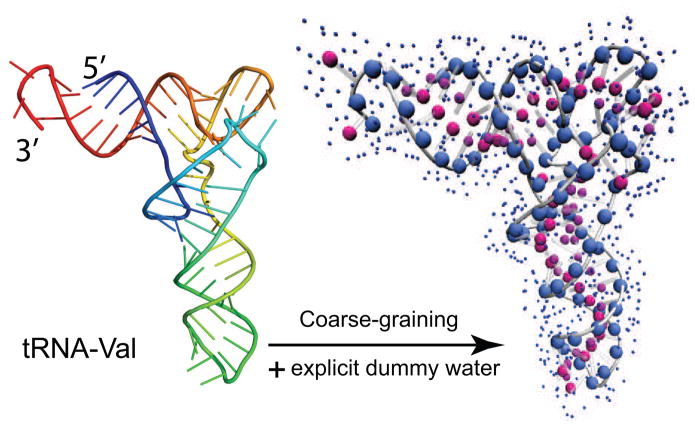
In addition to the RNA molecule itself, the hydration layer at the RNA surface also contributes to the total scattering.23,26,27,53,54 The bound water molecules in the hydration layer collectively display a higher electron density than that of the bulk solvent. Here, the excess electron density, relative to the bulk, is modeled by soaking the RNA molecule in a layer of explicit water molecules. In the same fashion as for protein scattering calculations,22 an explicit solvent representation is used for RNA scattering to account for the excess electron in the hydration layer. Both the RNA and water are effectively coarse-grained to take advantage of the low-resolution nature of SAXS data. An effective structure factor for TIP3P water molecules can be determined by the use of Eq. (7), and has already been parameterized.22 The water molecules are taken from a pre-equilibrated TIP3P waterbox at bulk solvent density (ρs = 0.334 e/Å3 at 20 °C). Water particles overlapping with the RNA molecule are deleted, and only those within 3.5 to 6.5 Å away from the RNA are kept. It results in an hydration layer of about 3 Å in thickness. The pre-equilibrated waterbox facilitates the solvation of the biomolecule, while preserving the explicit representation of the hydration layer. The water particles make a collective contribution to the total scattering, by representing excess hydration electron density as in Eq. (8). In this sense, they are not actual water molecules. Figure 2 shows the water particles representation for tRNA. At this point, a full solvated RNA molecular system is ready for SAXS calculations according to Eq. (9).
Figure 2.
Coarse-graining for RNA scattering. (left) Cartoon representation of the 3D structure of valine transfer RNA (tRNA; PDB entry 2K4C), colored from blue at the 5′ end to red at the 3′ end. (right) The 3D structure is coarse-grained into the two-particle representation, where the backbone particles are large blue spheres, and the sidechain in red. In addition, explicit water molecules are placed surrounding the RNA molecule and shown as small blue dots.
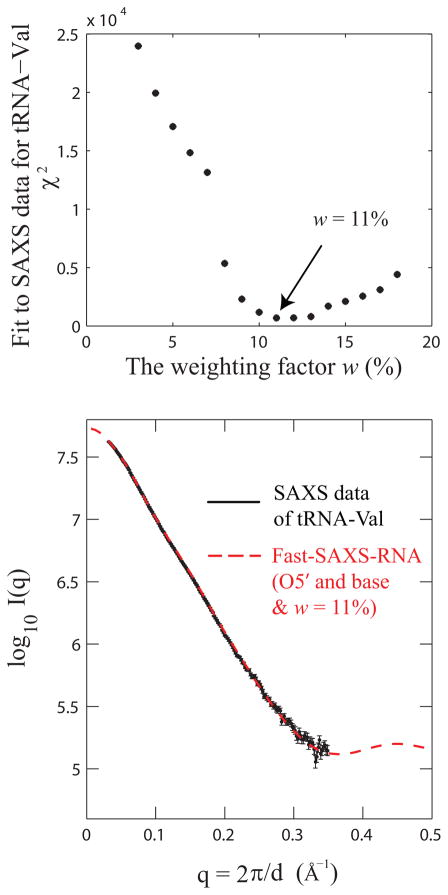
To calibrate the excess hydration electron density around RNA, an optimal value for the weighting factor w of the hydration contribution can be assigned using available experimental SAXS data. The recently solved tRNA-Val (PDB entry 2K4C) was used as a model system for this calibration. 35 Under the Fast-SAXS-RNA framework (Eq. (9)), SAXS profiles of tRNA are calculated for various values of w. A χ2 score is then calculated according to Eq. (10) to account for the difference between theoretical and experimental profiles. Finally, the scattering amplitude of water molecules is determined by best-fitting to SAXS data. Figure 3 shows the χ2 difference between the computed and experimental SAXS profiles as a function of w. The result indicates that a value of w = 11% is optimal to reproduce the experimental SAXS data of tRNA (Figure 3). It also suggests that the excess hydration electron density is higher for the tRNA (w = 11%) than that of the lysozyme protein (w = 3%).22 The higher excess hydration electron density might be caused by high occupancy of water molecules in both the major and minor grooves of the RNA helices.55–57 Since each nucleotide has three pairing faces (Watson-Crick, Sugar and Hoogsteen, according to the Leontis-Westhof nomenclature), only one face is involved in base pairs (usually the Watson-Crick face) and the other two polar faces are left exposed to hydration (the Hoogsteen faces in major grooves, and the Sugar faces in minor grooves). In addition, each phosphate group has a net negative charge in solution, which attracts mono and divalent cations and contributes to the excess electron density in the hydration layer.
Figure 3.
Hydration layer contribution for RNA scattering. The contribution of the hydration layer is calibrated using the experimental SAXS data and the solution structure for a transfer RNA (tRNA; PDB entry 2K4C). (top) Fit of the solution structure to the SAXS data as a function of the weighting factor w. A value of w = 11% is optimal to fit the SAXS data. (bottom) Comparison of the experimental (black) and computed (red) SAXS profiles.
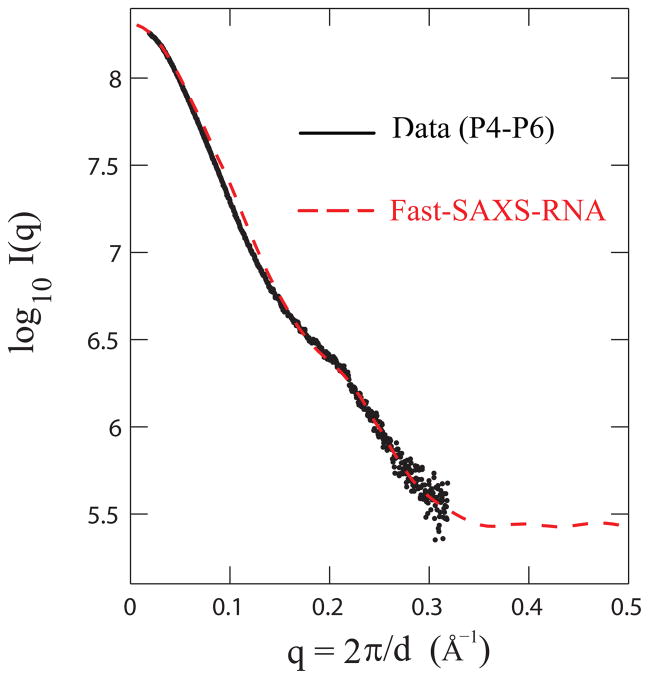
We note that computing SAXS profiles is not sensitive to the detailed water placement in the hydration layer; instead, it dependents only on the collective effect that the hydration layer makes as a whole to the total scattering. To illustrate this point, the total effective excess electron density is modeled by two factors: the weighting factor w and an hydration layer thickness d. As illustrated in the case of the lysozyme protein,22 varying the weighting factor w and the thickness d can still capture the essential features of computed SAXS profile. In other words, the hydration contribution to the total scattering, as long as the net excess electron contribution is conserved, remains similar. In addition, we observe that the coarse-graining of RNA molecules using Fast-SAXS-RNA can well reproduce theoretical SAXS profiles using an all-atom-based approach (Supplementary Figure 8). Taken together, an experimentally-calibrated hydration contribution is obtained for a complete Fast-SAXS-RNA method. The calibration procedure is then tested on the SAXS data of the P4-P6 group I intron fragment by its crystal structure (Figure 4). This test provides the validation on the contribution of the hydration later to the total scattering profile.
Figure 4.
Model validation of the Fast-SAXS-RNA method. The two-particle model with the hydration layer is validated using the experimental SAXS data and the crystal structure for the P4-P6 fragment of group I intron (P4-P6; PDB entry 1GID). Comparison of the experimental (black) and Fast-SAXS-RNA computed (red) SAXS profiles. The χ2 difference (Eq. (10)) between these two curves is 1.8 × 10−3.
RNA Conformational Sampling
To test the ability of the Fast-SAXS-RNA method in identifying the native fold and evaluating the usefulness of SAXS data in RNA structure prediction, large decoy sets were generated for three different RNA molecules, namely tRNA, P4-P6, and a RNA dimer. The decoy sets were generated using the MC-Fold and MC-Sym pipeline,16 which produces all-atom RNA 3D structures. The all-atom models allow for proper nucleotide volumes and electron densities. We capitalize on the generator’s built-in knowledge of RNA architectural principles, essentially encoded in Nucleotide Cyclic Motifs (NCMs) and in the ability of MC-Sym to explicitly model non-canonical and long-range base triples. For each RNA molecule, two sets of ensemble models were generated, in high and low resolutions to cover different regimes of the fold space (see Methods). For the RNA dimer, the method was further tested with the use of SAXS by making decoy models of alternate secondary structures.
Application to tRNA
For the tRNA conformational sampling, the set tRNA_low has models with RMSD ranging from 5.6 to 25.5 Å (O5′-only), hence at a low resolution regime. The set tRNA_high has models ranging from 3.1 to 12.7 Å, at a higher resolution regime. Supplementary Figure 9 shows the conformational sampling for tRNA. The latter set includes only L-shaped models, while the former features several additional shapes such as H- and T-shapes. Surprisingly, decoys from the tRNA_high set, with RMSD values of up to 12.7 Å, still look native-like. RMSD values of less than 3 Å seem to be quite difficult to obtain, even by making use of an all-atom model generator and explicit long-range and base triple pairings.
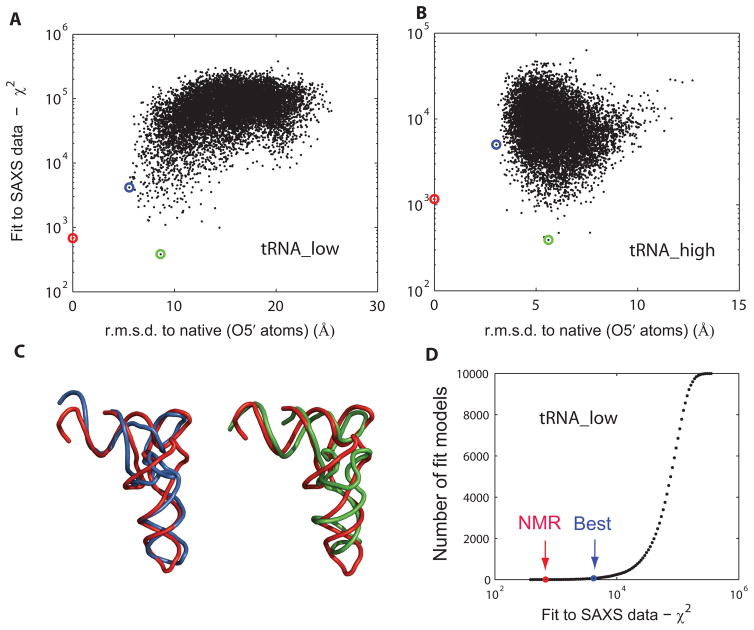
For each decoy within a set, a theoretical SAXS profile is first computed by Fast-SAXS-RNA, according to Eq. (9) (optimal weighting factor w = 11%). The theoretical profile is then compared to the experimental data via Eq. (10), by producing a χ2 score. Lower χ2 score indicates higher fidelity to the experimental SAXS profile. Decoys within a set are subsequently sorted by their χ2 score. Figure 5A and B shows the plot of χ2 against RMSD for both the tRNA_low and tRNA_high sets. It shows that the SAXS-based χ2 scores serve as a good indicator for selecting top structural candidates from decoys in the tRNA_low set. In fact, only 61 models (out of ten thousand) have a lower χ2 score than the lowest-RMSD model in the tRNA_low set. The result suggests that SAXS data are capable to filter 3D models in RNA structure prediction in a low-resolution regime and significantly accelerate the search for the native fold. The ability of identifying the top 1% decoy tRNA_val models by χ2 scores demonstrates that one can pinpoint only this small subset as representative folds. These low-resolution models can further offer a starting point for a next-step structural refinement (which is beyond the scope of this work). As illustrated by Figure 5C, the best models according to a χ2 criterion have a similar overall shape. The cumulative plot in Figure 5D further shows that the lowest-RMSD model is quite close to the solution structure, with a certain χ2 cutoff. For the high-resolution set, a ranking based on a χ2 score is not capable of capturing the finer structural differences between decoys (Figure 5B). Because of the low-resolution nature of SAXS data, most models in the tRNA_high set have similar overall shapes and thus have undistinguished χ2 scores. Nonetheless, the correlation between RMSD and χ2 in the tRNA_low set suggests that as a proof-of-principle study SAXS data can be used as input for a score function to locate these low-resolution models especially when a native structure is not available.
Figure 5.
Application to tRNA. Two decoy sets are used: tRNA_low and tRNA_high. Each set contains 10,000 models (including the solution structure) covering different regimes of the conformational space. Plot of fit to the SAXS data χ2 as a function of RMSD to the solution structure (PDB entry 2K4C), for tRNA_low (A) and tRNA_high (B), respectively. Lower χ2 values indicate a better fit. RMSD is computed over all O5′ atoms. The solution structure is indicated in red, the lowest-RMSD model in blue and the best SAXS-fit model in green. (C) Representative tRNA_low decoy set models. Optimal superposition of the best lowest-RMSD model (blue; 5.6 Å) and the best SAXS-fit model (green; 8.6 Å) on the solution structure (red). (D) Cumulative model plot as a function of the fit to SAXS data χ2. Indicated are the positions of the solution structure (NMR) and the best lowest-RMSD model (Best). There are 61 models (out of ten thousand) which display better χ2 values than the best lowest-RMSD model. The q-ranges from qmin = 0.05 Å−1 to qmax = 0.32 Å−1 were used for tRNA χ2-score calculations.
We also note that the use of the full SAXS spectrum of tRNA_val up to q ~ 0.3 Å−1 can be advantageous. Traditional use of SAXS data is to derive the radius of gyration (Rg) from the low-q region using a Guinier fit.58 Here, the χ2 scores, which makes use of the full SAXS spectrum, are strongly correlated with the r.m.s.d. values of decoy models in the tRNA_low set (Figure 5A). In contrast, such a funnel-like correlation feature does not show up in the plot between Rg and r.m.s.d. (Supplementary Figure 10), suggesting that Rg is not capable of discriminating native-like folds of tRNA_val. Therefore, the SAXS-based χ2 scores serve well as a indicator for correlating with native tRNA models by taking advantage of the full SAXS spectrum.
Application to P4-P6
Two sets of models were generated for the P4-P6, representing low and high resolution resolution regimes, respectively. The set P4-P6_low has models with RMSD ranging from 13.3 to 49.7 Å (O5′-only). The set P4-P6_high has models with RMSD from 6.9 to 14.2 Å. Even though the range of RMSD in the P4-P6_high set is large compared to tRNA_high, one has to keep in mind that P4-P6 has twice as many nucleotides than in tRNA, and that small modeling errors in connecting the stems produce large deviations. Nonetheless, the models compare favorably to those constructed by other methods (e.g., FARNA59 and NAST18). Supplementary Figure 11 shows the conformational sampling for P4-P6.
The P4-P6_low decoy set offers the most wide range of conformations (Figure 6A). Most decoy models are in an extended conformation, where two stems (P6-P4-P5 and P5a-P5c) form a long double-helical structure with a 180 degrees angle (Figure 11a). Other decoys includes the native-like U-shape, where a zero degree angle between these two stems (Figure 11b), as well as some decoys with a relative angle between 0 and 180 degrees. Hence, it is striking that the use of SAXS data is capable to identify the U-shaped native fold of P4-P6 from the low-resolution decoys (Figure 6A). In contrast, the P4-P6_high set, which is generated with the explicit use of the tetraloop-receptor long-range 3D contact, offers a different decoys set in Figure 6B where the funnel-like correlation between χ2 and RMSD is lost (compared to Figure 6A), although the slope of the distribution of χ2 values against RMSD remains positive. Figure 6C shows the superimposition between the native U-shape structure (red), the best RMSD model (blue), and the best SAXS fit with the lowest χ2 (green). Similar to tRNA-val, the results demonstrate that the SAXS data P4-P6 is able to identify its native U-shape fold from the pool of decoys in the P4-P6_low set. From the standpoint of structural modeling, one can use the resulting top models to further design new local structure probing experiments (such as cross-linking), which can provide insights into details about structural organizations of aligned sequences. Nonetheless, since the plot of χ2 against RMSD shows a sign of positive correlation (Figure 6B), it appears that χ2 can still keep track of the extended shape of P4-P6 in this P4-P6_high set. From the cumulative plot, only 40 models (out of ten thousand) have better χ2 than the lowest-RMSD model (Figure 6D). As more quality SAXS data become available,60 this result indicates that one can expect the use of SAXS data offers the top 1% best SAXS fit models in the search for native-like folds.
Figure 6.
Application to P4-P6. Two decoy sets are used: P4-P6_low and P4-P6_high. Each set contains approximatively 10,000 and 9,000 models (including the crystal structure). Plot of fit to the SAXS data χ2 of P4-P6 as a function of RMSD to its crystal structure (PDB entry 1GID), for P4-P6_low (A) and P4-P6_high (B), respectively. The crystal structure is indicated in red, the lowest-RMSD model in blue and the best SAXS-fit in green. (C) Representative P4-P6_low decoy set models. Optimal superposition of the best lowest-RMSD model (blue; 13.3 Å) and the best SAXS fit model (green; 16.0 Å) on the crystal structure (red). (D) Cumulative model plot as a function of the fit to the SAXS data (χ2). Indicated are the positions of the Crystal structure (Xtal) and the best lowest-RMSD model (Best). There are 40 models which display better χ2 values than the best RMSD model. The q-ranges from qmin = 0.02 Å−1 to qmax = 0.32 Å−1 were used for P4-P6 χ2-score calculations.
Application to an RNA Dimer
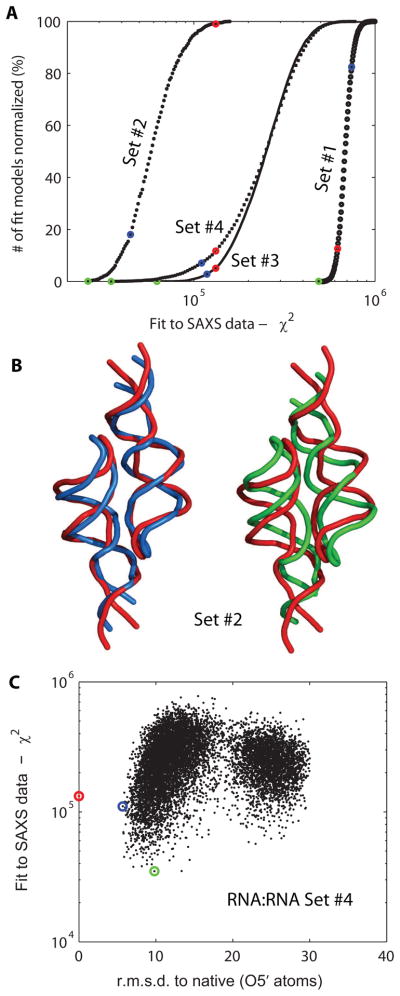
In this section, the ability of the method to identify the multimeric state and various secondary structures of an RNA hairpin is tested. The hairpin contains both a GNRA tetraloop and its receptor, allowing dimerization in solution (the tetraloop of one monomer would dock into the receptor in the other monomer, and vice-versa). Supplementary Figure 12 shows all the multimeric states and secondary structures tested, in a total of four different decoy sets. Figure 7A shows the fit to SAXS data for the four conformational states corresponding to the four sets. Conformational set #2 with its RMSD range close to the native structure has the best fit to the SAXS data, since it features dimers that are doubly-docked. Interestingly, several models from this set display lower SAXS χ2 scores than the solution structure (PDB entry 2JYH).40 This suggests that conformational set #1 has the poorest χ2 scores and the largest deviation from SAXS data among the four sets. It is well separated from the native homodimer set #2 in χ2 values. This separation demonstrates that one should be able to tell from SAXS data that the dimeric form is more favorable than the monomeric form. Conformational set #4 includes models with only one tetraloop-receptor interaction formed and overlaps with set #2. Most of models in set #3 with the four-way junction have poorer SAXS ranking scores than those in set #4, suggesting that this state is less likely to be observed in solution. Figure 7B shows the superposition of the models with the best ranking score (green) and the lowest RMSD (blue) with the solution structure (red). Figure 7C shows the plot of χ2 vs RMSD for set #4. The results suggest that the SAXS ranking helps to identify the models of the RNA dimer with lower RMSD (though keeping in mind that the doubly-docked state can happen fortuitously in that decoy set).
Figure 7.
Application to an RNA dimer. (A) Cumulative model plot as a function of the fit to SAXS data χ2. A total of four decoy sets, from #1 to #4, are compared. These decoy sets address various multimerization states and secondary structures (see Methods). Since the number of models in each decoy set is different, the cumulative plot has been normalized to the fraction of total number of decoys in the set. For each set, the solution structure is highlighted in red (PDB entry 2JYH), the best lowest-RMSD model in blue, and the best SAXS-fit in green. For decoy set #1, the solution structure is considered to be the monomer unit. (B) Representative models from decoy set #2. The best SAXS-fit model (green; 7.5 Å) and best RMSD model (blue; 4.7 Å) optimally superimposed on the solution structure (red). (C) Plot of fit of SAXS data χ2 against RMSD, for models in decoy set #4. The solution structure is highlighted in red, and blue for the best RMSD model and green for the best SAXS-fit model.
Given the intrinsic low-resolution nature of SAXS, the information context is sufficient to distinguish the native state among many multimerization states for a small RNA hairpin. The symmetric homodimer state (2-docked) is identified as the best fit to the SAXS data against the asymmetric one (1-docked) and an alternative secondary structure, even though the decoy sets have the similar radius of gyration Rg or the maximum distance Dmax. Clearly, the usage of the full SAXS spectrum instead of single parameters like Dmax or Rg is required for a proper identification (Supplementary Table 1).
Concluding Discussion
A rapid coarse-grained method for calculating the SAXS profile from complex nucleic acid structures has been developed. The method has been termed Fast-SAXS-RNA. The computer program Fast-SAXS-RNA will be released under the GNU General Public License.
The method is built on a reduced two-particle representation for each nucleotide. While it is possible to treat proteins based on a reduced representation with a single particle per residue,22 the present results indicate that a two-particle representation to achieve the desirable accuracy in the calculation of SAXS patterns in the case of tRNA structures. A single-particle-based SAXS calculation is unable to reproduce accurately the experimental profile, particularly beyond q = 0.1 Å (Supplementary Figure 8). Furthermore, the excess electron density at the RNA surface is taken into account in the Fast-SAXS-RNA calculation by explicit construction of a hydration layer. The amplitude of water scattering was calibrated from tRNA-Val data, and further tested on P4-P6 domain with good agreement with SAXS data.
As expected, coarse-graining RNA molecules and their surrounding solvent greatly accelerates the computation of SAXS profiles. For example, within the framework of the Debye formalism, computing the scattering of a protein without surrounding water molecules is faster by a factor of N2 (where N = 16 is the average number of atoms per group). It should be noted that the gain in speed is less pronounced when explicit dummy water molecules are included in the calculation, although a direct comparison with atomistically detailed solvent has not been attempted.
The utility of Fast-SAXS-RNA becomes obvious when it is combined with RNA 3D structure generators. Here, the advantage of using MC-Sym was to build all-atom models with proper excluded volumes and electronic densities. Besides, the MC-Pipeline offers a series of utility tools for managing RNA 3D structure decoys, including a general filtering process that allows one to upload various types of structural data. Because of the significant reduction in computational cost for testing a model, it is possible to rank, order, and filter large ensemble of 3D models extremely efficiently. For tRNA, P4-P6, and the RNA dimeric complex, usage of SAXS data as a constraint succeeds to filter out most non-native folds and identify well-fit models at a low-resolution level. Hence, the incorporation of SAXS data in modeling offers an alternative mean to dramatically narrow down the conformational search. It is our hope that this strategy will enable the rapid characterization and structural refinement of RNA models by exploiting increasingly available SAXS data.
Supplementary Material
Table 1: Various parameters for the RNA dimer decoy sets (see Supplementary Figure 12). Mean values for the radius of gyration (Rg, in Å) and maximum width (Dmax, in Å) are reported for each set. These do not include the contribution of the explicit hydration layer. Numbers in parenthesis are the standard deviations. N is the number of decoys in the set.
Figure 8: SAXS scattering profiles of various N-particle models. Theoretical SAXS profiles of C3′-only, O5′-only and the two-particle models (this work) are compared against an all-atoms model. For the sake of comparison, the contribution of the explicit hydration layer is not taken into account. The model structure used is tRNA (PDB entry 2K4C).
Figure 9: Conformational sampling for tRNA. (top) Conformational sampling of the tRNA_low decoy set. (a) Sequence and secondary structure used in the modeling process. Stem/loops are colored as follows: acceptor, green; D, cyan; anticodon, orange and T, yellow. (b) and (c) Twenty centroid centers, in thin lines, optimally superimposed on the solution structure (PDB file 2K4C), in thick lines. Colors used are the same as in (a). Centroids range in RMSD from 8.0 to 21.5 Å. (bottom) Conformational sampling of the tRNA_high decoy set. (d) Sequence and secondary structure used in the modeling process. Here, base triples 8-14-21, 9-23-12 and 22-46-13, along with long-range base pairs 18–55, 19–56 and 15–48 are explicitly modeled. (e) and (f) Twenty centroid structures, in thin lines, are optimally superimposed on the solution structure, in thick lines. Colors used are the same as in (d). Centroids range in RMSD from 4.3 to 7.8 Å.
Figure 10: Plot of Rg vs r.m.s.d of tRNA_val from the decoy set of tRNA_low. The red line indicates the Rg value of the native fold. The result suggests that the use of Rg alone, which can be derived from the low-q region of SAXS data, is not sufficient to discriminate the native-like fold in the tRNA_low decoy set.
Figure 11: Conformational sampling for P4-P6. (a) Sequence and secondary structure used in the modeling process. Uncolored nucleotides have been taken from the crystal structure (PDB entry 1GID); in particular, the P5c hairpin and the tetraloop receptor have not been sampled. Two decoy sets have been generated; P4-P6_low and P4-P6_high, whose only difference is the use of a long-range base pair 153–250 which enforces the U-shape in models in the P4-P6_high decoy set. (b) and (c) Twenty centroid structures, in thin lines, are optimally superimposed on the crystal structure, in thick lines. Colors used are the same as in (a). Centroids are taken from the P4-P6_high decoy set. Centroids range in RMSD from 7.6 to 10.3 Å.
Figure 12: Conformational sampling for the RNA dimer. A total of four decoy sets, #1 to #4, have been generated. (Top) Sequences and secondary structures for each decoy sets. Set #1 represents the monomer unit, which is an RNA hairpin that contains both a tetraloop-receptor (grey) and a tetraloop (orange). Set #2 represents homodimers, for which the tetraloop of monomer A (yellow) is docked into the receptor of monomer B (blue), and vice-versa, producing a doubly-docked configuration. Set #4 is similar to set #2, however it only imposes the docking of one monomer unit into the other. Hence, the double-docked configuration in this set would be fortuitous. Set #3 uses a different secondary structure, which part of two hairpins stems are fused to one another, producing a four-way junction. (Bottom) Twenty centroid centers aligned on monomer A (yellow) are shown for each set.
This material is available free of charge via the Internet at http://pubs.acs.org/.
Acknowledgments
We thank Drs. Alexander Grishaev and Ad Bax for providing the SAXS data of tRNA-Val, Drs. Jan Lipfert and Sebastian Doniach for providing the SAXS data of P4-P6, and Drs. Xiaobing Zuo, Samuel Butcher, and Yu-Xing Wang for providing the SAXS data of RNA dimer. This work was supported by the National Institute of Health (SY and BR) via a NCI grant (No. CA093577), and by the Canadian Institutes of Health Research (CIHR) and the Natural Sciences and Engineering Research Council (NSERC) of Canada (FM). MP holds Ph.D. scholarships from the NSERC and the Fonds Québécois de la Recherche sur la Nature et les Technologies. FM is a member of the Centre Robert-Cedergren of the Université de Montréal.
References
- 1.Putnam CD, Hammel M, Hura GL, Tainer JA. Quart Rev Biophys. 2007;40:191–285. doi: 10.1017/S0033583507004635. [DOI] [PubMed] [Google Scholar]
- 2.Doniach S. Chem Rev. 2001;101:1763–1778. doi: 10.1021/cr990071k. [DOI] [PubMed] [Google Scholar]
- 3.Koch MHJ, Vachette P, Svergun DI. Quart Rev Biophys. 2003;36:147–227. doi: 10.1017/s0033583503003871. [DOI] [PubMed] [Google Scholar]
- 4.Hura GL, Menon AL, Hammel M, Rambo RP, Poole FL, Tsutakawa SE, Jr, FEJ, Classen S, Frankel KA, Hopkins RC, jae Yang S, Scott JW, Dillard BD, Adams MWW, Tainer JA. Nat Meth. 2009;6:606–612. doi: 10.1038/nmeth.1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tsuruta H, Irving T. Curr Opin Struct Biol. 2008;18:601–608. doi: 10.1016/j.sbi.2008.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ibel K, Stuhrmann HB. J Mol Biol. 1975;93:255–265. doi: 10.1016/0022-2836(75)90131-x. [DOI] [PubMed] [Google Scholar]
- 7.Jacques DA, Trewhella J. Protein Sci. 2010;19:642–657. doi: 10.1002/pro.351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lipfert J, Chu VB, Bai Y, Herschlag D, Doniach S. J Appl Crystal. 2007;40:s229–s234. [Google Scholar]
- 9.Lipfert J, Doniach S. Annu Rev Biophy Biomol Struct. 2007;36:307–327. doi: 10.1146/annurev.biophys.36.040306.132655. [DOI] [PubMed] [Google Scholar]
- 10.Svergun DI, Petoukhov MV, Koch MH. Biophys J. 2001;80:2946–2953. doi: 10.1016/S0006-3495(01)76260-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bernado P, Mylonas E, Petoukhov MV, Blackledge M, Svergun DI. J Am Chem Soc. 2007;129:5656–5664. doi: 10.1021/ja069124n. [DOI] [PubMed] [Google Scholar]
- 12.Zheng W, Doniach S. J Mol Biol. 2002;316:173–187. doi: 10.1006/jmbi.2001.5324. [DOI] [PubMed] [Google Scholar]
- 13.Ali M, Lipfert J, Seifert S, Herschlag D, Doniach S. J Mol Biol. 2010;396:153–165. doi: 10.1016/j.jmb.2009.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Das R, Baker D. Proc Natl Acad Sci USA. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ding F, Sharma S, Chalasani P, Demidov VV, Broude NE, Dokholyan NV. RNA. 2008;14:1164–1173. doi: 10.1261/rna.894608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parisien M, Major F. Nature. 2008;452:51–55. doi: 10.1038/nature06684. [DOI] [PubMed] [Google Scholar]
- 17.Martinez HM, Jacob V, Maizel J, Shapiro BA. J Biomol Struct Dyn. 2008;25:669–84. doi: 10.1080/07391102.2008.10531240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jonikas MA, Radmer RJ, Laederach A, Das R, Pearlman S, Herschlag D, Altman RB. RNA. 2009;15:189–199. doi: 10.1261/rna.1270809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Frellsen J, Moltke I, Thiim M, Mardia KV, Ferkinghoff-Borg J, Hamelryck T. PLoS Comput Biol. 2009;5:e1000406. doi: 10.1371/journal.pcbi.1000406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walther D, Cohen FE, Doniach S. Journal of Applied Crystallography. 2000;33:350–363. [Google Scholar]
- 21.Svergun D, Barberato C, Koch MHJ. J App Crystal. 1995;28:768–773. [Google Scholar]
- 22.Yang S, Park S, Makowski L, Roux B. Biophys J. 2009;96:4449–4463. doi: 10.1016/j.bpj.2009.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bragg L, Perutz MF. Proc Roy Soc A. 1952;213:425–435. [Google Scholar]
- 24.Cromer DT, Mann JB. Acta Cryst A. 1968;24:0567–7394. [Google Scholar]
- 25.Fraser RDB, MacRae TP, Suzuki E. J Appl Crystal. 1978;11:693–694. [Google Scholar]
- 26.Svergun DI, Richard S, Koch MHJ, Sayers Z, Kuprin S, Zaccai G. Proc Natl Acad Sci USA. 1998;95:2267–2272. doi: 10.1073/pnas.95.5.2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Merzel F, Smith JC. Proc Natl Acad Sci USA. 2002;99:5378–5383. doi: 10.1073/pnas.082335099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Koizumi M, Hirai H, Onai T, Inoue K, Hirai M. J Appl Cryst. 2007;40:s175–s178. [Google Scholar]
- 29.Harker D. Acta Crystal. 1953;6:731–736. [Google Scholar]
- 30.Guo DY, Smith GD, Griffin JF, Langs DA. Acta Cryst A. 1995;51:945–947. doi: 10.1107/s0108767395010038. [DOI] [PubMed] [Google Scholar]
- 31.Guo DY, Blessing RH, Langs DA, Smith GD. Acta Cryst D. 1999;55:230–237. doi: 10.1107/S0907444998008208. [DOI] [PubMed] [Google Scholar]
- 32.Grishaev A, Wu J, Trewhella J, Bax A. J Am Chem Soc. 2005;127:16621–16628. doi: 10.1021/ja054342m. [DOI] [PubMed] [Google Scholar]
- 33.Debye P. Ann Phys (Leipzig) 1915;46:809–823. [Google Scholar]
- 34.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 35.Grishaev A, Ying J, Canny MD, Pardi A, Bax A. J Biomol NMR. 2008;42:99–109. doi: 10.1007/s10858-008-9267-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Major F, Turcotte M, Gautheret D, Lapalme G, Fillion E, Cedergren R. Science. 1991;253:1255–1260. doi: 10.1126/science.1716375. [DOI] [PubMed] [Google Scholar]
- 37.Major F. Computing in Science and Eng. 2003;5:44–53. [Google Scholar]
- 38.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Kundrot CE, Cech TR, Doudna JA. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 39.Laederach A, Chan JM, Schwartzman A, Willgohs E, Altman RB. RNA. 2007;13:643–650. doi: 10.1261/rna.381407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zuo X, Wang J, Foster TR, Schwieters CD, Tiede DM, Butcher SE, Wang Y-X. J Am Chem Soc. 2008;130:3292–3293. doi: 10.1021/ja7114508. [DOI] [PubMed] [Google Scholar]
- 41.Lee JC, Cannone JJ, Gutell RR. J Mol Biol. 2003;325:65–83. doi: 10.1016/s0022-2836(02)01106-3. [DOI] [PubMed] [Google Scholar]
- 42.Krasilnikov AS, Mondragon A. RNA. 2003;9:640–643. doi: 10.1261/rna.2202703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fuller W, Hodgson A. Nature. 1967;215:817–821. doi: 10.1038/215817a0. [DOI] [PubMed] [Google Scholar]
- 44.Levitt M. Nature. 1969;224:759–763. doi: 10.1038/224759a0. [DOI] [PubMed] [Google Scholar]
- 45.Klingler TM, Brutlag DL. Proc Int Conf Intell Syst Mol Biol. 1993:225–233. [PubMed] [Google Scholar]
- 46.Murphy FL, Cech TR. Biochemistry. 1993;32:5291–5300. doi: 10.1021/bi00071a003. [DOI] [PubMed] [Google Scholar]
- 47.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Szewczak AA, Kundrot CE, Cech TR, Doudna JA. Science. 1996;273:1696–1699. doi: 10.1126/science.273.5282.1696. [DOI] [PubMed] [Google Scholar]
- 48.Leontis NB, Westhof E. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bouchard P, Lacroix-Labonte J, Desjardins G, Lampron P, Lisi V, Lemieux S, Major F, Legault P. RNA. 2008;14:736–748. doi: 10.1261/rna.824308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ponder JW, Richards FM. J Comput Chem. 1987;8:1016–1024. [Google Scholar]
- 51.Wang J, Cieplak P, Kollman PA. J Comput Chem. 2000;21:1049–1074. [Google Scholar]
- 52.Chacón P, Morán F, Díaz J, Pantos E, Andreu J. Biophys J. 1998;74:2760–2775. doi: 10.1016/S0006-3495(98)77984-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Perkins SJ. Biophysical Chemistry. 2001;93:129–139. doi: 10.1016/s0301-4622(01)00216-2. [DOI] [PubMed] [Google Scholar]
- 54.Hubbard S, Hodgson K, Doniach S. J Biol Chem. 1988;263:4151–4158. [PubMed] [Google Scholar]
- 55.Auffinger P, Hashem Y. Curr Opin Struct Biol. 2007;17:325–333. doi: 10.1016/j.sbi.2007.05.008. [DOI] [PubMed] [Google Scholar]
- 56.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. Curr Opin Chem Biol. 2008;12:619–625. doi: 10.1016/j.cbpa.2008.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen S-J. Annu Rev Biophy. 2008;37:197–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Guinier A, Fournet G. Small-angle scattering of x-rays. Wiley; New York: 1955. [Google Scholar]
- 59.Das R, Kudaravalli M, Jonikas M, Laederach A, Fong R, Schwans JP, Baker D, Piccirilli JA, Altman RB, Herschlag D. Proc Natl Acad Sci USA. 2008;105:4144–4149. doi: 10.1073/pnas.0709032105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rambo RP, Tainer JA. RNA. 2010;16:638–646. doi: 10.1261/rna.1946310. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table 1: Various parameters for the RNA dimer decoy sets (see Supplementary Figure 12). Mean values for the radius of gyration (Rg, in Å) and maximum width (Dmax, in Å) are reported for each set. These do not include the contribution of the explicit hydration layer. Numbers in parenthesis are the standard deviations. N is the number of decoys in the set.
Figure 8: SAXS scattering profiles of various N-particle models. Theoretical SAXS profiles of C3′-only, O5′-only and the two-particle models (this work) are compared against an all-atoms model. For the sake of comparison, the contribution of the explicit hydration layer is not taken into account. The model structure used is tRNA (PDB entry 2K4C).
Figure 9: Conformational sampling for tRNA. (top) Conformational sampling of the tRNA_low decoy set. (a) Sequence and secondary structure used in the modeling process. Stem/loops are colored as follows: acceptor, green; D, cyan; anticodon, orange and T, yellow. (b) and (c) Twenty centroid centers, in thin lines, optimally superimposed on the solution structure (PDB file 2K4C), in thick lines. Colors used are the same as in (a). Centroids range in RMSD from 8.0 to 21.5 Å. (bottom) Conformational sampling of the tRNA_high decoy set. (d) Sequence and secondary structure used in the modeling process. Here, base triples 8-14-21, 9-23-12 and 22-46-13, along with long-range base pairs 18–55, 19–56 and 15–48 are explicitly modeled. (e) and (f) Twenty centroid structures, in thin lines, are optimally superimposed on the solution structure, in thick lines. Colors used are the same as in (d). Centroids range in RMSD from 4.3 to 7.8 Å.
Figure 10: Plot of Rg vs r.m.s.d of tRNA_val from the decoy set of tRNA_low. The red line indicates the Rg value of the native fold. The result suggests that the use of Rg alone, which can be derived from the low-q region of SAXS data, is not sufficient to discriminate the native-like fold in the tRNA_low decoy set.
Figure 11: Conformational sampling for P4-P6. (a) Sequence and secondary structure used in the modeling process. Uncolored nucleotides have been taken from the crystal structure (PDB entry 1GID); in particular, the P5c hairpin and the tetraloop receptor have not been sampled. Two decoy sets have been generated; P4-P6_low and P4-P6_high, whose only difference is the use of a long-range base pair 153–250 which enforces the U-shape in models in the P4-P6_high decoy set. (b) and (c) Twenty centroid structures, in thin lines, are optimally superimposed on the crystal structure, in thick lines. Colors used are the same as in (a). Centroids are taken from the P4-P6_high decoy set. Centroids range in RMSD from 7.6 to 10.3 Å.
Figure 12: Conformational sampling for the RNA dimer. A total of four decoy sets, #1 to #4, have been generated. (Top) Sequences and secondary structures for each decoy sets. Set #1 represents the monomer unit, which is an RNA hairpin that contains both a tetraloop-receptor (grey) and a tetraloop (orange). Set #2 represents homodimers, for which the tetraloop of monomer A (yellow) is docked into the receptor of monomer B (blue), and vice-versa, producing a doubly-docked configuration. Set #4 is similar to set #2, however it only imposes the docking of one monomer unit into the other. Hence, the double-docked configuration in this set would be fortuitous. Set #3 uses a different secondary structure, which part of two hairpins stems are fused to one another, producing a four-way junction. (Bottom) Twenty centroid centers aligned on monomer A (yellow) are shown for each set.
This material is available free of charge via the Internet at http://pubs.acs.org/.