A Method for Functional Network Connectivity Among Spatially Independent Resting-State Components in Schizophrenia

Abstract

Functional connectivity of the brain has been studied by analyzing correlation differences in time courses among seed voxels or regions with other voxels of the brain in patients versus controls. The spatial extent of strongly temporally coherent brain regions co-activated during rest has also been examined using independent component analysis (ICA). However, the weaker temporal relationships among ICA component time courses, which we operationally define as a measure of functional network connectivity (FNC), have not yet been studied. In this study, we propose an approach for evaluating FNC and apply it to functional magnetic resonance imaging (fMRI) data collected from persons with schizophrenia and healthy controls. We examined the connectivity and latency among ICA component time courses to test the hypothesis that patients with schizophrenia would show increased functional connectivity and increased lag among resting state networks compared to controls. Resting state fMRI data were collected and the inter-relationships among seven selected resting state networks (identified using group ICA) were evaluated by correlating each subject’s ICA time courses with one another. Patients showed higher correlation than controls among most of the dominant resting state networks. Patients also had slightly more variability in functional connectivity than controls. We present a novel approach for quantifying functional connectivity among brain networks identified with spatial ICA. Significant differences between patient and control connectivity in different networks were revealed possibly reflecting deficiencies in cortical processing in patients.

INTRODUCTION

Developments in functional imaging in the past two decades have allowed for significant advances in our understanding of the complex relationships and interactions among distributed brain regions underlying cognition. An active area of neuroimaging research involves examining the “functional connectivity” of spatially remote brain regions. Functional connectivity analyses allow the characterization of inter-regional neural interactions during particular cognitive or motor tasks or merely from spontaneous activity during rest. Previous functional connectivity analysis approaches have relied on choosing individual seed voxels and subsequently constructing cross-correlation maps of other voxels with respect to the chosen seed voxels (Biswal, et al. 1995; Biswal, et al. 1997; Cordes, et al. 2002; Cordes, et al. 2000; Lowe, et al. 1998).

Another useful method to examine functional connectivity is independent component analysis (ICA) (Calhoun, et al. 2001b; Esposito, et al. 2005; Garrity, et al. 2007; McKeown, et al. 1998), particularly as applied to “resting state” scans, which are relatively easy to obtain and do not suffer from performance confounds in cognitively-impaired patient groups (Beckmann, et al. 2005; Greicius, et al. 2004; Kivinienri, et al. 2001). ICA is a method for recovering underlying signals from linear mixtures of these signals and draws upon higher-order signal statistics to determine a set of “components” that are maximally independent of each other (Calhoun and Adali 2006). The use of ICA in these studies effectively finds and characterizes functional networks in data collected during the performance of a task as well as in resting state fMRI data. For instance, van de Ven, et al., used spatial differences across ICA-generated components’ intensity to determine functional connectivity levels (Van de Ven, et al. 2004). ICA has been found to be useful and able to capture the complex nature of fMRI time courses while also producing consistent spatial components (Turner and Twieg 2005). Rakapakse et al., performed analyses using structural equation modeling to find connectivity between regions identified using spatial ICA in healthy individuals while performing a task (Rajapakse, et al. 2006).

While these techniques are effective for analyzing dysfunctional integration of activations in various regions’ time series in brains, to date there has been no study of group differences in the temporal relationship among spatial components. Within a given component, the regions are by definition strongly temporally coherent due to the ICA assumption of linear mixing. In this paper we focus not upon these strongly coherent time courses, rather we consider weaker dependencies among components. In spatial ICA the images are maximally independent, but the time courses are not independent and can exhibit considerable temporal dependencies. These temporal dependencies among components are significant, but not as large as those between regions within a component (were this the case they would likely have been included within a single component) (Calhoun, et al. 2003). A technique to determine functional temporal connectivity among components and to evaluate group differences in these relatively weaker connections is proposed in this paper. In this paper, we define functional network connectivity (FNC) as the temporal dependency among the ICA components. In contrast to connectivity studies which focus upon the correlation between a single seed region of interest and the other brain regions, we focus instead upon the temporal connectivity among functional networks (components) estimated from ICA.

In order to show the practical relevance of our technique, we apply the methods described in this paper to compare FNC in patients with schizophrenia versus healthy controls. Schizophrenia is a chronic, disabling mental disorder that is diagnosed on the basis of a constellation of psychiatric symptoms and longitudinal course (APA 2000). The disease impairs multiple cognitive domains including memory, attention and executive function (Heinrichs and Zakzanis 1998). Although the causes and mechanisms of schizophrenia are still unclear, a hypothesis of neural network ‘disconnection’ has been proposed. This proposal assumes that schizophrenia arises from dysfunctional integration of a distributed network of brain regions (Friston and Frith 1995) or a misconnection syndrome of neural circuitry leading to an impairment in the smooth coordination of mental processes, sometimes described as “cognitive dysmetria” (Andreasen, et al. 1999).

Many researchers have examined the possibility of ’disconnection’ in psychiatric groups by analyzing brain function with functional connectivity methods (Bokde, et al. 2006; Friston 1995; Friston and Frith 1995; Frith, et al. 1995; Herbster, et al. 1996; Josin and Liddle 2001; Liang, et al. 2006; Liddle, et al. 1992; Mikula and Niebur 2006). For example, in a sample of patients with schizophrenia, Liang, et al., found disrupted functional integration of widespread brain areas, including a decreased connectivity among insula, temporal lobe, prefrontal lobe and corpus striatum and an increased connectivity between the cerebellum and other brain areas, during resting-state by analyzing correlations between brain regions (Liang, et al. 2006). Similarly, Meyer-Lindenberg, et al., reported pronounced disruptions of distributed cooperative activity in frontotemporal interactions in schizophrenia in selected regions of interest in positron emission tomography (PET) brain scans on working memory task (Meyer-Lindenberg, et al. 2001). Other task-related studies reported a lack of interaction between right anterior cingulate and other brain regions (Boksman, et al. 2005), disrupted integration between medial superior frontal gyrus and both the anterior cingulate and the cerebellum (Honey, et al. 2005), as well as reduced functional connectivity in frontotemporal regions of subjects with schizophrenia (Lawrie, et al. 2002). Although these studies help identify problems with typical functional integration among important brain regions, they do not examine patients to see if there is disruption in the relationship of activity within one large networks of brain regions with another. It follows that patients with schizophrenia may not only have deficits in the relationship of one brain region to another, but that their cognitive and behavioral deficits might be related to dysfunction of entire networks of regions failing to properly communicate with one another.

In the study, we focused on examining FNC differences between a group of patients with schizophrenia and a demographically-matched control sample. Based upon two of our recent studies showing less task-specific activation (Calhoun, et al. 2006a) and more high frequency fluctuations in the default mode (Garrity, et al. 2007) in schizophrenia patients versus healthy controls, we hypothesized that patients would show increased connectivity among ICA component networks, possibly reflecting less specialized cognitive processing. Also, based on a prior study showing delayed hemodynamic brain activity in schizophrenia (Ford, et al. 2005), we predicted that patients would show increased latency of peak hemodynamic signal change in each network compared to activity changes in healthy controls. Although we do not directly test the disconnection hypothesis in this work, the proposed methods would permit such tests using the proper experimental paradigm. Indeed, the results of this analysis are consistent with the existence of misconnected neural circuitry in subjects with schizophrenia, through findings that likely depict an increased dependence among a wider array of less efficient brain regions in schizophrenia, a possible manifestation of a generalized cognitive deficit.

Our general approach can be outlined as follows: we first use ICA to extract resting state network time courses in patients with schizophrenia and healthy controls (Beckmann, et al. 2005; Garrity, et al. 2007). After additional data filtering for noise removal, the time series between all pair-wise combinations of these networks are further analyzed to determine the maximal lagged correlation between networks (this was done both to mitigate the impact of latency difference upon the correlation and also to provide the possibility of evaluating the latency differences). Significant correlations within groups, differences in correlation between groups, and differences in lags between groups were computed. A resampling technique was used to validate the significance of the group differences. We also tested the robustness of the detected differences in connectivity by testing multiple independent sub-samples of patients and controls.

MATERIALS AND METHODS

Participants and Paradigm description

Data from 29 patients with schizophrenia [age 38.36±11.26 years (19–58 years) and 25 healthy controls (age 38.62±11.127 years (20–59 years)] were drawn from IRB-approved studies, with written subject consents, at the Olin Neuropsychiatry Research Center (ONRC). Prior to inclusion in the study, healthy participants were screened to ensure they were free from DSMIV Axis I or Axis II psychopathology [assessed using the SCID-IV (Spitzer, et al. 1996)] and also interviewed to determine that there was no history of psychosis in any first-degree relatives. Patients met DSM-IV criteria for schizophrenia on the basis of a structured clinical interview (SCID-IV) (First, et al. 1995) and review of the case file. The control group included 18 males and 7 females; the patient group consisted of 22 males and 7 females. Eighty percent of controls and 89.7% of patients were right-handed. The two groups were matched for mean age (p>0.811), proportion gender (p>0.747) and handedness (p>0.248). We selected slightly more participants in the patient group due to reported presence of greater variance in patterns in schizophrenic subjects with different symptom profiles (Liddle 1992).

Image Acquisition

FMRI scans were collected using a 3.0 Tesla Siemens Allegra scanner, equipped with 40 mT/m gradients and a standard quadrature head coil. The functional scan was acquired using gradient-echo echo-planar imaging with the following parameters (repeat time (TR) = 1.86s, echo time (TE) = 27 ms, field of view (FOV) = 24 cm, acquisition matrix = 64×64, flip angle (FA) = 70°, slice thickness (ST) = 3 mm, gap = 1mm). After excluding the first six dummy scans, during which magnetization steady state was being reached, 162 scans were used for analysis. During the scan, all subjects were instructed to rest quietly in the scanner, without sleeping. Post-scan questionnaire confirmed subjects’ alertness level during the scan.

Preprocessing

Data were preprocessed using the Statistical Parametric Mapping software package, SPM2 (http://www.fil.ion.ucl.ac.uk/spm/). Data were motion corrected, spatially smoothed with a 10 mm³ full width half-maximum Gaussian kernel, spatially normalized into the standard Montreal Neurological Institute space, and then converted to the standard space of Talairach and Tournoux (Talairach and Tournoux 1988) using an algorithm developed by Matthew Brett (http://imaging.mrccbu.cam.ac.uk/imaging/MniTalairach).

Component Identification

Group spatial ICA was conducted for all 54 participants using the infomax algorithm (Bell and Sejnowski 1995). Two separate group spatial ICAs were also conducted on controls and patients to ensure that the resulting components had similar resting state fluctuations in the two groups as in the resulting components attained from all 54 participants combined. Data were decomposed into thirty components using the GIFT software (http://icatb.sourceforge.net/, version 1.3b). Dimension estimation, to determine the number of components, was performed using the minimum description length criteria, modified to account for spatial correlation (Li, et al. 2006). Single subject time courses and spatial maps were then computed (called back-reconstruction), during which the aggregate components and the results from data reduction are used to compute the individual subject components (Calhoun, et al. 2001a).

Component Selection

A systematic process was used to inspect and select the components of interest from the 30 estimated components (Stevens, et al. 2006). The association of each component’s spatial map with a priori probabilistic maps of gray matter, white matter, and cerebral spinal fluid within standardized brain space (MNI templates provided in SPM2) helped to identify those components whose patterns of correlated signal change were largely consisted of gray matter versus non-gray matter. Components with high correlation to a priori localized CSF or white matter, or with low correlation to gray matter, suggested that they may be artifactual rather than representing hemodynamic change. Correlation analysis indicated that no component corresponded to the spatial distribution of white matter. Visual inspection of discarded components suggested that they represented eye movements, head motion, or cardiac-induced pulsatile artifact at the base of the brain. Seven components were selected as of interest for further analysis.

Analysis in GIFT also produced time courses for the 7 selected components for each of the 54 subjects. Prior to computing correlations, component time courses were filtered through a band-pass Butterworth filter, with cut-off frequencies set at 0.0372 Hz and 0.372 Hz, the frequency range implicated in previous resting state analysis (Cordes, et al. 2001).

Correlation and lag computation for patients and controls

The ICA algorithm assumes that the time courses of cortical areas within one component are synchronous (Calhoun, et al. 2004). Though the components are spatially independent, significant temporal correlations can exist between them. We examined this possibility directly by computing a constrained maximal lagged correlation. Using this approach, we computed a correlation and a lag value for each subject.

The time courses from the seven components for all subjects were first interpolated to enable detection of sub TR hemodynamic delay differences in patients with schizophrenia (Calhoun, et al. 2000; Ford, et al. 2005). The maximal lagged correlation was then examined between all pair-wise combinations where the number of combinations of 7 components, taken 2 at a time results in 7!/(2!(7–2)!) = 21 possible combinations. In other words, let ρ represent correlation between two time courses, X̄ and Ȳ of dimension T×1 units, where T represents the number of time points in the time course. Let i_o represent the starting reference of the two original time courses, and Δi represent the non-integer change in time (seconds). Assume X̄ at initial reference point i_o (X̄_io), and Ȳ circularly shifted Δi units from reference point of i_o (Ȳ_io+Δ_i), then ρ_io+Δ_i at this configuration of the two time courses can be calculated as follows:

$${\rho }_{i_o+\mathrm{\Delta }i}=\frac{({\overline{X}}_{i_o}^{\mathrm{T}})({\overline{Y}}_{i_o+\mathrm{\Delta }i})}{\sqrt{({\overline{X}}_{i_o}^{\mathrm{T}}{\overline{X}}_{i_o})}\times \sqrt{({\overline{Y}}_{i_o+\mathrm{\Delta }i}^{\mathrm{T}}{\overline{Y}}_{i_o+\mathrm{\Delta }i})}}$$

The lag between time courses X̄_io and Ȳ_io+Δi is Δi (commonly denoted as δ) in seconds. Therefore, vectors ρ̄ can be calculated between time courses X̄ and Ȳ, at each instance when Ȳ is circularly shifted Δi units from −5 to +5 seconds. The maximal correlation value from ρ̄ and corresponding lag, δ_ρ̄max, was saved for time courses X̄ and Ȳ.

Correlation and lag values were calculated for all subjects and were later averaged for control and patient group separately, where correlation values represented the dependency of two (out of 7) resting state networks on each other. Using the Student’s t-test, statistically significant correlation combinations from the 21 possible combinations were extracted for patients and controls separately (p < 0.05), resulting in maps of functional network connectivity for each group. Lag values corresponding to the significant correlation combinations were also extracted for each group. These lag values represent the amount of delay between two correlated component time courses averaged across patients and averaged across controls. We predicted that patients would exhibit more significantly correlated functional networks than would controls $(\mathrm{i}.\mathrm{e}.\mathit{\text{length}}({\overline{\rho }}_{\text{max}}^{\mathit{\text{patients}}})>\mathit{\text{length}}({\overline{\rho }}_{\text{max}}^{\mathit{\text{controls}}})),$ where length represents the number of significantly correlated connections in each group.

Correlation and lag computation for group difference

Five statistically significant differences in correlations values for patients versus controls were identified using a two sample t-test. To control for multiple comparisons, amore conservative p-value of p<0.01 [corrected for multiple comparisons using the false discovery rate (Genovese, et al. 2002)] was used for significance cut-off. We again predicted that most of the significant connectivity found from group difference would consist of higher correlation for patients than controls (i.e. ρ_patients > ρ_controls).

Furthermore, connectivity combinations with statistically significant (p<0.01) lag values,δ̄_ρ̄max, were also identified using a two sample t-test of the difference between averaged control and patient lags. This test not only enabled us to visualize the sequence of hemodynamic activity between two components in patients versus controls but also revealed the amount of mean lag during activation from one component to the other for both groups. Due to the delayed brain activity in patients with schizophrenia found in a previous study (Ford, et al. 2005), we predicted that patients will show greater lag between significantly correlated components than controls (i.e. δ_ρcontrol < δ_ρpatient).

Connectivity Validation

Because we used a relatively large sample size of fifty-four subjects, we were able to validate the results by repeating the experiment on subsets of the data to determine whether the same types of connectivity were present. Thus, to test for consistency, the methods described above were repeated twenty times. In each of the twenty trials, functional connectivity was observed between fifteen randomly selected patients and fifteen random controls drawn from the full set of 54 subjects. Significant connectivity was recorded for each group during each trial including significant correlations within groups, differences in correlation between groups, and differences in lags between groups.

In addition, we used a resampling technique to determine whether the mean correlation in controls is significantly different than the mean correlation in patients. We randomly relabeled patients and controls and computed, the mean correlation difference between shuffled controls and patients group in order to build a null distribution. We then calculated a student t-test determined whether the result was significantly different than the mean correlation difference in actual controls and patients group.

RESULTS

Component Selection and Visualization

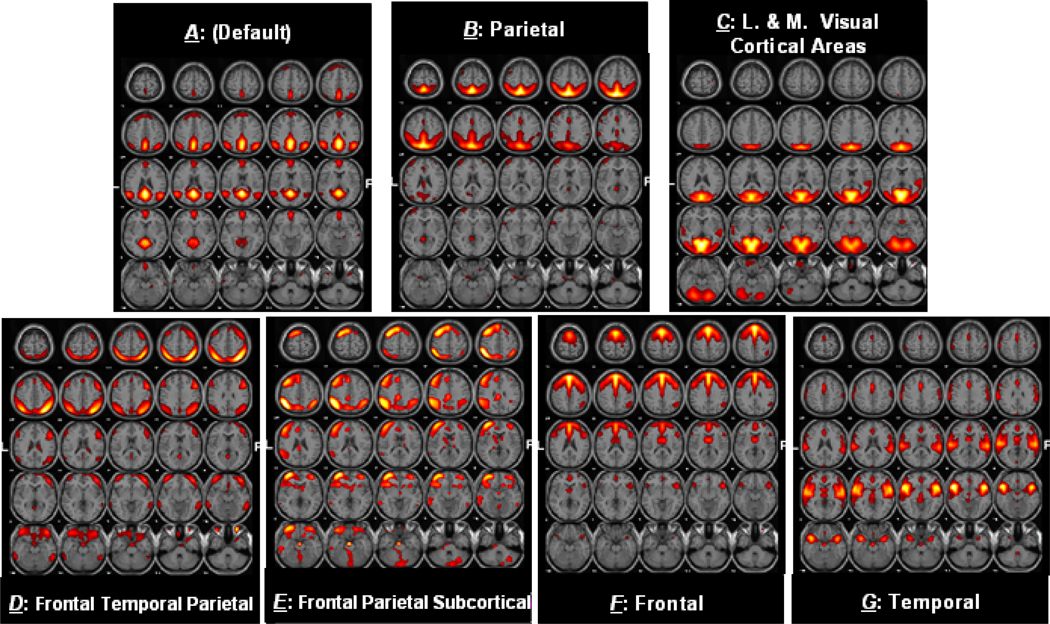
Figure 1 shows the seven components (A–G) selected for connectivity analysis.Table 1 summarizes the components selected, along with the regions of activation as well as the Brodmann areas (BA) in which activations occur. The results from the separate patient and control ICA analyses were similar to what is show in Figure 1 and indeed led to the same results as the full analysis.

Figure 1. Activation Maps for selected Components.

Activation maps for 7 resting state networks selected for correlation and lag analysis

Table 1 (a–g). Regions Activated in Controls and Patients during Resting State.

Voxels above threshold were converted from MNI to Talairach coordinates and entered into a database to provide anatomic and functional labels for the left (L) and right (R) hemispheres. The volume of activated voxels in each area is provided in cubic centimeters (cc). Within each area, the maximum t-value and its coordinate are provided. NS = Not significant

Region	Brodmann Area	Volume (cc) L/R	Random Effects: max T (x,y,z) L/R
Component A: (Default Mode)
Precuneus	31;7;23;39;19	19.9/17.6	26.3(0,−46,31)/26.4(3,−46,31)
Cingulate Gyrus	31;23;24	8.7/5.5	25.4(−3,−43,31)/25.0(3,−42,35)
Posterior Cingulate	31;23;30;29;18	10.6/8.7	24.2(−7,−57,24)/22.2(7,−50,27)
Cuneus	7;30;18;19;23;31;17	6.2/4.5	22.2(−3,−66,32)/22.2(3,−63,32)
Superior Temporal Gyrus	39;22;13;38	8.2/5.4	19.9(−52,−56,28)/22.1(49,−60,28)
Middle Temporal Gyrus	39;19;22;21	4.7/6.1	17.1(−52,−60,24)/20.7(45,−60,28)
Supramarginal Gyrus	40;39	3.8/2.6	20.5(−52,−56,32)/20.1(52,−56,32)
Angular Gyrus	39;40	2.2/2.4	19.2(−52,−60,32)/19.8(52,−60,32)
Inferior Parietal Lobule	40;39;7	5.1/5.2	18.5(−52,−56,36)/19.4(45,−59,36)
Parahippocampal Gyrus	30;27;18;19;36;35	2.5/1.8	15.0(−14,−47,7)/14.9(14,−47,7)
Superior Parietal Lobule	7	0.8/2.7	8.6(−7,−62,53)/14.9(38,−66,45)
Lingual Gyrus	19;18;30	2.8/1.8	14.0(−14,−47,2)/12.6(10,−54,3)
Medial Frontal Gyrus	10;11;8;9;6	11.4/8.4	12.0(0,54,1)/11.7(3,54,1)
Superior Frontal Gyrus	10;9;8;11	8.1/6.4	10.7(−21,43,39)/11.0(7,54,−3)
Superior Occipital Gyrus	39;19	0.0/1.0	NS/10.2(38,−73,29)
Middle Frontal Gyrus	8;9	1.5/1.3	8.8(−24,36,40)/7.1(38,19,40)
Paracentral Lobule	5;31;4;6	1.1/0.4	8.4(0,−38,48)/8.1(3,−38,48)
Anterior Cingulate	32;42	1.1/0.9	7.9(0,47,−2)/8.0(3,47,−2)
Thalamus		0.3/0.4	7.8(−10,−37,10)/6.7(7,−34,2)
Inferior Temporal Gyrus	20;21	1.3/1.2	7.1(−59,−8,−19)/7.0(59,−8,−22)
Fusiform Gyrus	20	0.4/0.1	6.6(−59,−5,−26)/5.8(59,−15,−22)
Insula	13	0.5/0.0	6.3(−28,−40,19)/5.1(28,−40,19)
Caudate	Caudate Tail	0.4/0.0	6.1(−24,−40,19)/NS
Component B: Parietal
Superior Parietal Lobule	7;40;5	11.6/10.0	25.8(−7,−65,57)/22.0(3,−65,57)
Precuneus	7;19;39;31	29.1/23.4	25.5(−7,−62,61)/23.6(3,−72,49)
Postcentral Gyrus	7;5;2;40;1;3	10.7/8.7	20.6(−7,−55,65)/20.1(3,−54,69)
Paracentral Lobule	5;31;6;4;7	6.0/3.5	18.5(0,−38,48)/16.8(3,−45,60)
Cingulate Gyrus	31;32;24;23	12.3/5.0	18.2(−7,−45,44)/14.4(3,−32,43)
Inferior Parietal Lobule	40;39;7	17.8/10.9	17.3(−45,−42,52)/13.8(42,−42,52)
Cuneus	19;7;18;31	3.6/3.3	13.7(−10,−66,32)/13.7(7,−76,37)
Angular Gyrus	39	1.7/0.1	13.1(−31,−59,36)/7.4(38,−73,33)
Sub−Gyral	7;31;40;39	0.6/0.9	11.5(−21,−52,56)/11.5(10,−32,43)
Superior Occipital Gyrus	19;39	1.0/0.8	11.0(−35,−77,33)/11.1(35,−77,33)
Middle Frontal Gyrus	9;10;46;6;11	8.1/0.9	10.6(−38,46,27)/6.6(38,42,27)
Medial Frontal Gyrus	6;9;32;8;25	1.4/0.1	10.4(−7,−21,47)/5.8(7,−21,47)
Middle Temporal Gyrus	39;19	0.9/0.1	9.7(−38,−73,29)/5.8(38,−80,25)
Superior Frontal Gyrus	10;9;11	3.8/0.9	9.5(−38,49,22)/6.6(38,39,27)
Supramarginal Gyrus	40	0.9/0.4	8.5(−55,−36,35)/7.4(38,−42,35)
Anterior Cingulate	32;24	1.3/0.3	8.2(−7,32,23)/6.7(3,22,24)
Posterior Cingulate	29;23;30	1.5/0.1	7.9(−7,−44,6)/5.5(3,−33,22)
Superior Temporal Gyrus	22;38	1.0/0.0	7.7(−55,13,−4)/NS
Inferior Frontal Gyrus	9;10;47;46;11;44	1.7/0.1	7.3(−55,18,24)/5.7(24,30,−20)
Parahippocampal Gyrus	30;36;34;35	0.4/0.2	7.1(−7,−40,6)/5.3(31,−32,−25)
Uncus	34;28	0.3/0.0	6.8(−17,6,−19)/NS
Component C: Visual Cortical Areas
Lingual Gyrus	18;19;17;30	17.8/16.8	20.1(−7,−78,0)/23.4(7,−64,3)
Cuneus	30;18;23;17;19;7;31	21.6/20.9	20.8(−14,−67,16)/23.3(10,−64,7)
Posterior Cingulate	30;31;23;29;18	8.1/6.9	21.0(−14,−64,16)/22.6(10,−64,11)
Precuneus	31;23;19;18;7;39	12.7/11.9	19.6(−10,−67,20)/19.5(7,−70,20)
Middle Occipital Gyrus	18;19;37	13.9/12.3	18.2(−14,−88,17)/18.1(21,−88,13)
Inferior Occipital Gyrus	18;17;19	3.8/3.9	12.5(−21,−89,−7)/16.8(21,−85,−3)
Parahippocampal Gyrus	19;18;30;37;36;27	5.7/3.3	16.1(−21,−58,−5)/13.9(21,−58,−1)
Fusiform Gyrus	19;18;37;20	10.4/6.0	15.8(−24,−61,−4)/14.7(24,−65,−4)
Superior Occipital Gyrus	19;39	1.3/1.0	14.5(−28,−80,25)/12.0(31,−80,25)
Middle Temporal Gyrus	39;19;37;22;21	8.6/8.9	14.2(−42,−74,12)/12.0(38,−74,16)
Sub−Gyral	19;39	0.4/0.2	10.0(−14,−44,−5)/13.2(17,−55,−5)
Inferior Temporal Gyrus	37;19;20	1.1/1.0	10.4(−49,−68,0)/9.5(42,−71,0)
Cingulate Gyrus	31	0.4/0.2	10.1(0,−60,24)/9.3(3,−60,28)
Superior Temporal Gyrus	22;41;39;21;42;29;13	6.0/9.1	8.9(−55,−27,5)/9.7(49,−34,6)
Transverse Temporal Gyrus	41;42	0.3/1.2	6.3(−49,−27,10)/9.5(45,−30,10)
Superior Parietal Lobule	7	0.3/0.3	7.6(−24,−73,45)/7.8(24,−73,45)
Insula	29;13;22;40	0.0/0.5	NS/7.8(45,−27,14)
Precentral Gyrus	6;4	0.0/0.9	NS/5.8(59,−5,33)
Component D: Frontal Temporal Parietal
Superior Parietal Lobule	7;40	8.2/10.2	14.1(−42,−59,53)/16.8(38,−59,53)
Inferior Parietal Lobule	40;7;39	12.3/14.8	13.4(−42,−55,53)/15.7(45,−55,53)
Precuneus	7;19;39	5.7/9.9	11.9(−42,−69,41)/15.3(28,−69,49)
Angular Gyrus	39;40	1.9/2.1	9.5(−45,−66,36)/11.9(45,−63,36)
Postcentral Gyrus	5;40;2;1;3;7	1.9/4.5	9.8(−59,−38,52)/10.8(42,−45,60)
Middle Frontal Gyrus	11;10;46;47;9;6;8	9.7/20.3	10.1(−38,54,−14)/10.7(45,40,−17)
Sub-Gyral	39;10;37;40	0.0/0.4	NS/10.4(31,−59,40)
Inferior Frontal Gyrus	47;46;10;44;9;45;11	1.5/8.6	9.4(−45,37,−17)/9.4(52,38,2)
Superior Frontal Gyrus	8;11;10;9;6	1.8/3.1	7.4(−35,50,−14)/9.2(42,16,49)
Middle Temporal Gyrus	39;20;21;37	2.2/4.3	8.6(−62,−45,−13)/8.9(49,−60,32)
Supramarginal Gyrus	40;39	0.6/1.1	7.6(−55,−56,36)/8.9(52,−49,36)
Cuneus	19;7	0.0/0.5	5.2(−28,−83,37)/8.7(28,−83,37)
Superior Occipital Gyrus	19;39	0.2/0.6	6.6(−38,−77,33)/8.6(35,−77,33)
Superior Temporal Gyrus	39;38	0.3/0.9	5.8(−55,−63,28)/8.3(49,−56,32)
Inferior Temporal Gyrus	20;37	1.1/1.5	7.9(−59,−48,−13)/7.6(62,−51,−9)
Precentral Gyrus	9;4;6	0.0/0.6	NS/7.4(45,19,36)
Fusiform Gyrus	37	0.1/0.3	5.7(−55,−52,−13)/6.2(55,−48,−17)
Medial Frontal Gyrus	8;6	0.2/0.1	6.0(0,33,40)/5.6(3,33,40)
Component E: Frontal Parietal Subcortical
Inferior Parietal Lobule	40;39;7	15.2/6.0	14.5(−49,−49,40)/9.7(45,−52,44)
Insula	13;47	1.5/0.4	13.6(−31,17,−5)/9.1(31,17,−5)
Middle Frontal Gyrus	10;46;11;6;8;9;47	39.4/6.0	13.5(−35,51,2)/9.2(35,47,−6)
Inferior Frontal Gyrus	47;46;10,45;13;9;44	15.6/1.5	13.0(−31,20,−5)/9.2(38,48,2)
Supramarginal Gyrus	40	4.0/1.1	12.7(−42,−46,35)/8.3(38,−46,35)
Superior Frontal Gyrus	10;8;6,9;11	19.9/2.0	12.7(−31,54,−3)/8.3(28,51,−6)
Sub-Gyral	47;40;10;39;8;37;9;32	1.0/0.6	12.6(−35,48,2)/9.4(35,48,2)
Angular Gyrus	39	1.4/0.3	11.5(−38,−59,40)/6.5(35,−59,36)
Precentral Gyrus	9;6;44	1.9/0.0	11.4(−42,19,40)/NS
Extra-Nuclear	47;13	0.5/0.4	11.3(−31,17,−8)/8.7(31,17,−8)
Precuneus	39;19;7;31	5.3/1.7	10.8(−38,−63,36)/7.0(31,−63,40)
Claustrum		1.3/0.6	10.7(−28,17,−1)/7.7(28,13,−4)
Superior Parietal Lobule	7;40	3.9/1.9	10.7(−38,−55,48)/9.5(38,−59,49)
Superior Temporal Gyrus	39;22	1.2/0.1	9.7(−38,−56,32)/6.0(31,−53,32)
Medial Frontal Gyrus	9;6;10;8;32	6.9/0.2	9.2(−10,36,31)/6.6(24,44,6)
Cingulate Gyrus	31;32;23;24;6	5.4/0.7	8.8(−7,−25,34)/7.1(3,−26,30)
Anterior Cingulate	32;10;24;42;9	4.1/0.3	8.7(−14,35,23)/5.9(24,41,2)
Postcentral Gyrus	2;1;40	0.6/0.0	8.5(−55,−29,39)/NS
Middle Temporal Gyrus	39;37;21;20;22	3.9/0.2	8.3(−45,−60,32)/5.2(55,−51,−5)
Lingual Gyrus	18	0.3/0.7	5.6(−3,−83,−19)/7.7(10,−79,−19)
Lentiform Nucleus		1.6/1.3	7.6(−24,17,−1)/7.6(21,17,−8)
Inferior Temporal Gyrus	20;37	0.9/0.0	6.6(−49,−28,−10)/NS
Posterior Cingulate	23	0.2/0.0	6.5(−7,−29,26)/NS
Thalamus		0.1/0.4	5.4(−14,−6,9)/5.9(10,−7,0)
Caudate		0.3/0.3	5.9(−14,14,−1)/5.9(10,7,0)
Fusiform Gyrus	37;18;19	0.0/0.2	5.8(−45,−34,−6)/5.6(17,−83,−22)
Component F: Frontal
Superior Frontal Gyrus	8;6;9;10	31.7/30.1	24.1(0,23,49)/21.6(3,23,49)
Medial Frontal Gyrus	8;6;9;10;32	18.7/17.4	23.2(0,26,48)/22.3(3,19,45)
Cingulate Gyrus	32;24;6;31;23	11.4/8.4	20.1(0,29,32)/21.2(3,29,32)
Anterior Cingulate	32;24;33;42	6.1/5.2	17.7(0,35,23)/17.8(3,35,23)
Middle Frontal Gyrus	9;8;6;10;46;11;47	27.2/29.5	14.2(−45,19,40)/16.6(38,26,36)
Precentral Gyrus	9;6;4;44	4.8/9.7	13.6(−45,19,36)/16.5(38,22,36)
Sub-Gyral	8;32;9;6;4;40	1.4/1.6	11.7(−14,23,44)/12.2(17,26,44)
Paracentral Lobule	31;6	1.0/0.5	11.4(0,−11,42)/8.8(3,−11,46)
Inferior Frontal Gyrus	9;45;44;47;46;6;13	6.8/11.5	10.1(−52,12,33)/11.3(49,18,24)
Superior Temporal Gyrus	38;22;39	0.0/1.1	5.5(−49,20,−12)/7.8(52,17,−8)
Caudate		2.7/1.9	7.6(−14,−3,17)/7.4(14,4,12)
Inferior Parietal Lobule	40;39;7	0.0/4.2	NS/7.4(45,−52,40)
Thalamus		1.2/1.2	7.0(−14,−3,13)/6.8(10,−3,13)
Postcentral Gyrus	3;4	0.0/1.0	NS/6.6(21,−28,55)
Supramarginal Gyrus	40	0.0/0.5	NS/6.5(52,−49,36)
Lentiform Nucleus		0.3/0.2	6.5(−14,4,8)/5.7(14,0,8)
Insula	47;13	0.0/0.3	6.5(−14,4,8)/5.7(14,0,8)
Component G: Temporal
Insula	13;47;29;40;22;45	7.2/8.4	28.2(−42,10,−4)/20.1(45,0,0)
Inferior Frontal Gyrus	47;45;13;44;10;46;9	11.1/8.3	26.7(−42,13,−4)/16.8(42,13,−4)
Superior Temporal Gyrus	22;38;42;41;13;29;21	19.7/17.3	26.0(−49,10,−8)/22.6(52,0,0)
Extra-Nuclear	13;47	0.6/0.7	23.9(−42,10,−8)/16.7(42,6,−8)
Claustrum		3.4/4.7	20.8(−35,10,−1)/18.7(38,−7,−3)
Transverse Temporal Gyrus	42;41	1.4/1.7	20.0(−59,−17,9)/18.7(59,−17,9)
Postcentral Gyrus	40;43;2;1;3	4.2/3.9	19.9(−62,−23,18)/18.3(62,−23,14)
Precentral Gyrus	6;44;13;43	3.9/4.5	17.8(−49,−10,9)/19.4(55,4,8)
Sub-Gyral	13;21;38	1.0/0.9	19.1(−42,3,−8)/15.9(42,0,−8)
Middle Temporal Gyrus	21;22;38;39	3.0/1.1	17.9(−59,0,−4)/15.2(59,−4,−4)
Inferior Parietal Lobule	40	2.2/2.6	17.3(−62,−23,22)/14.2(55,−33,22)
Lentiform Nucleus		2.3/1.8	12.6(−31,3,0)/11.4(31,−10,−3)
Cingulate Gyrus	32;24	2.1/0.6	10.9(0,9,41)/9.7(3,9,41)
Middle Frontal Gyrus	47;11;46	0.5/0.3	10.7(−49,37,−2)/9.2(45,34,−5)
Subcallosal Gyrus	34	0.0/0.2	NS/9.9(24,3,−11)
Anterior Cingulate	32;24;42	1.8/0.6	9.6(−3,32,19)/8.6(0,38,2)
Medial Frontal Gyrus	32;6	0.3/0.1	9.5(0,6,45)/8.2(3,6,45)
Thalamus		0.4/0.3	9.4(−7,−13,5)/9.1(3,−13,5)
Parahippocampal Gyrus		0.0/0.4	8.9(−31,−1,−11)/9.1(31,−4,−11)
Caudate		0.1/0.1	8.4(−10,4,4)/8.8(35,−17,−7)
Superior Frontal Gyrus	6	0.2/0.0	8.5(−3,6,49)/NS

Correlation and lag computation for Patients and Controls

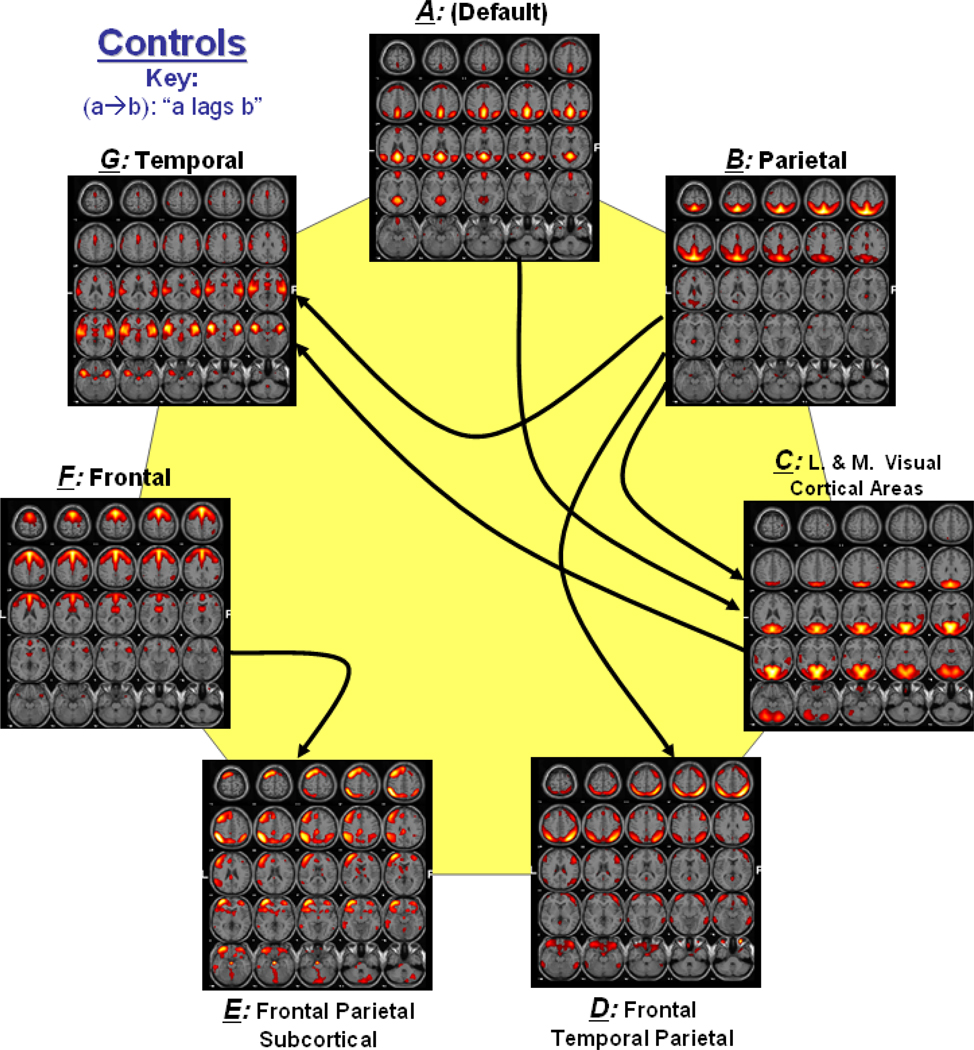
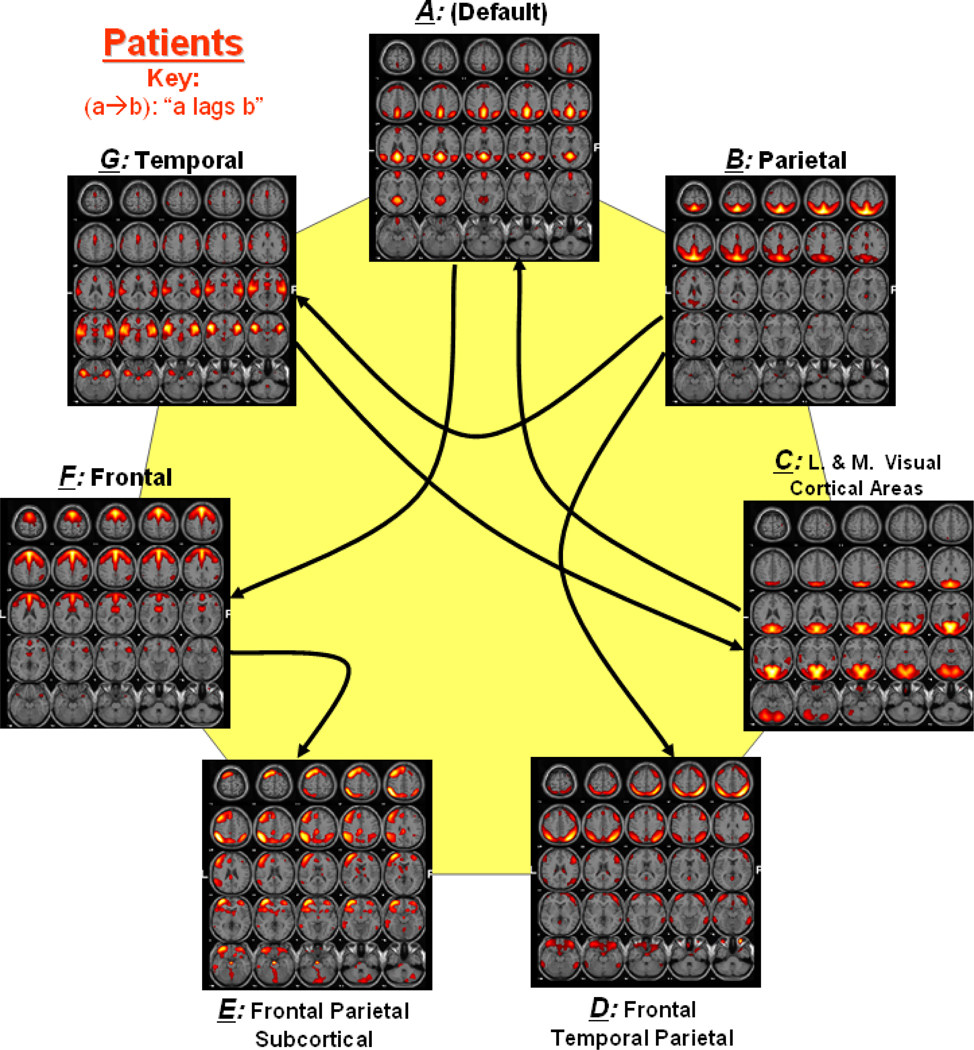
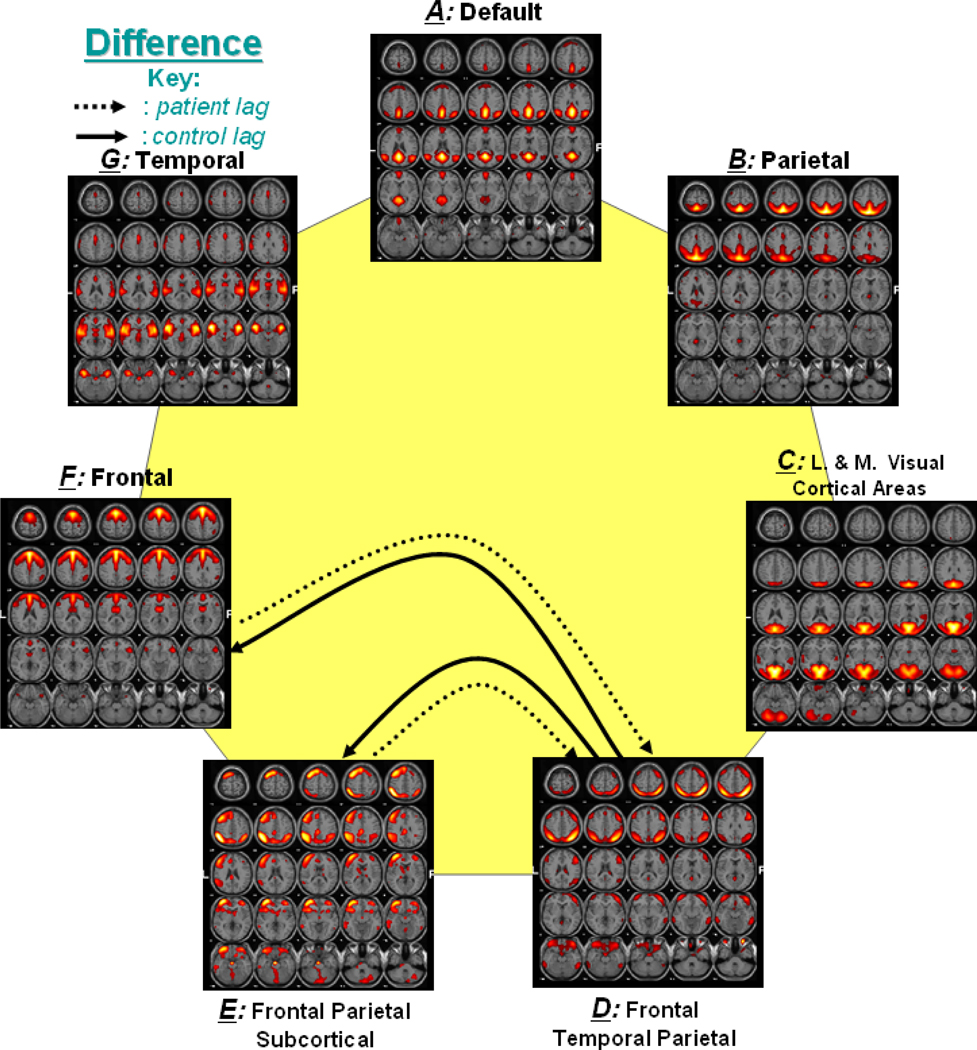
Figure 2 shows a functional network connectivity (FNC) diagram for controls in which significantly correlated components are represented by an arrow. Figure 3 shows a similar connectivity diagram for patients. The direction of each arrow represents the lag between the two connected components. For example, in Figure 2, an arrow connects components B and D, representing that component B lags component D by certain time units. Both controls and patients show significant connectivity between components B and D, components E and F as well as between components B and G. Connectivity of components A and F is only found in patients, while the connectivity of components B and C is only found in controls. The direction of lag differs between patients and controls for components A and C as well as C and G. It is also noticed that controls show an additional connection with component B, while patients show an additional connection with component A.

Figure 2. Functional Network Connectivity in Controls.

Solid lines show the significant correlation connections in controls. The arrow represents the direction of the delay between two components. For example (a → b) represents that component a lags component b by some calculated seconds among all controls.

Figure 3. Functional Network Connectivity in Patients.

Dotted lines show the significant correlation connections in patients from the 21 possible correlation combinations. The arrow represents the direction of the delay between two components. For example (a → b) represents that component a lags component b by some calculated seconds among all patients.

Correlation and lag computation for group difference

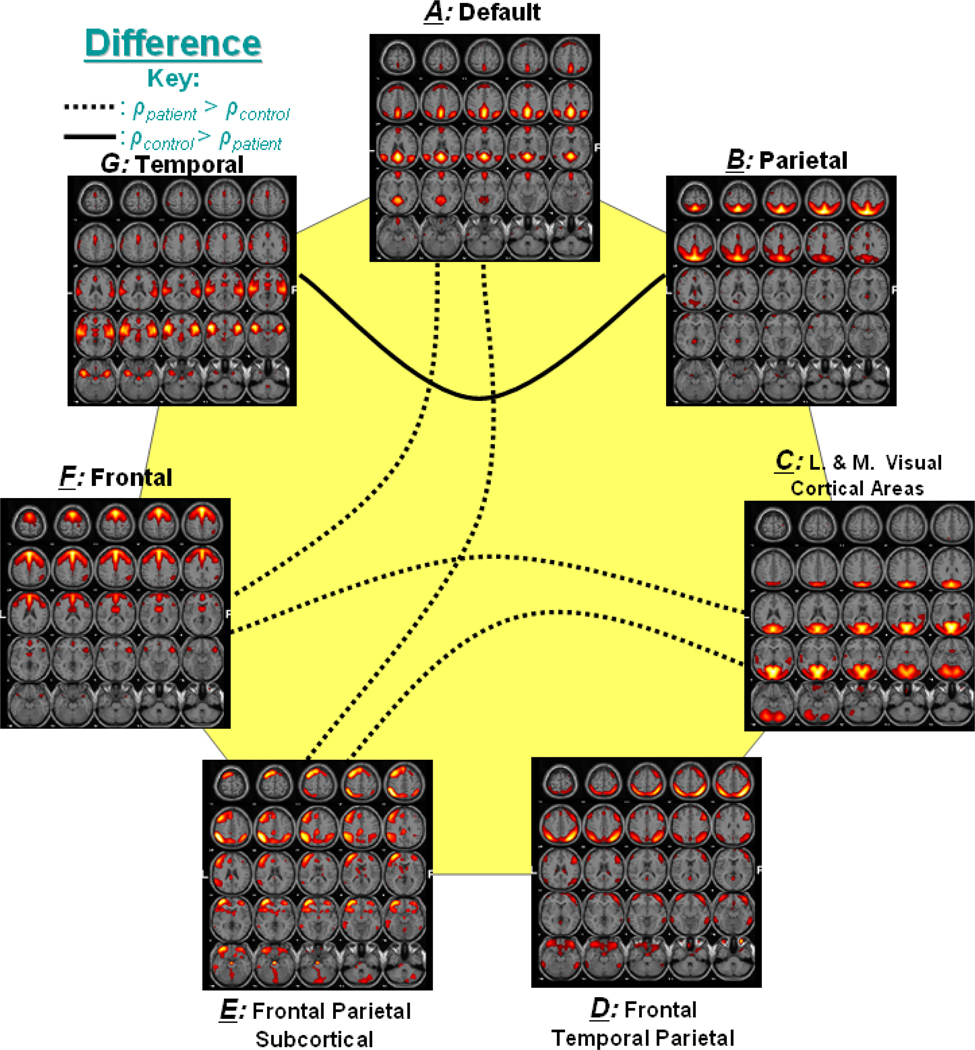
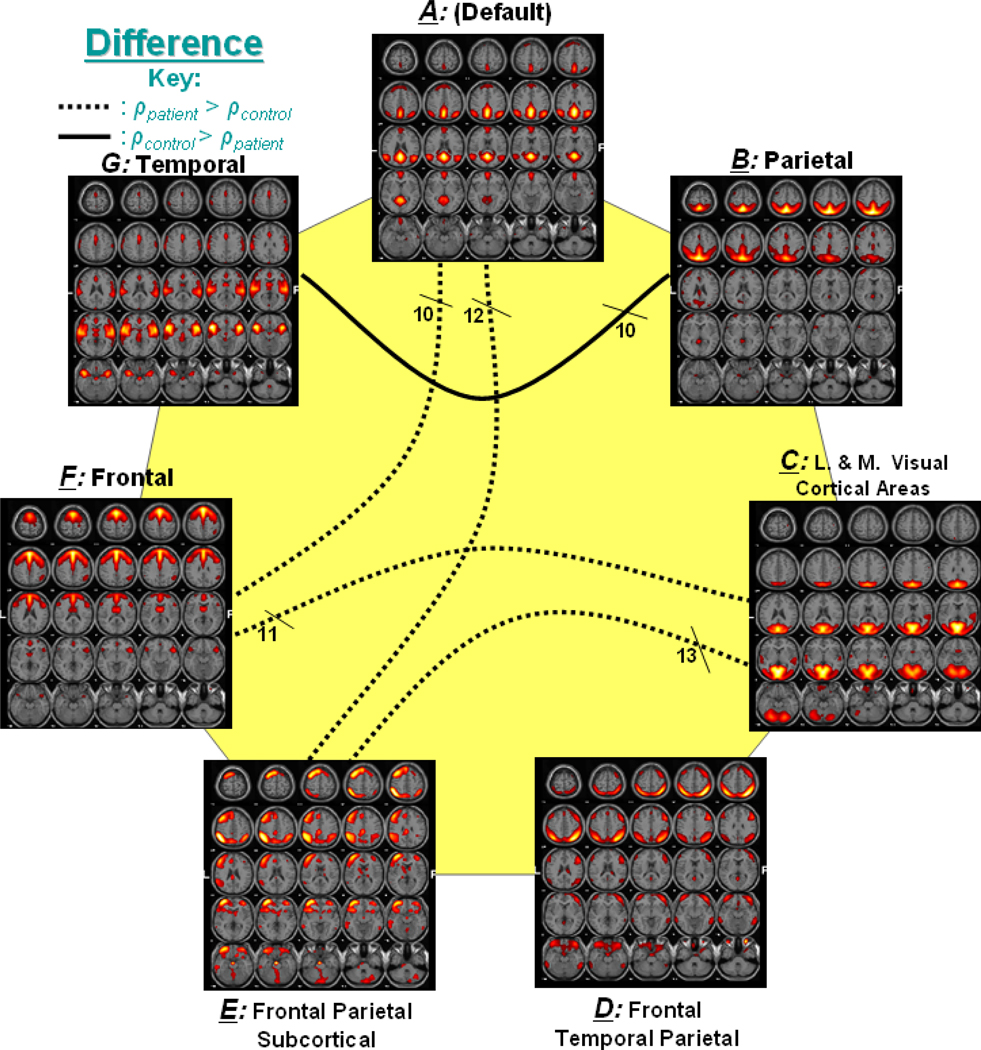
Figure 4 represents the significant correlation found among group differences. In the figure, a dotted line represents connectivity in which patients had higher mean correlation than controls, while a solid line represents connectivity with higher correlation for controls. For example, components A and F, which show significant correlation difference, are connected with a dotted line to indicate that patients had greater mean correlation values than controls for this connection.

Figure 4. Significant Correlation between Group Differences.

Out of 21 possible correlation combinations between 7 components, only 5 combinations passed the two sample t-test (p < 0.01). The solid line represents the significant connectivity where controls have higher mean correlation than patients, while dotted line represents connectivity where patients have higher mean correlation. Presence of dotted lines rejects the hypothesis that controls should have more correlation between two components than patients.

Figure 5 shows the significant lag among components for group differences. In the figure, dotted and solid lines are used to represent significant lag networks in patients and controls, respectively. The arrow in the lines represents the lag between the connecting components. For example, a dotted line between component D and F shows that in patients, component F becomes activated after the activation of component D.

Figure 5. Significant Lag between Group Differences.

Two sample t-test was also performed for significant lag among the 21 possible networks (p < 0.01). 2 functional networks show significant lag difference between patients and controls. Dotted lines show the direction of lag for patients, while solid lines shows the same for controls.

Connectivity Validation

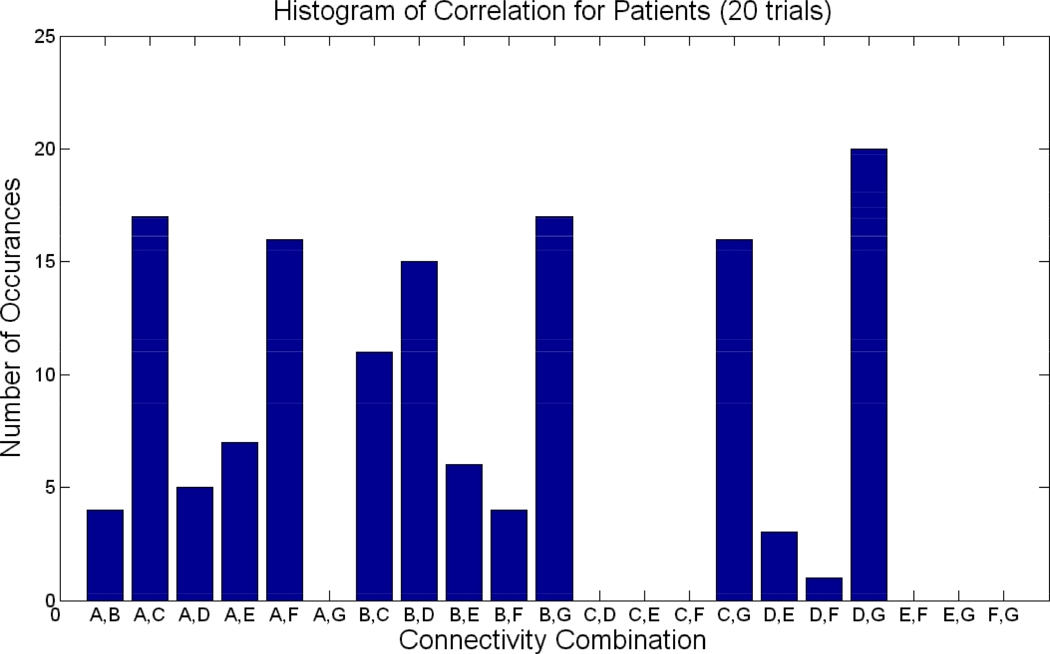
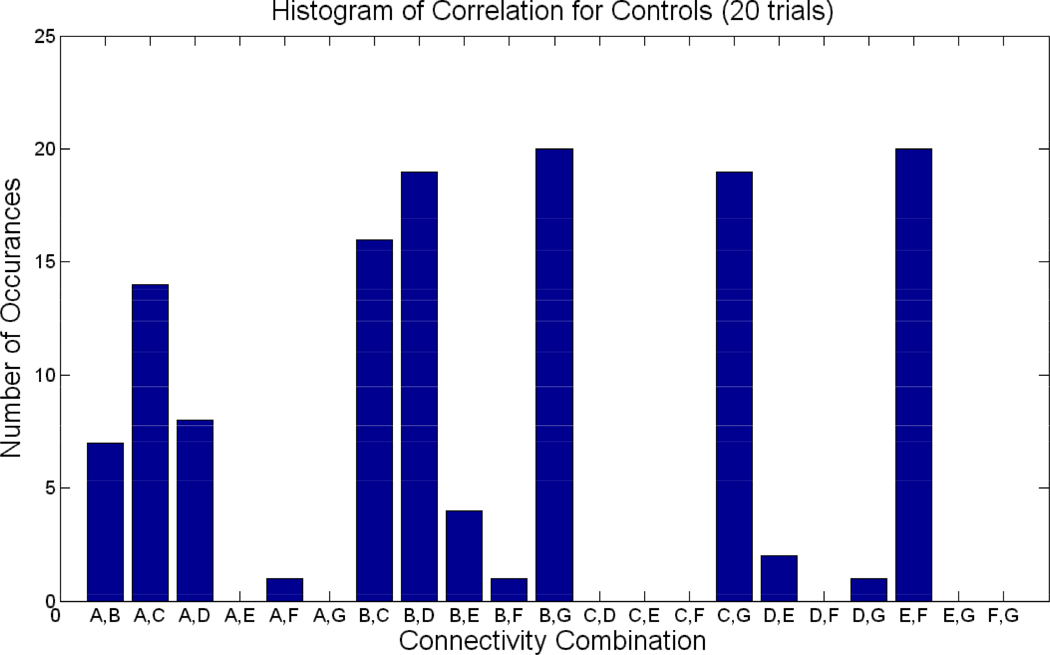
Twenty trials of the experiment were performed in which ten control and ten patients were randomly drawn a subjected to a t-test analysis. Figure 6 shows the number of times each of the 21 combination was selected as significant in the 20 trials for patients (p<0.05). Figure 7 shows the histogram of significant correlations for controls. For example, the connection between B and G was significant at many instances in both controls and patients. FNC with default mode (A) and various other components (D, E, and F) were mostly significant in patients, but not so much in controls. Overall, patients show more variance in the FNC combinations selected at each of the 20 trials than controls. For example, controls show 12 combinations to have occurred once or never; while in patients, many fewer combinations occurred once or less than 1 time (8).Similarly, in controls, four combinations occurred 19 or more (20) times, while inpatients, only 1 combination occurred at least 19, or greater, times.

Figure 6. Connectivity for Patients over 20 trials.

Histogram of significant connectivity found in patients over 20 trials. X-axis represents the 21 possible combinations for correlations, while the y –axis represents the number of times a particular combination appeared to be significant in the 20 trials.

Figure 7. Connectivity for Controls over 20 trials.

Histogram of significant connectivity found in controls over 20 trials. X-axis represents the 21 possible combinations for correlations, while the y –axis represents the number of times a particular combination appeared to be significant in the 20 trials.

Furthermore, the group difference analysis was also validated. Figure 8 shows the number of times the 5 connections in Figure 4 were selected as significant during the 20 trials. The numbers of times the connections occurred varied from 10 to 13. The validation confirmed (with 100% accuracy) that patients indeed showed greater correlation in 4 of the 5 connections, while controls showed greater correlation in connections B and G. The repetition of significant lag analysis in Figure 5 revealed consistent results in that components D–E and D–F appeared significant (p<0.01) 13 and 14 times, respectively, in the 20 trials. In the occurrences, component D lagged E in controls 92%, while component E lagged D in patients 85% of the time. Similarly, component D lagged F in controls 100%, while component F lagged D in patients 79% of the time.

Figure 8. Group Difference Correlation over 20 trials.

The number of times the 5 connections in Figure 4 were selected as significant during the 20 trials. The solid line represents the significant connectivity where controls have higher mean correlation than patients, while dotted line represents connectivity where patients have higher mean correlation.

Significance levels of group difference analysis were also calculated from the resampling approach. Table 2 shows resulting significant mean correlation difference between controls and patients. The columns report results from boot strapping technique in which 13 controls and patients are randomly shuffled from one group to the other and the means and standard deviations of the correlation differences are again computed. Finally, a one-sample t-test was performed to compare whether the mean difference correlation of shuffled groups was significantly different than the mean difference correlation of actual groups (p>0.01). Out of 21 combinations, the top 5 significantly different combinations (p<3.5E-08, uncorrected) are the same as the 5 significantly different combinations in Figure 4; in support of our finding that the patient and control group indeed has significantly different correlations for the 5 combinations selected.

Table 2. Correlation Validation Using Resampling Technique.

Mean correlation difference between controls and patients is reported. Then a boot strapping technique is used in which 13 controls and patients are randomly shuffled from one group to the other and the means and standard deviations of the correlation differences are again computed. Lilliefors test was then performed to ensure that mean correlation of shuffled group followed a normal distribution. Finally, a one-sample t-test was performed to compare whether the mean difference correlation of shuffled groups was significantly different than the mean difference correlation of actual groups (p>0.01).

Component Combination	Mean (all controls - patients)	Standard Deviation (all controls- patients)	Mean (mixed controls- patients) 20 runs	Standard Deviation (Mixed controls- patients) 20 runs	Lilliefors test (checks for normal distribution in 20 runs) [0 = accept Ho]	t-test (compares means from 20 runs to single actual mean (column 2) [0 = accept Ho]	p_values from t-test (uncorrected)
a,e	−0.17912	0.06073	0.01217	0.03923	0	1	4.71E-11
a,f	−0.15501	0.00122	0.00425	0.04400	0	1	1.60E-10
b,g	0.16687	0.11875	−0.00257	0.03804	0	1	4.40E-09
c,e	−0.13941	0.03925	0.00919	0.02929	0	1	1.77E-09
c,f	−0.10562	0.03844	−0.00765	0.01821	0	1	3.41E-08

DISCUSSION

ICA was successfully used to identify resting-state components in healthy controls and patients with schizophrenia and to identify differences in functional network connectivity among these components. We were able to identify several inter-connected networks present during resting and then examine temporal dependencies between them by computing the maximal lagged temporal correlation between the ICA time courses.

The identified resting state networks are included in Figure 1 (a–g). Figure 1a represents the "default-mode" network, which reflects an ensemble of cortical regions typically deactivated during demanding cognitive tasks in fMRI studies (Raichle, et al. 2001). Using functional connectivity, this network can be conceptualized and studied as a "stand-alone" function or system. Major regions in component A include the precuneus, anterior cingulate and posterior cingulate gyri. Additional regions include the superior and middle temporal and frontal gyri, the inferior parietal lobule and parahippocampal gyrus. Briefly, these regions are thought to be related to subject’s recognition, social communication, working memory and some auditory demands. The fluctuations in this network have been cited in numerous studies to increase during resting state and suspend during specific goal-directed behaviors (Garrity, et al. 2007; Raichle, et al. 2001).

Component B (in Figure 1b), in general, represents resting state hemodynamic activity fluctuations in the parietal regions. Along with the parietal lobule, significant regions include postcentral, anterior and posterior cingulate gyri, along with precuneus and middle frontal cortex. In general, the parietal lobule is used during visuo-spatial interaction. Regions present in component C include major visual cortical areas, such as the occipital gyrus along with activations in other areas such as lingual and fusiform gyri, cuneus and precuneus. Component D includes regions in frontal, temporal and parietal gyri, while component E shows covarying regions not only in frontal and temporal gyri, but also in subcortical regions, which include thalamus, caudate, and other basal ganglia regions. The function of the basal ganglia can be described as a brain relay station where commands, such as “stop reading”, get forwarded to the appropriate brain regions for processing. The dominant regions in component D are related to visual perceptual abnormalities reported in schizophrenia (Levy, et al. 2000).

The medial frontal gyrus dominates component F. Other covarying regions in component F include anterior cingulate and precentral gyrus as well as superior frontal gyrus. In general, these regions control the brain’s executive functions and have been cited to show abnormalities in schizophrenia brains (Chan, et al. 2006). Regions in component G include superior temporal and inferior frontal gyrus, responsible for auditory processing and language comprehension, along with insula which is the affective sensory region. Several studies cite frontal and temporal gyrus as partially responsible for auditory hallucinations found in schizophrenia (Gaser, et al. 2004).

Apart from just identifying neural networks present during ‘resting state’, the primary purpose of this paper was to examine functional network connectivity (FNC), or the temporal relationships among the identified components. Connectivity of the ‘default mode’ component (A) with other components was present more consistently in patients than controls. Although we did not explicitly examine connectivity strength in relation to measurements of active psychosis, it is reasonable to speculate that the increased default mode FNC in patients may be the results of distraction due to hallucinatory experiences and/or delusional preoccupations. Increased FNC of the default mode with other components in patients also could indicate greater dependency of brain regions in the default mode network on the function of other neural circuits (or vice versa) during resting state. We also observed directional differences in lag among components (i.e. C→A in patients, while A→C in controls).

There were other group differences in the relationship among component time courses. Although controls showed greater correlations than patients in one functional network (B–G), more networks existed in which patient correlations were significantly higher than controls. This trend of higher correlation in patients (i.e. ρ_controls < ρ_patients) might be related to the attentional deficits in schizophrenia (Jorm, et al. 2005). Controls, on the other hand, may have a better ability to persist in a single mental state with patients more variable. This is also consistent with our recent findings showing more rapid fluctuations in the default mode network in patients verses controls (Garrity, et al. 2007). This idea is indirectly supported by the significant connection B→C in only controls because the brain regions in component B have been linked to focused attention and decision making (Paulus, et al. 2002). In addition, reduced fluctuations in frontal and parietal regions have been attributed as a possible concomitant of deficit symptoms in schizophrenia (Pearlson 2000). In contrast, brain regions identified in component C assist in visual image processing and recognition (Kim, et al. 2005). In particular, fusiform gyrus and other object/face recognition areas are abnormal in schizophrenia (Dickey, etal. 2003). Therefore, the absence of functional connection between B and C may hint higher order control deficits over sensory association process in patients that appears intact in healthy controls, however this would need to be directly tested in a future study.

Furthermore, the B–G connectivity shows higher correlation in controls than patients, which agrees with previous studies since these components are related to mental timekeeping and self-ordered behavior, commonly disturbed in schizophrenia (Ganzevles and Haenen 1995). Two of the 4 connections among components in which patients show higher correlation than controls relate to component E. This is also consistent with previous studies finding abnormal function of basal ganglia regions in schizophrenia minds show dysfunction and decreased activations in the basal ganglia (Gaser, et al.2004; Menon, et al. 2001). The increased connectivity of these networks with that depicted in component E may suggest a need for dependency on other components to make up for the lack of function in component E’s regions.

The validation of our results through analysis of subsets of data lends additional support to our various conclusions. The large-scale (54 subjects) and small-scale (15 subjects/trial for 20 trials) analysis of functional connectivity in controls showed very consistent results. The five connectivity networks found in the large-scale analysis of correlation group difference (A and E, A and F, B and G, C and E, C and F) also manifested significantly in the small-scale analysis of multiple trials; however, the smaller-scale model of the study showed patients connectivity to be more scattered, with more connections occurring between 3 and 18 times, than never or always occurring (0–2 or 19–20 times), while control connectivity was more consistent, with most occurrences either less than 2 times, or greater than 19 times. We had anticipated this greater variance in patterns in schizophrenic subjects on account of the previously reported differences in patterns of brain activity in patients with different symptom profiles (Liddle 1992). Regardless of the few differences in the large-scale and small-scale analysis of correlation, the consistent similarities suggest this technique may identify important differences between patients and controls, which may also be useful for classification (although further work is needed to test this). Furthermore, the repeatability of results between two diagnostic groups also implies robustness of results, regardless of gender, age or education. Further validation of our results using the resampling technique confirmed that the mean correlation differences between patients and controls were indeed significantly different.

Group difference results for lag calculations (Figure 5) were not analyzed in detail because the lag difference is only meaningful if the correlations between the processes are also significant (i.e. if the shape of the two time courses is similar). Since the combinations with significant lag do not also have significant correlations for either controls or patients (i.e. connections D–E and D–F are not present in Figure 2 or Figure 3), the lags differences are not reported.

In summary, we describe a general method for studying network connectivity, which is demonstrated in a study of patients with schizophrenia and healthy controls. In agreement with our hypotheses, patients showed slightly greater number of significant correlation connectivity as controls in 54 subject analysis, as well as in individual runs for the 20 trial validation $(\mathrm{i}.\mathrm{e}.\mathit{\text{length}}({\overline{\rho }}_{\text{max}}^{\mathit{\text{patients}}})>\mathit{\text{length}}({\overline{\rho }}_{\text{max}}^{\mathit{\text{controls}}})).$ Furthermore, patients had higher correlation values than controls in most of the significant functional networks. We also found increased functional network connectivity in patients versus controls with respect to the default mode which has been described as involved in “internal” versus “external” focus (Raichle, et al. 2001). The increased connectivity of other networks to the default mode network may be related to hallucinations, although future work is needed to confirm this speculation.

An advantage of our approach to study the dependencies between functional networks was that it allowed us to examine weak, but significant, connectivity among strongly connected networks. We plan to explore the covariation between the symptom expression and the outcome measures within the schizophrenia group in future work. Although we used a correlational approach in this paper, one could also use other dependency measures, such as mutual information or Granger causality, to study the differences in FNC in healthy controls versus patients with schizophrenia. Furthermore, structural equation modeling techniques will be considered in future work to study multiple dependencies among networks. We also hope to apply this method to ICA results from EEG data and incorporate the newly derived FNC diagrams with the ones found through fMRI analysis (Calhoun, et al. 2006b; Liu and Calhoun 2007). Covariations between ICA components has previously been studied using EEG in the context of a visual task, although in this case short-term covariation was studied (Makeig, et al. 2004). In summary, we propose a general method for studying functional network connectivity (weak, but significant temporal dependencies between temporally coherent networks) and demonstrate it in a study of patients with schizophrenia and healthy controls. Our approach revealed several novel findings, and may help improve our understanding of schizophrenia as well as other mental disorders.