Bias-Corrected Diagonal Discriminant Rules for High-Dimensional Classification

Summary

Diagonal discriminant rules have been successfully used for high-dimensional classification problems, but suffer from the serious drawback of biased discriminant scores. In this paper, we propose improved diagonal discriminant rules with bias-corrected discriminant scores for high-dimensional classification. We show that the proposed discriminant scores dominate the standard ones under the quadratic loss function. Analytical results on why the bias-corrected rules can potentially improve the predication accuracy are also provided. Finally, we demonstrate the improvement of the proposed rules over the original ones through extensive simulation studies and real case studies.

1. Introduction

Class prediction using high-dimensional data such as microarrays has been recognized as an important problem since the seminal work of Golub et al. (1999). A variety of methods have been developed and compared, including Discriminant Analysis and its extensions (Dudoit et al., 2002; Ghosh, 2003; Zhu and Hastie, 2004; Huang and Zheng, 2006; Wu, 2006; Shen et al., 2006; Guo et al., 2007; Pang et al., 2009), Random Forests (Breiman, 2001; Statnikov et al., 2008), Support Vector Machines (Furey et al., 2000; Lee et al., 2004; Vapnik and Kotz, 2006), Dimension Reduction Methods (Antoniadis et al., 2003; Dai et al., 2006) and Nearest Shrunken Centroids Methods (Tibshirani et al., 2002, 2003; Wang and Zhu, 2007; Dabney and Storey, 2007). Also see review papers with extensive comparison studies by Dudoit et al. (2002), Lee et al. (2005), and Statnikov et al. (2008).

In high-dimensional microarray data classification, it is common that the number of training samples, n, is much smaller than the number of features examined, p. This “large p small n” paradigm has posed numerous statistical challenges to most classical classification methods, such as the well-known linear discriminant analysis (LDA) and the quadratic discriminant analysis (QDA), because the sample covariance matrices are singular. This greatly limits the usage of both methods in high-dimensional data classification. To overcome the singularity problem, various approaches that rely on a diagonal approximation to the covariance matrices have been proposed. This leads to the so-called diagonal discriminant rules, which have been widely used for high-dimensional data (Dudoit et al., 2002; Speed, 2003; Tibshirani et al., 2003; Dettling, 2004; Ye et al., 2004; Dabney, 2005; Lee et al., 2005; Pique-Regi et al., 2005; Asyali et al., 2006; Noushath et al., 2006; Shieh et al., 2006; Wang and Zhu, 2007; Natowicz et al., 2008; Pang et al., 2009). In practice, the most commonly used diagonal discriminant rules for high-dimensional data are the diagonal LDA (DLDA) and the diagonal QDA (DQDA) rules introduced by Dudoit et al. (2002). Due to the relatively small n, the diagonal discriminant rules, which ignore the correlation among features, performed remarkably well compared with the more sophisticated methods in terms of both accuracy and stability (Dudoit et al., 2002; Dettling, 2004; Lee et al., 2005; Pang et al., 2009). In addition, DLDA and DQDA are easy to implement and not very sensitive to the number of predictor variables (Dudoit et al., 2002). Bickel and Levina (2004) conducted a theoretical study of this phenomenon and proved that diagonal discriminant rules can indeed outperform Fisher’s LDA when p > n.

The diagonal discriminant rules have been shown to perform well for high-dimensional data with small sample sizes, but suffer from the serious drawback of biased discriminant scores. In this paper we propose to correct the biases in the discriminant scores of diagonal discriminant analysis. Before we proceed, it is worth pointing out that the idea of bias correction in discriminant analysis is not entirely new (Ghurye and Own, 1969; Moran and Murphy, 1979; McLachlan, 1992). For instance, Moran and Murphy (1979) proposed several bias correction methods for the plug-in discriminant scores under the condition that the sample size for each class, n_k, is larger than p. However, the improvement of their bias-corrected rules is not significant (James, 1985; McLachlan, 1992), mainly because the dominant term of the bias, p/n_k, is not large. This has, at least partially, discouraged the popularity of the previously proposed bias-corrected discriminant rules. For microarray data, however, the ratio p/n_k can be very large. As a consequence, the commonly used discriminant rules, e.g., DQDA and DLDA, may result in low prediction accuracy, especially when the design is fairly unbalanced.

The remainder of the paper is organized as follows. In Section 2, we introduce the notation and briefly review the diagonal discriminant rules. In Section 3, we derive the bias-corrected estimators of the discriminant scores and show that they dominate the original ones. In Section 4, we present some analytical results on why the bias-corrected rules can potentially increase the overall prediction accuracy. We then conduct extensive simulation studies to investigate the performance of the proposed methods in Section 5, and apply them to three real microarray data sets in Section 6. Finally, we conclude the paper in Section 7 with discussions and future directions.

2. Diagonal Discriminant Analysis

Suppose we have K distinct classes and samples from each class follow a p-dimensional multivariate normal distribution with mean vector μ_k and covariance matrix Σ_k, where k = 1, ···, K. Assume we observe n_k i.i.d. random samples from the kth class, that is,

$${\mathit{x}}_{k,1},\dots ,{\mathit{x}}_{k,n_k}\stackrel{i.i.d.}{\sim }\mathit{MVN}({\mathit{\mu }}_k,{\mathrm{\sum }}_k).$$

The total sample size is then $n={\sum }_{k=1}^K{n}_k$. The principal goal of discriminant analysis is to predict the class label for a new observation, y. Let π_k denote the prior probability of observing a sample from the kth class with ${\sum }_{k=1}^K{\pi }_k=1$. The QDA decision rule is to assign y to class $arg{min}_k{d}_k^Q(\mathit{y})$, where $d_k^Q(\mathit{y})$ is the discriminant score defined as in Friedman (1989), that is,

$$d_k^Q(\mathit{y})={(\mathit{y}-{\mathit{\mu }}_k)}^T{\mathrm{\sum }}_k^{-1}(\mathit{y}-{\mathit{\mu }}_k)+ln\mid {\mathrm{\sum }}_k\mid -2ln{\pi }_k.$$

Minimizing $d_k^Q(\mathit{y})$ over k is equivalent to maximizing the corresponding posterior probabilities.

In practice, the population parameters of the multivariate normal distributions are unknown and usually are estimated from the training data set, with μ_k by the sample means, ${\widehat{\mathit{\mu }}}_k=\frac{1}{n_k}{\sum }_{i=1}^{n_k}{\mathit{x}}_{k,i}$, and Σ_k by the sample covariance matrices, ${\widehat{\mathrm{\sum }}}_k=\frac{1}{n_k-1}{\sum }_{i=1}^{n_k}({\mathit{x}}_{k,i}-{\widehat{\mathit{\mu }}}_k){({\mathit{x}}_{k,i}-{\widehat{\mathit{\mu }}}_k)}^T$. In addition, the prior probability π_k is commonly estimated by n_k/n and treated as a constant in classification problems (Friedman, 1989; Guo et al., 2007). The above estimates of parameters lead to the following sample version of $d_k^Q(\mathit{y})$,

$${\widehat{d}}_k^Q(\mathit{y})={(\mathit{y}-{\widehat{\mathit{\mu }}}_k)}^T{\widehat{\mathrm{\sum }}}_k^{-1}(\mathit{y}-{\widehat{\mathit{\mu }}}_k)+ln\mid {\widehat{\mathrm{\sum }}}_k\mid -2ln{\pi }_k.$$ (1)

One important special case of QDA is to assume that the covariance matrices are all the same, i.e., Σ_k = Σ for all k. This leads to LDA, with the simplified discriminant score given by

$$d_k^L(\mathit{y})={(\mathit{y}-{\mathit{\mu }}_k)}^T{\mathrm{\sum }}^{-1}(\mathit{y}-{\mathit{\mu }}_k)-2ln{\pi }_k.$$

The corresponding sample version of $d_k^L(\mathit{y})$ is then

$${\widehat{d}}_k^L(\mathit{y})={(\mathit{y}-{\widehat{\mathit{\mu }}}_k)}^T{\widehat{\mathrm{\sum }}}^{-1}(\mathit{y}-{\widehat{\mathit{\mu }}}_k)-2ln{\pi }_k,$$ (2)

with the pooled sample covariance matrix estimate $\widehat{\mathrm{\sum }}=\frac{1}{n-K}{\sum }_{k=1}^K(n_k-1){\widehat{\mathrm{\sum }}}_k$.

QDA and LDA are expected to perform well if the multivariate normal assumption is satisfied and good “plug-in” estimates of the population parameters are available (Friedman, 1989). In general, LDA is more popular than QDA, largely due to its simplicity and robustness to the violations of the underlying distribution assumption and the common covariance matrices assumption (James, 1985). To make LDA work, we require that n ≥ p to ensure the non-singularity of Σ̂. Similarly for QDA, we require that n_k ≥ p for each class.

When p is greater than n, we may regularize the covariance matrix estimates with generalized matrix inverse or shrinkage to address the singularity problem. However, these estimators are usually unstable due to the limited number of observations (Guo et al., 2007). In 2002, Dudoit et al. proposed to use DQDA and DLDA for classifying tumors using microarray data. Specifically, they assumed the covariance matrices to be diagonal by replacing the off-diagonal elements of Σ̂_k or Σ̂ with zeros. For DQDA, we have ${\widehat{\mathrm{\sum }}}_k=\text{diag}({\widehat{\sigma }}_{k1}^2,\dots ,{\widehat{\sigma }}_{kp}^2)$, which simplifies Equation (1) to

$${\widehat{d}}_k^Q(\mathit{y})=\sum _{i=1}^p{(y_i-{\widehat{\mu }}_{ki})}^2/{\widehat{\sigma }}_{ki}^2+\sum _{i=1}^{p}ln{\widehat{\sigma }}_{ki}^2-2ln{\pi }_k.$$ (3)

For DLDA, we have $\widehat{\mathrm{\sum }}=\text{diag}({\widehat{\sigma }}_1^2,\dots ,{\widehat{\sigma }}_p^2)$, which simplifies Equation (2) to

$${\widehat{d}}_k^L(\mathit{y})=\sum _{i=1}^p{(y_i-{\widehat{\mu }}_{ki})}^2/{\widehat{\sigma }}_i^2-2ln{\pi }_k.$$ (4)

3. Bias-Corrected Diagonal Discriminant Analysis

In this section, we first show that ${\widehat{d}}_k^Q(\mathit{y})$ and ${\widehat{d}}_k^L(\mathit{y})$ are biased. We then propose several bias-corrected estimators for the discriminant scores and demonstrate their superiority over the original ones. Denote Equation (3) as

$${\widehat{d}}_k^Q(\mathit{y})={\widehat{L}}_{k1}+{\widehat{L}}_{k2}-2ln{\pi }_k,$$

where ${\widehat{L}}_{k1}={\sum }_{i=1}^p{(y_i-{\widehat{\mu }}_{ki})}^2/{\widehat{\sigma }}_{ki}^2$ and ${\widehat{L}}_{k2}={\sum }_{i=1}^{p}ln{\widehat{\sigma }}_{ki}^2$. Denote the true discriminant score as

$$d_k^Q(\mathit{y})=L_{k1}+L_{k2}-2ln{\pi }_k,$$

where $L_{k1}={\sum }_{i=1}^p{(y_i-{\mu }_{ki})}^2/{\sigma }_{ki}^2$ and $L_{k2}={\sum }_{i=1}^{p}ln{\sigma }_{ki}^2$. In Web Appendix A, we show that the following two estimators are unbiased for L_k1 and L_k2, respectively,

$$\begin{array}{l}{\stackrel{\sim }{L}}_{k1}=\frac{n_k-3}{n_k-1}{\widehat{L}}_{k1}-\frac{p}{n_k},\\ {\stackrel{\sim }{L}}_{k2}={\widehat{L}}_{k2}-p\{\mathrm{\Psi }(\frac{n_k-1}{2})-ln(\frac{n_k-1}{2})\},\end{array}$$

where Ψ(·) is the digamma function (Abramowitz and Stegun, 1972). Based on the above two unbiased estimators, we define

$${\stackrel{\sim }{d}}_k^Q(\mathit{y})={\stackrel{\sim }{L}}_{k1}+{\stackrel{\sim }{L}}_{k2}-2ln{\pi }_k,$$

which is a bias-corrected discriminant score of DQDA. We refer to the corresponding rule as the bias-corrected DQDA (BQDA).

For DLDA, we denote Equation (4) as ${\widehat{d}}_k^L(\mathit{y})={\widehat{L}}_k-2ln{\pi }_k$ and the corresponding true discriminant score as $d_k^L(\mathit{y})=L_k-2ln{\pi }_k$, where ${\widehat{L}}_k={\sum }_{i=1}^p{(y_i-{\widehat{\mu }}_{ki})}^2/{\widehat{\sigma }}_i^2$ and $L_k={\sum }_{i=1}^p{(y_i-{\mu }_{ki})}^2/{\sigma }_i^2$. Also in Web Appendix A, we show that the following estimator is unbiased for L_k,

$${\stackrel{\sim }{L}}_k=\frac{n-K-2}{n-K}{\widehat{L}}_k-\frac{p}{n_k},$$

which leads to the bias-corrected DLDA (BLDA) with

$${\stackrel{\sim }{d}}_k^L(\mathit{y})={\stackrel{\sim }{L}}_k-2ln{\pi }_k.$$

Further, in Appendix A we have that

Theorem 1

Under the quadratic loss function, we have

1. the discriminant score of BQDA, ${\stackrel{\sim }{d}}_k^Q$, dominates the discriminant score of DQDA, ${\widehat{d}}_k^Q$, when n_k > 5; and

2. the discriminant score of BLDA, ${\stackrel{\sim }{d}}_k^L$, dominates the discriminant score of DLDA, ${\widehat{d}}_k^L$, when n > K + 4.

The maximum likelihood estimators (MLE), ${\widehat{\sigma }}_{ki,ML}^2=\frac{n_k-1}{n_k}{\widehat{\sigma }}_{ki}^2$, are also common for estimating ${\sigma }_{ki}^2$ (Guo et al., 2007). By plugging ${\widehat{\sigma }}_{ki,ML}^2$ into Equation (3), we obtain the discriminant score of MLE-based DQDA (MQDA). In practice, there is usually no clear indication between ${\widehat{\sigma }}_{ki,ML}^2$ and ${\widehat{\sigma }}_{ki}^2$, as to which estimator performs better when n is small. It is worth pointing out that, when the bias correction technique is applied, DQDA and MQDA lead to the same discriminant score so that we do not need to distinguish the two methods any more. A similar result can be established for the MLE-based DLDA (MLDA).

4. Prediction Accuracy

In this section we compare the performance of the bias-corrected discriminant rules with that of the original ones. The prediction accuracy is a common measure for evaluating the performance of a discriminant rule. It is defined as the proportion of samples classified correctly in the test set and is usually used for a balanced experimental design (Dudoit et al., 2002). However, when the design is unbalanced, a classification method favoring the majority class may have a high prediction accuracy (Qiao and Liu, 2009). There are many evaluation criteria for unbalanced designs, e.g., G-mean, F-measure, recall, class-weighted accuracy, among others (Chen et al., 2004; Cohen et al., 2006; Qiao and Liu, 2009). All of the above performance metrics can be viewed as functions of the classification matrix formed by the probabilities Pr(True Class = i, Predicted Class=j). Each metrix has its own advantages and limitations (Chen et al., 2004; Cohen et al., 2006). In this study, we apply the class-weighted accuracy (CWA) criterion (Cohen et al., 2006), which is defined as

$$\mathit{CWA}=\sum _{k=1}^K{w}_k{a}_k,$$

where a_k are the per-class predication accuracies and w_k are non-negative weights with ${\sum }_{k=1}^K{w}_k=1$. For simplicity, we assume equal weights, i.e., w_k = 1/K, and set the prior probability π_k = 1/K as well. Note that CWA is equivalent to one of the criteria proposed by Qiao and Liu (2009), which they referred to as the “mean within group error with one-step fixed weights” criterion.

In what follows we establish some analytical results for the bias-corrected rules. For simplicity of exposition, we consider the binary classification (K = 2) with the following three assumptions:

1. the variances are known and equal (without loss of generality, we assume that ${\sigma }_{ki}^2=1$);

2. n₁ < n₂, i.e., the class 1 is the minority class and the class 2 is the majority class; and

3. the covariance matrix of the test data is diagonal.

Under the above assumptions, we have ${\widehat{d}}_k^L={\sum }_{i=1}^p{(y_i-{\widehat{\mu }}_{ki})}^2$ for DLDA, and ${\stackrel{\sim }{d}}_k^L={\widehat{d}}_k^L-p/n_k$ for BLDA. Denote $\widehat{D}={\widehat{d}}_1^L-{\widehat{d}}_2^L$. For DLDA, we assign y to the minority class if D̂ < 0; otherwise, we assign it to the majority class. For BLDA, the decision boundary is $U=p(\frac{1}{n_1}-\frac{1}{n_2})$ instead of a usual zero. It is easy to see that the expected change of prediction accuracy caused by the bias correction, Pr _D̂,k, is given as

$${Pr}_{\widehat{D},k}=Pr(0<\widehat{D}<U\mid \mathit{y}\in \text{class}\text{k}),k=1,2.$$

Note that for an unbalanced design, the prediction accuracy of the minority class always increases and that for the majority class always decreases because of the bias correction. The overall CWA change, Pr_Δ, is given as

$${Pr}_{\mathrm{\Delta }}={Pr}_{\widehat{D},1}-{Pr}_{\widehat{D},2},$$ (5)

where a positive Pr_Δ indicates an overall improvement on the classification performance.

By the Lindeberg condition of the central limit theorem (Lehmann, 1998), it can be shown that when p → ∞, D̂ converges in distribution to N (−δ + U, 4b₁δ + c) if y is from class 1, and D̂ converges in distribution to N (δ + U, 4b₂δ + c) if y is from class 2, where $\delta ={\sum }_{i=1}^p{({\mu }_{1i}-{\mu }_{2i})}^2$, b₁ = 1 + 1/n₂, b₂ = 1 + 1/n₁ and $c=2p\{(2n_1+1)/n_1^2+(2n_2+1)/n_2^2\}$. Note that δ is the squared Euclidean distance between two samples. Further, we have

Theorem 2

Under Assumptions (i) – (iii), the overall CWA change, Pr_Δ, is positive when 0 < δ/p ≤ 2 and p → ∞.

The proof of Theorem 2 is shown in Appendix B. Theorem 2 suggests that the bias correction improves the overall predication accuracy as p goes large and δ is bounded by 2p. It is also worth mentioning that the proposed decision boundary U is asymptotically optimal under certain situations. By the definition of Pr_Δ, it is easy to see that the optimal decision boundary, U_opt, can be achieved at the intersection of the two limiting normal distributions, N (−δ + U, 4b₁δ + c) and N (δ + U, 4b₂δ + c). When δ is not large and/or the sample sizes, n₁ and n₂, are at least moderately large, we have 4b₁δ + c ≈ 4b₂δ + c and thus U_opt ≈ U. In general, as 4b₁δ + c < 4b₂δ + c, U_opt is slightly larger than U when δ is close to zero, and vice versa when δ is large. Note that U_opt depends on the quantity of δ so it is unknown in practice. Simulation study (not shown) indicates that the discriminant rules based on U and an estimated Û_opt perform similarly when an accurate estimate of the unknown δ can be obtained. While if a less accurate estimate of δ is employed, the performance of Û_opt can be unsatisfactory. In addition, U_opt is obtained only in the asymptotic sense so it may not work well when p is small. For the above reasons, in what follows we will only focus on the decision boundary U but not Û_opt. Note that the cross-validation (CV) method can be used as an alternative to select the decision boundary. Simulation study (not shown) indicates that it performs similarly as U when the sample size of each class is large. While for a small n₁ or n₂, CV is unstable and consequently the performance of BLDA is not satisfactory, as indicated in Braga-Neto and Dougherty (2004), Fu et al. (2005) and Isaksson et al. (2008).

When p is small, the overall change of CWA is given as

$${Pr}_{\mathrm{\Delta }}={\int }_{-\infty }^{+\infty }{Pr}_{\widehat{D}\mid \mathit{y}}{f}_1(\mathit{y})d\mathit{y}-{\int }_{-\infty }^{+\infty }{Pr}_{\widehat{D}\mid \mathit{y}}{f}_2(\mathit{y})d\mathit{y},$$ (6)

where $f_t(\mathit{y})={\prod }_{i=1}^p\phi (y_i,{\mu }_{ti},{\sigma }_{ti}^2)$ is the joint density function, and Pr_D̂|y is the expected change of prediction accuracy given an observation y. One way to obtain Pr_Δ in Equation (6) is to use the numerical integration approach as shown in Appendix C.

5. Simulation Studies

In this section, we conduct extensive simulation studies to assess the performance of different discriminant rules under various settings. We explain in detail both simulation designs and results of the simple binary classification, as well as some more complicated scenarios such as the multiple classification.

5.1 Simulation Design

We draw n_k training samples, x_k,i, and m_k test samples, y_k,j, from a G-dimensional multivariate normal distribution, ${\mathit{x}}_{k,i},{\mathit{y}}_{k,j}\stackrel{i.i.d.}{\sim }\mathit{MVN}({\mathit{\mu }}_k,{\mathrm{\sum }}_k)$, where i = 1, …, n_k and j = 1, …, m_k. Usually G is large for microarray studies. For binary classification problem, we have K = 2. Note that we only choose p genes from all G genes for classification based on certain feature selection criteria.

We first evaluate CWA directly under different simulation settings with the assumptions stated in Section 4. We assume that all p genes are informative and the differences of the two group means are the same across all p genes. Note that if we increase p, the overall strength of the signal, $\delta ={\sum }_{i=1}^p{({\mu }_{1i}-{\mu }_{2i})}^2$, becomes stronger and eventually both the bias-corrected methods and the biased methods will classify samples with 100% accuracy. To visualize the comparison results for different p values, we fix δ as a constant. For large p, we compute the change of CWA directly from Equation (5); otherwise, CWA is approximated by integrating Equation (6) numerically. In both cases, we assume genes are independent from each other with variances equal to one. When the genes are dependent with unknown variances, we go through the regular classification procedure to estimate the prediction accuracy as outlined below.

Next we consider simulation settings that are closer to real data structures where genes are correlated to each other. We set the first g genes are informative, e.g., μ_1i = 0.5 and μ_2i = 0, i = 1, …, g, and the rest of (G − g) genes have μ_1i = μ_2i = 0, i = g + 1, …, G. Note that no feature selection procedure is involved here yet. We select the first p genes for classification. If p ≤ g, all p genes are informative. If p > g, all of the g informative genes and (p − g) non-informative genes are selected. Usually we let g ≪ G due to the fact that most of the genes are not differentially expressed in microarray experiments, e.g., G = 10, 000 and g = 50. Similarly as in Guo et al. (2007), we use block diagonal correlation structures to model the dependence among genes. Specifically, we partition the G genes into H equal sized blocks with H = G/g. We have

$${\mathrm{\sum }}_k=\left(\begin{array}{cccc}{\mathrm{\sum }}_{k,1}& 0& \cdots & 0\\ 0& {\mathrm{\sum }}_{k,2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\mathrm{\sum }}_{k,H}\end{array}\right),$$

where the hth block on the diagonal line is defined as

$${\mathrm{\sum }}_{k,h}=\left(\begin{array}{cccc}{\sigma }_{k,h,1,1}^2& {\sigma }_{k,h,1,2}^2& \cdots & {\sigma }_{k,h,1,g}^2\\ {\sigma }_{k,h,2,1}^2& {\sigma }_{k,h,2,2}^2& \cdots & {\sigma }_{k,h,2,g}^2\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{k,h,g,1}^2& {\sigma }_{k,h,g,2}^2& \cdots & {\sigma }_{k,h,g,g}^2\end{array}\right),$$

with ${\sigma }_{k,h,i,j}^2={\rho }^{\mid i-j\mid }{\sigma }_{k,h,i,i}{\sigma }_{k,h,j,j}$ and the pre-defined correlation coefficient ρ. We simulate the diagonal elements ${\sigma }_{k,h,i,i}^2$ from the uniform distribution, U(0.5, 1.5). To model the situation with equal covariance matrices between two classes, we set Σ = Σ₁ = Σ₂; otherwise, we use Σ₁ ≠ Σ₂.

The simulation design of multiple classification is similar to that of binary classification. For simplicity, we consider the following three-class case where the first g genes are informative with μ_1i = 0.5, μ_2i = 0, and μ_3i = −0.5, i = 1, …, g. We choose the two-fold cross-validation scheme to estimate CWA. Specifically for each simulation, we randomly take two-thirds of the samples from each class as the training set and the rest as the test set, i.e., n_k/(m_k +n_k)=2/3. The average CWA is computed by repeating this random division and testing procedure 100 times for each simulation and then averaging for 1,000 simulations.

5.2 Simulation Results

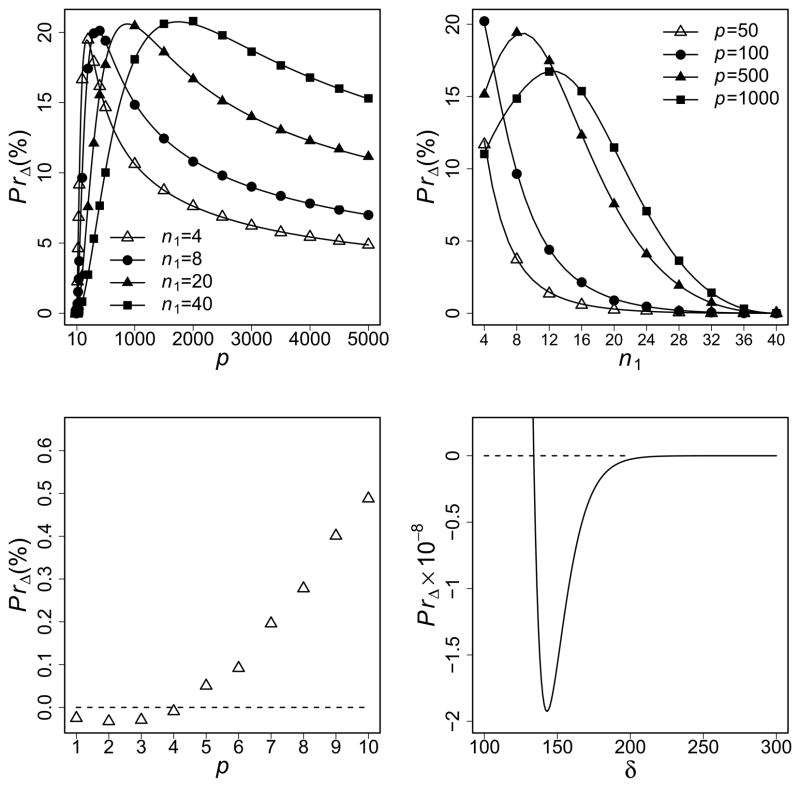
Results that assess the CWA change assuming constant variances are shown in Figure 1. The sum of squared mean vector difference is set as δ = 10 (except for the lower right panel of Figure 1). The positive Pr_Δ values, i.e., overall changes of CWA, indicate that the bias-corrected discriminant rules outperform the original ones (the top panels). The Pr_Δ values computed from Equation (5) are very close to those from Equation (6) even when p is as small as 10. In the upper left panel, we fix the degree of unbalance, n₂/n₁ = 5, and vary p. We observe that as p increases, Pr_Δ increases sharply first and then decreases slowly after reaching its maximum value. The tail becomes heavier when n₁ increases, that is, the improvement always keeps for large sample sizes. For example, with n₁ = 20 and n₂ = 100, we still have about 5% gain of CWA at p = 100 and the maximum 20.6% is reached at p = 874. In the upper right panel, n₂ is fixed at 40. When n₁ changes from 4 to 40, Pr_Δ decreases as n₁ increases for small p. For large p, Pr_Δ increases first then decreases as n₁ increases. For example, when p = 500, the maximum improvement of 19.4% can be obtained at n₁ = 10. The bottom panels show that we may have Pr_Δ < 0 under certain conditions. The lower left panel shows that Pr_Δ is negative when p < 5 and increases with p (n₁ = 4 and n₂ = 20). The lower right panel shows that Pr_Δ becomes negative when δ > 133.9 and reaches a minimum at δ = 142.9 (n₁ = 4, n₂ = 20, and p = 50).

Figure 1.

Pr_Δ as functions of different factors (p, n₁ and δ). The solid lines represent results using Equation (5). The symbols on the lines represent results using Equation (6). The dashed lines represent Pr_Δ = 0. We set n₂/n₁ = 5 except for the upper right panel and δ = 10 except for the lower right panel. Upper left: the results for different values of n₁ are shown. Upper right: the results for different values of p are shown (n₂ = 40). Lower left: use Equation (6) for small p (n₁ = 4). Lower right: use Equation (5) for large δ (n₁ = 4 and p = 50).

The bias-corrected discriminant scores do not always outperform the original ones (Section 4). Under certain conditions, we may have Pr_Δ < 0 (Figure 1, the bottom panels). This implies that either (i) a very small number of features is selected, or (ii) a strong signal exists in differentiating the two classes. In practice, a classifier with more than 50 features is often used for classification in microarray analysis (Dudoit et al., 2002; Lee et al., 2005; Golub et al., 1999). Simulation studies suggest Pr_Δ increases rapidly as p increases (Figure 1, the left panels). When the signal is strong, e.g., 2p = 100 < δ, both bias-corrected methods and the original methods work quite well. Simulation studies suggest that Pr_Δ ≈ 0 (Figure 1, the lower right panel).

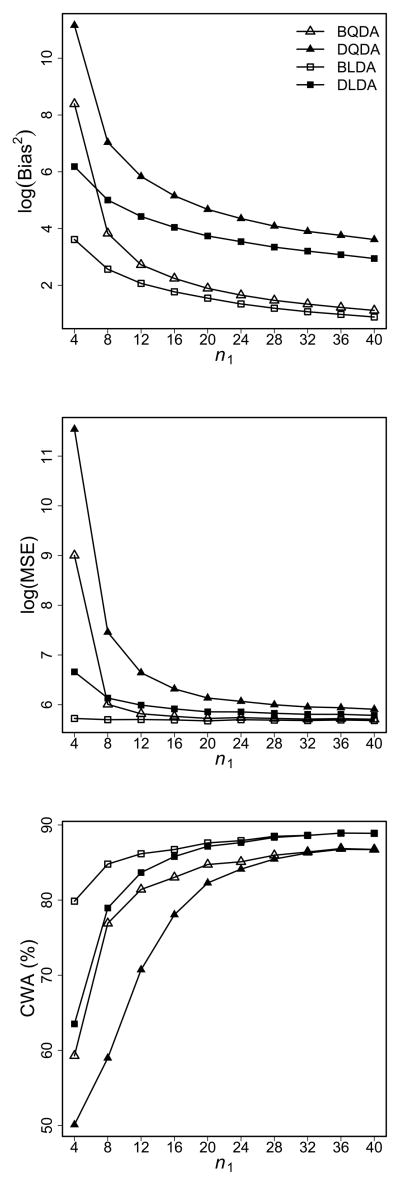
For the more general simulation settings, we set ρ = 0.3, H = 200, and G = 10, 000. We use the equal diagonal covariance matrix to generate samples for both classes. The left column of Figure 2 shows the simulation results for p = 100, n₂ = 40, and n₁ varying from 4 to 40. We examine the accuracy of the proposed bias-corrected discriminant scores in terms of the squared biases (Bias²) and the mean squared errors (MSE) in logarithmic scales for the top and middle panels. We observe that both BQDA and BLDA have smaller Bias² and MSE compared with their biased counterparts. When n₁ increases, the difference between unbiased and biased discriminant rules decreases. The bottom panel shows the corresponding results of CWA. Similar as those in Figure 1, the improved prediction accuracy of bias-corrected discriminant scores is consistent, with larger improvement happens at smaller sample sizes with higher degrees of unbalance, and becomes indistinguishable for the balanced data.

Figure 2.

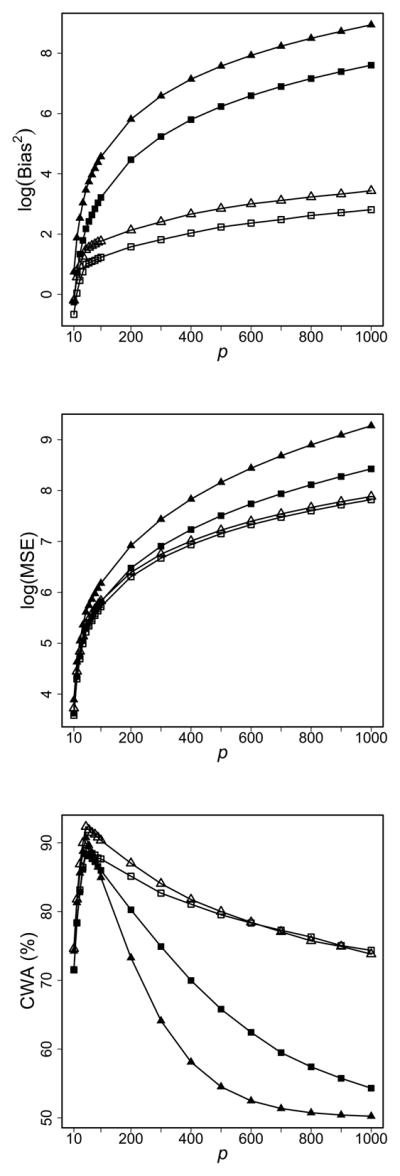
Comparison between bias-corrected discriminant rules and the original ones. Left column: n₂ = 40 and p = 100. Right column: n₁ = 20 and n₂ = 100. Top row: Bias² in logarithmic scale. Middle row: MSE in logarithmic scale. Bottom row: CWA.

The right column of Figure 2 displays the effect of p on the estimation and prediction accuracy (n₁ = 20 and n₂ = 100). It is clear that the bias-corrected discriminant scores provide more accurate and more stable estimates than the original ones consistently (the top and middle panels). The bottom panel shows that the bias-corrected scores have slight improvement when p is small, e.g., CWA increases about 1% for BQDA versus DQDA when p = 10. The improvement becomes more evident when p increases, e.g., CWA increases 6.9% for BQDA versus DQDA at p = 100. CWA of all methods peak around p = g. As more non-informative genes are included in the classifier, the class predication will tend to be random with a final CWA at 50%. However, we observe that even for such situations the bias-corrected discriminant rules still outperform the biased ones.

For multiple classification, we consider three sets of designs: 1) keep n₁ = n₃; 2) keep n₂ = n₃; 3) keep n₂/n₃ = 1/2. For all settings, we vary n₁ and n₂ the same way as in the binary classification settings. In the left columns of Web Figures 1–19, n₁ varies from 4 to 40 with n₂ = 40 and p = 100. In the right columns, p varies from 10 to 1000 with sample sizes fixed. We observe similar patterns as in binary classification simulation studies. For the results of using unequal covariance matrices and MLE-based discriminant rules (MLDA and MQDA), see Web Figures. As in Guo et al. (2007), we also conduct simulations with a feature selection procedure (Section 6) and incorporate different degrees of correlations, e.g., ρ = 0.5 or 0.7. The comparisons also have similar patterns as shown for binary classifications (see Web Figures). As the simulation results suggest, the improved performance of the bias-corrected discriminant rules over the original ones is evident for unbalanced classification analyses, especially when the degree of unbalance, e.g., the ratio n₂/n₁, is far from 1.

6. Case Studies

In this section, we apply the proposed bias-corrected methods to three real microarray data sets and compare them with several other popular classification methods, including the original diagonal discriminant analysis (DQDA, DLDA, MQDA and MLDA), support vector machines (SVM), and k-nearest neighbors (kNN). SVM is a supervised machine learning method that aims to find a separating hyperplane into the input space which maximizes the margin between classes (Boser et al., 1992). It is one commonly used classification method for high-dimensional data with small sample sizes. See for example in Ye et al. (2004), Lee et al. (2005) and Shieh et al. (2006). kNN is a simple algorithm that classifies a sample by the majority voting of its neighbors. This non-parametric classification method is widely used in discriminant analysis and works well in many studies (Dudoit et al., 2002; Lee et al., 2005). In this study we use the radial basis kernel for SVM and take the 3 nearest neighbors in Euclidean distance for kNN.

For the binary classification, we first analyze the B-cell lymphoma (BCL) data set in Shipp et al. (2002). The authors applied the weighted voting classification algorithm to differentiate diffuse large B-cell lymphoma (DLBCL) from follicular lymphoma (FL), a related germinal centers B-cell lymphoma. The gene expression data based on oligonucleotide microarray are available for 58 DLBCL and 19 FL pre-treatment biopsy samples with 6,817 genes. Although DLBCL and FL have different responses to cancer therapy, they share similar morphologic and clinical features over time. The authors showed that the two types of tumors may be distinguished by using their molecular markers. The second data set studied embryonal tumor of central nervous system (CNS), about which little is known biologically, but is believed to have heterogeneous pathogenesis (Pomeroy et al., 2002). The authors investigated the molecular heterogeneity of the most common brain tumor type, medulloblastomas, including primarily the desmoplastic subclass and the classic subclass. The desmoplastic subclass is often seen with a high frequency with Gorlin’s syndrome. They analyzed 9 desmoplastic samples and 25 classic samples with oligonucleotide microarrays of 6,817 genes. The results suggested that the Sonic Hedgehog (SHH) signaling pathway is involved in the pathogenesis of desmoplastic medulloblastoma. In the same study, the authors also investigated the problem of distinguishing multiple types of embryonal CNS tumors at gene expression level. In the original data set, there are 60 medulloblastomas, 10 malignant gliomas, 10 AT/RT (5 CNS, 5 renal-extrarenal), 6 supratentorial PNETs and 4 normal cerebellums. We exclude the class of normal samples in the study as BQDA requires a minimum of four training samples and one test sample for each class.

All data sets with raw intensity values can be downloaded from the Broad institute website (http://www.broad.mit.edu) and are pre-processed with the standard microarray data preprocessing R package from Bioconductor (http://www.bioconductor.org). We normalize all of the data sets with Robust Multichip Average (RMA) as described in Irizarry et al. (2003). The array control probe sets are removed from analysis after normalization. As in Dudoit et al. (2002), we perform a simple gene selection procedure using the ratios of the between-groups sum of squares (BSS) to the within-groups sum of squares (WSS) for the training set. Specifically, for the jth gene, the ratio is

$$\frac{\mathit{BSS}(j)}{\mathit{WSS}(j)}=\frac{{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{({\overline{x}}_{k.j}-{\overline{x}}_{\mathrm{..}j})}^2}{{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{(x_{\mathit{kij}}-{\overline{x}}_{\mathrm{..}j})}^2},$$

where x̄.._j is the averaged expression values across all samples and x̄_k.j is that across samples belonging to the kth class. We select the top p genes with the largest BSS/WSS ratios for classification. Similar to the simulation studies in Section 5, we randomly divide the samples of each class into the training set and the test set. The training sample size for the smallest class varies from 4 to n₁ + m₁ − 1 (we always set the first class be the smallest one), where n₁ + m₁ is the total sample size for the smallest class. For other classes, we hold the same number of samples, m₁, for testing, and use the rest for training. We repeat this procedure 1,000 times and report the average CWA for each method.

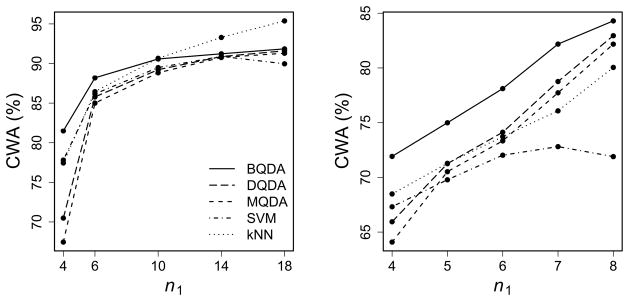
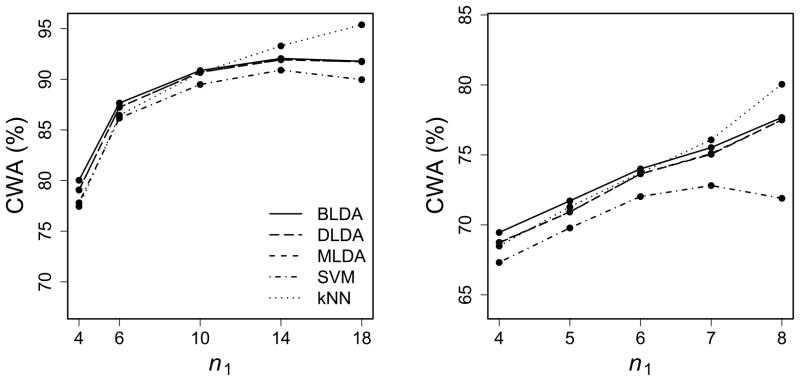
The results for the binary classification are summarized in Figure 3, where CWA is treated as a function of n₁ with p = 100.

Figure 3.

CWA (%) as a function of n₁ for the DLBCL (left) and CNS (right) data sets. The top two panels show the comparison of QDA-based methods; the bottom two panels show the comparison of LDA-based methods. All panels include SVM and kNN.

It is clear that the performance of the bias-corrected rules is consistenly better than that of the original ones. It is also interesting to see that the large improvement by the bias correction may result in the change of order of CWA. For example, in the top right panel, when n₁ = 4, BQDA performs the best, even when SVM and kNN have higher CWA than DQDA and MQDA. Similar patterns of CWA keep for different p values (results not shown). Although there is little difference between the MLE and the sample variance estimator when n_k is large, for data sets with small sample sizes, MQDA usually has lower prediction accuracy than DQDA (the top panels) while MLDA performs slightly better than DLDA (the bottom panels).

For the multi-class classification, we show the results with only one test sample but at a series number of selected features p in Table 1. We observe that the bias-corrected discriminant rules outperform the other methods for all p values, among which BQDA performs the best when p ≥ 100 and BLDA performs the best when p < 100 (Table 1 with the top ranked CWA highlighted).

Table 1.

CWA (%) for the multi-class CNS data set

p	10	50	100	150	200
BQDA	68.480	73.618	78.438	76.160	75.180
DQDA	63.517	68.630	69.735	69.253	69.303
MQDA	62.923	68.152	69.165	68.955	69.185
BLDA	68.643	77.082	76.040	73.807	72.655
DLDA	68.135	74.703	75.415	73.715	72.137
MLDA	68.230	74.807	75.422	73.723	72.155
SVM	63.415	71.405	74.838	74.038	72.473
kNN	61.520	61.830	62.817	63.770	63.570

7. Discussion

For high-dimensional data such as microarrays, we face the challenge of building a reliable classifier with a limited number of samples. For instance, a typical microarry study has expression levels for thousands of genes but less than one hundred samples. Much smaller sample sizes (< 10) are also common in practice. Diagonal discriminant analysis has been recommended for high-dimensional data classification problem with remarkably good performance (Dudoit et al., 2002; Lee et al., 2005). However, the conventional estimators of diagonal discriminant scores may not be reliable as they are all biased. In this paper, we proposed several bias-corrected discriminant rules that improve the overall prediction accuracy in both simulation studies and real case studies. The bias-corrected methods improve the prediction of the minority class, but sacrifice some performance for the majority class in terms of the per-class prediction accuracy. In reality, the minority class, e.g., representing some rare disease samples, is often of interest and may deserve more weight. Here we show that generally the bias-corrected methods offer higher CWA than the corresponding biased ones, even with the equal weights. The improvement may be affected by many factors, among which the sample size of minority class, n₁, the degree of unbalance, n₁/n₂, and the number of features selected, p, are the most important ones.

When the design is balanced, the bias-corrected rules perform similarly as the original ones, even though the bias-corrected rules provide better estimator of discriminant scores. Specifically, BLDA performs exactly the same as DLDA, and BQDA performs similarly as DQDA. For unbalanced designs, the change of CWA is non-trivial. As shown in Sections 5 and 6, the bias-corrected methods outperform their biased counterparts under all simulation settings and real case studies when n₂/n₁ > 1 and p is large. The improvement is evident when the sample size of the minority class in the training class (n₁) is small. When n₁ is large, the improvement is still not trivial as long as the ratio of n₂/n₁ keeps. For the DLBCL data set with 18 training samples in the minority class, the overall performance improvement is still observable with only 100 genes selected for classification. To make the bias-corrected rules work, BQDA requires n_k ≥ 4, and BLDA requires n ≥ K + 2 which is less restrictive than BQDA. Most of the public available microarray data sets satisfy such requirements.

One possible future research is to propose a regularization between BLDA and BQDA as those in Friedman (1989), Guo et al. (2007) and Pang et al. (2009). To stabilize the variances of ${\widehat{d}}_k^Q(\mathit{y})$ and ${\widehat{d}}_k^L(\mathit{y})$, or equivalently to correct their second-order biases is also of interest. Specifically, we will incorporate the bias correction together with the shrinkage technique in Tong and Wang (2007) and Pang et al. (2009). The rationale behind the shrinkage estimation is to trade off the increased bias for a possible “significant decrease” in the variance (James and Stein, 1961; Radchenko and James, 2008). As a consequence, the good performance of the shrinkage-based discriminant rules is mainly because of the largely reduced variances in the corresponding discriminant scores (Pang et al., 2009). Nevertheless, the bias terms still remain, and more likely, the biases will be larger than that in the original diagonal discriminant scores owing to the impact of shrinkage. Motivated by this, we expect that to correct the biases for the shrinkage-based discriminant rules can be of great interest.

Finally, we reiterate that the diagonal matrix assumption used is somewhat restrictive, so it might be necessary to drop such condition and obtain similar results for more general covariance matrices. Storey and Tibshirani (2001) suggested that the clumpy dependence (i.e., the block diagonal matrix) is a likely form of dependence in the setting of microarray data analysis. This is also mentioned in Langaas et al. (2005). Inspired by this, one natural extension is to propose the bias-corrected rules for the covariance matrix Σ_k = diag(Σ_k,1, …, Σ_k,H), where H is the total number of blocks. To calculate the expectation of L̂_k1 and L̂_k2 under the block diagonal covariance matrix, the following well-known results can be used (Das Gupta, 1968),

$$\begin{array}{l}E({\widehat{\mathrm{\sum }}}_k^{-1})=\frac{n_k-1}{n_k-p-2}E({\mathrm{\sum }}_k^{-1}),\\ E(log\mid {\widehat{\mathrm{\sum }}}_k\mid )=log\mid {\mathrm{\sum }}_k\mid -plog(n_k-1)+\sum _{i=1}^p\mathrm{\Psi }(\frac{n_k-1}{2}),\end{array}$$

where Σ̂_k is the sample covariance matrix of class k. In addition, to avoid the singularity problem, it needs to be assumed that each block size is not bigger than the sample size.

8. Supplementary Materials

Web Appendix and Figures referenced in Sections 3–5 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.

Appendix A: the proof of theorem 1

1. Recall that ${\stackrel{\sim }{d}}_k^Q$ is an unbiased estimator of $d_k^Q$ while ${\widehat{d}}_k^Q$ is biased. To verify $\mathit{Var}({\stackrel{\sim }{d}}_k^Q)<\mathit{Var}({\widehat{d}}_k^Q)$, it suffices to show

   $$\frac{n_k-2}{n_k-1}\mathit{Var}({\widehat{L}}_{k1})+\mathit{Cov}({\widehat{L}}_{k1},L_{k2})>0.$$ (A1)
   Denote $J_k={\displaystyle \sum _{i=1}^p}\frac{{(y_i-{\mu }_{ki})}^4}{{\sigma }_{ki}^4}$, when n_k > 5, we have

   $$\mathit{Var}({\widehat{L}}_{k1})=\frac{2{(n_k-1)}^2}{{(n_k-3)}^2(n_k-5)}\{J_k+\frac{2(n_k-2)}{n_k}{L}_{k1}+\frac{(n_k-2)}{n_k^2}p\}.$$
   For Cov(L̂_k1, L̂_k2), note that $ln\{{\widehat{\sigma }}_{ki}^2(n_k-1)/{\sigma }_{ki}^2\}\sim ln{\chi }_{n_k-1}^2$ (Chan, 2006). We have

   $$E(\frac{ln{\widehat{\sigma }}_{ki}^2}{{\widehat{\sigma }}_{ki}^2})=\frac{n_k-1}{(n_k-3){\sigma }_{ki}^2}\{\mathrm{\Psi }(\frac{n_k-3}{2})-ln(\frac{n_k-1}{2{\sigma }_{ki}^2})\}.$$
   Thus

   $$\mathit{Cov}({\widehat{L}}_{k1},{\widehat{L}}_{k2})=-\frac{2(n_k-1)}{{(n_k-3)}^2}(L_{k1}+\frac{p}{n_k}).$$
   Then Equation A1 can be simplified to

   $$J_k+\frac{n_k^2-3n_k+8}{n_k(n_k-2)}{L}_{k1}+\frac{n_k+4}{n_k^2(n_k-2)}p>0,$$

   which holds for any n_k > 5.

2. The proof of (ii) is skipped since it is essentially the same as that of (i).

Appendix B: the proof of theorem 2

For ease of notation, denote

$$\begin{array}{l}{\nu }_t={(-1)}^t\delta +U,\\ {\tau }_t^2=4b_t\delta +c.\end{array}$$

Note that for any integers 0< n₁ < n₂, we have $U=p(\frac{1}{n_1}-\frac{1}{n_2})<2p$. We establish Theorem 2 via the following two steps.

1. When 0 < δ ≤ U < 2p (i.e., δ − U ≤ 0 < δ). As τ₁ < τ₂, we have

   $$\begin{array}{l}{Pr}_{\widehat{D},1}=\mathrm{\Phi }(\frac{\delta }{{\tau }_1})-\mathrm{\Phi }(\frac{\delta -U}{{\tau }_1})\\ >\mathrm{\Phi }(\frac{\delta }{{\tau }_2})-\mathrm{\Phi }(\frac{\delta -U}{{\tau }_2})\\ >\mathrm{\Phi }(\frac{\delta +U}{{\tau }_2})-\mathrm{\Phi }(\frac{\delta }{{\tau }_2})\\ =\mathrm{\Phi }(\frac{U-{\nu }_2}{{\tau }_2})-\mathrm{\Phi }(\frac{-{\nu }_2}{{\tau }_2})\\ ={Pr}_{\widehat{D},2}.\end{array}$$

   The second inequality is obtained as the standard normal density is a unimodal function and the interval [ $\frac{\delta -U}{{\tau }_2},\frac{\delta }{{\tau }_2}$] contains the mode. The last equality is obtained by the symmetry of the standard normal density function.

2. When U < δ ≤ 2p (i.e., 0 < δ − U < δ ≤ 2p). Denote the length of interval [ $\frac{\delta -U}{{\tau }_1},\frac{\delta }{{\tau }_1}$] as I₁ = U/τ₁, and the length of interval [ $\frac{\delta }{{\tau }_2},\frac{\delta +U}{{\tau }_2}$] as I₂ = U/τ₂. We have I₁ > I₂ as τ₁ < τ₂. Thus by the monotone decreasing property of the N(0, 1) density on (0, ∞), as long as the lower bound of I₁ is not larger than that of I₂, i.e., if $\frac{\delta -U}{{\tau }_1}\le \frac{\delta }{{\tau }_2}$, we can claim that Theorem 2 holds.

In what follows we verify the condition $\frac{\delta -U}{{\tau }_1}\le \frac{\delta }{{\tau }_2}$, or equivalently to verify that

$$\frac{\delta -U}{\delta }\le \frac{{\tau }_1}{{\tau }_2}.$$ (A2)

By the condition that δ ≤ 2p, the left hand side of the Equation (A2) is

$$\begin{array}{l}\text{LHS}=1-\frac{p}{\delta }(\frac{1}{n_1}-\frac{1}{n_2})\\ \le 1-\frac{1}{2}(\frac{1}{n_1}-\frac{1}{n_2})\\ =1-\frac{n_2-n_1}{2n_1{n}_2}.\end{array}$$

Meanwhile, by Lemmas 1 and 2 shown below, the right hand side of Equation (A2) is

$$\text{RHS}=\sqrt{\frac{{\tau }_1^2}{{\tau }_2^2}}>\sqrt{\frac{4b_1\delta }{4b_2\delta }}=\sqrt{\frac{n_1{n}_2+n_1}{n_1{n}_2+n_2}}>1-\frac{n_2-n_1}{2n_1{n}_2}.$$

Hence, Equation (A2) is established and Theorem 2 holds.

Lemma 1

For any 0 < a < b, the function f(x) = (a + x)/(b + x) is a monotone increasing function of x on (0, ∞).

Lemma 2

For any integers 0 < n₁ < n₂, we have

$$\sqrt{\frac{n_1{n}_2+n_1}{n_1{n}_2+n_2}}\ge 1-\frac{n_2-n_1}{2n_1{n}_2}.$$

Appendix C: Pr_Δ in equation (6)

Under the assumptions in Section 4, note that if y is given, we can write $\widehat{D}={\widehat{d}}_1^L-{\widehat{d}}_2^L$ as a linear combination of two independent non-central chi-square random variables, both with p degrees of freedom, i.e.,

$$\widehat{D}=\frac{1}{n_1}{\chi }_p^2({\lambda }_1)-\frac{1}{n_2}{\chi }_p^2({\lambda }_2),$$

where ${\lambda }_k={\sum }_{i=1}^p{n}_k{(y_i-{\mu }_{ki})}^2$. The expected change of CWA for any fixed observation is defined as Pr _D̂|y = Pr(0 < D̂ < U|y). One way to obtain Pr _D̂|y is to use the inversion formula of probability characteristic function (Durrett, 1996), i.e.,

$${Pr}_{\widehat{D}\mid \mathit{y}}=\frac{1}{2\pi }\underset{T\to \infty }{lim}{\int }_{-T}^T\frac{1-e^{-i\eta U}}{i\eta }\mathcal{T}(\eta )d\eta ,$$

where (η) is the characteristic function for D̂, and

$$\mathcal{T}(\eta )={\left[\frac{n_1{n}_2}{(n_1-2i\eta )(n_2+2i\eta )}\right]}^{\frac{p}{2}}\mathit{exp}(\frac{i{\lambda }_1\eta }{n_1-2i\eta }-\frac{i{\lambda }_2\eta }{n_2+2i\eta }).$$

To compute Pr_Δ in Equation (6), we can sample y from both classes and integrate Pr _D̂|y numerically.