Metamers of the ventral stream

Abstract

The human capacity to recognize complex visual patterns emerges in a sequence of brain areas known as the ventral stream, beginning with primary visual cortex (V1). We develop a population model for mid-ventral processing, in which non-linear combinations of V1 responses are averaged within receptive fields that grow with eccentricity. To test the model, we generate novel forms of visual metamers — stimuli that differ physically, but look the same. We develop a behavioral protocol that uses metameric stimuli to estimate the receptive field sizes in which the model features are represented. Because receptive field sizes change along the ventral stream, the behavioral results can identify the visual area corresponding to the representation. Measurements in human observers implicate V2, providing a new functional account of this area. The model explains deficits of peripheral vision known as “crowding”, and provides a quantitative framework for assessing the capabilities of everyday vision.

Introduction

The ventral visual stream is a series of cortical areas that represent spatial patterns, scenes, and objects¹. Primary visual cortex (V1) is the earliest and most thoroughly characterized area. Individual V1 cells encode information about local orientation and spatial frequency², and simple computational models can describe neural responses as a function of visual input³. Significant progress has also been made in understanding later stages, such as inferotemporal cortex (IT), where neurons exhibit complex object-selective responses⁴. However, the transformations between V1 and IT remain a mystery.

Several observations from physiology and theory can help constrain the study of this problem. A key finding is that receptive field sizes increase along the ventral stream. Many models of visual pattern recognition^5–10 have proposed that increases in spatial pooling provide invariance to geometric transformations (e.g., changes in position or size). In addition, it is well established that within individual areas, receptive field sizes scale linearly with eccentricity, and that this rate of scaling is larger in each successive area along the ventral stream, providing a signature that distinguishes different areas^11–13.

We hypothesize that the increase in spatial pooling, both in successive ventral stream areas, and with eccentricity, induces an irretrievable loss of information. Stimuli that differ only in terms of this lost information will yield identical population-level responses. If the human observer is unable to access the discarded information, such stimuli will be perceptually indistinguishable; thus, we refer to them as metamers. Visual metamers were crucial to one of the earliest and most successful endeavors in vision science —the elucidation of human trichromacy. Behavioral experiments predicted the loss of spectral information in cone photoreceptors 100 years before the physiological mechanisms were confirmed¹⁴. The concept of metamerism is not limited to trichromacy, however, and a number of authors have used it to understand aspects of pattern or texture vision^15–17.

Here, we develop a population-level functional model for ventral stream computation beyond V1 that allows us to synthesize, and examine the perception of, a novel type of visual metamer. The first stage of the model decomposes an image with a population of oriented V1-like receptive fields. The second stage computes local averages of nonlinear combinations of these responses over regions that scale in size linearly with eccentricity, according to a scaling constant that we vary parametrically. Given a photographic image, we synthesize distinct images with identical model responses, and ask whether human observers can discriminate them. From these data we estimate the scaling constant that yields metameric images, and find that it is consistent with receptive field sizes in area V2, suggesting a new functional account of representation in that area.

Our model also provides an explanation for the phenomenon of “visual crowding”^18,19, in which humans fail to recognize peripherally presented objects surrounded by clutter. Crowding has been hypothesized to arise from compulsory pooling of peripheral information^20–23, and the development of our model was partly inspired by evidence that crowding is consistent with a representation based on local texture statistics²⁴. Our model offers an instantiation of this hypothesis, providing a quantitive explanation for the spacing and eccentricity dependence of crowding effects, generalizing them to arbitrary photographic images, and linking them to the underlying physiology of the ventral stream.

Results

The model is motivated by known facts about cortical computation, human pattern vision, and the functional organization of ventral stream receptive fields. The V1 representation uses a bank of oriented filters covering the visual field, at all orientations and spatial frequencies. “Simple” cells encode a single phase at each position; “complex” cells combine pairs of filters with the same preferred position, orientation, and scale, but different phase²⁵.

The second stage of the model achieves selectivity for compound image features by computing products between particular pairs of V1 responses (both simple and complex) and averaging these products over local regions, yielding local correlations. Correlations have been shown to capture key features of naturalistic texture images, and have been used to explain some aspects of texture perception^17,26,27. Correlations across orientations at different positions yield selectivity to angles and curved contours, as suggested by physiological studies of area V2^28–32. Correlations across frequencies encode features with aligned phase or magnitude (e.g., sharp edges or lines)^17,33, and correlations across positions capture periodicity. Finally, local correlations are compatible with models of cortical computation that propose hierarchical cascades of linear filtering, point non-linearities, and pooling^{5–9,25,34,35} (see Methods).

Last, we must specify the pooling regions over which pairwise products of V1 responses are averaged. Receptive field sizes in the ventral stream grow approximately linearly with eccentricity, and the slope of this relationship (i.e., the ratio of receptive field diameter to eccentricity) increases in successive areas (see Fig. 1 and Supplementary Methods). In our model, pooling is performed by weighted averaging, with smoothly overlapping functions that grow in size linearly with eccentricity, parameterized with a single scaling constant (see Methods and Supplementary Fig. 1).

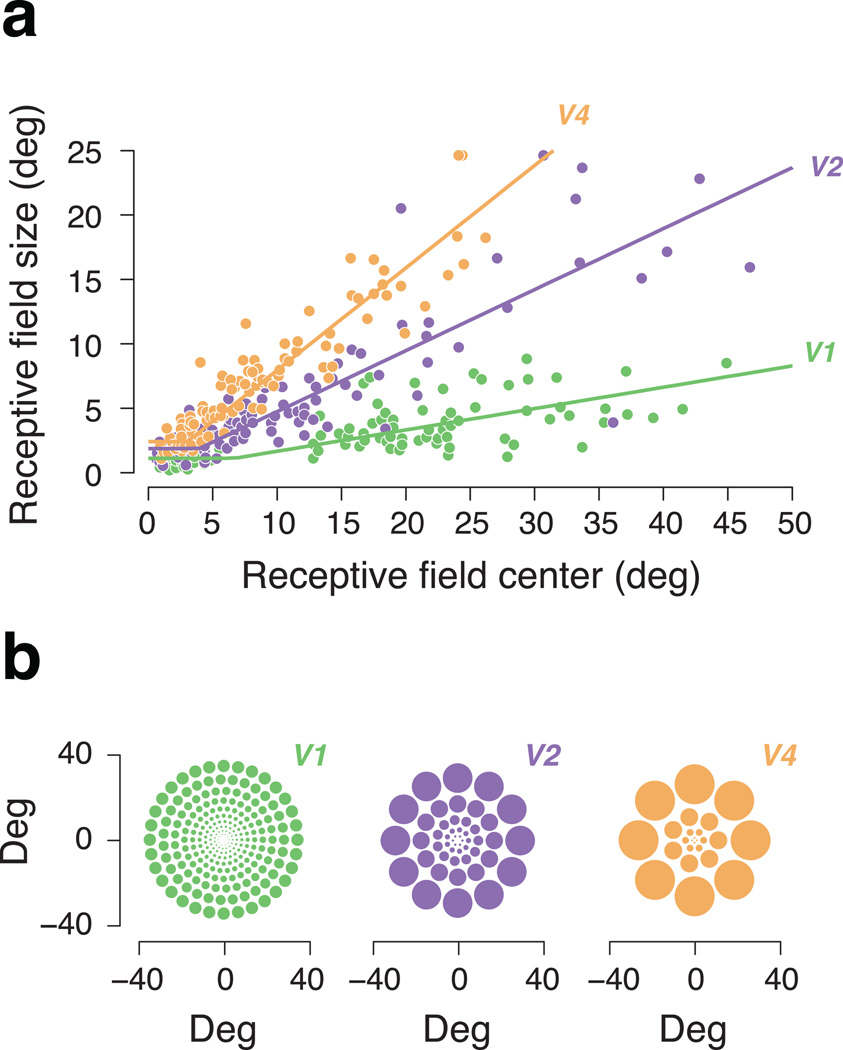
Figure 1.

Physiological measurements of receptive field size in macaque. (a) Receptive field size (diameter) as a function of receptive field center (eccentricity) for visual areas V1, V2, and V4. Data adapted from Gattass et al. (1981) and Gattass et al. (1988), the only studies to measure receptive fields in all three macaque ventral stream areas with comparable methods. The size-to-eccentricity relationship in each area is well described by a “hinged” line (see Supplementary Methods for details and an analysis of a larger set of ten physiological data sets). (b) Cartoon depiction of receptive fields with sizes based on physiological measurements. The center of each array is the fovea. The size of each circle is proportional to its eccentricity, based on the corresponding scaling parameter (slope of the fitted line in panel a). At a given eccentricity, a larger scaling parameter implies larger receptive fields. In our model, we use overlapping pooling regions (linear weighting functions) that uniformly tile the image and are separable and of constant size when expressed in polar angle and log eccentricity (Supplementary Fig. 1).

Generation of metameric stimuli

If our model accurately describes the information captured (and discarded) at some stage of visual processing, and human observers cannot access the discarded information, then any two images that produce matching model responses should appear identical. To directly test this assertion, we examine perceptual discriminability of synthetic images that are as random as possible while producing identical model responses¹⁷. First, model responses (Fig. 2a) are computed for a full-field photograph (e.g., Fig. 2b). Then synthetic images are generated by starting from Gaussian white noise and iteratively adjusting them (using a variant of gradient descent) until they match the model responses of the original (see Methods).

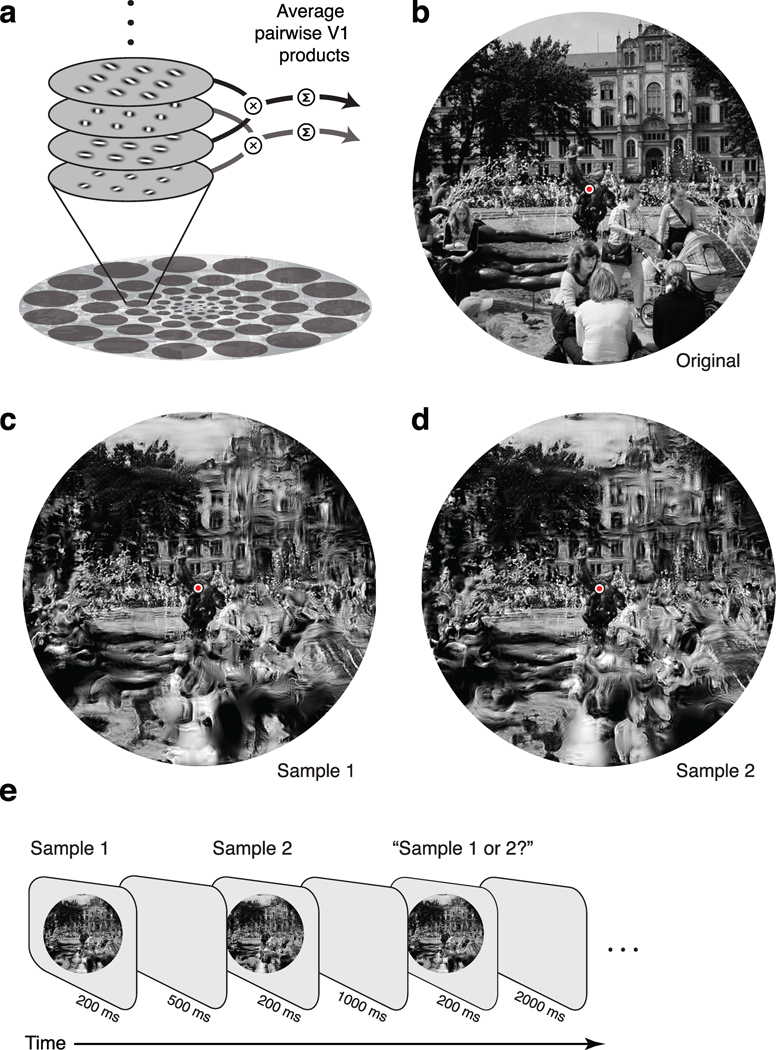
Figure 2.

Mid-ventral model, metameric stimuli, and experimental task. (a) In each spatial pooling region, the image is first decomposed using a population of model V1 cells (both simple and complex), varying in their preferred orientation and spatial frequency. Model responses are computed from products of the filter outputs across different positions, orientations, and scales, averaged over each of the pooling regions. (b) An original photograph of the Brunnen der Lebensfreude in Rostock, Germany (courtesy of Bruce Miner). (c–d) Image samples, randomly selected from the set of images that generated model responses identical to those of the original (panel b). The value of the scaling parameter (used to determine the pooling regions of the model) was selected to yield 75% correct performance in discriminating such synthetic images (see Fig. 4). The two images, when viewed with fixation at the center (red dot), should appear nearly identical to the original and to each other, despite gross distortions in the periphery (for example, a woman's face is scrambled, and dissolves into the spray of the fountain). (e) Psychophysical “ABX” task. Human observers viewed a sequence of two synthetic stimuli, each randomly selected from the set of all images having model responses matched to an original image, followed by a third image that was identical to one of the first two. Observers indicated which of the first two images matched the third.

Figure 2c–d shows two such synthetic images, generated with a scaling constant (derived from the experiments described below) that yields nearly indiscriminable samples. The synthetic images are identical to the original near the intended fixation point (red circle), where pooling regions are small, but features in the periphery are scrambled, and objects are grossly distorted and generally unrecognizable. When viewed with proper fixation, however, the two images appear nearly identical to the original and to each other.

Perceptual determination of critical scaling

To test the model more formally, and to link it to a specific ventral stream area, we measured the perceptual discriminability of synthetic images as a function of the scaling constant used in their generation. If the model, with a particular choice of scaling constant, captures the information represented in some visual area, then model-generated stimuli will appear metameric. If the scaling constant is made larger, the model will discard more information than the associated visual area, and model-generated images will be readily distinguishable. If the model scaling is made smaller, the model discards less information, and the images will remain metameric. Thus, we seek the largest value of the scaling constant such that stimuli appear metameric. This critical scaling should correspond to the scaling of receptive field sizes in the area where the information is lost.

As a separate control for the validity of this paradigm, we examined stimuli generated from a “V1 model” that computes pooled V1 complex cell responses³⁶ (i.e., local spectral energy, see Supplementary Fig. 2). The critical scaling estimated for these stimuli should match the receptive field sizes of area V1. Since the mid-ventral model includes a larger and more complex set of responses than the V1 model, we know a priori that the critical scaling for the mid-ventral model will be as large or larger than for the V1 model, but we do not know by how much.

For each model, we measured the ability of human observers to distinguish synthetic images generated for a range of scaling constants (using an “ABX” task, see Fig. 2e and Methods). All four observers exhibit monotonically increasing performance as a function of scaling constant (Fig. 3). Chance performance (50%) indicates that the stimuli are metameric, and roughly speaking, the critical scaling is the value at which each curve first rises above chance.

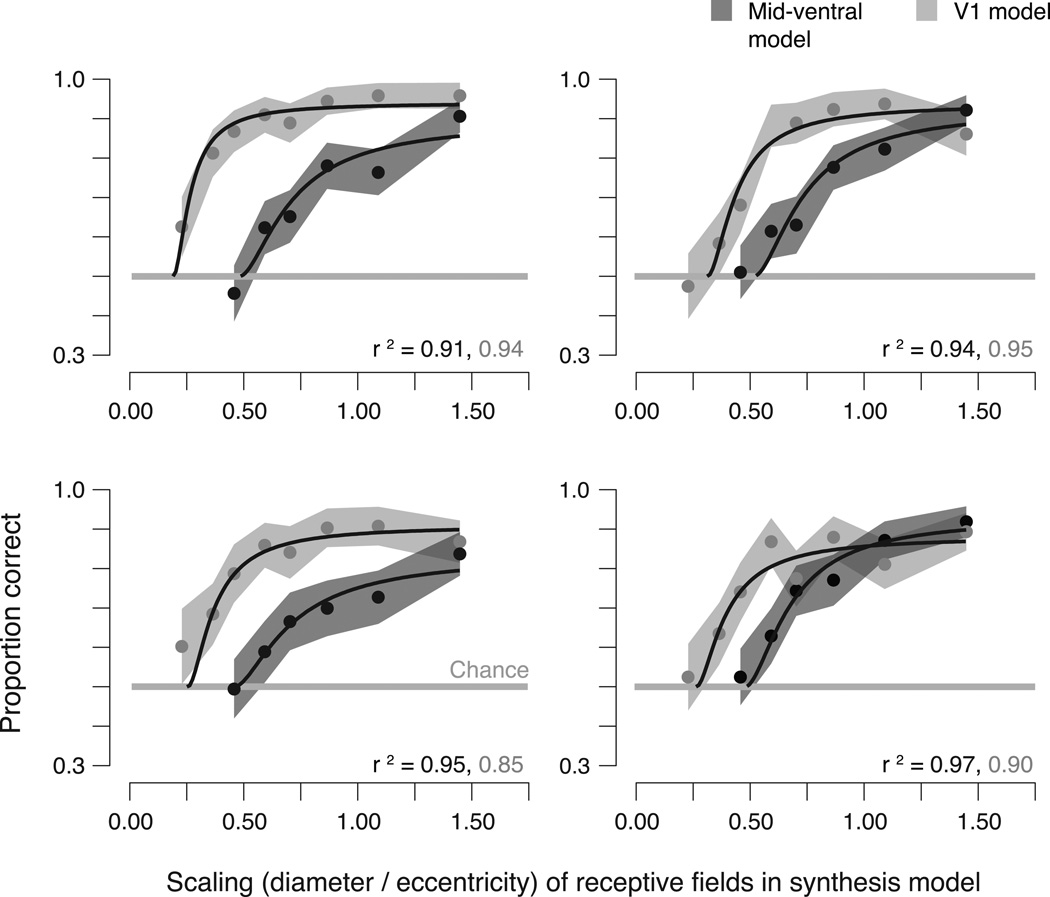
Figure 3.

Metamer experiment results. Each panel shows, for an individual observer, the proportion of correct responses in the ABX task, as a function of the scaling parameter (ratio of receptive field diameter to eccentricity) of the model used to generate the stimuli. Data are averaged over stimuli drawn from four naturalistic images. Dark gray points: mid-ventral model (see Fig. 2). Light gray points: V1 model (see Supplementary Fig. 2). Shaded region, 68% confidence interval obtained using bootstrapping. Gray horizontal line: Chance performance. Black lines: Performance of observer model with critical scaling and gain parameters chosen to maximize the likelihood of the data for each individual observer (see Methods and Results). r² values for the fits indicated at the bottom of each plot.

To obtain an objective estimate of the critical scaling values, we derived an observer model that uses the same ventral stream representation used to generate the matched images. The inputs to the observer model are two images that are matched over region sizes specified by scaling s. Assume that the observer computes responses to each of these images with receptive fields that grow in size according to a fixed (but unknown) critical scaling s₀. Their ability to discriminate the two images depends on the difference between the two sets of responses. We derived (see Supplementary Methods) a closed-form expression for the dependency of this difference on s. This expression is a function of the observer’s scaling parameter, s₀, as well as a gain parameter, α₀, which controls their overall performance. We used signal detection theory³⁷ to describe the probability of a correct answer, and fit the parameters (s₀, α₀) to the data of each subject by maximizing their likelihood (see Methods).

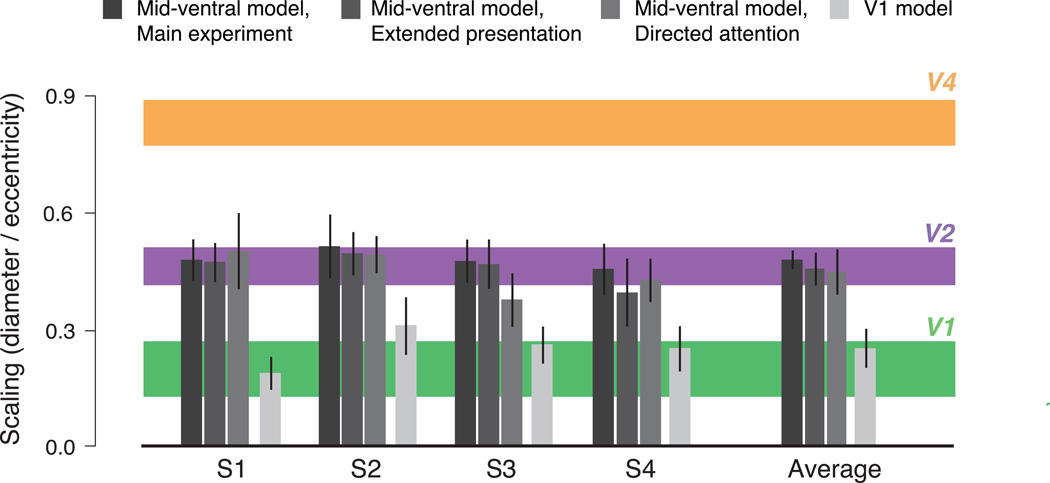
The observer model provides an excellent fit to individual observer data for both the V1 and mid-ventral experiments (Fig. 3). Critical scaling values (s₀) are highly consistent across observers, with most of the between-subject variability captured by differences in overall performance (α₀). As expected, the simpler V1 model requires a smaller scaling to generate metameric images. Specifically, critical scaling values for the V1 model are 0.26 ± 0.05 (mean ± sd), whereas values for the mid-ventral model are roughly twice as large (0.48 ± 0.02).

Estimation of physiological locus

We now compare the psychophysically estimated scaling parameters to physiological estimates of receptive field size scaling in different cortical areas. Functional magnetic resonance imaging has been used to measure “population receptive fields” in humans by estimating the spatial extent of a stimulus that contributes to the hemodynamic response across different regions of the visual field¹³. Although these sizes grow with eccentricity, and across successive visual areas, they include additional factors such as variability in receptive field position and non-neural hemodynamic effects, which may depend on both eccentricity and visual area. We thus chose to compare our results to single-unit electrophysiological measurements in non-human primates. Receptive field size estimates vary systematically, depending on the choice of stimuli and the method of estimation, so we combined estimates reported for ten different physiological data sets to obtain a distribution of scaling values for each visual area. This analysis yields values of 0.21 ± 0.07 for receptive fields in V1, 0.46 ± 0.05 for those of V2, and 0.84 ± 0.06 for those of V4 (mean with 95% confidence intervals, see Supplementary Methods). Moreover, for studies that used comparable methods to estimate receptive fields in both V2 and V1, the average receptive field sizes in V2 are approximately twice the size of those in V1, for both macaque and human^11,13,38.

As expected, the critical scaling value estimated from the V1 metamer experiment is well matched to the physiological estimates of receptive field scaling for V1 neurons. For the mid-ventral model, the critical scaling is roughly twice that of the V1 model, is well matched to receptive field sizes of V2 neurons, and is substantially smaller than than those of V4. We take this as compelling evidence that the metamerism of images synthesized using our mid-ventral model arises in area V2.

Robustness to bottom-up and top-down performance manipulations

If metamerism reflects a structural limitation of the visual system, governed by the eccentricity-dependent scaling of receptive field sizes, the effects should be robust to experimental manipulations that alter observer performance without changing the spatial properties of the stimuli. To test this, we performed two variants of the mid-ventral metamer experiment, designed to alter performance through bottom-up and top-down manipulations of the experimental task.

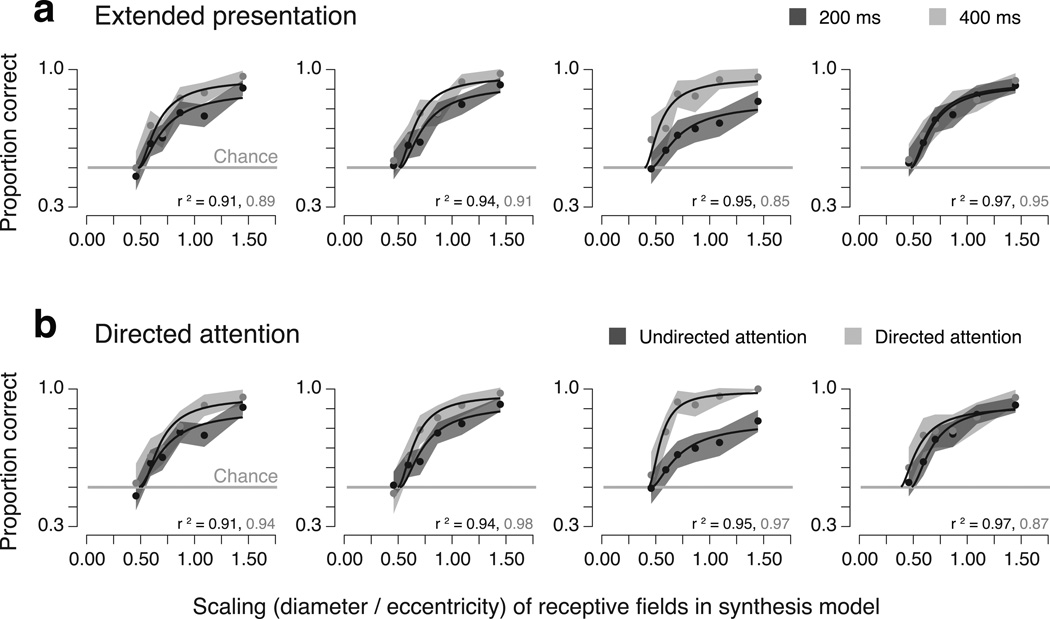
First, we repeated the original experiment with doubled presentation times (400 ms instead of 200 ms). Fitting the observer model to data from four observers (Fig. 4a), we find that the gain parameter (α₀) is generally larger to account for increases in performance, but that the critical scaling (s₀) is statistically indistinguishable from that estimated in the original experiment (p = 0.18, two-tailed paired t-test).

Figure 4.

Metamer control experiments. Each column shows data and fitted psychometric functions for an individual observer. Both experiments use stimuli generated by the mid-ventral model. (a) Metamer experiment with extended presentation time. Light gray points: 400 ms presentation time. Dark gray points: 200 ms presentation time (replotted from Fig. 3). Shaded region: 68% confidence interval obtained using bootstrapping. Gray horizontal line: chance performance. (b) Metamer experiment with directed attention. Light gray points: observers were directed with an attentional cue indicating the region with the largest change (see Methods). Dark gray points: undirected attention (replotted from Fig. 3). Shaded region: same as panel a.

In a second control experiment, we manipulated endogenous attention. At the onset of each trial, a small arrow was presented at fixation, pointing toward the region in which the two subsequently presented stimuli differed most (see Methods). The fitted gain parameter is again generally larger, accounting for improvements in performance, but the critical scaling is statistically indistinguishable from that estimated in the original experiment (p = 0.30; two-tailed paired t-test) (Fig. 4b). In both control experiments, the increase in gain varies across observers, and depends on their overall performance in the original experiment (some observers already have near-maximal performance).

The full set of critical scalings estimated for all four observers, across all experiments, are summarized in Figure 5, along with the physiological estimates for scaling of receptive fields. The scaling for the two control experiments are similar to those of the original experiment, are closely matched to the scaling of receptive fields found in area V2, and are much greater than the scaling found in the V1 metamer experiment (p = 0.0064, extended presentation task, p = 0.0183, attention task; two-tailed paired t-test).

Figure 5.

Summary of fitted critical scaling parameters for all experiments. Error bars: 95% confidence intervals on parameter estimates obtained through bootstrapping. Colored horizontal lines: receptive field scaling as measured physiologically in each visual area, based on a meta-analysis combining across ten data sets (see Supplementary Methods for details and references). Thickness of lines indicates 95% confidence interval.

Relationship to visual crowding

Our model implies severe perceptual deficits in peripheral vision, some of which are revealed in the well-studied phenomenon known as “visual crowding”^18,19. Crowding has been hypothesized to arise from pooling or statistical combination in the periphery^20–24, and thus emerges naturally from our model. Crowding is typically characterized by asking observers to recognize a peripheral target object flanked by two distractors at varying target-to-flanker spacings. The “critical spacing” at which performance reaches threshold increases proportional to eccentricity^18,19, with reported rates ranging from 0.3 to 0.6. Our estimates of critical scaling for the mid-ventral model lie within this range, but the variability across crowding studies (which arises from different choices of stimuli, task, number of targets and flankers, and threshold) renders this comparison equivocal. Moreover, a direct comparison of these values may not even be warranted, because it implicitly relies on an unknown relationship between the pooling of the model responses and the degradation of recognition performance.

We performed an additional experiment to determine directly whether our mid-ventral model could predict recognition performance in a crowding task. The experimental design was inspired by a previous study linking statistical pooling in the periphery to crowding²⁴. First, we measured observers’ ability to recognize target letters presented peripherally (6 deg) between two flanking letters, varying the target-to-flanker spacing to obtain a psychometric function (Fig. 6a). We then used the mid-ventral model to generate synthetic metamers for a subset of these peripherally-presented letter stimuli, and measured the ability of observers to recognize the letters in these metamer stimuli under foveal viewing. Recognition failure (or success) for a single metamer cannot alone indicate crowding (or lack thereof), but average performance across an ensemble of metamer samples quantifies the limitations on recognizability imposed by the model.

Figure 6.

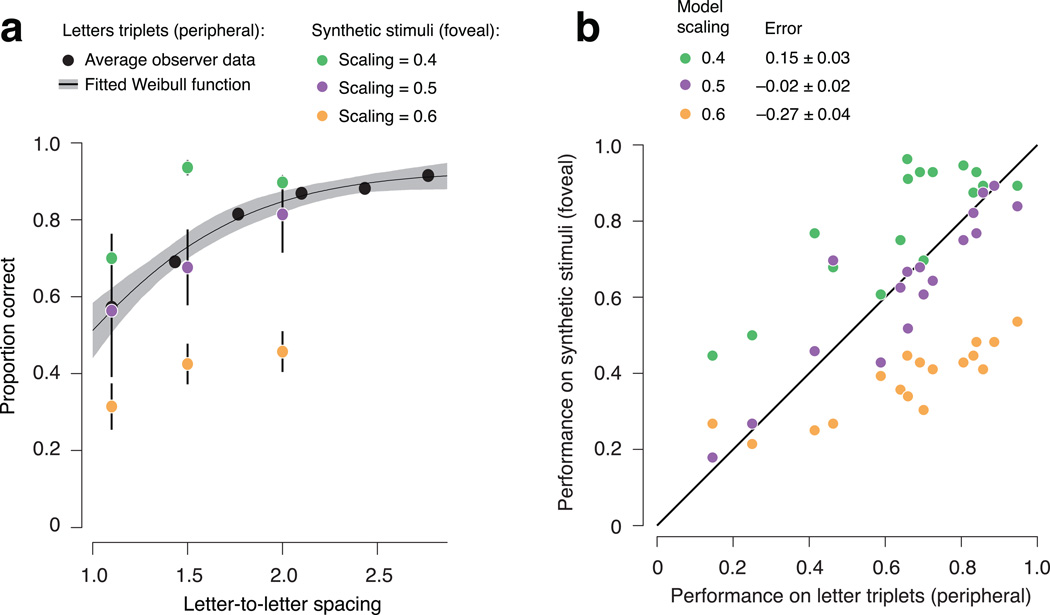
Crowding experiment. (a) Recognition performance for two different kinds of stimuli: peripherally viewed triplets of letters, and foveally viewed stimuli synthesized to produce model responses identical to their corresponding letter triplets. Black dots: average recognition performance for a peripheral letter between two flankers, as a function of letter-to-letter spacing (n = 5 observers). Black line: best fitting Weibull function. Gray shaded region: 95% confidence interval for fit obtained through bootstrapping. Synthetic stimuli were generated for spacings yielding approximately 50%, 65%, and 80% performance, based on the average psychometric function. Colored dots: average recognition performance for model-synthesized stimuli (foveally viewed). Different colors indicate the scaling parameter used in the model (purple: 0.5, orange: 0.4, green: 0.6). Error bars: standard deviation across observers. (b) Comparison of recognition performance for the peripheral letter triplets (from the psychometric function in panel a) and the foveally-viewed synthetic stimuli (colored dots from panel a). Each point represents data from a single observer for a particular spacing and scaling. Two observers performed an additional condition at a larger eccentricity (not shown in panel a), to extend the range of performance levels (the six left-most points).

Average recognition performance for the metamers is well matched to that of their corresponding letter stimuli (Fig. 6a), for metamers synthesized with scaling parameter s = 0.5 (the average critical scaling estimated for our human observers). For metamers synthesized with scaling parameters of s = 0.4 or s = 0.6, performance is significantly higher or lower, respectively (p < 0.0001; two-tailed paired t-test across observers and conditions). These results are consistent across all observers, at all spacings, and for two different eccentricities (Fig. 6b).

Discussion

We have constructed a model for visual pattern representation in the mid-level ventral stream, based on local correlations amongst V1 responses within eccentricity-dependent pooling regions. We have developed a method for generating images with identical model responses, and used these synthetic images to show that: (1) when the pooling region sizes of the model are set correctly, images with identical model responses are indistinguishable (metameric) to human observers, despite severe distortion of features in the periphery; (2) the critical pooling size required to produce metamericity is robust to bottom-up and top-down manipulations of discrimination performance; (3) critical pooling sizes are consistent with the eccentricity dependence of receptive field sizes of neurons in ventral visual area V2; and (4) the model can predict degradations of peripheral recognition known as “crowding”, as a function of both spacing and eccentricity.

Perceptual deficits in peripheral vision have been recognized for centuries. Most early literature focuses on the loss of acuity that results from eccentricity-dependent sampling and blurring in the earliest visual stages. Crowding is a more complex deficit³⁹. In a prescient article in 1976, Jerome Lettvin gave a subjective account of this phenomenon, describing letters embedded in text as having “lost form without losing crispness”, and concluding that “the embedded [letter] only seems to have a ‘statistical’ existence.”²⁰ Lettvin’s article seems to have drifted into obscurity, but these ideas have been formalized in recent literature that explains crowding in terms of excessive averaging or pooling of features^21–24. Balas et. al. (2009), in particular, hypothesized that crowding is a manifestation of the representation of peripheral visual content with local summary statistics. They showed that human recognition performance for crowded letters was matched to that of foveally viewed images synthesized to match the statistics of the original stimulus (computed over a localized region containing both the letter and flankers).

Our model provides an instantiation of these pooling hypotheses that operates over the entire visual field, which, in conjunction with the synthesis methodology, enabled several scientific advances. First, we validated the model with a metamer discrimination paradigm, which provides a more direct test than comparisons to recognition performance in a crowding experiment. Second, the parameterization of eccentricity dependence allowed us to estimate the size of pooling regions, and thus to associate the model with a distinct stage of ventral stream processing. Third, the full-field implementation allowed us to examine crowding in stimuli extending beyond a single pooling region, and thus to account for the dependence of recognition on both eccentricity and spacing — the defining properties of crowding¹⁸.

Finally, the fact that the model operates on arbitrary photographic images allows generalization of the laboratory phenomenon of crowding to complex scenes and everyday visual tasks. For example, crowding places limits on reading speed, because only a small number of letters around each fixation point are recognizable⁴⁰. Model-synthesized metamers can be used to examine this “uncrowded” window (Fig. 7a). We envision that the model could be used to optimize fonts, letter spacings, or line spacings for robustness to crowding effects, potentially improving reading performance. There is also some evidence linking dyslexia to crowding with larger-than-normal critical spacing^18,41,42, and the model might serve as a useful tool for investigating this hypothesis. Additional examples are provided in Figure 7b–c, which show how camouflaged objects, which are already difficult to recognize foveally, blend into the background when viewed peripherally.

Figure 7.

Effects of crowding on reading and searching. (a) Two metamers, matched to the model responses of a page of text from the first paragraph of Herman Melville’s “Moby Dick”. Each metamer was synthesized using a different foveal location (the letter above each red dot). These locations are separated by the distance readers typically traverse between fixations (Pelli et al., 2007). In each metamer, the central word is largely preserved; farther in the periphery the text is letter-like but scrambled, as if taken from a non-latin alphabet. Note that the boundary of readability in the first image roughly coincides with the location of the fixation in the second image. We emphasize that these are samples drawn from the set of images that are perceptually metameric; although they illustrate the kinds of distortions that result from the model, no single example represents “what an observer sees” in the periphery. (b) The notoriously hard-to-find “Waldo” (character with the red and white striped shirt) blends into the distracting background, and is only recognizable when fixated. Cross-hairs surrounding each image indicate the location of the fovea used by the model during synthesis. (c) A soldier in Afghanistan wears patterned clothing to match the stoney texture of the environment, and similarly blends into the background.

The interpretation of our experimental results relies on assumptions about the representation of, and access to, information in the brain. This is perhaps best understood by analogy to trichromacy¹⁴. Color metamers occur because information is lost by the cones and cannot be recovered in subsequent stages. But color appearance judgements clearly do not imply direct, conscious, access to the responses of those cones. Analogously, our experiments imply that the information loss ascribed to areas V1 and V2 cannot be recovered or accessed by subsequent stages of processing (two stimuli that are V1 metamers, for example, should also be V2 metamers). But this does not imply that observers directly access the information represented in V1 or V2. Indeed, if observers could access V1 responses, then any additional information loss incurred when those responses are combined and pooled in V2 would have no perceptual consequence, and the stimuli generated by the mid-ventral model would not appear metameric.

The loss of information in our model arises directly from its architecture — the set of statistics, and the pooling regions over which they are computed — and this determines the set of metameric stimuli. Discriminability of non-metameric stimuli depends on the strength of the information preserved by the model, relative to noise. As seen in the presentation time and attention control experiments, manipulations of signal strength do not alter the metamericity of stimuli, and thus do not affect estimates of critical scaling. These results are also consistent with the crowding literature. Crowding effects are robust to presentation time⁴³, and attention can increase performance in crowding tasks while yielding small or no changes in critical spacing^19,44. Certain kinds of exogenous cues, however, may reduce critical spacing⁴⁵, and perceptual learning has been shown to reduce critical spacing through several days of intensive training⁴⁶. If either manipulation were found to reduce critical scaling (as estimated from a metamer discrimination experiment), we would interpret this as arising from a reduction in receptive field sizes, which could be verified through electrophysiological measurements.

From a physiological perspective, our model is deliberately simplistic: We expect that incorporating more realistic response properties (e.g., spike generation, feedback circuitry) would not significantly alter the information represented in model populations, but would render the synthesis of stimuli computationally intractable. Despite the simplicity of the model, the metamer experiments do not uniquely constrain the response properties of individual model neurons. This may again be understood by analogy with the case of trichromacy: color matching experiments constrain the linear subspace spanned by the three cone absorption spectra, but do not uniquely constrain the spectra of the individual cones¹⁴. Thus, identification of V2 as the area in which the model resides does not imply that responses of individual V2 neurons encode local correlations. Our results, however, do suggest new forms of stimuli that could be used to explore such responses in physiological experiments. Within a single pooling region, the model provides a parametric representation of local texture features¹⁷. Stochastic stimuli containing these features are more complex than sine gratings or white noise, but better controlled (and more hypothesis driven) than natural scenes or objects, and are thus well suited for characterizing responses of individual cells⁴⁷.

Finally, one might ask why the ventral stream discards such a significant amount of information. Theories of object recognition posit that the growth of receptive field sizes in consecutive areas confers invariance to geometric transformations, and cascaded models based on filtering, simple nonlinearities, and successively broader spatial pooling have been used to explain such invariances measured in area IT^8–10,48. Our model closely resembles the early stages of these models, but our inclusion of eccentricity-dependent pooling, and the invariance to feature scrambling revealed by the metamericity of our synthetic stimuli, seems to be at odds with the goal of object recognition. One potential resolution of this conundrum is that the two forms of invariance arise in distinct parallel pathways. An alternative possibility is that a texture-like representation in the early ventral stream provides a substrate for object representations in later stages. Such a notion was suggested by Lettvin, who hypothesized that “texture, somewhat redefined, is the primitive stuff out of which form is constructed”²⁰. If so, the metamer paradigm introduced here provides a powerful tool for exploring the nature of invariances arising in subsequent stages of the ventral stream.

Methods

Model

The model is a localized version of the texture model of Portilla and Simoncelli (2000), which used global correlations to represent homogeneous visual textures.

Multi-scale multi-orientation decomposition

Images are partitioned into subbands by convolving with a bank of filters tuned to different orientations and spatial frequencies. We use a particular variant known as the “steerable pyramid”, which has several advantages over common alternatives (e.g., Gabor filters, orthogonal wavelets), including direct reconstruction properties (beneficial for synthesis), translation invariance within subbands, and rotation invariance across orientation bands¹⁷. A Matlab implementation is available at http://www.cns.nyu.edu/~lcv/software.php. The filters are directional third derivatives of a lowpass kernel, and are spatially localized, oriented, anti-symmetric, and roughly one octave in spatial frequency bandwidth. We use a set of 16 filters – rotated and dilated to cover four orientations and four scales. In addition, we include a set of even-symmetric filters of identical Fourier amplitude (Hilbert transforms of the original set)¹⁷. Each subband is subsampled at its associated Nyquist frequency, so that the effective spacing between filters is proportional to their size. Each filter pair yields two phase-sensitive outputs representing responses of V1 simple cells, and the square root of the sum of their squared responses yields a phase-invariant measure of local orientation magnitude, representing responses of V1 complex cells^17,25.

Mid-ventral model

The second stage of the model computes products of pairs of V1 responses tuned to neighboring orientations, scales, and positions. Specifically:

1. Products of responses at nearby spatial locations (within +/− three samples in each direction), for both the simple cells (capturing spectral features such as periodicity), and complex cells (capturing spatially displaced occurrences of similarly oriented features).

2. Products of complex cell responses with those at other orientations (capturing structures with mixed orientation content, such as junctions or corners) and with those at adjacent scales (capturing oriented features with spatially sharp transitions such as edges, lines, and contours).

3. Products of the symmetric filter responses with phase-doubled filter responses at the next coarsest scale. These phase relationships between filters at adjacent scales distinguish lines from edges, and can also capture gradients in intensity arising from shading and lighting¹⁷.

It is worth noting that these products may be represented equivalently as differences of squared sums and differences (i.e., 4ab = (a + b)² − (a − b)²), which might provide a more physiologically plausible form²⁵. We also include three marginal statistics (variance, skew, kurtosis) of the low-pass images reconstructed at each scale of the course-to-fine process, as was done in the original texture model¹⁷. All of the model responses are pooled locally (see next section).

Pooling regions

Pairwise products are spatially pooled by computing windowed averages (i.e., local correlations). The weighting functions for these averages are smooth and overlapping, and arranged so as to tile the image (i.e., they sum to a constant). These functions are separable with respect to polar angle and log eccentricity, which guarantees that they grow linearly in size with eccentricity (see examples in Supplementary Fig. 1). Weighting in each direction is defined in terms of a generic “mother” window, with a flat top and squared cosine edges:

$$f(x)=\{\begin{array}{cc}{\text{cos}}^2(\frac{\pi }{2}\left(\frac{x+t+1/2}{t})+\frac{\pi }{4}\right)\hfill & \hfill -\frac{1}{2}-\frac{t}{2}<x\le -\frac{1}{2}+\frac{t}{2}\\ 1\hfill & \hfill -\frac{1}{2}+\frac{t}{2}<x\le \frac{1}{2}-\frac{t}{2}\\ -{\text{cos}}^2(\frac{\pi }{2}\left(\frac{x-t-1/2}{t}\right)+\frac{\pi }{4})+1\hfill & \hfill \frac{1}{2}-\frac{t}{2}<x\le \frac{1}{2}+\frac{t}{2}\end{array}$$

These window functions tile when spaced on the unit lattice. The parameter t specifies the width of the transition region, and is set to 0.5 for our experiments. For polar angle, we require an integer number N_θ of windows between 0 and π. The full set is:

$$h_n(\theta )=f\left(\frac{\theta -[w_{\theta }n-\frac{w-t}{2}]}{w_{\theta }}\right),w_{\theta }=\frac{2\pi }{N_{\theta }},n=0\dots N_{\theta }-1$$

where n indexes the windows, w_θ is width. For log eccentricity, an integer number of windows is not required. However, to equate boundary conditions across scaling conditions in our experiments, we require that the outermost window is centered on the radius of the image (e_r). And for computational efficiency, we also do not include windows below a minimum eccentricity (e₀ – approximately half a degree of visual angle in our experiments). For eccentricities less than this, pooling regions are extremely small, and constrain the model to reproduce the original image. Between the minimum and maximum eccentricities, we construct N_e windows:

$$g_n(e)=f\left(\frac{\text{log}(e)-[\text{log}(e_0)+w_e(n+1)]}{w_e}\right),w_e=\frac{\text{log}(e_r)-\text{log}(e_0)}{N_e},n=0\dots N_e-1$$

n indexes the windows, w_e is the width,. The number of windows N_e determines the ratio of radial width to eccentricity, and this value is reported as the scaling (e.g. Fig. 4–5). Although this specification requires an integer number of windows between the inner and outer boundary, we can achieve an arbitrary scaling by releasing the constraint on the endpoint location (e.g. when synthesizing images based on psychophysical estimates of critical scaling, Fig. 6–7). For each choice of scaling, we choose an integer number of polar-angle windows (N_θ) that yields an aspect ratio of radial width to circumferential width of approximately 2. There are few studies on peripheral receptive field shape in the ventral stream, but our choice was motivated by reports of radially elongated receptive fields and radial biases throughout the visual system^49,50. Future work could explore effects of both the scaling and the aspect ratio on metamericity.

The windows must be applied at different scales of the pyramid. For each window, we create an original window in the pixel domain, and then generate low-pass windows to be applied at different scales by blurring and sampling the original (i.e., we construct a “Gaussian pyramid”). The full set of two dimensional windows are approximately invariant to global rotation or dilation: shifting the origin of the log-polar coordinate system in which they are defined would reparameterize the model without changing the class of metameric stimuli corresponding to a particular original image.

V1 model

The model for our V1 control experiment uses the same components described above. We use the same linear filter decomposition, and then square and pool these responses directly, consistent with physiological experiments in V1³⁶. This model does not include the local correlations (i.e. pairwise products) used in the mid-ventral model. Both the V1 model and the mid-ventral model collapse the computation into a single stage of pooling, instead of cascading the mid-ventral model computation on top of a V1 pooling stage (and previous stages, such as the retina and LGN). This kind of simplification is common in modeling sensory representations, and allowed us to develop a tractable synthesis procedure.

Synthesis

Metameric images are synthesized to match a set of measurements made on an original image. An image of Gaussian white noise is iteratively adjusted until it matches the model responses of the original. Synthesizing from different white noise samples yields distinct images. This procedure approximates sampling from the maximum entropy distribution over images matched to a set of model responses¹⁷. We use gradient descent to perform the iterative image adjustments. For each set of responses, we compute gradients, following the derivations in Portilla and Simoncelli (2000) but including the effects of the window functions. Descent steps are taken in the direction of these gradients, starting with the low-frequency subbands (i.e., coarse-to-fine). For autocorrelations, gradients for each pooling region are combined to give a global image gradient on each step. Gradient step sizes are chosen to stabilize convergence. For the cross correlations, single-step gradient projections are applied to each pooling region iteratively.

We used 50 iterations for all images generated for the experiments. Parameter convergence was verified by measuring one minus the mean squared error normalized by the variance. For samples synthesized from the same original image, this metric was 0.99 ± 0.015 (mean ± standard deviation) across all images and scalings used in our experiments. As an indication of computational cost, synthesis for a scaling of s = 0.5 took approximately 6 to 8 hours on a linux workstation with 2.6 GHz dual Opteron 64-bit processor and 32 GB RAM. Smaller scaling values require more time. The entire set of experimental stimuli took approximately one month of computing time to generate.

Synthesis sometimes required more steps to converge for artificial stimuli, such as those created for the crowding experiments (Fig. 6), so we used 100 iterations for those syntheses. In addition, for the text images (Fig. 7), whose pixels are highly kurtotic (due to a nearly binary distribution of pixel values), we obtained cleaner and more stable synthesis results by imposing global kurtosis and skew once, over the whole image, on each synthesis iteration.

Experimental stimuli

Stimuli were derived from four naturalistic photographs, three from the authors’ personal collection, and one courtesy of Rob Miner. One image depicts a natural scene (trees and shrubbery), and the other three depict people and man-made objects. Psychophysical results were similar for the four images. For each photograph, we synthesized three images for each of six values of the scaling parameter s. Piloting showed that performance was at chance for the smallest value tested, so we did not generate stimuli at smaller scalings, which would have been computationally taxing because of very large number of pooling regions. The V1 model was simpler, allowing us to synthesize stimuli for three smaller scaling values.

Psychophysics

Eight observers (ages 24–32, six male, two female) with normal or corrected-to-normal vision participated. One observer was an author; all others were naive to the purposes of the experiment. Four observers participated in the metamer experiments (described in this section), and five observers participated in the crowding experiments (described below). One observer participated in both. Protocols for selection of observers and experimental procedures were approved by the human subjects committee of New York University and all subjects signed an approved consent form.

Four observers participated in all four metamer experiments. Along with the main experiment (with our mid-ventral model), there were three control experiments (V1 model, extended presentation time, and directed endogenous attention). Two observers (S3 and S4) were tested with eye tracking (see below), with stimuli presented on a 22” flat screen CRT monitor at a distance of 57 cm. Two observers (S1 and S2) were tested tested without eye tracking, with stimuli presented on a 13 “ flat screen LCD monitor at a distance of 38 cm. In both displays, all images were presented in a circular window subtending 26 deg of visual angle and blended into the background with a 0.75 deg wide raised cosine. A 0.25 deg fixation square was shown throughout the experiment.

Each trial of the “ABX” task (Fig. 3) used two different synthesized image samples, matched to the model responses of a corresponding original image. At the start of each trial, the observer saw one image for 200 ms. After a 500 ms delay, the observer saw the second image for 200 ms. After a 1000 ms delay, the observer saw one of the two images, repeated, for 200 ms. The observer indicated with a key press whether the third image looked more like the first (“1”) or the second (“2”). During the experiment, observers received no feedback regarding the correctness of their responses. Before the experiment, each observer performed a small number of practice trials (~5), with feedback, to become familiar with the task.

In the mid-level ventral experiment, we used four original images and six scaling conditions, and created three synthetic images for each original / scaling combination. This yielded 12 unique ABX sequences per condition. In each block of the experiment, observers performed 288 trials, one for each combination of image (4), scaling (6), and trial type (12). Observers performed four blocks (1152 trials). The V1 experiment was identical, except that it included 9 scaling conditions, resulting in 384 trials per block. Observers performed three blocks (1152 trials). Blocks were performed on different days, so the observer never saw the same stimulus sequence twice in the same session. Psychometric functions and parameter estimates were similar across blocks, suggesting that observers did not learn any particular image feature.

We performed two further control experiments using the stimuli from the mid-ventral metamer experiment. The first of these was identical to the main experiment except that presentation time was lengthened to 400 ms. Each observer performed either two or three blocks (576 or 864 trials). The second experiment was also identical to the main experiment except that at the beginning of each trial a small line (1 deg long) emanating from fixation was presented for 300 ms, with a 300 ms blank period before and after. On each trial, we computed the squared error (in the pixel domain) between the two to-be-presented images, and averaged the squared error within each of six radial sections. The line cue pointed to the section with largest squared error. Each observer performed two blocks (576 trails).

Eye tracking

Two observers (S3 and S4) were tested while their gaze positions were measured (500 Hz, monocular) with an Eyelink 1000 (SR Research) eye tracker, for all four metamer experiments. A 9-point calibration was performed at the start of each block. We analyzed the eye position data to discard trials where the observer broke fixation. We first computed a “fixation” location for each block by averaging eye positions over all trials. This was used as fixation, rather than the physical screen center, to account for systematic offset due to calibration error. We then computed, on each trial, the distance of each gaze position from fixation. A trial was discarded if any gaze position exceeded 2 deg from fixation. We discarded 5% of trials for the first observer (across all four experiments), and 17% for the second. Using a more conservative (1 deg) threshold increased the number of discarded trials, but did not substantially change psychometric functions or critical scaling estimates. By only including trials with stable fixation, we ruled out the possibility that systematic differences in fixation among scaling conditions, presentation conditions, or models, could account for our results.

Fitting the psychometric function

We assume an observers‘ performance in the ABX experiment is determined by a population of mid-ventral neurons whose receptive fields grow with eccentricity according to scaling parameter s₀, and their performance depends on the total squared difference of those responses computed on the two presented images. Because each response is a spatial average, we can approximate the squared difference as a function of the scaling s used to synthesize the images, relative to the observer’s critical scaling s₀ (see Supplementary Methods):

$$d^2(s)\propto \{\begin{array}{cc}\alpha (1-s_0^2/s^2),\hfill & \hfill s>s_0\\ 0\hfill & \hfill \text{otherwise}\end{array}$$

The gain factor, α, controls the discriminability, and is expected to differ for each model parameter. If we assume the overall discriminability of the two images arises from a weighted average of these squared differences across all model parameters, it will have the same functional form, with an overall gain factor of α_0.. We used simulations to validate this approximation. Signal detection theory³⁷ predicts performance in the ABX task as a function of d²,

$$P_c=\mathrm{\Phi }(d^2/\sqrt{2})\mathrm{\Phi }(d^2/2)+\mathrm{\Phi }(-d^2/\sqrt{2})\mathrm{\Phi }(-d^2/2)$$

where Φ is the cumulative distribution function of the Gaussian. We fit values of the gain factor (α₀) and the critical scaling (s₀) for each subject, by maximizing the likelihood of the raw data. Bootstrapping was used to obtain confidence intervals for parameters.

Crowding

Five observers participated in the crowding experiments (one of whom also participated in the metamer experiments). Each observer performed two tasks: a peripheral recognition task on triplets of letters, and a foveal recognition task on synthesized stimuli. In the former, each trial began with a 200 ms presentation of three letters in the periphery, arranged along the horizontal meridian. Letters were uppercase, in the Courier font, and 1 deg in height. The “target” letter was centered at 6 deg eccentricity, and the two “flanker” letters were presented left and right of the target. All three letters were drawn randomly from the alphabet without replacement. We varied the center-to-center spacing between the letters, from 1.1 deg to 2.8 deg (all large enough to avoid letter overlap). Observers had 2 s to identify the target letter with a key press (1 out of 26 possibilities, chance = 4%). Observers performed 48 trials for each spacing. For each observer, performance as a function of spacing was fit with a Weibull function by maximizing likelihood. Spacings of 1.1, 1.5, and 2 deg corresponded to approximately 50%, 65%, and 80% performance respectively; these spacings were used to generate synthetic stimuli for the foveal task (see below). To extend our range of performance, two observers were run in an additional condition (8 deg eccentricity, 0.8 letter size, 1 deg spacing) yielding approximately 20% performance. For these observers, the same condition was included in the foveal task.

We used the mid-ventral model to synthesize stimuli matched to the letter triplets. To reduce the number of images that had to be synthesized (computational cost is high for the small scaling parameters), we synthesized stimuli containing triplets along eight radial arms, but eccentricity, letter size, font, and letter-to-letter spacing were otherwise identical. For each image of triplets we generated nine different synthetic stimuli: three different spacings (1.1, 1.5, 2 deg) for each of three different model scalings (0.4, 0.5, 0.6) centered roughly around the average critical scaling estimated in our initial metamer experiment. We synthesized stimuli for 56 unique letter triplets; letter identity was balanced across the experimental manipulations. On each trial of the foveal recognition task, one of the triplets from the synthesized stimuli was presented for 200 ms, and the observer had 2 s to identify the middle letter. The observer saw each unique combination of triplet identity, spacing, and scaling only once. Trials with different spacings were interleaved, but the three different model scalings were performed in separate blocks (with random order).