Extra-Classical Tuning Predicts Stimulus-Dependent Receptive Fields in Auditory Neurons

Abstract

The receptive fields of many sensory neurons are sensitive to statistical differences among classes of complex stimuli. For example, excitatory spectral bandwidths of midbrain auditory neurons and the spatial extent of cortical visual neurons differ during the processing of natural stimuli compared to the processing of artificial stimuli. Experimentally characterizing neuronal nonlinearities that contribute to stimulus-dependent receptive fields is important for understanding how neurons respond to different stimulus classes in multiple sensory modalities. Here we show that in the zebra finch, many auditory midbrain neurons have extra-classical receptive fields, consisting of sideband excitation and sideband inhibition. We also show that the presence, degree, and asymmetry of stimulus-dependent receptive fields during the processing of complex sounds are predicted by the presence, valence, and asymmetry of extra-classical tuning. Neurons for which excitatory bandwidth expands during the processing of song have extra-classical excitation. Neurons for which frequency tuning is static and for which excitatory bandwidth contracts during the processing of song have extra-classical inhibition. Simulation experiments further demonstrate that stimulus-dependent receptive fields can arise from extra-classical tuning with a static spike threshold nonlinearity. These findings demonstrate that a common neuronal nonlinearity can account for the stimulus dependence of receptive fields estimated from the responses of auditory neurons to stimuli with natural and non-natural statistics.

Introduction

Sensory neurons are characterized by the stimuli that modulate their firing (Haberly, 1969; Welker, 1976; Theunissen et al., 2001), and the stimulus features that evoke spiking responses define the neuron's receptive field (RF). The RF may be measured using simple stimuli such as tones or bars of light. In auditory neurons, the classical receptive field (CRF) is characterized by the frequency and intensity ranges of pure tones that evoke spiking responses (Schulze and Langner, 1999). The RFs of sensory neurons estimated from responses to complex stimuli such as vocalizations or natural scenes are called spectrotemporal or spatiotemporal receptive fields (STRFs), which are characterized by computing linear estimates of the relationship between stimulus features and neural responses. In auditory neurons, STRFs are linear models of the spectral and temporal features to which neurons respond during the processing of complex sounds (Theunissen et al., 2000).

The STRFs of some sensory neurons are sensitive to statistical differences among classes of complex stimuli (Blake and Merzenich, 2002; Nagel and Doupe, 2006; Woolley et al., 2006; Lesica et al., 2007; Lesica and Grothe, 2008; David et al., 2009; Gourévitch et al., 2009). Previous studies have proposed that stimulus-dependent changes in the linear approximation of the stimulus–response function may maximize the mutual information between stimulus and response (Fairhall et al., 2001; Escabí et al., 2003; Sharpee et al., 2006; Maravall et al., 2007), facilitate neural discrimination of natural stimuli (Woolley et al., 2005, 2006; Dean et al., 2008), and correlate with changes in perception (Webster et al., 2002; Dahmen et al., 2010). In principle, stimulus-dependent STRFs could arise if neurons adapt their response properties to changes in stimulus statistics (Sharpee et al., 2006) or if neurons have static but nonlinear response properties (Theunissen et al., 2000; Christianson et al., 2008). In the case of nonlinear response properties, different classes of stimuli drive a neuron along different regions of a nonlinear stimulus–response curve. Determining the degree to which RF nonlinearities influence stimulus-dependent STRFs and experimentally characterizing such nonlinearities are important for understanding how neurons respond to different stimulus classes in multiple sensory modalities.

Here we tested the hypothesis that major nonlinear mechanisms in auditory midbrain neurons are extra-classical receptive fields (eCRFs), which are composed of sideband excitation and/or inhibition and which modulate spiking responses to stimuli that fall within CRFs (Allman et al., 1985; Vinje and Gallant, 2002; Pollak et al., 2011). Songbirds were studied because they communicate using spectrotemporally complex vocalizations and because their auditory midbrain neurons respond strongly to different classes of complex sounds, allowing the direct comparison of spectrotemporal tuning to different sound classes. From single neurons, we estimated STRFs from responses to song and noise, computed CRFs from responses to single tones, and tested for the presence of eCRFs from responses to tone pairs. For each neuron, we measured the correspondence between stimulus-dependent STRFs and the presence, valence (excitatory or inhibitory), and frequency asymmetry (above or below best frequency) of eCRFs. Lastly, we used simulations to demonstrate that subthreshold tuning with a static spike threshold nonlinearity can account for the observed stimulus dependence of real midbrain neurons.

Materials and Methods

Surgery and electrophysiology.

All procedures were performed in accordance with the National Institutes of Health and Columbia University Animal Care and Use policy. The surgery and electrophysiology procedures are described in detail by Schneider and Woolley (2010). Briefly, 2 d before recording, male zebra finches were anesthetized, craniotomies were made at stereotaxic coordinates in both hemispheres, and a head post was affixed to the skull using dental cement. On the day of recording, the bird was given three 0.03 ml doses of 20% urethane. The responses of single auditory neurons in the midbrain nucleus mesencephalicus lateralis dorsalis (MLd) were recorded using glass pipettes filled with 1 m NaCl (Sutter Instruments), ranging in impedance from 3 to 12 MΩ. Neurons were recorded bilaterally and were sampled throughout the extent of MLd. We recorded from all neurons that were driven (or inhibited) by any of the search sounds (zebra finch songs, samples of modulation-limited noise). Isolation was ensured by calculating the signal-to-noise ratio of action potential and non-action potential events and by monitoring baseline firing throughout the recording session. Spikes were sorted offline using custom MATLAB software (MathWorks).

Stimuli.

We recorded spiking activity while presenting song, noise, and tones from a free-field speaker located 23 cm directly in front of the bird. Upon isolating a neuron, we first played 200 ms isointensity-pure tones [70 dB sound pressure level (SPL)] to estimate the neuron's best frequency (BF), and then presented isofrequency tones at the BF to construct a rate-intensity function. We next presented isointensity pure tones ranging in frequency between 500 and 8000 Hz (in steps of 500 Hz) and tone pairs comprised of the BF paired with all other frequencies. The two tones in a pair were each presented at the same intensity as the single tones, resulting in sounds that were louder than the individual tones. We chose the intensity such that the rate-intensity function at the BF was not saturated and was typically 70 dB SPL (for 56% of neurons). If the neurons were unresponsive at 70 dB (8%) or if their rate-intensity functions were saturated (36%), we presented the tones at higher or lower intensities, respectively. After collecting the tone responses, we pseudorandomly interleaved 20 renditions of unfamiliar zebra finch song and 10 samples of modulation-limited noise (Woolley et al., 2005), a spectrotemporally filtered version of white noise that has the same spectral and temporal modulation boundaries as zebra finch song (see Fig. 1). Each song and noise sample was presented 10 times. Song and noise samples were ∼2 s in duration and were matched in root means square (RMS) intensity (72 dB SPL). Lastly, we collected a complete tone CRF by playing 10 repetitions each of 200 ms pure tones that varied in frequency between 500 and 8000 Hz (in steps of 500 Hz) and intensity between 20 and 90 dB SPL (in steps of 10 dB).

Figure 1.

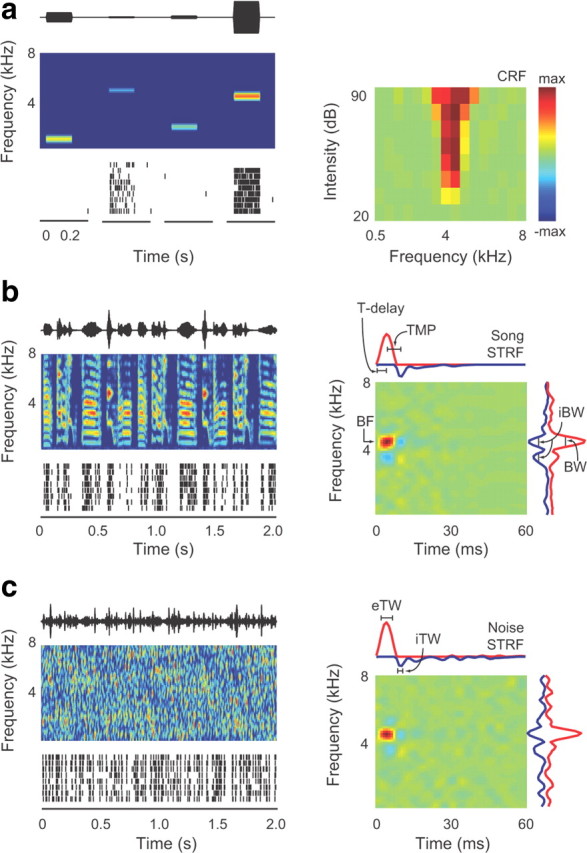
Auditory neurons are characterized by their receptive fields. a–c, Sound pressure waveforms of example stimuli are shown in the top left. Spectrograms, in which sound intensity is indicated by color, are in the middle. Red is high and blue is low. Spike trains evoked by 10 presentations of the sound shown above are at the bottom. a, Responses to pure tones were used to measure a neuron's classical receptive field (CRF, right). Color indicates response strength, which is the driven firing rate minus the spontaneous firing rate at each frequency–intensity combination. Red regions show higher firing rates compared with spontaneous firing rates, and blue regions show lower firing rates (maximum = 145 spikes/s). As with most neurons we recorded, this neuron was not inhibited by any single frequency–intensity combination and therefore the CRF has no blue regions. b, c, Spectrotemporal receptive fields were calculated independently from responses to song (b) and noise (c). STRFs are on the right. Red regions of the STRF show frequencies correlated with increased firing rates, and blue regions show frequencies correlated with decreased firing rates. Measurements of STRF parameters are indicated in b and c.

Estimating STRFs.

Spectrotemporal receptive fields were calculated from responses to song and noise stimuli by fitting a generalized linear model (GLM) with the following parameters: a two-dimensional linear filter in frequency and time (k, the STRF), an offset term (b), and a 15 ms spike history filter (h) (Paninski, 2004; Calabrese et al., 2011). The conditional spike rate of the model is given as λ:

In Eq. 1, x is the log spectrogram of the stimulus and r(t − j) is the neuron's spiking history. The log likelihood of the observed spiking response given the model parameters is as follows.

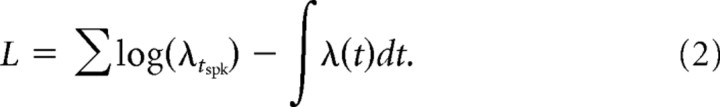In Eq. 2, t_spk denotes the spike times and the integral is taken over all experiment times. We optimized the GLM parameters (k, b, and h) to maximize the log-likelihood.

The STRFs had 3 ms time resolution and 387.5 Hz frequency resolution. The analyses presented here focus on the STRF parameters, because the offset term and spike history filter differ only minimally between song and noise GLMs and contribute marginally and insignificantly to differences in predictive power. Before analyzing STRFs, we performed a 3× up-sampling in each dimension using a cubic spline.

To validate each GLM STRF as a model for auditory tuning, we used the STRF to predict 10 spike trains in response to song and noise samples that were played while recording but were not used in the STRF estimation. We then compared the predicted response to the observed response by creating peristimulus time histograms (PSTHs) from the observed and predicted responses (5 ms smoothing) and calculating the correlation between the observed and predicted PSTHs.

Characterizing STRFs.

From each STRF, we measured two parameters relating to the scale of the STRF. The “Peak” of each STRF was the value of the largest single pixel. The “Sum” of each STRF was the sum of the absolute values of every STRF pixel. To parameterize spectral tuning, we calculated the BF and bandwidth (BW) by setting negative STRF values to 0, projecting the STRF onto the frequency axis, and smoothing the resulting vector with a 4-point Hanning window (David et al., 2009). We used a similar method to calculate the BW of the inhibitory region of the STRF (iBW), by first setting positive STRF values to zero. For the example neurons in Figure 5, the spectral profiles were calculated without setting negative STRF values to 0. The BF was the frequency where the excitatory spectral projection reached its maximum, and the BW was the range of frequencies within which the spectral projection exceeded 50% of its maximum.

Figure 5.

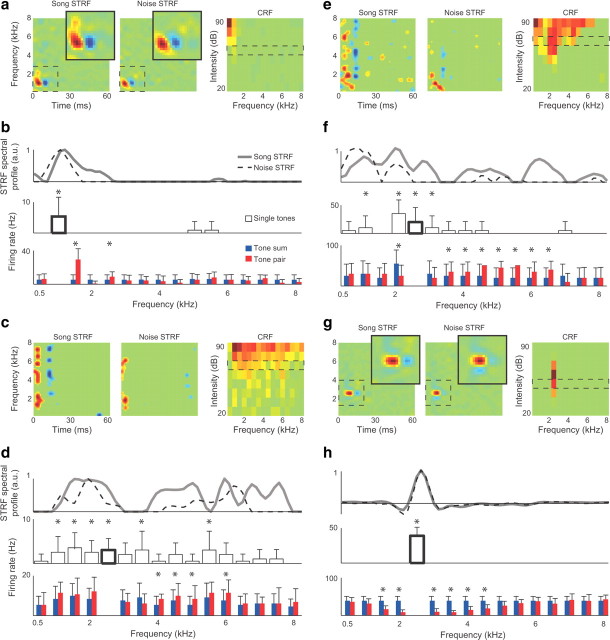
Extra-classical excitation measured with tone pairs. a, c, e, g, The song STRF, noise STRF, and CRF for four representative single neurons. The intensity that is enclosed by a dashed box within the CRF shows the intensity at which tones were presented for these experiments (60, 70, 70 and 50 dB, respectively). The darkest red pixel in each CRF corresponds to the maximum response strengths, which are 59.2 Hz (a), 17.5 Hz (c), 65 Hz (e), and 31 Hz (g). Green pixels show response strength of zero. b, d, f, h, The top row shows the spectral profiles of song and noise STRFs. The middle row shows the strength of the neural responses (firing rate, mean + SD) to isointensity pure tones ranging in frequency between 0.5 and 8 kHz. Asterisks indicate frequencies that drove responses significantly above baseline (p < 0.05) and were therefore in the CRF. The bold bar marks the frequency that was used as the BF in the tone pair experiments (1, 2.5, 2.5,and 2.5 kHz, respectively). The bottom row shows the response to tone pairs (red) comprised of the BF played simultaneously with tones ranging from 0.5 to 8 kHz and the sum of the two tones played independently (b, d, f) or the BF played alone (h) (blue). Significant differences between the blue and red bars at frequencies outside of the CRF show the eCRF. Asterisks (*) indicate frequencies that interacted significantly with the BF (p < 0.05). In b, d, f these interactions were excitatory. In h, these interactions were inhibitory. The top, middle, and bottom panels share the same frequency axis.

To measure temporal tuning, we created separate excitatory and inhibitory temporal profiles by projecting the STRF onto the time axis after setting negative and positive STRF values to 0, respectively. For both temporal projections, we used only the range of frequencies comprising the excitatory BW. The temporal delay (T-delay) was the time from the beginning of the STRF to the peak of excitation. The temporal modulation period (TMP) was the time of peak excitation to the time of peak inhibition. The excitatory and inhibitory temporal widths (eTW and iTW) measured the durations for which excitation and inhibition exceeded 50% of their maxima. The excitation–inhibition index (EI index) was the sum of the area under the excitatory temporal profile (a positive value) and inhibitory temporal profile (a negative value) normalized by the sum of the absolute values of the two areas. The EI index ranged from +1 to −1, with positive values indicating greater excitation than delayed inhibition.

Comparing song and noise STRFs.

To determine the degree to which STRF parameters varied between the song and noise STRFs of single neurons, we first calculated the range of values that each parameter could take, observed across all neurons and both STRF types. For example, the minimum excitatory BW observed across all neurons was 131 Hz, and the maximum BW was 5377 Hz. The range of BWs across all neurons and all STRFs was 5246 Hz. For each neuron, we then calculated the difference between each parameter as a fraction of the range observed across all STRFs. For example, the song and noise STRFs of a single neuron had BWs of 2295 and 1082 Hz, respectively. The difference between these bandwidths was 1213 Hz. Expressed as a fraction of the range, this BW difference was 0.23, indicating that the difference between song and noise STRF BWs for this neuron covered 23% of the range of BWs observed across all neurons. Parameters that varied widely across neurons but only slightly between song and noise STRFs for a single neuron had low values (e.g., BF). Parameters that varied substantially between the song and noise STRFs had values closer to 1 (e.g., TMP). We report the mean and SD of parameter values as a fraction of their observed range.

To determine the degree to which the 10 STRF parameters accounted for differences in predictive power between the song and noise STRFs of single neurons, we used a multivariate regression model. Each predictor variable was the absolute value of the difference between the song and noise STRFs for a single STRF parameter. The predictor variables included 10 STRF parameters, 45 interaction terms, and an offset term. To determine the variance explained by differences in single STRF parameters, we used each parameter in a linear regression model with a single predictor variable plus an offset term. The explainable variance calculated from partial correlation coefficients of the multivariate model (data not shown) was lower than the explainable variance reported from the single-variable models, but the STRF parameters that predicted the most variance were the same in both cases.

Measuring classical and extra-classical RFs.

We used responses to pure tones and tone pairs to measure classical and extra-classical tuning. Here, we define the CRF as the range of frequency–intensity combinations that modulate spiking significantly above or below the baseline firing rate. We define the eCRF as consisting of frequency–intensity combinations that do not modulate the firing rate when presented alone, but do modulate the firing rate during simultaneous CRF stimulation. For stimuli composed of pairs of tones, both tones were presented simultaneously. To determine whether a tone frequency evoked a significant response, we compared the distribution of driven spike counts to the distribution of baseline spike counts (Wilcoxon rank-sum test, p < 0.05). To determine whether a tone frequency provided significant extra-classical excitation, we measured whether the spike count when the pair was presented simultaneously (n = 10) exceeded the sum of the spike counts when the tones were presented independently (n = 100). To determine whether a tone frequency provided significant extra-classical inhibition, we measured whether the spike count when the pair was presented simultaneously (n = 10) was less than the spike count when the BF was presented alone (n = 10). We used two criteria to ensure that our estimates of eCRF BW were conservative. First, eCRF BWs only included frequencies that did not drive significant responses when presented independently. Second, eCRF BWs only included frequencies that were continuous with the CRF. We interpolated the single-tone and tone-pair tuning curves 3× to achieve greater spectral resolution.

The temporal patterns of neural response to tones and tone pairs differed across the population of recorded midbrain neurons. Some neurons responded with sustained firing throughout the stimulus duration, whereas other neurons fired only at the sound onset. For the majority of neurons (89%), using the full response (0–200 ms) and using only the onset response (0–50 ms) resulted in highly similar eCRF BWs. Therefore, to maintain consistency across neurons, we counted spikes throughout the entire stimulus duration for every neuron.

Because we performed 16 statistical tests to determine the eCRF for each neuron (one for each frequency channel), we considered using an adjusted p value that corrected for multiple comparisons to minimize type 1 errors (false positives). Using this stricter criterion (Bonferroni-corrected, p < 0.0031), we found that 9 of 24 neurons no longer had significant excitatory eCRFs. To determine whether these 9 neurons were false positives, we analyzed the frequency channels of each neuron's excitatory eCRF relative to the frequency channels of its CRF. We reasoned that false positives could occur at any frequency channel, whereas real interactions should only occur at frequency channels that are continuous with the CRF. For each of the 9 neurons, the eCRF frequency channels were always continuous with the CRF. The likelihood of observing this pattern simply by chance is 3 in 1000, indicating that the eCRFs of these neurons are likely to be real interactions, rather than false positives. To avoid incurring an inordinate number of false negatives, we used a significance threshold of p < 0.05 in all subsequent analyses.

Simulating neurons.

Using a generative model, we simulated neurons with varying firing rate, BF, BW, iBW, eTW, iTW, EI index, Peak, and Sum. These simulated parameters were chosen from the ranges observed in real MLd neurons. We also systematically varied two other parameters, the spike threshold and the shape of the spectral profile. We used three different spectral profiles, one with subthreshold excitation, one with subthreshold inhibition, and one without subthreshold excitation or inhibition.

For simulated neurons with subthreshold inhibition, we set the spike threshold to the value of the “resting membrane potential,” such that any stimuli that fell within the STRF's excitatory region increased firing probability, and any stimuli that fell within the STRF's inhibitory sidebands decreased firing probability. For neurons with excitatory subthreshold tuning or without subthreshold tuning, we used two values for the spike threshold. The first value was equal to the resting membrane potential, such that any stimuli that fell within the bandwidth of the STRF increased the firing probability. The second value was depolarized relative to the resting potential. For neurons with extra-classical excitation, weak stimuli or stimuli that fell at the periphery of the spectral profile caused changes in membrane potential but did not alone increase the firing probability. Adjusting this threshold decreased the range of frequencies that evoked spikes. For the neurons without extra-classical tuning, this threshold did not significantly change the range of frequencies that evoked spikes.

For each stimulated neuron, we used a generative model to simulate spiking responses to 20 songs and 10 renditions of modulation-limited noise. We first convolved each STRF (k) with the stimulus spectrogram (x). The spiking responses were generated using a modified GLM with the following time varying firing distribution:

where arg max() represents a rectifying nonlinearity that sets all negative values equal to zero and θ represents the difference between the resting membrane potential and the spiking threshold. The differences between the generative model and the GLM-fitting model are as follows: (1) the offset term (b) has been removed, and a new offset term (θ) has been placed outside of the exponential function; and (2) the spike history terms have been removed. For these simulations, the only parameter that we systematically changed was θ, which determined whether or not the model neuron possessed subthreshold tuning. When θ equaled 0, the resting membrane potential was very near the spiking threshold, and the model could not have subthreshold excitation but could have subthreshold inhibition. When θ was negative, the model could have subthreshold excitation. Larger positive values of θ produced higher spontaneous rates, which we did not observe in real MLd neurons. Therefore, we did not simulate neurons with positive θ values. For these simulations, θ was set to 0 (for neurons with subthreshold inhibition) or −1.5 (for neurons with subthreshold excitation or no extra-classical tuning). Our simulation results are robust to a range of θ values; the difference between song and noise STRFs decreased as θ approached 0 and increased as θ became more negative. As θ approached −3, the firing rates decreased substantially. We did not choose θ (−1.5) to optimize the differences between song and noise STRFs, but instead chose a value that accurately captured this effect without resulting in firing rates that were substantially lower than those observed in real MLd neurons. We generated spike trains from a binomial distribution with a time-varying mean described by λ. For each song and noise stimulus, we simulated 10 unique spike trains. Using these spike trains, we fit GLMs using the standard GLM method (see above, Estimating STRFs), which does not include the subthreshold tuning term, θ. We compared the excitatory bandwidths of the resulting song and noise STRFs.

Results

Characterizing the STRFs and CRFs of single auditory midbrain neurons

The primary goal of this study was to identify potential mechanisms whereby the STRFs of single neurons differ during the processing of different sound classes. We first characterized the degree and functional relevance of stimulus-dependent STRFs in 134 single midbrain neurons. We recorded neural responses to pure tones that varied in frequency and intensity and to two classes of complex sounds that differed in their spectral and temporal correlations, zebra finch song and modulation-limited noise (Woolley et al., 2005, 2006), referred to as noise from here on (Fig. 1a–c, left). From responses to pure tones, we measured each neuron's CRF (Fig. 1a, right). The CRF is comprised of frequency–intensity combinations that drive a neuron to fire above (or below) the baseline firing rate. Frequency–intensity combinations that do not modulate firing are said to lie outside of the CRF. From responses to song and noise, we determined the presence and extent of stimulus-dependent STRFs by calculating two STRFs for each neuron—one song STRF and one noise STRF (Fig. 1b,c, right). To measure STRFs, we fit a GLM that maps the spiking response of single neurons onto the spectrogram of the auditory stimuli (Paninski, 2004; Calabrese et al., 2011).

From each STRF, we obtained three measures of spectral tuning. The best frequency or BF is the frequency that drives the strongest neural response (Fig. 1b). The excitatory and inhibitory bandwidths (BW and iBW, respectively) are the frequency ranges that drive excitatory or inhibitory responses (Fig. 1b). We obtained five measures of temporal tuning. The temporal delay, T-delay, is the time to peak excitation in the STRF, and the temporal modulation period, TMP, is the time lag between the peaks of excitation and inhibition (Fig. 1b). The temporal widths are the durations of excitation and inhibition, eTW and iTW, respectively (Fig. 1c). The excitation–inhibition index, EI index, is the balance between excitation and delayed inhibition. We also measured two parameters from the STRF scale, the maximum value of the STRF (Peak) and the sum of the absolute value of every STRF pixel (Sum).

STRF spectral bandwidth is stimulus-dependent

Figure 2a shows the song and noise STRFs of three neurons that are representative of the range of stimulus-dependent STRFs that we observed across the population of recorded neurons. The neuron on the top row has stimulus-independent song and noise STRFs. The song and noise STRFs of the neurons in the middle and bottom rows differ in their spectral and temporal tuning, indicating stimulus dependence. For the neuron in the middle row, the song STRF has a broader excitatory BW and stronger delayed inhibition than does the noise STRF. For the neuron in the bottom row, the noise STRF has an excitatory region that is broader in frequency (BW) and in time (eTW).

Figure 2.

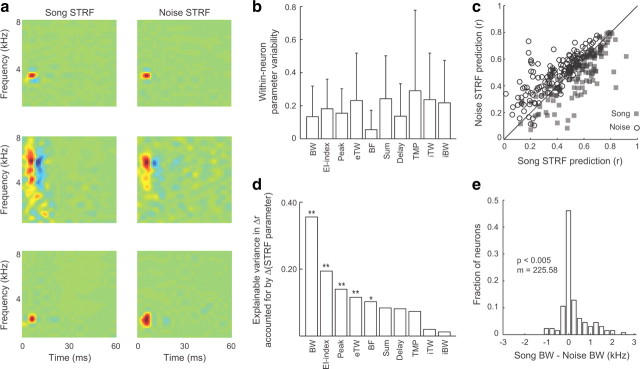
STRF excitatory bandwidth is stimulus-dependent. a, Song STRFs (left) and noise STRFs (right) for three representative MLd neurons. Song and noise STRFs of the neuron in the top row are highly similar. The neurons in the middle and bottom rows have song and noise STRFs that differ in their spectral and temporal tuning. b, Song and noise STRFs differ at the single neuron level. Each bar shows the degree (mean + SD) of differences between song and noise STRFs for single neurons, normalized by the range of each parameter observed across all neurons. EI index is the normalized ratio of excitation and inhibition and Sum is the sum of the absolute values of all pixel values in the STRF. Other abbreviations are as described in Figure 1. c, Song and noise STRFs were used to predict neural responses to novel within-class and between-class stimuli. Across the population of neurons, STRFs were significantly better at predicting neural responses to within-class stimuli compared with between-class stimuli (p = 3 × 10⁻¹⁰). d, The degree to which STRFs differentially predicted responses to within-class and between-class stimuli can be accounted for by differences in the measured parameters of song and noise STRFs. Together, the STRF parameters accounted for 72% of the difference in STRF predictions between sound classes (Δr). Each bar shows the fraction of this variance accounted for by the STRF parameters used independently. Differences in BW alone accounted for more than one-third of the explainable variance (*p < 0.05; **p < 0.01). e, The distribution of bandwidth differences across the population of recorded neurons shows that many neurons respond to a different range of frequencies during the processing of song compared with noise and that the distribution is biased toward broader song STRFs (mean = 225.58 Hz, p < 0.005).

At the single neuron level, a subset of tuning parameters differed substantially between the song and noise STRFs of some neurons (Fig. 2b), indicating stimulus-dependent STRFs during the processing of song compared to noise. To determine whether the differences between song and noise STRFs were significant, we used each STRF to predict neural responses to within-class and between-class stimuli and measured the correlation between the predicted and actual responses (Woolley et al., 2006). If the differences between song and noise STRFs were significant, STRFs should more accurately predict the neural response to within-class stimuli compared to between-class stimuli. We found that song STRFs predicted neural responses to song stimuli significantly better than did noise STRFs, and vice versa for noise STRFs (p = 3 × 10⁻¹⁰) (Fig. 2c), indicating that differences between the song and noise STRFs were significant for these neurons.

We next measured how much of the difference in predictive power between song and noise STRFs could be accounted for by differences in the 10 tuning parameters measured from the STRFs. Using all of the parameters together in a multivariate model accounted for 72.6% of the variance in predictive power (Δr), showing that the parameters we measured from the STRFs account for a large fraction of the difference in their predictive power. Comparing Figure 2, b and d shows that the stimulus parameters that vary the most between the song and noise STRFs of single neurons are not the parameters that best account for between-class differences in STRF predictive power. Differences in BW alone accounted for more than one-third of the explainable variance (36%), far more than any other single STRF parameter (Fig. 2d). Because differences in BW were the most important for predicting differences in predictive power, subsequent analyses were focused on this tuning parameter.

For some neurons, the song BW was broader than the noise BW, and vice versa for other neurons. Across the population of recorded neurons, song and noise STRF BWs were substantially different (> 250 Hz) for 38% of neurons, and neurons generally had broader song than noise STRFs (p < 0.005) (Fig. 2e). These results show that, on average, song STRFs have significantly broader bandwidths than do noise STRFs.

Stimulus spectral correlations and the eCRF hypothesis

To explore the physiological bases of the observed stimulus-dependent STRFs, we first examined the statistical differences between song and noise. Communication vocalizations such as human speech and bird song are characterized by strong spectral and temporal correlations, whereas artificial noise stimuli have much weaker correlations (Fig. 3a) (Chi et al., 1999; Singh and Theunissen, 2003; Woolley et al., 2005). To quantify the strength of spectral correlations in the stimuli presented to these neurons, we calculated the average spectral profile of song and noise stimuli for every 20 ms sound snippet, and the profiles were then aligned at their peaks and averaged (Fig. 3b). The results show that, in song, energy in one frequency channel tends to co-occur with energy in neighboring frequency channels. Alternatively, in noise, energy tends to be constrained to a narrow frequency band.

Figure 3.

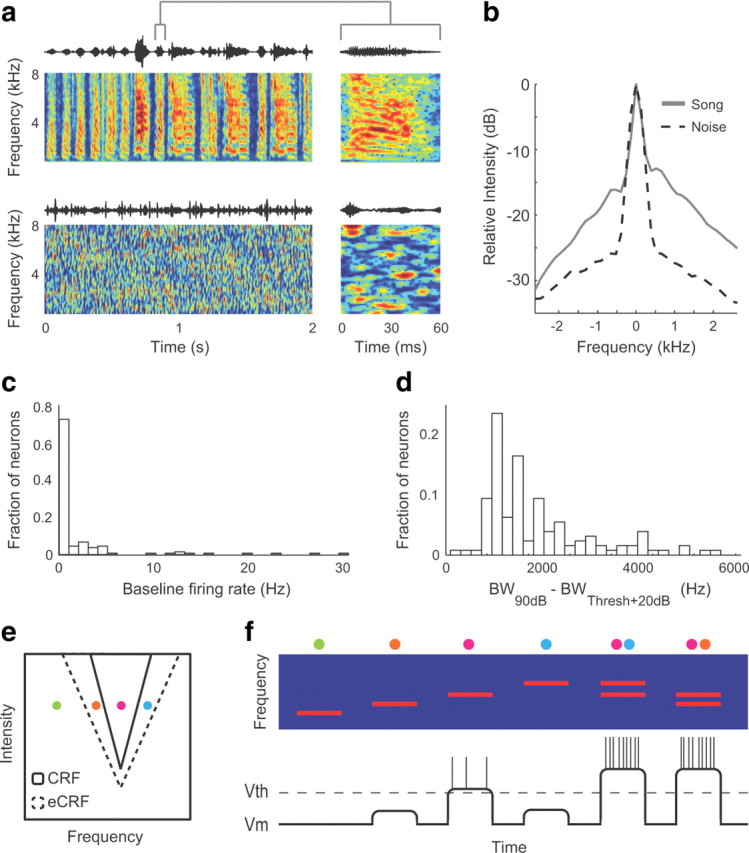
Correlated stimuli could modulate neural responses by recruiting subthreshold inputs. a, Song and noise stimuli have different correlations. Spectrograms of 2 s samples of song (top) and noise (bottom) are on the left and 60 ms samples of song and noise are on the right. b, The average spectral profiles of 20 ms samples of song (solid line) and noise (dashed line) aligned at their peaks (i.e., the spectral autocorrelation). Song energy is more correlated across multiple contiguous frequency bands than is noise energy. c, Histogram showing the average baseline firing rate recorded during the 1 s of silence preceding stimulus presentation. d, Histogram showing the difference in excitatory bandwidth measured from pure tones at 90 dB SPL and at 20 dB above each neuron's threshold. Bandwidth expands substantially as sound intensity increases. e, A model of a neuron with V-shaped excitatory classical (solid lines) and extra-classical (dashed lines) receptive fields. The colored dots represent isointensity tone stimuli at four different frequencies. Tones that fall within the solid V evoke spiking responses. Tones that fall within the dashed V evoke subthreshold changes in membrane potential, but not spikes. f, The top shows a spectrogram of the stimuli shown in e. Dots at the top of the spectrogram show the location of each stimulus in the neuron's receptive field. A diagram of changes in membrane potential and spiking activity (vertical lines) during each stimulus is shown below.

The strong spectral correlations in song and the weaker spectral correlations in noise led to the hypothesis that energy simultaneously present across a wide range of frequencies could recruit nonlinear tuning mechanisms during song processing that are not recruited during noise processing. Subthreshold tuning allows some stimuli to cause changes in the membrane potential of sensory neurons without leading to spiking responses. Subthreshold tuning has been described in auditory and visual neurons and could potentially contribute to stimulus-dependent encoding (Nelken et al., 1994; Schulze and Langner, 1999; Tan et al., 2004; Priebe and Ferster, 2008). The auditory neurons from which we recorded had low baseline firing rates (Fig. 3c) and CRF BWs that broadened substantially with increased stimulus intensity (Fig. 3d), suggesting that these midbrain neurons may receive synaptic input from frequencies outside of the CRF that remains subthreshold in responses to single tones.

An illustration of this type of tuning for auditory neurons is shown in Figure 3e. The solid triangle shows a V-shaped tuning curve or CRF. Stimuli that fall within the CRF evoke spikes, while stimuli that fall outside the CRF do not. Surrounding the CRF is a second triangle representing the eCRF. Stimuli that fall within the eCRF, but not within the CRF, cause changes in membrane potential, but not spikes, and can facilitate or suppress spiking responses to stimuli that fall within the CRF. Figure 3f shows representative responses of a neuron with the CRF and eCRF depicted in Figure 3e to four different isointensity tones, depicted as dots in Figure 3e, and to combinations of those tones. Although only the red tone evokes spikes when played alone, the firing rate in response to the red tone increases when it is presented simultaneously with tones that fall in the eCRF (orange or blue tones). In this model of a threshold nonlinearity, the spiking response to tone pairs is a nonlinear combination of the spiking responses to the two individual tones, even though changes in the membrane potential follow a purely linear relationship. This diagram illustrates that spectrally correlated stimuli such as tone pairs, harmonic stacks, or vocalizations could change the range of frequencies that is correlated with spiking by recruiting synaptic input outside of the CRF. If midbrain neurons have eCRFs, the broadband energy of song will fall within the CRF and eCRF more frequently than will the more narrowband energy of noise, which could lead to differences in excitatory STRF BW.

Tone pairs reveal extra-classical excitation and inhibition

To test the hypothesis that auditory midbrain neurons have eCRFs and that the combined stimulation of CRFs and eCRFs leads to stimulus-dependent STRFs, we first measured the presence/absence and valence (excitatory or inhibitory) of eCRFs in midbrain neurons. For each neuron, we presented single tones ranging from 500 to 8000 Hz interleaved with tone pairs comprised of the BF presented simultaneously with a non-BF tone. To test for the presence of eCRFs, we measured whether tone pairs evoked spike rates that differed significantly from those predicted by the sum of the two tones presented independently (excitatory eCRFs) or the response to the BF presented alone (inhibitory eCRFs) (Shamma et al., 1993). Tone pairs that evoked spike rates higher than the sum of the responses to the tones presented independently indicated extra-classical excitation at the non-BF frequency (Fig. 4a). Tone pairs that evoked lower spike rates than the response to the BF indicated extra-classical inhibition at the non-BF frequency (Fig. 4b). Frequency channels were considered part of the eCRF only if they were continuous with the CRF.

Figure 4.

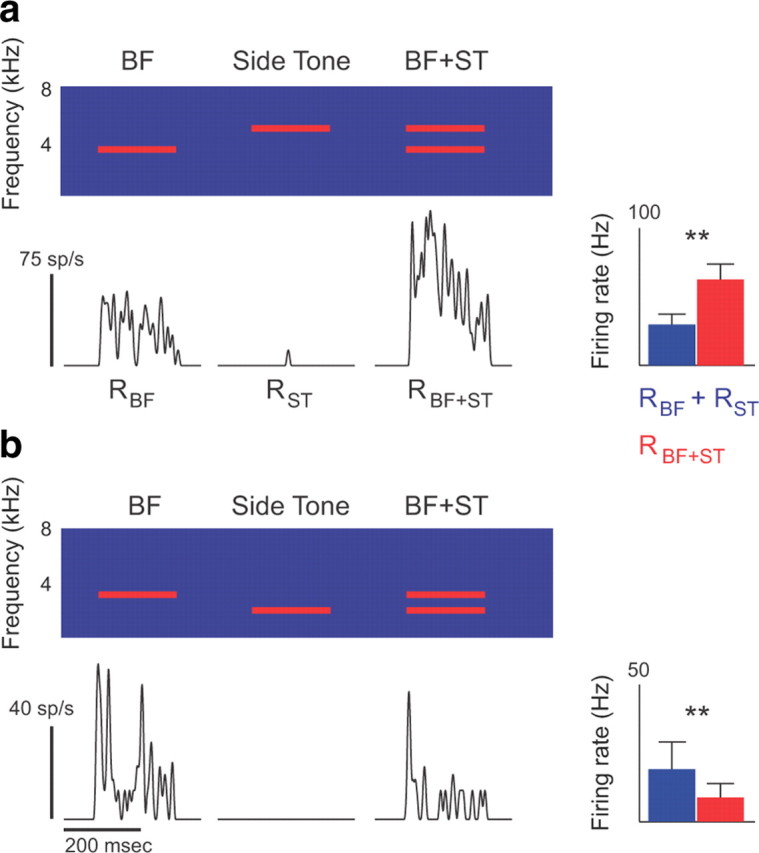
Paired tones reveal extra-classical excitation and inhibition. a, b, The top panel shows the spectrogram of three successive stimuli: a pure tone at the neuron's BF, a side tone (ST) near the BF but outside of the CRF, and the two tones presented simultaneously. The black PSTHs below show the average neural response to each stimulus. The bar graphs at the right show the firing rates in response to multiple presentations of tone pairs (R_BF+ST, red; mean + SD), and the sum of firing rates in response to the two tones (BF and ST) played independently (R_BF + R_ST, blue). In a, the tone pair produced significantly higher firing rates than predicted by the two tones played independently, indicating extra-classical excitation. In b, the tone pair produced significantly lower firing rates, indicating extra-classical inhibition.

Excitatory eCRFs were observed in 29% of neurons. Figure 5, a–f, shows three representative neurons for which the responses to tone pairs revealed extra-classical excitation. For these neurons, the song STRF had a wider BW than the noise STRF, and single pure tones evoked action potentials in either a narrow range of frequencies (Fig. 5b, middle) or a broad range of frequencies (Fig. 5d,f, middle). Although tones outside of the CRF did not evoke action potentials when presented alone, a subset of second tones significantly increased the response to the BF when presented concurrently (middle and bottom), indicating that their facilitative effect was driven by subthreshold excitation. On average, the range of frequencies comprising the CRF and eCRF exceeded the range of single tones that evoked action potentials at the highest intensity presented (90 dB SPL) by >1400 Hz (Wilcoxon signed-rank test, p < 0.001), indicating that at least some frequencies in the eCRF would not evoke spikes at any sound intensity.

Extra-classical inhibitory tuning was observed in 30% of neurons. For the neuron in Figure 5, g and h, the song and noise STRFs had very similar excitatory BWs. Probing the receptive field with tone pairs revealed that this neuron received broad inhibitory input at frequencies above and below the BF (Fig. 5 h), showing that inhibitory eCRFs (sideband inhibition) can lead to STRFs with similar excitatory BWs. On average, inhibitory eCRFs had a BW of 1160 Hz beyond the borders of the CRF (range, 500–4667 Hz). Only one neuron had both excitatory and inhibitory eCRFs, which were located on opposite sides of the BF. The remaining neurons (41%) had no eCRFs.

Extra-classical receptive fields predict stimulus-dependent STRFs

Across the population of 84 neurons for which we measured eCRFs, the valence (excitatory or inhibitory) of the eCRF largely determined the relationship between song and noise STRF excitatory bandwidths. On average, neurons with extra-classical excitation had wider song STRF BWs than noise STRF BWs (p = 3 × 10⁻⁴) (Fig. 6a). Although not significant, neurons with extra-classical inhibition tended to have highly similar song and noise STRF BWs or wider noise STRFs than song STRFs (p = 0.08). Neurons with no extra-classical tuning had highly similar song and noise STRF BWs (p = 0.87).

Figure 6.

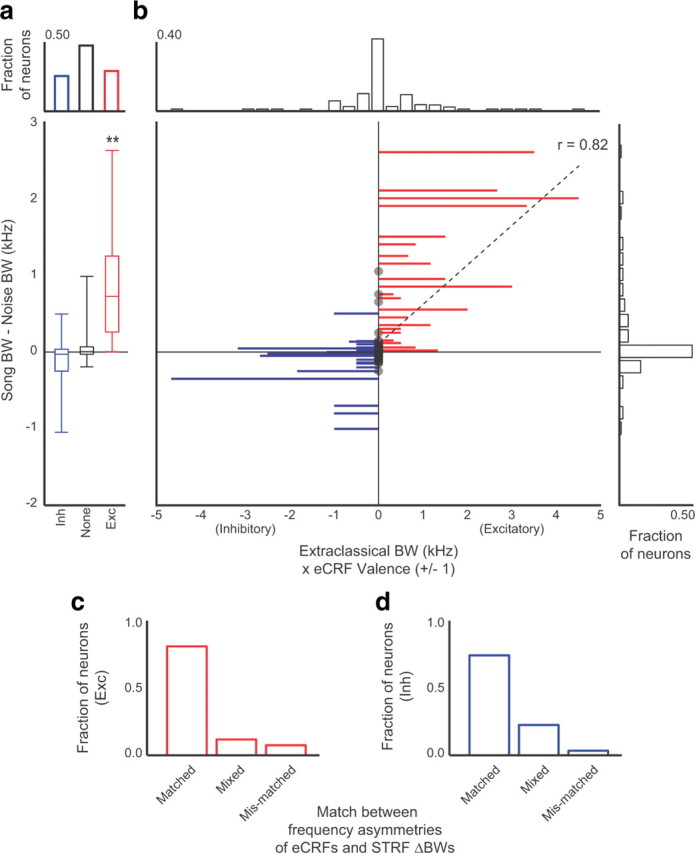
Extra-classical tuning predicts stimulus-dependent STRFs. a, The fraction of neurons with inhibitory (blue), excitatory (red), or no eCRFs (black) is at the top. The differences between the song and noise STRF BWs for the neurons in each group are given below. The center line of each box is the median of the distribution, and the outer box edges show the 25th and 75th percentiles. Bar ends mark the upper and lower bounds of each distribution. The distributions were all significantly different (p < 0.05, Wilcoxon rank-sum test). The STRF differences in the excitatory group were significantly greater than zero (**p < 0.005, Wilcoxon signed-rank test). b, Plot showing the relationship between stimulus-dependent spectral tuning and eCRFs for individual neurons. Each line shows the extent (Hz) and valence [excitatory (Exc) or inhibitory (Inh)] of extra-classical tuning for a single neuron. Red lines extending to the right show neurons with extra-classical excitation. Blue lines extending to the left show neurons with extra-classical inhibition. Black circles indicate neurons with no extra-classical tuning. The location of the line on the ordinate shows the difference between the song STRF and noise STRF BWs. The histograms show the distributions of extra-classical bandwidths (top) and STRF bandwidth differences (right). c, d, For neurons with excitatory eCRFs, the extra-classical excitation was typically asymmetric with respect to BF (either in lower frequencies, or in higher frequencies). Similarly, differences in the song and noise STRF BWs were also asymmetric with respect to BF. c, The fraction of neurons for which excitatory eCRFs had the same (matched) frequency asymmetry as STRFs. Neurons with mixed asymmetries include those with excitatory eCRFs but no differences in STRF BW, and those with differences in STRF BW but no eCRF. Neurons with mismatched asymmetries had eCRFs and STRF BW differences in frequency channels on opposite sides of the BF. d, The fraction of neurons for which inhibitory eCRFs had matched, mixed, or mismatched asymmetries.

At the single neuron level, the presence and valence of extra-classical tuning predicted the presence, direction, and degree of differences between song and noise STRF excitatory bandwidths. Extra-classical excitation, shown as red lines extending to the right in Figure 6b, was found in neurons that had broader song STRFs than noise STRFs. Extra-classical inhibition, shown as blue lines extending to the left, was found in neurons with highly similar song and noise STRFs and in neurons for which the noise STRF BW was wider than the song STRF BW. The valence and bandwidth of the eCRFs were highly correlated with the difference between the song and noise STRF BWs (r = 0.72, p < 4 × 10⁻¹⁴). When the linear relationship was calculated for the subset of neurons with no eCRFs or excitatory eCRFs, this correlation was particularly strong (r = 0.82, p < 4 × 10⁻⁵), indicating that excitatory eCRFs have a strong influence on the spectral bandwidths of song and noise STRFs.

The frequency asymmetry of eCRFs predicts STRF asymmetry

For many neurons, the song and noise STRF excitatory BWs were substantially different, but the differences occurred on only one side of the BF: only in frequencies higher than the BF (>BF) or only in frequencies lower than the BF (<BF). For the majority of neurons (87%), eCRFs were also located asymmetrically around the BF. Across the population, neurons were equally likely to have their eCRFs in frequency channels above or below the BF. We use the term asymmetry to describe both the frequency range of the eCRF and the frequency range for which one STRF BW differed from the other. For example, if the excitatory bandwidths of the song and noise STRFs had the same lower boundary, but the song STRF extended into higher frequencies than the noise STRF, the STRF asymmetry was above the BF (>BF). Song and noise STRF BWs were considered different if the high or low extents of their excitatory regions differed by >250 Hz.

For each neuron we determined whether the asymmetry of the STRF BWs matched the asymmetry of the eCRF. Of neurons with excitatory eCRFs, 81% had STRF differences with matched asymmetries (Fig. 6c), while only 7% had mismatches between eCRF and STRF asymmetries. The remaining 12% of neurons had excitatory eCRFs but did not have STRF differences > 250 Hz. Of the neurons with inhibitory eCRFs, 74% had matched asymmetries compared to 3% that had mismatches between STRF and eCRF asymmetries (Fig. 6d). Of the remaining 23% of neurons, the majority had extra-classical inhibition but stimulus-independent STRFs, indicating that inhibitory eCRFs can function to stabilize STRF BW between stimulus classes. These results indicate that the frequencies that contribute extra-classical tuning are in agreement with the frequency ranges over which song and noise STRFs differ.

Simulated neurons with subthreshold tuning exhibit stimulus-dependent STRFs

The strong correlations between stimulus-dependent STRFs and the degree, valence, and asymmetry of extra-classical tone tuning suggest that eCRFs serve as a nonlinear mechanism for stimulus-dependent processing of complex sounds. Furthermore, these results suggest that extra-classical excitation leads to broader song STRFs than noise STRFs, while extra-classical inhibition leads to no stimulus-dependent tuning or broader noise STRFs. To explicitly test whether a threshold model incorporating subthreshold tuning can serve as a mechanism for stimulus-dependent processing of complex sounds with differing stimulus correlations, we simulated three classes of neurons: (1) neurons with extra-classical excitation; (2) neurons with extra-classical inhibition; and (3) neurons with no extra-classical tuning.

The left panel of Figure 7a shows the neural response to isointensity pure tones for a simulated neuron with extra-classical excitation. Tone frequencies that caused the membrane potential to cross the firing threshold (Vth) led to increased firing rates. Tones that caused changes in the membrane potential that deviated from the resting potential (Vr) but remained below Vth caused only subthreshold responses, without modulating the firing rate. At the resting potential shown, approximately half of the neuron's bandwidth was subthreshold, meaning that only 50% of the frequencies that modulated the membrane potential caused an increase in firing rate. The right panel of Figure 7a shows a STRF with the same spectral profile as the left panel. The temporal profile of this STRF was modeled based on the temporal tuning properties observed in real midbrain neurons.

Figure 7.

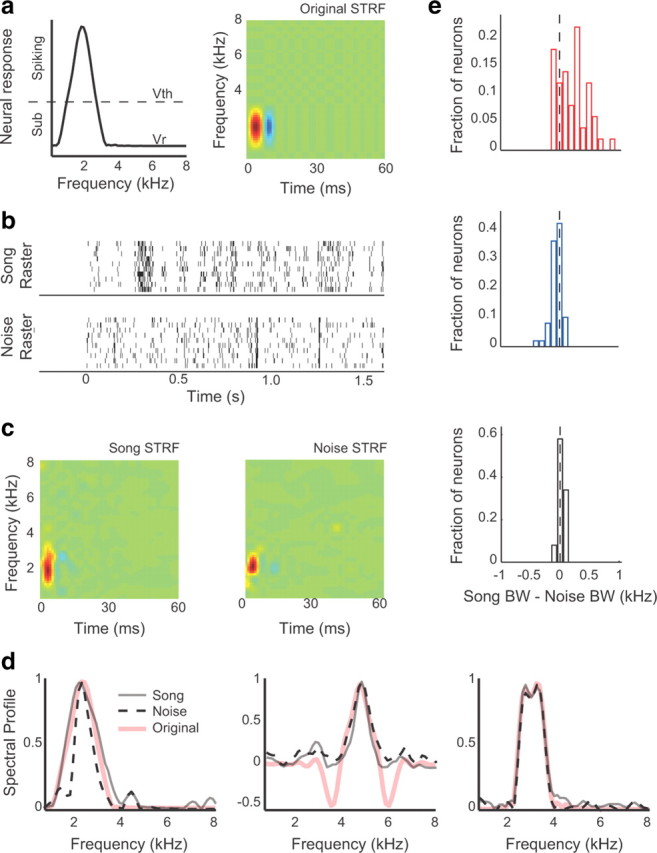
Simulated neurons with eCRFs and a spiking threshold exhibit stimulus-dependent STRFs. a, The neural response to isointensity tones for a simulated neuron with subthreshold excitation is on the left. Frequencies that cause the neural response to exceed spike threshold (Vth) lead to an increased spiking probability and are in the CRF. Frequencies that cause the neural response to deviate from the resting potential (Vr) but not cross Vth do not evoke spikes and are in the eCRF. A STRF with the same frequency tuning as the spectral profile is on the right. b, Spike trains were simulated using the STRF in a as a generative model. The top raster shows 10 spike trains in response to a single song, and the bottom raster shows 10 spike trains in response to a single noise sample. c, Separate song and noise STRFs were computed from the simulated spike trains to 20 songs and 10 noise stimuli, generated using the STRF in a. d, The spectral profile of the original STRF used in the generative model (pink), along with the spectral profiles of the resulting song STRF (solid gray) and the resulting noise STRF (dashed black). The left shows the spectral profiles of the neuron described in a–c, which had extra-classical excitation. The middle shows the spectral profiles for a simulated neuron with extra-classical (sideband) inhibition. The right shows the spectral profiles for a neuron with no extra-classical tuning. e, Histograms showing the difference in excitatory bandwidth between the song and noise STRFs of simulated neurons with extra-classical excitation (top), extra-classical inhibition (middle), and no extra-classical tuning (bottom). For neurons with extra-classical excitation and inhibition, the difference between song and noise STRF BWs was significantly different than 0 (p < 0.002, both comparisons) and highly similar to the BW differences that were measured experimentally.

Using the STRF in Figure 7a, we simulated spike trains to the song and noise stimuli presented to real midbrain neurons (Fig. 7b), and from these responses we calculated separate song and noise STRFs (Fig. 7c). Figure 7d shows the spectral profiles for song and noise STRFs calculated from example-simulated neurons with extra-classical excitation (left), inhibition (middle), or no extra-classical tuning (right). For the neuron with extra-classical excitation, the song STRF had a broader BW than the noise STRF. For the neuron with extra-classical inhibition, the noise STRF had a broader BW. The neuron with no extra-classical tuning had highly similar song and noise STRF BWs.

Across a population of 150 simulated neurons, the difference in bandwidth between song and noise STRFs was predicted by the presence and valence of extra-classical tuning (Fig. 7e). For neurons that were modeled with extra-classical excitation, the song STRFs were substantially broader than the noise STRFs, as observed in real midbrain neurons (top; p = 0.0001; mean difference, 215.1 Hz). For neurons that were modeled with extra-classical inhibition, the song and noise STRFs were similar, but the noise STRFs were, on average, slightly broader (middle; p = 0.0002; mean difference, −54.42 Hz). Neurons that were modeled without extra-classical receptive fields had highly similar song and noise STRFs (bottom; mean difference, 25.58 Hz). Further simulations showed that V-shaped tuning curves, such as those simulated in neurons with excitatory eCRFs, are not sufficient for stimulus-dependent tuning but must be coupled with a spike threshold that allows some neural responses to remain subthreshold (data not shown). These simulations demonstrate that simple threshold nonlinearity can account for the observed stimulus dependence of song and noise STRFs.

Discussion

The results of this study demonstrate that subthreshold tuning is an important nonlinearity that leads to stimulus-dependent auditory receptive fields. We found that STRFs estimated from neural responses to noise predict neural responses to song less well than do song STRFs, the BWs of excitatory eCRFs were highly correlated with differences in song and noise STRF BWs (Fig. 6), and eCRF BWs exceeded the range of frequencies encompassed by the CRF. Extra-classical RFs, such as those described here, have been shown to facilitate the discrimination of conspecific and predator signals in the weakly electric fish (Chacron et al., 2003), increase the information about complex visual scenes encoded by single neurons (Vinje and Gallant, 2002), and underlie selective neural responses to complex stimuli in the visual system (Priebe and Ferster, 2008). The current findings show that eCRFs are a major non-linearity in the auditory processing of complex sounds and that they account for a large fraction of stimulus-dependent STRF BWs.

Stimulus-dependent STRFs arise from nonlinear tuning

Differences in STRFs estimated during the coding of different sound classes such as song and noise could arise from multiple mechanisms, including RF adaptation (Sharpee et al., 2006) or static nonlinearities (Priebe et al., 2004; Priebe and Ferster, 2008). Our findings are unlikely to be due to long-term RF adaptations. First, we used short duration song and noise stimuli and interleaved their presentation, an experimental design that did not allow for long-term RF adaptation, which has been estimated to require processing of the same stimulus for >2 s. Our results align more closely with the short time scale adaptations that have been observed in the auditory forebrain (Nagel and Doupe, 2006; David et al., 2009).

Our findings suggest that stimulus-dependent STRFs in the songbird auditory midbrain are largely accounted for by a static nonlinearity composed of subthreshold excitation and, to some extent, subthreshold inhibition. The effects that we observe can be explained by a combination of differing spectral correlations in the two classes of sounds (Fig. 3a,b), the shape of the synaptic input across frequencies as revealed by eCRFs (Figs. 5–7), and spike threshold (Fig. 7). The spike threshold nonlinearity that we demonstrate here has been described previously in simulation experiments (Christianson et al., 2008) and is similar to the “iceberg effect” that is described for visual neuron RFs, for which subthreshold tuning can be much broader than tuning measured from spiking alone (for review, see Priebe and Ferster, 2008). Spike threshold has been shown to influence complex tuning properties in the primary visual cortex (Priebe et al., 2004; Priebe and Ferster, 2008), the rat barrel cortex (Wilent and Contreras, 2005), and the auditory system (Zhang et al., 2003; Escabí et al., 2005; Chacron and Fortune, 2010; Ye et al., 2010).

Influences of inhibitory eCRFs on STRF tuning

Differences between song and noise STRF BWs were strongly predicted by the extent of excitatory eCRFs (r² = 0.67) but were largely unrelated to the extent of inhibitory eCRFs (r² = 0.07). Although inhibitory eCRFs did not predict STRF BW differences, they did appear to constrain the BW of song and noise STRFs. In particular, 94% of neurons with inhibitory eCRFs had highly similar song and noise STRF BWs (ΔBW < 100 Hz) or broader noise STRF BWs. This is in strong contrast to neurons with excitatory eCRFs, for which song STRF BWs were broader than noise STRF BWs, but noise STRF BWs were never broader than song STRF BWs (Fig. 6a,b).

Many neurons had strong inhibitory sidebands when probed with tone pairs, but these inhibitory regions were largely absent from the song and noise STRFs. Why do STRFs lack inhibitory sidebands when frequencies outside of the eCRF can have a profound influence on spiking activity? The STRF inhibitory sidebands may be less pronounced than would be predicted by tone pair responses for the same reason that they are undetectable when presenting pure tones. In particular, the auditory midbrain neurons we studied had low baseline firing, and inhibition can only be detected when a stimulus contains energy that spans both the excitatory CRF and the inhibitory eCRF. If presented alone, energy in the inhibitory eCRF has no influence on the firing rate of a neuron without spontaneous activity. Thus, stimulus energy in the inhibitory sideband can have differential effects on the firing pattern depending on the stimulus features with which it is presented. And because STRFs show the average effect of a particular spectrotemporal feature on spiking activity, the inhibitory effects of the sideband may be averaged out.

Using tone pairs to estimate eCRFs

Measuring eCRFs from extracellular recordings such as those studied here are based on the assumption that subthreshold neural responses can be detected when they are coincident with a normally suprathreshold response. The presentation of tone pairs or other spectrally complex stimuli has previously been used to uncover extra-classical inhibition (Suga, 1965; Ehret and Merzenich, 1988; Yang et al., 1992, Shamma et al., 1993; Nelken et al., 1994; Schulze and Langner, 1999; Sutter et al., 1999; Escabí and Schreiner, 2002, Noreña et al., 2008) and excitation (Fuzessery and Feng, 1982, Nelken et al., 1994; Schulze and Langner, 1999) in multiple species and auditory areas. Although this technique provides an indirect measure of extra-classical tuning, these results are supported by experiments that directly recorded synaptic currents or membrane potentials using whole cell or intracellular techniques (Fitzpatrick et al., 1997; Zhang et al., 2003; Machens et al., 2004; Tan et al., 2004; Xie et al., 2007).

The response to a single tone is often a dynamic interaction between excitation and inhibition that stabilizes over the course of tens or hundreds of milliseconds (Tan et al., 2004). The tone pairs that we used in these experiments were presented concurrently. We therefore measured the effects that eCRF stimulation has on simultaneous BF stimulation without explicitly probing temporal interactions among frequency channels. By delaying the tones relative to one another, future work can examine the temporal effects that eCRF stimulation exerts upon CRF responses (Shamma et al., 1993; Andoni et al., 2007). The use of temporally delayed side tones may be especially interesting in brain areas where STRFs are inseparable in frequency and time. Most auditory midbrain neurons in the zebra finch have highly separable STRFs (Woolley et al., 2009), suggesting that stimulation with coincident tones captures the majority of interactions across frequency channels in these neurons.

Implications for vocalization coding

The importance of eCRFs and spike threshold during the processing of vocalizations is supported by previous studies in multiple brain areas of many species (Fuzessery and Feng, 1983; Mooney, 2000; Woolley et al., 2006; Holmstrom et al., 2007). In particular, our findings are in close agreement with similar studies of bat vocalization processing. For example, many neurons in the bat midbrain show nonlinear responses to discontinuous combinations of tones at frequencies that are contained in social calls (Leroy and Wenstrup, 2000; Portfors and Wenstrup, 2002), and these vocalizations are more accurately predicted by receptive fields estimated using combinations of tones that fall within and outside of the CRF (Holmstrom et al., 2007). Also in the bat midbrain, contiguous belts of excitation and inhibition shape the neural selectivity for the direction of frequency sweeps that are features of vocalizations (Fuzessery et al., 2006; Pollak et al., 2011). The similarity of our results to previous demonstrations of extra-classical tuning in the bat midbrain suggests that eCRFs may be a conserved mechanism for shaping neural responses to vocalizations (Klug et al., 2002, Xie et al., 2007).

In higher order auditory regions of the songbird brain, some neurons respond with higher firing rates to conspecific songs compared to synthetic stimuli (Grace et al., 2003; Hauber et al., 2007) or heterospecific songs (Stripling et al., 2001; Terleph et al., 2008), and neurons in vocal control nuclei respond preferentially to a bird's own song (Margoliash and Konishi, 1985; Doupe and Konishi, 1991). The stimulus-dependent tuning that we observe in the songbird auditory midbrain differs from the firing rate selectivity for songs that is observed in the songbird forebrain, but spike threshold may contribute to both forms of stimulus-dependent responses. For example, intracellular recordings in the vocal control nucleus HVc (Mooney, 2000) and the auditory forebrain (Bauer et al., 2008) show that spike threshold plays an integral role in firing rate selectivity for conspecific song and a bird's own song. Therefore, subthreshold tuning and spike threshold are likely to contribute to both stimulus-dependent STRFs and stimulus-selective responses along the auditory pathway.