Estimation and Variable Selection for Semiparametric Additive Partial Linear Models (SS-09-140)

Abstract

Semiparametric additive partial linear models, containing both linear and nonlinear additive components, are more flexible compared to linear models, and they are more efficient compared to general nonparametric regression models because they reduce the problem known as “curse of dimensionality”. In this paper, we propose a new estimation approach for these models, in which we use polynomial splines to approximate the additive nonparametric components and we derive the asymptotic normality for the resulting estimators of the parameters. We also develop a variable selection procedure to identify significant linear components using the smoothly clipped absolute deviation penalty (SCAD), and we show that the SCAD-based estimators of non-zero linear components have an oracle property. Simulations are performed to examine the performance of our approach as compared to several other variable selection methods such as the Bayesian Information Criterion and Least Absolute Shrinkage and Selection Operator (LASSO). The proposed approach is also applied to real data from a nutritional epidemiology study, in which we explore the relationship between plasma beta-carotene levels and personal characteristics (e.g., age, gender, body mass index (BMI), etc.) as well as dietary factors (e.g., alcohol consumption, smoking status, intake of cholesterol, etc.).

1 Introduction

Additive partial linear models (APLMs) are a generalization of multiple linear regression models, and can be regarded as a special case of generalized additive nonparametric regression models (Hastie and Tibshirani, 1990) as well. APLMs allow an easier interpretation of the effect of each variable and are preferable to completely nonparametric additive models, because APLMs combine both parametric and nonparametric components when it is believed that the response variable depends on some variables in a linear way but is nonlinearly related to the remaining independent variables.

Estimation and inference for APLMs have been well studied in literature (Stone, 1985; Opsomer and Ruppert, 1997), with backfitting algorithm generally used for estimation. Opsomer and Ruppert (1999) studied the asymptotics of the kernel-based backfitting estimators. Liang et al. (2008) suggested that a kernel-based estimation procedure is available for APLMs without an undersmoothing requirement, and applied APLMs to study the relationship between environmental chemical exposures and semen quality. When there are multiple nonparametric terms, it is both useful and required that estimation and inference methods be efficient and computationally easily implemented. Additionally, this implementation should be able to be achieved in a commonly used computational environment like R. Kernel-based procedures (Opsomer and Ruppert, 1999; Liang et al. 2008) are intuitively attractive and theoretically justifiable, but computationally inexpedient; Spline-based procedures (Li, 2000) are computationally expedient, but theoretically unreliable. Challenged by these demands and the drawbacks in the existing literature, we propose approximating the nonparametric components by using polynomial splines. With the models becoming linear, the resulting estimators for the linear components are therefore easily calculated, and of most importance still asymptotically normal.

Motivated by a dataset from a nutritional epidemiology project (see the details in Section 4), we study variable selection for APLMs. To the best of our knowledge, no variable selection procedures are available for APLMs. Best subset selection is commonly used to select significant variables in regression models. It examines all possible candidate subsets and selects the final subset by some criterion such as the Akaike information criterion (AIC) (Akaike, 1973) and the Bayesian information criterion (BIC) (Schwarz, 1978), which combine statistical measures of fit with penalties for increasing complexity (number of predictors). However, the best subset selection has two fundamental limitations. First, it is computationally infeasible to do subset selection when the number of predictors is large. Second, it is extremely variable because of its inherent discreteness (Breiman, 1996; Fan and Li, 2001). Stepwise selection is often used to reduce the number of candidate subsets. However, it still suffers from the high variability. Instead, Tibshirani (1996) proposed a regression method using L₁ penalty, the LASSO, that is similar to ridge regression but can shrink some coefficients to 0, and thus implement variable selection. Fan and Li (2001) proposed a very general variable selection framework by using a smoothly clipped absolute deviation (SCAD) penalty. The choice of the SCAD penalty function encompasses the usually used variable selection approaches as special cases (see Section 2.2 for details). Most importantly the SCAD-based approach holds appealing statistical properties, as Fan and Li (2001) demonstrated. This approach has become popular and been widely studied in literature by, for instance, Fan and Li (2002) for Cox models, Li and Liang (2008) for semiparametric models, and Liang and Li (2009) for partially linear models with measurement errors. Xie and Huang (2009) and Ni, Zhang, and Zhang (2009) studied the variable selection for partially linear models with a divergent number of linear covariates, and established the selection consistency and asymptotic normality. The former used polynomial splines and the latter used the smoothing spline to approximate the nonparametric function. Since partially linear models have only one nonparametric component, they are not as flexible as APLM. In contrast to that in partially linear models, estimation or variable selection is much more difficult in APLM. Ravikumar et al. (2008, 2009) investigated high-dimensional nonparametric sparse additive models (SpAM), developed a new class of algorithms for estimation and discussed asymptotic properties of their estimators. SpAM are more general but lack of the simplicity property of APLM, which are more appropriate when some covariates are not continuous.

In this paper we will develop a SCAD-based variable selection procedure for APLMs combining the spline approximation. This combination overcomes a potential problem of how to define the objective function if a backfitting algorithm is used. Furthermore, employing spline approximation can still make our variable selection procedure have the oracle property, which is the best theoretical performance any procedure pursues.

The rest of the article is organized as follows. Section 2 introduces the estimation and SCAD-based variable selection procedures for APLMs, and presents the theoretical results. Numerical comparisons and simulation studies are given in Section 3. Section 4 examines in detail the nutritional data to illustrate the procedure. Section 5 concludes the article with a discussion. All technical details are given in the Appendix.

2 Estimation and Variable Selection Procedure

Suppose that {(X₁, Z₁, Y₁), …, (X_n, Z_n, Y_n)} is an iid random sample of size n from an APLM

$$Y={\mathit{X}}^{\mathrm{T}}\beta +\sum _{k=1}^K{g}_k(Z_k)+\epsilon ,$$ (1)

where X = (X₁, … , X_d)^T and Z = (Z₁, … , Z_K)^T are the linear and nonparametric components, g₁, … , g_K are unknown smooth functions, β = (β₁, …, β_d) is a vector of unknown parameters, and the model error ε has the conditional mean zero and finite variance σ² given (X, Z). To ensure identifiability of the nonparametric functions, we assume that E{g_k(Z_k)} = 0 for k = 1, …, K.

2.1 Spline Approximation

Let g₀ = g₀₁ (z₁) + ⋯ + g_0K (z_K) and β₀ be the true additive function and the true parameter values. For simplicity, we assume that the covariate Z_k is distributed on a compact interval [a_k, b_k], k = 1, …, K, and without loss of generality, we take all intervals [a_k, b_k] = [0, 1], k = 1, …, K. Under some smoothness assumptions, g_0ks can be well approximated by spline functions. Let S_n be the space of polynomial splines on [0, 1] of degree ϱ ≥ 1. We introduce a knot sequence with J_n interior knots

$$t_{-\varrho }=\dots =t_{-1}=t_0=0<t_1<\dots <t_{J_n}<1=t_{J_n+1}=\dots =t_{J_n+\varrho +1},$$

where J_n increases when sample size n increases, with the precise order given in Condition (C4). Then S_n consists of functions ξ satisfying

1. ξ is a polynomial of degree ϱ on each of the subintervals I_j = [t_j, t_j+1), j = 0, …, J_n − 1, I_Jn = [t_Jn, 1];

2. for ϱ ≥ 2, ξ is ϱ − 1 continuously differentiable on [0, 1].

Equally spaced knots are used in this article for simplicity of proof. However other regular knot sequences can also be used, with similar asymptotic results. Let h = 1/ (J_n + 1) be the distance between neighboring knots.

We will consider the additive spline estimates ĝ of g₀ based on the independent random sample (X_i, Z_i, Y_i), i = 1, …, n. Let G_n be the collection of functions g with the additive form g (z) = g₁ (z₁)+⋯+g_K (z_K), where each component function g_k ∈ S_n and ${\sum }_{i=1}^n{g}_k(Z_{ik})=0$.

We would like to find a function g ∈ G_n and a value of β that minimize the following sum of squared residuals function

$$L(g,\beta )=\frac{1}{2}{\sum _{i=1}^n[Y_i-\{g({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}]}^2,g\in G_n.$$ (2)

For the k-th covariate z_k, let b_j,k (z_k) be the B-spline basis functions of degree ϱ. For any g ∈ G_n, one can write

$$g(z)={\mathrm{\gamma }}^{\mathrm{T}}\mathit{b}(\mathbf{z}),$$ (3)

where b (z) = {b_j,k (z_k), j = −ϱ,…, J_n, k = 1,…, K}^T, and the spline coefficient vector γ = {γ_j,k, j = −ϱ, …, J_n, k = 1,…, K}^T. Thus the minimization problem in (2) is equivalent to find a value of β and γ to minimize

$$\ell (\mathrm{\gamma },\beta )=\frac{1}{2}{\sum _{i=1}^n[Y_i-\{{\mathrm{\gamma }}^{\mathrm{T}}\mathit{b}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}]}^2.$$ (4)

We denote the minimizer as β̂ and γ̂ = {γ̂_j,k, j = −ϱ,…, J_n, k = 1, …, K}^T. Then the spline estimator of g₀ is ĝ = γ̂^Tb(z), and the centered spline estimator of the component g_k is

$${\widehat{g}}_k(z_k)=\sum _{j=-\varrho }^{J_n}{\widehat{\mathrm{\gamma }}}_j{b}_{j,k}(z_k)-\frac{1}{n}\sum _{i=1}^n\sum _{j=-\varrho }^{J_n}{\widehat{\mathrm{\gamma }}}_j{b}_{j,k}(Z_{\mathit{ik}}),$$

for k = 1, …, K. The above estimation approach can be easily implemented with existing linear models in any statistics software.

For simplicity of notation, write T = (X, Z). Let m₀ (T) = g₀ (Z) + X^T β₀, Γ (z) = E(X|Z = z), X̃ = X − Γ (Z), and Q^⊗2 = QQ^T for any matrix or vector Q. The next theorem shows that the estimators β̂ of β₀ is root-n consistent and asymptotically normal although the convergence rate of the estimators of the nonparametric component g₀ is slower than root-n (Lemma A.4). Its proof is given in the Appendix.

Theorem 1

Under the conditions (C1)-(C5) given in Appendix, $\sqrt{n}(\widehat{\beta }-{\beta }_0)$ converges to N (0, D⁻¹ ΣD⁻¹) in distribution where D = E(X̃^⊗2) and Σ = E(ε²X̃^⊗2). Furthermore, if ε and (X, Z) are independent, $\sqrt{n}(\widehat{\beta }-{\beta }_0)\to N(0,{\sigma }^2{\mathbf{D}}^{-1})$, where σ² = E (ε²).

2.2 SCAD-penalty variable selection procedure

Penalized likelihood has been widely used for non- and semi-parametric models to trade off model complexity and estimation accuracy. A comprehensive survey of these fields was given by Ruppert et al. (2003). The penalized objective function we used is defined as

$${ℒ}_P(\beta ,\mathrm{\gamma })=\frac{1}{2}{\sum _{i=1}^n[Y_i-\{{\mathrm{\gamma }}^{\mathrm{T}}\mathbf{B}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}]}^2+n\sum _{j=1}^{d}p{\mathrm{\lambda }}_j(|{\beta }_j|),$$ (5)

where pλ_j (·) is a penalty function with a tuning parameter λ_j, which may be chosen by a data-driven method. See Liang and Li (2009) for a detailed discussion of the choice of the tuning parameter. Minimizing ℒ_P (β, γ) with respect to β results in a penalized least squares estimator β̂. It is worth noting that the penalty functions and the tuning parameters are not necessarily the same for all coefficients. For instance, we want to keep important variables in the final model, and therefore should not penalize their coefficients.

The penalized sum of squared residuals function (5) provides a general framework of variable selection for APLMs. Taking the penalty function to be the L₀-penalty (also called the entropy penalty in the literature), namely, $p{\mathrm{\lambda }}_j(|{\beta }_j|)=0.5{\mathrm{\lambda }}_j^{2}I\{|{\beta }_j|\ne 0\}$, where I {·} is an indicator function, we may extend the traditional variable selection criteria, including the AIC (Akaike, 1973), BIC (Schwarz, 1978), and RIC (Foster and George, 1994), for the APLM:

$$\ell (\mathrm{\gamma },\beta )+\frac{n}{2}\sum _{j=1}^d{\mathrm{\lambda }}_j^{2}I\{|{\beta }_j|\ne 0\}$$ (6)

as ${\sum }_{j=1}^{d}I\{|{\beta }_j|\ne 0\}$ equals the size of the selected model. Specifically, the AIC, BIC, and RIC correspond to ${\mathrm{\lambda }}_j\equiv \sqrt{2/n\sigma }$, $\sqrt{\log (n)/n\sigma }$ and $\sqrt{\log (d)/n\sigma }$ respectively. Note that Bridge regression (Frank and Friedman, 1993) is equivalent to the L_q-penalty p_λ(|β_j|) = q⁻¹λ|β_j|^q; the LASSO (Tibshirani, 1996; Zou, 2006) corresponds to the L₁-penalty, and SCAD corresponds to the following smoothly clipped absolute deviation penalty function

$$p_{\mathrm{\lambda }}(|\beta |)=\{\begin{array}{ll}\mathrm{\lambda }|\beta |,& \mathbf{if}0\le |\beta |<\mathrm{\lambda };\\ \frac{(a^2-1){\mathrm{\lambda }}^2-{(|\beta |-a\mathrm{\lambda })}^2}{2(a-1)},& \mathbf{if}\mathrm{\lambda }\le |\beta |<a\mathrm{\lambda };\\ \frac{(a+1){\mathrm{\lambda }}^2}{2},& \mathbf{if}|\beta |\ge a\mathrm{\lambda };\end{array}$$

where a = 3.7. As demonstrated in Fan and Li (2001), SCAD is an improvement of LASSO in terms of modeling bias, and of bridge regression with q < 1 in terms of stability. It also has an oracle property.

We now present the sampling property of the resulting penalized least squares estimate. Let ${\beta }_0={({\beta }_{10},\dots ,{\beta }_{d0})}^{\mathrm{T}}={({\beta }_{10}^{\mathrm{T}},{\beta }_{20}^{\mathrm{T}})}^{\mathrm{T}}$ be the true value of β. Without loss of generality, assume that β₁₀ consists of all nonzero components of β₀, and β₂₀ = 0. Let s denote the length of β₁₀. Write $a_n={\max }_{1\le j\le d}\{|{p^{\prime }}_{{\mathrm{\lambda }}_j}(|{\beta }_{j0}|)|,{\beta }_{j0}\ne 0\}$, $b_n={\max }_{1\le j\le d}\{|{p^{″}}_{{\mathrm{\lambda }}_j}(|{\beta }_{j0}|)|,{\beta }_{j0}\ne 0\}$, $k_n={\{{p^{\prime }}_{{\mathrm{\lambda }}_1}(|{\beta }_{10}|)\mathrm{sgn}({\beta }_{10}),\dots ,{p^{\prime }}_{\mathrm{\lambda }s}(|{\beta }_{s0}|)\mathrm{sgn}({\beta }_{s0})\}}^{\mathrm{T}}$, and ${\sum }_{\mathrm{\lambda }}=\mathrm{diag}\{{p^{″}}_{{\mathrm{\lambda }}_1}(|{\beta }_{10}|),\dots ,{p^{″}}_{\mathrm{\lambda }s}(|{\beta }_{s0}|)\}$. Denote X₁ as the vector comprised by the first s elements of X. We have the following theorem, whose proof is given in the Appendix.

Theorem 2

Suppose that a_n = O(n^−1/2), b_n → 0, and the regularity conditions (C1)-(C5) in the Appendix hold. Then (I) With probability approaching one, there exists a local minimizer β̂ of ℒ_P (β,γ) such that ∥β̂ − β∥ = O_P(n^−1/2). (II) Furthermore, if λ_j → 0, n^1/2λ_j → ∞, and

$$\underset{n\to \infty }{\mathrm{lim\; inf}}\underset{u\to 0^{+}}{\mathrm{lim\; inf}}{p}_{{\mathrm{\lambda }}_j}^{\prime }(u)/{\mathrm{\lambda }}_j>0,$$ (7)

then, with probability approaching one, the root-n consistent estimator β̂ in (I) satisfies (a) β̂₂ = 0, and (b) β̂₁ has an asymptotic normal distribution

$$\sqrt{n}\{E({\stackrel{\sim }{\mathit{X}}}_1^{\otimes 2})+{\sum }_{\mathrm{\lambda }}\}[{\widehat{\beta }}_1-{\beta }_{10}+\{E({\stackrel{\sim }{\mathit{X}}}_1^{\otimes 2})+{{\sum }_{\mathrm{\lambda }}\}}^{-1}{k}_n]\stackrel{D}{\to }N(\mathbf{0},{\sum }_s),$$

where Σ_s = var (εX̃₁).

Theorem 2 indicates that the SCAD-penalty variable selection procedure can effectively identify the significant components, with the associated estimators holding the oracle property.

3 Simulation studies

In this section, the finite sample performance of the proposed procedure is investigated by Monte Carlo simulations. We numerically compare estimation accuracy and complexity of models selected by SCAD, LASSO and BIC. We use the local quadratic approximation algorithm of Fan and Li (2001) to implement the SCAD and LASSO procedures, and select the tuning parameter by generalized cross-validation (GCV) in both simulation studies and the real data example in Section 4.

Let g₁(z) = 5 sin (4πz) and g₂(z) = 100{exp(−3.25z) − 4 exp(−6.5z) + 3 exp(−9.75z)}. We simulate 100 data sets consisting of n = 60, 100, and 200 observations from the model

$$\mathit{Y}={\mathit{X}}^{\mathrm{T}}\beta +g(\mathit{Z})+\sigma \epsilon ,$$

where β = (3, 1.5, 0, 0, 2, 0, 0, 0)^T, σ = 1, 3, 5, and the components of X and ε are standard normal. X and ε are independent. The correlation between x_i and x_j is ρ^|i−j| with ρ = 0.5. We consider three cases: (i) g(Z) = g₁(Z₁); (ii) g(Z) = g₂(Z₂); and (iii) g(Z) = g₁(Z₁) + g₂(Z₂). Z₁ and Z₂ are independent uniformly distributed on [0, 1]; i.e., in the first two cases, there is only one nonparametric component, while in the third case there are two nonparametric components.

Cubic B-splines are used to approximate the nonparametric functions as described in Section 2.1. To determine the number of knots in the approximation, we examined several (say M) models, with the number of knots from 2 to 12 for each nonparametric component. In other words, M = 11 in both Case (i) and Case (ii), and M = 11² = 121 in Case (iii). In each case, the M linear prediction models are taken into account, and the model with the smallest median of relative model error when compared to the full model, which includes all covariates, is taken to be the final selected model.

Simulation results are presented in Tables 1-3, in which the columns labeled with “C” give the average number of the five zero coefficients correctly set to 0, the columns labeled with “I” give the average number of the three nonzero coefficients incorrectly set to 0, and the columns labeled “MRME” give the average of the median of relative model errors, which is defined as the ratio of model error comparing the selected model to the full model. The rows with “SCAD” and “LASSO” stand respectively for the penalized least squares with the SCAD penalty and the LASSO penalty. “BIC” stands for the best subset selection using the selection criterion BIC. The row “Oracle” stands for the oracle estimates computed by using the true model Y = β₁X₁ + β₂X₂ + β₅X₅ + g(Z) + σε. The oracle estimates always set the 5 zero coefficients correctly to zero and do not set any of the 3 nonzero coefficients to zero.

Table 1.

Simulation Results for Case (i)

n	method	σ = 1			σ = 3			σ = 5
		C	I	MRME	C	I	MRME	C	I	MRME
60	scad	4.49	0	0.852	4.39	0.12	0.899	4.29	0.61	0.903
	lasso	3.38	0	0.882	3.49	0.02	0.75	3.41	0.31	0.723
	bic	4.66	0	0.869	4.76	0.14	0.948	4.57	0.86	0.969
	oracle	5	0	0.662	5	0	0.68	5	0	0.635
100	scad	4.45	0	0.838	4.44	0.03	0.87	4.35	0.32	0.947
	lasso	3.31	0	0.906	3.53	0	0.775	3.4	0.09	0.768
	bic	4.84	0	0.876	4.8	0.03	0.88	4.77	0.6	1.036
	oracle	5	0	0.717	5	0	0.704	5	0	0.706
200	scad	4.4	0	0.798	4.37	0	0.818	4.38	0.03	0.788
	lasso	3.27	0	0.884	3.37	0	0.829	3.37	0	0.797
	bic	4.91	0	0.803	4.88	0	0.916	4.9	0.06	0.772
	oracle	5	0	0.723	5	0	0.668	5	0	0.693

Table 3.

Simulation Results for Case (iii)

n	method	σ = 1			σ = 3			σ = 5
		C	I	MRME	C	I	MRME	C	I	MRME
60	scad	4.43	0	0.924	4.39	0.28	1.045	4.37	0.74	1.01
	lasso	3.52	0	1.072	3.68	0.1	0.922	3.67	0.26	0.783
	bic	4.32	0	0.939	4.42	0.31	1.077	4.43	0.87	1.012
	oracle	5	0	0.802	5	0	0.802	5	0	0.752
100	scad	4.41	0	0.926	4.49	0.02	0.957	4.28	0.35	1.052
	lasso	3.58	0	1.028	3.58	0	0.964	3.56	0.09	0.883
	bic	4.6	0	0.939	4.77	0.05	0.977	4.66	0.65	1.112
	oracle	5	0	0.8	5	0	0.782	5	0	0.784
200	scad	4.44	0	0.881	4.45	0	0.953	4.45	0.06	0.973
	lasso	3.42	0	1.022	3.48	0	0.995	3.41	0.01	0.891
	bic	4.84	0	0.9	4.79	0	0.988	4.86	0.11	1.021
	oracle	5	0	0.821	5	0	0.806	5	0	0.797

The results for SCAD, BIC, and LASSO of correctly and incorrectly selected covariates show a similar pattern as those obtained by Fan and Li (2001) for linear models. In all three cases, BIC performs the best to correctly set coefficients to 0, followed by SCAD and LASSO. However, BIC has the highest average number of coefficients erroneously set to 0, followed by SCAD and LASSO. This indicates that BIC is the most aggressive method in terms of excluding variables, while LASSO is the most conservative and tends to include more variables.

As for the MRME, SCAD performs the best when the sample size is large or the error variance is small , while LASSO performs the best when the sample size is small or the error variance is large. The performance of BIC is worse than, although sometimes close to, SCAD for most of the time.

Overall, SCAD and BIC have the best performances in our simulations. Compared to BIC, SCAD has the higher prediction accuracy by slightly increasing the model complexity. In other words, SCAD selects more variables to reduce the prediction error. Furthermore, SCAD is much more computationally efficient than the best subset selection method using BIC, because the latter examines all the subset combinations and the number of all combinations is exponentially proportional to the total number of variables.

4 A Nutritional Study

It is well known that there is a direct relationship between beta-carotene and cancers such as lung, colon, breast, and prostate cancer (Fairfield and Fletcher, 2002). Some observational epidemiological studies have shown that beta carotene can not only effectively prevent cancer because beta carotene has powerful antioxidant properties, but can also help clean the body of free radicals that can cause cancer. Sufficient beta carotene supply can also strengthen the body’s autoimmune system, making it more effective in fighting degenerative diseases such as cancer. Clinicians and nutritionists are therefore interested in the relationship between serum concentrations of beta-carotene and other factors such as age, smoking status, alcohol consumption, and dietary intake because this information may be potentially useful in clinical decision-making and individualization of therapy. For example, Nierenberg et al. (1989) found that dietary carotene and female were positively related to beta-carotene levels, while cigarette smoking and body mass index (BMI) were negatively related to beta-carotene levels. Age was not associated with beta-carotene levels to a statistically significant extent. Faure et al. (2006) recently found that beta-carotene concentration depends on gender, age, smoking status, dietary intake, and location of residence. Examination of this relationship therefore shows diverse results so far, and there is insufficient evidence to draw a convincing conclusion regarding the relationship between beta-carotene and these factors.

A closer investigation of the methods used in these publications indicates that the investigators usually used either a simple analysis of variance(ANOVA) method or linear models to explore the relationship between beta-carotene and other factors, then expressed the factors that influence the beta-carotene concentration. As data sets from nutritional observational studies or clinical trials are far too complicated to comprehend with a linear model or simple statistical methods, using advanced statistical techniques is necessary in order to appropriately model the relationship. We examine a dataset from a nutritional epidemiology study in which we are interested in the relationships between the plasma beta-carotene levels and personal characteristics, including AGE, GENDER, BMI, and other factors: CALORIES (number of calories consumed per day), FAT (grams of fat consumed per day), FIBER (grams of fiber consumed per day), ALCOHOL (number of alcoholic drinks consumed per week), CHOL (cholesterol consumed mg per day), BETADIET (dietary beta-carotene consumed mcg per day), SMOKE2 (smoking status [1=former smoker, 0=never smoked], and SMOKE3 (smoking status [1=current smoker, 0=never smoked]). There was one extremely high leverage point in alcohol consumption that was deleted prior to any analysis. See Nierenberg et al. (1989) for a detailed description of the data. A general linear model was used to fit this dataset and the results are presented in the left panel of Table 4. These results indicate that only BMI, FIBER, GENDER, and SMOKE3 are statistically significant, while the other five variables (AGE, CALORIES, FAT, ALCOHOL, and CHOL) are not significant. However, a closer study shows that the relationship between the logarithm of beta-carotene levels and AGE and CHOL may be nonlinear. We therefore fitted the same dataset using the R function gam and found that the beta-carotene level seems to be linearly related to BMI, CALORIES, FAT, FIBER, ALCOHOL and BETADIET, but nonlinearly related to AGE and CHOL. Figure 1 shows the patterns of AGE and CHOL, which indicates a positive correlation before 45 years old or after 65 years old, and a slightly negative correlation between 45 and 65. Interestingly, we obtain a concave curve of the pattern of CHOL.

Table 4.

Results for the nutritional study. Left panel: Estimated values, associated standard error, and P-value by using the ordinary least squares. Right panel: Estimates, associated standard errors of the coefficients using the APLM with the proposed variable selection procedures.

	LS				APLM
	Est.	s.e	z value	Pr(> |z|)	SCAD (s.e.)	LASSO (s.e.)	BIC (s.e.)
BMI	-0.976	0.202	-4.829	< 10−4	-0.947(0.189)	-0.948(0.173)	-1.001(0.188)
CALORIES	0	0	-0.457	0.648	0(0)	0(0)	0(0)
FAT	-0.002	0.003	-0.711	0.477	0(0)	-0.001(0.001)	0(0)
FIBER	0.027	0.012	2.352	0.019	0.021(0.007)	0.019(0.007)	0.025(0.008)
BETADIET	0.137	0.073	1.889	0.06	0.046(0.027)	0.101(0.051)	0(0)
GENDER	0.277	0.135	2.06	0.04	0.194(0.088)	0.201(0.096)	0(0)
ALCOHOL	0.043	0.048	0.901	0.368	0(0)	0(0)	0(0)
SMOKE2	-0.068	0.091	-0.742	0.458	0(0)	0(0)	0(0)
SMOKE3	-0.286	0.13	-2.191	0.029	-0.245(0.097)	-0.224(0.096)	-0.293(0.117)
AGE	0.005	0.003	1.724	0.086
CHOL	-0.015	0.114	-0.133	0.894

Figure 1.

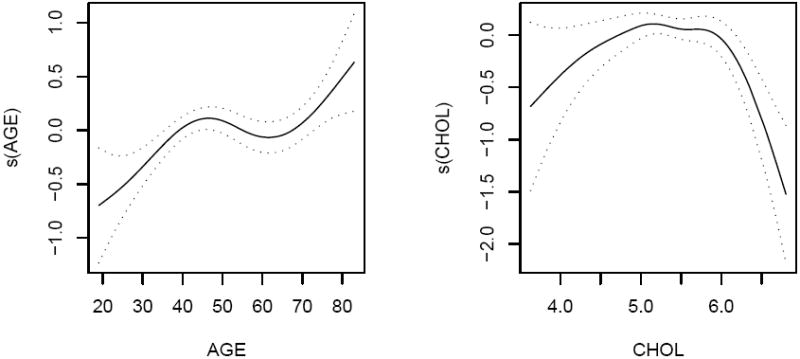
The patterns of AGE and CHOL with ±s.e. using the R function, gam, for the dataset from a nutritional study.

In this section, we use an APLM and the proposed procedures to study the relationship between beta-carotene and other factors, i.e., beta-carotene concentration linearly depends on covariates BMI, CALORIES, FAT, FIBER, ALCOHOL, BETADIET, GENDER and SMOKE2/3 but is nonlinearly related to the remaining covariates AGE and CHOL. We attempt to identify which linear covariates should be included in our final model and appropriately fit the nonlinear unknown functions, which can objectively reflect their impact on beta-carotene level and avoid misleading conclusions. To this end, we use the following model to fit the nutritional dataset, and then apply SCAD, LASSO and BIC procedures for variable selection.

$$\begin{array}{lll}\log (\mathrm{beta}­\mathrm{carotene})& =& {\beta }_0+{\beta }_1\mathrm{BMI}+{\beta }_2\mathrm{CALORIES}+{\beta }_3\mathrm{FAT}+{\beta }_4\mathrm{FIBER}\\ & & +{\beta }_5\mathrm{BETADIET}+{\beta }_6\mathrm{GENDER}+{\beta }_7\mathrm{ALCOHOL}+{\beta }_8\mathrm{SMOKE}2\\ & & +{\beta }_9\mathrm{SMOKE}3+g_1(\mathrm{AGE})+g_2(\mathrm{CHOL})+\epsilon .\end{array}$$

To determine the number of knots in the cubic B-splines approximation of the nonparametric components AGE and CHOL, we examine the number of knots from 2 to 9 for each component and choose the number which makes the model has the smallest relative mean squared error when compared to the full model. As a result, for the nonparametric component AGE, 2 and 5 knots are chose in SCAD and LASSO respectively. For the nonparametric component CHOL, 2 knots are used in both SCAD and LASSO. The tuning parameters selected by GCV are 0.035 and 0.015 for SCAD and LASSO respectively.

The estimated coefficients and their standard errors are listed in the right panel of Table 4. SCAD confirms that BMI, FIBER, BETADIET, GENDER, and SMOKE3 are significant, while LASSO also identifies FAT as being significant. But BIC indicates that only BMI, FIBER, and SMOKE3 are significant. The standard errors of these non-zero coefficients based on the APLM are consistently smaller than the corresponding ones based on the linear fitting. The estimated values using different methods under the APLM setting are similar, but there are differences in magnitude. The estimated curves of the two nonparametric components, AGE and CHOL, are similar to those in Figure 1, and therefore are not shown here. It is worthwhile to mention that the effects of AGE and CHOL are not only significant, but also should not be described by linear functions.

5 Discussion

We proposed a very effective routine by using a regression spline technique, then used an advanced variable selection procedure to identify which linear predictors should be included in our model fitting. There are three principal advantages of our method over the published ones: (i) it avoids any iterative algorithms and computational challenges; (ii) the estimators of the linear components, which are of primary interest, are still asymptotically normal; and (iii) the variable selection procedure holds the oracle property. Combining the idea here and that of Liang and Li (2009), we believe a similar procedure can be developed for partially linear additive models with error-prone linear covariates. The approach is possibly extended to generalized additive partial linear models and the situation with longitudinal data (Lin and Carroll, 2001). However, these extensions are by no means straightforward, and require further efforts.

It would appear possible, at least in principle, to extend our methods to cases in which the numbers of linear components and nonparametric components are diverging. An alternative is a combination of the methods of Xie and Huang (2009) and Ravikumar et al. (2009). One main challenge is how to establish asymptotic properties of the methods and to give theoretical justifications. A detailed investigation of these issues needs a lot of efforts and is certainly worthwhile, but is beyond the scope of this article.

An important question commonly raised among nutritionists is whether available scientific data support an important role of beta-carotene in the prevention of pathologic conditions such as cancer. The research process leads to the demonstration of a causal relationship between nutritional factors and beta-carotene. In this paper, we have proposed the use of an APLM to describe such a relationship because the APLM model can parsimoniously reflect the influence of covariates in linear or nonlinear forms. It is believed that APLMs and the proposed approach can be used in the study of datasets from other biomedical research.

Table 2.

Simulation Results for Case (ii)

n	method	σ = 1			σ = 3			σ = 5
		C	I	MRME	C	I	MRME	C	I	MRME
60	scad	4.44	0	0.774	4.48	0.14	0.937	4.32	0.69	1.028
	lasso	3.28	0	1.017	3.41	0.02	1.003	3.47	0.35	0.889
	bic	4.6	0	0.792	4.74	0.19	0.983	4.58	0.88	1.058
	oracle	5	0	0.673	5	0	0.674	5	0	0.662
100	scad	4.49	0	0.784	4.46	0.03	0.874	4.47	0.38	1.017
	lasso	3.58	0	1.044	3.5	0	0.996	3.58	0.11	0.963
	bic	4.85	0	0.784	4.76	0.03	0.907	4.78	0.61	1.041
	oracle	5	0	0.747	5	0	0.655	5	0	0.681
200	scad	4.4	0	0.768	4.31	0	0.805	4.31	0.03	0.87
	lasso	3.29	0	1.006	3.38	0	0.983	3.36	0	0.91
	bic	4.89	0	0.767	4.89	0.01	0.839	4.84	0.08	0.954
	oracle	5	0	0.716	5	0	0.644	5	0	0.677

Appendix

Throughout the article, let ||·|| be the Euclidean norm for vectors. For any matrix A, denote its L₂ norm as ${\parallel \mathbf{A}\parallel }_2={\sup }_{\parallel \mathbf{u}\parallel \ne 0}\frac{\parallel \mathbf{Au}\parallel }{\parallel \mathbf{u}\parallel }$. Let ${\parallel \phi \parallel }_{\infty }={\sup }_m|\phi (m)|$ be the supremum norm of a function φ on [0,1].

Following Stone (1985) and Huang (2003), for any measurable functions φ₁, φ₂ on [0, 1]^K, define the empirical inner product and the corresponding norm as

$${\langle {\phi }_1,{\phi }_2\rangle }_n=n^{-1}\sum _{i=1}^n{\phi }_1({\mathit{Z}}_i){\phi }_2({\mathit{Z}}_i),{\parallel \phi \parallel }_n^2=n^{-1}\sum _{i=1}^n{\phi }^2({\mathit{Z}}_i).$$

Let f(z) be the joint density of Z. If φ₁ and φ₂ are L²-integrable, define the theoretical inner product as

$$\langle {\phi }_1,{\phi }_2\rangle ={\mathit{\int }}_{{\left[0,1\right]}^K}{\phi }_1(\mathit{z}){\phi }_2(\mathit{z})f(\mathit{z})d\mathit{z}$$

with the corresponding induced norm ${\parallel \phi \parallel }_2^2={\mathit{\int }}_{{\left[0,1\right]}^K}{\phi }^2(\mathit{z})f(\mathit{z})d\mathit{z}$. Let ${\parallel \phi \parallel }_{nk}^2$ and ${\parallel \phi \parallel }_{2k}^2$ be the empirical and theoretical norm of a univariate function φ on [0, 1], defined by

$${\parallel \phi \parallel }_{nk}^2=n^{-1}\sum _{i=1}^n{\phi }^2(Z_{ik}),{\parallel \phi \parallel }_{2k}^2={\mathit{\int }}_0^1{\phi }^2(z_k)f_k(z_k)d{z}_k,$$

where f_k is the density of Z_k for k = 1, …, K. Define the following centered version spline basis

$$b_{j,k}^{\ast }(z_k)=b_{j,k}(z_k)-\frac{{\parallel b_{j,k}\parallel }_{2k}}{{\parallel b_{j-1,k}\parallel }_{2k}}{b}_{j-1,k}(z_k),\forall k=1,\dots ,K,j=-\varrho +1,\dots ,J_n$$ (A.1)

with the standardized version given for any k = 1, …, K,

$$B_{j,k}(z_k)=\frac{b_{j,k}^{\ast }(z_k)}{{\parallel b_{j,k}^{\ast }\parallel }_{2k}},\forall j=-\varrho +1,\dots ,J_{n.}$$ (A.2)

Notice that finding the (γ, β) that minimizes (4) is mathematically equivalent to finding the (γ, β) that minimizes

$$\frac{1}{2}{\sum _{i=1}^n\left[Y_i-\{{\mathbf{\gamma }}^{\mathrm{T}}\mathbf{B}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}\right]}^2,$$

where B (z) = {B_j,k (z_k), j = −ϱ + 1, …, J_n, k = 1, …, K}^T. Then the spline estimator of g₀ is ĝ(z) = γ̂^TB (z) and the centered spline estimators of each component function are

$$\widehat{g_k}(z_k)=\sum _{j=-\varrho +1}^{J_n}{\widehat{\mathrm{\gamma }}}_j{B}_{j,k}(z_k)-\frac{1}{n}\sum _{i=1}^n\sum _{j=-\varrho +1}^{J_n}{\widehat{\mathrm{\gamma }}}_j{B}_{j,k}(Z_{ik}),k=1,\dots ,K.$$

In practice, basis {b_j,k, j = −ϱ + 1, …, J_n, k = 1, …, K}^T is used for data-analytic implementation, and the mathematically equivalent expression (A.2) is convenient for asymptotic analysis.

A.1 Assumptions

The following are some conditions necessary to obtain Theorems 1 and 2. Let r be a positive integer, and ν ∈ (0, 1] be such that p = r + ν > 1.5. Let ℋ be the collection of functions g on [0, 1] whose r-th derivative, g^(r) exists and satisfies the Lipschitz condition of order ν:

$$|g^{(r)}(z^{\prime })-g^{(r)}(z){|\le C|z^{\prime }-z|}^{\nu },\mathit{for}0\le z^{\prime },z\le 1,$$

where and below C is a generic positive constant.

• (C1)Each component function g_0k ∈ ℋ, k = 1, …, K.
• (C2)The distribution of Z is absolutely continuous and its density f is bounded away from zero and infinity on [0, 1]^K.
• (C3)
  The random vector X satisfies that for any vector ω ∈ R^d

  $$c{\parallel \mathit{\omega }\parallel }^2\le {\mathit{\omega }}^{\mathrm{T}}E({\mathit{X}}^{\otimes 2}|\mathit{Z}=z)\mathit{\omega }\le C{\parallel \mathit{\omega }\parallel }^2,$$

  where c is a positive constant.
• (C4)The number of interior knots J_n satisfies: n^1/(2p) ≪ J_n ≪ n^1/3. For example, if p = 2, we can take J_n ~ n^1/4 log n.
• (C5)The projection function Γ (z) has an additive form, i.e., Γ (z) = Γ₁(z₁) + … + Γ_K(z_K), where Γ_k ∈ ℋ, E[Γ_k(Z_k)] = 0 and E[Γ_k(Z_k)]² < ∞, k = 1, …, K.

A.2 Technical Lemmas

According to the result of de Boor (2001, page 149), for any function η ∈ ℋ and n ≥ 1, there exists a function η̃ ∈ S_n such that ||η̃ − η||_∞ ≤ Ch^p. Recall that B(z) = {B_j,k(z_k), j = −ϱ + 1, …, J_n, k = 1, …, K}^T. For g₀ satisfying (C1), we can find γ̃ = {γ̃_j,k, j = −ϱ + 1, …, J_n, k = 1, …, K}^T and an additive spline function g̃ = γ̃^TB (z) ∈ G_n, such that

$${\parallel \stackrel{\sim }{g}-g_0\parallel }_{\infty }=O(h^p).$$ (A.3)

In the following, let

$$\stackrel{\sim }{\beta }=\underset{\beta }{\mathrm{arg\; min}}\frac{1}{2}{\sum _{i=1}^n[Y_i-\{\stackrel{\sim }{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}]}^2.$$ (A.4)

Denote m_0i ≡ m₀(T_i) = g₀(Z_i) + X_i^Tβ₀, and

$${\stackrel{\sim }{m}}_0(\mathit{t})=\stackrel{\sim }{g}(\mathit{z})+{\mathit{x}}^{\mathrm{T}}{\beta }_0,{\stackrel{\sim }{m}}_{0i}\equiv {\stackrel{\sim }{m}}_0({\mathit{T}}_i)=\stackrel{\sim }{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}{\beta }_0.$$ (A.5)

Lemma A.1

Under Conditions (C1)-(C4),

$$\sqrt{n}(\stackrel{\sim }{\beta }-{\beta }_0)\to N(\mathbf{0},{\mathbf{A}}^{-1}{\mathbf{\sum }}_1{\mathbf{A}}^{-1}),$$

where A = E (X^⊗2) and Σ₁ = E (ε²X^⊗2).

Proof

Let $\widehat{\mathit{\delta }}=\sqrt{n}(\stackrel{\sim }{\beta }-{\beta }_0)$. Note that β̃ minimizes $\frac{1}{2}{{\sum }_{i=1}^n[Y_i-\{\stackrel{\sim }{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\beta \}]}^2$, so, δ̂minimizes

$${\stackrel{\sim }{l}}_n(\mathit{\delta })=\frac{1}{2}\sum _{i=1}^n[{\{Y_i-({\stackrel{\sim }{m}}_{0i}+n^{-1/2}{\mathit{\delta }}^{\mathrm{T}}{\mathit{X}}_i)\}}^2-{\{Y_i-{\stackrel{\sim }{m}}_{0i}\}}^2].$$

By expansion, one has

$${\stackrel{\sim }{l}}_n(\mathit{\delta })=-n^{-1/2}\sum _{i=1}^n(Y_i-{\stackrel{\sim }{m}}_{0i}){\mathit{\delta }}^{\mathrm{T}}{\mathit{X}}_i+2^{-1}{\mathit{\delta }}^{\mathrm{T}}{\mathbf{A}}_n\mathit{\delta },$$

where ${\mathbf{A}}_n=\frac{1}{n}{\sum }_{i=1}^n{\mathit{X}}_i^{\otimes 2}=\mathbf{A}+o_P(1).$ Observe that

$$\begin{array}{ll}& n^{-1/2}\sum _{i=1}^n(Y_i-{\stackrel{\sim }{m}}_{0i}){\mathit{X}}_i=n^{-1/2}\sum _{i=1}^n[Y_i-\{\stackrel{\sim }{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}{\beta }_0\}]{\mathit{X}}_i\\ =& n^{-1/2}\sum _{i=1}^n[Y_i-\{g_0({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}{\beta }_0\}]{\mathit{X}}_i+n^{-1/2}\sum _{i=1}^n\{g_0({\mathit{Z}}_i)-\stackrel{\sim }{g}({\mathit{Z}}_i)\}{\mathit{X}}_i\\ =& n^{-1/2}\sum _{i=1}^n{\epsilon }_i{\mathit{X}}_i+n^{-1/2}\sum _{i=1}^n\{g_0({\mathit{Z}}_i)-\stackrel{\sim }{g}({\mathit{Z}}_i)\}{\mathit{X}}_i.\end{array}$$

By (A.3) and Condition (C3), the absolute value of the second term on the right-hand side of the above equation is

$$|n^{-1/2}\sum _{i=1}^n\{g_0({\mathit{Z}}_i)-\stackrel{\sim }{g}({\mathit{Z}}_i)\}{\mathit{X}}_i|\le n^{-1/2}\sum _{i=1}^n|{\mathit{X}}_i|{\parallel \stackrel{\sim }{g}-g_0\parallel }_{\infty }=O_P(n^{1/2}{h}^p)=o_P(1).$$

Thus,

$${\stackrel{\sim }{l}}_n(\mathit{\delta })=-n^{-1/2}\sum _{i=1}^n{\epsilon }_i{\mathit{\delta }}^{\mathrm{T}}{\mathit{X}}_i+2^{-1}{\mathit{\delta }}^{\mathrm{T}}\mathbf{A}\mathit{\delta }+o_P(1),$$

and the convexity lemma of Pollard (1991) implies that

$$\widehat{\mathit{\delta }}={\mathbf{A}}^{-1}{n}^{-1/2}\sum _{i=1}^n{\epsilon }_i{\mathit{X}}_i+o_P(1).$$

It follows that $\sqrt{n}(\stackrel{\sim }{\beta }-{\beta }_0)\to N(\mathbf{0},{\mathbf{A}}^{-1}{\sum }_1{\mathbf{A}}^{-1}).$

Denote

$${\mathbf{V}}_n=n^{-1}{\sum }_{i=1}^n\left\{\begin{array}{cc}{\{\mathbf{B}({\mathit{Z}}_i)\}}^{\otimes 2}& \mathbf{B}({\mathit{Z}}_i){\mathit{X}}_i^{\mathrm{T}}\\ {\mathit{X}}_i{\mathbf{B}}^{\mathrm{T}}({\mathit{Z}}_i)& {\mathit{X}}_i^{\otimes 2}\end{array}\right\}.$$ (A.6)

The following lemma indicates that the Hessian matrix V_n is bounded, which will be used in Lemma A.3.

Lemma A.2

Under Conditions (C1)-(C4), for the random matrix V_n defined in (A.6), there exists a positive constant C such that ${\parallel {\mathbf{V}}_n^{-1}\parallel }_2\le C,a.s.$

Proof

We first derive the lower and upper bound of the eigenvalue of matrix V_n. For any vectors ω₁ = {ω_j,k, j = −ϱ + 1, …, J_n, k = 1, …, K} ∈ R^(J_n+ϱ)K and ω₂ ∈ R^d, let $\omega ={({\omega }_1^{\mathrm{T}},{\omega }_2^{\mathrm{T}})}^{\mathrm{T}}$, then one has

$${\omega }^{\mathrm{T}}{\mathbf{V}}_n\omega ={\omega }_1^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n{\{\mathbf{B}({\mathit{Z}}_i)\}}^{\otimes 2}{\omega }_1+{\omega }_2^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n{\mathit{X}}_i^{\otimes 2}{\omega }_2+2{\omega }_1^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n\mathbf{B}({\mathit{Z}}_i){\mathit{X}}_i^{\mathrm{T}}{\omega }_2.$$

Lemma 1 of Stone (1985) provides a constant c > 0 such that

$${\parallel \sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2\ge c\sum _{k=1}^K{\parallel \sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2.$$

According to Theorem 5.4.2 of DeVore and Lorentz (1993), Condition (C2) and the definition of B_j,k in (A.2), there exist constants C^′_k > c^′_k > 0 such that for any k = 1, …, K

$$c_k^{\prime }{\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}^2\le \parallel \sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2\le C_k^{\prime }\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}^2.$$

Thus there exist constants C₀ > c₀ > 0 such that

$$c_0{\parallel {\omega }_1\parallel }^2\le {\parallel \sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2\le C_0{\parallel {\omega }_1\parallel }^2.$$

By Lemma A.8 in Wang and Yang (2007), we have

$$A_n\equiv \underset{g_1,g_2\in G_n}{\sup }\left|\frac{{\langle g_1,g_2\rangle }_n-\langle g_1,g_2\rangle }{{\parallel g_1\parallel }_2{\parallel g_2\parallel }_2}\right|=O\left\{{(\log n/nh)}^{1/2}\right\},a.s.$$ (A.7)

It is clear to see that

$$\begin{array}{ll}& (1-A_n){\parallel \sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2\le {\omega }_1^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n{\{\mathbf{B}({\mathit{Z}}_i)\}}^{\otimes 2}{\omega }_1\\ =& {\parallel \sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_{2,n}^2\le (1+A_n){\parallel \sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\omega }_{j,k}{B}_{j,k}\parallel }_2^2.\end{array}$$

Therefore,

$$c{\parallel {\omega }_1\parallel }^2\le {\omega }_1^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n{\{\mathbf{B}({\mathit{Z}}_i)\}}^{\otimes 2}{\omega }_1\le C{\parallel {\omega }_1\parallel }^2,a.s.$$

Next,

$$\begin{array}{lll}{\omega }_{\mathrm{2}}^{\mathrm{T}}{n}^{-1}\sum _{i=1}^n{\mathit{X}}_i^{\otimes 2}{\omega }_2& =& {\omega }_{\mathrm{2}}^{\mathrm{T}}E({\mathit{X}}^{\otimes 2}){\omega }_2+{\omega }_{\mathrm{2}}^{\mathrm{T}}[n^{-1}{\sum }_{i=1}^n\{{\mathit{X}}_i^{\otimes 2}-E({\mathit{X}}^{\otimes 2})\}]{\omega }_2\\ & =& {\omega }_{\mathrm{2}}^{\mathrm{T}}E({\mathit{X}}^{\otimes 2}){\omega }_2+{\parallel {\omega }_2\parallel }^2{o}_{a.s.}(1),\end{array}$$

and according to Condition (C3), $c{\parallel {\omega }_{\mathrm{2}}\parallel }^2\le {\omega }_2^{\mathrm{T}}{n}^{-1}{\sum }_{i=1}^n{\mathit{X}}_i^{\otimes 2}{\omega }_2\le C{\parallel {\omega }_2\parallel }^2,\mathrm{a.s.}$ Then $|{\omega }_1^{\mathrm{T}}{n}^{-1}{\sum }_{i=1}^n\mathbf{B}({\mathit{Z}}_i){\mathit{X}}_i^{\mathrm{T}}{\omega }_2|=o(\parallel {\omega }_1\parallel \parallel {\omega }_2\parallel ),\mathrm{a.s.}$ Thus

$$c{\parallel \omega \parallel }^2\le {\omega }^{\mathrm{T}}{\mathbf{V}}_n\omega \le C{\parallel \omega \parallel }^2,\mathrm{a.s.}$$ (A.8)

Let λ_max (V_n) and λ_min (V_n) be the maximum and minimum eigenvalues of V_n. Algebra and (A.8) show that ${\parallel {\mathbf{V}}_n\parallel }_2={\mathrm{\lambda }}_{\max }({\mathbf{V}}_n)\le C$ and ${\parallel {\mathbf{V}}_n^{-1}\parallel }_2={\mathrm{\lambda }}_{\min }^{-1}({\mathbf{V}}_n)\le c^{-1},\mathrm{a.s.}$

In the following, denote $\mathit{\theta }=\left(\begin{array}{c}\mathrm{\gamma }\\ \beta \end{array}\right),\stackrel{\sim }{\mathit{\theta }}=\left(\begin{array}{c}\stackrel{\sim }{\mathrm{\gamma }}\\ \stackrel{\sim }{\beta }\end{array}\right),\widehat{\mathit{\theta }}=\left(\begin{array}{c}\widehat{\mathrm{\gamma }}\\ \widehat{\beta }\end{array}\right),{\widehat{l}}_n(\mathit{\theta })=\ell (\mathrm{\gamma },\beta )$ and

$${\stackrel{\sim }{m}}_i\equiv \stackrel{\sim }{m}({\mathit{T}}_i)=\stackrel{\sim }{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\stackrel{\sim }{\beta }={\stackrel{\sim }{\mathrm{\gamma }}}^{\mathrm{T}}\mathbf{B}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\stackrel{\sim }{\beta }.$$ (A.9)

Lemma A.3

Under Conditions (C1)-(C4), $\parallel \widehat{\mathit{\theta }}-\stackrel{\sim }{\mathit{\theta }}\parallel =O_P\left\{J_n^{1/2}(h^p+n^{-1/2})\right\}.$

Proof

Note that

$${\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\widehat{\mathit{\theta }}}-{\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}={\frac{{\partial }^2{\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\mathrm{T}}}|}_{\mathit{\theta }=\overline{\mathit{\theta }}}(\widehat{\mathit{\theta }}-\stackrel{\sim }{\mathit{\theta }}),$$

where θ̄ is between θ̂ and θ̃. So

$$\widehat{\mathit{\theta }}-\stackrel{\sim }{\mathit{\theta }}=-{\left({\frac{{\partial }^2{\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\mathrm{T}}}|}_{\mathit{\theta }=\overline{\mathit{\theta }}}\right)}^{-1}{\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}.$$

Next write

$${\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}={{\left\{{\left(\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathrm{\gamma }}\right)}^{\mathrm{T}},{\left(\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \beta }\right)}^{\mathrm{T}}\right\}}^{\mathrm{T}}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}=-\sum _{i=1}^n(Y_i-{\stackrel{\sim }{m}}_i)\{\mathbf{B}({\mathit{Z}}_i),{\mathit{X}}_i\},$$

where

$$\begin{array}{ccc}{\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathrm{\gamma }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}& =& -\sum _{i=1}^n(Y_i-m_{0i})\mathbf{B}({\mathit{Z}}_i)+\sum _{i=1}^n\{\stackrel{\sim }{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}\mathbf{B}({\mathit{Z}}_i)\\ & & +\sum _{i=1}^n{\mathit{X}}_i^{\mathrm{T}}(\stackrel{\sim }{\beta }-{\beta }_0)\mathbf{B}({\mathit{Z}}_i),\end{array}$$

$${\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \beta }|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}=-\sum _{i=1}^n(Y_i-m_{0i}){\mathit{X}}_i+\sum _{i=1}^n\{\stackrel{\sim }{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\mathit{X}}_i+\sum _{i=1}^n{(\stackrel{\sim }{\beta }-{\beta }_0)}^{\mathrm{T}}{\mathit{X}}_i^{\otimes 2}.$$

Observing that

$$\parallel -\frac{1}{n}\sum _{i=1}^n(Y_i-m_{0i})\mathbf{B}({\mathit{Z}}_i)\parallel ={\left[\sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\left\{\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{B}_{j,k}(Z_{\mathit{ik}})\right\}}^2\right]}^{1/2},$$

and

$$E\left[\sum _{k=1}^K\sum _{j=-\varrho +1}^{J_n}{\left\{\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{B}_{j,k}(Z_{\mathit{ik}})\right\}}^2\right]\le C{J}_n/n,$$

we have $\parallel -\frac{1}{n}{\sum }_{i=1}^n(Y_i-m_{0i})\mathbf{B}({\mathit{Z}}_i)\parallel =O_P\left\{{(J_n/n)}^{1/2}\right\}.$ By Condition (C4), equation (A.3) and Lemma A.1,

$$\begin{array}{c}\parallel \frac{1}{n}\sum _{i=1}^n\{\stackrel{\sim }{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}\mathbf{B}({\mathit{Z}}_i)\parallel =O_P(J_n^{1/2}{h}^p),\\ \parallel \frac{1}{n}\sum _{i=1}^n{(\stackrel{\sim }{\beta }-{\beta }_0)}^{\mathrm{T}}{\mathit{X}}_i\mathbf{B}({\mathit{Z}}_i)\parallel =O_P\{{(J_n/n)}^{1/2}\}.\end{array}$$

Therefore, $\parallel {\frac{1}{n}\frac{\partial {\stackrel{\sim }{l}}_n(\mathit{\theta })}{\partial \mathrm{\gamma }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}\parallel =O_P\left\{J_n^{1/2}(h^p+n^{-1/2})\right\}.$ Similarly, one has

$$\begin{array}{c}\parallel \frac{1}{n}\sum _{i=1}^n(m_{0i}-Y_i){\mathit{X}}_i\parallel =\parallel \frac{1}{n}\sum _{i=1}^n{\epsilon }_i{\mathit{X}}_i\parallel =O_P\left\{{(J_n/n)}^{1/2}\right\},\\ \parallel \frac{1}{n}\sum _{i=1}^n\{\stackrel{\sim }{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\mathit{X}}_i\parallel =O_P(J_n^{1/2}{h}^p),\\ \parallel \frac{1}{n}\sum _{i=1}^n{\left(\stackrel{\sim }{\beta }-{\beta }_0\right)}^{\mathrm{T}}{\mathit{X}}_i{\mathit{X}}_i^{\mathrm{T}}\parallel =O_P\left\{{(J_n/n)}^{1/2}\right\}.\end{array}$$

Thus $\parallel {\frac{1}{n}\frac{{\stackrel{\sim }{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}\parallel =O_P\left\{J_n^{1/2}(h^p+n^{-1/2})\right\}.$ For the second order derivative, one has

$${\frac{1}{n}\frac{{\partial }^2{\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\mathrm{T}}}|}_{\mathit{\theta }=\overline{\mathit{\theta }}}={\frac{1}{n}\left\{\begin{array}{cc}\frac{{\partial }^2{\widehat{l}}_n(\mathit{\theta })}{\partial \mathrm{\gamma }\partial {\mathrm{\gamma }}^{\mathrm{T}}}& \frac{{\widehat{l}}_n(\mathit{\theta })}{\partial \mathrm{\gamma }\partial {\beta }^{\mathrm{T}}}\\ \frac{{\widehat{l}}_n(\mathit{\theta })}{\partial \beta \partial {\mathrm{\gamma }}^{\mathrm{T}}}& \frac{{\widehat{l}}_n(\mathit{\theta })}{\partial \beta \partial {\beta }^{\mathrm{T}}}\end{array}\right\}|}_{\mathit{\theta }=\overline{\mathit{\theta }}}={\mathbf{V}}_n.$$

According to Lemma A.2, ${\parallel {\mathrm{V}}_n^{-1}\parallel }_2=O_P(1)$. Thus

$$\parallel \widehat{\mathit{\theta }}-\stackrel{\sim }{\mathit{\theta }}\parallel \le {\parallel {\mathbf{V}}_n^{-1}\parallel }_2\parallel {\frac{1}{n}\frac{\partial {\widehat{l}}_n(\mathit{\theta })}{\partial \mathit{\theta }}|}_{\mathit{\theta }=\stackrel{\sim }{\mathit{\theta }}}\parallel =O_P\{J_n^{1/2}(h^p+n^{-1/2})\}.$$

Lemma A.4

Under (C1)-(C4), ∥ĝ − g₀∥₂ = O_P{(J_n/n)^1/2}, ∥ĝ − g₀∥_n = O_P{(J_n/n)^1/2}, and ∥ĝ_k − g_0k∥_2k = O_P{(J_n/n)^1/2} and ∥ĝ_k − g_0k∥_nk = O_P{(J_n/n)^1/2}, for k = 1, …, K.

Proof

According to Lemmas A.2 and A.3, ${\parallel \widehat{g}-\stackrel{\sim }{g}\parallel }_2^2$ is equal to ${\mathit{\int }}_{{[0,1]}^K}{(\widehat{g}-\stackrel{\sim }{g})}^2(z)f(z)dz={(\widehat{\mathrm{\gamma }}-\stackrel{\sim }{\mathrm{\gamma }})}^{\mathrm{T}}{(\langle B_{j,k},B_{j^{\prime },k^{\prime }}\rangle )}_{\underset{1\le k,k^{\prime }\le K}{-\varrho \le j,j^{\prime }\le J_n,}}(\widehat{\mathrm{\gamma }}-\stackrel{\sim }{\mathrm{\gamma }})\le C{\parallel \widehat{\mathrm{\gamma }}-\stackrel{\sim }{\mathrm{\gamma }}}_2^2$, thus ∥ĝ − g̃∥₂ = O_P{J_n^1/2(h^p + n^−1/2)} and

$$\begin{array}{lll}{\parallel \widehat{g}-g_0\parallel }_2& \le & {\parallel \widehat{g}-\stackrel{\sim }{g}\parallel }_2+{\parallel \stackrel{\sim }{g}-g_0\parallel }_2=O_P\{J_n^{1/2}(h^p+n^{-1/2})\}+O_P(h^p)\\ & =& O_P\{J_n^{1/2}(h^p+n^{-1/2})\}.\end{array}$$

By Lemma 1 of Stone (1985), ∥ĝ_k − g_0k∥_2k = O_P {J_n^1/2 (h^p + n^−1/2)}, 1 ≤ k ≤ K. Equation (A.7) then implies that ∥ĝ − g̃∥_n = O_P {J_n^1/2 (h^p + n^1/2)}. Then

$$\begin{array}{lll}{\parallel \widehat{g}-g_0\parallel }_n& \le & {\parallel \widehat{g}-\stackrel{\sim }{g}\parallel }_n+{\parallel \stackrel{\sim }{g}-g_0\parallel }_n=O_P\{J_n^{1/2}(h^p+n^{-1/2})\}+O_P(h^p)\\ & =& O_P\{J_n^{1/2}(h^p+n^{-1/2})\}.\end{array}$$

Similar to (A.7),

$$\underset{g\in S_n}{\sup }\left|\frac{{\parallel g\parallel }_{nk}}{{\parallel g\parallel }_{2k}}-1\right|=O_P\left\{{(\log n/nh)}^{1/2}\right\},k=1,\dots ,K,$$

thus ∥ĝk − g_0k∥_nk = O_P {J_n^1/2 (h^p + n^−1/2)}, for any k = 1, …, K. The desired result follows by Condition (C4).

Lemma A.5

Under Conditions (C1)-(C4), one has

$$\frac{1}{n}\sum _{i=1}^n{\stackrel{\sim }{\mathit{X}}}_i\mathrm{\Gamma }{({\mathit{Z}}_i)}^{\mathrm{T}}(\widehat{\beta }-{\beta }_0)=O_P(n^{-1/2}),$$ (A.10)

$$\frac{1}{n}\sum _{i=1}^n\{\widehat{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\stackrel{\sim }{\mathit{X}}}_i=O_P(n^{-1/2}).$$ (A.11)

Proof

We first show (A.11). Let s (z, g) = g(z)x̃. Note that

$$E{\{s(\mathit{Z},\widehat{g})-s(\mathit{Z},g_0)\}}^2=E{\{(\widehat{g}-g_0)({\mathit{Z}}_i){\stackrel{\sim }{\mathit{X}}}_i\}}^2\le O({\parallel \widehat{g}-g_0\parallel }_2^2).$$

By Lemma A.2 of Huang (1999), the logarithm of the ε-bracketing number of the class of functions

$${\mathit{A}}_1(\delta )=\{s(·,\widehat{g})-s(·,g_0):g\in {\mathit{G}}_n,{\parallel g-g_0\parallel }_2\le \delta \}$$

is c {(J_n + ϱ) log (δ/ε) + log (δ⁻¹)}, so the corresponding entropy integral

$$J_{[]}(\delta ,{\mathit{A}}_1(\delta ),{\parallel ·\parallel }_2)\le c\delta \{{(J_n+\varrho )}^{1/2}+{\log }^{1/2}({\delta }^{-1})\}.$$

According to Lemma 7 of Stone (1986) and Lemma A.4,

$${\parallel \widehat{g}-g_0\parallel }_{\infty }\le c{J}_n^{1/2}{\parallel \widehat{g}-g_0\parallel }_2=O_P(n^{-1/2}{J}_n).$$

Lemma 3.4.2 of van der Vaar and Wellner (1996) implies that, for r_n = (n/J_n)^1/2,

$$\begin{array}{ll}& E\left|\frac{1}{n}\sum _{i=1}^n\{\widehat{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\stackrel{\sim }{\mathit{X}}}_i-E\left[\{\widehat{g}(\mathit{Z})-g_0(\mathit{Z})\}\stackrel{\sim }{\mathit{X}}\right]\right|\\ \le & n^{-1/2}C{r}_n^{-1}\{{(J_n+\varrho )}^{1/2}+{\log }^{1/2}(r_n)\}\left[1+\frac{C{r}_n^{-1}\{{(J_n+\varrho )}^{1/2}+{\log }^{1/2}(r_n)\}}{r_n^{-2}\sqrt{n}}{C}_0\right]\\ \le & O(1)n^{-1/2}{r}_n^{-1}\{{(J_n+\varrho )}^{1/2}+{\log }^{1/2}(r_n)\}.\end{array}$$

By Condition (C4), O (n^−1/2J_n) = o (1). Thus, one has

$$E\left|\frac{1}{n}\sum _{i=1}^n\{\widehat{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\stackrel{\sim }{\mathit{X}}}_i-E\left[\{\widehat{g}(\mathit{Z})-g_0(\mathit{Z})\}\stackrel{\sim }{\mathit{X}}\right]\right|=o(n^{-1/2}).$$

By the definition of X̃, for any measurable function φ, E {φ (Z) X̃} = 0. Hence (A.11) holds. Similarly, (A.10) follows from Lemma 3.4.2 of van der Vaar and Wellner (1996) and Lemma A.3.

Lemma A.6

Under the conditions of Theorem 2, with probability tending to 1, for any given β₁ satisfying that ∥β₁ − β₁₀∥ = O_p(n^−1/2) and any constant C,

$${ℒ}_P\left\{\left(\begin{array}{c}{\mathit{\beta }}_1\\ \mathbf{0}\end{array}\right),\mathrm{\gamma }\right\}=\underset{\parallel {\mathit{\beta }}_2\parallel \le C{n}^{-1/2}}{\min }{ℒ}_P\left\{\left(\begin{array}{c}{\mathit{\beta }}_1\\ {\mathit{\beta }}_2\end{array}\right),\mathrm{\gamma }\right\}.$$

Proof

To prove that the minimum is attained at β₂ = 0, it suffices to show that with probability tending to 1, as n → ∞, for any β₁ satisfying ∥β₁ − β₁₀∥ = O_P(n^−1/2), and ∥β₂∥ ≤ Cn^−1/2, ∂ℒ_P(β)/∂β_j and β_j have the same signs for β_j ∈ (−Cn^−1/2, Cn^−1/2), for j = s + 1, … , d. It follows by the similar arguments as given in the proof of Theorem 1 that,

$${{\ell }^{\prime }}_j(\beta )\equiv \frac{\partial \ell (\widehat{\mathrm{\gamma }},\beta )}{\partial {\beta }_j}=n\left\{\frac{1}{n}\sum _{i=1}^n{\mathrm{\Omega }}_j(Y_i,{\mathit{T}}_i)-{(\beta -{\beta }_0)}^{\mathrm{T}}{R}_j+o_P(n^{-1/2})\right\},$$

where Ω_j (Y_i, T_i) is the jth element of −ε_iX̃_i and R_j is the jth column of E(X̃^⊗2). Note that ∥β − β₀∥ = O_P(n^−1/2) by the assumption. Thus, n⁻¹ ℓ′_j(β) is of the order O_P (n^−1/2). Therefore, for any zero β_j and j = s + 1, … , d,

$$\begin{array}{ll}\frac{\partial {ℒ}_P(\beta ,\mathrm{\gamma })}{\partial {\beta }_j}& ={{\ell }^{\prime }}_j(\beta )+n{p^{\prime }}_{{\mathrm{\lambda }}_{jn}}(|{\beta }_j|)\mathrm{sgn}({\beta }_j)\\ & =n{\lambda }_{\mathit{jn}}\{{\lambda }_{jn}^{-1}{p^{\prime }}_{{\lambda }_{jn}}(|{\beta }_j|)\mathrm{sgn}({\beta }_j)+O_p(\frac{1}{\sqrt{n}{\lambda }_n})\}\end{array}.$$

Because ${\mathrm{lim\; inf}}_{n\to \infty }{\mathrm{lim\; inf}}_{{\beta }_j\to 0^{+}}{\lambda }_{\mathit{jn}}^{-1}{p}_{{\lambda }_{\mathit{jn}}}^{\prime }(|{\beta }_j|)>0$ and $\sqrt{n}{\mathrm{\lambda }}_{jn}\to \infty$, the sign of the derivative is completely determined by that of β_j. Thus the desired result is obtained.

A.3 Proof of Theorem 1

According to Condition (C5), the projection function Г (z) = Г₁(z₁) + … + Г_K(z_K), where the theoretically centered function Г_k ∈ ℋ. By the result of de Boor (2001, page 149), there exists an empirically centered function Г̃_k ∈ S_n, such that ║Г̃_k − Г_k║_∞ = O_P (h^p), = k = 1, …, K. Denote Г̃ (z) = Г̃₁(z₁) + … + Г̃ _K(z_K) and clearly Г̃ ∈ G_n. Define a class of functions

$${ℳ}_n=\{m(x,z)=g(z)+x^{\mathrm{T}}\beta :g\in G_n\}.$$ (A.12)

For any υ ∈ R^d, let m̂ (x, z) = ĝ(z) + x^Tβ̂ and m̂ _υ = m̂ (x, z) + υ^T{x − Г̃(z), then m̂_υ = {ĝ(z) − υ^TГ̃(z)} + (β̂ + υ)^Tx ∈ ℳ_n. Note that m̂_υ minimizes the function ${\widehat{l}}_n(m)=1/2{\sum }_{i=1}^n{\{Y_i-m({\mathit{X}}_i,{\mathit{Z}}_i)\}}^2$ for all m ∈ ℳ_n when υ = 0, thus ${\frac{\partial }{\partial \mathit{\upsilon }}{\widehat{l}}_n({\widehat{m}}_{\mathit{\upsilon }})|}_{\mathit{\upsilon }=0}=0$. Denote

$${\widehat{m}}_i\equiv \widehat{m}({\mathit{X}}_i,{\mathit{Z}}_i)=\widehat{g}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\widehat{\beta }={\widehat{\mathrm{\gamma }}}^{\mathrm{T}}\mathbf{B}({\mathit{Z}}_i)+{\mathit{X}}_i^{\mathrm{T}}\widehat{\beta },$$ (A.13)

and X̃_i = X_i − Г (Z_i), then

$$\begin{array}{ll}\mathbf{0}& \equiv {\frac{\partial }{\partial \mathit{\upsilon }}{\widehat{l}}_n({\widehat{m}}_{\mathit{\upsilon }})|}_{\mathit{\upsilon }=0}=-\sum _{i=1}^n(Y_i-{\widehat{m}}_i)\{{\mathit{X}}_i-\stackrel{\sim }{\mathrm{\Gamma }}({\mathit{Z}}_i)\}=-\sum _{i=1}^n(Y_i-{\widehat{m}}_i){\stackrel{\sim }{\mathit{X}}}_i+O_P(h^p)\\ & =-\sum _{i=1}^n{\epsilon }_i{\stackrel{\sim }{\mathit{X}}}_i+\sum _{i=1}^n({\widehat{m}}_i-m_{0i}){\stackrel{\sim }{\mathit{X}}}_i+O_P(h^p).\end{array}$$ (A.14)

Note that

$$\widehat{m}(x,z)-m_0(x,z)={(\widehat{\beta }-{\beta }_0)}^{\mathrm{T}}\stackrel{\sim }{x}+{(\widehat{\beta }-{\beta }_0)}^{\mathrm{T}}\mathrm{\Gamma }(z)+\widehat{g}(z)-g_0(z).$$

We can rewrite the second term ${\sum }_{i=1}^n({\widehat{m}}_i-m_{0i}){\stackrel{\sim }{\mathit{X}}}_i$ in (A.14) as

$$\left(\sum _{i=1}^n{\stackrel{\sim }{\mathit{X}}}_i^{\otimes 2}\right)(\widehat{\beta }-{\beta }_0)+\left\{\sum _{i=1}^n{\stackrel{\sim }{\mathit{X}}}_i\mathrm{\Gamma }{({\mathit{Z}}_i)}^{\mathrm{T}}\right\}(\widehat{\beta }-{\beta }_0)+\sum _{i=1}^n\{\widehat{g}({\mathit{Z}}_i)-g_0({\mathit{Z}}_i)\}{\stackrel{\sim }{\mathit{X}}}_i.$$

By Lemma A.5, one has

$$\frac{1}{n}\sum _{i=1}^n({\widehat{m}}_i-m_{0i}){\stackrel{\sim }{\mathit{X}}}_i=\left\{E({\stackrel{\sim }{\mathit{X}}}^{\otimes 2})+o_P(1)\right\}(\widehat{\beta }-{\beta }_0)+o_P(n^{-1/2}).$$ (A.15)

Combining (A.14), (A.15) and Condition (C4), one has

$$\mathbf{0}=-\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{\stackrel{\sim }{\mathit{X}}}_i+\left\{E({\stackrel{\sim }{\mathit{X}}}^{\otimes 2})+o_P(1)\right\}(\widehat{\beta }-{\beta }_0)+o_P(n^{-1/2}).$$

Thus the desired distribution of β̂ follows.

A.4 Proof of Theorem 2

Let τ_n = n^−1/2 + a_n. It suffices to show that for any given ζ > 0, there exists a large constant C such that

$$P\left\{\underset{\parallel \mathit{\upsilon }\parallel =c}{\sup }{ℒ}_P({\beta }_0+{\tau }_n\mathit{\upsilon },\mathrm{\gamma })<{ℒ}_P({\beta }_0,\mathrm{\gamma })\right\}\ge 1-\zeta .$$ (A.16)

Denote

$$\begin{array}{ccc}{D}_{n,1}& =& \frac{1}{2}\sum _{i=1}^n[{\left\{Y_i-\left({\widehat{\gamma }}^{\mathrm{T}}\mathbf{B}\left({\mathit{Z}}_i\right)+{\mathit{X}}_i^{\mathrm{T}}\left({\mathit{\beta }}_0+{\tau }_n\upsilon \right)\right)\right\}}^2\\ & & -{\left\{Y_i-\left({\widehat{\gamma }}^{\mathrm{T}}\mathbf{B}\left({\mathit{Z}}_i\right)+{\mathit{X}}_i^{\mathrm{T}}{\mathit{\beta }}_0\right)\right\}}^2]\end{array}$$

and $D_{n,2}=n{\sum }_{j=1}^S\{p{\mathrm{\lambda }}_n(|{\beta }_{j0}+{\tau }_n{\upsilon }_j|)-p{\mathrm{\lambda }}_n(|{\beta }_{j0}|)\}$, where s is the number of components of β₁₀. Note that pλ_n (0) = 0 and pλ_n (|β|) ≥ 0 for all β. Thus,

$${ℒ}_P({\beta }_0+{\tau }_n\mathit{\upsilon },\mathrm{\gamma })-{ℒ}_P({\beta }_0,\mathrm{\gamma })\ge D_{n,1}+D_{n,2}.$$

Let m̂_0i = γ̂^TB(Z_i) + X_i^Tβ₀. For D_n,1, note that

$$D_{n,1}=\frac{1}{2}\sum _{i=1}^n[{\{Y_i-({\widehat{m}}_{0i}+{\tau }_n{\mathit{\upsilon }}^{\mathrm{T}}{\mathit{X}}_i)\}}^2-{(Y_i-{\widehat{m}}_{0i})}^2].$$

A mimic of the proof for Theorem 1 indicates that

$$D_{n,1}=-{\tau }_n{\mathit{\upsilon }}^{\mathrm{T}}\sum _{i=1}^n{\epsilon }_i{\stackrel{\sim }{\mathit{X}}}_i+\frac{1}{2}{\tau }_n^2{\mathit{\upsilon }}^{\mathrm{T}}\mathbf{D}\mathit{\upsilon }+O_P(1),$$ (A.17)

where the orders of the first term and the second term are O_P (n^1/2τ_n) and O_P (nτ_n²), respectively. For D_n,2, by the Taylor expansion and the Cauchy-Schwartz inequality, n⁻¹D_n,2 is bounded by

$$\sqrt{s}{\tau }_n{a}_n\parallel \mathit{\upsilon }\parallel +{\tau }_n^2{\omega }_n{\parallel \mathit{\upsilon }\parallel }^2=C{\tau }_n^2(\sqrt{s}+{\omega }_{n}C).$$

As w_n → 0, both the first and second terms on the right-hand side of (A.17) dominate D_n,2, by making C sufficiently large. Hence (A.16) holds for a sufficiently large C.

We now prove part (II). From Lemma A.6, it follows that β̂₂ = 0. Let ${\widehat{\beta }}_1^{\ast }=\sqrt{n}({\widehat{\beta }}_1-{\beta }_{10})$, ${\widehat{m}}_{i1}={\widehat{\gamma }}^{\mathrm{T}}\mathbf{B}({\mathit{Z}}_i)+{\mathit{X}}_{i1}^{\mathrm{T}}{\beta }_{10}$, and $m_{i1}=g_0^{\mathrm{T}}({\mathit{Z}}_i)+{\mathit{X}}_{i1}^{\mathrm{T}}{\beta }_{10}$. Then, β̂₁* minimizes

$$\frac{1}{2}\sum _{i=1}^n\left[{\left\{Y_i-({\widehat{m}}_{i1}+n^{-1/2}{\mathit{X}}_{i1}^{\mathrm{T}}{\widehat{\beta }}_1^{\ast })\right\}}^2-{(Y_i-{\widehat{m}}_{i1})}^2\right]+n\sum _{j=1}^{s}p{\mathrm{\lambda }}_{jn}(|{\beta }_j|).$$ (A.18)

Denote ℓ_nl (β^*₁) the first term in (A.18), then

$${\ell }_{n1}({\beta }_1^{\ast })=-n^{-1/2}\sum _{i=1}^n(Y_i-{\widehat{m}}_{i1}){\mathit{X}}_{i1}^{\mathrm{T}}{\beta }_1^{\ast }+2^{-1}{({\beta }_1^{\ast })}^{\mathrm{T}}\left\{\frac{1}{n}\sum _{i=1}^n{\mathit{X}}_{i1}^{\otimes 2}\right\}{\beta }_1^{\ast }.$$ (A.19)

Using the arguments similar to the proofs for (A.15) and (A.17) yields

$${\ell }_{n1}({\beta }_1^{\ast })=-n^{-1/2}\sum _{i=1}^n{\widehat{\beta }}_1^{\ast }(Y_i-m_{i1}){\stackrel{\sim }{\mathit{X}}}_{i1}+\frac{1}{2}{\widehat{\beta }}_1^{\ast \mathrm{T}}E({\stackrel{\sim }{\mathit{X}}}_1^{\otimes 2}){\widehat{\beta }}_1^{\ast }+o_P(1).$$

Using the Convexity Lemma (Pollard, 1991) and combining (A.18), one has

$$\left(E({\stackrel{\sim }{\mathit{X}}}_1^{\otimes 2})+{\sum }_{\mathrm{\lambda }}\right){\widehat{\beta }}_1^{\ast }+n^{1/2}{\kappa }_n=n^{-1/2}\sum _{i=1}^n(Y_i-m_{i1}){\stackrel{\sim }{\mathit{X}}}_{i1}+o_P(1).$$

Hence the asymptotic normality is derived.