Fundamentals of three-dimensional reconstruction from projections

Abstract

Three-dimensional reconstruction of an object mass density from the set of its two-dimensional line projections lies at a core of both single-particle reconstruction technique and electron tomography. Both techniques utilize electron microscope to collect a set of projections of either multiple objects representing in principle the same macromolecular complex in an isolated form, or a subcellular structure isolated in situ. Therefore, macromolecular electron microscopy can be seen as a problem of inverting projection transformation to recover the distribution of the mass density of the original object. The problem is interesting in that in its discrete form it is ill-posed and not invertible. Various algorithms have been proposed to cope with the practical difficulties of this inversion problem and their differ widely in terms of their robustness with respect to noise in the data, completeness of the collected projection data set, errors in projections’ orientation parameters, abilities to efficiently handle large data sets, and other obstacles typically encountered in molecular electron microscopy. Here, we review the theoretical foundations of three-dimensional reconstruction from line projections followed by an overview of reconstruction algorithms routinely used in practice of electron microscopy.

Introduction

The two electron microscope-based techniques that provide insight into three-dimensional (3D) organization of biological specimens, namely single particle reconstruction (SPR) and electron tomography (ET), are often stated as a problem of 3D reconstruction from 2D projections. While one can argue that the main challenge of these techniques is the establishment of the orientation parameters of 2D projections, which is necessary condition for 3D reconstruction, there is no doubt that the 3D reconstruction itself plays a central role in understanding how SPR and ET lead to 3D visualization of the specimen. Indeed, many steps of the respective data processing protocols for ET and SPR are best understood in terms of the 3D reconstruction problem. For example, the ab initio determination of a 3D model in SPR, both using Random Conical Tilt approach (Radermacher et al., 1987) and common lines methodology (Crowther et al., 1970b; Goncharov et al., 1987; Penczek et al., 1996; van Heel, 1987), is deeply rooted in the nature of the relationship between an object and its projections. Refinement of a 3D structure, as done using either real-space 3D projection alignment (Penczek et al., 1994) or Fourier space representation (Grigorieff, 1998) depends on correct accounting for 3D reconstruction idiosyncrasies. The principle and limitations of resolution estimation of the reconstructed 3D object using Fourier Shell Correlation (FSC) or Spectral Signal-to-Noise Ratio (SSNR) methodology can only be explained within the context of 3D reconstruction algorithms (Penczek, 2002). Therefore, even a brief introduction into SPR and ET principles has to include an explanation of the foundations of the methods of 3D reconstruction from projections.

Imaging the density distribution of a 3D object using a set of its 2D projections can be considered an extension of computerized tomography (from Greek τέμνειν, to section), which was originally developed for reconstructing 2D cross-sections (slices) of a 3D object from its 1D projections. The first practical application of the methods proposed for the reconstruction of an interior mass distribution of an object from a set of its projections dates back to 1956 when Bracewell reconstructed sun spots from multiple projection views of the Sun from the Earth (Bracewell, 1956). Bracewell is also credited with the introduction of the first semi-heuristic reconstruction algorithm known as filtered backprojection (FBP), which is still commonly used in CT scanners. In 1967, DeRosier and Klug performed 3D reconstruction of a virus capsid vy taking advantage of its icosahedral symmetry (Crowther et al., 1970b; DeRosier and Klug, 1968). In 1969 Hoppe proposed 3D high-resolution electron microscopy of non-periodic biological specimens (Hoppe, 1969), and his ideas later matured into what we today know as electron tomography (reconstruction of individual objects in situ) and single particle reconstruction (reconstruction of macromolecular structures by averaging projection images of multiple, but structurally identical isolated single particles). Tomography became a household name with the development of Computed Axial Tomography (CAT) by Hounsfield and Cormack (independently) in 1972. CAT was the first non-invasive technique that allowed visualization of the interior of living organisms.

Reconstruction algorithms are an integral part of the tomographic technique; without computer analysis and merging of the data it is all but impossible to deduce structure of an object from the set of its projections. Initially, the field was dominated by algorithms based on various semi-heuristic principles, and the lack of solid theoretical foundations caused some strong controversies. A question of both theoretical and practical interest concerns the minimum number of projections required for a faithful reconstruction, as algebraic and Fourier techniques seemed to lead to different conclusions (Bellman et al., 1971; Crowther and Klug, 1971; Gordon et al., 1970). Considering the quality of an early ET reconstruction of a ribosome, some claims might have been exaggerated (Bender et al., 1970). However, it was eventually recognized that mathematical foundations for modern tomography predate the field by decades and were laid out as purely theoretical problems: Radon considered the invertibility of an integral transform involving projections (Radon, 1986), and Kaczmarz sought an iterative solution of a large system of linear equations (Kaczmarz, 1993). Currently, the mathematics of reconstruction from projections problems is very well developed and understood (Herman, 2009; Natterer, 1986; Natterer and Wübbeling, 2001).

Even though the mathematical framework of tomography is well laid out, the field remains vibrant both in terms of theoretical progress and development of new algorithms. The main challenge is that the reconstruction of an object from a set of its projections belongs to a class of inverse problems, so one has to find practical approximations of the solution. While a continuous Radon transform with an infinite number of projections is invertible, in practice only a finite number of discretized projections can be measured. It is well known that in this case the original object cannot be uniquely recovered (Rieder and Faridani, 2003). To illustrate this statement we represent the problem as an algebraic one: we denote all projection data by a vector g, the original object by a vector d, and a projection matrix by P, which is almost always rectangular. The inverse reconstruction is stated as: given g and P, find d̂ such that Pd̂ = g. The inverse problem is called well-posed if it is uniquely solvable for each g and if the solution depends continuously on g. Otherwise, it is called ill-posed. Since P is rectangular in tomography, the inversion of projection transformation is necessarily ill-posed and is either over- or under-determined depending on the number of projections. Moreover, even if an approximate inverse (reconstruction algorithm) can be found, it is not necessarily continuous, which means that the solution of Pd̂ = g need not be close to the solution of Pd̂ = g^ε even if g^ε is close to g. A further difficulty is caused by the existence of ghosts in tomography. For discretized tomography, the set of projections is finite and data is sampled, and it can be shown that for any set of projection directions there exists a non-trivial object d̂₀ ≠ 0 whose projections calculated in the directions of measured data are exactly zero, that is Pd̂₀ = 0 (Louis, 1984). This implies that the reconstructed object can differ significantly from the original object but still agree perfectly with the given data, in other words, the discrete integral projection transformation is not invertible, even in the absence of noise. In practice, ghosts happen to be very high frequency objects (Louis, 1984; Maass, 1987) and their impact can be all but eliminated by a proper regularization of the inverse process.

It follows from the previous discussion that there are a number of practical difficulties associated with the problem of 3D reconstruction from 2D projections. The results of various reconstruction algorithms can differ noticeably, so the choice of reconstruction method within the context of SPR or ET can affect the results significantly. In addition, within the context of a specific algorithm, the methods used to minimize artifacts are somewhat arbitrary.

We tend to consider the problem of reconstruction from projections in SPR and ET to be a part of a broader field of tomographic reconstruction. However, it has to be stressed that what we typically encounter in EM differs considerably from the reconstruction problems in other fields and while the general theory holds, many issues arising within the context of SPT and ET do not have sound theoretical or even practical solutions. First, SPR and double-tilt ET are rare examples of “true” 3D reconstruction problems. In most applications, including single-axis ET, the 3D reconstruction from 2D projections can be decomposed into a series of semi-independent 2D reconstructions (slices of the final 3D object) from 1D projections. In this case, the problem is reduced to that of a 2D reconstruction and one can take advantage of a large number of well established and understood algorithms. Second, in SPR the data collection geometry cannot be controlled and the distribution of projections is random. This requires the reconstruction algorithm to be flexible with parameters that can be adjusted based on the encountered distribution of data. In SPR and double-tilt ET, the distribution of projection directions tend to be extremely uneven, so an effective algorithm must account for the varying spectral signal-to-noise (SSNR) conditions within the same target object. Furthermore, we also note that the problem of varying SSNR is compounded by the extremely low SNR of the data. Third, the uneven distribution of projection directions and experimental limitations of the maximum tilt in ET result in gaps in Fourier space, which not only makes the problem not invertible, but calls for additional regularization to minimize the artifacts. Fourth, unlike in other fields, orientation parameters in SPR and ET are known only approximately and the errors are both random and systematic. It follows that the 3D reconstruction algorithm should be considered within the context of the structure refinement procedure. Finally, to ensure a desirable SNR of the reconstructed object, the number of projections is typically much larger than their size (expressed in pixels). However, this dramatic oversampling places extreme computational demands on the reconstruction algorithms and therefore eliminates certain methods from consideration.

In this text I will provide a general overview of reconstruction techniques while focusing on issues unique to EM applications. I will first briefly describe the theory of reconstruction from projections and then analyze reconstruction algorithms practically used in EM with a focus on those that are implemented in major software packages and are routinely used. This is followed by a discussion of issues unique to 3D reconstruction of EM data, and in particular, those of correcting for the effects of the contrast transfer function (CTF) of the microscope.

The object and its projection

In structural studies of biological specimens, the settings of electron microscope are selected such that the collected 2D images are parallel beam 2D projections g (x) of a 3D specimen d(r). For a continuous distribution of projection directions τ, g forms an integral transformation of d called a ray transform (Natterer and Wübbeling, 2001):

$$g({\mathbf{x}}_{\mathit{\tau }})=\int d(\mathbf{r})d\mathit{\tau },\mathit{\tau }\perp \mathbf{x}.$$ (1)

Ray transform is an integral over straight line and transforms an nD function into a (n-1)D function. Ray transform is not to be confused with a Radon transform, which is realized as 1D projections of a nD function over (n-1)D hyperplanes. For 2D functions, ray and Radon transforms differ only in the notation. Here, we will concern ourselves with an inverse problem of recovering a 3D function from its 2D ray transform.

The projection direction τ is defined as a unit vector and in EM it is parametrized by two Eulerian angles τ (ϕ,θ) and the projection is formed on the plane x perpendicular to τ. Most cryo-EM software packages (SPIDER, IMAGIC, MRC, FREALIGN, EMAN2, SPARX) use the ZYZ convention of Eulerian angles which expresses the rotation of a 3D rigid body by the application of three matrices:

$$\left[\begin{array}{ccc}cos\psi & sin\psi & 0\\ -sin\psi & cos\psi & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\theta & 0& -sin\theta \\ 0& 1& 0\\ sin\theta & 0& cos\theta \end{array}\right]\left[\begin{array}{ccc}cos\varphi & sin\varphi & 0\\ -sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right].$$ (2)

Angle ψ is responsible for the in-plane rotation of the projection (Fig. 1) and is considered trivial as it does not affect information content of the ray transform. The two Eulerian angles ϕ, θ that define projection direction with the in-plane rotation ψ and in-plane translations t_x, t_y are in EM jointly referred to as projection orientation parameters. The distribution of projection directions may be conveniently visualized as a set of points on a unit half-sphere (Fig. 2).

Fig. 1.

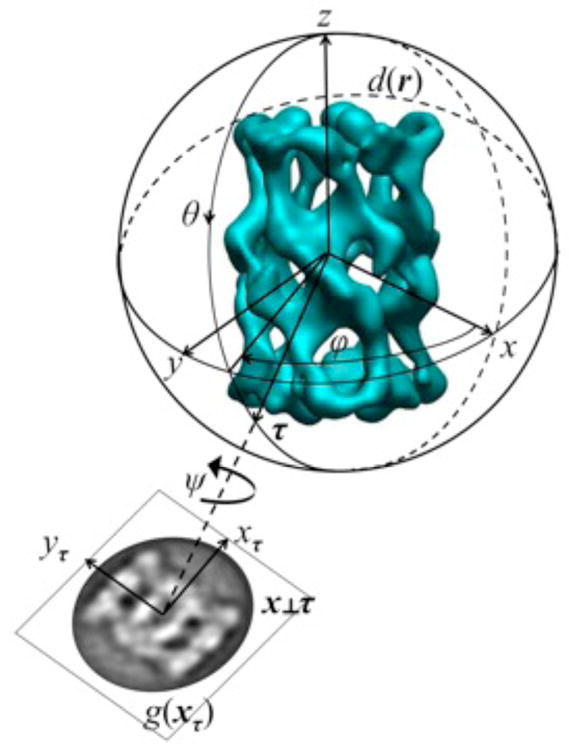
The projection sphere and projection g(x_τ) of d(r) along τ onto the plane τ ⊥ x. The convention of Eulerian angles as in Eq.2.

Fig. 2.

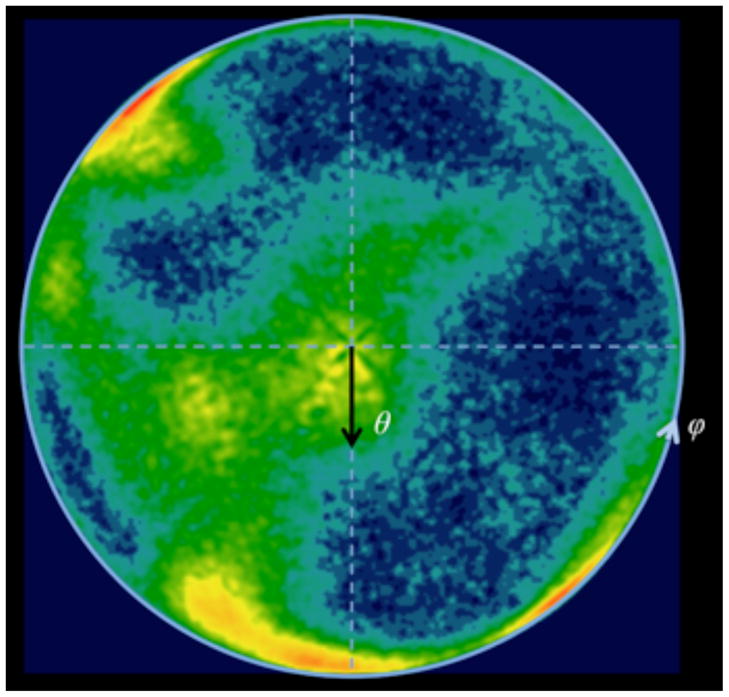
Distribution of projection directions τ (ϕ, θ) mapped on a half-sphere. The value of each point on the surface of the unitary sphere is equal to the number of projections whose directions given as vectors τ(ϕ, θ) (Eq.2) fall in its vicinity. All directions are mapped on a half-sphere 0 ≤ θ ≤ 90, 0 ≤ ϕ < 360, with directions 90 < θ ≤ 180 mapped to mirror-equivalent positions θ′ = 180 − θ, ϕ′ = 180 + ϕ. The 322,688 angles are taken from the 3D reconstruction of a Thermus thermophilus ribosome complexed with EF-Tu at 6.4 Å resolution (Schuette et al., 2009) and the occupancies are color-coded with red corresponding to maximum (130) and dark blue to minimum (0). There are no gaps in angular coverage at the angular resolution of the plot.

In Fourier space, the relationship between an object and its projection is referred to as the central section theorem: the Fourier transformation G of projection g of a 3D object d is the central (i.e., passing though the origin of reciprocal space) 2D plane cross-section of the 3D transform D and is perpendicular to the projection vector (Bracewell, 1956; Crowther et al., 1970b; DeRosier and Klug, 1968):

$$\mathcal{F}\left[g({\mathbf{x}}_{\mathit{\tau }})\right]=D({\mathbf{s}}_{\mathit{\tau }}),{\mathbf{s}}_{\mathit{\tau }}\perp \mathit{\tau }.$$ (3)

where by capital letter we denoted Fourier transform of a function and s is a vector of spatial frequencies. From Eq.3 it follows that the inversion of the 3D ray transform is possible if there is a continuous distribution of projections such that their 2D Fourier transforms fill without gaps 3D Fourier transform of the object. This requirement can be expressed as Orlov’s condition, according to which the minimum distribution of projections necessary for inversion of Eq.1 is given by the motion of the unit vector over any continuous line connecting the opposite points on the unit sphere (Orlov, 1976a). In 3D, single-axis tilt geometry used in electron tomography (ET) with the full range of projection angles is an example of a distribution of projection that ensures the invertibility of the ray transform.

Unlike the case in ET, imaged objects in SPR are randomly and non-uniformly oriented and the distribution of their orientations is beyond our control, so the practical impact of the Orlov’s condition in limited. Moreover, in EM the problem is compounded by the high noise level of the data. It is easy to see that single-axis tilt geometry would result in a highly nonuniform distribution of the Spectral Signal-to-Noise Ratio (SSNR) in the reconstructed 3D object (Penczek, 2002; Penczek and Frank, 2006). Hence, generally speaking, it is more desirable in SPR to have a possibly uniform distribution of projection directions as this will yield uniform distribution of SSNR. It clearly follows that uniform distribution of projection directions being redundant fulfills Orlov’s condition.

Taxonomy of reconstruction methods

The inversion formulae for a continuous ray transform are known: the solution for the 2D Radon transform was originally given by Radon (Radon, 1986) and his work was subsequently extended to higher dimensions and various data collection geometries (Natterer and Wübbeling, 2001). However, the applicability of these solutions towards the design of algorithms is limited. Simple discretization of analytical solutions is either not possible or does not lead to stable numerical algorithms. Moreover, as we have already pointed out, the discrete ray transform is not invertible, so practical ways of obtaining stable solutions have to be found. It is also necessary to account for particular data collection geometries and experimental limitations, such as limited or truncated view of the object.

The two main groups of reconstruction methods are the algebraic and the transform methods. The algebraic methods begin from discretization of the integral transformation Eq. 1. This leads to a system of linear equations that are typically overdetermined and whose solution yields the desired reconstructed object. The advantages of this approach are numerous: (1) the problem is immediately cast as an algebraic one, so one can take advantage of well established linear algebra numerical methods to find a solution, (2) discretization, sampling, and interpolation appear naturally and are simply embedded into the projection matrix P, and (3) there is no need to design methods to account for particular distribution of projection directions. Since the inverse of P normally does not exist, algebraic methods are with few exceptions iterative. While they are easy to implement, the significant disadvantage is that they are also extremely computationally intensive, especially in their applications to EM where the number of 2D projections is very large. It is also difficult to provide precise rules concerning the determination of the number of iterations required to obtain a desired quality of reconstruction.

The transform methods are based on the central section theorem Eq.3 and tend to rely on Fourier space analysis of the problem. The analysis of the problem is done using continuous functions and discretization is considered only during interpolation between polar and Cartesian systems of coordinates. Within the class of transform methods, there are further subdivisions. In the first subgroup of methods one constructs a Fourier space linear filter to account for particular distribution of projections, applies it in Fourier space to projection data, and reconstruction is typically performed in real space using filtered data and a simple backprojection algorithm. These algorithms are easy to implement, reasonably fast and straightforward to use, but for uneven distribution of projections, particularly in 3D, the filter functions are rather crude approximations of optimum solutions, so the results tend to be inferior. The second subgroup contains algorithms that directly and exclusively operate in Fourier space by casting the problem as one of Fourier space interpolation between polar system of coordinates of the projection data and Cartesian system of coordinates of the reconstructed object; collectively, these algorithms are known under the name of direct Fourier inversion. Their implementation tends to be challenging, but direct Fourier inversion is computationally very efficient and the ‘gridding’ algorithm from this group is currently considered the most accurate reconstruction method.

Reconstruction algorithms have to meet a number of requirements, some of which are in contradiction to each other, in order to be successfully applicable to EM data. The algorithm should be capable of handling very large data sets in excess of 10⁵ projection images that can be as large as 256² pixels or more. It should account for an uneven distribution of projection directions that is irregular and cannot be approximated by an analytical function and still be sufficiently fast to permit structure refinement by adjustments of projection directions. The algorithm should also minimize artifacts in the reconstructed object that are due to gaps in coverage of Fourier space; such artifacts tend to adversely affect refinement procedures. It should be capable of correcting for the CTF effects and of accounting for the uneven distribution of spectral SNR in the data and in 3D Fourier space. For larger structures, the algorithm should be capable of correcting for the defocus spread within the object. The reported resolution of a 3D reconstruction depends on the linear relations between parts of the structure and between reconstructions done from different subsets of the data. To ensure a meaningful resolution measure, the algorithm must be linear and shift invariant for otherwise the relative densities within the structure would be distorted, thus leading to incorrect interpretations of and in extreme cases meaningless reported resolutions. Lastly, when applied to ET problems, the algorithm should be able to properly account for slab geometry of the object and for the problem of partial and truncated views.

It is extremely unlikely that a single algorithm would yield optimum results with respect to a set of such diverse requirements. In most cases, the tradeoff is the computational efficiency, i.e., the running time. As we will see, iterative algebraic algorithms are the closest to the ideal, but they are very slow and require adjustments of numerous parameters whose values are not known in advance. In addition, some of the problems listed do not have convincing theoretical solutions. Taken together, it all assures that the field of 3D reconstruction from projections will remain fertile ground for the development of new methods and new algorithms.

Discretization and interpolation

In digital image processing, space is represented by a multi-dimensional discrete lattice. The 2D projections g_n(x) are sampled on a Cartesian grid {ka: k ∈ Zⁿ, − K/2 ≤ k < K/2} where n is the dimensionality of the grid of the reconstructed object, n-1 is the dimensionality of projections, $\mathbf{K}\in {\mathbf{Z}}_{+}^n$ is the size of the grid, and a is the grid spacing. In EM, the units of a are either Ångstroms or nanometers and we assume that the data is appropriately sampled, i.e., the pixel size is less than or equal to the inverse of twice the maximum spatial frequency present in the data a ≤ 1/2s_max. Since the latter is not known in advance, a practical rule of thumb is to select the pixel size to be about one-third of the expected resolution of the final structure, so that the adverse effects of interpolation are reduced.

The EM data (projections of the macromolecule) are discretized on a 2D Cartesian grid; however, each projection has a particular orientation in polar coordinates. Hence, an interpolation is required to relate the measured samples to the voxel values on the 3D Cartesian grid of the reconstructed structure. The backprojection step can be visualized as a set of rays with base a^d−1 and which are extended from projections The value of a voxel on the grid of the reconstructed structure is the sum of the ray values which intersect the voxel. One can select schemes that aim at approximation of the physical reality of the data collection, i.e., by weighting the contributions by the areas of the voxels intersected by the ray or by the lengths of the line segments that intersect (Huesman et al., 1977). To reduce the computation time, one usually assumes in electron microscopy that all the mass is located in the center of the voxel, in which case additional accuracy is achieved by application of tri- (or bi-) linear interpolation. The exception is the ART with blobs algorithm (Marabini et al., 1998) in which the voxels are represented by smooth spherically symmetric volume elements (for example Keiser-Bessel function).

In real space, both the projection and backprojection steps can be implemented in two different ways: as voxel driven or as ray driven (Laurette et al., 2000). If we consider a projection, in the voxel-driven approach the volume is scanned voxel by voxel. The nearest projection bin to the projection of each voxel is found, and the values in this bin and three neighboring bins are increased by the corresponding voxel value multiplied by the weights calculated using bi-linear interpolation. In the ray driven approach, the volume is scanned along the projection rays. The value of the projection bin is increased by the values in the volume calculated in equidistant steps along the rays using tri-linear interpolation. Because voxel- and ray-driven methods apply interpolation to projections or to voxels, respectively, the interpolation artifacts will be different in each case. Therefore, when calculating reconstructions using iterative algorithms that alternate between projection and backprojection steps, it is important to maintain consistency; that is, to make sure that matrix representing one step is the transpose of the matrix representing the other step. In either case, the computational complexity of each method is O(K³), which isthe same as for the rotation of a 3D volume.

In the reconstruction methods based on the direct Fourier inversion of the 3-D ray transform the interpolation is performed in Fourier space. Regrettably, it is difficult to design an accurate and fast interpolation scheme for the discrete Fourier space, so it is tempting to use interpolation based on Shannon’s sampling theorem (Shannon, 1949). It states that a properly sampled, band-limited signal can be fully recovered from its discrete samples. For the signal represented by K³ equispaced Fourier samples D_hkl, the value at the arbitrary location D(s_x, s_y, s_z) is given by (Crowther et al., 1970a):

$$D(s_x,s_y,s_z)=\sum _{h=0}^{K-1}\sum _{k=0}^{K-1}\sum _{l=0}^{K-1}{D}_{\mathit{hkl}}{w}_h(s_x)w_k(s_y)w_l(s_z),$$ (4)

where (Lanzavecchia and Bellon, 1994; Yuen and Fraser, 1979):

$$w_j(s)=\{\begin{array}{ll}\frac{sin\left(K\pi \left(s-k/K\right)\right)}{sin\left(\pi \left(s-k/K\right)\right)},\hfill & \text{K}\text{odd}\hfill \\ \frac{sin\left(K\pi \left(s-k/K\right)\right)}{tan\left(\pi \left(s-k/K\right)\right)},\hfill & \text{K}\text{even}\hfill \end{array}j=h,k,l.$$ (5)

For structures with symmetries such as icosahedral structures, the projection data are distributed approximately evenly, in which case Eq.4 can be solved to a good degree of accuracy by performing the interpolation independently along each of the three frequency axes (Crowther et al., 1970b). In this case, the solution to the problem of interpolation in Fourier space becomes a solution to the reconstruction problem. Crowther et al. solved it as an overdetermined system of linear equations equations and gave the following least-squares solution (Crowther et al., 1970b):

$${\widehat{\mathbf{D}}}_{\mathit{hkl}}={({\mathbf{W}}^T\mathbf{W})}^{-1}{\mathbf{W}}^T\mathbf{D}.$$ (6)

where D and D_hkl are written as 1D arrays D and D_hkl, respectively, and W denotes the appropriately dimensioned matrix of the interpolants in Eq.5. For general cases the above method is impractical because of the large size of the matrix W. More importantly, the samples in Fourier transforms of projection data are distributed irregularly, so the problem becomes that of interpolation between unevenly sampled data (on 2D planes in polar coordinates) and regularly sampled result (on 3D Cartesian grid) in which case Eq.6 in not applicable. We will discuss relevant algorithms in the section on direct Fourier inversion.

There is a tendency in EM to use simple interpolation schemes both in the design of reconstruction algorithms and in generic image processing operations. Particularly popular is bi- (or tri-) linear interpolation which is easy to implement and computationally very efficient but which also results in noticeable degradation of the image. The effect of interpolation methods is best analyzed in reciprocal space. Thus, nearest-neighbor (NN) interpolation is realized by assigning each sample to the nearest on-grid location on the target grid and effect is that of convolving the image with a rectangular with a width of one pixel independently along each dimension. In reciprocal space, the effect is that of multiplication by a normalized sinc function:

$$\text{sinc}(s)=\frac{sin(\pi s)}{\pi s}$$ (7)

where s is an absolute unitless frequency bounded above by 0.5: s_max = 0.5. The bi-linear interpolation is realized by assigning each sample to two locations on the target grid with fractional weights obtained as distances to nearest on-grid locations. This is equivalent to the convolution of the image with a triangular function, which in turn can be seen as equivalent to two convolutions with rectangular window. In reciprocal space, the effect is that of multiplication by sinc² (s). If interpolation is applied in real space, there is a loss of resolution due to suppression of high frequency, which at Nyquist frequency is 36% for NN interpolation and ~60% for bilinear interpolation (Fig. 3). At the same time, the accuracy of interpolation improves with the increased order of interpolation (Pratt, 1992). Higher order interpolation schemes, such as quadratic or B-splines improve the performance further but at significant computational cost.

Fig. 3.

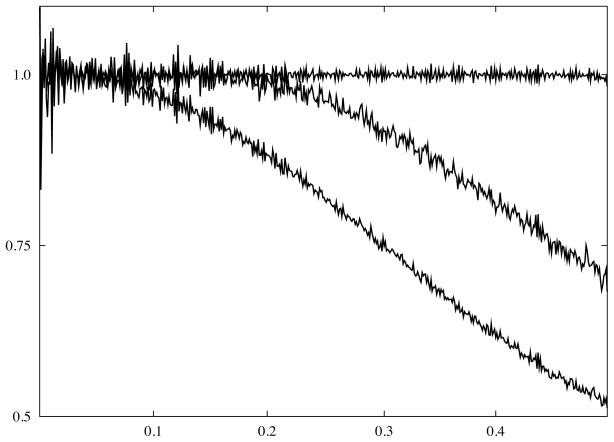
Suppression of high frequency information due to interpolation results in loss of resolution. A 2D 1024² image filled with Gaussian white noise was rotated by 45° and a ratio of rotationally averaged power spectrum of the rotated image to that of the original image was computed: bottom curve - bi-linear interpolation; middle curve - quadratic interpolation; top curve - “gridding”-based interpolation (Yang and Penczek, 2008). x-axis is given as normalized spatial frequency, i.e., 0.5 corresponds to Nyquist frequency.

Application of low-order interpolation schemes in Fourier space, in addition to the introduction of artifacts due to poor accuracy, will introduce difficult to account for fall-off of the image densities in real space. The fall-off will be be proportional to sinc or sinc² in real space depending on the interpolation scheme used. A standard approach to counteracting the adverse effects of interpolation is to oversample the data. As can be seen from Fig. 3, the often recommended three times oversampling reduces the suppression of high frequency information (or fall-off in real space) by bi-linear interpolation to ~10%. Such extreme oversampling increases the volume of 2D data nine times with a similar increase in computation time. We show in Fig. 3 that the so-called “gridding” method (discussed in the section on direct Fourier inversion) yields nearly perfect results in the entire frequency range when applied to interpolation. As the method all but eliminates the need for oversampling of the scanned data, the relative increase of computational demand is modest (Yang and Penczek, 2008).

The algebraic and iterative methods

The algebraic methods were derived based on the observation that when the projection equation Eq.1 is discretized, it forms a set of linear equations. We begin with forming two vectors: the first, g, contains pixels from all available N projections (in an arbitrary order), and the second, d, contains the voxels of the 3D object (in an order derived from the order of g by algebraic relations):

$${\mathbf{g}}_n=\left[\begin{array}{c}{g}_n^{k_1{k}_2}\\ ⋮\\ g_n^{l_1{l}_2}\end{array}\right],\mathbf{g}=\left[\begin{array}{c}{\mathbf{g}}_1\\ {\mathbf{g}}_2\\ ⋮\\ {\mathbf{g}}_N\end{array}\right],\mathbf{d}=\left[\begin{array}{c}{d}^{i_1{i}_2{i}_3}\\ ⋮\\ d^{j_1{j}_2{j}_3}\end{array}\right].$$ (8)

The exact sizes of d and g depend on the choice of support in 2D that can be arbitrary; similarly arbitrary can be the support of the 3D object. This freedom to select the region of interest constitutes a major advantage of iterative algebraic methods. Finally, the operation of projection is defined by the projection matrix P whose elements are the interpolation weights. The weights are determined by the interpolation scheme used; for the bi- and trilinear interpolations, the weights are between zero and one. The algebraic version of Eq.1 is:

$$\mathbf{g}=\mathbf{Pd}$$ (9)

Matrix P is rectangular and and the system of equation is overdetermined since the number of projections in EM exceeds linear size of the object in pixels. Eq.9 can be solved in a least-squares sense:

$$\widehat{\mathbf{d}}={({\mathbf{P}}^T\mathbf{P})}^{-1}{\mathbf{P}}^T\mathbf{g},$$ (10)

which yields a unique structure d̂ that minimizes |Pd − g|². Similarly as in the case of direct interpolation in Fourier space Eq.4, the approach introduced by Eq.10 is impractical because of the very large size of the projection matrix. Nevertheless, in the case of the single-axis tilt geometry, the full 3D reconstruction reduces to a series of independent 2D reconstructions, and it becomes possible to solve Eq.10 by using the Singular Value Decomposition (SVD) of the matrix P. The advantage of this approach is that for a given geometry the decomposition has to be calculated only once; thus, the method becomes very efficient if the reconstruction has to be performed repeatedly for the same distribution of projections or if additional symmetries, such as helical, are taken into account (Holmes et al., 2003).

In the general 3D case, a least-square solution can be found using one of the iterative approaches that take advantage of the sparsity of the projection matrix. The main idea is that the matrix P is not explicitly calculated or stored; instead, its elements are calculated in each iteration as needed. In the following, let L(d) be defined as follows:

$$L(\mathbf{d})={\mid \mathbf{Pd}-\mathbf{g}\mid }^2$$ (11)

The aim of Simultaneous Iterative Reconstruction Technique (SIRT) is to find a structure d that minimizes the objective function Eq.11. The algorithm begins by selecting the initial 3D structure d⁰ (usually set to zero) and proceeds by iteratively updating the current approximation dⁱ⁺¹ using the gradient of the objective function ∇L(d):

$${\mathbf{d}}^{i+1}={\mathbf{d}}^i-{\lambda }^i{\mathbf{P}}^T(\mathbf{P}{\mathbf{d}}^i-\mathbf{g})={\mathbf{d}}^i-{\lambda }^i({\mathbf{P}}^T\mathbf{P}{\mathbf{d}}^i-{\mathbf{P}}^T\mathbf{g}).$$ (12)

Setting the relaxation parameter λⁱ = λ = const yields Richardson’s algorithm (Gilbert, 1972).

SIRT is extensively used in single particle reconstruction (Frank, 2006) because it yields superior results under a wide range of experimental conditions (Penczek et al., 1992); additionally, in the presence of angular gaps in the distribution of projections, SIRT produces the least disturbing artifacts. Furthermore, SIRT offers considerable flexibility in EM applications. First, it is possible to accelerate the convergence by adjusting the relaxation parameters, i.e., by setting ${\lambda }^i=arg\underset{\lambda \ge 0}{min}L\left({\mathbf{d}}^i-\lambda \nabla L({\mathbf{d}}^i)\right)$ we obtain a steepest descent algorithm. Second, even faster convergence (in ~10 iterations) is achieved by solving Eq.12 using the conjugate gradient method; however, this requires the addition of a regularizing term to prevent excessive enhancement of noise. Such a term has the form |Bd|², where the matrix B is a discrete approximation of a Laplacian or higher order derivatives. Third, it is possible to take into account the underfocus settings of the microscope by including the CTF of the microscope and by solving the problem for the structure d that in effect will be corrected for the CTF:

$$L(\mathbf{d})=(1-\eta ){\mid \mathbf{SPd}-\mathbf{g}\mid }^2+\eta {\mid \mathbf{Bd}\mid }^2.$$ (13)

We introduced in Eq.13 a Lagrange multiplier η whose value determines the smoothness of the solution (Zhu et al., 1997), S is a matrix containing the algebraic representation of the space-invariant point spread functions (psf, i.e., the inverse Fourier transform of the CTF) of the microscope for all projection images. With this, Eq.13 can be solved using the following iterative scheme:

$${\mathbf{d}}^{i+1}={\mathbf{d}}^i-{\lambda }^i\left\{(1-\eta )\left({(\mathbf{SP})}^T(\mathbf{SP}){\mathbf{d}}^i-{(\mathbf{SP})}^T\mathbf{g}\right)+\eta {\mathbf{B}}^T\mathbf{B}{\mathbf{d}}^i\right\}$$ (14)

Both the psf and regularization terms are normally computed in Fourier space. Algorithms Eqs.13 and 14 are implemented in the SPIDER package (Frank et al., 1996).

The Algebraic Reconstruction Technique (ART) predates SIRT; in the context of tomographic reconstructions it was proposed by Gordon and coworkers (Gordon et al., 1970) and later it was recognized as a version of Kaczmarz’s method for iteratively solving Eq.1 (Kaczmarz, 1993). We first write Eq.9 as a set of systems of equations, each relating individual pixels g_l,l = 1,…, NK² in projections with voxels of the 3D structure:

$$g_l={\mathbf{P}}_l^T\mathbf{d},l=1,\dots ,{NK}^2$$ (15)

Note Eqs.9 and 15 are equivalent because of Eq.8 and $\mathbf{P}={\left[\begin{array}{cccc}{\mathbf{p}}_1& {\mathbf{p}}_2& \dots & {\mathbf{p}}_N\end{array}\right]}^T$. With this notation and a relaxation parameter 0 < μ < 2 ART consists of the following steps:

1. Set i = 0 and the initial guess of the structure d̂⁰.

2. For l = 1, …, NK², update

   $${\mathbf{d}}^{{\mathit{iNK}}^2+l}={\mathbf{d}}^{{\mathit{iNK}}^2+l-1}-\mu \left({\mathbf{P}}^T{\mathbf{d}}^{{\mathit{iNK}}^2+l-1}-g_l\right)\frac{{\mathbf{p}}_l}{\mid {\mathbf{p}}_l\mid }.$$ (16)

3. Set i → i +1; go to step 2.

Although the mathematical forms of the update equations in SIRT Eq.12 and in ART Eq. 16 appear at first glance to be very similar, there are profound differences between them. In SIRT, all voxels in the structure are corrected simultaneously after projections (P) and backprojections (P^T) of the current update of the structure are calculated. In ART, the projection/backprojection in Eq.16 involves only correction with respect to an individual pixel in a single projection immediately followed by the update of the structure. This results in a much faster convergence of ART as compared to SIRT. Further acceleration can be achieved by selecting the order in which pixels enter the correction in Eq.16. It was observed that if a pixel is selected such that its projection direction is perpendicular to the projection direction of the previous pixel, then convergence is achieved faster (Hamaker and Solmon, 1978; Herman and Meyer, 1993). Interestingly, a random order works almost equally well (Natterer and Wübbeling, 2001).

ART has been introduced into SPR as “ART with blobs” (Marabini et al., 1998) and is available in the Xmipp package (Sorzano et al., 2004). In this implementation the reconstructed structure is represented by a linear combination of spherically symmetric, smooth, spatially-limited basis functions, such as Kaiser-Bessel window functions (Lewitt, 1990; Lewitt, 1992; Matej and Lewitt, 1996). Introduction of blobs significantly reduces the number of iterations necessary to reach an acceptable solution (Marabini et al., 1998).

The main advantage of algebraic iterative methods is their applicability to various data collection geometries and to data with uneven distribution of projection directions. Indeed, as the weighting function that would account for particular distribution of projections does not appear in the mathematical formulations of SIRT Eq.12 and ART Eq.16, it would seem that both algorithms can be applied, with minor modifications, to all reconstruction problems encountered in EM. Moreover, a measure of regularization of the solution is naturally achieved by premature termination of the iterative process. However, this is not to say that iterative algebraic reconstruction algorithms do not have shortcomings. For most such methods, the computational requirements are dominated by the backprojection step, so it is safe to assume that the running times of both SIRT and ART will exceed that of other algorithms in proportion to the number of iterations (typically 10–200). Also, applications of SIRT or ART to unevenly distributed set of projection data will result in artifacts in the reconstructed object unless additional provisions are undertaken (Boisset et al., 1998; Sorzano et al., 2001). Finally, since the distribution of projection directions does not appear explicitly in the algebraic formulation of the reconstruction problem (as it does in the Fourier formulation as a weighting function), it is tempting to assume that algebraic iterative methods will yield properly reconstructed objects from very few projections or from data with major gaps in coverage of Fourier space (as in the cases of Random Conical Tilt, and both single- and double-axis tilts in ET). Not only extraordinary claims have been made, but grossly exaggerated results have been reported. As noted previously, reconstruction artifacts in ART and SIRT tend to be less severe than in other methods in the case of missing projection data; however, neither ART nor SIRT will fill gaps in Fourier space with meaningful information. With more aggressive regularization, as in Maximum Entropy iterative reconstruction, further reduction of artifacts might be possible, but no significant gain in information can be expected. The main reason is that while it is possible to obtain impressive results using simulated data, the limitations of EM data are poorly understood, as are the statistical properties of noise in EM data, CTF affects, and last but not least, errors in orientation parameters. In particular, the latter implies the system of equations Eq.9 is inconsistent, which precludes any major gains by using iterative algebraic methods in application to experimental EM data.

In ET, due to slab geometry of the object, the reconstruction problem is compounded by that of truncated views, i.e., depending on the tilt angle, each projection contains the projection of a larger or smaller extent of the object. Thus, the system of equations Eq.9 becomes inconsistent and strictly speaking algebraic methods are not applicable in this case. So far, the problem has met little attention in the design of ET reconstruction algorithms.

The iterative reconstruction methods can further constrain the solution by taking advantage of a priori knowledge, i.e., any information about the protein structure that was not initially included in the data processing, and introducing it into the reconstruction process in the form of constraints. Examples of such constraints include similarity to the experimental (measured) data, positivity of the protein mass density (only valid in conjunction with CTF correction), bounded spatial support, et cetera…. Formally, the process of enforcing selected constraints is best described in the framework of the Projections Onto Convex Sets (POCS) theory (Stark and Yang, 1998) that was introduced into EM by Carazo and co-workers (Carazo and Carrascosa, 1987) (also see insert reference to Penczek chapter on Image Restoration here).

Filtered Backprojection

The method of filtered backprojection (FBP) is based on the central section theorem. We will begin with the 2D case, in which the algorithm has a particularly simple form. Let us consider a function ϒ(s) describing, in Cartesian coordinates, the 2D Fourier transform of a 1D ray transforms g of a 2D object d. The inversion formula is obtained as:

$$\begin{array}{l}d(\mathbf{x})=\int \mathrm{\Upsilon }(\mathbf{s})exp(-2\pi i\mathbf{sx})d\mathbf{s}=\underset{0}{\overset{\pi }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}\mathrm{\Upsilon }(R,\psi )exp(-2\pi i\mathbf{x}\mathit{\tau })\mid R\mid \mathit{dRd}\psi \\ =\underset{0}{\overset{\pi }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}\mathcal{F}\left[g(x_{\psi })\right]exp(-2\pi i\mathbf{x}\mathit{\tau })\mid R\mid \mathit{dRd}\psi =\underset{0}{\overset{\pi }{\int }}{\mathcal{F}}^{-1}\left[\mid R\mid \mathcal{F}\left[g(x_{\psi })\right]\right]d\psi \\ =\mathit{Backprojection}\left[{\mathit{Filtration}}_{\mid R\mid }(g)\right]\end{array}$$ (17)

The FBP algorithm consist of the following steps: (i) compute a 1D Fourier transform of each projection, (ii) multiply the Fourier transform of each projection by the weighting filter |R| (a simple ramp filter), (iii) compute the inverse 1D Fourier transformes of the filtered projections, (iv) apply backprojection to the processed projections in real space to obtain the 2D reconstructed object. The FBP is applicable to ET single-axis tilt data collection, in which case the 3D reconstruction can be reduced to a series of axial 2D reconstructions (implemented in SPIDER (Frank et al., 1996)).

To introduce a 2D FBP for non-uniformly distributed projections, we note Eq.17 includes a Jacobian of a transformation between polar and Cartesian systems of coordinates |R|dRdψ. When the analytical form of the distribution of projections is known, we can use its discretized form as a weighting function in the filtration step. For an arbitrary distribution a good choice is to select weights c(|R|, ψ) such that the backprojection integral Eq.17 becomes approximated by a Riemann sum (Penczek et al., 1996):

$$c(\mid R\mid ,\psi )=\mid R\mid \mathit{dRd}\psi \to c(R_j,{\psi }_j)=R_j\frac{1}{2\pi }\frac{{\psi }_{j+1}-{\psi }_{j-1}}{2}=\frac{R_j\mathrm{\Delta }{\psi }_j}{2\pi }.$$ (18)

Weights given by Eq.18 yield good reconstruction if there are no major gaps in the distributions of projections, i.e., the data is properly sampled by projections. This requires:

$${\forall }_j\mathrm{\Delta }{\psi }_j\le r_{max}^{-1},$$ (19)

where r_max; is the radius of the object. For distributions which do not fulfill this condition, Bracewell proposed that weighting functions based on an explicitly or implicitly formulated concept of the “local density” of projections might be more appropriate (Bracewell and Riddle, 1967). For a 2D case of non-uniformly distributed projections, Bracewell et al. suggested the following heuristic weighting function:

$$c(R_j,{\psi }_j)=\frac{R_j}{{\displaystyle \sum _l}exp\left[-\mathit{const}{(\mid {\psi }_i-{\psi }_l\mid mod\pi )}^2\right]}$$ (20)

where the summation extends over all projection angles.

It has to be noted that it might be tempting to reverse the order of operations in FBP and arrive at the so-called backprojection-filtering reconstruction algorithm (BFP). It is based on the observation that the FT of the 2D object d is related to the FT of the backprojected object by a 2D weighting function ${\left(s_x^2+s_y^2\right)}^{1/2}=\mid \mathbf{s}\mid$, so the BFP is (Vainshtein and Penczek, 2008):

$$d(\mathbf{x})={\mathit{Filtration}}_{\mid \mathbf{s}\mid }[\mathit{Backprojection}(g)].$$ (21)

One can also arrive at the same conclusion by analyzing the point spread function of the backprojection step (Radermacher, 1992). While the results are acceptable for uniform distribution of projections, the approach does not yield correct results for non-uniform distributions (thus all interesting 3D cases). The reason is that in the discrete form of FBP Eq.17, the order in which the Jacobian weights given by Eq.18 (or obtained from suitable approximation) are applied to the projection data cannot be reversed. In other words, the sum of weighted projections cannot be replaced by a weighted sum of projections (see also the discussion on direct Fourier inversion algorithms).

For a non-trivial 3D reconstruction from 2D projections, the design of a good weighting function is challenging. First, in 3D there are no uniform distributions of projection directions. So, a reasonable criterion for an appropriate 3D weighting function is to have its backprojection integral approximate the Riemann sum, as in the 2D case (Eq.18). For example, the weighting function Eq.20 can be easily extended to 3D, but for a uniform distribution of projections it does not approximate well the analytical form of 3D Jacobian, which we consider optimal.

Radermacher (Radermacher, 1992; Radermacher et al., 1986) proposed a general weighting function (GWF) derived using a deconvolution kernel calculated for a given (nonuniform) distribution of projections and a finite length of backprojection. GWF is obtained by finding the response of the simple backprojection algorithm to the input composed of delta functions in real space:

$$c_{\mathit{GWF}}(s_x,s_y,s_z)=\frac{1}{{\displaystyle \sum _i}2r_{max}\text{sinc}\left(2r_{max}\pi w_{\mathit{\tau }}^i\right)},$$ (22)

where $w_{\mathit{\tau }}^i$ is a variable in Fourier space extending in the direction of the i’th projection direction τ(ϕ_i, θ_i). The GWF is consistent with the analytical requirement of Eq.17 as it can be shown that by assuming infinite support r_max → ∞ and continuous and uniform distribution of projection directions, one obtains in 2D the following: $c_{\mathit{GWF}}(s_x,s_y)={\left(s_x^2+s_y^2\right)}^{-}=\mid \mathbf{s}\mid$ (Radermacher, 2000).

The derivation of Eq.22 is based on the analysis of continuous functions and its direct application to discrete data results in reconstruction artifacts. In (Radermacher, 1992) it was proposed (a) to apply the appropriately reformulated GWF 2D projection data prior to the backprojection step and (b) to attenuate sinc functions in Eq.22 by Gaussian functions with decay depending on the radius of the structure or simply to replace sinc functions by Gaussian functions. This, however, reduces the concept of the weighting function corresponding to the deconvolution to that of the weighting function representing the “local density” of projections Eq.20. The general weighted backprojection reconstruction is implemented in the SPIDER (using Gaussian weighting functions) (Frank et al., 1996) and Xmipp (Sorzano et al., 2004) packages.

In (Harauz and van Heel, 1986) it was proposed that the calculation of the density of projections, and thus the weighting function, be based on the overlap of Fourier transforms of projections in Fourier space. Although the concept is general, its exposition is easier in 2D. If the radius of the object is r_max, the width of the Fourier transform of a projection is 1/r_max, which follows from the central section theorem Eq.3. Harauz and van Heel postulated that the weighting should be inversely proportional to the sum of geometrical overlaps between a given central section and the remaining central sections. For a pair of projections i and l, this overlap is:

$$o_{il}(R)=T[2r_{max}Rsin({\psi }_i-{\psi }_l)],$$ (23)

where T represents the triangle function. Also, due to Friedel symmetry of central sections the angles in Eq.23 are restricted such that 0 ≤ ψ_i − ψ_l ≤ (π/2). In this formulation, the overlap is limited to the maximum frequency:

$$R_{il}^{max}=\frac{1}{r_{max}sin({\psi }_i-{\psi }_l)},$$ (24)

in which case the overlap function becomes:

$$o_{il}(R)=\{\begin{array}{ll}1-R/R_{il}^{max}\hfill & \hfill 0\le R\le R_{il}^{max}\\ 0\hfill & \hfill R>R_{il}^{max}\end{array},$$ (25)

and the weighting function, termed an “exact filter” by the authors, is:

$$c(R,{\mathrm{\Psi }}_i)=\frac{1}{1+{\displaystyle \sum _{l\ne i}}{o}_{il}(R)}.$$ (26)

The weighting function Eq.26 easily extends to 3D; however, the calculation of the overlap between central sections in 3D (represented by slabs) is more elaborate (Harauz and van Heel, 1986). The method is conceptually simple and computationally efficient. Regrettably, Eq.26 does not approximate well the correct weighting for a uniform distribution of projections for which it should ideally yield c(R, Ψ_i) = R); it is easy to see that this is not the case by integrating Eq.26 over the entire angular range. The exact filter backprojection reconstruction is implemented in the IMAGIC (van Heel et al., 1996) and SPIDER packages (Frank et al., 1996).

The 3D reconstruction methods based on filtered backprojection are commonly used in single particle reconstruction because of their versatility, ease of implementation, and, in comparison with iterative methods, superior computational efficiency. Unlike iterative methods, there are no parameters to adjust, although it has been noted that the results depend on the value of the radius of the structure in all three weighting functions (Eqs.20, 22 and 26), so the performance of the reconstruction algorithm can be optimized for a particular data collection geometry by changing the value of r_max (Paul et al., 2004). Because evaluation of the weighting function involves calculation of pair-wise distances between projections, the computational complexity is proportional to the square of the number of projections and for large data sets methods from this class become inefficient. We also note that the weighting functions, both general and exact, remain approximations of the desired weighting function that would approximate the Riemann sum.

Direct Fourier inversion

Direct Fourier methods are based on the central section theorem in Fourier space Eq.3. The premise is that the 2D Fourier transforms of projections yield samples of the target 3D object on a non-uniform 3D grid. If the 3D inverse Fourier transform could be realized by means of the 3D inverse FFT, then one would have a very fast reconstruction algorithm. Unfortunately, application of 3D FFT has two non-trivial requirements: (1) accounting for the uneven distribution of samples and (2) recovering the samples on a uniform grid from the available samples on a non-uniform grid.

The most accurate Fourier reconstruction methods are those that employ non-uniform Fourier transforms, particularly the 3D gridding method (O’Sullivan, 1985; Schomberg and Timmer, 1995). In EM, a gridding-based Fast Fourier Summation (FFS) reconstruction algorithm was developed for ET (Sandberg et al., 2003) and implemented in IMOD (Kremer et al., 1996), while the Gridding-based Direct Fourier Reconstruction algorithm (GDFR) was developed specifically for SPR (Penczek et al., 2004). As we showed earlier, the optimum weights accounting for uneven distribution of projections should be such that their use approximates the integral over the distribution of samples through the Riemann sum. Such weights can be obtained as volumes of 3D Voronoi cells obtained from the distribution of sampling points (Okabe et al., 2000). In SPR EM, the number of projections, and thus the number of sampling points in Fourier space, is extremely large. Although the calculation of the gridding weights via the 3D Voronoi diagram of the non-uniformly spaced grid points would lead to an accurate direct Fourier method, the method is very slow and would require excessive computer memory. To circumvent this problem, GDFR introduces an additional step, namely the 2D reverse gridding method, to compute the Fourier transform of each 2D projection on a 2D polar grid. By means of the reverse gridding method, the samples of the 3D target object can be obtained on a 3D spherical grid, where the grid points are located both on centered spheres and on straight lines through the origin. Accordingly, it becomes possible to partition the sampled region into suitable sampling cells via the computation of a 2D Voronoi diagram on a unit sphere, rather than a 3D Voronoi diagram in Euclidean space (Fig. 4). This significantly reduces the memory requirements and improves the computational efficiency of the method, especially when a fast O(nlog n) algorithm for computing Voronoi diagrams on the unit sphere is employed (Renka, 1997).

Fig. 4.

Principle of the Gridding-based Direct Fourier 3D Reconstruction algorithm (GDFR). (a) 2D FFT of input projection image. (b) The reverse gridding is used to resample 2D Fourier input image into 2D polar Fourier coordinates. (c) “Gridding weights” are computed as cell areas of a 2D Voronoi diagram on a unit sphere (grey polygons) to compensate for the non-uniform distribution of the grid points. (d) Gridding using a convolution kernel with subsequent 3D inverse FFT yields samples on a 3D Cartesian grid. (e) Removal of weights in real space yields the reconstructed 3D object.

GDFR comprises four steps (Fig. 4):

1. The reverse gridding method is used to resample 2D input projection images into 2D polar coordinates.

2. The “gridding” step involves calculating for the Fourier transform of each projection the convolution ${\displaystyle \sum _i}\mathcal{F}[w]\ast (c\mathcal{F}[g_i])$,

   where c are “gridding weights” computed as cell areas of a 2D Voronoi diagram on a unit sphere that are designed to compensate for the non-uniform distribution of the grid points and [w] is an appropriately chosen convolution kernel. After processing all projections, this step yields samples of [w] * [d] on a Cartesian grid.

3. The 3D inverse FFT is used to compute $wd={\mathcal{F}}^{-1}[\mathcal{F}[w]\ast \mathcal{F}[d]]$ on a Cartesian grid.

4. The weights are removed using real-space division d = (wd)/w.

The reverse gridding in step 1 is obtained by reversing the sequence of steps (2–4) that constitute the proper gridding method:

1. The input image is divided in real space by the weighting function g/w.

2. The image is padded with zeros and 2D FFT is used to compute [g/w]

3. Gridding is used to compute [w] * [g/w] on an arbitrary non-uniform grid. In GDFR, this step yields 2D FTs of input projection images resampled into 2D Fourier polar coordinates.

Note the reverse gridding method does not require explicit gridding weights since the input 2D projection image is given on Cartesian grid, in which case the weights are constant. In addition, as step (c) results in a set of 1D Fourier central lines calculated using constant angular step, upon computing the inverse Fourier transforms they amount to a Radon transform of the projection, and after repeating the process for all available projections, they yield a Radon transform of a 3D object. Thus, GDFR, in addition to being a method of inverting of a 3D ray transform is also a highly accurate method of inverting a 3D Radon transform.

The GDFR method requires a number of parameters. First, we need a window function [w] whose support in Fourier space is “small”. To assure good computational efficiency of the convolution in step 2 of GDFR, this support was set to six Fourier voxels. In addition, to prevent division by zeroes in steps 1a and 4, the weighting function w must be positive within the support of the reconstructed object. A recommended window function is the separable, bell-shaped Kaiser-Bessel window (Jackson et al., 1991; O’Sullivan, 1985; Schomberg and Timmer, 1995) with parameters given in (Penczek et al., 2004).

The results of a comparison of selected reconstruction algorithms are shown in (Penczek et al., 2004; Vainshtein and Penczek, 2008). In a series of extensive tests it was shown that GDFR yields in a noise free case virtually perfect 3D reconstruction within the full frequency range, followed by SIRT and then weighted back-projection algorithms. It was also shown to be ~6 times faster than weighted back-projection methods, which is due to very time consuming calculation of weighting functions in the latter, and 17 times faster than SIRT.

Implementations of reconstruction algorithms in EM software packages

The theory of object reconstruction from a set of its line projections is well-developed and comprehensive. However, two issues of great concern for EM applications have not received sufficient attention: (1) the problem of reconstruction with transfer function correction or using projection data with non-uniform SSNR and (2) reconstruction using highly non-uniformly distributed or incomplete sets of projections. While some theoretical work have been pursued at early stages of the development of the field (Goncharov et al., 1987; Orlov, 1976a; Orlov, 1976b; Radermacher, 1988), currently used software packages are dominated by ad hoc solutions that are aimed at computational efficiency and convenience in data processing. More simply, a number of these ad hoc solutions stem from the history of the development of a given package.

The incorporation of the CTF correction of accounting for non-uniform distribution of the SSNR in projection data is relatively easy in iterative algebraic reconstruction algorithms, including both ART and SIRT, as can be seen from Eq.14. Iterative reconstruction cum CTF correction remains so far the only theoretically sound approach to the problem. The algorithm is only implemented in SPIDER (Zhu et al., 1997) with the additional requirement that the data be grouped by their respective defocus values in order to make the method computationally efficient; however, it does not appear to be in routine use.

Reconstruction methods based on backprojection and direct Fourier inversion methods require the implementation of a form of Wiener filter, which schematically is written as (see insert reference to Penczek chapter on Image Restoration here in this issue):

$$D=\frac{{\displaystyle \sum _n}{\mathit{CTF}}_n{\mathit{SSNR}}_n{G}_n}{{\displaystyle \sum _n}{\mathit{CTF}}_n^2{\mathit{SSNR}}_n+1}.$$ (27)

The summation in the numerator can be realized as a backprojection of the Fourier transforms of (n-1)D projections multiplied by their respective CTFs and SSNRs, so the result is nD. However, it is far from obvious how the summation in the denominator can be realized such that the result would have the intended meaning after the division is performed.

Cryo-EM software packages circumvent the difficulties listed above with the direct implementation of Eq.27 in various ways. In SPIDER, the routine approach is to group the projection data according to the assigned defocus values (Frank et al., 2000). Depending on the yield of particles, projection images from a single micrograph may constitute a “defocus group,” although larger groups are preferable. For each defocus group, an independent 3D reconstruction is computed using any of the algorithms implemented in the package. Finally, a “CTF-corrected” structure is calculated by merging all individual structures using the Wiener filter (Eq.27). While no doubt successful, this strategy makes it impossible to process data with very low particle yield per micrograph. In the current implementation of SPIDER, the anisotropy of SSNR of individual structures is not accounted for, in which case it is also not clear whether merging partial 3D structures can match the quality of a 3D reconstruction that would include CTF correction. In both IMAGIC and EMAN (including EMAN2), the 3D reconstruction is computed using the so-called class averages, i.e., images obtained by merging possibly similar 2D projection images of the molecule using the 2D version of a Wiener filter that includes CTF correction (Eq.27) or a similar approach. As class averages are corrected for the CTF effects, they can now be used in any 3D reconstruction algorithm. However, such 2D class averages have quite nonuniform distribution of SSNR and properly speaking this unevenness should be accounted for during the 3D reconstruction step. This would again require a reconstruction algorithm based on Eq.27 even though the CTF term is omitted, which is as difficult a problem as the original one.

There are two algorithms that implement Eq.27 directly using a simplified form of direct Fourier inversion and resampling of the non-uniformly distributed projection data onto a 3D Cartesian grid by a form of interpolation. In the FREALIGN package a modified tri-linear interpolation scheme is used to resample the data that leads to Eq.27 with additional weights accounting for interpolation (Grigorieff, 1998). However, it is not clear whether the uneven distribution of projection samples is taken into account. A simpler yet algorithm termed NN direct inversion is implemented in SPARX (Zhang et al., 2008). In this algorithm, the 2D input projections are first padded with zeroes to four times the size, 2D Fourier transformed, and samples are accumulated within the target 3D Fourier volume D using simple NN interpolation and a Wiener filter methodology based on Eq.27. After all 2D projections are processed, each element in the 3D Fourier volume is divided by the number of respective per-voxel counts of contributing 2D samples. Finally, a 3D weighting function modeled on Bracewell’s “local density” (Bracewell and Riddle, 1967) is constructed and applied to individual voxels of 3D Fourier space to account for possible non-uniform distribution of samples. This function is constructed to fulfill the following requirements:

1. For a given voxel, if all its neighbors are occupied, its weight is set to 1.0 (the minimum weight resulting from the procedure).

2. For a given voxel, if all its neighboring voxels are empty, the assigned weight has the maximum value.

3. Empty voxels located closer to the vacant voxel contribute more to its weight than those located further.

The resulting weighting function is:

$$w(h,k,l)=\frac{1}{1-\alpha {\displaystyle \sum _{i,j,m=-n}^n}l(h+i,k+j,l+m)exp(-\beta (i+j+m))},$$ (28)

where

$$l(h,k,l)=\{\begin{array}{cc}1& if{D}_{h,k,l}=0\\ 0& \mathit{otherwise}\end{array}.$$ (29)

β and n are constants whose values (0.2 and 3, respectively) were adjusted such that the rotationally averaged power spectrum is preserved upon reconstruction for selected test cases and α is a constant whose value depends is adjusted such that the first two normalization criteria listed above are fulfilled. As reported in (Zhang et al., 2008), the inclusion of weights significantly improves the fidelity of the NN direct-inversion reconstruction.

Accounting for uneven distribution of projections and for gaps in angular coverage is the second major problem which is not well resolved in EM reconstruction algorithms. There is strong evidence, both theoretical and experimental, that Riemann sum weights obtained using Voronoi diagrams yield optimum results in both 2D and 3D reconstruction algorithms,. However, this approach is valid only if the target space is sufficiently sampled by projection data. In the presence of major gaps, the weights obtained using this methodology tend to be exceedingly large and result in streaking artifacts in the reconstructed object. A similar argument can be applied to various “local density” weighting schemes in FBP algorithms, including ‘general’ and ‘exact’ filters. The problem is particularly difficult to solve for ET reconstructions in which contiguous subsets of projection data is missing. As long as the angular distribution of projections is even, one can apply a simple FBP algorithm with R-weighting (Eq.19) and ignore the presence of the angular gap. However, for more elaborate angular schemes (Penczek and Frank, 2006) or for double-tilt ET (Penczek et al., 1995) the angular dependence of the weighting function can no longer be ignored. Currently, there are no convincing methods that would yield proper weighting of the projection data within the measured region of Fourier space while avoiding excessive weighting of projections whose Fourier transforms are close to gaps in Fourier space.

The final group of commonly used EM algorithms are those that use a simplified version of the gridding approach. In the method implemented in EMAN, EMAN2, and in SPIDER, the gridding between projection data samples and a Cartesian target grid is accomplished using a truncated Gaussian convolution kernel. The gridding weights are ignored; instead, fractional Gaussian interpolants are accumulated on an auxiliary Cartesian grid and the final reconstruction is computed as the inverse Fourier transform of the gridded data divided by the accumulated interpolants. The method can be recognized as an implementation of Jackson’s original gridding algorithm (Jackson et al., 1991), which was subsequently phased out after the proper order of weighting was introduced (one can see that in Jackson’s method, the weights c that appear at the beginning of step 2 in the proper gridding scheme are used only in step 3).

Conclusions

The field of object reconstruction from a set of its projections underwent rapid development in the past five decades. While it was Computerized Axial Tomography that popularized the technique and drove much of the technical and theoretical progress, applications to studies of the ultrastructure of biological material rivaled these achievements by providing insight into biological processes on a molecular level. EM applications of tomography are distinguished by the predominance of ‘true’ 3D reconstruction from 2D projections, i.e., reconstructions that cannot be reduced to a series of 2D axial reconstructions. In addition, EM reconstruction algorithms have to handle problems that remain largely unique to the field, namely, the very large number of projection data, the incorporation of CTF correction, and compensating for the uneven distribution of projection data and gaps in coverage of Fourier space.

There is a great variety of reconstruction algorithms implemented in EM software packages. The first algorithms introduced in the 80s were generalizations of the FBP approach: general and exact filtrations. The arrival of cryo-preparation in the early 90s heralded the development of algorithms which can effectively process lower contrast and lower SNR data, and thus the focus shifted to algebraic iterative reconstruction methods: SIRT in SPIDER and ART with blobs in Xmipp. In the late 90s, the size of data sets increased dramatically. The first cryo reconstruction of an asymmetric complex (70S ribosome) was done using 303 particle images while most recent work on the same complex processed data sets with sizes exceeding 500,000 2D particle images (Schuette et al., 2009; Seidelt et al., 2009) closely followed by structural work on symmetric complexes. For example, recently published near-atomic structure of a group II chaperonin required ~30,000 particle images, which taking into account D8 point group symmetry of this complex corresponds to ~240,000 images (Zhang et al., 2010). This increase placed new demands on the reconstruction algorithms, mainly affecting the running times and computational efficiency of the algorithms, which resulted in a shift towards very fast direct Fourier inversion algorithms. Currently, virtually all major EM software packages include an implementation of a version of the method (EMAN, EMAN2, FREALIGN, IMOD, SPARX, SPIDER), with IMAGIC being most likely the only exception. We also note that the large increases in the number of projection images have only been accompanied by modest increases in the volume size (from 64 to ~256 voxels). This implies Fourier space is bound to be oversampled, and consequently, the problem of artifacts due to simple interpolation schemes used in most implementations is not as severe as it would be with a small number of images.

The limited scope of this review did not allow us to discuss some of the advanced subjects that remain of great interest in the EM field. In SPR one normally assumes that the depth of the field in the microscope is larger than the molecule size. This is not the case for larger biological objects, and certainly not for virus capsids. Efficient algorithms for correcting for the defocus spread within the structure have been proposed, but they are not as of yet widely implemented or tested (Philippsen et al., 2007; Wolf et al., 2006). Similarly, incorporation of a priori knowledge into reconstruction algorithms has been proposed early on, but relatively little has been accomplished in terms of the formal treatment of the problem (Sorzano et al., 2008). These and other issues pertinent to the problem of object reconstruction from projections in EM are often addressed in practical implementations using heuristic solutions. In addition, both SPR and ET are still rapidly developing as new ways of extracting information from EM data are being conceived. Methods such as resampling strategies in SPR (Penczek et al., 2006) or averaging of sub-tomograms in ET (Lucic et al., 2005) call for reevaluation of existing computational methodologies and possible development of new approaches that are more efficient and better suited for the problem at hand. Taken together with the fundamental challenges of the reconstruction problem, we are assured that reconstruction from projections will remain a vibrant research field for decades to come.