Resolution measures in molecular electron microscopy

Abstract

Resolution measures in molecular electron microscopy provide means to evaluate quality of macromolecular structures computed from sets of their two-dimensional line projections. When the amount of detail in the computed density map is low there are no external standards by which the resolution of the result can be judged. Instead, resolution measures in molecular electron microscopy evaluate consistency of the results in reciprocal space and present it as a one-dimensional function of the modulus of spatial frequency. Here we provide description of standard resolution measures commonly used in electron microscopy. We point out that the organizing principle is the relationship between these measures and the Spectral Signal-to-Noise Ratio of the computed density map. Within this framework it becomes straightforward to describe the connection between the outcome of resolution evaluations and the quality of electron microscopy maps, in particular, the optimum filtration, in the Wiener sense, of the computed map. We also provide a discussion of practical difficulties of evaluation of resolution in electron microscopy, particularly in terms of its sensitivity to data processing operations used during structure determination process in single particle analysis and in electron tomography.

Introduction

Resolution assessment in molecular electron microscopy is of paramount importance both in computational methodology of structure determination and in interpretation of final structural results. In rare cases, when a structure reaches near-atomic resolution, appearance of secondary structure elements, particularly helices, can serve as an independent validation of the correctness of the structure and at least approximate resolution assessment can be made. In most cases however, both in single particle analysis (SPR) and especially in electron tomography (ET), the amount of detail in the structure is insufficient for such independent evaluation and one has to resort to statistical measures for determining the quality of the results. For historical reasons, they are referred to as resolution measures, although they do not correspond directly to traditional notions of resolution in optics.

The importance of resolution assessment in SPR was recognized early on in the development of the field. The measures were initially introduced for two-dimensional (2D) work, and subsequently to extended for three-dimensional (3D) applications. There were a number of competing approaches introduced, such as Q-factor, Fourier Ring Correlation (FRC), and Differential Phase Residual (DPR). Ultimately, it was the relation of these measures to the Spectral Signal-to-Noise Ratio (SSNR) distribution in the resulting structure that provided a unifying framework for the understanding of the resolution issues in EM and their relationship to the optimum filtration of the results.

Resolution assessment of ET reconstruction remains one of the central issues that has resisted a satisfactory solution. The methodologies that have been proposed so far were usually inspired by SPR resolution measures. However, it is not immediately apparent that this is the correct approach since in standard ET there is no averaging of multiple pieces of data, the structure imaged is unique and no secondary structure elements are resolved. Hence, ideas of self-consistency and reproducibility of the results that are central to validation of SPR results do not seem to be directly transferable to the evaluation of ET results.

In this brief review, we will introduce the concept of resolution estimation in EM and what differentiates it from the concept of resolution traditionally used to characterize imaging systems in optics. We will point out that it is the self-consistency of the results that is understood as resolution in EM and we will show how this assessment is rooted in the availability of multiple data samples, i.e., 2D EM projection images of 3D macromolecules. By relating the commonly used Fourier Shell Correlation (FSC) measure to the SSNR we will show that, if certain statistical assumptions about the data are fulfilled, the concept of resolution is well-defined and interpretation of the results straightforward. In the closing section we will discuss current approaches to resolution estimation in ET and point the fundamental limitations that limit their usefulness.

Optical resolution versus resolution in electron microscopy

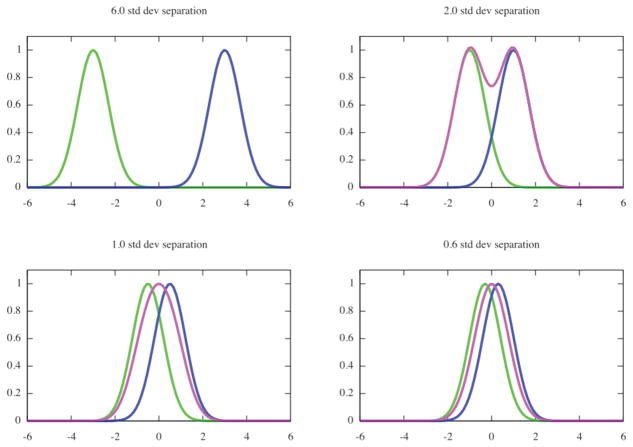
The resolution of a microscope is defined as the smallest distance between two points on a specimen that can still be distinguished as two separate entities. If we assume that the microscope introduces blurring that is expressed by a Gaussian function, then each of the point sources will be imaged as a bell-shaped object and the closer the two sources are, the worse the separation will be between the two maxima of the combined bells (Fig. 1). It is common to accept the resolution as the distance that is twice the standard deviation of the Gaussian blur. This concept of resolution is somewhat subjective, as one can presume different value at the minimum as acceptable and thus obtain different value for the resolution of the system. In the traditional definition there is no accounting for noise in the measurements. Finally, there is a logical inconsistency: if we know that the blurring function is Gaussian, we can simply fit it to the measured data and obtain accuracy of peak separation by far exceeding what the definition would suggest (den Dekker, 1997).

Fig. 1.

Optical resolution is defined as the smallest distance between two points on a specimen that can be distinguished as two separate entities. Assuming the blur introduced by the microscope to be Gaussian with a known standard deviation, the resolution is defined as a distance between points that equals at least one standard deviation. For distances smaller or equal one standard deviation, the observed pattern, i.e., sum of two Gaussian functions (green and blue) has an appearance of a pseudo-Gaussian with one maximum (magenta).

The theoretical resolution of an optical lens is ultimately limited by diffraction and therefore depends on the wavelength of the radiation used to image the object (light for light microscopy, electrons for electron microscopy, X-rays for X-ray crystallography and so on). In 2D, the Abbe criterion gives the resolution d of a microscope as:

$$d=0.61\frac{\lambda }{nsin\alpha }$$ (1)

where λ is the wavelength, n is the refractive index of the imaging medium (air, oil, vacuum), and α is half of the cone angle of light from the specimen plane accepted by the objective (half aperture angle in radians), in which case nsinα is the numerical aperture. This criterion stems from the requirement for the numerical aperture of the objective lens to be large enough to capture the first-order diffraction pattern produced by the source at the wavelength used. Numerical aperture is ~1 for light microscope, and ~0.01 for electron microscope. As the wavelength of light is 400–700 nm, the resolution of a light microscopes is ~250–420 nm. For electron microscopes, the electron wavelength λ depends on the h² accelerating voltage V. Within the classical approximation, $\lambda =\sqrt{\frac{h^2}{2\mathit{meV}}}$, where h is Planck’s constant, m is the mass and e the charge of the electron. For an accelerating voltage 100keV, λ = 0.0037 nm. The theoretical resolution of electron microscopes is 0.23 nm for an accelerating voltage 100keV ( λ = 0.003701nm) and 0.12 nm for 300keV ( λ = 0.001969 nm), and is mainly limited by the quality of electron optics. For example, spherical aberration correctors can significantly improve the resolution limit of electron microscopes.

While the resolution of electron microscopes is more than sufficient to achieve atomic resolution in macromolecular structural studies resolution of reconstructed 3D maps of biological specimens is typically worse by an order of magnitude. The resolution-limiting factors in EM include:

1. Wavelength of the electrons.

2. Quality of the electron optics (astigmatism, envelope functions).

3. Underfocus settings. Resolution of the TEM is often defined as the first zero of the contrast transfer function (CTF) at Scherzer (or optimum) defocus.

4. Low contrast of the data. This is due to both the electron microscope being mainly a phase contrast instrument with an amplitude contrast of less than 10% and the similar densities of ice surrounding the molecules and of protein (~0.97:1.36 g/cm³).

5. Radiation damage of imaged macromolecular complexes. Even if the electron dose is kept very low (~25e⁻/Ų), some degree of damage on the atomic level is unavoidable and regretfully virtually impossible to assess. In addition, exposure to the electron beam is likely to adversely affect structural integrity of both the medium and the specimen on the microscopic level (shrinkage, local shifts). These artifacts can be reduced in some cases by pre-irradiation of the sample.

6. Quality of recording devices. The current shift towards collecting EM data on CCD cameras means that there is additional strong suppression of high frequency signal due to the Modulation Transfer Function of the CCD. The advent of direct detection devices (DDD) should improve the situation (Milazzo et al., 2010).

7. Low Signal-to-Noise Ratio (SNR) level in the data. This stems from the necessity of keeping the electron dose at a minimum to prevent excessive radiation damage. It is generally accepted that the SNR of cryo data is less than one. The only practical way to increase the SNR of the result is by increasing the number of averaged individual projection images of complexes.

8. Presence of artifactual images in the data set. Due to the very low SNR and despite careful screening of windowed particles there is always a certain percentage of frames that contain objects that appear to be valid projection images, but in reality are artifacts. At present, there are no reliable methods that would allow detection of these artifactual objects or even to assess what might be their share in the sample.

9. Variability of the imaged molecule. This can be caused by natural conformational heterogeneity of the macromolecular assemblies due to fluctuations of the structure around the ground state or due to the presence of different functional states in the sample.

10. Accuracy of the estimation of the image formation model parameters, such as defocus, amplitude contrast, and also SSNR of the data, magnification mismatch and such.

11. Accuracy of alignment of projection images is limited by the very low SNR of the EM data, inhomogeneity of the sample, and limitations of computational methodologies.

Standard definitions of resolution are based on the assumption that it is possible to perform an experiment in which an object with known spacing is imaged in the microscope and the analysis of the result yields a point spread function of the instrument, and thus the resolution. This approach is not applicable to analysis of EM results since the main resolution-limiting factors include instability of the imaged object, high noise in the data, and computational procedures that separate the source data from the result. Thus, even if useful information about resolution of cryo-specimens can be deduced from the analysis of crystalline specimen that do not require orientation adjustment in a computer, practical assessment of resolution in SPR and ET requires more elaborate methodology that has to take into account statistical properties of the aligned and averaged data.

Principles of resolution assessment in EM

Assessment of resolution in EM concerns itself not so much with the information content of individual images or with the resolving power of the microscope as with the consistency of the result, which in 2D is the average of aligned images and in 3D the object reconstructed from its projection images. Moreover, following the example of the R-factor in X-ray crystallography, the analysis is cast in Fourier space and the result is presented as a function of the modulus of spatial frequency. The resolution in EM, if reported as a single number, is defined as a maximum spatial frequency at which the information content can be considered reliable. Again, the definition is subjective, as it is rather arbitrary what one considers reliable and much of the controversies still present in the EM field revolve around this problem although, as we will put forward later, the number by itself is inconsequential.

The resolution measures in EM evaluate the self-consistency of the result. The premise is to take advantage of the information redundancy: each Fourier component of the average/reconstruction is obtained by summing multiple Fourier components of input data at the same spatial frequency. These Fourier components are complex numbers, i.e., each comprises a real and an imaginary part and their possible representation is by vectors in a x–y system of coordinates, where the x-axis is associated with the real part and the y-axis with the imaginary part. The length of each vector is called its amplitude, and the angle between the vector and x-axis its phase. Thus, formation of an average, i.e., the summation of the Fourier transforms of images, can be thought of as a summation of such vectors for each spatial frequency. In this representation, assessment of the self-consistency of the result becomes a matter of testing whether vectors that were summed had similar phases, i.e., that the length of the sum of all vectors is not much shorter than the sum of lengths of individual vectors.

Indeed, if we consider a perfect case in which all images were identical the vectors would all have the same length and phase. Their sum then would be simply a vector whose length is the same as the sum of the lengths of each vector. The same result is obtained if the vectors have different lengths (amplitudes) but the same direction (phase). Thus, if both sums are the same, we would consider the EM data consistent. Conversely, if there is little consistency, the vectors would point in different directions, in which case the length of their sum would fall short of the sum of their lengths. In EM, the degree to which both sums agree is equated with the consistency of the results (phase agreement), and ultimately with the resolution. Again, this is not the resolution in the optical sense, as it says relatively little about resolving power of the instrument or even about our ability to distinguish between details in real space representation of the result. It is merely a measure that informs us on the consistency of the result for a particular spatial frequency, without even providing any information as to the cause of the inconsistency. For example, it is easy to see that both noise or structural inhomogeneity of the data will reduce consistency of the result as evaluated using the above recipe.

In what follows, we will assume a quite general Fourier space image formation model:

$$G_n=F+M_n$$ (1)

where F is the signal (i.e., the projection image of a macromolecular complex), M_n is noise, and G_n is the n’th observed image. For simplicity, we will omit the argument and assume that unless stated otherwise, all entities are functions of spatial frequency and the equation is written for a particular frequency.

There are four major resolution measures which have been introduced into the EM field. The Q-factor is defined as (van Heel and Hollenberg, 1980):

$$Q=\frac{\left|{\displaystyle \sum _{n=1}^N}{G}_n\right|}{{\displaystyle \sum _{n=1}^N}\mid G_n\mid }$$ (2)

It is easy to see that Q is zero for pure uncorrelated noise and one for a noise-free, aligned signal. We note that Eq.2 is a direct realization of the intuitive notion of consistency expressed as the length of a sum of complex numbers. However, as we shall see later, the ratio of squared sum to the sum of squares of G_n’s yields itself better to analysis (Baldwin and Penczek, 2005).

While the Q-factor is a particularly simple and straightforward measure, it did not gain much popularity for a number of reasons. First, to compute it for 2D data one has to compute the Fourier Transforms (FTs) of all the individual images, which at least at the time the measure was introduced might have been considered an impediment. Second, while Q-factor provides a measure of resolution for each pixel in the image, it needs to be modified to yield resolution per modulus of spatial frequency. Third, since Eq.2 includes moduli of Fourier components, it cannot be easily related to SSNR, which is defined as ratio of powers (squares) of the respective entities. Finally, it is not clear how to extend Eq.2 to 3D reconstruction from projections, which, as will be described later, would require accounting for the reconstruction process, uneven distribution of data points, and interpolation between polar and Cartesian systems of coordinates.

The Differential Phase Residual (DPR) (Frank et al., 1981) was introduced to address some of the shortcoming of the Q-factor. With DPR, it is possible to compare Fourier transforms of two images, which can be either 2D averages or 3D reconstructions. The weighted squared phase difference between the same frequency Fourier components is summed within a ring (in 2D) or a shell (in 3D) of approximately same spatial frequencies:

$$\mathit{DPR}(u,v;s)=\underset{q}{min}{\left|\frac{{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}{\left[\mathrm{\Delta }{\varphi }_{UV}({\mathbf{s}}_k)\right]}^2\left[\mid U({\mathbf{s}}_k)\mid +q\mid V({\mathbf{s}}_k)\mid \right]}{{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}\left[\mid U({\mathbf{s}}_k)\mid +q\mid V({\mathbf{s}}_k)\mid \right]}\right|}^{1/2}$$ (3)

where Δϕ_UV (s_k) is the phase difference between Fourier components of U and V, 2ε is a pre-selected ring/shell thickness, s =|s_k| is the magnitude of the spatial frequency, and k_s is the number of Fourier pixels/voxels in the ring/shell corresponding to frequency s. The DPR yields a 1D curve of weighted phase discrepancies as a function of s. Regrettably, the DPR is sensitive to relative normalization of u and v, so traditionally a minimum value with respect to the multiplicative normalization of v is reported (q in Eq.3). In order to assess the resolution of a set of images, the data set is randomly split into halves, two averages/reconstructions are computed and the DPR is evaluated using their FTs. A DPR equal to zero indicates perfect agreement while for two objects containing uncorrelated noise the expectation value of DPR is 103.9° (van Heel, 1987). The accepted cut-off value for resolution limit is 45°. Regrettably, there is no easy way to relate DPR to SSNR or any other resolution measure.

The regrettably Ring Correlation (FRC) (Saxton and Baumeister, 1982) was introduced to provide a measure that would be insensitive to linear transformations of the objects’ densities. For historical reasons, in 2D applications the measure is referred to as Fourier Ring Correlation while in 3D applications as Fourier Shell Correlation (FSC), even though the defintion remains the same:

$$\mathit{FSC}(u,v;s)=\frac{{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}U({\mathbf{s}}_k)V^{\ast }({\mathbf{s}}_k)}{{\left\{\left({\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}{\mid U({\mathbf{s}}_k)\mid }^2\right)\left({\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_r}}{\mid V({\mathbf{s}}_k)\mid }^2\right)\right\}}^{1/2}}$$ (4)

where the notation is the same as in Eq.3. FSC is a 1D function of the modulus of spatial frequency whose values are correlation coefficients computed between the Fourier transforms of two images/volumes over rings/shells of approximately equal spatial frequency. An FSC curve everywhere that is close to one everywhere reflects a strong similarity between u and v and an FSC curve with values close to zero indicates the lack of similarity between u and v. Predominantly negative values of FSC indicate that contrast of one of the images was inverted. Typically, FSC decreases with spatial frequency (although not necessarily monotonically) and various cut-off thresholds have been proposed for serving as indicators of the resolution limit. We postpone their discussion to the next section. Finally, we clarify that because u and v are real, their FTs are Friedel symmetric (i.e., U (s) = conjg(U (−s))), so the result of the summation in the numerator is real. Given that, we can write Eq.4 as:

$$\mathit{FSC}(u,v;s)=\frac{{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s/2}}\mid U({\mathbf{s}}_k)\left|\right|V({\mathbf{s}}_k)\mid cos\left(\mathrm{\Delta }{\varphi }_{UV}({\mathbf{s}}_k)\right)}{{\left\{\left({\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s/2}}{\mid U({\mathbf{s}}_k)\mid }^2\right)\left({\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -r\mid \le \epsilon }^{k_s/2}}{\mid V({\mathbf{s}}_k)\mid }^2\right)\right\}}^{1/2}}$$ (5)

It follows from Eq.5 that FSC is indeed a consistency measure, as it is an amplitude weighted sum of cosines of phase discrepancies between the Fourier components of two images. By comparing Eqs.3 and 5 we can also see that the normalization in FSC makes the measure better behaved.

Both DPR and FSC are computed using two maps. These can be either individual images or, more importantly, averages/3D reconstructions obtained from sets of images. The obvious application of these two measures is in the evaluation of resolution in structure determination by SPR. There are two possible approaches that reflect the overall methodology of the SPR. In the first approach, the entire data set is aligned and for the purpose of resolution estimation it is randomly split into halves. Next, the two averages/reconstructions are computed and compared using DPR or FSC. In the second approach, the data set is first split into halves, each subset is aligned independently, and the two resulting averages/reconstructions are compared using DPR or FSC. The second approach has a distinct advantage in that the problem of ‘noise alignment’ (Grigorieff, 2000; Stewart and Grigorieff, 2004) is avoided. As the orientation parameters of individual images are iteratively refined using the processed data set as a reference, the first approach has the tendency to induce self-consistency of the data set beyond what the level of signal in the data should permit. As a result, all the measures discussed in this chapter tend to report exaggerated resolution as they evaluate the degree of self-consistency of the data set. The problem is avoided by carrying out alignment independently.; however, this approach is not without its peril. Firstly, it is all but impossible to achieve ‘true’ independence in SPR; for example, the initial reference is often shared or at least obtained using similar principles. Secondly, one can argue that alignment of half of the available particles cannot yield results with quality comparable to that obtained by aligning the entire data set, abd this is of special concern when the data set is small. Thirdly, two independent alignments may diverge, in which case the reported resolution will be appropriately low, but the problem is clearly with the alignment procedure and not with the resolution as such. Therefore, as long as one is aware that the resolution estimated using the first approach is to some extent exaggerated, there is no significant disadvantgage to using it. Finally, we note that Q-factor and SSNR (to be introduced below) evaluate consistency of the entire data set, so they are not applicable to comparisons of independetly aligned sets of images.

The Spectral Signal-to-Noise Ratio (SSNR) can provide, like Q-factor, a per-pixel measure of the consistency of the data set, which also distinguishes it from both DPR and FRC that yield measures that are ‘rotationally averaged’ in Fourier space. SSNR was introduced for analyzing sets of 2D images and is defined as (Unser et al., 1987):

$$\mathit{SSNR}(\mathbf{s})=\{\begin{array}{ll}S(\mathbf{s})-1\hfill & \text{if}S(\mathbf{s})>1\hfill \\ 0\hfill & \text{if}S(\mathbf{s})\le 1\hfill \end{array},$$ (6)

where the spectral variance ratio S is:

$$S(\mathbf{s})=\frac{{\left|{\displaystyle \sum _{n=1}^N}{G}_n(\mathbf{s})\right|}^2}{\frac{N}{N-1}{\displaystyle \sum _{n=1}^N}{\mid G_n(\mathbf{s})-\overline{G}(\mathbf{s})\mid }^2},$$ (7)

with

$$\overline{G}(\mathbf{s})=\frac{1}{N}\sum _{n=1}^N{G}_n(\mathbf{s}).$$ (8)

Eqs.6–8 define a per-pixel SSNR. In the original contribution, Unser et al. introduced SSNR as a 1D function of the modulus of spatial frequency to maintain its correspondence to FRC:

$$\mathit{SSNR}(s)=\{\begin{array}{ll}S(s)-1\hfill & \text{if}S(s)>1\hfill \\ 0\hfill & \text{if}S(s)\le 1\hfill \end{array}$$ (9)

with the rotationally averaged spectral variance ratio defined as:

$$S(s)=\frac{{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}{\left|{\displaystyle \sum _{n=1}^N}{G}_n({\mathbf{s}}_k)\right|}^2}{\frac{N}{N-1}{\displaystyle \sum _{\mid \mid {\mathbf{s}}_k\mid -s\mid \le \epsilon }^{k_s}}{\displaystyle \sum _{n=1}^N}{\mid G_n({\mathbf{s}}_k)-G({\mathbf{s}}_k)\mid }^2}.$$ (10)

As we will demonstrate in the next section, the SSNR given by Eqs.9–10 yields results equivalent to FRC in application to 2D data.

Extension of the SSNR to resolution evaluation of a 3D object reconstructed from the set of its 2D projection was only partially successful. The main difficulty lies in accounting for the uneven distribution of projections and the proper inclusion of the interpolation step into Eq.9. To avoid a reliance on a particular reconstruction algorithm, Unser et al. (Unser et al., 2005) proposed first to estimate the SSNR in 2D by first comparing reprojections of the reconstructed structure with the original input projection data, and then averaging the contributions in 3D Fourier space to obtain the 1D dependence of the SSNR on spatial frequency. In addition, the authors proposed to estimate the otherwise difficult to assess degree of averaging of data by the reconstruction process by repeating the calculation of the 3D SSNR for simulated data containing white Gaussian noise. The ratio of the two curves, i.e., the one obtained from projection data and the other obtained from simulated noise, yields the desired true SSNR of the reconstructed object. Although the method is appealing in that it can be applied to any (linear) 3D reconstruction algorithm, a serious disadvantage is that the method actually yields a 2D SSNR of the input data, not the 3D SSNR of the reconstruction. This can be seen from the fact that in averaging the 2D contributions to the 3D SSNR, there is no accounting for uneven distributions of projections in Fourier space (insert reference to Penczek chapter on Fundamentals of 3D Reconstruction here).

It is straightforward, however, to extend Eqs.5–9 to a direct Fourier inversion reconstruction algorithm that is based on nearest-neighbor interpolation; additionally, the method can also explicitly take into account the Contrast Transfer Function correction necessary for cryo-EM data (Penczek, 2002; Zhang et al., 2008). It is also possible to introduce SSNR calculation to more sophisticated direct Fourier inversion algorithms that employ the gridding interpolation method, but this is accomplished only at the expense of further approximations and loss of accuracy (Penczek, 2002). As the equations are elaborate and the respective methods rarely used, we refer the reader to the cited literature for details.

The main advantage of evaluating 3D SSNR for 3D reconstruction applications is that the method can yield per-voxel SSNR distributions, and thus provide a measure of anisotropy in the reconstructed object. Given such a measure, it is possible to construct anisotropic Fourier filters that can account for the directionality of Fourier information, and thus potentially improve the performance of 3D structure refinement procedures in cryo-EM single particle reconstruction technique (Penczek, 2002). Outside of that, the equivalence between FSC and SSNR discussed in the next section limits the motivation for the development of a more robust SSNR measures for the reconstruction problem.

Fourier Shell Correlation and its relation to Spectral Signal-to-Noise Ratio

Currently, there is only one resolution measure in widespread use, which is namely the Fourier Shell Correlation. Besides the ease of calculation and versatility, the main reason for its popularity is its relation to the SSNR. This relation greatly simplifies the selection of a proper cutoff level for reported resolution, provides bases for the understanding of its relationship to optical resolution, and links resolution estimation to optimum filtration of the resulting average/structure. The SSNR is defined as a ratio of the power of the signal to the power of the noise. If we assume zero mean uncorrelated Gaussian noise, i.e., M_n ε N(0, σ²I), then the SSNR for our image formation model Eq.1 is:

$${\mathit{SSNR}}_{G_n}=\frac{{\mid F\mid }^2}{{\sigma }^2}.$$ (11)

The SSNR of an average of N images (Eq.8) is:

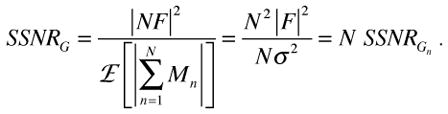(12)

Thus, the summation of N images that have identical signal and independent Gaussian noise increases the SSNR of the average N times. For 3D reconstruction, the relationship is much more complicated and difficult to compute because of the uneven coverage of 3D Fourier space by projections, and the necessity of the interpolation step between polar and Cartesian coordinates (see insert reference to Penczek chapter on Fundamentals of 3D Reconstruction here), the 3D SSNR in a reconstructed object is difficult to compute.

Given definitions of the FSC(s) Eq.4 and SSNR(s) Eqs.9–10, relationships between the two resolution measures are (for derivation see (Bershad and Rockmore, 1974; Frank and Al-Ali, 1975; Penczek, 2002; Saxton, 1978)):

$$\begin{array}{l}\mathit{FSC}(s)=\frac{\mathit{SSNR}(s)}{\mathit{SSNR}(s)+1}\\ \mathit{SSNR}(s)=\frac{\mathit{FSC}(s)}{1-\mathit{FSC}(s)}.\end{array}$$ (13)

For cases where the FSC was calculated by splitting the data set into halves, we have that (Unser et al., 1987):

$$\begin{array}{l}\mathit{FSC}(s)=\frac{\mathit{SSNR}(s)}{\mathit{SSNR}(s)+2}\\ \mathit{SSNR}(s)=2\frac{\mathit{FSC}(s)}{1-\mathit{FSC}(s)}.\end{array}$$ (14)

Eq.14 serves as a basis for establishing a cut-off for reporting resolution as a single number. Since in EM one would typically evaluate the data using FSC methodology, one needs a cut-off level that serves as an indicator of the quality of obtained results. Using the relationship between the FSC and SSNR, the decision can be informed, even though it remains arbitrary. Commonly accepted cut-off levels are: (1) the 3σ criterion that selects for a cut-off level the point where there is no signal in the resulta, i.e., SSNR falls to zero, in which case FSC=0 (van Heel, 1987); (2) the point at which noise begins to dominate the signal, i.e., SSNR=1 or FSC=1/3 (Eq.14); (3) the midpoint of the FSC curve, i.e., SSNR=2 or FSC=0.5, which is also often used for constructing a low-pass filter.

The usage of a particular cut-off threshold requires the construction of a statistical test that would tell us whether the obtained value is significant. Regrettably, the distribution of the correlation coefficient (in our case FSC) is not normal and rather complicated, so the test is constructed using Fisher’s z-transformation (Bartlett, 1993):

$$z=\frac{1}{2}log\frac{1+\mathit{FSC}}{1-\mathit{FSC}}=\mathit{arctanh}(\mathit{FSC}).$$ (15)

z has a normal distribution:

$$z\in N\left(\zeta =\frac{1}{2}log\frac{1+\rho }{1-\rho }+\frac{\rho }{k_s},1/\sqrt{k_s-3}\right)$$ (16)

where k_s is the number of independent sample pairs from which FSC was computed (see Eqs.4 and 5). In the statistical approach outlined here it is important to use the number of truly independent Fourier components, that is to account for Friedel symmetry and for point group symmetry of the complex, if present. Confidence intervals of z at 100(1−α )%, where α is the significance level, are:

$$z^{+}/-t_{\alpha /2}\frac{1}{\sqrt{k_s-3}}.$$ (17)

For example, for α = 0.05, $t_{\alpha /2}=1.96$, the confidence limits are $z^{+}/-\frac{1.96}{\sqrt{k_s-3}}$. Once the endpoints for a given value of z are established, they are transformed back to obtain confidence limits for the correlation coefficient (FSC):

$$FS{C}^{+}/-tanh\left(t_{\alpha /2}\frac{1}{\sqrt{k_s-3}}\right)=\frac{exp\left(2t_{\alpha /2}\frac{1}{\sqrt{k_s-3}}\right)-1}{exp\left(2t_{\alpha /2}\frac{1}{\sqrt{k_s-3}}\right)+1}$$ (18)

Finally, we note it is much simpler to test the hypothesis that FSC equals zero. Indeed, we first note that for small FSC, z ≃ FSC (Eq.16) and second for ρ = 0, $z\in N\left(0,1/\sqrt{k_s-3}\right)$. Assuming a significance level α = 0.026 corresponding to three standard deviations of a normal distribution, it follows that we can reject the hypothesis FSC = 0 when $\mathit{FSC}>3/\sqrt{k_s-3}$. The aforementioned is the basis of the 3σ criterion (van Heel, 1987) (Fig. 2). We add that the statistical analysis given above is based on the assumption that Fourier components in the map are independent and their number is k_s.

Fig. 2.

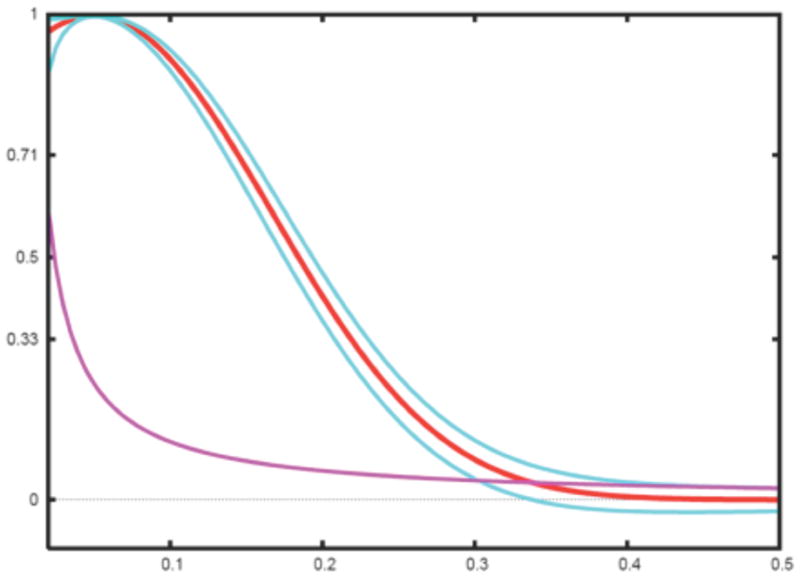
Simulated FSC curve (red) with confidence intervals plotted at ±3σ (blue) (Eq.18) and 3σ criterion curve (magenta) (van Heel, 1987).

The practical meaning of characterizing ‘resolution’ of a resultby a single number is unclear. Much has been written on the presumed superiority of one cut-off value over another, but little has been said on the practical difference between reporting resolution of the same result as say 12Å according to the 3σ criterion as opposed to 15Å based on the 0.5 cut-off. It has sometimes been claimed that some criteria are more ‘conservative’ than other and supposedly they can lead to Fourier filtration that would suppress interpretable details in the map, and yet no method of filtration is named (for example see exposition in (van Heel et al., 2000)). The debate is resolved quite simply if we recall the the FSC methodology yields a 1D function of the modulus of spatial frequency, which implies that it is the shape of the entire FSC curve that codes the ‘resolution’ and the quality of the results. Finally, the relations between FSC, SSNR, and optimum filtration should put the controversy to rest.

Wiener filtration methodology provides a means for constructing a Fourier linear filter that prevents excessive enhancement of noise and which uses SSNR distribution in the data. The method yields an optimum filter in the sense that the mean-square error between the estimate and the original signal is minimized (see insert reference to Penczek chapter on Image Restoration here):

$$\widehat{F}(s)=\frac{\mathit{SSNR}(s)}{\mathit{SSNR}(s)+1}G(s),$$ (19)

which, using the relation between SSNR and FSC Eq.13, is simply:

$$\widehat{F}(s)=\mathit{FSC}(s)G(s),$$ (20)

or, if FSC was computed using a data set split into halves (Eq.14), is:

$$\widehat{F}(s)=2\frac{\mathit{FSC}(s)}{\mathit{FSC}(s)+1}G(s).$$ (21)

We conclude that (1) the FSC function gives an optimum low-pass filter; (2) wherever the SSNR is high, the original structure is not modified, and the midpoint, i.e., FSC=0.5, corresponds to decrease of the amplitudes two times, while FSC=0 sets respective regions of Fourier space in filtered structure to zero; (3) in practice, FSC oscillates wildly around zero level and generally might be quite irregular, in which case it is preferable to approximate it by an analytical form of a selected digital filter (Gonzalez and Woods, 2002); (4) FSC is not necessarily a monotonically decreasing function of the modulus of spatial frequency, in particular, it may contain imprints of the dominating CTF, in which case an appropriate smooth filter has to be appropriately constructed. Finally, if the SSNR of a 3D map reconstructed from projections can be reliably estimated and if there is an indication of anisotropic resolution, a Wiener filter given by Eq.19 is applicable (with spatial frequency replacing its modulus as an argument) either directly or using an appropriate smooth approximation of the SSNR (Penczek, 2002).

The FSC measure has one more very useful application in that it can be used to compare two maps obtained using different experimental techniques. Most often it is used to compare EM maps with X-ray structures of the same complex. In this case, the resulting function is called Fourier Cross-Resolution (FCR) and its meaning is deduced from the relationship between FRC and SSNR. Usually, one assumes that a target the X-ray structure is error- and noise-free, in which case FRC yields the SSNR of the EM map:

$$\begin{array}{l}\mathit{SSNR}(s)=\frac{{\mathit{FCR}}^2(s)}{1-{\mathit{FCR}}^2(s)}\\ \mathit{FCR}(s)=\sqrt{\frac{\mathit{SSNR}(s)}{\mathit{SSNR}(s)+1}}.\end{array}$$ (22)

The selected cut-off thresholds are as follows for the FCR: SSNR=1 corresponds to FCR=0.71 and SSNR=2 to FCR=0.82. Thus, it is important to remember that for a reported resolution of an EM map based on FCR to mean the same as a reported resolution based on FSC, the cut-off thresholds have to be different and higher. Otherwise, the FCR function can be used directly in Eq.20 to obtain an optimum Wiener filtration of the result. Finally, it is important to stress that if there are reasons to believe that the target X-ray models and EM maps represent the same structure, at least within the considered frequency range, then the FCR methodology yields results that are much less marred by the problems prevalent in FSC resolution estimation. In particular, the difficult to avoid problem of alignment of noise has no influence on FCR results. Therefore, higher credence should be given to the FCR estimate of SSNR in the result, and hence also the FCR-based resolution.

Relation between optical resolution, self-consistency measures, and optimum filtration of the map

There is no apparent relationship between optical resolution which is understood as the ability of an imaging instrument to distinguish between closely spaced objects and resolution measures used in EM that are geared towards the evaluation of self-consistency of an aligned data set. Ultimately, the resolution of an EM map will be restricted by the final low-pass filtration based on the resolution curve (Eqs.19–21). First we consider two extreme examples: (1) the FSC curve, and thus the filter is Gaussian, (2) the resolution curve is rectangular, i.e., it is equal to one up to a certain stop-band frequency and zero in higher frequencies.

For the Gaussian shaped FSC curve, the traditional definition of resolution applies: using as a cut-off threshold 0.61, which is the value of a not-normalized Gaussian function at one standard deviation, one obtains that frequency corresponding to the Fourier standard deviation σ_S specifies the resolution. Application of the corresponding Fourier Gaussian filter corresponds to a convolution with a real space Gaussian function with a standard deviation ${\sigma }_r=\frac{1}{2\pi {\sigma }_s}$ that effectively limits the resolution to $2{\sigma }_r=\frac{1}{\pi {\sigma }_s}$, as per the traditional definition. For example, if ${\sigma }_s=\frac{1}{15}{Å}^{-1}$, the resolution of the filtered map would be 4.8Å. The reason it is so high is that the Gaussian filter decreases relatively slowly, which implies the filtered map contains significant amount of frequencies higher than the cut-off of one sigma. On the other hand, a Gaussian filter will also start suppressing amplitudes beginning from very low frequencies, which is the reason it should not be used for filtration of EM maps.

For a rectangular shaped FSC curve, one would apply a top-hat low-pass filter that would simply truncate the Fourier transform at the stop-band frequency s_c Å⁻¹ and thus obtain a map whose resolution is $1/s_cÅ$. This is a trivial consequence of the fact that the filtered map would not contain any higher frequencies. It would also appear that this is why it is often incorrectly assumed that a reported ‘resolution’ based on more or less arbitrarily selected cut-off level is equivalent to the actual resolution of the map. In either case, top-hat filters should be avoided as truncation of Fourier series results in real-space artifacts known as ‘Gibbs oscillations’, i.e., any step in real-space map will be surrounded by ringing artifacts in the filtered map whose amplitude is ~9% of the step’s amplitude (Jerri, 1998). If the original map was non-negative, Gibbs oscillations will also introduce negative artifacts into the filtered map. Gibbs phenomenon is particularly unwelcome in intermediate resolution EM maps, as ringing artifacts will appear as fine features on the surface of the complex and thus invite spurious interpretations. One has to be aware that all Fourier filters share, to a degree, this problem, particularly if they are steep in the transition regions. Therefore, filtration of the EM map has to be done carefully using dedicated digital filters and one must be aware of the trade-off between desired steepness of the filter in Fourier space with amplitudes of Gibbs oscillations.

A properly designed filter has to approximate well the shape of a given FSC curve and at the same time be sufficiently smooth to minimize ringing artifacts. One possibility is to apply low pass filtration in real space using convolution with a kernel. For example, if the kernel approximates a Gaussian function, it will only have positive coefficients, in which case both the ringing and negative artifacts are avoided. Regrettably, as discussed above, the practical applicability of Gaussian filtration in EM is limited. Another tempting approach is to use a procedure variously known as ‘binning’ or a ‘box convolution’ in which one replaces a given pixel by an average of neighboring pixels. This procedure is commonly, and incorrectly, often used for decimation of oversampled images (for example reduction of large micrographs). The procedure is simply a convolution of the input map with a rectangular function used as kernel. Since all coefficients of the kernel are the same, the resulting algorithm is particularly efficient. In addition, both ringing and negative artifacts are avoided and given that the method is fast, one can apply it repeatedly to approximate convolution with a Gaussian kernel (if repeated three times, it will approximate the Gaussian kernel to within 3%). However, the simple box convolution is deceptive, as the result is not what one would desire. This can be seen from the fact that the Fourier transform of a rectangular function is a sinc function, which is not band-limited and decreases rather slowly. Thus, paradoxically, simple box convolution does not suppress high-frequencies well and does not have a well-defined stop-band frequency. Finally, if if the method is used to decimate image, then it will result in aliasing, i.e., frequencies higher than the presumed stop-band frequency will appear in the decimated image as spurious lower frequencies, and resulting in real-space artifacts.

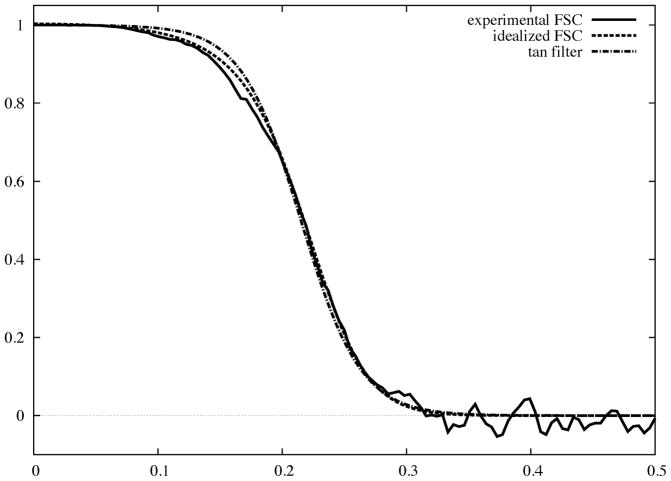
An advisable approach to filtration of an EM map is to select a candidate Fourier filter from a family of well-characterized prototypes and fit it to the experimental FSC curve. We note that under the assumption that the SSNR in EM image data is approximately Gaussian, the shape of the FSC curve can be modeled. Indeed, 1D rotationally averaged power spectra of macromolecular complexes in frequencies above 0.05 – 0.1Å⁻¹ are approximately constant at a level dependent on the number of atoms in the protein (Guinier and Fournet, 1955). This leaves SSNR as a ratio of the product of a squared envelope function of the data and the envelope function of misalignment to the power spectrum of the noise in the data. Both envelopes can be approximated, in the interesting frequency region, by Gaussian functions (Baldwin and Penczek, 2005; Saad et al., 2001) and the noise power spectrum by exponent of a low order polynomial (Saad et al., 2001), so an overall Gaussian function is a good approximation of the SSNR fall-off. Thus, for N averaged images we have:

$$\mathit{SSNR}(s)\simeq Nexp\left(-\frac{B_t}{4}{s}^2\right).$$ (23)

Using Eq.19, we obtain the shape of an optimum Wiener filter as (Fig. 3):

$$W(s)=\frac{Nexp\left(-\frac{B_t}{4}{s}^2\right)}{Nexp\left(-\frac{B_t}{4}{s}^2\right)+\gamma }$$ (24)

where γ accounts for the unknown normalization in Eq.23. While the filter approximates remarkably well the shape of a typical FSC curve, it remains non-zero in high frequencies, and so is not very well suited for practical applications. Incidentally, Eq.23 yields a simple relationship between resolution and the number of required images. More specifically, by using SSNR(s) = 1 as a resolution cut-off, we obtain that $\mathit{resolution}\sim {(lnN)}^{-\frac{1}{2}}$.

Fig. 3.

Experimental FSC curve encountered in practice of SPR (solid) plotted as a function of magnitude of spatial frequency with 0.5 corresponding to Nyquist frequency. We also show an idealized FSC curve (Eq.24) and a hyperbolic tangent filter (Eq.28) fitted to the experimental FSC.

A commonly used filter is the Butterworth filter:

$$W(s)=\frac{1}{{\left(1+{\left(s/c\right)}^q\right)}^{1/2}}$$ (25)

where c is the cut-off frequency and q determines the filter falloff. These two parameters are determined using two parameters, namely, a pass-band and stop-band frequencies denoted s_pass and s_stop, respectively:

$$q=2\frac{log\left(\frac{\epsilon }{\sqrt{a^2-1}}\right)}{log\left(\frac{s_{\mathit{pass}}}{s_{\mathit{stop}}}\right)},$$ (26)

$$c=\frac{s_{\mathit{pass}}}{{\epsilon }^{2/q}},$$ (27)

where ε= 0.882 and a = 10.624. Since the value of the Butterworth filter at s_pass is 0.8 and at s_stop is 0.09, it is straightforward to locate these two points given an FSC curve and then compute the values c and q that parametrize the filter.

The Butterworth filter has a number of desirable properties, but it approaches zero in high frequencies relatively slowly. In addition, it is not characterized by a cut-off point at 0.5 value, so it is not immediately apparent what the resolution of the filtered map is. Therefore, a preference might be given to the hyperbolic tangent filter (tanh) (Basokur, 1998), which is parameterized by the stop-band frequency at 0.5 value, denoted s_0.5, and width of the fall-off u:

$$W(s)=0.5tanh\left(\frac{\pi (s+s_{0.5})}{2{us}_{0.5}}\right)-0.5tanh\left(\frac{\pi (s-s_{0.5})}{2{us}_{0.5}}\right).$$ (28)

The shape of the tanh filter is controlled only by one parameter, amely its width. When the width approaches zero, the filter reduces to a top-hat filter (truncation in Fourier space) with the disadvantage of pronounced Gibbs artifacts. Increasing the width reduces the artifacts and results in a better approximation of the shape of the FSC curve. In comparison with the two previous filters, the values of the tanh filter approach zero more rapidly, which makes it better suited for use in refinement procedures in single particle analysis (Fig. 3).

Resolution assessment in electron tomography

The methodologies of data collection and calculation of the 3D reconstruction in electron tomography are dramatically different from those used in SPR and is more similar to those in computed axial tomography. There is only one object – a thin section of a biological specimen – and a tilt projection series is collected in the microscope by tilting the stage holding the specimen. As a consequence, three physical restrictions limit what can be accomplished with the technique: (1) total dose has to be limited to not far above that used in SPR to collect one image, so individual projection images in ET are rather noisy, (2) maximum tilt is limited to +/−60°–70°, so the missing Fourier information consitutes an inherent problem in ET, and (3) the specimen should be sufficiently thin to prevent multiple scattering, so the specimen thickness cannot exceed the free mean path of electrons in the substrate for a given energy and is in the range 100–300nm, and thus the imaged object is a slab. The projection images have to be aligned, but in ET the problem is simpler, since the data collection geometry in electron tomography can be controlled (within the limits imposed by the mechanics of the specimen holder and by the specimen dimensions), the initial orientation parameters are quite accurate.

The possible data collection geometries for ET are (1) single-axis tilting, which results in a missing wedge in coverage of Fourier space, (2) double-axes tilting, i.e., two single-axis series, with the second collected after rotating the specimen by 90° around the axis coinciding with the direction of the electron beam (Penczek et al., 1995), and (3) conical tilting, where the specimen tilt angle (60°) remains constant while the stage is being rotated in equal increments around the axis perpendicular to the specimen plane (Lanzavecchia et al., 2005). Regrettably, in all three data collection geometries, the Fourier information along the z-axis is missing, which all but eliminates from the 3D reconstruction features that are planar in x–y planes, thus making it difficult to study objects that are dominated by such features, such as membranes.

In ET there is only one projection per projection direction, so the evaluation of resolution based on the availability of multiple projections per angular direction, as practiced in SPR, is not applicable. The assessment of resolution in tomography has to include a combination of two key aspects of resolution evaluation in reconstructions of objects from their projections: (1) the distribution of projections should be such that the Fourier space is, as much as possible, evenly covered to the desired maximum spatial frequency; (2) the SSNR in the data should be such that the signal is sufficiently high at the resolution claimed. However, the quality of tomographic reconstructions depends on the maximum tilt angle used and on the data collection geometry, and yet neither of these factors is properly accounted for by resolution measures. While for slab geometry the loss of information expressed as a percentage of the Fourier space is very small, the easily noticeable, severe real space artifacts in tomography are mainly caused by the fact that the loss is entirely along one of the axes of the coordinate system, which results in anisotropic, object-dependent artifacts. In general, it is safe ot say that flat objects extending in a plane perpendicular to the missing wedge or cone axis will be severely deteriorated or that it might be entirely missing in the reconstruction.

There is no consensus on what should be a general concept of resolution in ET reconstructions, and the resolution measures currently in use in ET are either simply borrowed from SPR (mainly FSC) or slight adjustments of SPR methodologies. In three recently published papers devoted to resolution measures, the authors proposed solutions based on extensions of resolution measures routinely used in SPR. In (Penczek, 2002), the author proposed application to ET of a 3D SSNR measure developed for a class of 3D reconstruction algorithms that are based on interpolation in Fourier space and described in the earlier section. The 3D SSNR works well for isolated objects and within limited range of spatial frequencies. However, the measure requires calculation of the Fourier space variance, so it will yield correct results only to the maximum frequency limit within which there is sufficient overlap between Fourier transforms of projections. Consequently, its appeal for evaluation of ET reconstructions is limited. Similarly, it was suggesteed that the 3D SSNR measure proposed by Unser et al. (Unser et al., 2005) and discussed earlier can be made applicable to ET. Regrettably, its application to tomography is doubtful since, as as the case with the previous method, it requires sufficient oversampling in Fourier space to yield the correct result.

An interesting approach to resolution estimation was introduced by Cardone et al. (Cardone et al., 2005), who proposed to calculate, for each available projection, two 2D Fourier Ring Correlation (FRC) curves: (1) between selected projections and reprojections of the volume reconstructed using the whole set of projections and (2) between selected projections and reprojections of the volume reconstructed with the selected projection omitted. The authors showed that the ratio of these two FRC curves is related to the SSNR in the volume in the Fourier plane perpendicular to the projection direction, as per central section theorem. The authors propose to calculate the SSNR of the whole tomogram by summing the contributions from individual ratios. It is straightforward to note that the method suffers from the same disadvantages as the method by Unser et al.: (1) it does not account for the SSNR in the data lying in non-overlapping regions and (2) it does not yield the proper 3D SSNR because of the omission of reconstruction weights.

In order to adress the shortcomings of the method described in (Penczek and Frank, 2006) the authors propose to take advantage of inherent, even if only directional, oversampling of 3D Fourier space while using standard ET data collection geometries. By exploring these redundancies and by using the standard FSC approach the authors show that it is possible to: (1) calculate the SSNR in certain regions of Fourier space, (2) calculate the SSNR in individual projections in the entire range of spatial frequencies, and (3) infer/deduce the resolution in non-redundant regions of Fourier space by assuming isotropy of the data. Given the SSNR in projections and known angular step of projections, it becomes possible to calculate the distribution of the SSNR in the reconstructed 3D object. While the approach appears to be sound, results of experimental tests are lacking.

The main challenge of resolution estimation in ET is that imaged objects are not reproducible and they have inherent variability. Thus, unlike the case in crystallography or in single-particle studies, repeated reconstructions of the object from the same category will yield structures that have similar overall features, but are also significantly different. Hence, it is impossible to study resolution of tomographic reconstructions in terms of statistical reproducibility. Moreover, because of the dose limitations there is only one projection for each angular direction, so the standard approach to SSNR estimation based on dividing the data set into halves is not applicable. In order to develop a working approach, one has to consider two aspects of resolution estimation in ET: (1) angular distribution of projections and (2) estimation of the SSNR in the data. So far, a successul and generally accepted approach has not emerged.

Resolution assessment in practice

The theoretical foundations of the most commonly used EM resolution measure, the FSC, are very well developed and understood. This includes statistical properties of the FSC (Table 1), relation of the FSC to the SSNR, and the relation of FSC to optimum (Wiener) filtration of the results. Based on the these, it is straightforward to construct a statistical test that would indicate the significance of the results on the preselected significance level and through the relation of FSC to the SSNR, apply a proper filter to supress excessive noise. Nevertheless, practical use of resolution measures differs significantly among software packages and it is advisable to be aware of various factors that influence the results and to also know the details of implementation.

Table 1.

Taxonomy of EM resolution measures.

	relation to SSNR	statistical properties	computed using	applicable to
Q-factor	remote	somewhat understood	individual images	individual voxels
DPR	none	not understood	averages	2D & 3D
FSC	equivalent	understood	averages	2D & 3D
SSNR	-	understood	individual images	2D, approximations in 3D

The basic protocol of resolution assessment using FSC is straightforward:

1. Two averages/3D reconstructions are computed using either two ‘independently’ aligned data sets or by splitting the aligned data set randomly into halves,

2. The averages are preprocessed as follows:

   1. A mask is applied to suppress noise surounding the object.

   2. The averages may be padded with zeroes to kx the size (as a result, the FSC curve will have kx more sampling points) to obtain a finely sampled resolution curve.

   3. Other occasionally applied operations, particularly non-linear (for example, thresholding) will unduly increase the resolution.

3. The FSC curve is computed using Eq.4.

4. Optionally, confidence intervals are computed using Eqs.17–18 with proper accounting for the reduction of the number of degrees of freedom due to possible point-group symmetry of the complex.

5. An arbitrary cut-off threshold is selected in the range (0,1) with lower values given preference by more advantegous The decision is supported by appropriately chosen reference, ‘resolution’ is read from the FSC curve and solemnly reported.

6. A Wiener low-pass filter is constructed using the FSC curve either directly (Eq.19–21) or approximated using one of the candidate analytical filters (Eqs.24–28) and applied to the map.

7. Optionally, the power spectrum of the average/reconstruction is adjusted (see insert reference to Penczek chapter on Fundamentals of 3D Reconstruction here) based on the FSC curve and reference power spectrum (obtained from X-ray or SAXS experiments, or simply modeled). This power spectrum-adjusted structure is a proper model for interpretation.

Despite its popularity, the FSC has a number of well-known shortcomings that stem from the violation of underlying assumptions. The FSC is a proper measure of the SSNR in the average under the assumption that the noise in the data is additive and statistically independent from the signal. As in SPR the data has to be aligned in order to bring the signal in images into register, and it is all but impossible to align images without inducing some correlations into the noise component. Even if the data set is split into halves prior to the alignment to eliminate the noise bias, the two resulting maps have to be aligned to calculate the resolution, and this step introduces some correlations and undermines the assumption about noise independence. Second, if the data set contains projection images of different complexes or of different states of the same complex, the signal is no longer identical. Finally, even if the data is actually homogeneous, the alignment procedure may fail and may converge to a local minimum, so the solution will be incorrect but self-consistent and the resolution will appear to be significant.

In step 2 of the basic protocol outlined above, a mask is applied to the averages in real space to remove excessive background noise. However, because this step is equivalent to convolution in Fourier space with the Fourier transform of the mask, it results in additional correlations that will falsely ‘improve’ FSC results. In fact, application of the mask can be a source of grave mistakes in resolution assessment by FSC (or any other Fourier space-based similarity measure.) First, one has to consider the shape of the mask. It is tempting to use a mask whose shape closely follows the shape of the molecule. However, the design of such a mask is an entirely heuristic endeavour, as presence of noise, influences of envelope function, and filtration of the object make the notion of an ideal shape poorly defined. Many design procedures have been considered (Frank, 2006), but the problem remains without a general solution. As a result, for any particular shape, the mask has to be custom-designed by taking into account the resolution and noise level of the object. Worse yet, some software packages have “automasking” facilities that merely reflect the designer’s concept of what a “good” mask is and which contain key parameters not readily accessible to the user. The outcome of such “automasking” is generally unpredictable. The design of an appropriate mask is an important issue because the FSC resolution strongly depends on how close the mask follows the molecule shape and on how elaborate the shape is. More specifically, more elaborate shapes introduce stronger correlations in Fourier space, and thus “improve” the resolution.

Second, the Fourier transform of a purely binary mask, i.e., a mask whose values are one in the region of interest and zero elsewhere, has high amplitude ripples extending to the Nyquist frequencies, and will introduce strong correlations in Fourier space. Ideally, one would want to apply as a real-space mask a broad Gaussian function with a standard deviation equal to say half the radius of the structure; however, although such a mask minimizes the artifacts, it does not supress surronding noise very well. The best compromise is a mask that has a neutral shape, i.e., it does not follow the shape of the object closely such as a sphere or an elipsoid, which is equal to one in the region of interest zero outside, and where the two regions joined by a smooth transition region with a fall-off given by Gaussian, cosine, or tangent functions.

Third, if a mask is applied, which is almost always the case, one has to make sure that the tested objects are normalized properly. It is known that if we add a constant to pixel values prior to masking, the resolution will improve. In fact, by adding a sufficiently large number, one can obtain an arbitrarily high resolution using the FSC test. The appropriate approach is to compute the average of the pixel values within a transition region as discussed above (which for a sphere is a shell few pixels wide) and then subtract it before applying the mask.

In general, the masking operation changes the number of independent Fourier pixels, that is the number of degrees of freedom, but it is very difficult to give a precise number. This adversely affects the results of statistical criteria, particularly in the case of the 3σ criterion as when FSC approaches zero the curve oscillates widely and too low a threshold can dramatically change the resolution estimation. Non-linear operations such as thresholding or non-linear filters such as the median filter will also unduly ‘improve’ the resolution. Finally, various mistakes in the computational EM structure determination process will strongly affect resolution and overall shape of the FSC curve (Fig. 4).

Fig. 4.

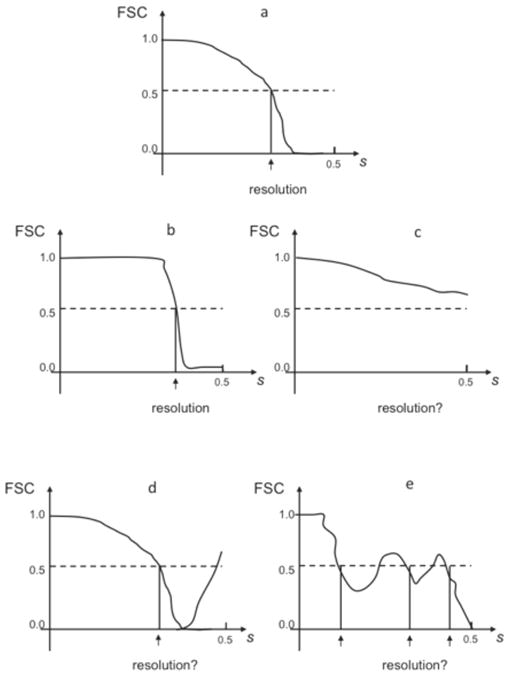
Typical FSC resolution curves encountered in practice of SPR. s - magnitude of spatial frequency with 0.5 corresponding to Nyquist frequency. (a) proper FSC curve remains one at low frequencies, which is followed by a semi-Gaussian fall-off (see Eq.24) and a drop to zero at around 2/3 of Nyquist frequency, in high frequencies oscillates around zero. (b) Artifactual “rectangular” FSC: remains one at low frequencies remains one, followed by a sharp drop, in high frequencies oscillates around zero. Typically it is caused by a combination of alignment of noise and a sharp filtration during the alignment procedure. (c) The FSC never drops to zero in the entire frequency range. Normally, this means that the noise component in the data was aligned, the result are artifactual and the resolution is undetermined. In rare cases it can also mean that the data was severely undersampled (very large pixel size). (d) After the FSC curve drops to zero, it increases again in high frequencies. This artifact can be caused by the low-pass filtration of the data prior to alignment, errors in the image processing code, mainly in interpolation, by the erroneous correction for the CTF, including errors in estimation of SSNR, and finally, incorrect parameters in 3D reconstruction programs (for example iterative 3D reconstruction was terminated too early). It can also mean that all images were rotated by the same angle. (e) FSC oscillates around 0.5. It means that data was dominated by one subset with the same defocus value or there is only one defocus group. The resolution curve is not incorrect per se, but it is unclear what the resolution is. The resulting structure will have strong artifacts in real space.

In the study of resolution estimation of maps reconstructed from projection images it is known that neither FSC nor SSNR yield correct results when the distribution of projection directions is strongly non-uniform. Any major gaps in Fourier space will result in overestimation of resolution and unless 3D SSNR is monitored for anisotropy, there is no simple way to detect the problem. Even if anisotropy is detected, the analytical tools that would help to assess its influence on resolution are lacking.

While the resolution measures described here provide specific numerical estimates of resolution, the ultimate assessment of the claimed resolution is always done by examining the appearance of the map. In SPR, when the resolution is in the subnanometer range, features related to secondary structure elements should be identifiable. In the range 5–10Å, α-helices should appear as cylindrical features while β-sheets as planar objects. At a resolution better than 5Å, densities approximating the protein backbone trace should be identifiable (Baker et al., 2007). Conversely, presence of small features at a resolution lower than ~ 8Å indicates that resolution was overestimated, that the map was not low-pass filtered properly, and/or that excessive correction for the envelope function of the microscope was applied (“sharpening” of the map). In ET it is also possible to assess the resolution by examining the resolvability of known features of the imaged biological material. These can include spacing in filaments, distances between membranes, or visibility of subcellular structures. It is certainly the case that in both SPR and ET 3D reconstructions are almost never performed in the total absence of some a priori information about the specimen, for example, the number of monomers and the number of subunits in macromolecular complexes, are generally known a priori. While this information might be insufficient to assess the resolution to a satisfying degree of accuracy, it can certainly provide sufficient grounds to evaluate the general validity of the results within the resolution limit claimed.