Global view of bionetwork dynamics: adaptive landscape

Abstract

Based on recent work, I will give a nontechnical brief review of a powerful quantitative concept in biology, adaptive landscape, initially proposed by S. Wright over 70 years ago, reintroduced by one of the founders of molecular biology and by others in different biological contexts, but apparently forgotten by modern biologists for many years. Nevertheless, this concept finds an increasingly important role in the development of systems biology and bionetwork dynamics modeling, from phage lambda genetic switch to endogenous network for cancer genesis and progression. It is an ideal quantification to describe the robustness and stability of bionetworks. Here, I will first introduce five landmark proposals in biology on this concept, to demonstrate an important common thread in theoretical biology. Then I will discuss a few recent results, focusing on the studies showing theoretical consistency of adaptive landscape. From the perspective of a working scientist and of what is needed logically for a dynamical theory when confronting empirical data, the adaptive landscape is useful both metaphorically and quantitatively, and has captured an essential aspect of biological dynamical processes. Though at the theoretical level the adaptive landscape must exist and it can be used across hierarchical boundaries in biology, many associated issues are indeed vague in their initial formulations and their quantitative realizations are not easy, and are good research topics for quantitative biologists. I will discuss three types of open problems associated with the adaptive landscape in a broader perspective.

Introduction

With the emergence of systems biology, the demands on quantitative handling of data have become increasingly great (Hood, 2003; Auffray et al., 2009). There have been two general and opposite methodologies available that have been very helpful in facilitating the progress. The statistical analysis generally focuses on data sets themselves, supplemented by biological understandings (Russell and Aloy, 2008; Han, 2008). The mechanistic modeling, on the other hand, focuses on the working of the biological phenomena, at suitable levels of physics, chemistry, and biology, supplemented by statistical analysis (Li et al., 2004; Ptashne, 2004; Zhu et al., 2004; Auffray and Nottale, 2008). The purpose of the present overview is, however, on a middle-ground approach: a stochastic process approach that can smoothly connect the two known methodologies (Zhu et al., 2007). This middle-ground approach has been applied recently to small bionetworks such as genetic switches (Black et al., 2003; Zhu et al., 2004; Raser and O'Shea, 2005; Chabot et al., 2007), and to those of complex diseases such as cancer (Ao, 2007; Ao et al., 2008) and to evolutionary processes (Ao, 2005a; Kussell and Leibler, 2005). Even at metabolic and physiological level, it shows a promising potential in bringing out salient biological properties (Qian et al., 2003; Ao, 2005b; Elf et al., 2007; Lee et al., 2007; Scott et al., 2007; Ao et al. 2008b; Hanson and Schnell, 2008).

The central concept in such stochastic dynamics approach is the adaptive landscape. It differs from the direct real time calculation or simulation type (Gillespie, 2007) in that it aims to get middle and long time behaviors. It also differs from those focusing on moments (Gadgil et al., 2006) but leans towards those of nonequilibrium thermodynamics approaches (Qian, 2005). In addition, it differs from other more formal stochastic approaches in biology but more from a mathematical point of view (Malyshev and Pirogov, 2008). The powerful adaptive landscape concept was first proposed by a great biologist a long time ago (Wright, 1932). Similar ones have been repeatedly and independently proposed in biology since then. It lies at the core in the formulation of evolutionary dynamics, the foundation of biology. It not only corresponds to the energy function in physical science (Ao, 2008), but also is a Lyapunov function in control theory of engineering (Ao, 2005a; Haddad and Chellaboina, 2008), the two fields strongly associated with systems biology. The idea is also closely related to the mathematical theory of large deviation (Feng and Kurtz, 2006; Liu, 2008; Varadhan, 2008; Zhou et al., 2008). Nevertheless, this concept has suffered certain conceptual and theoretical problems, and has been nearly forgotten by modern molecular biologists. Recently, in studying the stability and robustness of phage lambda genetic switch, we accidentally discovered the key to solve these conceptual and theoretical problems, and has shown its usefulness in systems biology.

In the present overview, I will give a short presentation on this important recent progress. I will start with discussions on five known ideas on the adaptive landscape. Some of them have been very successful, whereas, others are still in the metaphoric stage. Then I discuss the central issue on the adaptive landscape: its existence and consistency in biological sciences and beyond. Furthermore, I will discuss associated open problems in general terms, and conclude in the end. I hope to be able to convey the importance and powerfulness of the adaptive landscape in net work modeling, and hope that the open problems will draw the attention of quantitative biologists.

Biological roots of adaptive landscape

In this section, I show the usefulness, metaphorically and/or quantitatively, of the adaptive landscape concept in various subfields in biology, manifested by its numerous independent originations. It captures an essential part of dynamics in biological processes.

Population genetics

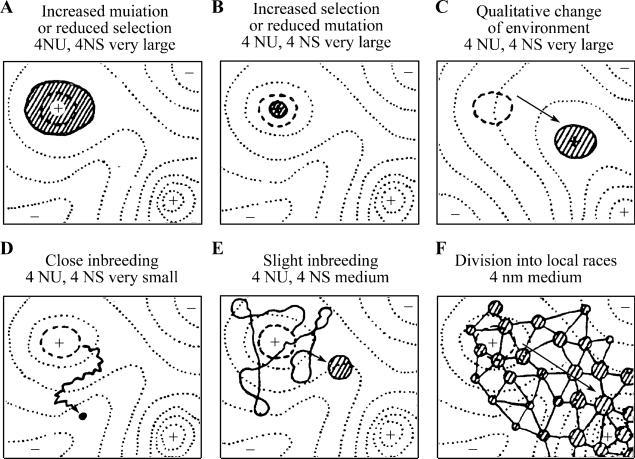
The concept of the adaptive landscape appears to be basic to describe evolutionary dynamics in biology. It has repeatedly and independently come up in various biological contexts. The most famous proposal, arguably the first, may be due to S. Wright, proposed in 1932 (Wright, 1932, 1988). There are several ways to express the key idea from today's perspective. Wright already used two opposite representations in his original proposal, in my opinion: the probabilistic distribution for an ensemble—a collection of large agents, and the trajectory for a single agent (Fig. 1). Such multiple representations have caused sustained confusion in the literature. In addition, Wright apparently recognized the generality of his proposal and had applied his concept far beyond the initial intended population genetics, a move seemed to have not been widely appreciated by biologists. I will discuss related issues in the next two sections, particularly that of a “flat” landscape situation. Nevertheless, such generality is vindicated by similar proposals from fields very far from population genetics, to be discussed in the rest of this section, and by its influence in other fields. For example, his concept of fitness landscape has been routinely used in statistical physics known as fitness landscape, though many researchers may not know its originator. Furthermore, conceptual problems encountered by Wright's adaptive landscape are also shared in different forms in other situations.

Fig. 1.

Wright's adaptive landscape schematically represented with a portion of the multidimensional landscape of genotypes of a single population with potential (fitness) contour, and his shifting balance theory. The most likely initial probability distribution of individual agents of a large population is indicated by the shaded area (A). There is a first increase in average fitness, represented by the shrinking shaded area (B). After some waiting time, the population transverses across a saddle configuration to another likely better fitness peak (C). C–E are the trajectory view of the same process to emphasize the small population limit, and F indicates the discreteness nature of space (from S. Wright, 1932).

Developmental biology

Independent of S. Wright, a similar concept was proposed by C.H. Waddington in 1940 and elaborated further in 1957 explicitly as a metaphor, at least so far, to understand the developmental process, known as developmental landscape (Waddington, 1957) (Fig. 2). I have not been aware of any realization of such developmental landscape directly corresponding to dynamical data. The interaction between developmental processes to both environmental and genetic factors can be discussed in Waddington's landscape (Waddington, 1957; Slack, 2002). The profound symmetry breaking idea embedded in such landscape captures an important aspect of developmental processes. It also vividly and graphically depicts the robustness and plasticity, the modern interpretations of Waddington's canonization.

Fig. 2.

Waddington's developmental landscape. The ball represents a cell, and the bifurcating system of valleys represents the bundles of trajectories in the functional space. Similar to Wright's shifting balance theory, such landscape indicates the possibility of transitions between different functional states (from C.H. Washington, 1957).

Gene regulation and genetic switch

In discussion of all-none genotypic phenomena, M. Delbruck (1949) proposed the possibility of bi-stable states in genetic systems (Fig. 3). He argued that such situations could be formed based on known physics and chemistry principles. A few years later, such phenomena were clearly observed experimentally (Novick and Weiner, 1957). Subsequently, an innovative and concrete molecular biological mechanism was proposed and further tested experimentally (Jacob and Monod, 1961). Nowadays, there exists an extensive quantitative and predictive study of such genetic switch systems (Ptashne, 2004; Zhu et al., 2004, 2007). The bio-switches have been one of the building elements in the study of systems biology. This is an example that once the dynamics is explicitly known, not only can the adaptive landscape be constructed quantitatively, but also various related questions, such as stability, robustness, etc., can be studied and compared with further experimental data.

Fig. 3.

Bi-stable genetic switch. The genetic switch idea was first proposed by M. Delbruck. Perhaps due to the brevity of his comment, or the obviousness (to him) of such an idea, M. Delbruck did not draw a bi-stable landscape. The landscape here is instead for phage lambda genetic switch, taken from Zhu et al. (2004). The regimes with dense equal potential lines are two attractive basins, the viable two stable states. The coordinates are the numbers of two proteins controlling the switch. It appears to be the first quantitative construction of such a landscape for genetic switch based on physics, chemistry, and biology principles (from Zhu et al., 2004).

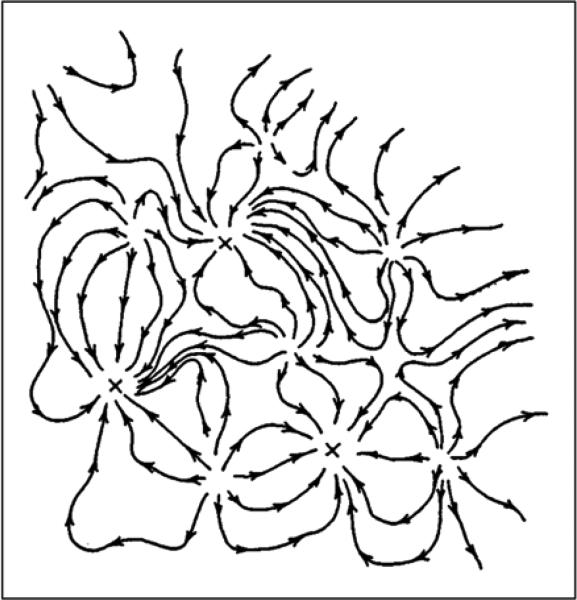
Neural dynamics and computing

An analog computer was proposed for neural dynamics in 1982 by J.J. Hopfield. It has inspired a tremendous amount of research activity, reviewed in perspective by Hopfield (1999). In this research program, the “energy” landscape can actually be constructed quantitatively for many interesting situations. A schematic illustration is given in Fig. 4. The stable states in the adaptive landscape represent the possible solutions from the neural network “computing”.

Fig. 4.

Hopfield's landscape for neural dynamics inspired computation in terms of the flow field. The stable points of the flow, marked by x, are possible answers. To initiate the computation, the initial location in state space must be given. A complex analog computer would have such a flow field in a very large number of dimensions (from Hopfield, 1999).

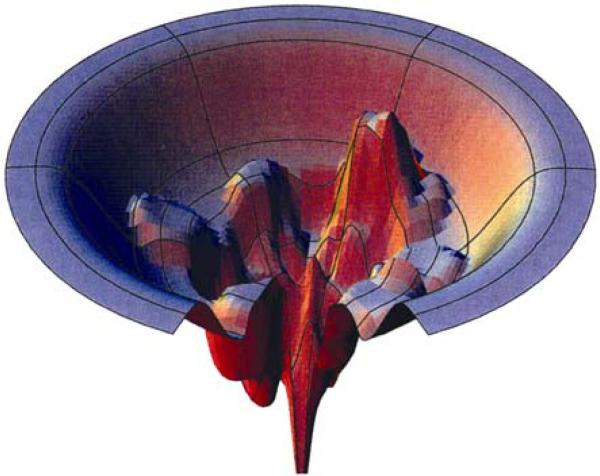
Protein folding

Perhaps the best-known recent example of landscape concept is from protein folding research, where such a concept has played both the metaphoric and quantitative roles during the past two decades. There is no doubt for researchers that such landscape exists. Nevertheless, computing it directly from the first principle in physics to detail the folding dynamics of amino acid chains has not been possible, not even in the foreseeable future with faster computers. A coarse-grain averaged landscape capturing the major features of folding dynamics is needed: both as a guidance to test hypotheses and as an intermediate quantitative realization. Indeed, such a landscape concept was proposed over 10 years ago (Bryngelson et al., 1995; Dill et al., 1995), which helps the researchers enormously to such extent that the protein folding dynamics has been announced as being solved by an optimistic group of experts (Fig. 5) (Service, 2008). It may be interesting to note that the various stages embedded in the funnel landscape corroborate well with the modular phenomena widely observed in biological systems.

Fig. 5.

Protein folding funnel landscape. It is a downhill run. A folding protein can follow many paths to its most energetically stable native (N) conformation (from Dill and Chan, 1997). More than ten orders of scale in energy have been involved, showing that such an idea can be used to link various hierarchical levels. The dynamical flow is somehow opposite to that in Waddington's developmental landscape.

Sampling of recent studies

An exhaustive list of all studies on dynamics in biology with adaptive landscapes is not possible in this short article, even though this concept has been somehow “forgotten” by modern molecular biologists. Instead, a few recent works in various subfields in biology are given here to indicate the usefulness of the concept.

The construction of an adaptive landscape for evolutionary dynamics in the wild has a few successful examples (Endler, 1988; Kauffman, 1993), where ecological factors are obviously important. The evolutionary history of a protein has been illustrated by its motion in a landscape constructible from experimental data (Lunzer et al., 2005). The possible evolutionary route for another protein was demonstrated in a similar fashion (Poelwijk et al., 2007). In additional to making use of landscape concept in genetic switch study (Zhu et al., 2004; 2008; Toulouse et al., 2005; Morelli et al., 2008; Yuan et al., 2008), similar investigations have been carried out into other important molecular biological processes, such as cell cycle (Wang et al., 2006; Zhang et al., 2006), signal transduction pathways (Lapidus et al., 2008), and cancer genesis and progression (Andrews 2002; Ao et al., 2008). The adaptive landscape immediately quantifies important concepts such as robustness and stability, and can be easily understood graphically. The quantitative realization of the concept has been further explored in discrete space (Walczak et al., 2005; Cao and Liang, 2008). The roles of such a concept have been quantitatively explored in various recent studies (Arnold et al., 2001; Holmstrom and Jensen, 2004; Waxman and Gavrilets, 2005; Hendry et al., 2006). Hence, it is evident that the adaptive landscape concept has been very useful both metaphorically and quantitatively in biology.

Major theoretical progress

Given such extensive support for the adaptive landscape concept and associated potential function, there is still a strong opposition on its usage ranging from biology, chemistry, and physics (Ao, 2005, 2008), and not necessarily confined to any particularly subfield in biology. Similar worries can be found in other fields (Ao, 2004). One would naturally wonder the reasons behind those numerous objections and rejections, which cannot be all trivial. Indeed, there were, and still are, a serious set of open problems. In this section, problems associated with the mathematical and conceptual side, its existence in a general setting, and in the domain of theoretical biology as redefined recently (Brenner, 1999), are discussed.

Origin of the problem and the current solution

It was already recognized shortly after Wright's proposal of adaptive landscape that there is a problem associated with a simple of view of evolutionary dynamics as fitness increasing process: always increasing mean fitness in the adaptive landscape. There are biologically meaningful and realizable cyclic dynamical processes in which the system can repeatedly visit its starting state infinitely. The challenge is to construct an adaptive landscape for such a process in a consistent manner. It was concluded that the fitness could not exist because its fitness should not increase when system comes back to its starting state. Because of lack of generic constructive method, this theoretical and mathematical problem remained open till 2004, to my knowledge. The challenge was formulated most explicitly for the case of limit cycle dynamics: finding such adaptive landscape with both local and global meanings. This challenge was taken up by me. It was found that a proper understanding of the adaptive landscape has to make use of the concept of probability or stochasticity, such as embedded in the so-called fundamental theorem of natural selection (Fisher, 1930; Li, 1955). After clarifying the controversies surrounding the fundamental theorem of natural selection and adaptive landscape, a consistent mathematical formulation for evolutionary dynamics was found (Ao, 2005), in which the quantified adaptive landscape as adaptive potential function is an integral part of the formulation. Specifically, the adaptive landscape for a limit cycle was explicitly and exactly constructed (Ao, 2005; Zhu et al., 2006; Wang et al., 2008). It was found that right at the limit cycle, the adaptive potential function takes the same value in the deterministic limit, a “flat” section of the adaptive landscape. The dynamics is still possible at the limit cycle because of the existence of a conservative dynamics, a part of dynamics largely overlooked in previous evolutionary studies.

Three independent dynamical elements of bionetworks

The general structure

Whereas it is not intended to give a full account of the construction, it will be helpful to show in more quantitative manner what the related quantities would look like. In a typical trajectory description, the dynamical equation would take the form of standard stochastic differential equation. With an appropriate time scale, it would read,

$${\partial }_{\mathrm{t}}\mathrm{q}=\mathrm{f}\left(\mathrm{q}\right)+{\mathrm{N}}_{\mathrm{I}}\left(\mathrm{q}\right)\zeta \left(\mathrm{t}\right),$$ (1)

where f and q are n-dimensional vectors and f a nonlinear function of q and possible time t, too. This implies that the network has n-node. The network variable of i-th allele is represented by q_i. Depending on the situation under consideration, the quantity q could, alternatively, be the populations of n species in ecology, the numbers of n proteins, or, the n coordinates in physical sciences. All quantities in this article are dimensionless: they are assumed to be measured in their own proper units. The collection of all q forms a real n-dimensional phase space. The noise ζ(t) is explicitly separated from the state variable to emphasize its independence, with l components. It is a standard Gaussian white noise function with zero average, and the covariance matrix element < ζ_i(t) ζ_j(t′) > = 2 δij (t – t′), and i, j =1, 2, ..., l. Here < > denotes the average over the noise variable { ζ(t) }, to be distinguished from the average over the distribution in phase space below. The variation is described by the noise term in Eq.(1) and the elimination and selection effect is represented by the force f. A further description of the noise term in Eq.(1) is through the diffusion matrix D(q), which is defined by the following matrix equation N_I^τ (q) N_I (q) = D(q) with N_I an n × I matrix and N_I^τ its transpose, which describes how the system is coupled to the noisy source. This is a generalization of the fundamental theorem of natural selection (Fisher, 1930) in population genetics. By construction, the diffusion matrix D is both symmetric and nonnegative. For the dynamics of the state vector q, all are needed from the noise term in Eq.(1). Nevertheless, it has not been clear how a consistent potential function, that is, a consistent adaptive landscape, could be constructed out of Eq.(1).

Recent study has shown that there is indeed a consistent way to construct the potential function from Eq.(1) (Ao, 2004; Kwon et al., 2005; Yin and Ao, 2006). We refer the readers to original articles for details. Here we simply quote the results. Eq.(1) can be transformed into the following equation,

$$[\mathrm{A}\left(\mathrm{q}\right)+\mathrm{T}\left(\mathrm{q}\right)]{\partial }_{\mathrm{t}}\mathrm{q}={\partial }_{\mathrm{q}}\psi \left(\mathrm{q}\right)+{\mathrm{N}}_{\mathrm{II}}\left(\mathrm{q}\right)\zeta \left(\mathrm{t}\right),$$ (2)

where the noise is from the same source as that in Eq.(1). The parameter denotes the influence of non-dynamical and external quantities. It should be pointed out that the potential function Ψ(q) may also implicitly depend on time t, if the original f does. The friction matrix A(q) is defined through the following matrix equation N_II^τ(q) N_II(q) = A(q). The anti-symmetric matrix T(q) represents the dynamics that would not change the value of Ψ(q). Those matrices are related to the diffusion matrix via [A + T ] [D + Q] = 1, and

$$[\mathrm{A}+\mathrm{T}]\mathrm{D}[\mathrm{A}-\mathrm{T}]=\mathrm{A},$$ (3)

with Q another anti-symmetric matrix. The connection to the deterministic force f (q) is via an anti-symmetric matrix equation

$${\partial }_{\mathrm{q}}\times \left\{[\mathrm{A}\left(\mathrm{q}\right)+\mathrm{T}\left(\mathrm{q}\right)]\mathrm{f}\left(\mathrm{q}\right)\right\}=0,$$ (4)

with ∂_q × the wedge differentiation in higher dimensions and

$${\partial }_{\mathrm{q}}\psi \left(\mathrm{q}\right)=[\mathrm{A}\left(\mathrm{q}\right)+\mathrm{T}\left(\mathrm{q}\right)]\mathrm{f}\left(\mathrm{q}\right).$$ (5)

Thus, Eq.(4) is precisely the potential function condition. It can be found via the integration over Eq.(5), independent of the integration routes connecting initial and final points. All A, T, Q, as well as the potential function Ψ(q) are uniquely determined by the diffusion matrix and the deterministic force f(q). It has been shown that the potential function Ψ(q) indeed plays precisely the role of adaptive landscape, as it has the role of “energy” function in physical sciences, and thus quantifies adaptive landscape, such as those in Figs. 1–5.

Because of the constraint between the noise and the diffusion matrix, there are only three independent dynamical quantities in Eq.(2): the potential function, the friction or diffusion matrix, and the anti-symmetric matrix represented by T. In terms of probability distribution function ρ(q, t) in the n-dimensional state space, the dynamics equation will take the form of the Fokker-Planck equation, or, in the discrete space situation, the Master equation. In its abstract form, such equation can be written as

$${\partial }_{\mathrm{t}}\rho (\mathrm{q},\mathrm{t})=\mathrm{L}(\mathrm{D},\mathrm{Q},\psi \left(\mathrm{q}\right))\rho (\mathrm{q},\mathrm{t}).$$ (6)

A technical discussion of three such independent dynamical elements can be found in Ao (2008).

An example

In one dimension, the above construction is relatively easy, because the anti-symmetric matrix does not exit. Given the deterministic force f(q) and diffusion constant (not a matrix function), the potential function can be analytically obtained, already known to physicist Langevin 100 years ago, and its additional mathematical subtle points have been fully recognized since 1950's. A related discussion can be found in standard references on stochastic differential equations (for example, references cited in Ao et al., 2007). The real important situation is in higher dimensions, where there is no time reversibility, or the detailed balance condition is absence. It can be illustrated with a generic two-dimensional case, which would include realistic situations such as phage lambda genetic switch. The following presentation closely follows that in Ao (2005b).

By introducing an auxiliary matrix G = D + Q = 1 / [A + T], the equations corresponding to Eq.(3) and (4) are,

$$\mathrm{G}+{\mathrm{G}}^{\tau }=2\mathrm{D},$$ (7)

and ∂_q × {G^–1 f (q)} = 0. In many realistic situations, such as in the phage lambda genetic switch, functions involved are smooth, which allows the possibility to use the gradient expansion, which turns the differential equations of Eq.(5) into an algebraic equation. For the first order, in terms of Jacobian of deterministic force f (q), which defines as, F₁₁ (q) = ∂₁ f₁ (q), F₁₂ (q) = ∂₂ f₁ (q), F₂₁ (q) = ∂₁ f₂ (q), F₂₂ (q) = ∂₂ f₂ (q), the potential condition becomes very simple,

$$\mathrm{G}{\mathrm{F}}^{\tau }-\mathrm{F}{\mathrm{G}}^{\tau }=0.$$ (8)

Thus, the auxiliary matrix G has been readily solved analytically and explicitly in this two-dimensional case under the gradient expansion: three linear equations in Eq.(7) and one linear equation in Eq.(8). Higher order gradient expansion is a successive procedure of solving such linear algebraic equations to the desired order. Once G is known, the potential function is Ψ(q) = ∫ dq[G^–1f(q)].

In my view, a consistent theoretical formulation has been here since 2005 (Ao, 2005a): major theoretical and mathematical issues associated with such stochastic evolutionary dynamics are solved, with respect to the construction (Ao, 2004; Kwon et al., 2005), the connection to other stochastic methods (Yin and Ao, 2006; Ao et al., 2007), and in relation to thermodynamics (Ao, 2008), along with some practical computing techniques (Ao, 2004; Kwon et al., 2005). Nevertheless, there are still theoretical issues meriting further discussions.

Adaptive landscape beyond its metaphoric role

The most clearly formulated “counterexample” in the literature against adaptive landscape was on limit cycle (Ao, 2005a). Other voiced objections, known to me, are all verbal and vague. For some to be valid, it would be helpful to formulate them explicitly and quantitatively. If my assessment of the situation is correct, based on recent theoretical constructions (Ao, 2005; Kwon et al., 2005; Yin and Ao, 2006) and applications to various concrete biological problems as discussed above, the answer to the above question is indeed positive on the theoretical level.

What is the effect of noise or drift?

It has been noticed that there are some situations where the landscape seems ill-defined (Ao, 2005a; Poelwijk et al., 2006). From the general theoretical framework (Ao, 2004; Kwon et al., 2005; Yin and Ao, 2006), a sure way to generate such uncertainty is in the no-noise limit. Mathematically, this limit is singular, that is, a procedure for this limit has to be specified. For completely deterministic dynamics, a potential function not only exists, and there can be infinitely many of them, perhaps more than what one would like to have. The noise or drift, including both genetic and environmental, is shown to be able to affect the adaptive landscape in a profound and quantitative manner: it is the quantity needed to make the adaptive landscape unique in a given situation, and can determine the outcome of dynamics. As discussed recently (Ao, 2004; Kwon et al., 2005; Yin and Ao, 2006), in the continuous trajectory representation of the dynamics, evolutionary dynamics can be uniquely decomposed into four components, with adaptive landscape, noise, adaptive (non-conserving) and conservative dynamics. The noise is connected to the adaptive dynamics by the F-theorem, an idea already embedded in Fisher's fundamental theorem of natural selection (Fisher, 1930; Li, 1955). Thus, there are actually three independent dynamical elements for a general evolutionary process. In the probability distribution representation of the dynamics such as in the form of Fokker-Planck equation (Ao, 2004; Kwon et al., 2005; Yin and Ao, 2006) or discrete Master equation (Ao, 2008), three independent dynamical elements indeed completely specify the dynamical equation. In particular, a complete evolutionary dynamics with “flat” adaptive landscape is possible. This way of decomposing dynamics has also been discussed in detail qualitatively in literature, though the conservative dynamics has not been explicitly expressed (Ao, 2005a). There is an interesting analogy here. I recall the situation of the fundamental theorem of arithmetic in high school mathematics: every natural number greater than one can be uniquely written as a product of prime numbers. Parallel to it, the present unique decomposition in evolutionary dynamics may be named the fundamental theorem of dynamics.

Evidently, the noise, variation, or drift is indispensible in bionetwork dynamics. An important difference between the fundamental theorem of natural selection (Fisher, 1930) and its recent extension as the F-theorem (Ao, 2005a) should be pointed out here. In the formulation of F-theorem no reference to adaptive potential function (or fitness landscape) is used. This suggests that the F-theorem is valid for any shape of adaptive landscape, near or far away from a local peak. In particular, this would imply that it applies to the flat landscape too. When applying it to a stationary state near a peak, which would be reached after a perturbation if waiting for sufficiently long time, there should be no change in average value of potential function, whereas, a finite variation would exist. This appears to be what has been observed experimentally, and is consistent with the F-theorem in the light of the present discussion, but has been interpreted by many biologists as evidence against the fundamental theorem of natural selection.

To summarize the situation in theoretical biology, there exists now a consistent and quantitative formulation of dynamics of any bionetwork, so long as its mathematical description is in the form of usual stochastic processes. The adaptive landscape, quantified as a potential function, has been naturally incorporated, which gives a graphical view on the global dynamics.

Open questions in broad perspective

There are other unclear and difficult issues associated with the concept of adaptive landscape. In this section, three levels of problems are classified, and the third one is of major concern to working quantitative biologists.

Conceptual domain

The first type is at a philosophical and linguistic level. It is known that there exist numerous definitions of fitness and associated adaptive landscape. Even if some of them may be equivalent to each other and may be correct, it cannot be so for all of them. This problem has already been noticed long ago (Ao, 2005), and its proper discussion is beyond the scope of the present article, though a critical evaluation of those in literature is clearly needed. Nevertheless, one cannot dispel the feeling that many discussions on this issue in the literature, by biologists, philosophers, and historians, indicate that most traditional biologists have not worked out of the shadows of past giants (Haldane, 2008).

The existence of adaptive landscape implies a profound concept in nature: an order or a priority in any dynamical process. This quantity is obviously connected to the Hamiltonian, or energy function, in physical sciences (Ao, 2005a, 2008). In addition, the discussion in the previous section demonstrated an intrinsic connection between the adaptive landscape and the noise or drift, which appears to be most eminent and distinct in the evolutionary dynamics, exemplified by S. Wright and R.A. Fisher. Further explorations on the implications of those important relationships are desirable at the level beyond biology, to lay a firm theoretical foundation for systems biology in particular and biology in general.

Theoretical domain

The second type of problems is in the theoretical biology domain: whether or not the adaptive landscape necessarily exists in the general framework of theoretical biology. Various related issues were discussed below. When the dynamics is known quantitatively, generically three independent dynamical components would be uniquely found, built upon the insights of Wright and Fisher. The adaptive landscape quantified as the potential function is one (Ao, 2005a, 2008). If this problem is not addressed properly, the debate on adaptive landscape would easily persist indefinitely, and its usage in real problems will be greatly reduced. One cannot dispel the feeling that this problem has not been considered seriously enough by theoretical biologists, and it is not the job of philosophers and historians unless their hands become wet.

Another important issue is the discrete versus continuous descriptions, exemplified by a current false prevalent argument that the Master equation is more fundamental in biology than the Fokker-Planck equation (Mehta et al. 2008). The fact is that the Master equation has usually been derived based on Fokker-Planck equation. It is true that for a given biological problem appropriate tools are needed: nobody wants to describe a bacterium starting from superstrings even if such theories exist. In the domain where two different methods are valid the same prediction should be expected. If not, there must be an inconsistency in theoretical treatment, which needs to be located. The possibility of generating very different results from apparently the same equation has been well known (Ao, 2007). The associated issue consists of another open problem.

The importance of potential function has been known in another important field, the dynamical systems theory for nonlinear systems. There has been a debate on the general existence of potential function, nevertheless, in the form of gradient systems versus vector field flow systems. To my best knowledge such debate has not been closed in mathematics (Holmes, 2005). The methodology reviewed here appears to provide a key insight to close this debate in dynamical systems.

The implications and applications of the novel construction of Lyapunov function in control theory of engineering have not yet been explored (Ao, 2005a; Haddad and Chellaboina, 2008; Milton et al., 2008).

Empirical domain

The third type is the concern of practicing biologists: how to construct and to use the adaptive landscape. For a given problem, even if all agree on the existence of adaptive landscape, its exact construction and analysis can be a daunting task. The protein folding problem discussed above is one such ideal example (Frauenfelder et al., 1991; Bryngelson et al., 1995; Dill et al., 1995; Wade, 2005). Whereas, the funnel type landscape is quantitatively crude and metaphoric, it provides a global picture on how folding dynamics are unfolding (Frauenfelder et al., 2006), and, better solutions and a quantitative understanding are reached under its step-by-step guidance (Thomas et al., 2005; Service, 2008).

In situations where the construction of adaptive landscape is still unclear, such as the developmental landscape, the metaphoric nature of the concept has been enormously helpful (Wright, 1988; Slack, 2002; Lunzer et al., 2005). Even in this situation, thanks to many biologists’ decades of dedicated study, a complete quantitative set is close to being ready for meaningful and predictive mathematical modeling (Oliveri et al., 2008). In cases such as phage lambda genetic switch, the landscape can be constructed quantitatively, which leads to solution of outstanding stability puzzle, along with quantitative predictions (Zhu et al., 2004, 2007). The constructed landscape can also be useful in improving the existing stochastic simulation methods (Hemberg and Barahona, 2007). Thus, new techniques for its construction are needed.

The most difficult situations are those where the metaphor is not enough and a quantitative description is immediately needed, but its clear construction is unknown at the beginning. The relevant construction has to be found by trial and error in research. This has been the situation encountered in population genetics (Endler, 1985), and is typical in biology, such as in the cancer dynamics (Ao et al., 2008). This may not be surprising. The examples above amply illustrate the hierarchical structure in biology: there are many hierarchical layers in the gap between the geno and pheno types (Ellegren and Sheldan, 2008), in addition to ecological and environmental factors. It is seldom that theoretical models work at first try, particularly those in population genetics striving to span over this huge hierarchical gap. I certainly share many of the skeptic's concerns on the use of adaptive landscape right at the genetic level. Such models may well be oversimplified, as already discussed by Haldane in a similar situation (Haldane, 2008), but it is not the reason to eliminate them, because it gener ates the information for improvement. Wright's adaptive landscape is, however, a unifying quantity applicable to multiple hierarchical layers. Evidently, practicing biologists, I included, have to study this hard in the foreseeable future.

Conclusions

Based on the above presentation, it appears that the adaptive landscape is one of the central concepts in the modeling of bionetwork dynamics. It can be used, and has been used, to describe bionetwork dynamics across many hierarchical layers. Open problems at all levels still exist. They serve to attract the attention of more quantitative biologists to move the field forward.

“There may still be a use for people who believe there is more in life and in biology than the applied biochemistry of the nucleic acids, always provided that they pay due regard to the man who has been trained to wield modern methods with precision and apply modern logical and mathematical facilities to the interpretation of his results.”

Franck Macfarlane Burnet, 1899 1985