Comparison of β-Sheets of Capped Polyalanine with those of the Tau-Amyloid Structure VQIVYK and VQIINK. A Density Functional Theory (DFT) Study

Abstract

We present ONIOM calculations using B3LYP/d95(d,p) as the high and AM1 as the low level on parallel β-sheets containing from two to ten strands of Ac-VQIVYK-NHMe, and Ac-VQIINK-NHMe, as well as, both parallel and antiparallel Ac-AAAAAA-NHMe. We find that the first two sequences form more stable sheets due to the additional H-bonding between the Q’s in the side chains of both and the N’s in the side chain of VQIINK-NHMe. However, the H-bonds in the amyloid chains are significantly weakened by attractive strain, which prevents all the interstrand H-bonds from achieving their optimal geometries simultaneously and requires high distortion energies for the individual strands in the sheets. The antiparallel Ac-AAAAAA-NHMe’s are generally more stable and more cooperative than the parallel sheets, principally due to the higher distortion energies of the latter.

INTRODUCTION

Amyloid fibrils can be associated with several diseases, either as a cause or a symptom. In Alzheimer’s disease, two different kinds of misfolding/aggregation occur: 1) Plaques of aggregated β-sheet-like proteins form, and 2) the peptide, tau, which normally promotes aggregation of tubulin to form the natural tubular material of neuron fibrils, instead forms other aggregates which result in neurons losing their neuron fibrils, and thus their function.¹

Amyloid fibrils result from the association of multiple individual peptide units into large clusters. The formation of these fibrils resembles a crystallization in one dimension, In fact, short peptides containing the key sequences of 4–6 residues necessary for the formation of several amyloids have been crystalized and subsequently used to seed amyloid formation from the relevant proteins,² and some of these same sequences when spliced into other proteins cause these to form amyloids.³ We have reported a preliminary communication detailing DFT calculations that show how the glutamine (Q) residues in one of these peptide sequences ³⁰⁶VQIVYK³¹¹, essential for amyloid formation from the protein, tau, contribute to the tendency of a small peptide of this sequence to form crystals and the tendency of tau to form amyloids.⁴ Another peptide sequence, ²⁷⁵VQIINK²⁸⁰, which for which no crystal structure has been reported, also causes fibril formation from tau.^5,6 The secondary structural motif most favorable for the association of many individual peptides should be the β-sheet, which can occur with adjacent peptide strands running either parallel or antiparallel. The crystal structure of the VQIVYK peptide shows it to form a pair of infinite parallel β-sheets that are associated via interdigitating nonpolar side chains.² A second polymorph was found that involves differences in the interdigitating side chains, but not the β-sheets. Tycko has reported that other amyloids assume in register β-sheets⁷ and Vaden has reported β-sheet formation in the dimer of tau in the gas phase.⁸

The above suggests two obvious questions: 1) why do some, but not all, peptide sequences easily form amyloid structures; and, 2) what physical characteristics of the residues in these sequences contribute to these tendencies? We have made some suggestions in our preliminary communication⁴ and we have very recently compared the energetics for the formation of the various possible β-sheets of a polyglycine hexapeptide.⁹ In this paper we consider this problem in much more detail by comparing association of the capped acetylVQIVYKmethylamide and acetylVQIINKmethylamide sequences with that of the all alanine, acetyl(A)₆methylamide, in both parallel and antiparallel forms. We shall show the complex situation to involve the difficulty of forming multiple optimal H-bonds between entities due to a phenomenon that we have called attractive strain,¹⁰ which is manifest in both experimental and theoretical studies on both biochemical and other self-assembling systems. Although obvious, one might note that since these amyloids are solid, they must be insoluble in their in vivo environment, which is presumably aqueous. Aqueous solvation energies of these sheets is, therefore, not relevant.

Among protein secondary structural motifs, β-sheets generally form in two distinct patterns. Antiparallel β-sheets most often occur when a polypeptide chain bends via a hairpin or turn and forms H-bonds to residues that are not very distant in the primary sequence of the chain. Since the peptide connectivity direction has made a 180 degree turn at the hairpin, the direction of the connectivity between the H-bonding sections becomes antiparallel. Antiparallel β-sheets can form from the interactions of multiple peptide strands, as well. Parallel β-sheets cannot form between proximate residues on the same strand. They can form between different peptide strands. Both antiparallel and parallel β-sheets can form from distal sections of the same peptide strand. The preference for antiparallel or parallel β-sheet formation can play an important role in protein structure. For example, amyloids generally require the formation of β-sheet-like structures that contain many strands. Crystal structures of amyloid-like structures can contain either the parallel or antiparallel motif.² However, large antiparallel β-sheets formed from one continuous strand may disfavor amyloids.

In this paper, we examine the interaction energies for both parallel and antiparallel β-sheets formed from two up to 10 strands of the capped peptide acetyl(Ala)₆NHMe and compare them with parallel β-sheets of two sequences from tau which are known to form amyloids, VQIVYK and VQIINK. Earlier DFT calculations on β-sheets have focused on antiparallel glycine-like fragments,^11–13 which tend to form an almost planar, or a rippled structure in addition to the pleated-sheet structure typical of most β-sheets.⁹ In another interesting paper, Perczel has explored the relative energies of b-sheets compared to other secondary structural motifs for short polyalanines containing up to 8 residues per strand.¹⁴

METHODS

We used the ONIOM^15,16 method as programmed in the Gaussian09¹⁷ suite of computer programs. ONIOM divides the system into up to three segments which can be treated at different levels of calculational complexity. Thus, one can treat the essential part of the system at the high level, while the less critical parts of the system might be calculated at the medium or low level. For this study we only used two levels (high and medium). We treated the backbones of the peptides (equivalent to a corresponding peptide containing only glycines) and the glutamine (Q) and asparagine (N) residues at the high level, with only the side chains that distinguish the other different residues from that of glycine at the medium level. The high level used hybrid DFT methods at the B3LYP/D95(d,p) level. This method combines Becke’s 3-parameter functional,¹⁸ with the non-local correlation provided by the correlation functional of Lee, Yang and Parr.¹⁹ In the ONIOM method, there are unsatisfied valences in the high level at the interface between it and medium level. These valences were satisfied by using the default method of capping them with a hydrogen atom in the direction of the connecting atom in the medium level with a C-H distance of 0.723886 times the C-C distance. We used the AM1²⁰ semiempirical molecular orbital method for the ONIOM medium level.

All geometries were completely optimized in all internal degrees of freedom and vibrational calculations performed to assure the geometries are true minima on the PESs for sheets containing up to five strands as there are no imaginary vibrational frequencies, and to obtain the vibrational frequencies used to calculate the enthalpies at 298K. The enthalpic corrections for sheets containing more than five strands was extrapolated from the data for three to five strands which increased linearly with the number of strands.

In a previous study of five 17-amino acid peptides,²¹ we found little difference in relative energies between this procedure and another where the side chains (in this case, the methyls) were subsequently optimized using DFT, with the (previously optimized) peptide chain held fixed. The current procedure also gave relative energies that agreed well with complete DFT optimizations for a series of five small 3₁₀-helical peptides.²² We have used this procedure with success for several previous studies of peptide structures,^4,22–26 and have shown it to compare favorably with other functional/basis set combinations for calculations n the gas phase water-dimer.²⁷

The counterpoise correction (CP) for basis set superposition error (BSSE) has been applied to all interaction energies and enthalpies using the single point a posteriori procedure,^28–31 as optimization of such large structures on a CP-corrected surface³² would have been too computationally intensive and the ONIOM and CP-optimization cannot be performed simultaneously using the GAUSSIAN 09 program. Balabin has recently emphasized the importance of BSSE correction for biochemical and other calculations.^33,34

Since the model for these calculations is solid-state, no solvation energies have been calculated and the lysine residues are assumed to be neutral to avoid proximate positive charges.

RESULTS AND DISCUSSION

Figure 1 and table 1 present the interaction energies for parallel and antiparallel β-sheets containing from two to 10 strands of the four hexapeptides capped with acetyl and NHMe. We have only considered the parallel forms for the amyloid forming sequences, but both forms for the polyalanines. For the latter, the antiparallel sheets are more stable for all of the sets of isomeric structures when corrected for BSSE using the counterpoise correction (CP), however, the parallel forms provide a better direct comparison to the amyloid sequences.

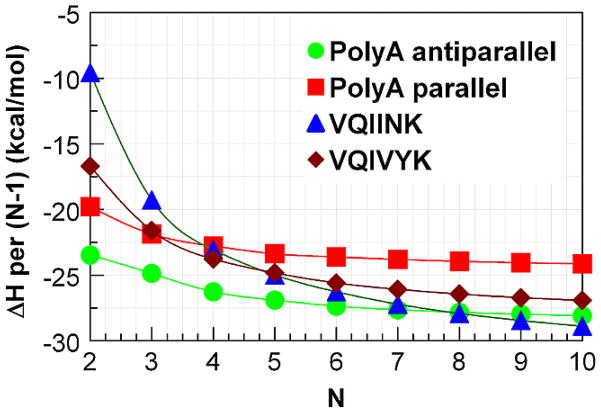
Figure 1.

Enthalpy of interaction divided by the number of interactions between adjacent strands (N-1) in a β-sheet containing N strands.

Table 1.

Energies for (Ac-VQIVYK-NHMe)_N, (Ac-VQIINK-NHMe)_N and parallel and anti-parallel (Ac-Ala₆-NHMe)_N β-sheets in kcal/mol.

N	H-bonds	ΔE/H-bond (CP)	Distortion/N	ΔE/H-bond (CP) from optimized strand	Δ/H-bond (CP) from optimized strand
VQIVYK
2	8	−5.91	13.54	−2.52	−2.09
3	16	−6.22	16.35	−3.16	−2.70
4	24	−6.34	17.40	−3.44	−2.97
5	32	−6.38	17.89	−3.59	−3.10
6	40	−6.42	18.24	−3.68	−3.20
7	48	−6.46	18.57	−3.75	−3.26
8	56	−6.48	18.80	−3.79	−3.30
9	64	−6.50	18.98	−3.83	−3.34
10	72	−6.52	19.16	−3.86	−3.37
VQIINK
2	9	−6.06	20.35	−1.54	−1.06
3	18	−6.15	21.25	−2.61	−2.14
4	27	−6.32	22.13	−3.04	−2.56
5	36	−6.39	22.50	−3.27	−2.78
6	45	−6.47	22.92	−3.41	−2.92
7	54	−6.55	23.34	−3.52	−3.02
8	63	−6.59	23.57	−3.60	−3.10
9	72	−6.63	23.74	−3.66	−3.16
10	81	−6.65	23.82	−3.71	−3.21
P
AAAAA
A
2	7	−5.95	8.89	−3.41	−2.83
3	14	−6.13	11.34	−3.71	−3.12
4	21	−6.16	12.18	−3.84	−3.25
5	28	−6.19	12.70	−3.92	−3.34
6	35	−6.20	13.06	−3.96	−3.37
7	42	−6.21	13.31	−3.99	−3.40
8	49	−6.22	13.50	−4.01	−3.42
9	56	−6.22	13.65	−4.03	−3.44
10	63	−6.23	13.76	−4.04	−3.45
AP
AAAAAA
2	7	−5.29	4.98	−3.86	−3.35
3	14	−6.02	9.00	−4.09	−3.55
4	21	−6.19	9.98	−4.29	−3.75
5	28	−6.29	10.67	−4.38	−3.84
6	35	−6.33	10.99	−4.45	−3.91
7	42	−6.37	11.32	−4.48	−3.95
8	49	−6.39	11.53	−4.51	−3.98
9	56	−6.41	11.71	−4.53	−4.00
10	63	−6.43	11.83	−4.55	−4.01

Parallel sheets

The two amyloid hexapeptides (VQIVYK and VQIINK) can only have H-bonding interactions between the side chains of the Q’s and N’s in adjacent strands in parallel β-sheets. In antiparallel sheets the Q’s and N’s in adjacent strands will extend on opposite sides of the sheet (precluding H-bonding between these side chains). We compare these sheets of these two hexapeptides (shown in figures 3 and 4) with those of analogous hexaalanine peptides (shown in figures 5 and 6) to highlight the differences in the energetics and structures of the amyloid forming sheets from the simple ployalanine (polyA) sheets.

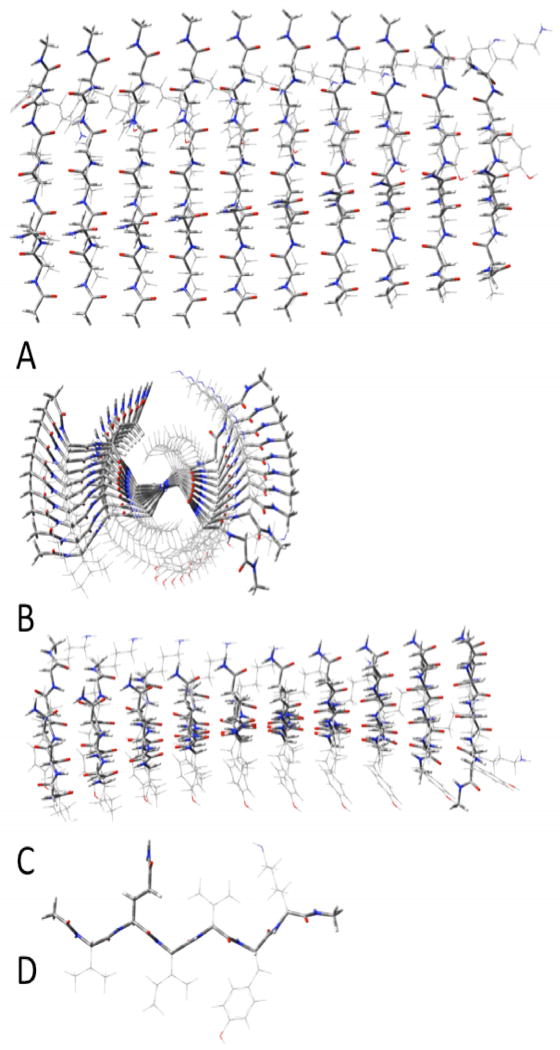
Figure 3.

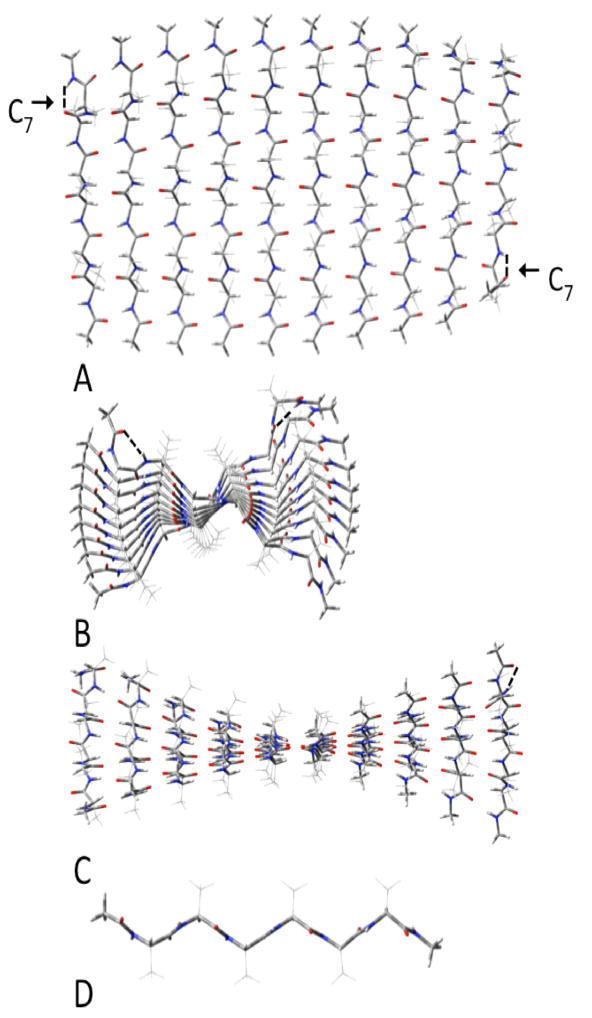
Parallel β-sheets of (acetylVQIVYKmethylamide)₁₀. A:top view; B: side view; C: end view; D innermost single strand.

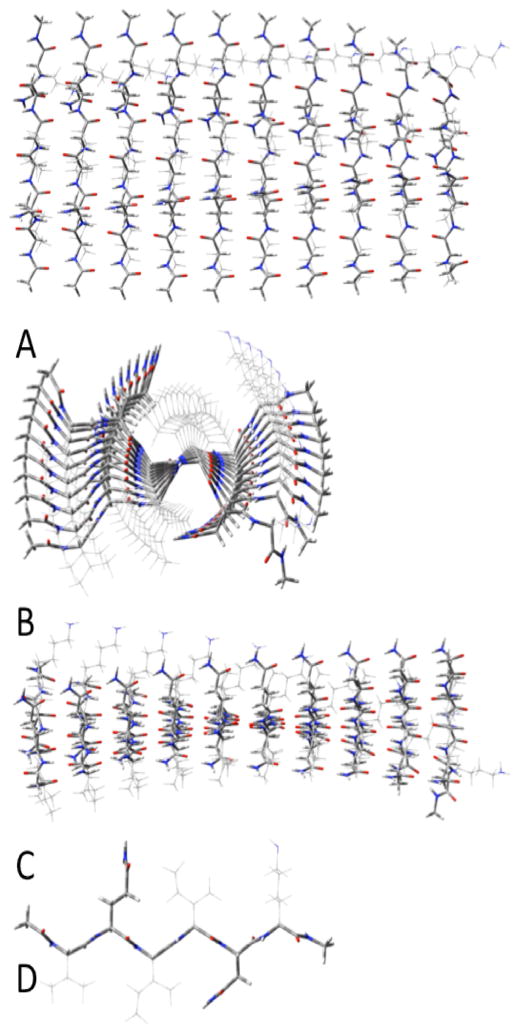
Figure 4.

Parallel β-sheets of (acetylVQIINKmethylamide)₁₀. A:top view; B: side view; C: end view; D innermost single strand.

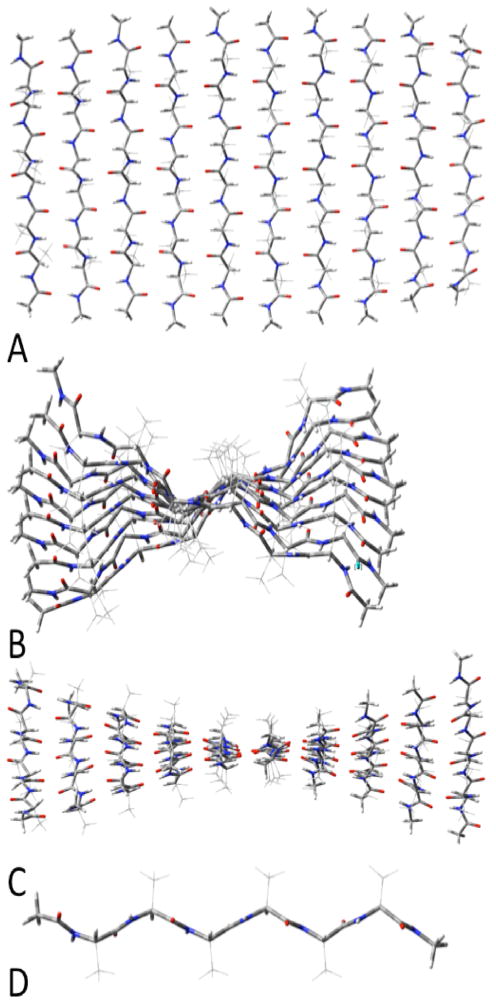
Figure 5.

Antiparallel β-sheets of (acetylAAAAAAmethylamide)₁₀. A:top view; B: side view; C: end view; D innermost single strand.

Figure 6.

Parallel β-sheets of (acetylAAAAAAmethylamide)₁₀. A:top view; B: side view; C: end view; D innermost single strand. The C₇ intrastrand H-bonds are noted at the top left and bottom right of A.

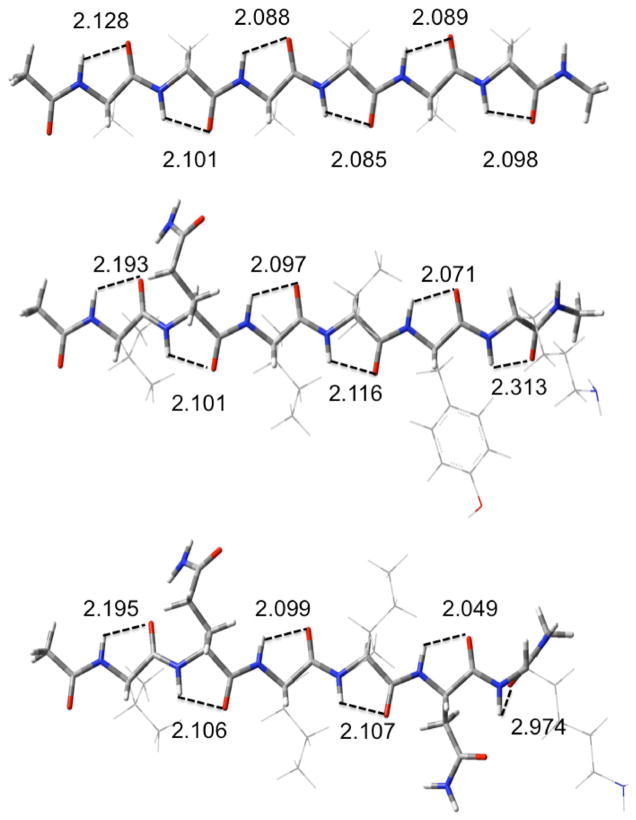
We decompose the interactions within the sheets into the H-bonding and distortion energies (see table 1) as we have recently done in our study of polyglycine β-sheets.⁹ We define the H-bonding energies as the interactions between the strands in the geometries of the optimized sheet, and the distortion energies as the energy required to change the geometry of the completely relaxed extended strand to that it assumes in the optimized sheet. This procedure has the advantage of allowing different conformations of the individual strands to be considered as starting points. The differences in energies between any arbitrary conformation of the free strand and the completely relaxed extended strand can easily be calculated and added as a constant. The structures of the extended strands contain slightly cooperative C₅-intrastrand cyclic H-bonds (indicated in figure 2), as previously reported.^35–39 The H-bonding interaction energies will not change, so the large aggregates do not need to be reoptimized. As seen from table 1, the CP-corrected H-bonding energies per H-bond become monotonically more negative as the number of strands increases for all cases studied. Those for the two forms of polyalanine have smaller H-bonding interactions than does (Ac-VQIINK-NHMe)_N for all values of N and for (Ac-VQIVYK-NHMe)_N for all values of N>2. However, the parallel polyalanine has individual H-bonding interactions that are slightly stronger than (Ac-VQIVYK-NHMe)_N for N=2, while the antiparallel form has weaker H-bonds for this value of N. This behavior is due to the formation of C₇-cyclic intrastrand H-bonding interactions in the parallel polyalanine sheets which lowers the energy of (only) these strands compared to the fully extended structure. This interaction occurs only in both of the terminal strands and can be seen in upper left and lower right corners of figure 6. As the sheets get larger, the relative contribution of this anomaly to the overall energetics decreases. We made many unsuccessful attempts to find an optimized structure without the C₇ interactions. The low cooperativity of the parallel polyalanine compared to both of the others causes it to reach the same asymptotic limit for ΔE of about −6.3 kcal/mol per H-bond, while antiparallel reaches one of about −6.5 kcal/mol. (Ac-VQIVYK-NHMe)_N, which has eight H-bonds between adjacent strands, reaches a limit of −6.6 kcal/mol/H-bond, while that for (Ac-VQIINK-NHMe)_N, with nine H-bonds between adjacent strands, reaches 6.7, due to the added cooperativity of the H-bonds between the side chains of Q and N. The distortion energies are expressed per strand (rather than per H-bond). These are consistently lowest for the antiparallel form of polyalanine. The distortion energies are significantly higher for (Ac-VQIVYK-NHMe)_N and (Ac-VQIINK-NHMe)_N. However, one must note that while the distortions for two forms of the polyalanines refer to the same optimized single strand, the optimized single strands for the two other aggregates have different geometric properties due to the different side-chains, as seen from figure 2.

Figure 2.

Structures of optimized extended single strands: Acetyl(A)₆NH₂CH₃ (A); acetylVQIVYKNH₂CH₃ (B);AcetylVQIINKNH₂CH₃ (C). C₅H-bond distances (Angstroms are indicated.

The difference in the energies per H-bond, taken together with the fact that (Ac-VQIVYK-NHMe)_N has one and (Ac-VQIINK-NHMe)_N two more H-bonds per adjacent interstrand interaction clearly favors the amyloids, while the distortion energy per strand works against them. The amyloid structures have consistently 4 to 5 kcal/mol more distortion per strand than the parallel, and 7–8 kcal/mol per strand more than the antiparallel polyalanine, as might be expected since the stronger attractive interactions will allow a tolerance of greater distortion. The ΔH/H-bond for the amyloids are the smallest of the structures. We attribute this observation to what we have called ‘attractive strain’ which occurs due to the difficulty of forming optimal H-bonds in several places simultaneously.¹⁰ However, the extra H-bonds per interaction more than compensate for the smaller ΔH’s, which make the amyloid structures the more stable.

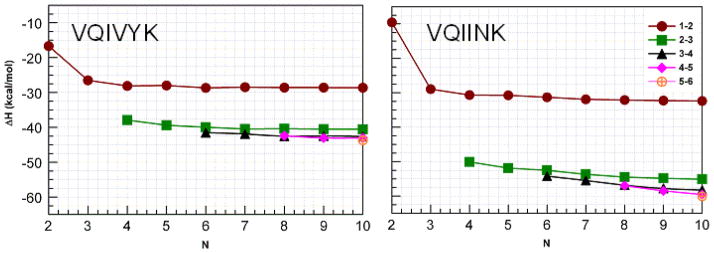
Figures 7 and 8 illustrate the interaction enthalpies between different types of interactions between adjacent strands for VQIVYK and VQIINK (figure 7) and the two forms of polyA (figure 8) in the manner we have previously used for other studies.^4,9,40,41 Comparison of VQIVYK with VQIINK reveals that the interaction enthalpy for the strands at the edge of the sheet (1–2) reach a similar asymptotic value for both structures. However, the interactions nearer the center of the sheets are much stronger for VQIINK. This behavior suggests that the N-N interactions in the side chains do not contribute substantially to the interactions between the strands at the ends of the sheets, but contribute much more substantially to the inner interactions.

Figure 7.

Interaction enthalpies for groups of H-bonds organized by chain length for sets of H-bond types indicated by the symbols. Note that the enthalpies for the first (1–2) and last (9–10) sets of H-bonds are the same as are the second (2–3) and penultimate (8–9) sets of H-bonds so interactions between only the first of each kind are plotted. Note that VQIVYK has eight H-bonds per set, while VQIINK has nine.

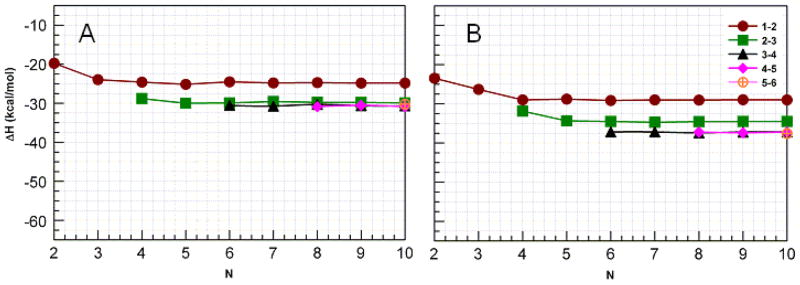
Figure 8.

Interaction enthalpies for groups of H-bonds organized by chain length for sets of H-bond types indicated by the symbols in β-sheets of parallel (A) and antiparallel (B) polyalanine. Note that the enthalpies for the first (1–2) and last (9–10) sets of H-bonds are the same as are the second (2–3) and penultimate (8–9) sets of H-bonds so interactions between only the first of each kind are plotted. There are seven H-bonds in each set.

For the polyA’s, H-bond cooperativity is evident from figure 8. For the antiparallel sheet (B), the H-bonds between the 1^st and 2^nd strands become more stable as strands are added, but reach their asymptotic limit when N= 4, while the H-bonds between strands 2 and 3, which are stronger than those between the first and second strands reach their limit at N=5 and the H-bonds between strands more towards the center of the larger sheets (again stronger than those between the 2nd and 3^rd strands) do not become stronger as the sheet grows larger. This cooperative behavior qualitatively resembles that previously reported for chains of formamides,⁴¹ and 4-pyridones,⁴⁰ but is much weaker. Interestingly, the antiparallel polyA sheets containing two or three strands are more stable than either of the amyloid forming sequences of the same size.

CONCLUSIONS

The two amyloid sequences, VQIVYK and VQIINK for parallel β-sheets are significantly more stable than those of similar sized peptides containing all alanine residues primarily due to the addition H-bonds formed between the Q’s in both VQIVYK and VQIINK and the N’s in VQIINK. The ΔE’s/H-bond (before distortion) reach more negative asymptotic limits for the amyloid sequences. However, the distortion energies of the strands in the amyloid-like structures are significantly higher than for the all alanine strands in their β-sheets due to the additional ‘attractive strain’ present in the amyloid-like sheets. As a result, the individual H-bonds of the amyloid sheets contribute less (including distortion) to the overall stabilities than those of the all alanine sheets. For the alanine sheets, the antiparallel sheet has more negative asymptotic ΔE’s/H-bond (before distortion), less distortion and stronger H-bonds (including distortion) for all sheets studied.