Kernel Machine Approach to Testing the Significance of Multiple Genetic Markers for Risk Prediction

Summary

There is growing evidence that genomic and proteomic research holds great potentials for changing irrevocably the practice of medicine. The ability to identify important genomic and biological markers for risk assessment can have a great impact in public health from disease prevention, to detection, to treatment selection. However, the potentially large number of markers and the complexity in the relationship between the markers and the outcome of interest impose a grand challenge in developing accurate risk prediction models. The standard approach to identifying important markers often assesses the marginal effects of individual markers on a phenotype of interest. When multiple markers relate to the phenotype simultaneously via a complex structure, such a type of marginal analysis may not be effective. To overcome such difficulties, we employ a kernel machine Cox regression framework and propose an efficient score test to assess the overall effect of a set of markers, such as genes within a pathway or a network, on survival outcomes. The proposed test has the advantage of capturing the potentially non-linear effects without explicitly specifying a particular non-linear functional form. To approximate the null distribution of the score statistic, we propose a simple resampling procedure that can be easily implemented in practice. Numerical studies suggest that the test performs well with respect to both empirical size and power even when the number of variables in a gene set is not small compared to the sample size.

1. Introduction

Genomic technologies permit systematic approaches to discovery that have begun to have a profound impact on biological research, pharmacology, and medicine. The ability to obtain quantitative information about the complete transcription profile of cells promises to be powerful means to explore basic biology, diagnose disease, facilitate drug development, and tailor therapeutics to specific pathologies (Young, 2000). The standard approach to analyzing genetic data is to identify important genes by assessing the marginal effects of individual genes on the phenotype of interest. However, when multiple genes are related to the phenotype simultaneously via a complex structure, such a single gene analysis may not be effective and may lead to a large number of false positives and false negatives especially when the signals are weak and results that are not reproducible (Vo et al., 2007). To overcome such difficulties, biological knowledge based learning methods have been advocated to integrate biological knowledge into statistical learning (Brown et al., 2000). One important approach is through the use of genetic pathways or networks. Results from pathway/network analysis are often more reliable and reproducible (Goeman et al., 2004, 2005).

To identify pathways that are associated with disease progression, one may test for the overall effect of a pathway on the risk of developing a clinical event. Goeman et al. (2005) proposed a score test under the standard proportional hazards model framework, where linear covariate effects are assumed. However, the functionality of the genes within a pathway are often complicated, and is likely to yield non-linear and non-additive effects on disease progression. We propose to incorporate such complex joint pathway effects with kernel machine learning. The kernel machine framework has been employed in various settings as a powerful machine learning tool to incorporate complex feature spaces (Vapnik, 1998; Scholkopf and Smola, 2002). For example, support vector machine has been successfully used for classifying and validating cancer subtypes (Furey et al., 2000; Ramaswamy et al., 2001; Lee and Lee, 2003). Linear and logistic kernel machine methods have been proposed to model pathway effects on continuous and binary outcomes (Liu et al., 2007, 2008). However, limited work using kernel methods has been done for survival data. Li and Luan (2003) considered a kernel Cox regression model for relating gene expression profiles to survival outcomes. However, no inference procedures were provided for the resulting estimates of the gene expression level effects.

We propose in this paper the use of the kernel machine Cox regression to derive a score test for assessing the pathway effect on survival outcomes. The proposed test has the advantage of capturing both linear and non-linear effects. For nonlinear effects, it does not require the specification of any particular parametric non-linear functional form. To approximate the null distribution of the score test, we propose a simple resampling procedure that can be easily implemented in practice. Numerical studies suggest that the test performs well with respect to both empirical size and power even when the number of variables in a gene set is not small compared to the sample size.

The rest of the paper is organized as follows. In section 2, we introduce the Cox proportional hazards kernel machine model. In section 3, we present the score test and procedures for approximating the null distribution of the proposed test. Simulation results are presented in Section 4.1 and the proposed procedures are illustrated by assessing the effects of various canonical pathways on breast cancer survival using a breast cancer gene expression study conducted by van de Vijver et al. (2002). In the example section, we also discuss simultaneous testing procedures to adjust for multiple comparisons when there are more than one pathway of interest.

2. The Cox Proportional Hazard Kernel Machine Model

Suppose we are interested in assessing the association between genetic measurements, Z_ptimes1, and the survival outcome T adjusting for covariates U. For example, Z could represent the gene expression levels within a pathway and U may represent additional covariates such as age and gender. Due to censoring, the survival time T is not always observable. Instead, we observe a bivariate vector (X,Δ), where X = min(T, C), Δ = I(T ≤ C) and C is the censoring time. We require the standard assumption that C is independent of T conditional on Z and U. The data for analysis consist of n i.i.d copies of random vectors {(X_i, Δ_i, Z_i, U_i), i = 1, …, n}. We assume that the survival time T relate to Z and U through the proportional hazards model (Cox, 1972):

$${\lambda }_{\mathbf{Z},\mathbf{U}}\left(t\right)={\lambda }_0\left(t\right)e^{{\gamma }^{{⊺}_{\mathbf{U}+h\left(\mathbf{Z}\right)}}}$$

where λ_Z,U(t) is the conditional hazard function given Z and U, λ₀(t) is the baseline hazard function, γ is an unknown covariate effect for U, and h(Z) is an unknown centered smooth function of Z.

Here, we are particularly interested in testing the null hypothesis H₀ : h(Z) = 0. If Z represents a genetic pathway/network, the null suggests that none of the genes in the pathway/network is associated with survival time conditional on U, i.e, no pathway/network effect. To test for such a hypothesis, one may consider a parametric or non-parametric specification for h(•). For example, if h(z) = β^Tz, the model becomes the standard Cox proportional hazard model (Cox, 1972). A score test for h(•) = 0 under such a framework has been considered by Goeman et al. (2005). However, such a test for linear effects may have limited power when the covariate effect is non-linear.

We consider a general parametric/non-parametric setting where we allow the functional form of h(•) to belong to a function space ${\mathcal{H}}_K$, generated by a given positive definite kernel function K(·, ·; ρ), where ρ is a possibly unknown scale parameter of the kernel function. By Mercer's Theorem (Cristianini and Shawe-Taylor, 2000), under regularity conditions, a kernel function K(·, ·; ρ) implicitly specifies a unique function space spanned by a particular set of orthogonal basis functions ${\left\{{\varphi }_l(\mathbf{z};\rho )\right)\}}_{l=1}^L$, where ${\varphi }_l(\mathbf{z};\rho )=\lambda {\left(\rho \right)}^{\frac{1}{2}}{\psi }_l(\mathbf{z};\rho )$, ${\left\{{\lambda }_l\left(\rho \right)\right\}}_{l=1}^L$ and ${\left\{{\psi }_l(\mathbf{z};\rho )\right)\}}_{l=1}^L$ are the eigenvalue and eigenfunctions of K(·, ·; ρ) such that $K({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )={\Sigma }_{l=1}^L{\lambda }_l\left(\rho \right){\psi }_l({\mathbf{z}}_1;\rho ){\psi }_l({\mathbf{z}}_2;\rho )$ and λ₁(ρ) ≥ λ₂(ρ) ≥ ⋯ ≥ λ_L(ρ) ≥ 0. The functional space ${\mathcal{H}}_K$ is essentially ${\mathcal{H}}_K=\stackrel{‒}{\left\{\varphi (\mathbf{z};\rho )\right\}}$, where $\stackrel{‒}{\left\{\mathbf{a}\right\}}$ denotes the function space spanned by basis functions a. This gives a primal representation of $h\in {\mathcal{H}}_K:h\left(\mathbf{z}\right)={\Sigma }_{l=1}^L{\beta }_l{\varphi }_l(\mathbf{z},\rho )$. One popular kernel function is the rth polynomial kernel $K({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )={(\rho +{\mathbf{z}}_1^{\mathrm{T}}{\mathbf{z}}_2)}^r$, where ρ is the intercept. For our present case, h(z) is centered and thus ρ may be set to 0. The first order polynomial kernel with r = 1 corresponds to the linear effect with h(z) = β^Tz and thus ${\mathcal{H}}_K=\stackrel{‒}{\left\{\varphi \left(\mathbf{z}\right)\right\}}=\stackrel{‒}{\{z_1,\cdots ,z_p\}}$. If r = 2, ${\mathcal{H}}_K=\stackrel{‒}{\left\{\varphi \left(\mathbf{z}\right)\right\}}=\stackrel{‒}{\{z_j,z_j,z_{j^{\prime }},j,j^{\prime }=1,\cdots ,p\}}$, i.e., a model with main effects, quadratic effects and two-way interactions. The kernel function $K({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )={\prod }_{j=1}^p(1+z_{1j}{z}_{2j})$ corresponds to the model with linear effects and all multi-way interactions, i.e. $\stackrel{‒}{\left\{{\varphi }_j\mathbf{z}\right\}}=\stackrel{‒}{\{z_j,{\prod }_{l=1}^2{z}_{jl},\cdots ,{\prod }_{l=1}^p{z}_{jl},jl=1,\cdots ,p,jl\ne jl\prime \text{if}l\ne l\prime \}}$. Another popular kernel is the Gaussian Kernel $K({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )=\text{exp}\{-{\parallel {\mathbf{z}}_1-{\mathbf{z}}_2\parallel }^2∕\rho \}$, where ${\parallel \mathbf{z}\parallel }^2={\mathbf{z}}^T\mathbf{z}$ and ρ is an unknown parameter. The Gaussian kernel generates the function space spanned by the radial basis functions. See Buhmann (2003) for the mathematical properties associated with this kernel function. Other kernel functions include the sigmoid, spline, Fourier and B-Spline kernels (Vapnik, 1998; Burges, 1998; Scholkopf and Smola, 2002). The kernel function can be viewed as a measure of similarity of gene profiles within the same pathway between two subjects. A choice of the kernels specifies a particular parametric/nonparametric model one is interested in fitting.

The explicit forms of the basis functions corresponding to K are generally difficult if not impossible to specify especially when p is not small and the function h is complex. Thus, it is generally difficult to estimate h based on its primal representation. On the other hand, estimating $h(\cdot )\in {\mathcal{H}}_K$ can be achieved by obtaining a dual representation of h with a given dataset. By the representer theorem (Kimeldorf and Wahba, 1970), any regularized estimator of $h(\cdot )\in {\mathcal{H}}_K$ with ${\parallel h\parallel }_{{\mathcal{H}}_K}^2$ being the penalty function can be represented as $h\left({\mathbf{Z}}_i\right)={\alpha }^{\mathrm{T}}\mathbb{K}\left(\rho \right)={\Sigma }_{j=1}^n{\alpha }_{j}K({\mathbf{Z}}_i,{\mathbf{Z}}_j;\rho )$, where α is the unknown regression parameter and $\mathbb{K}\left(\rho \right)$ is the n × n matrix with (i, j)^th element being K_ij(ρ) = K(Z_i, Z_j; ρ). The dual representation of h provides us a convenient way of assessing the effects of z on the outcome of interest without necessitating the specification of the basis functions.

Under the dual representation, the estimation of the unknown parameters {α, γ} could be facilitated by maximizing the penalized partial likelihood (PPL) function

$$\sum _{i=1}^n\int \log \left[\frac{\exp \{{\alpha }^{⊺}{\mathbf{K}}_i\left(\rho \right)+{\gamma }^{⊺}{\mathbf{U}}_i\}}{{\Sigma }_{l=1}^n{Y}_1\left(s\right)\exp \{{\alpha }^{⊺}{\mathbf{K}}_l\left(\rho \right)+{\gamma }^{⊺}{\mathbf{U}}_l\}}\right]d{N}_i\left(s\right)-\frac{\mathfrak{c}}{2}{\alpha }^{⊺}\mathbb{K}\left(\rho \right)\alpha .$$ (1)

where $Y_l\left(t\right)=I(X_l\ge t)$, ${\mathbf{K}}_i\left(\rho \right)={[K_{i1}\left(\rho \right),\dots ,K_{in}\left(\rho \right)]}^{\mathrm{T}}$, $N_i\left(t\right)=I(X_i\le t){\Delta }_i$ and $\mathfrak{c}$ is a penalty parameter. The PPL function (1) is closely related to the random effect Cox model:

$${\lambda }_{{\mathbf{Z}}_i,{\mathbf{U}}_i}\left(t\right)={\lambda }_0\left(t\right)\exp \{{\alpha }^{⊺}{\mathbf{K}}_i\left(\rho \right)+{\gamma }^{⊺}{\mathbf{U}}_i\}\text{with}\alpha =\tau ∊,E\left(∊\right)=0,\text{var}\left(∊\right)=\mathbb{K}{\left(\rho \right)}^{-}$$ (2)

where ∊ = (∊₁, ⋯, ∊_n)^T are the unobserved random effects, τ is the unknown variance component, and $\mathbb{K}{\left(\rho \right)}^{-}$ is Moore-Penrose generalized inverse of $\mathbb{K}\left(\rho \right)$. Specifically, if ∊ is further assumed to follow $N\{0,\tau \mathbb{K}{\left(\rho \right)}^{-}\}$, equation (1) corresponds to fitting (2) using the PQL approximation (Breslow and Clayton, 1993) and the penalty parameter c corresponds to the reciprocal of τ². Similar connections between the kernel machine penalized regression and the mixed effects models have been discussed in (Liu et al., 2007, 2008) for analyzing non-censored data.

3. Score Test for the Parametric/Non-parametric Function

The above connection between the PPL and the mixed effects model motivates us to employ the mixed effects model given in (2) and test the null hypothesis of no pathway effect by testing

$$H_0:\tau =0$$

since for a centered h, h(·) = 0 if and only if var{h(z)} = 0 for all z. Under the mixed effects framework, testing the variance being 0 for all z is equivalent to testing τ = 0.

3.1 Score Statistic

Since the null value of τ = 0 is on the boundary of the parameter space and the kernel matrix $\mathbb{K}\left(\rho \right)$ is not block diagonal, the distribution of the likelihood ratio statistic for H₀ : τ = 0 is non-standard. Here, we propose a score test based on the working model (2) which can be derived along the lines of Commenges and Andersen (1995). Specifically, let the partial likelihood function conditional on ε be

$${\mathcal{L}}_{∊}(\tau ;\rho ,\gamma )=\sum _{i=1}^n\int \text{log}\left[\frac{\text{exp}\{\tau {\mathbf{K}}_i{\left(\rho \right)}^{⊺}∊+{\gamma }^{⊺}{\mathbf{U}}_i\}}{\sum _{l=1}^n{Y}_1\left(s\right)\exp \{\tau {\mathbf{K}}_l{\left(\rho \right)}^{⊺}∊+{\gamma }^{⊺}{\mathbf{U}}_l\}}\right]d{N}_i\left(s\right).$$

If γ is known, then the score statistic is $\widehat{Q}(\rho ,\gamma )=E[{\{\partial {\mathcal{L}}_{∊}(\tau ;\rho ,\gamma )∕\partial \tau \}}^2\mid \mathcal{O}]+E\{{\partial }^2{\mathcal{L}}_{∊}(\tau ;\rho ,\gamma )∕\partial {\tau }^2\mid \mathcal{O}\}$, where $\mathcal{O}$ denotes the observed data. When γ is unknown as in most practical settings, we obtain the score statistic as $\widehat{Q}\left(\rho \right)=\widehat{Q}(\rho ,\widehat{\gamma })$, where $\widehat{\gamma }$ is the maximum partial likelihood estimator of γ under H₀ : h(z) = 0. It is straightforward to see that the resulting score statistic takes the form

$$\widehat{Q}\left(\rho \right)=\widehat{\mathbf{M}}{\left(\infty \right)}^{⊺}\mathbb{K}\left(\rho \right)\widehat{\mathbf{M}}\left(\infty \right)-n\widehat{q}\left(\rho \right).$$

where $\widehat{M}\left(s\right)={\{{\widehat{M}}_1\left(s\right),\cdots ,{\widehat{M}}_n\left(s\right)\}}^{\mathrm{T}}$, ${\widehat{M}}_i\left(s\right)=N_i\left(s\right)-{\int }_0^s{Y}_i\left(u\right)e^{{\widehat{\gamma }}^{\mathrm{T}{\mathbf{U}}_i}}d{\widehat{\Lambda }}_0\left(u\right)$, ${\widehat{\mathcal{S}}}^{\left(0\right)}\left(s\right)={\Sigma }_{j=1}^n{Y}_j\left(s\right)e^{{\widehat{\gamma }}^{{\mathrm{T}}_{U_j}}}$, ${\widehat{\mathcal{S}}}^{\left(k\right)}(s;\rho )={\Sigma }_{j=1}^n{Y}_j\left(s\right)e^{{\widehat{\gamma }}^{{\mathrm{T}}_{U_j}}}{\left\{{\mathbf{K}}_j{\left(\rho \right)}^{\mathrm{T}}∊\right\}}^k$, ${\widehat{\Lambda }}_0\left(s\right)={\Sigma }_{i=1}^n{\int }_0^{s}d{N}_i\left(u\right)∕{\widehat{\mathcal{S}}}^{\left(0\right)}\left(u\right)$, and

$$\widehat{q}\left(\rho \right)=n^{-1}\sum _{i=1}^n\int K_{ii}\left(\rho \right)Y_i\left(s\right)e^{{\widehat{\gamma }}^{⊺}{\mathbf{U}}_i}d{\widehat{\Lambda }}_0\left(s\right)-n^{-1}\sum _{i=1}^n\sum _{j=1}^n\int \frac{Y_i\left(s\right)Y_j\left(s\right)e^{{\widehat{\gamma }}^{⊺}{\mathbf{U}}_i+{\widehat{\gamma }}^{⊺}{\mathbf{U}}_j}{K}_{ij}\left(\rho \right)}{\widehat{\mathcal{S}}\left(0\right)\left(s\right)}d{\widehat{\Lambda }}_0\left(s\right).$$

In the Appendix, we show that $n^{-1}\widehat{Q}\left(\rho \right)=\widehat{\mathcal{W}}\left(\rho \right)-q\left(\rho \right)+o_p\left(1\right)$ which centers around 0, where $q\left(\rho \right)=\int [E\left\{K_{ii}\left(\rho \right){\tilde{Y}}_i\left(t\right)\right\}+{\omega }_{00}(t,t,\rho )∕E\left\{{\tilde{Y}}_j\left(t\right)\right\}]d{\Lambda }_0\left(t\right)$ which is the limiting mean of $\widehat{\mathcal{W}}\left(\rho \right)$,

$$\widehat{\mathcal{W}}\left(\rho \right)=\iint K({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )d{\widehat{\mathbb{W}}}_M\left({\mathbf{z}}_1\right)d{\widehat{\mathbb{W}}}_M\left({\mathbf{z}}_2\right)-2\int \left\{\int {\omega }_0(\mathbf{z},t,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)+{\widehat{\mathbf{W}}}_{\gamma }^{⊺}{\omega }_1(\mathbf{z},\rho )\right\}d{\widehat{\mathbb{W}}}_M\left(\mathbf{z}\right)+\iint {\omega }_{00}(t,s,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)d{\widehat{\mathbb{W}}}_{\lambda }\left(s\right)+{\widehat{\mathbf{W}}}_{\gamma }^{⊺}{\omega }_{11}\left(\rho \right){\widehat{\mathbf{W}}}_{\gamma }+2\int {\widehat{\mathbf{W}}}_{\gamma }^{⊺}{\omega }_{10}(s,\rho )d{\widehat{\mathbb{W}}}_{\lambda }\left(s\right)$$ (3)

${\widehat{\mathbb{W}}}_M\left(\mathbf{z}\right)=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{M}_{i}I({\mathbf{Z}}_i\le \mathbf{z})$, $M_i=M_i\left(\infty \right)$, $M_i\left(t\right)=N_i\left(t\right)-{\int }_0^t{\tilde{Y}}_j\left(s\right)d{\Lambda }_0\left(s\right)$, ${\tilde{Y}}_j\left(s\right)e^{{\gamma }_0^{\mathrm{T}}{\mathbf{U}}_j}$, ${\omega }_0(\mathbf{z},t,\rho )=E\left\{K({\mathbf{Z}}_i,\mathbf{z};\rho ){\tilde{Y}}_i\left(t\right)\right\}$, ${\omega }_1(\mathbf{z},\rho )=E\left\{K({\mathbf{Z}}_i,\mathbf{z};\rho ){\tilde{\mathbf{U}}}_i\right\}$, ${\tilde{\mathbf{U}}}_i={\mathbf{U}}_i\int {\tilde{Y}}_i\left(t\right)d{\Lambda }_0\left(t\right)$, ${\omega }_{00}(t,s,\rho )=E\left[K_{ij}\left(\rho \right){\tilde{Y}}_i\left(t\right){\tilde{Y}}_j\left(s\right)\right]$, ${\omega }_{11}\left(\rho \right)=E\left[K_{ij}\right]$ and ${\omega }_{10}(s,\rho )=E\left\{K_{ij}\left(\rho \right){\tilde{\mathbf{U}}}_i{\tilde{Y}}_j\left(s\right)\right\}$.

For the linear kernel with $K({\mathbf{Z}}_i,{\mathbf{Z}}_j;\rho )={\mathbf{Z}}_i^{\mathrm{T}}{\mathbf{Z}}_j$, $\widehat{Q}\left(\rho \right)$ is equivalent to the test statistic proposed in equation (4) of Goeman et al. (2005). In general, if the orthogonal basis functions ${\left\{{\varphi }_l(\cdot ;\rho )\right\}}_{l=1}^L$ for K(·, ·, ρ) with a given ρ are known and L is finite, then one may directly derive $\widehat{Q}\left(\rho \right)$ based on the primal representation $h\left(\mathbf{z}\right)={\Sigma }_{l=1}^L{\beta }_j{\varphi }_j(\mathbf{z};\rho )$. Specifically, assuming var(β_l) = τ² and cov(β_l, β_l′) = 0, one may obtain the same score statistic $\widehat{Q}\left(\rho \right)$ based on arguments given in Goeman et al. (2005, 2006). Furthermore, based on Lemma 4 of Goeman et al. (2006), one may argue that the score test based on $\widehat{Q}\left(\rho \right)$ is locally most powerful. However, deriving tests directly from basis functions may not be feasible as ${\left\{{\varphi }_l(\cdot ;\rho )\right\}}_{l=1}^L$ often cannot be specified explicitly and the parameter ρ is often unknown and not estimable under the null. Furthermore, Goeman et al. (2006) indicated that it is unclear how to approximate the null distribution of the score test statistic with a large L. Note that for many non-linear kernels such as the Gaussian kernel, L could be infinity even if p is fixed. The use of the kernel machine framework avoids the explicit specification of basis functions and allows us to derive the asymptotic null distribution of our proposed test as a process in ρ for a general kernel function.

3.2 Approximating the Score Test Statistic and Its Null Distribution

In the Appendix, we show that $n^{-1}\widehat{Q}\left(\rho \right)+q\left(\rho \right)$ converges weakly to the process $\mathcal{W}\left(\rho \right)$ defined in (A.3). For a fixed ρ, one may use the Satterthwaite method to approximate the distribution of $\mathcal{W}\left(\rho \right)$ using a rescaled χ² distribution, $c_0{\chi }_{d0}^2$. The scale parameter c₀ and the degrees of freedom (DF) d₀ can be estimated by matching the first two moments of $\mathcal{W}\left(\rho \right)$. The scaled χ² distribution has shown to provide a good approximation to the distribution of the score statistic for continuous and binary outcomes (Liu et al., 2007, 2008).

The effective DF d₀ decreases as we increase the correlation between covariates. Furthermore, d₀ increases slowly with p when the correlation is moderate/high, but more rapidly with p when the correlation is low. Thus with the same h(z), a higher correlation among Z is likely to yield a higher power of the score test and a more gradual power loss over increasing p. This suggests that the kernel machine score test improves the power for testing for the pathway effect by effectively borrowing information across different genes and accounting for between-gene correlation in calculating a data-adaptive DF. By doing so, it often results in a low DF test and increase the test power. Specifically, consider the case h(z) = β^Tz. The null hypothesis for no pathway effect, H₀ : h(z) = 0 is equivalent to H₀ : β = 0. The traditional testing approach based on a p-DF test would suffer from power loss if p is large. The kernel machine score test effectively accounts for the correlation among the genes and is often based on a much smaller DF d₀. For example, consider the extreme case if there are say 20 genes within a pathway and the genes are highly correlated, say correlation >0.95, the traditional 20-DF test for H₀ : β = 0 will have little power. One can show that d₀ is close to 1 by effectively accounting for the correlation between genes, and is hence much more powerful.

For the linear kernel $K({\mathbf{z}}_1,{\mathbf{z}}_2,\rho )=\rho +{\mathbf{z}}_1^{\mathrm{T}}{\mathbf{z}}_2$, the score test can be obtained based on $n^{-1}\widehat{Q}\left(0\right)$ with ρ = 0 since ρ corresponds to the intercept which would be absorbed by the unknown baseline hazard function. For the Gaussian kernel, the score test $n^{-1}\widehat{Q}\left(\rho \right)$ may depend on ρ. It is not difficult to see that under H₀, the kernel matrix $\mathbb{K}\left(\rho \right)$ disappears and hence the scale parameter ρ is inestimable. Davies (1987) studied the problem of a parameter disappearing under H₀ and proposed a score test by treating the score statistic as a Gaussian process indexed by the nuisance parameter ρ. Here, we propose to take a similar approach by considering the score test statistic

$$\widehat{S}=\underset{\rho \in \mathcal{I}}{\sup }\{n^{-1}\widehat{Q}\left(\rho \right)∕\widehat{\sigma }\left(\rho \right)\},$$

where $\mathcal{I}$ is the range of ρ to be considered and ${\widehat{\sigma }}^2\left(\rho \right)$ is a consistent estimator of ${\sigma }^2\left(\rho \right)=\text{var}\left\{\mathcal{W}\left(\rho \right)\right\}$ To approximate the limiting distributions of $\widehat{Q}\left(\rho \right)$ and $\widehat{S}$ in finite samples, we consider a resampling procedure which has been successfully used in the literature (Parzen et al., 1994; Cai et al., 2000; Park and Wei, 2003). Specifically, let $\mathcal{V}={({\mathcal{V}}_1,\cdots ,{\mathcal{V}}_n)}^{\mathrm{T}}$ be a vector of n i.i.d standard normal random variables generated independent of the data. For each set of $\mathcal{V}$, we obtain

$$\widehat{\mathcal{W}}\ast \left(\rho \right)=\iint K({\mathbf{z}}_1{\mathbf{z}}_2,\rho )d{\widehat{\mathbb{W}}}_M^{\ast }\left({\mathbf{z}}_1\right)d{\widehat{\mathbb{W}}}_M^{\ast }\left({\mathbf{z}}_2\right)-2\int \left\{\int {\widehat{\omega }}_0(\mathbf{z},t,\rho )d{\widehat{\mathbb{W}}}_{\lambda }^{\ast }\left(t\right)+{\widehat{\mathbf{W}}}_{\gamma }^{\ast ⊺}{\widehat{\omega }}_1(\mathbf{z},\rho )\right\}d{\widehat{\mathbb{W}}}_M^{\ast }\left(\mathbf{z}\right)+\iint {\widehat{\omega }}_{00}(t,s,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }^{\ast }\left(t\right)d{\widehat{\mathbb{W}}}_{\Lambda }^{\ast }\left(s\right)+{\widehat{\mathbf{W}}}_{\gamma }^{\ast ⊺}{\widehat{\omega }}_{11}\left(\rho \right){\widehat{\mathbf{W}}}_{\gamma }^{\ast }+2\int {\widehat{\mathbf{W}}}_{\gamma }^{\ast ⊺}{\widehat{\omega }}_{10}(s,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }^{\ast }\left(s\right)$$

where ${\widehat{\omega }}_0(\mathbf{z},s,\rho )$, ${\widehat{\omega }}_1(\mathbf{z},\rho )$, ${\widehat{\omega }}_{00}(t,s,\rho )$, ${\widehat{\omega }}_{10}(s,\rho )$ and ${\widehat{\omega }}_{11}\left(\rho \right)$ are the empirical counterparts of ${\omega }_0(\mathbf{z},t\rho )$, ${\omega }_1(\mathbf{z},\rho )$, ${\omega }_{00}(t,s,\rho )$, ${\omega }_{10}(s,\rho )$ and ${\omega }_{11}\left(\rho \right)$, ${\widehat{\mathbb{W}}}_M^{\ast }\left(\mathbf{z}\right)=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{\widehat{M}}_{i}I({\mathbf{Z}}_i\le \mathbf{z}){\mathcal{V}}_i$, ${\widehat{\mathbb{W}}}_{\Lambda }^{\ast }\left(t\right)=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{\widehat{W}}_{\Lambda i}{\mathcal{V}}_i$, ${\widehat{W}}_{\gamma }^{\ast }=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{\widehat{\mathbf{W}}}_{\gamma i}{\mathcal{V}}_i$, ${\widehat{W}}_{\Lambda i}$ and ${\widehat{\mathbf{W}}}_{\gamma i}$ the empirical counterparts of W_Λi which are defined in (A.1). It follows from similar arguments as given in Cai et al. (2000) that$\widehat{\mathcal{W}}\ast \left(\rho \right)$ conditional on the data converges weakly to $\mathcal{W}\left(\rho \right)$. To calculate the p-value for testing H₀ one may generate a large number, say B, realizations of $\mathcal{V}$ and obtain realizations of $\widehat{W}\ast \left(\rho \right)$, $\overrightarrow{\mathcal{W}}\ast \left(\rho \right)=\{{\widehat{\mathcal{W}}}_{\left(b\right)}^{\ast }\left(\rho \right),b=1,\dots ,B\}$. For any fixed ρ, the p-value of the test can be obtained as ${\Sigma }_{b=1}^{B}I\{{\widehat{\mathcal{Q}}}_{\left(b\right)}^{\ast }\left(\rho \right)>n^{-1}\widehat{Q}\left(\rho \right)\}∕B$ where ${\widehat{\mathcal{Q}}}_{\left(b\right)}^{\ast }\left(\rho \right)={\widehat{\mathcal{W}}}_{\left(b\right)}^{\ast }\left(\rho \right)-{\stackrel{‒}{q}}^{\ast }\left(\rho \right)$ and ${\stackrel{‒}{q}}^{\ast }\left(\rho \right)$ is the empirical mean of ${\overrightarrow{\mathcal{W}}}^{\ast }\left(\rho \right)$. Alternatively, one may estimate the first two moments of $\mathcal{W}\left(\rho \right)$ based on $\overrightarrow{\mathcal{W}}\ast \left(\rho \right)$ and then calculate the p-value based on thebone may χ² approximation. When ρ is unknown in practice, one may test H₀ based on the sup-statistic. The null distribution of $\widehat{S}$ can be approximated by the empirical distribution of $\{{\widehat{S}}_{\left(b\right)}^{\ast }={\text{sup}}_{\rho \in \mathcal{I}}\{{\widehat{\mathcal{Q}}}_{\left(b\right)}^{\ast }\left(\rho \right)∕\widehat{\sigma }\left(\rho \right)\},b=1,\dots ,B\}$ given the data, where ${\widehat{\sigma }}^2\left(\rho \right)$ is the empirical variance of $\overrightarrow{\mathcal{W}}\ast \left(\rho \right)$. To assess the significance for testing H₀, one may the p-value based on $\widehat{S}$ as ${\Sigma }_{b=1}^{B}I({\widehat{S}}_{\left(b\right)}^{\ast }>\widehat{S})∕B$.

3.3 Kernel PCA Approximation

An appropriate selection of the kernel function could potentially lead to improved power in detecting the signal. However, especially in finite sample, the complexity of the feature space corresponding to the kernel function may lead to a larger number of nuisance parameters and thus result in a loss in power. On the other hand, there often exists some correlations among the covariates and thus dimensionality reduction or so-called feature extraction may allow us to restrict the entire feature space to a sub-space of lower dimensionality. One approach to achieving such a goal is through kernel principal component analysis (PCA) (Scholkopf et al., 1998). We propose to investigate the effect of dimension reduction on the power of the score test. To this end, we take a singular value decomposition of the matrix $\mathbb{K}\left(\rho \right):\mathbb{K}\left(\rho \right)={\Sigma }_{\ell =1}^n{\nu }_{\ell }\left(\rho \right){\mathbf{e}}_{\ell }\left(\rho \right){\mathbf{e}}_{\ell }{\left(\rho \right)}^{\mathrm{T}}$, where ${\nu }_1\left(\rho \right)\ge {\nu }_2\left(\rho \right)\ge \cdots \ge {\nu }_n\left(\rho \right)\ge 0$ are the eigenvalues and $\{{\mathbf{e}}_{\ell }\left(\rho \right),\ell =1,\dots ,n\}$ are the corresponding eigenvectors. We assume that with a properly chosen ρ, the eigenvalues decay quickly and thus there exists an ${\ell }_0$ such that ${\Sigma }_{l=1}^{{\ell }_0}{\nu }_l\left(\rho \right)∕{\Sigma }_{l=1}^n{\nu }_l\left(\rho \right)\ge {\mathfrak{p}}_0$ where ${\mathfrak{p}}_0\in (0,1)$ is a prespecified constant. Consider the kernel PCA approximation to the original kernel matrix $\mathbb{K}\left(\rho \right)$, $\tilde{\mathbb{K}}\left(\rho \right)={\Sigma }_{l=1}^{{\ell }_0}{\nu }_{\ell }\left(\rho \right){\mathbf{e}}_{\ell }\left(\rho \right){\mathbf{e}}_{\ell }{\left(\rho \right)}^{\mathrm{T}}$. Let $\tilde{Q}\left(\rho \right)$ and $\tilde{\mathcal{W}}\left(\rho \right)$ be $\tilde{Q}\left(\rho \right)$ and $\tilde{\mathcal{W}}\left(\rho \right)$ with $\mathbb{K}\left(\rho \right)$ replaced by $\tilde{\mathbb{K}}\left(\rho \right)$, respectively. It is not difficult to show that $n^{-1}\tilde{\mathcal{W}}\left(\rho \right)={\Sigma }_{\ell =1}^{{\ell }_0}{\tilde{W}}_{\ell }{\left(\rho \right)}^2$, where ${\tilde{W}}_{\ell }\left(\rho \right)={\nu }_{\ell }{\left(\rho \right)}^{\frac{1}{2}}{n}^{-\frac{1}{2}}{\Sigma }_{i=1}^n[e_{\ell i}\left(\rho \right)M_i-\int {\omega }_{0\ell }(t,\rho )d{W}_{\Lambda i}\left(t\right)-{\omega }_{1\ell }{\left(\rho \right)}^{\mathrm{T}}{\mathbf{W}}_{\gamma i},e_{\ell i}\left(\rho \right)$ is the ith element of ${\mathbf{e}}_{\ell }\left(\rho \right)$, ${\omega }_{0\ell }(t,\rho )$ and ${\omega }_{1\ell }\left(\rho \right)$ are the respective limit of $n^{-1}{\Sigma }_{i=1}^n{e}_{\ell i}\left(\rho \right){\tilde{Y}}_i\left(t\right)$ and $n^{-1}{\Sigma }_{i=1}^n{e}_{\ell i}\left(\rho \right){\tilde{\mathbf{U}}}_i$. Based on the convergence properties of the eigenvectors to the eigenfunctions (Bengio et al., 2004; Zwald and Blanchard, 2006), one may view $\tilde{\mathbb{K}}\left(\rho \right)$ as an empirical kernel matrix corresponding to $K^{\left[{\ell }_0\right]}\left(\rho \right)$, the ${\ell }_0$-degenerated approximation of K (Braun, 2005). Thus, treating $\tilde{K}\left(\rho \right)$ as a new kernel matrix, the same arguments as given in the Appendix can be used to establish the limiting distribution of $\tilde{\mathcal{W}}\left(\rho \right)$ and justify the resampling method. For a given range of $\mathcal{I}$ of ρ, the final score test based on $\tilde{\mathbb{K}}$ could be obtained as $\tilde{S}={\text{sup}}_{\rho \in \mathcal{I}}\{n^{-1}\tilde{Q}\left(\rho \right)∕\tilde{\sigma }\left(\rho \right)\}$, where ${\tilde{\sigma }}^2$ is the estimated variance of $\tilde{\mathcal{W}}\left(\rho \right)$.

The kernel PCA approximation is equivalent to approximating $h\left(\mathbf{z}\right)={\Sigma }_{l=1}^L\beta {\varphi }_l(\mathbf{z},\rho )$ by $\tilde{h}\left(\mathbf{z}\right)={\Sigma }_{l=1}^L\beta {\varphi }_l(\mathbf{z},\rho )$. Based on truncated set of basis functions, one may approximate the leading term of the score statistic by $\tilde{\mathcal{W}}†\left(\rho \right)={\Sigma }_{l=1}^{{\ell }_0}{\lambda }_l\left(\rho \right){\left\{{\Sigma }_{i=1}^n{\psi }_l({\mathbf{Z}}_i,\rho ){\tilde{M}}_i\right\}}^2$. Based on Satterthwaite method, one may approximate the distribution of $\tilde{\mathcal{W}}†\left(\rho \right)$ as $c_0\left({\ell }_0\right){\chi }_{d_0\left({\ell }_0\right)}^2$ under H₀ and as $c_0\left({\ell }_0\right){\chi }_{d_0\left({\ell }_0\right)}^2\left\{\delta \left({\ell }_0\right)\right\}$ under the alternative. Both the DF d₀(ℓ₀) and the non-centrality parameter δ(ℓ₀) are dominated by the larger eigenvalues. Thus, we expect that the majority of the information about h to be captured by $\tilde{\mathbb{K}}$. Similar findings based on eigenvalue decomposition have been discussed in Goeman et al. (2006) for the linear model.

3.4 Practical Issues with the Choice of ρ

Although our simulation results show that the score test is not sensitive to the choice of ρ within a reasonable range $\mathcal{I}$. However, when ρ → 0 or ρ → ∞, the kernel matrix may become degenerated and thus it may become infeasible to draw inference. For example, when K is the Gaussian kernel, ρ → 0 corresponds to no similarity between subjects and ρ → ∞ corresponds to no heterogeneity between subjects. For both extreme cases, one may be unable to draw conclusion about the association between T and Z based on the given kernel. It is important to note that the eigenvalues of the kernel matrix does not decay when ρ → 0 and would be all 0 except for the first one when ρ → ∞.

For the Gaussian kernel, to prevent $\mathbb{K}\left(\rho \right)$ from being degenerated while including a sufficiently wide range of ρ, one may as determine the range of ρ based on the kernel PCA. Specifically, let ${\widehat{\ell }}_{\rho }$ denote the smallest ℓ such that ${\Sigma }_{l=1}^{\ell }{\nu }_1\left(\rho \right)∕{\Sigma }_{l=1}^n{\nu }_1\left(\rho \right)\ge {\mathfrak{p}}_0$. Then the range of ρ can be chosen as $\mathcal{I}[\text{min}\{\rho :{\widehat{\ell }}_{\rho }\le {\ell }_0\}$, $\text{max}\{\rho :{\widehat{\ell }}_{\rho }\ge 2\}]$. In practice, we recommend $\mathcal{I}$ with ${\ell }_0=\sqrt{n}$. The constants $\{2,\sqrt{n}\}$ are chosen to ensure that the rank of $\mathbb{K}\left(\rho \right)$ is not close to 1 and the eigenvalue of $\mathbb{K}\left(\rho \right)$ has a reasonable decay rate. See more discussions on the choice of ℓ₀ in the discussion section.

4. Simulation Studies

We conducted simulation studies to assess the performance of the proposed score test. Throughout, we generated Z from a multivariate normal with mean 0, unit variance and correlation ℘. We considered $\wp =0.5,0.2$, and 0 to represent a moderate, weak, and zero correlation among the Z's, respectively. For simplicity, no additional covariates were considered for numerical studies. The censoring was generated from an exponential with mean μ_C. For each configuration, we generated 2000 datasets to calculate the empirical size and 1000 datasets to calculate the empirical power. For each simulated dataset, we carried out the score test for two types of kernels: (1) Gaussian kernel with K_G(z₁, z₂; ρ) = exp{−∥z₁ − z₂∥²/ρ}; and (2) Linear kernel with $K_G({\mathbf{z}}_1,{\mathbf{z}}_2;\rho )=\text{exp}\{-{\parallel {\mathbf{z}}_1-{\mathbf{z}}_2\parallel }^2∕\rho \}$. For comparison, we evaluated the performance of the score test using $\mathbb{K}$ and the approximated kernel matrix $\widehat{\mathbb{K}}$ with $\mathfrak{p}=0.90$. We considered testing based on (a) sup statistic, $\widehat{S}$ and $\tilde{S}$, with K_G; (b) $K_G;\left(b\right)\widehat{Q}\left({\rho }_2\right)$ and $\widehat{Q}\left({\rho }_2\right)$ with K_G and ρ₂ being the upper bound of $\mathcal{I}$; and (c) $\widehat{Q}$ and $\tilde{Q}$ with K_L. For the resampling procedure, we let B = 1000. We considered n = 100 and 200; censoring proportion of 25% (μ_C = 3) and 50% (μ_C = 1), and p = 5, 10, and 100.

First, to examine the validity of our proposed testing procedure in finite samples, we generated data under the null model to assess the size of the score test. Specifically, we generated log T from an extreme value distribution and thus the survival time is independent of the covariates. The empirical sizes of the proposed tests are summarized in Table 1 for $\wp =0.5$ and Table 2 for $\wp =0.2$. We evaluated the performance of testing procedures based on various approximations to the null distribution: (i) the resampling procedure; (ii) the scaled χ² approximation; and (iii) the normal approximation as suggested in the literature. Across all the configurations, the empirical sizes for $\widehat{Q}\left({\rho }_2\right)$, $\tilde{Q}\left({\rho }_2\right)$, $\widehat{Q}$ and $\tilde{Q}$, are close to the nominal levels when the null is approximated based on the resampling and the scaled χ². The PCA based test appears to perform slightly better when p is large. This is in part due to the reduction in the DF. On the contrary, the normal approximations do not appear to work well in many of the settings. For example, when n = 100, p = 5, $\wp =0.5$ with 50% of censoring, the empirical sizes for $\{\widehat{Q}\left({\rho }_2\right),\tilde{Q}\left({\rho }_2\right)\}$ were (7.4%, 8.4%) based on the normal approximation, (5.8%, 5.5%) based on the resampling procedure and (5.5%, 6.2%) based on the χ² approximation. Similar patterns were observed for $\wp =0.2$ and larger p's.

Table 1.

Empirical sizes at type I error rate of 0.05 for the case when the genes are moderately correlated (℘ = 0.5). Testing was performed based on both the Gaussian kernel and the Linear kernel. For Gaussian kernel, we compared (i) sup-statistic with the original kernel (subscript $\widehat{S}$); (ii) sup-statistic with the kernel PCA including 90% of eigenvalues (subscript $\tilde{S}$); (iii) score test with ρ fixed at ρ₂ (upper bound of $\mathcal{I}$) with original kernel (subscript $\widehat{Q}$); (iv) score test at ρ₂ with kernel PCA (subscript $\tilde{Q}$). For the linear kernel, the testing was performed based on $\widehat{Q}$ and $\tilde{Q}$. The null distributions were generated based on (a) the resampling procedure (indexed by P); (b) the χ² approximation (indexed by χ²); and (c) the normal approximation (indexed by N).

				p = 5				p = 10				p= 100
Censoring %			50%		25%		50%		25%		50%		25%
Kernel		n	100	200	100	200	100	200	100	200	100	200	100	200
Gaussian	sup	$P_{\widehat{S}}$	5.8	4.1	4.5	4.2	4.0	5.2	4.0	4.3	5.1	5.2	5.1	4.0
		$P_{\tilde{S}}$	5.3	4.6	5.1	4.24	4.24	5.7	4.2	4.8	5.4	5.4	5.8	4.6
		$N_{\widehat{S}}$	7.8	6.4	6.4	6.2	6.0	7.6	5.4	6.1	6.4	6.8	7.0	5.6
		$N_{\tilde{S}}$	8.7	7.0	7.4	6.9	6.8	8.1	6.0	6.8	7.0	7.0	7.9	6.0
	ρ 2	$P_{\widehat{Q}}$	5.8	4.5	5.0	4.5	4.0	5.4	4.0	4.6	5.0	5.2	5.0	4.1
		$P_{\tilde{Q}}$	5.5	4.7	5.4	4.6	4.8	6.0	4.4	4.9	5.6	5.2	5.9	4.6
		$N_{\widehat{Q}}$	7.4	5.9	6.4	5.8	5.8	7.3	5.2	5.8	6.4	6.8	7.1	5.6
		$N_{\tilde{Q}}$	8.4	7.0	7.1	6.4	6.2	7.8	6.6	6.9	7.5	7.1	8.0	6.3
		${\chi }_{\widehat{Q}}^2$	5.5	4.4	4.8	4.4	4.0	5.5	4.1	4.6	5.2	5.2	5.2	4.4
		${\chi }_{\tilde{Q}}^2$	6.2	4.8	5.4	4.5	4.6	5.9	4.4	4.9	5.4	5.2	6.0	4.7
Linear		$P_{\widehat{Q}}$	4.5	6.0	3.9	5.6	5.2	4.0	4.7	4.8	5.8	4.9	6.0	4.6
		$P_{\tilde{Q}}$	4.2	5.9	4.4	5.3	5.2	4.2	4.8	4.6	5.8	5.0	6.1	4.6
		$N_{\widehat{Q}}$	6.0	7.2	5.8	6.8	7.0	5.2	6.2	6.4	7.5	6.9	7.6	6.0
		$N_{\tilde{Q}}$	5.7	7.5	5.8	6.7	6.8	5.4	6.2	6.8	7.6	7.0	7.8	6.0
		${\chi }_{\widehat{Q}}^2$	4.5	5.9	3.8	5.6	5.2	4.1	4.6	4.6	6.0	5.2	6.2	4.9
		${\chi }_{\tilde{Q}}^2$	4.2	5.8	4.3	5.2	5.2	4.2	4.7	4.7	6.0	5.2	6.2	5.0

Table 2.

Empirical sizes at type I error rate of 0.05 for the case when the genes are weakly correlated (℘ = 0.2). Testing was performed based on (i) sup-statistic with the original kernel (subscript $\widehat{S}$); (ii) sup-statistic with the kernel PCA including 90% of eigenvalues (subscript $\tilde{S}$); (iii) score test with ρ fixed at ρ₂ (upper bound of $\mathcal{I}$) with original kernel (subscript $\widehat{Q}$); (iv) score test at ρ₂ with kernel PCA (subscript $\tilde{Q}$). The null distributions were generated based on (a) the resampling procedure (indexed by P); (b) the χ² approximation (indexed by χ² ); and (c) the normal approximation (indexed by N).

				p = 5				p = 10				p =100
Censoring %			50%		25%		50%		25%		50%		25%
Kernel		n	100	200	100	200	100	200	100	200	100	200	100	200
Gaussian	sup	$P_{\widehat{S}}$	4.8	3.6	3.4	4.0	3.3	4.5	3.0	3.6	3.5	4.6	3.0	3.0
		$P_{\tilde{S}}$	5.4	4.5	4.9	4.6	4.2	5.4	4.2	4.1	5.2	5.3	5.4	4.4
		$N_{\widehat{S}}$	6.9	5.4	5.4	6.1	4.8	6.5	4.1	4.9	4.3	5.4	4.1	4.0
		$N_{\tilde{S}}$	10.	7.4	8.2	7.8	7.1	8.2	7.1	7.3	7.0	7.1	7.6	6.2
	ρ 2	$P_{\widehat{Q}}$	5.4	3.7	3.8	4.0	3.5	4.4	3.2	4.0	3.6	4.6	3.0	3.2
		$P_{\tilde{Q}}$	6.2	4.7	5.3	4.5	4.4	5.8	4.6	4.8	5.6	5.3	5.8	4.7
		$N_{\widehat{Q}}$	7.2	5.3	5.5	6.0	4.8	6.4	4.6	4.9	4.4	5.3	4.0	4.1
		$N_{\tilde{Q}}$	8.4	6.7	7.0	6.5	6.2	7.2	6.2	6.8	7.4	7.2	8.0	6.2
		${\chi }_{\widehat{Q}}^2$	5.2	3.6	3.6	4.0	3.4	4.8	3.3	4.0	3.6	4.8	3.2	3.3
		${\chi }_{\tilde{Q}}^2$	6.0	4.6	5.3	4.4	4.4	6.0	4.6	4.8	5.5	5.3	5.9	5.0
Linear		$P_{\widehat{Q}}$	4.1	5.6	4.2	5.1	4.3	3.4	3.2	3.6	4.0	4.3	4.0	3.4
		$P_{\tilde{Q}}$	4.4	5.5	4.1	5.4	4.4	3.7	3.7	4.1	4.4	4.5	4.5	3.4
		$N_{\widehat{Q}}$	6.0	7.1	5.8	6.7	5.8	4.9	5.1	4.8	5.4	5.4	5.0	4.4
		$N_{\tilde{Q}}$	6.2	7.3	5.9	6.6	6.2	5.2	5.3	5.4	5.6	5.4	5.4	4.6
		${\chi }_{\widehat{Q}}^2$	4.0	5.4	4.2	4.8	4.2	3.3	3.3	3.6	4.4	4.6	4.2	3.4
		${\chi }_{\tilde{Q}}^2$	4.2	5.3	4.2	5.2	4.4	3.7	3.8	4.0	4.6	4.8	4.4	3.6

Results reported in Tables 1 and 2 suggest that one may use the χ² approximation to assess the DF for the score test. For example, when the correlation is weak with $\wp =0.2$, the effective DF of $\widehat{Q}$ are about 3.9, 6.1, and 11.4 for p = 5, 10, and 100, respectively. When $\wp =0.5$, the DFs are 2.5, 2.9and 3.7, respectively. Thus, as we increase the correlation among Z, the effective DFs of the score test are much lower and do not increase much with the covariate dimension. This suggests that the kernel machine test effectively borrows information across genes within a pathway by accounting for their correlation to construct for a low-DF test and increase the power of the test. This shows an attractive feature of the kernel machine test as a powerful approach to detecting the pathway effect in high-dimensional data problems.

The tests based on $\widehat{S}$ and $\tilde{S}$ also perform well in maintaining the size. As expected, the performance improves as we increase n and/or decrease the censoring proportion. When p = 100 and $\wp =0.2$, the empirical sizes based on $\widehat{S}$ tends to be slightly lower than the nominal level. For such settings, the effective DF is large relative to n, and thus the standard large sample distribution theory may not hold for $\widehat{S}$ and $\widehat{Q}$ with a general K. On the other hand, the use of kernel PCA seems to reduce the effective DF and thus lead to $\tilde{S}$ with reasonable empirical sizes even with p = 100.

To assess the power of the proposed tests, we generated data from a proportional hazards model log T = h(Z) + ε, where ε follows an extreme value distribution. Two forms of h(·) was considered: (1) $h\left(\mathbf{Z}\right)=0.1{\Sigma }_{l=1}^5{Z}_l$ corresponding to a standard Cox model with linear effects, and (2) a complex functional form with $h\left(\mathbf{Z}\right)=Z_1^2+Z_2^2+\text{sin}\left(3Z_3\right)+\text{sin}\left(3Z_4\right)+\text{sin}\left(3Z_5\right)$. For each model, we generated p covariates with p = 5, 10, 100, and the event time T is only determined by the first 5 covariates based on the model. The empirical power was summarized in Table 3 for the standard Cox model and in Table 4 for the non-linear model.

Table 3.

Empirical power when h(Z) is linear at the type I error rate of 0.05 with p=5, 10, and 100 genes are used to fit the model while the true number of genes is 5. Testing was performed based on (i) sup-statistic with the original kernel (subscript $\widehat{S}$); (ii) sup-statistic with the kernel PCA including 90% of eigenvalues (subscript $\tilde{S}$); (iii) score test with ρ fixed at ρ₂ (upper bound of $\mathcal{I}$) with original kernel (subscript $\widehat{Q}$); (iv) score test at ρ₂ with kernel PCA (subscript $\tilde{Q}$). The null distributions were generated based on the resampling procedure (indexed by P).

			p = 5				p = 10				p = 100
Censoring %			50%		25%		50%		25%		50%		25%
Kernel		n	100	200	100	200	100	200	100	200	100	200	100	200
		Correlation = 0.5
Gaussian	sup	$P_{\widehat{S}}$	67	94	83	99	68	94	83	99	67	92	82	98
		$P_{\tilde{S}}$	68	94	85	99	69	94	85	99	68	92	83	99
	ρ 2	$P_{\widehat{Q}}$	69	95	86	99	69	94	84	100	67	92	82	98
		$P_{\tilde{Q}}$	72	96	88	99	71	94	86	100	69	92	84	99
Linear		$P_{\widehat{Q}}$	74	97	88	100	71	96	86	100	66	94	81	99
		$P_{\tilde{Q}}$	75	96	88	100	72	96	87	100	66	94	81	99
		Correlation = 0.2
Gaussian	sup	$P_{\widehat{S}}$	42	72	57	89	37	66	49	83	28	57	37	73
		$P_{\tilde{S}}$	49	78	65	92	42	70	56	86	34	61	48	76
	ρ 2	$P_{\widehat{Q}}$	43	74	59	90	38	67	50	84	28	57	37	73
		$P_{\tilde{Q}}$	54	82	69	94	45	72	60	87	34	62	48	76
Linear		$P_{\widehat{Q}}$	44	77	59	89	39	69	54	86	29	58	39	73
		$P_{\tilde{Q}}$	44	78	61	90	40	70	54	86	30	58	40	74

Table 4.

Empirical power when h(Z) is non-linear at the type I error rate of 0.05 with p =5, 10, and 100 genes used to fit the model while the true number of genes is 5. Testing was performed based on (i) sup-statistic with the original kernel (subscript $\widehat{S}$); (ii) sup-statistic with the kernel PCA including 90% of eigenvalues (subscript $\tilde{S}$); (iii) score test with ρ fixed at ρ₂ (upper bound of$\mathcal{I}$) with original kernel (subscript $\widehat{Q}$); (iv) score test at ρ₂ with kernel PCA (subscript $\tilde{Q}$). The null distributions were generated based on the resampling procedure (indexed by P).

			p = 5				p = 10				p = 100
Censoring %			50%		25%		50%		25%		50%		25%
Kernel		n	100	200	100	200	100	200	100	200	100	200	100	200
		Correlation = 0.5
Gaussian	sup	$P_{\widehat{S}}$	94	100	94	100	78	100	76	100	30	75	29	73
		$P_{\tilde{S}}$	84	100	85	100	70	99	69	98	31	75	31	73
	ρ 2	$P_{\widehat{Q}}$	54	97	56	96	32	81	34	82	21	55	22	56
		$P_{\tilde{Q}}$	19	36	21	40	13	21	17	26	10	17	12	18
Linear		$P_{\widehat{Q}}$	8	10	9	10	9	11	10	14	8	10	9	10
		$P_{\tilde{Q}}$	7	9	9	10	9	11	9	13	8	10	9	10
		Correlation = 0.2
Gaussian	sup	$P_{\widehat{S}}$	65	99	61	99	21	60	19	54	5	7	4	6
		$P_{\tilde{S}}$	30	89	29	87	10	20	10	16	6	6	5	6
	ρ 2	$P_{\widehat{Q}}$	17	35	16	33	8	15	9	13	5	6	4	6
		$P_{\tilde{Q}}$	11	16	12	15	8	9	8	9	5	6	5	6
Linear		$P_{\widehat{Q}}$	6	8	7	8	8	7	7	7	4	6	4	6
		$P_{\tilde{Q}}$	7	8	7	8	8	8	7	7	4	7	5	6

First, consider the case with moderate correlation $\wp =0.5$. For the standard Cox model, the best strategy would be based on K_L with p = 5 (i.e., using the true 5 genes). For a n = 100 with 50% of censoring, this best strategy achieves about 74% of power. When we fit the model with p = 100 by including additional 95 noise covariates, the power decreases to 66%. Thus, the score test appears to have reasonable power in detecting the signal even in the presence of a large number of noise features. The use of kernel PCA does not appear to affect the power for linear kernel. When K_G is used, the score test $\widehat{S}$ achieves about 67% of power with p = 5 and with p = 100. Applying kernel PCA test $\tilde{S}$ by thresholding the eigenvalues at $\mathfrak{p}=90\%$, the power remains almost identical. There appears to be little loss in power for using K_G compared to K_L when $\widehat{S}$ and $\tilde{S}$ are considered. This can in part be attributed to the fact that K_G is approximately K_L when ρ is relatively large (Liu et al, 2008). When h(z) is non-linear, the use of K_G resulted in a substantial improvement in power when compared to K_L. For example, with p = 5, n = 100 and 50% of censoring, the power is about 94% for $\widehat{S}$ and 8% with the linear kernel. Even when p = 100 and n = 200, the power was 75% based on $\widehat{S}$ and merely 8% based on $\widehat{Q}$. This suggests drastically amount of gain in power for employing K_G over K_L when the true effects are highly non-linear. Again, the power does not appear to decrease dramatically as we increase the number of noise covariates. This is likely due to the fact that the kernel machine test effectively accounts for the correlation between the covariates which results in little increase in the effective DF as p increases.

We next summarize how the results may be affected by the covariate correlation ℘. As we decrease ℘, the effective DF of the score statistics under the null increases which is likely to yield a power loss. This is consistent with the results shown in Table 3 and 4. For example, under the standard Cox model, the power of $\widehat{S}$ decreased from 83% to 49% when ℘ was decreased from 0.5 to 0.2, when p = 10, n = 100 and 25% censoring. Moreover, the power appears to decrease more rapidly with p when ℘ is small. When n = 100 and 25% censoring, as p increases from 5 to 100, the power of $\widehat{S}$ decreases from 83% to 82% when $\wp =0.5$ and from 57% to 37% when $\wp =0.2$. This is also expected since when ℘ is small, the effective DF increases more rapidly with p. One cannot borrow information across genes to improve power. In the extreme case that all genes are independent, the best test would need to be based on p DF. In pathway analysis, as genes are often correlated with pathway, one would expect a high power using the kernel machine test as it effectively borrow information across genes. It is also worth noting that when $\wp =0.2$ and the underlying effects are non-linear, there appears to be a substantial power loss by using $\tilde{S}$ which only includes PCAs that account for 90% of the total variation. Thus, for such settings, a higher threshold values should be considered to minimize the information loss. When the threshold value was increased to 99%, the difference between $\widehat{S}$ and $\tilde{S}$ becomes minimal with respect to power.

5. Example: Breast Cancer Gene Expression Study

Findings from genomic research hold great potential to improve disease outcomes for breast cancer patients. For example, the discovery that mutations in BRCA1 and BRCA2 genes increase the risk of breast cancer has radically transformed our understanding of the genetic basis of breast cancer, leading to improved management of high-risk women. A number of genomic biomarkers have been developed for clinical use, and increasingly, pharmacogenetic end points are being incorporated into clinical trial design (Olopade et al., 2008). Despite recent advances in understanding genetic susceptibility to breast cancer, it remains important to identify and understand molecular pathways of pathogenesis (Nathanson et al., 2001). Here, we are particularly interested in assessing whether various canonical pathways from the molecular signature database are related to breast cancer survival. Examples of these pathways include AKAP13, EGFR SMRTE and p53. Genetic alterations within AKAP13 are expected to provoke a constitutive Rho signaling, thereby facilitating the development of cancer (Wirtenberger et al., 2006). Epidermal growth factor receptor (EGFR) is a receptor tyrosine kinase and is expressed in a wide variety of epithelial malignancies including non-small-cell lung cancer, head and neck cancer, and breast cancer (Kuwahara et al., 2004; Nicholson et al., 2001). EGFR activation promotes tumor growth by increasing cell proliferation, motility, or angiogenesis, and by blocking apoptosis (Holbro et al., 2003). p53 mutation remains the most common genetic change identified in human neoplasia and is associated with more aggressive disease and worse overall survival in breast cancer (Gasco et al., 2002).

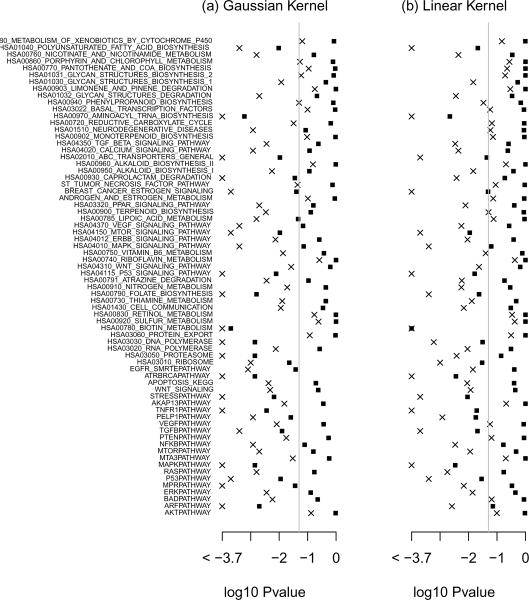
Here, we apply the proposed score test to assess the overall effect of various canonical pathways using a recent breast cancer study by van de Vijver et al. (2002). The primary goal of this study was to evaluate the performance of prognostic rules constructed based on microarray gene expression data from Van't Veer et al. (2002). There are a total of 260 patients with primary breast carcinomas from the Netherlands Cancer Institute. The median followup time was 8.8 years and there was about 75% of censoring. For illustration, we consider 70 pathways that are potentially related to breast cancer survival. The number of genes contained in a pathway ranges from 2 to 235 with a median of 22. We applied the the proposed score test with both the Gaussian based on ${\widehat{S}}_{{\mathcal{I}}_2}$ and the linear kernel based on $\widehat{Q}$. The p-value for the aforementioned 70 pathways are shown bin Figure 1. The score test identifies 56 (80%) pathways as significantly associated with breast cancer survival with p-value < 0.05 when the Gaussian kernel is used; and 46 (66%) when the linear kernel is used. For example, the AKAP13 pathway is significant with a p-value of 0.015 based on the Gaussian kernel but not significant with a p-value of 0.21 based on the linear kernel. For this pathway, there are a total of 10 genes and their effects appear to be non-linear. When comparing the fitted Cox model with linear effects only to the model with both linear and quadratic effects, the inclusion of quadratic effects yields an increase of 19.5 in the log partial likelihood with a p-value of 0.035. This also suggests the underlying effects of these genes are potentially non-linear.

Figure 1.

log₁₀ Pvalue for testing the overall effect of the 70 genetic pathways on breast cancer survival based on the kernel machine score test $\widehat{S}$ with Gaussian kernel and $\widehat{Q}$ with the linear kernel. The crosses and the squares represent p-values before and after adjusting for multiple comparisons, respectively. The results are based on B = 5000 bperturbations.

In settings where multiple pathways are under examination, it is important to adjust for multiple comparison. The proposed procedure can easily be extended to incorporate such an adjustment. Specifically, let $\widehat{S}\left(j\right)$ denote the observed score statistic for the jth pathway and $\widehat{S}\ast \left(j\right)$ represents null counterpart. Then the adjusted p-value can be obtained by comparing the observed score statistic $\widehat{S}\left(j\right)$ to the distribution of ${\widehat{S}}_{\text{max}}^{\ast }=\text{max}\{\widehat{S}\ast \left(1\right),\cdots ,\widehat{S}\ast \left(J\right)\}$. In practice, realizations of ${\widehat{S}}_{\text{max}}^{\ast }$ can be easily generated via the aforementioned resampling procedure. For b = 1, …, B, we generate a set of standard normal random variable ${\mathcal{V}}_{\left(b\right)}$ to calculate ${\widehat{S}}_{\left(b\right)}^{\ast }\left(1\right),\cdots ,{\widehat{S}}_{\left(b\right)}^{\ast }\left(J\right)$ simultaneously and obtain ${\widehat{S}}_{\text{max}\left(b\right)}^{\ast }$. The adjusted p-value for $\widehat{S}\left(j\right)$ can be calculated as $B^{-1}{\Sigma }_{b=1}^{B}I\{{\widehat{S}}_{\text{max}\left(b\right)}^{\ast }>\widehat{S}\left(j\right)\}$. After multiple comparisons, adjusting for 23 pathways remain significant when Gaussian kernel is used and 17 when Linear kernel is used. For example, without adjusting for multiple comparisons, the EGFR pathway is significantly associated with breast cancer survival with p-value 0.0008 based on the Gaussian kernel and 0.014 based on the linear kernel. However, after accounting for the fact that we tested 70 pathways, it remains significant with a p-value of 0.038 when the Gaussian kernel is used but no longer significant when the linear kernel is used.

6. Discussions

We develop a powerful kernel machine test to test for the parametric/nonparametric pathway effect for survival data. A key advantage of the kernel machine test is that it can effectively borrow information across genes within a pathway by accounting for between-gene correlation and yield a powerful test with a low DF test if the genes within a pathway are moderately correlated. Its power is shown not affected when the number of genes including noisy genes increases within a pathway as long as the genes are correlated. When the underlying effects of Z is complex, testing based on the Gaussian kernel could potentially lead to a substantial power gain when compared to testing with linear kernel which corresponds to the Goeman et al (2005) procedure. The R code for implementing the proposed testing procedures will be available upon request.

The scaled χ² approximation to the null distribution of $\widehat{Q}\left(\rho \right)$ provides us a venue to assess the effective DF for the proposed test. As one expects, the DF does not increase with p quickly when Z are moderately or highly correlated and thus under such settings, the proposed test works well even for large p. On the other hand, when there is little correlation between the genes, the effective DF would be of similar order as p and thus the test may perform poorly when p is in the similar magnitude as n. In this case, resampling methods such as the permutation procedure could be used to estimate the null distribution of the test.

For the Gaussian kernel, the selection of ρ plays an important role in the score test. Large sample approximation to the null distribution may perform poorly when ρ is too small or too large. We determine the range of ρ based on kernel PCA. It is important to note the trade-off between selecting different values of ℓ₀. A small ℓ₀ might result in a significant power loss due to approximating $\mathbb{K}$ with $\tilde{\mathbb{K}}$ while a large ℓ₀ may result in a higher effective DF and thus may also lead to efficiency loss. From Theorem 5.541 of Braun (2005), the projection error due to kernel PCA is approximately of order $O\left({\ell }_0^{-a}\right)$ for some a > 0 when the eigenvalues of the kernel function K decay at a polynomial rate and of order $O\left(e^{-b{\ell }_0}\right)$ for some b > 0 when the eigenvalues decay exponentially. It would be interesting to investigate the optimal thresholding value ℓ₀. Our simulation results suggest that in most cases, the score test with $\rho \in \mathcal{I}$ with respect to power and size.

Our proposed test adjust for covariates U under a linearity assumption on the effects of U. When the true effect of U is non-linear, the proposed test derived under the linearity assumption may have incorrect size. Thus, it is important to examine the appropriateness of the linearity assumption. In practice, since U involves clinical variables that are typically well studied, prior information is often available to pre-specified potentially non-linear functional forms for U. More robust procedures such as the regression spline could also be used to incorporate non-linear effects in U.

Appendix: Asymptotic Distribution for the Score Test Statistic

Throughout, we assume that $\rho \in [{\mathfrak{p}}_l,{\mathfrak{p}}_r]\in (-\infty ,\infty )$, Z is bounded, K(z₁, z₂, ρ) is continuously differentiable with respect to all of its arguments and is symmetric about z₁ and z₂, the conditional density of C given Z is continuous and bounded and the marginal density of C is bounded away from 0 on [0, τ]. We assume that the upper bound of the support of X, denoted by τ, is finite.

To derive the asymptotic distribution for $\widehat{Q}\left(\rho \right)$, we first note that ${\text{sup}}_{t\le \tau }\mid {\widehat{\Lambda }}_0\left(t\right)-{\Lambda }_0\left(t\right)\mid +\parallel \widehat{\gamma }-{\gamma }_0\parallel =o_p\left(1\right)$ (Fleming and Harrington, 1991), $n^{\frac{1}{2}}(\widehat{\gamma }-{\gamma }_0)=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{\mathbf{W}}_{\gamma i}+O_p\left(n^{-\frac{1}{2}}\right)$, ${\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)=n^{\frac{1}{2}}\{{\widehat{\Lambda }}_0\left(t\right)-{\Lambda }_0\left(t\right)\}=n^{-\frac{1}{2}}{\Sigma }_{i=1}^n{W}_{\Lambda i}\left(t\right)+O_p\left(n^{-\frac{1}{2}}\right)$, where γ₀ is the true value of γ,

$${\mathbf{W}}_{\gamma i}=\int {\mathbb{A}}^{-1}\left\{{\mathbf{U}}_i-\frac{{\mathfrak{S}}^{\left(1\right)}\left(t\right)}{{\mathfrak{S}}^{\left(0\right)}\left(t\right)}\right\}d{M}_i\left(t\right),W_{\Lambda i}\left(t\right)={\int }_0^t\frac{d{M}_i\left(s\right)-{\mathbf{W}}_{\gamma i}^{⊺}{\mathfrak{S}}^{\left(1\right)}\left(s\right)d{\Lambda }_0\left(s\right)}{{\mathfrak{S}}^{\left(0\right)}\left(s\right)}$$ (A.1)

$\mathbb{A}=\int \{{\mathfrak{S}}^{\left(2\right)}\left(t\right)-{\mathfrak{S}}^{\left(1\right)}{\left(t\right)}^{\otimes 2}\}{\mathfrak{S}}^{\left(0\right)}{\left(t\right)}^{-2}dE\left\{N_i\left(t\right)\right\}$, ${\mathfrak{S}}^{\left(k\right)}\left(t\right)=E\left\{{\tilde{Y}}_i\left(t\right){\mathbf{U}}_i^{\otimes k}\right\}$, ${\tilde{Y}}_i\left(t\right)=Y_i\left(t\right)e^{{\gamma }_0^{\mathrm{T}}{\mathbf{U}}_i}$ for any vector u, ${\mathbf{u}}^{\otimes 0}=1$, ${\mathbf{u}}^{\otimes 1}=\mathbf{u}$, and ${\mathbf{u}}^{\otimes 2}={\mathbf{uu}}^{\mathrm{T}}$. It follows that

$${\widehat{M}}_i=M_i-n^{-\frac{1}{2}}\int {\tilde{Y}}_i\left(t\right)d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)-{(\widehat{\gamma }-{\gamma }_0)}^{⊺}{\tilde{\mathbf{U}}}_i+O_p\left(n^{-1}\right).$$ (A.2)

We next write $n^{-1}\widehat{Q}\left(\rho \right)={\widehat{\mathcal{Q}}}_1\left(\rho \right)+{\widehat{\mathcal{Q}}}_2\left(\rho \right)+{\widehat{\mathcal{Q}}}_3\left(\rho \right)-\widehat{q}\left(\rho \right)$, where

$${\widehat{\mathcal{Q}}}_1\left(\rho \right)=n^{-1}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right)M_i{M}_j=\int K({\mathbf{z}}_1,{\mathbf{z}}_2,\rho )d{\widehat{\mathbb{W}}}_M\left({\mathbf{z}}_1\right)d{\widehat{\mathbb{W}}}_M\left({\mathbf{z}}_2\right)$$

$${\widehat{\mathcal{Q}}}_2\left(\rho \right)=2n^{-1}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right)({\widehat{M}}_i-M_i)M_j,{\widehat{\mathcal{Q}}}_3\left(\rho \right)=n^{-1}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right)({\widehat{M}}_i-M_i)({\widehat{M}}_j-M_j)$$

From (A.2), ${\widehat{\mathcal{Q}}}_2\left(\rho \right)=-2n^{-1}\int [\int \left\{{\Sigma }_{i=1}^{n}K({\mathbf{Z}}_i,\mathbf{z},\rho ){\tilde{Y}}_i\left(t\right)\right\}d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)-{\widehat{\mathbf{W}}}_{\gamma }^{\mathrm{T}}\left\{{\Sigma }_{i=1}^{n}K({\mathbf{Z}}_i,\mathbf{z},\rho ){\tilde{\mathbf{U}}}_i\right\}]d{\widehat{\mathbb{W}}}_M\left(\mathbf{z}\right)+o_p\left(1\right)$. By a uniform law of large numbers (ULLN, Pollard, 1990), ${\text{sup}}_{\mathbf{z},\rho ,t}\mid n^{-1}{\Sigma }_{i=1}^{n}K({\mathbf{Z}}_i\mathbf{z},\rho ){\tilde{Y}}_i\left(t\right)-{\omega }_0(\mathbf{z},t,\rho )\mid +{\text{sup}}_{\mathbf{z},\rho }\parallel n^{-1}{\Sigma }_{i=1}^{n}K({\mathbf{Z}}_i,\mathbf{z},\rho ){\tilde{U}}_i-{\omega }_1(\mathbf{z},\rho )\parallel =o_p\left(1\right)$. This, together with Lemma A1 of Bilias et al (1997), implies that

$${\widehat{\mathcal{Q}}}_2\left(\rho \right)=-2\int \left\{\int {\omega }_0(\mathbf{z},t,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)+{\widehat{\mathbf{W}}}_{\gamma }^{⊺}{\omega }_1(\mathbf{z},\rho )\right\}d{\widehat{\mathbb{W}}}_M\left(\mathbf{z}\right)+o_p\left(1\right)$$

Furthermore, ${\widehat{\mathcal{Q}}}_3\left(\rho \right)$ is asymptotically equivalent to

$${\widehat{\mathbf{W}}}_{\gamma }^{⊺}\left\{n^{-2}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right){\tilde{\mathbf{U}}}_i{\tilde{\mathbf{U}}}_j\right\}{\widehat{\mathbf{W}}}_{\gamma }+2{\widehat{\mathbf{W}}}_{\gamma }^{⊺}\int \left\{n^{-2}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right){\tilde{\mathbf{U}}}_i{\tilde{Y}}_j\left(s\right)\right\}d{\widehat{\mathbb{W}}}_{\Lambda }\left(s\right)\iint \left\{n^{-2}\sum _{i=1}^n\sum _{j=1}^n{K}_{ij}\left(\rho \right){\tilde{Y}}_i\left(t\right){\tilde{Y}}_j\left(s\right)\right\}d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)d{\widehat{\mathbb{W}}}_{\Lambda }\left(s\right).$$

This, together with a ULLN for U-processes (Nolan and Pollard, 1987) and Lemma A1 of Bilias et al. (1997), implies that ${\tilde{\mathcal{Q}}}_3\left(\rho \right)=\int \int {\omega }_{00}(t,s,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)d{\widehat{\mathbb{W}}}_{\Lambda }\left(s\right)+{\widehat{\mathbf{W}}}_{\gamma }^{\mathrm{T}}{\omega }_{11}\left(\rho \right){\widehat{\mathbf{W}}}_{\gamma }+2{\widehat{\mathbf{W}}}_{\gamma }^{\mathrm{T}}\int {\omega }_{10}(s,\rho )d{\widehat{\mathbb{W}}}_{\Lambda }\left(s\right)$. Lastly, by a ULLN and the consistency of $\widehat{\gamma }$, ${\widehat{\Lambda }}_0\left(t\right)$, ${\text{sup}}_{\rho }\mid \widehat{q}\left(\rho \right)-q\left(\rho \right)\mid =o_p\left(1\right)$. This, together with the approximations for ${\widehat{\mathcal{Q}}}_2$ and ${\widehat{\mathcal{Q}}}_3$, implies that $\widehat{\mathcal{Q}}\left(\rho \right)=\widehat{\mathcal{W}}\left(\rho \right)-q\left(\rho \right)+o_p\left(1\right)$.

We next derive the asymptotic distribution of $\tilde{\mathcal{W}}\left(\rho \right)$. First, both I(Z ≤ z) and M_i(t) have finite pseudo-dimensions $t{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right)$, implies that $\{{\widehat{\mathbb{W}}}_M\left(\mathbf{z}\right),{\widehat{\mathbb{W}}}_{\Lambda }\left(t\right),{\widehat{\mathbf{W}}}_{\gamma }\}$ converge jointly to zero-mean Gaussian processes ${\mathbb{W}}_M\left(\mathbf{z}\right)$, ${\mathbb{W}}_{\Lambda }\left(t\right)$ and W. Since $\widehat{\mathcal{W}}\left(\rho \right)$ is a smooth functional of ${\mathbb{W}}_M\left(\mathbf{z}\right)$, ${\mathbb{W}}_{\Lambda }\left(t\right)$ and W, it then follows from a strong representation theorem (Pollard, 1990) and Lemma A1 of Bilias et al (1997) that that $\widehat{\mathcal{W}}\left(\rho \right)$ converges weakly to the process

$$\mathcal{W}\left(\rho \right)=\iint K({\mathbf{z}}_1{\mathbf{z}}_2,\rho )d{\mathbb{W}}_M\left({\mathbf{z}}_1\right)d{\mathbb{W}}_M\left({\mathbf{z}}_2\right)-2\int \left\{\int {\omega }_0(\mathbf{z},t,\rho )d{\mathbb{W}}_{\Lambda }\left(t\right)+{\mathbf{W}}_{\gamma }^{⊺}{\omega }_1(\mathbf{z},\rho )\right\}d{\mathbb{W}}_M\left(\mathbf{z}\right)+\iint {\omega }_{00}(t,s,\rho )d{\mathbb{W}}_{\Lambda }\left(t\right)d{\mathbb{W}}_{\Lambda }\left(s\right)+{\mathbf{W}}_{\gamma }^{⊺}{\omega }_{11}\left(\rho \right){\mathbf{W}}_{\gamma }+2{\mathbf{W}}_{\gamma }^{⊺}\int {\omega }_{10}(s,\rho )d{\mathbb{W}}_{\Lambda }\left(s\right)$$ (A.3)