Abstract
Purpose: To mathematically model the relationship between CT measurements of emphysema obtained from images reconstructed using different section thicknesses and kernels and to evaluate the accuracy of the models for converting measurements to those of a reference reconstruction.
Methods: CT raw data from the lung cancer screening examinations of 138 heavy smokers were reconstructed at 15 different combinations of section thickness and kernel. An emphysema index was quantified as the percentage of the lung with attenuation below −950 HU (EI950). Linear, quadratic, and power functions were used to model the relationship between EI950 values obtained with a reference 1 mm, medium smooth kernel reconstruction and values from each of the other 14 reconstructions. Preferred models were selected using the corrected Akaike information criterion (AICc), coefficients of determination (R2), and residuals (conversion errors), and cross-validated by a jackknife approach using the leave-one-out method.
Results: The preferred models were power functions, with model R2 values ranging from 0.949 to 0.998. The errors in converting EI950 measurements from other reconstructions to the 1 mm, medium smooth kernel reconstruction in leave-one-out testing were less than 3.0 index percentage points for all reconstructions, and less than 1.0 index percentage point for five reconstructions. Conversion errors were related in part to image noise, emphysema distribution, and attenuation histogram parameters. Conversion inaccuracy related to increased kernel sharpness tended to be reduced by increased section thickness.
Conclusions: Image reconstruction-related differences in quantitative emphysema measurements were successfully modeled using power functions.
Keywords: CT; quantitative; section thickness; reconstruction kernel; lungs, emphysema
INTRODUCTION
Using multidetector CT (MDCT), the alterations in lung morphology produced by emphysema can be quantified by determining the percentage of lung tissue with attenuation below a specified threshold in Hounsfield units (HU).1 This parameter, referred to hereinafter as the CT emphysema index, has become accepted as an objective and clinically relevant means of measuring the extent of emphysema when comparing different populations. The noninvasive CT quantification of emphysema has resulted in the identification of differences in susceptibility to emphysema related to gender,2, 3 race,4 body habitus,5 and genes.6 It has also made the classification of patients with chronic obstructive pulmonary disease (COPD) into different emphysema phenotypes a realistic goal that may result in a greater understanding of pathogenesis and lead to more individualized therapy.7, 8, 9, 10, 11 Hence, potential future clinical applications of CT emphysema quantification include the monitoring of disease progression and the assessment of response to any new therapies designed to slow its progression.
The CT emphysema index does not correspond directly to the absolute amount of emphysema, but rather correlates with histologic measurements of emphysema.1, 12, 13, 14, 15 It is recognized that the measured value of the CT emphysema index will vary depending on the section thickness and reconstruction kernel used to generate images from the CT raw data. It has been found in several cohorts that either reducing the section thickness14, 15, 16 or increasing the sharpness of the reconstruction kernel17, 18, 19 resulted in an increase in the mean CT emphysema index. Other work has shown that these effects are related to the extent of emphysema in a nonlinear way, so that the difference in emphysema index with any two different reconstructions is smaller when the extent is either very small or very large, and larger for intermediate amounts of emphysema. For extremely severe emphysema, such as is found in some lung transplant candidates, these effects of section thickness and reconstruction kernel are reversed, so that thinner sections and sharper kernels result in lower emphysema index values.15 The mechanisms of these thickness and kernel effects have not been directly studied but may be related in part to differences in image noise levels and to differences in the degree to which the voxel attenuation coefficients at the lung air-tissue interfaces are altered by the reconstruction kernel.
This section thickness- and reconstruction kernel-related variation may limit the ability to compare CT measurements of emphysema among individuals whose images were generated using different reconstruction parameters. For studies comparing emphysema in different groups or in the same group over time, the impact of this variation on the ability to detect differences will depend on the actual size of the group differences and the degree of measurement variation, which in turn affect the needed size of the study population. To limit the impact of measurement variation, it is now recognized that section thickness and reconstruction kernel should be clearly specified and held constant in prospective cross-sectional and longitudinal studies. However, this may not be possible in studies analyzing existing CT examinations in which differing reconstruction parameters were used. Technical differences in image reconstruction among different scanner models add an additional unknown amount of measurement variation. The ability to normalize quantitative emphysema index values from images generated using different reconstruction parameters to a standard measurement scale would be very useful for these situations but has not previously been demonstrated.
Although CT emphysema index measurements vary depending on the image reconstruction parameters, the measurements using different parameters are correlated to each other and to histologic measurements of emphysema.14, 15 We therefore hypothesized that the relationship between CT emphysema index measurements obtained with different reconstruction techniques can be modeled mathematically, and that the relationship can be used to convert measurements using one reconstruction technique to those that would have been obtained with a different reconstruction. The purpose of this study was to test these hypotheses and to determine the accuracy of converting to a standard reference reconstruction technique.
MATERIALS AND METHODS
Approval to conduct this study was obtained from the Human Research Protection Office at our institution and included a waiver of informed consent for the use of existing data.
Subjects
The 138 subjects of this study were a subset of the 1880 participants in the National Lung Screening Trial (Ref. 20 , clinical trials.gov identifier NCT00047385)21 who had undergone screening for lung cancer using low-radiation-dose multidetector CT at our institution. This study was not part of the National Lung Screening Trial. The subjects included in the present study were those for whom CT raw data had been saved by a research coordinator when permitted by the daily workflow of the clinical CT service. There were 91 men and 47 women, with a mean ± standard deviation age of 61 ± 5 years. All subjects had a smoking history of at least 30 pack years, with a mean ± standard deviation of 61.5 ± 28.7 pack years. Data from this study population were used previously in an unrelated investigation.22
Imaging and image analysis
The CT scans were performed on a 16-MDCT scanner (Sensation 16, Siemens Healthcare, Erlangen, Germany) at end-inspiration using a low radiation dose technique. Technical parameters included 0.75 mm detector collimation, 120 kVp, 45 mAs, and 1.5 pitch for an effective tube current of 30 mAs. For each subject, a single raw data acquisition was used to reconstruct 15 sets of contiguous transverse images, each with a unique combination of one of three different section thicknesses (1, 2, and 5 mm) and one of five different body reconstruction kernels including Siemens B20f (smooth), B30f (medium smooth), B40f (medium), B50f (medium sharp), and B60f (sharp). The reconstructions were generated using a proprietary desktop version of software for the Sensation 16 scanner (Siemens).
Analysis of the CT images was performed using the pULMONARYANALYSISSOFTWARESUITEEMPHYSEMAPROFILER (VIDA Diagnostics, Iowa City, IA) computer program.23 This software produced histograms of lung voxel attenuation values after automatically outlining the lungs in the CT images. Emphysema was quantified by calculating the number of voxels within a given volume having attenuation less than −950 HU divided by the total number of voxels within that volume, a measurement referred to hereinafter as the emphysema index (EI950); thresholds at and near this level have been validated against tissue specimens using both standard clinical and low radiation dose scan techniques.1, 13, 14, 15 The software also divided the lungs into upper, middle, and lower thirds, allowing for calculation of both whole lung and regional partial-lung CT emphysema indices. Image noise was determined by measuring the standard deviation of the attenuation of air in circular or oval regions of interest within the trachea near the carina on three consecutive CT sections.
Modeling
Scatter plots were generated using the EI950 measured on 1 mm-B30f reconstructions as the dependent variable and the EI950 measured using each of the other 14 different reconstructions as the independent variable. The 1 mm-B30f reconstruction was chosen as the reference because similar techniques have provided very good correlation with quantitative emphysema histology,14, 15 and because a thin-section, low to medium spatial resolution reconstruction is generally preferred for emphysema quantification.24 Inspection of the scatter plots and preliminary curve-fitting analyses revealed that while the relationships of some reconstructions with the reference reconstruction appeared nearly linear, all could be fit very well with either quadratic or power functions. Subsequently, linear [f(x) = a + bx], quadratic [f(x) = a + bx + cx2], and power function [f(x) = axb] models were generated to relate the EI950 from each of the other 14 section thickness-kernel combinations to the EI950 of the 1 mm-B30f reference, using JMP 8.0 (SAS Institute, Cary, NC). For each model, data from all 138 subjects were used to determine best fit parameters using the least squares method.
Model selection
For each of the 14 section thickness-kernel combinations, the relative performance of the linear, quadratic, and power function models was ranked based on the value of the small sample size-corrected Akaike information criterion (AICc),25, 26 determined using JMP 8.0 (SAS Institute, Cary, NC). This statistical parameter provides a means for comparing the goodness of fit of different statistical models. The model with the lowest AICc was considered the best model for predicting the 1 mm-B30f EI950.26
For further assessment of goodness of fit, the model residuals, or difference between the model-predicted EI950 value for the 1 mm-B30f reconstruction and the actual value (referred to hereinafter as conversion errors), were examined. This included determination of the minimum, 5th percentile, 95th percentile, and maximum conversion errors. In addition, the coefficients of determination (R2 values) for each model were reviewed. Considering the AICc, the size of the conversion errors, and the coefficients of determination, a preferred model was then chosen for predicting the EI950 values of the reference reconstruction technique from the values of the other reconstruction techniques.
Model testing
The reliability of the preferred models was cross-validated by a jackknife approach using the leave-one-out method. For each of the 14 test reconstructions, model parameters were determined N times (where N equals the total number of study subjects or 138) using the data from N − 1 subjects, leaving a different subject out each time. From each model, a predicted EI950 at 1 mm-B30f was determined for each subject left out, and the model R2 values and conversion errors for each cycle were compiled for each reconstruction.
Model refinement
The various reconstructions represent different mathematical manipulations of image data from the same lungs in the same physical state. Since a perfect mathematical relationship (i.e., R2 = 1 and conversion errors = 0) was not found between the EI950 values of the different reconstructions, we postulated that the size of the conversion errors may be due to the individual subject differences in body size and the amount and distribution of emphysema. This was based on the consideration that these factors can lead to differences in image noise and to local differences in tissue attenuation measurements, respectively, both of which may influence the effects of the different reconstructions. Consequently, we investigated the relationship of image noise (which varies in part with individual body size), the spatial distribution of emphysema, and the lung voxel attenuation frequency (lung attenuation histogram) statistics to the size of conversion errors. This analysis was performed using data from all 138 subjects, for the reconstructions in which conversion was least successful (defined as those in which the 5th and 95th percentile conversion errors were 1.0 index percentage points or larger). Noise was measured as the standard deviation of air attenuation measured in the lower trachea; the spatial distribution of emphysema was quantified as the ratio of the EI950 in the upper third to the lower third of the lungs (U/L); and the lung attenuation histogram was characterized by its mean and standard deviation (SD). These four parameters were entered into separate multiple regression models for each reconstruction using the conversion error as the dependent variable, and backwards stepwise regression27 was performed using JMP 8.0, requiring a p value of 0.05 to retain a parameter, to determine whether these parameters were independently related to the size of the conversion error. These conversion error prediction models were then used to generate linear corrective terms for the predicted 1 mm-B30f EI950 values, and the R2 and conversion errors of the refined preferred models were examined.
RESULTS
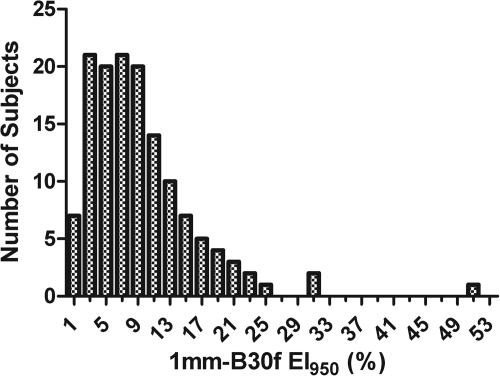
The frequency distribution of EI950 values for the 1 mm-B30f reconstruction is shown in Fig. 1. The mean ± standard deviation was 9.4 ± 6.9%, with a median of 8.0%. The mean ± standard deviation and range of EI950 measured for each section thickness-kernel combination are shown in Table Table I.. For reconstructions made with the same section thickness, using a sharper kernel produced a larger average EI950. For reconstructions that used the same kernel, thinner sections produced a larger average EI950.
Figure 1.
Frequency distribution of EI950 values for the 1 mm-B30f reconstruction.
Table 1.
The average ± standard deviation (range) EI950 at each section thickness-reconstruction kernel combination.
| B20f | B30f | B40f | B50f | B60f | |
|---|---|---|---|---|---|
| 1 mm | 8.43% ± 6.77% | 9.43% ± 6.86% | 10.85% ± 6.96 % | 19.83% ± 6.83% | 22.02% ± 6.49% |
| (0.71%–50.41%) | (0.90%–50.27%) | (1.15%–50.23%) | (4.44%–49.85%) | (5.93%–48.75%) | |
| 2 mm | 5.82% ± 6.23% | 6.37% ± 6.32% | 7.27% ± 6.45% | 14.28% ± 6.90% | 16.22% ± 6.77% |
| (0.27%–49.05%) | (0.32%–48.97%) | (0.43%–49.06%) | (2.02%–49.21%) | (2.70%–48.13%) | |
| 5 mm | 3.13% ± 5.06% | 3.28% ± 5.10% | 3.61% ± 5.19% | 7.04% ± 5.86% | 8.18% ± 5.93% |
| (0.08%–44.61%) | (0.09%–44.54%) | (0.10%–44.68%) | (0.51%–45.42%) | (0.62%–44.70%) |
Model selection
Results of the analysis comparing linear, quadratic, and power function prediction models are shown in Table Table II.. For each section thickness-kernel combination, the best model for predicting the 1 mm-B30f EI950 had a coefficient of determination (R2) greater than 0.950. Conversion errors (residuals) ranged from −5.25 to 6.02 emphysema index percentage points, though the largest 5th and 95th percentile conversion errors were less than half of these extreme values of the range as shown in Table Table II..
Table 2.
Best models as determined by AICc at each section thickness-kernel combination (reconstruction) to predict EI950 at 1 mm-B30f. The values for the parameters a, b, and c were determined by a least squares method.
| Conversion errorsa | ||||||
|---|---|---|---|---|---|---|
| Reconstruction | Best model | R2 | Min (%) | 5th %ile | 95th %ile | Max (%) |
| 1 mm-B20f | a*(EI950)b | 0.998 | −0.66 | −0.51 | 0.45 | 0.70 |
| 1 mm-B40f | a*(EI950)b | 0.998 | −0.66 | −0.44 | 0.52 | 0.83 |
| 1 mm-B50f | a*(EI950)b | 0.965 | −2.89 | −1.64 | 2.49 | 4.79 |
| 1 mm-B60f | a + b*(EI950) + c*(EI950)2 | 0.951 | −3.47 | −1.94 | 2.95 | 6.02 |
| 2 mm-B20f | a*(EI950)b | 0.985 | −2.58 | −1.60 | 1.27 | 2.09 |
| 2 mm-B30f | a*(EI950)b | 0.992 | −2.02 | −1.12 | 0.89 | 1.58 |
| 2 mm-B40f | a*(EI950)b | 0.998 | −1.27 | −0.58 | 0.44 | 0.88 |
| 2 mm-B50f | a*(EI950)b | 0.983 | −2.02 | −1.19 | 1.77 | 3.07 |
| 2 mm-B60f | a*(EI950)b | 0.970 | −2.73 | −1.59 | 2.34 | 4.46 |
| 5 mm-B20f | a*(EI950)b | 0.951 | −5.25 | −2.42 | 2.50 | 3.33 |
| 5 mm-B30f | a*(EI950)b | 0.961 | −4.98 | −2.28 | 2.06 | 2.89 |
| 5 mm-B40f | a*(EI950)b | 0.973 | −4.48 | −1.93 | 1.72 | 2.38 |
| 5 mm-B50f | a*(EI950)b | 0.997 | −1.09 | −0.58 | 0.49 | 1.48 |
| 5 mm-B60f | a + b*(EI950) + c*(EI950)2 | 0.991 | −3.03 | −1.02 | 0.96 | 2.37 |
Notes: Min—smallest conversion error among all 138 subjects. Max—largest conversion error among all 138 subjects. 5th%ile—5th percentile of all conversion errors among all 138 subjects. 95th%ile—95th percentile of all conversion errors among all 138 subjects.
Values are in index percentage points.
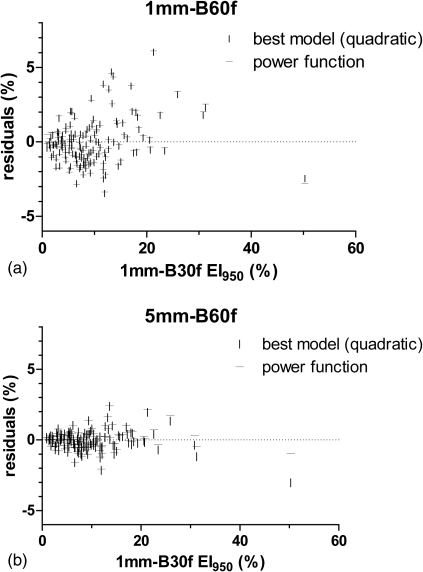
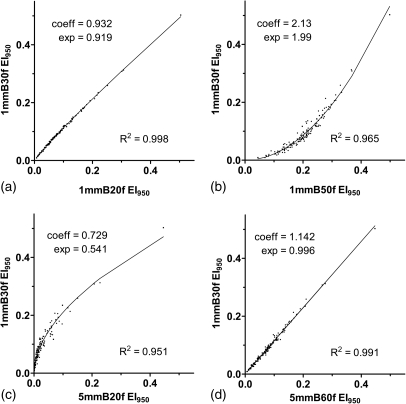
For all but two reconstructions (1 mm-B60f and 5 mm-B60f), the best model as determined by the AICc was a power function that used EI950 as the input variable. For these two cases, the best model was a quadratic function; however, R2 and analysis of the residuals showed that the best fit power function performed almost exactly as well as the best model (Table Table III.). For both, the difference in R2 between the power function and the model with the smallest AICc was less than 0.002. Additionally, the residuals for the power function differed minimally from the residuals for the best model (Fig. 2). Thus, for consistency and simplicity, we considered a power function (Fig. 3) to be the preferred mathematical conversion model for all reconstructions.
Table 3.
Comparison of the best model to the best fit EI950 power functions for the two reconstructions (1 mm-B60f) and (5 mm-B60f) for which the best model to predict the 1 mm-B30f EI950 was not a power function.
| Conversion errorsa | ||||||
|---|---|---|---|---|---|---|
| Model | R2 | Min (%) | 5th %ile | 95th %ile | Max (%) | |
| 1 mm-B60f | a + b*(EI950) + c*(EI950)2 | 0.951 | −3.47 | −1.94 | 2.95 | 6.02 |
| a*(EI950)b | 0.949 | −3.37 | −2.04 | 2.88 | 6.11 | |
| 5 mm-B60f | a + b*(EI950) + c*(EI950)2 | 0.991 | −3.03 | −1.02 | 0.96 | 2.37 |
| a*(EI950)b | 0.991 | −2.06 | −0.95 | 1.01 | 2.41 | |
Notes: Min— smallest conversion error among all 138 subjects. Max—largest conversion error among all 138 subjects. 5th%ile—5th percentile of all conversion errors among all 138 subjects. 95th%ile—95th percentile of all conversion errors among all 138 subjects.
Values are in index percentage points.
Figure 2.
Residual plots of the best models and power function models for the two reconstructions [1 mm-B60f in (a) and 5 mm-B60f in (b)] in which the best model for predicting the 1 mm-B30f emphysema index was not a power function.
Figure 3.
Scatter plots and power function fits relating the reference 1 mm-B30f reconstruction to (a) the 1 mm-B20f, (b) 1 mm-B50f, (c) 5 mm-B20f, and (d) 5 mm-B60f reconstructions. These are representative of the stronger (1 mm-B20f), weaker (1 mm-B50f and 5 mm-B20f), and intermediate (5 mm-B60f) fits.
Model testing
The results of the leave-one-out cross-validation using power functions to predict the 1 mm-B30f EI950 are presented in Table Table IV.. The R2 values for each reconstruction in the cross-validation (Table Table IV.) were virtually the same as those obtained with the entire data set (Table Table II.), with no to minimal difference between the smallest, mean, and largest R2 value among all 138 leave-one-out cycles.
Table 4.
Leave-one-out cross-validation using power functions to estimate 1 mm-B30f EI950 values from other reconstructions.
| Leave-one-out R2 values | Leave-one-out conversion errorsa | ||||||
|---|---|---|---|---|---|---|---|
| Reconstruction | Min | Mean | Max | Min (%) | 5th%ile | 95th%ile | Max (%) |
| 1 mm-B20f | 0.998 | 0.998 | 0.998 | −0.66 | −0.52 | 0.46 | 1.15 |
| 1 mm-B40f | 0.998 | 0.998 | 0.998 | −1.42 | −0.45 | 0.52 | 0.85 |
| 1 mm-B50f | 0.958 | 0.965 | 0.965 | −7.93 | −1.66 | 2.66 | 4.85 |
| 1 mm-B60f | 0.943 | 0.949 | 0.949 | −7.84 | −2.05 | 2.91 | 6.19 |
| 2 mm-B20f | 0.984 | 0.985 | 0.985 | −2.61 | −1.62 | 1.28 | 3.89 |
| 2 mm-B30f | 0.992 | 0.992 | 0.992 | −2.05 | −1.13 | 0.90 | 3.03 |
| 2 mm-B40f | 0.998 | 0.998 | 0.998 | −1.27 | −0.60 | 0.44 | 1.76 |
| 2 mm-B50f | 0.981 | 0.983 | 0.983 | −4.97 | −1.20 | 1.79 | 3.12 |
| 2 mm-B60f | 0.967 | 0.970 | 0.970 | −5.49 | −1.60 | 2.36 | 4.53 |
| 5 mm-B20f | 0.949 | 0.951 | 0.951 | −5.33 | −2.46 | 2.53 | 5.61 |
| 5 mm-B30f | 0.959 | 0.961 | 0.961 | −5.06 | −2.31 | 2.09 | 5.20 |
| 5 mm-B40f | 0.972 | 0.973 | 0.973 | −4.55 | −1.99 | 1.77 | 4.37 |
| 5 mm-B50f | 0.997 | 0.997 | 0.997 | −1.35 | −0.58 | 0.49 | 1.49 |
| 5 mm-B60f | 0.991 | 0.991 | 0.991 | −2.20 | −0.96 | 1.02 | 2.43 |
Notes: R2 and conversion error statistics are from 138 power function models generated for each reconstruction, leaving a different case out for each model. Min—smallest conversion error from the 138 power function models generated by leaving one case out. Max— largest conversion error from the 138 power function models generated by leaving one case out. 5th%ile—5th percentile of all conversion errors from the 138 power function models generated by leaving one case out. 95th%ile—95th percentile of all conversion errors from the 138 power function models generated by leaving one case out.
Values are in index percentage points.
The 5th and 95th percentile conversion errors for each reconstruction (Table Table IV.) also were very similar to those found with the entire data set (Table Table II.), being less than 3.0 index percentage points for all 138 leave-one-out cycles with all reconstructions, and less than 1.0 index percentage point for five reconstructions. However, either the minimum or the maximum conversion error (depending on the reconstruction) among the 138 leave-one-out iterations (Table Table IV.) was larger than that found with the entire data set (Table Table II.) for many reconstructions. The 1 mm smooth kernels (B20f and B40f), 2mm-B40f, and 5 mm sharp kernel (B50f and B60f) reconstructions all generated conversions that performed exceptionally well, with conversion errors smaller than 2.5 emphysema index percentage points for all subjects. The other reconstructions were less universally reliable, with conversion errors as high as 4.5–7.9 emphysema index percentage points in some subjects.
Refined model assessment
The analysis of factors potentially associated with the size of the model residuals (conversion errors) is shown in Table Table V.. Different combinations of the four variables assessed (noise, U/L, mean, and SD) were significantly associated with the size of the conversion errors for the different reconstructions, with R2 for the conversion error factor models ranging from 0.35 to 0.48. Noise and U/L were the only two variables present in every model. These variables together accounted for the largest proportion of the R2 of the models, with noise having the strongest association. Table Table V. also lists the range and 5th and 95th percentiles of the conversion errors for predicting the 1 mm-B30f EI950, and the R2 of the models, when these variables were used as linear corrective terms to the power functions. Comparison to the data in Tables 2, Table III. reveals that the addition of linear corrective terms resulted in only marginal improvement in R2 and conversion errors; this improvement was nearly as great correcting only for noise and U/L as correcting for all variables which were significant in the models.
Table 5.
Parameters related to conversion errors and their effects as linear correction terms to the power functions in estimating 1 mm-B30f EI950 values.
| Performance of modified power function modelsa | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correction for all significant parameters | Correction for noise and U/L only | |||||||||||
| Models for predicting conversion errors | Conversion errorc | Conversion errorc | ||||||||||
| Reconstruction | Parametersb | Model R2 | Min | 5th%ile | 95th%ile | Max | R2 | Min | 5th%ile | 95th%ile | Max | R2 |
| 1 mm-B50f | Noise, U/L | 0.35 | −4.2 | −1.3 | 1.7 | 3.4 | 0.978 | −4.2 | −1.3 | 1.7 | 3.4 | 0.978 |
| 1 mm-B60f | Noise, U/L, Mean, SD | 0.38 | −2.7 | −1.5 | 1.5 | 2.8 | 0.970 | −4.3 | −1.5 | 2.2 | 4.0 | 0.967 |
| 2 mm-B20f | Noise, U/L, Mean | 0.47 | −2.0 | −1.0 | 0.8 | 2.1 | 0.992 | −2.0 | −1.0 | 1.0 | 2.6 | 0.991 |
| 2 mm-B30f | Noise, U/L, Mean | 0.47 | −1.4 | −0.7 | 0.6 | 1.6 | 0.996 | −1.5 | −0.7 | 0.7 | 2.0 | 0.996 |
| 2 mm-B50f | Noise, U/L | 0.36 | −2.9 | −1.0 | 1.0 | 2.5 | 0.989 | −2.9 | −1.0 | 1.0 | 2.5 | 0.989 |
| 2 mm-B60f | Noise, U/L | 0.35 | −3.1 | −1.3 | 1.4 | 3.4 | 0.981 | −3.1 | −1.3 | 1.4 | 3.4 | 0.981 |
| 5 mm-B20f | Noise, U/L, Mean | 0.37 | −3.3 | −2.2 | 1.9 | 3.0 | 0.970 | −3.6 | −2.0 | 2.0 | 3.8 | 0.968 |
| 5 mm-B30f | Noise, U/L, Mean | 0.41 | −3.3 | −1.7 | 1.5 | 2.8 | 0.978 | −3.5 | −1.6 | 1.7 | 3.6 | 0.976 |
| 5 mm-B40f | Noise, U/L, Mean | 0.48 | −2.3 | −1.4 | 1.1 | 2.4 | 0.986 | −2.3 | −1.4 | 1.3 | 3.1 | 0.985 |
Notes: Reconstructions listed are those for which the 5th—95th percentile residuals were ≥ ±1.0 index percentage point. Min—smallest conversion error among all 138 subjects. Max—largest conversion error among all 138 subjects. 5th%ile—5th percentile of all conversion errors among all 138 subjects. 95th%ile—95th percentile of all conversion errors among all 138 subjects.
Predicted 1 mm-B30f EI950 = power function output + a(Noise) + b(U/L) + c(Mean) + d(SD) + e, where noise is the standard deviation of air in the trachea; U/L is the upper: lower EI950 ratio; mean is the mean lung attenuation; SD is the standard deviation of the mean lung attenuation; a, b, c, and d are coefficients determined by the residuals multiple regression model; and e is the residuals regression model intercept. Residuals are calculated as Actual 1 mm-B30f EI950 − Predicted 1 mm-B30f EI950.
Whole model p values all <0.0001; individual parameter p value ranges: Noise−8.9 × 10−19 − 1.5 × 10-4; U/L−3.5 × 10−13 − 0.02; mean −2.2 × 10−6 − 0.002; SD–(1.5 × 10−4 − 0.01).
Values are in index percentage points.
DISCUSSION
This study illustrates the degree of accuracy obtainable in estimating the EI950 that would have been measured with a specific reference reconstruction technique, using data from CT images generated using other reconstruction techniques. Lacking knowledge of the proprietary reconstruction algorithms, we used an empirical approach to determine which of several mathematical functions most closely model the relationship between the reference EI950 values and EI950 values measured from other reconstructions. Simple power functions based on the EI950 from the other reconstructions provided the most accurate conversions. The conversion accuracy was only marginally improved when the power functions were augmented by other variables that reflect individual subject differences in image noise, emphysema spatial distribution, and attenuation histogram characteristics.
The accuracy of the conversions varied for the different reconstructions. In particular, the 1 mm smooth kernel (B20f and B40f), 2mm-B40f, and 5 mm sharp kernel (B50f and B60f) reconstructions had highly reliable conversion formulas to predict 1 mm-B30f results. For reconstructions in which the conversion formulas did not perform as well, it was not because the mathematical function form did not approximate the trends in the data, as the R2 values were all 0.95 or higher. Instead, the entirety of the data could not be well described by any of the simple functions tested. In such cases, there were several individuals for whom the measured EI950 was the same with the tested reconstruction technique but different with the 1 mm-B30f reference technique, and vice-versa, so that some deviated more from the fitted curves.
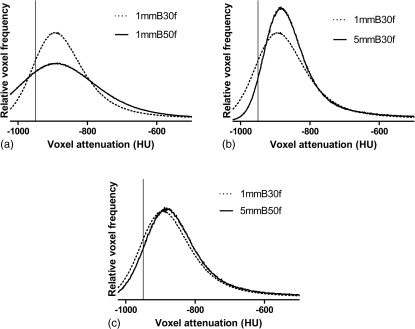
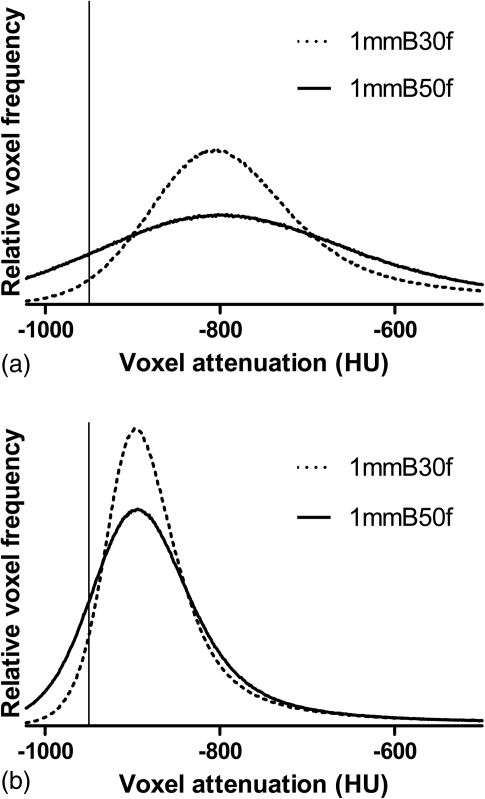
The trends in the performance of the different models and known effects of section thickness and kernel on lung attenuation histograms suggest some general principles regarding the relative ability to convert from other techniques to a thin-section, medium-smooth technique (1 mm-B30f EI950). When two reconstructions of a single raw data set use different section thicknesses (or reconstruction kernels), the histogram for the reconstruction with the thinner sections (or sharper kernel) will be broader and have a smaller peak value.16 This is a result of increased quantum noise as well as linear partial volume effects that arise as a consequence of the physical structure of the lung parenchyma.28 An example of this is shown in Fig. 4a, in this case as a result of using a sharper kernel. When using thicker sections or a smoother kernel to reconstruct images, the opposite effect may be seen, and the histogram will be narrower and more peaked [Fig. 4b].
Figure 4.
Lung voxel attenuation histograms generated from a single raw data acquisition. Dotted curves represent the histogram from 1 mm-B30f images. The solid curves are histograms from (a) 1 mm-B50f, (b) 5 mm-B30f, and (c) 5 mm-B50f reconstructions. Vertical lines are shown at −950 HU on each plot.
Because the mean and median attenuation differ minimally with different section thicknesses or kernels, these opposing effects can balance out to some degree when comparing histograms from thin section-smooth kernel reconstructions to histograms from thick section-sharp kernel reconstructions. The effect of using thicker sections (a narrower, more peaked histogram) counteracts the effect of using a sharper kernel (a broader, more spread out histogram). The end result is that the histogram for a 5 mm-B50f reconstruction is very similar in size, shape, and position to the histogram from a 1 mm-B30f reconstruction [Fig. 4c]. This likely explains why the conversion formula for predicting the 1 mm-B30f emphysema index from the 5 mm-B50f index was so surprisingly successful. For conversions without this balancing of two opposing effects, such as when converting from a 5 mm-smooth kernel or 1 mm-sharp kernel, the 1 mm-B30f emphysema index is relatively more difficult to predict with this level of accuracy in all individuals. Thus, our results suggest that the most accurate conversions can be made between reconstructions in which the lung attenuation histogram differences related to changing the section thickness are offset by the differences related to changing the kernel.
As previously noted, depending on the specific shape and position of the histograms, several different individuals may have the same emphysema index using one reconstruction technique and different indices using another (Fig. 5). The conversion error analysis was performed to look for variables that might be responsible for these individual differences and act as corrective terms to improve the conversion formulas. Image noise, the upper/lower EI950 ratio, and the whole lung attenuation histogram descriptors—mean and standard deviation—explained a substantial portion of the variance in residuals. The source of the remaining variance is unknown. Nevertheless, our analysis demonstrated that it should be possible to improve the conversion accuracy by taking these parameters into account. However, as shown by comparison of the conversion errors in Tables 2, Table V., the power functions alone performed quite well and did not leave much room for improvement in the vast majority of individuals.
Figure 5.
Lung voxel attenuation histograms from two subjects generated from 1 mm-B50f reconstructions (solid curves) and 1 mm-B30f reconstructions (dotted curves). The 1 mm-B50f emphysema index for both subjects is 13.7%. The best fit power function predicts a 1 mm-B30f emphysema index of 4.21%. The actual 1 mm-B30f emphysema indices are 2.66% for the subject in (a) and 5.69% for the subject in (b). Histograms have been normalized so that the total area under the curve is identical for each, and they are displayed on the same vertical scale. Vertical lines are shown at −950 HU on each plot.
To our knowledge, there have been no published results regarding the use of mathematical models to convert quantitative CT results among various reconstruction techniques. Prior studies of the effects of varying section thickness14, 15, 16 and reconstruction kernel15, 16, 17 are consistent with the trends seen in Table Table I.. We note that these trends represent average changes, and that the size of the effect of section thickness and kernel may vary in different individuals based on the severity of emphysema in a nonlinear manner.15 The range of emphysema severity represented in our population of heavy smokers, with EI950 of approximately 0–50% across most reconstruction techniques, is similar to the range of severity reported in other recent quantitative CT studies.15, 22, 29, 30
Some limitations of this study are recognized. First, the relationships presented here may be somewhat different for other CT scanner models or under different scanning conditions of kVp, mAs, and pitch. In addition, the EI950 values of our subject group were predominantly skewed toward the lower to mid portions of the overall range. This may have limited our ability to test the accuracy of the models in subjects with more extensive emphysema. Nevertheless, the models were quite reliable across our entire subject group. Finally, augmenting the power function models with linear correction factors based on the variables tested was only partially effective, and it is possible that other variables not recognized could provide more significant improvements.
CONCLUSION
There is growing recognition of the need to have technical standards in order to insure of the validity of quantitative CT measurement comparisons.31, 32, 33, 34 In this study, simple, robust mathematical models were found that allowed for reliable prediction of measurements from a specific reconstruction technique given data obtained using various other techniques. Since different CT manufacturers use different proprietary algorithms for image reconstruction, the specific results derived from this study may have limited applicability. The process used to generate these results, however, could be applied to find conversion formulas for other scanner models, or for other scanning conditions of kVp, mAs, and pitch. Applying this approach to convert EI950 values between different scanner models might also be possible, but would likely require the use of CT phantoms having numerous different simulated lung attenuation profiles that can be measured on different scanners. In the absence of current industry standards for CT scanners related to quantitative lung measurements, such empirical derivation of measurement conversion factors may be a feasible alternative that would allow more reliable comparison of results independent of the reconstruction parameters and scanner model used to obtain them.
ACKNOWLEDGMENTS
This research was supported by contracts from the Division of Cancer Prevention, National Cancer Institute, NIH, DHHS, and by National Heart, Lung, and Blood Institute grants P50 HL084922 and R01 HL72369. The authors thank Dr. Christine Berg, Dr. Richard Fagerstrom, and Dr. Pamela Marcus, Division of Cancer Prevention, National Cancer Institute, the Screening Center investigators and staff of the National Lung Screening Trial (NLST), Mr. Tom Riley and staff, Information Management Services, Inc., and Ms. Brenda Brewer and staff, Westat. Most importantly, the authors acknowledge the NLST participants, whose contributions made this study possible.
References
- Madani A., Zanen J., de Maertelaer V., and Gevenois P. A., “Pulmonary emphysema: Objective quantification at multi-detector row CT—comparison with macroscopic and microscopic morphometry,” Radiology 238, 1036–1043 (2006). 10.1148/radiol.2382042196 [DOI] [PubMed] [Google Scholar]
- Dransfield M. T., Washko G. R., Foreman M. G., Estepar R. S., Reilly J., and Bailey W. C., “Gender differences in the severity of CT emphysema in COPD,” Chest 132, 464–470 (2007). 10.1378/chest.07-0863 [DOI] [PubMed] [Google Scholar]
- Martinez F. J., Curtis J. L., Sciurba F., Mumford J., Giardino N. D., Weinmann G., Kazerooni E., Murray S., Criner G. J., Sin D. D., Hogg J., Ries A. L., Han M., Fishman A. P., Make B., Hoffman E. A., Mohsenifar Z., and Wise R., “Sex differences in severe pulmonary emphysema,” Am. J. Respir. Crit. Care Med. 176, 243–252 (2007). 10.1164/rccm.200606-828OC [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatila W. M., Hoffman E. A., Gaughan J., Robinswood G. B., and Criner G. J., “Advanced emphysema in African-American and white patients: Do differences exist?,” Chest 130, 108–118 (2006). 10.1378/chest.130.1.108 [DOI] [PubMed] [Google Scholar]
- Ogawa E., Nakano Y., Ohara T., Muro S., Hirai T., Sato S., Sakai H., Tsukino M., Kinose D., Nishioka M., Niimi A., Chin K., Pare P. D., and Mishima M., “Body mass index in male patients with COPD: Correlation with low attenuation areas on CT,” Thorax 64, 20–25 (2009). 10.1136/thx.2008.097543 [DOI] [PubMed] [Google Scholar]
- Demeo D. L., Hersh C. P., Hoffman E. A., Litonjua A. A., Lazarus R., Sparrow D., Benditt J. O., Criner G., Make B., Martinez F. J., Scanlon P. D., Sciurba F. C., Utz J. P., Reilly J. J., and Silverman E. K., “Genetic determinants of emphysema distribution in the national emphysema treatment trial,” Am. J. Respir. Crit. Care Med. 176, 42–48 (2007). 10.1164/rccm.200612-1797OC [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boschetto P., Miniati M., Miotto D., Braccioni F., De Rosa E., Bononi I., Papi A., Saetta M., Fabbri L. M., and Mapp C. E., “Predominant emphysema phenotype in chronic obstructive pulmonary,” Eur. Respir. J. 21, 450–454 (2003). [DOI] [PubMed] [Google Scholar]
- Boschetto P., Quintavalle S., Zeni E., Leprotti S., Potena A., Ballerin L., Papi A., Palladini G., Luisetti M., Annovazzi L., Iadarola P., De Rosa E., Fabbri L. M., and Mapp C. E., “Association between markers of emphysema and more severe chronic obstructive pulmonary disease,” Thorax 61, 1037–1042 (2006). 10.1136/thx.2006.058321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makita H., Nasuhara Y., Nagai K., Ito Y., Hasegawa M., Betsuyaku T., Onodera Y., Hizawa N., and Nishimura M., “Characterisation of phenotypes based on severity of emphysema in chronic obstructive pulmonary disease,” Thorax 62, 932–937 (2007). 10.1136/thx.2006.072777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim W. D., Ling S. H., Coxson H. O., English J. C., Yee J., Levy R. D., Pare P. D., and Hogg J. C., “The association between small airway obstruction and emphysema phenotypes in COPD,” Chest 131, 1372–1378 (2007). 10.1378/chest.06-2194 [DOI] [PubMed] [Google Scholar]
- Kim W. J., Hoffman E., Reilly J., Hersh C., Demeo D., Washko G., and Silverman E. K., “Association of COPD candidate genes with computed tomography emphysema and airway phenotypes in severe COPD,” Eur. Respir. J. 37, 39–43 (2011). 10.1183/09031936.00173009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller N. L., Staples C. A., Miller R. R., and Abboud R. T., “Density mask”. An objective method to quantitate emphysema using computed tomography,” Chest 94, 782–787 (1988). 10.1378/chest.94.4.782 [DOI] [PubMed] [Google Scholar]
- Gevenois P. A., De Vuyst P., de Maertelaer V., Zanen J., Jacobovitz D., Cosio M. G., and Yernault J. C., “Comparison of computed density and microscopic morphometry in pulmonary emphysema,” Am. J. Respir. Crit. Care Med. 154, 187–192 (1996). [DOI] [PubMed] [Google Scholar]
- Madani A., De Maertelaer V., Zanen J., and Gevenois P. A., “Pulmonary emphysema: Radiation dose and section thickness at multidetector CT quantification—comparison with macroscopic and microscopic morphometry,” Radiology 243, 250–257 (2007). 10.1148/radiol.2431060194 [DOI] [PubMed] [Google Scholar]
- Gierada D. S., Bierhals A. J., Choong C. K., Bartel S. T., Ritter J. H., Das N. A., Hong C., Pilgram T. K., Bae K. T., Whiting B. R., Woods J. C., Hogg J. C., Lutey B. A., Battafarano R. J., Cooper J. D., Meyers B. F., and Patterson G. A., “Effects of CT section thickness and reconstruction kernel on emphysema quantification relationship to the magnitude of the CT emphysema index,” Acad. Radiol. 17, 146–156 (2010). 10.1016/j.acra.2009.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemerink G. J., Kruize H. H., Lamers R. J., and van Engelshoven J. M., “CT lung densitometry: Dependence of CT number histograms on sample volume and consequences for scan protocol comparability,” J. Comput. Assist. Tomogr. 21, 948–954 (1997). 10.1097/00004728-199711000-00018 [DOI] [PubMed] [Google Scholar]
- Boedeker K. L., McNitt-Gray M. F., Rogers S. R., Truong D. A., Brown M. S., Gjertson D. W., and Goldin J. G., “Emphysema: Effect of reconstruction algorithm on CT imaging measures,” Radiology 232, 295–301 (2004). 10.1148/radiol.2321030383 [DOI] [PubMed] [Google Scholar]
- Ley-Zaporozhan J., Ley S., Weinheimer O., Iliyushenko S., Erdugan S., Eberhardt R., Fuxa A., Mews J., and Kauczor H. U., “Quantitative analysis of emphysema in 3D using MDCT: Influence of different reconstruction algorithms,” Eur. J. Radiol. 65, 228–234 (2008). 10.1016/j.ejrad.2007.03.034 [DOI] [PubMed] [Google Scholar]
- Hochhegger B., Irion K. L., Marchiori E., and Moreira J. S., “Reconstruction algorithms influence the follow-up variability in the longitudinal CT emphysema index measurements,” Korean J. Radiol. 12, 169–175 (2011). 10.3348/kjr.2011.12.2.169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- http://www.cancer.gov/nlst
- Aberle D. R., Berg C. D., Black W. C., Church T. R., Fagerstrom R. M., Galen B., Gareen I. F., Gatsonis C., Goldin J., Gohagan J. K., Hillman B., Jaffe C., Kramer B. S., Lynch D., Marcus P. M., Schnall M., Sullivan D. C., Sullivan D., and Zylak C. J., “The National Lung Screening Trial: Overview and study design,” Radiology 258, 243–253 (2011). 10.1148/radiol.10091808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilgram T. K., Quirk J. D., Bierhals A. J., Yusen R. D., Lefrak S. S., Cooper J. D., and Gierada D. S., “Accuracy of emphysema quantification performed with reduced numbers of CT sections,” AJR, Am. J. Roentgenol. 194, 585–591 (2010). 10.2214/AJR.09.2709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo J., Reinhardt J. M., Kitaoka H., Zhang L., Sonka M., McLennan G., and Hoffman E. A., “Integrated system for CT-based assessment of parenchymal lung disease,” IEEE Int. Symp. Biomed. Imaging 871–874 (2002). 10.1109/ISBI.2002.1029398 [DOI]
- J. D.Newell, Jr., “Quantitative computed tomography of lung parenchyma in chronic obstructive pulmonary disease: An overview,” Proc. Am. Thorac. Soc. 5, 915–918 (2008). 10.1513/pats.200804-034QC [DOI] [PubMed] [Google Scholar]
- Akaike H., Parzen E., Tanabe K., and Kitagawa G., Selected Papers of Hirotugu Akaike (Springer, New York, 1998). [Google Scholar]
- Burnham K. P. and Anderson D. R., “Multimodel inference: Understanding AIC and BIC in model selection,” Sociolog. Methods Res. 33, 261–304 (2004). 10.1177/0049124104268644 [DOI] [Google Scholar]
- Rawlings J. O., Pantula S. G., and Dickey D. A., Applied Regression Analysis: A Research Tool, 2nd ed. (Springer, New York, 1998). [Google Scholar]
- Kemerink G. J., Lamers R. J., Thelissen G. R., and van Engelshoven J. M., “CT densitometry of the lungs: Scanner performance,” J. Comput. Assist. Tomogr. 20, 24–33 (1996). 10.1097/00004728-199601000-00006 [DOI] [PubMed] [Google Scholar]
- Bankier A. A., De Maertelaer V., Keyzer C., and Gevenois P. A., “Pulmonary emphysema: Subjective visual grading versus objective quantification with macroscopic morphometry and thin-section CT densitometry,” Radiology 211, 851–858 (1999). [DOI] [PubMed] [Google Scholar]
- Gierada D. S., Pilgram T. K., Whiting B. R., Hong C., Bierhals A. J., Kim J. H., and Bae K. T., “Comparison of standard- and low-radiation-dose CT for quantification of emphysema,” AJR, Am. J. Roentgenol. 188, 42–47 (2007). 10.2214/AJR.05.1498 [DOI] [PubMed] [Google Scholar]
- Cosio M. G. and Snider G. L., “Chest computed tomography: Is it ready for major studies of chronic obstructive pulmonary disease?,” Eur. Respir. J. 17, 1062–1064 (2001). 10.1183/09031936.01.00225201 [DOI] [PubMed] [Google Scholar]
- Hoffman E. A., Reinhardt J. M., Sonka M., Simon B. A., Guo J., Saba O., Chon D., Samrah S., Shikata H., Tschirren J., Palagyi K., Beck K. C., and McLennan G., “Characterization of the interstitial lung diseases via density-based and texture-based analysis of computed tomography images of lung structure and function,” Acad. Radiol. 10, 1104–1118 (2003). 10.1016/S1076-6332(03)00330-1 [DOI] [PubMed] [Google Scholar]
- Reilly J., “Using computed tomographic scanning to advance understanding of chronic obstructive pulmonary disease,” Proc. Am. Thorac. Soc. 3, 450–455 (2006). 10.1513/pats.200604-101AW [DOI] [PubMed] [Google Scholar]
- Madani A., Keyzer C., and Gevenois P. A., “Quantitative computed tomography assessment of lung structure and function in pulmonary emphysema,” Eur. Respir. J. 18, 720–730 (2001). 10.1183/09031936.01.00255701 [DOI] [PubMed] [Google Scholar]