Secondary adaptation of memory-guided saccades

Abstract

Adaptation of saccade gains in response to errors keeps vision and action co-registered in the absence of awareness or effort. Timing is key, as the visual error must be available shortly after the saccade is generated or adaptation does not occur. Here, we tested the hypothesis that when feedback is delayed, learning still occurs, but does so through small secondary corrective saccades. Using a memory-guided saccade task, we gave feedback about the accuracy of saccades that was falsely displaced by a consistent amount, but only after long delays. Despite the delayed feedback, over time subjects improved in accuracy toward the false feedback. They did so not by adjusting their primary saccades, but via directed corrective saccades made before feedback was given. We propose that saccade learning may be driven by different types of feedback teaching signals. One teaching signal relies upon a tight temporal relation with the saccade and contributes to obligatory learning independent of awareness. When this signal is ineffective due to delayed error feedback, a second compensatory teaching signal enables flexible adjustments to the spatial goal of saccades and helps maintain sensorimotor accuracy.

INTRODUCTION

Accuracy is an important goal of sensorimotor behavior. In the face of uncertain and changing environments, both external and internal, sensorimotor systems have to adapt and maintain accurate registration. For example, the saccadic system controls ballistic eye movements called saccades that foveate images of interest and remain accurate despite aging, injury or fatigue. To maintain accuracy, the saccadic system must have adaptive processes to compensate for changes brought about by these conditions. Saccade adaptation is studied in the laboratory by artificially inducing visual error over blocks of trials and measuring adaptation, the learning that over time minimizes visual error. Typically, a visual saccade target is slightly displaced while a saccade to it is in flight, thereby creating an error or mismatch between the position of gaze at the end of the saccade and the visual target. Since people are effectively blind while a saccade is in flight, subjects are unaware of the shift, but nevertheless adapt the gain of saccades to match the displaced target over time (McLaughlin 1967).

Saccades, however, are guided not only by the external visual environment but are often controlled by internal goal states. Externally and internally guided saccades, which differ in the amount of time required to compute the saccade metrics, may also have different adaptive learning mechanisms. Visually guided saccades are externally-guided because they are generated in reaction to a salient visual target that captures attention and involve bottom-up neural processes. These types of saccades can be generated at short latencies ranging from 80–180ms in humans and involve limited amount of cortical processing. Importantly, visually guided saccades are automatic in that they are produced without any instruction or training. Visually guided saccades primarily involve early visual areas, the superior colliculus, and the brainstem, as opposed to higher cortical areas such as the frontal eye field (Braun et al. 1992; Fischer et al. 1993). Internally-guided saccades, on the other hand, are voluntary shifts of the eyes to non-salient or remembered targets and are thought to depend on a top-down signal that selects and maintains the location of the internal goal. For example, memory-guided saccades are generated to the remembered location of a target no longer present in the visual field. This requires precise encoding of the target location, maintenance of this information across time and the generation of an accurate saccade to the remembered location. The longer latencies of memory-guided saccades, which tend to be at least 100ms longer than visually guided saccades, reflect the additional amount of cortical processing and the additional involvement of higher cortical areas such as the frontal eye field (Dias and Segraves 1999; Pierrot-Deseilligny et al. 2004; Pierrot-Deseilligny et al. 1995).

Since the factors that guide saccade production can differ, they may also have different adaptation mechanisms. The vast majority of saccade adaptation studies has focused on visually guided saccades and has generally pointed to a low-level, automatic and obligatory learning process, which does not require awareness (Hopp and Fuchs 2004; Srimal et al. 2008). In comparison, very little is known about the adaptation of internally-guided, or “higher order” saccades. Most behavioral studies of higher order saccade adaptation have been transfer experiments, which are used to infer the degree to which different classes of saccades share the same adaptation mechanisms and pathways. Adaptation consistently transfers among various types of visually guided saccades suggesting a common pathway (Deubel 1999; Frens and van Opstal 1994; Hopp and Fuchs 2002) while adaptation transfer between visually guided and higher-order saccades has been reported inconsistently (Deubel 1995; 1999; Fujita et al. 2002). Moreover, even in cases where significant adaptation transfer was observed between visually guided and higher order saccades, the transfer was only partial, suggesting that these saccades may share overlapping but not identical neural pathways.

An important feature that determines whether adaptation occurs may be when the visual error signal is received relative to the end of a saccade. Studies of both visually guided (Bahcall and Kowler 2000) and memory-guided saccade adaptation (Fujita et al. 2002) in humans found that adaptation was greatly attenuated at delays longer than 400ms. One interpretation of these results is that adaptation depends on a “teaching signal” computed from feedback about the visual error following the primary saccade. Importantly, this teaching signal must arrive shortly after the primary saccade has been generated in order to successfully modify the gain of future saccades. Delaying feedback by a few hundred milliseconds interferes with adaptation.

Although these past studies clearly indicate that learning only occurs if feedback is given within a short time window following the primary saccade, they have limited their scope to the gain adaptation of primary saccades. In this study, we tested the hypothesis that during higher-order, specifically memory-guided saccade adaptation, learning still occurs, but via small secondary saccades following primary saccades that compensate for targeting inaccuracies. To test our hypothesis, we modified the standard memory-guided saccade task in two important ways. First, we provided false feedback about the location of the spatial memoranda. On a block of trials feedback was displaced by 2 degrees from the true position of the memoranda and we measured if subjects’ memory-guided saccades adapted to the displaced feedback target. Second, we delayed feedback to the subjects by 1–2s from the cue to initiate their saccade. By delaying feedback up to 2s, subjects had time to make adjustments (e.g., secondary corrective saccades) to their primary saccades. For comparison, we also tested subjects on a standard visually guided saccade adaptation task. We hypothesized that the two tasks induce qualitatively different mechanisms of adaptation. We predicted that learning during the visually guided saccade task would result in gain adaptation of primary saccades, the result of a low-level and automatic form of learning. During the memory-guided saccade task with delayed feedback, we predicted that directed secondary saccades generated before feedback would compensate for attenuated primary gain adaptation due to delayed visual error signals.

Our results indicate that although subjects were unaware of the target displacements during the visually guided saccade task, their saccade gains reduced towards the target location as expected. During the memory-guided saccade task, accuracy adapted mainly via small systematic secondary saccades that followed the initial memory-guided saccade and were made in the direction of the perturbation. These data highlight two qualitatively different forms of saccade learning. We propose that different types of feedback teaching signals can invoke saccade learning. One teaching signal depends upon a tight temporal coupling with the saccade and contributes to obligatory learning independent of awareness. When this learning mechanism is hampered due to delayed error signals, a second learning mechanism helps to maintain saccade accuracy.

MATERIALS AND METHODS

Subjects

Twelve healthy individuals (7 female, 5 male; 11 right-handed, 1 ambidextrous; ages between 18 and 40) gave written informed consent according to procedures approved by the human subjects Institutional Review Board at New York University, and were paid for participation.

Oculomotor and stimulus procedures

Subjects were seated in a darkened room 57 cm from a DELL LCD monitor (37cm × 30cm, 60 Hz refresh rate, 250 cd/m² luminance, 25 ms response time) with their heads stabilized via a chin-rest. Gray dots that subtended 1° of visual angle were used for fixation and target, except during inter-trial intervals when the fixation dot was blue. Two eyetracker systems were used to collect data. For half the subjects, eye position was recorded at 240 Hz with an infrared videographic camera (ASL 504; Applied Sciences laboratories, Bedford, MA). In-house software (Gramalkn, http://www.ryklinsoftware.com) was used to present stimuli, quantify saccade timing and amplitude, and modify visual displays contingent on eye position. Targeting saccades were detected when the eye position left a 1.5 ° radius circle centered on the fixation point. For rest of the subjects, eye position was recorded at 1000 Hz with an infrared videographic camera (Eyelink 2K; SR Research Ltd., Osgoode, Canada). Experiment Builder software available with the Eyelink camera was used to present stimuli, quantify saccade timing and amplitude, and modify visual displays contingent on saccade velocity. All eye-movement data were transformed to degrees of visual angle, calibrated using a third-order polynomial algorithm that fit eye positions to known spatial positions, and scored offline with in-house software (GRAPES). Saccades were detected when the eye velocity exceeded 30°/s shortly after the cue to make a saccade and were subsequently verified by visual inspection.

Visually guided saccade adaptation (VGSA) experiment

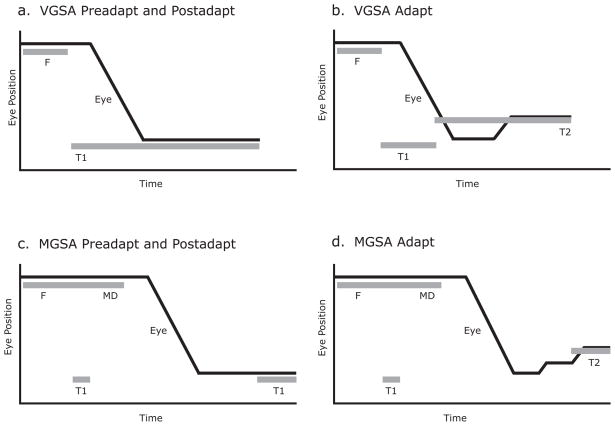
Pre-Adapt Trials (Figure 1a: Subjects maintained fixation (F, gray dot) for 1 or 1–2s, after which a target (T1, gray dot) appeared 16° to the left of fixation. Simultaneous with target onset, the fixation point disappeared and the subject made a saccade to the target location and then after 600–700ms another saccade back to the blue fixation dot when it reappeared for an inter-trial interval of 2 or 1–3s. The fixation dot reappeared in a new location (1 of 6 possible locations along the horizontal axis – 5, 6, 7, 8, 10 or 11°) and the target location was always 16° to the left of it. Adapt Trials (Figure 1b): The task was the same as during pre-adapt, except that when the saccade velocity exceeded 30°/s or crossed the 1.5° radius boundary, the target was stepped backward (lower eccentricity) by 2° along the horizontal axis (T2). Post-Adapt Trials (Figure 1a): Same as Pre-Adapt Trials.

Figure 1.

Experimental paradigms during visually guided saccade adaptation (VGSA) and memory-guided saccade adaptation (MGSA). a) Preadapt and postadapt trial structure for visually guided saccade adaptation (VGSA) were the same. A fixation dot, F, appeared for 1–2s followed by a target, T1. b) During VGSA adapt trials, the target, T1, was back-stepped to T2. c) Preadapt and postadapt trial structure during memory-guided saccade adaptation (MGSA) were the same. After 1–2s of a fixation dot, F, a target, T1, was briefly presented for 150ms. The fixation dot remained for a variable delay, MD (1–5s). After another 2 s, the target, T1, was presented again as feedback d) During MGSA adapt trials, the target, T1, was back-stepped to T2 during feedback.

Memory-guided saccade adaptation (MGSA) experiment

Pre-Adapt Trials (Figure 1c): Subjects maintained fixation (F, gray dot) for 1 or 1–2s, after which a target (T1, gray dot) was concurrently flashed 16° to the left of fixation for 150ms. The subjects were instructed to remember the location of the flashed target while maintaining fixation. After the disappearance of the target, subjects continued to maintain fixation for a delay of 1 – 5s (MD). At this point, the fixation point disappeared and this was the cue for subjects to make a saccade to the remembered location. 1 or 2s after the fixation disappeared, the flashed target was presented for the duration of 500–700ms (T1, feedback) and subjects foveated it before making a saccade to a blue fixation dot for the inter-trial interval of 2 or 1 – 3s. Adapt Trials (Figure 1d): The task was the same as during pre-adapt, except that the feedback target was always presented 2° to the right of the original flashed target (T2), thereby, providing the subjects with a consistent false feedback signal. Post-Adapt Trials (Figure 1a): Same as Pre-Adapt Trials.

In both experiments, subjects performed a block of pre-adapt (100 trials), a block of adapt (200 trials), followed by a block of post-adapt trials (100 trials). The same group of 12 subjects performed both the VGSA and MGSA experiments in counterbalanced order on separate days and all were naive to the experiment and the study’s goals. Subjects underwent a post-adaptation session to reverse any saccadic gain adaptation and prevent carry-over effects. After the conclusion of both experiments, half the subjects were asked whether they detected any target jumps in the VGSA paradigm. They were also asked whether they detected any systematic errors in the MGSA paradigm and if they employed any strategy to compensate for the errors.

Analysis

Calibrated eye-position data were converted to saccadic gain values in degrees of visual angle (saccadic gain = amplitude of saccade/target eccentricity) for subsequent analysis. For the VGSA experiment, we calculated the gain of the first or primary saccade elicited by the visual target and measured the reaction time to the saccade from the cue to generate a saccade. For the MGSA experiment, we calculated the gain of the primary saccade which denoted subjects’ first estimate of the remembered target location along with the reaction time from the cue to make a saccade. We also measured the position of the last fixation subjects made before feedback target was presented and denoted these spatial positions as secondary ‘gain’ values with respect to the original target. These secondary gain values reflect the subjects’ best estimate of the remembered location obtained by adjusting their first estimates (primary saccades). We measured the reaction time to the first and last secondary corrective saccade from the end of the primary saccade. Trials in the MGSA experiment where subjects made saccades during the delay period were discarded.

Magnitude and rate of gain adaptation

To determine the magnitude of adaptation and whether the gain change between the preadaptation trials and the adapted trials was significant, we calculated the mean of the gains during the last third of the preadaptation trials and the last third of the adapt trials and did a paired sample t-test.

We determined the rate constant of adaptation by fitting an exponential function of the following form (Fujita et al, 2002) to the adaptation data:

$$\text{a}(\text{t})={\text{a}}_{\text{x}}+({\text{a}}_0-{\text{a}}_{\text{x}})\text{e}{-}^{\text{t}/\tau }$$

where, a(t) = curve fitted gain for trial t, a_x = mean adaptive gain value; a₀ = mean preadaptive gain value; t = trial number; τ = time constant for adaptation. τ was calculated using a non-linear least squares algorithm.

State-space adaptation model

To quantify learning during both our experimental conditions, we fit our data to a state-space model based on a feedforward theory of motor learning involving internal models of sensorimotor transformation. The state-space model maps a number of input variables to a number of output variables via a set of state variables. Such state–space models can be used to represent the output of a visuomotor control system as a function of the input and of the hidden state of the system at a particular moment in time, i.e., within a given motor trial. More importantly, they can be used to describe the temporal dynamics of how the hidden state develops over time, i.e., how the visuomotor system learns from trial to trial. The model allows us place the learning process within a theoretical framework. Similar approaches have been used to model learning during saccade adaptation (Srimal et al, 2008), force-field reaching (Diedrichsen et al. 2005; Donchin et al. 2003; Smith et al. 2004; Thoroughman and Shadmehr 2000) as well as during sensorimotor adaptation to altered visual feedback (Cheng and Sabes 2006). The model we use is defined by two equations. The output equation states that the saccade gain produced on trial n (y_n) is determined by the adaptive state of the system (z_n) plus some random noise (ε_n).

$${\text{y}}_{\text{n}}={\text{z}}_{\text{n}}+{\epsilon }_{\text{n}}$$

Second, the state-update equation defines the adaptive state of the next trial z_n+1, as the current predicted gain, z_n, weighted by a retention factor (A) and updated by a certain proportion (B) of the difference between the actual saccade gain and the target perturbation on the current trial (y_n – u_n)

$${\text{z}}_{\text{n}+1}={\text{Az}}_{\text{n}}-\text{B}({\text{y}}_{\text{n}}-{\text{u}}_{\text{n}})$$

For each subject’s data, we used a non-linear least squares algorithm to solve for the A parameter, a measure of retention and the B parameter, an index of the amount of learning. To account for individual differences in inherent hypometricity, we set the starting value of z_n to be the mean gain of the first third of each subject’s preadaptive trials.

RESULTS

Magnitude and rate of adaptation during VGSA

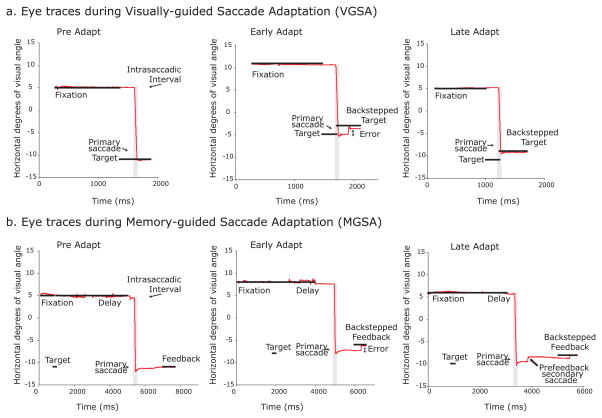
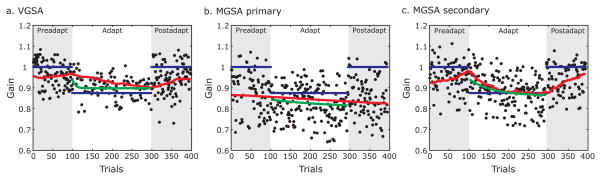
Figure 2a shows the eye traces for a representative subject at different epochs of the visually guided saccade adaptation (VGSA) task – preadapt, early adapt (first third of adapt trials) and late adapt (last third of adapt trials). During the preadapt block, the subject made a saccade from fixation to the peripheral target after it appeared. Starting from the adapt block, the target was back-stepped by 2° during the intrasaccadic interval. The subject overshot the back-stepped target and experienced a visual error signal at the end of the saccade. By the end of the adapt block, the primary saccade adapted to the back-stepped target and the subject no longer experienced visual error at the end of her saccade. During the adapt block, the gain of primary saccades reduced exponentially over the course of multiple trials. Figure 3a shows the adaptive gain change for a representative subject. During the preadapt block, saccade gains reached 88% of the visual target’s eccentricity on average. By the end of the adapt block, the average saccade amplitude shortened to 38% of the back-stepped distance, or about 0.76°. To quantify the rate of adaptation, we fit an exponential function to the saccade gains (green trace) and estimated a rate constant (τ) for the adaptation process. The example subject shown in Figure 3a adapted her saccades at a rate of τ =27 trials. Table 1 shows similar results for the other subjects, where the mean amount of adaptation was 60±6.9% of the back-step and the mean rate of adaptation (τ) was 42±9.3 trials. Overall, the mean saccade gains across subjects were significantly smaller when we compared the last third of adapt trials or late adapt trials during which we expect learning to asymptote to the last third or late pre-adapt trials in the VGSA condition, t(11)=8.38, p<10⁻⁵. On average, primary saccades were initiated 245±8.5ms after the cue to make a saccade.

Figure 2.

Example eye position traces from preadapt, early adapt and late adapt phases during visually guided saccade adaptation (VGSA) and memory-guided saccade adaptation (MGSA) from a representative subject. a) During VGSA preadapt trials, the primary saccades were normometric. During early VGSA adapt trials (i.e., first third of adapt trials), the primary saccades were still aimed towards the original target, therefore backstepping the target during the intrasaccadic interval caused the subject to experience a post-saccadic visual error. By late VGSA adapt trials (i.e., last third of adapt trials), the primary saccades had reduced amplitude to land on the back-stepped target and minimize post-saccadic error. b) During the course of MGSA preadapt trials, the subject made accurate primary saccades to the location of the flashed target and received true feedback. During early MGSA adapt trials, the subject made primary saccades to the original target, but the back-stepped target induced large post-feedback corrective saccades. By late MGSA adapt trials, the subject still made primary saccades to the original target, but also made prefeedback corrective saccades in the direction of the back-stepped feedback.

Figure 3.

Saccade gains before, during, and after adaptation from an example subject. a) During the visually guided saccade adaptation (VGSA) block, the target (blue trace) was back-stepped by 2° during the saccade. The saccade gain (black dots) steadily adapted to match the new target location at a characteristic exponential rate (green trace). State-space model fit of the predicted gain (z; red trace) during VGSA as the saccadic system adapted to the error signals. b) During the memory-guided saccade adaptation (MGSA) block, the feedback target gain was stepped 2o backward (blue trace). The primary saccade gains (black dots) did not adapt to match the feedback target gain (blue trace) as demonstrated by the flat exponential fit (green trace) and predicted gain (z, red trace). c) During the memory-guided saccade adaptation (MGSA) block, the secondary saccade gains (black dots) adapted to match the back-stepped feedback location at an exponential rate (green trace). The predicted gain (z; red trace) adapted to the error signals.

Table 1.

Mean and individual subject learning indices during visually guided and memory-guided saccade adaptation tasks

	VGSA										MGSA
	Primary saccades					Primary saccades					Secondary saccades
Sub	%	ax	τ	B	RTp	%	ax	τ	B	RTp	%	ax	τ	B	RTs	RTl	Q
1	78	0.896	46	0.011	270	−5	0.811	47	−0.004	440	29	0.852	1	−0.017	369	465	na
2	32	0.949	82	0.005	246	16	0.924	4	−0.006	303	81	0.864	13	0.049	281	458	na
3	42	0.862	4	0.005	226	36	0.785	473	0.006	620	99	0.858	30	0.031	173	182	na
4	38	0.898	27	0.012	254	27	0.804	162	0.0001	406	65	0.862	59	0.023	185	289	na
5	35	0.914	123	0.007	217	21	0.912	28	0.002	396	62	0.896	17	0.015	199	377	na
6	31	0.897	28	0.004	234	22	0.979	105	0.005	393	52	0.939	65	0.011	440	705	A,S
7	106	0.859	54	0.022	323	66	0.939	4	0.005	518	90	0.936	18	0.009	175	282	na
8	70	0.956	19	0.007	225	63	0.891	69	0.007	312	83	0.879	50	0.017	395	756	A,P,S
9	69	0.881	35	0.013	256	72	0.884	44	0.010	338	78	0.892	39	0.011	291	816	A,P
10	81	0.870	23	0.017	234	61	0.888	28	0.017	308	65	0.908	21	0.020	326	747	A,P,S,F
11	68	0.910	36	0.014	230	−4	0.894	231	0.005	366	36	0.888	43	0.011	419	1039	A,M
12	66	0.914	25	0.018	221	68	0.894	67	0.006	394	67	0.880	57	0.012	309	1002	A,M
Mean	60	0.901	42	0.011	245	34	0.884	105	0.004	400	68	0.888	34	0.016	297	593
S.E.	6.9	0.009	9.3	0.002	8.5	8.2	0.017	38.6	0.002	26.7	6.1	0.009	5.9	0.005	28.1	83.4

VGSA = visually guided saccade adaptation; MGSA = memory-guided saccade adaptation

% = amount of adaptation (percentage of backstep the saccade gain changed); a_x = asymptote of adaptation τ = rate constant of adaptation; B = model estimate of learning; RTp = reaction time to primary saccade from cue to make saccade (ms); RTs = reaction time to first prefeedback corrective saccade from end of primary saccade (ms); RTl = reaction time to last prefeedback corrective saccade from end of primary saccade (ms); Q = post-experiment questionnaire; A = aware of systematic error; P = stated that they attempted to adjust gain of primary saccades; S = stated that they attempted to modify primary saccade with secondary saccade adjustments; M = miscellaneous attempts to increase effort or attention; F = suspicious that feedback was displaced; na = data not available.

Magnitude and rate of adaptation during MGSA

During the memory-guided saccade adaptation (MGSA) paradigm, we measured the gain of the primary saccades as well as the gain of the final secondary saccade with respect to the original target before feedback. Figure 2b shows the evolution of saccades during the task for a representative subject. During the preadapt block, the subject remembered the location of the briefly flashed target while maintaining fixation and then made a saccade to the remembered location at the end of the delay. Feedback was provided by presenting the target at its original location. During the adapt block, feedback was presented at a location 2° less eccentric than that of the original target, causing subjects to make corrective saccades in the direction of the displaced feedback as the block progressed.

Primary saccade gains during the memory-guided task adapted to a variable degree across subjects. For example, the representative subject shown in Figure 3b made saccades that adapted to 27% of the backstepped target. However, the gains of primary saccades did not adapt at all in two other subjects. As shown in Table 1, the amount of primary saccade adaptation was variable across subjects and ranged from −5 to 72% of the back-stepped location with a mean value of 34±8.2%. A comparison of the late preadapt and adapt trials across subjects showed that the primary saccades did indeed reduce significantly in gain t(11)=4.41, p<0.005. The variability in the amount of primary gain adaptation was reflected in the rate constant of adaptation. The primary saccade gain of the example subject shown in Figure 3b adapted at a rate of τ =162 trials. The rate constant of adaptation across subjects ranged from 4 to 231 trials with a mean value of 105±39 trials (see Table 1).

As seen in Figure 2b, after multiple trials of experiencing memory-guided saccade errors, the representative subject started to make systematic secondary corrective saccades in the direction of the back-stepped target before feedback was provided. These secondary saccades adapted exponentially over the course of the adapt block in all subjects. Figure 3c shows the adaptive gain change for the same representative subject in Figure 3a. During the preadapt block, the secondary saccade gains were on average 95% of the target eccentricity, but by the end of the adapt block, they adapted significantly to 65% of the back-stepped distance, or about 1.3o at a rate of τ =59 trials. As detailed in Table 1, subjects adapted to 68±6.1% of the gain of the back-step at the mean rate of τ = 34±5.9 trials. The mean secondary saccade gains across subjects were significantly smaller during the last third of adapt trials when compared with the last third of preadapt trials in the MGSA condition, t(11)=10.34, p<10⁻⁶.

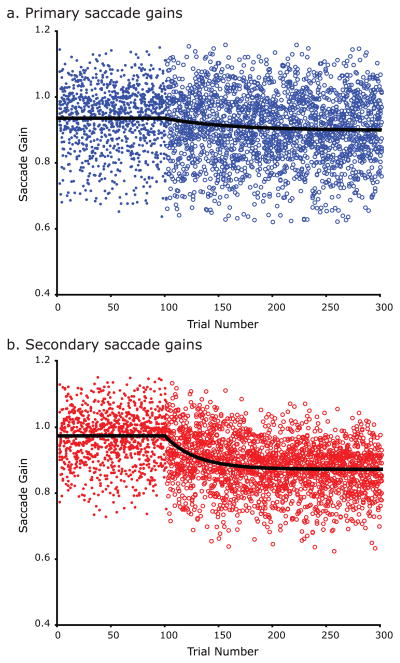
Next, we combined the saccade gains across subjects so we could compare adaptation of primary and secondary memory-guided saccades (Figure 4). As can be seen in Figure 4, adaptation was smaller and slower for primary saccades compared to secondary saccades. Even though primary saccades showed significant adaptation, they adapted to only 34% of the backstepped target location, while the secondary saccades adapted to 68% of the distance. The mean amount of primary saccade gain adaptation was significantly less than the mean amount of secondary saccade adaptation across subjects, t(11) = 4.91, p<10⁻³. Moreover, even for the subjects who showed partial primary saccade adaptation, the rate of adaptation for secondary saccades was greater than that of the primary saccades in 90% of the subjects, suggesting that in subjects where primary saccades adapted partially, the prefeedback secondary saccades may have been the main driving force behind learning.

Figure 4.

Saccade gains before and during adaptation during the memory-guided saccade task for the group of subjects. a) Primary saccade gains prior to the adaptation block are shown in filled blue dots. Primary saccade gains during the adaptation block are shown in blue circles. The black line is the exponential fit to the gains. b) Secondary saccade gains prior to the adaptation block are shown in filled red dots. Secondary saccade gains during the adaptation block are shown in red circles. The black line is the exponential fit to the gains. Learning is greater and faster in the secondary corrective saccades compared to the primary memory-guided saccades.

Comparison of adaptation magnitude and saccade latency during VGSA and MGSA

As expected, the response latencies of the primary memory-guided saccades were longer than visually guided saccades (400±26.7 vs. 245±8.5 ms). The average latencies for the first corrective saccade and last corrective saccade after the end of the primary saccade were 297±29.1 ms and 593±83.4 ms respectively. The extended duration between the primary and secondary corrective saccades argue against a pre-programmed sequence of corrective saccades which typically occur at much shorter latencies of 100–130 ms (Becker 1989). Moreover, we found no evidence of secondary saccades being independently adapted due to their proximity in time to target reappearance as there was no significant correlation between the amount of trial-by-trial secondary gain adjustment and the time period between the end of secondary saccades and target reappearance for any subject (r values ranged from −0.16 to 0.15; p values from 0.11 to 0.99). We also compared the amount of adaptation (i.e., the reduction in saccade gains during learning) between the VGSA and MGSA conditions, and found that subjects adapted their visually guided saccades significantly more than memory-guided primary saccades, t(11) = 2.80, p<0.05, but equal to memory-guided secondary saccades, t(11) = 0.82, p=0.43.

State-space model quantification of learning during VGSA and MGSA

Next, we fit the state-space model to each subject’s data from the VGSA and MGSA experiments and solved for the learning rate parameter, B to obtain a potentially more sensitive estimate of trial-by-trial learning. This parameter estimates how much weight was given to the error experienced on a current trial to predict the gain on the next trial. It provides an insight to the dynamic process of learning, unlike measures such as the percentage amount of adaptation or the rate constant of adaptation, which only provide a summary of the degree of overall learning. During VGSA, subjects significantly adapted their saccade gains by the end of the adapt block, mean B value = 0.011±0.002, t(11)=6.75, p<10⁻⁴ (mean A value = 0.999±0.0001). The individual subjects’ B values (shown in Table 1) positively correlated with the percentage of adaptation, r(10)=0.81, p<0.005 confirming that the B parameter was sensitive to learning. Figure 3a shows a plot of predicted gain derived from the model for all three stages of the VGSA experiment for a representative subject. The predicted gain (red line) is roughly exponential in form as the system changes gain during the adapt block to minimize the error between predicted visual error and the actual visual error.

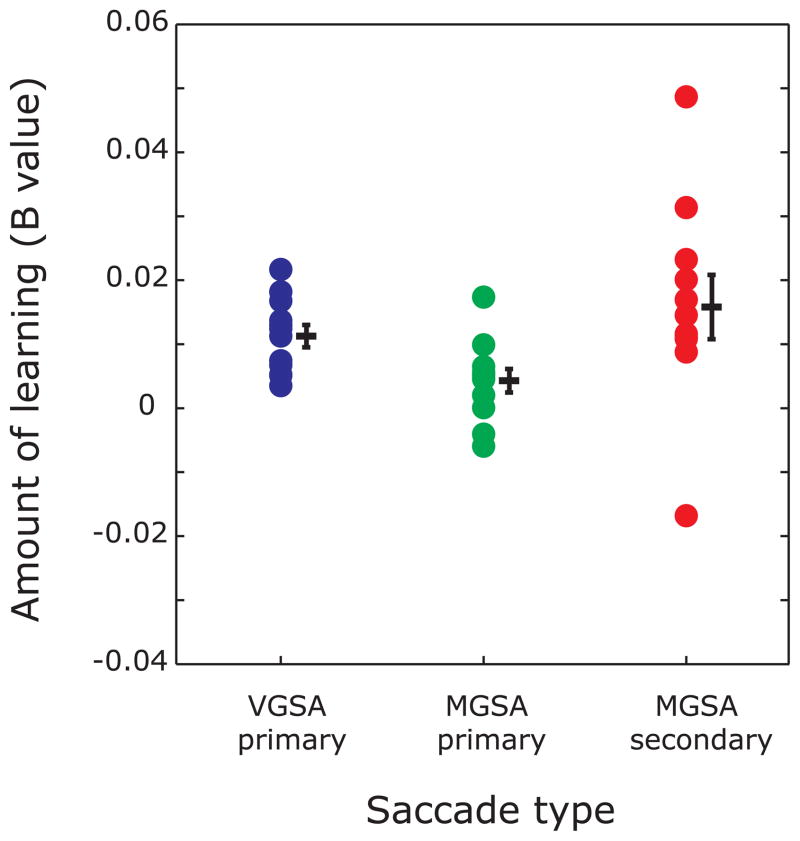
For the MGSA condition, we fit the primary saccade gains and secondary saccade gains separately with the state space model and estimated the amount of trial-by-trial learning in each case. For primary saccade gains, the amount of learning was significant with a mean B value = 0.004±0.002, t(11)=2.44, p = 0.03 (mean A value = 1.000±0.0001). The secondary saccade gains changed with learning as well, with B = 0.016±0.005, t(11) = 3.54, p<0.005 (mean A value = 0.999±0.0002). Table 1 shows the individual B values for the MGSA primary and secondary saccades. The individual B values for both primary and secondary saccades were correlated with the percentage amount of adaptation, r = 0.65; p<0.05 and r = 0.63; p<0.05 for primary and secondary saccades respectively. Recall that B estimates the degree to which the gain of a given saccade was influenced by the error experienced on the preceding trial. The B values estimated from secondary saccades were significantly greater than ones estimated from primary saccades, t(11)= 2.37, p<0.05, indicating that overall learning was driven more by secondary corrective saccades compared to primary saccades. Figure 3b shows a plot of predicted primary saccade gain (red trace) and Figure 3c shows a plot of predicted secondary saccade gain (red trace) as calculated by the state-space model for the course of an entire MGSA experiment for a representative subject. Figure 5 shows estimates of B for VGSA primary saccades, MGSA primary saccade and MGSA secondary saccades across all subjects.

Figure 5.

State-space model estimate of learning (B values) for each subject during visually guided saccade adaptation (VGSA) and memory-guided saccade adaptation (MGSA). B values for visually guided primary saccade adaptation (VGSA primary, blue), memory-guided primary saccade (MGSA primary, green) and secondary saccade adaptation (MGSA secondary, red) were significant across subjects indicating experienced error on current trial was significantly predictive of saccade gain on the subsequent trial during visually guided and memory-guided saccade adaptation. Memory-guided secondary saccade adaptation was significantly greater than memory-guided primary saccade adaptation indicating learning was mainly driven by secondary saccades. Each dot is an estimate of learning, B, for an individual subject. Lines and error bars represent sample mean and standard error for each condition.

Post-experiment subject responses

We asked a sub-sample of subjects (n=6) whether they detected any target or feedback displacements during the visually guided and memory-guided adaptation paradigms, and whether they used any strategies to improve their accuracy. None of the queried subjects reported being aware of the feedback target jumps in the VGSA or MGSA paradigms. One subject said he was suspicious, but only offered this after we revealed that the targets were being stepped. Each reported becoming aware of the consistent errors they were making during the MGSA paradigm. Importantly, they attributed the errors during MGSA to memory errors. As detailed in Table 1, subjects reported responding to their MGS errors with a variety of strategies. Two subjects stated that they attempted to adjust both their primary and secondary saccades. Two other subjects attempted to adjust either their primary or their secondary saccades and the last two subjects could not articulate their strategy beyond that they tried harder. In summary, during the MGSA, but not VGSA task, subjects reported being aware of their poor performance and making an effort to compensate for their errors.

DISCUSSION

The central nervous system continually adapts to internal and external perturbations in order to maintain an accurate calibration between vision and action. This adaptive process is obligatory, automatic, and does not require awareness of one’s inaccuracy or even volition (Mazzoni and Krakauer 2006; Srimal et al. 2008). Based on past research, adaptation occurs when feedback about the accuracy of movements is available at the time of the movement, but not when feedback is delayed for more than 400 ms (Bahcall and Kowler 2000; Fujita et al. 2002). Here, we provide evidence of motor learning during a memory-guided saccade task with feedback delays as long as 1600 ms. In this task, false feedback was presented to subjects to produce systematic errors in performance and induce learning. Subjects attempted to compensate for these errors on a trial-by-trial basis by adjusting their estimate of the remembered location to match the location of the false feedback. Learning mainly took place through adjustments in the secondary corrective saccades that followed the initial memory-guided saccade. We propose that this form of learning is qualitatively different from learning during standard saccade adaptation designs and provides new evidence on how sensorimotor systems employ multiple learning mechanisms to maintain accuracy.

Standard adaptation depends on feedback contemporaneous with movement

The adaptation of visually guided saccades is highly sensitive to the timing of the feedback signal and may depend on a feed-forward mechanism of learning. During our visually guided saccade adaptation (VGSA) paradigm, we back-stepped the target while subjects were in the midst of a saccade to the original location. This caused them to overshoot the target and experience a visual error signal as soon as their primary saccade had landed. Although subjects were not aware that we were moving the target, the saccadic system adapted the gain of the primary saccades towards the gain of the back-stepped target. Using a state space model of motor learning, we provided quantitative evidence that the error on the last trial lead to corrections in the gain of the next saccade.

Learning during visually guided saccade adaptation is thought to involve a feed-forward mechanism. Visually guided saccades are so fast (40 ms for a 10° saccade (Becker 1989)) that visual feedback cannot be used to guide online corrections. Instead, motor control theory (Kawato 1999; Wolpert and Kawato 1998) proposes a feed-forward mechanism for generating accurate saccades in the face of perturbations. This mechanism predicts the sensory consequences of a given motor command and updates this prediction using the actual error as a teaching signal to adjust forthcoming motor commands Anatomically, such a feed-forward learning mechanism may be present in the oculomotor vermis of the cerebellum (Hopp and Fuchs, 2002). During learning, temporal registration between motor command signals and the error signal is thought to change the spiking activity of the Purkinje cells, which in turn modifies the brainstem activity controlling saccade amplitudes (Albus 1971; Marr 1969). A number of motor control and conditioning studies suggest that this temporal specificity is critical for learning during visually guided saccade adaptation (Mauk et al. 2000; Ohyama et al. 2003; Thier et al. 2000). Therefore, a model of cerebellar feed-forward learning may provide a unified framework for understanding a wide range of learning behavior that occur at fast timescales and depend on a precise timing relationship between sensory and motor components.

Secondary adaptation during memory-guided saccades with delayed feedback

In contrast to adaptation in the context of feedback contemporaneous with saccade generation, we found evidence of a secondary adaptation mechanism dissociable from standard saccade adaptation in the context of delayed feedback. During our memory-guided saccade adaptation (MGSA) task, we asked subjects to remember the location of a briefly presented target and after a delay to make a saccade to its remembered location. For feedback, we represented the target, but at a displaced location. Critically, we presented feedback after at least 500ms, enough time for subjects to make corrections to their first approximation of the target location. Subjects rapidly compensated for errors by making systematic secondary saccade corrections to their first estimate of the remembered location (primary saccades) before feedback was presented. By measuring the prefeedback secondary saccades we were able to quantify this novel learning process.

Interestingly, unlike an earlier study on memory-guided saccade adaptation (Fujita et al. 2002), primary saccade adaptation was not the predominant source of learning in this study. We found little evidence that primary saccades adapted, which may be explained in terms of the cerebellar model of saccade plasticity. The long delay between the primary saccade motor command and the visual error signal in our experiment probably hampered the cerebellar learning process, which depends on tight temporal coupling between the two signals. It appeared that to compensate for impaired primary saccade adaptation, prefeedback secondary corrective saccades were made in the direction of the perturbation after the primary saccades. These late corrective saccades may reflect a form of learning that evolves over slower timescales and is not highly dependent on temporal specificity of the error signal.

Within the same framework of motor control theory, we propose that the accuracy of saccades can benefit from two types of teaching signals. One teaching signal is the difference between the primary saccade endpoint and the visual feedback (i.e., visual or retinal error). When feedback is available at the time of the saccade, learning depends on this teaching signal. When feedback is delayed, its temporal mismatch with the forthcoming primary saccade command weakens this learning process. In the context of adaptation during the MGSA task with delayed feedback, we observed a second, compensatory learning mechanism that must rely on another teaching signal. What might be the nature of this other teaching signal? First, we propose that it minimally involves a stored or maintained representation of the visual error. Second, this working memory representation, however, is likely to be distinct from the working memory representation of the position of the past visual cue. Third, since the majority of the learning took the form of secondary corrections to the primary memory-guided saccade, learning did not primarily result from an adjustment in the gain of the memory-guided saccade or the stored representation of the cued location. Instead, the representation of visual errors on past trials is primarily used for planning the small corrections made after the saccade is generated towards the memorized location. The first of these secondary corrections were generated at long latencies after the primary saccade (i.e., ~300ms) and fall in the range of volitional or internally guided saccades (Deubel 1995; Hopp and Fuchs 2004). It is unlikely that they were preprogrammed in conjunction with the primary saccade since corrective saccades that are preprogrammed have latencies as short as 100ms (Becker 1989). Subjects reported becoming aware that their performance worsened during the adaptation block, but importantly ascribed it to their fallible memory. Moreover, they reported using strategies to improve their performance and although self-reported strategies may not be reliable descriptors of actual behavior, they do indicate that, at the very minimum, subjects made an effort to compensate for their errors. These factors suggest that the secondary corrections may be voluntary and perhaps even strategic in nature where subjects become aware of their systematic errors and attempt to remedy them. However, we also found that the secondary saccades adapted gradually towards the backstepped target and then adapted gradually towards the original target in the post-adapt phase at rates comparable to those during visually guided saccade adaptation. While these gradual adaptation and de-adaptation rates may be due to learning in a noisy environment such as those present in memory-guided saccade tasks, they may also reflect a learning mechanism similar in nature to visually guided saccade adaptation. Therefore, while more study is required to conclusively establish whether the secondary teaching signal is strategic in nature, our data establishes that two mechanisms are occurring in parallel to control saccade metrics and maintain accuracy during our memory-guided saccade task. One mechanism utilizes information about the original target location to generate primary saccades, while the other accesses predictive information about the backstepped target location to generate secondary saccades. We can only speculate about the neural circuitry underlying this secondary teaching signal, but the frontal eye field (FEF), the posterior parietal cortex (PPC) and dorsolateral prefrontal cortex (DLPFC) are good candidate sites (Murtha et al. 2007; Curtis 2006). Extensive research has shown that FEF and the PPC are crucial for the generation of memory-guided saccades and the DLPFC are engaged in a wide variety of control and decision-based tasks, including spatial and mnemonic memory tasks (Curtis 2006; Curtis and D’Esposito 2004). Moreover, if lesioned, the FEF/PPC and DLPFC are known to cause systematic and variable errors, respectively, in memory-guided saccades (Dias and Segraves 1999; Li et al. 1999; Ploner et al. 1999).

Conclusions

In this study, we find evidence of two processes occurring in parallel to maintain saccade accuracy. One learning mechanism may involve precise calibration of a time-constrained teaching signal with the saccadic motor command to drive adaptation, and when this process is hampered, a second learning mechanism acts to compensate for saccadic errors, suggesting that the sensorimotor system can utilize multiple learning mechanisms in real life to maintain optimal registration between vision and action.