Bridging the gap between IMRT and VMAT: Dense angularly sampled and sparse intensity modulated radiation therapy

Abstract

Purpose: To propose an alternative radiation therapy (RT) planning and delivery scheme with optimal angular beam sampling and intrabeam modulation for improved dose distribution while maintaining high delivery efficiency.

Methods: In the proposed approach, coined as dense angularly sampled and sparse intensity modulated RT (DASSIM-RT), a large number of beam angles are used to increase the angular sampling, leading to potentially more conformal dose distributions as compared to conventional IMRT. At the same time, intensity modulation of the incident beams is simplified to eliminate the dispensable segments, compensating the increase in delivery time caused by the increased number of beams and facilitating the plan delivery. In a sense, the proposed approach shifts and transforms, in an optimal fashion, some of the beam segments in conventional IMRT to the added beams. For newly available digital accelerators, the DASSIM-RT delivery can be made very efficient by concatenating the beams so that they can be delivered sequentially without operator’s intervention. Different from VMAT, the level of intensity modulation in DASSIS-RT is field specific and optimized to meet the need of each beam direction. Three clinical cases (a head and neck (HN) case, a pancreas case, and a lung case) are used to evaluate the proposed RT scheme. DASSIM-RT, VMAT, and conventional IMRT plans are compared quantitatively in terms of the conformality index (CI) and delivery efficiency.

Results: Plan quality improves generally with the number and intensity modulation of the incident beams. For a fixed number of beams or fixed level of intensity modulation, the improvement saturates after the intensity modulation or number of beams reaches to a certain level. An interplay between the two variables is observed and the saturation point depends on the values of both variables. For all the cases studied here, the CI of DASSIM-RT with 15 beams and 5 intensity levels (0.90, 0.79, and 0.84 for the HN, pancreas, and lung cases, respectively) is similar with that of conventional IMRT with seven beams and ten intensity levels (0.88, 0.79, and 0.83) and is higher than that of single-arc VMAT (0.75, 0.75, and 0.82). It is also found that the DASSIM-RT plans generally have better sparing of organs-at-risk than IMRT plans. It is estimated that the dose delivery time of DASSIM-RT with 15 beams and 5 intensity levels is about 4.5, 4.4, and 4.2 min for the HN, pancreas, and lung case, respectively, similar to that of IMRT plans with 7 beams and 10 intensity levels.Conclusion: DASSIS-RT bridges the gap between IMRT and VMAT and allows optimal sampling of angular space and intrabeam modulation, thus it provides improved conformity in dose distributions while maintaining high delivery efficiency.

INTRODUCTION

A number of intensity modulation techniques are available to deliver high doses of radiation to the tumor while sparing the surrounding critical structures. These techniques include fixed-gantry IMRT (Ref. ¹) (typically, with five to ten beams) planned using beamlet-based optimization^{2, 3, 4, 5} or direct aperture optimization or segment-based optimization,^{6, 7, 8} volumetric modulated arc therapy (VMAT)^{9, 10, 11} (typically with one to two arcs), and Tomotherapy.^{12, 13} Each of these techniques captures certain aspect(s) of desirable features of radiation therapy (RT) but compromises in either dose distribution (in fixed-gantry IMRT and VMAT) or delivery efficiency (in Tomotherapy^™). Conventional IMRT often does not possess sufficient angular sampling required to spatially shape the doses for complicated clinical cases. Increasing the number of beams prolongs treatment delivery and makes practicality an issue. On the other hand, VMAT produces conformal dose distribution by continuously rotating the gantry while modulating the aperture shape and weight. Because each beam is limited to a single aperture in an arc-based delivery, it does not provide the desired beam intensity modulation in some or all directions. The use of multiple arcs may be an option to tackle the problem, but it does not address the need for modulation of each individual beam and thus nonoptimal. The purpose of fast delivery with VMAT may be defeated by redundant angular sampling when multiple arcs are employed. Theoretically, Tomotherapy with slice-by-slice binary modulation provides an uncompromised angular sampling and beam modulation, thus setting the limit for achievable dose conformity with coplanar beam configuration. Indeed, Bortfeld and Webb argued that Tomotherapy provides the greatest flexibility in shaping intensity landscapes and allows to deliver IMRT that comes close to the ideal case in the transverse plane.¹⁴ However, the approach suffers from inefficient delivery due to the narrow slice-by-slice coverage. As currently implemented, restricted use of low energy beam in Tomotherapy may also be suboptimal for some patients. A truly optimal RT scheme with uncompromised angular sampling, beam modulation, delivery efficiency, and possibly energy and collimator modulation when going from one gantry angle to another,¹⁵ is yet to be developed to utilize fully the technical capability of modern LINAC.

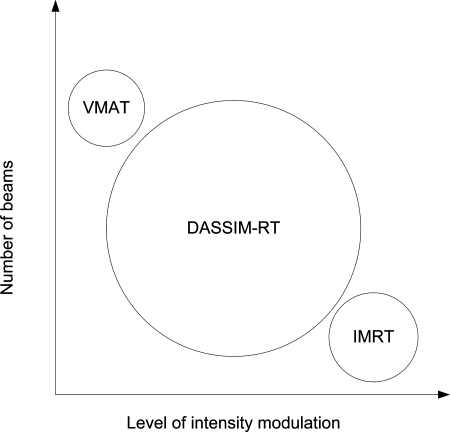
In this work, we propose an alternative treatment planning and delivery scheme to produce highly conformal dose distributions with uncompromised angular sampling and field specific intensity modulation, while still maintaining delivery efficiency. The new treatment modality, coined as dense angularly sampled and sparse intensity modulated RT (DASSIM-RT), is achieved by increasing the angular sampling of radiation beams while eliminating dispensable segments of the incident fields. The proposed method takes advantage of desirable features of both VMAT (by increasing the angular sampling) and fixed-gantry IMRT (by allowing multiple field specific segments). As shown in Fig. 1, DASSIM-RT explores a large area of uncharted territory in terms of the number of beams and level of intensity modulation and bridges the gap between conventional IMRT and VMAT, which have been portrayed as two different processes. For newly available digital LINACs, such as TrueBeam^™ (Varian Medical Systems, Palo Alto, CA), the DASSIM-RT delivery can be made efficient by the high dose-rate beams¹⁶ and by concatenating the beams in such way that they can be delivered sequentially in an automated fashion. The delivery time saved in this manner as well as through the removal of dispensable intrabeam modulation is used to increase the angular sampling. In this way, it is possible to achieve Tomotherapy-like dose distributions with cone beam segments shaped by MLC but with much greater delivery efficiency. This paper presents our feasibility study of DASSIM-RT with two modest goals: (1) demonstrating the potential dosimetric advantage of DASSIM-RT and (2) estimating the delivery efficiency of DASSIM-RT as compared with IMRT and VMAT.

Figure 1.

Schematic plot of DASSIM-RT, conventional IMRT, and VMAT in terms of the number of beams and level of intensity modulation. DASSIM-RT completes the phase space extended by interbeam and intrabeam modulation for radiation therapy.

METHOD AND MATERIALS

Treatment planning

Three previously treated cases, a head and neck (HN), a pancreas, and a lung cancer patient were selected. For each patient, we planned the treatment using Pinnacle^™ system (Philips Radiation Oncology Systems, Milpitas, CA), with different numbers of beams (5, 7, 11, 15, 23, 31, 61, and 90 in this study), uniformly distributed in the range of 0° to 360°. The average number of segments per beam was chosen to be 1, 2, 5, 8, 10 for the plans with 5 to 31 beams, and 1, 2, and 5 for the plans with 61 and 90 beams. For the HN case, a total dose of 66 Gy was prescribed to the planning target volume (PTV) over 33 fractions. For the pancreas patient, a total dose of 25 Gy was prescribed to the PTV over five fractions. For the lung patient, a total dose of 60 Gy was prescribed to the PTV over 30 fractions. 6 MV photons were chosen for the HN case and lung case, and 18 MV photons were chosen for the pancreas case. All plans were normalized in such a way that 95% of the PTV receives the prescribed dose. For comparison purpose, conventional VMAT plans with one and two full arcs across the 0° to 360° angular space were also generated for the two cases.

Dose volume histogram (DVH) and conformality index (CI) are used to compare the plans obtained using different number of beams and intrabeam modulation. Here, we follow the definition of Oozeer et al.¹⁷ for the CI. That is,

$$\mathrm{CI}=\mathrm{cover}\mathrm{factor}\times \mathrm{spill}\mathrm{factor},$$ (1)

where cover factor is the relative PTV receiving a dose greater than or equal to the prescription dose (fixed at 0.95 in this study), and spill factor is the ratio of PTV receiving a dose greater than or equal to the prescription dose to the total volume receiving the prescription dose. A perfect CI is 1. Additionally, we calculated the equivalent uniform dose^{18, 19, 20} (EUD) for the target and different organs at risk for the two cases as follows:

$$\mathrm{EUD}={\left(\frac{1}{n}\sum _{i=0}^n{d}_i^a\right)}^{1∕a},$$ (2)

where d_i is the dose received by voxel i, and n is the total number of voxels in the region of interest. In calculating EUD, we chose the values for parameter a to be 0.35, 1, and 2 for the target, parallel organs (such as liver and parotid glands), and serial organs (such as spinal cord and esophagus), respectively.

Estimation of dose delivery time

The increase in delivery time caused by the increased angular sampling can be partially or even fully compensated by the time gain from the reduction of intrabeam modulation. In a sense, the proposed DASSIM-RT shifts, in an optimal fashion, some of the segments in conventional IMRT to the added incident beams. By migrating MLC segments to otherwise unsampled beam angles, the solution space is effectively increased while maintaining a similar number of overall segments. The emergence of autofield sequencing, which eliminates the unnecessary operator control of gantry rotation during dose delivery, and the dramatically increased dose rate in modern digital LINACs make DASSIM-RT clinically practical.

The treatment delivery time (from the first beam on to the last beam off) for a step-and-shoot IMRT delivery with autofield sequencing consists of four parts: (1) beam-on time, (2) gantry rotation time, (3) extra time due to gantry acceleration and deceleration at each beam angle relative to a constant-speed gantry rotation, and (4) MLC leaf travel time. Thus, we can estimate the dose delivery time by

$$T\approx \frac{\mathrm{MU}}{\mathrm{DR}}+T_{\mathrm{G}}(1-\frac{1}{N_{\mathrm{B}}})+\Delta T_{\mathrm{G}}(N_{\mathrm{B}}-1)+T_{\mathrm{MLC}},$$ (3)

where MU is the plan-specific monitor units per fraction, DR is the dose rate used for plan delivery, T_G is the time required for a gantry rotation of 360° (fixed at 1 min), and N_B is the number of incident beams. The second term gives the time required for the gantry to rotate between the first and last gantry positions. ΔT_G is the extra time due to gantry acceleration and deceleration at an angle (fixed at 0.6 s or 1/100 min), which can be easily estimated from the dynamic log files on TrueBeam. The last term in Eq. 3 is the total MLC leaf travel time, which was estimated by summing the maximum leaf travel distances between consecutive MLC segments, assuming a constant leaf travel speed of 2 cm/s. The last term can be rewritten as ${\overline{T}}_{\mathrm{MLC}}(N_{\mathrm{S}}-N_{\mathrm{B}})$, i.e., the average MLC leaf travel time per segment times the total number of intrabeam segments (notice that N_S is the total number of segments). The reason we use intrabeam segments only is that the MLC leaf travel time between consecutive beams can be done during the gantry rotation. In general, the average leaf travel time depends on the size of the target and the overall complexity of the plan; however, for the same target and surrounding anatomy, ${\overline{T}}_{\mathrm{MLC}}$ is roughly equal for different plans.

The validity of Eq. 3 was examined by delivering six step-and-shoot treatment plans with different number of beams (5, 7, and 15) and intensity levels (5 and 10) on a TrueBeam. Given a plan for the patient cases, we first determined the required MU per fraction and then calculate the total MLC leaf travel time according to the planned MLC leaf positions for all the segments. The dose delivery time was then calculated according to Eq. 3. We compared the estimated dose delivery time for our DASSIM-RT plans and conventional IMRT plans.

RESULTS

Plan quality comparison

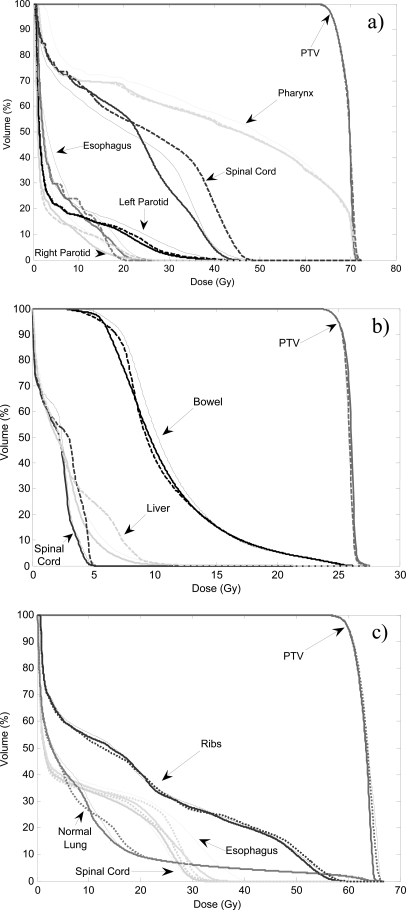
Figure 2 shows the DVHs of a DASSIM-RT plan with 15 beams and 5 intensity levels, an IMRT plan with 7 beams and 10 intensity levels, as well as a 2-arc VMAT plan. The DASSIM-RT and IMRT plans have similar number of segments (75 and 70, respectively) and take about the same amount of time to deliver. As can be seen from Fig. 2, all the plans have similar target coverage, whereas the DASSIM-RT plan has better organ sparing than IMRT and VMAT in all three patients. This is also evident from Table TABLE I., which shows similar EUD for the targets, while the EUDs of critical organs are generally smaller for the DASSIM-RT plans than that for the IMRT and VMAT plans. For instance, in the head and neck case, the EUD of spinal cord for the DASSIM-RT plan is lowered by 4.4 Gy compared with the IMRT plan, and the EUD of pharynx for the DASSIM-RT plan is lower by 2.5 Gy compared with the 2-arc VMAT plan.

Figure 2.

DVHs of a DASSIM-RT plan with 15 beams and 5 intensity levels (thick solid lines), an IMRT plan with 7 beams and 10 intensity levels (dashed lines), and a 2-arc VMAT plan (thin solid lines). (a) HN case; (b) pancreas case; (c) lung case. Target coverage is similar for all plans. The DASSIM-RT plan has better (and slightly better) organ sparing than IMRT (and VMAT) in all cases.

Table 1.

EUD of targets and OARs in the three cases for: IMRT plans with 7 beams and 10 intensity levels, DASSIM-RT plans with 15 beams and 5 intensity levels, and 2-arc VMAT plans. The dose-per-fraction effect is not taken into account in the pancreas case.

Patient	Organs	IMRT	DASSIM-RT	VMAT
Head and neck, 66 Gy in 33 fractions	PTV	69.3	69.3	69.4
	Spinal cord	28.6	24.2	25.0
	Esophagus	7.6	7.6	8.9
	Parotid glands	4.4	4.1	5.5
	Pharynx	39.1	39.0	41.5
Pancreas, 25 Gy in 5 fractions	PTV	25.8	26.0	25.8
	Spinal cord	3.3	2.6	2.5
	Liver	3.0	2.4	2.7
	Bowel	10.8	10.7	11.3
Lung, 60 Gy in 30 fractions	PTV	63.4	63.0	63.5
	Normal lung	8.3	8.2	8.5
	Spinal cord	14.3	13.7	13.6
	Esophagus	15.4	15.1	17.7
	Ribs	27.2	26.7	27.1

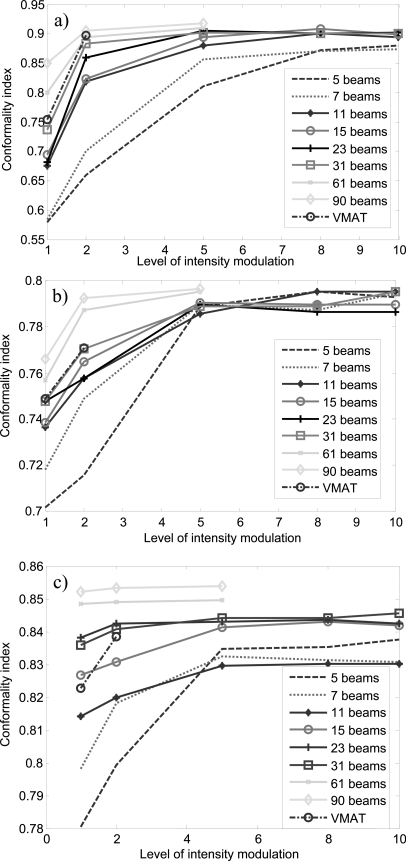
Figure 3 shows the CI versus the level of intensity modulation for all the DASSIM-RT, IMRT, and VMAT plans. As expected, given the same number of beams, CI increases with increasing level of intensity modulation and given the same level of intensity modulation, CI increases with increasing number of beams. It is worth noting that the improvement in CI diminishes with increasing levels of intensity modulation and saturates beyond a certain level. This turning point differs for different number of beams: CI saturates at lower levels of intensity modulation with more beams and vice versa. For instance, in the HN case, CI saturates around 5 intensity levels for 15 beams; while it saturates around 10 intensity levels for 7 beams. There is a gap in the final CI between conventional IMRT plans (5 and 7 beams) and DASSIM-RT plans (11 beams and more) in the HN and lung cases, indicating the benefit of more angular sampling in these cases. On the other hand, such a gap is not evident in the pancreas case. Notice the increase of CI from 2 to 5 intensity levels in the pancreas case, which is quite dramatic even for 31 beams. This may be an indication that intensity modulation is more important than angular sampling in this particular case. Interestingly, VMAT with one or two arcs did not beat the 61-beam DASSIM-RT plans with one or two intensity levels, respectively, in terms of the CI in any case. This is mainly because the segments from neighboring beams in VMAT are not completely independent due to the continuous gantry rotation; thus it does not achieve the full extent of intensity modulation as DASSIM-RT.

Figure 3.

The CI versus level of intensity modulation for all the DASSIM-RT, IMRT, and VMAT plans. (a) HN case; (b) pancreas case; (c) lung case.

Estimated dose delivery time

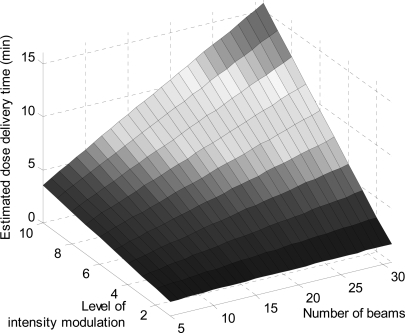
We first validated Eq. 3 by delivering six step-and-shoot treatment plans with different number of beams (5, 7, and 15) and intensity levels (5 and 10) on a TrueBeam. Autofield sequencing available in TrueBeam was used. We exported the planned MLC leaf positions and calculated the MLC travel time specifically for each plan. The actual delivery time ranges from around 7 to 13.5 min. The estimated delivery time differs from the actual one by 2.1% on average. The maximum relative difference in estimated and actual delivery time is around 3.9% (or 16 s), for a plan with the shortest delivery time (∼7 min). Delivery time of DASSIM-RT is of practical concern. To give a glimpse of how dose delivery time changes with different planning and delivery schemes, we show in Fig. 4 the estimated dose delivery time according to Eq. 3 with respect to the number of beams and level of intensity modulation for a treatment plan of 600 MU per fraction, where we have assumed a constant dose rate of 1400 MU/min and an average MLC leaf travel time of 3 s per segment. As expected, the dose delivery time increases with increasing number of beams and level of intensity modulation.

Figure 4.

Estimated dose delivery time with respect to the number of beams and level of intensity modulation for a treatment plan of 600 MU per fraction and a constant dose rate of 1400 MU/min.

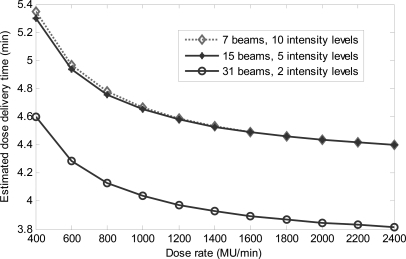
The dose rate dependence of the delivery time is shown in Fig. 5 for an IMRT plan and two DASSIM-RT plans in the head and neck case. For the DASSIM-RT plan with 15 beams and 5 intensity levels, the estimated dose delivery time is reduced from 5.3 min at 400 MU/min to about 4.5 min at 1400 MU/min—a 15% reduction. The benefit of higher dose rate in terms of shortened dose delivery time diminishes after 1400 MU/min; indeed, there is only a marginal decrease in the dose delivery time (around 4.4 min) at 2400 MU/min because the reduction in delivery time is primarily limited by the MLC leaf travel speed and gantry rotation speed (the two motions account for about 96% of the total delivery time). Increasing the MLC leaf travel speed and/or gantry rotation speed may prove to be a viable solution to reduce the dose delivery time to truly benefit from a high dose rate.

Figure 5.

Estimated dose delivery time with respect to dose rate for an IMRT plan and two DASSIM-RT plans in the HN case. The IMRT plan with 7 beams and 10 intensity levels and the DASSIM-RT plan with 15 beams and 5 intensity levels take about the same amount of delivery time at all dose rates.

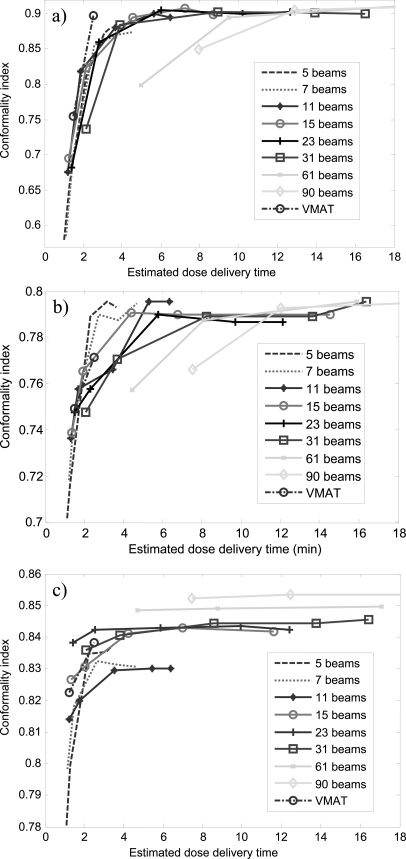
Figure 6 shows the CI versus estimated dose delivery time for all the DASSIM-RT, IMRT, and VMAT plans for all three cases. For the DASSIM-RT plan with 15 beams and 5 intensity levels, the estimated dose delivery time is around ∼4.5 min for all three cases. This is similar to the delivery time of conventional IMRT plans with 7 beams and 10 intensity levels in the three cases. The DASSIM-RT plan achieves better sparing for critical OARs than the IMRT plan for all the patients (Fig. 2 and Table TABLE I.). The main advantage of VMAT lies in its relatively fast delivery time (∼1.5 and ∼2.5 min for a 1-arc and 2-arc plan, respectively). However, it is less conformal than IMRT and DASSIM-RT plans, especially with a single arc.

Figure 6.

The CI versus estimated dose delivery time for all the DASSIM-RT, IMRT, and VMAT plans. (a) HN case; (b) pancreas case; (c) lung case. For ease of illustration, data points with estimated dose delivery time greater than 18 min are not shown.

DISCUSSION

IMRT and VMAT are currently widely used for RT of various cancers. Standard IMRT and VMAT make compromises in different aspects. The former achieves a reasonable dose distribution by intensity modulation with limited angular beam sampling. The level of intensity modulation is generally unconstrained and the resultant number of segments is usually large to generate a reasonable dose distribution. Due to the sparse angular sampling in IMRT, the conformity and maneuverability of the resultant dose distribution are often limited. On the other hand, while VMAT has sufficient angular sampling, it does not provide the desired intrabeam intensity modulation in some or all directions. Only in relatively simple cases that do not require substantial intensity modulation will single-arc VMAT be dosimetrically comparable to Tomotherapy.¹⁴ In certain clinical cases, single-arc VMAT may unduly compromise the quality of the dose distribution.

Some clarification on terminology is appropriate here. The current division of fixed-gantry IMRT and VMAT is largely historical. Up to this point, VMAT is typically referring to a rotational delivery (i.e., beam is on while gantry rotates and MLC moves), which include the RapidArc technique proposed by Otto,¹⁰ intensity modulated arc therapy (IMAT) originally proposed by Yu⁹ or alike.²¹ The major difference between the two mainly lies in how the arc-delivery treatment plan is obtained. The RapidArc approach restricts one aperture for each control point, which makes arc sequencing straightforward (the apertures in between two control points are obtained through linear interpolation with consideration of MLC motion constraint). Higher degree of intensity modulation is achieved through the use of multiple arcs. IMAT optimization also uses a large number of control points but allows intensity modulated fluence maps at each control point (or gantry angle). The realization of so obtained set of intensity modulated beams through a rotational arc is complicated and needs a sophisticated arc sequencing algorithm. More often than not, the arc sequencing can only approximately reproduce the fluence maps because only a few arcs (one–three arcs) are practical. In this paper, we have adopted this conventional view and use VMAT to refer to a rotational delivery (beam is on while gantry rotates). Likewise, the term of IMRT is used in a conventional sense to describe the dose delivery scheme of five to ten fixed gantry intensity modulated beams. Although the division between VMAT and IMRT is somewhat arbitrary, an important point that we wish to stress here is that a treatment scheme is generally characterized by two aspects: angular sampling and intrabeam modulation. With dense angular sampling (more than ten fixed gantry beams) and sparse intensity modulation, DASSIM-RT allows us to reach the solutions that are otherwise inaccessible in balancing the two aspects. The take-home message of this work is twofold: (1) for a given case, there exists an optimal combination of angular sampling and intrabeam modulation and this optimum is likely to be located somewhere between current VMAT and IMRT; and (2) with the availability of new generation digital accelerator with autofield sequencing, fixed-gantry IMRT of a large number of beams with reduced intrabeam modulations may be a favorable choice from the perspectives of optimality of the resultant dose distribution, delivery simplicity, and QA.

Generally speaking, intensity modulation is helpful in improving the dose uniformity. However, the benefit of increasing intrabeam modulation diminishes beyond a certain level. Intensity modulation alone is not sufficient to produce a desired dose distribution in general. Adequate angular sampling is important in order to achieve a high conformity in dose distributions, especially when treating complex cases, as sufficient angular sampling is essential for curving the high dose region. As the number of beams is increased, the number of segments can be reduced accordingly. The specific relation will, of course, be complicated and case dependent. Theoretically, modern IMRT is fundamentally dominated by the classical Shannon–Nyquist theorem, which sets the minimum angular sampling and intrabeam modulation in order to achieve a desired dose distribution. Although there is no rigorous proof, it is arguable and practically imaginable that multiple beams are necessary to better satisfy the Shannon–Nyquest theorem to achieve a conformal dose distribution. In reality, neither fixed-gantry IMRT nor VMAT is satisfactory for a broad spectrum of cases. The former may not have sufficient angular sampling, whereas the latter may fall short in providing sufficient intrabeam modulation. Angular sampling of beams is important to “spread” the dose, and intensity modulation is useful for intrabeam tradeoff. The benefits of increased angular sampling and intrabeam intensity modulation are evident from Fig. 3.

Two recent advancements in radiation therapy support the proposed DASSIM-RT in clinical practice. On the planning side, IMRT inverse planning with total-variation regularization has been proposed,^{22, 23} which is capable of dispensing unnecessary segments in intensity modulated beams to produce easily deliverable piece-wise constant fluence maps. The approach is also applicable to treatment with flattening filter free beams.^{16, 24} On the delivery side, it is now possible to concatenate a number of fixed gantry beams so that the delivery can proceed without manual intervention. This entirely eliminates the unnecessary operator’s time spent on the manual control of gantry rotation during dose delivery. The availability of high dose-rate beams may further facilitate the DASSIM-RT delivery. The recent development of the “burst mode” delivery on Siemens LINACs would also be a useful platform for the proposed DASSIM-RT planning and delivery scheme. In burst mode, no irradiation is allowed while the gantry or MLC leaves are moving. Instead, dose is delivered in bursts at a high dose rate (2000 MU/min) and only after an MLC segment shape has been completely formed. The new system is capable of delivering a wide array of clinically relevant treatment plans, and it was found that delivery times are significantly short.²⁵ The time saved from all these factors can be utilized to add extra beams or intensity modulation to achieve a more conformal dose distribution. We note that, practically, it is possible to incorporate dose delivery time formularized by Eq. 3 into the treatment plan optimization process, either as a part of the cost function or in the form of constraints.

VMAT represents a major deviation from conventional IMRT, but it complicates the QA process in clinical practice. DASSIM-RT, on the other hand, combines the useful features of conventional IMRT and VMAT and bridges the gap between what seems to be two different processes. Its QA can proceed in a similar manner as that of IMRT treatment. DASSIM-RT provides a timely solution to improve not only dose distribution but also the clinical QA process. Additionally, onboard kV imaging can be performed during switch from one gantry angle to another without the interference of the scatter photons from the treatment MV beam. Delivery scheme with a combination of partial arc(s) and fixed gantry beams is a special case of this scheme. A related delivery scheme is the smart arc,^™ where the resulting beam segments at a nodal point are distributed over a small angular interval surrounding that beam. However, the smart arc^™ currently implemented in the Raystation^™ and Pinnacle TPS enforces a fixed number of segments per arc; this system would have a variable number of segments with more refined apertures wherever necessary. Treatment with mixed energies (e.g., beams at different gantry angles use different energies) and collimator modulation¹⁵ is also made straightforward by DASSIM-RT. Finally, we mention that the approach is also applicable to non-LINAC machines such as a Cobalt machine with one or more sources.

For demonstration of feasibility, we have included a total of three patient cases of different disease sites. A statistically meaningful conclusion is thus not reached with the limited number of patients. The study, however, shed useful insights into the interplay between angular sampling rate and intrabeam modulation.

CONCLUSION

We have proposed a DASSIM-RT strategy to fully utilize the degree of freedom of angular and intensity modulation in unison. The DASSIM-RT uses a large number of intensity-sparsified beams to increase angular sampling and maintain the overall delivery time within a practically acceptable limit. The final dose distribution depends on the level of intensity modulation and angular sampling. A delivery scheme with dense angular sampling but sparse and field-specific intensity modulation provides a viable option to maximize the utility of modern LINAC and complete the “phase space” of modulated radiation therapy. The approach allows us to optimally distribute the delivery time among the angular sampling and intrabeam modulation. The treatment modality provides uncompromised dose distributions and at the same time maintains the delivery efficiency.