A joint model of longitudinal and competing risks survival data with heterogeneous random effects and outlying longitudinal measurements

Abstract

This article proposes a joint model for longitudinal measurements and competing risks survival data. The model consists of a linear mixed effects sub-model with t-distributed measurement errors for the longitudinal outcome, a proportional cause-specific hazards frailty sub-model for the survival outcome, and a regression sub-model for the variance-covariance matrix of the multivariate latent random effects based on a modified Cholesky decomposition. A Bayesian MCMC procedure is developed for parameter estimation and inference. Our method is insensitive to outlying longitudinal measurements in the presence of non-ignorable missing data due to dropout. Moreover, by modeling the variance-covariance matrix of the latent random effects, our model provides a useful framework for handling high-dimensional heterogeneous random effects and testing the homogeneous random effects assumption which is otherwise untestable in commonly used joint models. Finally, our model enables analysis of a survival outcome with intermittently measured time-dependent covariates and possibly correlated competing risks and dependent censoring, as well as joint analysis of the longitudinal and survival outcomes. Illustrations are given using a real data set from a lung study and simulation.

1. INTRODUCTION

In the past decades, much work has been done in the field of joint modeling of longitudinal and survival data. Joint models have been proposed to adjust inferences on longitudinal measurements in the presence of non-ignorable missing values due to dropout (Schluchter, 1992; DeGruttola and Tu, 1994; Little, 1995; Hogan and Laird, 1997; Henderson et al., 2000; Elashoff et al., 2007, 2008); to solve difficulties in Cox proportional hazards model arising from time-dependent covariates which are possibly missing at some event times or subject to substantial measurement error (Faucett and Thomas, 1996; Wulfsohn and Tsiatis, 1997; Faucett et al., 1998; Wang and Taylor, 2001; Xu and Zeger, 2001; Song et al., 2002; Brown and Ibrahim, 2003; Tseng et al., 2005; Ye et al., 2008); and to assess covariates effects on both endpoints simultaneously (Henderson et al., 2000; Zeng and Cai, 2005; Elashoff et al., 2007, 2008; Liu et al., 2008).

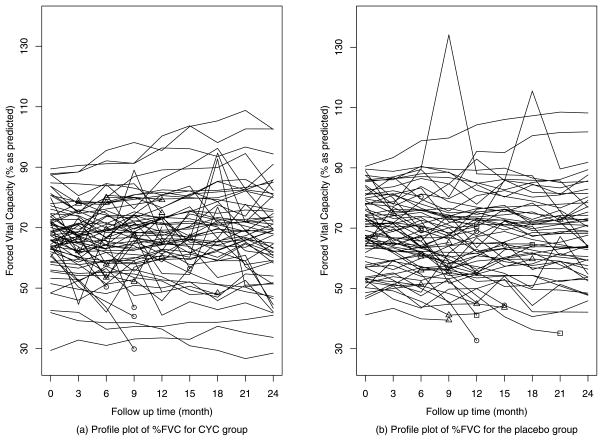
Most joint models in the literature assume a normal random error for the longitudinal sub-model. The normal model, however, can be sensitive to outliers or heavy-tailed data. For example, the profile plot of repeated measured FVC (Forced Vital Capacity) in Figure 1 reveals several suspiciously large values. We demonstrate in Section 3 that the normal model is sensitive to the extreme values. We also observe in a simulation study (see Tables 2, 3) that the regression and random effects parameters in a normal model can be seriously biased in the presence of outliers.

Figure 1.

(a)–(b) Profile plots of observed %FVC for CYC group vs. placebo group including potential outlying measurements: ○ for treatment failure or death; △ for informatively censored events; □ for noninformatively censored events.

Table 2.

Comparison of the joint model with a normal distribution versus that with a t-distribution for ε_ij (sample size = 250)

m	Parameter	True	Normal distribution			t-distribution
			Bias	SE	CP	Bias	SE	CP
250	Longitudinal
	Fixed effects
	β0	10	0.295	0.352	0.655	0.020	0.137	0.903
	β1	−1	0.059	0.735	0.927	−0.009	0.221	0.952
	β2	1.5	0.272	0.340	0.807	−0.015	0.155	0.949
	Survival
	Fixed effects
	γ11	0.8	−0.004	0.121	0.953	−0.011	0.130	0.923
	γ12	−1	0.042	0.286	0.927	0.002	0.248	0.954
	γ21	0.5	−0.025	0.128	0.927	−0.012	0.119	0.929
	γ22	−1	0.026	0.260	0.960	−0.034	0.255	0.959
	Random effects
	ν2	0.5	0.147	0.688	0.895	−0.004	0.308	0.939
	${\sigma }_{u1}^2$	2.5	−0.117	1.640	0.876	0.109	0.561	0.944
	σuv1	1.5	−0.018	0.890	0.931	0.036	0.514	0.949
	${\sigma }_{v1}^2$	1	0.253	0.713	0.949	0.063	0.585	0.959
	${\sigma }_{u0}^2$	0.5	0.719	0.967	0.887	0.039	0.259	0.938
	σuv0	−0.4	−0.492	2.905	0.840	0.002	0.297	0.908
	${\sigma }_{v0}^2$	0.5	0.054	0.530	0.895	−0.018	0.416	0.929

Note: The bold numbers represent relatively large biases.

Table 3.

Comparison of the joint model with a normal distribution versus that with a t-distribution for ε_ij (sample size = 500)

m	Parameter	True	Normal distribution			t-distribution
			Bias	SE	CP	Bias	SE	CP
500	Longitudinal
	Fixed effects
	β0	10	0.249	0.239	0.594	0.004	0.091	0.935
	β1	−14	−0.064	0.413	0.934	−0.026	0.157	0.936
	β2	1.5	0.231	0.239	0.791	−0.008	0.114	0.907
	Survival
	Fixed effects
	γ11	0.8	0.007	0.085	0.955	−0.004	0.081	0.947
	γ12	−1	−0.002	0.191	0.938	0.007	0.173	0.947
	γ21	0.5	−0.005	0.084	0.934	−0.010	0.087	0.931
	γ22	−1	0.011	0.182	0.934	−0.021	0.170	0.955
	Random effects
	ν2	0.5	−0.027	0.299	0.910	−0.006	0.192	0.931
	${\sigma }_{u1}^2$	2.5	−0.375	0.540	0.796	0.072	0.388	0.951
	σuv1	1.5	−0.013	0.457	0.959	−0.009	0.385	0.943
	${\sigma }_{v1}^2$	1	0.153	0.457	0.951	−0.015	0.396	0.927
	${\sigma }_{u0}^2$	0.5	1.266	1.129	0.575	0.050	0.154	0.939
	σuv0	−0.4	−0.204	0.699	0.868	−0.022	0.170	0.923
	${\sigma }_{v0}^2$	0.5	−0.051	0.292	0.877	−0.012	0.232	0.907

This paper proposes a new joint model of longitudinal and competing risks survival data. Our model consists of three sub-models: a linear mixed effects sub-model with a t-distributed measurement error, a cause-specific hazards sub-model for the survival outcome, and a variance-covariance sub-model for the multivariate latent random effects based on a modified Cholesky decomposition. A Bayesian MCMC method is developed for estimation and inference. Our model has several distinct features from existing models. The inference resulting from the linear mixed effects sub-model with a t-distributed measurement error is more robust to outlying longitudinal measurements or heavy-tailed data than its normal-error counterpart. Secondly, the cause-specific hazards sub-model for the survival outcome allows one to account for possibly correlated competing risks and dependent censoring. The random effects of the two sub-models induce the correlation between the longitudinal and survival outcomes. Finally, by extending the idea of Pourahmadi (1999), the sub-model for the variance-covariance matrix of the multivariate latent random effects based on a modified Cholesky decomposition allows for high-dimensional heterogeneous covariance matrices of the multivariate random effects and the resulting estimated covariance matrices are guaranteed to be positive definite. Our method also provides a framework for testing the homogeneous random effects assumption of a homogeneous joint model.

It is worth noting that compared to other robust methods such as Huber’s robust regression (Huber, 1973), the t-distribution based method is mathematically more tractable and computationally simple. The use of the t-distribution in applications with heavy-tailed or outlying data is well-developed in the literature. Lange et al. (1989) and Liu (1996) used it in linear and nonlinear regressions. Rosa et al. (2003) applied a class of normal/independent distributions (Lange and Sinsheimer, 1993), which include the t-distribution as a special case, in linear mixed effects models with ignorable missing data. Li et al. (2009) extended the idea to a robust joint model for longitudinal and survival data with possible non-ignorable missing data due to some terminating events. Our approach is distinct from Li et al. (2009) in several aspects. Our Bayesian MCMC method can easily handle high-dimensional random effects that otherwise complicates the likelihood-based method of Li et al. (2009). Secondly, Li et al. (2009) assume a homogeneous variance-covariance matrix for the random effects, while we allow heterogeneous random effects. Finally, the homogeneous variance-covariance assumption is untestable under the Li et al. (2009) model. Our model provides a useful framework to test this assumption.

This paper is organized as follows: in Section 2 we define the robust joint model and derive a Bayesian estimation procedure. In Section 3, we illustrate our method using a data set from scleroderma lung study (Tashkin et al., 2006). In Section 4, the performance of our method is examined by simulation. A discussion of the method is provided in Section 5. Technical details of the MCMC algorithm are deferred to the Appendix.

2. MODEL AND ESTIMATION

2.1 Robust joint model

Suppose there are m subjects in the study. For the i^th subject at time t, the longitudinal outcome Y_i(t) follows a linear mixed effects model:

$$Y_i(t)=X_i^{(1)}{(t)}^T\beta +Z_i{(t)}^T{U}_i+{\epsilon }_i(t)$$ (1)

where $X_i^{(1)}(t)$ and Z_i(t) are vectors of covariates associated with the fixed effects β (p × 1) and the random effects U_i (q×1) respectively. Assume that the measurement error ε_i(t) is t(0, σ², k) distributed with k degrees of freedom. Assume further that ε_i(t) ⊥ U_i and ε_i(t₁) ⊥ ε_i(t₂) for any t₁ ≠ t₂.

During follow-up, each subject may experience one of g distinct competing causes of failure or may be right censored. Let C_i = (T_i, D_i) be the competing risks survival data on subject i, where T_i is the failure or censoring time, and D_i assumes a value from 0, 1, … , g, with D_i = 0 indicating a noninformative censored event and D_i = k indicating the k^th failure type, k = 1, … , g. Dependent (or informative) censoring is treated as one of the g types of failures. The cause-specific hazards sub-model for the competing risks survival data is specified as follows:

$$\begin{array}{l}{\lambda }_k(t;X_i^{(2)}(t),v_i,{\gamma }_k,{\nu }_k)=\underset{h\to 0}{lim}\frac{P[t\le T_i<t+h,D_i=k\mid T_i\ge t,X_i^{(2)}(t),v_i,{\gamma }_k,{\nu }_k]}{h}\\ ={\lambda }_{0k}(t)exp\{X_i^{(2)}{(t)}^T{\gamma }_k+{\nu }_k{v}_i\}.\end{array}$$ (2)

The function ${\lambda }_k(t;X_i^{(2)},v_i,{\gamma }_k,{\nu }_k)$ is the instantaneous failure rate from cause k at time t given the vector of covariates $X_i^{(2)}(t)$ and the latent unknown factor v_i, in the presence of all other failure types. The regression coefficient ν_k represents the effect of the latent variable v_i with ν₁ set to 1 to ensure identifiability. The parameter γ_k represents the effects of the observed covariates $X_i^{(2)}(t)$ on cause k. We further assume that the k^th baseline hazard is a step function, ${\lambda }_{0k}(t)={\lambda }_{0k}^{(s)}$, for $t_k^{(s-1)}<t\le t_k^{(s)}$, where $0<t_k^{(1)}<\cdots <t_k^{(S^k)}<\infty$ is a partition of (0, ∞) and S^k indicates the number of steps for the k^th baseline hazard. The competing risks model is one of the useful methods to handle dependent censoring. The identification of dependent competing risks models in which each risk has a mixed proportional hazard specification with regressors, and the risks are dependent by way of the unobserved heterogeneity, or frailty components, has been proved by Abbring and Van den Berg (2003).

Assume that

$$W_i=\left(\begin{array}{c}{U}_i\\ v_i\end{array}\right)\sim N_{q+1}\left(\left(\begin{array}{c}\mathbf{0}\\ 0\end{array}\right),{\mathrm{\sum }}_i=\left(\begin{array}{cc}{\mathrm{\sum }}_{U_i}& {\mathrm{\sum }}_{U{v}_i}\\ {\mathrm{\sum }}_{U{v}_i}^T& {\sigma }_{v_i}^2\end{array}\right)\right).$$ (3)

Similar to Pourahmadi (1999), we model the covariance matrices Σ_i through a modified Cholesky decomposition $M_i{\mathrm{\sum }}_i{M}_i^T=H_i$, where H_i is a diagonal matrix with positive entries and M_i is the lower triangular matrix with −φ_i,jl as its (j, l)^th entry. This decomposition has a clear statistical interpretation: the below-diagonal entries of M_i are the negatives of generalized autoregressive parameters (GARP), φ_i,jl, in the autoregressive model

$$W_{ij}=\sum _{l=1}^{j-1}{\phi }_{i,jl}{W}_{jl}+e_{ij},j=1,\dots ,q+1.$$ (4)

The diagonal entries of H_i are the innovation variances (IV) $h_{ij}^2=var(e_{ij})$ and we have cov(e_ij, e_jk) = 0 if j ≠ k (1 ≤ j, k ≤ q + 1 and i = 1, … , m). The GARPs and the logarithms of the IVs are modeled with linear and log link functions:

$$\{\begin{array}{ll}{\phi }_{i,jl}=a_{i,jl}^T{\eta }_1\hfill & \text{for}i=1,\dots ,m\hfill \\ log{h}_{ij}^2=b_{ij}^T{\eta }_2\hfill & j=1,\dots ,q+1,l=1,\dots ,j-1\hfill \end{array}$$ (5)

where a_i,jl and b_ij are covariates, and η₁ and η₂ are low-dimensional parameter vectors. For example, a_i,jl and b_ij may contain group indicators, implying that the random effects covariances are heterogeneous. The homogeneous random effects assumption in existing joint models becomes a testable assumption within our model framework. Furthermore, the resulting estimated covariance matrix is guaranteed to be positive definite. The latent association between the longitudinal measurements and survival outcomes can be assessed by testing the hypothesis Σ _Uvi = 0.

2.2 Likelihood

The standard maximum likelihood method involves integrating out latent variables from the log-likelihood function which is difficult when dealing with high-dimensional variables. We develop a Bayesian estimation procedure and a Markov chain Monte Carlo (MCMC) method for estimation and inference. To make the sampling of σ² and β easier, we use the fact that the t-distributed error can be represented as ${\epsilon }_{ij}={\tau }_{ij}^{-1/2}{\epsilon }_{ij}$, where τ_ij |k ~ Gamma(k/2, k/2) is independent of U_i and ε_ij ~ N (0, σ²). We define the parameter set in the joint model as: Ω = {β, σ², γ, ν, λ₀, η₁, η₂}, where γ = (γ₁,γ₂, … , γ_g ), ν = (ν₂, … , ν_g ) and ${\lambda }_0=({\lambda }_{01}^{(1)},{\lambda }_{01}^{(2)},\dots ,{\lambda }_{0g}^{(S^g)})$. We assume that for each subject i the longitudinal data are independent of the survival data, given all the parameters in O, latent factors θ = (W, τ), and covariates (X_i, Z_i). For simplicity, we assume k is prespecified. Thus, the full likelihood function for Ω, conditional on the data (Y_i, C_i) for i = 1, … , m and covariates, is:

$$L(\mathrm{\Omega }\mid Y,C)\propto \prod _{i=1}^{m}p(Y_i,C_i\mid \mathrm{\Omega })=\prod _{i=1}^m{\int }_{\theta }p(Y_i\mid \theta ,\mathrm{\Omega })p(C_i\mid \theta ,\mathrm{\Omega })p(\theta \mid \mathrm{\Omega })d\theta$$ (6)

It is convenient to work directly with the joint distribution of the observed data (Y, C) and the unobservable random vector θ, conditional on Ω, which facilitates the MCMC implementation. The conditional joint density of (Y, C) and θ is:

$$\begin{array}{l}p(Y,C,\theta \mid \mathrm{\Omega })\\ =\prod _i^{m}p(Y_i\mid {\theta }_i,\mathrm{\Omega })p(C_i\mid {\theta }_i,\mathrm{\Omega })p({\theta }_i\mid \mathrm{\Omega })\\ \propto \prod _{i=1}^m\prod _{j=1}^{n_i}{\left(2\pi \frac{{\sigma }^2}{{\tau }_{ij}}\right)}^{-\frac{1}{2}}exp\left\{-\frac{{\tau }_{ij}}{2{\sigma }^2}{(Y_{ij}-X_{ij}^{(1)T}\beta -Z_{ij}^T{U}_i)}^2\right\}\\ \times \prod _{k=1}^g({({\lambda }_k(T_i))}^{I(D_i=k)}exp\{-H_k(T_i)\})\\ \times exp\{-\frac{1}{2}\sum _{j=1}^{q+1}[b_{ij}^T{\eta }_2+{\left(W_{ij}-\sum _{l=1}^{j-1}{a}_{\mathit{ijl}}^T{\eta }_1{W}_{il}\right)}^2\\ \times exp(-b_{ij}^T{\eta }_2)\left]\right\}\end{array}$$ (7)

where ${\lambda }_k(T_i)={\lambda }_{0k}(T_i)exp\{X_i^{(2)}(T_i){\gamma }_k+{\nu }_k{v}_i\}$ and

$$H_k(T_i)=exp({\nu }_k{v}_i)\sum _{s=1}^{S^k}I(T_i>t_k^{(s-1)}){\lambda }_{0k}^{(s)}\times {\int }_{t_k^{(s-1)}}^{\mathit{min}(T_i,t_k^{(s)})}exp(X_i^{(2)}(t){\gamma }_k)dt$$ (8)

2.3 Estimation and inference

Our Bayesian method involves a combination of direct sampling from the full conditional distribution, Metropolis-Hastings (MH) sampling (Hastings, 1970; Chib and Greenberg, 1995) and adaptive rejection sampling (ARS) (Gilks and Wild, 1992). We estimate the parameters by their posterior medians. Approximate 95% probability intervals are based on the 2.5^th and 97.5^th percentiles. Standard errors are obtained from the standard deviations of the posterior samples. The convergence of the Gibbs sampler is monitored by examining time series plots of the parameters over iteration and the Gelman and Rubin (1992) approach of using multiple chains.

We assume independent priors for O. We specify Normal priors for the parameters β, γ, ν, η₁ and η₂, leading to conjugate posteriors for β and some components of η₁. We use an inverse Gamma prior for the measurement error variance σ² and a gamma prior for each step of the k^th baseline hazard function λ_0k by which conjugate posterior distributions are easy to obtain. Because the full conditional distributions of the parameters β, σ², and ${\lambda }_{0k}^{(s)}$, (s = 1, … , S^g, k = 1, … , g) are standard distributions, drawing random variates from their full conditional distributions is straightforward. The full conditional distribution of the random variate τ_ij given k is also known. For other parameters and the random effects (U_i, v_i), we either use a Metropolis-Hastings step with the normal approximation to the full conditional distribution as the candidate distribution or apply the adaptive rejection sampling technique. The technical details on the sampling distributions are given in the Appendix.

The initial values of the parameters for sampling are obtained by modeling the longitudinal data and survival data separately by a linear mixed model and a cause-specific proportional hazards model. The initial value for ${\lambda }_{0k}^{(s)}$ (s = 1, … , S^k, k = 1, … , g) can be obtained by drawing a random variate from the gamma full conditional distribution described in the Appendix.

3. AN EXAMPLE

We apply the developed method to analyze a data set from a scleroderma lung study (SLS) (Tashkin et al., 2006) to evaluate the effectiveness of oral cyclophosphamide (CYC) for scleroderma lung disease. The SLS enrolled 158 patients, which were randomized to receive either CYC (79 patients) or placebo (79 patients) for 12 months. An additional year of follow-up was performed to determine if CYC effects persisted after treatment. The primary outcome is forced vital capacity (FVC, % predicted) which was measured at 3-month intervals from the baseline. Treatment failure was defined as a ≥ 15% (absolute) decrement in %FVC from baseline occurring at least 3 months into treatment that was sustained for at least 1 month.

Our analysis is based on the 6–24 months %FVC scores of 141 patients. The longitudinal profile of %FVC over time for the two groups (Figure 1) reveals some potential outliers. We are particularly concerned how these outlying data points would affect the joint model inference. We observe 14 treatment failures or deaths, 32 informative dropouts and 5 noninformative dropouts. A dropout is noninformative if there is no evidence showing that the dropout is related to the disease or the treatment, and informative otherwise. Since the informative dropout is potentially related to the patient’s disease condition, it causes not only non-ignorable missing data in %FVC, but also dependent censoring for treatment failure or death.

We consider two baseline factors in our joint model when assessing the CYC treatment effects: baseline %FVC (FVC₀), and lung fibrosis (FIB₀). It is suggested by clinicians that the beneficial effects of CYC on pulmonary function continue to increase after stopping treatment at 12 months and eventually begin to wane after 18 months. Therefore, we fit the following linear spline mixed effects model with a change point at month 18 for the longitudinal measurements %FVC:

$$\begin{array}{l}\%{\mathit{FVC}}_{ij}={\beta }_0+{\beta }_1{\mathit{FVC}}_{0i}+{\beta }_2{\mathit{FIB}}_{0i}+{\beta }_3{\mathit{CYC}}_i\\ +{\beta }_4{\mathit{Time}}_{ij}+{\beta }_5{({\mathit{Time}}_{ij}-18)}_{+}+{\beta }_6{\mathit{FVC}}_{0i}\\ \times {\mathit{CYC}}_i+{\beta }_7{\mathit{FIB}}_{0i}\times {\mathit{CYC}}_i+{\beta }_8{\mathit{Time}}_{ij}\\ \times {\mathit{CYC}}_i+{\beta }_9{({\mathit{Time}}_{ij}-18)}_{+}\times {\mathit{CYC}}_i\\ +Z_{ij}{U}_i+{\epsilon }_{ij}\end{array}$$ (9)

where U_i = (U_i1, U_i2)^T is the subject-specific random effects and the ε_ij is the mutually independent measurement errors. Since we include baseline %FVC as a fixed effect covariate, we don’t consider random intercept to avoid possible confounding effects and Z_ij = (Time_ij, (Time_ij − 18)₊).

A cause-specific competing risks sub-model was applied to model disease-related dropout (risk 1) and treatment failure or death (risk 2):

$${\lambda }_1(t)={\lambda }_{01}(t)exp({\gamma }_{11}{\mathit{FVC}}_{0i}+{\gamma }_{12}{\mathit{FIB}}_{0i}+{\gamma }_{13}{\mathit{CYC}}_i+{\gamma }_{14}{\mathit{FVC}}_{0i}\times {\mathit{CYC}}_i+{\gamma }_{15}{\mathit{FIB}}_{0i}\times {\mathit{CYC}}_i+v_i)$$ (10)

and

$${\lambda }_2(t)={\lambda }_{02}(t)exp({\gamma }_{21}{\mathit{FVC}}_{0i}+{\gamma }_{22}{\mathit{FIB}}_{0i}+{\gamma }_{23}{\mathit{CYC}}_i+{\gamma }_{24}{\mathit{FVC}}_{0i}\times {\mathit{CYC}}_i+{\gamma }_{25}{\mathit{FIB}}_{0i}\times {\mathit{CYC}}_i+{\nu }_2{v}_i).$$ (11)

The latent variables from both sub-models are assumed to have a multivariate normal distribution with mean zero and variance-covariance matrices

$${\mathrm{\sum }}_i=\left(\begin{array}{ll}{\mathrm{\sum }}_{U_i}\hfill & {\mathrm{\sum }}_{U{v}_i}\hfill \\ {\mathrm{\sum }}_{U{v}_i}^T\hfill & {\sigma }_{v_i}^2\hfill \end{array}\right).$$

We first test the homogeneous random effects covariance matrix assumption by considering subject-dependent covariates for a_ijl and b_ij. Specifically, we choose a_ijl = b_ij = (1, CYC_i), which allows heterogeneous covariance matrices for different treatment groups, and test the null hypothesis by examining if the 95% credible interval of CYC effects contains zero for all the GARP and IV parameters. None of the 95% CIs for CYC of all the covariance parameters exclude zero (results not shown here), suggesting no obvious violation of the homogeneous random effects covariances assumption.

We use independent noninformative prior distributions for all the parameters with relatively large variances. A 3-step baseline hazard function, with the time points defining the steps being equallysplit percentiles of the observed event times, is utilized for the informatively censored events and the event of treatment failure or death. Sensitivity analyses with 4- and 5-step baseline hazard functions are conducted and show no significant difference. The corresponding priors for the parameters are β₀ ~ N (70, 10³) and β_l ~ N (0, 10³) for l = 1, … , 9; σ² ~ IG(10⁻³, 10⁻³); γ_kr ~N (0, 10³) for k = 1, 2 and r = 1, … , 5; ${\lambda }_{0k}^{(s)}\sim \mathrm{\Gamma }(0.1,0.1)$ for s = 1, … , S^k and S¹ = S² = 3; ν₂ ~ N (0, 10⁵); and each element of η₁ and η₂ ~ N (0, 10⁵). We use 30,000 iterations of MCMC sampling chains following a 15,000-iteration “burn-in” period.

We identify 7 possible outlying data points by examining the residuals from our robust joint model. Table 1 compares results from a normal joint model with and without the outliers together with a model with a t-distributed error (k = 3) using all data points. The estimation procedure for the normal joint model is the same except that there is no need to estimate parameter τ_ij (Huang, 2008). First, the outliers are observed to be influential to the parameter estimates for the longitudinal endpoint. The t-model with all data and the normal model without outliers yield consistent conclusions. For example, both methods reveal a significant time trend in the placebo group before 18 months (β₁), which indicates a more steep decrease before 18 months in %FVC scores than that estimated from the normal joint model with all the data points. They also both identify a significant interaction (β₈) between the time trend (before 18 months) and the treatment group. In contrast, these effects are not significant using the normal method with all data points. Secondly, comparable estimates at the survival endpoint are obtained for all three models. Thirdly, all models identify a negative significant covariance Σ_U1v between the random slope before 18 months in the longitudinal model and the latent variable of the survival model, and a positive significant covariance Σ_U2v between the random slope after 18 months in the longitudinal model and the latent variable from the survival model, which indicates a dependence between the longitudinal measurement %FVC and the survival endpoint. We also observe a significant positive coefficient ν₂ which suggests a latent positive association between the two competing risks. Finally, the negative sign of Σ_U1v and positive sign of Σ_U2v together with the positive ν₂ indicate that before month 18, there is a lower risk of treatment failure or death and informative dropout for patients with higher than average increasing rate of %FVC over time; after 18 months, the trend is reversed due to the negative association between the two slopes. In summary, the longitudinal sub-model with a normal error is not robust against potential outliers in the longitudinal data, although the outliers may not have much impact on the estimation of the survival model parameters.

Table 1.

Analysis of 6–24 months scleroderma lung study data

	Normal distribution		t-distribution (κ = 3)
	With outliers	Without outliers	With outliers
	Estimate (95%CI)	Estimate (95%CI)	Estimate (95%CI)
Longitudinal outcome %FVC
Time (β1)	−0.13 (−0.30, 0.05)	−0.18 (−0.33, −0.02)	−0.20 (−0.36, −0.03)
Time18 (β2)	0.23 (−0.25, 0.74)	0.15 (−0.25, 0.53)	0.22 (−0.13, 0.56)
FVC0 (β3)	0.92 (0.83, 1.03)	0.88 (0.79, 0.98)	0.93 (0.85, 1.01)
FIB0 (β4)	−2.05 (−3.22, −0.94)	−1.83 (−2.84, −0.81)	−1.88 (−2.75, −0.99)
CYC (β5)	−1.38 (−3.66, 1.00)	−1.00 (−2.89, 0.88)	−1.12 (−2.83, 0.59)
FVC0 × CYC (β6)	0.11 (−0.04, 0.25)	0.15 (−0.02, 0.27)	0.09 (−0.01, 0.20)
FIB0 × CYC (β7)	2.03 (0.43, 3.69)	1.74 (0.32, 3.19)	2.25 (0.92, 3.52)
Time × CYC (β8)	0.26 (−0.01, 0.51)	0.23 (0.01, 0.45)	0.24 (0.01, 0.47)
Time18 × CYC (β9)	−0.64 (−1.33, 0.07)	−0.43 (−0.96, 0.13)	−0.41 (−0.92, 0.09)
p-value for H0:Overall CYC Effects=0	0.040	0.022	0.003
Cause-specific hazards (informatively censored events)
FVC0 (γ11)	−0.06 (−0.13, −0.01)	−0.06 (−0.12, −0.01)	−0.06 (−0.12, −0.01)
FIB0 (γ12)	0.21 (−0.28, 0.77)	0.21 (−0.29, 0.76)	0.21 (−0.27, 0.79)
CYC (γ13)	0.24 (−0.61, 1.20)	0.29 (−0.55, 1.21)	0.25 (−0.57, 1.18)
FVC0 × CYC (γ14)	0.11 (0.03, 0.18)	0.10 (0.03, 0.18)	0.11 (0.04, 0.19)
FIB0 × CYC (γ15)	0.13 (−0.58, 0.83)	0.12 (−0.61, 0.81)	0.08 (−0.63, 0.78)
Cause-specific hazards (treatment failure of death)
FVC0 (γ21)	0.01 (−0.07, 0.11)	0.02 (−0.06, 0.10)	0.01 (−0.07, 0.09)
FIB0 (γ22)	0.25 (−0.68, 1.22)	0.22 (−0.62, 1.13)	0.25 (−0.67, 1.20)
CYC (γ23)	−1.24 (−3.20, 0.35)	−1.19 (−3.29, 0.22)	−1.20 (−3.50, 0.34)
FVC0 × CYC (γ24)	−0.06 (−0.20, 0.08)	−0.07 (−0.20, 0.07)	−0.05 (−0.19, 0.09)
FIB0 × CYC (γ25)	−0.55 (−2.26, 1.07)	−0.52 (−2.12, 0.94)	−0.51 (−2.22, 1.02)
Random effects
ν2	3.34 (1.34, 8.35)	3.28 (1.42, 8.81)	3.25 (1.18, 7.84)
ΣU11	0.27 (0.20, 0.36)	0.28 (0.21, 0.37)	0.25 (0.19, 0.33)
ΣU12	−0.36 (−0.61, −0.18)	−0.32 (−0.53, −0.17)	−0.27 (−0.45, −0.15)
ΣU22	1.60 (0.89, 2.59)	0.93 (0.51, 1.61)	0.73 (0.39, 0.1.25)
${\sigma }_v^2$	0.40 (0.07, 1.59)	0.31 (0.05, 1.16)	0.35 (0.06, 1.31)
Covariance of Ui and vi
ΣUv1	0.25 (−0.53, −0.09)	−0.25 (−0.50, −0.09)	−0.23 (−0.47, −0.08)
ΣUv2	0.69 (0.24, 1.50)	0.42 (0.11, 1.02)	0.39 (0.11, 0.93)
Model fit
DIC	5693.08	5295.18	5089.35

Note: The bold numbers indicate the significant results (p-value < 0.05).

The models are assessed using the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002). The robust joint model gives the lowest DIC of 5089.35, which indicates the best fit. We note that there are several versions of DIC for missing data models (Celeux et al., 2006; Chen, 2006). Here we use the DIC constructed from the conditional distribution while treating both Ω and W as parameters because it is easy to compute. We conduct a small simulation to evaluate the DIC which selects 147 times out of 200 datasets and the effective dimension is always positive.

4. SIMULATION STUDY

We carry out a simulation study to assess the performance of our robust joint model and compare it to the joint model with a normal measurement error. The longitudinal measurements are simulated from the following random slope model:

$$Y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\beta }_2{X}_{2i}+U_i{t}_{ij}+{\epsilon }_{ij}$$ (12)

where τ_ij = 0, 0.15, 0.3, … , 3, represents the scheduled visit time and X_2i ~ Bernoulli(0.5) is a group indicator. We generate 1% outliers in the placebo group from normal distributions N (60, 100) and N (−60, 100) with rates 30% and 70%, respectively. The rest of the data have measurement error ε_ij ~ N (0, 5). We simulate two competing risks

failure times with the following cause-specific hazards:

$${\lambda }_1(t;X_{1i},X_{2i},v_i,{\gamma }_1)={\lambda }_{01}(t)\mathit{exp}\{{\gamma }_{11}{X}_{1i}+{\gamma }_{12}{X}_{2i}+v_i\}$$ (13)

$${\lambda }_2(t;X_{1i},X_{2i},v_i,{\gamma }_2,{\nu }_2)={\lambda }_{02}(t)\mathit{exp}\{{\gamma }_{21}{X}_{1i}+{\gamma }_{22}{X}_{2i}+{\nu }_2{v}_i\}$$ (14)

where X₁ ~ N (2, 1.0), and X₂ is shared with the longitudinal model. We use constant baseline hazards of 0.12 and 0.25 for risk 1 and risk 2, respectively, to generate the survival data. The random effects are generated from the multivariate normal distribution with covariance matrices Σ_i which are decomposed into the GARPs and IVs modeled with covariates a_ijl = b_ij = (1, X_2i). In other words, the covariance matrices are different in the two groups: strong positive correlation in one group and strong negative correlation in the other. The parameter values are given in Table 2. With this setup, the rate of risk 1 is approximately 0.44, the rate of risk 2 is 0.36 and the censoring rate is 0.20. Longitudinal responses are missing after the observed or censored event times. The average number of total longitudinal observations is 7.8 per subject. We use a vague prior of N (0, 10⁵) for each component of β, γ, ν, η₁ and η₂, IG(10⁻³, 10⁻³) for σ², and Γ(10⁻³, 10⁻³) for λ₀. The simulation is based on 200 Monte Carlo samples with a sample size of 250. The MCMC sampling is run using 5, 000 iterations, and the estimation results are based on the last 2, 500 iterations.

The bias, standard deviations of the posterior medians and coverage rate of 95% credible intervals are given in Table 2. In the presence of outliers, the joint model with a normal measurement error shows large bias for the longitudinal fixed effects β, the joint random effects covariance matrix parameters and ν₂. In particular, the group effect β₂ is overestimated since the outliers only exist in the placebo group and have a higher probability of being negative. Furthermore, these biases do not disappear for a large sample size of 500 (Table 3). In the contrast, our robust joint model yields much smaller biases for all the parameters. Both methods produce comparable estimates for the fixed effects for the competing risks survival endpoint.

5. DISCUSSION

We propose a robust joint model for longitudinal measurements and competing risks survival data with heterogeneous random effects. The robustness against potential outliers in the longitudinal measurements is achieved by specifying a t-distribution for the measurement error in the linear mixed effects sub-model. In addition, the proposed approach allows for high-dimensional random effects and heterogenous covariance matrices of the multivariate random effects, and the resulting estimated covariance matrices are guaranteed to be positive definite.

The t-distribution model is a robust model in two ways. First, with t-distributed random errors, τ_ij reweights the observations according to their residuals, and thus we are able to obtain robust estimation by downweighting the outliers. Secondly, we carried out simulation to compare the two models (t-model and normal model) when there were no outliers, that is, the underlying measurement error followed a zero-mean normal distribution. There are almost unbiased estimates for all the parameters in both methods and the simulated coverage probabilities are close to 0.95, although the joint model with the t-distribution produces a little bit larger standard errors for the parameters at the longitudinal endpoint.

We did some sensitivity analyses of the estimates to mis-specification of the variance-covariance structure and found out that we may obtain biased parameter estimates for the survival endpoint when combining the information of the longitudinal outcome if the correlation of the two endpoints is incorrectly modeled. Therefore, ignoring the heterogeneity can result in biased estimates and invalid inference.

The t-distributed error with k = 3 has demonstrated nice properties for the purpose of guarding against outliers in the longitudinal data in our numerical study, even though it can also be estimated as a parameter. General principles of parsimony suggest that k be fixed for small data sets and estimated for large ones (Lange et al., 1989). Lange et al. (1989) also suggest that estimated values of degree of freedom below 1 should be regarded with suspicion. In addition to the t-distribution, other normal/independent distributions (Lange and Sinsheimer, 1993), such as the slash distribution or the contaminated normal distribution, can be adapted for the measurement error in our robust joint model. Rosa et al. (2003) pointed out that the t process is the most commonly used thick-tailed distribution for robust inference which is often a good alternative to a Gaussian distribution; the contaminated normal distribution is more flexible but at the expense of an additional parameter, while the slash distribution is rarely encountered in the literature despite its relatively easier implementation in hierarchical modeling.

Our model can be extended to clustered data. Clustered data arise frequently from multi-site clinical trials, in which each site can be viewed as a cluster, or from studies across families, in which each family may be treated as a cluster. The cluster effect can easily be incorporated as a random effect or as a design vector for the GARP/IV parameters in order to take into account the heterogeneity across the cluster.

Finally, it is possible to extend our method to handle recurrent event data when each subject may repeatedly experience a certain event. Typical medical examples are multiple infection episodes and tumor recurrences. Zhang et al. (2008) considered a joint mixed-effects regression model for time series measures and recurrent events to analyze the air quality and respiratory symptom data. Their work may represent the first attempt to include a latent process in both the hazard and recovery rates of a recurrent event process. Extension of our joint model to incorporate recurrent event data would offer another promising approach. A possible choice of the sub-model for the recurrent event data is the semiparametric transformation models with random effects described by Zeng and Lin (2007).

APPENDIX A: FULL CONDITIONAL DENSITIES

This section provides details for the full conditional distributions of the parameters used in the Gibbs sampling algorithm. We use p(·) and p(·|·) to denote marginal and conditional densities, respectively. We denote the prior distribution by p₀(·). Based on the modified Cholesky decomposition, the random effects v_i can be written as $v_i={\sum }_{l=1}^q{a}_{\mathit{iql}}^T{\eta }_1{U}_{il}+e_{i,q+1}$ where $e_{i,q+1}\sim N(0,exp(b_{i,q+1}^T{\eta }_2))$. Instead of sampling v_i directly, we sample e_i,q+1, leading to a faster convergence rate.

1. Sample τ_ij from

   $$p({\tau }_{ij}\mid .)\sim \mathrm{\Gamma }\left(\frac{1+\kappa }{2},\frac{1}{2}\left[\kappa +\frac{1}{{\sigma }^2}{(Y_{ij}-{\beta }^T{X}_i^{(1)}(t_{ij})-U_i^{T}Z(t_{ij}))}^2\right]\right)$$
2. Sample σ² from

   $$p({\sigma }^2\mid .)\sim IG\left(\frac{{\sum }_{i=1}^m{n}_i}{2}+{\alpha }_1,\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^{n_i}{\tau }_{ij}\times {(Y_{ij}-{\beta }^T{X}_i^{(1)}(t_{ij})-U_i^{T}Z(t_{ij}))}^2+{\alpha }_2\right)$$

   where p₀(σ²) = Γ(α₁, α₂).

3. Sample β from

   $$p(\beta \mid .)\sim N({\left(\frac{{\sum }_{i=1}^m{X}_i^{(1)T}{S}_i{X}_i^{(1)}}{{\sigma }^2}+{\mathrm{\sum }}_{\beta }^{-1}\right)}^{-1}\times \left(\frac{{\sum }_{i=1}^m{X}_i^{(1)T}{S}_i(Y_i-Z_{i}Ui)}{{\sigma }^2}+{\mathrm{\sum }}_{\beta }^{-1}{\beta }_0\right),{\left(\frac{{\sum }_{i=1}^m{X}_i^{(1)T}{S}_i{X}_i^{(1)}}{{\sigma }^2}+{\mathrm{\sum }}_{\beta }^{-1}\right)}^{-1})$$

   where S_i = Diag (τ_ij) and p₀(β) = N (β₀, Σ_β)

4. Sample the random effects U_i from

   $$p(U_i\mid .)\propto N({\mu }_{U_i\mid Y_i},{\mathrm{\sum }}_{U_i\mid Y_i})\times \prod _{k=1}^{g}exp\left\{\left(\sum _{l=1}^q{a}_{\mathit{iql}}^T{\eta }_1{U}_{il}+e_{i,q+1}\right)\times {\nu }_{k}I(D_i=k)-H_k(T_i)\right\}$$

   where ${\mathrm{\sum }}_{U_i\mid Y_i}={(\frac{Z_i^T{S}_i{Z}_i}{{\sigma }^2}+{\mathrm{\sum }}_{u_i}^{-1})}^{-1},{\mu }_{U_i\mid Y_i}={\mathrm{\sum }}_{U_i\mid Y_i}[\frac{Z_i^T{S}_i(Y_i-X_i\beta )}{{\sigma }^2}]$, and ${\mathrm{\sum }}_{u_i}^{-1}=M_i^{\ast T}{H}_i^{\ast -1}{M}_i^{\ast },M_i^{\ast }$ is a q × q matrix consisting of the first q columns and rows of M_i, $H_i^{\ast }$ is a q × q matrix consisting of the first q columns and rows of H_i. We use the one-step Metropolis-Hastings algorithm to obtain the update in the sampling sequence with the normal density from the longitudinal data as the proposal density. The random effects U_i is obtained by first sampling a random variable form the conditional density based on the longitudinal data and then using the conditional likelihood contribution from the survival data to determine the acceptance of the new draw.

5. Sample η₁ from

   $$p({\eta }_1\mid .)\propto N({\left(\sum _{i=1}^m{Q}_i^T{H}_i^{\ast -1}{Q}_i\right)}^{-1}\left(\sum _{i=1}^m{Q}_i^T{H}_i^{\ast -1}{U}_i\right),{\left(\sum _{i=1}^m{Q}_i^T{H}_i^{\ast -1}{Q}_i\right)}^{-1})\prod _{k=1}^{g}exp\left\{\right(\sum _{l=1}^q{a}_{\mathit{iql}}^T{\eta }_1{U}_{il}+e_{i,q+1}){\nu }_{k}I(D_i=k)-H_k(T_i)\}{p}_0({\eta }_1),$$

   where Q_i is a q × q₁ matrix with first row Q_i1 = 0 and j^th row $Q_{ij}={\sum }_{l=1}^{j-1}{a}_{\mathit{ijl}}^T{U}_{il}$ for j = 2, …, q. We sample η₁ in two steps: sample the entries only involving U_i from the normal conditional density, sample the entries involving U_i and v_i with adaptive rejection sampling. It is worth noting that for the homogeneous case where the variance-covariance matrix Σ is diagonal, we have Σ = H and M = I. In this case, there is no need to sample η₁ and it should be set to zero in the sampling procedure.

6. Sample η₂ from

   $$p({\eta }_2\mid .)\propto exp[-\frac{1}{2}\sum _{i=1}^m(\sum _{j=1}^q\{b_{ij}^T{\eta }_2+{\left(U_{ij}-\sum _{l=1}^{j-1}{a}_{\mathit{ijl}}^T{\eta }_1{U}_{il}\right)}^2\times exp(-b_{ij}^T{\eta }_2)\}+b_{i,q+1}^T{\eta }_2+e_{i,q+1}^{2}exp(-b_{i,q+1}^T{\eta }_2)\left)\right]p_0({\eta }_2).$$

   We use a Metropolis-Hastings step with a normal approximation to the full conditional as the candidate distribution. For details, see Daniels and Pourahmadi (2002).

7. Sample γ_kr, k = 1, …, g, r = 1, …, R from

   $$p({\gamma }_{kr}\mid .)\propto exp\left[{\gamma }_{kr}\sum _{i=1}^{m}I(D_i=k)X_{ir}^{(2)}(T_i)-\sum _{i=1}^m{H}_k(T_i)\right]p_0({\gamma }_k).$$

   We use a Metropolis-Hastings step within the single component sampler to update the values of these parameters. For each of these parameters, we propose a normal density as the proposal density, which has the current value of the parameter as its mean and its standard deviation is set equal to four times the standard error of a maximum partial likelihood estimate from a standard Cox model (Wang and Taylor, 2001).

8. Sample ν_k with ARS from

   $$p({\nu }_k\mid .)\propto exp[\sum _{i=1}^{m}I(D_i=k){\nu }_k\left(\sum _{l=1}^q{a}_{\mathit{iql}}^T{\eta }_1{U}_{il}+e_{i,q+1}\right)-\sum _{i=1}^m{\int }_0^{T_i}{\lambda }_{0k}exp({\gamma }_k^T{X}_i^{(2)}+{\nu }_k\left(\sum _{l=1}^q{a}_{\mathit{iql}}^T{\eta }_1{U}_{il}+e_{i,q+1}\right))dt]p_0({\nu }_k).$$
9. Sample e_i,q+1 (i = 1, …, m) from

   $$p(e_{i,q+1}\mid .)\propto N(0,exp(b_{i,q+1}^T{\eta }_2))\times \prod _{k=1}^{g}exp[e_{i,q+1}{\nu }_{k}I(D_i=k)-H_k(T_i)].$$

   The sample is obtained by first sampling a candidate from the normal densities as its assumption and then using the conditional likelihood contribution from the survival data to determine the acceptance of the new draw.

10. Sample each piece of λ_0k (k = 1, … g) from

    $$p({\lambda }_{0k}^{(s)}\mid .)\propto \mathrm{\Gamma }({\alpha }_k^s,{\beta }_k^s)p_0({\lambda }_{0k}^{(s)}),$$

    where ${\alpha }_k^s={\sum }_{i=1}^{m}I(D_i=k,t_k^{(s-1)}<T_i\le t_k^{(s)})+1$ indicates the number of events occurring in the time interval $t_k^{(s-1)},t_k^{(s)}$, and ${\beta }_k^s={\sum }_{i=1}^{m}I(T_i>t_k^{(s-1)}){\int }_{t_k^{(s-1)}}^{min(T_i,t_k^{(s)})}exp({\gamma }_k^T{X}_i^{(2)}+{\nu }_k{v}_i)dt$, for s = 1, …, S^k