Abstract
The BK channel is a Ca2+ and voltage-gated conductance responsible for shaping action potential waveforms in many types of neurons. Type II BK channels are differentiated from type I channels by their pharmacology and slow gating kinetics. The β4 accessory subunit confers type II properties on BK α subunits. Empirically derived properties of BK channels, with and without the β4 accessory subunit, were obtained using a heterologous expression system under physiological ionic conditions. These data were then used to study how BK channels alone (type I) and with the accessory β4 subunit (type II) modulate action potential properties in biophysical neuron models. Overall, the models support the hypothesis that it is the slower kinetics provided by the β4 subunit that endows the BK channel with type II properties, which leads to broadening of action potentials and, secondarily, to greater recruitment of SK channels reducing neuronal excitability. Two regions of parameter space distinguished type II and type I effects; one where the range of BK-activating Ca2+ was high (>20 µM) and the other where BK-activating Ca2+ was low (~0.4–1.2 µM). The latter required an elevated BK channel density, possibly beyond a likely physiological range. BK-mediated sharpening of the spike waveform associated with the lack of the β4 subunit was sensitive to the properties of voltage-gated Ca2+ channels due to electrogenic effects on spike duration. We also found that depending on Ca2+ dynamics, type II BK channels may have the ability to contribute to the medium AHP, a property not generally ascribed to BK channels, influencing the frequency-current relationship. Finally, we show how the broadening of action potentials conferred by type II BK channels can also indirectly increase the recruitment of SK-type channels decreasing the excitability of the neuron.
Keywords: modeling, neuron, dentate gyrus, granule cell, potassium channel, patch clamp
Introduction
Neuronal large conductance Ca2+-activated K+ channels (BK) are activated by coincident depolarization and increases in intracellular Ca2+ generated by voltage-gated Ca2+ channel activation during the action potential spike (Faber and Sah 2003b). As a result, these channels are activated with a delay from the peak of the action potential, contributing to shaping the falling phase of the spike (Storm 1987a; 1987b; Golding et al. 1999) and the fast afterhyperpolarization (fAHP) (Lancaster and Nicoll 1987; Storm 1987a; 1987b).
In different systems BK channels either increase (Du et al. 2005; Gu et al. 2007) or decrease excitability (Nelson et al. 2005; Matthews et al. 2008). In CA1 hippocampal pyramidal neurons BK channels have secondary effects that increase excitability (Gu, et al., 2007). Increases in excitability also were observed in gain-of-function of BK channels in dentate gyrus granule neurons (Brenner et al. 2005). The mechanisms are two-fold: i) more rapid Na+ channel re-activation following each spike or ii) a decrease in the medium afterhyperpolarization (mAHP), produced by small conductance (SK) Ca2+-activated K+ currents or delayed rectifier K+ currents (Brenner et al. 2005; Gu et al. 2007).
BK channels are expressed from a single pore-forming α subunit and their diversity partly arises from tissue- and cell-specific expression of β accessory subunits (Orio et al. 2002). Of particular interest is the β4 subunit, an accessory protein highly expressed in the brain (Behrens et al. 2000; Brenner et al. 2000; Brenner et al. 2005). Knockout studies of the β4 subunit suggest that this protein may confer properties of the type II class of BK channels in the brain (Brenner et al. 2005). Type II BK channels are resistant to scorpion venoms, are slow-gated and are relatively less Ca2+ sensitive (Reinhart et al. 1989). A possible functional role of the β4 subunit may be to limit BK channel activation during action potentials, since knockout of β4 demonstrates a “gain-of-function” for BK channels as evidenced by sharpening of action potentials. Moreover, knockout animals also exhibit epileptiform activity, presumably due to a paradoxical increase in neuronal excitability.
Biophysical studies in heterologous expression systems demonstrate complex effects of the β4 subunit on BK channels. Effects of β4 on steady-state channel open probability are Ca2+-dependent. β4 increases channel open probability at high Ca2+ concentrations while reducing open probability at low Ca2+ concentrations (Ha et al., 2004; Wang et al., 2006b; Wang et al., 2009). Thus, without a measure of local Ca2+ that activate BK channels one cannot infer whether β4 will enhance or inhibit BK steady state currents. The other aspect of β4’s influence is its significant slowing of activation/deactivation kinetics. A likely explanation for the BK channel gain-of-function (in β4 subunit knockout animals) is that BK channel lacking β4 are faster activating and can better follow the time course of the action potential. The presence of the β4 subunit may therefore slow BK conductance, filtering and reducing channel activation.
We have performed computational modeling to better understand effects of β4 subunits on spike duration and neuronal excitability. The approach offers several advantages to understanding BK channel function. First, computational modeling overcomes the difficulty to ascribe direct effects of β4 on BK channel activation from secondary effects. For example, the antagonistic relationship between BK channel activation and voltage-dependent Ca2+ influx can be readily distinguished in a computational model. However, it is experimentally difficult to distinguish BK channel effects on Ca2+ channel activation from Ca2+ effects on BK channels. Second, acutely isolating β4 effects is not yet experimentally feasible, and inferring β4 function using the knockout mice cannot exclude the possible compensatory effects. On the contrary, not only is it possible to manipulate levels of β4 ‘expression’ using modeling, it is also possible to distinguish effects of steady-state and kinetic modulation on spike duration and neuronal excitability.
Starting with measurements of BK channel properties made under physiological K+ conditions, we constructed Hodgkin-Huxley-like, “representational” models of BK channels with and without the accessory β4 subunit. We then used these models to perform voltage- and current-clamp simulations to understand what aspects of neuronal parameter space (voltage-gated channels, Ca2+ dynamics, etc.) are affected by BK channels containing or lacking a β4 subunit. We show that within two regions of parameter space, largely governed by the intracellular Ca2+ transient and the density of BK channels, that the β4 subunit had largest influences on action potentials. As well, we utilized the representational BK channel model to make predictions of how BK channels alone and those with β4 subunits (type II BK channels) differentially affect action potential shape and output properties of neurons.
Experimental Procedures
Experiments
Patch Clamp Recording of HEK Cells
Experiments were performed with the mouse α subunit cDNA expression vector in pcDNA3 (Genbank accession number MMU09383, construct initiates with the MDAL translation initiation site), and mouse β4 (accession number NM 021452) in the Invitrogen vector pcDNA3.1Hygro(+). The α subunit cDNA contains alternative exons insertions at site 3 and site 6 (Ramanathan et al., 2000). Studies of the related β1 and β2 subunits indicate that BK channels can assemble with a less-than saturating number of accessory subunits (Wang et al., 2002). However, we do not have an understanding of the relative β4 stoichiometry in DG neurons, nor how reduced β4 stoichiometry affects BK channels. As such, we measured αβ4 channel gating properties with DNA transfection ratios that likely saturate BK channels with a full complement of β4 subunits. This was a ratio of 1:10 α to β4 subunit in 2–3 micrograms total DNA and 10 microliter lipofectamine reagent per 35 mm dish of HEK293 cells. After 5 hours of incubation, the cells were re-plated on glass coverslips and analyzed by electrophysiology for the following 1–3 days. GFP expression from cotransfection (0.2 microgram) of the Clontech EGFP-N1 vector was used to identify channel-expressing cells.
The external recording solution was composed of (in mM) 10 HEPES, 145 NaCl, 5 KCl, 1 MgCl2, 2 CaCl2, pH 7.2. Internal solutions were composed of a pH 7.2 solution of (in mM) 20 HEPES, 140 KMeSO3, 2 KCl. Intracellular Ca2+ were buffered with 5 mM EGTA (0.9 µM), HEDTA (3.4, 7.3 and 18 µM) or NTA (41 µM) and free Ca2+ concentration was measured using an Orion Ca2+-sensitive electrode (Orion Research, Inc.).
Analysis of Macroscopic Currents
Conductance-voltage (G-V) relationships were obtained using a test pulse followed by a step to a post-test voltage (0mV) to measure instantaneous tail current 200 microseconds after the test pulse. In experiments where Gmax were not reached, Gmax values at higher Ca2+ concentration from the same patch were used. G/Gmax-V data were fitted with the Boltzmann function: G /Gmax = 1 / (1+ eQF(V1/2 −V)/RT), where V is the test potential, V1/2 is the membrane potential at half-maximal conductance, Q is the equivalent gating charge (the slope of the Boltzmann function is RT/QF).
Computer Modeling
All simulations were performed using NEURON 7.2 (Hines and Carnevale 1997) on an Apple Macintosh computer. Curve fitting and all analyses were performed using IgorPro (Wavemetrics, Lake Oswego, OR).
The state variable for each channel (w) was calculated over time using a Crank-Nicholson method solving the time dependent equation
| (1) |
where w∞ is the steady-state Ca2+ and voltage (v) dependent variable and τw is the time constant, also both Ca2+- and voltage-dependent. Steady-state values were calculated based on experimentally-derived Boltzmann functions (Fig. 1B) where
| (2) |
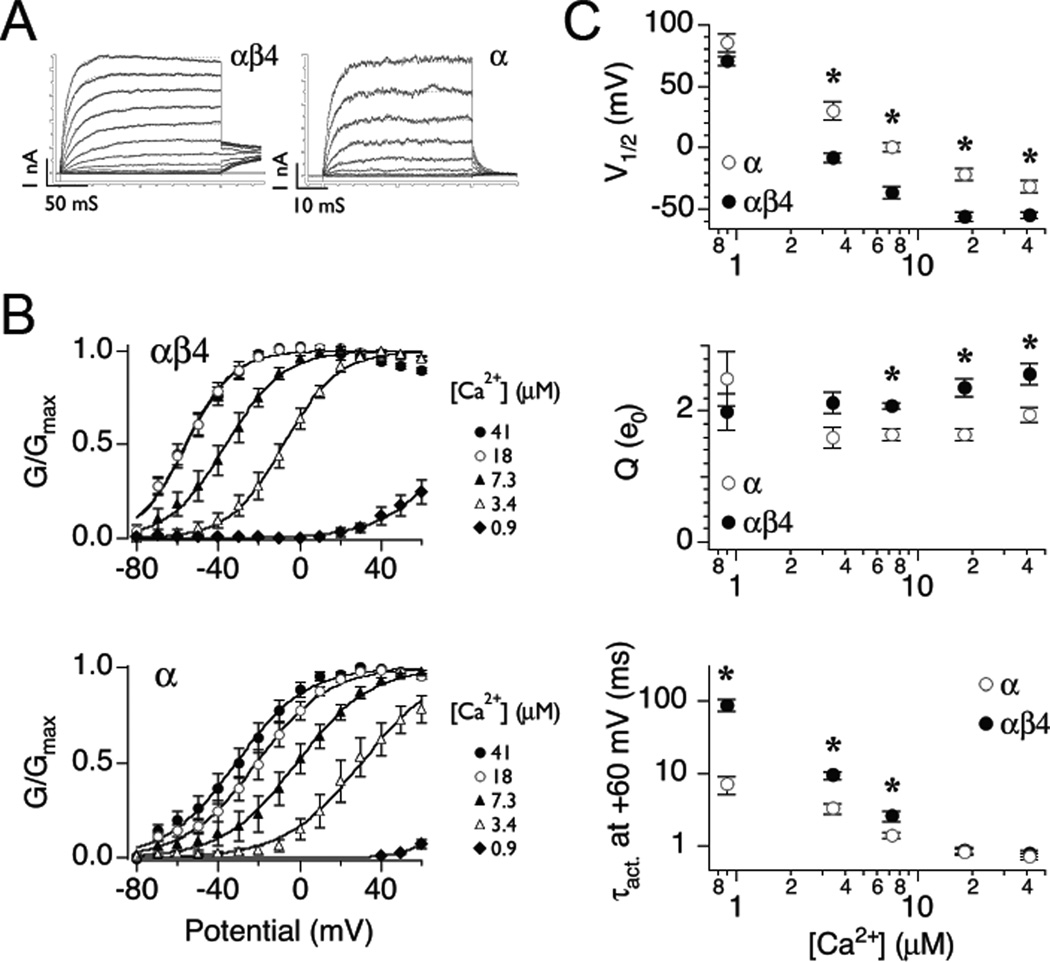
Figure 1. β4 shifts BK steady-state G-V relation to hyperpolarizing membrane potentials in ‘physiological’ external potassium.
A: A family of BK currents recorded from αβ4 (left) or α alone (right) channels in 3.4 µM Ca2+. Currents were evoked with 200 ms (αβ4) or 50 ms (α) depolarizing steps between −80 and 60 mV in 10 mV intervals. Current traces were fitted to single exponential (dashed curve) to estimate activation time constants. To reduce noise in the αβ4 current trace, the data was obtained by averaging five recordings. B: Mean G-V relations at different Ca2+ concentrations (µM) for αβ4 (top) and α (bottom). Solid curves represent fits to the Boltzmann function. (αβ4: 41 µM (n=9), 18 µM (n=6), 7.3 µM (n=6), 3.4 µM (n=6), 0.9 µM (n=5); α alone: 41 µM (n=11), 18 µM (n=7), 7.3 µM (n=6), 3.4 µM (n=5), 0.9 µM (n=3)). C: Pooled results for V1/2 (top), mean equivalent gating charge (Q, middle), and the activation time constant at +60 mV (bottom) plotted as a function of Ca2+ concentration. * p < 0.05 Student’s t-test for un-paired samples.
The time constant (τw) was determined from three functions. The first was a symmetrical double sigmoid function that described the voltage relationship of τw at a particular Ca2+ concentration
| (3) |
where f(v) ≥ 0.2 allowing the function to approach baselines in both directions and v’ was the adjusted potential
| (4) |
required for the Ca2+ dependence τw. The exponential function s(Ca) was used to “shift” the voltage-dependence of τw depending on Ca2+ concentration. Lastly, the magnitude of τw was also determined by the exponential function p(Ca). From these three functions (found in the legend for Figure 2), f(v), s(Ca), and p(Ca), τw was calculated by the equation:
| (5) |
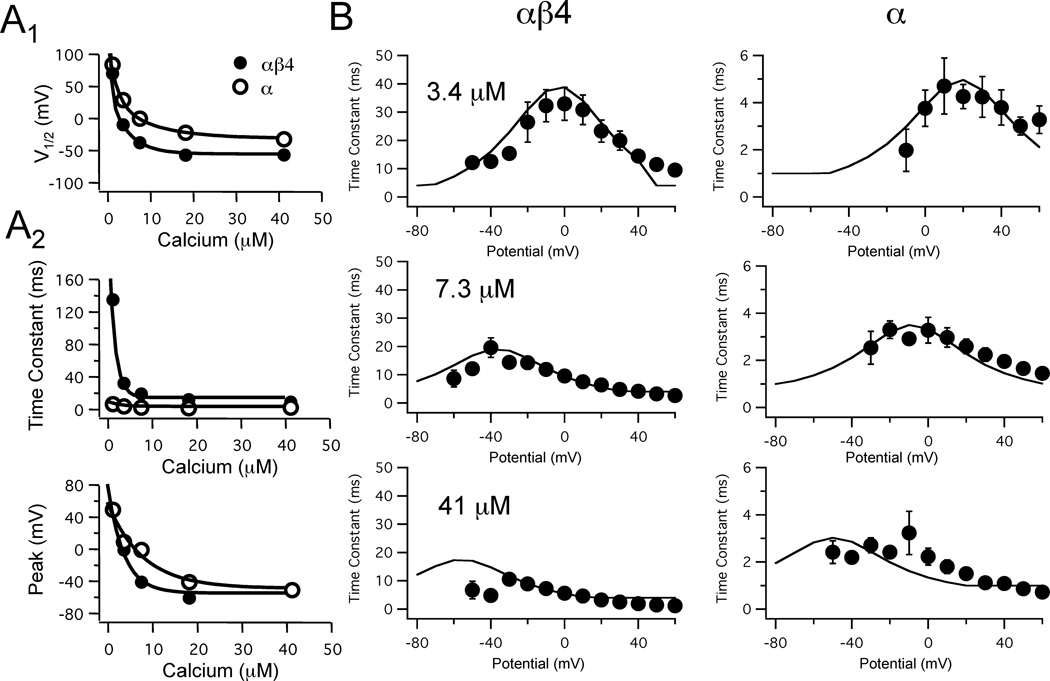
Figure 2. Models of BK channels with and without β4 accessory subunit.
A1: The Ca2+ dependence of channel activation was best fit by double exponential functions: and . Solid and filled circles are experimental data and the solid line is the best fit. A2: Relationship between Ca2+ and the voltage-dependence of the time constant for activation was determined by two parameters: maximum time constant (pαβ4 and pα) and the potential where the time constant was greatest (sαβ and sα) were best fit by single exponentials: pαβ4 (Ca 2+) = 13.7 + 234 ·e−720 Ca & pα (Ca) = 2.9 +6.3e−360Ca ; sαβ4 (Ca2+) = −30 + 137 ·e −280 Ca & sα(Ca) = −25.3+107.5e−120. Solid and filled circles are experimental data and the solid curves are the best fit. B: Single exponentials were obtained for BK currents (as in Fig. 1A) exposed to 41 µM Ca2+ (α: n = 11; αβ4: n = 10), 7.3 µM Ca2+ (α: n = 6; αβ4: n = 6), and 3.4 µM Ca2+ (α: n = 3; αβ4: n = 5). Symbols represent mean experimental data values and the error bars are SEM. The solid curves are the fit of the data for each concentration by equation 5.
Local Ca2+ dynamics sensed by the BK channels (eq. 6) were simulated as a shell beneath the plasma membrane (Sala and Hernandez-Cruz 1990; Yuen and Durand 1991) and controlled by Ca2+ influx, an exponential function regulating the rate of removal (τCa) from the shell (the diffusion of Ca2+), a parameter governing the thickness of the shell rapid Ca2+ buffering (S), and resting Ca2+ ([Ca]o). Varying the parameter S allowed us to change the amplitude of the Ca2+ transient without having to alter voltage-gated Ca2+ channels.
| (6) |
Simulations were performed using a model of a dentate granule cell modified from that of Aradi and Holmes (1999). The model included a voltage-dependent Na+ conductance (NaV), fast and slow delayed rectifier conductances (fKDR & sKDR, respectively), a slow Ca2+-dependent, voltage-independent K+ conductance (SK) where noted, and one of three possible (T, N, or L-type depending on the simulation) voltage-gated Ca2+ channels (Aradi and Holmes 1999). The dendrites contained the Na+ conductance and both fKDR & sKDR, while the axon contained only the NaV and fKDR. The somatic compartment contained NaV, fKDR, sKDR, one of either of the BK channels (α or αβ4), the SK conductance, and one of the voltage-gated Ca2+ channels in any particular simulation.
The Neuron Model Description Language “mod file” (Hines and Carnevale 2000) describing both the α subunit model and the αβ4 model, along with all necessary code demonstrating a representative simulation, will be made publicly available via the ModelDB database (https://senselab.med.yale.edu).
Results
Empirically derived BK channel models
In order to construct biophysical neuron models comparing how type I and type II BK channels affect action potentials a quantitative understanding of the channels’ voltage- and Ca2+-dependence on steady-state and kinetic properties are required. Functions describing these parameters can then be incorporated into a more complex biophysical neuronal model where, in turn, their interaction with other conductances on the simulated voltage response can be investigated (described below). Here we obtained these parameters from channels expressed in a heterologous system (see Methods). Specifically, BK channels with and without the β4 accessory subunit were studied under conditions where the external K+ concentration approximated physiological conditions. Macropatch inside-out currents were elicited from families of depolarizing steps for channels expressed with the accessory subunit, αβ4, or the α subunit alone (Fig. 1A). From these currents steady-state conductance-voltage plots (G-V) were obtained and fit with Boltzmann function (Fig. 1B) to obtain values for V1/2 and equivalent gating charge (Q) over a range of Ca2+ concentrations (Fig. 1C, top and middle panels). As expected, increasing Ca2+ concentration shifted activation curves to hyperpolarizing potentials for both the α subunit alone and with the accessory subunit (αβ4; Fig. 1B and 1C). Interestingly, β4 significantly reduced V1/2 at Ca2+ concentration greater than 3 µM in physiological K+. This differs from previous recordings under symmetrical K+, where β4 increases V1/2 below 20 µM Ca2+, but lowers it above (Wang et al. 2006). In contrast to V1/2, the equivalent voltage-dependence (Q) was relatively insensitive to Ca2+ concentration, though values for αβ4 channels were slightly higher than for the α subunit alone (Fig. 1C, middle panel). Again, this also differs from symmetrical K+, where β4 reduces Q at all Ca2+ concentration (Wang et al. 2006). Single time constants for channel activation were obtained from families of currents taken over a range of voltage-steps (Fig. 1A). In general, activation time constants decreased with Ca2+ concentration (Fig. 1C, bottom panel). At high concentrations, there was no significant difference in activation between BK channels with or without the accessory subunit. At lower Ca2+ concentrations (less than 10 µM) αβ4 channels activated significantly slower than α channels.
To model channel behavior, V1/2 values for either αβ4 or α BK channels, as determined above, were plotted against Ca2+ concentration and the relationship for each channel was best fit by a double exponential function (Fig. 2A1). These functions were then used to calculate the value of fractional opening at steady-state (see Methods equation 2). Next, we needed to determine the time-dependence for changes in fractional opening. Empirically-determined time constants (Fig. 2B) were used to generate equations approximating their Ca2+- and voltage-dependence. Two parameters were used to characterize how Ca2+ affected the voltage-dependent time constants for channel activation; the maximum time constant for current activation and the potential where the maximum time constant was observed. The Ca2+-dependence of these two parameters are shown in Figure 2A2. Both the maximum time constant and the potential where the maximum was reached, for either BK channel, were best fit by single exponential functions. Peak values for the time constants were greatest at Ca2+ concentrations less than 10 µM and it is within this range that the largest difference in time constants between the αβ4 and α were observed.
Using the two Ca2+-dependent functions empirically measured above (maximum time constant, peak shift potential), continuous functions for activation time constants across a physiological range of potentials and Ca2+ concentrations were calculated. It was assumed that these functions follow a symmetrical, double sigmoid relationship varying in amplitude (maximum time constant) and their voltage-dependence. Time constant functions for the αβ4 and α currents at three different Ca2+ concentrations are plotted against experimentally-obtained values and demonstrate reasonable overlap (Fig. 2B). For both αβ4 and α channels the functions shifted to more hyperpolarized potentials with increasing Ca2+ concentration. Most notably, however, the range of the time constants was much greater when the β4 was included, particularly at low Ca2+ concentrations. For example, at a low Ca2+ concentration (3.4 µM) the time constant at 0 mV was 33 ms, while with the α subunit alone it was 4 ms. Similarly, at high Ca2+ concentration (41 µM) the peak time constant at −40 mV for the αβ4 current was 9 ms, and 2 ms for the α subunit alone. At 0 mV there was less of a difference in time constants with high Ca2+ concentration.
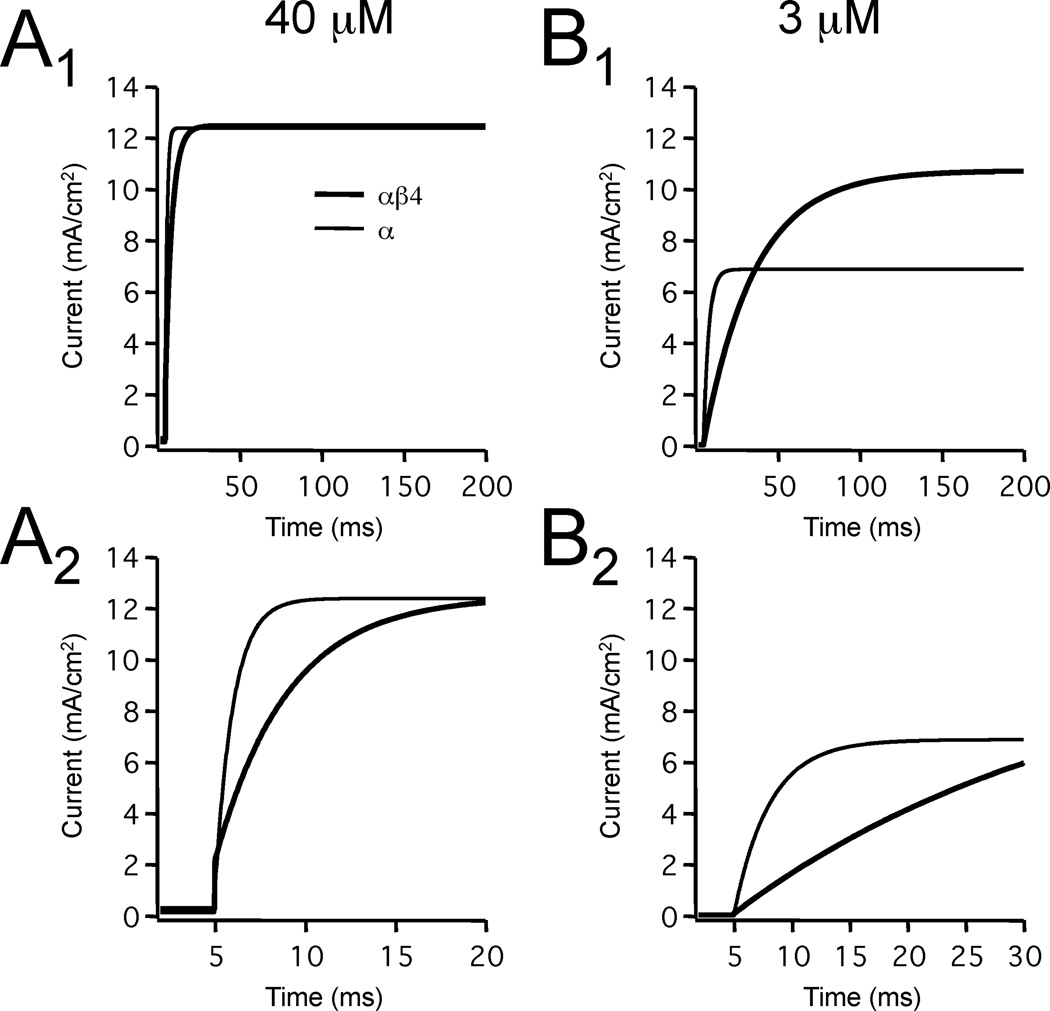
Simulated currents resulting from the activation of the two BK models by a voltage step, at two different Ca2+ concentrations, are illustrated in Figure 3. Either the αβ4 or α conductance was inserted into the soma of a model dentate granule cell (Aradi and Holmes 1999). Voltage-clamp simulations of a standard voltage-step protocol from a holding potential of −70 mV to a command potential of +40 mV was used to activate BK currents in the model. At a high Ca2+ concentration (40 µM) the activation for both the αβ4 and α currents were achieved within 20 ms, with the activation of the α current occurring faster (Fig. 3A). With a lower Ca2+ concentration (3 µM), although αβ4 had a larger steady-state current (Fig. 3B1), the slower activation of the αβ4 resulted in significantly less BK current than α alone over times scales less than 30 ms (Fig. 3B2).
Figure 3. Simulated currents produced by BK channels.
The soma of the model neuron was voltage clamped at −70 mV and stepped to +40 mV. Resulting currents for simulations containing either the αβ4 or α channel models are shown for two different fixed Ca2+ concentrations (A: 40 µM; B: 3 µM) at long (A1 and B1) or short (A2 and B2) time scales. As expected, the simulation lacking the β4 subunit clearly activates faster at either Ca2+ concentration. Note, however, that the difference in activation is more pronounced at the lower Ca2+ concentration.
Influence of β4 subunit on single action potentials
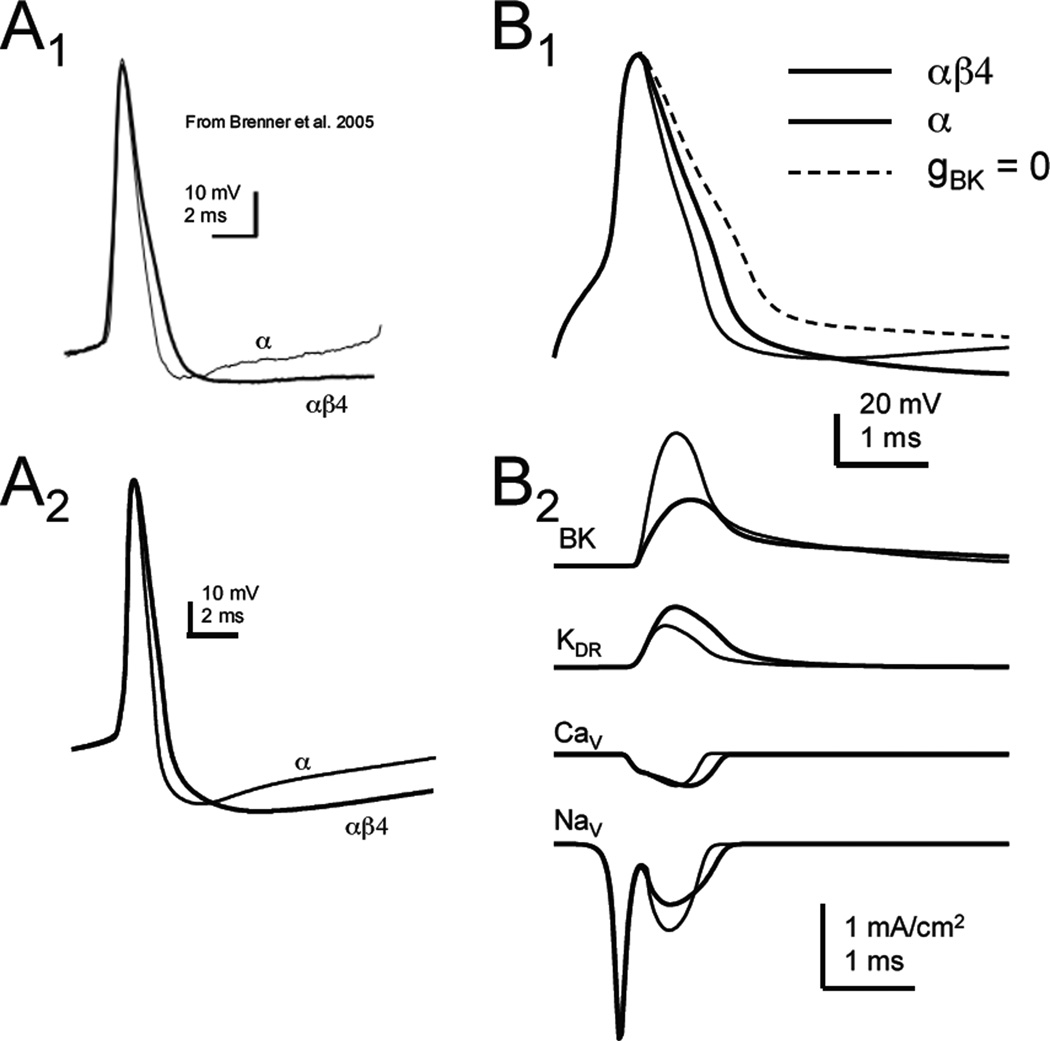
We next turned to current-clamp simulations to study how the interaction of voltage-gated Ca2+ entry and BK channel activation affected both the width of the action potential and the afterhyperpolarization. In mice lacking the β4 subunit, action potential half width of dentate gyrus granule cells is reduced by approximately 0.3 ms (Fig. 4A1) compared to wild type (WT) mice and the onset of the fast AHP (fAHP) occurs earlier (Brenner et al. 2005). Our simulations contained either the αβ4 or α BK channels, a fast Na+ channel, a fast and slow delayed rectifier K+ conductance, an L-type voltage-gated Ca2+ conductance (unless otherwise noted), and intracellular Ca2+ dynamics regulating BK channels (see Methods). In the simulations below, we adjusted parameters (BK channel density, amplitude of the Ca2+ transient, and intracellular Ca2+ dynamics) to obtain a difference in spike duration of at least 0.2 ms between models with and without the β4 subunit. No changes were made to the Na+ channel and delayed rectifier K+ conductances in all simulations. Examples of simulated spikes generated by the αβ4 and α BK channel models, generated either alone (Fig. 4B1) or as part of a train of action potentials (Fig. 4A2), qualitatively had the same features as spikes observed experimentally.
Figure 4. Effect of β4 or α BK channels on simulated action potentials.
A: Comparison of experimentally-measured spikes to simulated action potentials. Action potentials recorded in dentate gyrus granule cells (A1) from WT (αβ4) and KO (α) mice (from Brenner et al., 2005). A2: Simulated action potentials generated as part of a train of spikes for both the αβ4 and α BK models. B1: Single action potentials produced in models containing either the αβ4 or α BK channels. A spike from a model lacking BK channels is shown for comparison (dashed line, gBK = 0). B2: Ion currents underlying the action potential for either αβ4 or α BK models. Currents shown: BK, delayed rectifier (KDR), L-type voltage-gated Ca2+ channels (CaV), and fast voltage-gated Na+ channels (NaV).
Compared with a model lacking any BK channels, both the αβ4 and αBK models shorten the duration of the spike (Fig. 4B1). It is important to note that the influence of αβ4 BK channels on the action potential waveform is minimal in some studies of dentate gyrus granule cells, where the blockade of BK channels with paxilline has little effect (Brenner, et al., 2005; but see Muller et al., 2007). The α BK model had the greatest effect as it produced approximately twice as much BK current as the αβ4 model (Fig. 4B2). Other conductances in the model were affected by the change in spike width, secondarily to the difference in BK channels. Both the delayed rectifier current (KDR) and voltage-gated Ca2+ currents were enhanced by the wider spike produced in the αβ4 model. Voltage-gated Na+ currents during the upstroke were not different between the two models, as expected. During the downstroke, the non-inactivated portion of the Na+ current was less in the αβ4 BK model (compared to the α BK model) where the spike was wider and there was greater inactivation of the Na+ conductance.
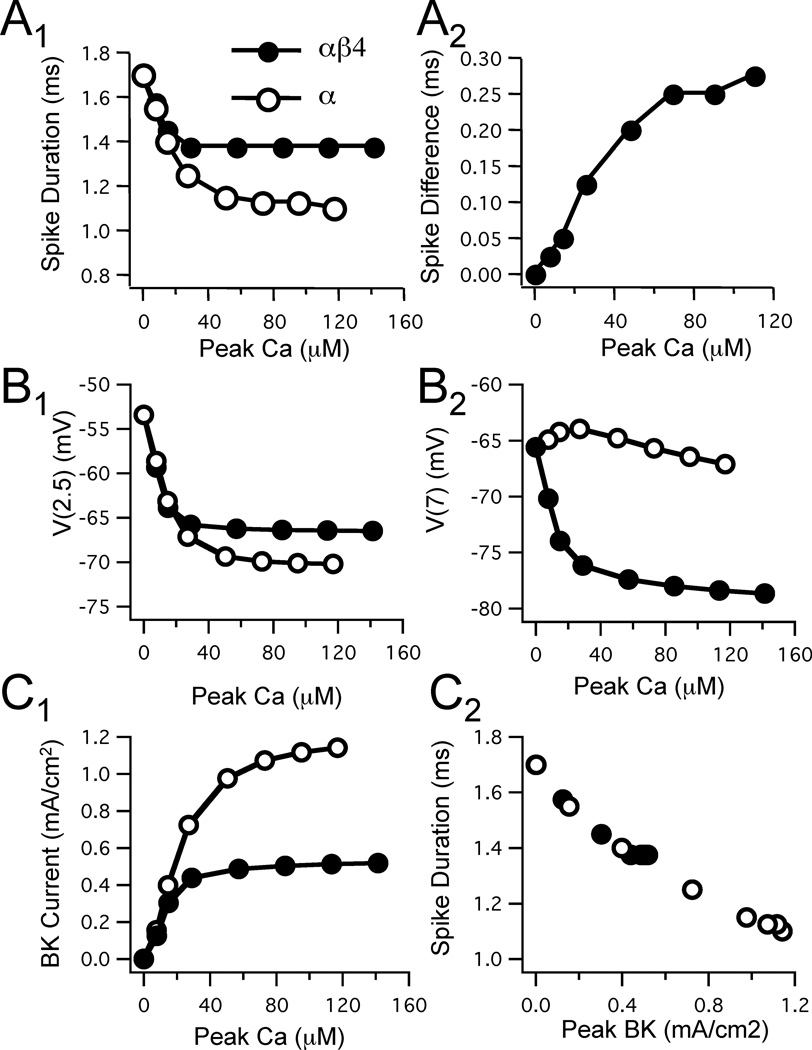
We examined the effects of varying the local Ca2+ concentration sensed by the BK channels. This was accomplished by systematically adjusting the amplitude of Ca2+ concentration sensed by the BK channels by scaling Ca2+ accumulation following Ca2+ influx (see Methods Eq. 6). This approach allowed us to alter Ca2+ concentration without introducing electrogenic effects produced by varying voltage-gated Ca2+ entry. Single action potentials, elicited by a 1 ms depolarizing current pulse (2 nA), were triggered to generate a local Ca2+ transient with peak amplitudes that varied between 0–120 µM. BK channel densities of 0.05–0.3 S/cm2 achieved a difference in spike width greater than 0.2 ms between the two models (same density was used for either of the two channel types). At the lowest part of the range of [Ca2+], the density of BK was approximately 20-fold greater than used in Aradi and Holmes (1999).
The relationship between Ca2+ concentration sensed by the BK channels and the subsequent effect on action potential duration (measured at −40 mV) for either the αβ4 or α BK model is shown in Figure 5A1. With increasing peak Ca2+ concentration spike duration decreased for both models. However, the α BK model saturated at greater Ca2+ level and had greater sharpening of the action potential than the αβ4 BK model. Spike duration decreased in the α BK model by ~0.6 ms (from 0 to saturating Ca2+ influx) and saturated at the 100 µM range. In contrast, the αβ4 BK conferred a maximum 0.3 ms sharpening of the action potential. This effect saturated at ~30 µM. The difference in spike duration between the two models (αβ4 vs α) increased with the amplitude of the Ca2+ transient and maximized to near 0.3 ms when peak concentrations reached above 60 µM (Fig. 5A2).
Figure 5. Spike waveforms are differentially affected in αβ4 and α BK channel models with varying Ca2+ transient levels.
A: Effect of varying Ca2+ transient amplitude on the difference in spike duration between models (gCa=4.5 mS/cm2; gBK=0.05 S/cm2). A1: Increasing Ca2+ transient amplitude reduced action potential duration for both models at concentrations above 20 µM. A2: The difference in spike width increased as a function of the average Ca2+ transient amplitude (average of peak Ca2+ transient produced by αβ4 and α BK models) up to ~60 µM. B: Presence of β4 affects afterpotentials in the model neurons. Afterspike potentials were measured at two time points: 2.5 ms and 7 ms after the onset of the stimulus. B1: Plot of the spike afterpotentials at the earlier time point (2.5 ms) as a function of Ca2+ transient amplitude. Both αβ4 and α BK models expressed a fAHP. B2: Plot of the spike afterpotentials at the later time point (7 ms) shows that for models lacking the β4 subunit an afterdepolarization (ADP) was elicited across all Ca2+ ranges, in contrast to models with the β4 subunit where a medium AHP was expressed. C: Relationship between Ca2+, BK channel current, and spike width. C1: Peak BK current is plotted against varying Ca2+ transient amplitude illustrating the larger current produced by the model lacking the β4 subunit. C2: Spike duration for the same two models plotted for varying BK currents showing the relationship between BK current and its effect on spike duration.
As mentioned above, in dentate gyrus granule cells the presence of the β4 subunit not only widens action potential duration, but also alters the afterhyperpolarization phase compared to cells lacking the accessory subunit (Brenner et al., 2005). The presence of the β4 subunit in our models not only affected spike repolarization, but also delayed the afterhyperpolarization converting a fAHP into a medium AHP (mAHP). We quantified this shift by measuring the potential after a spike at two time points; 2.5 and 7 ms after the current stimulus, respectively. As plotted in Figure 5B1, the early potential (measured at 2.5 ms) became more hyperpolarized with increasing BK channel activation. The αβ4 BK model was less sensitive to increasing Ca2+ concentration than the α BK model, consistent with its slower kinetics. At the later time point, the α BK model exhibited an afterdepolarization (ADP) that was only slightly Ca2+ sensitive and peaked at concentrations of ~20 µM (Fig. 5B2). In contrast, the αβ4 BK model produced a mAHP at this latency that was strongly Ca2+ sensitive up to concentrations over 40 µM.
The relationship between peak BK current and spike-mediated Ca2+ transients is illustrated in Figure 5C1. When peak Ca2+ concentrations were below 20 µM the relationship between Ca2+ concentration and peak BK current was approximately linear and there was no difference between the models. With higher concentrations the αβ4 BK current saturated below that for the α BK currents, with a difference between the αβ4 and α BK currents becoming apparent when the peak of the Ca2+ transient exceeded 20 µM. The difference in BK current amplitude between the two models translated into a difference in spike duration. Sharper spikes (shorter spike duration) were produced by the α BK channels, compared to models containing the αβ4 BK channels. This resulted from a near doubling of the BK current by the α channels, in spite of the fact that Ca2+ influx was somewhat less in models with α BK channels due to narrower spikes (see also Fig. 4B2). To show that for both αβ4 and α BK channel models the effect of varying BK current on spike duration is the same, both models fall along the same relationship for peak BK current plotted against spike duration (Fig. 5C2).
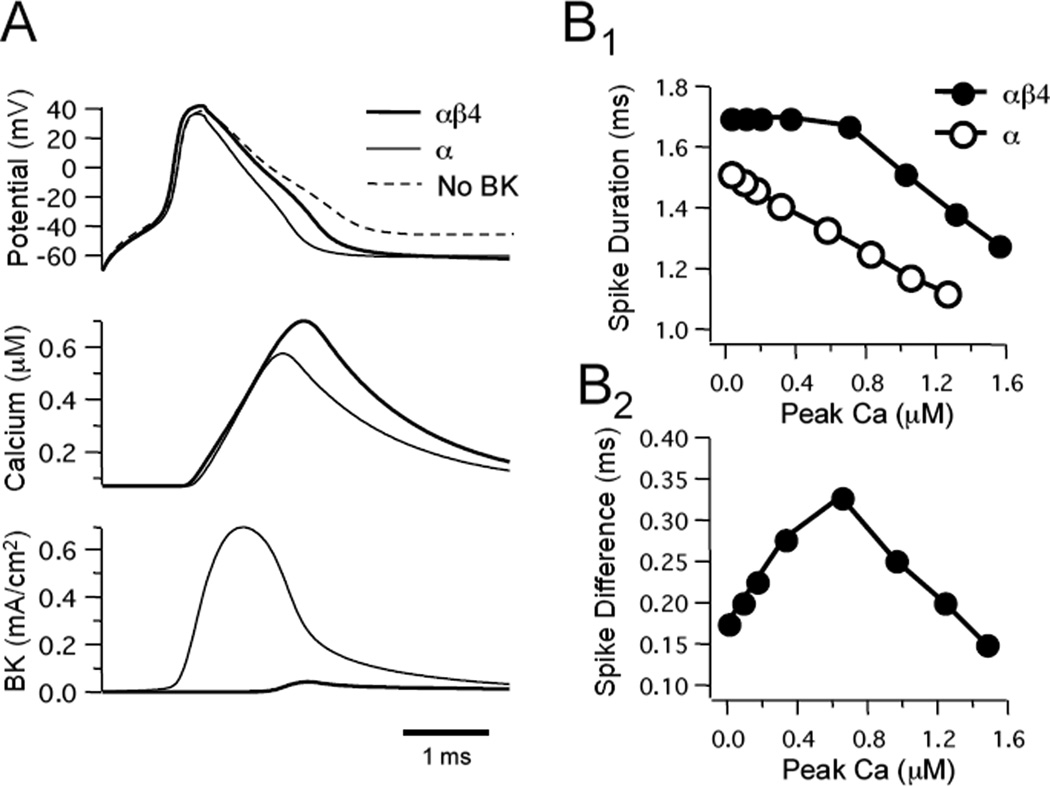
We noticed that the greatest difference in kinetics occurred within a lower range of Ca2+ concentrations (see Fig. 2). To study how a lower Ca2+ concentration might differentially affect the two models, we adjusted the amplitude of the Ca2+ transient to achieve approximately 100-fold lower amplitudes (less than 1 µM). However, with smaller Ca2+ transients action potentials failed to activate a sufficient BK conductance to affect spike width (not shown). To compensate for the ineffective conductance in the “low Ca2+ configuration”, BK channel density was increased to yield a difference in spike width (Fig. 6A). To observe a 0.2 ms difference between the two models a BK channel density of 20 S/cm2 or greater was required (compared to 0.05–0.3 S/cm2). The relationship between Ca2+ influx and BK channel activation was now somewhat different than seen with the previous “high Ca2+ configuration”. In particular, there was a greater difference in the current produced by BK channels. When αβ4 BK channels were inserted there was a ~93% decrease in the BK current compared with the α BK model (Fig. 6A). In contrast, there was approximately a 50% decrease for the high Ca2+ configuration. Also in contrast to the high Ca2+ configuration, varying the Ca2+ transient produced a relatively monotonic change in spike duration with a range of Ca2+ of 0–1.6 µM for the α BK model, while an effect on action potential width didn’t occur until ~0.6 µM for the αβ4 model (Fig. 6B1). As a result, the difference in spike duration was maximal when the Ca2+ transient peaked between 0.6–0.8 µM (Fig. 6B2).
Figure 6. A difference in spike duration between αβ4 and α models can be elicited with small Ca2+ transients if countered by an increase in gBK.
A: Spikes (top traces), Ca2+ transients (middle traces), and BK current (lower traces) produced when Ca2+ transient amplitude was low and BK channel density was elevated to 40 S/cm2 (low Ca2+ configuration). Note that the peak Ca2+ transient was less than 1 µM (compare with ranges in Figure 4). B: Effect of varying Ca2+ transient amplitude, by varying the Ca2+ buffering factor CB, on spike duration (B1). The difference in spike width between the two models (B2) (difference between αβ4 and α models) was greatest when Ca2+ peaked at approximately 0.6 µM for a channel density of gBK = 40 S/cm2.
It is important to point out that input resistance (RN) and membrane time constant (τm) were affected by the increase in BK channel density required for the low Ca2+ configuration. Most notably, with a larger density of α BK channels both RN and τm were less. In the high Ca2+ configuration (lower BK channel density) for either αβ4 or α BK channels RN = 247 MΩ and τm 39 ms. In the low Ca2+ configuration (higher BK channel density) there was no effect on the passive parameters for αβ4 BK channels. In contrast, for α BK channels the increased channel density resulted in a greater resting membrane conductance and thereby dropping the passive parameters (RN = 214 MΩ and τm = 36 ms). Given that neuronal BK channels have a low affinity for Ca2+, and are not observed to be active at rest suggest that these model parameters are not applicable to most neurons. Therefore, the remaining simulations were performed using the high Ca2+ configuration.
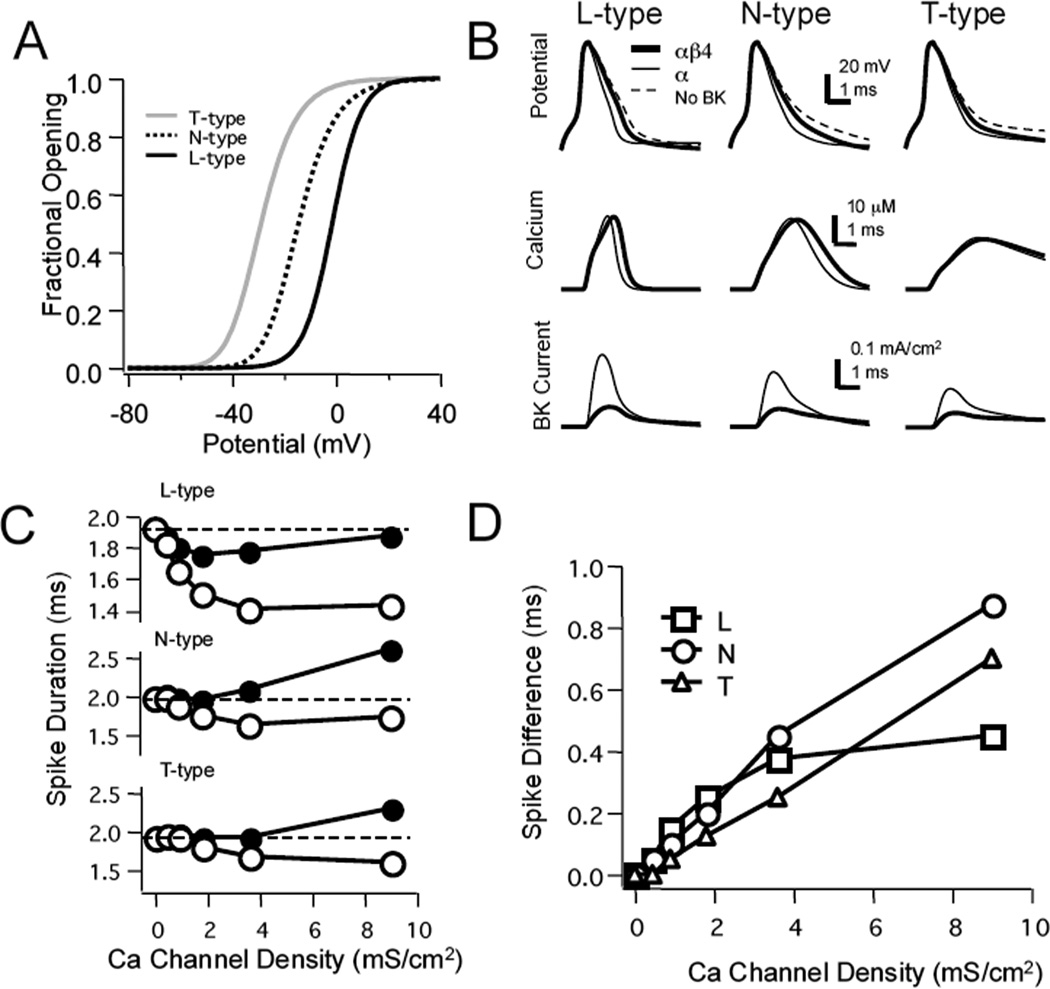
We next examined how Ca2+ channel density and the type of Ca2+ channel affected BK modulation of spike waveforms. Three different voltage-gated Ca2+ conductances were compared over a range of conductance densities representing fast-inactivating (T-type), higher threshold inactivating (N-type), and high-threshold, non-inactivating (L-type) Ca2+ channels (Fig. 7A). Sharpening of the action potential waveform was produced in both αβ4 and α BK models by all three sources of Ca2+ compared to models lacking BK channels (Fig. 7B). Interestingly, when T-type channels were the sole course of Ca2+ the difference in spike waveform between αβ4 and α BK models had little effect on Ca2+ influx. The relationship between Ca2+ channel density and spike duration for all three sources of Ca2+ is shown in Figure 7C. Spike duration generally was reduced in the α BK channel model with increasing T-, N-, or L-type channel density. In contrast, αβ4 models were less sensitive to Ca2+ channel density and T- and N-type channels increased spike duration at higher densities compared to models with L-type channels due to greater electrogenic effects on spike duration. The greater Ca2+ current broadened action potential duration countering the effect of BK channels.
Figure 7. Differential effects of varying the density and type of Ca2+ channels.
A: three types of voltage-gated Ca2+ channels were compared; a low-threshold, fast inactivating T-type channel, a higher-threshold, inactivating N-type conductance, and a high-threshold, non-inactivating L-type channel (the latter was used in all previous simulations). Fractional G-V plots for the three channel types are shown. B: Effect of different Ca2+ channels (gCa=3.6 mS/cm2; gBK=0.05 S/cm2) on spike waveforms when there were no BK channels present in the simulations (dashed line) and for simulations with either the αβ4 or α channel models. C: Spike duration plotted against varying Ca2+ channel density for models containing L- (top), N- (middle), or T- (bottom) type Ca2+ channels. Spike duration for models containing αβ4 BK channels (filled circles) and α BK channel (open circles) are plotted. Dashed lines represent spike duration when no Ca2+ channels were in the model. Note that for the αβ4 BK channel models N- and T-type channels produced broader spikes at higher Ca2+ channel densities. D: Effect of varying Ca2+ channel density on the difference in spike duration between simulations using the αβ4 or α channel models. The difference in spike duration increased with channel density for all three types of channels, saturating to near 0.4 ms for the L-type channel. In contrast, the difference increased throughout the range of densities when either the T- or N-type channels were engaged.
Overall, with greater Ca2+ channel density there was an increase in the difference in spike duration between αβ4 and α BK models (Fig. 7D). When L-type channels were the sole source of Ca2+ the difference in spike width saturated at approximately 0.4 ms. In contrast, when either N- or T-type channels were used the spike difference continued to increase nearly linearly within the range of densities studied. For these channels, at high Ca2+ channel densities (greater than 4 mS/cm2) spike width was affected not only by BK currents, but also by the electrogenic broadening of the spike by the Ca2+ channels (Fig. 7C). At higher densities, the greater difference was promoted not only by increased spike sharpening, but broadening of spikes by the larger Ca2+ current in αβ4 (Fig. 7C).
The amplitude and time course of the Ca2+ transient is affected not only by the magnitude of the Ca2+ transient, but also its kinetics. This is determined by a number of factors governing Ca2+ removal including fast buffering, diffusion, and extrusion/sequestration (see Eq. 6). We examined how varying the time constant for Ca2+ removal (τCa) affected BK currents and, in turn, spike waveforms. The effect of varying τCa on spike duration was similar to varying the amplitude of the Ca2+ transient. With increasing values of τCa, and therefore increasing amplitude of the Ca2+ transient, there was increased BK channel activation and decreased action potential duration for both models. Values of τCa of 0.1 ms or greater were required to achieve a 0.2 ms difference in spike duration between the two models. Consistent with the smaller αβ4 BK currents, spikes in the αβ4 BK model were wider than for the α BK model (simulations not shown).
Influence of β4 subunit on firing output
The observation that the β4 subunit affected the afterhyperpolarization phase of the action potential waveform both experimentally (Brenner et al., 2005) and in our simulations suggested that the presence of this subunit might directly affect firing rates by increasing interspike intervals. However, it has previously been shown that when firing rates of dentate gyrus granule cells were compared between WT and β4 KO mice, no direct effect was observed (Brenner et al. 2005). Rather, it was shown that β4 had an indirect, secondary action on firing rates. Blocking BK channels in WT granule cells had no effect on firing output, while blocking SK channels (a Ca2+-depenent K+ conductance) with apamin increased firing output. Conversely, blocking BK channels in cells lacking the β4 subunit decreased firing rates, again secondary to SK channel activation (Table 1).
Table 1.
Experimental constraints
| Spike duration | FI Slope | |||
|---|---|---|---|---|
| Condition | WT (αβ4) | KO (α) | WT (αβ4) | KO (α) |
| Control | ++ | + | ++ | +++ |
| Paxilline | ++ | ++ | ++ | ++ |
| Apamin | ++ | ++ | +++ | +++ |
++ : no difference from WT control
+ : less than WT control
+++ : greater than WT control
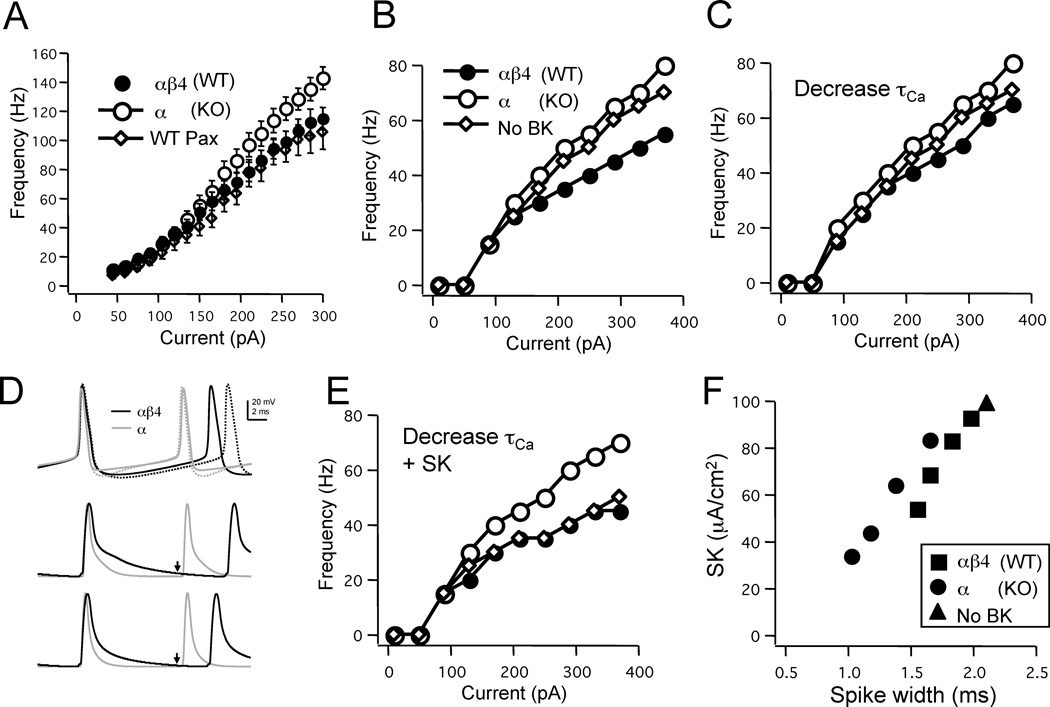
To explore how the two BK channel models’ shaping of spike waveform might, in turn, control neuronal firing we next studied the instantaneous frequency-current (F-I) relationship, quantifying the output firing rate of spike trains in response to varying input current driving the neuron. The general slope of this relationship represents the “gain” of the cell; for a given change in input current, it tells us how much change in firing output is achieved. In dentate gyrus granule cells recorded from slices, the F-I relationship for neurons lacking the β4 subunit were significantly more excitable and exhibited a greater slope compared to neurons from WT animals containing β4 (Fig. 8A). When BK channels were blocked with paxilline (in cells from either WT or KO mice), the F-I slope was the same as for the WT (One way ANOVA, F=3.959, df=46, p<0.05; Dunnett multiple comparison test).
Figure 8. Direct and secondary effects of BK channels on output firing.
A: Instantaneous frequency-current (FI) relationships averaged between the first three spikes in dentate gyrus granule cells from wild type (WT) animals (n=22), mice lacking the β4 subunit (KO; n=19), and WT mice exposed to the BK channel blocker paxilline (WT Pax; n=6). The slope of the FI relationship was greatest for the cells from KO mice, while they were the same for both the WT and WT exposed to paxilline. In experiments where the SK channel blocker apamin was present, the FI relationship for WT cells, but not β4 KO were increased (not shown). B: Simulations with a Ca2+ recovery time constant of 1 ms failed to replicate the relationship between FI curves; the αβ4 BK model had a direct effect on firing rate and the model lacking BK channels had an FI curve with the same slope as the α BK model. C: Decreasing the Ca2+ recovery time constant to 0.2 ms eliminated the direct effect of the αβ4 BK current on FI slope. D: The direct effect of the αβ4 BK model on interspike interval was due to the slow deactivation of the BK current. Action potentials (top traces) produced in either model with a 1 ms (dotted traces) or 0.2 ms (solid traces) Ca2+ recovery time constant (τCa). Note that the increased fAHP for the α BK model and the greater mAHP in the αβ4 BK model. Normalized BK channel currents (bottom traces) illustrating how the slower deactivation of the αβ4 BK model occurs when the Ca2+ recovery time constant is 1 ms (arrows) resulting in the larger mAHP. E: Addition of an SK conductance replicates the experimentally observed effect of the BK channels in neuronal input/output. F: Spike width affects SK channel current that, in turn, results in the secondary effects on interspike interval.
In contrast to the in vitro data, when no BK channels were included in the model (as if we were blocking BK channels) the slope was nearly the same as for the α BK channel model, while at the same time the αβ4 BK model had a direct effect depressing spiking output (Fig. 8B). The mechanism appeared to be through an enhanced mAHP αβ4 BK model that increased interspike interval and therefore decreased firing rates (Fig. 8D). Although our model was able to capture the effects of the two channels on spike waveform, over a large range of parameter space it failed to reproduce the experimentally-observed F-I relationship. This suggested that slower channel kinetics (Fig. 1 & 2) alone cannot account for β4 subunit influence of excitability. We therefore investigated other parameters that perhaps limit any direct effect of the αβ4 BK model on excitability.
One parameter that could limit the direct effect of the β4 subunit would be a decrease in αβ4 BK channel density. It has been observed that the presence of the β4 subunit reduces BK channel density by ~55% (Brenner et al., 2005). Varying the relative density of αβ4 BK channels to α BK channels produced a nearly linear difference in F-I slope. But even a 50% reduction in αβ4 BK channels was not sufficient to eliminate the direct effect on interspike interval (simulations not shown).
As mentioned above, we surmised that the direct effect of the αβ4 BK model was due to the mAHP. This is inconsistent with the general concept that BK channels rapidly deactivate after a spike and contribute to a fast but not medium component of the AHP (Faber and Sah 2003b). Therefore, we sought to find a parameter in the model that would influence the rate of channel deactivation following a spike. Other than modifying channel kinetics, which would affect spike waveform, the only parameter that could influence channel deactivation after the spike was the time constant for Ca2+ removal (τCa). We found that decreasing τCa from 1 ms to a value of 0.2 ms removed much of the direct effect of the αβ4 BK model on the F-I relationship (Fig. 8C). This change indeed decreased the BK current associated with the afterhyperpolarization phase (Fig. 8D). It is important to note that τCa could be decreased further, but below 0.1 ms where Ca2+ transients were below 10 µM, the channel no longer had a significant effect on spike duration. Therefore there was an optimum range of τCa that satisfied not only the effect of the two different BK channel models on spike waveform, but also did not produce a direct BK channel effect on interspike interval.
Neither voltage-gated Na+ or K+ (KDR) channels contributed to secondary effects on firing output. Voltage-gated Na+ channels were re-activated slightly more in the αβ4 BK model where the mAHP was greater in amplitude and duration, but not sufficiently to affect excitability (not shown).
As mentioned above, blockade of SK channels by apamin has been shown to eliminate the secondary effects of BK channels on firing output (Brenner et al. 2005). In an attempt to simulate the F-I curves seen in vitro we added an SK Ca2+-dependent current to the model, which would be influenced solely by Ca2+ influx controlled by spike duration. As expected, addition of this current reduced the slope of the F-I relationship for all three models (Fig. 8E), but exerted its effect proportional to spike width, and therefore Ca2+ influx (Fig. 8F). Therefore, SK had a greater influence on F-I slope for models containing broader action potentials (i.e. αβ4 channels or no BK channels at all). As a result, a density of SK channels was found where both the αβ4 BK model and the model lacking any BK channels exerted a similar F-I slope, but at the same time was less than the slope produced by the α BK model (Fig. 8E).
Discussion
A primary focus of this study was to understand how BK channels with distinct properties, such as those with or without the accessory β4 subunit, affect action potential shape and neuronal excitability. Our major finding was that the differential effects of β4 subunits on the Ca2+ and voltage-dependent properties of BK channels, within discrete ranges of parameter space, can account for experimentally-observed changes to action potential waveform and, in turn, their indirect effects on excitability.
Biophysical studies of BK channels indicate that the β4 subunit has two effects on BK channels; an increase in steady-state conductance and a slowing of channel activation (Fig. 1). In the context of action potentials, these properties are expected to have opposing effects on K+ channel function, promoting and reducing action potential repolarization, respectively. The computational model supports the hypothesis that it is primarily the effect of β4 on kinetics, rather than steady-state properties (V1/2, Q), that is responsible for the attenuated current and, in turn, broadening of the action potential observed in the presence of β4. Here, under physiological K+, we found that β4 enhanced, rather than reduced, steady-state open probability. This is in contrast to previous observations where modulatory effects of β4 were characterized in heterologous expression systems under high bi-ionic K+ concentrations (Wang et al. 2006). Because the presence of the β4 subunit decreased the threshold for activation this property on its own would be expected to enhance the BK current, not depress it. The models also demonstrate that the effect of the β4 subunit does not require a difference in BK channel density; total BK channel conductance was equivalent for simulations of when the β4 subunit was either present or absent. Thus, the difference in kinetics and, in turn, the change in spike duration between the two types of BK channels is sufficient to account for variations in neuronal excitability.
Importance of Ca2+ dynamics
BK channels are activated by an increase in intracellular Ca2+ that shifts their voltage-dependence into a range sensitive to action potentials. This Ca2+ transient is determined by the properties and density of voltage-gated Ca2+ located near BK channels (Cox et al. 1997; Muller et al. 2007; Fakler and Adelman 2008), how Ca2+ concentration is locally controlled (i.e. buffering, diffusion, sequestration), and the properties of BK channels themselves. The concentrations required for this change are generally thought to be in the tens of micromolar range (Cox et al. 1997; Muller et al. 2007; Fakler and Adelman 2008). We found that the slower activation kinetics, at relatively lower Ca2+ concentrations (see Fig. 1C), provided by the β4 subunit readily explains why these channels are minimally activated by spikes and, in turn, have little effect on spike waveform. However, at the same time the slower kinetics also dictate that after a spike the protracted closing of any activated channels will produce a deeper and prolonged mAHP. As a result, the interspike interval should also be extended, thereby resulting in a direct inhibitory effect on excitability. This is inconsistent with experimental observations where there is no direct effect of the αβ4 BK channel on interspike interval. The current view is that the influence of β4 on excitability is produced as a secondary effect through SK channels (Brenner et al. 2005).
Here we found that only when the Ca2+ transient near the BK channels decays at a fast enough rate is the deactivation of the αβ4 BK channel fast enough to prevent elongation of the interspike interval (Fig. 8D). This is consistent with recent work by Muller et al. (2007) that support the hypothesis that the source of Ca2+ activating BK channels should be within a very close proximity and that the Ca2+ sensor must be one of low affinity (Cox et al. 1997; Muller et al. 2007; Fakler and Adelman 2008). In such a high Ca2+ configuration a relatively lower, albeit “tuned”, density of BK channels was required and was comparable to densities used in other simulations (Moczydlowski and Latorre 1983; Aradi and Holmes 1999; Shao et al. 1999; Ly et al. 2010). That said, we also found a second range of parameter space that has a more constrained range of Ca2+ transient, while requiring a significantly larger BK channel density to compensate for less channel activation. Further experiments will be required to test whether this predicted region of parameter space has a physiological relevance. It could be that different sets of BK channels might work together within both regions of parameter space to regulate spike waveform (Kaufmann et al. 2009; Kaufmann et al. 2010) or other factors might permit BK channel activation within lower Ca2+ ranges (Soom et al., 2008; Yan and Aldrich 2010).
If we make the assumptions that either of the two BK channel types (αβ4 and α) are equally situated near voltage-gated Ca2+ channels (Muller et al. 2007), the density of Ca2+ channels is the same, and the sole source of Ca2+ is influx through Ca2+ channels, and not intracellular release, our simulations suggest that Ca2+ kinetics (produced by rapid buffering, diffusion, etc.) associated with Ca2+ binding to BK channels has to be fast and within a limited time scale. This is required so that i) the transient reaches an amplitude that differentially activates the two channels thereby producing a difference in spike duration (Fig. 5C) and ii) it is fast enough so that the BK current doesn’t directly affect interspike interval (Fig. 8D). Alternatively, such constraints might not be necessary and the explanation for why in the presence of the β4 subunit there are no direct effects on excitability is due to factors associated with BK channel co-localization with Ca2+ channels. If β4 subunits perturb the spatial relationship between voltage-gated Ca2+ channels and BK channels the two may no longer be positioned such that BK channels are maximally affected by Ca2+ influx. This is a reasonable hypothesis given that the β4 subunit may affect channel density and distribution (Wynne et al., 2009).
Our simulations make experimentally-testable predictions with respect to sources of Ca2+ and spike waveform. In many neurons both L- and N-type channels are colocalized with BK channels (Grunnet and Kaufmann 2004; Berkefeld et al. 2006; Fakler and Adelman 2008), though it is not known whether Ca2+ from T-type channels can activate them as well. Berkefeld et al. (2006) demonstrated in oocytes co-expressing BK αβ4 channels with either L-, N-, or P/Q type channels that there is differential activation of the resulting K+ current produced by a spike-like waveform. Our simulations predict that fast-gated BK channels (those lacking the β4 subunit) sharpen and contribute to repolarization in response to any one of a range of Ca2+ channels (T, N, or L-type). In contrast, αβ4 BK channels appear to contribute significantly to repolarization only in response to L-type Ca2+ channels (Fig. 7C). The electrogenic (action potential broadening) effect of N- or T-type channels countered the outward current produced by αβ4 BK channels (spike width was widened, not sharpened).
β4 regulation of firing output
The role of type II BK channels on neuronal excitability is poorly understood. BK channels often are shown to affect the downstroke of the action potential and the fAHP (Faber and Sah 2003a). These simulations allow us to infer that type II BK channels, due to slow deactivation conferred by β4, are specialized to influence the afterhyperpolarization more so than the downstroke. That said, in dentate gyrus granule cells where type II BK channels are expressed, there is still little direct effect on interspike interval (Fig. 8A). In contrast, our modeling suggests that type I BK channels (or BK channels lacking β4) have a more profound effect on the downstroke of the action potential, and in turn spike duration, and generation of a fAHP.
Because BK channels deactivate quickly following repolarization of action potentials they generally do not directly affect firing rates (Faber and Sah 2003b). However, some examples exist where BK channels do reduce action potential firing rates (Nelson et al. 2005; Meredith et al. 2006; Matthews et al. 2008). Over a wide range of parameter space in our models αβ4 channels influenced firing rates because their slower gating deepened a mAHP and extended the interspike interval. But if the Ca2+ transient was fast enough (but not too fast as to limit effects on spike duration), the mAHP was not as large while there was still a significant broadening of the spike.
Activation of BK currents limit firing rates in some neurons (Nelson et al., 2003; Mathews et al., 2009), while in others they can enhance excitability, presumably through secondary mechanisms such as the reactivation of voltage-gated Na+ conductances (McKay and Turner, 2004; Gittis et al., 2005). A recent modeling study by Ly et al. (2010) demonstrated how BK currents interacting with M- or H-currents can differentially control spiking output, and would therefore likely be influenced by β4 accessory subunits (Ly et al. 2010). Dentate granule cells lack significant H-current expression (Santoro et al., 2000) and the impact of M-currents on dentate granule cell excitability remains to be determined. Here, we found little interaction between BK channels and voltage-gated Na+ conductances (Fig. 8B) and our model was most consistent with an influence of spike duration on SK currents (Brenner et al. 2005). In the absence of the β4 subunit there was greater K+ current during the downstroke of a spike (Fig. 4B). With a sharper spike there was less Ca2+ entry (Fig. 4B; Johnston and Wu 1994; Sabatini and Regehr 1997; Giese et al. 1998) and, in turn, less SK channel activation (Fig. 8).
Summary
We have shown using computational modeling how type I and type II BK channels can shape action potential waveforms and that different regions of parameter space can differentially affect spike repolarization, the afterhyperpolarization, and in turn a neuron’s firing output. Our models of these BK currents should readily be applicable to more extensive study of the differential effects of type I and type II BK channels on more realistic neuron models and their interaction with other membrane conductances to influence neuronal excitability and firing output.
Highlights.
-
>
We empirically derived properties of BK channels, with and without the β4 accessory subunit
-
>
In a biophysical neuron model we studied how these two BK channel types modulate action potentials
-
>
We show that the slow kinetics provided by β4 subunits leads to spike broadening
-
>
The effect was observed in two regions of parameter space, based on high and low Ca2+ amplitudes.
-
>
β4 subunits may endow BK channels with the ability to contribute to the medium AHP
Acknowledgements
This work was supported by NIH grant NS052574 (R.B.), AHA grant BGIA2390030 (B.W.), and an award from the San Antonio Life Sciences Institute (SALSI) research enhancement fund.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aradi I, Holmes WR. Role of multiple calcium and calcium-dependent conductances in regulation of hippocampal dentate granule cell excitability. J Comput Neurosci. 1999;6:215–235. doi: 10.1023/a:1008801821784. [DOI] [PubMed] [Google Scholar]
- Behrens R, Nolting A, Reimann F, Schwarz M, Waldschutz R, Pongs O. hKCNMB3 and hKCNMB4, cloning and characterization of two members of the large-conductance calcium-activated potassium channel beta subunit family. FEBS Lett. 2000;474:99–106. doi: 10.1016/s0014-5793(00)01584-2. [DOI] [PubMed] [Google Scholar]
- Berkefeld H, Sailer CA, Bildl W, Rohde V, Thumfart JO, Eble S, Klugbauer N, Reisinger E, Bischofberger J, Oliver D, Knaus HG, Schulte U, Fakler B. BKCa-Cav channel complexes mediate rapid and localized Ca2+-activated K+ signaling. Science. 2006;314:615–620. doi: 10.1126/science.1132915. [DOI] [PubMed] [Google Scholar]
- Brenner R, Chen QH, Vilaythong A, Toney GM, Noebels JL, Aldrich RW. BK channel beta4 subunit reduces dentate gyrus excitability and protects against temporal lobe seizures. Nat Neurosci. 2005;8:1752–1759. doi: 10.1038/nn1573. [DOI] [PubMed] [Google Scholar]
- Brenner R, Jegla TJ, Wickenden A, Liu Y, Aldrich RW. Cloning and functional characterization of novel large conductance calcium-activated potassium channel beta subunits, hKCNMB3 and hKCNMB4. J Biol Chem. 2000;275:6453–6461. doi: 10.1074/jbc.275.9.6453. [DOI] [PubMed] [Google Scholar]
- Cox DH, Cui J, Aldrich RW. Allosteric gating of a large conductance Ca-activated K+ channel. J Gen Physiol. 1997;110:257–281. doi: 10.1085/jgp.110.3.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du W, Bautista JF, Yang H, Diez-Sampedro A, You SA, Wang L, Kotagal P, Luders HO, Shi J, Cui J, Richerson GB, Wang QK. Calcium-sensitive potassium channelopathy in human epilepsy and paroxysmal movement disorder. Nat Genet. 2005;37:733–738. doi: 10.1038/ng1585. [DOI] [PubMed] [Google Scholar]
- Faber ES, Sah P. Ca2+-activated K+ (BK) channel inactivation contributes to spike broadening during repetitive firing in the rat lateral amygdala. J Physiol. 2003a;552:483–497. doi: 10.1113/jphysiol.2003.050120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faber ES, Sah P. Calcium-activated potassium channels: multiple contributions to neuronal function. Neuroscientist. 2003b;9:181–194. doi: 10.1177/1073858403009003011. [DOI] [PubMed] [Google Scholar]
- Fakler B, Adelman JP. Control of K(Ca) channels by calcium nano/microdomains. Neuron. 2008;59:873–881. doi: 10.1016/j.neuron.2008.09.001. [DOI] [PubMed] [Google Scholar]
- Giese KP, Storm JF, Reuter D, Fedorov NB, Shao LR, Leicher T, Pongs O, Silva AJ. Reduced K+ channel inactivation, spike broadening, and after-hyperpolarization in Kvbeta1.1-deficient mice with impaired learning. Learn Mem. 1998;5:257–273. [PMC free article] [PubMed] [Google Scholar]
- Gittis AH, Moghadam SH, du Lac S. Mechanisms of sustained high firing rates in two classes of vestibular nucleus neurons: differential contributions of resurgent Na, Kv3, and BK currents. J. Neurophys. 2005;104:1625–1634. doi: 10.1152/jn.00378.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding NL, Jung HY, Mickus T, Spruston N. Dendritic calcium spike initiation and repolarization are controlled by distinct potassium channel subtypes in CA1 pyramidal neurons. J Neurosci. 1999;19:8789–8798. doi: 10.1523/JNEUROSCI.19-20-08789.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grunnet M, Kaufmann WA. Coassembly of big conductance Ca2+-activated K+ channels and L-type voltage-gated Ca2+ channels in rat brain. J Biol Chem. 2004;279:36445–36453. doi: 10.1074/jbc.M402254200. [DOI] [PubMed] [Google Scholar]
- Gu N, Vervaeke K, Storm JF. BK potassium channels facilitate high-frequency firing and cause early spike frequency adaptation in rat CA1 hippocampal pyramidal cells. J Physiol. 2007;580:859–882. doi: 10.1113/jphysiol.2006.126367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha TS, Heo MS, Park CS. Functional effects of auxiliary beta4-subunit on rat large-conductance Ca(2+)-activated K(+) channel. Biophys J. 2004;86:2871–2882. doi: 10.1016/S0006-3495(04)74339-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. Expanding NEURON's repertoire of mechanisms with NMODL. Neural Comput. 2000;12:995–1007. doi: 10.1162/089976600300015475. [DOI] [PubMed] [Google Scholar]
- Johnston D, Wu SM. Foundations of Cellular Neurophysiology. Cambridge: MIT Press; 1994. [Google Scholar]
- Kaufmann WA, Ferraguti F, Fukazawa Y, Kasugai Y, Shigemoto R, Laake P, Sexton JA, Ruth P, Wietzorrek G, Knaus HG, Storm JF, Ottersen OP. Large-conductance calcium-activated potassium channels in purkinje cell plasma membranes are clustered at sites of hypolemmal microdomains. J Comp Neurol. 2009;515:215–230. doi: 10.1002/cne.22066. [DOI] [PubMed] [Google Scholar]
- Kaufmann WA, Kasugai Y, Ferraguti F, Storm JF. Two distinct pools of large-conductance calcium-activated potassium channels in the somatic plasma membrane of central principal neurons. Neuroscience. 2010;169:974–986. doi: 10.1016/j.neuroscience.2010.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster B, Nicoll RA. Properties of two calcium-activated hyperpolarizations in rat hippocampal neurones. J Physiol. 1987;389:187–203. doi: 10.1113/jphysiol.1987.sp016653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ly C, Melman T, Barth AL, Ermentrout GB. Phase-resetting curve determines how BK currents affect neuronal firing. J Comput Neurosci. 2010 doi: 10.1007/s10827-010-0246-3. [DOI] [PubMed] [Google Scholar]
- Matthews EA, Weible AP, Shah S, Disterhoft JF. The BK-mediated fAHP is modulated by learning a hippocampus-dependent task. Proc Natl Acad Sci U S A. 2008;105:15154–15159. doi: 10.1073/pnas.0805855105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews EA, Disterhoft JF. Blocking the BK channel impedes acquisition of trace eyeblink conditioning. Learn. Mem. 2009;16:106–109. doi: 10.1101/lm.1289809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKay BE, Turner RW. Kv3 K+ channels enable burst output in rat cerebellar Purkinje cells. Eur J Neurosci. 2004;20:729–739. doi: 10.1111/j.1460-9568.2004.03539.x. [DOI] [PubMed] [Google Scholar]
- Meredith AL, Wiler SW, Miller BH, Takahashi JS, Fodor AA, Ruby NF, Aldrich RW. BK calcium-activated potassium channels regulate circadian behavioral rhythms and pacemaker output. Nat Neurosci. 2006;9:1041–1049. doi: 10.1038/nn1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moczydlowski E, Latorre R. Gating kinetics of Ca2+-activated K+ channels from rat muscle incorporated into planar lipid bilayers. Evidence for two voltage-dependent Ca2+ binding reactions. J Gen Physiol. 1983;82:511–542. doi: 10.1085/jgp.82.4.511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller A, Kukley M, Uebachs M, Beck H, Dietrich D. Nanodomains of single Ca2+ channels contribute to action potential repolarization in cortical neurons. J Neurosci. 2007;27:483–495. doi: 10.1523/JNEUROSCI.3816-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson AB, Gittis AH, du Lac S. Decreases in CaMKII activity trigger persistent potentiation of intrinsic excitability in spontaneously firing vestibular nucleus neurons. Neuron. 2005;46:623–631. doi: 10.1016/j.neuron.2005.04.009. [DOI] [PubMed] [Google Scholar]
- Orio P, Rojas P, Ferreira G, Latorre R. New disguises for an old channel: MaxiK channel beta-subunits. News Physiol Sci. 2002;17:156–161. doi: 10.1152/nips.01387.2002. [DOI] [PubMed] [Google Scholar]
- Ramanathan K, Michael TH, Fuchs PA. beta subunits modulate alternatively spliced, large conductance, calcium-activated potassium channels of avian hair cells. J Neurosci. 2000;20:1675–1684. doi: 10.1523/JNEUROSCI.20-05-01675.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhart PH, Chung S, Levitan IB. A family of calcium-dependent potassium channels from rat brain. Neuron. 1989;2:1031–1041. doi: 10.1016/0896-6273(89)90227-4. [DOI] [PubMed] [Google Scholar]
- Sabatini BL, Regehr WG. Control of neurotransmitter release by presynaptic waveform at the granule cell to Purkinje cell synapse. J Neurosci. 1997;17:3425–3435. doi: 10.1523/JNEUROSCI.17-10-03425.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sala F, Hernandez-Cruz A. Calcium diffusion modeling in a spherical neuron. Biophys J. 1990;57:313–324. doi: 10.1016/S0006-3495(90)82533-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santoro B, Chen S, Luthi A, Pavlidis P, Shumyatasky GP, Tibbs GR, Siegelbaum SA. Molecular and functional heterogeneity of hyperpolarization-activated pacemaker channels in the mouse CNS. J Neurosci. 2000;20:5264–5275. doi: 10.1523/JNEUROSCI.20-14-05264.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao LR, Halvorsrud R, Borg-Graham L, Storm JF. The role of BK-type Ca2+-dependent K+ channels in spike broadening during repetitive firing in rat hippocampal pyramidal cells. J Physiol. 1999;521(Pt 1):135–146. doi: 10.1111/j.1469-7793.1999.00135.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shruti S, Clem RL, Barth AL. A seizure-induced gain-of-function in BK channels is associated with elevated firing activity in neocortical pyramidal neurons. Neurobio. Dis. 2008;30:323–330. doi: 10.1016/j.nbd.2008.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song X, Su W, Chen L, Ji JJ. Functional expression of large-conductance Ca(2+)-activated potassium channels in lateral globus pallidus neurons. Neuroscience. 2010;169:1548–1556. doi: 10.1016/j.neuroscience.2010.06.026. [DOI] [PubMed] [Google Scholar]
- Soom M, Gessner G, Heuer H, Hoshi T, Heinemann SH. A mutually exclusive alternative exon of slo1 codes for a neuronal BK channel with altered function. Channels. 2008;2:278–282. doi: 10.4161/chan.2.4.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storm JF. Action potential repolarization and a fast after-hyperpolarization in rat hippocampal pyramidal cells. J Physiol. 1987a;385:733–759. doi: 10.1113/jphysiol.1987.sp016517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storm JF. Intracellular injection of a Ca2+ chelator inhibits spike repolarization in hippocampal neurons. Brain Res. 1987b;435:387–392. doi: 10.1016/0006-8993(87)91631-3. [DOI] [PubMed] [Google Scholar]
- Wang B, Brenner R. An S6 mutation in BK channels reveals beta1 subunit effects on intrinsic and voltage-dependent gating. J Gen Physiol. 2006;128:731–744. doi: 10.1085/jgp.200609596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Rothberg BS, Brenner R. Mechanism of beta4 subunit modulation of BK channels. J Gen Physiol. 2006;127:449–465. doi: 10.1085/jgp.200509436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Rothberg BS, Brenner R. Mechanism of increased BK channel activation from a channel mutation that causes epilepsy. J Gen Physiol. 2009;133:283–294. doi: 10.1085/jgp.200810141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YW, Ding JP, Xia XM, Lingle CJ. Consequences of the stoichiometry of Slo1 alpha and auxiliary beta subunits on functional properties of large-conductance Ca2+-activated K+ channels. J Neurosci. 2002;22:1550–1561. doi: 10.1523/JNEUROSCI.22-05-01550.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wynne PM, Puig SI, Martin GE, Treistman SN. Compartmentalized beta subunit distribution determines characteristics and ethanol sensitivity of somatic, dendritic, and terminal large-conductance calcium-activated potassium channels in the rat central nervous system. J Pharmacol Exp Ther. 2009;329:978–986. doi: 10.1124/jpet.108.146175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J, Aldrich RW. LRRC26 auxiliary protein allows BK channel activation at resting voltage without calcium. Nature. 2010;466:513–516. doi: 10.1038/nature09162. [DOI] [PubMed] [Google Scholar]
- Yuen GL, Durand D. Reconstruction of hippocampal granule cell electrophysiology by computer simulation. Neuroscience. 1991;41:411–423. doi: 10.1016/0306-4522(91)90337-n. [DOI] [PubMed] [Google Scholar]