Abstract
Accurate segmentation of neonatal brain MR images remains challenging mainly due to their poor spatial resolution, inverted contrast between white matter and gray matter, and high intensity inhomogeneity. Most existing methods for neonatal brain segmentation are atlas-based and voxel-wise. Although active contour/surface models with geometric information constraint have been successfully applied to adult brain segmentation, they are not fully explored in the neonatal image segmentation. In this paper, we propose a novel neonatal image segmentation method by combining local intensity information, atlas spatial prior, and cortical thickness constraint in a single level-set framework. Besides, we also provide a robust and reliable tissue surface initialization for the proposed method by using a convex optimization technique. Thus, tissue segmentation, as well as inner and outer cortical surface reconstruction, can be obtained simultaneously. The proposed method has been tested on a large neonatal dataset, and the validation on 10 neonatal brain images (with manual segmentations) shows very promising results.
Keywords: Neonatal tissue segmentation, atlas-based segmentation, convex optimization, coupled level sets
1. Introduction
Accurate segmentation of neonatal brain magnetic resonance (MR) images into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) has important implications for normal brain development studies, as well as for the diagnosis and treatment evaluation of neurodevelepmental disorders such as autism. Manual segmentation of neonatal brain structures is tedious, time consuming, and also lacks of reproducibility. Therefore, it is necessary to develop automatic techniques for neonatal brain segmentation. However, despite of the success of segmentation methods developed for adult brain images, it still remains challenging to segment neonatal brain images due to poor spatial resolution, ambiguous tissue intensity distributions (Prastawa et al., 2005; Shi et al., 2010a), as well as different levels of inverted contrast between WM and GM at different parts of neonatal brain (Xue et al., 2007).
To obtain more reliable segmentation results, atlas-based methods are widely used (Warfield et al., 2000; Cocosco et al., 2003; Prastawa et al., 2005; Weisenfeld and Warfield, 2009; Shi et al., 2010a). For example, Prastawa et al. (2005) proposed an atlas-based approach for neonatal brain segmentation. They generated an atlas by averaging three semi-automatic segmented neonatal brain images and then adopted the expectation-maximization (EM) scheme with inhomogeneity correction to achieve tissue classification of GM, CSF, myelinated and unmyelinated WM. Warfield et al. (2000) proposed an age-specific atlas from multiple subjects and an iterated tissue-segmentation-and-atlas-alignment strategy to improve the neonatal tissue segmentation. Shi et al. (2010a) proposed a new framework for performing neonatal brain tissue segmentation by using a subject-specific tissue probabilistic atlas generated from the follow-up data of the same subject. Comprehensive reviews on the atlas-based segmentation methods can be referred to (Kuklisova-Murgasova et al., 2011). Most of the above-mentioned neonatal segmentation methods are voxel-wise, although neighborhood information is incorporated in some studies. Geometric information, which describes the boundary between tissue structures and also constrains the relative locations of different boundaries, is not fully explored. In fact, the geometric information can be used in tissue segmentation to manage the ambiguous tissue distributions, especially for neonatal brain images.
One of the most effective ways of incorporating geometric information for tissue segmentation is to use active contour/surface models (Gooya et al., 2008; Shi and Karl, 2008; Shi et al., 2007). These models are able to provide smooth and closed contours/surfaces as final segmentation, which is not guaranteed in voxel-based segmentation methods. In fact, geometrically, the human cerebral cortex is a thin, folded sheet of GM, with a nearly constant thickness at a range of [1 5]mm for neonatal brains. To obtain a detailed geometric representation of the cortex, many algorithms have been proposed using explicit or implicit surface representation (Xu et al., 1999; Zeng et al., 1999; MacDonald et al., 2000; Goldenberg et al., 2002; Han et al., 2004; Xue et al., 2007). In these methods, adaptive fuzzy c-means (AFCM) algorithm (Pham and Prince, 1999) or EM-MRF segmentation scheme (Xue et al., 2007) are typically used to obtain an initial tissue classification, or local boundary indicator functions to derive the inner and outer interfaces of cortex (Zeng et al., 1999). Then, the tissue classification or interfaces of cortex are transformed into surface tessellation and the surfaces are further deformed with a self-intersection checking, smooth regularization, or thickness constraint. However, there are two main drawbacks for these methods. First, the initial segmentation is crucial to the final result. If the initial segmentation is not good enough, the errors are difficult to be corrected during the surface evolution procedure. In this way, the final result can be not accurate as well. Second, the AFCM algorithm and EM algorithm are sensitive to the initialization and typically converge to a local optimum (Vovk et al., 2007; Dempster et al., 1977), and also the local boundary indicator functions are sensitive to the image noise.
In this paper, we proposed a novel framework for neonatal image segmentation based on convex optimization and coupled level sets. We first use a convex optimization to derive a preliminary segmentation, which then forms an initialization for the following coupled level sets. Finally, the coupled level sets are constructed by refining the surfaces defined on the boundaries among WM, GM, CSF, and background, which will further segment the neonatal brain image based on the local intensity information, atlas spatial prior, and cortical thickness constraint. In contrast to the methods in (Xu et al., 1999; Zeng et al., 1999; MacDonald et al., 2000; Goldenberg et al., 2002; Han et al., 2004; Xue et al., 2007), our framework allows for random initialization. Even when the preliminary segmentation is in question, the following coupled level sets can still robustly locate the correct boundaries.
2. Method
In this paper, we present a novel surface-based segmentation method, utilizing local intensity information, atlas spatial prior, and cortical thickness constraint, for segmentation of neonatal MR brain images in to GM, WM, and CSF. We adopt the local Gaussian distribution fitting (LGDF) energy (Wang et al., 2009), which describes local image intensities by Gaussian distributions with different means and variances. The means and variances of local intensities are spatially varying functions, which enable the model to deal with intensity inhomogeneities. A prior knowledge from atlases is then combined with the LGDF energy to regularize the segmentation and further increase the ability in handling the inhomogeneities. Based on the fact that the cortex has a nearly constant thickness, a constraint of cortical thickness can provide useful geometric information to guide more accurate segmentation. Accordingly, these three terms are finally incorporated into the coupled level sets in such a way that the surfaces are driven by the LGDF and spatial prior, while the distance between the inner and the outer surfaces of cortex remains within a predefined range by an additional cortical-thickness constraint term. We also propose a novel initialization method for this coupled level sets by using convex optimization, which allows for the random initializations. The contributions of this paper are two-fold:
a) we propose a novel coupled-level-sets based neonatal image segmentation method by combining local intensity information, atlas spatial prior, and cortical thickness constraint in a level-set framework.
b) we propose a robust initialization based on the convex optimization for the coupled level sets by using the global image statistical information and atlas spatial prior.
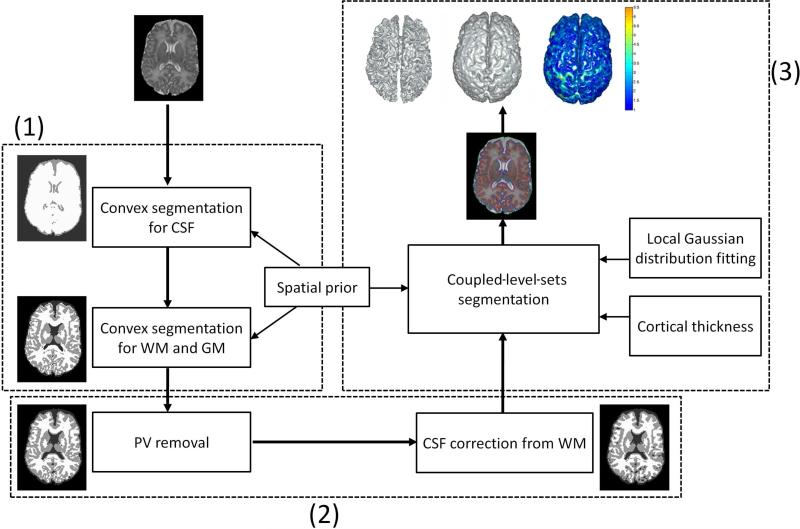
An overview of the proposed framework is shown in Fig. 1. The framework consists of three steps: (1) Preliminary segmentation for CSF, WM and GM, as shown in the left panel of Fig. 1; (2) Partial Volume (PV) removal and correction of the mislabeled CSF from WM, as shown in the bottom panel; and (3) Coupled level sets based segmentation, as shown in the top-right panel. Steps (1) and (2) form an initialization for the step (3). For better emphasizing our contribution, we will first introduce step (3) in Section 2.1, and then steps (1) and (2) in Sections 2.2 and 2.3, respectively. The following sections describe the method in detail.
Figure 1.
The proposed framework for neonatal brain segmentation.
2.1. Neonatal segmentation using coupled level sets
In this section, we propose an implicit level set method based on local intensity distribution fitting, spatial prior, and cortical thickness constraint for neonatal brain segmentation. Let Ω be the image domain, I be a given image, and be a set of disjoint image regions, such that , , , where N refers to the number of regions. Instead of modeling the intensities of each tissue by a global Gaussian distribution, we model the intensities of the neighborhood of each voxel x by a spatial Gaussian distribution. Based on our previous work in (Wang et al., 2009), the Gaussian probability density with spatially varying means ui(x) and variances is defined as,
| (1) |
where I(y) is the intensity of voxel y in the neighborhood of the current voxel x. In fact, we can replace by a Gaussian kernel ωσ with scale σ to control the size of the neighborhood (Li, 2006; Li et al., 2008a, 2007, 2008b). Based on maximum a posteriori probability (MAP), we can thus define a local Gaussian distribution fitting energy:
| (2) |
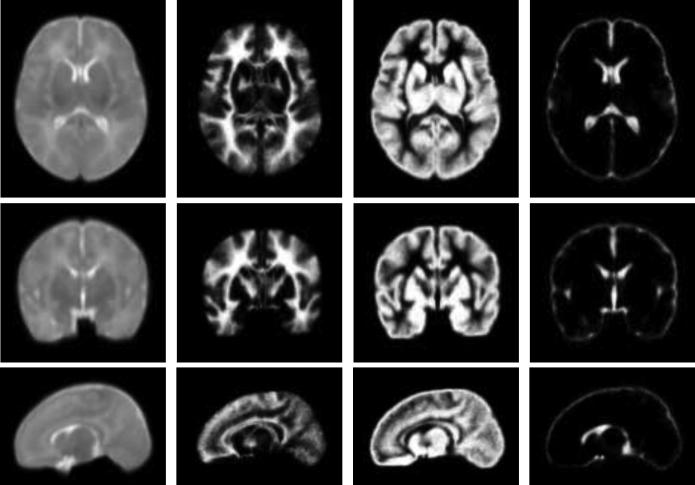
It is worth noting that local intensity means ui(x) and variances are the spatially varying functions, which are crucial in handling the inhomogeneity. Due to large overlap in the tissue distribution, it is necessary to use spatial prior priori for guiding the segmentation. The spatial prior used in this paper is given by a neonatal atlas1 (Shi et al., 2011), shown in Fig. 2. This atlas was constructed from 95 neonatal subjects, segmented by our previous longitudinal-based segmentation method (Shi et al., 2010a). For a given subject image, by using HAMMER algorithm (Shen and Davatzikos, 2002) to warp the atlas image into the subject image space, we can derive spatial prior information priori for WM, GM and CSF, respectively, for the subject image. In the following, we propose a new energy function which combines the local Gaussian distribution fitting energy and spatial prior knowledge priori given by the neonatal brain atlases,
| (3) |
Figure 2.
The probabilistic brain atlas of neonatal brains. From left to right: the T2 average image, and the spatial prior probability values for WM, GM and CSF. From top to bottom: axial view, coronal view and sagittal view.
The ultimate goal is to minimize for all the voxels x in the image domain Ω, which directs us to define an energy function as the following double integral:
| (4) |
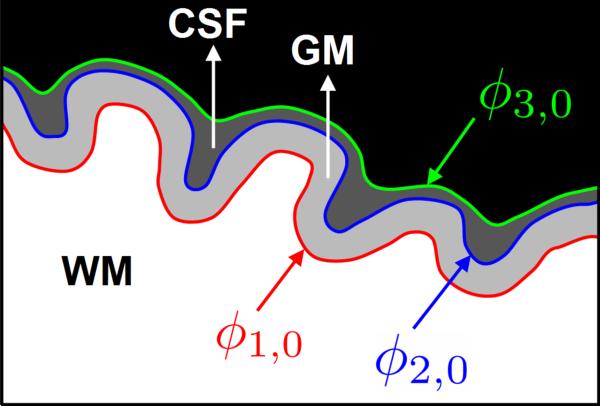
We can use one or multiple level set functions to represent a partition . For neonatal segmentation, we use three level set functions ϕ1, ϕ2 and ϕ3 to represent WM, GM, CSF and background. As illustrated in Fig. 3, the zero-level surfaces of ϕ1, ϕ2 and ϕ3 are the interfaces of WM/GM, GM/CSF, and CSF/background, respectively.
Figure 3.
A cartoon drawing illustrating the definition of the three interfaces, where ϕ1,0, ϕ2,0 and ϕ3,0 are the zero-level surfaces of ϕ1, ϕ2 and ϕ3, respectively.
Let Φ = (ϕ1, ϕ2, ϕ3). Using Heaviside function H, the energy function based on the LGDF energy and atlas spatial prior can be defined as
| (5) |
where is the length term to maintain a smooth contour/surface during evolution, as controlled by ν. (When ν is big, the contour/surface is smooth; The coefficient ν is determined based on our experience.)
Mi(Φ) are defined as,
| (6) |
By calculus of variations, it can be shown that the parameters ui(x) and that minimize the energy functional in Eq. (5) for a fixed Φ are given by
| (7) |
and
| (8) |
Note that the formulas of ui(x) and in Eqs. (7) and (8) are also presented in (Brox, 2005; Rosenhahn et al., 2007; Brox and Cremers, 2007), which were, however, empirically defined, instead of being derived from a variational principle.
Minimization of the energy function in Eq. (5) with respect to ϕi is achieved by solving the gradient descent flow equations as follows,
| (9) |
where
| (10) |
and
| (11) |
As proposed in (Zeng et al., 1999; Goldenberg et al., 2002), the cortical layer has a nearly constant thickness which can be used to guide the surface evolutions. To utilize the cortical structural information, we design a coupled level set to constrain the distance of zero-level surfaces of ϕ1 and ϕ2 within a reasonable range. Let the allowed distance be [d D]. We adopt the coupling functions h(·) and ci(ϕj) in (Paragios, 2001; Zeng et al., 1999), where h(x) is a function that h(x) = 1 when the distance between the two surfaces is within an acceptable range, otherwise h(x) = 0, and ci(ϕj) is another coupling function that maintains the distance within an acceptable range. Therefore, we write
| (12) |
where h(·) and ci(ϕj) are defined as
| (13) |
and
| (14) |
where f is the constant that determines the range of the preferable values for the distance [d+f, D−f] (Unless otherwise specified, the parameter f = 1 is used as default). There are two advantages of this design. First, the image-based force [−δ(ϕ1)H(ϕ2)(e1 − e2)H(ϕ3)] guides the surface evolution only when the distance between the two surfaces is within an acceptable range. Second, when the distance is beyond the acceptable range, this force does not affect the evolutions, but the second term c1(ϕ2)|∇ϕ1| is activated which will deflate the surface if the distance is below the minimum acceptable value, and inflate the surface if the distance is beyond the maximum acceptable value.
In a similar way, we write a new evolution equation for ϕ2,
| (15) |
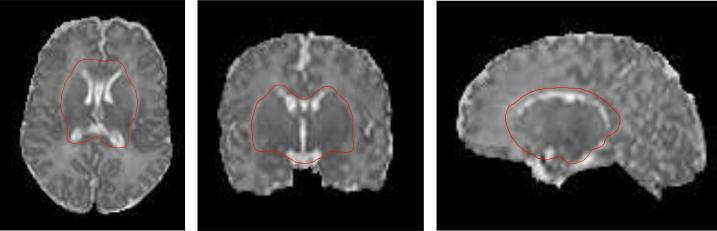
Note that the thickness is not constant for the subcortical GM, therefore we should not put any cortical-thickness constraint on the subcortical GM regions. To this end, we define a mask in the template space to include ventricular CSF, its surrounding GM/WM tissues, and other subcortical GM regions, as similarly proposed in (Shi et al., 2010b). Then, by warping this mask to the subject image under segmentation (Shen and Davatzikos, 2002), we can obtain the mask for the ventricular CSF and subcortical GM regions of the subject, where the cortical thickness constraint will not be imposed. As shown in Fig. 4, the mask is indicated by the red curves. In these subcortical regions, only local Gaussian distribution fitting and atlas prior are employed to guide the segmentation.
Figure 4.
Topological template, used as a subcortical mask, displayed in three orthogonal sections.
With the combination of local Gaussian distribution fitting energy, spatial prior knowledge, and cortical thickness constraint, the proposed method is able to achieve accurate segmentation for the neonatal MR images. However, as the 3D convolution operations have to be performed at every iteration, the proposed method is computationally expensive. Thus, a good initialization for the proposed coupled-level-sets method is necessary not only to save time, but also to help avoid being trapped into local minima. In the following section, we will propose a robust initialization method based on the convex optimization.
2.2. Preliminary Segmentation for CSF, WM and GM
Considering the tissue intensity distribution is more overlapping between GM and WM while not with CSF, we propose two steps for initial segmentation. First, CSF is identified from the brain image by classifying the brain image into CSF, WM+GM, and background (BG). Second, the WM+GM are further separated into WM and GM. Similar strategy was also employed in other papers (Liu et al., 2007; Ekin and Jasinschi, 2006; Cappabianco et al., 2010), showing better performance than that obtained by simultaneous extraction of CSF, WM and GM as done in the conventional methods. To address the issue of the intensity inhomogeneity, we adopt a joint segmentation and inhomogeneity estimation scheme. Specifically, we first logarithmically transform the intensities in order to make the bias b additive. We then use two segmentation variables u1 and u2, which take values between 0 and 1, to represent the membership functions of three regions with M1 = u1u2, M2 = u1(1 − u2), and M3 = (1 − u1). The intensities of each region are characterized by a global Gaussian distribution with mean and variance as (ci, ). The atlas spatial prior priori is also utilized for segmentation. We then propose the following minimization scheme for segmenting the image into the regions of CSF, (WM+GM) and BG,
| (16) |
where the probability pi(x) can be expressed as:
| (17) |
and the last two terms in (16) are the total variations of u1 and u2. By constraining both u1 and u2 to be [0, 1], the minimization problem is separately convex in each segmentation variable ui, when (ci, σi, b) are fixed (Bresson and et al., 2007; Chan et al., 2006). In fact, the minimization problem in (16) can be written as:
| (18) |
where
| (19) |
The following theorem states the existence of a global minimizer for the energies E1 and E2 in (18):
Theorem 1. Suppose that u2 is fixed, if u1* is any minimizer of E1(., ci, σi, b), then for almost every η ∈ [0, 1] we have that the binary function
is also a global minimizer of E1(., ci, σi, b).
Similarly, suppose that u1 fixed, if u2* is any minimizer of E2(., ci, σi, b), then for almost every η ∈ [0, 1] we have that the binary function
is also a global minimizer of E2(., ci, σi, b).
Proof: The proof is the same as the one proposed in (Bresson and et al., 2007; Chan et al., 2006; Mory and Ardon, 2007).
Therefore, the proposed method allows for random initializations and we can easily use the Split Bregman method (Goldstein et al., 2009) to minimize u1 and u2 (see Appendix for detail).
The global mean c and variance can be easily solved. For the fixed (u1, u2, ci, σi), the bias field b can be determined by
| (20) |
In view of the slowly varying property of the bias field, using the technique in (Li et al., 2008a) we can derive a smooth bias field in this form,
| (21) |
where * is the convolution operation, and g is a lowpass filter, such as a mean-filter kernel or a Gaussian-filter kernel. In this paper, we set g = ωσ.
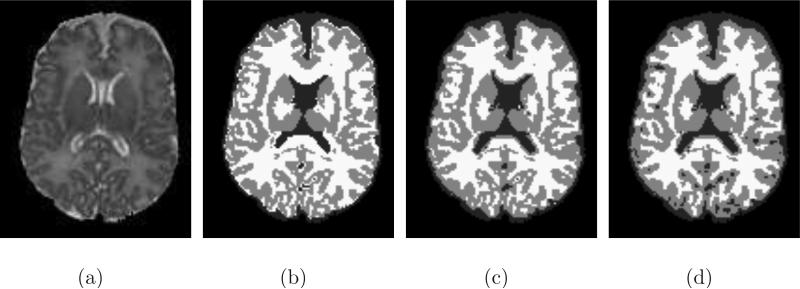
After preliminary segmentation for CSF, we further apply the scheme to segment WM+GM into WM and GM. The energy is the same as Eq. (16). With these two convex models, we can achieve a good preliminary segmentation for the neonatal brain images. For example, Fig. 5(a) shows a slice of neonatal brain. Fig. 5(b) shows the preliminary segmentation result obtained by these convex models. Note that, in all the neonatal image segmentation experiments in this paper, we randomly initialize the constants ci and the segmentation variables ui.
Figure 5.
Demonstration of preliminary tissue segmentation steps. From left ro right: (a) Original slice; (b) Preliminary segmentation; (c) PV removal; and (d) Correction of CSF.
2.3. Partial Volume (PV) Removal and CSF Correction from WM
After preliminary segmentation, we find that many voxels between CSF and GM are incorrectly classified as WM due to partial volume effect. This is a common phenomenon that happens in neonatal brain images because the MR intensity for the unmyelinated WM lies between CSF and GM and thus the intensities of the mixed voxels between CSF and GM are similar to the intensities of WM. In (Xue et al., 2007), Xue et al. proposed a technique based on EM algorithm and Markov random field (MRF) to remove the effect of PV. In this paper, we adopt rather simple but effective scheme to handle PV problem based on the observation that the misclassified WM are commonly surrounded by the CSF and GM. For each segmented WM voxel, in its neighborhood with size of w × w × w, let the number of WM, GM and CSF/BG be NWM, NGM, and NCSF, respectively. If NWM ≤ a, while NGM > NCSF ≥ b, then this WM should be set as GM. If NWM ≤ a, while NCSF > NGM ≥ c, then this WM should be set as CSF. In this paper, we set a = 3, b = 3, c = 6, w = 3 for all experiments. Fig. 5(c) shows the correction result achieved by our PV removal scheme. In our experiment, we also find that there are some CSF voxels in sulci that are incorrectly labeled as WM. In this case, we adopt a scheme proposed in (Xue et al., 2007), which is based on the observation that these mislabeled CSF are unconnected with true WM volume, to correct these misclassified CSF from WM. Fig. 5(d) shows the correction result for CSF. This preliminary result will be used as a good initialization for the coupled-level-sets method in Section 2.1.
3. Experimental Results
In this paper, we choose to use T2 images for neonatal brain segmentation since they have better intensity contrast than T1 images. Data were acquired from a 3T Siemens scanner. T2 images of 70 axial slices were obtained with imaging parameters: TR=7380 ms, TE=119 ms, Flip Angle=150, acquisition matrix=256×128, and resolution= 1.25×1.25×1.95mm3. T2 images are resampled to 1×1 × 1mm3. Standard preprocessing steps such as skull stripping (Shattuck and Leahy, 2001) and bias correction (Sled et al., 1998) were performed. In our experiments, we set the allowable thickness for cortex as [1, 5] mm, ν = 0.5 for Eq. (5), and ν = 0.25 for Eq. (16). The functions δ and H are regularized as in (Chan and Vese, 2001). The level set functions are reinitialized at every iteration using fast marching method (Sethian, 1999).
To measure the overlap rate between two segmentations, we employ Dice ratio (DR) (Dice, 1945), which is defined as . DR ranges from 0 to 1, corresponding to the worst and the best agreement between labels of two segmentations.
3.1. Parameter optimization
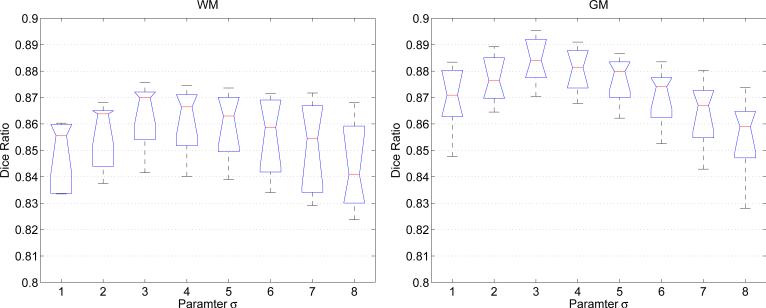
It is necessary to examine the influence of the scale parameter σ in ωσ on the segmentation results of the proposed method. The parameter σ allows the use of intensity information in regions at a controllable scale, from small neighborhood to the entire domain. In fact, for a subject with more severe level of intensity inhomogeneity, we shall select a relatively smaller σ. The parameter σ are chosen from 1 to 8 and applied to the 8 training subjects. The average Dice ratio is shown in Fig. 6. It can be seen that when the scale is very small, e.g., σ = 1 where only the current voxel and its nearest neighbor voxels are considered, insufficient image information is collected and the segmentation performance is thus limited. When the scale increases, better estimation of local intensity distribution is obtained and thus the segmentation performance is gradually improved. When the scale becomes very big, the resulting large image neighborhood starts to suffer from the intensity inhomogeneity and thus obtain worse segmentation performance. This inverted-U shape performance can be observed from Fig. 6. In this paper, we set σ = 3 for all the experiment results reported below.
Figure 6.
Segmentation accuracy on 8 training subjects with respect to the change of the scale parameter σ.
3.2. Result on a synthetic image
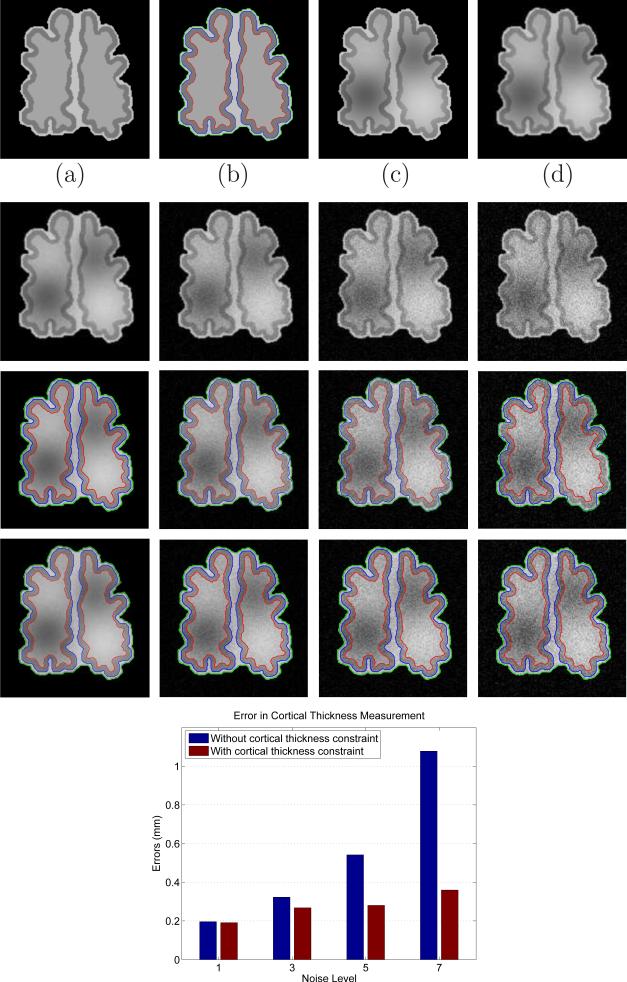
To evaluate the effect of the cortical thickness constraint in the final cortical thickness measurement, we apply our method to a synthetic neonatal image with different noise levels. Fig. 7(a) shows a synthetic brain image with variable cortical thickness, where the exact location of the object boundaries are known, as indicated by curves with different colors in Fig. 7(b). The size of Fig. 7(a) is 159×169, resolution is 1×1 mm2, and intensities of WM, GM and CSF in the Fig. 7(a) are 160, 120, and 190, respectively. The range of cortical thickness is [1 5] mm. Fig. 7(c) is obtained by corrupting Fig. 7(a) with intensity inhomogeneity, which was simulated by using polynomial basis functions (Leemput et al., 1999) with values ranged from 0.70 to 1.30 over the brain area. After corrupting with inhomogeneity field, we also use a Gaussian kernel with size of 3×3 and sigma=1 to further blur the image to simulate the partial volume effect, as shown in Fig. 7(d). The second row shows four noisy images obtained by adding Gaussian noise with standard deviations 1, 3, 5, and 7 to Fig. 7(d). The third and fourth rows present the results of the proposed method without and with cortical thickness constraint, respectively. In this experiment, we use the parameter f = 0. It can be clearly seen that the proposed method without cortical thickness constraint cannot accurately delineate the cortical boundaries, especially for the images with high noise level. In contrast, the proposed method with cortical thickness constraint can still accurately delineate the cortical boundaries. We further show, by quantitative comparison on the error in cortical thickness measurement, that our method with cortical thickness constraint produces more accurate results than that without cortical thickness constraint. Here, we define the cortical thickness on the inner cortical contour. Specifically, cortical thickness in the ground-truth contours in Fig. 7(b) is simply defined in this paper as the shortest distance between any given point on the inner cortical contour (i.e., the red contour) and its closest point on the outer cortical contour (i.e., the blue contour). The similar cortical thickness can be measured for the contours estimated by our method in other subfigures of Fig. 7. In this way, for each point in the inner cortical contour of the ground-truth contours in Fig. 7(b), we can find its closest point on each estimated inner cortical contour by our method, and then we can compare their difference on cortical thickness measures, which can be averaged on the whole inner cortical contours to finally get the average error for each segmentation result. The last row of Fig. 7 shows the error in cortical thickness measurement at different noise levels. The y-axis denotes thickness error in mm, while the x-axis denotes different noise level. It can be seen that the proposed method (with the cortical thickness constraint) produces a more accurate measurement than the method without the cortical thickness constraint.
Figure 7.
Experiment result on a synthetic image. (a) Original image with size= 159×169, and resolution= 1×1 mm2; (b) Ground truth; (c) Synthetic image obtained by adding intensity inhomogeneity to (a); (d) Synthetic image obtained by blurring (c). The second row shows the images corrupted by Gaussian noise with standard deviations of 1, 3, 5, and 7. The third and fourth rows show the results without and with cortical thickness constraint, respectively. The last row shows the errors in cortical thickness measurement.
3.3. Results on real neonatal images
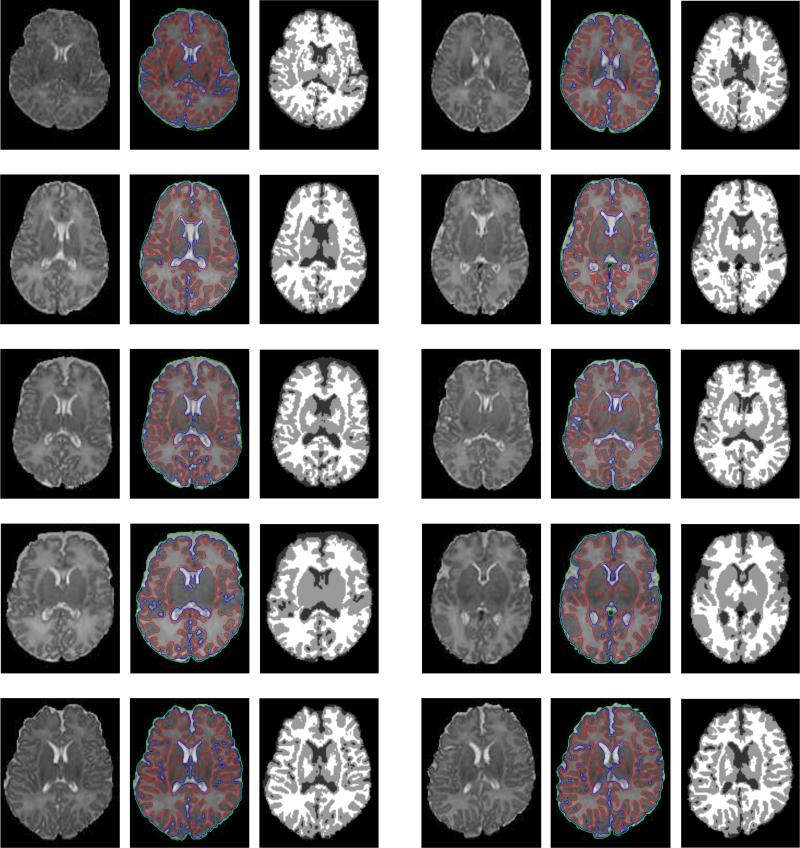
For validation of our method, images from 10 real neonates with manual segmentation are used, as shown in Fig. 8. The columns 1 and 4 of Fig. 8 show the original MR T2 slices, with the corresponding segmentation results of our coupled-level-sets method shown in columns 2 and 5, respectively. To better view the results, we also present the hard tissue segmentations of WM, GM and CSF in columns 3 and 6, respectively. Visual inspection of these results shows that WM, GM and CSF are reasonably segmented.
Figure 8.
Results of the proposed method on real neonatal images. For each part, from left to right: original T2 slices, segmentation by the proposed method and its corresponding hard segmentation.
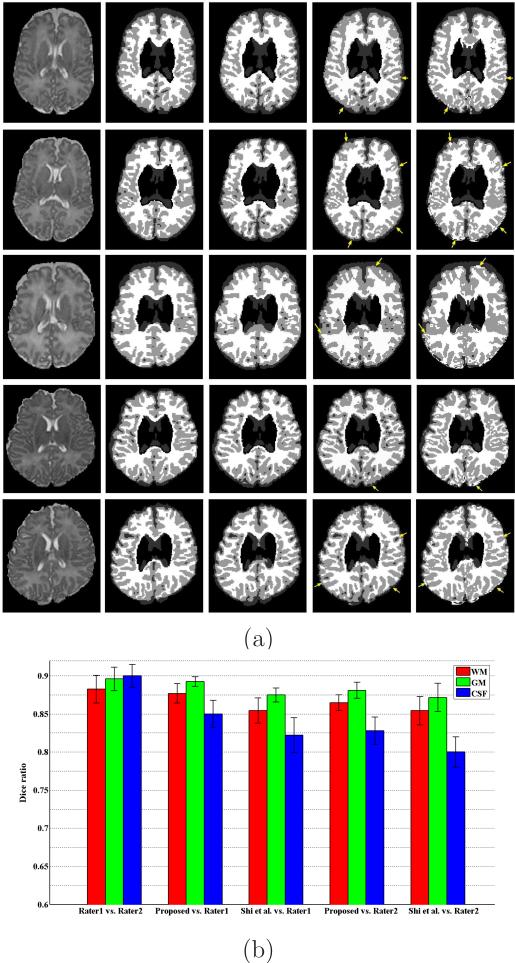
Validation of the automatic segmentation results is difficult because ground truth is not available. For comparison, we use the manual segmentations by experts as our golden standard. Fig. 9(a) shows the segmentation results of five representative subjects by two expert raters (columns 2 and 3) and by our method (column 4). As atlas-based segmentation method is popular for neonatal brain segmentation, we do another comparison with the standard atlas-based segmentation method as proposed by Shi et al. (Shi et al., 2010a), with their results shown in the last column of Fig. 9(a). By visual inspection, our results are comparable with those produced by expert raters. Compared with the method of Shi et al., our method achieves more accurate results, especially at locations indicated by the yellow arrows in the figure. Note that the tissue contrast in subcortical regions is very low; as a result, it is very difficult to segment subcortical regions, even for manual raters, thus the manual raters leave these regions as unsegment regions (as we can see from columns 2 and 3). Accordingly, we exclude these regions from the quantitative evaluation of different segmentation algorithms. Fig. 9(b) shows the mean and standard deviation of DR values of WM, GM and CSF segmentations of all 10 subjects. The first pair of bars shows the comparison between the two manual segmentations. By taking the manual segmentations from rater 1 as ground-truth, we can make quantitative comparison with our proposed method and Shi et al.'s method, respectively, with results given in the second and third pairs of bars of Fig. 9(b). We can observe that our proposed automatic segmentation method achieves comparable segmentation performance as the manual rater. Compared with Shi et al.'s method, our proposed method achieves higher DR values. The superior performance of the proposed method can also be observed from the last two pairs of bars, in which we take the manual segmentation of rater 2 as ground truth for quantitative comparison.
Figure 9.
Comparison of segmentation accuracy on WM and GM for 10 subjects by different methods. (a) Segmentation results on five representative subjects. From left to right: original MR T2 images; manual segmentations by rater1; manual segmentations by rater2; results by our proposed method; and results by the method of Shi et al.. (b) Dice ratios of WM, GM and CSF for 10 subjects by different methods. Note that subcortical regions are excluded from the quantitative evaluation of different segmentation algorithms.
3.4. Standard atlas-based segmentation vs Convex segmentation vs Coupled level set segmentation
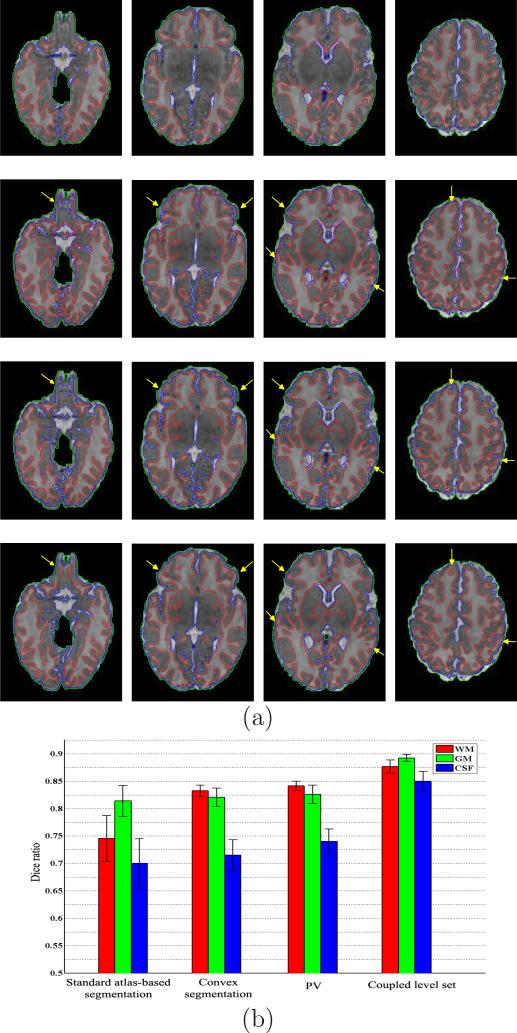
In this section, we compare the performances of the standard atlas-based algorithm, the proposed convex segmentation, and the subsequent coupled-level-sets based segmentation. In Fig. 10(a), we present segmentation results of 4 representative slices of the subject N0075-1-2. The first row shows the results of standard atlas-driven EM approach with bias correction and PV removal (as implemented in SPM software2), from which we can observe that the segmented WM is much smaller than it should be. Note that the same neonatal atlas is used as priori knowledge for guiding tissue segmentation in the standard atlas-driven EM approach. The second row show the results of convex segmentation. It can be seen that convex segmentation has achieved a more accurate segmentation result than the atlas-driven EM approach, especially for WM. However, in some places as indicated by the yellow arrows, the WM has been incorrectly labeled as GM, and the outer cortical boundaries are not accurately delineated. Even after the PV removal, as shown in the third row, some incorrect segmentations still exist. Fortunately, in the subsequent coupled-level-sets based segmentation, most errors have been corrected, and by visual comparison, the coupled-level-sets based segmentation achieves higher accuracy. By taking the manual segmentation from rater 1 as ground truth, we shows DR values of WM, GM and CSF for all 10 subjects by different segmentation methods in Fig. 10(b). It can be seen that the convex segmentation achieve a higher accuracy than the atlas-based approach, especially for WM. The accuracy is further improved slightly after PV removal and considerably improved after using the coupled-level-sets based segmentation, especially for the GM.
Figure 10.
Standard atlas-based approach vs Convex segmentation vs Coupled-level-set based segmentation. (a) The first row shows the results of standard atlas-based approach; the second and third rows show the results of convex segmentation without and with PV removal; the fourth row shows the results of the coupled-level-sets. (b) Dice ratios for all 10 subjects by different segmentation methods.
4. Discussion and conclusion
We have presented a novel coupled-level-sets based segmentation method for neonatal brain images. Our method effectively utilizes local image information, atlas prior knowledge, and cortical thickness constraint for guiding the segmentation by specially integrating them into a coupled-level-sets method. We also provide a robust initialization method using convex optimization for this coupled-level-sets method. Our proposed method has been tested on a large neonatal dataset, and the validation on 10 subjects with manual segmentations shows very promising results.
The average total computation time is around 36 minutes for the segmentation of a 256×256×198 image with a spatial resolution of 1×1×1mm3 on a PC with 2.5 GHz Pentium4 processor. In this computational time, 8 minutes are used for convex segmentation, 1 minute is used for PV correction, and 27 minutes are used for the coupled-level-sets based segmentation. Overall, the proposed segmentation framework is able to achieve satisfactory segmentation results within a reasonable computational time.
Reported cortical thicknesses from post-mortem data in adults are in the range of 1.3-4.5 mm (von Economo, 1929; Rockel et al., 1980; Henery and Mayhew, 1989). In vivo MR-based measurements from Sisodiya et al. (1996) were reported to have a mean thickness of 3.2 mm. Although, to the best of our knowledge, there are currently no studies measuring the physical cortical thickness in neonatal brain, we conservatively set the acceptable range as 1-5 mm. The thickness constraint term in the evolution equations (12) and (15) efficiently takes the advantage that the human cerebral cortex is a thin, folded sheet of GM with a nearly constant thickness. However, the equations (12) and (15) are defined empirically, instead of being strictly derived by minimizing an energy functional. In our future work, we will investigate this problem. We will also apply our proposed method to more data sets currently acquired in our institute.
The proposed method cannot separate the myelinated WM from unmyelinated WM. This may be addressed by developing a 4D atlas which includes explicit modeling of areas of myelinated WM, as suggested by Kuklisova-Murgasova et al. (2011). On the other hand, due to the existence of lots of unmyelinated WM around the central GM regions in the neonatal stage, the contrast between GM and WM in the central regions is quite low. As a result, it is difficult to segment central GM regions, even for the manual experts. In the future, we will include diffusion tensor image (DTI) to guide the segmentation (Liu et al., 2007) since we find that DTI can provide better information for white matter, thus it may be useful for guiding better segmentation for central regions of neonatal brain images.
Research highlight.
▶A novel coupled-level-sets based neonatal image segmentation method is proposed. ▶The proposed method combines atlas spatial prior, and cortical thickness constraint in a level-set framework. ▶A robust initialization method using convex optimization is proposed for this coupled-level-sets method. ▶The proposed method has been tested on a large neonatal dataset with promising results.
Appendix
We only consider the minimization of the energy E1 of Eq. (18), while the minimization of the energy E2 can be solved in the same manner. For the sake of clarity, we write the minimization problem E1 as follows,
| (22) |
Following (Goldstein et al., 2009), we introduce a new vectorial function . For the 3D case, , where dx, dy and dz are the components of the vector along x, y and z axises, respectively. (Note that the meaning of x, y and z is different from the previous sections, where x and y denote the voxels of the image). To weakly enforce the resulting equality constraint, we add a quadratic penalty function. Thus, we can get the following unconstrained problem
| (23) |
where μ is a balance parameter.
In order to strictly enforce the constraint , we add a new vector, , inside of the quadratic penalty function above. By applying Bregman iteration (Goldstein et al., 2009; Osher et al., 2005; Bregman, 1967) to the unconstrained problem (23), we derive the following sequence of optimization problems, for t ≥ 0:
| (24) |
| (25) |
For the fixed , we can derive the Euler-Lagrange equation of optimization problem (24) with respect to u1:
| (26) |
where △ is the Laplacian operator. Note that we omit the superscript t for simplicity.
By using central discretization for the Laplacian operator and backward difference for the divergence operator, a fast approximated solution for (26) is:
| (27) |
where (i, j, k) is the position in 3D image coordinate.
For the fixed u1, the minimization solution is performed using following formula (Wang et al., 2007):
| (28) |
Similarly, we can solve the minimization problem E2 with respect to u2.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
This neonatal atlas is available in our website for download: https://www.med.unc.edu/bric/ideagroup/free-softwares.
References
- Bregman L. The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming. USSR Computational Mathematics and Mathematical Physics. 1967;7:200–217. [Google Scholar]
- Bresson X, et al. Fast global minimization of the active contour/snake model. J. Math. Imaging Vis. 2007;28(2):151–167. [Google Scholar]
- Brox T. Ph.D. thesis. Faculty of Mathematics and Computer Science, Saarland University; Germany: 2005. From pixels to regions: Partial di erential equations in image analysis. [Google Scholar]
- Brox T, Cremers D. SSVM07. Ischia, Italy: 2007. On the statistical interpretation of the piecewise smooth Mumford-Shah functional. pp. 203–213. [Google Scholar]
- Cappabianco FAM, Falcao AX, Yasuda CL, Udupa JK. Tech. rep. Institute of Computing, University of Campinas; Mar, 2010. MR-Image Segmentation of Brain Tissues based on Bias Correction and Optimum-Path Forest Clustering. [Google Scholar]
- Chan T, Vese L. Active contours without edges. IEEE Trans. Imag. Proc. 2001 February;10(2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- Chan TF, Esedoglu S, Nikolov M. Algorithms for finding global minimizers of image segmentation and denoising models. SIAM J. Appl. Math. 2006;66(5):1632–1648. [Google Scholar]
- Cocosco CA, Zijdenbos AP, Evans AC. A fully automatic and robust brain MRI tissue classification method. Medical Image Analysis. 2003;7(4):513–527. doi: 10.1016/s1361-8415(03)00037-9. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the em algorithm. JOURNAL OF THE ROYAL STATISTICAL SOCIETY, SERIES B. 1977;39(1):1–38. [Google Scholar]
- Dice L. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- Ekin A, Jasinschi R. A robust thresholding method with applications to brain mr image segmentation.. 14th European Signal Processing Conference; Florence, Italy. 2006. [Google Scholar]
- Goldenberg R, Kimmel R, Rivlin E, Rudzsky M. Cortex segmentation: a fast variational geometric approach. IEEE Trans. Med. Imag. 2002;21(2):1544–1551. doi: 10.1109/TMI.2002.806594. [DOI] [PubMed] [Google Scholar]
- Goldstein T, Bresson X, Osher S. CAM Report 09-06. UCLA; 2009. Geometric applications of the split bregman method: Segmentation and surface reconstruction. [Google Scholar]
- Gooya A, Liao H, Matsumiya K, Masamune K, Masutani Y, Dohi T. A variational method for geometric regularization of vascular segmentation in medical images. IEEE Transactions on Image Processing. 2008;17(8):1295–1312. doi: 10.1109/TIP.2008.925378. [DOI] [PubMed] [Google Scholar]
- Han X, Pham DL, Tosun D, Rettmann ME, Xu C, Prince JL. Cruise: Cortical reconstruction using implicit surface evolution. NeuroImage. 2004;23(3):997–1012. doi: 10.1016/j.neuroimage.2004.06.043. [DOI] [PubMed] [Google Scholar]
- Henery C, Mayhew T. The cerebrum and cerebellum of the fixed human brain: e cient and unbiased estimates of volumes and cortical surfaces areas. J Anat. 1989;167:167–180. [PMC free article] [PubMed] [Google Scholar]
- Kuklisova-Murgasova M, Aljabar P, Srinivasan L, Counsell SJ, Doria V, Serag A, Gousias IS, Boardman JP, Rutherford MA, Edwards AD, Hajnal JV, Rueckert D. A dynamic 4d probabilistic atlas of the developing brain. NeuroImage. 2011;54(4):2750–2763. doi: 10.1016/j.neuroimage.2010.10.019. [DOI] [PubMed] [Google Scholar]
- Leemput V, Maes K, Vandermeulen D, Suetens P. Automated model-based bias field correction of MR images of the brain. IEEE Trans. Med. Imag. 1999;18(10):885–896. doi: 10.1109/42.811268. [DOI] [PubMed] [Google Scholar]
- Li C. Active contours with local binary fitting energy. IMA Workshop on New Mathematics and Algorithms for 3-D Image Analysis. Jan, 2006.
- Li C, Huang R, Ding Z, Gatenby C, Metaxas D, Gore J. A variational level set approach to segmentation and bias correction of medical images with intensity inhomogeneity. MICCAI. 2008a;LNCS 5242(II):1083–1091. doi: 10.1007/978-3-540-85990-1_130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Kao C, Gore J, Ding Z. Implicit active contours driven by local binary fitting energy. CVPR. 2007:1–7. [Google Scholar]
- Li C, Kao C, Gore JC, Ding Z. Minimization of region-scalable fitting energy for image segmentation. IEEE Trans. Image Process. 2008b October;17(10):1940–1949. doi: 10.1109/TIP.2008.2002304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T, Li H, Wong K, Tarokh A, Guo L, Wong ST. Brain tissue segmentation based on DTI data. NeuroImage. 2007;38(1):114–123. doi: 10.1016/j.neuroimage.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacDonald D, Kabani N, Avis D, Evans AC. Automated 3-d extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage. 2000;12(3):340–356. doi: 10.1006/nimg.1999.0534. [DOI] [PubMed] [Google Scholar]
- Mory B, Ardon R. Fuzzy region competition: A convex two-phase segmentation framework. SSVM07. 2007:214–226. [Google Scholar]
- Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularization method for total variation-based image restoration. SIAM Multiscale Modeling and Simulation. 2005;4:460–489. [Google Scholar]
- Paragios N. A variational approach for the segmentation of the left ventricle in mr cardiac images. VLSM'01. 2001:153–160. [Google Scholar]
- Pham D, Prince J. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans. Med. Imag. 1999;18(9):737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- Prastawa M, Gilmore JH, Lin W, Gerig G. Automatic segmentation of mr images of the developing newborn brain. Medical Image Analysis. 2005;9(5):457–466. doi: 10.1016/j.media.2005.05.007. [DOI] [PubMed] [Google Scholar]
- Rockel A, Hiorns R, Powel T. The basic uniformity in structure of the neocortex. Brain. 1980;103:221–224. doi: 10.1093/brain/103.2.221. [DOI] [PubMed] [Google Scholar]
- Rosenhahn B, Brox T, Weickert J. Three-dimensional shape knowledge for joint image segmentation and pose tracking. Int'l J. Comp. Vis. 2007 July;73(3):242–262. [Google Scholar]
- Sethian J. Level Set Methods and Fast Marching Methods. Cambridge University Press; Cambridge: 1999. [Google Scholar]
- Shattuck D, Leahy R. Automated graph-based analysis and correction of cortical volume topology. IEEE TMI. 2001;20(11):1167–1177. doi: 10.1109/42.963819. [DOI] [PubMed] [Google Scholar]
- Shen D, Davatzikos C. Hammer: Hierarchical attribute matching mechanism for elastic registration. IEEE Trans. Med. Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. Neonatal brain image segmentation in longitudinal MRI studies. NeuroImage. 2010a;49(1):391–400. doi: 10.1016/j.neuroimage.2009.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F, Shen D, Yap P, Fan Y, Cheng J, An H, Wald L, Gerig G, Gilmore J, Lin W. Cents: Cortical enhanced neonatal tissue segmentation. Hum Brain Mapp. 2010b doi: 10.1002/hbm.21023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F, Yap P-T, Wu G, Jia H, Gilmore JH, Lin W, Shen D. Infant brain atlases from neonates to 1- and 2-year-olds. PLoS ONE. 2011 doi: 10.1371/journal.pone.0018746. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Karl W. A real-time algorithm for the approximation of level-set-based curve evolution. Image Processing, IEEE Transactions on. 2008 may;17(5):645–656. doi: 10.1109/TIP.2008.920737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y, Thompson PM, Dinov I, Osher S, Toga AW. Direct cortical mapping via solving partial di erential equations on implicit surfaces. Medical Image Analysis. 2007;11(3):207–223. doi: 10.1016/j.media.2007.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sisodiya S, Free S, Fish D, Shorvon S. Mri-based surface area estimates in the normal adult human brain: evidence for structural organisation. J Anat. 1996;188:425–438. [PMC free article] [PubMed] [Google Scholar]
- Sled J, Zijdenbos A, Evans A. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imag. 1998 January;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- von Economo C. The cytoarchitectonics of the human cerebral cortex. Oxford University Press; London: 1929. [Google Scholar]
- Vovk U, Pernus F, Likar B. A review of methods for correction of intensity inhomogeneity in MRI. IEEE Trans. Med. Imag. 2007 March;26(3):405–421. doi: 10.1109/TMI.2006.891486. [DOI] [PubMed] [Google Scholar]
- Wang L, He L, Mishra A, Li C. Active contours driven by local gaussian distribution fitting energy. Signal Processing. 2009;89(12):2435–2447. [Google Scholar]
- Wang Y, Yin W, Zhang Y. CAAM Technical Report TR07-10. Department of Computational and Applied Mathematics; 2007. A fast algorithm for image deblurring with total variation regularization. [Google Scholar]
- Warfield SK, Kaus M, Jolesz FA, Kikinis R. Adaptive, template moderated, spatially varying statistical classification. Medical Image Analysis. 2000;7(4):43–55. doi: 10.1016/s1361-8415(00)00003-7. [DOI] [PubMed] [Google Scholar]
- Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain MRI. NeuroImage. 2009;47(2):564–572. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C, Pham DL, Rettmann ME, Yu DN, Prince JL. Reconstruction of the human cerebral cortex from magnetic resonance images. IEEE Trans. Med. Imag. 1999;18(6):467–480. doi: 10.1109/42.781013. [DOI] [PubMed] [Google Scholar]
- Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, Rueckert D, Hajnal JV. Automatic segmentation and reconstruction of the cortex from neonatal MRI. NeuroImage. 2007;38(3):461–477. doi: 10.1016/j.neuroimage.2007.07.030. [DOI] [PubMed] [Google Scholar]
- Zeng X, Staib L, Schultz R, Duncan J. Segmentation and measurement of the cortex from 3D MR images using coupled surfaces propagation. IEEE Trans. Med. Imag. 1999;18(10):100–111. doi: 10.1109/42.811276. [DOI] [PubMed] [Google Scholar]