Abstract
The olfactory glomerulus is the locus of information transfer between olfactory sensory neurons and output neurons of the olfactory bulb. Juxtaglomerular cells (JGCs) may influence intraglomerular processing by firing plateau potentials that support multiple spikes. It is unclear what inward currents mediate this firing pattern. In previous work, we characterized potassium currents of JGCs. We focus here on the inward currents using whole cell current clamp and voltage recording in a rat in vitro slice preparation, as well as computer simulation.
We first showed that sodium current was not required to mediate plateau potentials. Voltage clamp characterization of calcium current (ICa) determined that ICa consisted of a slow activating, rapidly inactivating (τ10%–90% rise 6–8ms, τinactivation 38–77ms) component Icat1, similar to T-type currents, and a sustained (τinactivation≫500ms) component Icat2, likely composed of L-type and P/Q-type currents. We used computer simulation to test their roles in plateau potential firing.
We robustly modeled Icat1 and Icat2 to Hodgkin-Huxley schemes (m3h and m2, respectively) and simulated a JGC plateau potential with 6 conductances: calcium currents as above, potassium currents from our prior study (A-type Ikt1, D-type Ikt2, delayed rectifier Ikt3), and a fast sodium current (INa). We demonstrated that Icat1 was required for mediating the plateau potential, unlike INa and Icat2, and its τinactivation determined plateau duration. We also found that Ikt1 dictated plateau potential shape more than Ikt2 and Ikt3. The influence of these two transient and opposing conductances suggests a unique mechanism of plateau potential physiology.
Keywords: olfactory bulb, glomerulus, calcium current, potassium current, plateau potential, simulation
1. INTRODUCTION
Odor identity and concentration are represented by the combinatorial activation of distinct sets of glomeruli at the surface of the olfactory bulb (OB) (Stewart et al., 1979; Rubin and Katz, 1999; Mori et al., 1999; Johnson and Leon, 2000; Xu et al., 2003). Each glomerulus is a processing unit, receiving unique olfactory nerve input from olfactory sensory neuron (OSN) axons expressing the same olfactory receptor, which is then modulated by interactions with dendrites of interneurons and the projection neurons, mitral and tufted (M/T) cells (Ressler et al., 1994; Vassar et al., 1996; Mombaerts et al., 1996).
Juxtaglomerular cells (JGCs) are a heterogeneous group of neurons whose somata are near the border of an individual glomerulus, receiving input from OSNs and participating in complex synaptic interactions with other JGCs and M/T cells (Pinching and Powell, 1971a,b). JGCs are made up of interneurons such as periglomerular cells (PGCs) and short axon cells (SACs), as well as a subgroup of superficial tufted cell called external tufted cells (ETCs) (Pinching and Powell, 1971c; Shipley and Ennis, 1996).
In response to brief input, certain JGCs fire long lasting responses (Wellis and Scott, 1990; McQuiston and Katz, 2001; Hayar et al., 2004a; Zhou et al., 2006). One type of long lasting response is the spike burst, generated specifically by ETCs in a spontaneous and rhythmic fashion (McQuiston and Katz, 2001; Hayar et al., 2004a). In rat, ETC bursts are driven by persistent sodium current INa,P (Hayar et al., 2004a), and in mouse by INa,P and a low voltage activated (LVA) calcium current showing features of both T-type and L-type calcium current (Liu and Shipley, 2008). They also possess hyperpolarization-activated current (Ih) that may promote burst rhythmicity (Cadetti and Belluzzi, 2001; Liu and Shipley, 2008).
These ETC bursts may coordinate glomerular excitation through extensively branched primary dendrites giving numerous dendrodendritic synapses to other glomerular neurons (Pinching and Powell, 1971b; Pinching and Powell, 1971c; McQuiston and Katz, 2001; Hayar et al., 2004a; Zhou et al., 2006; Antal et al., 2006), as well as on physiological evidence that they can excite glomerular interneurons and mitral cells (Hayar et al., 2004b; Murphy et al., 2005; De Saint Jan et al., 2009) and engage in mutually electrical coupling (Hayar et al., 2005; Kosaka and Kosaka, 2005). In addition, inhibitory PGC activity prevents glomerular excitation by suppressing this critical ETC pathway (Gire and Schoppa, 2009).
Alternatively, some PGCs and ETCs fire plateau potentials spontaneously at low frequencies (McQuiston and Katz, 2001; Zhou et al., 2006). Despite extensive work on ETC burst mechanism and function, less is known regarding JGC plateau potential physiology. Input-output relationships in these neurons suggest that they can convert high frequency synaptic input into low frequency output (Zhou et al., 2006), but the network effect of this is unknown.
The mechanism of plateau potential firing is also less clear than the burst mechanism of ETCs. Ih may play a role in the excitability of PGCs and the rhythmic firing of JGC plateau potentials (Cadetti and Belluzzi, 2001; Zhou et al., 2006). Regarding the inward currents that create JGC plateau potentials, it is thought that they are low voltage-activated and not dependent on intracellular calcium (Zhou et al., 2006). Plateau potential persistence in extracellular TTX, sensitivity to 250μM extracellular nickel, and insensitivity to 200μM extracellular cadmium suggested a critical role for T-type calcium currents (Zhou et al., 2006; McQuiston and Katz, 2001). Such currents may be dendritically located (Zhou et al., 2006). This suggests that the plateau potential mechanism may be different than that of ETC bursts.
Low voltage activated (LVA) calcium current has been studied previously in other JGC subtypes. GABAergic PGCs in rat OB possess LVA calcium current, but it is blocked by dihydropyridines and cadmium and not by nickel, suggesting that these PGCs differ from plateau potential-firing PGCs (Murphy et al., 2005). Dopaminergic PGCs in mouse OB possess a T-type current, but it is blocked by 100μM nickel and 100μM cadmium (Pignatelli et al., 2005). However, dopaminergic PGCs are not plateau potential-firing, and in this context T-type channels instead generates a subthreshold current that, along with INa,P, supports repetitive spiking in the absence of synaptic input (Puopolo et al., 2005). Therefore, it seems that plateau potential-firing neurons of the rat glomerulus possess a different LVA current to enable such prolonged depolarizations. This LVA current may be similar to that found in bursting mouse ETCs mentioned above, given that mouse ETC LVA current also promotes prolonged depolarizations and displays similar nickel sensitivity (Liu and Shipley, 2008).
In our accompanying study (Masurkar and Chen, 2011), we characterized the outward potassium currents of JGCs. Here, we pursued study of the calcium current of the JGCs with two purposes. First, we sought more specific evidence that JGCs possess a T-type calcium current that could mediate the plateau potential. Second, we created a single compartment computational model of plateau potential firing based on our characterizations. This enabled us to overcome pharmacological limitations and determine which inward currents (calcium, sodium) and potassium currents were critical for plateau potential generation.
2. EXPERIMENTAL PROCEDURES
2.1 Animal use and care
Animal experimentation protocols were reviewed and approved by the Yale University Animal Care and Use Committee. Sprague Dawley (Rattus norvegicus) rats, 12 to 21 days old, were anesthetized with 1.2g/kg urethane (intraperitoneal) until unresponsive to tail pinch and decapitated according to aforementioned committee guidelines. The number of animals used was minimized.
2.2 Slice preparation and solutions
Olfactory bulbs were extracted in chilled (4°C) and oxygenated (95% 02, 5% CO2) artificial cerebrospinal fluid (ACSF), composed of 124mM NaCl, 2mM CaCl2, 3mM KCl, 1.25mM NaH2PO4, 26mM NaHCO3, 1.3mM MgSO4, and 10mM dextrose at pH 7.4. Horizontal slices of 400μm thickness were made with a rotorslicer (Dosaka) and immediately immersed in oxygenated ACSF at 34°C for 15 to 20 minutes. Slices were maintained in oxygenated ACSF at room temperature for up to 8 hours.
For Na+ washout experiments, slice preparation ACSF was made using a HEPES buffer (140mM NaCl, 3mM KCl, 1.3mM MgSO4, 2mM CaCl2, 10mM HEPES, 10mM dextrose). Oxygenation was achieved with 100% O2.
Extracellular drugs (cadmium, nickel, mibefradil, TTX) were dissolved in ddH20 except for nimodipine, which was dissolved in 100% EtOH such that final ethanol concentration was 0.02%. These stock solutions were stored in refrigeration, except for TTX, which was stored at −20°C.
2.3 Current clamp recording
JGCs were recorded in whole cell mode using a Kgluconate-EGTA internal solution (130mM Kgluconate, 10mM HEPES, 0.2mM EGTA, 4mM MgATP, 0.3mM Na3GTP, and 10mM Na2phosphocreatine), adjusted to pH 7.3–7.4 with KOH.
JGCs were visually identified via an infrared camera (Hamamatsu C2400-07ER) on an upright microscope (Olympus BX50WI) employing differential interference contrast microscopy with a 40X water immersion objective. JGCs were identifiable by their large somata at the deep border of glomeruli. Based on their size, we felt that these cells were similar to the external tufted cells and larger periglomerular cells that have been morphologically identified and shown to exhibit plateau potentials (McQuiston and Katz, 2001; Zhou et al., 2006). In unpublished work, we have also demonstrated that some of these cells give glutamatergic output, and are therefore most likely external tufted cells (results not shown). Current clamp whole cell recordings were made with the Axoclamp 2A and 2B amplifiers in bridge balance current clamp mode. Data were acquired with Pclamp 9.0 software at 10–20kHz sampling rate. Pipettes of resistance 8–12MΩ were pulled from borosilicate glass tube with filament (1.20mm outer/0.69mm inner diameter; Sutter) using a P-97 Flaming/Brown micropipette puller (Sutter). The recording chamber contained ACSF heated to 33–37°C.
For Na+ washout experiments, HEPES-buffer control ACSF was replaced with an ACSF in which Na+ was replaced with equimolar Tris (140mM TrisCl, 3mM KCl, 1.3mM MgSO4, 2mM CaCl2, 10mM HEPES, and 10mM dextrose).
2.4 Voltage clamp recording
For voltage clamp characterization of calcium current, the following intracellular solution was used: 100mM CsMES, 10mM TEA-Cl, 10mM EGTA, 0.5mM CaCl2, 10mM HEPES, 5mM MgATP, 10mM Na2phosphocreatine, and 0.5mM Na3GTP at pH 7.4 (CsMES internal solution). The EGTA and CaCl2 clamped internal calcium concentration to a known level of approximately 80nM, resulting in a theoretical Ca2+ reversal potential of +134mV. However, due to nonlinear properties of lipid membrane (Goldman, 1943; Hodgkin and Katz, 1949), the apparent reversal potential by linear extrapolation of IV curves was much less (+35mV).
The following were added to ACSF for further calcium current isolation: 1 μM TTX to block fast Na+ current, 3mM CsCl to block hyperpolarization-activated current (Ih), 50μM D-APV to block NMDAR-mediated glutamatergic input, and 20μM CNQX to block AMPAR-mediated glutamatergic input. Calcium replacement with barium (Hagiwara et al., 1975) was not done in order to study the native kinetics and amplitudes of calcium currents in the JGC.
Pipettes were pulled as above to 3–5MΩ (initial series resistance below 20MΩ) and tips were coated with dental wax to reduce capacitance. An axoclamp 200B amplifier was used for recordings in whole cell voltage clamp cSEVC mode.
JGCs were first identified by morphology as above. Plateau potential firing was confirmed before dialysis with K+ channel blocking internal solution by testing responses to olfactory nerve (ON) input in extracellular gigaseal mode just prior to break-in. The ON layer was preserved in the coronal acute slices, and its stimulation was elicited by placing a large tip pipette (1MΩ) filled with ACSF or a concentric bipolar stimulating electrode (25μm diameter tip) that was connected to electrical isolator, which controlled current amplitude of stimulation. Nerve was stimulated with one shock of 0.05–0.2ms width and less than 0.1mA amplitude.
After JGC identification, pipette capacitance was compensated and membrane was ruptured. The cell was dialyzed at resting membrane potential for several minutes. Series resistance (Rs), along with membrane capacitance (Cm), was compensated (with 10μs lag) to at least 80% correction and prediction for kinetics and activation/inactivation experiments and at least 65% for pharmacology experiments. If uncompensated Rs exceeded 20MΩ the recording was discontinued.
Currents were P/4 leak subtracted online. Data were sampled and filtered at 2 or 5kHz based on presumed Nyquist rate dependent on low pass filtering by the series resistance at 1/2πRsCm (with uncompensated Rs usually much less than 20MΩ, this cutoff frequency was typically much higher than ~250Hz). When possible, protocols were repeated and averaged. All voltages were corrected for a liquid junction potential of 10mV between ACSF and CsMES internal solution, measured according to a KCl salt bridge-based method (Neher, 1992). All experiments were performed at 33–37°C.
2.5 Computer simulation
Currents were assumed to be generated by homogeneous conductances undergoing state transitions according to a Hodgkin-Huxley scheme for activation (m) and inactivation (h) (Hodgkin and Huxley, 1952):
| [1] |
where
| [2] |
| [3] |
for activation (m) and analogous equations for inactivation (h). Current amplitude was determined by the following:
| [4] |
We determined experimental values to simulate these equations based on modifications of prior methods (Connor and Stevens, 1971c; Huguenard and McCormick, 1992). Briefly, during voltage clamp experiments, m∞X(Vm) was assumed to be equivalent to G/Gmax(Vm) obtained by the steady state activation protocol. This involved measuring peak current (Ipeak) generated at different test potentials from a given holding potential. This holding potential was chosen where current was maximally recovered from inactivation, and required the assumption that activation occurred much faster than inactivation to establish peak current. This held true in the case of the transient currents. Conductance value was determined by the following and normalized for each cell by dividing my the maximal conductance:
| [5] |
The value of X was determined for each transient current by fitting Boltzmann functions of the appropriate power to G/Gmax(Vm) and then examining how well macroscopic current generated in NEURON simulations fit experimentally recorded traces (see below and Results). Similarly, h∞(Vm) was assumed to be equivalent to I/Imax, derived from the steady state inactivation protocol which generated I/Imax for a given test potential as a function of holding potential. Test potential had been chosen to maximize activation and isolation of the current of interest. We assumed Y = 1, as in most conductance models.
The time constants, τm(Vm) and τh(Vm) could be constructed by measuring the rate of activation/deactivation and inactivation/recovery from inactivation, respectively. Time constant of activation was determined from the 10%–90% rise time of currents elicited in the activation protocol as follows. Because different schemes were used (X=1,2,3…), converting the rise time (trise) to a time constant required different conversion factors for each value of X, derived by solving for trise = t90–t10 in the following system of equations:
| [6] |
| [7] |
This lead to a scaling factor as follows:
| [8] |
Time constant of deactivation was determined by monoexponential fits to decay current elicited by stepping voltage to hyperpolarized potentials after current activation to a given test potential. The function τm(Vm) was constructed by combining these two functions. We assumed that the closing of a channel needed only one of the X number of m gates to deactivate, and therefore each time constant was scaled by 1/X based on the scheme being tested (Huguenard and McCormick, 1992). Time constant of inactivation was determined from monoexponential fits to decay of currents elicited in the activation protocol. Time constant of recovery from inactivation was determined by monoexponential fits to recovery of current after different durations of a hyperpolarized holding potential. The function τh(Vm) was constructed by combining these two functions.
The NEURON simulation environment version 5.9 (Hines and Carnevale, 1997) was used to simulate currents and a single compartment neuron containing these currents. The morphological parameters of the cell were chosen to match capacitative transients produced in these cells in current clamp, as well as capacitance in ranges seen in voltage clamp. These and the passive parameters are shown in Table 3. Currents were modeled using equations fit to m∞X(Vm), h∞Y(Vm), τ m(Vm), and τ h(Vm) wherever possible, and incorporated in NMODL. For simulations generated completely de novo (Icat1, Ikt1, Ikt2), the following differential equation was used in NEURON to actively compute m(Vm,t), and analogously for h(Vm,t):
| [9] |
Table 3.
Passive and active parameters related to JGC single compartment model
| Parameter | Value |
|---|---|
| L | 43μm |
| Diam | 43μm |
| Ra | 35.4 ohm*cm |
| Rm | 111 MΩ |
| Cm | 1μF/cm2 |
| Gpas | 1.55×10−4 S/cm2 |
| Epas | −63.5mV |
| Ina density | 100 pS/μm2 |
| Icat1 density | 0.0025 S/cm2 |
| Icat2 density | 0.003 S/cm2 |
| Ikt1 density | 0.00375 S/cm2 |
| Ikt2 density | 0.00074 S/cm2 |
| Ikt3 density | 14 pS/μm2 |
For Icat2, Ikt3, and INa, we based simulations on code used in previously published models (Traub et al., 2003; Mainen et al., 1995; Shen et al., 1999, respectively). Simulation runs were computed with time step of 0.025ms.
2.6 Statistical Analysis
Numerical averages are presented with standard error values, unless otherwise noted. P-values were obtained by Welch’s unpaired T-test. Correlations were evaluated using Pearson coefficient (r values presented).
3. RESULTS
3.1 The role of sodium current in JGC plateau potential generation
Though previous studies have shown that JGC plateau potentials are not blocked by extracellular TTX (McQuiston and Katz, 2001; Zhou et al., 2006), ruling out classical fast and persistent Na+ conductances as mediators of the firing pattern, there existed the possibility that TTX-resistant sodium currents could play a role (Yoshida and Matsuda, 1979). This was addressed in one study (McQuiston and Katz, 2001), in which plateau potentials persisted when extracellular Na+ was replaced with choline, and when the cell was dialyzed with QX-314, a lidocaine derivative Na+ channel blocker. However, neurons have variable permeability to choline (Partridge et al., 1994). Furthermore, QX-314 is known to also block calcium current (Talbot and Sayer, 1996).
We therefore aimed to block all Na+ currents by replacing extracellular sodium with impermeable Tris+ base (see Methods). Figure 1A shows a typical plateau potential, elicited in whole cell mode via a small current injection, before and after sodium replacement (n = 8). We waited well after the preliminary action potential was eliminated to consider sodium to be effectively washed out. Indeed, the underlying depolarization of the plateau potential persisted with Na+ gradient eliminated. We calculated the area of the plateau potential, measured as the product of half-maximal amplitude (Vmax,1/2) and plateau duration at Vmax,1/2, before and after experimental manipulation. Figure 1B shows that the area of the plateau potential, as a percent of area before Na+ replacement, is only slightly reduced (77.9 +/− 16.5%). For comparison, in another set of cells, we made this measurement before and after addition of TTX (n = 10). As a percent of control, plateau potential area on average was similar after TTX (109.5% +/− 61.5%).
Figure 1. Role of Na+ ions in JGC plateau potential firing.
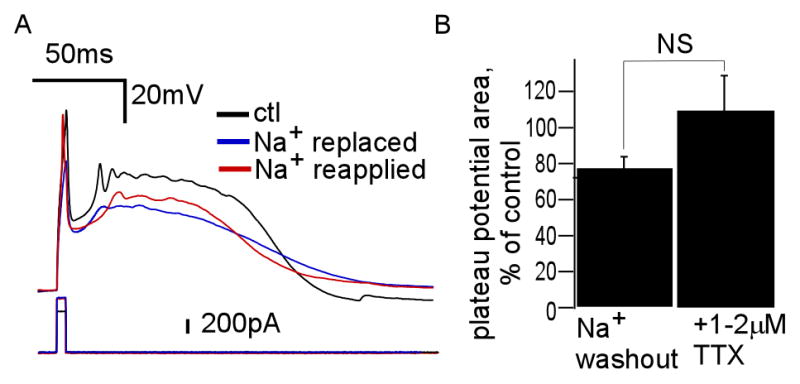
(A) JGC plateau potential before (black) and after replacement (blue) of extracellular Na+ with Tris+, with return of action potential after extracellular sodium reapplication (red) (n = 8). (B) Average remaining plateau potential area, as percent of control, after reduction of Na+ by Na+ replacement (left) and pharmacological blockade of Na+ channels (right) with extracellular TTX (n = 10, p = 0.15).
3.2 Calcium current in JGCs: fast (Icat1) and slow (Icat2) components
With evidence in our prior study eliminating calcium-mediated processes as generators of plateau potentials (Zhou et al., 2006), and with evidence above against a critical role for Na+ current, the most likely candidate to mediate the plateau potential seemed to be voltage dependent calcium currents (VGCCs). Previous work established that the plateau potential was sensitive to 250μM to 1mM extracellular nickel but not 200 to 400μM extracellular cadmium (McQuiston and Katz, 2001; Zhou et al., 2006). Though this supported that T-type calcium currents were driving the plateau potential, at such elevated (>100μM) concentrations, multiple subtypes of calcium current were likely blocked by either cation (Fox et al., 1987; Zamponi et al., 1996). Mibefradil, a T-type calcium channel blocker of debatable specificity (Avery and Johnston, 1997; Randall and Tsien, 1997), also produced inconclusive results for the same reasons (data not shown).
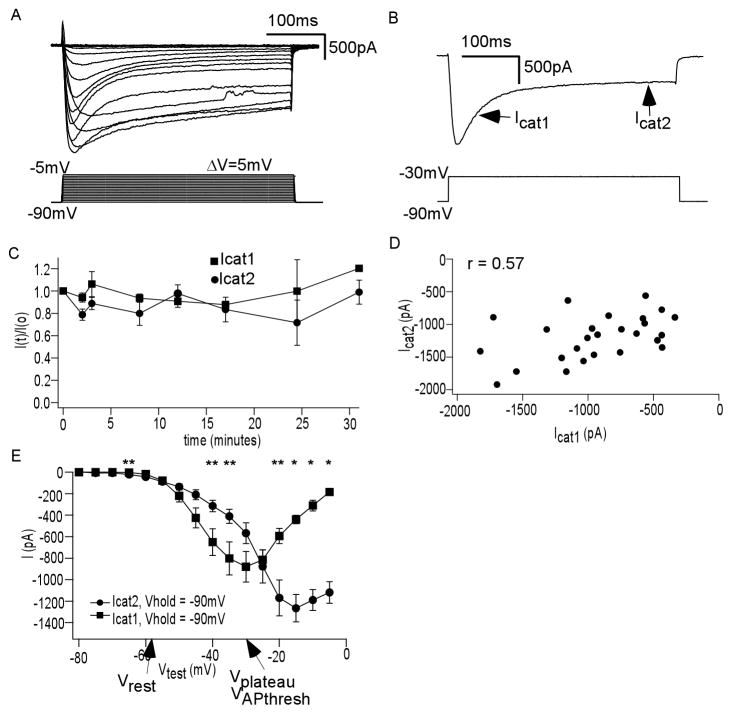
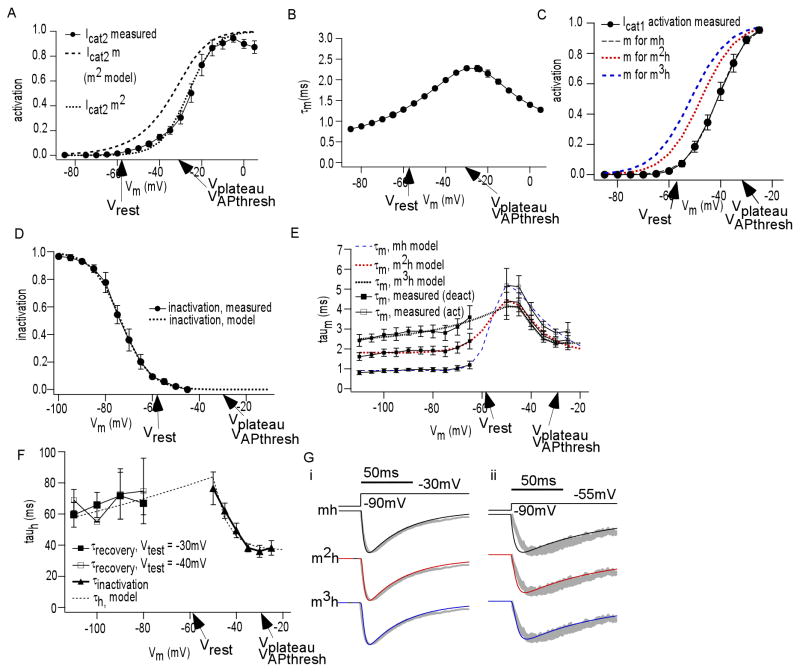
Due to this limitation of pharmacology, we turned to voltage clamp characterization. We isolated the calcium current (ICa) as described in the Methods. ICa was evoked by 5mV step depolarizations from an adequately hyperpolarized holding potential, chosen to relieve most currents from inactivation (Vhold = −90mV). Figure 2A shows typical currents generated from this protocol (n = 14). ICa had two components (Figure 2B): one transient (Icat1), one more sustained (Icat2). Icat1 decayed with time constants much less than 100ms, and we measured its amplitude as the difference of between the ICa peak and the sustained current ICa2 at 200ms. Icat2 often had decay time constants well exceeding 500ms.
Figure 2. Ca2+ current (ICa) of JGCs: rapidly inactivating Icat1 and very slowly inactivating Icat2.
(A) ICa (above) elicited by step depolarizations of 5mV from −90mV (below) (n = 14) (B) At test potential of −30mV, ICa clearly had a rapidly inactivating (Icat1) and a more sustained (Icat2) component. (C) Ratios of each current’s amplitude in time to its amplitude at the beginning of recording indicate stability of recording to 31 minutes (n = 12) (D) Plot of maximum Icat1 and Icat2 in each cell recorded indicate no consistent ratio (n = 27, Pearson r = 0.57). (E) Average current-voltage curves, from protocol as in Figure 2A, for Icat1 (square) and Icat2 (circle), show distinct relationships. Key plateau potential shape parameters are noted (n = 8, * p<0.0005, **p<0.05)
We were able to obtain stable, consistent recordings of each component for up to 31 minutes (Figure 2C, n = 12). Figure 2D shows a plot of the maximum current amplitudes of each component for all recorded cells (n = 27). The ratios of the two components varied widely, with Icat2/Icat1 ranging from 0.52–3.12 and with correlation coefficient (Pearson r) of 0.57. Therefore, it seemed more likely that ICa was generated by at least two different populations of voltage dependent current, rather than one current with two kinetic components, as is found with N-type current (Plummer and Hess, 1991). This was further supported by the average current-voltage relation (IV curve), as in Figure 2E (n = 8). Resting membrane potential (Vrest), action potential threshold (VAPthresh), and plateau voltage range (Vplateau) are delineated on the graph based on values obtained in the accompanying potassium current study (Masurkar and Chen, 2011). Note that the IV curve of Icat1 reaches its peak at lower voltages than Icat2 and that it is higher in amplitude between Vrest and Vplateau. However, both currents possessed activation thresholds near the resting membrane potential of these JGCs.
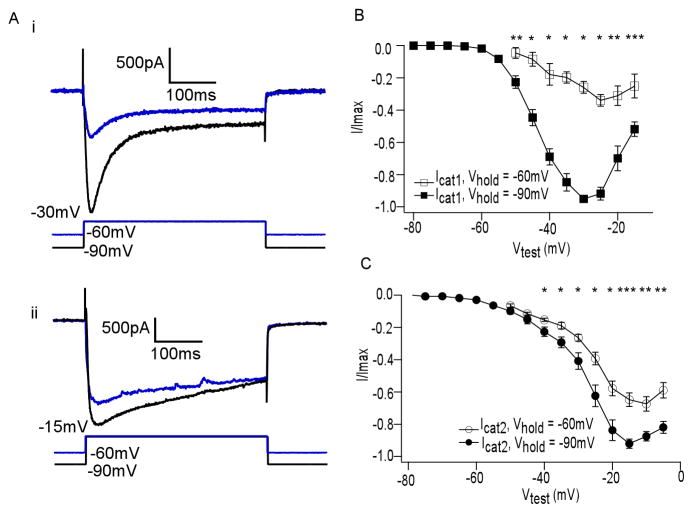
To gather more evidence that these were distinct currents, we attempted to separate the two components by assessing the effect of holding potential on peak amplitude. We repeated IV curves at two different holding potentials, one high (−60mV) and one low (−90mV). Icat1 had peak activation at −30mV, as in Figure 2E. However, Icat1 elicited from −60mV was lower in amplitude than that elicited from −90mV (Figure 3Ai). A similar comparison with a test potential of −15mV, at which Icat2 peaked, demonstrated that this sustained current was not as affected by manipulation of holding potential (Figure 3Aii). The influence of holding potential was quantified across a range of test potentials in Figures 3B and 3C, showing the average normalized IV curves for Icat1 and Icat2, respectively (n = 8). This again confirmed the distinctness of these two components. Furthermore, the voltage dependence of Icat1 resembled the voltage dependence of the plateau potential in the presence of TTX, as demonstrated in our prior work (Zhou et al., 2006).
Figure 3. Icat1 is more sensitive than Icat2 to steady state voltage changes.
(A) (i) Ica elicited by a −30mV test potential, at which Icat1 had peak activation, from two different holding potentials Vhold: −90mV (black) and −60mV (blue). (ii) Ica elicited by a −30mV test potential, at which Icat2 had peak activation, from two different holding potentials Vhold: −90mV (black) and −60mV (blue) (n = 8; *p<0.002, **p<0.005, ***p<0.02). (B) Plot of average normalized Icat1 versus test potential (Vtest), repeated at two values of Vhold, shows dependence on steady state holding potential (C) Plot of average normalized Icat2 versus test potential (Vtest), repeated at two values of Vhold, shows less dependence on steady state holding potential (n = 8, *p<0.05, **p<0.005, ***p<0.0005)
To be able to test the role of each current in plateau potentials, we tried to separate the two currents by using combinations of nickel, cadmium, nimodipine, and mibefradil. However, this was unsuccessful in that recordings were often unstable and results obtained were again nonspecific (data not shown).
3.3 Further characterization of Icat1
To overcome this pharmacological limitation, our strategy for assessing the function of Icat1 was to fully characterize the voltage dependence and kinetics to permit simulation and development of a model for plateau potential generation in which Icat1 could be selectively removed and altered in silico.
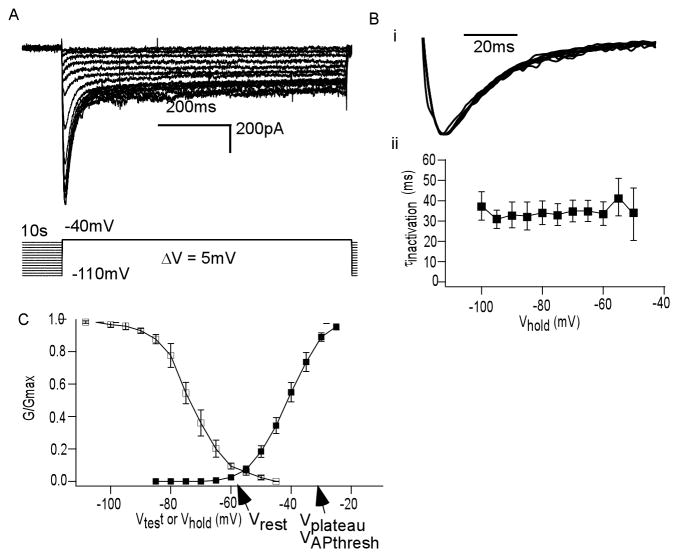
To study steady state inactivation of this current, we varied Vhold from −45mV to −110mV. We used a test pulse (Vtest) to −40mV so Icat1 would be activated but minimally contaminated by Icat2. Shown in Figure 4A are currents generated by this inactivation protocol, demonstrating reduced Icat1 at depolarized holding potentials (n = 7). Figure 4Bi shows an overlay of the normalized Icat1 for each Vhold in a given inactivation protocol. The similarity between each normalized trace within the protocol demonstrated that the currents generated in this voltage range are likely from a uniform population of voltage activated currents. We quantify this in Figure 4Bii, showing that the time constant of inactivation (τinactivation) is on average consistent at each Vhold (n = 7). The values for τinactivation were obtained by a fitting the decay of Icat1 to monoexponential decay.
Figure 4. Icat1 displays smooth steady state inactivation and activation.
(A) ICa (above) elicited by inactivation protocol (below) in which Vhold was varied for a given Vtest (B) (i) Superimposed normalized Icat1 traces from a single inactivation protocol shows overlap (ii) Plot of time constant of inactivation (τinactivation) of Icat1 elicited at each Vhold, averaged over many cells, shows consistency over holding potentials (C) Plot of steady state inactivation versus Vhold, derived from data in Figure 4A. Superimposed is steady state activation versus Vtest, derived from IV curve of Figure 2E. Key plateau potential shape parameters are noted.
Steady state inactivation, as a function of Vhold, was determined by dividing current amplitudes by the maximum elicited within a protocol (I/Imax). Figure 4C demonstrates that Icat1 smoothly inactivated with voltage (n = 7). This also reveals that Icat1 is approximately 90% inactivated at Vrest. Shown with the steady state inactivation curve is the steady state activation curve. IV curve of Icat1 from figure 2D was converted into an activation curve by dividing current by the driving force, and normalizing this conductance (G) by the maximum (Gmax) for each protocol per neuron (n = 14). This confirmed that Icat1 displayed smooth activation with voltage, typical of uniform voltage gated currents.
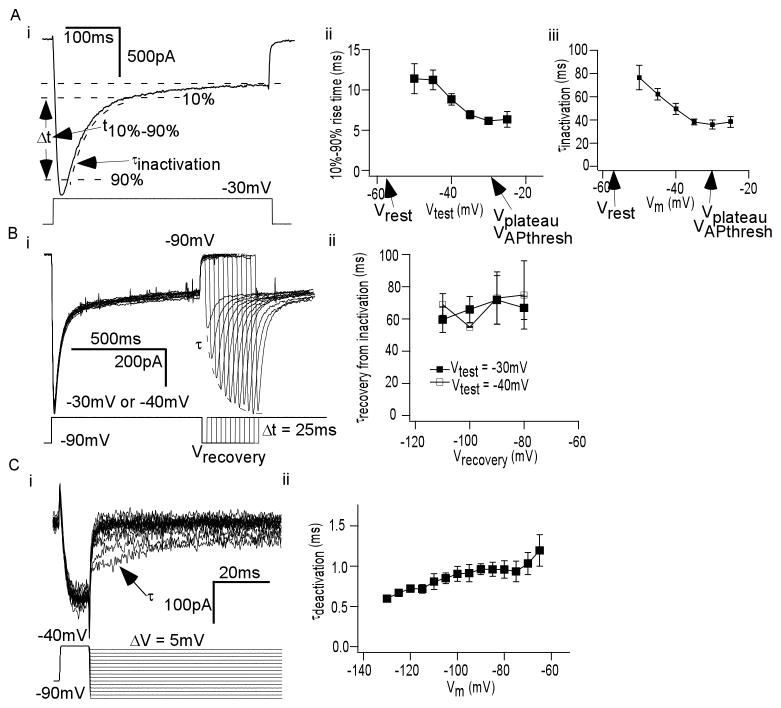
To measure kinetics of activation and inactivation, we analyzed currents from the IV curve of Figure 2. Delineated in Figure 5Ai is the method by which these were measured. Briefly, time to peak was measured by assessing the time needed to rise from 10% of maximum to 90% of maximum. For inactivation rate, τinactivation was obtained as described above. Shown in Figures 5Aii and 5Aiii are plots delineating how t10%–90%max (n = 5) and τinactivation (n = 5) smoothly vary with voltage, respectively. Notable was that τinactivation resembled the duration of the plateau potential.
Figure 5. Kinetics of Icat1.
(A) (i) 10%–90% rise time and τinactivation were extrapolated as shown from currents elicited as in Figure 2A (ii) Plot of 10%–90% rise time versus Vtest. (iii) Plot of τinactivation versus Vtest. Key plateau potential shape parameters are noted. (B) (i) ICa (above) elicited from voltage protocol (below) to study Icat1 recovery from inactivation (ii) Plot of τrecovery from nactivation of Icat1 versus recovery potential (Vrecovery), at two values of Vtest: −30mV (filled square) and −40mV (open square) (C) (i) ICa (above) elicited from voltage protocol (below) to study time constant of deactivation (τdeactivation) for Icat1 (ii) Plot of τdeactivation versus Vrepolarization.
The time constant of recovery from inactivation (or τrecovery from inactivation) was measured as function of Vhold as follows. Icat1 was evoked by a Vtest from a negative Vhold, fully inactivated, exposed to a recovery potential (Vrecovery) for different durations, and evoked again at the same Vtest (Figure 5Bi). Icat1 amplitude recovery with time was fit to a monoexponential to obtain τrecovery from inactivation. We tested τrecovery from inactivation at two values for Vrecovery: −30mV and −40mV. Shown in Figure 5Bii is a plot of how τrecovery from inactivation varied with recovery potential (n = 4–5 for each recovery potential). Interestingly, the time course of recovery from inactivation for Icat1 was in the same range as the frequencies of rhythmic plateau potential generation.
Time constant of deactivation (τdeactivation), as a function of Vm, was measured by eliciting Icat1 with brief Vtest to −30mV, and then rapidly stepping to various potentials once Icat1 reached its peak (Figure 5Ci). The resulting tail current decays were fit to monoexponentials to obtain τdeactivation. Shown in Figure 5Cii is a graph of how τdeactivation smoothly varied with voltage (n = 5).
3.4 Simulation of calcium currents
To simulate the calcium currents of JGCs, we approximated the total ICa as a sum of Icat1 and Icat2. We simulated Icat2 by modifying an existing model for L-type conductance, which used an m2 Hodgkin-Huxley scheme, without inactivation (Traub et al., 2003). Shown in Figure 6A is a fit of the simulation activation curve to our experimental data. The experimental activation curve was generated from the activation protocol similar to the method used for Icat1. Figure 6B shows the kinetics of activation for the simulation. Equations for this model are in Table 1.
Figure 6. Simulation of Icat2 and Icat1.
(A) (i) Steady state activation of Icat2 versus Vtest, derived from Figure 2E. Superimposed is Icat2 m∞(Vm) (broad dash). Its square, Icat2 m∞2(Vm) (fine dash), overlaps the experimental activation curve (solid line). Function modified from Traub et al., 2003. (B) Time constant of activation (τm) as function of Vm for Icat2 (Traub et al., 2003) (C) Three Boltzmann functions m∞(Vm) (m – black dash, m2 – red dash, m3 – blue dash) that, when raised to the appropriate power (1,2,3), all closely fit the measured activation curve of Icat1 (solid line). For clarity, each is shown prior to this exponentiation. (D) Boltzmann function h∞(Vm) and measured steady state inactivation of Icat1. This was used for all three Icat1 models (mh, m2h, m3h). (E) Experimental τactivation (open square) and τdeactivation (filled square), as functions of Vm, were both scaled appropriately for each of the three schemes (see Methods and Figures 5A, 5C). Superimposed are three τm(Vm) curves, fit to these scaled experimental data (m – black, m2 – red, m3 – blue). These were used for each Icat1 model (mh, m2h, m3h). (F) Experimental τinactivation and τrecovery from inactivation, as functions of Vm (see Figures 5A, 5B). Superimposed is τh(Vm) fit, used in all Icat1 models (mh, m2h, m3h) (G) Three models were generated from descriptions in 6A–F. (i) Simulated Icat1 evoked by Vtest of −30mV, using each scheme (mh - black, m2h - red, m3h - blue). Superimposed (gray) is average experimentally recorded Icat1 at this Vtest. The m3h scheme shows the best fit. (ii) Simulated Icat1 evoked by Vtest of −55mV, using each scheme (mh - black, m2h - red, m3h - blue). Superimposed (gray) is experimentally recorded Icat1 at this Vtest. The m3h scheme shows the best fit. Key plateau potential shape parameters are noted throughout.
Table 1.
Activation equations for models of JGC calcium, sodium, and potassium currents
| scheme | minf(Vm) | tm(Vm) | |||||
|---|---|---|---|---|---|---|---|
| Icat1 | m3h |
|
|
||||
| Icat2 | m2 |
|
|
||||
| INa | m3h |
|
|
||||
| Ikt1 | m4h |
|
|
||||
| Ikt2 | m2h |
|
|
||||
| Ikt3 | m |
|
|
To simulate Icat1 we employed our extensive characterization of steady state activation, inactivation, and kinetics. Because models for transient VGCCs, the T-type currents, have used mh, m2h, and m3h schemes (De Schutter and Bower, 1994; Jaffe et al., 1994; Huguenard and McCormick, 1992; Lee et al., 2003; Wang et al., 1991a), we tested all three for fitness. Shown in Figure 6C are three Boltzmann curves which, when raised to the power of n = 1 or 2 or 3, robustly overlapped the experimental activation curve m∞ curve. Shown in Figure 6D is the Boltzmann curve fit to the steady state inactivation plot (h∞ curve).
For kinetics, we simulated τm by a function fit to the combination of τdeactivation and τactivation. For the latter, for each model scheme (mh, m2h, and m3h), we converted experimental t10%-90%max to an appropriately scaled exponential time constant τactivation according to the number of m components (see Methods). This led to three different τm functions. The converted data and fits for each model are shown in Figure 6E. For τh, we fit functions to the grouping of tinactivation with trecovery from inactivation, as shown in Figure 6F. Because all three models had one inactivation particle, the same τh function was used for all three. These fits generated m(Vm,t) and h(Vm,t) to complete each simulation. For each scheme, in simulated voltage clamp, we generated currents at one subthreshold (Vtest = −55mV) and one suprathreshold (Vtest = −30mV) test potential to test which model fit best to an average of experimental traces for the same test potentials. As shown in Figure 6Gi and Figure 6Gii, the m3h current best fit the experimental traces. Equations for this model are in Tables 1 and 2.
Table 2.
Inactivation equations for models of JGC calcium, sodium, and potassium currents
| scheme | hinf(Vm) | τh(Vm) | |||||
|---|---|---|---|---|---|---|---|
| Icat1 | m3h |
|
|
||||
| INa | m3h |
|
|
||||
| Ikt1 | m4h |
|
|
||||
| Ikt2 | m2h |
|
|
3.5 Single compartment modeling of JGC plateau potential firing
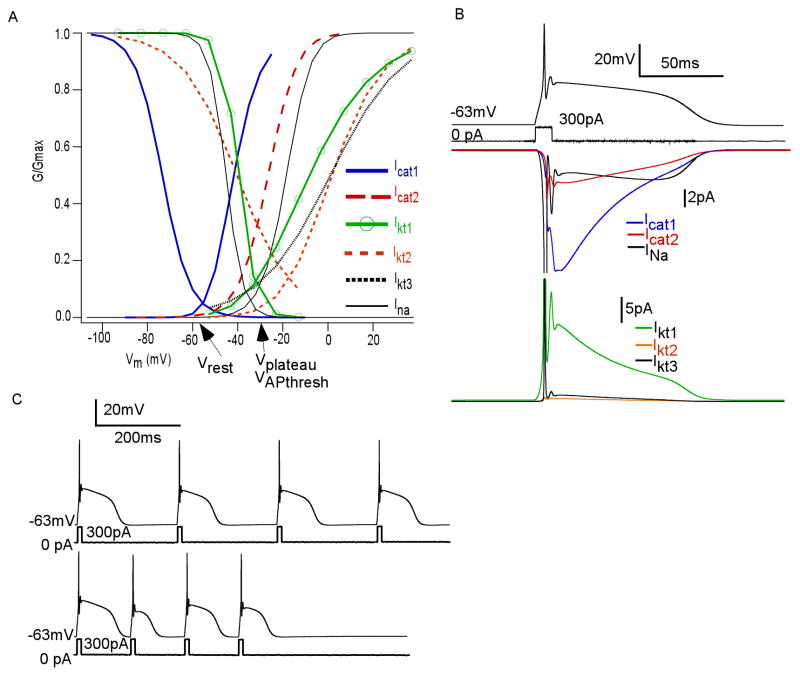
We combined our simulations of calcium current with those for the three potassium currents (Ikt1, Ikt2, Ikt3) in the accompanying study (Masurkar and Chen, 2011), and a previously published fast sodium current INa (Shen et al., 1999), to generate a single compartment model of plateau potential firing in JGCs (equations in Tables 1 and 2). Ikt1 is an A-type current, Ikt2 is a D-type current, and Ikt3 is a delayed rectifier. We used passive properties to be consistent with range of whole cell capacitance (Cm) and resistances (Rm) in our voltage clamp recordings, modulated to recreate capacitative transients recorded in current clamp (Table 3). Conductance values of each calcium and potassium current were based on ranges noted in voltage clamp recordings, normalized by cell capacitance. Ratios of Icat2:Icat1 and Ikt3:Ikt2:IKkt1 were also noted in our recordings and used to guide conductance density choices. We modulated these values, as well as that of the sodium current, to align reasonably with standardized recordings of plateau potentials. Calcium-activated potassium currents were not included, as we have previously shown these currents play minimal roles in shaping the salient features of the plateau potential (Zhou et al., 2006; Masurkar and Chen, 2011).
The summary of the model is shown in Figure 7A, demonstrating all m∞ and h∞ curves for the 6 conductances of the simulation, and Table 3, which shows parameters for conductance values and passive characteristics. An example of a simulated plateau potential at resting membrane potential (Vrest = −63mV) is shown in Figure 7B. Below is shown the time course of each ion current used in the model. The model demonstrated similar electrical properties to experimental recordings. For example, repetetive firing of plateau potentials is limited to certain frequencies (Zhou et al., 2006). Our simulation also showed this property. Robust plateau potentials could be induced by current input every 240ms (Figure 7C, above), but when inputs were delivered every 130ms there was variation in plateau duration (Figure 7C, below). Note that 240ms is three times τrecovery from inactivation for Icat1 at this Vrest.
Figure 7. Simulation of JGC plateau potentials.
(A) Summary of all m∞(Vm) and h∞(Vm) curves for the 6 currents used for the simulation (B) The multiconductance model well simulates a plateau potential in response to current input (top). Time courses of inward currents (middle) and outward currents (bottom) are shown. Note prominance of Icat1 (blue - middle) and Ikt1 (green - bottom) during the plateau (C) The model preserves intrinsic frequency preference of recurrent plateau potentials, as evidenced by consistently shaped plateau potentials with current injection every 240ms (above) but not when every 130ms (below).
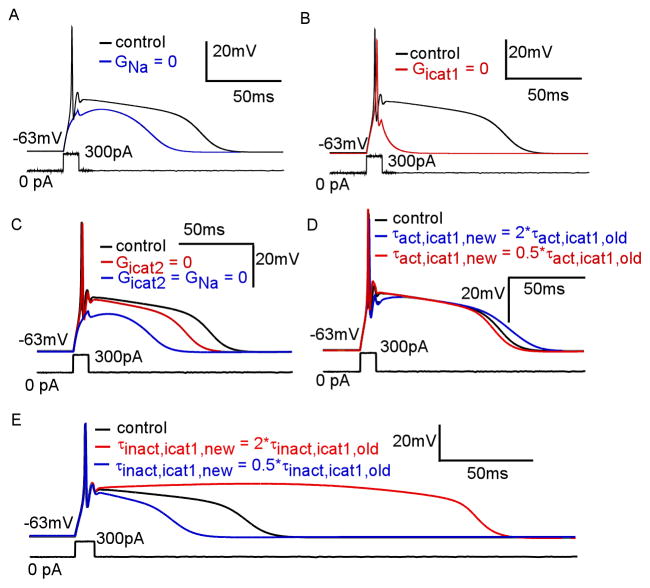
We then used the simulation to explore the roles of inward currents in plateau potential generation. In Figure 8A, we show that a significant afterdepolarization persists in the absence of sodium current, as we have found experimentally. This shows that Icat1 and Icat2 both support the plateau potential under these conditions. In Figure 8B, we selectively removed Icat1 to demonstrate that Icat2 and INa cannot support the plateau potential. In Figure 8C, we selectively remove Icat2 to show that Icat1 together with INa can generate the plateau potential. These simulations indicate that Icat1 is necessary, though not necessarily sufficient, for generating the plateau potential. In Figure 8C we removed only Icat2 to demonstrate that a depolarizing potential persists, driven by Icat1 and INa. In the same figure, removal of both INa and Icat2 reduced, but did not eliminate, the depolarizing potential mediated by Icat1 alone.
Figure 8. Role of inward currents in JGC plateau potentials.
(A) Response of simulated JGC to current injection before (black) and after (blue) removal of sodium conductance shows persistence of a depolarizing potential (B) Model response to current injection before (black) and after (red) removal of Icat1 conductance shows critical dependence on Icat1 (C) Simulated JGC plateau potential (black), after removal of Icat2 conductance (red), and after removal of both Icat2 and INa conductances (blue) shows persistence of a small depolarizing potential (D) JGC plateau potential simulation with Icat1 τactivation at control values (black), increased by factor of 2 (blue), and decreased by factor of 2 (red) shows some dependence of plateau duration on Icat1 activation kinetics (E) JGC plateau potential simulation with τinactivation at control values (black), increased by factor of 2 (red), and decreased by factor of 2 (blue), demonstrates significant dependence of plaeau duration on Ikt1 inactivation kinetics
We exploited the ability to manipulate Icat1 to further explore which aspects of the current were critical for plateau potential timing. Since the plateau potential level is at approximately −30 mV, where the activation and inactivation processes of Icat1 are dominant over deactivation and recovery from inactivation, we sought to manipulate these values and test their effect on the plateau potential. Figure 8D demonstrates a plateau potential generated with alternate forms of Icat1 in which τactivation was increased and decreased by a factor of two. This manipulation caused slight variation in plateau duration. In Figure 8E, we show the plateau potential generated with τinactivation increased and decreased by a factor of two showed much more variation. Therefore, the inactivation kinetics of Icat1 greatly influence plateau potential shape.
We then explored the role of potassium currents. For each potassium current we increased and decreased conductance by 25%. In Figure 9A is shown the effects of such modulations of Ikt1. This demonstrated that this atypical A-current had a wide influence over the potential, including spike amplitude, spike delay, plateau amplitude, and plateau duration. In Figures 9B and 9C we similarly altered the conductance values of Ikt2 and Ikt3. These manipulations did not have much effect.
Figure 9. Role of potassium currents in plateau potential generation.
(A) Simulated JGC plateau potential (black), after increasing Ikt1 conductance by 25% (red), and after decreasing Ikt1 conductance by 25% (blue) demonstrates dependence of plateau duration on this conductance magnitude (B) Simulated JGC plateau potential (black), after increasing Ikt2 conductance by 25% (red), and after decreasing Ikt2 conductance by 25% (blue) shows almost no variation (C) Simulated JGC plateau potential (black), after increasing Ikt3 conductance by 25% (red), and after decreasing Ikt3 conductance by 25% (blue), also shows almost no variation.
4. DISCUSSION
In this study we first demonstrated that JGC plateau potentials are primarily mediated by voltage gated calcium currents and not by sodium influx. We then characterized the two components of JGC calcium current: a slow activating, rapidly inactivating (τ10%–90% rise 6–8ms, τinactivation 38–77ms) component Icat1 and a sustained (τinactivation≫500ms) component Icat2. To overcome limitations of pharmacological separation, we created a 6-conductance computer model of JGC plateau potentials to then demonstrate that Icat1 was the most critical inward current for plateau potential generation and that Ikt1, an A-type potassium current, was the most important outward current for plateau potential shape.
INa,P influences burst and plateau potential firing in several neuronal subtypes (Kay et al., 1998; Hsiao et al., 1998; Jahnsen and Llinas 1984a; Jahnsen and Llinas 1984b; Li and Bennett, 2003), including OB ETCs (Hayar et al., 2004a; Liu and Shipley, 2008). Prior studies showed that this current does not mediate the JGC plateau potential (McQuiston and Katz, 2001; Zhou et al., 2006), and in the present study we used another pharmacologic manipulation to suppress Na+ current (Tris+ replacement) and demonstrate that this did not abolish the plateau potential either. Nevertheless, fast Na+ currents are likely still critical as a trigger, because an action potential is probably needed to activate the other inward currents involved plateau potential generation. The mild reduction in plateau potential area by our manipulation implied that sodium ions also contributed to plateau amplitude and duration. This could come in the form of TTX-resistant Na+ currents, nonspecific cation currents, or current from Na+-Ca2+ exchangers.
Icat1 likely represents a uniform population of currents based on the smoothly voltage-dependent activation, inactivation, and kinetics. Additionally, we demonstrated that τinactivation was stable over a wide range of holding potentials. Rapidly inactivating VGCCs include T-type, R-type, and N-type currents. Immunohistochemical evidence exists for all of these calcium subtypes in the glomerular layer (Ludwig et al., 1997; Talley et al., 1999).
The half maximal voltage (V1/2) for inactivation was −74.0mV, which is similar to that of typical whole cell T-current and T-type channels (Coulter et al., 1989; Monteil et al., 2000a; Monteil et al., 2000b; Klockner et al., 1999), R-current (Soong et al., 1993; Randall and Tsien, 1997), and N-current (Stea et al., 1999). However, the activation V1/2 of Icat1 is −40.5mV, approximately 10mV hyperpolarized to that of the R-current (Soong et al., 1993; Randall and Tsien, 1997) and 40–50mV hyperpolarized to that of the N-currents (Nowycky et al., 1985). Notably, all three T-type channel subtypes have been shown to have a similar activation V1/2 to Icat1 (−44mV and −46mV: Monteil et al., 2000a; Monteil et al., 2000b; Klockner et al., 1999).
Activation occurred on the order of 2–8ms, similar to classical whole cell T-type current (Carbone and Lux, 1984; Coulter et al., 1989) and the CaV3.3 T-channel (Klockner et al., 1999). However, R-type currents (Randall and Tsien, 1997; Soong et al., 1993) and N-type currents (Stea et al., 1999) can also activate at these rates. Deactivation occurred very quickly, in less than 1.5ms. Although this was much faster than typical T-type current (Huguenard and McCormick, 1992; Randall and Tsien, 1997), both CaV3.1 and CaV3.3 currents display such rapid kinetics (Talavera and Nilius, 2006a; Talavera and Nilius 2006b; Chemin et al., 2001). The R-type and N-type currents can also deactivate similarly (Randall and Tsien, 1997; Buraei et al., 2005).
With τinactivation of 40–80ms, Icat1 decays rate resembles that of classical whole cell LVA current (Fedulova et al., 1985) and CaV3.3, but is slow compared to CaV3.2 and CaV3.1 (Monteil et al., 2000a; Monteil et al., 2000b; Klockner et al. 1999). This inactivation rate is faster than R-type (Randall and Tsien, 1997; Soong et al., 1993) and N-type currents (Stea et al., 1999). Interestingly, reticular thalamic neurons fire low threshold bursts of longer duration than thalamic relay neurons, and this difference is attributed to expression of CaV3.3 versus the faster decaying T-type variants (Huguenard and Prince, 1992; Talley et al., 1999). Icat1 time constant of recovery from inactivation ranged from 50–80ms, which was lower than that of the classical T-current (Coulter et al., 1989), cloned T-type channel variants (Perez-Reyes, 2003), and R-current (Randall and Tsien, 1997).
Icat1 therefore was most likely a T-type current, with a component most likely comprised of CaV3.3. Indeed, immunohistochemical evidence supports presence of CaV3.1 and CaV3.3 in the OB glomeruli (Talley et al., 1999; Klugbauer et al., 1999). Furthermore, these variants of T-current display less sensitivity to nickel block than CaV3.2 (Lee et al., 1999), which may explain the requirement of high concentrations of extracellular nickel to block the plateau potential itself. Such pharamacological differences also occur between reticular thalamic bursts and thalamic relay bursts based on similar calcium channel expression differences (Joksovic et al., 2005).
As mentioned previously, LVA calcium current was identified in rat GABAergic PGCs (Murphy et al., 2005), with a major component identified as L-type based on sustained time course and sensitivity to dihydropyridines and cadmium, but not to nickel (Murphy et al., 2005). In the same cells, some of which could fire bursts, a transient LVA current was identified that also activated above −60mV. Comparing IV curves, it appears that Icat1 inactivates with a similar rate, but may activate at slightly more depolarized potentials. It is possible that this T-current from GABAergic PGCs is represented partially in our study, as we recorded a general population of JGCs. The T-current of dopaminergic PGCs (Pignatelli et al., 2005) has slightly hyperpolarized activation compared to Icat1, with peak current at −35mV and V1/2 of −45.3mV. We do not think that this current contributed to Icat1 because these cells were spike firing only. The LVA current of bursting mouse ETCs has similar features as Icat1, activating with V1/2 of −37.1mV and inactivating with τinact of −62ms (Liu and Shipley, 2008). Certainly Icat1 could partially reflect this current, as ETCs are included in these recordings.
Icat2 likely reflected a composite of multiple calcium currents. The activation V1/2 (−25 mV) is similar to that of P/Q type currents (Llinas et al., 1989; Sather et al., 1993) rather than L-type currents (Fox et al., 1987). All are found in the olfactory bulb glomerular layer (Ludwig et al., 1997).
Though multicompartment models account better for electrotonic effects, single compartment models have been very useful to explore burst and plateau potential mechanisms in other neurons (McCormick and Huguenard, 1992; Genet and Delord, 2002). Our simulation of plateau potential firing demonstrated that Icat1 was necesssary but not sufficient for generating the plateau potential, but still more critical than the other two depolarizing currents (Icat2, INa). The necessity for Icat1 was consistent with the finding that the voltage dependence of the current was similar to that of the plateau potential itself, as measured experimentally in our prior study (Zhou et al., 2006) and simulated in this study. Additionally, inactivation kinetics of Icat1 strongly dictated plateau potential duration. This suggests a mechanism in which T-type currents are dominant, as in thalamic relay neurons (Coulter et al., 1989), trigeminal neurons (Hsiao et al., 1998), and the Purkinje cell (Pouille et al., 2000).
We also found that atypical A-current Ikt1 was more influential on plateau potential shape than the atypical D-current Ikt2 and delayed rectifier Ikt3. Several factors likely contribute to this. First, compared to Ikt2, this current activates at more hyperpolarized membrane potentials to interact with INa and Icat1 in the plateau potential voltage range. Also, this current activates much more quickly than Ikt2 and thus can influence the action potential. Although Ikt3 shows equivalent activation in the plateau voltage region, it activates at approximately half the rate of Ikt1 and the overall slope of its activation curve is lower. It is therefore less poised to influence spike and plateau shape. The importance of the A-current to plateau potential firing has also been demonstrated in cerebellar Purkinje cell (Wang et al., 1991b; Serodio and Rudy, 1998; Wang and Schreurs, 2006). However, Purkinje cell plateau potentials are also more reliant on currents similar to Ikt2 and Ikt3, similar to subthalamic nucleus plateau potentials (Midtgaard, 1995; Otsuka et al., 2001; Genet and Delord, 2002; McKay et al., 2005). This may be related to the unique features of potassium currents in JGCs, as well as the unique properties of Icat1 with which Ikt1 interacts.
As discussed in the accompanying paper (Masurkar and Chen, 2011), the limitations to our study stem from the drawbacks of single electrode voltage clamp (space clamp), the possibility of transmitter-mediated modulation of ionic currents, and recordings from a heterogeneous group of neurons (JGCs) that include different neuron types (ETCs and PGCs). We are however encouraged by the consistency of current measurements and ratios across the large number of neurons targeted, and the similarity between the characteritics of currents recorded here and of those expressed in the OB gomerulus. Lastly, we have noticed little variation in plateau potential generation when all ionotropic and metabotropic glutamatergic and GABAergic input is blocked (data not shown).
5. CONCLUSION
In summary, we demonstrate through current clamp recordings, voltage clamp characterization, and computer simulations, that transient calcium current (Icat1) and transient potassium current (Ikt1) are the most critical currents for driving and shaping the plateau potentials of olfactory bulb JGCs. Though this was done with calcium-activated potassium currents minimized, we have shown previously that plateau potential shape is minimally influenced by such conductances (Zhou et al., 2006; Masurkar and Chen, 2011). The voltage dependence, kinetics, and pharmacology of Icat1 reflect the calcium channels found in the OB glomerulus, CaV3.1 and CaV3.3.
These findings further suggest that T-type and A-type currents are important loci for controlling and modulating JGC function, and in turn odorant processing in the olfactory glomerulus. Lastly, we have developed the first working model of JGC plateau potentials. This, together with prior models of other PGCs (Pignatelli et al., 2005) and mitral cells (Shen et al., 1999; David et al., 2008 ), could be used to advance existing simulations of small OB networks (Davison et al., 2003; Rubin and Cleland 2006; Karnup et al., 2006; Migliore and Shepherd 2008) to better reflect the complex glomerular layer processing that contributes to odor information processing in the OB.
RESEARCH HIGHLIGHTS.
Olfactory juxtaglomerular cells fire plateau potentials of unclear mechanism.
We recorded their calcium current, showing a transient and sustained component.
We created a model of plateau potential firing based on these recordings.
The model showed that transient calcium current generates the plateau potential.
The model also showed that transient potassium current is also critical.
Acknowledgments
We thank Dr. G. Shepherd for guidance, Dr. S. Nagayama and Dr. M. Fletcher for critically reading the manuscript, and Dr. W. Xiong for technical assistance. This work was supported by National Institute of Deafness and Other Communication Disorders Grants DC-003918 and DC-009666 (W.C.), DC-000086 and DC-004732 (G. M. Shepherd), and a National Institutes of Health Medical Scientist Training Program Grant (A.M.).
Abbreviations
- TEA
tetramethylammonium
- MES
methanesulfonate
- TTX
tetrodotoxin
- EGTA
glycol-bis(2-aminoethylether)-N,N,N′,N′-tetraacetic acid
- D-APV
D-2-amino-5-phosphonovaleric acid
- CNQX
6-cyano-7-nitroquinoxaline-2,3-dione
- AMPA
2-amino-3-(5-methyl-3-oxo-1,2-oxazol-4-yl)propanoic acid
- NMDA
N-Methyl-D-aspartic acid
- HEPES
4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid
- ATP
Adenosine-5′-triphosphate
- GTP
Guanosine-5′-triphosphate
6. GLOSSARY
- Olfactory bulb
The first area of the brain to receive and process primary olfactory sensory information from olfactory sensory neurons
- Glomerulus
A spherical 50–100μm of neuropil and the locus of information transfer between olfactory sensory neurons and output neurons of the olfactory bulb, as well as the site of modulation of this transfer by interneurons. Several hundred glomeruli form the first layer of the olfactory bulb
- Mitral cell
An excitatory output neuron of the olfactory bulb, whose axons project to olfactory cortex, and whose dendrites are within the glomerulus and cell body is deep to the glomerular layer
- Tufted cell
Another excitatory output neuron of the olfactory bulb, whose soma is more superficial than that of a mitral cell
- Juxtglomerular cell
A group of neurons whose cell bodies lie around the border of a glomerulus. They include external tufted, periglomerular, and short axons cells
- External tufted cell
The most superficially located tufted cell
- Periglomerular cell
A chemical heterogeneous group of interneurons within the glomerular layer show dendrites and axons pariticipate in synaptic interactions with other glomerular processes. They can be GABAergic, dopaminergic, or release other neurotransmitters
- Short axon cell
An excitatory interneuron thought mediate interglomerular inhibition
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Antal M, Eyre M, Finklea B, Nusser Z. External tufted cells in the main olfactory bulb form two distinct subpopulations. Eur J Neurosci. 2006;24:1124–1136. doi: 10.1111/j.1460-9568.2006.04988.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avery RB, Johnston D. Ca2+ channel antagonist U-92032 inhibits both T-type Ca2+ channels and Na+ channels in hippocampal CA1 pyramidal neurons. J Neurophysiol. 1997;77:1023–1028. doi: 10.1152/jn.1997.77.2.1023. [DOI] [PubMed] [Google Scholar]
- Beurrier C, Congar P, Bioulac B, Hammond C. Subthalamic nucleus neurons switch from single-spike activity to burst-firing mode. J Neurosci. 1999;19:599–609. doi: 10.1523/JNEUROSCI.19-02-00599.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buraei Z, Anghelescu M, Elmslie KS. Slowed N-type calcium channel (CaV2.2) deactivation by the cyclin-dependent kinase inhibitor roscovitine. Biophys J. 2005;89:1681–1691. doi: 10.1529/biophysj.104.052837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cadetti L, Belluzzi O. Hyperpolarisation-activated current in glomerular cells of the rat olfactory bulb. Neuroreport. 2001;12:3117–3120. doi: 10.1097/00001756-200110080-00027. [DOI] [PubMed] [Google Scholar]
- Carbone E, Lux HD. A low voltage-activated, fully inactivating Ca channel in vertebrate sensory neurones. Nature. 1984;310:501–502. doi: 10.1038/310501a0. [DOI] [PubMed] [Google Scholar]
- Chemin J, Monteil A, Dubel S, Nargeot J, Lory P. The alpha1I T-type calcium channel exhibits faster gating properties when overexpressed in neuroblastoma/glioma NG 108–15 cells. Eur J Neurosci. 2001;14:1678–1686. doi: 10.1046/j.0953-816x.2001.01796.x. [DOI] [PubMed] [Google Scholar]
- Connor JA, Stevens CF. Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. J Physiol. 1971;213:31–53. doi: 10.1113/jphysiol.1971.sp009366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulter DA, Huguenard JR, Prince DA. Calcium currents in rat thalamocortical relay neurones: kinetic properties of the transient, low-threshold current. J Physiol. 1989;414:587–604. doi: 10.1113/jphysiol.1989.sp017705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David F, Linster C, Cleland TA. Lateral dendritic shunt inhibition can regularize mitral cell spike patterning. J Comput Neurosci. 2008;25:25–38. doi: 10.1007/s10827-007-0063-5. [DOI] [PubMed] [Google Scholar]
- Davison AP, Feng J, Brown D. Dendrodendritic inhibition and simulated odor responses in a detailed olfactory bulb network model. J Neurophysiol. 2003;90:1921–1935. doi: 10.1152/jn.00623.2002. [DOI] [PubMed] [Google Scholar]
- De Saint Jan D, Hirnet D, Westbrook GL, Charpak S. External tufted cells drive the output of olfactory bulb glomeruli. J Neurosci. 2009;29:2043–2052. doi: 10.1523/JNEUROSCI.5317-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Schutter E, Bower JM. An active membrane model of the cerebellar Purkinje cell. I. Simulation of current clamps in slice. J Neurophysiol. 1994;71:375–400. doi: 10.1152/jn.1994.71.1.375. [DOI] [PubMed] [Google Scholar]
- Fedulova SA, Kostyuk PG, Veselovsky NS. Two types of calcium channels in the somatic membrane of new-born rat dorsal root ganglion neurones. J Physiol. 1985;359:431–446. doi: 10.1113/jphysiol.1985.sp015594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox AP, Nowycky MC, Tsien RW. Kinetic and pharmacological properties distinguishing three types of calcium currents in chick sensory neurones. J Physiol. 1987;394:149–172. doi: 10.1113/jphysiol.1987.sp016864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser DD, MacVicar BA. Cholinergic-dependent plateau potential in hippocampal CA1 pyramidal neurons. J Neurosci. 1996;16:4113–4128. doi: 10.1523/JNEUROSCI.16-13-04113.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genet S, Delord B. A biophysical model of nonlinear dynamics underlying plateau potentials and calcium spikes in purkinje cell dendrites. J Neurophysiol. 2002;88:2430–2444. doi: 10.1152/jn.00839.2001. [DOI] [PubMed] [Google Scholar]
- Gire DH, Schoppa NE. Control of on/off glomerular signaling by a local GABAergic microcircuit in the olfactory bulb. J Neurosci. 2009;29:13454–13464. doi: 10.1523/JNEUROSCI.2368-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagiwara S, Ozawa S, Sand O. Voltage clamp analysis of two inward current mechanisms in the egg cell membrane of a starfish. J Gen Physiol. 1975;65:617–644. doi: 10.1085/jgp.65.5.617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayar A, Karnup S, Ennis M, Shipley MT. External tufted cells: a major excitatory element that coordinates glomerular activity. J Neurosci. 2004;24:6676–6685. doi: 10.1523/JNEUROSCI.1367-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayar A, Karnup S, Shipley MT, Ennis M. Olfactory bulb glomeruli: external tufted cells intrinsically burst at theta frequency and are entrained by patterned olfactory input. J Neurosci. 2004;24:1190–1199. doi: 10.1523/JNEUROSCI.4714-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayar A, Shipley MT, Ennis M. Olfactory bulb external tufted cells are synchronized by multiple intraglomerular mechanisms. J Neurosci. 2005;25:8197–8208. doi: 10.1523/JNEUROSCI.2374-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of the giant axon of the squid. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hounsgaard J, Mintz I. Calcium conductance and firing properties of spinal motoneurones in the turtle. J Physiol. 1988;398:591–603. doi: 10.1113/jphysiol.1988.sp017059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsiao CF, Del Negro CA, Trueblood PR, Chandler SH. Ionic basis for serotonin-induced bistable membrane properties in guinea pig trigeminal motoneurons. J Neurophysiol. 1998;79:2847–2856. doi: 10.1152/jn.1998.79.6.2847. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. J Neurophysiol. 1992;68:1373–1383. doi: 10.1152/jn.1992.68.4.1373. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, Prince DA. A novel T-type current underlies prolonged Ca(2+)-dependent burst firing in GABAergic neurons of rat thalamic reticular nucleus. J Neurosci. 1992;12:3804–3817. doi: 10.1523/JNEUROSCI.12-10-03804.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe DB, Ross WN, Lisman JE, Lasser-Ross N, Miyakawa H, Johnston D. A model for dendritic Ca2+ accumulation in hippocampal pyramidal neurons based on fluorescence imaging measurements. J Neurophysiol. 1994;71:1065–1077. doi: 10.1152/jn.1994.71.3.1065. [DOI] [PubMed] [Google Scholar]
- Jahnsen H, Llinas R. Electrophysiological properties of guinea-pig thalamic neurones: an in vitro study. J Physiol. 1984;349:205–226. doi: 10.1113/jphysiol.1984.sp015153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahnsen H, Llinas R. Ionic basis for the electro-responsiveness and oscillatory properties of guinea-pig thalamic neurones in vitro. J Physiol. 1984;349:227–247. doi: 10.1113/jphysiol.1984.sp015154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson BA, Leon M. Modular representations of odorants in the glomerular layer of the rat olfactory bulb and the effects of stimulus concentration. J Comp Neurol. 2000;422:496–509. doi: 10.1002/1096-9861(20000710)422:4<496::aid-cne2>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- Joksovic PM, Bayliss DA, Todorovic SM. Different kinetic properties of two T-type Ca2+ currents of rat reticular thalamic neurones and their modulation by enflurane. J Physiol. 2005;566:125–142. doi: 10.1113/jphysiol.2005.086579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnup SV, Hayar A, Shipley MT, Kurnikova MG. Spontaneous field potentials in the glomeruli of the olfactory bulb: the leading role of juxtaglomerular cells. Neuroscience. 2006;142:203–221. doi: 10.1016/j.neuroscience.2006.05.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay AR, Sugimori M, Llinas R. Kinetic and stochastic properties of a persistent sodium current in mature guinea pig cerebellar Purkinje cells. J Neurophysiol. 1998;80:1167–1179. doi: 10.1152/jn.1998.80.3.1167. [DOI] [PubMed] [Google Scholar]
- Klockner U, Lee JH, Cribbs LL, Daud A, Hescheler J, Pereverzev A, Perez-Reyes E, Schneider T. Comparison of the Ca2 + currents induced by expression of three cloned alpha1 subunits, alpha1G, alpha1H and alpha1I, of low-voltage-activated T-type Ca2 + channels. Eur J Neurosci. 1999;11:4171–4178. doi: 10.1046/j.1460-9568.1999.00849.x. [DOI] [PubMed] [Google Scholar]
- Klugbauer N, Marais E, Lacinova L, Hofmann F. A T-type calcium channel from mouse brain. Pflugers Arch. 1999;437:710–715. doi: 10.1007/s004240050836. [DOI] [PubMed] [Google Scholar]
- Kosaka K, Kosaka T. synaptic organization of the glomerulus in the main olfactory bulb: compartments of the glomerulus and heterogeneity of the periglomerular cells. Anat Sci Int. 2005;80:80–90. doi: 10.1111/j.1447-073x.2005.00092.x. [DOI] [PubMed] [Google Scholar]
- Kuzmiski JB, Barr W, Zamponi GW, MacVicar BA. Topiramate inhibits the initiation of plateau potentials in CA1 neurons by depressing R-type calcium channels. Epilepsia. 2005;46:481–489. doi: 10.1111/j.0013-9580.2005.35304.x. [DOI] [PubMed] [Google Scholar]
- Lee JH, Gomora JC, Cribbs LL, Perez-Reyes E. Nickel block of three cloned T-type calcium channels: low concentrations selectively block alpha1H. Biophys J. 1999;77:3034–3042. doi: 10.1016/S0006-3495(99)77134-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SC, Hayashida Y, Ishida AT. Availability of low-threshold Ca2+ current in retinal ganglion cells. J Neurophysiol. 2003;90:3888–3901. doi: 10.1152/jn.00477.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Bennett DJ. Persistent sodium and calcium currents cause plateau potentials in motoneurons of chronic spinal rats. J Neurophysiol. 2003;90:857–869. doi: 10.1152/jn.00236.2003. [DOI] [PubMed] [Google Scholar]
- Liu S, Shipley MT. Multiple conductances cooperatively regulate spontaneous bursting in mouse olfactory bulb external tufted cells. J Neurosci. 2008;28:1625–1639. doi: 10.1523/JNEUROSCI.3906-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Sugimori M, Lin JW, Cherksey B. Blocking and isolation of a calcium channel from neurons in mammals and cephalopods utilizing a toxin fraction (FTX) from funnel-web spider poison. Proc Natl Acad Sci U S A. 1989;86:1689–1693. doi: 10.1073/pnas.86.5.1689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig A, Flockerzi V, Hofmann F. Regional expression and cellular localization of the alpha1 and beta subunit of high voltage-activated calcium channels in rat brain. J Neurosci. 1997;17:1339–1349. doi: 10.1523/JNEUROSCI.17-04-01339.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Joerges J, Huguenard JR, Sejnowski TJ. A model of spike initiation in neocortical pyramidal neurons. Neuron. 1995;15:1427–1439. doi: 10.1016/0896-6273(95)90020-9. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Huguenard JR. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992;68:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- McKay BE, Molineux ML, Mehaffey WH, Turner RW. Kv1 K+ channels control Purkinje cell output to facilitate postsynaptic rebound discharge in deep cerebellar neurons. J Neurosci. 2005;25:1481–1492. doi: 10.1523/JNEUROSCI.3523-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McQuiston AR, Katz LC. Electrophysiology of interneurons in the glomerular layer of the rat olfactory bulb. J Neurophysiol. 2001;86:1899–1907. doi: 10.1152/jn.2001.86.4.1899. [DOI] [PubMed] [Google Scholar]
- Midtgaard J. Spatial synaptic integration in Purkinje cell dendrites. J Physiol Paris. 1995;89:23–32. doi: 10.1016/0928-4257(96)80548-1. [DOI] [PubMed] [Google Scholar]
- Migliore M, Shepherd GM. Dendritic action potentials connect distributed dendrodendritic microcircuits. J Comput Neurosci. 2008;24:207–221. doi: 10.1007/s10827-007-0051-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mombaerts P, Wang F, Dulac C, Chao SK, Nemes A, Mendelsohn M, Edmondson J, Axel R. Visualizing an olfactory sensory map. Cell. 1996;87:675–686. doi: 10.1016/s0092-8674(00)81387-2. [DOI] [PubMed] [Google Scholar]
- Monteil A, Chemin J, Bourinet E, Mennessier G, Lory P, Nargeot J. Molecular and functional properties of the human alpha(1G) subunit that forms T-type calcium channels. J Biol Chem. 2000;275:6090–6100. doi: 10.1074/jbc.275.9.6090. [DOI] [PubMed] [Google Scholar]
- Monteil A, Chemin J, Leuranguer V, Altier C, Mennessier G, Bourinet E, Lory P, Nargeot J. Specific properties of T-type calcium channels generated by the human alpha 1I subunit. J Biol Chem. 2000;275:16530–16535. doi: 10.1074/jbc.C000090200. [DOI] [PubMed] [Google Scholar]
- Mori K, Nagao H, Yoshihara Y. The olfactory bulb: coding and processing of odor molecule information. Science. 1999;286:711–715. doi: 10.1126/science.286.5440.711. [DOI] [PubMed] [Google Scholar]
- Murphy GJ, Darcy DP, Isaacson JS. Intraglomerular inhibition: signaling mechanisms of an olfactory microcircuit. Nat Neurosci. 2005;8:354–364. doi: 10.1038/nn1403. [DOI] [PubMed] [Google Scholar]
- Neher E. Correction for liquid junction potentials in patch clamp experiments. Methods Enzymol. 1992;207:123–131. doi: 10.1016/0076-6879(92)07008-c. [DOI] [PubMed] [Google Scholar]
- Nowycky MC, Fox AP, Tsien RW. Three types of neuronal calcium channel with different calcium agonist sensitivity. Nature. 1985;316:440–443. doi: 10.1038/316440a0. [DOI] [PubMed] [Google Scholar]
- Otsuka T, Murakami F, Song WJ. Excitatory postsynaptic potentials trigger a plateau potential in rat subthalamic neurons at hyperpolarized states. J Neurophysiol. 2001;86:1816–1825. doi: 10.1152/jn.2001.86.4.1816. [DOI] [PubMed] [Google Scholar]
- Partridge LD, Muller TH, Swandulla D. Calcium-activated non-selective channels in the nervous system. Brain Res Brain Res Rev. 1994;19:319–325. doi: 10.1016/0165-0173(94)90017-5. [DOI] [PubMed] [Google Scholar]
- Perez-Reyes E. Molecular physiology of low-voltage-activated t-type calcium channels. Physiol Rev. 2003;83:117–161. doi: 10.1152/physrev.00018.2002. [DOI] [PubMed] [Google Scholar]
- Pignatelli A, Kobayashi K, Okano H, Belluzzi O. Functional properties of dopaminergic neurones in the mouse olfactory bulb. J Physiol. 2005;564:501–514. doi: 10.1113/jphysiol.2005.084632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinching AJ, Powell TP. The neuron types of the glomerular layer of the olfactory bulb. J Cell Sci. 1971;9:305–345. doi: 10.1242/jcs.9.2.305. [DOI] [PubMed] [Google Scholar]
- Pinching AJ, Powell TP. The neuropil of the glomeruli of the olfactory bulb. J Cell Sci. 1971;9:347–377. doi: 10.1242/jcs.9.2.347. [DOI] [PubMed] [Google Scholar]
- Pinching AJ, Powell TP. The neuropil of the periglomerular region of the olfactory bulb. J Cell Sci. 1971;9:379–409. doi: 10.1242/jcs.9.2.379. [DOI] [PubMed] [Google Scholar]
- Plummer MR, Hess P. Reversible uncoupling of inactivation in N-type calcium channels. Nature. 1991;351:657–659. doi: 10.1038/351657a0. [DOI] [PubMed] [Google Scholar]
- Pouille F, Cavelier P, Desplantez T, Beekenkamp H, Craig PJ, Beattie RE, Volsen SG, Bossu JL. Dendro-somatic distribution of calcium-mediated electrogenesis in purkinje cells from rat cerebellar slice cultures. J Physiol. 2000;527(Pt 2):265–282. doi: 10.1111/j.1469-7793.2000.00265.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randall AD, Tsien RW. Contrasting biophysical and pharmacological properties of T-type and R-type calcium channels. Neuropharmacology. 1997;36:879–893. doi: 10.1016/s0028-3908(97)00086-5. [DOI] [PubMed] [Google Scholar]
- Ressler KJ, Sullivan SL, Buck LB. Information coding in the olfactory system: evidence for a stereotyped and highly organized epitope map in the olfactory bulb. Cell. 1994;79:1245–1255. doi: 10.1016/0092-8674(94)90015-9. [DOI] [PubMed] [Google Scholar]
- Rubin BD, Katz LC. Optical imaging of odorant representations in the mammalian olfactory bulb. Neuron. 1999;23:499–511. doi: 10.1016/s0896-6273(00)80803-x. [DOI] [PubMed] [Google Scholar]
- Rubin DB, Cleland TA. Dynamical mechanisms of odor processing in olfactory bulb mitral cells. J Neurophysiol. 2006;96:555–568. doi: 10.1152/jn.00264.2006. [DOI] [PubMed] [Google Scholar]
- Sather WA, Tanabe T, Zhang JF, Mori Y, Adams ME, Tsien RW. Distinctive biophysical and pharmacological properties of class A (BI) calcium channel alpha 1 subunits. Neuron. 1993;11:291–303. doi: 10.1016/0896-6273(93)90185-t. [DOI] [PubMed] [Google Scholar]
- Serodio P, Rudy B. Differential expression of Kv4 K+ channel subunits mediating subthreshold transient K+ (A-type) currents in rat brain. J Neurophysiol. 1998;79:1081–1091. doi: 10.1152/jn.1998.79.2.1081. [DOI] [PubMed] [Google Scholar]
- Shen GY, Chen WR, Midtgaard J, Shepherd GM, Hines ML. Computational analysis of action potential initiation in mitral cell soma and dendrites based on dual patch recordings. J Neurophysiol. 1999;82:3006–3020. doi: 10.1152/jn.1999.82.6.3006. [DOI] [PubMed] [Google Scholar]
- Shepherd GM, et al. Olfactory Bulb. In: Shepherd GM, editor. Synaptic Organization of the Brain. New York: Oxford; 2004. pp. 165–216. [Google Scholar]
- Shipley MT, Ennis M. Functional organization of olfactory system. J Neurobiol. 1996;30:123–176. doi: 10.1002/(SICI)1097-4695(199605)30:1<123::AID-NEU11>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- Soong TW, Stea A, Hodson CD, Dubel SJ, Vincent SR, Snutch TP. Structure and functional expression of a member of the low voltage-activated calcium channel family. Science. 1993;260:1133–1136. doi: 10.1126/science.8388125. [DOI] [PubMed] [Google Scholar]
- Stea A, Dubel SJ, Snutch TP. alpha 1B N-type calcium channel isoforms with distinct biophysical properties. Ann N Y Acad Sci. 1999;868:118–130. doi: 10.1111/j.1749-6632.1999.tb11282.x. [DOI] [PubMed] [Google Scholar]
- Stewart WB, Kauer JS, Shepherd GM. Functional organization of rat olfactory bulb analysed by the 2-deoxyglucose method. J Comp Neurol. 1979;185:715–734. doi: 10.1002/cne.901850407. [DOI] [PubMed] [Google Scholar]
- Talavera K, Nilius B. Biophysics and structure-function relationship of T-type Ca2+ channels. Cell Calcium. 2006;40:97–114. doi: 10.1016/j.ceca.2006.04.013. [DOI] [PubMed] [Google Scholar]
- Talavera K, Nilius B. Evidence for common structural determinants of activation and inactivation in T-type Ca2+ channels. Pflugers Arch. 2006;453:189–201. doi: 10.1007/s00424-006-0129-7. [DOI] [PubMed] [Google Scholar]
- Talbot MJ, Sayer RJ. Intracellular QX-314 inhibits calcium currents in hippocampal CA1 pyramidal neurons. J Neurophysiol. 1996;76:2120–2124. doi: 10.1152/jn.1996.76.3.2120. [DOI] [PubMed] [Google Scholar]
- Talley EM, Cribbs LL, Lee JH, Daud A, Perez-Reyes E, Bayliss DA. Differential distribution of three members of a gene family encoding low voltage-activated (T-type) calcium channels. J Neurosci. 1999;19:1895–1911. doi: 10.1523/JNEUROSCI.19-06-01895.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Buhl EH, Gloveli T, Whittington MA. Fast rhythmic bursting can be induced in layer 2/3 cortical neurons by enhancing persistent Na+ conductance or by blocking BK channels. J Neurophysiol. 2003;89:909–921. doi: 10.1152/jn.00573.2002. [DOI] [PubMed] [Google Scholar]
- Vassar R, Chao SK, Sitcheran R, Nunez JM, Vosshall LB, Axel R. Topographic organization of sensory projections to the olfactory bulb. Cell. 1994;79:981–991. doi: 10.1016/0092-8674(94)90029-9. [DOI] [PubMed] [Google Scholar]
- Wang D, Schreurs BG. Characteristics of IA currents in adult rabbit cerebellar Purkinje cells. Brain Res. 2006;1096:85–96. doi: 10.1016/j.brainres.2006.04.048. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J, Rogawski MA. A model of the T-type calcium current and the low-threshold spike in thalamic neurons. J Neurophysiol. 1991;66:839–850. doi: 10.1152/jn.1991.66.3.839. [DOI] [PubMed] [Google Scholar]
- Wang Y, Strahlendorf JC, Strahlendorf HK. A transient voltage-dependent outward potassium current in mammalian cerebellar Purkinje cells. Brain Res. 1991;567:153–158. doi: 10.1016/0006-8993(91)91449-b. [DOI] [PubMed] [Google Scholar]
- Wellis DP, Scott JW. Intracellular responses of identified rat olfactory bulb interneurons to electrical and odor stimulation. J Neurophysiol. 1990;64:932–947. doi: 10.1152/jn.1990.64.3.932. [DOI] [PubMed] [Google Scholar]
- Xu F, Liu N, Kida I, Rothman DL, Hyder F, Shepherd GM. Odor maps of aldehydes and esters revealed by functional MRI in the glomerular layer of the mouse olfactory bulb. Proc Natl Acad Sci U S A. 2003;100:11029–11034. doi: 10.1073/pnas.1832864100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida S, Matsuda Y. Studies on sensory neurons of the mouse with intracellular-recording and horseradish peroxidase-injection techniques. J Neurophysiol. 1979;42:1134–1145. doi: 10.1152/jn.1979.42.4.1134. [DOI] [PubMed] [Google Scholar]
- Zamponi GW, Bourinet E, Snutch TP. Nickel block of a family of neuronal calcium channels: subtype- and subunit-dependent action at multiple sites. J Membr Biol. 1996;151:77–90. doi: 10.1007/s002329900059. [DOI] [PubMed] [Google Scholar]
- Zhou Z, Xiong W, Masurkar AV, Chen WR, Shepherd GM. Dendritic calcium plateau potentials modulate input-output properties of juxtaglomerular cells in the rat olfactory bulb. J Neurophysiol. 2006;96:2354–2363. doi: 10.1152/jn.00003.2006. [DOI] [PubMed] [Google Scholar]