Radiative Transport Based Frequency Domain Fluorescence Tomography

Abstract

We report the development of radiative transport model based fluorescence optical tomography from frequency domain boundary measurements. The coupled radiative transport model for describing NIR fluorescence propagation in tissue is solved by a novel software based on the established Attila^™ particle transport simulation platform. The proposed scheme enables the prediction of fluorescence measurements with non-contact sources and detectors at minimal computational cost. An adjoint transport solution based fluorescence tomography algorithm is implemented on dual grids to efficiently assemble the measurement sensitivity Jacobian matrix. Finally, we demonstrate fluorescence tomography on a realistic computational mouse model to locate nM to μM fluorophore concentration distributions in simulated mouse organs.

1. Introduction

Small animal imaging can play an integral role in elucidating the biomolecular aspects of disease and health, as well as in confirming the in vivo molecular action of therapeutic drug candidates. While nuclear medicine with gamma and beta emitters will continue to offer the “gold standards” of molecular imaging owing to the exquisite sensitivities and the ability to isotopically label drugs, the convenience associated with fluorescence labels suggests a prominent role of optical imaging in drug discovery. The objective of fluorescence optical tomography is to recover interior maps of fluorescence yield and/or fluorophore lifetime distribution from boundary fluorescence measurements. A variety of fluorescence tomography systems and approaches have been proposed in the recent years, which utilize both steady state [1, 2] and time varying NIR excitation sources [3–7]. While steady state measurements of fluorescence light intensity on the tissue boundary can be used to recover only the fluorophore yield distributions, time varying measurements with pulsed or intensity modulated excitation enables the additional recovery of fluorophore lifetime distribution and maybe less susceptible to changes in endogenous tissue properties [8, 9]. Since light multiply scatters in tissue, standard backprojection based image reconstruction algorithms may not be applicable for accurate image reconstruction. Hence, model based tomography schemes which account for scattering and attenuation of light in biological tissue by solving a photon transport model are typically employed in optical tomography. [10] In the model based tomography framework, the forward problem step consists of solving a light transport model to predict boundary fluorescence measurements for a given interior fluorophore distribution, and the known excitation source placement on the tissue boundary. The predicted measurements are compared with the experimentally observed boundary measurements, and the interior image map is then iteratively updated to minimize the difference between the predicted and observed measurements. The diffusion approximation to the equation of radiative transfer is the predominant forward model used in optical tomography because of its ease of implementation, and wide availability of numerical solvers for solving diffusion equations in arbitrary domains. The limitations of diffusion approximation for predicting boundary measurements in optically thin media (i.e. when absorption is comparable or dominates scattering), small distances between illumination and collection points, and the presence of void or strongly forward scattering tissue regions, all have been explored by both theoreticians and experimentalists [11–18]. These limitations of diffusion approximation are particularly concerning for small animal imaging, primarily because of the limited volumes of the 20–25 gram mice typically used in drug discovery and molecular medicine studies. To adequately apply diffusion approximation for model based image reconstruction in small animal tomography, Culver et. al. [4] and Ntziachristos et. al. [19] suspended the imaged animals in matching scattering media such as Intralipid solution, resulting in signal loss due to additional light scattering and attenuation in the matching media.

1.1. Radiative Transport Equation for the Forward Problem

To address the shortcomings of diffusion model based optical tomography, other investigators use the more general radiative transport equation (RTE) to model photon propagation in biological tissue. Since, analytical solutions of the RTEs are not applicable to conditions of heterogeneous backgrounds and physiological geometries pertinent to biomedical imaging, most of the prior published work has focused on the development of numerical techniques. RTE models the angular distribution of light flux at every point in the domain of interest. Numerical schemes for solving RTE need to discretize the solution in both angle and space. Discrete ordinates angular discretization schemes (called S_N methods) are widely used for solving RTE. In S_N methods, RTE is allowed to hold only over a discrete set of angles belonging to a user specified quadrature set. Dorn [20] and Hielscher et al. [21] pioneered radiative transport model based optical tomography by numerically solving RTE with a S_N method coupled with an upwind step differencing based spatial discretization of light flux on a regular grid [12,22,23]. In later work, they extended the method to continuous wave fluorescence optical tomography. [24] Step differencing methods are limited to slab like geometries, and the convergence of RTE solution with upwind step differencing is strongly dependent on the grid spacing. Ren et. al. [25] proposed a discrete ordinates finite volume discretization based method for solving the frequency domain radiative transport equation. Finite volume methods can handle arbitrary geometries discretized with unstructured tetrahedral meshes, but they suffer from the same numerical inefficiencies as the step differencing schemes especially with respect to the convergence rates and the mesh resolution needed for accurate solutions. To obtain accurate solutions, the grid spacing should be on the order of mean transport length, which is approximately 1mm in biological tissue, thus increasing the computational burden of RTE model based optical tomography.

In this contribution, we demonstrate for the first time model based frequency domain fluorescence optical tomography with a proven RTE solver which couples the S_N scheme to a discontinuous Galerkin finite element method (DGFEM) based spatial differencing scheme. Our approach allows the use of unstructured tetrahedral meshes to describe arbitrary geometries like the finite volume methods do, however, unlike the finite volume methods, the accuracy of RTE solution with DGFEM differencing schemes is mesh independent, hence allowing the use of coarser meshes.

1.2. Inverse Problem Considerations for RTE

Model based optical tomography requires the computation of sensitivity function of each measurement to the unknown image voxels. The computation of sensitivity or Jacobian matrix is a major bottleneck governing the efficiency of RTE model based tomography. In related methods, where the tomography problem is posed as an optimization problem, the computation of the gradient vector of the optimization cost function is required. The optimization cost function describes the difference between the model predicted and the actual observed measurements in an L₂ norm sense and the gradient vector represents the sensitivity of the cost function to unknown image voxels. In the literature, Klose et al. [26] have proposed a reverse automated differentiation (RAD) based strategy for the cost function gradient computation in RTE based tomography. RAD was initially advocated by Christianson et al. [27] for optical tomography, and later utilized by Roy and Sevick [28] for diffuse fluorescence tomography. RAD requires the storage of all steps involved in the forward RTE computation, and to compute the sensitivity or derivative of a given function of measurements, chain rule of differentiation is used to step backward through the stored forward computation steps. While fast, RAD is limited to forward RTE computation with the straightforward source iteration techniques. In highly scattering media like biological tissue, source iterations for solving the discretized RTE system converge slowly. Diffusion Synthetic Acceleration schemes which have been proposed in the nuclear engineering community to speed up the convergence of source iterations significantly, add up a number of intermediate steps to the forward RTE computation and makes the application of storage based schemes like RAD difficult. As a result, RAD based sensitivity computations have not been shown to incorporate the powerful diffusion synthetic acceleration based source iteration. In an alternative RTE model based optical tomography application, Dorn [29, 30] has shown the use of adjoint RTE solution for computing the sensitivity of measurement functions to the unknown image map. Dorn used the discrete ordinates upwind step differencing scheme to solve the forward and adjoint radiative transport equations and solved the diffuse optical tomography problem on a two dimensional model problem. In this contribution, we demonstrate an efficient tomography scheme which utilizes adjoint RTE solution on unstructured tetrahedral meshes for computing the measurement sensitivity functions. As a diffusion synthetic acceleration scheme is implemented, the forward and adjoint RTE computations are fast compared to plain source iterations.

1.3. Non-Contact Fluorescence Optical Tomography

The development of a noncontact tomography system that does not require the immersion of an animal in a scattering solution and enables lossless propagation of photons from excitation sources to the tissue boundary, and from tissue boundary to the detectors, should improve sensitivity and light budget considerations. Non-contact imaging with both the excitation sources and detectors delivering and collecting light through nonscattering media, requires modeling of highly directional photon transport. The approach requires a high order of S_N discretization to avoid ray effect anomalies [31]. On the other hand, only a moderate S_N order is needed within the animal itself, where photon scattering is forward and approaches isotropic scattering within a few mean transport paths. In this work, we implemented a hybrid strategy, which breaks up RTE solution into uncollided and collided photon fluxes. The uncollided component from the excitation source is computed semi-analytically to produce a distributed source inside the animal body, wherein a moderate S_N order is used for computing the collided flux RTE solution. The scalar light flux at the non-contact detectors is computed semi-analytically by using a high order S_N quadrature set and integrating through the detector field of view along the rays passing through animal body. This hybrid RTE scheme using the first scattered distributed source (FSDS) and the last collided integrated detection allows highly accurate yet fast solution in non-contact imaging conditions.

The paper is organized into the following sections: in section-2 we briefly describe (i) the DGFEM based S_N computations with the implementation of (ii) FSDS and (iii) last collided integration based non-contact fluorescence imaging, followed by (iv) the derivation of adjoint RTE solution based fluorescence tomography. In section-3 we describe the generation of a synthetic MRI derived mouse phantom and outline the computational experiments to validate RTE model based fluorescence tomography. In section-4 we report the results on efficiency and accuracy gains for FSDS/last collided integration method, the sensitivity matrix computations, and the simulated image reconstructions on the computational mouse phantom. In section-5, we conclude by summarizing the innovations and describing ongoing work to implement RTE based tomography.

2. Methods

The coupled radiative transport equations describing the generation and propagation of fluorescence in frequency domain are written as:

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )+\left[{\mathrm{\sum }}_T^x(\mathbf{r})+\frac{i\omega }{c_x}\right]{\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )-Q_{\mathit{scat}}^x=S_x(\mathbf{r},\omega ,\mathbf{\Omega })$$ (1)

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_m(\mathbf{r},\mathbf{\Omega },\omega )+\left[{\mathrm{\sum }}_T^m(\mathbf{r})+\frac{i\omega }{c_m}\right]{\stackrel{\sim }{\mathrm{\Phi }}}_m(\mathbf{r},\mathbf{\Omega },\omega )-Q_{\mathit{scat}}^m=S_m(\mathbf{r},\omega ,\mathbf{\Omega })$$ (2)

$$\begin{array}{l}{Q}_{\mathit{scat}}^{x,m}={\mu }_s^{x,m}(\mathbf{r}){\int }_{4\pi }p(\mathbf{\Omega }·{\mathbf{\Omega }}^{\prime }){\stackrel{\sim }{\mathrm{\Phi }}}_{x,m}(\mathbf{r},{\mathbf{\Omega }}^{\prime },\omega )d{\mathbf{\Omega }}^{\prime }\\ S_m(\mathbf{r},\omega ,\mathbf{\Omega })=\frac{1}{4\pi }{\int }_{4\pi }\frac{\nu (\mathbf{r}){\mu }_{af}^x(\mathbf{r})}{1+i\omega \tau (\mathbf{r})}{\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )d\mathbf{\Omega }\\ {\mathrm{\sum }}_T^{x,m}(\mathbf{r})={\mu }_s^{x,m}(\mathbf{r})+{\mu }_{ai}^{x,m}(\mathbf{r})+{\mu }_{af}^{x,m}(\mathbf{r}),\eta (\mathbf{r})=\nu (\mathbf{r}){\mu }_{af}^x(\mathbf{r})\end{array}$$ (3)

Herein, Φ̃ denotes the angle dependent fluence, with subscripts x and m denoting excitation and emission wavelengths respectively; c_x,m is the velocity of light in the medium; ${\mathrm{\sum }}_T^{x,m}(\mathbf{r})$ is the spatially varying attenuation coefficient (cm⁻¹); ω is the modulation frequency; ${\mu }_s^{x,m}(\mathbf{r})$ is the scattering coefficient (cm⁻¹); ${\mu }_{ai}^{x,m}(\mathbf{r})$ is the absorption due to chromophores (cm⁻¹); ${\mu }_{af}^{x,m}(\mathbf{r})$ is the absorption due to fluorophores; ν(r) is quantum efficiency of the fluorophore and τ(r) denotes the lifetime of the fluorophore; S_x (r, ω, Ω) is the boundary excitation source; $Q_{\mathit{scat}}^{x,m}$ denotes the scattering source, wherein p(Ω · Ω′) is the phase function identifying the probability of a photon scattering from the direction Ω′ to Ω. Herein, we treat the spatially varying fluorescence yield η(r) denoted by the product $\nu (\mathbf{r}){\mu }_{af}^x(\mathbf{r})$ as the unknown parameter. A model based tomography approach for determining the fluorescence yield map in the tissue from boundary measurements requires the solution of multiple forward and adjoint transport problems corresponding to the source-detector locations. In the following, we describe the discrete ordinate based angular and discontinuous finite element based spatial differencing scheme for solving the coupled transport equation system (1)–(2). Equations (1)–(2) are coupled only in the forward direction with the solution Φ̃_x(r, Ω, ω) for Equation (1) determining the external source for Equation (2). For sake of brevity, we will present the solution steps for Equation (1) only, as an analogous procedure applies for Equation (2).

2.1. RTE solver

The transport equation solver for optical fluorescence modelling was developed on top of a pre-existing general purpose radiation transport analysis system Attila^™ (Transpire Inc. Gig Harbor, WA, USA). Attila^™ was initially developed at the Los Alamos National Laboratory [32], Los Alamos, NM, USA. In Attila^™ numerical solution of transport equation involves two steps: (i) angular discretization by discrete ordinates method, (ii) spatial discretization by discontinuous finite element based differencing and the solution of the resulting linear systems with source iteration method coupled with diffusion synthetic acceleration(DSA).

2.1.1. Discrete Ordinates Angular Discretization

As a first step before applying discrete ordinates angular discretization, the scattering phase function p(Ω · Ω′) is expanded in terms of Legendre polynomials P_l(Ω · Ω′):

$$p(\mathbf{\Omega }·{\mathbf{\Omega }}^{\prime })=\sum _{l=0}^M\frac{2l+1}{4\pi }{b}_l{P}_l(\mathbf{\Omega }·{\mathbf{\Omega }}^{\prime })$$ (4)

Here b_l are the Legendre expansion coefficients. For b_l = g^l, where g is the tissue anisotropy or mean cosine of the scattering angle (< Ω · Ω′>), Equation (4) is reduced to the well known Henyey-Greenstein phase function [33].

Next the angular fluence Φ̃_x(r, Ω, ω) is expanded in terms of spherical harmonic functions $Y_l^m(\mathbf{\Omega })$ and associated moments ${\phi }_l^m(\mathbf{r})$

$${\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )=\sum _{l=0}^{\infty }\sum _{m=-l}^{m=l}{\phi }_l^m(\mathbf{r})Y_l^m(\mathbf{\Omega }),{\phi }_l^m(\mathbf{r})={\int }_{4\pi }{Y}_l^m({\mathbf{\Omega }}^{\prime }){\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},{\mathbf{\Omega }}^{\prime },\omega )d{\mathbf{\Omega }}^{\prime }$$ (5)

Typically only a finite number of spherical harmonic moments L are used to limit computation time. After substituting equations (4) and (5) into (3), the scattering source can be written as:

$$Q_{\mathit{scat}}^x=\sum _{l=0}^L\frac{2l+1}{4\pi }\sum _{m=-l}^{m=l}{\mu }_s^x{g}^l{\phi }_l^m(\mathbf{r})Y_l^m(\mathbf{\Omega })$$ (6)

Within the discrete ordinate approximation, the transport equation is satisfied exactly only for a finite set of angles Ω_n, n = 1, 2…N, which is chosen to form a quadrature set that solves the angular integral involved in the scattering source (5). Applying the discrete ordinates approximation, we obtain a coupled system of N equations:

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_n^x(\mathbf{r})+{\mathrm{\sum }}_t^x(\mathbf{r}){\stackrel{\sim }{\mathrm{\Phi }}}_n^x(\mathbf{r})-Q_{\mathit{scat}}^x(\mathbf{r},{\mathbf{\Omega }}_n)=S_x(\mathbf{r},{\mathbf{\Omega }}_n),{\stackrel{\sim }{\mathrm{\Phi }}}_n^x(\mathbf{r})={\stackrel{\sim }{\mathrm{\Phi }}}^x(\mathbf{r},{\mathbf{\Omega }}_n)$$ (7)

The coupling term for system (7) results from quadrature based evaluation of the spherical harmonic moments ${\phi }_l^m(\mathbf{r})$:

$${\phi }_l^m(\mathbf{r})=\sum _{n=1}^N{Y}_l^m({\mathbf{\Omega }}_n){\stackrel{\sim }{\mathrm{\Phi }}}_n^x(\mathbf{r},{\mathbf{\Omega }}_n)w_n,w_n>0,\sum _n{w}_n=1$$ (8)

The accuracy of solution increases with the number of discrete ordinate directions chosen, with the corresponding increase in computation time. Weakly scattering regions require a higher angular quadrature order to reduce ray effect anomalies.

2.1.2. LLD spatial discretization and solution with DSA

The discrete ordinates system of equations (7) is solved by discretizing the domain into an unstructured tetrahedral mesh which enables the modeling of physiological geometries encountered in biomedical imaging. Attila^™ employs a lumped linear discontinuous (LLD) differencing scheme. The LLD based spatial discretization enables higher solution accuracy at coarser mesh resolutions compared to the more prevalent first order continuous spatial differencing schemes. Each tetrahedral element is treated as a discontinuous finite element (DFEM) with 4 unknowns at the corner points. Each corner point is unique to a tetrahedron, hence the angular fluence is discontinuous across element faces. DFEM based differencing equations are detailed in References [34, 35] and are not repeated here. Fully discretized discrete ordinates system with 4 × N_ordinates × N_elements is solved by the source-iteration(SI) method. SI methods converge slowly for problems with significant within energy-group scattering which is the case with optical imaging. Attila^™ implements a diffusion synthetic acceleration (DSA) scheme to improve the convergence rate of the SI method. Restricting the scattering source expansion (6) to the first term, a typical SI iteration coupled with the acceleration step for nth ordinate direction can be written as:

$${\mathbf{\Omega }}_n·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_n^{x,k+1/2}(\mathbf{r})+{\mathrm{\sum }}_t^x(\mathbf{r}){\stackrel{\sim }{\mathrm{\Phi }}}_n^{x,k+1/2}(\mathbf{r})={\mu }_s^x{\phi }_0^{0,k}+S_x(\mathbf{r},{\mathbf{\Omega }}_n)$$ (9)

$$-\nabla ·\frac{1}{3{\mathrm{\sum }}_t^x(\mathbf{r})}\nabla \delta {\phi }_0^{0,k+1}+{\mu }_a^x\delta {\phi }_0^{0,k+1}={\mu }_s^x\left({\phi }_0^{0,k+1/2}-{\phi }_0^{0,k}\right)$$ (10)

$${\phi }_0^{0,k+1}={\phi }_0^{0,k+1/2}+\delta {\phi }_0^{0,k+1}$$ (11)

where k is the iteration index. The diffusion calculation (10) is performed to estimate the error in scalar fluence $\delta {\phi }_0^{0,k+1}$. Attila^™ implements a DSA scheme developed by Wareing, Larson and Adams [36,37], wherein the diffusion equation is discretized to a continuous finite element form on the same grid as used for the DFEM discretization of discrete ordinates equations as described in Reference [36]. To conduct an SI sweep, that is to solve equations (9) to (11) over all discrete ordinate directions and for each tetrahedron, the angular flux unknowns need to be arranged into a block lower triangular form. On an unstructured mesh, this involves ordering the elements in such a way that for traversal through a given ordinate direction, the ordered element list results in a block lower triangular form. The sweeping order is established once and reused for subsequent iterations. [36]

2.2. First scattered distributed source computation

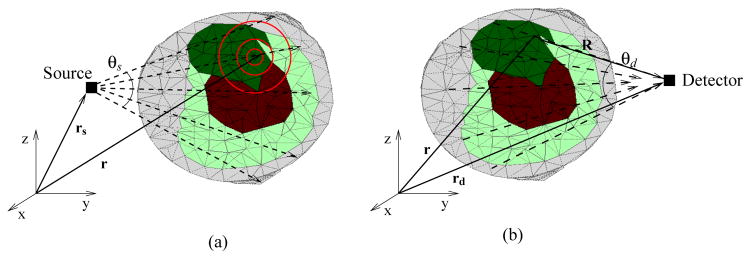
A high order angular quadrature set is needed to avoid ray effects in transport equation solutions for weakly scattering media. Most biological tissues are strongly scattering and a low order angular approximation provides sufficient accuracy. However, for imaging applications in which the animal is surrounded by non-scattering media and a non-contact illumination is used, a higher order quadrature is necessary to resolve the transport of excitation photons to the animal boundary. As depicted in Figure 1(a), these computations can be carried out efficiently by breaking the transport calculation in two stages: (i) computing an analytical ray trace of unscattered photons through out the imaged domain, followed by (ii) a low angular quadrature based numerical transport solution with the uncollided photons acting as external sources of photons. Consider a unit strength isotropic source located at r_s, then the excitation transport equation can be written as:

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )+\left[{\mathrm{\sum }}_T^x(\mathbf{r})+\frac{i\omega }{c_x}\right]{\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )-Q_{\mathit{scat}}^x=\frac{1}{4\pi }\delta (\mathbf{r}-{\mathbf{r}}_s)$$ (12)

Figure 1.

(a) FSDS source illustration: Rays are traced from the source position r_s to every position in the meshed volume r for describing the uncollided photon distribution, which sets up the volume source for scattered photons. (b) Last collided integration at the detector: once the source iterations for solving the angular flux in the domain have converged, the detected flux is calculated by integrating along the rays from the detector position r_d towards the points r in the domain which are in the FOV of the detector.

Splitting the angular excitation fluence into unscattered (superscript “unsc”) and scattered (superscript “sc”) components, we have:

$${\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )={\stackrel{\sim }{\mathrm{\Phi }}}^{x,\mathit{unsc}}(\mathbf{r},\mathbf{\Omega },\omega )+{\stackrel{\sim }{\mathrm{\Phi }}}^{x,sc}(\mathbf{r},\mathbf{\Omega },\omega )$$ (13)

The excitation transport equation (12) for the unscattered and scattered components can now be written as:

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}^{x,\mathit{unsc}}(\mathbf{r},\mathbf{\Omega },\omega )+\left[{\mathrm{\sum }}_T^x(\mathbf{r})+\frac{i\omega }{c_x}\right]{\stackrel{\sim }{\mathrm{\Phi }}}^{x,\mathit{unsc}}(\mathbf{r},\mathbf{\Omega },\omega )=\frac{1}{4\pi }\delta (\mathbf{r}-{\mathbf{r}}_s)$$ (14)

$$\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}^{x,sc}(\mathbf{r},\mathbf{\Omega },\omega )+\left[{\mathrm{\sum }}_T^x(\mathbf{r})+\frac{i\omega }{c_x}\right]{\stackrel{\sim }{\mathrm{\Phi }}}^{x,sc}(\mathbf{r},\mathbf{\Omega },\omega )-Q_{\mathit{scat}}^{x.sc}=Q_{\mathit{scat}}^{x,\mathit{unsc}}$$ (15)

In (15), the term $Q_{\mathit{scat}}^{x,\mathit{unsc}}$ is the additional scattering source due to the uncollided photon distribution and is evaluated by substituting the solution Φ̃^x,unsc(r, Ω, ω) of (14) into (6). The analytical solution of (14) is given by:

$${\stackrel{\sim }{\mathrm{\Phi }}}^{x,\mathit{unsc}}(\mathbf{r},\mathbf{\Omega },\omega )=\delta \left(\mathbf{\Omega }-\frac{\mathbf{r}-{\mathbf{r}}_s}{\mid \mathbf{r}-{\mathbf{r}}_s\mid }\right)\frac{1}{4\pi }\frac{e^{-d(\mathbf{r},{\mathbf{r}}_s)}}{{\mid \mathbf{r}-{\mathbf{r}}_s\mid }^2}$$ (16)

Here, d(r, r_s) is the optical path between r and r_s. [31] Optical path d is the line integral of the total cross section along the line of photon travel. For the frequency domain excitation transport equation, it can be expressed as:

$$d(\mathbf{r},{\mathbf{r}}_s)={\int }_0^{\mid \mathbf{r}-{\mathbf{r}}_s\mid }\left[{\mathrm{\sum }}_T^x\left(\mathbf{r}-R^{\prime }\frac{\mathbf{r}-{\mathbf{r}}_s}{\mid \mathbf{r}-{\mathbf{r}}_s\mid }\right)+\frac{i\omega }{c_x}\right]d{R}^{\prime }$$ (17)

The spherical harmonic moments of the unscattered photon flux can be computed by substituting (16) into (5):

$${\phi }_l^{m,\mathit{unsc}}=Y_l^m\left(\frac{\mathbf{r}-{\mathbf{r}}_s}{\mid \mathbf{r}-{\mathbf{r}}_s\mid }\right)\frac{1}{4\pi }\frac{e^{-d(\mathbf{r},{\mathbf{r}}_s)}}{{\mid \mathbf{r}-{\mathbf{r}}_s\mid }^2}$$ (18)

Equations (16) and (17) define the volume distributed source Q_scat for the transport equation corresponding to the scatter component (15).

2.3. Last Collided integration method

For imaging small animals surrounded by non-scattering media, wherein the light collectors are located away from the animal body, a high angular quadrature order is needed to obtain accurate numerical RTE solution at the collector locations. To avoid the ensuing computational burden, Attila^™ implements a last collided integration approach, that can be used to rapidly obtain accurate scalar photon flux at distant collectors without inflating the discrete ordinates quadrature set. With the last collided integration approach, the scattered flux is computed precisely only in the animal volume and not in the clear region surrounding the animal. The concept of last collided integration at the detectors is illustrated in Figure-1b for a hypothetical photon collector positioned at r_d. A moderate angular discretization, which is enough for approximating the nearly diffusive NIR photon propagation in tissue is used in the entire domain surrounding the animal and collector locations. The scalar flux at the collector is not computed directly from the numerical transport solution, but is obtained via postprocessing on the numerical transport solution by the application of integral transport theory. The last collided approach implemented in Attila^™ follows from the integral form of the transport equation described in reference [31]. We will present the outline of the method for the excitation transport equation. Equation (1) can be transformed into the following integral equation for obtaining the angular flux at the collector location r_d:

$$\begin{array}{l}{\stackrel{\sim }{\mathrm{\Phi }}}_x({\mathbf{r}}_d,\mathbf{\Omega },\omega )={\int }_0^{R}d{R}^{\prime }Q({\mathbf{r}}_d-R^{\prime }\mathbf{\Omega })e^{(-d({\mathbf{r}}_d,{\mathbf{r}}_d-R^{\prime }\mathbf{\Omega }))}+{\stackrel{\sim }{\mathrm{\Phi }}}_x({\mathbf{r}}_d-R\mathbf{\Omega },\mathbf{\Omega },\omega )e^{-d({\mathbf{r}}_d,{\mathbf{r}}_d-R^{\prime }\mathbf{\Omega })}\\ Q({\mathbf{r}}_d-R^{\prime }\mathbf{\Omega })=Q_{\mathit{scat}}^x({\mathbf{r}}_d-R^{\prime }\mathbf{\Omega })+S_x({\mathbf{r}}_d-R^{\prime }\mathbf{\Omega }),\mathbf{\Omega })\end{array}$$ (19)

Where, R is the distance along the direction Ω looking backward towards the imaged volume from the detector position r_d; d is the optical path between r_d and r_d − R′Ω as defined earlier in (17). If R is extended to the boundary of the computation domain, then the second term represents the contribution due to boundary conditions. Upon extending R to infinity and under vacuum boundary conditions, the scalar or angle integrated flux at the collector position reduces to:

$${\mathrm{\Phi }}_x({\mathbf{r}}_d,\omega )=\int d\mathbf{\Omega }{\int }_0^{\infty }d{R}^{\prime }Q({\mathbf{r}}_d-R^{\prime }\mathbf{\Omega })e^{(-d({\mathbf{r}}_d,{\mathbf{r}}_d-R^{\prime }\mathbf{\Omega }))}$$ (20)

The collected flux can be computed after the numerical solution of the transport equation, by utilizing (20) directly. After the S_N iterations have converged, the scattering source Q(r) is known everywhere in the domain. The infinite integral in (20) is computed only in the problem domain as Q(r) vanishes outside of it. Most importantly as the scattering cross-section μ_s is zero in the clear region surrounding the imaged animal, it doesn’t contribute to detected scalar flux. Hence, the inaccuracies in the numerical transport solution in the clear region due to inadequate spatial and/or angular discretization do not propagate to the computation of detected scalar photon flux. Even high angular quadrature orders such as S₅₀ or S₁₀₀ can be used to solve (20) as these computations are semi-analytic and fast compared to the transport S_N iterations. As a special case, detector specific quadrature sets as needed for fiber optic based NIR measurements can also be generated. [18] In the results section, we demonstrate the accuracy and efficiency gains of the last collided integration approach for the forward RTE model.

2.4. Solution of the RTE based inverse imaging problem

For brevity, we write the coupled frequency domain excitation and emission transport equations as a block linear system:

$$\left[\begin{array}{cc}{H}_x& 0\\ -B_{xm}& H_m\end{array}\right]\left[\begin{array}{c}{\stackrel{\sim }{\mathrm{\Phi }}}_x\\ {\stackrel{\sim }{\mathrm{\Phi }}}_m\end{array}\right]=\left[\begin{array}{c}{S}_{ex}\\ 0\end{array}\right]$$ (21)

$$H_{x,m}=\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_{x,m}+\left[{\mathrm{\sum }}_T^{x,m}(\mathbf{r})+\frac{i\omega }{c_{x,m}}\right]-Q_{\mathit{scat}}^{x,m}$$ (22)

$$B_{xm}{\stackrel{\sim }{\mathrm{\Phi }}}_x=\frac{1}{4\pi }{\int }_{4\pi }\frac{\nu (\mathbf{r}){\mu }_{af}^x(\mathbf{r})}{1+i\omega \tau (\mathbf{r})}{\stackrel{\sim }{\mathrm{\Phi }}}_x(\mathbf{r},\mathbf{\Omega },\omega )d\mathbf{\Omega }$$ (23)

The general fluorescence tomography problem involves the determination of discretized fluorescence absorption coefficient ${\mu }_{\mathbf{af}}^{\mathbf{x}}=\{{\mu }_{{af}_i}^x\}$, i = 1, 2…N from a set of discrete boundary measurements of scalar emission fluence z = {z_j}, j = 1, 2…M, where z_j is defined as: $z_j={\int }_{{\theta }_j}{\stackrel{\sim }{\mathrm{\Phi }}}_m^j$. θ_j is the angular aperture of the j^th photon collector. The measurements z depend nonlinearly on the unknown fluorescence absorption ${\mu }_{\mathbf{af}}^{\mathbf{x}}$. The tomography problem can be linearized if a first order Taylor series expansion about a initial fluorescence map ${\mu }_{\mathbf{a}{\mathbf{f}}_{\mathbf{0}}}^{\mathbf{x}}$ is used to describe the boundary fluorescence measurements:

$$\mathbf{z}-{\mathbf{z}}_0=\mathbf{J}·\left({\mu }_{\mathbf{af}}^{\mathbf{x}}-{\mu }_{\mathbf{a}{\mathbf{f}}_{\mathbf{0}}}^{\mathbf{x}}\right)\mathbf{J}={\left[\frac{\partial \mathbf{z}}{\partial {\mu }_{\mathbf{af}}^{\mathbf{x}}}\right]}_{{\mu }_{\mathbf{af}}^{\mathbf{x}}={\mu }_{\mathbf{a}{\mathbf{f}}_{\mathbf{0}}}^{\mathbf{x}}}$$ (24)

Where J is the jacobian sensitivity matrix with dimensions of M×N, where M is the number of measurements and N is the number of unknowns. Calculation of the Jacobian matrix dominates the computational cost of typical optical tomography algorithms. A member of the matrix J corresponding to the sensitivity of j^th measurement with respect to the k^th unknown image voxel can be expressed as:

$${\mathbf{J}}_{jk}=\frac{\partial z_j}{\partial {\mu }_{{af}_k}^x}=\frac{{\int }_{{\theta }_j}\partial {\stackrel{\sim }{\mathrm{\Phi }}}_m^j}{\partial {\mu }_{{af}_k}^x}=<D_j,\frac{\partial {\stackrel{\sim }{\mathrm{\Phi }}}_m}{\partial {\mu }_{{af}_k}^x}>$$ (25)

Where D_j(r, Ω) = δ(r − r_dj) for Ω in θ_j, 0 otherwise and

$$<D_j,\frac{\partial {\stackrel{\sim }{\mathrm{\Phi }}}_m}{\partial {\mu }_{{af}_k}^x}>={\int }_{4\pi }{D}_j\frac{\partial {\stackrel{\sim }{\mathrm{\Phi }}}_m}{\partial {\mu }_{{af}_k}^x}d\mathbf{\Omega }$$

Here, r_dj is the spatial position of the j^th collector and D_j(r, Ω) is a modified Dirac delta function which characterizes its spatial and angular response. J can be efficiently computed by employing the adjoint transport equation. We define the adjoint system for j^th detector with response D_j as:

$$\left[\begin{array}{cc}{H}_x^{\ast }& -B_{xm}^{\ast }\\ 0& H_m^{\ast }\end{array}\right]\left[\begin{array}{c}{\stackrel{\sim }{\mathrm{\Psi }}}_x^j\\ {\stackrel{\sim }{\mathrm{\Psi }}}_m^j\end{array}\right]=\left[\begin{array}{c}0\\ D_j\end{array}\right]$$ (26)

Here, $H_{x,m}^{\ast }$ are the adjoint transport operators. For vacuum boundary conditions, H^* is defined as:

$$H_{x,m}^{\ast }=-\mathbf{\Omega }·\nabla {\stackrel{\sim }{\mathrm{\Phi }}}_{x,m}+\left[{\mathrm{\sum }}_T^{x,m}(\mathbf{r})-\frac{i\omega }{c_{x,m}}\right]-Q_{\mathit{scat}}^{x,m}$$ (27)

The adjoint operator $B_{xm}^{\ast }$ is obtained by taking the complex transpose of B_xm

$$B_{xm}^{\ast }{\stackrel{\sim }{\mathrm{\Psi }}}_m=\frac{1}{4\pi }{\int }_{4\pi }\frac{\nu (\mathbf{r}){\mu }_{af}^x(\mathbf{r})}{1-i\omega \tau (\mathbf{r})}{\stackrel{\sim }{\mathrm{\Psi }}}_{x}d\mathbf{\Omega }$$ (28)

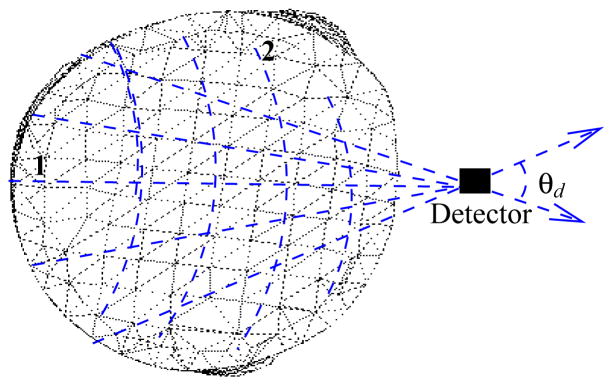
It can be observed that the adjoint transport operator for photon propagation in frequency domain is reversed in direction and time(phase) with respect to the forward operators. Figure 2 illustrates the adjoint source positioned at the collector location.

Figure 2.

Detectors are modelled as adjoint sources with photon directions directed outwards and the propagation is backwards in time(phase). Computation is carried out by the two step FSDS method, wherein, in step-1 the unscattered flux is calculated through analytical ray tracing, and in step-2, the unscattered flux distribution acts as the volumetric source for S_N transport iterations for determining the scattered adjoint flux.

The particle flow from the adjoint source is directed outwards from the animal body, as against the inwards particle flow used for forward RTE simulations. The jk^th element of the Jacobian matrix (25) can then be expressed in terms of the adjoint solutions Ψ̃_x,m by exploiting the definition of the adjoint operator:

$$J_{jk}=<D_j,\frac{\partial {\stackrel{\sim }{\mathrm{\Phi }}}_m}{\partial {\mu }_{{af}_k}^x}>=<{\stackrel{\sim }{\mathrm{\Psi }}}_x^j,\frac{\partial H_x}{\partial {\mu }_{{af}_k}^x}{\stackrel{\sim }{\mathrm{\Phi }}}_x>+<{\stackrel{\sim }{\mathrm{\Psi }}}_m^j,\frac{\partial B_{xm}}{\partial {\mu }_{{af}_k}^x}{\stackrel{\sim }{\mathrm{\Phi }}}_x>$$ (29)

The first term on the R.H.S of (29) can be dropped upon invoking the Born approximation, wherein the excitation field is assumed not to be perturbed by the presence of fluorescent target. The adjoint solution ${\stackrel{\sim }{\mathrm{\Psi }}}_m^j$ does not depend on the particular image voxel index k, hence in a linearized tomography algorithm, the adjoint solutions ${\stackrel{\sim }{\mathrm{\Psi }}}_m^j$ can be precomputed and stored for all M collector locations. The Jacobian matrix can then be assembled on demand provided the forward solutions Φ̃_x corresponding to all excitation sources are available. The computation of the terms $\partial B_{xm}/\partial {\mu }_{{af}_k}^x$ depends upon the discretization scheme employed, but it is straightforward as the operator B_xm depends linearly on ${\mu }_{af}^x$. In fact, J doesn’t even need to be explicitly constructed. Iterative solution methods such as algebraic reconstruction technique or conjugate gradient least squares, only require matrix-vector products involving J, and they can be implemented directly with (29) once the respective forward and adjoint RTE solutions are available. As J is illposed, stable Born linearization based image reconstruction in a single iteration requires J to be overdetermined (M > N). Frequency domain measurements produce two measurements per source-collector pair in the form of amplitude and phase, hence allowing the use of a lesser number of source-detectors compared to steady state measurements. In the results section, we present RTE model based fluorescence reconstructions from synthetic data based upon the solution of (24).

3. Synthetic Mouse Phantom and Computational Experiments

We tested the developed RTE solution scheme and conducted simulated tomography experiments on the MOBY mouse dataset made available by the Johns Hopkins University. [38] MOBY phantom is a collection of NURBS (Non-uniform Rational B-Splines) curves and surfaces defining the various mouse organs and it has been employed by other researchers. [39] We converted the NURBS based mouse organ descriptions into a standard CAD (computer aided design) format STEP, and the geometries were simplified in a solid modelling software SolidWorks^™. The major organs in the mouse torso were modelled along with the skull, ribs, and the spinal structure. The modelled organs along with the optical properties obtained from literature [40, 41] in the wavelength range of 600 – 850nm are listed in Table-1 and for the purposes of this feasibility study, assumed to be wavelength independent. As shown in Figure 3, a highly refined tetrahedral mesh 127466 elements was generated with the mesh generator incorporated within the Attila^™ platform, and used to generated simulated measurement datasets. The mouse was simulated as being positioned in a 2.9 cm diameter cylinder surrounded by water, for the purposes of investigating delivery and collection of light through a non-scattering media, while avoiding the complications arising out of partial refraction and reflection effects at the animal boundary.

Table 1.

Optical properties used for synthetic mouse phantom organs [40,41]

Organ/Tissue	Absorption μa(cm−1)	Scattering μs(cm−1)	Ratio $\frac{{\mu }_s(1-g)}{{\mu }_a}$
Lungs	8.4	35.9	0.2137
Heart	0.35	167	8.114
Stomach	1.2	200	16.67
Gut	1.2	200	16.67
Kidneys	0.01	73.3	1100
Spleen	2.8	13	1.024
Bladder	1.25	50.8	2.03
Liver	6.5	143.7	1.11
Body (muscle)	1	40	1.2
Water	0.011	0	0

Figure 3.

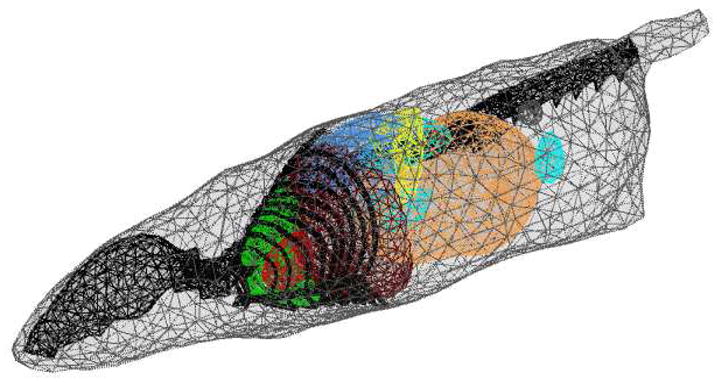
Finite element model of the synthetic mouse derived from the MOBY phantom. Major organs listed in Table-1 were modeled. The mesh consisted of 127466 tetrahedral elements.

Two sets of computational experiments were performed to illustrate RTE model based fluorescence tomography. In the first synthetic experiment, we validated the computational efficiency and accuracy gains obtained by implementing the FSDS/last collided integration approach for solving the RTE based forward problem. Measurements were generated by simulating uptake of 1μM Indocyanine Green dye in the kidneys of the MOBY phantom. As shown in Figure 4 a source placed at the circumferential ring near the kidney locations was switched on, with measurements computed at all the collection sites on the same ring. The sensitivity of the solution to angular discretization was evaluated by first using a high order S₁₂ angular discretization, and P₆ level Legendre polynomial expansion for the scattering source in the entire domain which includes both the animal and the surrounding media with sources and detectors. With the triangular tchebychev quadrature set employed, S₁₂ discretization results in N_angles = 12 * 12 + 12 = 156 discrete angles in the unit sphere. P₆ expansion was used to account for the highly forward directed excitation source. Other measurements were generated with a lower order S₄ angular quadrature (4 * 4 + 4 = 20 discrete angles) and P₃ level Legendre expansion for the scattering source, while using different last collided integration schemes for obtaining the simulated measurements.

Figure 4.

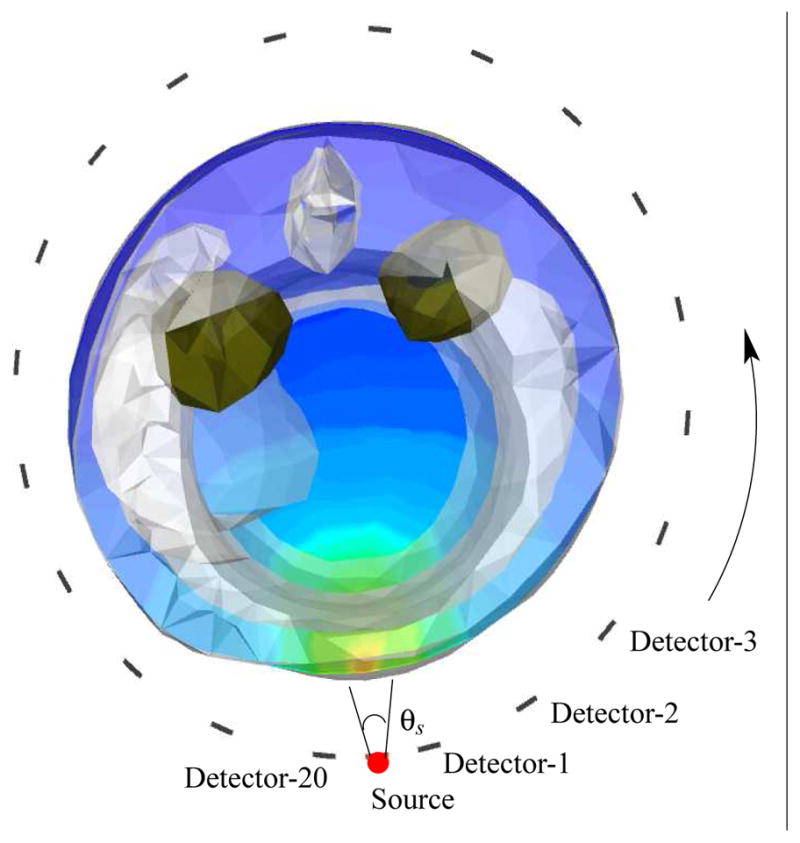
Simulation setup for validating the last collided detector flux integration approach. The kidneys shown in green shade were simulated to have the uptake of 1 μM ICG. θ_s: the source aperture was 20 degrees. Detectors were placed 18 degrees apart.

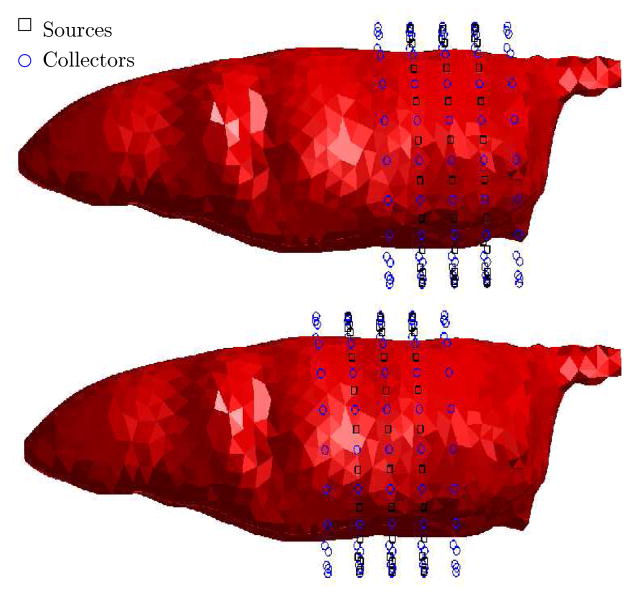
The second set of computational experiments were conducted to demonstrate RTE model based tomographic determination of single and multiple fluorescent targets in small animal volumes. Synthetic measurements corresponding the uptake of 10nM ICG dye in the bladder, and the uptake of 1μM ICG in both the kidneys were generated. The sources and collectors were modelled as points with a 20 degree numerical aperture, creating a cone shape equivalent to the effective collimation in the fiber optic cable. Rings of sources and collectors were simulated to be at axial intervals of 0.5 cm, with 20 circumferentially spaced sources and collectors at each axial location as shown in Figure 5. 2% white noise was added to the simulated measurements. Five source-detector rings placed 0.5cm apart around the mouse torso between kidneys and bladder were used. While all the 100 detectors on the five rings were employed, only the data from 60 sources on the middle 3 rings were used for reconstruction. Frequency domain measurement data was simulated on the refined mesh illustrated in figure 3 with the endogenous optical properties of different organs listed in Table-1. A linearized Born type tomography algorithm described in section 2.4 was used to obtain the 3-D images of reconstructed fluorescence absorption on a different mesh than that used for generating synthetic data or for computing forward/adjoint solutions.

Figure 5.

Source-Collector locations for fluorescence tomography simulations: top figure depicts the source and collector rings for generating synthetic data corresponding to 10nM uptake of ICG in mouse bladder, bottom figure depicts the source/collector rings for generating synthetic data corresponding to 1μM uptake of ICG in both the kidneys. Middle three rings contain both the sources and collectors. Each ring was simulated to contain 20 sources and 20 collectors.

Computations were carried out on a 16 node Beowulf cluster, with dual opteron 2.2 GhZ processors and 8 GB of system memory per node. Typically one processor was allocated to handle one forward/adjoint computation.

4. Results

4.1. Effect of FSDS and last collided integration schemes

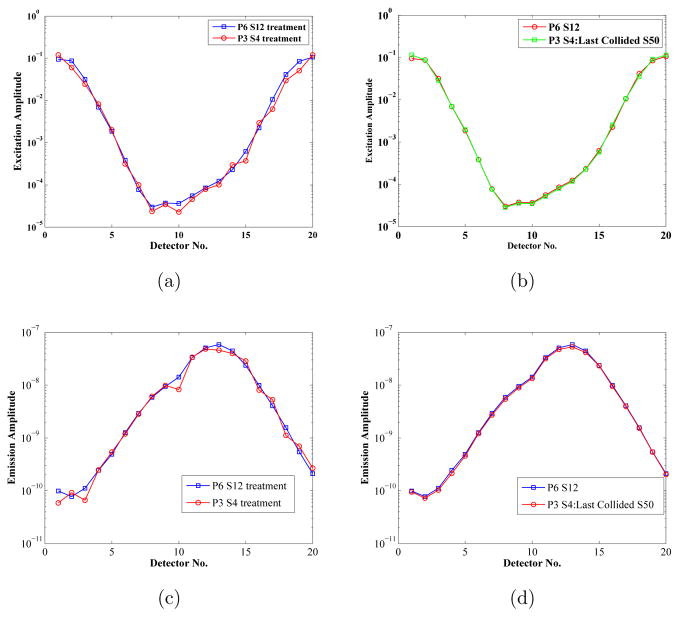
Figures 6(a) and 6(c) depict the excitation and fluorescence emission amplitudes at the detectors positions shown in Figure 4 for the high order P₆-S₁₂ approximation based numerical solution and the low order P₃-S₄ simulation. As expected, the P₃-S₄ solution oscillated around the high order solution, because S₄ quadrature order was not enough to simulate the highly directional photon transport in water surrounding the mouse phantom. Figures 6b and 6d depict the two solutions again, but with the detector flux from P₃-S₄ solution calculated by an S₅₀ order last collided integration on the primary numerical solution according to (20). An S₅₀ quadrature order fills in the unit sphere with 2550 angles, which is sufficient to integrate the scatter solution in animal body, while the last collided approach rejects the ray effect analogies in the non-scattering media surrounding the phantom. In Table-2, the computational times and the mean squared error with the P₆-S₁₂ solution is reported for the P₃-S₄ solution and the last collided integrations with orders S₁₀, S₅₀, and S₁₀₀. The P₆-S₁₂ solution at over 12000 seconds is the most expensive, while the P₃-S₄ solution at about 700 seconds is fast but most inaccurate. The computational times required by increasing orders of last collided integrations differ only marginally from the cost of stand alone P₃-S₄ solution. The accuracy increases with quadrature level up until S₅₀.

Figure 6.

Demonstration of the accuracy improvements with last collided post processing

Table 2.

Computation speed and accuracy gains obtained with the last collided method: for the P_mS_n entries in the first column, m stands for the spherical harmonic expansion order of the scattering source, and n indicates the angular discretization order. LC_k indicates that last collided integration with angular discretization of order k was performed to get the scalar flux at the collector locations. Column 3 and 4 list the mean squared error (MSE) in the scalar flux solutions with respect to the P₆S₁₂ solution.

Angular Discretization	Compute Time(s)	MSE:Excitation	MSE:Emission
P3S4	710.22	0.2651	0.2257
P3S4 : LC10	710.24	0.1498	0.0839
P3S4 : LC50	710.26	0.0809	0.0612
P3S4 : LC100	710.25	0.0788	0.0613
P6S12	12490.02	0	0

4.2. Fluorescence reconstructions

To reconstruct the fluorescence absorption images from the synthetic measurement datasets corresponding to ICG uptake in kidneys and bladder as described in the previous section, we first need to generate the Jacobian sensitivity matrix of measurements with respect to the unknown image voxels. The forward and adjoint computations needed to compute the Jacobian matrix (29) were carried out on a separate mesh from the synthetic data generation mesh depicted in Figure 3. This was done to prevent the possibility of any inadvertent inverse crime, as well as to mimic the real small animal imaging, wherein the endogenous optical property distribution of the small animals will not be precisely known. The forward/adjoint solution mesh used for image reconstruction studies is depicted in Figure 7. The only prior knowledge used in the construction of the tetrahedral mesh was the knowledge of the phantom boundary which can be obtained by a variety of methods including Xray CT, micro-MRI, or PET transmission scans, or by the newly reported optical projection techniques [42]. For carrying out the forward/adjoint calculations, we assumed the endogenous absorption and scattering in the entire phantom to be uniform and equal to the optical properties of the muscle tissue listed in Table-1. Since the muscle comprises the largest component of the synthetic mouse phantom, the assumption of a single bulk optical property of an intact animal is most practical for applications. The unknown fluorescence absorption map was discretized on a separate voxelized grid with 2mm cells to limit the number of unknowns as depicted in Figure 7. Figure 8 illustrates the measurement sensitivity plot for a typical source-detector pair. These profiles are similar to but less broad than that obtained in diffusion model based tomography schemes. The image reconstructions were carried out by solving the Equation (24) with the least squares algorithm LSQR implemented in MATLAB (Mathworks, Inc., Natwick, MA). No explicit regularization was used, however the LSQR iterations were truncated at 300.

Figure 7.

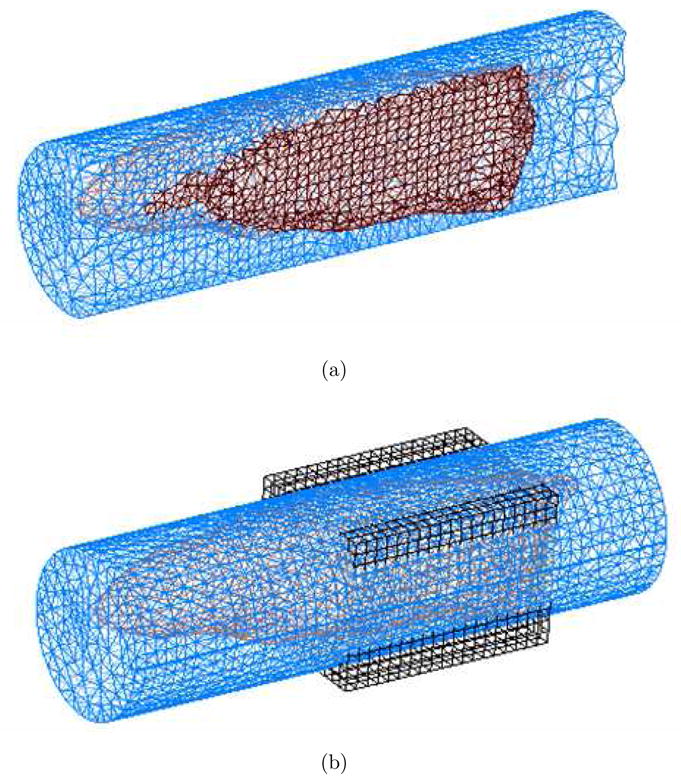
Meshes used for parameter description and forward/adjoint simulations involved in RTE model based tomography: (a) a uniform tetrahedral mesh was used to solve for forward and adjoint RTE solutions needed to generate the Jacobian sensitivity matrix. (b) the unknown parameter was discretized on a separate piecewise discontinuous voxelized grid.

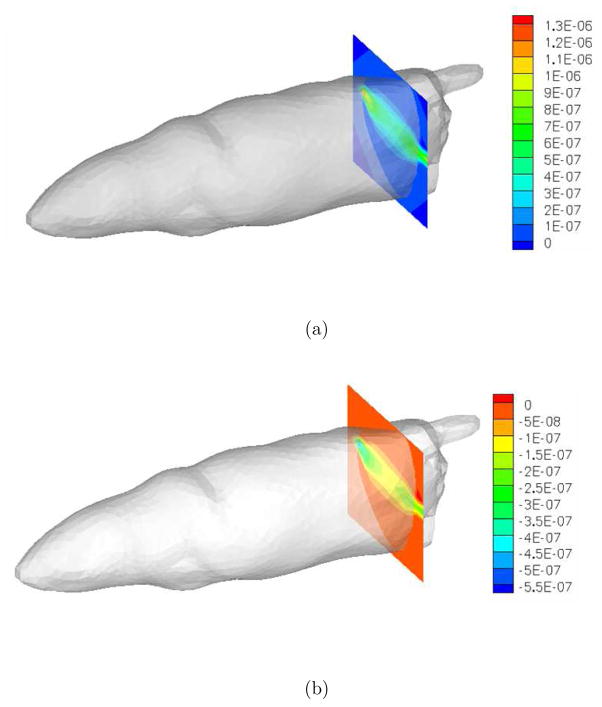
Figure 8.

Illustration of RTE based Jacobian sensitivity matrix for fluorescence tomography for a typical source-detector pair: (a) real component, (b) imaginary component

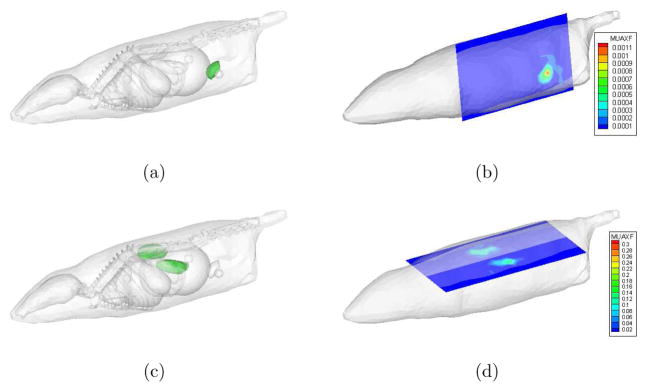
The true and reconstructed fluorescence images are depicted in Figure 9. The true magnitudes of fluorescence absorption in 0.598cm⁻¹ in kidneys, and 0.00598cm⁻¹ in the bladder. The recovered magnitudes of approximately 0.15cm⁻¹ in the kidneys and 0.0005cm⁻¹ in the bladder, demonstrate the sensitivity of RTE model based tomography to relative variations in fluorophore concentration. Absolute determination of fluorescence absorption is not feasible with only one linearized tomography iteration for this highly illposed problem. The computational time for the solution of the linear system defined in Equation (24) was under 2 minutes. As only one linearization about the initial fluorescence map of ${\mu }_{af}^x(\mathbf{r})=0$ was carried out, the forward and adjoint solutions corresponding the 60 sources and 100 detectors were precomputed on the Beowulf cluster. Each forward/adjoint computation took approximately 10 minutes and calculations for different sources and detectors were carried out in parallel to the extent possible.

Figure 9.

Inverse image reconstruction results: (a,c) The true fluorescence probe locations were in the kidneys and the bladder, (b,d) the reconstructed images for the fluorophore absorption in the bladder and kidneys. Slices drawn through the voxelized parameter grid are shown. There were no significant artifacts(see attached movies.)

5. Conclusions

In this contribution, we have demonstrated a RTE model based fluorescence tomography algorithm for frequency domain optical tomography in small animal geometries. To the best of our knowledge, this is the first demonstration of a frequency domain fluorescence tomography algorithm utilizing the coupled RTE equations. Further, we have shown the application of a robust RTE solver based on the established Attila^™ nuclear engineering particle transport simulation platform. The high computational expense of RTE model based tomography has been minimized by a combination of advances which include: (i) the discontinuous finite element differencing on unstructured tetrahedral meshes for mesh independent convergence of solution on arbitrary geometries, (ii) application of diffusion synthetic acceleration for rapidly solving source iterations. (iii) first scattered distributed source and last collided integration at detectors for rapidly and accurately predicting RTE solutions, when sources and detectors are separated from the animal volume with clear media, and (iv) utilization of adjoint RTE solution to efficiently assemble the measurement sensitivity Jacobian matrix. The dual mesh based image reconstruction scheme reported in this manuscript will be extended to employ adaptive meshes [43,44] in our future work, resulting in image resolution and further speedup as demonstrated in our prior work on large volume diffuse fluorescence optical tomography. The image reconstructions have been carried out with the prior knowledge limited to the animal geometry, and this contribution marks our first step towards hybrid structural-molecular small animal tomography systems, which utilize animal structure information from established modalities like Xray CT, and seek to determine the distribution of molecularly targeting fluorescence probes without a priori information of interior endogenous optical properties. The robust and rapid deterministic transport solution schemes on animal geometries will also impact bioluminescence tomography applications. [45,46]