Models of cardiac electromechanics based on individual hearts imaging data

Abstract

Current multi-scale computational models of ventricular electromechanics describe the full process of cardiac contraction on both the micro- and macro- scales including: the depolarization of cardiac cells, the release of calcium from intracellular stores, tension generation by cardiac myofilaments, and mechanical contraction of the whole heart. Such models are used to reveal basic mechanisms of cardiac contraction as well as the mechanisms of cardiac dysfunction in disease conditions. In this paper, we present a methodology to construct finite element electromechanical models of ventricular contraction with anatomically accurate ventricular geometry based on magnetic resonance and diffusion tensor magnetic resonance imaging of the heart. The electromechanical model couples detailed representations of the cardiac cell membrane, cardiac myofilament dynamics, electrical impulse propagation, ventricular contraction, and circulation to simulate the electrical and mechanical activity of the ventricles. The utility of the model is demonstrated in an example simulation of contraction during sinus rhythm using a model of the normal canine ventricles.

1 Introduction

Cardiac disease remains the leading cause of death in the developed world. Despite the large body of research devoted to understanding cardiac electromechanical function, significant gaps in knowledge are still present due to the complexity of cardiac structure, electrophysiology, and mechanics. A main challenge in studying cardiac electrom-echanics is experimental difficulty in direct observation and manipulation of the processes that underlie cardiac electrical and mechanical activity. Computational modeling circumvents these experimental limitations by providing the framework to test hypotheses and to gain insights into the relationship between heart structure and electromechanical function.

During the last decade, models of cardiac electromechanics have been developed and used to improve knowledge regarding cardiac pump function (for review see Kerckhoffs et al. (2006)). The initial modeling attempts represented the ventricles as idealized geometries of cylindrical and elliptical shapes (Janz and Grimm 1972; Arts et al. 1979; Feit 1979; Bovendeerd et al. 1992). Studies using such models have provided insights into the effects of ventricular chamber volume, wall thickness, and fiber geometry on ventricular mechanics. Within the past decade, more sophisticated finite element models that incorporate averaged anatomically realistic geometries obtained from histological sections have been developed (Guccione et al. 1995; Vetter and McCulloch 2000; Usyk et al. 2002; Stevens et al. 2003). These models have improved predictive capabilities over the idealized cylindrical or elliptical models since the simulated strains and stresses in the ventricular walls are better aligned with experimental measurements (Guccione et al. 1995).

While these anatomically realistic models represent an important achievement in cardiac modeling and particularly in electromechanics, they are associated with several shortcomings. First, such models are difficult and time consuming to construct. Indeed, only three anatomical models suitable for modeling cardiac mechanics have been developed thus far, namely those of the rabbit (Vetter and McCulloch 1998), the canine (Nielsen et al. 1991), and the pig ventricles (Stevens et al. 2003). Obtaining the geometries for these models involves the labor-intensive procedure of histological sectioning of multiple heart preparations that takes months to complete. Because these models were developed from averaged measurements, they cannot represent, in simulation studies, the inherent variability in ventricular and fiber geometry among individual hearts. Finally, this class of models has additional limitations in the finite element mesh (such as small opening at the left ventricular apex (Guccione et al. 1995; Usyk et al. 2002), as well as discontinuities in fiber and laminar sheet orientations in certain regions arising from their representation as angles interpolated on the finite elements in the mesh (Nielsen et al. 1991).

Recent advancements in magnetic resonance (MR) and diffusion tensor (DT) MR imaging of the heart have made possible the development of a new class of anatomically accurate heart models. MR and DTMR scans provide information regarding the individual ventricular geometry as well as fiber and laminar sheet structure of each heart (Helm et al. 2005a). Unlike histological sectioning, MR and DTMR imaging of the heart takes hours to complete. We have recently developed a methodology to create electrical models of the heart from MR and DTMR imaging data (Vadakkumpadan et al. 2009b); these models have been used successfully to study problems in cardiac arrhythmogenesis and defibrillation (Vadakkumpadan et al. 2009b).

The goal of this paper is to present a novel methodology for the generation of anatomically accurate electromechanical models of the heart directly from ex-vivo high resolution MR and DTMR cardiac images. The presented methodology overcomes the limitations described above by enabling the rapid reconstruction of the geometry and fiber architecture of individual hearts, and by employing a novel finite element mechanical mesh topology and a tensor representation of fiber and laminar sheet structure. We present here the full pipeline of electromechanical model development that includes MR and DTMR image segmentation, creation of mechanical and electrical finite element meshes, modeling electrical and mechanical activity in the ventricles, and coupling of the mechanical model with a model of the circulatory system. This pipeline is illustrated with the development of models of a normal canine heart, a failing canine heart, and a normal human heart. Finally, simulations of electromechanical activity using the normal canine heart are performed to demonstrate feasibility and usefulness of this novel methodology.

2 Methodology: image-based model development

The electromechanical model of the heart is composed of two main components, an electrical component and a mechanics component. The components represent two coupled finite element models, both based on the cardiac imaging data. The methodology for the semi-automated generation of the electromechanical model consists of (1) segmenting the ventricles from the imaging data, (2) generating the non-linear hexahedral finite element mesh for the cardiac mechanics component from the segmented images, (3) incorporating fiber and sheet structure into the mechanics mesh, (4) generating the linear, mixed-type finite element mesh for the electrical component from that of the mechanics component and incorporating fiber and sheet structure in the electrical mesh, and finally, (5) representing the electrical and mechanical properties of the heart. The numerical methods for solving the equations of electromechanical activity in the model are also described.

2.1 MR and DTMR image segmentation

MR and DTMR image data sets acquired previously ex-vivo from normal canine, failing canine, and human hearts were used in this study; these are publicly available (Helm et al. 2004). The data acquisition techniques can be found in (Helm et al. 2005b, 2006). The images were segmented as described in our previous paper (Vadakkumpadan et al. 2009a,b). Briefly, a level-set segmentation was first performed on the MR image stacks to separate the myocardium from the suspension media. Next, the ventricles were segmented from the atria using a semi-automatic approach. For every tenth slice within the MR image stack, landmark points were manually seeded to identify the atrioventricular border, which were determined by the location of the valves and gray level differences. The landmarks for the remaining slices were obtained by linearly interpolating the manually identified points. A 3D cubic spline was then fitted through the landmark points to generate a surface that represents the atrioventricular border. From the segmented images, a surface mesh composed of triangular elements (red ventricular surface of Fig. 1a) was generated using the software package Tarantula, the latter based on the octree meshing technique described in Prassl et al. (2009). The surface mesh served as a guide for the creation of the finite element mesh of the mechanics model component.

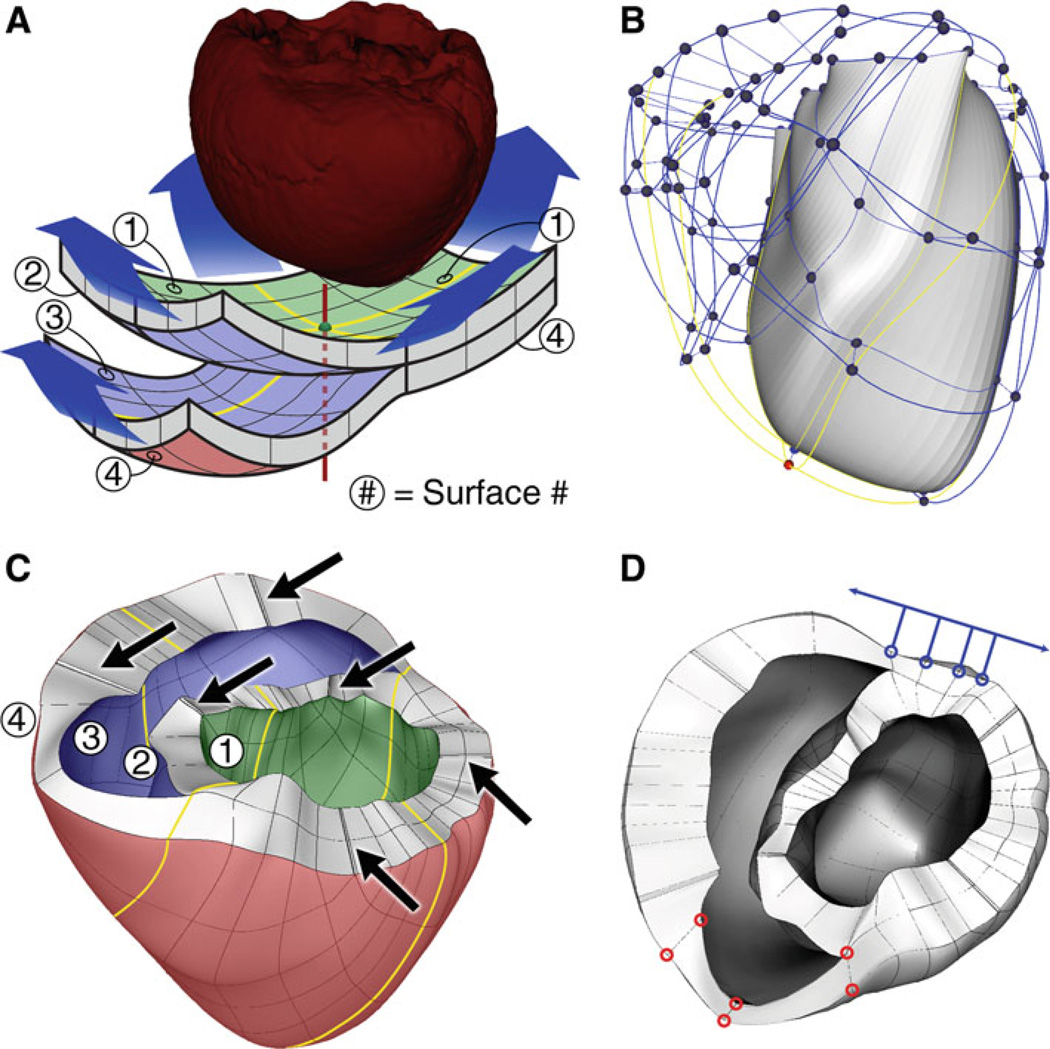
Fig. 1.

a Fitting the mechanics mesh to the ventricular geometry obtained from segmenting the MR imaging stacks. b The initial mechanics mesh. The LV is solid and the RV is transparent. The yellow lines correspond to those in panel A. c Final mechanics mesh. The arrows point to locations where corner elements were removed. d Locations at which boundary conditions were applied. See text for details

2.2 Finite element mesh for the mechanics component of the cardiac electromechanical model

The mechanics mesh was composed of non-linear hexahedral Hermite-based finite elements. Using such elements maintained the continuity of strain and was appropriate for maintaining incompressibility constraints (Onate et al. 2004). The structure of the mesh consisted of two 6×6-element layers, as shown in Fig. 1a. The portion of the mesh where the two layers are attached formed the left ventricle (LV); the upper, detached layer formed the septum; and the remaining lower layer formed the right ventricle (RV). The colored surfaces in Fig. 1a defined the endocardium and epicardium of the ventricles, with the green surface being the LV endocardium, the blue surface forming the RV endocardium, and red surface defining the epicardium. The red vertical axis represented the geometric center of the mesh and passed through the central nodes of each surface (colored nodes in Fig. 1a and b).

The surface nodes of the two mesh layers were manipulated manually to fit the surface mesh generated from the segmented images. In doing so, the first step was to choose the position of the RV endocardial apex; the central node of the blue surface was selected for that and the RV endocardial apex was manually positioned there. The central nodes of the green and red surfaces were placed on the LV endocardial and epicardial surfaces, respectively, at the locations nearest to the RV endocardial apex.

Next, the green surface was deformed by manipulating its nodes to fit the shape of the segmented LV endocardium (i.e. the endocardium of the LV free wall and of the LV side of the septum). The outermost nodes were spaced evenly and placed around the base of the LV endocardium. The remaining green surface nodes were manipulated to conform to the shape of the LV endocardium.

The RV endocardium was defined by the nodes located on the blue surface. The nodes at the free edges of the blue surface were placed around the RV endocardial base. Similar to the node fitting for the LV endocardium, the remaining nodes of the blue surface were manipulated to conform to the segmented RV endocardium. The epicardium was defined by the nodes located on the red surface, with the nodes on the outer edges of the red surface distributed along the epicardial base.

After completing the described manual process, the finite element mesh roughly resembled the segmented ventricular geometry. The least-squares method was used to better fit the nodal coordinates and their derivatives to the segmented epicardial and endocardial surfaces using an algorithm described elsewhere (Nielsen et al. 1991; Helm et al. 2005b). For the nodes that resided within the LV midwall, the spatial coordinates and their derivatives were calculated as the averages of the values at the corresponding nodes on the epicardium and endocardium.

After the fitting process, the corner elements of the mesh, which are located near the base, became almost prisms (elements with nearly triangular faces), which results in ill-conditioned Jacobians of the Hermite interpolation. The mesh was therefore refined by decreasing the size of these elements and increasing the size of the elements adjacent to them, while retaining the overall shape of the mesh. These shrunken corner elements were then removed from the mesh (arrows in Fig. 1c). Finally, finite elements adjacent to the corner elements were split to distribute the ventricular volume more evenly among elements. As a result, the initial mesh of 72 elements (Fig. 1b) evolved into a final hexahedral mesh of 172 elements and 356 nodes (Fig. 1c). To ensure continuity with respect to the global coordinates rather than the local finite element coordinates, all derivatives at the nodes were defined with respect to the arc length, as done in Nielsen et al. (1991).

2.3 Fiber interpolation and fitting in the mechanics finite element mesh

Fiber and laminar sheet structural information for each heart was obtained from the DTMR image data set. It has been well established, based on comparisons with histological studies, that the primary, secondary, and tertiary eigenvectors of the water diffusion tensors are aligned with the fiber direction, with the direction transverse to the fiber direction and in the plane of the laminar sheet, and with the direction normal to the laminar sheet, respectively (Hsu et al. 1998; Scollan et al. 1998;Chen et al. 2003;Helm et al. 2005a). Therefore, to incorporate fiber and laminar sheet architecture in the model, tensors and tensor gradients were defined at each node of the finite element mesh and interpolated within the finite elements using Hermite interpolation. The eigenvectors of the tensors in the interpolated tensor field represented the fiber and laminar sheet structure in the reconstructed hearts, as validated previously (Helm et al. 2005a).

Interpolation was performed in a vector space of tensors, introduced previously by Arsigny et al. (2006), in the framework of which addition of two tensors A₁ and A₂ and multiplication of a tensor A by a scalar k of the vector space were:

$$\mathbf{\{}\begin{array}{l}{\mathit{A}}_{\mathbf{1}}\oplus {\mathit{A}}_{\mathbf{2}}=\text{exp}(\text{ln}({\mathit{A}}_{\mathbf{1}})+\text{ln}({\mathit{A}}_{\mathbf{2}}))\hfill \\ k\otimes A=\text{exp}(k\text{ln}(A))\hfill \end{array}.$$ (1)

For positive definite symmetric matrices, these operations become:

$$\mathbf{\{}\begin{array}{l}{\mathit{A}}_{\mathbf{1}}\oplus {\mathit{A}}_{\mathbf{2}}={\mathit{A}}_{\mathbf{1}}{\mathit{A}}_{\mathbf{2}}\hfill \\ k\otimes A=A^k={({\mathit{\text{UDU}}}^T)}^k={\mathit{\text{UD}}}^k{\mathit{U}}^T=\mathit{U}\left[\begin{array}{ccc}{\lambda }_1^k& 0& 0\\ 0& {\lambda }_2^k& 0\\ 0& 0& {\lambda }_3^k\end{array}\right]{\mathit{U}}^T,\hfill \end{array}$$ (2)

where U is an orthogonal matrix and D is a diagonal matrix of eigenvalues λ₁, λ₂ and λ₃. Using the operations in Eqs. (1) and (2), the Hermite interpolation was defined as:

$$A={\displaystyle \mathbf{\prod }{\mathit{A}}_{\mathit{i}}^{{\psi }_i},}$$ (3)

where ψ_i are the Hermite basis functions as described in Nielsen et al. (1991), and A_i are the tensors and tensor gradients with respect to the arc-lengths assigned to the nodes of each finite element.

The method for tensor fitting to the DTMR image data, which uses the least-squares method in a metric space of tensors, was similar to that of angle fitting (Nielsen et al. 1991). The tensors and the tensor gradients at the nodes of the mesh were found using the least-squares method by minimizing the sum of the squared distances between the DTs from the DTMR image data and the tensors from the interpolated tensor field. The log-Euclidean metric applied in the least-squares method was:

$$d({\mathit{A}}_{\mathbf{1}},{\mathit{A}}_{\mathbf{2}})={(\text{Trace}{\{\text{ln}({\mathit{A}}_{\mathbf{1}})-\text{ln}({\mathit{A}}_{\mathbf{2}})\}}^2)}^{\frac{1}{2}}.$$ (4)

To remove artifacts that appear when voxels of MR images represent both ventricular tissue and surrounding media at the epicardial and endocardial surfaces, the approximated tensor field was regularized. Regularization of the tensor field using the log-Euclidean metric in Eq. (4) was performed by introducing a penalty term Reg(s) to the least-squares method; the latter was derived from the norm of the tensor field gradient:

$$\mathbf{\{}\begin{array}{l}\text{Reg}(s)=\frac{n_s\gamma }{V_t}{\displaystyle \int s^{2}dV}\hfill \\ s^2={\displaystyle {\sum }_j\left[\text{Trace}{\left\{{\displaystyle {\sum }_i\frac{\partial {\mathrm{\Psi }}_i}{\partial x_j}\text{ln}({\mathit{A}}_{\mathit{i}})}\right\}}^2\right],}\hfill \end{array}$$ (5)

where integration was performed over the volume of the finite elements, n_s is the number of samples (tensors) in the DTMR image data set, V_t is the tissue volume of the ventricles, γ = 1.0 is the penalty factor, and $\frac{\partial {\mathrm{\psi }}_i}{\partial x_j}$ are the derivatives of the Hermite basis functions with respect to a fixed set of global coordinates, x_j.

To analyze the quality of the approximation, the angle α between the unit eigenvector of the DTMR-derived tensor (v_d) and that of the approximated tensor (v_a) was calculated as

$$\alpha =\frac{180}{\pi }\times \mathbf{\{}\begin{array}{ll}\beta ,\hfill & \beta <\frac{\pi }{2}\hfill \\ \pi -\beta ,\hfill & \text{otherwise}\hfill \end{array},$$ (6)

where β = arccos(v_d ○ v_a). By definition, this angle is less than 90 degrees. The error in the tensor approximation was defined as the root mean square (RMS) of the angles α_f and α_l. Angle α_f is the angle between the primary eigenvectors of the approximated tensor and the DTMR-derived tensor. The angle between the tertiary eigenvectors of these two tensors was defined as α_l. Since primary, secondary, and tertiary eigenvectors were perpendicular to each other, RMS of the angle between secondary eigenvectors was redundant and excluded from analysis.

2.4 Generation of finite element mesh, and fiber and laminar sheet architecture for the electrical component of the cardiac electromechanical model

Unlike the finite element mesh for the mechanics component, the mesh for the electrical component of the cardiac electromechanics model was composed of linear finite elements. The mechanics mesh served as the basis for the electrical mesh generation to ensure that the geometries of both meshes were exactly the same. First, the mechanical mesh was processed into a binarized image stack. Then, this image stack was inputted into the meshing software Tarantula, to generate a mixed-type finite element mesh (Prassl et al. 2009) for the electrical component of the model. The resulting electrical mesh consisted of approximately 1,400,000 nodes and 1,700,000 elements.

Fiber and laminar sheet orientation was assigned to each element in the electrical mesh by first finding the centroid of the element and then applying Newton’s method to map that centroid to its corresponding location in the mechanics mesh. The fiber orientation at that location in the mechanics mesh was then assigned to the corresponding finite element of the electrical mesh.

2.5 Representing the electrical and mechanical properties of the heart in the model

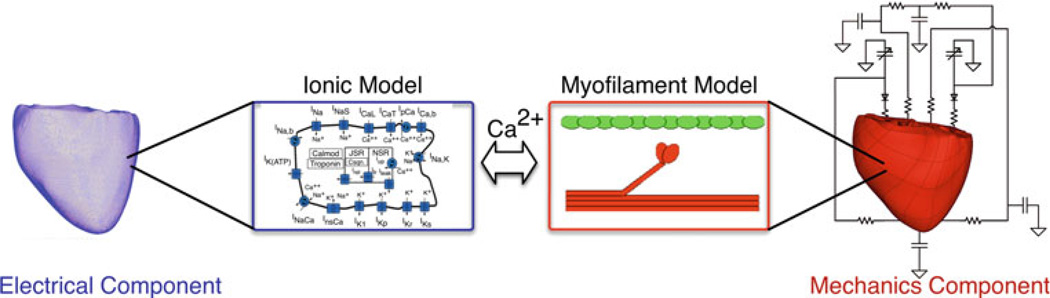
Figure 2 presents a schematic of the electrical and mechanics components of the electromechanical model of the heart and their coupling. Mathematical description of cardiac tissue behavior in the electrical component of the model was based on the monodomain representation of the myocardium (Plank et al. 2008). Electrical activity at the cellular level was represented by a membrane kinetics model; the choice of the membrane kinetics model depends on the particular species to which the modeled heart belongs and could incorporate electrophysiological remodeling associated with cardiac disease. The anisotropic electrical properties were initially based on conductivity values reported by Roberts and Scher (1982) which were then adjusted until electrical propagation during sinus activity matched those reported by Durrer et al. (1970). Mathematical description of cardiac contraction in the mechanics component was based on continuum models of cardiac mechanics (Guccione et al. 1995; Vetter and McCulloch 2000; Usyk et al. 2002), with the myocardium assumed to be orthotropic, hyper-elastic, nearly-incompressible material, the passive mechanical properties of which were defined by an exponential strain energy function (Usyk et al. 2002). Generation of active stress at the level of the single myocyte was described by the model of cardiac myofilament contraction; the model by Rice et al. (2008) was used as the baseline model, to which modifications could be made to account for species differences and for changes resulting from cardiac disease. The active tension generated by the myofilament model depended on the stretch ratio in the direction of the myofilament (i.e., the ratio of fiber length before and after deformation) and its temporal derivative. Active tension defined the component of the Cauchy stress tensor that acted in the local fiber direction (Kerckhoffs et al. 2003). The fiber and laminar sheet structure determined the orthotropic electrical conductivity and passive mechanical properties of the myocardium.

Fig. 2.

Schematic diagram of the electromechanics model

The electrical and mechanics components were weakly coupled to minimize the computational effort; the membrane kinetics model was incorporated in both the electrical and mechanics components. The local electrical activation times (time of cellular depolarization), which were obtained using the electrical component, determined the instants at which the combined ionic and cardiac myofilament model in the mechanics component was stimulated. By employing this method of weak coupling, cooperative binding of Ca to Troponin C was represented, which was necessary in order to reproduce the experimental force-length relationship for cardiac muscle.

To determine the appropriate boundary conditions for the mechanical deformation of the ventricles in the mechanics component of the model, publically available animation frames of Cine-MRI (INRIA, Asclepios Research Project) were analyzed; they revealed that the portion of the ventricle near the orifice of the pulmonary artery in the RV remained stationary during contraction. Additionally, the movement of the posterior wall surface near the septum was found to be restricted to a single direction in the short-axis plane tangent to the surface of the ventricles. These boundary conditions were then implemented in the model by fixing the positions of the red nodes and restricting the movement of the blue nodes to the direction indicated by the blue arrow (Fig. 1d). In addition, the movement of the entire ventricular base was restricted to a fixed plane perpendicular to the longitudinal axis of the ventricles, similar to previous studies (Usyk et al. 2002).

The eletromechanical model of the ventricles was coupled to a model of the circulatory system representing the systemic and pulmonic circulations (Kerckhoffs et al. 2007).The method of coupling between the electromechanical and circulatory models was different from that used in previous electromechanical models, in which the intraventricular pressure was calculated in several iterations by using the penalty term until an estimation of the intraventricular pressure that minimizes the error in intraventricular volume is obtained (Usyk et al. 2002).

In the present modeling approach, the intraventricular pressures were added as additional unknown variables in the non-linear system of stress equilibrium in the finite element method. To do so, the volumes of the LV (V_L) and RV (V_R) were expressed as functions of the degrees of freedom x_s of the endocardial surface nodes using the divergence theorem. These functions are the left hand side of two new equations added to the non-linear system:

$$\mathbf{\{}\begin{array}{l}{V}_L(x_s)=V_{\text{circ},L}\hfill \\ V_R(x_s)=V_{\text{circ},R}\hfill \end{array},$$ (7)

where V_circ,L and V_circ,R are the LV and RV volumes calculated from the circulatory model, respectively. The pressures of the LV (P_L) and RV (P_R) were added to the vector of unknowns in the system of non-linear equations. As a result of these changes in the system of equations, two extra columns, composed of the derivatives of all equations with respect to P_L and P_R, were added to the Jacobian of the system. Because pressure was a constant multiplier in the weak form of the stress equilibrium equation, no additional computations were required to construct these two columns. Finally, the equations in (7) were differentiated with respect to x_s and added as two extra rows to the Jacobian.

This modification simplified the algorithm of coupling the electromechanical model with the circulatory system model and improved the performance of the numerical calculations, since our method does not require pressure perturbation steps to compute the ventricular compliance matrix, as done in previous studies (Kerckhoffs et al. 2007). The initial conditions of the circulatory model were determined from the elastic model of ventricular contraction (for details see (Kerckhoffs et al. 2007)).

2.6 Numerical methods

The procedure for solving the equations of the model’s electrical component was described in details elsewhere (Plank et al. 2008); therefore, only numerical methods for mechanics component are discussed below. The final system of equations for the mechanics component took the form of a differential algebraic system after the spatial integration over the finite elements was performed using Gaussian quadrature. This system consisted of ODEs for the state variables of the ionic, myofilament and circulatory models (γ), and quasi-static equations of stress equilibrium with respect to the finite element mesh node parameters, x, and their temporal derivatives, $\frac{\mathrm{d}x}{\mathrm{d}t}$:

$$\mathbf{\{}\begin{array}{l}\frac{d\gamma }{\mathrm{d}t}=F(x,\frac{\mathrm{d}x}{\mathrm{d}t},\gamma ,t)\hfill \\ g(x,\gamma )=0\hfill \end{array}.$$ (8)

where the vector of functions F is the right side of the ODEs and g is the function that is derived from numerical integration over the finite elements and which relates x to γ in the algebraic system. The differential algebraic system (8) can be solved by differentiating the function g and solving the resulting system of ODEs. Because differentiation of the algebraic equations in the system (8) was complicated, the ODEs were integrated and the resulting system of algebraic equations was solved at each time step (Campbell et al. 2009). To ensure stability, a semi-implicit numerical scheme was implemented. In this semi-implicit scheme, x_k+1 (the value of x at the next integration step) was used for extrapolation of $\frac{\mathrm{d}x}{\mathrm{d}t}$ and for integration of the first equation in (7) at the current time step k; it was found from the algebraic equation g(x_k+1, γ_k+1) = 0. The state variables γ were extrapolated at the time step k+1 using the right side of ODE s:

$$\mathbf{\{}\begin{array}{l}g(x_{k+1},{\gamma }_k+hF(x_{k+1},x_{k+1}^{\prime },{\gamma }_k,t_k))=0\hfill \\ x_{k+1}^{\prime }=\frac{x_{k+1}-x_k}{h}\hfill \end{array},$$ (9)

where h is the time step. The resulting non-linear system of algebraic Eq. (9) was solved with respect to x_k+1, which, in turn, were used to obtain γ_k+1 by integrating the ODEs in (8). The latter, repeated integration of ODEs was performed since some equations of the system for γ were stiff, and a more robust method of integration rather than the forward Euler was needed. The algebraic system of Eq. (9) was solved using the Newton-Raphson method.

Integration of ODEs was performed using the CVODE solver with Backward Differentiation Formulas method (Cohen and Hindmarsh 1996). The direct solver (SuperLU or MUMPS) through the PETSc interface (Balay et al. 2007) was employed to solve the linear system of equations. In the simulations presented in Sect. 4, a time step of 0.1 and 0.01 ms was used for the mechanical and electrical solution, respectively. A 30-second episode of ventricular contraction took 24 h on 16 CPU for electrical and mechanics meshes with ~1,400, 000 and ~8,500 degrees of freedom, respectively.

To analyze the convergence of the numerical solution with respect to decreases in spatial discretization, the mechanical mesh was refined twice. At each refinement, the largest edges of the finite elements were split in half. After the first and second refinements, the maximum edge length was less than 20 and 10mm, respectively. The numbers of degrees of freedom were 11,308 and 43,540 for each respective mesh.

The ventricles were passively dilated to the respective enddiastolic pressures, which were determined from the initial mesh of 172 elements, and the overall changes in total strain energy with decreasing spatial discretization were calculated, as done in the study by Vetter and McCulloch (2000). The strain energy decreased by 0.023 and 0.013% after the first and the second finite element mesh refinements, demonstrating convergence of the numerical solution. These values are less than the tolerance used by Vetter and McCulloch (0.5%). In addition, a point-wise comparison of fiber strain throughout the ventricular volume was performed. The average difference in fibre strain was 0.003 ± 0.005 and 0.002 ± 0.004 after the first and the second refinement, further demonstrating convergence. Changes in total strain energy and differences in fiber strain were also calculated at end-systole in the actively contracting ventricular model. The changes in strain energy were 1.6%, 0.29% after first and second refinement. Average fiber strain differences at end-systole were 0.019 ± 0.017 and 0.017 ±0.014. Although these values are larger than those for the passively dilated ventricles, they still demonstrate convergence.

For all meshes, decreasing the time step from 0.1 to 0.05 ms and from 0.05 to 0.025 ms resulted in changes in strain energy of less than 0.004% and in average fiber strain of less than 0.00008, which were significantly smaller than the overall changes in strain energy with the decrease in spatial discretization calculated at end-systole.

3 Analysis of the error in the approximation of the ventricular surfaces, and fiber and laminar sheet architecture

In illustration of the approach presented above, mechanics meshes were generated from high resolution MR scans of normal canine, failing canine, and normal human ventricles (Fig. 3). The error in the mechanics mesh surface fitting to the surfaces of the segmented ventricles was defined as the root mean square (RMS) of the Euclidian distance between epicardial and endocardial surfaces of the mechanics mesh and the triangulated surfaces of the ventricles from the segmented image. The error was larger for the failing canine and the human ventricles, owing to the larger sizes of these hearts when compared to the normal canine heart. The RMS error was 0.7mm for the normal canine mesh, 2mm for the failing canine mesh, and 3.5mm for the human mesh. The relatively large RMS error for the human heart was due to the fact that the posterior side of the human heart was slightly deformed prior to imaging, resulting in a more complex shape than that of the canine.

Fig. 3.

Anterior view of the finite element mechanics meshes. From left to right: normal canine, failing canine, and human ventricles

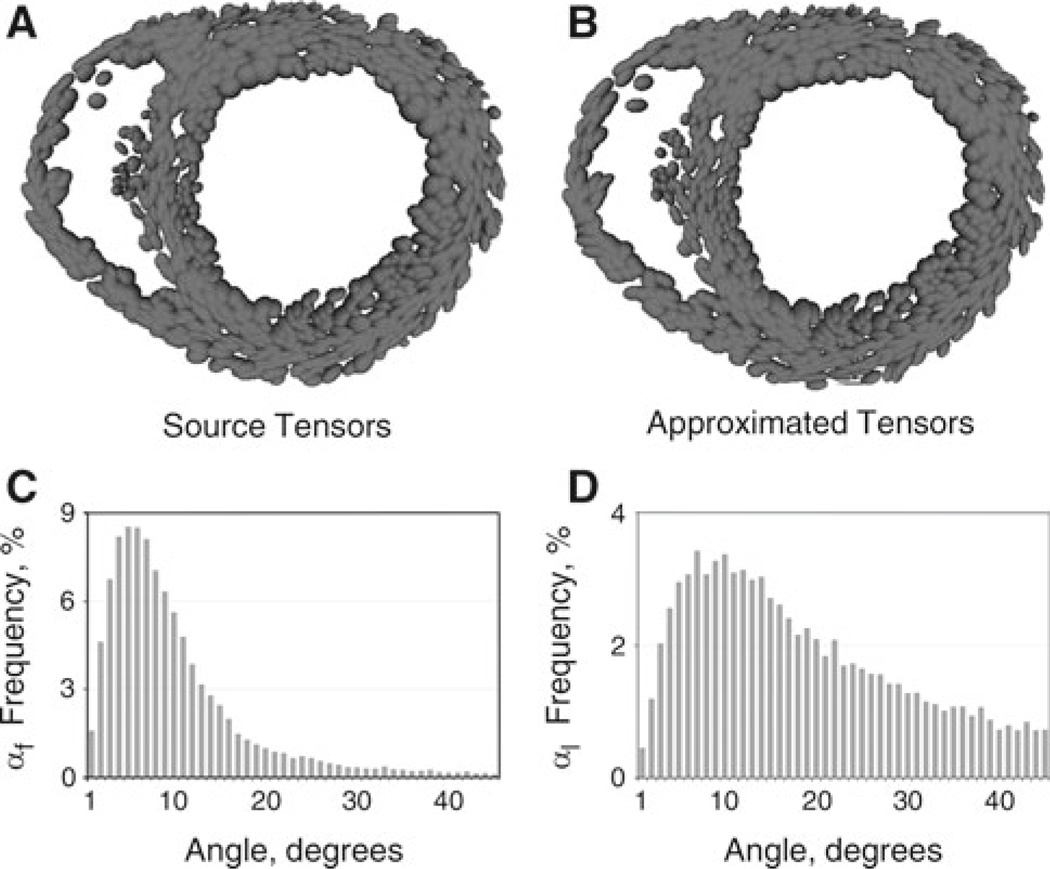
Local tensors from the raw DTMR image stack and local tensors from the approximated tensor field are visualized as ellipsoids in a short-axis view of the normal canine ventricles in Fig. 4a and b. Figure 4 shows good qualitative match between diffusion and approximated tensors. To analyze the quantitative error in the tensor approximation, the distribution of the angles between approximated tensor and DT eigenvectors was analyzed. These angles were calculated using Eq. (6). The frequency distribution, in the ventricular volume, of the angle between eigenvectors of the DTMR-derived and the approximated tensors is shown in Fig. 4c (fiber directions) and d (the normals to the laminar sheets) before regularization.

Fig. 4.

Tensor interpolation and comparison with the original DTMR imaging data for the normal canine ventricles. Tensors from DTMR images (a) and approximated tensors (b) are represented as ellipses, where the lengths of each axis correspond to the DT eigenvalues. Frequency distribution bar graphs of the angles α_f (c) and α_l (d)

In the graph, values greater than 45 degrees were not shown due to the relatively low frequency of angle distribution within this range. Statistical characteristics of the angle distribution are shown in Table 1. RMS of the α_f distribution was 15.6 degrees and resulted from minimizing the inherent DTMR fiber approximation noise. Regularization increased the RMS of the α_f distribution by 0.6 degrees owing to the fact that it increased the difference in the angle between the original fiber orientation at the endocardium, which was poorly defined in DTMR images, and the approximated fiber orientation. The much larger RMS of α_l (33 degrees) was due to the smaller statistical difference between the secondary and tertiary eigenvalues, resulting in difficulties in resolving the laminar sheet orientation (Helm et al. 2005a,b). Similar shapes of the frequency distributions of α_f and α_l were obtained for the failing canine and human hearts (not shown).

Table 1.

Characteristics of the distribution of the angle between the eigenvectors of the diffusion and the approximated tensors for the normal canine heart

	Before regularization		After regularization
	αf, fiber direction	αl, normal to laminar sheets	αf, fiber direction	αl, normal to laminar sheets
RMS	15.6	33	16.2	36.1
25% Percentile	4.459	9.894	4.63	10.42
Median	7.529	19.4	7.773	20.36
75% Percentile	12.38	36.4	12.84	37.1
Mean	10.73	26.23	11.7	27.40
Std. deviation	11.33	21.60	11.75	22.07

All values are in degrees

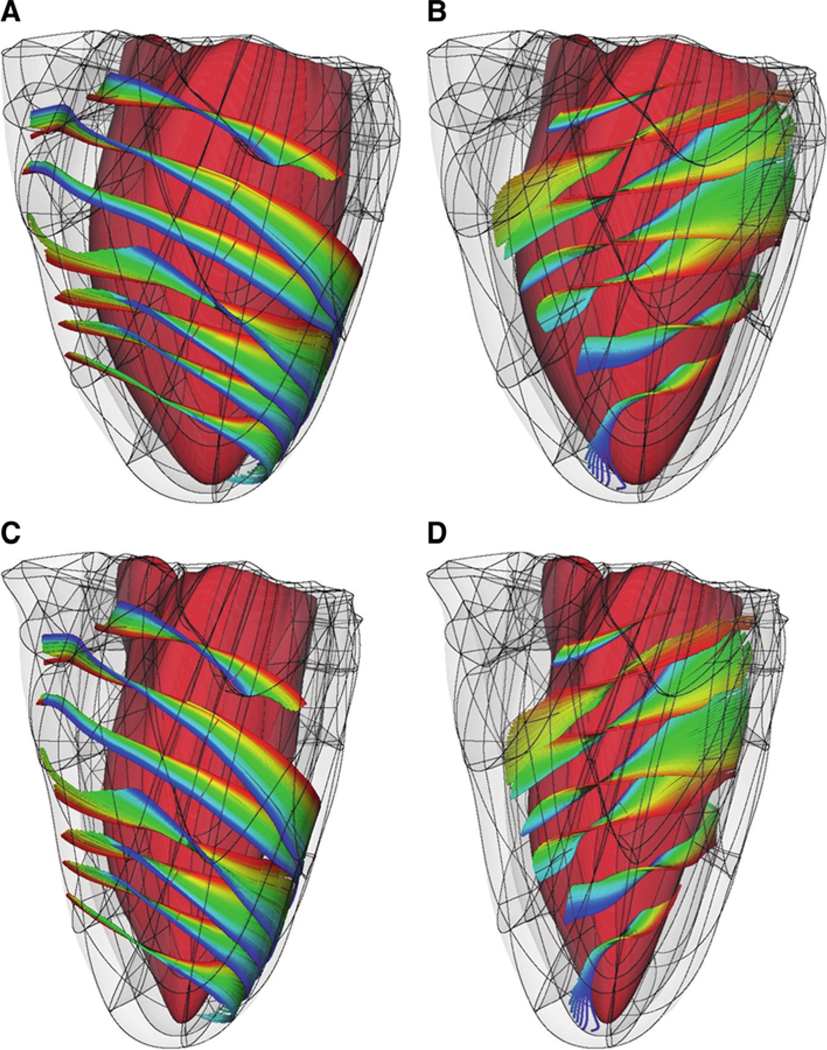
Figure 5 presents the fiber organization near the epicardium (Fig. 5a) and the endocardium (Fig. 5b) of the LV anterolateral wall. The fiber organization is qualitatively similar to the fiber structure described previously (Nielsen et al. 1991), as obtained from histological sectioning.

Fig. 5.

Fiber architecture of the normal canine ventricles at end-diastole (a, b) and end-systole (c, d). For clarity of visualization, fibers near the epicardium (a, c) and near the endocardium (b, d) are shown separately. The colors trace individual fibers

4 An example of cardiac electromechanical modeling: the normal canine heart

To demonstrate the feasibility of using the described modeling approach to simulate cardiac electromechanical function, several cardiac cycles during sinus rhythm were simulated in the normal canine ventricles. The membrane kinetics were represented by the Greenstein et al. (Greenstein et al. 2006) canine ionic model. The cellular myofilament dynamics were represented by the biophysical model of Rice et al. (2008), which was modified for the canine heart. To ensure that the duration of all cardiac phases matched experimental values (Ashikaga et al. 2007), the variables f_app and h_f of the Rice et al. model (2008) were scaled by 10 and 0.2, respectively.

Sinus rhythm in the normal canine heart was simulated by stimulating the endocardium at specific timings and locations to replicate electrical activation originating from the Purkinje network. The timings and locations were adjusted until the surface activation pattern matched experimental data (Durrer et al. 1970; Spach and Barr 1975). Figure 5 shows the ventricles (with a representation of the fibers) at two stages of the cardiac cycle, end-diastole (Fig. 5, panels a and b) and end-systole (Fig. 5, panels C and D).

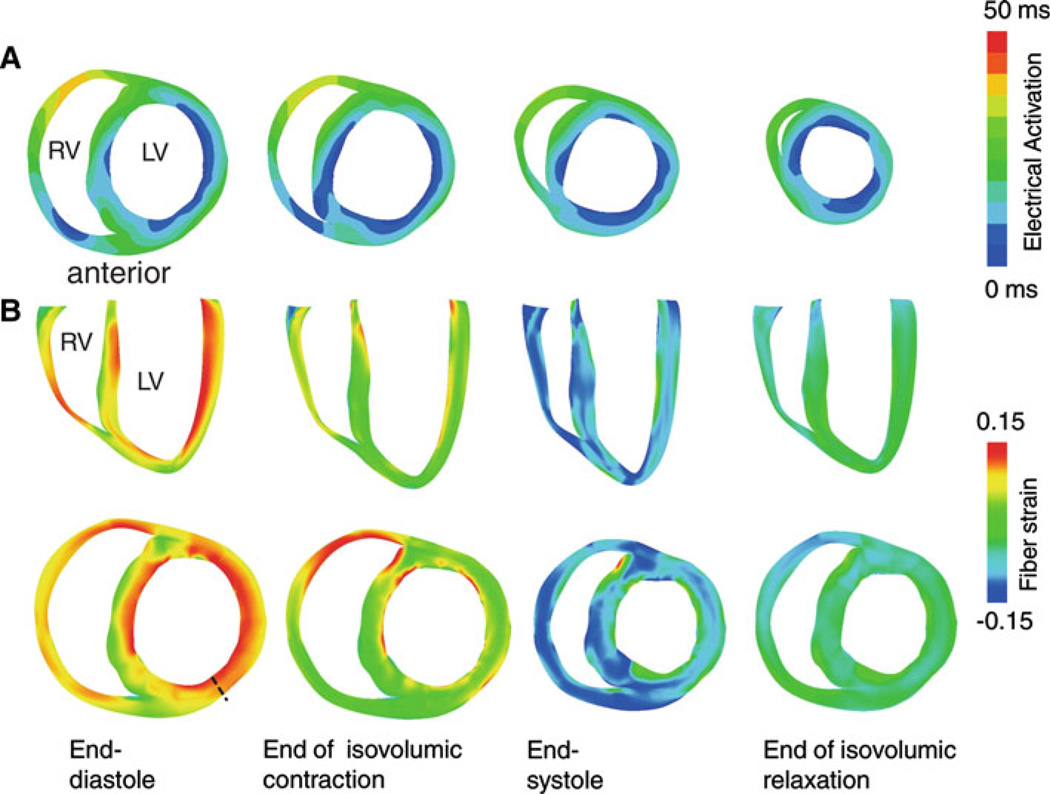
Figure 6a presents transmural maps of electrical activation in a short-axis view of the ventricles during sinus rhythm. The electrical activation wave commenced at the LV side of the septum, at the endocardium of the LV anterolateral wall, and at the RV endocardium near the junction of the RV free wall and septum, consistent with experimental data (Durrer et al. 1970; Spach and Barr 1975). The corresponding fiber strain distribution during the different phases of cardiac contraction is shown in Fig. 6b. At the end of the ventricular filling phase, myofiber strain was positive throughout the ventricles, as indicted by the fiber strain maps in the first column of Fig. 6b. At the end of the isovolumic phase of contraction, maximal myofiber shortening was observed at the early activated regions: the septum, the LV anterolateral wall, and the RV anterior wall (Fig. 6b, second column). At end-systole, maximal myofiber shortening occurred at the LV midwall (Fig. 6b, third column). This observation agreed with the experimentally documented larger amplitude of shortening at the midwall when compared to that in myocardial layers located closer to the wall surface (Ashikaga et al. 2004, 2007). Strain at the beginning of myofiber relaxation is shown in the last column of Fig. 6b.

Fig. 6.

Electrical activation and transmural fiber strain during sinus rhythm. a Isochronal maps of electrical activation in a short-axis view during sinus rhythm. b Transmural fiber strain during the cardiac cycle in long-axis (top) and short-axis (bottom) views. The undeformed (stress-free) state was the reference state for strain calculation

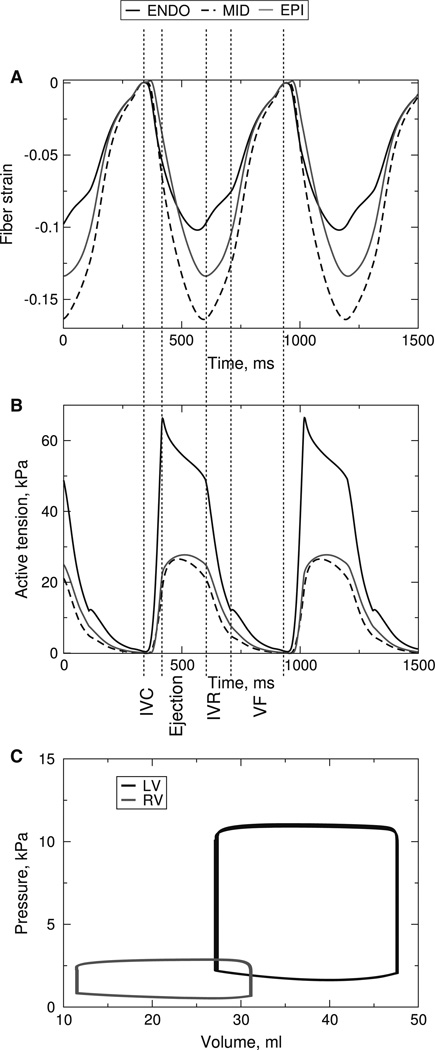
The temporal traces of transmural strain and active tension, and pressure-volume loops are shown in Fig. 7. The fiber strain traces (Fig. 7a) were obtained from the mid-base of the ventricles at locations along the thick black line in Fig. 6b. They demonstrate myofiber prestretching, as illustrated by the positive fiber strain, during the isovolumic phase of contraction, which agrees with experimental findings (Ashikaga et al. 2007). The model was further validated with original experimental data from a novel ultrasound-based experimental approach called electromechanical wave imaging, which utilizes very high frame rate ultrasound to determine the onset of active contraction by constructing maps of incremental strain rate (Provost et al. 2010). Details of this validation study and quantitative comparisons between experimental and simulation results can be found elsewhere (Provost et al. In Review).

Fig. 7.

a Fiber strain for different wall depths at the mid-base of the anterior left ventricular wall. The end-diastolic state is the reference state for the strain calculations. b Active tensions at the same locations as in panel A. c LV and RV pressure-volume loops during the cardiac cycles. IVC: isovolumic contraction, IVR: isovolumic relaxation, VF: ventricular filling

In addition to transmural strain, the model provides information regarding the stress distribution, which is difficult to obtain experimentally. Figure 7b shows the active tension at the same transmural locations as in Fig. 7a. The maximum tension at the midwall is less than that at the endocardium or epicardium due to the faster myofiber shortening at the midwall during the ejection phase. The magnitude of the tension at the endocardium is the largest due to the largest end-diastolic strain, with the undeformed stress-free state of the ventricles as the reference state (data not shown). The model also provides information about the global variables of ventricular contraction, such as ventricular pressure and volume. Pressure-volume loops for LV and RV are shown in Fig. 7c.

5 Discussion

This report presents a new methodology to construct electromechanical models of ventricular contraction based on MR and DTMR images. The full pipeline of electromechanical model development, which includes reconstruction of the ventricular geometry from MR and DTMR scans, generation of the finite element meshes, representation of fiber and laminar sheet architecture, and modeling of electrical and mechanical activity, is presented. The methodology is then employed to generate anatomical finite element models of the normal canine, the failing canine, and the human ventricles. Lastly, the normal canine geometry is used to simulate several contraction beats, demonstrating the utility of the electromechanical model.

Previous ventricular electromechanical models incorporated ventricular geometries and fiber architecture that were obtained from histological sections. However, collecting histological data for these models took as long as several months per model, thus, only three histology-based anatomical models have been developed. On the other hand, obtaining MR and DTMR scans of an ex-vivo heart is, in comparison, a relatively fast procedure (up to a day). When it is combined with the novel semi-automatic procedure that we have developed here, generating a whole-heart electromechanical model can be completed in a span of a couple of days at most.

To accurately simulate ventricular contraction, a new approach to the construction of the finite element mesh for the mechanics component of the model was designed. The finite element mesh consisted of the two layers of hexahedral elements, which were “wrapped” around the ventricles. Previous mechanics meshes had a small opening at the LV apex and thus incorporated redundant nodes there. In our methodology, the redundant nodes were instead located at the base of the ventricles. Since the boundary conditions for all electromechanical models of the ventricles are applied at the base and there are inherent errors associated with these boundary conditions, inclusion of the redundant nodes at the base did not lead to additional numerical errors in simulations of mechanical deformations. There are other mesh topologies that can be used to avoid singularities at the apex, such as the butterfly topology (Wenk et al. 2010). However, such topologies do not allow for the use of the Hermite interpolation scheme (Fernandez et al. 2004), which has the advantage of maintaining continuity of strain across the borders of the finite elements.

Our methodology also incorporates a novel use of tensors to describe ventricular fiber and laminar sheet architecture that is based on interpolation methods developed for brain imaging (Arsigny et al. 2006). This approach overcomes limitations associated with the use of angle interpolation to define the fiber and sheet architecture (Nielsen et al. 1991; Helm et al. 2006) in previous models. Interpolation of angles may result in spatial angle changes greater than 180 degrees, which results in discontinuities; thus, additional nodes have to be introduced manually into the mesh. However, this procedure only decreases the numerical error arising from the discontinuities without eliminating it. Our methodology employs tensors to represent the fiber and laminar sheet structure. Interpolating tensors and tensor gradients, in contrast to interpolating angles, results in a continuous representation throughout the mesh, thus eliminating any errors associated with discontinuities resulting from the angle interpolation.

Reconstructing the ventricular geometry from MR and DTMR images also allows for the development of individual electromechanical models of the heart. Our methodology thus provides the capabilities to generate electromechanical models of the heart for any species under normal or pathological conditions. The electromechanical models with individual anatomically accurate geometry and fiber architecture and detailed biophysical representations of both electrical and mechanical activity provide a modeling framework of unprecedented detail that can be used to successfully address issues related to both disturbances in heart rhythm and the efficacy of the cardiac pump.