Application of Clustering Analyses to the Diagnosis of Huntington Disease in Mice and Other Diseases with Well-Defined Group Boundaries

Abstract

Nuclear magnetic resonance (NMR) spectroscopy has emerged as a technology that can provide metabolite information within organ systems in vivo. In this study, we introduced a new method of employing a clustering algorithm to develop a diagnostic model that can differentially diagnose a single unknown subject in a disease with well-defined group boundaries. We used three tests to assess the suitability and the accuracy required for diagnostic purposes of the four clustering algorithms we investigated (K-means, Fuzzy, Hierarchical, and Medoid Partitioning). To accomplish this goal, we studied the striatal metabolomic profile of R6/2 Huntington disease (HD) transgenic mice and that of wild type (WT) mice using high field in vivo proton NMR spectroscopy (9.4 Tesla). We tested all four clustering algorithms 1) with the original R6/2 HD mice and WT mice, 2) with unknown mice, whose status had been determined via genotyping, and 3) with the ability to separate the original R6/2 mice into the two age subgroups (8 and 12 wks old). Only our diagnostic models that employed ROC-supervised Fuzzy, unsupervised Fuzzy, and ROC-supervised K-means clustering passed all three stringent tests with 100% accuracy, indicating that they may be used for diagnostic purposes.

1. INTRODUCTION

The ability to utilize common clustering methods in order to develop diagnostic biomarker models that can accurately render a differential diagnosis of a single unknown subject in a given disease state has yet to be demonstrated. Typically, in the vast majority of the cases, common clustering analyses are employed to classify data into two or more groups. For example, in the case of a disease where there are three well-defined groups of subjects (normal, pre-symptomatic, and symptomatic), if a sufficient amount of data of all three of those groups is available, then a common clustering analysis may classify correctly the subjects in the data into three clusters corresponding to the aforementioned three groups. If, on the other hand, a common clustering analysis is presented with the data of a single unknown subject, i.e. it is not known to which of the aforementioned three groups the subject belongs, then, to the best of our knowledge, no common clustering analysis will be able to identify/diagnose that single subject. The ability, therefore, to employ a common clustering analysis in order to develop a diagnostic biomarker model (DBM) that can be used to accurately diagnose a single unknown subject in a disease with well-defined group boundaries constitutes a novel approach. Moreover, and more importantly, this approach has significant implications for the biomedical and clinical sciences because it makes possible the transference of clustering analysis from the research area, i.e. identification of groups in data, to the clinical area, i.e. identification/diagnosis of a single subject.

In two previous studies, using the NMR spectroscopy data we examined mathematical approaches in connection with the identification and assessment of key biomarkers in a disease state, as well as with the development of diagnostic biomarker models and clinical change assessment models [1,2]. In the present study, we investigated four clustering methods (K-means, Fuzzy, Hierarchical, and Medoid Partitioning) that are popular in the medical sciences in connection with the development of diagnostic biomarker models.

Clustering theories first gained popularity in the 1960’s, when biologists and social scientists took a keen interest in exploring ways of finding groups in their data [3]. A decade later, aided by advancements in computers, clustering methods were used in medicine, psychiatry, archaeology, anthropology, economics, and finance [4]. Today, there are various clustering methods, K-means, Fuzzy, Hierarchical, Medoid Partitioning, Clustering Regression, etc., and they are used routinely in every scientific field with a focus from the macrocosm to the microcosm – from studying the internal structure of dark matter halos in a set of large cosmological N-body simulations to trying to discover groups of genes in microarray analysis and to predicting protein structural classes [5–12].

As Kaufman et al. [3] remarked, “Cluster analysis is the art of finding groups in data.” The objective of all clustering methods is to classify N subjects (observations) with P independent variables (IVs) into K clusters according to the spatial relationships among the subjects – subjects in the same clusters are maximally similar, whereas subjects in different clusters are maximally dissimilar. By design, therefore, the primary objective of every clustering method is the correct determination of the number of groups into which a given set of data can be partitioned, and that in itself constitutes, by far, the most difficult task that a clustering analysis has to do. As it so happens, in the medical sciences, especially in the area of diagnostics, the number of groups is known. In our study of experimental Huntington disease (HD), for example, we know a priori that we have two, and only two, groups of mice: a mouse can be either normal wild type (WT) or an R6/2 (HD) mouse. We can therefore ask a clustering method not to waste time examining all the possible clustering outcomes but to focus instead in classifying all of our subjects (data) into only two clusters. This constitutes a significant bypass of the most difficult course – both in terms of obstacles and potential pitfalls – that a clustering analysis has to traverse. This holds true for any other disease where the number of groups is known. If, for example, we studied a disease with three groups, including the normal group, then we would pre-set the number of clusters to three.

Availing ourselves of the aforementioned significant theoretical advantage, we sought to answer the question of whether it was possible to use a common clustering method to ultimately render a differential diagnosis of a single unknown subject in a disease with well-defined group boundaries. To address this question, we first developed a clustering approach that made it possible to use a common clustering method for such a purpose, and we subsequently investigated four clustering methods (K-means, Fuzzy, Hierarchical, and Medoid Partitioning) by applying them to the in vivo analysis of the striatal metabolomic profile of R6/2 transgenic mice with Huntington disease (HD) and WT mice using proton nuclear magnetic resonance (¹H NMR) spectroscopy. We first assessed the clustering models in an unsupervised way. Then, we introduced the concept of employing ROC curve analysis with the express purpose of supervising the clustering models in order to increase their accuracy, and we subsequently assessed the performance of the ROC-supervised clustering models and compare it to that of their unsupervised counterparts. Our ultimate goal was to accomplish the following two objectives:

1. Construct diagnostic biomarker models (DBMs) that could accurately diagnose R6/2 mice as a prototype for the diagnosis of diseases. Since HD is a neurodegenerative disease with well-defined group boundaries (WT vs. R6/2), since genotyping is available for the R6/2 mice, and since genotyping is the gold standard, we would use HD to test the accuracy of our DBMs.

2. Subject all four clustering methods to thorough, stringent tests in order to assess their strengths, weaknesses, and overall suitability for diagnostic applications.

2. METHODS

2.1. ANIMAL METHODS

2.1.1. R6/2 Transgenic mice

Original R6/2 mice were purchased from the Jackson Laboratories (Bar Harbor, ME, USA) and bred by crossing transgenic males and wild type (WT) females at 5 weeks of age. Offspring were genotyped according to established procedures [13] and the Jackson Laboratory. All animal breeding and all animal experiments described in this study were performed in accordance to the procedures approved by the University of Minnesota Institutional Animal Care and Use Committee. This study was specifically approved by the aforementioned Institutional Committee.

2.1.2. Animal Preparation

Prior to the in vivo ¹H NMR (proton nuclear magnetic resonance) scanning, all animals were anesthetized and maintained thus throughout the duration of the scanning procedure. The anesthesia used was a gas mixture (O₂: N₂O = 1:1) containing 1.25–2.0% of isoflurane that flowed throughout the cylindrical chamber wherein the spontaneously breathing animals were placed. The temperature inside the chamber was maintained at 30° C by the circulation of warm water on the outside surface of the chamber. The duration of the ¹H NMR scanning was approximately 1hr.

2.1.3. In Vivo ¹H NMR Spectroscopy

All ¹H NMR scans were conducted with a 9.4 T/31 cm magnet (Magnex Scientific, Abingdon, UK) equipped with an 11 cm gradient coil insert (300 mT/m, 500 ls) and strong custom-designed second order shim coils (Magnex Scientific, Abingdon, UK) [14]. The position of the volume of interest (VOI) was selected based on multi-slice RARE images. The VOI was centered in the left striatum at the level of the anterior commissure. The size of the VOI, which varied from7–12 μL, was adjusted to fit the anatomical structure of the left striatum, as well as to exclude the lateral ventricle and, thus, to minimize partial volume effects (inclusion of a tissue other than the target tissue). The striatum was selected as the area of interest because it consists to a large extent of the medium spiny projection neurons, which are GABA-ergic, and which, more importantly, constitute the initial and preferential target of HD. It is in this structure of the brain and in this neuronal population that HD first manifests itself and its destructive force. At the end stage, following extensive neuronal cell loss in the striatum, the disease evinces itself in other brain areas, such as the cerebral cortex, globus pallidus, and – to a smaller extent – the substantia nigra, the thalamus, the cerebellum, etc [15].

Thirty mice (17 WT and 13 R6/2) were scanned according to the aforementioned procedure. Of the 17 WT mice, 8 were 8 wks old and 9 were 12 wks old; whereas of the 13 R6/2 mice, 7 were 8 wks old and 6 were 12 wks old. Those 30 mice were used in the development of the diagnostic biomarker models (DBMs) of all three analytical mathematical approaches. In addition, 31 unknown mice (11 R6/2 and 20 WT) were also scanned according to the aforementioned procedure and were used to test all three DBMs. All of those 31 unknown mice were extraneous to the development of the three DBMs, and their status had been ascertained via genotyping.

Spectral analysis resulted in the identification and individual quantification of 15 metabolites. By combining the obtained individual absolute concentrations of creatine (Cr) and phosphocreatine (PCr), we created the Cr+PCr and PCr/Cr metabolites (variables) in order to obtain information about the total striatal creatine (free and phosphorylated), as well as about the ratio of those two metabolites. In the case of glycerophosphorylcholine (GPC) and phosphorylcholine (PC), we were not able to separate those two and obtain individual concentrations. We were able, however, to obtain the absolute concentration of the sum of GPC and PC, which represents the total striatal phosphorylated choline. All of the 15 striatal metabolites we were able to identify and quantify individually as a result of the high magnetic field spectrometer we used (9.4 Tesla), as well as the two metabolites (variables) we created, are shown in Table 1.

Table 1.

Names & abbreviations of all metabolites detected, measured, and evaluated in the study.

No.	Metabolite Symbol	Metabolite Name
1	Cr	creatine
2	PCr	phosphocreatine
3	Cr+PCr	creatine + phosphocreatine
4	PCr/Cr	phosphocreatine/creatine
5	GABA	γ-aminobutyric acid
6	Glc	glucose
7	Gln	glutamine
8	Glu	glutamate
9	GSH	glutathione
10	GPC+PC	glycerophosphorylcholine + phosphorylcholine
11	Lac	lactate
12	MM	macromolecules
13	mIns	myo-Inositol
14	NAA	N-acetylaspartate
15	NAAG	N-acetylaspartylglutamate
16	PE	phosphorylethanolamine
17	Tau	Taurine

Since both of our animal groups (WT & R6/2) comprised two age subgroups (8-wk old & 12-wk old mice), the time dependent variable was collapsed, so the developed models would be applicable from 8–12 weeks of age – a most important time period in the progression of the disease in R6/2 mice, as well as a significant portion of the observed lifespan of the R6/2 mice. The development of all of the subsequent clustering DBMs, therefore, was based on the data of the aforementioned 13 R6/2 mice [seven at 8 wks of age & six at 12 wks of age] and 17 WT mice [eight at 8 wks of age & nine at 12 wks of age]. For more details on animal methods, as well as on spectra obtainment and processing, please see our previous study [16].

2.2. STATISTICAL SOFTWARE & GRAPHICS

For all clustering runs, we used the statistical software by NCSS 2007, Kaysville, Utah, USA.

2.3. COMPUTER PROGRAMS

Computer programs were written using MATLAB R2010a by The MathWorks, Inc., Natick, MA, USA.

2.4. DIAGNOSTIC BIOMARKER MODELS (DBMs)

2.4.1. Development of Clustering DBMs

We used the data of our original 30 mice (17 WT and 13 R6/2) to develop all four clustering DBMs, each based on one of the following four common clustering methods: K-means, Fuzzy, Hierarchical, and Medoid Partitioning. For those three clustering methods that allow the preselection of the number of groups (K-means, Fuzzy, and Medoid Partitioning), we set the number of clusters to two since in the disease of our interest, HD, there are only two groups (WT vs. R6/2 mice). As we discussed earlier, that in itself can increase the accuracy of a clustering method considerably. Then, we ran each of those four clustering methods unsupervised, i.e. we input all of our 17 variables (concentrations of 17 metabolites measured by NMR spectroscopy), and assessed their performance. Since our goal was to apply those clustering methods for diagnostic purposes, which means that accuracy is of the utmost importance, we wanted to find out which was the best possible setting of each of those four methods. We assessed the best possible setting of a given clustering method by the following two ways. First, by the clustering results, i.e. by whether or not all 30 of our original mice were classified into the correct cluster (identified correctly in terms of being WT or R6/2). Secondly, by how good the “fitting” of a particular setting is. In general, that is known as “Goodness of Fit.” In the case of the ideal fitting, the clusters are very tight, and their centers are very far apart. In the case of the worst fitting, the clusters are widely dispersed, and their centers are very close to each other. We used the internal statistics of a particular clustering method to assess the fitting of all of its settings. In order to find out which was the best possible setting (both in terms of results and fitting) of a particular clustering method, we used receiver operating characteristic (ROC) curve analysis.

Briefly, ROC curve analysis is a theory of probabilities. It studies two probabilities, namely, sensitivity and (1-specificity), in order to determine a third probability, namely, the area under the curve (AUC). The ROC AUC probability is basically an assessment of the discriminating power of a given variable with respect to the two groups involved. If the AUC of a given variable is equal to 1.00, then that means that according to that variable, the two groups involved can be separated with 100% accuracy. A variable with perfect discrimination between the two groups has an AUC=1.00, whereas a variable with the poorest discrimination between the two groups has an AUC=0.50 (chance probability). For a more detailed account on the properties, methodology, and applications of ROC curve analysis, please see our previous study [1]. Since ROC curve analysis allows us to assess our variables [also referred to henceforward as independent variables (IVs)] in terms of discriminating power with respect to our two groups (WT vs. R6/2), we used the results of ROC curve analysis (Table 2) to determine the best possible setting of a given clustering method by supervising it, i.e. by inputting only those IVs that met a certain AUC threshold value. To be more specific, first we entered only those IVs (metabolite concentrations) that had an AUC > 0.70 (70%), then only those that had an AUC > 0.80, then only those with an AUC > 0.90, and finally only those with an AUC > 0.98. By assessing in each of those cases both the clustering results and the fitting, we were able to determine the best possible setting for each of the four clustering methods.

Table 2.

Rank of all metabolites based on their discriminating power (AUC) from ROC curve analysis.

ROC CURVE ANALYSIS
Metabolite	AUC	AUC Rank
Cr+PCr	1.00000	1
Gln	0.98897	2
Cr	0.98832	3
NAA	0.98198	4
GSH	0.94052	5
GPC+PC	0.90301	6
mIns	0.89978	7
PCr	0.87023	8
PE	0.83667	9
Tau	0.72888	10
NAAG	0.69632	11
Glc	0.58495	12
Glu	0.58179	13
PCr/Cr	0.53852	14
GABA	0.52209	15
Lac	0.52187	16
MM	0.50067	17

Having, thus, determined the best possible setting for each of the four clustering methods, we used that setting to develop a clustering DBM for each of those four clustering methods. A clustering DBM comprises the following: 1) The 30 original mice (17 WT and 13 R6/2) – the WT mice are in rows # 1–17, and the R6/2 mice are in rows # 18–30; 2) the input IVs as determined by the best possible setting; and 3) the unknown mouse is in row #31. If, for example, the best possible setting was attained by using only those IVs that had an AUC > 0.98, then only those IVs (Cr+PCr, Gln, Cr, and NAA)(Table 2) are used by the clustering DBM. That also means that in the case of the unknown mouse, i.e. the mouse whose status we would like to determine, we enter its NMR spectroscopy concentration values for the aforementioned four IVs, i.e. Cr+PCr, Gln, Cr, and NAA.

The underlying rationale upon which a clustering DBM is predicated can be stated as follows: If in a given disease, such as HD in our case, where the normal and the pathological states are well defined, we used a number of subjects from each of the two groups; if the status of all of those original subjects were definitively known (in the case of HD, genotyping is the gold standard); and if we used the best setting of a clustering method, i.e. one that gave us the best separation and discrimination between the two clusters of our original subjects; then we would have the best chance of identifying the status of an unknown subject because this clustering model would have the sole task of deciding into which of the two predetermined and pre-established clusters the unknown subject should be classified based on its data. This clustering DBM can be developed and applied in any disease for diagnostic purposes provided that the pathological and normal states in that disease are well defined.

For comparison purposes, and in a similar fashion as the one outlined above, we also developed unsupervised clustering DBMs, which used all of our 17 IVs.

2.4.2. All Clustering Analyses

We subjected all clustering DBMs (both unsupervised and supervised) to the following three tests:

Test 1

Identification of our original 30 mice, which were intrinsic to the development of all DBMs. This is a necessary first test in that a DBM has to demonstrate that it has the prerequisite discriminating accuracy to classify correctly the original 30 mice, which were used in the development of that DBM. It is by no means a foregone conclusion that a DBM can pass this test with 100% accuracy. This is a mandatory test for a diagnostic model.

Test 2

Identification of 31 unknown mice, which were extraneous to the development of all DBMs. This is the validation test, and as such, it is by far the most important test. A DBM is asked to identify/diagnose 31 unknown mice. These 31 mice were new and different from the 30 original mice used in the development of that DBM. The status of these 31 unknown mice had been determined by genotyping, which is the gold standard in HD. A DBM would be presented with one of those 31 unknown mice at a time and asked to identify/diagnose that single unknown mouse. Typically, the sample size of the validation test is between 1/3 and 1/2 of the original sample size that was used to develop a model. In our case, the validation sample size is > 100% the original sample size (31 vs. 30 respectively). This is both a mandatory and a most important test for a diagnostic model.

Test3

Identification of our 13 original R6/2 mice with respect to their two age groups: 8 wk-old and 12 wk-old. Seven of those R6/2 mice were scanned at the age of 8 weeks and six of them were scanned at the age of 12 weeks. This is a test designed to assess the sensitivity of a DBM with respect to the progression of the disease. Those R6/2 mice that were scanned at the age of 12 weeks are more impaired than those R6/2 mice that were scanned when they were 8 weeks old. This is an optional test for a diagnostic model because it deals exclusively with the population that has the disease (R6/2 mice, in our case). Unlike the preceding two tests, this one does not assess discriminating ability between the normal controls (WT) and those who have the disease (R6/2). It is administered with the sole purpose of showing whether a diagnostic model has a sensitivity that extends outside the area of diagnosis and into the area of the progression of the disease. As such, therefore, this test can only reveal exceptional ability on the part of a diagnostic model, but it cannot constitute a diagnostic criterion per se.

All three of the aforementioned tests were administered in the same manner to all clustering DBMs (both unsupervised and supervised); and all clustering DBMs were assessed, first, for accuracy and, secondly, for clustering fitting.

For all of the clustering analyses, and for all of their settings in connection with the first test, we entered our data (subjects) in the following order: rows #1–17 were the WT mice and rows #18–30 were the R6/2 mice. For all of the clustering analyses, and for all of their settings in connection with the second test, we entered our data (subjects) in the following order: rows #1–17 were the original 17 WT mice, rows #18–30 were the original 13 R6/2 mice, and row #31 was an unknown mouse. For all of the clustering analyses, and for all of their settings in connection with the third test, we entered our data (subjects) in the following order: rows #1–7 were the 8-wk old R6/2, whereas rows #8–13 were the 12-wk old R6/2 mice.

2.4.3. K-Means Clustering Analysis (KMCA)

The K-means clustering algorithm was developed and introduced by Hartigan [4]. It seeks to classify N subjects (observations) with P IVs into K clusters until the within-cluster sum of squares is minimized, that is to say until the within-cluster variance is minimized. KMCA is ideally suited for partitioning a large number of subjects (observations) into a small number of clusters [17].

KMCA conditions

There is only one condition: all IVs have to be continuous.

In our case, all of our IVs are continuous – they are concentrations of metabolites.

Outliers

Despite a number of subjects with outlying metabolite values, we decided to do nothing about them in order to further test not only the KMCA but also the rest of the clustering methods. Moreover, in our previous studies [1,2], where we investigated a number of analytical mathematical approaches and other data analysis/mining methods using the same ¹H NMR spectroscopy data, we made no alterations to the data in connection with outlying observations. Therefore, in order to be able to compare the results of those approaches and methods investigated in those studies with the results of the clustering approaches investigated in this study, we decided to make no alterations to the data here, as well.

Missing Values

One of our R6/2 mice had a missing GSH value. We used the mean GSH value of the R6/2 mice to impute the missing value.

Minimum, Maximum, and Reported Number of Clusters

As we explained above, we set the minimum, maximum, and reported number of clusters equal to 2.

2.4.4. Fuzzy Clustering Analysis (FCA)

The Fuzzy clustering algorithm we used was introduced by Kaufman et al. [3]. FCA is different from all other clustering analyses in that it seeks to ascribe cluster membership probabilities to every data point. For example, p_ik is the probability that subject i (row i) belongs in cluster k. If, let us say, we have 30 subjects and three clusters, then the probability that subject 1 belongs in cluster 1 is p₁₁, the probability that it belongs in cluster 2 is p₁₂, and the probability that it belongs in cluster 3 is p₁₃. As is the case with every probability, p_ik ≥ 0 *with i=1, 2, 3, … N and k=1, 2, 3, … K (N is the total number of subjects, and K is the total number of clusters)+ and p₁₁+ p₁₂+ p₁₃=1. Instead of classifying a subject into one, and only one, cluster, which is what all the other clustering analyses do, FCA classifies a subject into all clusters according to its cluster membership probabilities (p_ik). This “fuzzification” in the classification of a subject into a particular cluster renders FCA – at least theoretically – less sensitive to outliers. FCA seeks to minimize the function F, which comprises all cluster membership probabilities and distances in such a way that their grand sum represents the total amount of dissimilarity, or the total amount of dispersion, for all subjects in all clusters.

FCA conditions

As far as FCA is concerned, there are no conditions.

Missing Values

Once again, we used the same method as described above in the KMCA section to impute the one missing value from our data.

Distance Method

We selected Euclidean distance (the shortest distance between two points) as opposed to Manhattan distance (the distance defined by the sum of the two sides of a right angle triangle that are perpendicular to each other).

Scaling Method

We chose Standard Deviation as the scaling method for our continuous IVs.

Minimum, Maximum, and Reported Number of Clusters

Just as we did above in the case of KMCA, we set the minimum, maximum, and reported number of clusters equal to 2.

2.4.5. Hierarchical Clustering Analysis (HCA)

In addition to KMCA and FCA, we investigated all eight of the agglomerative hierarchical clustering algorithms that are available in the NCSS 2007 statistical software. Of those eight algorithms, the “Group Average” gave us the best results, and it is to that we will refer henceforth.

As we mentioned earlier, the objective of any clustering analysis is to classify N subjects with P IVs into K clusters so that both the within-cluster similarities and the between-cluster dissimilarities are maximized. Hierarchical Clustering Analysis (HCA) seeks to accomplish that via the following way: first, assign every subject into a cluster all by itself (N subjects into N clusters); then calculate all distances among all clusters; then take the clusters C₁ and C₂, to which the shortest between-cluster distance corresponds, and merge them, i.e. place the subjects in those two clusters into one new cluster; and start the process anew and continue until there is one cluster left in the end.

For our runs, we chose the following:

Clustering Method (algorithm)

As was mentioned above, we chose the Group Average algorithm.

Distance Method

We selected Euclidean distance.

Scaling Method

We chose Standard Deviation.

Cluster Cutoff

Since we knew we had two groups, we would select the cluster cutoff value that gave us two clusters.

2.4.6. Medoid Partitioning Clustering Analysis (MPCA)

We tried two medoid algorithms: the one introduced by Spath [18] and the one introduced by Kaufman et al. [3]. Of those two, the latter gave us better results, and our referring to MPCA henceforth will pertain only to the Kaufman and Rousseeuw algorithm.

The algorithm of MPCA [the Kaufman and Rousseeuw algorithm (PAM: Partitioning around Medoids)] [3] seeks, via an iterative cluster member exchange, to minimize the total distance between the members within each cluster.

For our runs, we chose the following:

Clustering Method (algorithm)

We used the Kaufman – Rousseeuw algorithm.

Distance Method

We selected Euclidean distance.

Scaling Method

We chose Standard Deviation.

Minimum, Maximum, and Reported Number of Clusters

We set all three equal to 2.

3. RESULTS

3.1. K-MEANS CLUSTERING ANALYSIS (KMCA)

First, we ran KMCA unsupervised, i.e. with all 17 IVs (metabolites). Pertaining to the first test, KMCA correctly classified all of the 30 original mice into their appropriate group as either R6/2 (Cluster 2) or WT (Cluster 1) [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)]. Therefore, in this case, the sensitivity=1 and the (1-specificity)=0.

The positive Likelihood Ratio [(+)LR] [19,20] is:

(+)LR= (sensitivity)/(1-specificity) = 1/0 → ∞

The negative Likelihood Ratio [(−)LR] [19,20] is:

(−)LR= (1-sensitivity)/(specificity) = 0/1=0

Table S1 (Supplementary Material) shows in detail the above results. More specifically, the unsupervised KMCA classified all of the WT mice (17) into Cluster 1 and all of the R6/2 mice (13) into Cluster 2.

The general results of all KMCA runs, including those of the aforementioned run, appear in Table 3.

Table 3.

Summary of the results of all four clustering methods in connection with all three tests. Each clustering method was tested both in an unsupervised and ROC-supervised way. All unsupervised settings were run with all 17 IVs. In the case of the first and second test, all clustering methods were run with the top four most significant IVs according to the ROC curve analysis performed between the WT and the R6/2 mice. In the case of the third test, all clustering methods were run with the top two most significant IVs according to the R6/2 ROC curve analysis performed between the 8-wk old and the 12-wk old R6/2 mice. The internal statistic of a clustering method assesses the clustering fitting of that method in a given setting.

SUMMARY OF TEST RESULTS
	KMCA		FCA		HCA		MPCA
	Unsupervised (17 Variables)	ROC-Supervised (4 Variables)	Unsupervised (17 Variables)	ROC-Supervised (4 Variables)	Unsupervised (17 Variables)	ROC-Supervised (4 Variables)	Unsupervised (17 Variables)	ROC-Supervised (4 Variables)
TEST 1 ID of original 30 mice	% Correct		% Correct		% Correct		% Correct
17 WT	17/17 (100%)	17/17 (100%)	17/17 (100%)	17/17 (100%)		17/17 (100%)	17/17 (100%)	17/17 (100%)
13 R6/2	13/13 (100%)	13/13 (100%)	13/13 (100%)	13/13 (100%)		13/13 (100%)	13/13 (100%)	13/13 (100%)
Total	30/30 (100%)	30/30 (100%)	30/30 (100%)	30/30 (100%)	*	30/30 (100%)	30/30 (100%)	30/30 (100%)
(+) Likelihood Ratio	1/0 → ∞	1/0 → ∞	1/0 → ∞	1/0 → ∞		1/0 → ∞	1/0 → ∞	1/0 → ∞
(−) Likelihood Ratio	0/1=0	0/1=0	0/1=0	0/1=0		0/1=0	0/1=0	0/1=0
Internal Statistic	%Var=65.76	%Var=22.04	AS=0.312	AS=0.655	CC=0.873	CC=0.913	AS=0.312	AS=0.655
TEST 2 ID of 31 unknown mice
20 WT	20/20 (100%)	20/20 (100%)	20/20 (100%)	20/20 (100%)		20/20 (100%)	20/20 (100%)	20/20 (100%)
11 R6/2	10/11 (90.91%)	11/11 (100%)	11/11 (100%)	11/11 (100%)		11/11 (100%)	9/11 (81.82%)	10/11 (90.91%)
Total	30/31 (96.77%)	31/31 (100%)	31/31 (100%)	31/31 (100%)	*	31/31 (100%)	29/31 (93.55%)	30/31 (96.77%)
(+) Likelihood Ratio	0.909/0 → ∞	1/0 → ∞	1/0 → ∞	1/0 → ∞		1/0 → ∞	0.818/0 → ∞	0.909/0 → ∞
(−) Likelihood Ratio	0.091	0/1=0	0/1=0	0/1=0		0/1=0	0.182	0.091
TEST 3 ID of original 13 R6/2 mice		(R6/2)-ROC-Supervised (2 Variables)		(R6/2)-ROC-Supervised (2 Variables)		(R6/2)-ROC-Supervised (2 Variables)		(R6/2)-ROC-Supervised (2 Variables)
7 R6/2 8 wks old	7/7 (100%)	7/7 (100%)	7/7 (100%)	7/7 (100%)			7/7 (100%)	7/7 (100%)
6 R6/2 12 wks old	6/6 (100%)	6/6 (100%)	6/6 (100%)	6/6 (100%)			6/6 (100%)	6/6 (100%)
Total	13/13 (100%)	13/13 (100%)	13/13 (100%)	13/13 (100%)	*	*	13/13 (100%)	13/13 (100%)
(+) Likelihood Ratio	1/0 → ∞	1/0 → ∞	1/0 → ∞	1/0 → ∞			1/0 → ∞	1/0 → ∞
(−) Likelihood Ratio	0/1=0	0/1=0	0/1=0	0/1=0			0/1=0	0/1=0
Internal Statistic	%Var=66.12	%Var=33.78	AS=0.235	AS=0.525	CC=0.832	CC=0.840	AS=0.235	AS=0.525

^(*)The results of this setting made little sense

(%Var): Percent Variation – the lower, the better the clustering

(AS): Average Silhouette – the higher, the better the clustering

(CC): Cophenetic Correlation – the higher, the better the clustering

The Goodness-of-Fit criterion for KMCA is based on the within-cluster sum of squares, which is precisely what the KMCA algorithm is striving to minimize [4]. With every run, we obtained a value for the Percent of Variation, which is the percentage of the within-cluster sum of squares for the number of clusters reported with respect to the within sum of squares without clustering [4,17]. The smaller the Percent of Variation, the better. In the above run of KMCA, i.e. when we entered all 17 IVs and ran it unsupervised, and with regard to the first test, the Percent of Variation was 65.76.

We then subjected the unsupervised KMCA to the second test. The order of the entry of the data was as follows: the first 17 subjects (#1–17) were the WT mice, the next 13 subjects (#18–30) were the R6/2 mice. This order remained fixed for all of the KMCA runs in connection with the second test. As we mentioned above, we had 31 unknown mice, which were extraneous to all of our mathematical analyses, and the status of which had been determined via genotyping. We entered each of those 31 unknown mice one at a time in row #31, and then ran the KMCA 31 times, each time entering the data of one of the 31 unknown mice in row #31, and each time asking the KMCA to classify the unknown mouse into one of the two groups. In effect, what we did here was to ask the KMCA each time to make a decision in terms of which of the two clusters (WT or R6/2) the “unknown” mouse in row #31 belonged. KMCA correctly determined the status of 30/31 unknown mice [20/20 WT mice (100% correct) and 10/11 R6/2 mice (90.91% correct), with a total accuracy of 30/31 unknown mice (96.77% correct)]. Therefore, for the second test, KMCA exhibited a sensitivity=0.909 and a (1-specificity)=0 [(+)LR=0.909/0 → ∞ and (−)LR=0.091].

Next, we subjected the unsupervised KMCA to our third test. More specifically, we wanted to know whether unsupervised KMCA was sensitive enough to detect the metabolomic differences caused by the progression of the disease between our two R6/2 subgroups, i.e. between the 8-wk old R6/2 and the 12-wk old R6/2 mice. Physiologically, we know that the progression of HD will effect alterations in the metabolite concentrations of the cells in the striatum area of the brain. A diagnostic model, therefore, should be sensitive enough to detect those alterations in the time span of four weeks. We entered all of the 17 IVs and our 13 R6/2 mice [(7) 8-wk old & (6) 12-wk old] in the following manner: rows #1–7 the seven 8-wk old ones and rows #8–13 the six 12-wk old ones. Unsupervised KMCA correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)]. In this case, the sensitivity=1 and the (1-specificity)=0. For this run, the Percent of Variation was 66.12.

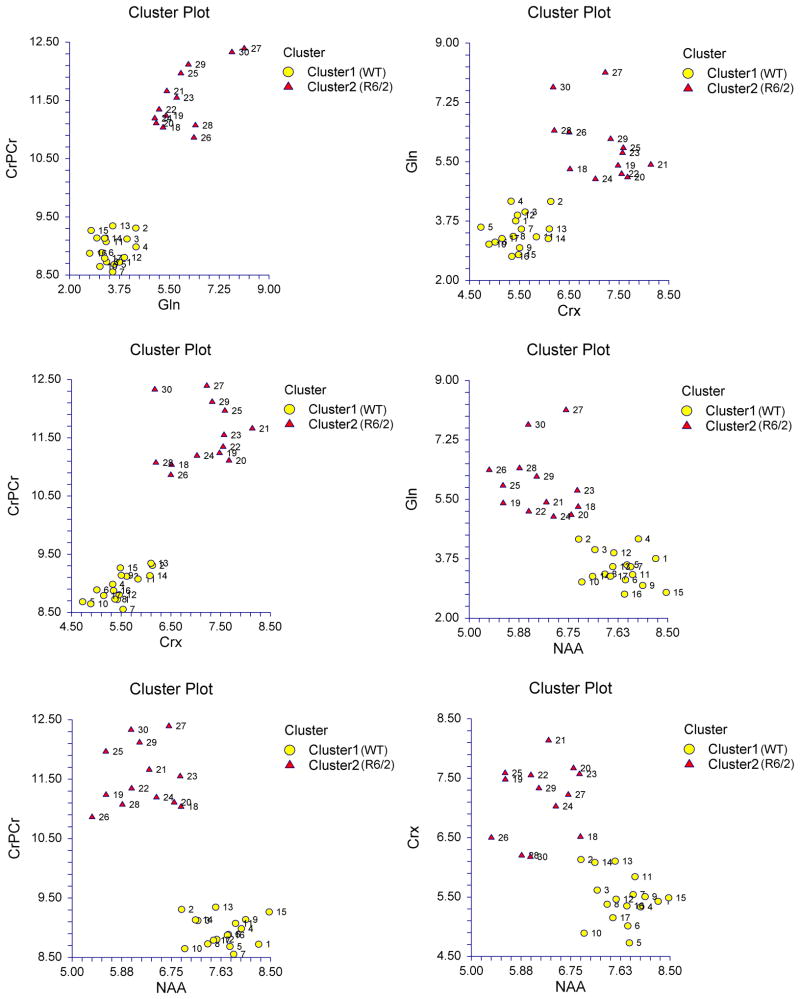
Since our goal was to find the best possible KMCA setting, in other words, the one that would give us the best separation between the WT & the R6/2 mice, and use that setting to develop a DBM (diagnostic biomarker model), we also availed ourselves of the results of the ROC curve analysis. We therefore ran the KMCA with the top ten most significant IVs according to ROC curve analysis (AUC > 70%) (see Table 2); then with the top nine most significant IVs (AUC > 80%); then with the top seven IVs (AUC > 90%); and finally, with the top four most significant IVs (AUC > 98%). In every one of those ROC-supervised settings, KMCA correctly identified and classified our two groups of mice. The best setting, however, was the one in which we used the top four most significant IVs (AUC > 98%) because that is the one that yielded the lowest Percent of Variation (22.04). The Percent Variation values for the intermediate settings were as follows: 43.67 for the top 10 IVs, 39.46 for the top 9 IVs, and 33.29 for the top 7 IVs. We should point out here three things: 1) The best ROC-supervised KMCA setting represented a considerable improvement over the unsupervised KMCA setting (22.04 vs. 65.76 Percent of Variation respectively). 2) All of the above ROC-supervised KMCA settings were better than the unsupervised KMCA setting according to their aforementioned Percent of Variation values. 3) The best KMCA setting was, therefore, the best ROC-supervised KMCA setting. Table S2 shows the results of the best ROC-supervised KMCA setting (with top four IVs and Percent Variation = 22.04). It correctly identified all of the 30 original mice [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)] [sensitivity=1; (1-specificity)=0]. More specifically, all of the WT mice were classified into Cluster 1, whereas all of the R6/2 into Cluster 2. Dist 1 and Dist 2 are the distances of each subject from the center of Cluster 1 and Cluster 2 respectively. Figure 1(A–F) depicts the separation of the two groups (WT & R6/2) into two clusters (Cluster 1 and Cluster 2 respectively) according to the aforementioned best KMCA setting; the top four most significant IVs are plotted against each other in the six possible ways. It is worth noting here that those biomarkers (metabolites) that have larger AUCs yielded clusters that are tighter and more separated than biomarkers that have smaller AUCs. For example, in Figure 1A, wherein Cr+PCr [most significant biomarker according to ROC curve analysis (AUC=1.00) (see Table 2)] is plotted vs. Gln [second most significant biomarker (AUC=0.98897)], the resulting clusters have greater separation and smaller spreads than the clusters in the Figure 1F resulting from plotting Cr [third most significant biomarker (AUC=0.98832)] vs. NAA [fourth most significant biomarker (AUC=0.98198)]. As one moves from Figure 1A to 1F, one can observe that the two clusters become more dispersed and their separation distance diminishes.

Figure 1. Separation of the original WT & R6/2 mice by the best KMCA setting (ROC-supervised KMCA).

The top four most significant IVs (AUC > 98%), namely, Cr+PCr, Gln, Cr, and NAA, yielded not only the best ROC-supervised KMCA setting but also the best KMCA setting. Those four IVs are plotted against each other (A–F). The WT mice (#1–17) are depicted in Cluster 1 (yellow circles), whereas the R6/2 mice (#18–30) are depicted in Cluster 2 (red triangles). IVs with larger AUCs yielded clusters that are tighter and more separated than IVs with smaller AUCs. For example, in (A), wherein Cr+PCr [most significant IV according to ROC curve analysis (AUC=1.00) (see Table 2)] is plotted vs. Gln [second most significant IV (AUC=0.98897)], the resulting clusters have greater separation and smaller spreads than the clusters in (F) resulting from plotting Cr [third most significant IV (AUC=0.98832)] vs. NAA [fourth most significant IV (AUC=0.98198)]. As one moves from (A) to (F), one can observe that the two clusters become more dispersed and their separation distance diminishes.

As we stated above, the most difficult task of a clustering analysis, by far, is the determination of the appropriate number of clusters into which a given set of data can be partitioned. Since in our case that is known a priori, in other words, we know beforehand that we have only two groups, that can bestow upon a clustering analysis a large advantage and put it in a position where it can be very successful and accurate. Taking advantage of this theoretical observation, we subjected the best KMCA setting – the one that gave us the best separation between the WT and the R6/2 mice, i.e. the setting that gave us the lowest total dissimilarity (dispersion) between the two clusters (Percent Variation = 22.04) – to our second test. Using the same methodology as in the case of the unsupervised KMCA, we ran this ROC-supervised KMCA setting 31 times in order to identify the status of the 31 unknown mice. It correctly determined the status of all of the 31 unknown mice [20/20 WT mice (100% correct) and 11/11 R6/2 mice (100% correct), with a total accuracy of 31/31 unknown mice (100% correct)] [sensitivity=1; (1-specificity)=0]. Table S3 shows the results of the best KMCA setting with respect to one of the unknown mice, which is in row #31. This ROC-supervised KMCA correctly identified that unknown mouse as an R6/2 (confirmed via genotyping); more specifically, it classified all of the WT mice (rows #1–17) into Cluster 1, all of the R6/2 mice (rows #18–30) into Cluster 2, and the unknown mouse (row #31) into Cluster 2, i.e. in the same cluster as all of the R6/2 mice. We should note here that the total accuracy of the unsupervised KMCA with regard to the second test was 96.77% (30/31 unknown mice), whereas that of the ROC-supervised KMCA was 100% (31/31 unknown mice) [Table 3].

Subjecting the best ROC-supervised setting of KMCA to the third test was the next task. The third test concerns itself exclusively with the R6/2 mice; more specifically, it assesses the ability of a given model to discriminate between the two R6/2 groups: the 8-wk old vs. the 12-wk old. The ROC curve analysis with which we supervised KMCA in the first and second test, and the results of which appear in Table 2, was designed to assess the ability of all 17 IVs to discriminate between the WT and the R6/2 mice. Clearly, as far as the third test was concerned, we had to perform another ROC curve analysis, one that would deal exclusively with the 13 original R6/2 mice, and one that would assess all of the 17 IVs in terms of their ability to discriminate between the 8-wk old and the 12-wk old R6/2 mice. The top 5 most significant IVs (metabolites) in the discrimination between the two R6/2 groups according to their AUC value as determined by the R6/2 ROC curve analysis are: 1) TTau (AUC=0.97515) [Transformed Tau in order to meet normality criteria], 2) GPC+PC (AUC=0.95167), 3) Glu (AUC=0.94598), 4) Lac (AUC=0.94456), and 5) Gln (AUC=0.94319). The best R6/2 ROC-supervised KMCA setting was the one that employed only the top two most significant IVs (AUC>95%), i.e. TTau and GPC+PC; this setting gave us the lowest Percent of Variation value (33.78) of all settings; and it is this setting that we used for the third test. The R6/2-ROC-supervised KMCA correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)] [sensitivity=1; (1-specificity)=0]. Table S4 shows those results. More specifically, the R6/2-ROC-supervised KMCA classified all of the 8 wk-old R6/2 mice into Cluster 1 and all of the 12 wk-old R6/2 mice into Cluster 2 (Percent of Variation=33.78). Compared with its counterpart, i.e. the unsupervised KMCA setting (Percent of Variation=66.12), the R6/2-ROC-supervised KMCA was a considerably better setting (Percent of Variation=33.78), that is to say, it yielded tighter clusters.

All of the aforementioned test results of KMCA are summarized in Table 3.

3.2. FUZZY CLUSTERING ANALYSIS (FCA)

We first ran FCA unsupervised, i.e. with all 17 IVs. In connection with the first test, the unsupervised FCA correctly classified all of the 30 original mice into their appropriate group as either R6/2 or WT [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)] [sensitivity=1; (1-specificity)=0].

There are three Goodness-of-Fit criteria for FCA, all of which are discussed at great length by Kaufman et al. [3]. We chose the most common, namely, the “Silhouette Coefficient” (SC). SC takes values from -1 to 1. If SC=0, then the method of classifying a subject into a particular cluster is no better than the chance method (50-50). If SC=1, then a subject is perfectly classified; the amount of dissimilarity between that subject and other subjects in the same cluster is extremely small in comparison with the amount of dissimilarity between it and subjects from other clusters. If SC=-1, then a different classification method is warranted. If one calculates the average value of all SCs (for all subjects), that constitutes the Average Silhouette (AS) value for the whole clustering analysis for the number of the reported clusters. The closer the value of the Average Silhouette is to 1, the better the classification by fuzzy clustering is. We used the Average Silhouette (AS) to assess the clustering fitting of all FCA settings.

In connection with the first test, the aforementioned unsupervised FCA yielded: Average Silhouette = 0.311791.

Having used the same methodology as the one explained in the case of KMCA, we subjected the unsupervised FCA to the second test. It correctly determined the status of all of the 31 unknown mice [20/20 WT mice (100% correct) and 11/11 R6/2 mice (100% correct), with a total accuracy of 31/31 unknown mice (100% correct)] [sensitivity=1; (1-specificity)=0].

In connection with the third test, the unsupervised FCA correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)] [sensitivity=1; (1-specificity)=0]. In this case, Average Silhouette = 0.234672.

Just as we did in the case of KMCA, we ran FCA with the top ten most significant IVs according to ROC curve analysis (AUC > 70%) [Table 2]; then with the top nine most significant IVs (AUC > 80%); then with the top seven IVs (AUC > 90%); and finally, with the top four most significant IVs (AUC > 98%). In every one of those settings, the ROC-supervised FCA correctly identified and classified our two groups of mice. The best setting, however, just like in the case of KMCA, was the one in which we used the top four most significant IVs (AUC > 98%) because that is the one that yielded the highest value for the Average Silhouette [Average Silhouette = 0.654794]. This, incidentally, shows that, at least in clustering analysis, using more IVs is not necessarily better.

Table S5 shows the results of the aforementioned best FCA setting (top four most significant IVs) in connection with the first test. This ROC-supervised FCA correctly identified all of the 30 original mice [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)] [sensitivity=1; (1-specificity)=0]. More specifically, all of the WT mice were classified into Cluster 1, whereas all of the R6/2 into Cluster 2. Prob in 1 & Prob in 2 are the membership probabilities of each subject in Cluster 1 and Cluster 2 respectively. The Cluster Medoids Section of Table S5 shows the cluster average metabolite concentration values with respect to the four metabolites (IVs) (top four most significant according to ROC curve analysis) used in this setting. Subjects # 7 and # 29 were the medoids (closest to the center) of Cluster 1 and Cluster 2 respectively for this setting, as they had the highest probability of belonging to their respective cluster (0.9111 and 0.8826 respectively).

Next, we subjected this ROC-supervised FCA to the second test in the same manner as we did in the case of KMCA. The ROC-supervised FCA correctly determined the status of all of the 31 unknown mice [20/20 WT mice (100% correct) and 11/11 R6/2 mice (100% correct), with a total accuracy of 31/31 unknown mice (100% correct)] [sensitivity=1; (1-specificity)=0]. Table S6 shows the results of the ROC-supervised FCA with respect to one of the unknown mice, which is in row #31. The ROC-supervised FCA correctly identified that unknown mouse as a WT (confirmed via genotyping); more specifically, it classified all of the WT mice (rows #1–17) into Cluster 1, all of the R6/2 mice (rows #18–30) into Cluster 2, and the unknown mouse (row #31) into Cluster 1, i.e. in the same cluster as all of the WT mice.

Using the R6/2 ROC curve analysis, explained above in the case of KMCA, we subjected the R6/2-ROC-supervised FCA to the third test. It correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)] [sensitivity=1; (1-specificity)=0]. In this case, Average Silhouette = 0.525337. Table S7 shows those results. More specifically, the R6/2-ROC-supervised FCA classified all of the 8 wk-old R6/2 mice into Cluster 1 and all of the 12 wk-old R6/2 mice into Cluster 2. The Cluster Medoids Section shows the cluster average metabolite concentration values with respect to the two metabolites TTau and GPC+PC (top two most significant according to the R6/2 ROC curve analysis) (AUC>95%) used in this setting. Subjects # 3 and # 10 were the medoids (closest to the center) of Cluster 1 and Cluster 2 respectively for this setting, as they had the highest probability of belonging to their respective cluster (0.9199 and 0.9159 respectively).

As was the case with KMCA, the ROC-supervised settings of FCA were considerably better than their respective unsupervised counterparts in that they yielded tighter clusters; the former had considerably higher Average Silhouette value than the latter.

All of the aforementioned test results of FCA are summarized in Table 3.

3.3. HIERARCHICAL CLUSTERING ANALYSIS (HCA)

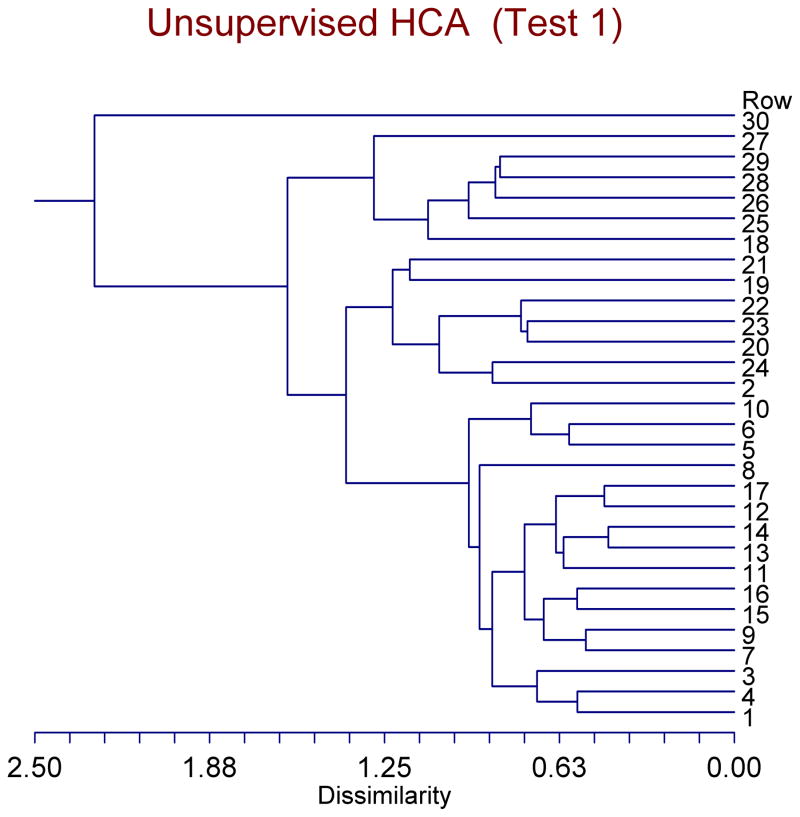
In the same manner we did in the case of KMCA and FCA, we tested the unsupervised HCA with our three tests. The unsupervised HCA failed all of our three tests. In each of those tests, the unsupervised HCA yielded results that made little sense. Figure 2 depicts the results of the unsupervised HCA in connection with the first test. Rows #1–17 are the WT mice, whereas rows #18–30 are the R6/2 mice. Looking in the area where there are only two clusters (Dissimilarity range of ~ 1.63–2.26), one can see that subject #30 was classified into one cluster all by itself, and that all other 29 subjects were classified into the other cluster. This classification makes little sense.

Figure 2. Dendrogram classification of the original mice (17 WT & 13 R6/2) according to unsupervised HCA.

Rows #1–17 are the WT mice, whereas rows #18–30 are the R6/2 mice. Looking at the area where there are only two clusters (Dissimilarity range of ~ 1.63–2.26), one can see that subject #30 was classified into one cluster all by itself, and that all other 29 subjects were classified into the other cluster. This classification makes little sense.

The Goodness-of-Fit criteria for HCA are 1) the Cophenetic Correlation (CC) coefficient, which measures the degree of similarity (the closer to 1 it is, the better); 2) Δ(0.5); and 3) Δ(1.0) [21,17]. The last two measure the degree of dissimilarity, and, hence, the closer to 0 they are, the better [17]. With respect to the first and third test, the aforementioned unsupervised HCA gave the following CC coefficients respectively: 0.873 and 0.832.

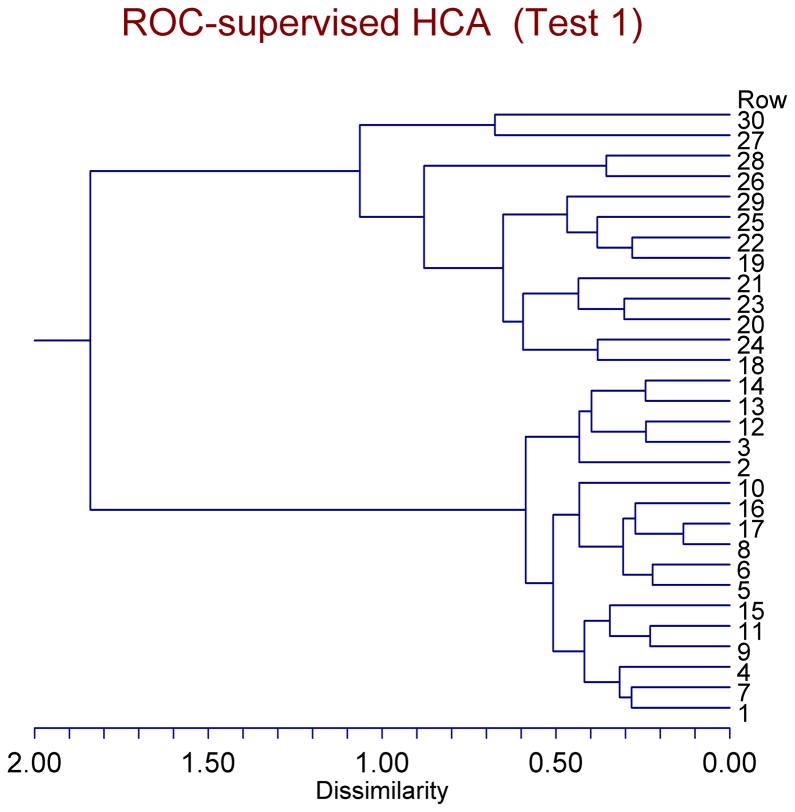
Next, we ran ROC-supervised settings of HCA. Just as we did with our previous clustering analyses, we ran HCA with the top 10 most significant IVs (AUC > 70%) according to ROC curve analysis, then with the top 9 IVs (AUC > 80%), then with the top 7 IVs (AUC > 90%), and finally with the top 4 IVs (AUC > 98%). ROC-supervised HCA failed the first test, i.e. to classify correctly all of the 30 original mice into the two groups (clusters) (WT and R6/2), when run with the top 10 most significant IVs (AUC > 70%) [17/17 WT mice (100% correct) & 12/13 R6/2 mice (92.31% correct) → with a total accuracy of 29/30 original mice (96.67% correct)]. However, ROC-supervised HCA did correctly identify and classify all of the 30 original mice into the two groups in the last three settings, i.e. when we used the top 9, top 7, and top 4 most significant IVs. Of those last three successful settings, the last one [with the top 4 most significant IVs according to ROC curve analysis (AUC > 98%)] was the best setting of all ROC-supervised, as well as of all unsupervised, HCA settings in that it yielded the highest Cophenetic Correlation coefficient (0.913287) and the lowest Δ(0.5) *0.171784+ and Δ(1.0) *0.204949+. This ROC-supervised HCA, with the top 4 most significant IVs, as was mentioned, successfully passed our first test: [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)] [sensitivity=1; (1-specificity)=0]. Figure 3 depicts, in the form of a dendrogram, the results of the best ROC-supervised HCA in connection with the first test. Rows #1–17 are the WT mice, whereas rows #18–30 are the R6/2 mice. Looking in the area where there are only two clusters (Dissimilarity range of ~ 1.1–1.8), one can see that subjects # 1–17 (all of the WT mice) were classified into the lower cluster, whereas subjects #18–30 (all of the R6/2 mice) were classified into the upper cluster.

Figure 3. Dendrogram classification of the original mice (17 WT & 13 R6/2) according to ROC-supervised HCA.

Rows #1–17 are the WT mice, whereas rows #18–30 are the R6/2 mice. The ROC-supervised HCA correctly identified all of the 30 mice. Looking in the area where there are only two clusters (Dissimilarity range of ~ 1.1–1.8), one can see that subjects # 1–17 (all of the WT mice) were classified into the lower cluster, whereas subjects #18–30 (all of the R6/2 mice) were classified into the upper cluster. The top four most significant IVs (AUC > 98%) according to ROC curve analysis were used in this setting, and the Cophenetic Correlation Coefficient is 0.913287.

In connection with the second test, the aforementioned ROC-supervised HCA correctly determined the status of all of the 31 unknown mice [20/20 WT mice (100% correct) and 11/11 R6/2 mice (100% correct), with a total accuracy of 31/31 unknown mice (100% correct)] [sensitivity=1; (1-specificity)=0]. Figure S1 shows, in the form of a dendrogram, the results of the ROC-supervised HCA in connection with the second test, and with respect to one of the unknown mice, which is in row #31. Rows #1–17 are the WT mice, whereas rows #18–30 are the R6/2 mice. The ROC-supervised HCA correctly identified that unknown mouse as an R6/2 (confirmed via genotyping). More specifically, looking in that area of the dendrogram where there are only two clusters (Dissimilarity range of ~ 1.2–1.7), one can see that subjects # 1–17 (all of the WT mice) were classified into the lower cluster, whereas subjects #18–30 (all of the R6/2 mice) and # 31 (the unknown mouse) were classified together into the upper cluster.

Using the R6/2 ROC curve analysis, we subjected the R6/2-ROC-supervised HCA to the third test. As was the case with all of the unsupervised HCA settings, the results of the R6/2-ROC-supervised HCA made little sense. In a dendrogram presentation, Figure S2 depicts the results of the R6/2-ROC-supervised HCA in connection with the third test. Rows #1–7 are the 8 wk-old R6/2 mice, whereas rows #8–13 are the 12 wk-old R6/2 mice. Looking in the area where there are only two clusters (Dissimilarity range of ~ 1.4–2.4), one can see that subject #13 was classified all by itself into the upper cluster, whereas all of the remaining subjects were classified into the lower cluster. That, of course, makes little sense. The CC coefficient was 0.840.

We should point out here that, just like in the case of the previous two clustering methods, the ROC-supervised settings of HCA exhibited better clustering ability than the unsupervised HCA as was indicated by the CC (Cophenetic Correlation) coefficient, including the case of the R6/2-ROC-supervised HCA, even though it failed the third test. We observed that the successful ROC-supervised HCA settings, including the 31 settings for the 31 unknowns, all had a CC > 0.884, with 91% of those settings having a CC > 0.900.

All of the aforementioned test results of HCA are summarized in Table 3.

3.4. MEDOID PARTITIONING CLUSTERING ANALYSIS (MPCA)

With respect to the first test, the unsupervised MPCA correctly classified all of the 30 original mice into their appropriate group as either R6/2 (Cluster 2) or WT (Cluster 1) [17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct)] [sensitivity=1; (1-specificity)=0].

The Goodness-of-Fit criterion for MPCA is the Silhouette Coefficient (SC), or simply Silhouette Value, which was discussed at length in the Fuzzy Clustering Analysis section earlier [3]. The average value of all individual SC values constitutes the Average Silhouette (AS) value for the whole clustering analysis for the number of the reported clusters. Once again, the closer this value is to 1, the better the classification, or partitioning, by the MPCA. The aforementioned unsupervised MPCA gave AS=0.312 in connection with the first test.

Pertaining to the second test, the unsupervised MPCA incorrectly classified 2 out of the 31 unknown mice. More specifically, it correctly classified 20/20 WT mice (100% correct) and 9/11 R6/2 mice (81.82% correct), with a total accuracy of 29/31 unknown mice (93.55% correct) [sensitivity=0.818; (1-specificity)=0; (+)LR=0.818/0 → ∞; (−)LR=0.182].

With regard to the third test, the unsupervised MPCA correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)] [sensitivity=1; (1-specificity)=0]. In this case the AS=0.235, which is the same value as the one yielded by the unsupervised FCA in connection with this test. Table S8 shows the above results. More specifically, the unsupervised MPCA classified all of the 8 wk-old R6/2 mice into Cluster 1 and all of the 12 wk-old R6/2 mice into Cluster 2. The Average Silhouette (AS) value was 0.235. “Average Distance Within” is the average distance of a subject with respect to all other members of the same cluster, whereas “Average Distance Neighbor” is the average distance of a subject with respect to all members of the other cluster.

Availing ourselves of the results of the ROC curve analysis (Table 2), we ran MPCA first with the top 10 most significant IVs (AUC > 70%), then with the top 9 IVs (AUC > 80%), then with the top 7 IVs (AUC > 90%), and finally with the top 4 IVs (AUC > 98%). In every one of those settings, the ROC-supervised MPCA correctly identified and classified the 30 original mice into the two groups (clusters) (WT and R6/2). The best setting, however, just like in the case of all previously discussed clustering analyses, was the one in which we used the top four most significant IVs (AUC > 98%) because that is the one that yielded the highest value for the Overall Average Silhouette (AS=0.6548). More specifically, the results of the best ROC-supervised MPCA (top four IVs) pertaining to the first test were as follows: 17/17 WT mice (100% correct) & 13/13 R6/2 mice (100% correct) → with a total accuracy of 30/30 original mice (100% correct) [sensitivity=1; (1-specificity)=0]. Table S9 shows those results. As can be seen, all of the WT mice (rows #1–17) were classified into Cluster 1, whereas all of the R6/2 mice (rows #18–30) were classified into Cluster 2. The Average Silhouette (AS) value was 0.655.

In connection with the second test, the ROC-supervised MPCA misclassified 1 out of the 31 unknown mice. More specifically, it correctly classified 20/20 WT mice (100% correct) and 10/11 R6/2 mice (90.91% correct), with a total accuracy of 30/31 unknown mice (96.77% correct) [sensitivity=0.909; (1-specificity)=0; (+)LR=0.909/0 → ∞; (−)LR=0.091]. Table S10 shows the misclassification of the aforementioned unknown mouse. As can be seen, the unknown mouse (row #31), whose status had been determined to be R6/2 by genotyping, was classified into Cluster 1, together with all the WT mice (rows #1–17). All of the R6/2 mice (rows #18–30) were classified into Cluster 2. It is worth pointing out here that the fact that the individual Silhouette Value of the unknown mouse (row #31) is close to zero (0.0157) indicates that the decision on the classification of that mouse was hardly better than the chance decision (50-50).

With regard to the third test, the R6/2-ROC-supervised MPCA correctly identified and classified all of our R6/2 mice into their respective two subgroups [(Cluster 1): 7/7 8 wk-old R6/2 mice (100% correct) & (Cluster 2): 6/6 12 wk-old R6/2 mice (100% correct) → with a total accuracy of 13/13 original R6/2 mice (100% correct)] [sensitivity=1; (1-specificity)=0]. In this case, AS = 0.525. Table S11 shows those results. As can be seen, the R6/2-ROC-supervised MPCA classified all of the 8 wk-old R6/2 mice into Cluster 1 and all of the 12 wk-old R6/2 mice into Cluster 2. By direct comparison of the R6/2-ROC-supervised MPCA (Table S11) with the unsupervised MPCA (Table S8), one can see that the former constitutes a considerable improvement of the latter. The individual Silhouette value of every subject is higher in the case of the R6/2-ROC-supervised MPCA, indicating a considerably better overall clustering power. For instance, looking at the most difficult subject in terms of classification (row #8), one can see that the Silhouette value of that subject in the R6/2-ROC-supervised MPCA is nearly sixteen times higher than the one in the unsupervised MPCA (0.1949 vs. 0.0122).

All of the aforementioned test results of MPCA are summarized in Table 3.

4. DISCUSSION

Our results demonstrate that certain clustering methods can be employed for the development of clustering diagnostic biomarker models (DBMs) that can render a differential diagnosis of a single unknown subject in diseases where the boundaries between the pathological and the normal are well defined, such as neurodegenerative diseases, cancer, etc. (Table 3). In particular, FCA passed all three of our tests with 100% accuracy, both when run unsupervised and when run supervised by ROC curve analysis. The ROC-supervised KMCA also passed all three of our tests with 100% accuracy.

More specifically, of all the clustering methods we investigated, FCA was the only one to pass all three of our tests both unsupervised and when supervised by ROC curve analysis. The fact, therefore, that FCA proved to be the most accurate and the most consistent clustering method in our study, provides strong evidence for the robustness of the FCA algorithm and, more importantly, for its suitability for diagnostic applications. Given that the ROC-supervised FCA evinced considerably greater clustering ability than the unsupervised FCA [greater AS value both for Test 1 and 3 (Table 3)], it stands to reason that FCA aided by ROC curve analysis is, according to our investigation, the best clustering method for the development of accurate diagnostic biomarker models.

The ROC-supervised KMCA also passed all of our three tests, and it proved that it is the second most robust clustering method according to our study. The fact that the unsupervised KMCA passed the first and the third test, and that it failed the second test by missing just one of the 31 unknown subjects, redounds greatly to the innate clustering ability of the KMCA algorithm. That and the demonstrated accuracy of the KMCA aided by ROC curve analysis provide compelling support for the employment of the ROC-supervised KMCA for the development of accurate diagnostic biomarker models.

MPCA passed the first and the third test both in the unsupervised and in the ROC-supervised condition. The second test, however, proved particularly difficult for MPCA. Even the ROC-supervised MPCA was not able to pass the second test, although it demonstrated better accuracy than the unsupervised MPCA. Those results, as well as the high accuracy required of a diagnostic biomarker model, argue against the employment of MPCA for diagnostic purposes. HCA demonstrated by far the lowest accuracy and consistency of all clustering methods according to our investigation. It was the only method that failed all of our three tests when run completely unaided. Even when aided by the R6/2 ROC curve analysis, HCA failed to classify correctly the 13 original R6/2 mice into their two subgroups. All other clustering methods were able to do so and pass the third test both in the unsupervised and the R6/2-ROC-supervised way. Insofar as the diagnosis of diseases constitutes the end goal, or, equivalently, in any task requiring a high degree of accuracy, using HCA would not constitute a wise choice according to the results of our study.

We should point out here that there are at least two possible explanations for the poor results on the part of HCA. First, of all the methods we examined, HCA is the only one that does not allow the preselection of the number of clusters [21,17]. As was stated earlier, knowing beforehand the number of clusters significantly increases the accuracy of a clustering method. Since in the diagnosis of a disease, the number of groups (clusters) is known, the inability to preset the number of clusters and, thus, to significantly increase the accuracy of the algorithm constitutes a major disadvantage on the part of HCA. Secondly, of all the clustering methods we examined, HCA is the only one that lacks an iterative capability [3,21,17]. Once a subject is assigned into a cluster, HCA’s algorithm does not re-assess the impact of that classification to the entire model by re-examining all possible intra- and inter-clustering subject relationships. A misclassified subject, especially in the early stages of the clustering process, will inevitably impair the accuracy of the final results to a large extent. The fact that HCA also failed the third test when run supervised by the R6/2 ROC curve analysis further evidences the inappropriateness of its use for diagnostic purposes, where a high degree of accuracy is necessary.

Apropos of the aforementioned results and observations, we should interject here the following remarks. Today, clustering methods have found their way in the main stream of biomedical research. Owing to significant advances of technology, such as the ability to gather information about large numbers of genes or proteins, vast amounts of data can be generated; and nowhere is that more evident than in the fields of genomics and proteomics. Confronted by such a plethora of generated data, researchers have little choice but to resort to data mining methods, such as clustering analyses. On account of a host of reasons, ranging from ease of use to the undeniable convenience afforded by the visual presentation of results (dendrograms or other branch-like graphs), HCA, in one form or another, has become the data tool of choice. Many researchers routinely entrust their data to HCA and predicate their study conclusions on the results provided by HCA [22–25].

Theoretically, according to their individual internal statistics, all four clustering methods demonstrated considerably better clustering ability when run supervised by ROC curve analysis compared with their unsupervised counterparts. That was indeed the case for all ROC supervised settings of all four clustering methods in connection with all three tests, including the 31 runs for the 31 unknowns for each method in the second test. This theoretical evidence, attesting to the significantly superior clustering ability of the ROC-supervised settings of all four clustering methods, was not the only evidence; in terms of results, i.e. in terms of classification accuracy, the ROC-supervised settings proved to be considerably more accurate than their respective unsupervised settings. Nowhere was this manifested in a more obvious way than in the case of HCA. The unsupervised HCA settings all yielded results that were not meaningful; whereas, in connection with the first and second test, the ROC-supervised HCA settings passed both of those tests (100% total accuracy) [Table 3]. Regarding the second test, the ROC-supervised settings of both KMCA and MPCA demonstrated higher accuracy than their respective unsupervised settings: the total accuracy of the former improved from 96.77% to 100%, whereas the total accuracy of the latter improved from 93.55% to 96.77%.

It is interesting to note that the internal statistic of FCA, Average Silhouette (AS), is the same as the one employed by MPCA. The fact that all FCA settings yielded the same AS value as their MPCA counterparts attests to the similarity of the algorithms of the two clustering methods, both of which were introduced by Kaufman et al. [3]. In this case, we have two different clustering methods which employ the same internal statistic, and which are applied to the same data. That, however, constitutes the entire extent of similarity between those two methods. FCA’s probability based algorithm, with its fuzzification capability, proved to be superior not only to that of MPCA but also to the ones of the rest of the clustering methods.

Unlike in the case of other more complex multivariate analyses, such as linear discriminant analysis, regression methods, etc., clustering analyses do not impose the fulfillment of any conditions (normality, equality of variance, etc.) as a prerequisite for their use. This renders clustering analyses an easy option, especially when the volume of the data is large. However great this versatility and ease of use may be, one should be aware of the limitations of clustering diagnostic biomarkers. If in a particular disease state or disorder there is no clear separation between the affected and the normal, then the two clusters/groups will be, under the best conditions, widely dispersed and close to each other; and that will not be conducive to the development of an accurate diagnostic model. Another significant limitation in the development of a clustering diagnostic model has to do with the particular field of a disease. If, for example, in a disease state or a disorder there is no definitive diagnosis (gold standard), then one will not be able to definitively ascertain the status of the original subjects required to build the model. If the status of all of the original subjects is not known definitively, that would compromise the accuracy of the developed diagnostic model. Alzheimer disease constitutes such a case. Finally, as is always the case in statistics, larger samples confer larger accuracy. In our case, if a larger number of original subjects were used, that would minimize the impact of outlying or biovariability cases within all groups involved, and that, in turn, would increase the accuracy of the developed diagnostic model.

In conclusion, as was mentioned earlier, in the vast majority of the cases, clustering methods are typically used to find groups in data. That indeed constitutes the predominant employment of clustering methods from physics to the medical sciences [5–12,26,27]. In this study, we introduced and demonstrated the method whereby a clustering algorithm may be used to develop a clustering diagnostic biomarker model that can be used to accurately diagnose a single unknown subject in a disease with well-defined group boundaries. This is important because in a number of diseases, the gold-standard diagnostic test is invasive, expensive, and/or may be available only post-mortem. In the process of developing our clustering diagnostic biomarker models, we investigated four different clustering methods, and we assessed them in terms of clustering accuracy and fitting by subjecting them to three tests, including the validation test with unknown subjects. We also introduced the concept of supervising all four investigated clustering methods with ROC curve analysis in order to increase their accuracy. Although we utilized an animal model with Huntington disease (HD), and although the technology we used was NMR spectroscopy, the clustering diagnostic approach we developed in this study can be applied to other disease states with well-defined group boundaries using any type of platform technology to quantify outcome measures.