Statistical Approaches for the Analysis of DNA Methylation Microarray Data

Abstract

Following the rapid development and adoption in DNA methylation microarray assays, we are now experiencing a growth in the number of statistical tools to analyze the resulting large-scale data sets. As is the case for other microarray applications, biases caused by technical issues are of concern. Some of these issues are old (e.g. two-color dye bias and probe- and array-specific effects), while others are new (e.g. fragment length bias and bisulfite conversion efficiency). Here, I highlight characteristics of DNA methylation that suggest standard statistical tools developed for other data types may not be directly suitable. I then describe the microarray technologies most commonly in use, along with the methods used for pre-processing and obtaining a summary measure. I finish with a section describing down-stream analyses of the data, focusing on methods that model percentage DNA methylation as the outcome, and methods for integrating DNA methylation with gene expression or genotype data.

Introduction

Variation in the epigenome, the distribution of DNA-related modifications and structural features that inform the packaging of the DNA, can confer a host of specialized functions to different cells with the same genome. In humans, there are more than 200 cell types (Strachan and Read 1999), each with distinct epigenomic landscapes that shape their specific transcriptomes. Recognizing the importance of understanding these landscapes, large-scale projects such as the NIH Roadmap Epigenomics Project (http://www.roadmapepigenomics.org/), the Human Epigenome Project (http://www.epigenome.org) and the International Human Epigenome Consortium (http://ihec-epigenomes.org) were launched (Task and Board 2008). A series of reviews, commentaries, and research articles by leading experts, was recently published in Nature Biotechnology (October 2010).

One of the best studied epigenetic marks in mammals is DNA methylation, which overwhelmingly presents itself in the form of 5-methylcytosine residues found in CpG dinucleotides. Nevertheless, 5-methylcytosine residues can also occur in other sequence contexts (Lister et al. 2009). The totality of DNA methylation marks present in a mammalian genome is referred to as its methylome. DNA methylation has normal function in embryonic development, X-chromosome inactivation, genomic imprinting (Bird 2002), and allele-specific methylation unrelated to imprinting (Tycko 2010). Aberrant DNA methylation is seen in a variety of human diseases ranging from neurological and autoimmune disorders to cancer (Portela and Esteller 2010; Wang et al. 2010). Because DNA methylation is a stably inherited mark, it has generated great interest in its possible use as a biomarker for environmental exposures, clinical decision making, or predicting patient outcome (Laird 2003). Because it is reversible, it has become a desirable target for therapeutic intervention (Kelly et al. 2010).

Technologies

A recent review describes the daunting technical challenges of analyzing the human methylome (Laird 2010). The most common experimental methods require an amplification step prior to the analysis of CpG dinucleotides. However, CpG methylation information is lost upon amplification, due to the fact that both cytosine and 5-methylcytosine residues base pair with guanine. Thus, some sort of a priori modification to the DNA is needed to preserve information concerning DNA methylation status. The current gold-standard methodology is bisulfite conversion that results in cytosines being converted to uracil residues, while leaving 5-methylcytosines intact. The resulting template DNA can be amplified and sequenced (aka bisulfite sequencing) allowing single-base resolution of DNA methylation patterns. Whole-genome bisulfite sequencing has recently been applied towards obtaining the human methylome (Li et al. 2010; Lister et al. 2009), but is still too cost prohibitive to be used in a general laboratory setting.

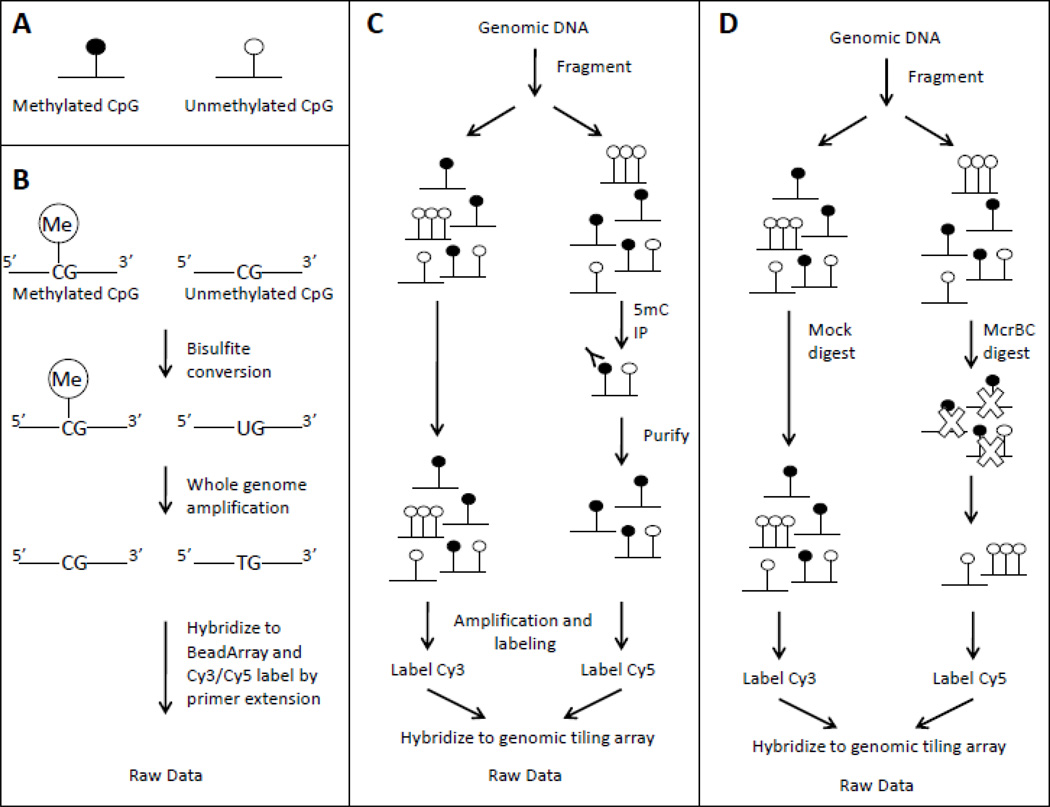
Microarray-based methods are presently the most affordable discovery tool available for genome-wide DNA methylation analysis. The dollar savings are obtained at the cost of lower resolution data with lower accuracy compared to bisulfite genomic sequencing. There are three main microarray-based approaches, each using a different method to treat the DNA in a methylation-dependent context prior to amplification or hybridization: bisulfite treatment (Bibikova et al. 2006), affinity enrichment (e.g. MeDIP (Weber et al. 2005) and MBDCap (Rauch et al. 2006)), and restriction digestion (e.g. HELP (Oda et al. 2009) and CHARM (Irizarry et al. 2008)) (Figure 1). Interpreting the data generated from these different platforms requires careful attention. Even the basic assessment of DNA methylation can vary depending on whether one is measuring the proportion of total fluorescent signal intensity due to CpG methylation (Beta value), or the log ratio of the intensity from methylation-enriched compared to total input fractions (M value) (Du et al. 2010; Irizarry et al. 2008). At the same time, within-sample and between-sample artifacts occur in the data, as seen with other types of microarrays that examine gene expression, genotype, or copy number variation. Although many of the statistical issues surrounding the use of microarrays may be familiar, the different properties of DNA methylation data suggests alternate statistical solutions.

Figure 1.

Three main approaches to DNA methylation microarray analysis. A) Black circles denote methylated CpGs and white circles denote unmethylated CpGs. B) Illumina’s bisulfite treatmentbased approach. Cy3/Cy5 labeling varies between Infinium I and Infinium II probes, C) Affinity enrichment using methylcytosine immunoprecipitation (IP) D) Methylation-sensitive restriction digestion using McrBC.

Characteristics of DNA methylation

Several key properties of DNA methylation are relevant for data preprocessing. First, CpGs and DNA methylation are non-randomly distributed throughout mammalian genomes. Second, DNA methylation is associated with CpG density; regions sparse in CpGs are highly methylated and regions dense in CpGs (CpG islands) are typically unmethylated (Ordway and Curran 2002). As total fluorescence signal (the general readout in microarray studies) is related to GC-content, oligonucleotide probes with high GC-content provide high signal intensity, DNA methylation levels are inversely related to total fluorescence signal. This has implications for within-array normalization procedures, as popular methods used for gene expression studies assume independence of these two quantities (e.g. loess normalization for two-color microarray experiments and background correction procedures for one-color microarray experiments). A third important consideration, one with potential to impact between-array normalization procedures, is that the overall amount of DNA methylation may vary between samples. This argues against the use of standard quantile normalization, perhaps the most frequently applied method for microarray gene expression data. I will review preprocessing methods that take into consideration these characteristics of DNA methylation data, followed by a discussion of several different methods for obtaining better summary estimates of absolute DNA methylation.

One common measure of DNA methylation is fraction methylation, a measure bounded between zero and one, with variance a function of the mean. These distributional properties have motivated the development of novel statistical methods for the investigation of biological hypotheses. The questions are familiar, testing for differential DNA methylation between classes, or looking for novel subgroups in data. Below I highlight a few statistical methods that use percent methylation as the outcome variable.

I begin with a review of statistical methods for preprocessing the data to remove technical artifacts. The description of preprocessing methods is complicated by the use of different technologies; however, the concerns of probe-level and sample-level biases are shared by all. I describe the methods separately by microarray type, first describing approaches proposed for enrichment-based tiling arrays, followed by a discussion of methods for Illumina’s BeadArray assays that interrogate specific CpG dinucleotides or small groups of CpG dinucleotides. Then I address methods for evaluating different biological questions. I begin with a summary of methods for the analysis of data from a single platform. This is followed by a description of methods for the integration of multiple data types.

Methods

Pre-processing microarray data

Enrichment-based microarrays

In an enrichment-based study, the input DNA usually undergoes random fragmentation and is split into two fractions, one of which is enriched for methylated (or unmethylated) DNA while the second is left untreated (total input). The enriched fraction and total input are differentially labeled with fluorescent dyes (e.g Cy3 and Cy5), and co-hybridized to a single microarray (Figures 1C & 1D). Different custom microarrays exist, as illustrated by a recent microarray used for CHARM assays which examined 4.6 million CpGs (Ji et al. 2010). In such experiments, DNA methylation is typically quantified using an M value, with higher values indicating more methylation. For MeDIP-enrichment, the M value is the log₂ ratio of the intensity from the methylation-enriched (R) and the control (G) (total input) fractions (=log₂(R/G).) For CHARM, the ratio is between the total input fraction, G, and the methyl-depleted fraction, R (M=log₂(G/R).)

Quality Assessment

The quality of individual probes and samples is assessed prior to adjusting for technical artifacts. Individual probe quality is evaluated by comparing the signal intensity to the signal from control probes that measure background noise and cross-hybridization (Aryee et al. 2010; Thompson et al. 2008). Aryee et al. (2010) assign probes a quality score based on their percentile rank among the control probes having the same GC-content, and exclude from their analysis probes assigned low scores (e.g. < 75%) across the majority of samples. Outlier arrays are identified by the array quality score, the average of the probe quality scores on the array. A useful tool for identifying spatial artifacts on the array is a heatmap of the probe intensity by array location (Thompson et al. 2008).

Within-array normalization

A primary objective of within-array normalization for two-color arrays is to remove intensity-related dye biases in the log₂ ratio, M. Other issues include background fluorescence and nucleotide-specific effects on the probes. Issues specific to restriction digestion methods are restriction cut-site density and fragment length bias.

A standard method to remove dye bias for two-color gene expression microarray studies is to obtain the residuals from the fit of a loess curve of M versus A, where M is the difference in log fluorescence signals between two samples (the majority of probes assumed to show no difference) and A(=log₂ sqrt(RxG)) is the average of the (log) signals from the two dyes (Yang et al. 2002). The method’s success is attributed to the independence between M and A, and the fact that M estimates background for the majority of probes. Neither statement is true for methylation log ratios. First, independence between M and A is violated because of the relationship between DNA methylation to average fluorescence intensity via its association with GC-content. Second, for DNA methylation microarrays M measures methylation enrichment in a single sample (enriched fraction compared to total input), so that its average captures the average level of methylation and not background. In light of these properties, researchers have proposed to correct for dye bias using a subset of probes selected from CpG-free regions and known to be unmethylated (Irizarry et al. 2008; Ordway et al. 2006). Irizarry (2008) adapt the loess method developed for gene expression data to fit a loess regression of M versus A on a subset of probes from CpG-free regions to capture only background artifacts (for details, see (Aryee et al. 2010)). In an extension of their work, Aryee et al. (2010) propose to correct for background fluorescence using a modification to the popular normal-exponential convolution model (Irizarry et al. 2003; Silver et al. 2009). In the convolution model, the true signal is estimated by assuming that the measured signal is the sum of true signal and experimental noise, and the signal and noise follow exponential and normal distributions, respectively. The recently proposed modification is to use CpG-free probes to estimate the distribution for background noise, and to estimate the true signal from the convolution stratified on GC-content. The combination of background correction and loess normalization methods is designed to reduce bias towards zero in the log ratio for low intensities, and remove the non-linear effects of dye-bias.

Model-based methods provide an alternate approach to correct for dye bias in microarray studies (Potter et al. 2008; Song et al. 2007). Potter et al. (2008) propose a linear model to correct for effects of dye-bias, probe-sequence, and restriction cut-site density. Using linear regression, they develop two models, extending ideas developed for model-based analysis of tiling arrays (MAT) (Johnson et al. 2006) and GC-robust multiarray analysis (GC-RMA) (Wu et al. 2004). They compare their method to MA2C (Song et al. 2007), another method to correct for dye-bias arising from sequence-specific effects, showing that their model does a better job at normalizing data for a sample run as the comparison group on multiple arrays. Without exploring the extent of DNA methylation differences on their platform, the authors assume that the 200,000+ probes in the microarray primarily measure background noise. As this assumption could be violated depending on the tissues hybridized, a backward selection approach to remove differentially methylated regions prior to estimating model parameters could be adopted (Johnson et al. 2006). A comparison of model-based and loess-based approaches has not been done and would be of interest.

Fragment length biases in signal intensities are seen for some, but not all, restriction-based methods (e.g. bias for HELP (Thompson et al. 2008) but not CHARM (Aryee et al. 2010)). Thompson et al. (2008) propose a quantile normalization approach to normalize signal intensities across fragment lengths. The approach is similar to between-array quantile normalization used by robust multiarray analysis (RMA) for gene expression data, except the quantiles are aligned using windows for data sorted by increasing fragment size. Thompson et al. (2008) show that this approach removes fragment length bias from the estimates of the methylation log ratio, M.

Between-array normalization

The goal of between-array normalization is to remove technical artifacts incurred when running samples on separate arrays. A common assumption of the methods used for gene expression data is that the distribution of measures is the same across samples. However, in many studies of DNA methylation, such as the comparison of tumor to normal cells, or the stem cells to differentiated cells, substantial differences in total DNA methylation levels exist (Jones and Baylin 2007; Lister et al. 2009). Even within a single cell type, total DNA methylation content can vary by age (Fuke et al. 2004). Therefore, normalization methods that allow for different DNA methylation distributions may be desired. One approach to correct for some between-array artifacts is to apply a within-array method that sets the true zero level (e.g. by correcting for background fluorescence).

Recently, Aryee et al. (2010) propose removing between-array artifacts using subset quantile normalization (Wu and Aryee 2010), an approach that normalizes the data based on a subset of probes selected to exhibit the same behavior across samples. For DNA methylation studies, CpG-free probes that are independent of DNA methylation are used for this subset. Selecting negative control probes that cover the spectrum of GC-content is desired to span the dynamic range of the signal probes. Prior to normalizing the enriched channel, a common baseline is established by normalizing the total input channel. Here, Aryee et al. (2010) assume equivalent quantities of input DNA across samples, and assign each probe to its median value. Since establishing a common baseline should not introduce bias in probe-specific effects between the fractions analyzed, the probes for the enriched and total input fractions are adjusted by the same amount. Next, samples in the enriched fraction undergo subset quantile-normalization. In step one, the quantile normalization of the CpG-free (control) probes creates an empirical reference distribution. In step two, a weighted average of the empirical reference distribution and a normal mixture distribution creates a target distribution that allows the mapping of probes beyond the range of the empirical distribution.

Table 1 lists a summary of current statistical solutions to address within-array and between-array technical biases.

Table 1.

Preprocessing of DNA methylation microarray data

Normalization	Bias	Statistical Method	Reference
Within-array	Dye-bias for two-color microarrays Dye-bias + sequence bias + restriction cut-site density	Loess normalization, using a subset of CpG- free regions Linear model	Ordway et al. (2006); Irizarry et al. (2008) Potter et al. (2008)
	Background fluorescence	Normal-exponential convolution, using CpG-free regions to estimate the background distribution and stratifying on GC content	Aryee et al. (2010)
	Fragment length	Quantile normalization by fragment length	Thompson et al. (2008)
Between-Array	Array-specific effects	Subset quantile normalization	Aryee et al. (2010)

Metric

The methylation log ratio (M), comparing enriched to a total input channel, is the typical measure from an enrichment microarray. Also of interest to many investigators is the estimate of absolute percent methylation. Recent papers have proposed methods for obtaining estimates of absolute percent methylation from M values (Aryee et al. 2010; Down et al. 2008; Pelizzola et al. 2008). However, when the goal is to identify differentially methylated regions (aka DMRs), M values seem to be preferred as noise may be introduced when estimating absolute percent methylation.

At any single genomic location the M value can be highly variable. Correlations in DNA methylation state in 1-kb regions (Eckhardt et al. 2006), suggests that measures will be improved by smoothing. A common choice is a linear weighting of probes within a 1-kb (or smaller) window of their target probe; the weight is a linear function of the distance from the probes to the center of the target probe, taking on the value one at the center, and the value zero 500-bp up- or downstream (Pelizzola et al. 2008). Analyses to identify differentially methylated regions use the smoothed M values.

Methods to estimate absolute percent DNA methylation from microarray data have been proposed for experiments using MeDIP enrichment (Down et al. 2008; Pelizzola et al. 2008) or CHARM (Aryee et al. 2010). For studies using MeDIP enrichment, Pelizolla et al. (2008) propose the mathematical modeling of the enrichment measures from a fully methylated DNA sample, as a calibration for estimating relative and absolute DNA methylation from experimental samples. Their smoothed measure of enrichment, a weighted average of M values, is modeled as a function of the expected methylation level, which for a fully methylated sample is the weighted average of the number of CpGs. The non-linear relationship between enrichment and expected value is captured by a 4-parameter logistic model. The parameters from this model are then used to estimate absolute and relative DNA methylation levels from experimental samples run using the same design and protocol. Down et al. (2008) propose a Bayesian approach to estimate absolute DNA methylation, modeling the effect of the density of methylated CpGs on the (loess-)normalized M values. Their method does not require the analysis of a fully methylated sample for calibration as required by the previous approach; instead, it uses assumptions that DNA methylation only occurs at CpGs and that regions of low CpG density are methylated. The computational time of the method is reduced in regions of high-CpG density by assuming high-correlation of methylation state. In CpG dense regions they group CpGs in windows, assume they would have the same methylation state, and infer the methylation status at each CpG as a deconvolution problem. The distribution of methylation states given one or multiple sets of MeDIP-chip output, can be estimated using standard Bayesian techniques. For studies using CHARM, Aryee et al. (2010) propose an empirical Bayes method to estimate absolute percent methylation from (unsmoothed) M values.

Targeted bisulfite sequencing microarray

An alternate microarray approach relies in measuring bisulfite converted DNA. Illumina adapted its BeadArray technology for genotyping to recognize bisulfite-converted DNA for methylation analysis (Figure 1B). They design bead types to measure specific target sequences, measuring multiple beads per bead type. The bead types are summarized by the average signal for the methylated (Me) and unmethylated (Un) alleles. Illumina reports a Beta value for the methylation level of the interrogated site, where

$$\text{Average Beta}=\frac{\text{Max}(\text{Me},0)}{\text{Max}(\text{Me},0)+\text{Max}(\text{Un},0)+100}.$$ (1)

Quality Assessment

Illumina provides a variety of control probes for determining data quality. The negative control probes and the bisulfite conversion probes are used to identify weak bead types and failed samples, respectively. Illumina recommends filtering bead types for which the signal intensity does not fluoresce above the non-specific background of the negative controls in the same channel. Arrays with a high probe failure rate (e.g. > 10%) are often omitted from the analysis. Arrays are also omitted if the bisulfite conversion probes indicate that they failed the bisulfite conversion step.

Within-array normalization

Although the preprocessing of BeadArrays for gene expression data has received recent statistical attention (Dunning et al. 2008; Shi et al. 2010; Xie et al. 2009), less has been reported for DNA methylation BeadArrays (Lynch et al. 2009). Illumina has developed three platforms: GoldenGate, Infinium HumanMethylation27 (H27K), and Infinium HumanMethylation450 (H450K). They all use two fluorescent dye colors; however, the chemistries to recognize the bisulfite-converted sequence vary by platform. GoldenGate uses its own extension, ligation, and PCR-based assay. Alternatively the H27K BeadArray uses Infinium I, and the H450K BeadArray uses both Infinium I and II primer extension assays. Both the original GoldenGate and the new Infinium II assays label methylated and unmethylated alleles from the same target sequence using different fluorescent colors making dyebias a concern. For the Infinium I assay, color is determined by the base 5’ of the targeted CpG so that methylated and unmethylated alleles at the same target are measured using the same color. Dye-bias is not a concern, but background fluorescence will bias average Beta values towards 0.5 for low intensity bead types.

Illumina’s GenomeStudio software offers some within-array normalization methods for the GoldenGate and H450K BeadChip data. Recently, investigators have begun to access bead-level data for the Infinium arrays, exploring alternate methods of pre-processing the signal. One use of the negative control probes is to correct for background fluorescence in the way explored for gene expression data (Shi et al. 2010). However, the distribution of signal intensities does not resemble that for gene expression data, suggesting that alternate models may be desirable. Given these challenges, this is an active area of research.

Between-array normalization

There is also a paucity of studies addressing between-array normalization for DNA methylation BeadArray data sets. In a study aimed at identifying epigenetic signatures of ovarian cancer, Teschendorf et al. (Teschendorff et al. 2009) compared five different strategies for normalizing hundreds of H27K BeadArrays. They used singular value decomposition to identify the top 20 components of variation in the normalized Beta matrix and tested associations between the top components of variation and unwanted factors such as batch, DNA input, and bisulfite conversion (BSC) efficiency measured using the control probes on the BeadArrays. They identified multiple statistically significant associations with unwanted factors if they did not normalize the data, or if they used quantile normalization on either the beta values directly, or separately by signal intensities for the methylated and unmethylated bead types prior to computing Beta values. They were most successful in removing associations with unwanted factors while maintaining associations with age and case-control status when they adjusted for batch, DNA input, and BSC efficiency in a linear regression model.

Metric

BeadArray assays are based on the bisulfite conversion of template DNA followed by enzymatic incorporation of fluorescent dNTPs. This is summarized as the fluorescence of the previously defined methylated (Me) and unmethylated (Un) alleles. The fluorescent signals obtained from multiple beads surveying a particular CpG dinucleotide(s) are averaged, after outlier removal. The summary proposed by the manufacturer is the percent of total fluorescence due to methylation (see equation (1)). To compare Illumina measures to M-values from different platforms, Irizarry et al. (2008) used a log-ratio for the Illumina data, M = log₂ Me/Un. The relationship between the Beta value and M-value is captured by a logistic function on the log₂ scale (M = log₂ Beta/(1-Beta)) (Du et al. 2010).

Methylome experiments

Many of the statistical questions posed for gene expression data, such as differences in abundance levels, cluster analysis and class prediction, are now being assessed for DNA methylation. An earlier review of the literature found many statistical methods utilized mixture-model approaches (Siegmund and Lin 2007). This theme is continued in some more recent work (Khalili et al. 2009; Sun et al. 2009). Here, I highlight some methods that have been used for modeling the Beta value as the outcome, a measure that takes on values between zero and one and has a variance related to its mean.

A variety of methods have been applied for the simple goal of studying differential DNA methylation in subgroups of samples (e.g. t-tests, non-parametric tests, generalized linear regression with a quasibinomial logit link) (Bell et al. 2011; Du et al. 2010; Marsit et al. 2009; Noushmehr et al. 2010). A recent paper compared using t-tests with unequal variance to t-test with equal variances on the logit-transformed data (M-value) (Du et al. 2010). Their results favored using the M-values instead of Beta-values for testing differential DNA methylation; however, the result was based on a data from eight arrays. In an analysis of 77 HapMap samples, researchers compared DNA methylation to genotype by first normalizing the Beta-values to N(0,1) prior to analysis using linear regression (Bell et al. 2011). The authors report that their results were robust to whether they measured DNA methylation using a normalized Beta-value or the log₂-ratio M-value. An alternate approach to data transformation and using standard methods is to apply Beta regression (Ferrari and Cribari-Neto 2004). Beta regression is designed for modeling proportions, continuous outcome bounded by zero and one, allowing for differences in both the mean and precision. A preliminary analysis of Infinium H27K data on 56 colorectal tissues suggests that Beta regression may be more sensitive for detecting differential DNA methylation than data transformation followed by tests that assume normality (unpublished data).

The non-normal distribution of Beta values has also motivated the development of a novel clustering algorithm (Houseman et al. 2008). The method, Recursive-Partitioning-Mixture Model (RPMM) is similar to the Hierarchical Ordered Partitioning and Collapsing Hybrid (HOPACH) (van der Laan and Pollard 2003) approach developed for gene expression data, but uses a Beta mixture model to split the samples between subgroups. The method shows all the benefits of a conventional mixture model approach, with the added computational efficiency due to recursive partitioning steps. More recently, the method has been applied in a semi-supervised (SS) manner to identify subclasses that are related to patient survival, leading to SS-RPMM (Koestler et al. 2010).

Data integration

Studies analyzing DNA methylation in conjunction with other molecular data are becoming more common (Jeong et al. 2010; Loss et al. 2010; Noushmehr et al. 2010; Zhang et al. 2010). Jeong et al. (2010) use an empirical Bayes model to combine microarray-based gene expression and DNA methylation data, in situations with few biological replicates. They model average gene expression levels and average DNA methylation levels in drug-resistant and WT cell lines, and their main output is the joint posterior distribution of the difference of expression and difference of DNA methylation levels. They then divide the distribution into nine quadrants based on whether the expression is up-regulated, unchanged, or down-regulated and DNA methylation is hypomethylated, unchanged, or hypermethylated, when comparing drug-resistant to WT cell lines. They can then compute the posterior probabililty of belonging to any one class, to classify a gene into its most likely category.

Loss et al. (2010) propose a method to identify epigenetically regulated genes from the quantification of DNA methylation-expression associations across larger numbers of samples. Using cluster analysis, they reduce the dimensionality of the DNA methylation data prior to studying its association with gene expression. After clustering, they match the averaged DNA methylation levels to gene probe sets if they occur within a 20-kb window of each other. Then, an exponential curve, E = ae^−bxM + c, is fitted to the expression and methylation data, where E is the expression measure and M the DNA methylation measurement, the exponential curve capturing the non-linear association often observed between gene expression and DNA methylation levels. Loci are ranked based on the proportion of variance in expression that is explained by DNA methylation. Other interesting statistical approaches have been developed for combining data of different types, but so far applications using the methods have focused on gene expression and single nucleotide polymorphism (SNP) (Parkhomenko et al. 2007, 2009), gene expression and copy number variation (Shen et al. 2009; Witten and Tibshirani 2009), or gene expression and microRNA variation (Agius and Campbell 2009).

Novel visualization approaches have also been proposed for genome-wide comparisons (Krzywinski et al. 2009; Noushmehr et al. 2010). Krzywinski et al. (2009) developed Circos, a visualization tool that creates circular displays of epigenomic data, aligning the molecular data in concentric circles to facilitate the comparison of molecular features by genomic intervals. An alternative to visualizing raw (or summary) data is to create a figure of the results from a statistical analysis. The volcano plot, a plot of –log10 p-values against effect size (e.g. log fold-change) is a method for visualizing associations from microarray studies. A new starburst plot is proposed to combine information from two volcano plots, and is applied for a study of DNA methylation and gene expression (Noushmehr et al. 2010). The starburst plot is a scatter-diagram of -log10 FDR adjusted p-values from testing differential gene expression versus the same from testing differential DNA methylation, with information on direction of effect (positive/negative) captured by multiplying the log-transformed p-value by +1/−1. This figure allows researchers to assess whether loci showing increases (decreases) in DNA methylation also show down (up)-regulation in gene expression. Although it may be desirable that DNA methylation and gene expression are measured from the same samples, the starburst plot can be applied as a meta-analysis tool, combining data from different samples (Wolff et al. 2010). Although initially used to explore associations with disease state, the figure could also be used to show associations between DNA methylation and gene expression with genotype. In general, combined analyses will continue to expand since they can be accomplished in a cost-effective manner by using the publicly available data, such as data sets found in the National Center for Biotechnology Information (NCBI) Gene Expression Omnibus (GEO) database (http://www.ncbi.nlm.nih.gov/geo/).

Discussion

Statistical tools for the pre-processing of DNA methylation microarrays have only recently begun appearing in the literature, and inherent biases of different microarray platforms are still being quantified (Kuan et al. 2010; Robinson et al. 2010b). Platform-specific statistical analysis pipelines are under development, with the methods for CHARM being perhaps the most advanced. Thus far, there has been little overlap in statistical approaches by different laboratories for both pre-processing and down-stream analysis; however, I expect this to change. With the increasing number of large studies using microarrays, I anticipate that more comparative studies of statistical approaches will be forthcoming resulting in more overlap in approaches between labs.

Table 2 summarizes a variety of statistical software created for the analysis of epigenomic data. Many of the tools described in this review are available as R packages from Bioconductor (http://www.bioconductor.org). The entire statistical analysis pipeline for CHARM, from pre-processing to differential methylation analysis, is available from Bioconductor (Aryee et al. 2010). Also available are the packages MEDME, for modeling experimental data with MeDIP enrichment (Pelizzola et al. 2008), HELP for the analytical pipeline for data from the HELP assay (Thompson et al. 2008), beadarray (Dunning et al. 2007) and lumi (Du et al. 2008) for analyzing Illumina BeadArray data, and MEDIPS for the analysis of MeDIP-enriched data analyzed by sequencing (Chavez et al. 2010). At the R-Forge web site is Repitools, for the analysis of epigenomic data from enrichment-based microarrays (Statham et al. 2010). Batman for the analysis of MeDIP enrichment data is available as a suite of Java scripts (Down et al. 2008). Software for sequencing methods, not reviewed here, include PASH 3.0 (Coarfa et al. 2010) and edgeR, another Bioconductor package (Robinson et al. 2010a).

Table 2.

Software for the analysis of DNA methylation data

Software	Purpose	URL	Reference
charm	Modified Loess normalization; Modified normal-exponential convolution; subset quantile normalization; estimate absolute DNA methylation using empirical Bayes	http://www.bioconductor.org	Aryee et al. (2010)
HELP	Quantile normalization by fragment length for data generated using HELP assay	http://www.bioconductor.org	Thompson et al. (2010)
beadarray	For Illumina BeadArray data	http://www.bioconductor.org	Dunning et al. (2007)
lumi	For Illumina BeadArray data	http://www.bioconductor.org	Du et al. (2008)
MEDME	Estimate absolute DNA methylation from MeDIP study	http://www.bioconductor.org	Pelizolla et al. (2008)
MEDIPS	Analysis of MeDIP-seq data, with functions useful for other types of enrichment (MBD-seq) or sequence data (ChIP-seq)	http://www.bioconductor.org	Chavez et al. (2010)
Batman	Estimate absolute DNA methylation from MeDIP study	http://tdblade.gurdon.cam.ac.uk/software/batman	Down et al. (2008)
RPMM	Cluster analysis of Illumina beta values	http://www.bioconductor.org	Houseman et al. (2008)
Circos	Visualization tool	http://mkweb.bcgsc.ca/circos	Krzywinski et al. (2009)
Repitools	Analysis of epigenomic data from enrichment-based microarrays	http://repitools.r-forge.rproject.org	Statham et al. (2010)
PASH 3.0	Analysis of Bisulfite Sequence data	http://www.brl.bcm.tmc.edu/pash/pashDownload. rhtml	Coarfa et al. (2010)
edgeR	Analysis of Bisulfite Sequence data	http://www.bioconductor.org	Robinson et al. (2010a)

One area I have not covered in this review is methods for the analysis of batch effects. Batch effects, a huge concern in DNA methylation studies (Leek et al. 2010), are not discussed because present approaches to handling them use standard software developed for gene expression data (Zhang et al. 2010). This is an area that remains to be explored, taking into consideration the distinguishing characteristics of DNA methylation. Another statistical issue not addressed in the literature and specific to Illumina BeadArrays, is the variation in the precision of Beta values due to the random number of beads measured on an array. For gene expression BeadArray data, there is increasing interest in using the information on technical variation from the bead-level data in the statistical analysis (Dunning et al. 2008; Kim and Lin 2010). Presently, there is no corresponding literature for DNA methylation analysis.

Finally, as with genotyping and RNA expression studies, the current technological push is to use genome-wide sequencing for digital summaries of the data (Bock et al. 2010; Harris et al. 2010). The arrival of sequence data will be certain to raise new issues and require the development of new tools. However, with these new data in hand, the future will be in developing methods to integrate data of different types (genetic, epigenetic, RNA and protein expression) in order to better understand human development and health.