Image Restoration in Cryo-electron Microscopy

Abstract

Image restoration techniques are used to obtain, given experimental measurements, the best possible approximation of the original object within the limits imposed by instrumental conditions and noise level in the data. In molecular electron microscopy, we are mainly interested in linear methods that preserve the respective relationships between mass densities within the restored map. Here, we describe the methodology of image restoration in structural electron microscopy, and more specifically, we will focus on the problem of the optimum recovery of Fourier amplitudes given electron microscope data collected under various defocus settings. We discuss in detail two classes of commonly used linear methods, the first of which consists of methods based on pseudoinverse restoration, and which is further subdivided into mean-square error, chi-square error, and constrained based restorations, where the methods in the latter two subclasses explicitly incorporates non-white distribution of noise in the data. The second class of methods is based on the Wiener filtration approach. We show that the Wiener filter-based methodology can be used to obtain a solution to the problem of amplitude correction (or “sharpening”) of the electron microscopy map that makes it visually comparable to maps determined by X-ray crystallography, and thus amenable to comparable interpretation. Finally, we present a semi-heuristic Wiener filter-based solution to the problem of image restoration given sets of heterogeneous solutions. We conclude the chapter with a discussion of image restoration protocols implemented in commonly used single particle software packages.

Introduction

The goal of image restoration is to produce the best possible estimate, within the limits imposed by instrumental conditions, of the original object given its experimental realization and the noise level. The instrumental limitations are expressed by the point spread function (psf) and its Fourier space transform, the transfer function, while the noise level, termed Signal-to-Noise Ratio (SNR), is conveniently expressed as a ratio of the power of the signal to the power of noise. The distribution of signal-to-noise ratio in Fourier space is given as a function of spatial frequency and is called Spectral SNR (SSNR); regrettably, there is no simple relationship between SNR and SSNR. Relations between an object and its realizations are expressed by image formation models that can be quite complicated; they can for example depend on localization of the object or be nonlinear. In single particle electron microscopy (EM) the generally accepted model is linear, with additive noise, and with spatially invariant psf (at least within the area of the imaged object). Given an accurate image formation model and precise knowledge of all its parameters, image restoration methods can inform us on how closely we can recover the original image from its experimental realizations.

The effectiveness of image restoration methods depends on the accuracy of the image formation model, i.e., how closely it corresponds to the physical reality of the image formation process, and its ability to precisely establish values of all the parameters of the model as well as statistical properties of random entities included in the model, such as noise. Fortunately, the linear, weak-phase-object approximation of the image formation process in the electron microscope has been experimentally tested, and has been shown to be accurate, and for well-behaved materials, in agreement with experimental results to resolution exceeding 1Å. For frozen-hydrated biological specimens, dose limitations and beam-induced specimen and media distortions make testing more challenging, but the agreement still appears to be excellent and more accurate image formation models did not result in significantly improved image restoration (Angert et al., 2000). Hence, data processing methods implemented in single particle software packages employ the standard model with some parameters taken as settings of the microscope (accelerating voltage, spherical aberration constant, magnification, which together with digitization settings yields effective pixel size), some as generally accepted experimental values (amplitude contrast), and some determined from the data (defocus setting).

A separate category of image formation parameters characterise the random components of the image such as: the spectral properties of the imaged data and also of noise in the data, and the associated envelope functions that describe suppression of high frequency information by the microscope and scanning process. The accuracy of these estimates is not very good and the difficulties are compounded by the lack of accepted analytical models for individual components. Finally, we have the suppression of information due to the alignment process necessary to establishing spatial orientations of the collected projection images. For small errors, this loss can be expressed as an additional envelope function (Baldwin and Penczek, 2005; Jensen, 2001).

In cryo-EM the goal of image restoration is to recover the distribution of electron densities within the imaged macromolecular complex, or, in the 2D case, its projection image. Since the EM image formation process is linear, it is possible in principle for quantitative electron microscopy to yield measurements of atomic densities within the imaged material (Langmore and Smith, 1992). In practice, a more modest but perfectly acceptable goal is to obtain a restored image whose densities are linearly related to those in the original structure. If the linear relationship is perturbed, the interpretation of the final map might be incorrect; hence, image restoration methods should be linear to preserve the desired relationship between the specimen and the restored structure. This essentially excludes from consideration methods based on non-linear goal functions, such as Maximum Entropy. Nevertheless, there is room for incorporation of non-linear constraints that encapsulate a priori knowledge about the macromolecular complex, such as nonnegativity of the densities. The appropriate framework is given by the Projections Onto Convex Sets (POCS) theory (Stark and Yang, 1998).

The goals of image restoration are distinct from those of image enhancement. The former is expressed as a well-defined mathematical objective and is aimed at recovery of the original image while keeping distortions due to unavoidable amplification of noise at a minimum. The latter can be broadly described as a set of techniques aimed at modification of the image that facilitate interpretation or visual appreciation of the results. These can range from simply colouring the subunits of a macromolecular complex to make them easily distinguishable, to sophisticated non-linear image processing methods that are tuned to enhance particular features, e.g., components of a given size or shape. Image enhancement methods may be quite elaborate; however, since its goals of image enhancement are task-specific and often loosely defined, its methods are generally heuristics and are unrelated to models used in image restoration that are rooted in the physics of image formation.

In this work, we will describe the methodology of image restoration in cryo-EM single particle reconstruction (SPR), and more specifically, we will focus on the problem of the optimum recovery of Fourier amplitudes given EM data collected under various defocus settings. The linear theory of image restoration is very well developed (Carazo, 1992; Gonzalez and Woods, 2002; Jain, 1989; Pratt, 1992) and the methods used in SPR are standard. The problem is challenging because of the unique form of the Contrast Transfer Function (CTF) of the electron microscope that has numerous zero crossings whose number and locations depend on the underfocus setting of the microscope that are difficult to control precisely. Thus, we will present the standard criteria, namely the Mean Squared Error (MSE) and the Minimum Mean Squared Error (MMSE), with an emphasis on the CTF-correction aspects. Finally, we will discuss limitations of the image restoration methodology that are mainly caused by the low accuracy of data SSNR estimation and the intrinsic heterogeneity of the processed data set. We close with a description of a semi-heuristic approach to image restoration based on a Wiener filter methodology that is meant to alleviate the problems of currently prevalent methods. We note that the step of 3D reconstruction from projections is also part of image restoration methodology in cryo-EM, but because it is a broad subject, we devoted to it an independent contribution which we refer the reader to for details (insert reference to Penczek chapter on Fundamentals of 3D Reconstruction here).

Image formation model in electron microscopy

Within the linear, weak-phase-object approximation of the image formation process in the microscope (Wade, 1992), 2D projections represent line integrals of the 3D Coulomb potential of the macromolecule convoluted with the psf of the microscope:

$$g_n\left(\mathbf{x}\right)=ps{f}_n\left(\mathbf{x}\right)\ast e_n\left(\mathbf{x}\right)\ast \left[\int d\left({\mathbf{T}}_n\mathbf{r}\right)dz+m_n^S\left(\mathbf{x}\right)\right]+m_n^B\left(\mathbf{x}\right)$$ (1)

where g_n denotes the n'th observed 2D projection image, e is the inverse Fourier transform of the envelope function, x = [x y]^T is a vector of coordinates in the plane of projections, r = [r_x r_y r_z 1]^T is a vector of coordinates associated with the macromolecule, T is the 4×4 transformation matrix given by

$$T(\mathbf{R},\mathbf{t})=\left[\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill \mathbf{t}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],\left[\begin{array}{c}\hfill \mathbf{x}\hfill \\ \hfill z\hfill \\ \hfill 1\hfill \end{array}\right]=\mathbf{Tr},$$ (2)

with t = [t_x t_y 1]^T being the shift vector denoting translation of the object (and its projection) in the x-y plane (translation in z is irrelevant due to the projection operation), and R(ψ ,θ, ϕ) is the 3×3 rotation matrix specified by three Eulerian angles (Baldwin and Penczek, 2007). Finally, m^B and m^S denote two additive noises, the first of which is a coloured background noise. The second, m^S, is attributed to the residual scattering by the solvent and the support carbon film; if used, it is assumed to be white and affected by the transfer function of the microscope in the same way as the imaged macromolecule is. Both types of noise are assumed to be zero mean, mutually uncorrelated, independent between projection images and uncorrelated with the signal:

$$E\left[m_i^k\right]=0,k=S,B,$$ (3a)

$$E\left[m_i^k{m}_j^l\right]=\{\begin{array}{cc}0\hfill & \mathrm{if}i\ne j\hfill \\ {\sigma }_i^{k,l^2}\hfill & \mathrm{if}i=j\hfill \end{array}\phantom{\}},k,l=S,B,$$ (3b)

$$E\left[d_i{m}_i^k\right]=0,k=S,B.$$ (3c)

Model (1) is in many respects semi-empirical. In principle, signal from amorphous ice should not be affected by the CTF; in practice however, the buffer in which the protein is purified contains ions and it is possible to observe CTF effects by imaging frozen buffer alone. It is also debatable whether the envelope function should have the same shape for all components included in the equation. Envelope functions of electron microscopes have been extensively studied and one can identify envelope functions for finite source size, energy spread, drift, specimen charging effects, and multiple inelastic-elastic scattering. Furthermore, one can also identify envelope functions corresponding to the modulation transfer function of the recording medium, which is usually film or CCD camera (for discussion see (Zhu et al., 1997)). In Fourier space however all these functions appear as products of each other, and since these functions are either Gaussian functions or well approximated by Gaussian functions in the frequency range relevant for single particle work, and it is impossible in practice to independently retrieve all their parameters from the data, it has become customary in the field to use just one function, namely the Gaussian envelope function (E). This function is characterized in Fourier space by the so-called B-factor (B):

$$E\left(s\right)=\exp \left(-\frac{B}{4}{s}^2\right)$$ (4)

where s is the modulus of spatial frequency. While the accepted form simplifies the analysis, the choice of both the terminology and form adopted are somewhat unfortunate as the unit of the B-factor is Ų (surface area!). A more useful characterisation is a standard deviation of the associated Gaussian function:

$${\sigma }_B=\sqrt{\frac{2}{B}},$$

which not only has units of spatial frequency, but is also naturally interpretable as the spatial frequency at which amplitudes of the Fourier transform of the image decrease to ~60% of their original value. It follows from the previous that at frequency 3σ_B, the amplitudes of the Fourier transform of the image decrease to ~1% of their original value. Thus, σ_B = 0.05Å^– (resolution of 20Å)corresponds to B=200Ų in B-factor idiom, while σ_B = 0.04Å^– (resolution of 25Å) to B=312Ų.

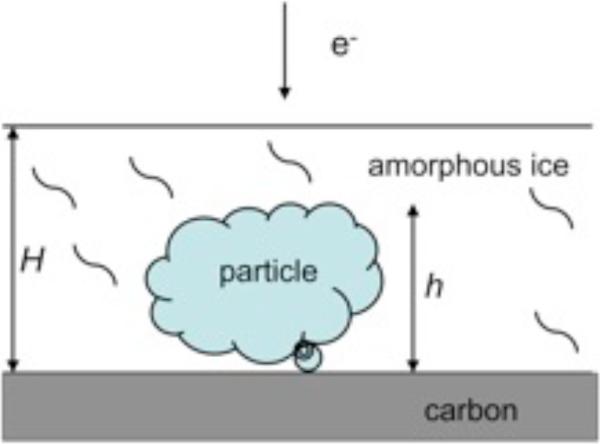
The noise included in Eq.1 is referred to as background noise and in some EM data analysis protocols it has become common to assume that it can be estimated from samples of the background selected from micrographs or simply from areas surrounding windowed particles. In practice however, the situation is more complicated. If there is no carbon film and if the solvent is appropriately thin, the contribution of solvent to the noise affecting the projection image will be much less than what the estimates obtained from background areas would suggest, as some of the buffer will be displaced by the protein (Fig.1). Regrettably, while the effective height of the particle can be easily estimated, it is all but impossible to obtain reliable measurements of ice thickness. It is therefore advisable to keep in mind that while the model Eq.1 reflects physical reality of the image formation in cryo-EM to a good extent, its exact form is a compromise between what is theoretically justifiable and what is experimentally and computationally tractable.

Fig.1.

Biological particle suspended in a layer of amorphous ice with an optional thin carbon layer support. Depending on the specimen, the size h of the particle is between fifty and few thousand Ångstroms. The ice thickness H should not exceed the particle size by much.

In Fourier space, Eq.1 is written by taking advantage of the central section theorem: the Fourier transform of a projection is a Fourier plane (perpendicular to the beam direction) of a rotated Fourier transform of a 3D object:

$$G_n\left(\mathbf{s}\right)=CTF(\mathbf{s};\Delta z_n)E_n\left(\mathbf{s}\right)\left[{\phantom{\mid }\left(D\left(\mathbf{Ts}\right)\right)\mid }_{s_z=0}+M_n^S\left(\mathbf{s}\right)\right]+M_n^B\left(\mathbf{s}\right)$$ (5)

The capital letters denote Fourier transforms of objects appearing in (1) while CTF (a Fourier transform of the psf) depends, among other parameters that are set very accurately (such as the accelerating voltage of the microscope), on the defocus setting Δz_n and the amplitude contrast ratio 0 ≤ A < 1 that reflects presence of absorption and thus the amplitude contrast in the images. For the range of frequency considered, A is assumed to be constant and the CTF is written in terms of the phase perturbation function γ as:

$$CTF(\mathbf{s};\Delta z)=\sqrt{1-A^2}\sin \left(\gamma (s;\Delta z)\right)-A\cos \left(\gamma (s;\Delta z)\right)$$ (6)

where s = |s| is the magnitude of spatial frequency and where for simplicity we assumed the absence astigmatism. The phase perturbation function is (Scherzer, 1949):

$$\gamma (s;\Delta z)=2\pi \left(-\frac{1}{2}\Delta z\lambda s^2+\frac{1}{4}{C}_s{\lambda }^3{s}^4\right),$$ (7)

where C_s is the spherical aberration constant and, ignoring relativistic effects, $\lambda =\sqrt{\frac{h^2}{2m{e}^{-}V}}$ is the wavelength of electrons (h - Planck's constant, m and e^- - electron mass and charge, respectively, V - voltage of the microscope).

While what is given here can be written as 2D functions, thus accommodating possible astigmatism, in practice almost all cryo-EM data processed is astigmatism-free. Hence, without loss of generality we will write subsequent expressions as 1D functions of the modulus of spatial frequency. For simplicity we may write:

$$\begin{array}{cc}\hfill g_n\left(\mathbf{x}\right)& =ps{f}_n\left(\mathbf{x}\right)\ast e_n\left(\mathbf{x}\right)\ast \int d\left({\mathbf{T}}_n\mathbf{r}\right)dz+m_n\left(\mathbf{x}\right)\hfill \\ \hfill & =ps{f}_n\left(\mathbf{x}\right)\ast e_n\left(\mathbf{x}\right)\ast f\left(\mathbf{x}\right)+m_n\left(\mathbf{x}\right)\hfill \end{array}$$ (8)

$$\begin{array}{cc}\hfill G_n\left(\mathbf{s}\right)& =CTF(\mathbf{s};\Delta z_n)E_n\left(\mathbf{s}\right){\phantom{\mid }\left(D\left(\mathbf{Ts}\right)\right)\mid }_{s_z=0}+M_n\left(\mathbf{s}\right)\hfill \\ \hfill & =CTF(\mathbf{s};\Delta z_n)E_n\left(\mathbf{s}\right)F\left(\mathbf{s}\right)+M_n\left(\mathbf{s}\right)\hfill \end{array}$$ (9)

where m is the effective noise containing both the background noise and the CTF-affected contributions from solvent and/or carbon support layer.

Due to linearity of the Fourier transform, assumptions Eqs.3a-c hold for Fourier transforms of the respective entities in Eqs.5 and 9. In addition, we assume that in Fourier space noise is approximately uncorrelated between spatial frequencies:

$$E\left\{M_n\left(\mathbf{s}\right)M_n\left(\mathbf{u}\right)\right\}={\sigma }_n^2\left(\mathbf{s}\right)\delta (\mathbf{s}-\mathbf{u})=P_n\left(\mathbf{s}\right)\delta (\mathbf{s}-\mathbf{u}),$$ (10)

where based on the assumption that the noise has zero mean, we equated its Fourier space variance with its power spectrum (PW). The rotationally averaged PW of the observed image calculated as the expected value of its squared Fourier intensities (Eq.5), is given by:

$$\begin{array}{cc}\hfill P_g\left(s\right)& =CT{F}^2\left(s\right)\cdot E^2\left(s\right)\cdot (P_f\left(s\right)+P_m^S\left(s\right))+P_m^B\left(s\right)\hfill \\ \hfill & =CT{F}^2\left(s\right)\cdot E^2\left(s\right)\cdot P_f\left(s\right)+P_m\left(s\right).\hfill \end{array}$$ (11)

We assume the power spectrum of the 3D structure to be isotropic, so we can replace it by the (averaged) power spectrum of 2D projections.

Based on Eqs.1, 9 and 11, the SSNR can be understood either as a ratio of rotationally averaged PWs, and thus a 1D function of modulus of spatial frequency, or a multidimensional function describing frequency dependence of SSNR in Fourier space (Penczek, 2002). Moreover, there exist in cryo-EM several different understandings of what SSNR represents. A generic one is to define SSNR as a ratio of the power of the “ideal” signal to the power of noise:

$$SSNR\left(\mathbf{s}\right)=\frac{P_f\left(\mathbf{s}\right)}{P_m\left(\mathbf{s}\right)}.$$ (12)

In Eq.12, the details of image formation are excluded. In a definition of SSNR that is commonly used, both the CTF and the envelope function are incorporated into the effective signal, thus making it closely related to the data (Ludtke et al., 1999; Ludtke and Chiu, 2002). We term this definition SSNR^Data and it is written as:

$$SSN{R}^{Data}\left(\mathbf{s}\right)=\frac{CT{F}^2\left(\mathbf{s}\right)E^2\left(\mathbf{s}\right)P_f\left(\mathbf{s}\right)}{P_m\left(\mathbf{s}\right)}.$$ (13)

Finally, we can consider the SSNR of the average of EM images (or a 3D reconstruction) that will be corrected for the CTF effects using one of the methods discussed below, but will not necessarily have the correct distribution of Fourier amplitudes and is also affected by alignment errors. The latter can be easier considered as a source of noise, or as yet another envelope function (Baldwin and Penczek, 2005). In recognition of alignment as a major source of errors in EM structure determination, we will term the SSNR of the average SSNR^Ali:

$$SSN{R}^{Ali}\left(\mathbf{s}\right)=\frac{E^{Al{i}^2}\left(\mathbf{s}\right)P_f\left(\mathbf{s}\right)}{P_m^{Ali}\left(\mathbf{s}\right)}.$$ (14)

The relationships among the three SSNRs introduced above are not necessarily straightforward, particularly in light of the fact that the same SSNR can be estimated using different experimental approaches (see next section). Nevertheless, the difference between SSNR (Eq.12) and SSNR^Data (Eq.13) lies chiefly in the inclusion of the CTF and envelope function in the latter, so the choice between them is mainly a matter of convenience or of the particular data processing protocol used. For example, in some approaches one would attempt to directly estimate the effective power of the signal, i.e., CTF(s)E(s)P_f(s), from the data, and in others, estimation of the envelope is separate from estimation of the power of the signal. The latter may be estimated using independent experiments, such as X-ray crystallography or SAXS (Gabashvili et al., 2000; Ludtke et al., 2001).

In what follows we will focus on the problem of recovering either f or d given projection images g under the assumption that alignment parameters are approximately known. We also assume that the PW of the 3D structure d is isotropic and that the set of 2D projections g_n samples the entire Fourier space, in which case the rotationally averaged sum of PWs of available 2D projections faithfully represent the rotational PW of the original, albeit initially unknown, 3D structure. Finally, whenever we discuss the restoration of a 3D object from its 2D projections, we will largely ignore the difficulties associated with the problem of the reconstruction of an object from a set of its projections; a comprehensive review of reconstruction methods is given in (insert reference to Penczek chapter on Fundamentals of 3D Reconstruction here). Instead, we will focus on the restoration of the proper distribution of the Fourier amplitudes of the reconstructed object given artifacts introduced by the CTF and fall-off due to the envelope function E.

Estimation of image formation model characteristics

In this section we will briefly describe the current state of art in estimation of image formation characteristics. In the last decade there was a surge of publications devoted to the study of estimation of CTF parameters and the resulting computational methods were either incorporated into existing software packages (Huang et al., 2003; Penczek et al., 1997; Saadet al., 2001; Sorzano et al., 2007; van Heel et al., 2000; Velazquez-Muriel et al., 2003) or made available as independent applications (Mallick et al., 2005; Mindell and Grigorieff, 2003; Sander et al., 2003; Yang et al., 2009; Zhou et al., 1996). The CTF is determined from the collected micrographs and the methods used are typically automated with supporting Graphical User Interface (GUI) that allows examination and, if necessary, adjustment of the results. While all methods allow determination of basic image formation parameters such as defocus, sometimes amplitude contrast and astigmatism, others will also yield envelope functions and other more complex characteristics. Overall, a user can always find a CTF-estimation utility that will provide the required functionality; regrettably however, there is no established standard in the mathematical form of the CTF used by developers. In the following publications (Huang et al., 2003; Penczek et al., 1997; Saad et al., 2001; Sander et al., 2003; Velazquez-Muriel et al., 2003), in addition to the different sign conventions used, amplitude contrast is also defined differently in each case.

The initial steps of CTF parameters estimation are common to all methods. Two parameters of the CTF Eqs.6-7 are simply taken from the microscope settings and are considered accurate: the accelerating voltage (i.e., the wavelength of electrons) and the spherical aberration constant. The amplitude contrast can in principle be fitted, but very often is assumed to be constant and for cryo data is set in the range of 6-12%. This leaves the defocus and amount and direction of astigmatism, the estimations of which are possible if accurate estimates of PWs of micrographs are available.

Depending on the package, power spectra are either computed from the entire micrograph field (Zhu et al., 1997) or from windowed particles (Saad et al., 2001). The advantages of the first approach are: (1) the larger amount of averaged data and larger window sizes improve the statistical properties and resolution of the estimate, and (2) since CTF estimation precedes the particle picking step, it is possible to use CTF information to improve the efficiency of automated particle picking (Huang and Penczek, 2004). The second approach makes it possible to use the information about particle regions and background noise regions to compute additional characteristics of the image formation process. Typically, a 2D estimate of the PW is rotationally averaged, and either a low-order polynomial is fitted to a set of local minima of the resulting 1D PW or a constrained optimization is used to obtain curves bracketing the 1D PW (Huang et al., 2003; Mallick et al., 2005; Yang et al., 2009). The curve “beneath” the PW is associated with the background noise of Eq.8 and is subtracted. The repeated fit yields the curve bracketing the background-subtracted PW from “above”, and this curve is used in a direct fit of the analytical form of CTF Eq.6 to 1D data. The fit is typically restricted to the intermediate range of spatial frequencies within which the 1D PW agrees well with the model. In the low frequency region the noise in the data seems to increase rapidly, while in the high frequency region, the statistical properties of the data seem to change, thus precluding reliance on the simple analytical form of the bracketing curves (Huang and Penczek, 2004). It is possible to use the thus obtained value of defocus as an initial guess in the subsequent analysis of astigmatism in 2D PWs (Huang and Penczek, 2004; Mallick et al., 2005). In the SPARX implementation (Hohn et al., 2007), the initial parameters obtained from estimates based on the entire micrograph are used as initial estimates and are subsequently refined using PWs obtained from windowed particles.

There are two competing approaches both to the initial steps of CTF parameters estimation and the estimation of the envelope function and SSNR in the data. One can either rely on analytical functions to represent the characteristics and fit them to the data, as was initially put forward in a pioneering study by Saad et al. (Saad et al., 2001), or use the estimated PWs directly to represent image formation characteristics required in subsequent cryo-EM data processing. In the former approach, the selected analytical functions are in general simple, and the choices might either have a theoretical basis, as in using a Gaussian function to represent the envelope function, or be heuristic, as in the use of exponents of low-order polynomials for the envelope function (Huang et al., 2003; Saad et al., 2001). The latter approach is used in EMAN2 (Steven Ludtke, personal communication). In both approaches, it is necessary to estimate PWs from micrograph regions that contain projection data (P_g of Eq.8) [and from background noise regions, usually aptly available in micrographs or in areas surrounding windowed particles (P_m of Eq.8) . If there were no errors and if the image formation model (Eq.5) were to hold exactly, one would have:

$$CT{F}^2\left(s\right)\cdot E^2\left(s\right)\cdot P_f\left(s\right)=P_g\left(s\right)-P_m\left(s\right).$$ (15)

Since CTF parameters have already been estimated, one would then only need to know the (1D) PW P_f of the molecular complex imaged to estimate the envelope function E. There are several ways to carry this out: (1) obtain independent experimental measurements of the 1D PW P_f either from SAXS experiments (Gabashvili et al., 2000; Saad et al., 2001) or from X-ray crystallography (possibly computed from atomic coordinates of the model of the complex), (2) use the 1D PW of a complex of similar size and shape as the resulting differences are negligible in comparison with other uncertainties inherent in the analysis of Eq.15, (3) use an analytical curve fitted to the data from either (1) or (2), (4) use a simple analytical model that approximates the shape of typical macromolecular complexes well. Next, the background-subtracted 1D PW Eq.15 is divided by P_f, and the fit of a curve bracketing the result from above yields the envelope function E (Fig.2).

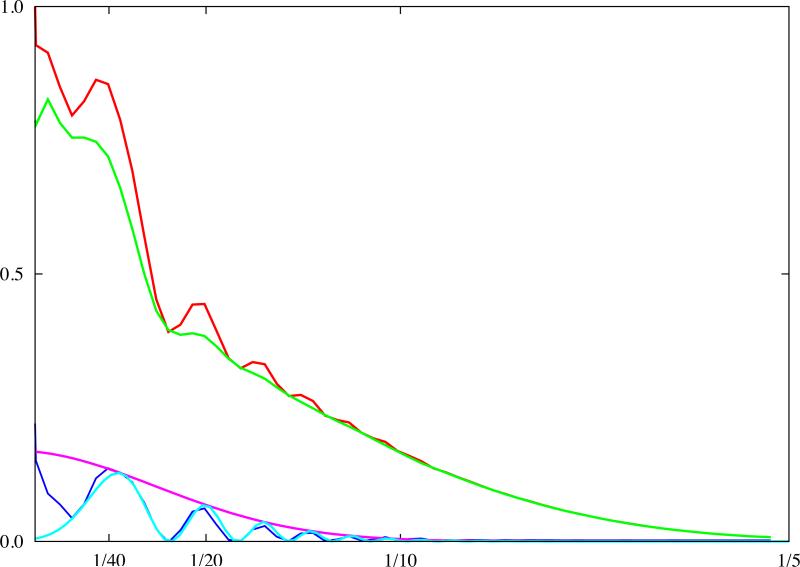
Fig.2.

Estimation of image formation model characteristics. The PW (red) was computed using particles windowed from a single micrograph (70S ribosomes on carbon support, accelerating voltage 300kV). The background noise PW (green) was computed from areas surrounding windowed particles. The defocus (2.95μm) was estimated using background-subtracted PW (blue) and the envelope function (magenta) modelled by a Gaussian function. The fitted CTF shows excellent agreement with the experimental PW (light blue). Analysis was done using the e2ctf.py utility of EMAN2. The vertical axis is in arbitrary units, and the horizontal axis corresponds to modulus of spatial frequency [1/Å].

Analytical model of 1D rotationally averaged power spectrum of macromolecular complexes in solution

The shape of 1D PWs of proteins was studied by Guinier and Fournet (Guinier and Fournet, 1955), who noticed that the overall shape of the curve mainly depends on the size of the protein. The authors suggested an approximation by a two-component function where: (1) the low-frequency region is modeled by a Gaussian function whose standard deviation is related to the effective diameter of the protein in real space, and (2) the PW in frequencies higher than $\sim \frac{1}{8}{\mathrm{Å}}^{-1}$ is assumed to be constant at a level dependent on the number of atoms in the protein. This model does not agree very well with the 1D PWs of pseudo-electron densities obtained from computational conversion of atomic coordinates of selected macromolecular complexes available in the PDB database. On the other hand, it is is also debatable whether such a procedure faithfully represents the physical reality and “true” PWs of complexes in solution. One can also dispute the usefulness of SAXS PWs since different buffer conditions or protein concentration may modify the shape of the PW in comparison to that observed in EM. In addition, small angle scattering in physical image formation process is different than that in electron microscopy. Reliance on PDB models can be justified by the simplicity of the procedure and by the fact that X-ray models, when available, are considered gold standards in the cryo-EM community. Furthermore, X-ray models are widely used for comparisons and for docking (Volkmann and Hanein, 2003), so macromolecular complexes, even if obtained used different techniques, look ‘familiar’ when they have the same PWs as X-ray atomic models.

The empirical model used in SPARX (Hohn et al., 2007) is heuristic, meets expectations, was thoroughly tested using numerous X-ray crystallographic model and was found to fit the data very well (Z. Huang and P.A. Penczek, unpublished results):

$$P_f\left(s\right)=\exp \left(t_1+\frac{t_2}{{\left(\frac{s}{t_3}+1\right)}^2}\right)+\exp \left(t_4-0.5{\left(\frac{s-t_5}{t_6^2}\right)}^2\right),$$ (16)

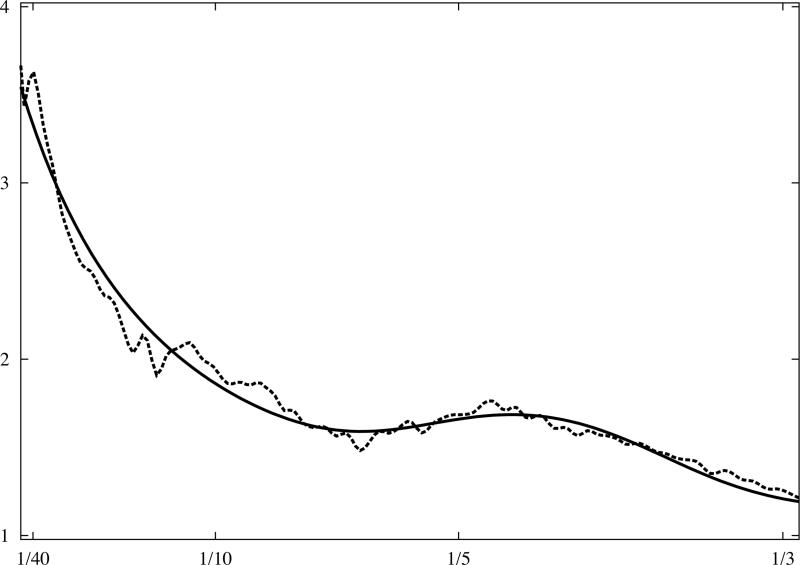
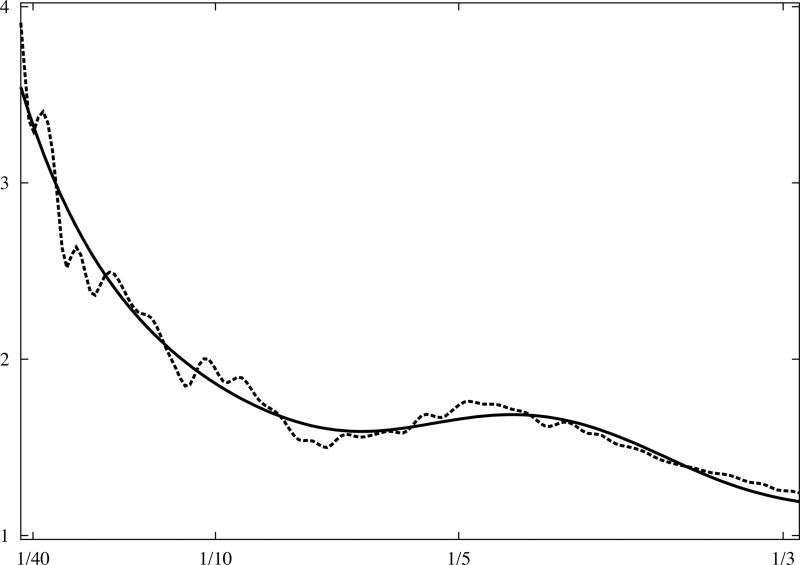
where t₁ and t₄ are scaling parameters which do not influence the shape of the curve; the first term is responsible for the general shape, and the second, the Gaussian function, represents the beta-beta spacing which results in a broad peak at $\sim \frac{1}{5}{\mathrm{Å}}^{-1}$ (Fig.3). It can be shown that the model effectively depends on only two parameters, namely (t₂,t₃), and with minimal adjustment can represent a very broad range of macromolecular complexes, virtually irrespective of their shapes.

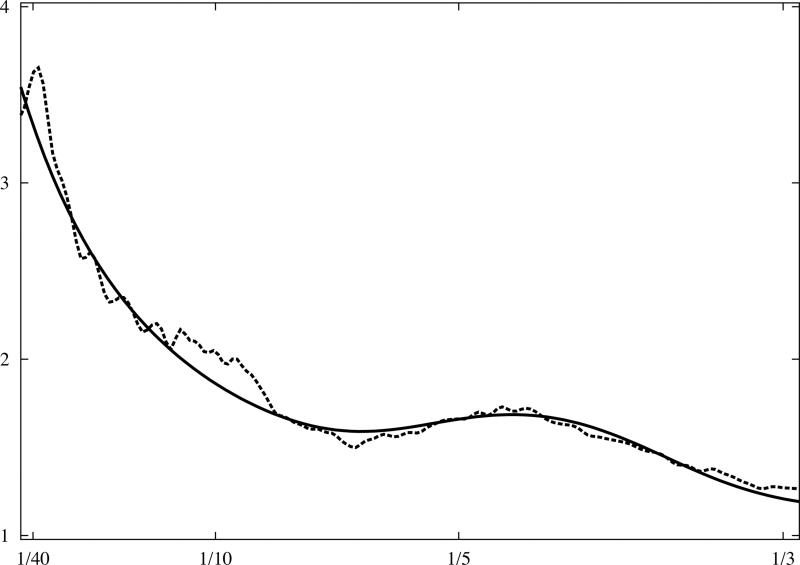
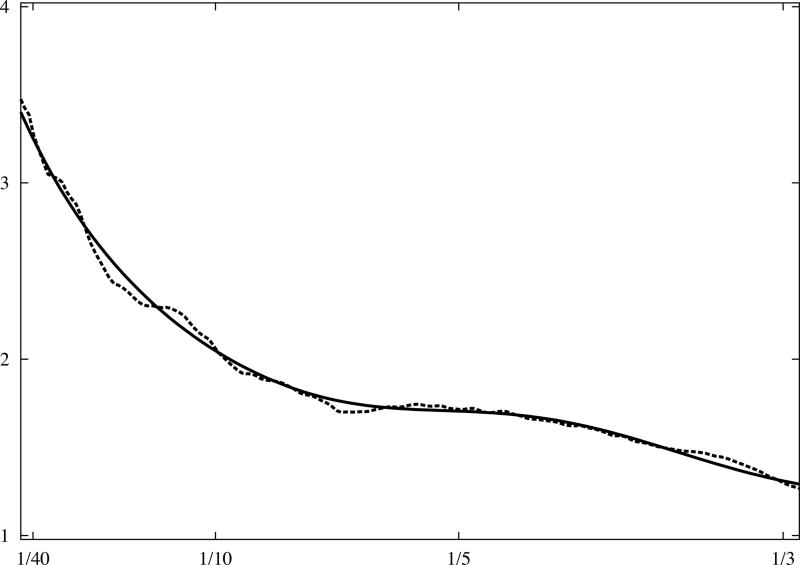
Fig.3.

Analytical model of 1D rotationally averaged power spectrum of macromolecular complexes. X-ray crystallographic atomic models were converted to discrete 3D electron density maps using tri-linear interpolation and voxel size 1.0Å. Eq.16 was fitted to rotationally averaged 3D power spectra of all maps. The vertical axis is in arbitrary units, and the horizontal axis corresponds to modulus of spatial frequency [1/Å]. (a) 20S proteasome, 630kDa (PDB:1J2Q), (b) GroEL chaperonin, 715kDa (PDB:1KP8), (c) calmodulin-dependent protein kinase II (CaMKII), 205kDa (PDB:1HKX), (d) 70S ribosome, ~2,000kDa (PDB:2AVY). Power spectra of complexes (a-c) were modelled using the same parameters as in Eq.16 while the power spectrum of ribosome (d) required minor adjustments.

Pseudoinverse restoration - mean-square and chi-square error criteria

Closed form solutions

In MSE pseudoinverse restoration we seek an estimate F̂ of the original signal that fits the observed EM images in the mean-square error sense (MSE criterion):

$$\underset{\widehat{F}}{\min }{\mathcal{L}}_{MSE}\left(\widehat{F}\right)=\underset{\widehat{F}}{\min }E\left\{\sum _n{\Vert G_n\left(\mathbf{s}\right)-CT{F}_n\left(\mathbf{s}\right)\cdot E_n\left(\mathbf{s}\right)\cdot \widehat{F}\left(\mathbf{s}\right)\Vert }^2\right\}$$ (17)

The MSE criterion has a number of desirable properties in that: (1) it corresponds to the “total power” of the data, i.e., it is equivalent to $\underset{\widehat{F}}{\max }E\left\{{\Vert \widehat{F}\Vert }^2\right\}$ (Penczek et al., 1992), (2) it is a quadratic form of F̂, so in principle a global minimum exists (a unique solution of Eq.17), (3) it is differentiable with respect to F̂, so when there is no closed form solution, an efficient iterative algorithms for seeking the minimum can be employed.

The most straightforward approach to pseudoinverse restoration is to ignore the presence of noise, in which case, for a single EM image, the solution of Eq.17 has the form:

$$\widehat{F}\left(\mathbf{s}\right)=\{\begin{array}{cc}\frac{1}{CTF\left(\mathbf{s}\right)E\left(\mathbf{s}\right)}G\left(\mathbf{s}\right)\hfill & \mathrm{if}CTF\left(\mathbf{s}\right)\ne 0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (18)

In practice, a more sensible approach is to select a small constant ε and thus obtain:

$$\widehat{F}\left(s\right)=\{\begin{array}{cc}\frac{1}{CTF\left(\mathbf{s}\right)E\left(\mathbf{s}\right)}G\left(\mathbf{s}\right)\hfill & \mathrm{if}\mathrm{abs}(CTF\left(\mathbf{s}\right))>\epsilon \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (19)

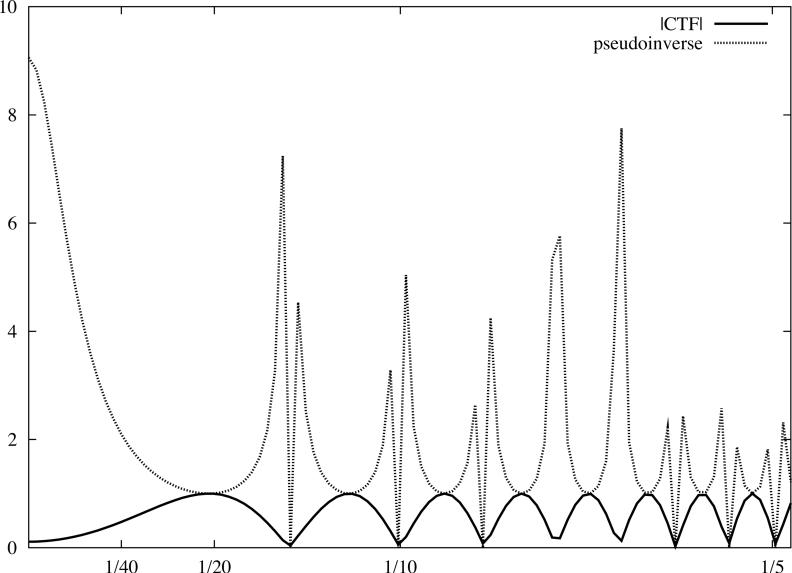
However, even if we were prepared to tolerate an enhancement of noise due to the division by the envelope function, it turns out that strong artifacts in the real space representation of the ‘restored’ image would result from setting to zero those parts of the image F whose spatial frequencies correspond to small absolute values of the CTF. In addition, for a single image, sections of its Fourier transform are irretrievably lost. Therefore, it is difficult to have a meaningful pseudoinverse based CTF correction of a single underfocused EM image as the information in some regions of Fourier space cannot be restored (Fig.4a).

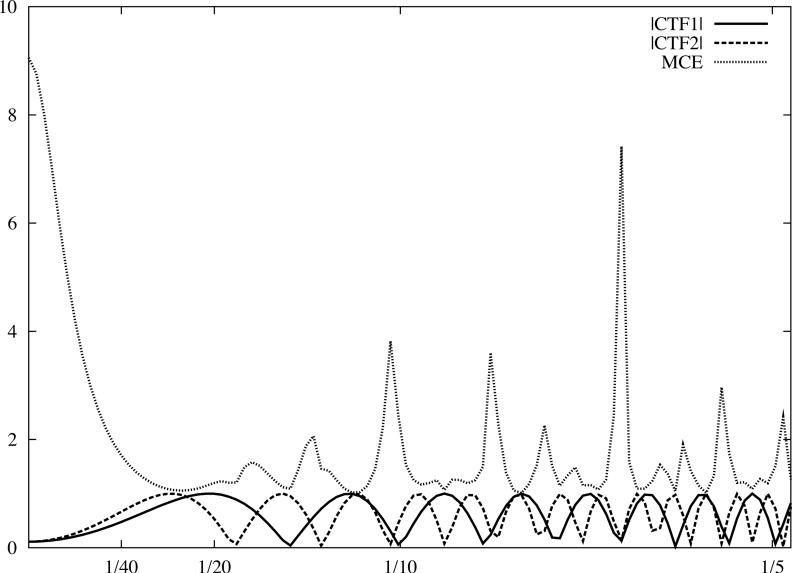
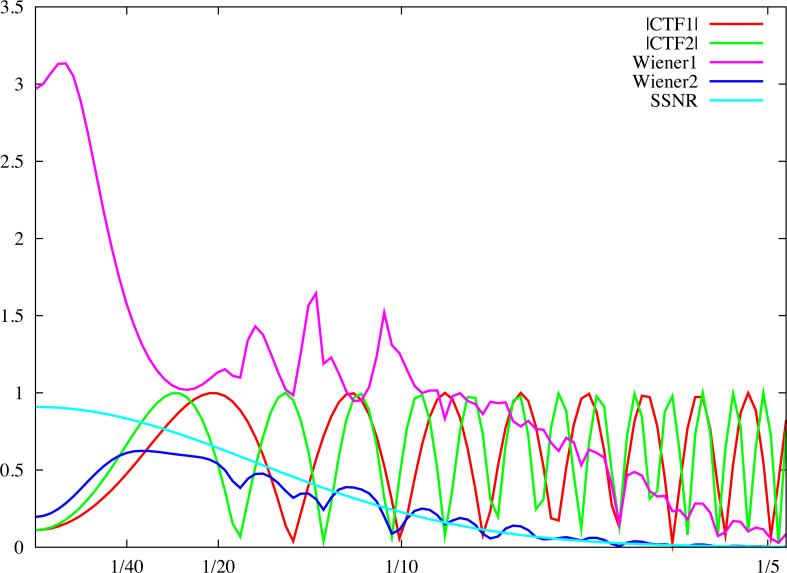
Fig.4.

Linear cryo-EM image restoration filters. The horizontal axis corresponds to modulus of spatial frequency [1/Å]. (a) CTF (accelerating voltage 300kV, amplitude contrast 10%, defocus 1.0μm) and the pseudoinverse filter (Eq.19) with ε = 0.02. (b) Two CTFs, first as in (a), the second with defocus 1.6μm, and the Mean Square Error filter (Eq.26) with the variance of data omitted. (c) Wiener filters (Eq.42) plotted assuming the SSNR is the same for each CTF and is given by a Gaussian function. For the first filter (magenta), the maximum SSNR is set to 20 while for the second filter (blue), it is set to 0.9. Note that identical filters can be obtained using the CMCE filter (Eq.31) with regularisation function U set to the inverse of the SSNR of the data. For clarity, we plotted moduli of the CTF function.

A standard approach to overcoming the problem of information loss due to zeros in CTF is to collect EM data using a wide range of defocus settings to obtain images affected by a range of different CTFs. If the defocus settings of the microscope are selected properly, it is possible to collect the data in such a way so that the full range of Fourier space information can be recovered. We also include the presence of frequency-dependent noise that leads to a mean chi-square error (MCE) criterion: in MCE pseudoinverse restoration we seek an estimate F̂ of the original signal that fits the observed EM images in the chi-square sense:

$$\underset{\widehat{F}}{\min }{\mathcal{L}}_{MCE}\left(\widehat{F}\right)=\underset{\widehat{F}}{\min }E\left\{\sum _n\frac{{\Vert G_n\left(\mathbf{s}\right)-CT{F}_n\left(\mathbf{s}\right)\cdot E_n\left(\mathbf{s}\right)\cdot \widehat{F}\left(\mathbf{s}\right)\Vert }^2}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}\right\}.$$ (20)

To solve the problem, we express the solution as a linear combination of the input data:

$$\widehat{F}\left(\mathbf{s}\right)=\sum _{n=1}^N{w}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)$$ (21)

and we minimize criterion Eq.20 with respect to the weights w_n (s).

In the derivation, since noise in the data, in Fourier space, is uncorrelated with respect to spatial frequencies, we will omit the argument s. By combining Eqs.20 and 21 we obtain:

$${\mathcal{L}}_{MCE}\left(\widehat{F}\right)=E\left\{\sum _n\frac{{\Vert G_n\Vert }^2}{{\sigma }_{M_n}^2}-2\mathrm{Re}\left(\left(\sum _n\frac{CT{F}_n{E}_n{G}_n}{{\sigma }_{M_n}^2}\right){\left(\sum _n{w}_n{G}_n\right)}^{\ast }\right)+\left(\sum _n\frac{{\Vert CT{F}_n{E}_n\Vert }^2}{{\sigma }_{M_n}^2}\right){\Vert \sum _n{w}_n{G}_n\Vert }^2\right\}.$$ (22)

To find the minimum, we differentiate with respect to w_k, set derivatives to zero, and substitute G_n by its form given by the image formation model Eq.9:

$$\frac{\partial {\mathcal{L}}_{MCE}\left(\sum _n{w}_n{G}_n\right)}{\partial w_k}=E\left\{\left(F\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2}{{\sigma }_{M_n}^2}+\sum _n\frac{CT{F}_n{E}_n{M}_n}{{\sigma }_{M_n}^2}\right){(CT{F}_k{E}_{k}F+M_k)}^{\ast }-\left(\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2}{{\sigma }_{M_n}^2}\right)\left(F\sum _n{w}_{n}CT{F}_n{E}_n+\sum _n{w}_n{M}_n\right){(CT{F}_k{E}_{k}F+M_k)}^{\ast }\right\}=0.$$ (23)

The expected value of Eq.23 yields a set of N equations:

$$P_f\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2}{{\sigma }_{M_n}^2}+1=\left(\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2}{{\sigma }_{M_n}^2}\right)\left(P_f\sum _n{w}_{n}CT{F}_n{E}_n+w_k\frac{{\sigma }_{M_k}^2}{CT{F}_k{E}_k}\right),$$ (24)

which can be simultaneously solved by taking advantage of the fact that the term $P_f{\sum }_n{w}_{n}CT{F}_n{E}_n$ is shared. The final form of the weighting term is:

$$w_k=\frac{CT{F}_k{E}_k}{{\sigma }_{M_k}^2}/\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2}{{\sigma }_{M_n}^2}.$$ (25)

The image restored from N EM images collected with different defocus setting is thus obtained using the following equation (Ludtke, 2001):

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^N\frac{CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}}{\sum _{n=1}^N\frac{CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}}.$$ (26)

By multiplying the numerator and denominator of Eq.26 by the PW of the original structure f, the MCE solution can be written as a function of the SSNR either as that of the data (Eq.13) (Ludtke, 2001):

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^N\frac{1}{CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)}SSN{R}_n^{Data}\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}^{N}SSN{R}_n^{Data}\left(\mathbf{s}\right)},$$ (27)

or the ideal SSNR:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)}.$$ (28)

The three forms Eqs.26-28 are not mathematically equivalent as Eq.27 is aesthetically unappealing due to implied divisions by the zeros of CTFs, or, equally problematic, divisions by the zeroes of $SSN{R}_n^{Data}$ (the two should coincide).

The MCE image restoration given by Eq.28 has the following properties (Fig.4b):

1. For a large number of images collected at approximately uniformly distributed defocus settings, the impact of the filter can be considered separately for two spatial frequency regions consisting of, respectively: (a) frequencies lower than the frequency of the first extremum of ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)$, and (b) frequencies higher than the frequency of the first extremum. In the first region, all CTFs have approximately the same shape irrespective of the defocus settings, and their values for s → 0 are given by the amplitude contrast A. Hence, the result of the restoration is an enhancement of the very low frequencies by A times (we assumed that envelope functions are scaled such that E(0) = 1); moreover, the degree of this enhancement does not depend on the SSNR. In the second region consisting of the higher frequencies, under the aforementioned assumptions, the denominator will be approximately constant, so the restoration corresponds to the summation of EM images multiplied by their respective CTFs and weighted relative to each other by differences in the envelope function and noise level.

2. For a small number of images, or for data sets for which for some spatial frequencies ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)\simeq 0$, the MCS-based restoration will be affected by artifacts shared with the pseudoinverse solution Eq.18. In 2D applications, this is unlikely to happen; however, if Eq.28 is used in the context of 3D reconstruction from projections, divisions by very small numbers in the denominator of Eq.28 will result in very unpleasant real-space artifacts. In some applications, this is prevented by inclusion of a small additive heuristic parameter in the denominator (Böttcher and Crowther, 1996; Grigorieff, 1998).

3. The solution does not depend on the form or scaling of the PW of the target, ideal image.

4. The solution does not depend on the absolute scaling of the SSNR but rather on differences between the SSNRs of different images. Since P_f is the same for all images, practically speaking we are only concerned with the PW of the background noise P_mn (recall $P_{m_n}={\sigma }_{M_n}^2$). In other words, if we let P_m denote the average PW of the background noise, then for the PW of the individual images we can write P_mn = P_m + ΔP_n. It follows that image restoration with Eq.28 depends only mildly on the average distribution of background noise and it is the deviation ΔP_n that is decisive. Since in cryo-EM PW of the noise is determined from the data and deviations ΔP_n are small in comparison with P_m, one would have to have a sufficiently accurate method of determining P_mn to justify the inclusion of SSNR_n (or P_mn) in the image restoration. Otherwise, errors in the determination of P_mn will propagate into the restored image and result in the deterioration of its SSNR.

Constrained closed form restoration

An elegant way to address the shortcomings of pseudoinverse restorations Eqs.26-28 is to constrain the desired solution by imposing on it “smoothness”. Given a high-pass filter U (s), we seek to minimize the quantity

$$\underset{\widehat{F}}{\min }{\mathcal{L}}_{CMCE}\left(\widehat{F}\right)=\underset{\widehat{F}}{\min }E\left\{{\Vert U\left(\mathbf{s}\right)\widehat{F}\left(\mathbf{s}\right)\Vert }^2\right\},$$ (29)

subject to the condition that:

$$\sum _n\frac{{\Vert G_n\left(\mathbf{s}\right)-CT{F}_n\left(\mathbf{s}\right)\cdot E_n\left(\mathbf{s}\right)\cdot \widehat{F}\left(\mathbf{s}\right)\Vert }^2}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}=1.$$ (30)

As in the previous section, we obtain the solution by introducing the Lagrange multiplier 1/γ and thus obtain the following constrained mean chi-square error (CMCE) restoration:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^N\frac{CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}}{\sum _{n=1}^N\frac{CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}+\gamma U^2\left(\mathbf{s}\right)}$$ (31)

As expected, the solution reduces to MCE restoration for γ = 0 and for γ → ∞ becomes a sum of input images multiplied by their respective CTFs and envelope functions. It should also be noted that although the mathematical forms of the CMCE restoration and the Wiener filter (which will be discussed in a later chapter) are very similar, the assumptions underlying their derivations are entirely different (Fig.4c). We will return to the apparent similarity of the two solutions later.

The CMCE restoration Eq.31 has significant advantages over MCE pseudoinverse Eq. 28 in that the possibility of division by zero is eliminated, and artifacts due to divisions by small values in the denominator can be minimized by a proper selection of the constant γ. In the following, to better understand the behavior of CMCE restoration, we assume that the high-pass filter U(s) is given by an inverse Gaussian function, in which case Eq.31 becomes:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\exp \left(-\frac{s^2}{2{\sigma }^2}\right)\sum _{n=1}^N\frac{CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}}{\exp \left(-\frac{s^2}{2{\sigma }^2}\right)\sum _{n=1}^N\frac{CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)}{{\sigma }_{M_n}^2\left(\mathbf{s}\right)}+\gamma },$$ (32)

Eq. 32 is simply a low-passed version of the pseudoinverse restoration Eq.26 with the difference that with the appropriate choices of γ and σ, any impact of the denominator becomes negligible in high frequencies.

Iterative solution

A standard method of solving least-squares problem (LSQ) of the type given by Eq.17 is by an iterative process which takes advantage of the fact that the goal function is differentiable and employs iterations of the type:

$${\widehat{F}}^{l+1}\left(\mathbf{s}\right)={\widehat{F}}^l\left(\mathbf{s}\right)+{\eta }^l\nabla \mathcal{L}\left({\widehat{F}}^l\right)={\widehat{F}}^l\left(\mathbf{s}\right)+{\eta }^l\sum _n{E}_n\left(\mathbf{s}\right)\cdot CT{F}_n\left(\mathbf{s}\right)(G_n\left(\mathbf{s}\right)-CT{F}_n\left(\mathbf{s}\right)\cdot E_n\left(\mathbf{s}\right)\cdot {\widehat{F}}^l\left(\mathbf{s}\right)).$$ (33)

Note complex conjugation in Eq. 33 is omitted since both the CTF and E are real. The relaxation parameter for the l'th iteration is denoted by η^l > 0 ; note that by setting η^l = η = const > 0 we obtain Richardson's algorithm (Richardson, 1910). With properly chosen relaxation parameters, the algorithm will converge to a solution of Eq.17 that is most similar to the prototype image F̂⁰ (s) in the least squares sense. The prototype image is usually a blank image filled with zeroes or an acceptable approximation to the solution obtained using one of the fast direct methods.

Termination of the algorithm after a finite number of iterations is a form of regularization of the solution as it will yield an image that roughly corresponds to one that could be obtained from the Singular Value Decomposition (SVD) approach generated by a subset of dominating eigenvectors. The main disadvantages of the iterative method (Eq.33) include significant computational effort, slow convergence rate, and lack of clear guidelines on what the number of iterations and values of relaxation parameters should be, (which in practice have to be established by trial and error), all of which make the method only moderately attractive. Furthermore, the iterative method (Eq.33) yields images of essentially the same quality as closed-form solutions, but requires a much larger computational effort. However, the iterative method also has a significant advantage in that it can serve as basis for more sophisticated image restoration algorithms. For example, division by zero is not a problem despite the presence of (overlapping) zeroes of CTFs since Eq.33 does not involve division by CTFs. For a spatial frequency for which all CTFs are equal to zero the final image can simply inherit the value from the prototype image, and thus make use of available a priori information. When combined with additional regularization provided by early termination of the algorithm, the iterative method yields a solution which has fewer artifacts (particularly if CTFs have overlapping zeroes or very small values) and is “smoother,” and hence more agreeable to the eye.

It is possible to dramatically improve the rate of convergence by using more advanced methods for solving Eq.17 while taking advantage of the simple form of the derivative shown in Eq.33. In many applications it is possible to use steepest decent, conjugate gradients, or limited-memory BFGS optimization methods (Yang et al., 2005). One can also incorporate explicitly rational regularization terms, for example by constraining the Laplacian of the real space solution F̂ (Zhu et al., 1997), which can also be expressed as a low-pass filtration in Fourier space resulting in an algorithm with iterations of the type:

$${\widehat{F}}^{l+1}\left(\mathbf{s}\right)={\widehat{F}}^l\left(\mathbf{s}\right)-\gamma {\eta }^l{U}^{-2}\left(\mathbf{s}\right){\widehat{F}}^l\left(\mathbf{s}\right)+{\eta }^l\sum _n{E}_n\left(\mathbf{s}\right)\cdot CT{F}_n\left(\mathbf{s}\right)(G_n\left(\mathbf{s}\right)-CT{F}_n\left(\mathbf{s}\right)\cdot E_n\left(\mathbf{s}\right)\cdot {\widehat{F}}^l\left(\mathbf{s}\right)),$$ (34)

where the notation has the same meaning as in Eq.31. The improvements outlined above not only accelerate convergence, but also yield solutions less affected by the noise and artifact-inducing inconsistencies in the data.

Finally, in application to 3D reconstruction from projections, iterative methods offer the only mathematically sound approach to reconstruction with CTF correction. For reasons that exceed the scope of this review, there are neither direct Fourier inversion nor filtered backrprojection algorithms that include CTF correction; the only consistent approach is to use a 3D version of Eq.33 and obtain a solution iteratively (Yang et al., 2005; Zhu et al., 1997).

Constrained solutions - incorporation of a priori information

The main advantage of iterative methods is that it is straightforward to incorporate a priori knowledge about the solution, particularly if it is given as a non-linear constraint, such as non-negativity of solution. The theory of Projections Onto Convex Sets (POCS) offers an elegant and comprehensive paradigm within which various ideas, often articulated in an intuitive, heuristic fashion, can be properly expressed and analyzed (Stark and Yang, 1998). In the scope of this section, we will take “projection” to mean the enforcement of certain types of constraints on the solution, and not the integral in the context of the image formation model (Eq.1). We also note that there are attempts to express constraints as additional sets of linear equations to be solved simultaneously with the 3D reconstruction problem, but they are either designed specifically for structures with icosahedral symmetry (Zheng et al., 2000), or still atinitial stages of development (Sorzano et al., 2008).

In POCS, one considers sets whose elements are images, which can be either 2D or 3D . For example, one can consider a set of non-negative images or a set of frequency-limited images. Given k convex sets of images C_i, i = 1,...,k, methodology based on the theory of POCS methodology can be used to find an image that lies in the intersection C₀ of all the given sets, and thus simultaneously satisfies all constraints and hence has the desired properties. If we denote by ${\mathcal{P}}_i$ the projection onto convex set C_i, then the sequence of iterations

$$f_{l+1}={\mathcal{P}}_1{\mathcal{P}}_2\dots {\mathcal{P}}_k{f}_l$$ (35)

will converge to an image in the intersection C₀ for any initial image f₀; if C₀ is empty, then the procedure will not terminate. Assuming C₀ is non-empty, the properties of the solution will depend on the properties of the initial image f₀. The exception is if C₀ consists of just a single image, which normally does not happen.

Examples of often used constraints are: non-negativity (negative elements in the image are set to zero), compact support (image is multiplied by a binary mask), and predefined Fourier amplitudes (the corresponding POCS projection sets the Fourier amplitudes of an image to predefined values while imposing no restrictions on phases). It is easy to see that there are images that could fulfill all three constraints simultaneously, and for limited resolution data, the number of such images will be very large. However, under favorable conditions, the procedure based on repeated applications of these constraints can be shown to converge in the limit to the so-called super-resolution. The method was developed independently by Papoulis (Papoulis, 1975) and Gerchberg (Gerchberg, 1974). While the former was concerned with the extrapolation of a band-limited signal from a part of the original real-space signal, the latter dealt with the problem of reconstruction of the signal from its Fourier spectrum given to the diffraction limit. In X-ray crystallography, the Papillose-Gerchberg (PG) algorithm is known as “solvent flattening” (Wang, 1985). POCS provides a comprehensive framework within which the PG algorithm can be understood, in addition to being a theoretical basis for the development of additional constraints (Sezan, 1992).

In cryo-EM, the initial motivation for exploring POCS based methods was due to the missing cone problem resulting from application of the Random Conical Tilt method for ab initio protein structure determination (Radermacher et al., 1987). Tilt-pairs of electron micrographs are collected and the presence of predominant view on the zero-tilt micrograph leads to a simple and robust way of determining all necessary 3D orientation parameters by using the readout from the microscope goniometer and 2D in-plane alignment of zero-degree, thus presumably identical, 2D projection views. Regrettably, the method leaves undetermined a conical-shaped region of Fourier space in the 3D reconstructed volume, and the angle of the cone is typically 40 degrees. As a result, the 3D structure is severely distorted and elongated in the direction of the cone. Some effort has been put into POCS-based recovery of the missing region (Carazo and Carrascosa, 1987), and although some reduction of the elongation has been reported, the results were at best modest (Akey and Radermacher, 1993; Radermacher et al., 1994). A related problem in electron tomography is the missing wedge of the single-axis tilt series of EM projection data (20-30 degrees opening), which is caused by the limited tilting range of the microscope; there have been some attempts to rectify the problem using POCS approaches (Carazo, 1992).

POCS is an attractive approach to the problem of restoration of cryo-EM macromolecular structure; however, the practical application of POCS based methods is problematic for a number of reasons. Neither the theory of POCS nor the POCS based methods developed so far account for errors in the 3D results. And while it is easy to demonstrate significant improvements using simulated, error-free data, even modest amounts of noise make the gains doubtful. One possible approach to the aforementioned issues is to consider POCS within a broader context of the structure determination procedure, including refinement of orientation parameters. So far however, no significant effort in this direction has been reported (for a possible solution, see (Yang et al., 2005)).

Wiener filter - the minimum mean-squared error criterion

In images restored using pseudoinverse methods, noise can be excessively amplified for some spatial frequencies. This not only produces unpleasant artifacts in real space, but also creates serious problems in iterative alignment procedures, which tend to emphasize artifacts in reference images. A method that prevents excessive enhancement of noise by taking advantage of the estimate of the SSNR distribution in the data is based on minimization of mean-square error (MMSE) between the estimate and the original signal:

$$\underset{\widehat{F}}{\min }{\mathcal{L}}_{MMSE}\left(\widehat{F}\right)=\underset{\widehat{F}}{\min }E\left\{{\Vert F\left(\mathbf{s}\right)-\widehat{F}\left(\mathbf{s}\right)\Vert }^2\right\}.$$ (36)

Wiener filter in restoration of an image using EM data with varied defocus settings

As previously noted, we seek the solution in a form of linear combination of input data:

$$\widehat{F}\left(\mathbf{s}\right)=\sum _n{w}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)$$ (37)

and we minimize Eq.36 with respect to filter coefficients w_n (s). To find the minimum, we differentiate Eq.36 with respect to w_k, set derivatives to zero and obtain a set of N equations:

$$\begin{array}{cc}\hfill \frac{\partial {\mathcal{L}}_{MMSE}}{\partial w_k}& =\frac{\partial }{\partial w_k}E\left\{{\Vert F-\sum _n{w}_n{G}_n\Vert }^2\right\}\hfill \\ \hfill & =E\left\{\left(F-\sum _n{w}_n{G}_n\right)G_k^{\ast }\right\}=0,\hfill \end{array}$$ (38)

where for simplicity we omitted the dependence on spatial frequency. In Eq.38, we substitute G_n by its form given by the image formation model (Eq.8). The expectation value yields the following set of equations:

$$CT{F}_k{E}_k{P}_{f_k}\left(1-\left(\sum _n{w}_{n}CT{F}_n{E}_n\right)\right)-w_k{P}_{m_k}=0,$$ (39)

which can be solved by noting that the term ${\sum }_n{w}_{n}CT{F}_n{E}_n$ is shared:

$$w_k=\frac{CT{F}_k{E}_k{P}_f}{P_{m_k}}/\left(\sum _n\frac{{\mid CT{F}_n{E}_n\mid }^2{P}_f}{P_{m_k}}+1\right).$$ (40)

Weights w_k are coefficients of the Wiener filter, which means the result is dependent on the ratio of the PW of the signal to the PW of noise:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)\frac{P_f\left(\mathbf{s}\right)}{P_{m_n}\left(\mathbf{s}\right)}{G}_n\left(\mathbf{s}\right)}{\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)\frac{P_f\left(\mathbf{s}\right)}{P_{m_n}\left(\mathbf{s}\right)}+1}.$$ (41)

It is customary to express the Wiener filter as a function of SSNR, so, using definition Eq.9, we obtain:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)+1}.$$ (42)

The difference between the Wiener filter Eq.42 and the MCE pseudoinverse restoration Eq.28 appears to be minimal since they differ merely by the addition of one in the denominator. However, this constant has a significant impact on the outcome of the restoration as it lends the Wiener filter the following desired properties: (a) it sets to zero those frequency regions in the input data for which CTF or the envelope function or the SSNR are zero, and (b) it mitigates the enhancement of amplitudes in regions where combined signal ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)$ is low and depends on the combined value of SSNR in this region.

The mathematical forms of the Wiener filter Eq.42 and the constrained mean-square restoration CMCE Eq.31 are all but identical. Nevertheless, the motivations and meanings behind them are entirely different. The Wiener filter will yield a solution similar to the original signal, as permitted by the SSNR level in the data, while CMCE will yield a “smooth” solution that is constrained by its chi-square fit to the data. The main difference is that the Wiener filter does not contain any free parameters, since in principle at least all its terms should be derived either from the experimental settings or from analysis of the data, whereas in CMCE, both the shape of the high-pass filter U (s) and constant γ are entirely arbitrary and depend on the decision of the user. In the context of SPR, it remains to be seen whether it is possible in practice to determine characteristics of the image formation process with an accuracy sufficient to justify usage of the Wiener filter instead of the heuristic CMCE.

The properties of the Wiener filter are best exemplified by the two limiting cases of input images with very high SSNR and those with very low SSNR. In the former case, we obtain:

$${\widehat{F}}_{SSNR\to \infty }\left(\mathbf{s}\right)=\frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)E_n^2\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)}.$$ (43)

Eq.43 simply coincides with the MCE pseudoinverse restoration Eq.28. This reinforces the intuitive notion that unlimited enhancement of amplitudes in regions where products of CTFs and envelope functions are small only makes sense when the power of the noise is negligible relative to the power of the signal, in which case the enhancement of the former will not deteriorate the overall appearance of the image.

For input data that has very low SSNR, i.e., the signal is dominated by noise, the Wiener filter Eq.42 is reduced to:

$${\widehat{F}}_{SSNR\to 0}\left(\mathbf{s}\right)=\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)E_n\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right).$$ (44)

Eq.44 simply means that under low SSNR conditions there should be no enhancement of amplitudes; to the contrary, all images should be multiplied by their CTFs and envelope functions, which under standard EM imaging conditions corresponds to low-pass filtration of the data. Eq.44 has no counterpart in MSE or MCE frameworks and is unique to the MMSE statement of the restoration problem.

In general, the Wiener filter image restoration given by Eq.42 has the following properties (Fig.4c):

1. For a large number of images collected at approximately uniformly distributed defocus settings, the impact of the filter Eq.42 can be considered separately for two spatial frequency regions consisting of, respectively, : (a) frequencies lower than the frequency of the first extremum of ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)$, and (b) frequencies higher than the first extremum. In the first region, all CTFs have approximately the same shape irrespective of the defocus settings, so the enhancement for s → 0 is given by $\frac{A^2{\sum }_{n=1}^{N}SSN{R}_n\left(\mathbf{s}\right)+1}{A{\sum }_{n=1}^{N}SSN{R}_n\left(\mathbf{s}\right)}$, which for large SSNRs corresponds to the MCE solution. In the second region consisting of higher frequencies, the denominator will be approximately constant, so the restoration corresponds to the summation of EM images multiplied by their respective CTFs. However, unlike the case in MCE, the variations in the denominator depend on the SSNR values and decrease with decreasing values of the SSNR.

2. For a small number of images or for data sets for which ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)\simeq 0$ for some spatial frequencies, the value of the Wiener filter approaches zero, which is markedly different from the MCE solution. This advantage of the Wiener filter makes it the method of choice in direct Fourier inversion 3D reconstruction from projection algorithms in EM (Zhang et al., 2008).

3. The solution depends both on the scaling and frequency dependance of the SSNR. Thus, in protocols where the PW of the signal is obtained from independent experiments or computed from X-ray crystallographic models, while the PW of the background noise is estimated from the data, the additional free variable in the image restoration Eq.42 is the relative scaling between the two. It is easy to see that the results depend heavily on this parameter and an incorrect scaling cannot be easily accounted for in subsequent data processing steps.

Proper applications of the image restoration methods outlined above vary depending on the dimensionality of the data (2D versus 3D) and the goal (alignment, 3D reconstruction, PW adjustment or “sharpening” of EM map). In 2D applications, the incorrect enhancement of amplitudes in the low frequencies region can adversely influence the alignment results. Furthermore, the problem is compounded by the need to process heterogeneous data sets, in which case, strictly speaking, neither of the methods reviewed in this section are applicable without modifications. On the other hand, it is the case that in 2D applications each pixel (spatial frequency s) of the restored image has the same number of contributing data images. This, combined with the fact that it would be rare to have a selection of defocus settings such that ${\sum }_{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)\simeq 0$, imply that the quality of restoration in higher frequency regions is less critical than in lower frequency regions, and the practical differences between MCE, the iterative methods, or the Wiener filter become of secondary consideration.

Wiener filter (MMSE) restoration in cryo-EM has many appealing properties, but it also has significant disadvantages. While the solution is better behaved than what one would obtain from MCE e pseudoinverse restoration and is less likely to be affected by artifacts, it also depends to a much higher degree on the proper estimation of all the image formation characteristics. In particular, the proper scaling and general shape of envelope functions and SSNR distributions are of paramount importance. More importantly, the MMSE criterion cannot be easily used in alignment procedures. Specifically, if we introduce a dependence on the orientation parameters of images G_n, then the MSE (Eq.17) and MCE (Eq.20) criteria yield to a well-known method of finding the optimum values of these parameters using a cross-correlation function (CCF) (obtained from an inverse Fourier transform of a product in reciprocal space). A similar line of reasoning implies that Eq.36 in combination with Eq.31 would yield a solution for finding the optimum orientations of images G_n, under the assumption that an ideal template is given. Regrettably, this reasoning cannot be applied to the MMSE criterion, and has no applicability to EM in general, since such a template is not available. In addition, it can be easily shown that the Wiener filter average (i.e., the restored image) Eq.42 does not minimize the variance of the data set with respect to the alignment parameters.

Wiener filter in image filtration and amplitude correction (“sharpening”)

The Wiener image restoration technique described in the previous section is based on the assumption that a reasonable approximation of the SSNR in the data can be established. However, as exemplified by Eq.11, the most comprehensive SSNR characterization of EM results would include accounting for the deterioration due to alignment errors, expressed either as an additional envelope function, additional variance, or both (Baldwin and Penczek, 2005). It would be appropriate to include this information in the restoration of the average by either MCE or Wiener methodology; regrettably, it is more typically the case that information about SSNR of the average becomes available only after the average has been calculate. This SSNR of the result is often referred to as a resolution of the averagereconstruction and is typically estimated using the Fourier Shell Correlation (FSC) methodology (insert reference to Penczek chapter on Resolution Measures here). Thus, the problem is circular: to properly restore the average, one would have to know its SSNR, but the SSNR can be obtained only after the average has been computed . The issue has never been satisfactorily resolved in the EM data processing methodology, and it is customary to apply a post-filtering of the average, thus breaking the calculation of average into two steps (Penczek, 2008).

The image formation model of a CTF-corrected cryo-EM 2D average or a 3D reconstruction v of a macromolecular complex f is given, in Fourier space, as:

$$V\left(\mathbf{s}\right)=E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)F\left(\mathbf{s}\right)+M\left(\mathbf{s}\right),$$ (45)

where E is the average of the effective envelope functions E_n that appeared in Eq.9, E^Ali is the envelope function due to alignment errors and errors in the image restoration step that resulted in average V, and M is the background noise of Eq.9 (albeit reduced due to the averaging/reconstruction step). As before, we assume that the noise is zero mean, uncorrelated between spatial frequencies and uncorrelated with the signal. The Wiener filter derivation for model Eq.45 follows steps Eqs.37-40 and yields:

$$\begin{array}{cc}\hfill \widehat{F}\left(\mathbf{s}\right)& =\frac{E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)\frac{P_f\mathbf{s})}{P_m\left(\mathbf{s}\right)}}{E^2\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)\frac{P_f\left(\mathbf{s}\right)}{P_m\left(\mathbf{s}\right)}+1}V\left(\mathbf{s}\right)\hfill \\ \hfill & =\frac{E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)SSN{R}_f\left(\mathbf{s}\right)}{E^2\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)SSN{R}_f\left(\mathbf{s}\right)+1}V\left(\mathbf{s}\right)\hfill \\ \hfill & =\frac{1}{E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)}\frac{SSN{R}_v\left(\mathbf{s}\right)}{SSN{R}_v\left(\mathbf{s}\right)+1}V\left(\mathbf{s}\right).\hfill \end{array}$$ (46)

Most properties of the Wiener filter Eq.42 are shared by the filter given by Eq.46.

The straightforward application of Eq.46 is in a low-pass filtration of the average/reconstruction emerging from the cryo-EM refinement procedure. In this case, one would neglect correcting for the two envelope functions and take advantage of the simple relationship between the SSNR of the average and the FSC to obtain the appropriate filter (insert reference to Penczek chapter on Resolution Measures here). The full form of Eq. 46 provides a solution to the problem of restoration of the rotationally-averaged profile of the PW of the average/reconstruction v; this procedure is sometimes referred to as sharpening the result. To derive it, we first note that even though SSNR_v is known, it is all but impossible to estimate the product of two envelope functions. A sensible approach, described in an earlier section, is to independently estimate both the rotational average of the PW of the ideal structure P_f (s) and that of the background noise in the average/reconstruction P_m (s). Given this and the image formation model in Eq.45, we obtain:

$$E^2\left(s\right)E^{Al{i}^2}\left(s\right)\frac{P_f\left(s\right)}{P_m\left(s\right)}=\frac{P_v\left(s\right)}{P_m\left(s\right)}-1,$$ (47)

Using Eq 47 we can write the Wiener filter Eq.46 as:

$$\widehat{F}\left(\mathbf{s}\right)=E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)\frac{P_f\left(\mathbf{s}\right)}{P_v\left(\mathbf{s}\right)}V\left(\mathbf{s}\right).$$ (48)

The product of the envelope functions is obtained independently using FSC methodology and is simply:

$$E\left(\mathbf{s}\right)E^{Ali}\left(\mathbf{s}\right)=\sqrt{SSN{R}_v\left(s\right)\frac{P_m\left(\mathbf{s}\right)}{P_f\left(\mathbf{s}\right)}}.$$ (49)

The expression for filtration combined with PW adjustment (“sharpening”) of the EM average/reconstruction is:

$$\widehat{F}\left(\mathbf{s}\right)=\{\begin{array}{cc}\sqrt{\frac{SSN{R}_v\left(s\right)P_m\left(s\right)}{P_v\left(s\right)}}\sqrt{\frac{P_f\left(s\right)}{P_v\left(s\right)}}V\left(\mathbf{s}\right)\hfill & if\frac{SSN{R}_v\left(s\right)P_m\left(s\right)}{P_v\left(s\right)}<1\hfill \\ \sqrt{\frac{P_f\left(s\right)}{P_v\left(s\right)}}V\left(\mathbf{s}\right)\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (50)

Eq.50 has many appealing properties: (1) it contains only entities which can be easily computed from the data, namely, SSNR_v, FSC_v and PW of the background noise in the average/reconstruction (which can be computed from the area surrounding the object), and (2) the result does not depend on normalizations of PWs of the ideal object and background noise, both of which are difficult to establish. Furthermore, in regions where SSNR is high, P_m should be close to zero, and the additional condition in Eq.50 prevents excessive amplification of amplitudes in V.

Image restoration for sets of heterogeneous images

The image restoration techniques described in the preceding sections are based on the assumption that the signals the EM projection images of a macromolecular complex) in Eq.1 are identical. This however is rarely the case and it might be more appropriate to consider various degrees to which this assumption holds in practice. An EM data set will always contain a certain percentage of non-particles, i.e., objects that passed both automated particle selection as well as visual scrutiny, but do not represent valid views of the imaged complex and are instead artifacts that have strong low frequency components and which are often found in micrographs. Furthermore, many macromolecular complexes naturally exist as a mixture of various conformations, so the sample cannot be considered homogeneous. Very often processed sample contains a mixture of complexes in various functional states, for example some may have ligands bound.

It is a straightforward to conclude that in the case of heterogeneous samples, the images restoration techniques described above are strictly speaking not applicable as they are based on the assumption that the signal is identical and images are in the same orientations. Indeed, if a Wiener filter (Eq.42) were applied to a heterogeneous data set, we would obtain:

$$\widehat{F}(s\to 0)=\frac{A\sum _{n=1}^{N}SSN{R}_n^{Data}{G}_n}{A^2\sum _{n=1}^{N}SSN{R}_n^{Data}+1}\simeq \frac{ASSN{R}^{Data}\sum _{n=1}^N{G}_n}{A^{2}SSN{R}^{Data}+1/N}\simeq \sum _{n=1}^N\frac{1}{A}{G}_n,$$ (51)

where we assumed that envelopes and SNRs are approximately the same for all particles in very low frequency range. It follows from Eq.51 that since all images G_n are different (in the sense that the signal components F are different), the average will be formed from individual images whose low frequency component was enhanced A times. A typical value of the amplitude contrast ratio (A) is 0.1, so the enhancement will be ~10 times, the result of which are very blurry images.

Phase flipping

There are a number of possible heuristic solutions to the problem outlined above. One such solution, adopted in numerous single particle packages (Ludtke et al., 1999; Tang et al., 2007; van Heel et al., 1996), is to disregard the information about CTF-induced amplitude changes in EM images and correct the data only for the sign of the CTF, and thus obtain the correct signs of phases in Fourier space. Consequently, this heuristic is known as “phase-flipping”:

$${\tilde{G}}_n\left(\mathbf{s}\right)=sign\left(CT{F}_n\left(\mathbf{s}\right)\right)G_n\left(\mathbf{s}\right).$$ (52)

The appeals of phase-flipping are: (1) signs of phases in images collected under different defocus settings become consistent, so it is possible to apply efficient alignment procedures such as those based on image invariants (Marabini and Carazo, 1996; Schatz and van Heel, 1990; Schatz and van Heel, 1992); (2) the problem of excessive low-frequencies in the average is circumvented; (3) the CTF correction process can be decomposed into a number of steps, thus allowing for more elaborate CTF correction to be applied in later stages of data processing. Advantages of using phase-flipped data, even if they are only used in the early stages of data processing, do not outweigh the disadvantages. A significant disadvantage is the omission of CTF amplitude weighting, so the average computed from phase-flipped images will have excessive amount of noise, and thus suboptimal SNR.

The reciprocal space adaptive Wiener filter

We begin by proposing that the desired amplitude-weighted Wiener filter based restoration ] should be such that in the case of a heterogeneous data set the overall effect of the restoration should result in a PW of the restored image that corresponds to the average of the PWs of the individual images. We note that the previous neither implies nor assumes that the PWs of averaged images cannot be changed, as in the phase-flipping approach. To construct such an amplitude-preserving restoration, we impose the additional constraint on the Wiener filter (Eq.42) requiring that the effective amplitude modification for each spatial frequency should be one:

$$\forall \mathbf{s}:\frac{\sum _{n=1}^{N}q\left(\mathbf{s}\right)\mid CT{F}_n\left(\mathbf{s}\right)\mid SSNR\left(\mathbf{s}\right)}{\sum _{n=1}^{N}q\left(\mathbf{s}\right)CT{F}_n^2\left(\mathbf{s}\right)SSNR\left(\mathbf{s}\right)+1}=1,$$ (53)

where for simplicity we omitted envelope functions and the per-image dependence of SSNR. From Eq.53 it follows that the additional normalization factor should be:

$$q\left(\mathbf{s}\right)=\frac{1}{SSNR\left(\mathbf{s}\right)\left(\sum _{n=1}^N\mid CT{F}_n\left(\mathbf{s}\right)\mid -\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)\right)}.$$ (54)

With this the Wiener filter (Eq.42) is reduced to:

$$\widehat{F}\left(\mathbf{s}\right)=\frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}^N\mid CT{F}_n\left(\mathbf{s}\right)\mid },$$ (55)

in which case the restoration becomes a simple CTF-weighted averaging.

To obtain a continuous transition between restoration methods geared for strictly homogeneous (Eq.28) data sets and strictly heterogeneous (Eq.55) data sets, we propose the following form of the reciprocal space adaptive Wiener filter:

$$\widehat{F}\left(\mathbf{s}\right)=\alpha \left(\mathbf{s}\right)\cdot \frac{\sum _{n=1}^{N}CT{F}_n\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)G_n\left(\mathbf{s}\right)}{\sum _{n=1}CT{F}_n^2\left(\mathbf{s}\right)SSN{R}_n\left(\mathbf{s}\right)},$$ (58)

where α(s) depends on the parameter N_g, a user specified parameter denoting the number of homogeneous subsets in the data set:

$$\alpha \left(\mathbf{s}\right)=\frac{N-N_g}{N-1}+\frac{N_g-1}{N-1}\cdot \frac{\sum _{n=1}^{N}CT{F}_n^2\left(\mathbf{s}\right)}{\sum _{n=1}^N\mid CT{F}_n\left(\mathbf{s}\right)\mid }.$$ (59)

The reciprocal space adaptive Wiener filter offers a significant advantage over ‘phase flipping’ as it incorporates proper amplitude weighting of images, thereby maximizing SSNR per each spatial frequency s. It also provides a mechanism for a continuous and intuitive, albeit heuristic, transition between restoration of purely homogeneous and purely heterogeneous EM data sets.

Discussion

All restoration methods discussed in this review require knowledge of the parameters of the image formation model. These parameters can be derived from analysis of the data, some with a high degree of accuracy (e.g. defocus), while for others (e.g. envelopes, SSNR) there is no consensus on whether their accuracy is sufficient to benefit alignment procedures. Curiously, although elaborate CTF estimation methods have been implemented and used, there are no published studies that would demonstrate that the resolution of the final structure improves if estimates of the SSNR of the data, envelope functions, and background noise are included. Hence, in the absence of conclusive evidence, there are at least three possible approaches to the treatment of the relationship between the image formation model and image restoration: (1) ignore the subtleties, set SSNR of the data to a constant, and adjust the parameters of alignment procedures based on other considerations, (2) model all curves by analytical functions and fit them to the data in the hope that this will reduce uncertainties, (3) use characteristics such as background noise distribution or SSNR as estimated directly from the data. The latter approach has a significant advantage of being applicable to any data without adherence to any particular model, but at the same time any statistical fluctuations in the characteristics drawn directly from the data are passed on to the alignment procedures unchecked.

All the restoration methods presented here yield solutions that appear very similar, e.g., the mathematical forms of the CMCE and Wiener filter are nearly identical. However, the motivations and meanings of the parameters of the respective solutions can be quite different, and the user should be aware which parameters are arbitrary and can be set based on heuristics and alignment results, and which should be derived experimentally from the data. It is also apparent that 2D image restoration is less sensitive to the choice of restoration method since the main difficulty is in the inhomogeneity of the data. Hence we propose a practical solution in terms of a reciprocal space adaptive Wiener filter whose main parameter is the number of homogeneous classes that one assumes are present in the data set. In 3D image restoration, particularly in 3D reconstruction algorithms that incorporate CTF correction, it is necessary to use a form of regularization to avoid artifacts in the resulting 3D structure, in which case CMCE, iterative methods and Wiener filters are the only possibilities, while MCE is not applicable. Again, there is relatively little work published on the 3D reconstruction/CTF correction algorithms and there is no consensus on how to best accommodate large SSNR variations in reciprocal space.

Major single particle software packages differ significantly in the way that image restoration issues are handled, and s published descriptions are minimal for a number of the packages. Hence, a comprehensive comparison among the different packages is a difficult task at best. At the risk of not representing the methods actually used adequately, one can characterize the methodology implemented in the respective packages as follows:

1. In SPIDER (Frank et al., 1996), SSNR is treated as constant and can be set by the user. The 3D reconstruction is done by grouping 2D projection data according to defocus settings, and 3D reconstruction is performed for each group independently. The resulting volumes are merged using a Wiener filter with constant SSNR. However, since SPIDER is a general purpose image processing package, advanced users tend to implement their own strategies, including phase flipping and others.

2. In IMAGIC (van Heel et al., 1996), data is aligned and clustered in 2D, initially using phased-flipped data; subsequently, only amplitudes are adjusted in the 3D reconstruction step(van Heel et al., 2000).

3. In EMAN1 (Ludtke et al., 1999), the sequence of data processing steps follows that in IMAGIC, e.g., the CTF correction is done for 2D projection images, but the major difference is in the incorporation of image formation characteristics using analytical functions fitted to the data.

4. EMAN2 (Tang et al., 2007) inherits the general strategy of EMAN1 but employs a a modernized approach to image restoration based on characteristics derived from the data, thus omitting the fitting step and making the process more robust and widely applicable.

5. In SPARX (Hohn et al., 2007) the 3D reconstruction algorithm incorporates CTF correction and both 2D and 3D rely on variations of the reciprocal space adaptive Wiener filters with some image formation characteristics derived from the data. SPARX follows the open source philosophy of SPIDER in allowing users to implement customized strategies by taking advantage of its extensive library of general image processing commands.

Since image restoration methods in single particle reconstruction software packages are incorporated into the structure determination protocols, it is very difficult to perform comparative testing. Such tests would require repetition of the entire structure determination process, and the results would be influenced by other differences among the packages. Although a consensus is unlikely to be reached soon, there is much that could be done towards carrying out a comprehensive treatment of image formation characteristics. A number of the solutions adopted are heuristic and it should be possible to reach an understanding as to why heuristics are necessary since the physics of image formation in EM is well understood. Similarly, even if the trend is to rely on image formation characteristics directly derived from the data, as implemented in EMAN2, it is possible that more robust and less error-prone approaches can be developed by a reexamination of the theory and the introduction of appropriate constraints to the fitting process.