Assessing the contribution of heterogeneous distributions of oligomers to aggregation mechanisms for polyglutamine peptides

Abstract

Polyglutamine aggregation is associated with neurodegeneration in nine different disorders. The effects of polyglutamine length and peptide concentration on the kinetics of aggregation were previously analyzed using a homogeneous nucleation model that assumes the presence of a single bottleneck along the free energy profile G(n), where n denotes the number of polyglutamine molecules. The observation of stable, soluble oligomers as intermediates along aggregation pathways is refractory to the assumptions of homogeneous nucleation. Furthermore, the analysis of in vitro kinetic data using a specific variant of homogeneous nucleation leads to confounding observations such as fractional and / or negative values for estimates of the critical nucleus size. Here, we show that the homogeneous nucleation model is inherently robust and is unlikely to yield fractional values if the underlying process is strictly homogeneous with a free energy profile G(n) that displays a sharp maximum at n=n*, where n* corresponds to the critical nucleus. Conversely, a model that includes oligomers of different size and different potentials for supporting turnover into fibrils yields estimates of fractional and / or negative nucleus sizes when the kinetic data are analyzed using the assumption of a homogeneous process. This model provides a route to reconcile independent observations of heterogeneous distributions of oligomers and other non-fibrillar aggregates with results obtained from analysis of aggregation kinetics using the assumption of a homogeneous nucleation model. In the new model, the mechanisms of fibril assembly are governed by the relative stabilities of two types of oligomers viz., fibril-competent and fibril-incompetent oligomers, the size of the smallest fibril competent oligomer, and rates for conformational conversion within different oligomers.

1. Introduction

Nine different neurodegenerative disorders including Huntington's disease [1] are associated with polyglutamine expansions [2]. In these diseases, the age-of-onset and severity at onset are inversely correlated with polyglutamine expansion lengths [3]. Expanded polyglutamine tracts have all the hallmarks of being intrinsically disordered regions [4-9] although this does not translate into their classification as canonical random coils [10]. Polyglutamine regions destabilize their host protein thereby increasing its susceptibility to proteolysis [11-21]. Products of proteolysis are rich in unprocessed polyglutamine regions [22, 23], which are prone to aggregation [6, 24-30] as well as recruitment and sequestration [6, 31, 32] of polyglutamine-rich regions from other proteins, specifically transcription factors [33-46]. Together, aggregation as well as recruitment and sequestration form a gain-of-function / loss-of-function route to toxicity. In the gain-of-function paradigm, soluble, oligomeric intermediates are currently implicated, albeit in unresolved ways, with consequences for trafficking [47], interactions with membranes [48, 49], and protein quality control [50-57]. The loss-of-function paradigm implicates unwarranted interactions with polyglutamine expansions leading to the loss of essential proteins. The proteins involved in polyglutamine expansion disorders are different from each other in terms of their sequences and functions. Their only shared attribute is the association with disease on account of mutant polyglutamine expansions. As a result, much effort has been focused on understanding the conformational properties and aggregation mechanisms of polyglutamine-rich sequences.

Constructs for biophysical investigation

Studies based on homopolymeric or quasi-homopolymeric polyglutamine constructs are directly relevant to the situation in vivo because mechanisms formulated to explain the behavior of synthetic peptides serve as references for interpreting the effects of naturally occurring flanking sequences and heterotypic interactions in the cellular milieu. Reports from molecular simulations [8, 9, 58-63] have focused on analyzing the conformational properties and oligomerization [64, 65] of homopolymeric polyglutamine. In biophysical studies, the poor solubility of homopolymeric polyglutamine [25] necessitates the use of flanking charged residues including one [10] or two [6, 26-28, 66-70] pairs of flanking lysines or pairs of oppositely charged flanking residues [71]. The implicit assumption is that these charges do not alter the intrinsic conformational preferences and intermolecular associations. Recent experimental investigations [69] and computational studies [72] call this assumption into question. At this juncture, the effects of naturally occurring flanking sequences remain unresolved because of conflicting interpretations of in vitro data [67, 73] and these interpretations being called into question by in silico results [72].

The need for a thermodynamic framework for aggregation

The goal of understanding the “gatekeeping” [74, 75] or other modulating effects of flanking sequences on polyglutamine aggregation is reminiscent of thermodynamic linkage models [76] for analyzing the effects of ligand on the self-assembly of macromolecules into large aggregates. One can develop a linkage analysis for the effect of ligands in cis, namely flanking sequences on the polyglutamine-length dependent driving forces for aggregation [77]. This is likely to be feasible by drawing from the rich literature of the physics of phase transitions – a topic that has been reviewed recently [78]. Specifically, phase equilibria of polymer solutions modeled as quasi-binary mixtures provide thermodynamic constraints on aggregation mechanisms. At this juncture, systematic thermodynamic characterization of driving forces for polyglutamine aggregation remains unavailable. Instead, Scherzinger et al. [29, 30] used in vitro aggregation experiments to show that the overall rate of aggregation in polyglutamine-rich systems increases with polyglutamine length and peptide concentration. One of the necessary (but insufficient) hallmarks of a nucleation-dependent mechanism is the presence of a lag phase that can be eliminated by adding pre-formed aggregates to the reaction mixture [79, 80]. Scherzinger et al. showed that lag times could be reduced / eliminated with the addition of pre-formed aggregates. Subsequently, Wetzel and coworkers established the necessary set of protocols to disaggregate synthetic polyglutamine peptides of the form K₂-Q_N-K₂ [6, 81, 82]. A key step was ensuring the absence of seeds such that the starting peptide concentration c_t can be reliably confined to the monomer pool.

Homogeneous nucleation

Chen et al. [83] adapted the homogeneous nucleation model of Ferrone [79] to analyze their data for the time course of aggregation of K₂-Q_N-K₂ peptides. In this model, the Gibbs free energy of a species with n molecules can be written as follows: G(n+1) − G(n) > 0 for n < n* whereas, G(n+1) − G(n) < 0 for n > n*. Here, n* is the size of the critical nucleus that forms a single, well-defined bottleneck that kinetically partitions the reaction mixture between a pool that is dominantly monomeric (because the monomer is the thermodynamically favored state for pre-nuclear species) and large aggregates that for polyglutamine are assumed to be fibrillar. By assuming that pre-nuclear species are in rapid pre-equilibrium with each other and postulating that the rates of elongation of nuclei and fibrils are equivalent, Chen et al. analyzed the time courses for aggregation of K₂-Q_N-K₂ peptides. Of particular relevance is the expression for Δ(t), which measures the concentration of monomeric material that is incorporated into the growing fibril. It can be shown that Δ(t) ∼ t² for the early stages of homogeneous nucleation. If one assumes that the only relevant species are monomers and large aggregates, then the time course for monomer loss can be used as a proxy for Δ(t) and analyzed at different overall peptide concentrations to extract an estimate for the critical nucleus size n*. For brevity, we shall use the acronym ETM (for Early Time course Model) when using the variant of homogeneous nucleation that is based on the t² dependence of Δ(t).

In studies of K₂-Q_N-K₂ peptides, Chen et al. [83] used ETM and obtained values of 0.98, 0.68, and 0.59, as estimates of n* for N=28, 36, and 47, respectively. They rounded these estimates up to the nearest integer to conclude that monomers form the critical nucleus for polyglutamine aggregation. Folding of individual molecules is rate-limiting because it is presumed to be thermodynamically unfavorable by ca. 12-15 kcal/mol, and becomes less unfavorable as polyglutamine length increases [66]. Parameters from the model were used to predict the age-of-onset of Huntington's disease by connecting the accumulation of large fibrillar species to the onset of disease.

Issues with homogeneous nucleation

Bernacki and Murphy [84] have shown that the t² dependence for the early time course of Δ(t) is not restricted to homogeneous nucleation. They also raised concerns about certifying a specific mechanism by following only one side of the reaction viz., monomer loss kinetics because this imposes strong assumptions on the model that is inferred from the analysis. The nature of the proposed rate-limiting unimolecular conformational transition remains speculative, although mutagenesis studies [28] and inferences drawn from analysis of morphologies of high molecular weight aggregates [27] were extrapolated to suggest that the transition involves a conversion to β-sheets. Within smaller species, specifically for monomers, a heterogeneous ensemble of collapsed structures is preferred for homopolymeric polyglutamine irrespective of chain length. Computational studies of homopolymeric constructs show that the preference for heterogeneity at the monomer level leads to significant entropic bottlenecks for forming β-sheet conformations [64]. It was shown that disorder prevails even when the entropic penalties for sampling the requisite dihedral angles have been pre-paid [65]. Conversely, ordered β-sheets emerge as one of the possible outcomes of intermolecular interfaces within aggregates of growing size [65]. This idea is consistent with results [83] demonstrating that the rate of elongation of K₂-Q_N-K₂ peptides was considerably slower than diffusion suggesting that the ordered template that forms upon nucleation needs to be deformed to promote elongation by a so-called “dock-and-lock” mechanism, which requires the mixing / entanglement of chain degrees-of-freedom at intermolecular interfaces. Several studies report the presence of stable oligomers [57, 85-92] that form early and are either on-pathway to the fibril or act as off-pathway sinks. Additionally, recent attention in the aggregation literature has focused on the effects of fragmentation of larger species [93] and the positive cooperativity between fragmentation and assembly because it increases the concentration of growing ends [94-96].

The presence of heterogeneous distributions of species of different sizes and morphologies can confound the analysis of aggregation kinetics that relies on the strict assumptions of homogeneous nucleation. Of particular interest are two sets of observations that result from the application of ETM to processes that are presumed to follow homogeneous nucleation. These are the observations of fractional values for n*, which was reproduced in recent analysis of kinetic data for shorter K₂Q_N-K₂ constructs [97]. Secondly, when Thakur et al. [67] applied the ETM analysis to monomer loss kinetics for synthetic peptide mimics of the exon 1 encoded region of huntingtin, they obtained negative values as estimates for n*. Here, we ask if fractional and / or negative values for n* point to inherent non-robustness of the ETM analysis or if it might point to contributions from underlying heterogeneities such as oligomers of different sizes and potential for growing into fibrils.

In the analysis that follows, we first introduce the details of the analysis based on ETM. The effects of specific approximations in ETM are quantified by comparing it to the classical homogeneous nucleation model developed by Oosawa and Kasai [98] or OKM that makes fewer approximations. We re-derive the t² dependence for Δ(t) as a limiting form of OKM. We then fix the nucleus size and assess the contributions due to experimental errors on the robustness of the procedure used to estimate n* from real data. In particular, we show that if the underlying process adheres to homogeneous nucleation with an integer-sized nucleus, then fractional values for n* are inconsistent with the inherent robustness we demonstrate for the ETM analysis. Following the introduction of a schematic that postulates a mechanism for fibril formation through rapid accumulation of stable oligomers, we proceed to show how the homogeneous nucleation model can be generalized to investigate the effects of heterogeneities. When such a model is analyzed using ETM, we show that it yields estimates for n* that can be fractional and also negative under certain circumstances. Overall, the analysis presented here might serve two purposes: First, it shows how the ETM analysis itself can serve as a useful diagnostic for testing the assumption of homogeneous nucleation. Secondly, our analysis provides a route for incorporating the effects of heterogeneous distributions of oligomers.

2. The homogeneous nucleation model

To facilitate our analysis, we first describe the main features of homogeneous nucleation. We consider a generic, step-wise polymerization reaction for species A:

$$\begin{array}{c}A+A\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{A}_2;K_2=\frac{k_2}{k_{-2}}=\frac{\left[A_2\right]}{{\left[A\right]}^2}\\ ⋮\\ A_i+A\underset{\underset{k_{-(i+1)}}{\leftharpoondown }}{\overset{k_{i+1}}{\rightharpoonup }}{A}_{i+1};K_{i+1}=\frac{k_{i+1}}{k_{-(i+1)}}=\frac{[A_{i+1}]}{[A_i][A]}\end{array}$$ (1)

In Equation (1), the K's are equilibrium constants, the k's are rate constants, and square brackets denote concentrations of different species or more precisely, their activities. Only the initial (dimerization) step and the generalization for later steps are shown. In the Ferrone approach, the accumulation of species up to the critical nucleus of size n* are assumed to be in a rapid pre-equilibrium because formation of the nucleus is rate limiting. Accordingly,

$$n^{\ast }A\underset{k_{-n\ast }}{\overset{k_{n\ast }}{\rightleftharpoons }}{A}_{n\ast };K_{n\ast }=\frac{k_{n\ast }}{k_{-n\ast }}=\frac{\left[A_{n\ast }\right]}{{\left[A\right]}^{n\ast }}$$ (2)

Equation (2) identifies one of the important parameters in the homogeneous nucleation model, viz., K_n*, the equilibrium constant that describes the thermodynamic stability of the critical nucleus. The net rate of formation of growing polymer ends is defined using:

$$\frac{d{c}_p}{dt}=k_{+}^{\ast }{c}_{\ast }[A]-k_{-}^{\ast }{c}_{\ast }=K_{n\ast }\cdot {[A]}^{n\ast }\cdot (k_{+}^{\ast }[A]-k_{-}^{\ast })$$ (3)

In Equation (3), c_* denotes the concentration of nuclei and c_p the concentration of growing ends. The pre-equilibrium in Equation (2) was used to obtain an expression in terms of [A]. If we assume rate constants that are independent of aggregate size for species larger than the nucleus, then the rate of incorporation of monomer into the growing polymer is governed by:

$$\frac{d(c_t-[A])}{dt}=\frac{d\Delta }{dt}=c_p\cdot (k_{+}[A]-k_{-})$$ (4)

Here, c_t is the total monomer concentration at t = 0. During the early stages of the polymerization reaction, one can assume that c_t and [A] are similar. Additionally, because post-nucleation processes favor downhill polymerization, the rates for monomers dissociating from either a polymer or from a species larger than n* are assumed to be equivalent and negligibly small. These assumptions are summarized in Equation (5).

$$k_{-}^{\ast }=k_{-}\approx 0;k_{+}^{\ast }=k_{+};[A]\approx c_t=\text{const.}$$ (5)

We can combine Equations (3) and (4) to obtain:

$$\frac{d^2\Delta }{d{t}^2}=\frac{d}{dt}(c_p{k}_{+}{c}_t)=k_{+}{c}_t\frac{d{c}_p}{dt}=K_{n\ast }{k}_{+}^2{c}_t^{n\ast +2}$$ (6)

Equation (6) can be integrated to estimate the rate of incorporation of monomers into the growing polymer during the initial stages of a polymerization reaction in which a well-defined, homogeneous nucleation event is followed by irreversible, kinetically uniform, downhill addition of monomers. This yields:

$$\Delta (t)=\frac{1}{2}{K}_{n\ast }{k}_{+}^2{c}_t^{n\ast +2}{t}^2$$ (7)

and

$$\frac{d\text{ln}\left(\frac{d^2\Delta }{d{t}^2}\right)}{dln{c}_t}=(n^{\ast }+2)\cdot K_{n\ast }{k}_{+}^2{c}_t^{n\ast +1}\cdot \frac{c_t}{K_{n\ast }{k}_{+}^2{c}_t^{n\ast +2}}=n^{\ast }+2$$ (8)

For a given value of c_t, Equation (7) suggests the existence of a time interval where Δ(t) increases linearly with t². Regression analysis in this region yields an estimate for the slope $s(c_t)=\frac{K_{n\ast }{k}_{+}^2{c}_t^{n\ast +2}}{2}$ [83]. Performing this regression analysis using measurements for the early time course to quantify Δ(t) for different values of c_t allows the determination of the nucleus size, n* by estimating the slope of the plot of ln[s(c_t)] against ln(c_t), which should be n*+2. Using mass conservation and the assumption of a homogeneous process, i.e., the absence of intermediates such as oligomers, Chen et al. [83] proposed that the rate of change of Δ(t) can be inferred directly from the rate of loss of monomers.

2.1 General expression for Δ(t) given the assumption of homogeneous nucleation

The expressions developed thus far, particularly Equations (6) – (8) are limited to the analysis of early time courses for the rate at which monomers are incorporated into growing polymers. Oosawa and Kasai [98] showed that for k₊[A] ≫ k₋ i.e., when nucleus formation and elongation are irreversible and the initial concentration of nuclei is zero, the rate at which monomers are incorporated into polymers can be written in terms of $k_{n\ast }^{\text{eff}}$, the effective rate of formation of nuclei as:

$$\begin{array}{c}\text{ln}\left(\frac{1+x}{1-x}\right)=t\sqrt{2n^{\ast }{k}_{+}{k}_{n\ast }^{\text{eff}}{c}_t^{n\ast }}\\ x^2=1-{\left(\frac{[A]}{c_t}\right)}^{n\ast }=1-{\left(1-\frac{\Delta }{c_t}\right)}^{n\ast }\approx \frac{n^{\ast }\Delta }{c_t}\text{for small values of}\left(\frac{\Delta }{c_t}\right)\end{array}$$ (9)

For x² < 1, which corresponds to the early time limit, one can expand the logarithmic term in Equation (9) as a power series in x. Truncation of this series at the first-order term and subsequent algebraic manipulation yields an expression for Δ(t) shown below:

$$\Delta (t)=\frac{1}{2}{k}_{n\ast }^{\text{eff}}{k}_{+}{c}_t^{n\ast +1}{t}^2$$ (10)

Comparing the expressions in Equations (7) and (10), we find that the two models can be matched if we set $k_{n\ast }^{\text{eff}}=K_{n\ast }{c}_t{k}_{+}$, which is consistent with the definition of $k_{n\ast }^{\text{eff}}$. The limiting form of the Oosawa-Kasai result yields an expression that shows the t² dependence for Δ(t) during the early stages of the reaction.

2.2 Comparative analysis of the two models for homogeneous nucleation

Equation (9) allows us to assess the validity of the approximations made in arriving at Equation (7) and the conclusions drawn from analysis of measurements that leads to estimates for n* from plots of ln[s(c_t)] against ln(c_t). Using Equation (10) and the definition of $k_{n\ast }^{\text{eff}}$, we generated artificial data over a full time course (defined as the time taken to reach equilibrium) and this allows us to test the robustness of the analysis outlined in Equation (7). It is worth emphasizing that the Oosawa-Kasai model is also built on the assumption of homogeneous nucleation. The motivation for our comparative analysis is as follows: If the estimates for n* are overly sensitive to the approximations that lead up to Equations (7) and (8), then experimental errors may be large and a re-analysis using a more complete model of aggregation is in order. Conversely, if we find that the estimate of n* is fairly robust to errors and approximations, then we can make inferences regarding the validity of the assumption of a homogeneous nucleation process. In all applications of the homogeneous nucleation model to study aggregation of polyglutamine containing systems, the estimates for n* end up being fractional values and they also show considerable variability with polyglutamine length and flanking sequences. At issue is whether such behavior can be better explained by the presence of a heterogeneous distribution of oligomers with different intrinsic abilities for turning over into fibrils. Contributions from such species are ignored in the assumption of a homogeneous process.

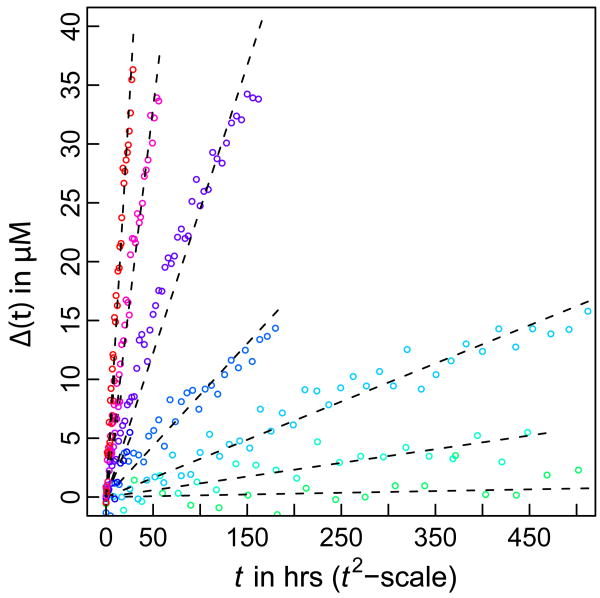
We generated data for the time course of Δ(t) using parameters reported in the literature [83]. Specifically, we set k₊ = 10⁴ M⁻¹s⁻¹, K^n* = 2.7 × 10⁻⁹, and n*=1. Panel A of Figure 1 shows plots of Δ(t) versus t for values of c_t ranging from 10 μM – 100 μM. As expected, the expression in Equation (7) applies only over a limited time scale. However, panel B of Figure 1 shows that the approximation for Δ(t) is reasonable during the early stages of the reaction. Given this agreement, we tested the quality of the proposed linear relationship between Δ(t) and t² by comparing the simulated data from the Oosawa-Kasai model that plots Δ(t) against t² to linear fits to these data (Figure 2). The quality of the agreement between the simulated data and linear fits suggests that the analysis proposed in Equation (8), i.e., calculating the slope of the double logarithmic plot of ln[s(c_t)] against ln(c_t) should provide a reliable estimate of the nucleus size. That this is the case is shown in Figure 3, which shows that the ETM reproduces the value of (n*+2)= 3, which was used to generate the simulation data for Δ(t) at different c_t values.

Figure 1. Simulated time course for aggregation.

Panel A shows the entire time course of aggregation according to Equation (7) (blue dashed curves) and Equation (9) (solid red curves). Panel B shows a magnification focusing on the early time course and demonstrates the validity of the t² dependence for Δ(t) during the early stages. In the interest of clarity, Δ(t) is plotted against t² in panel B and in both panels, each pair of curves (red and blue) corresponds to a specific value for c_t and these values are shown in panel A.

Figure 2. Assessment of the linear relationship between Δ(t) and t².

The red circles denote solutions to the Oosawa-Kasai model summarized in Equation (9) and the black dashed lines denote the results of linear regression, which show reasonable agreement with the full solution.

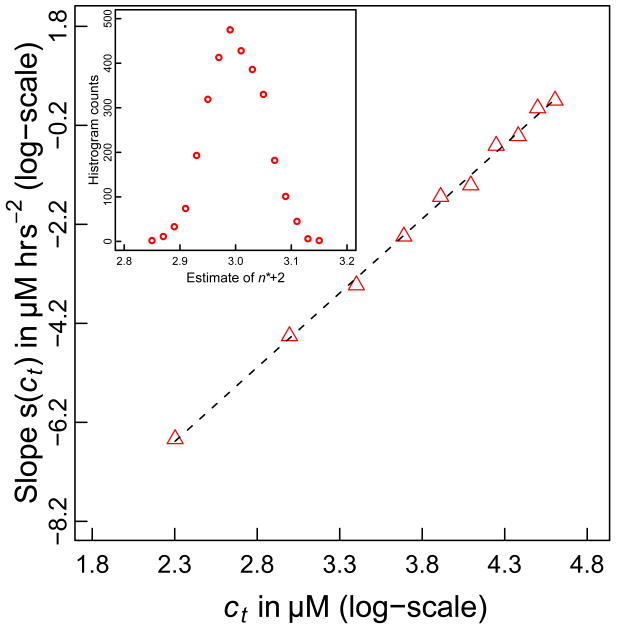
Figure 3. Estimating n* using the double logarithmic plot.

This figure plots ln[s(c_t)] against ln(c_t). The slope of the resultant straight line equals n*+2, from which we can estimate n*. For the current plot, we obtain a slope of 2.971, which is concordant with the value of n*=1 that was used to generate the data in Figures 1-2. The inset shows a histogram of estimates for n*+2 based on 3,000 independent trials and analysis such as shown in Figures 1 and 2. This distribution has a mean of 3.01 and a standard deviation of 0.048.

We further assessed the robustness of the analysis by quantifying the effects of noise on the estimate of n*. Of particular relevance is the delineation of the time interval that corresponds to the initial stages of the reaction, a time interval we designate as t_c. For different values of c_t we varied t_c from 10% to 60% of the total time course for Δ(t) and found that the analysis of the double logarithmic plot yields a normal distribution of values for the estimate of n*+2, with a mean value of 3.0 and standard deviation of 0.06. Additionally, if arbitrariness in defining the initial phase is removed, i.e., a similar criterion is applied for choosing the initial phase for all values of c_t, then the slope of the double logarithmic plot is exactly 3.0. These two results suggest that for a truly homogeneous process, errors involved in choosing a value for t_c lead to negligible variations in the estimate for n*+2.

2.3 Implications of comparative analysis for polyglutamine aggregation mechanisms

The preceding discussion highlights the robustness of the approach shown in Equation (8) for a strictly homogeneous process with a well-defined nucleus size. Our assessment of the robustness of the ETM analysis focused on quantifying the effects of noise / errors in defining the early stages of the reaction process. Chen et al. [83] applied the methods described above to analyze kinetic data for the rate of loss of soluble material. Measurements were performed at different values of c_t for peptides of the form K₂-Q_N-K₂ with N=28, 36, and 47, respectively. For these three constructs, their analysis of the double logarithmic plots yielded slopes of 2.98, 2.68, and 2.59, from which they estimated a value of n*=1 for all constructs as the nearest integer value to the fractional values they obtained. As noted above, for a strictly homogeneous process the estimates for n* should be robust and reasonably insensitive to errors in defining the interval t_c for the extent of reaction used to extract ln[s(c_t)].

The fractional values for n* are at odds with the expected robustness of the analysis for estimating n*, providing aggregation follows homogeneous nucleation. There are other errors that might arise from difficulties in accurately measuring the fraction of unaggregated material that remains in the supernatant. Such errors are unlikely to be systematic during the early stages of the reaction and can be overcome through multiple independent measurements. An additional source of error might pertain to the number of c_t values for which the time courses of Δ(t) are measured. Chen et al. used four different concentrations that span a reasonable range of concentrations.

Bernacki and Murphy [84] demonstrated that kinetic data using monomer loss as the only experimental readout for aggregation may be fit with a variety of different mechanistic models including the homogeneous nucleation. Distinguishing between models was shown to be difficult in the absence of more detailed data, in particular the complimentary readout of fibril numbers and sizes. Similarly, Morris et al. [99] demonstrated that a mechanism termed “the Finke-Watzky model of nucleation followed by autocatalytic surface growth” fits several independent sets of protein aggregation data reasonably well with only two free parameters. Neither approach accounted for the effects of heterogeneities in the (effective) nucleation and / or the elongation steps. Heterogeneous distributions of oligomers can act as defects for homogeneous nucleation specifically if different oligomers vary in their intrinsic potential for turning over into fibrils. In the following sections we will review the evidence from experimental work and atomistic simulations that jointly suggest a role for heterogeneous distributions of oligomers in polyglutamine aggregation.

3. A scheme for incorporating heterogeneous distributions of oligomers into polyglutamine aggregation mechanisms

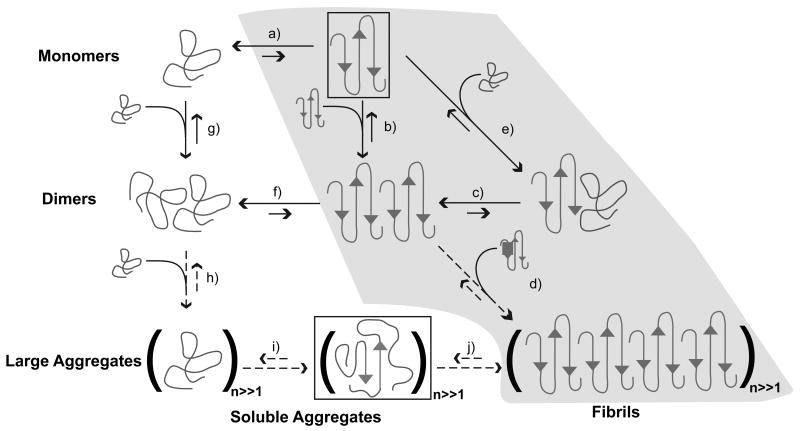
Figure 4 summarizes an alternative “two-stage” mechanism that integrates findings from atomistic simulations and biophysical experiments [65]. In this proposal, disordered globules associate reversibly to form a distribution of molten oligomers. If p(n) denotes the distribution of oligomer sizes, then the peak and width of this distribution will in all likelihood vary with polyglutamine length and the nature of the sequences that flank the polyglutamine expansion on the N- and C-termini. Inter-peptide interfaces are thermodynamically favored to peptide-solvent interfaces because chains within oligomers are solvated by other chains. Since intra- and intermolecular interactions are thermodynamically equivalent, individual chains within clusters can expand / contract freely and this facilitates the requisite conformational rearrangements needed to converge upon energetically favorable conformations with high β-content in large aggregates. As a result, oligomers of the same size can be distinguished by the conformational preferences of individual chains within the oligomer leading to additional heterogeneities in the reaction mixture.

Figure 4. Schematic of possible aggregation pathways for polyglutamine in vitro.

Here, n denotes the number of polyglutamine molecules within a disordered aggregate and n_F denotes the number of polyglutamine molecules within an ordered amyloid fibril. The ordered amyloid fibril rich in β-sheets is shown in the bottom right corner of the schematic. The gray shaded region encompasses steps (a), (e), (c), and (d) and depicts the homogeneous nucleation proposal of Chen et al. [83]. Studies of the thermodynamics of step (a), indicate that the formation of ordered conformations is thermodynamically unfavorable. Monomeric polyglutamine prefers disordered, collapsed conformations, left of step (a). Step (b) pertains to the thermodynamics of interactions between chains that adopt ordered conformations. However, the likelihood that chains will sample the associations shown in step (b) is very small because this is tied to the equilibria in step (a), which requires the population of the conformations with high β-content. Similarly, step (f) shows that disordered dimers are thermodynamically favored to dimers with high β-contents in individual chains. This is the result of linkage to step (a) as discussed above. The aggregates achieved in step (h) are likely to be large (in terms of n) and exhibit spherical, “liquid-like” [102-104] organization of polyglutamine chains around each other. Step (i) depicts a slow conformational conversion of individual / small numbers of chains to β-sheets. This slow step is likely to lead to the creation of an ordered template for fibril formation via monomer or oligomer addition and elongation to yield the ordered amyloid fibril.

3.1 Development of a model that explicitly accounts for a heterogeneous distribution of oligomers

We consider a model in which monomers in solution rapidly associate to give rise to a distribution of oligomers. This model is motivated by the schematic shown in Figure 4. For simplicity, we consider oligomer formation through monomer addition alone. At equilibrium:

$$\begin{array}{c}A+A\rightleftharpoons A_2;K_2=\frac{[A_2]}{{[A]}^2}\\ A_i+A\rightleftharpoons A_{i+1};K_{i+1}=\frac{[A_{i+1}]}{[A_i][A]}\end{array}$$ (11)

In Equation (11), A is the aggregating species, square brackets denote concentrations (more precisely activities), and the K_i are equilibrium constants that quantify the stability of species i. We can generate equations for the populations of individual species, f_i, by observing conservation of mass:

$$\begin{array}{c}{f}_i=\frac{[A_i]}{c_t}=\frac{[A]}{c_t}\cdot \prod _{j=2}^i{K}_j[A]\\ c_t=\sum _{i=1}^{\infty }i[A_i]\end{array}$$ (12)

Here, c_t is the total concentration of aggregating material and Equation (12) provides an implicit relationship between the concentration of free monomer and the total monomer concentration. We shall consider the case where the infinite sum in Equation (2) is approximated by a finite sum; this is reasonable since we focus on soluble oligomers. We define a maximum oligomer size i_max by setting K_i to be zero for i > i_max. Equation (12) then becomes:

$$\begin{array}{l}{f}_i=\{\begin{array}{c}\frac{[A]}{c_t}\cdot \prod _{j=2}^i{K}_j[A]\text{for}i<i_{max}\\ 0.0\text{for}i\ge i_{max}\end{array}\hfill \\ c_t=\sum _{i=1}^{i_{max}}i[A_i]\hfill \end{array}$$ (13)

Next, we assume a slow and irreversible conversion of large oligomers A_i with i ≥ i_min to fibrillar or more accurately to protofibrillar species:

$$\begin{array}{c}{A}_{i_{min}}\stackrel{k_{i_{min}}}{\to }{F}_{i_{min}}\\ A_{i_{min}+1}\stackrel{k_{i_{min}+1}}{\to }{F}_{i_{min}+1}\\ ⋮\\ A_{i_{max}}\stackrel{k_{i_{max}}}{\to }{F}_{i_{max}}\end{array}$$ (14)

In Equation (14), F_i denotes a fibrillar species composed of i monomers. We propose that fibrillar species form through a unimolecular process, which requires an internal re-arrangement as sketched in Figure 4. Due to the slowness of the process we can assume that the oligomer distribution re-equilibrates rapidly (pre-equilibrium assumption). We write a rate equation for fibril formation nucleated by unimolecular conformational conversion within any of the oligomers of size i ≥ i_min as:

$$\begin{array}{c}\frac{d\left[F_i\right]}{dt}=k_i\left[A_i\right]=k_i\left[A\right]\cdot \prod _{j=2}^i{K}_j\left[A\right]\\ \frac{d{c}_p}{dt}=\sum _{i=i_{min}}^{i_{max}}{k}_i\left[A_i\right]=\sum _{i=i_{min}}^{i_{max}}{k}_i\left[A\right]\cdot \prod _{j=2}^i{K}_j\left[A\right]\end{array}$$ (15)

In Equation (15), c_p is the total concentration of growing ends (independent of the size of the particular fibril nucleus) and each k_i denotes the rate of nucleation within an oligomer of size i. Consequently, we can treat elongation via monomer addition as:

$$\begin{array}{c}{F}_i+A\underset{\underset{k_{-}}{\leftharpoondown }}{\overset{k_{+}}{\rightharpoonup }}{F}_{i+1}\\ \frac{d{c}_f}{dt}=k_{+}{c}_p[A]-k_{-}{c}_p\\ \frac{d^2{c}_f}{d{t}^2}=k_{+}{c}_p\frac{d[A]}{dt}+(k_{+}[A]-k_{-})\cdot \sum _{i=i_{min}}^{i_{max}}{k}_i[A]\cdot \prod _{j=2}^i{K}_j[A]\end{array}$$ (16)

Here, k₊ is the elongation rate constant for monomer addition, k₋ is the rate constant for monomer loss from a growing fibril, and c_f is the total concentration of monomers incorporated into fibrils.

If we focus on the initial rate of aggregation and treat fibril elongation as being irreversible and homogeneous we may assume, at least for certain values of K_i, that the free monomer concentration [A] is static and determined by its pre-equilibrium value in the absence of any fibrillar aggregates. This concentration a₀ is obtained implicitly via Equation (13). Then, we can integrate Equation (16) similar to Equation (7):

$$c_f(t)=\frac{1}{2}{k}_{+}{t}^2{a}_0\cdot \sum _{i=i_{min}}^{i_{max}}{k}_i{a}_0\cdot \prod _{j=2}^i{K}_j{a}_0$$ (17)

Through the generalizations introduced leading up to Equation (16) we are in a position to assess the role of oligomers and rate limiting steps within oligomers on the concentration dependence of the initial rate of aggregation. In the proposed model i_max is the size of the largest soluble oligomer and i_min is the size of the smallest oligomer that can support conversion into a fibril / protofibrils.

From Equation (17) we see that the slope of a double logarithmic plot still convolves elongation and nucleation processes. Secondly, we recognize that the effective dependence on total concentration is not guaranteed to yield a well-defined integer as the slope of a double logarithmic plot since it depends on the relationship between a₀ and c_t, which is given by Equation (13). This relationship convolves contributions from the significant population of off-pathway, i.e., oligomers of size i < i_min that are incapable of converting to fibrils and the heterogeneity of the nucleation mechanism itself, which determines the rate of conversion of different oligomers to fibrils. The slope of a double logarithmic plot convolves elongation and nucleation processes, as is the case with the original analysis. Additionally, the slope is now directly proportional to the free monomer concentration and to the fraction of fibril competent species. Because the latter quantity depends on a_o and includes terms that range from 1 to $a_o^{i_{min}}$, we can expect slopes i.e., n*+2 values ranging from unity (yielding negative values for n*) to i_min+1. Importantly, Equation (17) recovers the ETM expression i.e., Equation (7) if both i_min and i_max are equal to two. The only difference is that the pre-equilibrium constant K_n* becomes a pre-equilibrium dimerization constant K₂ and that the bimolecular nucleus elongation rate constant k*₊ becomes a unimolecular nucleation rate constant k₂.

3.2 Analysis of the effects of heterogeneous oligomer distributions using the ETM approach

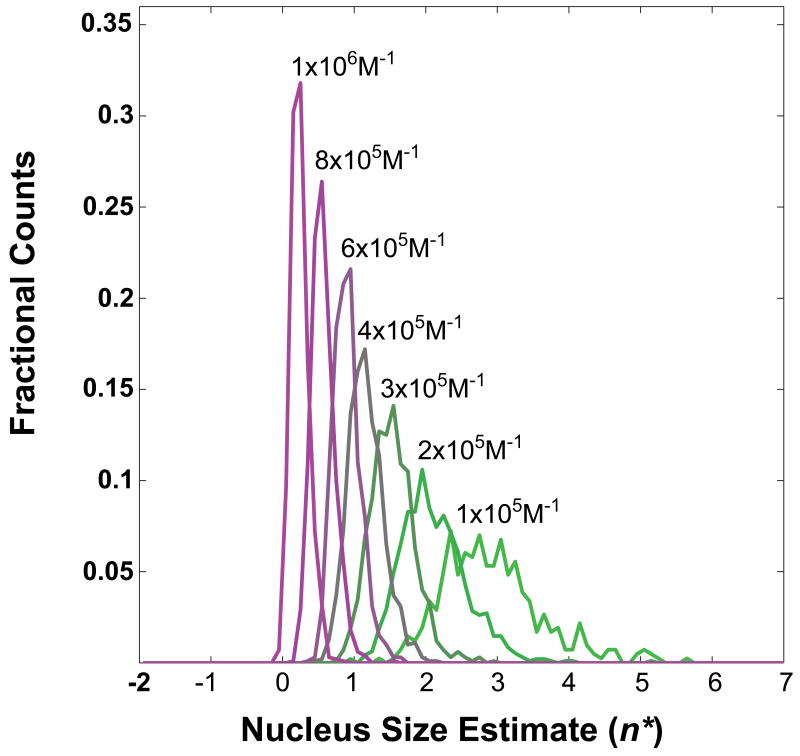
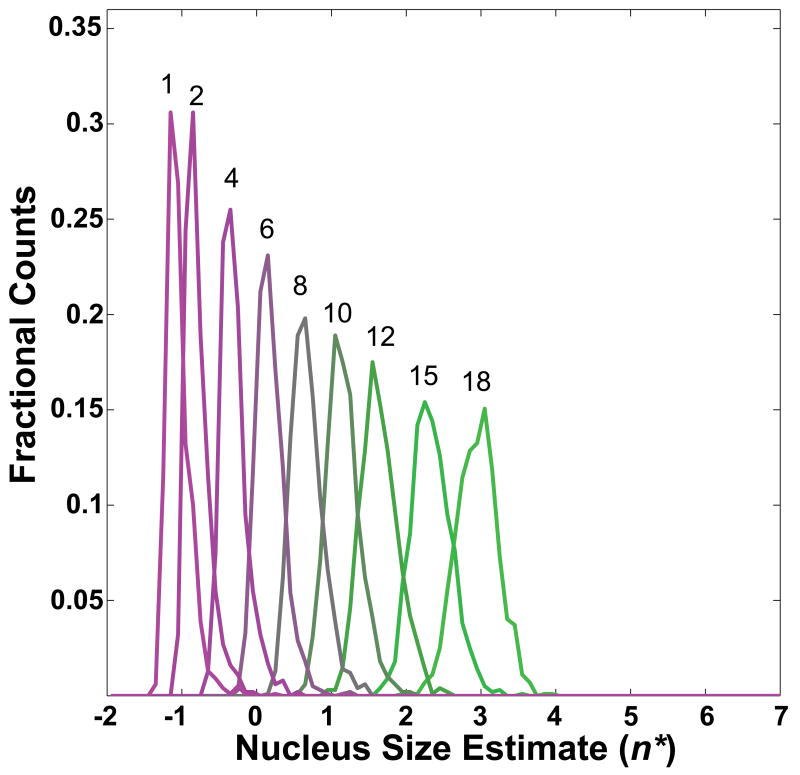
We demonstrate the influence of oligomers that have different potentials for turning over to fibrils by quantifying their effects on estimates of apparent nucleus sizes, n*. Simulated data were generated using values for k_i that were sampled from a normal distribution, the parameters of which were held constant throughout (mean and standard deviation are 10⁻²s⁻¹; values are adjusted to zero if drawn as negative). Additionally, we set i_max = 20 in all of our simulations. Figure 5 shows histograms of apparent nucleus size estimates for a minimum fibril-forming oligomer of size i_min = 10 and for different values of the mean of the distribution of K_i. The variance for the underlying distribution was fixed at 10⁵M⁻¹. Every histogram represents 10³ simulated datasets. Within each dataset, 450 free monomer concentrations up to the high μM-range were used to obtain species distributions and total concentrations via Equation (13). Linear regression of the logarithm of the constant terms in Equation (17) plotted against ln(c_t) yielded estimates for n*+2 according to Equation (8). To mimic experimental conditions, only values for c_t of 1-500 μM were considered for the linear regression. Figure 6 shows a plot that is analogous to the plot in Figure 5. Here, i_min is varied and the mean of the K_i is fixed to 4×10⁵M⁻¹.

Figure 5. Distribution of apparent nucleus sizes obtained from analysis of simulated data for a heterogeneously nucleated process – effect of oligomer stabilities.

While the model includes the presence of heterogeneous distributions of oligomers, the data were analyzed using the homogeneous nucleation model. The plot shows histograms of apparent nucleus sizes for a minimum fibril-forming oligomer with 10 monomers, i.e., i_min=10. Each histogram corresponds to different values for the mean of the distribution of K_i and each curve is labeled with the appropriate value used.

Figure 6. Distribution of apparent nucleus sizes obtained from analysis of simulated data for a heterogeneously nucleated process – effect of varying i_min.

In contrast to Figure 5, here we fix all K_i = 4×10⁵M⁻¹ and obtain the distribution of n* values for different values of i_min. Each curve is labeled with the value of i_min used in the calculations. As i_min decreases, so does the estimated value for n*.

Figures 5 and 6 show that applying the methods of Chen et al. to processes with built-in heterogeneities such as the presence of oligomers of varying sizes, stabilities, and potential for transforming to fibrils will yield estimates for the nucleus size that depend strongly on the parameters that give rise to heterogeneities. If most of the aggregating material exists in fibril-incompetent forms (small K_i and / or large i_min), the apparent nucleus size is large but smaller than i_min and fractional values for n* are readily observed. If, however, large fractions of the aggregating material are present in soluble oligomers that are large enough to promote fibril formation (large K_i and / or small i_min), then the smallest apparent nucleus size is close to zero (corresponding to a slope of 2.0) and can be less than zero. This finding is also consistent with the autocatalytic surface growth mechanism proposed by Morris et al., whose analysis of the initial rate dependence on total concentration would similarly yield a slope of 2.0 [99].

4. Conclusions

Our investigations have focused on understanding the implications of heterogeneous distributions of oligomers for aggregation kinetics that are analyzed using the ETM variant of homogeneous nucleation. Accounting for the presence of oligomers and multiple routes to fibrillar / protofibrillar forms provides a plausible explanation for fractional and / or negative values for n*. By comparing the approximate solution used by Chen et al. for Δ(t) to the full solution derived from the classical model of Oosawa and Kasai we were able to delineate the time interval 0 < t ≤ t_c over which the t² dependence of Δ(t) is reasonable. We then investigated the effects of uncertainty in defining t_ci.e., the extent of uncertainty in delineating the reaction for which the approximation of [A] ≈ c_t is valid. This analysis demonstrated that the estimate of n* is rather robust to the introduction of uncertainties in defining t_c. Consequently, for a truly homogeneous nucleation process, estimates of fractional values for n* might provide a reasonable basis to question the assumption of a homogeneous process [100].

It is worth emphasizing that the assumption of heterogeneous distributions of oligomers is not the only way to obtain fractional values of n* using the ETM analysis. In fact, for homogeneous nucleation the specific shape of the free energy profile G(n) can lead to fractional values of n*. This is because the concentration of super nuclei, i.e., species of size n > n* is proportional to exp[−z²(n − n*)²] [100] where z is the so-called Zeldovich factor that quantifies the curvature of the free energy profile G(n) at n = n*. The smaller the value of z, the broader the free energy maximum, and the greater the likelihood that the nucleus size will be a fractional value around n* because clusters with aggregate numbers in the vicinity of n* have similar free energy values. Conversely, for higher values of z, the free energy profile becomes sharper and the nucleus size will converge upon n* with high precision. It is also worth emphasizing that focusing on the curvature of the free energy profile cannot yield a negative estimate for the nucleus size. Consequently, the formalism presented in this work is different from this “blended homogeneous nucleation model” because we sought to develop a model that rationalizes the observations of oligomers in experiments [68, 69, 90].

We generalized the homogeneous process to be a two-stage process in conformity with the scheme introduced in Figure 4. In this scheme, a distribution of oligomers can form in a thermodynamically downhill fashion. Fibril formation requires a unimolecular conversion of individual chains within one or more of oligomers into a conformation that is competent for templated growth. Oligomers can be classified as being fibril competent or incompetent based on their ability to support the requisite unimolecular conversion of individual chains into conformations that can support templated growth. Incorporation of heterogeneities into the model followed by application of the ETM analysis to the resultant kinetics shows how the methodology leads to an estimate of fractional as well as negative values for n*. The relative stabilities of different oligomeric species (fibril competent / incompetent species) and the size of the smallest fibril competent oligomer (i_min) contribute to determining the estimated values for n*. The model outlined in this work provides a quantitative framework for the proposal of “nucleated conformational conversion within oligomers” put forth by Serio et al. [101].