The use of analytical sedimentation velocity to extract thermodynamic linkage

Abstract

For 25 years, the Gibbs Conference on Biothermodynamics has focused on the use of thermodynamics to extract information about the mechanism and regulation of biological processes. This includes the determination of equilibrium constants for macromolecular interactions by high precision physical measurements. These approaches further reveal thermodynamic linkages to ligand binding events. Analytical ultracentrifugation has been a fundamental technique in the determination of macromolecular reaction stoichiometry and energetics for 85 years. This approach is highly amenable to the extraction of thermodynamic couplings to small molecule binding in the overall reaction pathway. In the 1980’s this approach was extended to the use of sedimentation velocity techniques, primarily by the analysis of tubulin-drug interactions by Na and Timasheff. This transport method necessarily incorporates the complexity of both hydrodynamic and thermodynamic nonideality. The advent of modern computational methods in the last 20 years has subsequently made the analysis of sedimentation velocity data for interacting systems more robust and rigorous. Here we review three examples where sedimentation velocity has been useful at extracting thermodynamic information about reaction stoichiometry and energetics. Approaches to extract linkage to small molecule binding and the influence of hydrodynamic nonideality are emphasized. These methods are shown to also apply to the collection of fluorescence data with the new Aviv FDS.

Introduction

Analytical ultracentrifugation (AUC) has been a fundamental technique in the determination of macromolecular reaction stoichiometry and energetics [1–6]. Although sedimentation equilibrium was considered to be the most rigorous approach to extract macromolecular self-association constants, sedimentation velocity has evolved to become the method of choice for these studies. This transition was, in part, facilitated by the fundamental studies performed by Na and Timasheff [7–11] on vinblastine-induced self-association of tubulin. Sedimentation velocity was appropriate to this system because tubulin is highly unstable during a sedimentation equilibrium experiment time frame and the indefinite polymer distribution induced is very broad and difficult to analyze by equilibrium methods. These studies focused on the thermodynamic linkage between tubulin self-association and the binding of vinblastine. Subsequent sedimentation velocity studies on the vinca alkaloid system have focused on the energetic coupling to pH, Mg²⁺ and salt concentrations, and nucleotide binding [12] as well as the translational connection between binding affinity and drug potency [13].

A recent review on the use of weight average sedimentation coefficient (s_w) analysis for interacting systems [14] concluded that systems best investigated by sedimentation velocity include unstable systems, complex systems involving intermediates, cooperative monomer-Nmer systems, systems with slow kinetics, and systems involving conformational changes in the absence of self-association. The focus of this approach was on fitting s_w as a function of macromolecule or ligand concentration. However, the development of direct boundary fitting methods such as SEDANAL [15] places the analysis of sedimentation velocity data for interacting systems in a more rigorous position because 1) the raw data are directly fitted and 2) models can be compared by standard statistical tools. This is similar to the impact of the NONLIN program on the rigorous analysis of sedimentation equilibrium data [16]. A powerful feature of SEDANAL is the ModelEditor that allows the user to input custom fitting models that may be required for a complex biological system or experimental design. For example, sedimentation velocity analysis has been used to define the stoichiometries and stepwise binding constants for assembly of the RNA-activated protein kinase PKR on activating and inhibitory RNAs and to distinguish among alternative assembly models [17]. This work highlights the ability of physical methods like AUC to extract detailed reaction mechanisms from rigorous thermodynamic data. More importantly, it emphasizes that hetero-molecular binding can thermodynamically couple to macromolecular assembly as a means to regulate that assembly. This type of thermodynamic linkage has been a major topic of discussion and investigation at the Gibbs conference since its inception.

The use of sedimentation velocity approaches introduces the potential influence of hydrodynamic and thermodynamic nonideality [15, 18]. This was a significant factor in early Model E studies done at high concentrations on plasma proteins in the 1950’s [19]. Nonideality was exacerbated by the necessity of using high protein concentrations with the schlieren optical system. The presence of nonideality in hydrodynamic data has been minimized (not eliminated) by the development of the new Beckman XLA/XLI and the current practice of performing experiments on dilute protein concentrations. This is completely dependent upon the details of the system being studied because nonideality is dependent upon the charge (the primary charge effect) and the excluded volume of the macromolecular species. Thus, nucleic acids, highly charged proteins, intrinsically disordered proteins, coiled-coil complexes and highly extended complexes will all exhibit significant hydrodynamic nonideality. Furthermore, the development of the Aviv FDS has allowed investigators to perform sedimentation velocity experiments in plasma [20–22], the delivery buffer for many therapeutic antibodies and peptides. These conditions will also be dominated by nonideality effects.

In many allosteric systems, self-association is thermodynamically linked to ligand binding. Figure 1 illustrates a generic linked system in which dimerization of protein is linked to binding of one ligand [19]. The goal of a rigorous thermodynamic analysis of such a linkage scheme is to determine the energetics of protein dimerization, ligand binding, and the linkage free energy coupling these processes,ΔG_c. In the example shown in Figure 1, the coupling free energy is given by

Figure 1.

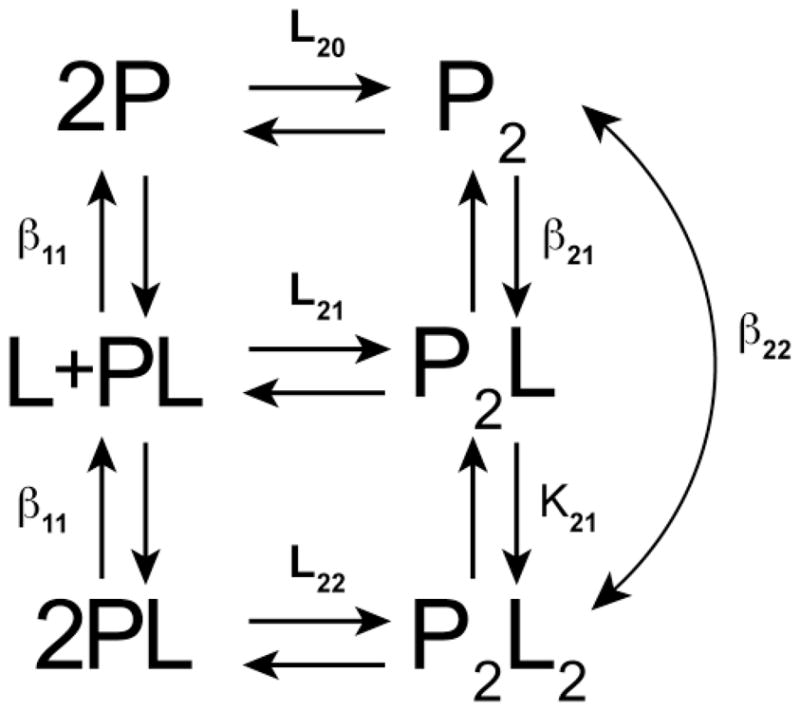
Model for thermodynamic linkage of protein dimerization and ligand binding. Adapted from Figure 6–5 in reference [19]. P is protein and L is ligand. The binding constants are defined as follows: L₂₀ is the dimerization constant for unliganded P, L₂₂ is the dimerization constant for the PL complex, L₂₁ is the dimerization constant for interaction of P and PL,β₁₁ is the constant for L binding to P,β₂₁ is the constant for L binding to P₂, K₂₁ is the constant for L binding to P₂L andβ₂₂ =β₂₁K₂₁ is the overall constant for interaction of two ligands with P₂ to produce P₂L₂.

$$\mathrm{\Delta }{G}_C=-\mathit{RT}ln\frac{{\beta }_{22}}{{\beta }_{11}^2}=-\mathit{RT}ln\frac{L_{22}}{L_{20}}$$ (1)

In principle, linkage can be defined from ligand binding isotherms obtained at various protein concentrations or by analysis of protein dimerization at various ligand concentrations. Sedimentation equilibrium measurements continue to be extensively used to define the linkage for ligand binding to self-association. In the case of biotin binding and dimerization of the BirA repressor, ligand-enhanced association is an activator of activity [23]. In the case of HIV reverse transcriptase, binding of nonnucleoside inhibitors can either enhance or weaken dimerization [24]. In the examples below, we illustrate the advantages of sedimentation velocity in the analysis of linkage energetics in two systems: enhancement of PKR dimerization by heparin and inhibition of the dimerization of the ATP-dependent motor protein SecA by signal peptide. For a third system we emphasize the consequences of nonideality on the measurement of the energetics of a weakly dimerizing pegylated protein system and demonstrate the necessity to take nonideality into account for biopharmaceutical preparations.

Experimental and Analysis Methods

Detailed protocols for performing and analyzing sedimentation velocity experiments have been published in various formats by the authors [1, 2, 6, 25, 26]. Here, we point out a few key experimental issues when performing and analyzing sedimentation velocity experiments. In all cases, samples should be carefully equilibrated with buffer. The cells should be filled to maximize the sedimentation distance, with 5.9 cm being the target meniscus position. Filling velocity cells to only 6.1 – 6.2 cm, a common practice today, discards useful information, thereby diminishing resolution. We recommend matching the reference and sample meniscii with a synthetic boundary centerpiece or meniscus matching centerpeice, especially if interference optics are being used. Care must be taken to properly align cells in the rotor [27], although the effects of misalignment have only been studied for characterizing aggregation and not reversible interacting systems, the focus of this review. For our purposes, the advantage of SV is that the aggregates usually spin out of the way and do not impact analysis, although this strongly depends upon the scans used for analysis and how big the aggregates are relative to the interacting species. The rotor must be equilbrated at the target temperature for at least one hour before starting the run. The optics must be properly aligned and cleaned to maximize signal/noise. Alignment primarily pertains to interference optics although proper focus depth is critical for FDS data collection. While there are no hard and fast rules, the run should be carried out long enough so that the smallest species sediments at least 2/3 of the distance between the meniscus and base. A proper rotor speed should be chosen to provide sufficient fractionation of species and reasonable diffusional broadening while permitting a sufficient number of scans to be collected during the run. Rather than using a fixed time interval between scans, we recommend collecting data as rapidly as the optical system permits. This is primarily an issue with the absorbance optics where scan rates are slow.

The primary methods of analysis described in this review involve 1) generation of g(s*) sedimentation coefficient distribution functions using the time derivative method [28, 29], 2) analysis of s_w isotherms [14, 30] and 3) direct boundary fitting approaches based upon a hypothesis derived from g(s*) and s_w analysis, [15]. These methods have been reviewed extensively by the authors [1, 2, 14, 15, 17, 25, 26] and we only highlight a few features here. The dcdt time-derivative method involves subtracting pairs of closely spaced velocity scans to remove time-independent systematic noise, transforming them from radial space to s* space, and then averaging those difference curves (dc/dt) to improve signal-to-noise. After a final transformation, the apparent sedimentation coefficient distribution function g(s*) is then plotted as a function of protein concentration. One of the main advantages of g(s*) analysis is demonstrated below where normalized plots are used to show the evolution of a reaction boundary to reveal a reaction mechanism. This visual approach is a powerful method for hypothesis building about the molecular characteristics of the systems. One of the useful features of g(s*) analysis is that it preserves the details of the boundary shape, showing not only the effects of transport due to sedimentation but also that due to both diffusion and reversible macromolecular interaction. By superimposing g(s*) curves that have been normalized to the plateau concentration obtained over a range of loading concentrations, one can see immediately whether the system is interacting or noninteracting or non-ideal. For interacting systems the shapes of the curves are characteristic of the stoichiometry [31].

Direct boundary fitting with SEDANAL usually assumes the system is in rapid reversible thermodynamic equilibrium during sedimentation; however, analysis can also be done while incorporating kinetic effects, typically by floating both K_a and k_off. Recent examples of incorporating kinetic effects include the methods papers by Correia and Stafford [2, 25] and two papers on kinetically limited dimerization reactions [32, 33]. The models constructed with the ModelEditor linked to SEDANAL include a series of parameters for each species, including MW, s, density increment or (1-ῡρ) information, extinction coefficient or coefficients if multiple signals are combined in the global fit, hydrodynamic nonideality (k_s) and thermodynamic nonideality (BM₁). In the latest version, one can fit for D or f/f₀ for each species. These parameters can be constrained or fit, and they can be linked to reasonable assumptions such as M₂ = 2×M₁, or extinction coefficients are constant on a weight basis for homo-oligomers and weight average values for hetero-oligomers.

In order to extract thermodynamic parameters from sedimentation velocity data, we prefer to directly fit data to the transcendental Lamm equations that describe the linked sedimentation and diffusion process (see Figures 3 and 8). This is the most statistically rigorous method of analysis. As implemented in SEDANAL, this approach directly probes and extracts information about the shape of the reaction boundary during sedimentation. Other software platforms that are also capable of direct boundary fitting of sedimentation velocity data include SEDPHAT [30] and ULTRASCAN [34]. However, SEDANAL is the only package that allows the user to input arbitrary fitting models that may be required for particular biological systems or experimental designs.

Figure 3.

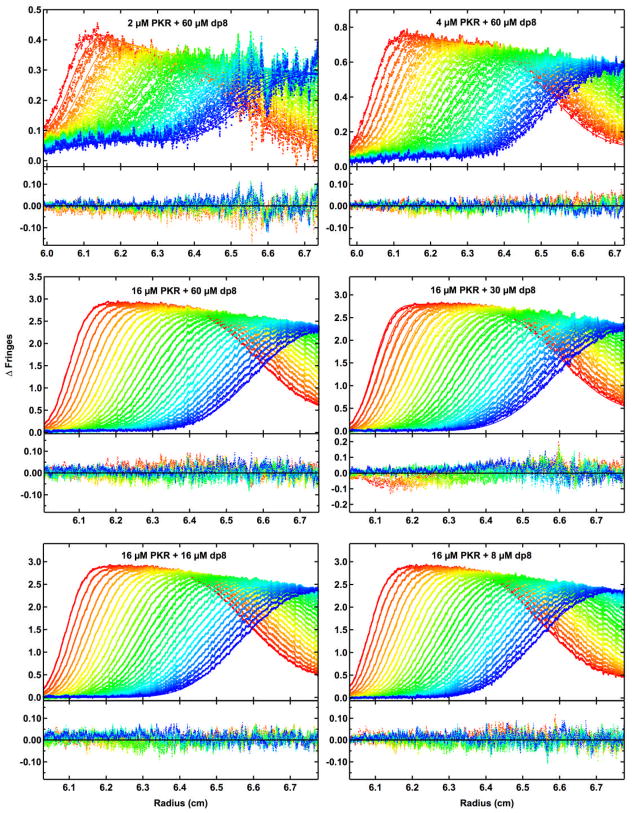
Global analysis of sedimentation velocity difference curves for dp8 binding to PKR. The data were subtracted in pairs for six data channels collected at the following concentrations: A, 2 μM PKR + 60 μM dp8; B, 4 μM PKR + 60 μM dp8; C, 16 μM PKR + 60 μM dp8; D,16 μM PKR + 30 μM dp8; E, 16 μM PKR + 16 μM dp8 and F, 16 μM PKR + 8 μM dp8. The data (58 difference scans for each channel) were globally fit to the binding model depicted in Figure 1 with an RMS deviation of 0.0191 fringes. The value of β₁₁ was fixed at 4.02×10⁶ M⁻¹ based on the anisotropy titration of bdp8 binding to PKR, L₂₀ was fixed at 2.00×10³ M⁻¹ from our previous analysis of PKR dimerization [42], L₂₁ was constrained as the geometric mean of L₂₀ and L₂₂, s_dp8 was fixed at 1.17 S from published data [84], s_PKR was fixed at 3.52 S [42], s_(PKR)2 was estimated as 5.0 S based on the sedimentation analysis of the phosphorylated PKR dimer [85], s_(PKR)2-dp8 was estimated as 5.5 S and the ratio of s_(PKR-dp8)2 to s_PKR-dp8 was constrained to be 1.5. The top panels show the data (points) and fit (solid lines) and the bottom panels show the residuals (points). Conditions: rotor speed, 50,000 RPM; temperature, 20°C; inteference optics; scan interval, one minute. This figure was adapted from reference [46].

Figure 8.

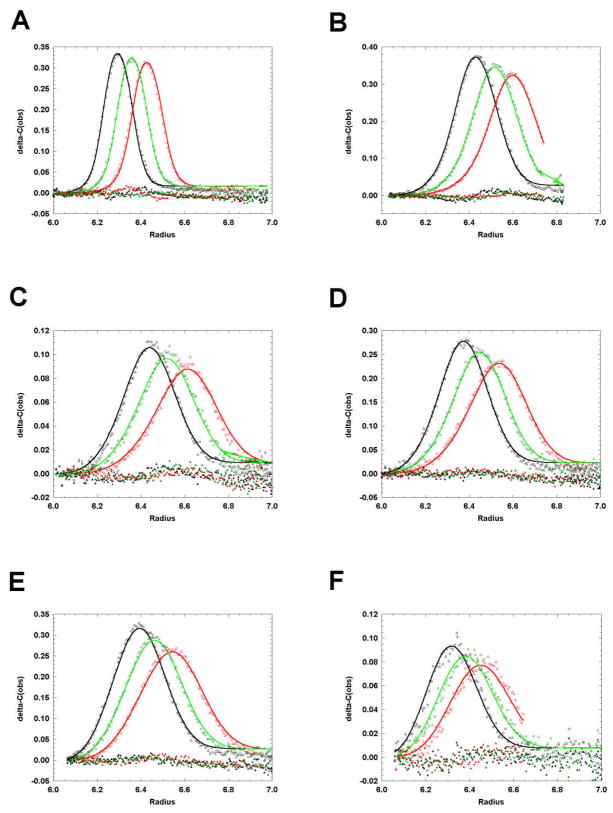
Global analysis of sedimentation velocity data to a nonideal monomer-dimer model using SEDANAL. The data are plotted asΔc vs r. The red points are the data, the green lines are the best fit and the blue points are the residuals. The best fit parameters are: K₂ = 3.25 ×10⁵ [3.04 ×10⁵ – 3.44 ×10⁵] M⁻¹; s₁ = 0.850 [0.841 – 0.860] S; s₂ = 1.56 [1.55 – 1.57] S; k_s = 0.389 [0.385 – 0.395] L/g; RMS = 0.0088 fringes. BM₁ was held at a calculated value of 0.113 L/g as explained in the text. The ranges are the 95% confidence limits using F-statistics according to equation 35 in reference [86]. (A) 1.5 g/L, 280 nm; (B) 0.5 g/L, 280 nm; (C) 0.17 g/L, 280 nm; (D) 0.17 g/L, 220 nm; (E) 0.056 g/L, 220 nm; (F) 0.019 g/L, 220 nm.

PKR

The RNA-activated protein kinase PKR plays a key role in the innate immunity response to viral infection [35, 36]. PKR is induced by interferon in a latent form that is activated by binding dsRNA to undergo autophosphorylation. PKR consists of an N-terminal dsRNA binding domain (dsRBD), containing two tandem copies of the dsRNA binding motif (dsRBM) [37] and a C-terminal kinase, with a ~90 amino acid linker lying between these domains. Although an autoinhibition mechanism was originally proposed for the activation of PKR by dsRNA, recent data have accumulated in support of a dimerization model [38, 39]. A minimum of 30 bp of dsRNA are required to bind two PKRs and to activate autophosphorylation, supporting a model where the role of the dsRNA is to bring two or more PKR monomers in close proximity to enhance dimerization via the kinase domain [40, 41]. PKR dimerizes weakly in solution with K_d ~ 500μM and dimerization is sufficient to activate PKR in the absence of RNA [42]. In addition to RNA, PKR can be activated by several polyanionic compounds including heparin, a highly sulfated glycosaminoglycan [43]. Activation does not require the presence of the dsRBD [44], indicating that heparin does not bind at the same site as dsRNA. Deletion mutagenesis studies have located the binding site at a region within the kinase domain [45]. The minimal-sized heparin capable of activating PKR is an octasaccharide [44].

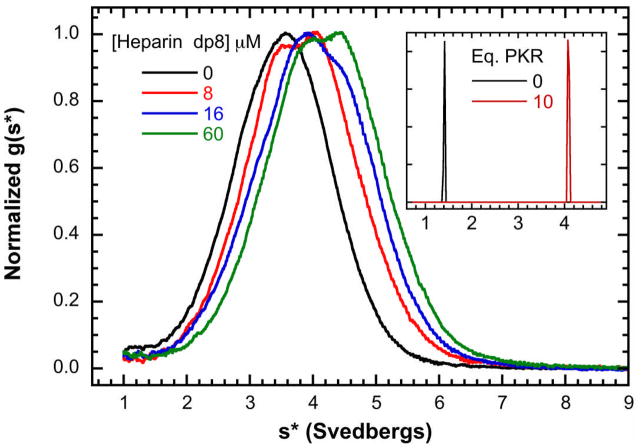
Because of the importance of dimerization in the activation of PKR by dsRNA [17, 39], we hypothesized that heparin may activate by enhancing PKR dimerization and have investigated the mechanism using analytical ultracentrifugation [46]. Qualitative, model-independent analysis of the effects of heparin binding by sedimentation velocity was very useful early in the study for proposing a testable mechanism. Figure 2 shows a titration of a fixed concentration of PKR (16 μM, ~1 mg/ml) with heparin octasaccharide (dp8). The data were transformed using the time derivative method to produce normalized g(s*) sedimentation coefficient distributions [28, 29]. In the absence of dp8, PKR exists predominantly as a monomer with a sedimentation coefficient near 3.5 S. Upon addition of the lowest concentration of dp8 (0.5 eq.) a second peak near 4 S forms. At higher dp8 concentrations the distributions continue to shift to the right.

Figure 2.

Sedimentation velocity analysis of dp8 binding to PKR. A) Normalized g(s*) distributions obtained at a fixed concentration of PKR (16 μM) with the indicated concentration of of dp8: 0 μM (black), 8 μM (red), 16 μM (blue) and 32 μM (green). The distributions are normalized by peak maximum. Conditions: rotor speed, 50,000 RPM; temperature, 20°C; inteference optics; scan interval, one minute. Note that the free dp8 is not resolved in these distributions because the the scan range was chosen to emphasize the higher-s features and diffusional broadening reduces resolution of the low-s region in the time derivative method. Inset: bdp8 binding to PKR analyzed by fluorescence-detected sedimentation velocity. c(s) distributions of 250 nM bdp8 (black) and 250 nM bdp8 + 10 eq. PKR (red). Conditions: rotor speed, 50,000 RPM; temperature, 20°C; fluorescence optics.

In principle an increase in sedimentation coefficient may be associated with the mass increase upon binding of dp8, a conformational change to a more compact shape or PKR oligomerization. We addressed this ambiguity by fluorescence-detected sedimentation velocity using conjugate of dp8 with Bodipy-Fl (bdp8). The inset to Figure 2 shows c(s) distributions [47] of 250 nM free bdp8 and in the presence of a 10-fold excess of PKR. The free oligosaccharide has a sedimentation coefficient of ~ 1.4 S. Addition of PKR shifts the sedimentation to ~ 4.1 S, as was observed using interference optics at higher concentrations. Analysis of weight-average sedimentation coefficients obtained from a titration of 15 nM bdp8 with PKR fit well to a simple 1:1 binding model with K_d = 387 nM, which is similar to the value obtained from a direct fluorescence anisotropy titration (K_d = 224 ± 27 nM, data not shown). The increase in the PKR sedimentation coefficient from ~3.5 to ~4 S upon binding dp8 is larger than expected based on the mass increase and indicates that heparin binding induces PKR to adopt a more compact shape. The g(s*) distributions shift to the right with increasing protein concentration from 2–16μM in samples containing a high saturating concentration of dp8, suggesting that heparin binding is thermodynamically linked to PKR dimerization.

The thermodynamic linkage was quantitatively resolved by global analysis of sedimentation velocity data obtained at multiple PKR and dp8 concentrations to the linkage model in Figure 1 using SEDANAL [15]. Using such a complex model it is best to constrain as many parameters as possible. We were able to fix β₁₁ based on the bdp8 binding measurements as well as several sedimentation coefficients (see legend to Figure 3). We also made the simplifying assumptions that L₂₁ is equal to the geometric mean of L₂₀ and L₂₂ and similarly

$${\beta }_{21}={\left[{\beta }_{11}\sqrt{{\beta }_{22}}\right]}^{1/2}$$ (2)

Figure 3 shows a global SEDANAL fit of six data channels to the linkage model. A good fit is obtained with RMS= 0.0191 fringes a best fit value of L₂₂= 7.37 (6.59, 8.27) × 10³ M⁻¹. These data indicate that dp8 indeed enhances PKR dimerization by about 4-fold, corresponding to a coupling energy of ΔG_c = − 0.80 kcal/mol. A significantly worse fit is obtained if we deliberate fix L₂₂ to equal the dimerization constant of free PKR (RMS = 0.0222), confirming that the linkage is required to describe the data. Although heparin binding induces only a modest enhancement in PKR dimerization, it is sufficient to activate the kinase by initiating an autocatalytic phosphorylation cascade [42].

SecA

In prokaryotes and eukaryotes, the general secretion (Sec) pathway is the major route for transport of proteins across and into the cytoplasmic member [48, 49]. These proteins contain an amino-terminal, signal peptide that earmarks them for transport. In Escherichia coli, the translocase comprises the protein-conducting channel SecYEG and the ATP-dependent motor protein SecA [50, 51]. SecA docks with SecYEG and guides preprotein translocation via this channel [51–57]. The oligomeric state of SecA during translocation is controversial and there is evidence for both monomeric and dimeric forms [55, 58–63]. Furthermore, it has been reported that SecA self-association is modulated by interactions with signal peptide [61, 63] and acidic phospholipids [58, 63].

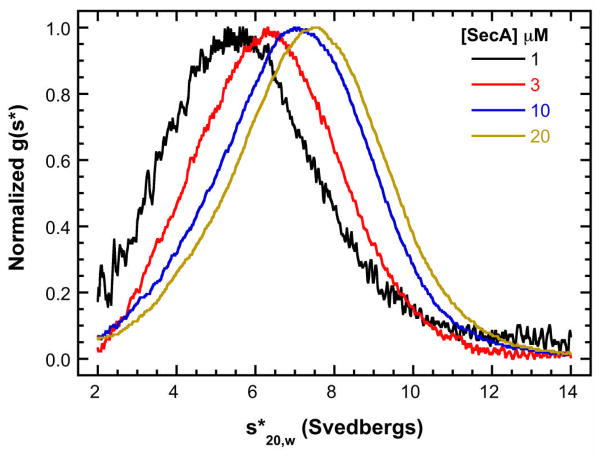
As a first step in the quantitative analysis of SecA self-association during protein translocation, we have used analytical ultracentrifugation to define SecA dimerization in solution and the linkage with salt, temperature and signal peptide binding [64]. Figure 4 shows the normalized g(s*) distributions obtained at multiple concentrations of SecA (1–20 μM) in 400 mM KCl (20 mM HEPES, pH 7.5, 400 mM KCl, 0.5 mM EDTA, and 0.1 mM TCEP). The peak of the normalized g(s*) distribution shifts to the right with increasing SecA concentration, indicating that SecA reversibly associates. The increase in the weight-average sedimentation coefficient from ~5.5 to ~7.5 S is consistent with a monomer-dimer equilibrium. Global analysis with SEDANAL of the complete dataset using this model yields a dimer dissociation constant of K_d = 18.6μM [64]. It was previously noted that SecA dimerization is strongly dependent on salt concentration [65]. Using the high sensitivity afforded by fluorescence detection of a SecA labeled with Alexa Fluor 488, we were able to measure high-affinity SecA dimerization and demonstrated that K_d varies dramatically with salt, ranging from 14 nM in 100 mM KCl up to 40.4μM in 500 mM KCl. A Wyman linkage plot of lnK vs. ln [KCl] has a slope of −5.26, indicating that ~ 5 ions are released upon dimerization.

Figure 4.

Sedimentation velocity analysis of SecA self-association. Normalized g(s*) distributions of 1 μM (black), 3 μM (red), 10 μM (blue), and 20 μM (brown) SecA in a buffer containing 400 mM KCl. The distributions are normalized by peak maximum. This figure was adapted from reference [64].

There are significant discrepancies in the literature regarding the effect of signal peptide binding on SecA dimerization. These may be related to the different methods and experimental conditions used to assay the oligomeric state of SecA. We took advantage of fluorescence detection to directly monitor the effects of signal peptide dimerization of labeled labeled SecA without interference from free peptide. Measurements were performed at 200 mM KCl with signal peptide concentrations ranging from 1 to 100 μM. Figure 5 shows that apparent K_d for SecA dimerization increases about 9-fold over this range of peptide concentration, indicating that ligand binding is thermodynamically linked to SecA dimerization. We analyzed these data making the same simplifying assumptions as we did for the PKR-dp8 system. However, in this case the ligand does not induce a conformational change in the protein and it also does not contribute to the sedimentation data. Thus, there is little advantage to be gained in direct global analysis of the sedimentation velocity data. Also, we were not able to directly measure β₁₁ because labeling of the signal peptide affected binding. Based on the linkage model in Figure 1, the dependence of K_d,app on [peptide] is given by

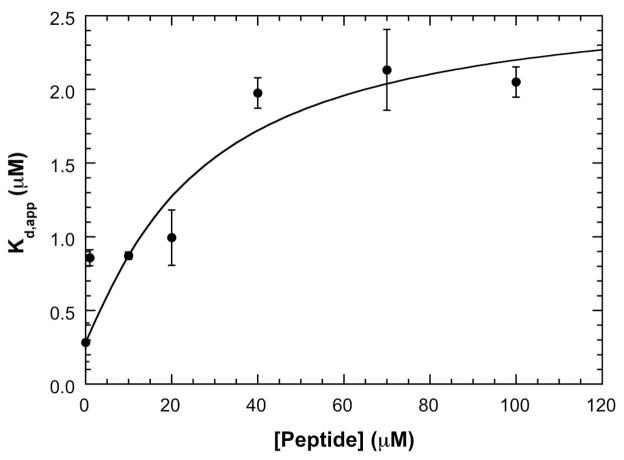
Figure 5.

Dissociation of the SecA dimer by signal peptide. A) Plot of apparent dimer dissociation constants (K_d,app) vs. signal peptide concentration. SecA dimer dissociation constants were obtained at 200 mM KCl by sedimentation velocity measurements using fluorescence optics. The solid line is a fit of the data to equation 3 performed as described in the text. The best-fit parameters are: β₁₁ = 0.158 (μM) ⁻¹ and β₂₂ = 0.00264 (μM) ⁻². This figure was adapted from reference [64].

$$K_{d,\mathit{app}}=K_d\frac{{(1+{\beta }_{11}[L])}^2}{1+{\beta }_{22}^{1/4}{\beta }_{11}^{1/2}[L]+{\beta }_{22}{[L]}^2}$$ (3)

This model fits that data well, with best-fit values ofβ₁₁ = 0.158μM⁻¹ (K_d = 1/β₁₁ = 6.32 μM) and ${\beta }_{22}=0.00264\mu {\text{M}}^{-2}({\text{K}}_{\text{d},\text{app}}=\sqrt{1/{\beta }_{22}}=19.5\mu \text{M})$. The coupling free energy given by equation (1) corresponds toΔG_c =1.31 kcal/mol.

Analysis of thermodynamically non-ideal interacting systems

Weakly associating protein-protein interacting systems are perhaps among the most difficult to analyze experimentally. The equilibrium constants and virial coefficients are highly correlated over a wide range of concentration making their independent determination extremely difficult if not impossible. One of the most difficult systems to analyze is the weakly associating monomer-dimer, non-ideal system [16, 66]. At the relatively high concentrations required to observe significant self-association, deviations from thermodynamic ideality also become significant and must be taken into account if the energetics of the interactions are to be accurately quantified. The problem is to determine both the value of the association constant K₂ and the value of the activity coefficients y_i and their concentration dependence. The standard Gibbs free energy for this interaction is given byΔG^o = −RTln(K₂) but we can measure only K_2,app and will have to also measure the non-ideality terms in order to determine K₂. The expected isotherm for a monomer-dimer system has a characteristic functional dependence on the activity of the monomer which must be deconvoluted from the data in order to reveal the underlying non-ideality. For velocity data this dependence is revealed as a slowing and sharpening of the boundary. For example, Figure 6 presents the normalized g(s*) distributions for a pegylated protein that exhibits nonideal monomer-dimer behavior. Pegylated hIFN-α2a (Pegasys), manufactured by Hoffmann La Roche, Inc., is a covalent conjugate of hIFN-α2a with a single 40 kD branched bis-monomethoxy-polyethylene glycol (PEG) chain [67]. With increasing concentration (9×) from 0.019 to 0.17 mg/ml, the distribution shifts to the right indicating an increase in dimer concentration. However, at 26× and 90× higher concentrations the distributions shift centripetally and sharpen, reflecting the influence of both hydrodynamic nonideality (k_s) and thermodynamic nonideality (BM₁). This can be described by the following two equations [15, 68]

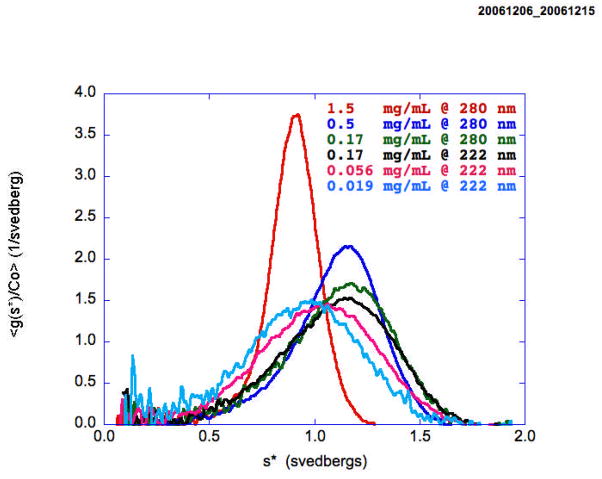
Figure 6.

Sedimentation profiles of a pegylated protein as a function of loading concentration showing the initial shift to the right at low concentrations as dimer is being formed followed by a shift to the left as the non-ideality starts to dominate the process. The three highest concentrations were measured at 280 nm and the three lowest at 220 nm with both 3 mm and 12 mm centerpieces.

$$s(c)=\frac{s_0}{(1+k_{s}c)}$$ (4)

and

$$D(c)=D_0\frac{(1+2{BM}_{1}c)}{(1+k_{s}c)}$$ (5)

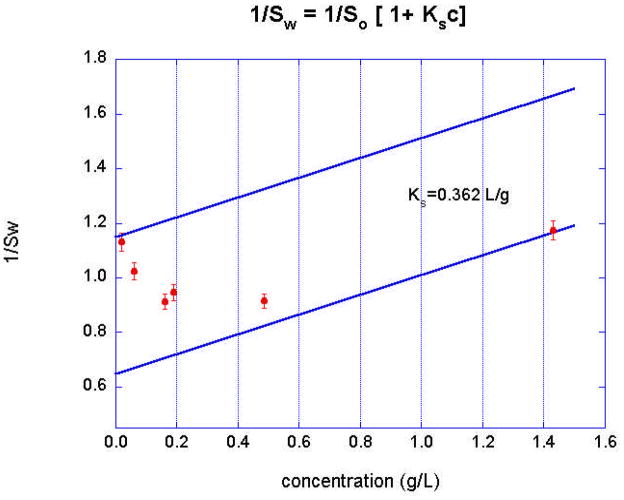
The thermodynamic nonideality term BM₁ reflects the contribution of both charge (the Donnan effect) and excluded volume [66, 68, 69]. While the effects of hydrodynamic nonideality have been extensively considered in the literature, the theory for k_s is less rigorously defined, although it too depends upon the charge and the excluded volume [18, 70]. It is common practice to empirically determine k_s from a plot of 1/s_w vs. weight concentration, where s_w is the weight-average sedimentation coefficient. This accounts for the shift in s_w,app to lower values in the distributions observed in Figure 6 as the concentration is increased. An example of this 1/s_w vs. concentration plot for a nonideal monomer-dimer system is in Figure 7. Note that a broad (90×) concentration range is required to observe the full transition from monomer to dimer. These six data sets can be globally fit with SEDANAL to extract both the energetics and the hydrodynamic nonideality terms defined in equations 4 and 5 (Figure 8). The straight lines in Figure 7 represent the concentration dependence of the sedimentation coefficient of the monomer and the dimer, respectively, using the value of k_s obtained from the global fit (Figure 8) to all the data. It is worth pointing out here that pegylation of biopharmaceutical proteins will primarily cause an excluded volume effect on nonideality. The large value of k_s reported here (0.389 L/g) is likely due to entrainment of solvent components by the hydrated PEG chains in addition to simple swelling [71]. A calculated value for BM₁=0.113 L/g (c.f. equations 12-9 and 12-10 in reference [72]) was used for fitting.

Figure 7.

Plot of inverse weight average sedimentation coefficient, 1/s_w, according to equation 4 vs loading concentration, showing the effects of both association and non-ideality. The straight lines represent the expected concentration dependence of the sedimentation coefficient of the monomer and the dimer, respectively, using the value of k_s obtained from the global fit (Figure 8) to all the data.

Discussion

We have presented a number of examples were sedimentation velocity has been useful for extracting linkage thermodynamics for a self-associating or a nonideal system. The analysis methods described are widely applicable in diverse biological systems, as demonstrated by numerous examples from the authors’ laboratories. These examples include motor domains [73], hexameric RNA binding proteins [74], hetero-associations [75], Ca⁺²-mediated nonideal dimerization [76], phosphorylation-dependent transcription factor associations [77], ligand-mediated oligomerization [78], indefinite associations [13], Anti-TRAP self-association and binding to TRAP [79], PKR self-association [42] and its interactions with RNA [40, 41, 80] and heparin [46]. The summary presented in this manuscript is hopefully a convenient and accessible resource for users of sedimentation velocity approaches.

Future progress in this area is being driven by two factors. First, the Aviv Fluorescence Detection System (FDS) is now installed in over 22 laboratories world wide, including in the labs of two of the authors, and there have been greater than 33 publications using this optical system. A major advantage of this optical system is the ability to selectively study a labeled macromolecule in a complex solvent or medium such as plasma. This brings up the second factor that sedimentation velocity AUC is one of the few biophysical methods that can be used for highly nonideal systems and greatly expands our ability to work under more biologically relevant interaction conditions. In addition to plasma, measurements can be performed in cell lysates or in the presence of synthetic crowding agents or osmolytes (see manuscript by Auton, et al in this issue). These factors will be a great asset for biophysicists interested in understanding in vivo or cellular interactions. In the context of biopharmaceuticals, there is evidence that a therapeutic antibody and its antigen may form different complexes in serum than in dilute solution [20]. Thus, there is great interest in studying antibody-antigen interactions and therapeutic peptides in plasma.

The problems introduced by non-ideality for both interacting and non-interacting systems were solved almost a decade ago by including the appropriate non-ideality coefficients, both hydrodynamic and thermodynamic, in the global fitting program SEDANAL [15]. For weakly associating systems, it is necessary to work at high concentrations, where nonideality must be taken into account, in order to populate the oligomeric species. Uncharged, globular proteins have the smallest contributions to non-ideality, on the order of 0.006 L/g, so that for concentrations above 1–2 g/L, the excluded volume contribution to non-ideality will start to become significant. If the macromolecules are either highly charged at low ionic strength or are very asymmetric, the effects will become significant at much lower concentrations. An example of such a system is the self-association of Troponin C [76] which showed measurable non-ideality in 0.5M NaCl in sedimentation equilibrium experiments. Currently, SEDANAL is the only direct boundary fitting software program that is capable of separately accounting for both hydrodynamic non-ideality in the frictional coefficient and thermodynamic non-ideality from excluded volume and charge effects in sedimentation velocity experiments. Concentration dependence of the frictional coefficient and concentration dependence due to excluded volume or charge effects are treated rigorously by separating the hydrodynamic and thermodynamic non-ideality terms. Others [16, 68, 81] have combined the effects in a single coefficient in a Taylor series approximation to first order in concentration.

The major challenges to progress in these areas involve theoretical understanding of the nonideality that dominates solution interactions in plasma and cells. This has been investigated and is referred to as molecular crowding [69]. Sedimentation equilibrium measurements have been used extensively to analyze excluded volume effects. In principle, this approach should apply to pegylated proteins such as the sample in Figures 6–8, depending upon the degree of modification and how they are modified, at a single site or at many multiple sites. Our focus is on hydrodynamic techniques and the use and interpretation of k_s values. In practical terms equations (4) and (5) are implemented in SEDANAL as are equations with higher order terms involving 2nd order hydrodynamic effects (k’sc²) and third virial coefficients (CM₁c²). We are currently investigating whether or not higher order terms are required to fit and interpret phenomena like the Johnston-Ogston effect [82] for samples sedimented in plasma (D. Lyons and J.J. Correia, manuscript submitted). Both charge and excluded volume impact hydrodynamic nonideality k_s. The origin of the primary charge effect which slows sedimentation is well understood to be due to the counter ions associated with the macromolecule. Considerations based upon sedimentation velocity results in plasma suggest the charge effect on k_s is due to a relaxation effect of the expanded Debye ion cloud associated with the macromolecular charge [66, 68]. This increase in apparent radius of the macromolecule is associated with a corresponding increase in the effective Stokes resulting in an increased backflow of solvent which is proportional to the macromolecular concentration. At high protein concentrations these interactions can include weak nonspecific protein association with that cloud causing increases in sedimentation rates. Excluded volume effects on k_s are usually treated as volume fraction [70], where the fraction of volume occupied by hard spherical particles is given by φ = v_effc [2], and where v_eff is the specific volume of the effective hard spherical particle in units of inverse w/v concentration. Studies on the degree and kind of pegylation on a model system might be a useful experimental approach. Some work in this area has already been done showing that doubly pegyated hen egg white lysozyme exhibits concentration dependence of similar magnitude to what we observe here with a k_s of 0.46 L/g (Table 17 in reference [83]). Thus, the future does look bright, albeit challenging, for the continuing application of sedimentation velocity approaches to complex biological interactions.

Summary

The focus of this manuscript, told in three stories, is how to use sedimentation velocity to extract thermodynamic linkage information for interacting systems. We propose three simple steps: 1) do a series of runs as a function of macromolecular and/or ligand concentration, 2) plot g(s*) and s_w data and hypothesize a model, and 3) fit the data to that model by global direct boundary fitting. The examples presented outline the ease and utility as well as the power of this widely used approach.

Research Highlights.

• Analysis of SV data allows the determination of reaction mechanism and energetics.

• Thermodynamic linkage to small molecule binding can be readily extracted by SV experiments.

• Reaction mechanisms can be determined by comparison of a family of normalized g(s) distributions.

• Analysis of thermodynamic coupling is best performed by direct boundary fitting with SEDANAL.

• The study of nonideal solutions by SV is a growing area of research in biopharmaceuticals.