Performance of the MRI-Based Virtual Bone Biopsy in the Distal Radius: Serial Reproducibility and Reliability of Structural and Mechanical Parameters in Women Representative of Osteoporosis Study Populations

Abstract

Serial reproducibility and reliability critically determine sensitivity to detect changes in response to intervention and provide a basis for sample size estimates. Here, we evaluated the performance of the MRI-based Virtual Bone Biopsy in terms of 26 structural and mechanical parameters in the distal radius of 20 women in the age range of 50 to 75 years (mean = 62.0 years, S.D. = 8.1 years), representative of typical study populations in drug intervention trials and fracture studies. Subjects were examined three times at average intervals of 20.2 days (S.D. = 14.5 days) by MRI at 1.5 T field strength at a voxel size of 137×137×410 μm³. Methods involved prospective and retrospective 3D image registration and auto-focus motion correction. Analyses were performed from a central 5×5×5 mm³ cuboid subvolume and trabecular volume consisting of a 13 mm axial slab encompassing the entire medullary cavity. Whole-volume axial stiffness and sub-regional Young’s and shear moduli were computed by finite-element analysis. Whole-volume-derived aggregate mean coefficient of variation of all structural parameters was 4.4% (range 1.8% to 7.7%) and 4.0% for axial stiffness; corresponding data in the subvolume were 6.5% (range 1.6% to 13.0%) for structural, and 5.5% (range 4.6% to 6.5%) for mechanical parameters. Aggregate ICC was 0.976 (range 0.947 to 0.986) and 0.992 for whole-volume-derived structural parameters and axial stiffness, and 0.946 (range 0.752 to 0.991) and 0.974 (range 0.965 to 0.978) for subvolume-derived structural and mechanical parameters, respectively. The strongest predictors of whole-volume axial stiffness were BV/TV, junction density, skeleton density and Tb.N (R² 0.79 – 0.87). The same parameters were also highly predictive of sub-regional axial modulus (R² 0.88 – 0.91). The data suggest that the method is suited for longitudinal assessment of the response to therapy. The underlying technology is portable and should be compatible with all general-purpose MRI scanners, which is appealing considering the very large installed base of this modality.

1. Introduction

Osteoporosis is characterized by low bone mineral density (BMD) [1and impaired bone architecture [2] leading to decreased bone strength and increased fracture risk. While BMD measured with dual-energy X-ray absorptiometry (DXA) has been shown to only moderately predict bone strength [3], trabecular bone (TB) there is significant evidence that microarchitecture provides independent information on mechanical competence and fracture risk in vivo [4-7].

In vivo three-dimensional (3D) micro-magnetic resonance (μMR) imaging now allows resolution of TB structure at the distal extremities [8, 9]. Quantitative structural parameters derived from 3D μMR images can describe TB microarchitecture in terms of scale [10, 11], topology [12-14] and orientation [15, 16]. Furthermore, finite element (FE)-based mechanical analysis of μMR images has shown promise for assessing mechanical properties determining bone strength [17-19]. Target applications include fracture risk assessment (e.g. [4, 20-22]) and evaluation of drug efficacy (e.g. [23, 24]).

An important performance criterion for any quantitative imaging technique of TB is its reproducibility. The few prior articles addressing the problem have been confined to small numbers of test subjects who are not representative of typical study populations [25-29].

The present study examines the variability and reproducibility of commonly evaluated structural and mechanical parameters derived from μMR images in a class of subjects where osteoporotic fractures typically occur. Toward this goal the distal radius of twenty female subjects were imaged at three time points and the relationships between structural and mechanical parameters were investigated with an improved version of the virtual bone biopsy (VBB) analysis protocol previously developed in the authors’ laboratory [23, 28, 30]. This work provides data on the variability and reproducibility of μMR image-based structural and mechanical parameters obtained from a group of older women, representative of typical study populations in osteoporosis intervention studies.

2. Materials and Methods

2.1 Subjects

Twenty women in the age range of 50 to 75 years (mean = 62.0 years, S.D. = 8.1 years) were recruited for this study (17 postmenopausal, three premenopausal). Sixteen subjects were Caucasian and 4 were African American. Body mass index (BMI) ranged from 18.4 to 29.4 kg/m² (mean = 24.90 kg/m², S.D. = 3.00 kg/m²). Exclusion criteria included a history of fracture or treatment for osteoporosis, a BMI greater than 30 kg/m², and the presence of primary bone cancer or metastases to the bone. The University of Pennsylvania Institutional Review Board approved this study, and all subjects signed a written informed consent prior to participation.

Each subject was scanned three times over the course of 8 weeks. The mean interval between was 20.2 days (S.D. = 14.5 days). According to findings of Ahlborg et al. [31], changes in BMD in the distal radius within this time interval should be negligible.

2.2 Image Acquisition and Processing

2.2.1 Overview of Virtual Bone Biopsy Process

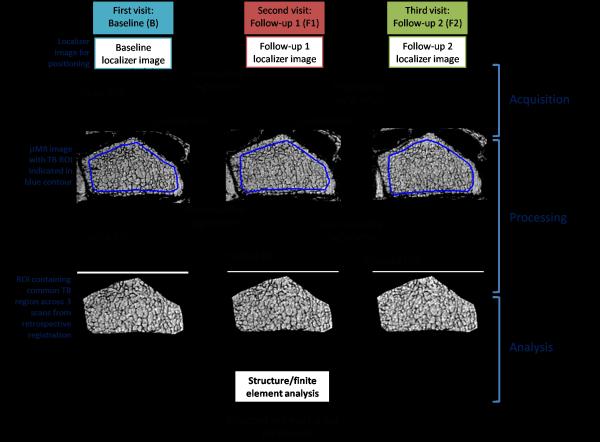
TB structural and mechanical parameters were extracted from μMR images following a protocol, previously referred to as the virtual bone biopsy (VBB) [23, 28, 30] modified as described below. The VBB processing protocol was implemented in C++ and Matlab (The Mathworks Inc., Natick, MA) and automated to minimize human intervention. Fig. 1 outlines the processing steps required for analysis of the data from the three time points.

Fig. 1.

VBB protocol of three imaging visits. Key steps include image acquisition, processing and analysis.

2.2.2 Image Acquisition

Images of the right distal radius were acquired on a Siemens 1.5T MAGNETOM Sonata MR scanner (Siemens Medical Solution, Erlangen, Germany), using a transmit-receive elliptical birdcage wrist radiofrequency coil (InsightMRI, Worcester, MA). The coil was positioned at the center of an immobilization vacuum bag (VacFixTM, Soule Medical Systems Inc., Tampa, FL, USA) and attached to the base of the positioning device (Fig. 2).

Fig. 2.

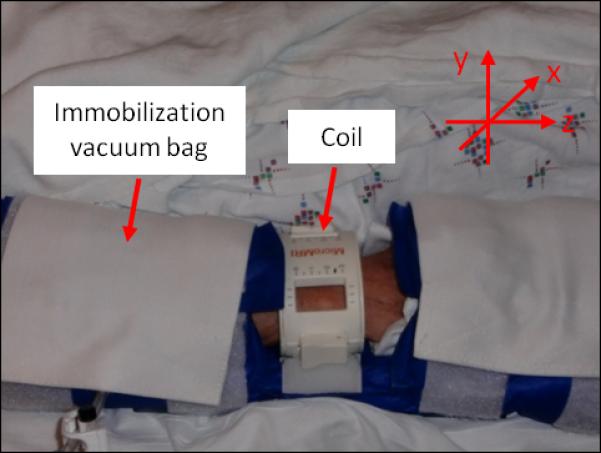
Imaging setup and positioning.

Subjects were positioned feet-first, supine, with the right forearm parallel to the magnet bore axis (z-axis) adjacent to the subject’s body. The birdcage coil was centered at the subject’s ulnar styloid process. The vacuum bag was then secured around the arm using Velcro straps prior to evacuation. Straps were placed over the upper and lower portions of the arm to the scanner bed and a small sand bag was situated over the device to help minimize involuntary motion.

The imaging region-of-interest (ROI) was a 70×42×13 mm³ slab centered 7 mm proximal to the most proximal tip of the epiphyseal line (remnant of the growth plate) of the right radius. The initial ROI positioning of the wrist was first prescribed with a number of orthogonal 2D localizer sequences. Upon follow-up visits, the 13 mm slab was selected by means of prospective registration [32]. This registration procedure was performed on a stand-alone laptop computer and the alignment parameters were manually entered into the MR scanner software so that the imaging ROI of the follow-up μMR images were coincident with that of the baseline while the subject was in the scanner. Micro-MR images were subsequently acquired with an improved 3D fast large-angle spin echo (FLASE) sequence [33] at 137×137×410 μm³voxel size in a total scan time of 10 min 26 sec.

2.2.3 Image processing

Computation of Structural Parameters

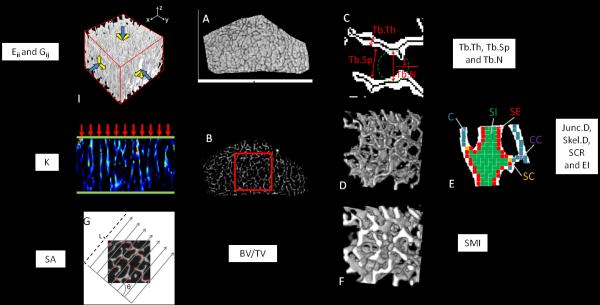
Images obtained at the three time-points were subjected to a series of processing steps. First, image blurring due to translational and rotational subjects movement during the scan were corrected using an auto-focusing motion correction algorithm [34] with normalized gradient square (NGS) value as the image sharpness metric. Subsequently, the ROI common to the three time points were isolated and retrospectively registered [35] (Fig. 1) followed by correction for intensity variations of the registered ROIs resulting from the sensitivity profile of the RF coil [11]. The intensity corrected images (Fig. 3A) were then converted to bone volume fraction (BVF) images (Fig. 3B) based on the fraction of TB occupying each voxel relative to pure bone (which was assigned a value of 100%).

Fig. 3.

Process for extraction of structural and mechanical parameters. Parameters are derived from both whole TB volume and subvolume unless specified. A. Center slice of a μMR image of the whole TB volume ROI after retrospective registration and segmentation of region common to baseline and follow-up images; B. Bone volume fraction (BVF) image of A yielding BV/TV. Region in box indicates analysis subvolume; C. Fuzzy distance transform based computation of trabecular thickness, spacing and number; D. 3D rendered binarized skeleton after sinc-interpolation; E. Digital topological analysis classification of skeleton voxels; F. 3D rendering of a subvoxel processed and binarized image yielding structure model index; G. Computation of mean intercept length yielding structural anisotropy (subvolume only); H. FE analysis providing estimation of axial stiffness K (whole TB volume only); I. FE analysis of subvolume compressive and shear moduli (E_ii and G_ij, where i, j = {x, y, z}).

Structural and mechanical parameters were derived from the entire 3D TB volume as well as from a 5×5×5 mm³ subvolume region extracted from the center of TB region, as indicated by the red square in Fig. 3B.

A series of structural parameters, both conventional and parameters relating to topology, the latter having proven their usefulness for fracture discrimination [4, 30] and sensitivity to intervention [23, 36] were derived from the BVF image for both whole TB volume and parallelepiped subvolume: Overall volumetric BVF (BV/TV) was calculated as the average of the voxel BVF values over total volume. Fuzzy distance transform [10] (Fig. 3C) was applied to calculate the average 3D trabecular thickness (Tb.Th) from the BVF image. Using the definitions in [37] and the calculated Tb.Th, the average trabecular spacing (Tb.Sp) and trabecular number (Tb.N) were computed. The BVF images were further sinc-interpolated by factor of 3×3×9 to 46 μm³ isotropic voxel size followed by binarization and skeletonization [38] for digital topological analysis (DTA) [12]. DTA classifies each voxel from a skeletonized BVF image into surface (S), curve (C) and their mutual junctions (CC, SC and SS). Further classification distinguishes between voxels located in the interior or edge of the respective curves or surfaces (CI, SI, CE and SE) (Fig. 3D and E). Based on the DTA voxel classification, junction density (Junc.D) and skeleton density (Skel.D) were calculated to characterize the counts of junction-type voxels and all voxels in the skeleton respectively over the TB volume. Two topological parameters, surface-to-curve ratio (SCR) and erosion index (EI) were computed based on digital topological analysis (DTA) [12] to describe the TB network integrity. SCR is the ratio of the sum of all surface-type voxels (SE, SI, SC and SS) divided by the sum of all curve-type (CE, CI and CC) voxels as a measure of the relative plate versus rod character of the TB network. EI is the ratio of the sum of voxel types expected to increase upon bone resorption (CI, CE, CC and SE), divided by the sum of those expected to decrease upon such a process (surface-type voxels). The structure model index (SMI), another topological parameter that characterizes the overall plate- versus rod-likeness of the network [39], was calculated from subvoxel processed [40] binary BVF images at 46 μm³ isotropic voxel size (Fig. 3F). SMI ranges from 0 to 3 corresponding to an all-plates or all-rods configuration, respectively. Finally, structural anisotropy (SA) was calculated for the parallelepiped TB subvolume. The eigenvalues of the fabric tensor along the three axis were obtained by means of the 3D mean intercept length technique [41] applied to the subvolume (Fig. 3G) as described by Wald et al. [16]. SA was computed as the ratio of the largest to smallest eigenvalue.

Computation of Mechanical Parameters

Following conversion of voxels of the BVF images to hexahedral (brick) FE elements with dimensions corresponding to voxel size, two sets of FE simulations were performed: (1) axial compression on whole TB volume yielding axis stiffness (K) along the bone’s major loading direction (Fig. 3H), and (2) Young’s and shear moduli (denoted E and G, respectively) along the three orthogonal directions of the 5×5×5 mm³ TB subvolume (Fig. 3I), as described previously [18, 42]. The bone tissue material properties were chosen as isotropic and linearly elastic with each element’s Young’s modulus (YM) being linearly proportional to the voxel BVF value, i.e. YM = (15 GPa) × (BVF value), while Poisson’s ratio was kept constant at 0.3 for all elements. FE computations were carried out on a dual quad-core Xeon 3.16 GHz desktop computer equipped with 40 GB of RAM using a custom-developed solver.

Axial stiffness was estimated along bone’s longitudinal axis by applying a constant displacement (^~1% strain) to all FE nodes in the proximal face of the FE mesh while keeping those in the distal face constrained [43]. The unknown displacements at each FE node were then found by minimizing the total strain energy of the system. Finally, K was computed as the ratio of the resulting stress on the proximal face to the applied strain. Young’s and shear moduli E_ii and G_ij (i, j = {x, y, z}) were obtained analogously for the TB subvolumes via compression and shear tests along the three orthogonal directions.

2.3 Statistical Analyses

For each subject, coefficients of variation (CV) were calculated for all parameters across the three time-points and an average CV was obtained for all 20 subjects as the root mean square average across all subjects (denoted RMS-CV) as a measure of global variability across the three time-points. In addition, the intra-class correlation coefficient (ICC) was computed as a measure of reliability via one-way analysis of variance (ANOVA) [44]. Further, the ratio of the RMS difference between the parameters derived from the whole TB volume and subvolume to the average of whole TB volume mean and subvolume mean (RMSD/μ_Ave)1 across the three measurement time-points was calculated for each parameter and subject as a normalized measure of relative difference between the parameter values derived from the two regions. Axial stiffness K was compared with subvolume modulus E_zz. In order to evaluate associations among structural parameters as well as between structural and mechanical, mean values were obtained from the three time-points for each parameter and subject, and the Pearson correlation coefficient calculated. All statistical analyses were performed with Matlab (The Mathworks Inc., Natick, MA) with p < 0.05 set to denote statistical significance.

$$\mathit{RMSD}∕{\mu }_{\mathit{Ave}}=\sqrt{\frac{{\sum }_{n=1}^{20}{\left(X_W\left(n\right)-X_S\left(n\right)\right)}^2}{20}}/\left(\frac{{\stackrel{‒}{X}}_W+{\stackrel{‒}{X}}_S}{2}\right)\times 100\%,$$ 1

where X_w and X_s are the data of whole Tb volume and subvolume of parameter X respectively. ${\stackrel{‒}{X}}_i,i=\{W,S\}$, is the mean of parameter X over all 20 subjects and three time-points.

3. Results

For all subjects, TB patterns were well matched across the three time points after prospective registration (Fig. 1). Autofocus motion correction resulted in an average improvement in NGS values of 1.8% (S.D. = 1.3%).

The pool of twenty subjects provided a wide range in structural and mechanical parameters. Fig. 4 provides an example of two subjects differing substantially in their structural and mechanical measures. RMS-CVs, ICCs, means and ranges for all parameters derived from whole TB volumes and subvolumes μMR images are presented in Tables 1 and 2 respectively. For the data derived from whole-section TB volumes, aggregate RMS-CVs were 4.4% (range 1.8% - 7.7%) and 4.0% for all structural parameters and axial stiffness K respectively. SMI was the structural parameter having the lowest RMS-CV, whereas SCR and EI were the highest. Aggregate whole-volume ICC was 0.976 (range 0.947 - 0.986) and 0.992 for all structural parameters and K, respectively. The structural parameter having the lowest ICC was Tb.Th, whereas the highest were BV/TV and SMI. Results from TB subvolume analysis yielded an aggregate RMS-CV of 6.5% (range 1.6% - 13.0%) and 5.5% (4.6% to 6.5%) for all structural and mechanical parameters, respectively. For subvolume structural and mechanical parameters, aggregate ICC were 0.946 (range 0.752 - 0.991) and 0.974 (0.965 - 0.978). For both regions the composite topological parameters had greater intra-subject variance, however, their larger ranges resulted in ICCs of similar magnitude as those of other structural parameters. There was no significant difference in the sample means across the three time-points for all parameters from whole TB volumes or subvolumes (all p ≥ 0.88).

Fig. 4.

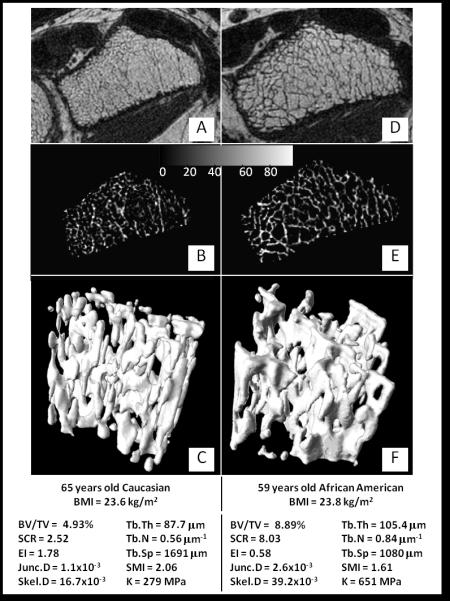
Image data from two study subjects with widely differing structural characteristics: A, D) center slice of acquired (unprocessed) μMR images; B, E) segmented trabecular region grayscale BVF images; C, F) 3D renderings of TB subvolume (Image surface rendered with v3d [45]).

Table 1.

Global means and reproducibility measures for each of the structural and mechanical parameters evaluated for the whole TB volume.

Parameters		Mean	Range	RMS-CV (%)	ICC
Structural	BV/TV (%)	7.08	[4.93, 8.89]	2.9	0.986
	SCR	4.24	[2.39, 8.03]	7.7	0.984
	EI	1.20	[0.58, 2.08]	7.7	0.965
	Junc.D	2.23×10−3	[1.10×10−3, 2.93×10−3]	5.8	0.982
	Skel.D	30.9×10−3	[16.7×10−3, 39.6×10−3]	4.8	0.982
	Tb.Th (μm)	95.2	[87.7, 105.4]	2.0	0.947
	Tb.N (μm−1)	0.74	[0.56, 0.87]	3.3	0.979
	Tb.Sp (μm)	1272	[1060, 1691]	3.5	0.977
	SMI	1.92	[1.61, 2.47]	1.8	0.986
Mechanical	K (MPa)	477	[279, 655]	4.0	0.992

Table 2.

Global means and reproducibility measures for structural and mechanical parameters evaluated from a TB subvolume.

Parameters		Mean	Range	RMS-CV (%)	ICC
Structural	BV/TV (%)	7.14	[4.17, 8.20]	3.7	0.978
	SCR	2.97	[1.08, 5.50]	13.0	0.947
	EI	1.91	[0.90, 4.69]	12.9	0.981
	Junc.D	1.40×10−3	[0.40×10−3, 2.05×10−3]	9.5	0.960
	Skel.D	21.5×10−3	[8.8×10−3, 27.0×10−3]	6.0	0.975
	SA	1.85	[1.68, 2.03]	1.6	0.967
	Tb.Th (μm)	103.04	[96.52, 110.53]	3.7	0.752
	Tb.N (μm−1)	0.69	[0.43, 0.84]	5.9	0.950
	Tb.Sp (μm)	1377	[1088, 2216]	6.1	0.962
	SMI	1.98	[1.70, 2.77]	2.1	0.991
Mechanical	Exx (MPa)	238	[148, 337]	5.9	0.978
	Eyy (MPa)	340	[188, 450]	6.5	0.965
	Ezz (MPa)	687	[372, 858]	5.6	0.969
	Gxy (MPa)	135	[85, 172]	5.2	0.977
	Gyz (MPa)	166	[103, 222]	4.6	0.978
	Gzx (MPa)	212	[116, 272]	5.1	0.974

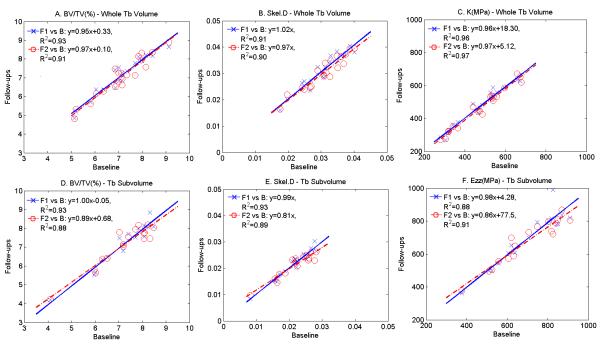
Fig. 5 shows correlations of baseline versus follow-up values for BV/TV, Skel.D and K to illustrate the level of serial reproducibility. For all test-retest correlations, R² > 0.88 (p < 10⁻⁷) with slopes of the regression lines close to unity (mean = 0.95, range = 0.8 to 1.0). For all parameters, whole-volume RMS-CVs were lower than their subvolume counterparts. Consistent with this result were ICCs, which were greater for the whole-volume than for the subvolume data, except for SMI (Table 1 and 2). For the parameters shown in Fig. 5, subvolume data exhibited greater clustering (i.e. narrower inter-subject distribution) than those derived from the whole TB volume. Inter-region comparison (whole volume versus subvolume) yielded correlation coefficients ranging from 0.32 to 0.88. Except for Tb.Th, all structural and mechanical parameters showed moderately high correlations (R²≥ 0.72, p < 0.001, Table 3). On the other hand, the normalized differences between whole volume and subvolume-derived parameters, expressed in terms of RMSD/μ_Ave varied greatly (4.7% to 64.5%). We note that RMSD/μ_Ave of SCR, EI, Junc.D, Skel.D and K-E_zz all exceeded 35%, thereby suggesting that these parameters are particularly sensitive to spatial heterogeneity.

Fig. 5.

Test-retest plots of selected parameters derived from whole TB volume (top) and TB subvolume (bottom): crosses: follow-up 1 versus baseline; circles: follow-up 2 versus baseline, all p < 10⁻⁷.

Table 3.

Comparison between parameters derived from whole TB volume and subvolume

	Structural									Mechanical
	BV/TV	SCR	EI	Junc.D	Skel.D	Tb.Th	Tb.N	Tb.Sp	SMI	K-Ezz
R2	0.78	0.87	0.76	0.72	0.79	0.32	0.79	0.75	0.88	0.78
RMSD/μAve (%)	6.92	37.62	64.45	48.19	37.48	8.82	9.17	12.73	4.71	37.68

^aNote: Sub-volume parameter E_zzis correlated with whole bone axial stiffness K. All p < 0.001.

Table 4 provides data for inter-parameter relationships for whole TB volume and subvolume parameters. For the former all correlations were statistically significant. However, for the TB subvolume, no correlation was found between SA versus SCR, EI, Tb.Th, Tb.N, and SMI versus Tb.Th and Junc.D, Skel.D, Tb.N, presumably due to the significant structural heterogeneity (see, for example, Fig. 4). For whole TB volume and subvolume, BV/TV, Junc.D and Skel.D had strong (R²≥ 0.87) positive and negative correlations with Tb.N and Tb.Sp. Further, BV/TV, Junc.D and Skel.D were highly correlated with each other (R²≥ 0.89). SCR and Tb.Sp showed strong negative correlations with their complementary parameters EI and Tb.N (R²≥ 0.76). Finally, whole volume and subvolume SCR were strongly correlated with Tb.Th and Tb.N in (R²≥ 0.82). Relationships between individual structural and mechanical parameters from whole TB volume and subvolume are reported in Table 5. All whole-volume structural parameters were significantly correlated with axial stiffness K (0.24 ≤ R²≤ 0.87), being strongest for BV/TV, Junc.D, Skel.D, Tb.N (all positive) while Tb.Sp had a strong negative correlation (R²≥ 0.79). The remaining correlations were either positive or negative and of smaller magnitude. Subvolume analysis indicated most structural parameters to be highly correlated with the Young’s moduli, except Tb.Th, which only moderately correlated with E_yy (R² = 0.45), and SA, which also only moderately correlated with E_yy and E_zz (R² = 0.31 and 0.40). BV/TV strongly correlated with E_yy, E_zz, G_yz and G_zx (R²≥ 0.76), and Junc.D and Tb.N were strongly correlated with E_zz and G_zx (R²≥ 0.73). Skel.D had a strong and positive correlation with E_yy, E_zz and G_zx (R²≥ 0.82). Tb.Sp was negatively correlated with all moduli, particularly strongly with E_zz (R² = 0.82). SCR was positively, while EI and SMI were negatively associated with elastic moduli.

Table 4.

Inter-parameter correlations(R²) for whole TB volume and subvolume

Whole TB volume	SCR	EI	Junc.D	Skel.D	Tb.Th	Tb.N	Tb.Sp	SMI
BV/TV	0.60*	(−)0.65*	0.89*	0.93*	0.50*	0.93*	(−)0.92*	(−)0.69*
SCR		(−)0.84*	0.35**	0.46*	0.82*	0.37**	(−)0.37**	(−)0.54*
EI			(−)0.44**	(−)0.51*	(−)0.69*	(−)0.47*	0.50*	0.49*
Junc.D				0.95*	0.30^	0.92*	(−)0.91*	(−)0.54*
Skel.D					0.36**	0.93*	(−)0.93*	(−)0.63*
Tb.Th						0.25***	(−)0.27***	(−)0.48*
Tb.N							(−)0.99*	(−)0.58*
Tb.Sp								0.58*

TB subvolume	SCR	EI	Junc.D	Skel.D	Tb.Th	Tb.N	Tb.Sp	SMI	SA
BV/TV	0.49*	(−)0.61*	0.93*	0.96*	0.16***	0.94*	(−)0.95*	(−)0.78*	0.26***
SCR		(−)0.76*	0.37**	0.47*	0.39**	0.94**	(−)0.37**	(−)0.48*	NS
EI			(−)0.49*	(−)0.55*	(−)0.32**	(−)0.48*	0.54*	0.52*	NS
Junc.D				0.95*	NS	0.90*	(−)0.87*	(−)0.66*	0.35**
Skel.D					NS	0.89*	(−)0.89*	(−)0.76*	0.38**
Tb.Th						NS	NS	(−)0.30***	NS
Tb.N							(−)0.95*	(−)0.66*	NS
Tb.Sp								0.81*	(−)0.23***
SMI									NS

^*Note: p<0.001,

^**p<0.01,

^***p<0.05,

NS: p>0.05. (−) indicates negative correlation.

Table 5.

Correlations (R²) between structural and mechanical parameters.

		Mechanical parameters
		Whole- volume	Subvolume
		K	Exx	Eyy	Ezz	Gxy	Gzx	Gyz
Structural parameters	BV/TV	0.79*	0.51*	0.76*	0.91*	0.66*	0.83*	0.76*
	SCR	0.41**	0.26***	0.40**	0.48*	0.39**	0.60*	0.46**
	EI	(−)0.44**	(−)0.23***	(−)0.54*	(−)0.49*	(−)0.42**	(−)0.67*	(−)0.43**
	Junc.D	0.79*	0.38**	0.71*	0.88*	0.51*	0.73*	0.61*
	Skel.D	0.87*	0.45**	0.82*	0.89*	0.61*	0.84*	0.67*
	Tb.Th	0.24***	NS	0.45***	NS	NS	NS	NS
	Tb.N	0.82*	0.44**	0.67*	0.88*	0.60*	0.74*	0.70*
	Tb.Sp	(−)0.80*	(−)0.45**	(−)0.68*	(−)0.82*	(−)0.59*	(−)0.73*	(−)0.68*
	SMI	(−)0.59*	(−)0.41**	(−)0.58*	(−)0.68*	(−)0.44**	(−)0.66*	(−)0.54*
	SA	NA	NS	0.31***	0.40**	NS	NS	NS

Note: (−) indicates negative correlation.

^*p<0.001,

^**p<0.01,

^***p<0.05,

NS: p>0.05.

NA: not available.

4. Discussion

Several structural imaging studies based on either MRI or HR-pQCT have reported reproducibility data [25, 27-29, 46, 47]. However, all were limited in terms of the number of subjects examined or the type of structural or mechanical parameters assessed, and most involved only young, compliant subjects. Further, except for one, all reported CV only, rather than the much more informative ICC, which is representative of sensitivity. While a low CV is indicative of high reproducibility, it is not a measure of sensitivity, as previously pointed out. In an investigation at 1.5T Newitt et al. [25] reported CV ranges of 2 – 4% in 2D structural and 4 – 9% in 3D FE mechanical parameters derived from the MR images acquired at the distal radius in eight healthy subjects ages 24 - 62 years, obtained at three time points within a 60-minute period. From seven subjects (24-62 years) without disease known to affect bone by Pothuaud et al. [27], found CVs ranging from 3.5 % to 6% for structural measures derived with a 3D-line skeleton graph analysis method performed on 1.5T MR images. Gomberg et al. [28] reported CVs of 4 – 7% in the 3D structural parameters on distal radii and tibias from six healthy volunteers ages 23 – 38 years. More recently, Zuo et al. [29] and also Bhagat et al. [46] reported a better reproducibility in 2D and 3D structural parameters from 7T images acquired from six and five healthy adults. Wald et al. [47] examined reproducibility at 3T in seven healthy volunteers, finding precision to range from 1-5%.

Structural parameters derived from HR-pQCT images showed somewhat lower variability. In an early study Muller et al. [48] calculated BV/TV, Tb.N, Tb.Th and Tb.Sp from HR-pQCT images of six healthy young male volunteers, reporting a CV of less than 0.5% and ICC of 0.98. Subsequently, Laib et al. [49] reported a mean root-mean square error of 1.6% for Tb.N from nine healthy postmenopausal women. In a larger study Boutroy et al. [50] scanned 15 healthy women three times with HR-pQCT within a 1-month period obtaining CVs of 2.5-4.4% for similar parameters.

In distinction to the prior work, the present study provides insight into the precision achievable in patient populations typically studied to evaluate fracture susceptibility or treatment efficacy, by having examined a large number of structural and mechanical measures, in terms of both, an average coefficient of variation (RMS-CV) as well as ICC, which are substantially different performance measures in 20 postmenopausal women. The former is typically used as a measure of the average variability for repeat measurements but is not a sufficient metric for power estimates. For example, a low CV value, while desirable in itself, may mitigate the parameter’s ability to distinguish subjects if the detectable inter-subject variability is small. By contrast, the ICC, which compares intra- to inter-subject variances, is more informative. The data in Tables 1 and 2 provide some insight in this respect. For example, we note that the composite topological parameters SCR and EI have relatively large RMS-CV (since they are composed of two or more parameters, each associated with an uncertainty). However, this deficiency is largely offset by their much larger range compared to some of the conventional parameters. For example, for the whole TB volume data (Table 1) the range for SCR was 235%, versus 55% for Tb.N, yielding ICCs of 0.98 for both measures in spite of the much larger CV of the former parameter (7.7 versus 3.3%). It is interesting to note that while there are large differences in CVs (ranging from 1.8 to 7.7% (whole bone, Table 1) and 1.6 to 13% (subvolume, Table 2) ICCs were almost uniformly in the 0.95 to 0.99, except for subvolume regionally measured Tb.Th (R² = 0.75). The data thus suggest the majority of the parameters to have comparable detection sensitivity. The sensitivity of topological parameters to relatively subtle changes in trabecular network architecture, in response to treatment or depletion of hormone levels, have been amply demonstrated from an analysis of in vivo MR images, in both animals and humans. Large increases in SCR, for example, following hormone supplementation, suggesting closure of perforations secondary to bone accrual, have been reported in several recent studies, in spite of the relatively low measurement precision [23, 36]. Lastly, given the degrees of freedom equals to 40 { (measurements − 1) × subjects = 40} on C which the statistics in this study are based, there is significant confidence as a basis of power estimates for future longitudinal studies.

Achievement of adequate reproducibility requires a number of precautions and appropriate technology. The thickness of trabeculae is approximately 100-150 μm. Therefore, very small movements (usually involuntary subject movement) during the scan adversely affect the accuracy and precision of the derived structural and mechanical parameters. In this study, a retrospective motion correction algorithm was applied to all images to enhance the sharpness of images corrupted by small in-plane translational and rotational motion [34].

Another requirement for achieving serial reproducibility is image registration, which ensures that the follow-up images are superimposable onto the baseline images. While prospective registration is known to be accurate to about 1 mm and 1° [32] retrospective registration was employed to ensure that exactly the same ROIs are analyzed across the three time point, thereby further reducing positioning variability, particularly important for sub-region analysis due to the inherent heterogeneity of the bone’s structural make-up. Since TB is not rigidly connected to the surrounding soft-tissue, retrospective registration of μMR images was accomplished based on the ROI containing only TB, which was isolated by a semi-automated segmentation procedure.

A few comments are needed to made regarding parameters that are difficult to quantify at in vivo resolution due to their sensitivity to image voxel size. These comprise trabecular thickness and SMI. Tb.Th was derived with the aid of the fuzzy distance transform technique [10], along with Tb.N and Tb.Sp. Trabecular thickness derived from in vivo images is often referred to as “apparent” considering the difficulty of obtaining accurate measures of this quantity. However, Saha and Wehrli [10] had previously shown that accurate measurement is possible in the regime of in vivo imaging and, in fact, that the method is able to detect treatment effects as in a study examining the structural implications of dexamethasone exposure and its reversal in a rabbit model of corticosteroid-induced osteoporosis[10, 51, 52]. SMI, a measure of the plate-strut characteristics of the trabecular network [53] is not generally evaluated in vivo because of the difficulty in reliably quantifying the surface area at low resolution. Here we computed SMI after subvoxel processing [40], a technique that entails up-sampling the μMR images to isotropic voxel size and redistributing the bone in a non-linear fashion. The approach has the property of mimicking data acquisition at higher resolution. It is thus rewarding that this parameter can be reliably measured with high precision under retention of its sensitivity as suggested by an ICC of 0.99 for both whole bone and sub-region (Tables 1 and 2).

In this work we have examined the performance of the method for both the entire trabecular volume as well as for a sub-region. The correlations (R²) between whole volume and subvolume-derived parameters were all on the order of 0.8 except for Tb.Th, which was much weaker (Table 3). However, among the parameters that correlated strongly, only BV/TV, SMI, Tb.Th and Tb.N had RMSD/μ_Ave ratios less than 10%, suggesting that the actual values derived from whole volume were not comparable for many of the parameters even though they followed similar trends, an observation attributed to regional heterogeneity. Therefore, direct comparison between parameters from whole TB volume and subvolume is not appropriate. The results also suggest that construction of a parameter map for the whole volume from subvolume regional kernels could provide a useful representation of the variations in the structure and mechanical properties of the volume.

The correlation matrix of Table 4 provides some insight into the interdependence of structural parameters. BV/TV was strongly correlated with Junc.D, Skel.D, Tb.N and Tb.Sp (all R²> 0.89), suggesting the latter to provide very limited additional information. Moreover, EI and SCR, as well as Tb.N and Tb.Sp, based on their definitions, are reciprocally related to one another and, not surprisingly, are strongly correlated with each other (R²> 0.95). Overall, we note that some of the subvolume-derived quantities were not correlated. SMI and SCR were negatively correlated as expected, but only moderately so, even though both are measures of the plate/rod architecture.

This study has some limitations. Even though demonstration of accuracy was not an objective, we note that anisotropic resolution may cause errors in some of the parameters (even though topological parameters are inherently dependent on resolution). Here, the images were acquired at a voxel size 137×137×410 μm³ (with the lower resolution in axial direction) and interpolated to isotropic voxel size prior analysis, which is known to overestimate plate density yielding, for example, greater values of the topological surface-to-curve ratio than corresponding measures obtained from images acquired at isotropic voxel size [47]. Similarly, structural anisotropy appears to be overestimated at anisotropic voxel size. The typically used voxel size in μMRI of trabecular bone is dictated by SNR limitations even though in recent work it has been shown that isotropic voxel size of 160 μm yields adequate SNR for structural and mechanical analysis of images acquired at the distal extremities at 3T field strength. However, we are more concerned about the technique’s ability to detect change, which is expressed by the ICC. Recent work involving simulations of homogeneous and heterogeneous erosion based on high-resolution μCT images of trabecular bone, showed that after downsampling of the images to mimic in vivo MR resolution and addition of noise, the resulting changes in structural parameters were detectable with high significance for a bone loss of 5% [54]. Lastly, the derived mechanical parameters are sensitive to the processing algorithms used for obtaining bone volume fraction images, skeletonization needed for digital topological analysis, threshold settings, etc., will require standardization to allow comparison of the data among users.

5. Conclusions

The data in this work provide insight into the performance achievable by μMRI at 1.5T field strength for quantifying structural and mechanical parameters in the distal radius of older women representative of typical study populations evaluated in drug intervention trials. The results in terms of intraclass correlation coefficients suggest expected errors in the range of 1-4% (ICC 0.96-0.99). The work also emphasizes the importance of methodology for minimization of reproducibility errors from subject motion and positioning. Lastly, the data have implications on sample size estimates in future longitudinal studies involving structural MRI.

Highlights.

• > The performance of the MRI-based Virtual Bone Biopsy was evaluated in the data from 20 women representative of osteoporosis study populations.

• > Reproducibility and reliability of 26 structural and mechanical parameters in the distal radius were assessed.

• > The work describes the methodology for minimization of reproducibility errors from subject motion and positioning.

• > Expected errors of repeated imaging is in the range of 1-4%.