Abstract
Background
Clinically relevant endpoints cannot be routinely targeted with reasonable power in a small study. Hence, proof-of-concept studies are often powered to a primary surrogate endpoint. However, in acute heart failure (AHF) effects on surrogates have not translated into clinical benefit in confirmatory studies. Although observing an effect on one of many endpoints due to chance is likely, observing concurrent positive trends across several outcomes by chance is usually unlikely.
Methods
Pre-RELAX-AHF, which compared 4 relaxin doses with placebo in AHF, has shown favourable trends versus placebo (one-sided P < 0.10) on six of nine clinical endpoints in the 30 μg/kg/day group. To illustrate evaluation of multiple, correlated clinical endpoints for evidence of efficacy and for dose selection, a permutation method was applied retrospectively. By randomly re-assigning the treatment group to the actual data for each of the 229 subjects, 20,000 permutation samples were constructed.
Results
The permutation P value for at least six favourable trends among nine endpoints in any dose groups was 0.0073 (99.9% CI 0.0053–0.0093). This is higher than would be expected if the endpoints were uncorrelated (0.00026), but much lower than the probability of observing one of nine comparisons significant at the traditional two-sided P < 0.05 (0.74). Thus, the result was unlikely due to correlated endpoints or to chance.
Conclusions
Examining consistency of effect across multiple clinical endpoints in a proof-of-concept study may identify efficacious therapies and enable dose selection for confirmatory trials. The merit of the approach described requires confirmation through prospective application in designing future studies.
Keywords: Heart failure, Statistics, Clinical trials, Phase II
Introduction
Cardiovascular medicine has made dramatic advances in recent decades, partly due to effective discovery programs that have successfully progressed through the phases of development. Proof-of-concept studies must provide a strong bridge between mechanistic, pharmacokinetic and pharmacodynamic studies, and confirmatory studies for efficacy. These studies often have designs for effects of new interventions on a single primary outcome. Since a small sample size (of up to 350 patients) has insufficient power for clinically significant treatment targets (such as dyspnea relief or cardiovascular death), many proof-of-concept studies address surrogate endpoints so as to have adequate power. However, positive effects on such surrogate endpoints (e.g., wedge pressure, BNP) may not translate into obvious clinical benefit in later studies. For instance, if an efficacious intervention does not affect a surrogate this will lead to a false-negative proof-of-concept study result and may lead to abandoning the intervention and not pursuing the intervention in confirmatory studies. On the other hand, ineffective interventions may have apparent positive effects on surrogates (false-positive) leading to unnecessary confirmatory studies in which the true lack of efficacy is discovered after years of futile effort [1]. Consequently, the selection of endpoints for proof-of-concept studies has become a major challenge in acute heart failure (AHF) research.
A possible solution to this dilemma is to design proof-of-concept studies to explore whether a therapy demonstrates consistent indications of a possible clinical benefit for multiple endpoints that are relevant to the disease. If an intervention’s effect is examined on six endpoints—for instance, symptoms, recurrent disease, readmission, death, quality of life and functional improvement—having a positive effect on one of them (for example, symptoms only) and no effect on the other endpoints may represent a chance finding and not a real beneficial effect. If, on the other hand, the intervention improves symptoms, reduces disease recurrence and re-admissions and improves quality of life, the probability that all these beneficial effects are the result of chance and not a real benefit of the intervention is low. Subsequent studies can then confirm the therapy’s potential benefit.
We have investigated the value of this approach in the Preliminary study of RELAXin in Acute Heart Failure (Pre-RELAX-AHF) [2, 3]. The purposes of this study were to assess the potential clinical efficacy of the new intervention, to choose a dose from among four active doses for further study, to assess the distributions of the endpoints, and to re-assess the sample size needed for a subsequent confirmatory study. Although the protocol identified primary and secondary endpoints, the analysis plan recognized that the sample size did not provide adequate power to detect statistically significant differences, and so the overall pattern of results was to guide the dose selection for the subsequent confirmatory study. In the main study manuscript [3], a consistent, U-shaped dose response was described across multiple endpoints recognized as treatment targets in AHF, but given the modest sample size, many of their P values were not statistically significant at the traditional two-sided 0.05 level. In this paper, we examine the usefulness of a method, called a permutation criterion, for quantitatively evaluating the totality of the data for evidence of efficacy and for choosing among multiple doses.
Methods
A permutation criterion, also known as a re-randomization criterion, is a statistical method based on the distribution of all possible results when treatment groups are reassigned to subjects. A permutation sample is generated by taking the observed data for each subject, and randomly re-assigning the treatment group to the subjects in the same ratio as in the original sample. This procedure is then repeated multiple times to obtain many permutation samples. The statistical assessments of interest are generated for each permutation sample. If the treatment has an effect, then one would expect the observed pattern of results to occur rarely among these re-randomized samples. Fisher’s exact test, with which many researchers are familiar, is a permutation test for a single dichotomous endpoint.
In a proof-of-concept study with multiple endpoints, criteria can be established for evidence of efficacy and for choosing a dose. A possible criterion for evidence of efficacy can be based on P values from univariate pairwise comparisons of each dose with placebo for all candidate endpoints; e.g., positive ‘trends’ with one-sided P < 0.10 (equivalent to two-sided P < 0.20 favouring active drug) for the majority of the endpoints is applicable, and its occurrence by chance can have assessment across permutation samples. The dose with the most positive trends among the endpoints could be the selected dose. With this criterion, the number of positive trends in each dose group is calculated, and the proportion of permutation samples with that number or more positive trends is computed. This proportion represents the probability of obtaining at least the observed number of positive trends by chance alone. Thus, no adjustment for multiple endpoints is needed, as the single global null hypothesis that all nine endpoints for each dose are no different or worse than placebo is being assessed (with a single associated permutation P value) against the alternative of a preponderance of results in favour of at least one dose. The criterion for dose selection may be further restricted, for example, by further requiring nonnegative trends (one-sided P > 0.90, equivalent to two-sided P < 0.20 favouring placebo).
Pre-RELAX-AHF was a parallel-group, randomized, dose-ranging study in 234 patients with AHF [2, 3] (ClinicalTrials.gov identifier NCT00520806). Patients with dyspnea, pulmonary congestion, elevated BNP or NT-pro-BNP, mild to moderate renal impairment, and systolic blood pressure >125 mmHg were randomly assigned within 16 h of presentation to 48 h of continuous IV infusion of placebo, or 10, 30, 100, or 250 μg/kg/day relaxin in a 3:2:2:2:2 ratio. The study complied with the Declaration of Helsinki and was approved by appropriate ethics committees. All patients gave written, informed consent prior to study participation. Five randomized subjects were not treated with study drug and were excluded from the analyses. Subject self-report of dyspnea and physician-assessed heart failure signs and symptoms were recorded at 6, 12, and 24 h, daily through day 5, and at day 14 following randomization. Subjects were contacted at days 30 and 60 to obtain rehospitalization information and vital status and at day 180 to ascertain vital status. This proof-of-concept study was conducted to determine whether a confirmatory study for IV relaxin was warranted in this patient population, and, if so, to identify a dose, to select endpoints, and to provide a basis for sample size calculations. The pattern of results across nine clinical outcomes was evaluated with one-sided P values <0.10 in favour of active treatment considered indicative of potential efficacy. The endpoints of interest and the analytic method used to compare groups with respect to each outcome are given in Table 1.
Table 1.
Statistical analysis of outcomes of interest
| Variable | Statistical test | Effect measure |
|---|---|---|
| Moderately or markedly better dyspnoea at 6, 12, and 24 h as assessed by Likert scale | Wald chi-square from logistic regression model adjusted for region | Odds ratio |
| Area under the curve representing the change from baseline to Day 5 in dyspnoea as assessed by Visual Analog Scale (VAS) | F test from analysis of variance model adjusted for region | Mean difference |
| Worsening heart failure to Day 5 | Wilcoxon rank sum test of days to WHF (no WHF assigned 6 days) | Mean score difference |
| Increase ≥25% in serum creatinine from baseline to Day 5 | Wald chi-square from logistic regression model adjusted for region | Odds ratio |
| Increase ≥0.3 mg/dL in serum creatinine from baseline to both Day 5 and Day 14 | Wald chi-square from logistic regression model adjusted for region | Odds ratio |
| Length of initial hospital stay | Wilcoxon rank sum test stratified by region (in-hospital death assigned max + 1 days) | Mean difference |
| Days alive out of hospital to Day 60 | Wilcoxon rank sum test stratified by region | Mean difference |
| Cardiovascular death or rehospitalization for heart failure or renal failure to Day 60 | Wald chi-square from Cox regression | Hazard ratio |
| Cardiovascular death to Day 180 | Fisher’s exact test of incidence densities | Odds ratio |
For this study, 20,000 permutation samples were generated by re-randomizing the 229 treated patients (with all their data kept intact) 20,000 times. This number of samples would allow estimation of a permutation P value of 0.01 within ±0.0023 with 99.9% confidence. Each permutation sample had a 61-patient placebo group and 40-, 42-, 37-, and 49-patient groups for 10, 30, 100, 250, μg/kg/day relaxin. For each permutation sample, comparisons of each relaxin dose group versus placebo for each of the nine outcomes of interest described in Table 1 were conducted, and the number of such assessments with positive trends in favour of that dose group was calculated. The maximum number of positive trends among the four dose groups was then taken for each permutation sample as the criterion for expressing efficacy of the best dose across the nine endpoints; for example, if 0, 2, 3, and 4 positive ‘trends’ were observed among the four dose groups, then the maximum was 4 for that sample. The proportion of permutation samples for which their maximum number of favourable trends across the four dose groups is at least as large as that actually observed for the study is the single P value for the global null hypothesis that none of the four doses are better than placebo for any of the nine endpoints, and such assessment has adjustment for the multiplicity in its 4 × 9 = 36 underlying comparisons.
Results
The results observed in the 229 subjects enrolled in Pre-RELAX-AHF have been described in detail [3]; one-sided P values observed in these subjects for the outcomes of interest are given in Table 2. Statistical assessments for six of the nine variables comparing relaxin 30 μg/kg/day to placebo in the study had one-sided P < 0.10, indicating results that favoured relaxin. The number of favourable P values for the 10, 100, and 250 μg/kg/day groups were lower, and the higher dose groups had outcomes with unfavourable direction (one-sided P > 0.90). The 30 μg/kg/day was chosen for a confirmatory study [3]. This dose group had the greatest number of favourable outcomes with one-sided P < 0.10, and had no unfavourable results with one-sided P > 0.90 (equivalent to a two-sided P value <0.20).
Table 2.
One-sided P values observed in Pre-RELAX-AHF for comparisons of each dose group with placebo
| Endpoint | Relaxin 10 μg/kg/day | Relaxin 30 μg/kg/day | Relaxin 100 μg/kg/day | Relaxin 250 μg/kg/day |
|---|---|---|---|---|
| Moderately or markedly better dyspnea at 6, 12, and 24 h by Likert scale | 0.268 | 0.022† | 0.860 | 0.569 |
| Dyspnoea VAS area under the change from baseline curve from baseline to Day 5 | 0.077† | 0.055† | 0.082† | 0.154 |
| Time to worsening heart failure to Day 5 (no WHF assigned 6 days) | 0.376 | 0.145 | 0.201 | 0.077† |
| Increase ≥25% in serum creatinine from baseline to Day 5 | 0.310 | 0.874 | 0.977‡ | 0.937‡ |
| Increase ≥0.3 mg/dL in serum creatinine from baseline to both Day 5 and Day 14 | 0.565 | 0.550 | 0.765 | 0.907‡ |
| Length of initial hospital stay (in-hospital death assigned max + 1 day) | 0.181 | 0.089† | 0.373 | 0.102 |
| Days alive out of hospital to Day 60 | 0.200 | 0.082† | 0.202 | 0.024† |
| Cardiovascular death or rehospitalization for heart failure or renal failure to Day 60 | 0.160 | 0.026† | 0.117 | 0.043† |
| Cardiovascular death to Day 180 | 0.075† | 0.023† | 0.083† | 0.265 |
| No. of one-sided P values <0.1 (trends) out of 9 supporting dose | 2 | 6 | 2 | 3 |
| No. of one-sided P values >0.9 (trends) out of nine against dose | 0 | 0 | 1 | 2 |
One-sided P < 0.5 favours relaxin and P > 0.5 favours placebo
† One-sided P < 0.10 corresponds to two-sided P < 0.20 favouring relaxin
‡ One-sided P > 0.90 corresponds to two-sided P < 0.20 favouring placebo
Table 3 illustrates results for 10 of the 20,000 permutation samples, each of which was constructed by randomly reassigning the treatment group label to the 229 subjects’ actual data. For each permutation sample, the effect estimate and P value for each of the 9 endpoints for each of the 4 permuted dose group comparisons against placebo—a total of 36 comparisons—were computed. Results for 3 of these 36 comparisons (one permuted dose group compared against placebo for 3 of the 9 endpoints), and the number of endpoint comparisons out of 9 with a positive trend for that dose group, are shown for the 10 illustrative permutation samples in Table 3.
Table 3.
Example of results for 10 permutation samples for comparison of the 30 μg/kg/day relaxin dose group versus placebo for 3 of the 9 outcomes of interest
| Sample | # (+) trends out of 9* | Mod/marked better dyspnea at 6, 12, and 24 h | VAS AUC to Day 5 | Persistent renal impairment | |||
|---|---|---|---|---|---|---|---|
| Effect | P value† | Effect | P value† | Effect | P value† | ||
| 1 | 0 | 0.972 | 0.523 | −785.614 | 0.928 | 1.853 | 0.807 |
| 2 | 0 | 0.768 | 0.717 | −421.809 | 0.784 | 1.385 | 0.649 |
| 3 | 2 | 2.586 | 0.034 | 1096.705 | 0.019 | 0.957 | 0.472 |
| 4 | 1 | 1.238 | 0.339 | −249.908 | 0.680 | 0.272 | 0.123 |
| 5 | 0 | 1.135 | 0.394 | −213.555 | 0.654 | 1.633 | 0.744 |
| 6 | 2 | 0.995 | 0.504 | −907.511 | 0.957 | 0.873 | 0.429 |
| 7 | 1 | 1.224 | 0.347 | 721.538 | 0.087 | 1.591 | 0.754 |
| 8 | 1 | 1.257 | 0.312 | 799.000 | 0.068 | 1.048 | 0.524 |
| 9 | 2 | 1.886 | 0.089 | −374.060 | 0.758 | 0.920 | 0.450 |
| 10 | 1 | 1.856 | 0.091 | 101.700 | 0.425 | 0.973 | 0.484 |
* Positive (+) trend defined as one-sided P < 0.10
† One-sided P < 0.5 favours relaxin and P > 0.5 favours placebo. One-sided P < 0.10 corresponds to two-sided P < 0.20 favouring relaxin, while one-sided P > 0.90 corresponds to two-sided P < 0.20 favouring placebo
Table 4 contains the P values computed across the 20,000 permutation samples. Computed as the proportion of permutation samples where the number of positive trends was as large or larger than the possible values 1 through 9, these represent the probability of observing that number of positive trends or more by chance. The permutation P value for any dose versus placebo (given in the next to last column of Table 4) was computed as the proportion of permutation samples where the maximum number of positive trends in any dose group was at least as large as the respective possible value, and represents a P value adjusted for the multiple comparisons across the four dose groups. In Pre-RELAX-AHF, the maximum number of positive trends (one-sided P values < 0.10) was six among the nine tested and was observed in the relaxin 30 μg/kg/day group; the permutation P value for this observed result (with multiplicity adjustment for four doses) was 0.0073 (99.9% confidence interval 0.0053–0.0093). As one might expect, the multiplicity-adjusted permutation P value for observing six of nine one-sided P values < 0.10 with the further restriction that all nine P values ≤ 0.90 (indicating no negative trends) in any dose group was slightly smaller: 0.0072 (99.9% CI 0.0052–0.0092). Table 4 additionally shows permutation P values for six or more positive trends for each dose versus placebo without adjustment for multiplicity and they are 0.0022, 0.0021, 0.0017, and 0.0017 for the 10, 30, 100, 250 μg/kg/day doses, and their similarity supports the comparable utility of this criterion to identify departures from chance for the respective doses. These unadjusted P values clearly exceed the binomial probability of 0.000064 for at least six one-sided P values ≤ 0.10 among nine independent assessments by chance reflecting the correlations among the nine endpoints.
Table 4.
Probability estimated from 20,000 permutation samples of given number of positive trends or more out of 9 outcomes of interest
| Number of one-sided P < 0.1 (in favour of active treatment) | P value for comparison of permuted dose group | Relaxin dose group(s) in which result observed (μg/kg/day) | ||||
|---|---|---|---|---|---|---|
| 10 μg v. placebo | 30 μg v. placebo | 100 μg v. placebo | 250 μg v. placebo | Any dose group v. placebo | ||
| 1 | 0.5080 | 0.5056 | 0.4983 | 0.5053 | 0.8810 | |
| 2 | 0.2120 | 0.2130 | 0.2062 | 0.2179 | 0.5240 | 10 , 100 |
| 3 | 0.0758 | 0.0783 | 0.0727 | 0.0838 | 0.2333 | 250 |
| 4 | 0.0249 | 0.0289 | 0.0249 | 0.0310 | 0.0911 | |
| 5 | 0.0075 | 0.0081 | 0.0072 | 0.0089 | 0.0288 | |
| 6 | 0.0022 | 0.0021 | 0.0017 | 0.0017 | 0.0073 | 30 |
| 7 | 0.0004 | 0.0006 | 0.0003 | 0.0004 | 0.0019 | |
| 8 | 0 | 0.0001 | 0 | 0 | 0.0003 | |
| 9 | 0 | 0 | 0 | 0 | 0.0000 | |
Discussion
Results across multiple outcomes in Pre-RELAX-AHF suggest that relaxin may have a beneficial effect on clinical endpoints in AHF and that the 30 μg/kg/day relaxin dose may be promising for further study. Of the 4 doses studied, this dose group was the only group to meet the criterion of a majority of endpoints with one-sided P < 0.10 favouring relaxin compared to placebo; it had the greatest number of favourable endpoints with one-sided P < 0.10 (6 of 9), and it had no unfavourable result with a one-sided P value > 0.90. Through a permutation criterion, we have shown that the probability of observing such an extreme number of favourable trends in any dose group by chance alone is <1%. Thus, it is unlikely that the observed effect on clinical endpoints for the 30 μg/kg/day dose is a chance finding. We conclude that 30 μg/kg/day relaxin has potential clinical efficacy in the treatment of AHF, and so its effects on dyspnea relief and 60-day mortality and morbidity—endpoints found to be responsive to therapy in this proof-of-concept study—are being assessed in an ongoing RELAX-AHF-1 confirmatory study.
Dose selection and proof of activity are often based on a surrogate endpoint (such as a biomarker) for which a study with small sample sizes can have insufficient power. However, such a surrogate endpoint may not be predictive of the drug’s effect on clinical outcomes in a confirmatory study. Reliance on a single, primary, surrogate outcome measure in proof-of-concept studies may lead to decisions that would not be confirmed, including false-positive results driven by an effect of the intervention on the surrogate but no activity on the disease, false-negatives and the abandoned development of potentially beneficial therapies, or in the selection of an inappropriate dose for further study. A novel approach that has been recently incorporated into the design of cardiovascular clinical trials is to examine multiple clinical outcomes for evidence of a drug’s activity and worthiness for further evaluation.
Several studies have evaluated multiple clinical endpoints, but the approach taken in integrating results across these multiple endpoints has varied. One approach is to assign a score to each subject by assigning values based on results over the endpoints. For example, in the African-American Heart Failure Trial (AHeFT), subjects were assigned a rank score from −6 to +2 based on weighted values for all-cause mortality, first heart failure rehospitalization, and quality of life score [4]. This ranked composite outcome was then used as the primary outcome for comparing treatment groups. A similar criterion has been proposed for use in trials of mechanical circulatory support devices [5], and in AHF studies [6]. In the end, the risks of the therapy must be weighed against the potential benefit, and an advantage of the ranked individual outcome is that the risks and benefits to the individual patient are incorporated in the criterion. The disadvantage of such an approach, however, is in the difficulty interpreting the criterion: several different outcome combinations could result in the same score, and a therapy might affect some components in one direction and others in a different direction. Simpler, three-category ordered outcomes (success, unchanged, failure) have been used in several AHF programs, including the REVIVE studies evaluating levosimendan [7] and the PROTECT studies [8, 9] evaluating rolofylline. In designing such criteria, individual components must be chosen and weighted such that a favourable score reflects benefit outweighing risk to a meaningful degree.
Another potentially useful approach in exploratory studies where the most sensitive endpoint to the therapy is unknown is to analyse multiple endpoints individually and look for consistency of results across the endpoints. For example, in the design of the CUPID study, researchers considered as evidence of efficacy “improvement” (two-sided P < 0.2 for an endpoint with favourable point estimates for other endpoint(s) within the domain) in 2 of 5 efficacy ‘domains’ on a study-level, or two-sided P < 0.2 on a subject-level composite outcome of success/unchanged/failure based on improvement in at least one efficacy endpoint without worsening on any others [10]. They estimate the probability of a ‘false-positive’ given this approach to be <0.10 assuming a lack of correlation among the domains.
Other approaches involve computation of a global statistic across multiple endpoints. A multivariate test such as Hotelling’s T 2 allows comparison of groups regarding multiple endpoints simultaneously, but can be insensitive to situations in which individual endpoints are not statistically significant, but the pattern of results suggests efficacy [11]. O’Brien [11] suggested a global rank-sum-type test, based on a simple or weighted sum of ranks across the individual endpoints. This method is powerful only if the treatment effects on all endpoints are in the same direction. This limitation could be handled with a step-down approach to testing each individual endpoint given rejection of a global null hypothesis of no effect [12], or through weighting of the individual endpoints in an attempt to create an overall benefit-to-risk measure.
The permutation criterion described here allows an assessment of multiple endpoints simultaneously with consideration of the direction of the treatment effect. The method is flexible, and can be adapted to examine different hypotheses. In Pre-RELAX-AHF, we have computed a multiplicity adjusted P value based on the number of endpoints with favourable trends, given the observed data including the correlation structure, allowing an informed decision regarding the role of chance in the findings. Results of the RELAX-AHF-1 study will either confirm or refute the efficacy of the selected relaxin dose on primary and secondary endpoints chosen from among those in the proof-of-concept study.
A common misconception is that evaluating several clinical outcomes simultaneously increases the probability of a false signal [13]. Although it is true that the probability of obtaining at least one “positive” result from a long list of potential variables is higher than the nominal P value used for each of the multiple outcomes, requiring demonstration of multiple concurrent effects does not necessarily increase the likelihood of a chance finding. Assuming independence (or no correlation) among the clinical outcomes of interest, the probability of observing the pairwise comparison of a dose and placebo for one of nine endpoints significant at the traditional, one-sided 0.025 level by chance alone would be 0.184, while the chance of observing at least six of nine positive trends (with one-sided P ≤ 0.10) versus placebo in would be 0.000064. As the correlation between the endpoints increases, the chance of observing multiple concomitant trends becomes higher. If the nine variables were very highly correlated (e.g., all correlations ≥0.9), the chance of observing six of nine positive trends (one-sided P < 0.10) would approach 0.15 [14], while if they were perfectly correlated (all correlations = 1.0) the probability would be 0.10. The value calculated for the present study (0.0017) is higher than one would expect if all the endpoints were independent reflecting a modest correlation among the variables. Therefore, observing six of nine positive trends in Pre-RELAX-AHF is not likely to be the result of either a chance finding or that these were basically six expressions of identical phenomena highly correlated with each other.
We have applied this approach to the Pre-RELAX-AHF database retrospectively. Although the endpoints examined are recognized as important endpoints in AHF studies [15, 16], the nine endpoints selected and the analytic method for examining them concurrently were not identified prospectively; thus, the proposed approach should be considered untried. The approach could be applied prospectively when designing future studies by identifying the endpoints to be examined and the criteria for evidence of efficacy and dose selection a priori. The acceptable false-positive rate should be chosen, and then power calculations conducted to determine the number of subjects needed. Once the study is completed, results observed in the study population should be compared against the criteria chosen for evidence of effect and dose selection, and permutation P values computed for the observed results. Each of these design elements is considered in further detail below.
Choice of endpoints
When designing these studies, endpoints should be included that would be appropriate for a confirmatory study. While surrogate endpoints might be included in addition to clinical endpoints as evidence of effect in a proof-of-concept study, these endpoints would probably not be selected as primary endpoints in a confirmatory study. One should also consider that the more endpoints examined, the lower the probability of observing a majority of favourable trends by chance alone. For example, if the endpoints selected were uncorrelated, the probability of at least four of seven positive trends by chance alone is 0.0027, while for at least five of nine, it is 0.00089. As described above, correlation among the endpoints reduces the ability to determine effects by observing multiple trends and is analogous to reducing the number of endpoints, thus increasing the probability of observing multiple positive trends by chance alone. Therefore, endpoints should be selected that are not too highly correlated with one another. However, this may introduce a dilemma since it may not be known a priori which endpoint within a ‘domain’ might be most sensitive to the treatment. One example is dyspnoea relief which could be measured using either a Likert scale where the patient compares their symptoms to baseline or a visual analogue scale where the patient rates their symptoms at each point in time and effects could be measured either at 6 and 24 h or over 5 days. A possible solution is to compute an overall P value within each domain, and then proceed with the evaluation of potential efficacy across domains as described here for individual endpoints.
Once the proof-of-concept study is complete, the choice of endpoints as primary in the confirmatory study must be guided by both statistical and other concerns. Endpoints with favourable results in the proof-of-concept study would seem to have a higher probability of demonstrating a treatment effect than untested ones or ones without evidence of effect. Choosing the endpoints with the lowest P values must be balanced, however, with study objectives. For the RELAX-AHF-1 study, two primary endpoints were chosen from among those tested in the proof-of-concept study: moderately or markedly better dyspnea reported on the Likert scale at 6, 12, and 24 h; and the area under the change in dyspnea visual analogue scale score from baseline to day 5. Although these were not the two endpoints with the lowest P values in Pre-RELAX-AHF, the confirmatory study is designed primarily to evaluate relaxin’s effect on dyspnea relief, and a positive finding for either of these endpoints would likely support regulatory approval for this indication.
Choice of criteria for evidence of efficacy and dose selection
A criterion for acceptance of proof of concept illustrated here was a simple majority of endpoints favouring the test treatment and with a positive trend at the one-sided 0.10 level. A criterion for evidence of effect based on a majority of endpoints has been accepted in other research fields. For example, the ACR20 composite endpoint in rheumatoid arthritis defines a responder as a patient who has at least five of seven endpoints with at least 20% improvement, although this criterion is applied to individual patients within a group rather to comparisons between two groups [17]. The P value for a comparison between two groups represents a standardized effect size that accounts for sample size. For a continuous endpoint with equal sample sizes in the two groups, one-sided P ≤ 0.10 corresponds to 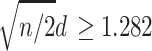 , where d is the standardized effect size (i.e., the ratio of the difference between the groups’ means versus the standard deviation). With 50 subjects per group, one-sided P ≤ 0.10 corresponds to d ≥ 0.256—a small effect size with potential clinical relevance [18].
, where d is the standardized effect size (i.e., the ratio of the difference between the groups’ means versus the standard deviation). With 50 subjects per group, one-sided P ≤ 0.10 corresponds to d ≥ 0.256—a small effect size with potential clinical relevance [18].
Other criteria for evidence of efficacy could be constructed, for example, by accepting ‘positive trends’ on surrogate markers but requiring that clinical endpoint(s) demonstrate positive trends as well. The choice of criterion should be driven by consideration of an acceptable false-positive rate which could be estimated through simulations taking into account the correlations among the chosen endpoints and assuming no treatment effect. After the study is completed, the permutation P value can be calculated using the observed results with actual correlation structure.
The dose selection criterion for the confirmatory study suggested here was to choose the dose with the most favourable trends. It might be possible in a proof-of-concept study for more than one dose group to satisfy the criterion demonstrating potential efficacy. If one dose group was not clearly superior to the other, both doses could be explored further in the confirmatory study.
Power and sample size considerations
How many subjects to include in proof-of-concept studies is an important consideration. With the approach described here, the power obtained to detect a majority of endpoints with positive trends is greater than that required for each individual endpoint. If the endpoints were independent, 65% power for each of nine endpoints would provide approximately 83% power to detect five of nine favourable trends. Of course, higher correlations among the endpoints may result in less power than that calculated assuming independence. To estimate power correctly for such studies, one should assume somewhat higher correlations than expected and strive to include more rather than fewer patients. Power calculations can be achieved through simulations which preferably should be based on real data from previous programs rather than theoretical assumptions. This underlines the importance of sharing data freely among different stake holders in research.
Limitations
Balancing apparent efficacy and potential safety concerns may not be possible through purely statistical methods. The method described in this paper is a novel approach to assessing potential activity of new therapies, but shares the limitation with other statistical approaches that safety concerns may in some cases be related to single or very few extreme events that do not approach statistical significance. Hence, final decisions on whether a new therapy should be further explored must involve clinical judgment balancing efficacy and safety.
Conclusions
Examination of consistency of findings across multiple clinical endpoints in a proof-of-concept study may be useful in identifying efficacious therapies, and in selecting a dose from among several tested. The permutation method described allows a determination of the role of chance in these findings. In this retrospective analysis, application of this method to the Pre-RELAX-AHF proof-of-concept study shows that the multiplicity adjusted P value for observing at least 6 of the 9 AHF endpoints examined with a one-sided P value < 0.10 favouring active treatment in one of 4 dose groups by chance alone was <1%. These data and analyses have been used to design the ongoing RELAX-AHF-1 confirmatory study, which will assess the efficacy of the selected relaxin dose primarily in relieving dyspnoea and secondarily in reducing morbidity and mortality in AHF patients. The merit of the approach described requires confirmation through prospective application in designing future proof-of-concept studies.
Acknowledgments
The authors thank Jill El-Khorazaty, Michael Hussey, and Daniela Sotres for their review and helpful comments. Pre-RELAX-AHF was sponsored by Corthera, Inc., a subsidiary of Novartis Pharmaceuticals Corp. (San Mateo, California).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Abbreviations
- AHF
Acute heart failure
- CI
Confidence interval
- IV
Intravenous
References
- 1.Gheorghiade M, Pang PS. Are BNP changes during hospitalization for heart failure a reliable surrogate for predicting the effects of therapies on post-discharge mortality? J Am Coll Cardiol. 2009;53(25):2349–2352. doi: 10.1016/j.jacc.2009.01.075. [DOI] [PubMed] [Google Scholar]
- 2.Maier LS, Baumhakel M, Bohm M. Hotline sessions presented at the American College of Cardiology Congress 2009. Clin Res Cardiol. 2009;98(6):345–352. doi: 10.1007/s00392-009-0023-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Teerlink JR, Metra M, Felker GM, Ponikowski P, Voors AA, Weatherley BD, et al. Relaxin for the treatment of patients with acute heart failure (Pre-RELAX-AHF): a multicentre, randomised, placebo-controlled, parallel-group, dose-finding phase IIb study. Lancet. 2009;373(9673):1429–1439. doi: 10.1016/S0140-6736(09)60622-X. [DOI] [PubMed] [Google Scholar]
- 4.Franciosa JA, Taylor AL, Cohn JN, Yancy CW, Ziesche S, Olukotun A, et al. African-American Heart Failure Trial (A-HeFT): rationale, design, and methodology. J Card Fail. 2002;8(3):128–135. doi: 10.1054/jcaf.2002.124730. [DOI] [PubMed] [Google Scholar]
- 5.Felker GM, Anstrom KJ, Rogers JG. A global ranking approach to end points in trials of mechanical circulatory support devices. J Card Fail. 2008;14(5):368–372. doi: 10.1016/j.cardfail.2008.01.009. [DOI] [PubMed] [Google Scholar]
- 6.Allen LA, Hernandez AF, O’Connor CM, Felker GM. End points for clinical trials in acute heart failure syndromes. J Am Coll Cardiol. 2009;53(24):2248–2258. doi: 10.1016/j.jacc.2008.12.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cleland JG, Freemantle N, Coletta AP, Clark AL. Clinical trials update from the American Heart Association: REPAIR-AMI, ASTAMI, JELIS, MEGA, REVIVE-II, SURVIVE, and PROACTIVE. Eur J Heart Fail. 2006;8(1):105–110. doi: 10.1016/j.ejheart.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 8.Cotter G, Dittrich HC, Weatherley BD, Bloomfield DM, O’Connor CM, Metra M, et al. The PROTECT pilot study: a randomized, placebo-controlled, dose-finding study of the adenosine A1 receptor antagonist rolofylline in patients with acute heart failure and renal impairment. J Card Fail. 2008;14(8):631–640. doi: 10.1016/j.cardfail.2008.08.010. [DOI] [PubMed] [Google Scholar]
- 9.Massie BM, O’Connor CM, Metra M, Ponikowski P, Teerlink JR, Cotter G, et al. Rolofylline, an adenosine A1-receptor antagonist, in acute heart failure. N Engl J Med. 2010;363(15):1419–1428. doi: 10.1056/NEJMoa0912613. [DOI] [PubMed] [Google Scholar]
- 10.Hajjar RJ, Zsebo K, Deckelbaum L, Thompson C, Rudy J, Yaroshinsky A, et al. Design of a phase 1/2 trial of intracoronary administration of AAV1/SERCA2a in patients with heart failure. J Card Fail. 2008;14(5):355–367. doi: 10.1016/j.cardfail.2008.02.005. [DOI] [PubMed] [Google Scholar]
- 11.O’Brien PC. Procedures for comparing samples with multiple endpoints. Biometrics. 1984;40(4):1079–1087. doi: 10.2307/2531158. [DOI] [PubMed] [Google Scholar]
- 12.Lehmacher W, Wassmer G, Reitmeir P. Procedures for two-sample comparisons with multiple endpoints controlling the experimentwise error rate. Biometrics. 1991;47(2):511–521. doi: 10.2307/2532142. [DOI] [PubMed] [Google Scholar]
- 13.Hernandez AF, Granger CB. Advancing care for acute heart failure–no time to relax. Lancet. 2009;373(9673):1401–1402. doi: 10.1016/S0140-6736(09)60653-X. [DOI] [PubMed] [Google Scholar]
- 14.Anand SP, Murray SC, Koch GG. Sample size calculations for crossover thorough QT studies: satisfaction of regulatory threshold and assay sensitivity. J Biopharm Stat. 2010;20(3):587–603. doi: 10.1080/10543400903582000. [DOI] [PubMed] [Google Scholar]
- 15.Felker GM, Pang PS, Adams KF, Cleland JG, Cotter G, Dickstein K, et al. Clinical trials of pharmacological therapies in acute heart failure syndromes: lessons learned and directions forward. Circ Heart Fail. 2010;3(2):314–325. doi: 10.1161/CIRCHEARTFAILURE.109.893222. [DOI] [PubMed] [Google Scholar]
- 16.Cotter G, Voors AA, Weatherley BD, Pang PS, Teerlink JR, Filippatos G, et al. Acute heart failure clinical drug development: from planning to proof of activity to Phase III. Cardiology. 2010;116(4):292–301. doi: 10.1159/000318048. [DOI] [PubMed] [Google Scholar]
- 17.Felson DT, Anderson JJ, Boers M, Bombardier C, Chernoff M, Fried B, et al. The American College of Rheumatology preliminary core set of disease activity measures for rheumatoid arthritis clinical trials. The Committee on Outcome Measures in Rheumatoid Arthritis Clinical Trials. Arthritis Rheum. 1993;36(6):729–740. doi: 10.1002/art.1780360601. [DOI] [PubMed] [Google Scholar]
- 18.Cohen J. Statistical power analysis for the behavioral sciences. 2. Hillsdale: Lawrence Erlbaum Associates, Inc.; 1988. [Google Scholar]


