Creation of Computerized 3D MRI-Integrated Atlases of the Human Basal Ganglia and Thalamus

Abstract

Functional brain imaging and neurosurgery in subcortical areas often requires visualization of brain nuclei beyond the resolution of current magnetic resonance imaging (MRI) methods. We present techniques used to create: (1) a lower resolution 3D atlas, based on the Schaltenbrand and Wahren print atlas, which was integrated into a stereotactic neurosurgery planning and visualization platform (VIPER); and (2) a higher resolution 3D atlas derived from a single set of manually segmented histological slices containing nuclei of the basal ganglia, thalamus, basal forebrain, and medial temporal lobe. Both atlases were integrated to a canonical MRI (Colin27) from a young male participant by manually identifying homologous landmarks. The lower resolution atlas was then warped to fit the MRI based on the identified landmarks. A pseudo-MRI representation of the high-resolution atlas was created, and a non-linear transformation was calculated in order to match the atlas to the template MRI. The atlas can then be warped to match the anatomy of Parkinson's disease surgical candidates by using 3D automated non-linear deformation methods. By way of functional validation of the atlas, the location of the sensory thalamus was correlated with stereotactic intraoperative physiological data. The position of subthalamic electrode positions in patients with Parkinson's disease was also evaluated in the atlas-integrated MRI space. Finally, probabilistic maps of subthalamic stimulation electrodes were developed, in order to allow group analysis of the location of contacts associated with the best motor outcomes. We have therefore developed, and are continuing to validate, a high-resolution computerized MRI-integrated 3D histological atlas, which is useful in functional neurosurgery, and for functional and anatomical studies of the human basal ganglia, thalamus, and basal forebrain.

Introduction

Despite impressive gains in medical imaging during the last two decades, significant challenges remain when visualizing the structure of the living brain. The resolution and contrast of standard in vivo magnetic resonance imaging (MRI) is well below that required to visualize subnuclei and fiber tracts of the basal ganglia, thalamus, and brainstem. Since image-guided neurosurgery for Parkinson's disease often targets subnuclei of the thalamus, subthalamic area, basal ganglia, and brainstem, reliable targeting needs to be supplemented with invasive neurophysiological methods. Furthermore, advances in functional brain imaging have allowed increasing visualization of activation in subcortical brain areas, but only low-resolution atlases are available for interpretation of these changes. Most available print atlases of the human brain delineate subcortical nuclei in tissue sectioned in three planes, derived from different hemispheres using multiple brains (Olszewski and Baxter, 1954; Talairach, 1957; Schaltenbrand and Bailey, 1959; Van Buren and Maccubbin, 1962; Andrew et al., 1969; Van Buren and Borke, 1972; Schaltenbrand and Wahren, 1977; Afshar et al., 1978; Talairach and Tournoux, 1988). Bertrand and Thompson published the first computerized digitized atlas, which was derived from the Schaltenbrand print atlas. This atlas could be mapped to stereotactic ventriculograms using constrained affine transformations (Bertrand et al., 1973). The atlas was used in stereotactic neurosurgery of the thalamus and basal ganglia, and also served as the basis for functional atlases of deep brain stimulation responses (Hardy et al., 1979a,b,c, 1981). A variety of digital atlases have since been created from original print versions (Yoshida, 1987; Kazarnovskaya et al., 1991; Hardy et al., 1992; Niemann et al., 1994; Nowinski et al., 1997; Sramka et al., 1997; Yeo and Nowinski, 1997; Niemann and van Nieuwenhofen, 1999; Yelnik et al., 2000; Berks et al., 2001).

Challenges faced when creating computerized 3D digital atlases from print atlases include: (1) Print atlases often have low inter-slice resolution and variable inter-slice distances. Reconstructed nuclei data may be fractured, reducing atlas utility. Furthermore, minor errors in photographic representations in stereotactic space can result in a shift between reconstructed slices, making image integration difficult in 3D space. Robust reconstruction algorithms that account for slice-to-slice variability, and anatomical differences between the atlas and patient data, can help enhance the quality of 3D visualization and atlas integration (St-Jean et al., 1998; Chakravarty et al., 2006a, 2008). (2) Differences in stereotaxic location of nuclear structures may be noted when comparing data derived in different planes from different hemispheres. Simple representation of the three planes of a print atlas is therefore not useful in computerized atlas aided analysis of neurosurgical plans, since the data sets do not match in all planes. (St-Jean et al., 1998; Niemann and van Nieuwenhofen, 1999; Nowinski et al., 2005, 2008; Chakravarty et al., 2006a,b, 2008, 2009; Sather and Patil, 2007; Yelnik et al., 2007). Multiplanar reconstruction from a unique histological data set is more useful (St-Jean et al., 1998) although only low resolution is obtained in most cases due to lack of detail in the source data. (3) Histological artifacts related to different stains (e.g., myelin, Nissl) can be problematic, especially in large sections, limiting proper identification of outlines of nuclei and tracts. Furthermore, thalamic nuclear nomenclature is highly complex, making it difficult to provide reliable outlines in multiplanar 3D mode on the basis of an initially low-resolution data set. (4) Tissue inhomogeneity can occur due to shear stress on sectioning, and artifacts can result from histological processing and slice mounting, further reducing the ability to interpret the underlying anatomy. For this reason, it is necessary to apply computerized reconstruction methods to minimize slice-to-slice variations in tissue morphology and staining intensity. (5) Classical atlases such as that of Schaltenbrand are based largely on detailed histological delineations using Hassler's nomenclature (Hassler et al., 1965; Schaltenbrand and Wahren, 1977). This terminology, which includes a distinct parcellation of the thalamus, has proved useful for neurosurgeons, and classical anatomists. Correspondence in 3D atlas space of Hassler's terminology with more commonly used thalamic nomenclature based on work in human and non-human primates would be desirable (Hirai and Jones, 1989b).

Here, we summarize our recent work on the creation and implementation of two digitized 3D atlases of subcortical structures. We first created a lower resolution atlas based on axial slices derived from the Schaltenbrand and Wahren print atlas (St-Jean et al., 1998; Atkinson et al., 2002; Strafella et al., 2004; Duval et al., 2006; Tyvaert et al., 2009). More recently, we created a higher resolution atlas derived from a new set of coronal histological slices, with delineation of thalamic and basal forebrain nuclei based on multiple terminologies (Chakravarty et al., 2006a,b, 2009; Duval et al., 2006). We concurrently developed novel tools for the creation of volumetric voxel-based 3D atlases from histological data sets, and methods for effective integration of the digitized atlases with canonical high-resolution MRI scans, or individual participant or patient MRIs. Availability of high-resolution digitized deformable atlases of subcortical nuclei will greatly aid in image-guided neurosurgery in subcortical areas, and in interpretation of structural and functional brain imaging data.

Materials and Methods

Two computerized 3D atlases were created. The first atlas was created using the Schaltenbrand and Wahren print atlas. Details of image processing used for atlas development are presented in the Section “Results.” This atlas was integrated into VIPER, a stereotactic visual integration platform for enhanced reality (St-Jean et al., 1998). VIPER allows visualization of stereotactic tools, electrodes, and virtual lesions in the 3D atlas space. The second atlas was created using the postmortem brain of a middle-aged man who died of a non-neurological cause. The brain was fixed in 10% buffered formalin, hemi-sectioned in the mid-sagittal plane, and blocked to obtain the thalamus, basal ganglia, basal forebrain, and temporal lobe of the left hemisphere. The brain was then embedded in paraffin, and sectioned in the coronal plane, perpendicular to the AP–PC plane (Chakravarty et al., 2006a). Pairs of 15 μm thick slices were sampled from this data set at 0.70 mm intervals, yielding a total of 86 pairs of slices across the block. For each pair of slices, one was stained with Luxol Fast Blue for myelin, while the other was stained with a Nissl stain for neurons and glia. Subsequent image processing for atlas development is presented in the Section “Results.” Computerized software used for image analysis included Adobe Photoshop 7, and MINC image analysis tools developed at the McConnell Brain Imaging Centre at the MNI (available at: http://www.bic.mni.mcgill.ca/ServicesSoftware).

Results

Initial creation of a 3D digitized atlas with a surgical planning platform

We initially created a digitized computerized 3D version of the atlas of Schaltenbrand and Wahren (St-Jean et al., 1998). The digital atlas was created from an axial data set with varying slice thickness of 0.5–3 mm due to the slice-to-slice distance variations in the original photographic plates (Schaltenbrand and Wahren, 1977). The 2D contour data was extracted into a vector format. Hermite polynomials were applied in order to interpolate the 2D contour data to achieve a 0.5-mm isotropic voxel resolution in the reconstructed 3D data set.

A methodology was then developed to create a customized version of the Schaltenbrand and Wahren atlas which can be automatically integrated to a patient's MRI scan on a routine basis. The reconstructed 3D digital atlas was first warped to fit Colin27, a widely used high resolution, high signal-to-noise canonical reference MRI volume, which is derived by averaging 27 T1-weighted MRI scans of the same participant (Collins et al., 1995; Holmes et al., 1998). Two hundred fifty homologous point-pairs of landmarks were manually identified on both the digitized atlas and the canonical volume using REGISTER (Macdonald et al., 1994). The volumetric version of the Schaltenbrand atlas was then warped to the reference MRI using Bookstein's 3D thin-plate-spline interpolation approach (Bookstein, 1989). The result of this initial labor-intensive step is a 3D volumetric MRI-integrated reference atlas of the basal ganglia and thalamus.

The MRI-integrated reference digital atlas may then be integrated to individual patient MRI scans using a non-labor-intensive automated process. An automated non-linear intensity matching algorithm, ANIMAL (Collins et al., 1995), is applied to generate a transform which matches a patient's MRI to the Colin27 MRI average. Application of the inverse of this transformation allows integration of the 3D digital atlas into the patient's MRI reference space. The MRI-integrated atlas can also be used in the VIPER stereotactic platform, which allows visualization of stereotactic targets, neurosurgical instruments (deep brain stimulation leads, leukotomes, retractable searching electrodes), and lesions in the atlas and MRI spaces (St-Jean et al., 1998).

Development of a higher resolution 3D digitized atlas with incorporation of multiple nomenclatures of nuclei of the thalamus, basal ganglia, and basal forebrain

While the previously described 3D atlas proved very useful (St-Jean et al., 1998; Atkinson et al., 2002; Strafella et al., 2004; Duval et al., 2006; Van Der Werf et al., 2006; Tyvaert et al., 2009; Duerden et al., 2011) it has limited inherent inter-slice resolution, and contains a limited number of subcortical nuclear structures. Furthermore, the atlas does not present an analysis of homologies between Hassler's terminology and the more recent terminology of Jones and Hirai, based on the so-called “Anglo-American” school and work in non-human primates. In order to help overcome these limitations, we created a new higher resolution atlas with more detailed outlines of subcortical subnuclei, including reference to multiple anatomical nomenclatures (Chakravarty et al., 2006a, 2009). The new digital atlas is derived from a single set of high resolution, thin-slice histological data of the basal ganglia, basal forebrain, and thalamus. Consecutive pairs of slices were sampled from this data set at 0.70 mm intervals, and one set was stained with Luxol Fast Blue for myelin, while the other was stained with a Nissl stain for neurons and glia. A total of 86 pairs of slices across the block was analyzed. The atlas contains 105 anatomical structures that were manually delineated by neuroanatomists (GB, AFS, VVR) on the myelin and Nissl stained histological data, using multiple source terminologies for the thalamus, basal ganglia, basal forebrain, and amygdala (Figures 1A,B) Within the thalamus, nuclear boundaries were identified according to the terminologies of Hassler (Schaltenbrand and Wahren, 1977), and of Hirai and Jones (Hirai and Jones, 1989a,b). Detailed work is now continuing in the basal forebrain with further reference to the terminology of Brockhaus, Gloor, Heimer and colleagues, and Paxinos and Mai (Gloor, 1997; Heimer et al., 1997; Mai et al., 2008).

Figure 1.

Outline of nuclei of the human thalamus on a coronal Myelin–Nissl stained section. The section is taken at the level of the sensory thalamus. Thalamic nuclei are outlined using the terminology in Schaltenbrand's atlas according to Hassler (A), with homologous outlines using the terminology of Hirai and Jones (B).

The histological data were then reconstructed in 3D using methods described in detail in our previous work (Chakravarty et al., 2006a, 2008, 2009). First, an optimized version of the ANIMAL algorithm was developed for slice-to-slice non-linear registration, and was applied throughout the reconstructed data set to minimize morphological misalignment between slices. An intensity correction algorithm was also developed for optimization of the histological data, accounting for staining inhomogeneities, and other processing artifacts, such as tearing, local compression, shearing, or stretching (Malandain et al., 2004; Chakravarty et al., 2005). The correction scheme matches local neighborhoods in each slice using a least-trimmed squares estimator, in order to build a voxel-by-voxel multiplicative field to correct for local variations in image intensities between slices (Chakravarty et al., 2006a).

In order to develop a tool for visualization and understanding of the 3D relationships of the basal ganglia, thalamus, and basal forebrain, two atlas data sets were derived from the contours manually defined on the original histological data. The first, a voxel-based atlas, was created with labels assigned to each voxel of the reconstructed histological volume, facilitating investigation of the nuclear boundaries when navigating through the transverse, sagittal, or coronal slices of the volume (Figures 2A–D). The second is a geometric atlas which extracts structures using a marching cubes algorithm (Cline et al., 1987), and enables visualization of the 3D relationship of subcortical nuclei and tracts. The result is a volumetric 3D atlas with 105 separately labeled structures including the basal ganglia, thalamus, subthalamic area, basal forebrain, and temporal lobe (Figure 2I).

Figure 2.

Different 3D atlas representations and integration with a high-contrast, high-resolution MRI (Colin27) (A). Histological volume created from the original coronal data (C). Axial reconstruction of the histological volume created from the original coronal brain slices (B). Coronal voxel-label atlas created from the contours identified on the histological atlas (D). Reformatted axial views created from the 3D voxel-label atlas (E,G). Pseudo-MRI from original coronal data (E), with a reformatted axial view (G). The pseudo-MRI is created by modifying the intensity of the labels in the voxel-label atlas (B) to a high-contrast, high-resolution MRI templates (F,H) The pseudo-MRI is then used to estimate a non-linear transformation which matches the atlas to a high-resolution template MRI volume, or directly to a patient or participant's MRI (I). 3D geometric atlas created from the 3D surface rendering of labels in the voxel-label atlas (B).

Once the 3D voxel-based atlas was completed, two separate methods were used to integrate the atlas to a patient or participant MRI (Holmes et al., 1998; Chakravarty et al., 2008). In the first strategy, also used in our initial atlas (St-Jean et al., 1998), multiple homologous points were identified in the atlas and on the Colin27 MRI. An affine transformation was then used to fit the atlas to the Colin27 MRI. ANIMAL can then be used to aid in atlas integration with the patient or participant MRI. In a second strategy, a novel pseudo-MRI (Figures 2E,G) was created by matching the intensity of basal ganglia nuclei, thalamus, and internal capsule in the voxel-label atlas (Figures 2B,D) to the corresponding structures on Colin27 MRI (Figures 2F,H). The pseudo-MRI atlas is then warped to the Colin27 brain using ANIMAL. The same transform is then applied to the voxel-based atlas, resulting in integration of the atlas with the Colin27 template. The resulting atlas-integrated Colin27 MRI can then be warped to the target patient MRI using standard MRI-to-MRI non-linear registration techniques such as the ANIMAL algorithm. As an alternative, the pseudo-MRI can be directly integrated with the patient MRI, with comparable results (St-Jean et al., 1998; Chakravarty et al., 2008).

Applications of the atlases

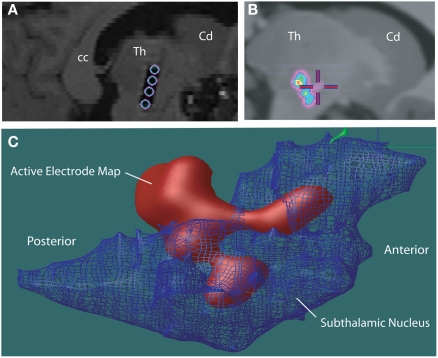
The two atlases have been adapted to a number of applications in human, including incorporation with a surgical planning platform (St-Jean et al., 1998), analysis of microelectrode responses in the subthalamic nucleus during cortical transcranial magnetic stimulation (Strafella et al., 2004), analysis of fMRI–EEG data in patients with epilepsy (Tyvaert et al., 2009), confirming the stereotactic position of the sensory thalamus (Figures 3A–F) by correlating the atlas with stimulation induced sensory responses (Chakravarty et al., 2005, 2008). The atlases have also been used to clarify the location of effective thalamic lesions for medically intractable tremor, and in determining the position of deep brain stimulation electrodes (Atkinson et al., 2002). Display of lesions, or active electrode contacts from multiple patients, in a common probabilistic atlas-integrated space, allows for statistical analysis of differences in clinical outcome. For example, our recent analysis of (Chakravarty et al., 2006b) motor outcome after subthalamic stimulation indicates that the most effective electrodes for relief of appendicular manifestations of Parkinson's disease (Figures 4A–C) are located in the posterior and lateral part of the subthalamic nucleus, and dorsal to the nucleus, in the region of the zona incerta and ventral thalamus (Chakravarty et al., 2006b; Sadikot et al., 2006).

Figure 3.

(A–D) Voxel-label atlas of the basal ganglia and thalamus integrated into a high-contrast high-resolution MRI (Colin27). (E,F) The sensory thalamus is isolated in the atlas and represented on coronal and sagittal views. The average stereotactic position of the somatosensory responses obtained during stereotactic neurosurgery in the thalamus from nine patients is integrated into the same MRI. The somatosensory responses were obtained using a curved retractable stimulator, and the position of hand/arm area responses from multiple patients was analyzed in the atlas-integrated reference space. The circle represents the 90% probability map of somatosensory responses, which map to the rostral portion of the ventral posterior somatosensory nucleus of the thalamus.

Figure 4.

(A) Post-operative sagittal T1-weighted MRI scan of a patient who underwent insertion of subthalamic stimulators for Parkinson's disease. The hypointense signal artifact shows the four electrode contacts (Medtronic 3387) that traverse the subthalamic nucleus, identified during surgery using an array of five microelectrodes (“Ben's Gun” array). The electrode contacts are within, and dorsal to the subthalamic nucleus. Abbreviations: cc, corpus callosum; Cd, caudate; Th, thalamus. (B) The automatic non-linear image matching and automatic labeling (ANIMAL) algorithm was used to integrate each patent's MRI scan with the canonical high-resolution MRI (Colin27), resulting in a common space for evaluation of electrode positions from different patients. A probabilistic average map of active contacts of subthalamic stimulators associated with the best outcome for motor symptoms of the contralateral side is shown. (C) The voxel-labeled 3D atlas was integrated with the probabilistic volume map of the most effective active electrode contacts in patients with Parkinson's disease with subthalamic stimulator implants. The subthalamic nucleus is represented as a net. A 90% probability map of most effective electrode positions shows they are localized in the dorsolateral subthalamic nucleus, and areas dorsal and posterior to the subthalamic nucleus, including the zona incerta, Forel's fields, and ventral thalamus.

In addition to surgical targeting, the VIPER platform provides a useful method for virtual in vivo “histological” analysis of effective and less effective lesions or DBS lead positions for tremor (Atkinson et al., 2002). The MRI-integrated reference atlas was also used to display electrophysiological responses from the internal capsule or the subthalamic nucleus in a common reference space (Strafella et al., 2004; Duerden et al., 2011). Finally, the atlases are also used in analysis of subcortical functional activation in multiple modalities, including PET and fMRI. For example, the atlas was recently used to demonstrate that activation of intralaminar nuclei occurs prior to anterior thalamic nuclei in patients with generalized spike and wave epilepsy studied by fMRI–EEG (Tyvaert et al., 2009).

Discussion

When digital atlases were first used for integration with patient's stereotactic ventriculograms, CT scans, or MRI scans, linear transformations mapping the atlas to patient data were estimated to register an atlas to an individual patient scan (Bertrand et al., 1973; Hardy et al., 1980a,b, 1981; Yoshida, 1987; Yeo and Nowinski, 1997). Atlas integration by simple linear scaling of axial, sagittal, or coronal data sets is limited by the fact that the three planes are necessarily derived from different hemispheres of different individuals. This results in variations of the position of structures in stereotaxic space (Niemann and van Nieuwenhofen, 1999; Nowinski, 2004; Nowinski et al., 2007), which is especially important to note when attempting to scale the three representations of nuclear structures into the triplanar MRI space of a patient or individual participant. Attempts at creating 3D atlas versions from histological data are limited by the quality, triplanar anatomical correspondence, and resolution of the initial data set. We have developed methods for partially correcting for artifacts resulting from variations in staining intensity, shear, and inter-slice distance variations, allowing creation of a lower resolution 3D data set based on the Schaltenbrand and Wahren Atlas. The missing inter-slice data in the original data set was accounted for using Hermite cubic polynomials allowed for creation of smooth 3D structures. The lower resolution 3D atlas was integrated to a stereotactic platform that allows surgical tool representation and creation of virtual lesions in atlas space. The utility of computerized 3D atlases can be limited by the accuracy of the method used for integration into patient or participant target imaging. In order to overcome the limitations of linear scaling methods used for atlas integration into patient data, our group was one of the first to apply non-linear transformations which warp a digital atlas to fit pre-operative or post-operative patient MRI data, accounting for local variations in the anatomy (St-Jean et al., 1998; Atkinson et al., 2002).

To improve atlas resolution, we created a new high-resolution 3D data set from histological data from a middle-aged man who died from a non-neurological cause. Thalamic atlases, especially those created for stereotactic neurosurgery, mainly use Hassler's detailed parcellation of the thalamus. More recent work has emphasized homologies between parcellations in non-human primates and humans (Jones, 2007). In the work of Hirai and Jones, cytoarchitecture and tract-tracing data based on connections of the monkey thalamus, were harmonized with that of human thalamic parcellation based on myelo-architecture and histochemical stains (Walker, 1938; Hirai and Jones, 1989b; Jones, 2007). In creating our higher resolution 3D atlas, we therefore undertook to present nomenclature using both commonly applied terminologies, allowing precise 2D and 3D homology between the nomenclature used by the Hassler school and that of Jones and Hirai. We also compared terminologies for basal forebrain and amygdala nuclei used in the Schaltenbrand atlas (Schaltenbrand and Wahren, 1977), with the more recent atlas of Paxinos and Mai (Mai et al., 2008), and the work of Brockhaus (Gloor, 1997). To date, our atlas boundaries are derived from myelin and Nissl stains. Other authors have provided important additional data sets based on chemical anatomy, particularly the calcium binding proteins, which provide useful additional information compared to traditional cytoarchitectonic and histochemical parcellations (Morel et al., 1997; Mai et al., 2004, 2008; Yelnik et al., 2007; Bhattacharjee et al., 2008; Bardinet et al., 2009; Krauth et al., 2010).

Many groups use template based procedures to warp atlases to pre-operative patient data. Once the atlas has been customized to an MRI, a non-linear transformation can be estimated to match the anatomy between the atlas and the template. Essentially, the atlas matching problem is then simplified to the standard MRI-to-MRI non-linear registration problem (Chakravarty et al., 2009). For example, D'Haese et al. developed a combined anatomical and electrophysiological atlas (D′Haese et al., 2005; Pallavaram et al., 2010) which integrated subcortical delineations and electrophysiological intraoperative recordings from the subthalamic nucleus registered to a template created from the average of pre-operative data. This group noted that the choice of template was crucial for the accuracy of subsequent atlas customization due to the differing underlying anatomies between populations suffering from neurodegenerative diseases and the template. Other groups have suggested that non-linear transformations should be used with caution in the atlas customization procedure as they may abnormally deform the morphology of the subcortical neuroanatomy (Yelnik et al., 2007; Bardinet et al., 2009). Their work uses histological and MRI data prospectively acquired from a single subject, and they demonstrate impressive target-localization accuracy using only affine transformations. The work of these authors has been validated using intraoperative recordings and post-operative electrode location.

Work from our group argues that non-linear transformations alone may be suboptimal for pre-operative atlas-based target identification (Chakravarty et al., 2009). Pre-operative planning is limited by the accuracy of the warping techniques used. Validation of non-linear registration algorithms is a notoriously difficult problem given the lack of a universally accepted “gold-standard” (Chakravarty et al., 2009; Klein et al., 2009). Many groups simply use anatomical correspondence between intraoperative recordings and post-operative electrode locations to validate their findings. However, we propose it is important to borrow heavily from the medical image processing community where several methods have been proposed for the validation of non-linear registration algorithms (Hellier et al., 2003; Robbins et al., 2004; Chakravarty et al., 2009; Klein et al., 2009).

We have applied our atlases to a wide variety of applications, including use in a stereotactic planning platform (St-Jean et al., 1998), probabilistic analysis of thalamic lesions used for alleviation of tremor (Atkinson et al., 2002), analysis of the stereotactic location of the human sensory thalamus using information obtained during intraoperative stimulation (Figures 3E,F) or following activation visualized by functional brain imaging (Chakravarty et al., 2008), probabilistic analysis of the topography and location of motor fibers of the posterior limb of the internal capsule obtained using intraoperative stimulation (Duerden et al., 2011), and probabilistic analysis of the location of effective and less effective subthalamic nucleus stimulation electrodes (Chakravarty et al., 2006b; Sadikot et al., 2006). Ongoing work includes further application of the atlas to functional neurosurgery, analysis of positions of subcortical lesions or electrodes, interpretation of subcortical functional activation data, and use with in vivo tractography. Future work by our group and many others, will involve creation of additional computerized atlases based on diverse chemical anatomy data, and atlas integration with functional data obtained using functional brain imaging, physiological responses obtained during neurosurgery, or with anatomical tractography information.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.