The Network Autocorrelation Model using Two-mode Data: Affiliation Exposure and Potential Bias in the Autocorrelation Parameter

Social Network Analysis (SNA) has been widely used to measure the degree of social influences on behavior change based on social theory. SNA has been used to model various forms of network influence on individual behavior using the so-called network autocorrelation model (Doreian, 1980a, 1981, 1990; Dow, 2007; Dow, Burton, White, & Reitz, 1984; Leenders, 2002; Mizruchi & Neuman, 2008; Ord, 1975; Paez, Darren, & Volz, 2008; Smith, 2004). It has been a workhorse for modeling theories of social influence by measuring and statistically testing network effects on individual behaviors. Similarly, in diffusion of innovation studies, the network exposure model (Burt, 1987; Marsden & Friedkin, 1993; Valente, 1995, 2005) has been widely employed to measure the extent to which individuals are exposed to an innovation in the network, which is then presumed to influence the timing of his or her adoption of innovation. The network exposure model can be used to model behavioral outcomes as being influenced simultaneously by local- and network-level effects and provides a mapping of social theories with statistical estimation (Leenders, 2002) by specifying the appropriate weight matrix (W) for different network influence processes (Valente, 1995).

The standard network approaches for mapping social influence have been limited in their operationalization by specifying a weight matrix W based on a single mode (actor-by-actor) network. W is a N × N weight matrix with elements w_ij representing the extent to which actor j (alter) influences actor i (ego). For example, research using network exposure to substance use has shown a correlation between individual use and exposure to friends’ use of substances (Alexander, Piazza, Mekos, & Valente, 2001; Cleveland & Wiebe, 2003; Cleveland, Wiebe, & Rowe, 2005; Crosnoe, 2002, 2006; Crosnoe, Muller, & Frank, 2004; Hall & Valente, 2007; Haynie, 2001). Peer influence based on friendship relations, however, is only one of the many ways peers come into contact with one another and potentially influence each other’s behavior.

In this paper, we extend the existing one-mode network exposure model by developing a new influence model of “affiliation exposure” that statistically tests the affiliation effect within a network autocorrelation framework. We believe this new model will allow analysis of social influences previously not available with network exposure type models, and thus opening entirely new information vistas for exploration and examination. In the proposed “affiliation exposure model,” the weight matrix W is the converted affiliation matrix using the off-diagonal values of the co-membership matrix. The diagonal of the converted matrix (i.e., the number of events participated in by each actor) is used as a covariate in subsequent regression analysis. It is known that the one-mode network autocorrelation model contains potential biases in the estimation of the structural parameter (Dow, Burton, & White, 1982; Mizruchi & Neuman, 2008; Neuman & Mizruchi, 2010; Paez, et al., 2008; Smith, 2004, 2009) under certain conditions. In particular, a recent simulation study has shown negative bias in the estimate of the autocorrelation parameter ρ (i.e., estimated ρ tends to be lower than the population ρ) and this tendency becomes more pronounced with higher density in random graphs (Mizruchi & Neuman, 2008). This bias is reported to hold across other types of well-known networks including the star, caveman, and small-world structures (Neuman & Mizruchi, 2010).

Given these results, we decided it was prudent to see if a similar bias was present in the affiliation exposure model, and so we have conducted a simulation study to examine the statistical bias in the Maximum Likelihood (ML) estimates of autocorrelation parameter ρ. To maximize our ability to compare our results with prior reports, we have chosen to match many of the independent parameters of the simulation performed earlier by Mizruchi & Neumann (2008). Given the bias observed in the one-mode autocorrelation model, we will explore potential bias in the two-mode version of the network effects model¹, i.e., a bias in the autocorrelation parameter ρ for the affiliation exposure. As in the one-mode case, we will investigate the network density levels at which bias in the autocorrelation parameter potentially become pronounced.

In this study, two-mode actor-by-events bipartite graphs were randomly generated based on a Poisson-distributed outdegree (i.e., conditioning on the expected number of events, λ, for each actor which is the mean number of events each actor participated in). Using a range of different densities of simulated bipartite graphs, along with varying levels of network autocorrelation ρ and event total local effect γ, we explore the extent to which the density of the affiliation network affects the degree of bias in the parameter estimates derived from the model. We will show that the autocorrelation parameter tends to be biased with increased density, and this negative bias becomes increasingly pronounced as γ (the main effect of event participation) approaches zero. We will conclude by discussing the implications of our findings for estimating affiliation exposure models, and how including the diagonal (outdegree) values seem to help stabilize the estimates (in the presence of noise) of the model and help mitigate the systemic negative bias.

This study conceptualizes social influence based on co-membership in organizations, events, or activities, and proposes a new way of operationalizing affiliation-based network influence derived from two-mode network data within a network autocorrelation modeling framework. It assumes that co-membership is a structural feature that defines individual social identities and increases the probability of forming acquaintances (McPherson 1982). Affiliation-based social influence is conceptually different from friends’ influence in that it assumes that social influence is not limited to positive-affective ties. Borgatti and Everett (1997), in their discussion of classic women-by-event affiliation data (A. Davis, Gardner, & Gardner, 1941), pointed out that the strength of social proximity of a pair of women who attended the same events reflects not only a positive-affective tie but also a non-liking/negative-affective tie (i.e., having a competitive relationship), thus still being closely familiar with and influenced by each other (p.246).

1. Two-mode network data

In SNA, structural variables are measured based on a distinct set of entities, which are referred to as “mode” (Wasserman & Faust, 1994). In the one-mode network, structural variables are measured on a single set of nodes (N) within a given network boundary, and network data are represented as a sociomatrix X, composed of N rows (nominating nodes) and N columns (receiving nodes), with elements of X=x_ij equal to 1 if a node i (row) nominated a node j (column) as a given relation, and 0 otherwise.

In the two-mode network data, structural variables are measured on two sets of nodes. Usually, the first mode is a set of actors within a given network boundary, and the second mode is a set of events with which the actors in the first set are affiliated. Such two-mode networks are referred to as affiliation networks with each actor (indexed in row) with each event (indexed in column) in the N×K matrix form A_ij, with the entry of A=a_ij equal to 1 if row actor n_i is affiliated with column event j, and 0 otherwise. Two-mode network or affiliation networks are also referred to as bipartite graphs, membership networks (Breiger, 1974), or hypernetworks (McPherson, 1982).

2. Analysis of affiliation networks

There are primarily two current approaches to analyzing affiliation networks. The first approach is to analyze the two-mode network data directly without transformation. Many studies have developed such techniques to analyze “raw” two-mode networks including Q-Analysis (Doreian, 1980b; Freeman, 1980), Galois lattices (Freeman & White, 1993; Roth & Bourgine, 2005; Wasserman & Faust, 1994), correspondence analysis (Faust, 2005; Roberts Jr., 2000), blockmodeling (Doreian, Batagelj, & Ferligoj, 2004), centrality measures (Bonacich, 1991; Borgatti & Everett, 1997; Faust, 1997), overlapping membership (Bonacich, 1978), structural similarity (Borgatti & Everett, 1992), clustering (Borgatti & Everett, 1997; Robins & Alexander, 2004), degree distributions (Newman, Strogatz, & Watts, 2001; Newman, Watts, & Strogatz, 2002; Robins & Alexander, 2004), exponential random graph models (Agneessens, Roose, & Waege, 2004; Faust, Willert, Rowlee, & Skovretz, 2002; Skovretz & Faust, 1999; Wang, Sharpe, Robins, & Pattison, 2009), and identification of positions in affiliation network (Field, Frank, Riegle-Crumba, & Mullera, 2006).

The second approach for studying two-mode networks is to convert the data into two (or more) one-mode networks, either as an actor-by-actor network or an event-by-event one. The process of converting a two-mode network into its one-mode versions is frequently described as the projection of the bipartite graph onto the unipartite space of actors or events only. In a projected actor-by-actor matrix, each pair of actors is connected if they share at least one common event. In particular, these one-mode “projection” networks are frequently constructed by either multiplying the affiliation (N×K) matrix A with its transpose (i.e., AA′) or multiplying the transpose of the affiliation matrix with itself (i.e., A′A). The resulting converted matrices are symmetric, valued, 1-mode matrices that record the co-membership relation for each actor (N×N matrix C=AA′) or the overlapping relations for each event (K×K matrix T=A′A). Essentially, in the individual, actor-by-actor case the co-membership (C) off-diagonal entries count the number of events jointly affiliated with for each pair of actors, and the diagonal entries count the total number of events each actor is affiliated with. In the event-by-event case the off-diagonal entries count the total number of actors jointly affiliated by each pair of events, and diagonal entries count the total number of actors affiliated with each event. To date, the projected one-mode networks are usually dichotomized², and then analyzed using conventional network analytic techniques.

Using either of the two approaches described above, various types of collaboration networks have been studied that include: the networks of movie actors where two actors are linked if they co-appear in the same movie (Watts & Strogatz, 1998), the networks of scientists where two scientists are linked if they co-author a paper (Newman, 2001a, 2001b, 2001c), the network of words where two words are linked if they co-occur in the same sentence (Ferrer & Sole, 2001), the interlocking networks of board of directors where two directors are linked together if they are members of the same board (Conyon & Muldoom, 2004; G. F. Davis & Mizruchi, 1999; Mizruchi, 1996; Robins & Alexander, 2004). Additionally, some other network studies have conducted combined analysis of bipartite graphs with projections of them (Guillaume, Le Blond, & Latapy, 2004; Latapy, Magnien, & Vecchio, 2008; Newman, et al., 2001; Robins & Alexander, 2004) to examine how network features differ among two methods.

It is generally accepted, however, that directly analyzing bipartite graphs provides a richer understanding of two-mode structures than analysis using the projected 1-mode data only, since much information in the original bipartite structure (such as information about path lengths of three or more and information about nodes with a single affiliation) is lost during the projection process (Latapy, et al., 2008; Robins & Alexander, 2004; Wang, et al., 2009). None the less, using the projected 1-mode matrix is appropriate when theoretical attention is being focused on one type of the two social entities (Robins & Alexander, 2004) and primary interest lies in how the actors/events are connected via the events/actors (Borgatti & Everett, 1997).

The analysis presented here is based on a projected, non-binarized one-mode analysis that focuses on the actor-to-actor network (AA′, rather than the event-to-event network A′A) since our theoretical attention is on the actors rather than the events, and thus our primary interest lies in the co-membership among actors via the events. This co-membership is the backbone of modeling the affiliation-based social influence within a network autocorrelation framework where the unit of analysis is the individual actor, but before introducing the affiliation exposure model, the following section will review the general formula of a network exposure model for one-mode data.

3. Network Exposure Model

The general formula of the network exposure E (for N actors) has been introduced and developed (Valente, 1995, 2005), which is defined as:

$$\underset{\_}{E}=\frac{{\displaystyle \sum _{j=1}}{W}_{ij}{Y}_j}{{\displaystyle \sum _{j=1}}{W}_{ij}}\mathit{for}i,j=1,\cdots ,Ni\ne j$$ (1)

Where E is the N-by-1 exposure vector, W_ij is a social network weight matrix, and Y_j is a vector of j’s behavioral attribute (j = 1, …, N; j ≠ i). By specifying different weight matrices W, the general exposure model measures different types of social influence. There have been two contrasting one-mode network approaches to studying social influence and measuring interpersonal proximity, (1) “structural cohesion” which measure direct and indirect connectivity among actors and (2) “structural equivalence” which measures network positions in terms of the similarity of actors’ profiles of relations (Burt, 1987; Marsden & Friedkin, 1993; Valente, 1995).

Social influence based on cohesion is founded on solidarity relations such as friendship or advice relations (Marsden & Friedkin, 1993) and presumes that individuals are influenced by other actors in the network with whom an individual has direct ties. This type of social influence is termed “relational exposure” (Valente, 1995), which is computed by using a one-mode adjacency matrix, X_ij, as a specification of weight matrix W_ij, with X_ij = 1 if an actor i nominates an actor j in a given positive relationship, and X_ij = 0 otherwise. By multiplying X_ij by nominated actors’ behavior y_j and normalizing by the row-sum of X_ij (i.e., actor i’s outdegree, X_i+), the resulting normalized relational exposure of E_i measures the mean level of nominated actors js who have behavioral attribute of y_j in an ego network.

On the other hand, social influence based on structural equivalence emphasizes competition between ego and alter. The more similar two people are in the network, the more substitutable they are and this may lead to increased feelings of competition. It has been shown that individuals are more likely to adopt innovations as their structurally equivalent alters adopt (Burt 1987). People who occupy similar structural positions (in terms of patterns of relations with all other actors in the network) will influence each other, and this type of social influence is termed as “positional exposure” (Valente, 1995). “Positional exposure” is calculated by using the one-mode adjacency matrix of X_ij, to compute structural equivalence matrix of S_ij that is based on any of the profile similarity relations between all pairs of actors³. Although social influence based on structural equivalence extends the frame of reference from ego’s neighbors to the network as a whole, it is still limited to conceptualizing social influence based on one-mode social network data. It should be noted that various coding schemes can be considered in defining the weight matrix W (Tiefelsdorf, Griffith, & Boots, 1999). For the simplicity of interpretation, the most frequently used row-sum standardization, or W-coding scheme, was used in this study.

4. Development of the Affiliation Exposure Model

We now introduce a new way of conceptualizing social influence based on co-membership with events, and we call this type of social influence “affiliation exposure.” In the specification of W_ij in the network exposure model, “affiliation exposure” uses the converted one-mode matrix C (= AA′) that records the co-membership relations (i.e., the number of events each pair of actors attended in common) in a network, thus representing the affiliation-based social influence. The diagonal is the count of the number of events each actor is affiliated with and this is extracted for inclusion in the subsequent statistical network autocorrelation analysis as an independent variables (discussed later). The diagonal is set to zero in the calculation of exposure. By multiplying C_ij by each co-participant’s attribute y_j and normalizing it by row-sum C_i+ (ignoring the diagonal), the resulting affiliation exposure vector of F is defined as follow:

$$\underset{\_}{F}=\frac{{\displaystyle \sum _{j=1}}{C}_{ij}{Y}_j}{{\displaystyle \sum _{j=1}}{C}_{ij}}\mathit{for}i,j=1,\cdots ,Ni\ne j$$ (2)

Affiliation exposure, F, measures the degree each actor is exposed to attribute Y based on the extent of co-participation among the actors. More specifically, the affiliation exposure measures the mean level of attribute of Y_j that is weighted by the proportion of all events each pair of actors co-participated in. For example, if an actor participated in three events with one alter, and a single event with another alter, then the first alter’s influence (“exposure”) is three times greater than the second alter’s influence. In the next section, we situate the affiliation exposure term within network autocorrelation framework, and examine potential bias of network autocorrelation parameters and local event parameter estimates for various levels of density in converted matrix C.

5. Network autocorrelation model

In the standard linear OLS regression model, y = Xβ + ε, random variable of error term is based on the assumption of being independently and identically distributed (i.i.d.) with mean zero and equal variances, σ²I. However, in the analysis of network data, the independence assumption for the error terms is violated due to correlation among error terms. The network autocorrelation model (Doreian, 1980a, 1981, 1990; Dow, 1984; Ord, 1975) was developed to deal with the issue of the network autocorrelation in the regression analysis. There have been two families of network autocorrelation models, which are (1) network effects model and (2) network disturbances model. This study uses the network effects model (Doreian, Teuter, & Wang, 1984) which is more straightforward to model social influence than network disturbances model (Doreian, 1980a; Dow, et al., 1984; Ord, 1975)⁴ The network exposure model assumes that social influence occurs when individuals are exposed to a behavior by their network contacts. The exposure is estimated via the network effect model. Network effects model is based on the assumption that social influence occurs through the dependency among responses to the dependent variable (Leenders, 2002). It treats the network autocorrelation as a parameter and models the autoregressive effects on outcome variable:

$$\text{y}=\rho \text{Wy}+\text{X}\beta +\epsilon ,\epsilon \sim N(0,{\sigma }^2\text{I})$$ (3)

where y is a (N × 1) vector for values of a dependent variable, X is an (N × h) matrix of values for the N actors on h independent variables with unit row vector for the intercept term, β is a (h × 1) vector of regression coefficients, ρ is a scalar estimate of autocorrelation parameter, and W is a (N × N) weight matrix with its element w_ij representing the degree to which y_i depends on y_j. The W matrix can be row or column normalized to unity⁵, which determines how social influence is allocated among alters in the network, thus altering the strength of influence for a particular influencer (Leenders, 2002). It is important to note that in relation to the network exposure model, Wy term with row-normalized W matrix corresponds to the values of exposure term (E) defined in the equation (1).

The network effect model for affiliation exposure is defined as:

$$\text{y}=\rho \text{Wy}+\text{X}\beta +\gamma \text{D}+\epsilon ,\epsilon \sim N(0,{\sigma }^2\text{I})$$ (4)

where y, X, β, ρ, and ε are defined as in equation (3), Wy is equivalent to F in equation (2) with W being a (N × N) row-normalized co-membership matrix C, D represents the number of events participated in for each actor (the diagonal entries of C matrix (i.e., C_ij; i = j)) ranging from 0 to event size K, and γ is a corresponding regression parameter. One other difference between the network effects model based on the one-mode binary matrix and the two-mode version is the addition of γD term in the model. The D term is a measure of levels of participation in events or activities, and γ reflects its effect on the behavior of interest (y). For example, in a study assessing the effects of joint participation in team sports on alcohol use, the γ term assesses the association between the number of teams each person belongs to and alcohol use. The proposed approach includes the prediction (y) in the regression model and thus making it a self or autocorrelation design that focuses on reducing the errors in its predictions (which may not be covered by a finite manifold). Consequently, it does not require the clustering and uniform statistical space assumptions which were made in the Getis-Ord statistics (Getis & Ord, 1992). In the next section, we will explore potential bias in the autocorrelation parameter ρ by simultaneously controlling for the effects of X and D (the events total).

As for the estimation procedures in network autocorrelation model⁶, Maximum Likelihood Estimation (Anselin, 1988; Doreian, 1981; Ord, 1975) has been widely used and believed to be the preferred method for estimating the parameters of the network autocorrelation model for over two decades (Leenders, 2002). The likelihood function to be estimated is defined as follows (Doreian, 1981; Doreian, et al., 1984):

$$\begin{array}{l}\ell (y)=\mathit{const}-(N/2)ln\omega +ln\mid A\mid +(1/2\omega )(y^{\prime }{A}^{\prime }Ay-2{\beta }^{\prime }{X}^{\prime }Ay+{\beta }^{\prime }{X}^{\prime }X\beta )\\ \mathit{where}A=\text{I}-\rho W,\omega ={\sigma }^2\end{array}$$ (5)

The above equation is minimized with respect to ω, ρ, and β (see Doreian, 1981 for more detailed formula). Previous simulation studies, however, have shown that the network autocorrelation model contains potential biases in its estimation of the structural parameter (Dow, et al., 1982; Mizruchi & Neuman, 2008; Neuman & Mizruchi, 2010; Paez, et al., 2008; Smith, 2004). Specifically, a recent simulation study has shown a negative bias in the estimate of network effects autocorrelation parameter ρ (i.e., estimated ρ tends to be lower than the population ρ), and report that this tendency becomes more pronounced with higher density in random graphs (Mizruchi & Neuman, 2008) and holds across other types of well-known networks including star, caveman, and small-world structures (Neuman & Mizruchi, 2010).

This present simulation study explores the potential bias in the two-mode version of network effects model, that is, the degree of bias in the autocorrelation parameter ρ for the affiliation exposure term (F).

6. Simulation procedure

We conducted a series of simulations to examine the extent to which the Maximum Likelihood estimate of autocorrelation parameter ρ might be biased in the network effects model for given levels of density in the co-membership matrix C. In general, we followed and extended the simulation procedures conducted by Mizruchi and Neuman (2008) where the bias in the autocorrelation parameter was examined for one-mode, randomly-generated graphs (with a specified set of densities and population ρ values). The reason for this is to facilitate the comparison of the reported one-mode results with the two-mode results.

When analyzing a two-mode network, there are two ways to base a density computation. The first is based on the original actor by event (N × K) affiliation network A (Borgatti & Everett, 1997)⁷, and the second is based on the projected (N × N) co-membership matrix C (Wasserman & Faust, 1994). This study used the latter basis since the density of C, the co-membership matrix, is the main component of the W matrix in the affiliation exposure model and as such the density measures the degree of interaction among actors through shared events. In the simulation, a range of different network “densities” are specified using binarized co-membership matrix C to test the association of bias with network density, and to be comparable with the one-mode case by Mizruchi and Newman (2008) analysis. W uses the following expression of “density” that assumes any non-zero value to indicate the presence of a tie between two actors:

$${\mathrm{\Delta }}_{(c)}=\frac{1}{N}\sum _{i=1}^N\left\{\frac{1}{N-1}\sum _{j=1}^N\left(C_{ij}>0\right)\right\}=\frac{{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^N}\left(C_{ij}>0\right)}{N(N-1)}\mathit{for}i,j=1,\cdots ,Ni\ne j$$ (6)

In other words, we are using the average normalized out-degree score, and this is mathematically equivalent to other common one-mode (binary) density calculation formulations. The density of C (Δ _(c)), however, is, in part, a function of the expected number of events each actor participated in (i.e., Poisson parameter λ) but they are not linearly related, which prevented us from obtaining a closed-form solution. Therefore, we have instead employed a linear-interpolation approach to obtaining an estimate of the needed lambda (λ) values for the desired densities in C (Δ _(c)) within ±1%. We will discuss this procedure in more detail in the next section.

Generating random bipartite graph

Our simulation uses a Poisson outdegree distribution⁸ with parameter λ to generate random bipartite graphs A, where a random variable of A_i+ (sum of row i of matrix A) represents the number of events participated in for an actor i (i=1, …, N), and the expected number of events each actor participated becomes E(A_i+) = λ. We have chosen the Poisson outdegree distribution since we assume a homogeneity in the distribution (i.e., no actors are very different from the average number of events participated in), indicating the normal and expected behavior when taking an actor at random⁹ (Latapy, et al., 2008). Additionally, these values are based on several empirical affiliation studies which reported the average number of organized sports activities participated in (K=13) by middle-school students (N >= 100), which approximated a Poisson distribution.

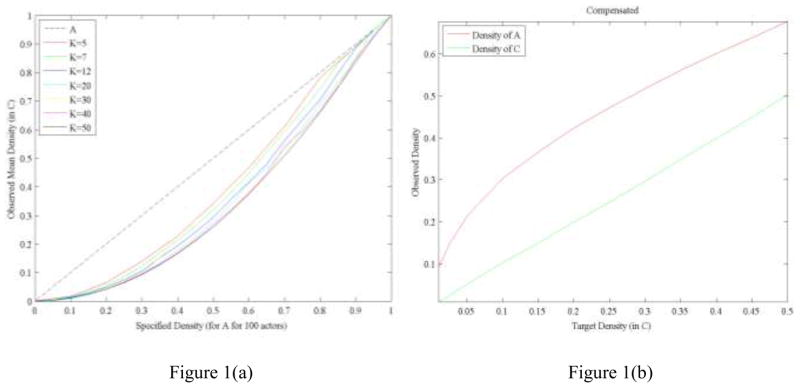
There are two steps to generate the random bipartite graphs used in this study¹⁰. First, we generated binary actor-by-event bipartite graphs drawn uniformly at random constrained on Poisson outdegree distribution with densities (in A matrix) ranging from 0.05 to 0.95 in increments of 0.05. For each targeted density value, we generated 100 random bipartite graphs. Then, we converted these observed random bipartite graphs into one-mode co-membership matrices and computed corresponding densities (by using Δ_(c)). Figure 1 shows the non-linear relationship between the theoretical density values (as determined by λ divided by event size) and the actual observed densities in C for a variety of K values (event size) and 100 actors.

Figure 1.

Plots of observed densities in the generated networks. (a) The dotted line is the mean density of the A matrix, and the solid lines are the densities of the corresponding C matrices. This demonstrates that the density of A as determined by λ (the mean number of events participated in) is non-linearly related to the density of C, the corresponding co-membership matrix. (b) Results of the density compensation procedure, where the lower straight line is the desired density in C and the upper curve is the density of A that is required. Because of the non-linear relationship of λ to the density in C (see text), a linear-interpolation of the λ parameter was used based on the resulting density in C.

Since the simulation will treat the density of the C matrix as one of the independent parameters, we compensated for the non-linear relationship shown in Figure 1(a) by interpolating a “corrected” density parameter for the A matrix such that the corresponding C matrix density (Δ _(c)) would match the target value. The result of this process is shown in the Figure 1(b) example in which K=20 and 100 actors. The targeted (x-axis) and observed densities (y-axis) now match within ±1% (solid green line). For illustrative purposes, the dotted red line shows the density of A required to reliably generate the targeted density in the C matrix. In other words, simply incrementing by fixed amounts of the average number of events in the simulated affiliation networks does not provide correspondingly incremental densities in the resulting C matrix. As an example, to obtain a target density of Δ_(c)=0.15, a density of 0.37 (see Figure 1b) in the affiliation matrix must be generated, which required a corresponding λ value of 6.08 on a matrix with 100 actors and 20 events¹¹. In the second step, we generated 100 random bipartite graphs at each target density level (Δ _(c)) using the corresponding estimated λ values, and these were the graphs used in the subsequent analysis (parameter specification will be discussed later).

Simulation procedures

Our simulation procedure¹² was implemented as follows:

• Step (1)

  Number of actors is 100, and the maximum number of events is K=10 (thus forming a 100-actor by 10-events affiliation matrix A).

• Step (2)

  Targeted density, Δ_(c), in the (100 × 100) co-membership matrix C (Δ _(c)) was initiated at 0.05 and incremented by 0.05 to 0.90 with corresponding estimated λ values to be {1.80, 2.56, 3.16, 3.65, 4.10, 4.54, 4.93, 5.29, 5.66, 6.03, 6.35, 6.69, 7.07, 7.48, 7.81, 8.18, 8.61, 9.06}.

• Step (3)

  We randomly generated three covariate variables X plus the unit vector for the intercept term and corresponding set of regression coefficients (three β values plus an α value) from a standard normal distribution (with a mean of 0 and standard deviation of 1). We have also specified a vector of error term ε drawn from a standard normal distribution with mean zero and standard deviation of σ=1.0. However, the previous study indicated that negative bias could be attributed to the specification of model noise in the simulation by showing that reduction in the variance of the residuals (i.e. and thus improving the fit of the models) by setting the standard deviation (σ) of the residuals from unity to 0.1 contributed significantly to remove most of the bias in the sampling distributions of ρ (Mizruchi & Neuman, 2008). Therefore, the present simulation specified σ=1 (since it is a more conservative approach) and also a σ=0.1. Additionally, the diagonal entries of C matrix (i.e., C_ij; i=j) were constructed to estimate event total effect, which was defined as the D term in the network effects model.

• Step (4)

  The population (true) value of the autocorrelation parameter (ρ) was set to {−0.8, −0.5, −0.2, −0.1, 0.0, 0.1, 0.2, 0.5, 0.8}¹³ and the population event total parameter (γ) was set to {0.0, 0.25, 0.5, 0.75, 1.0}. We used combinations of ρ, γ, Δ _(c) for the parameter space to be simulated. For each combination we performed a trial by running 100 replications of our model, which yield 9(ρ) × 5(γ) × 18 (Δ_(c)) × 100 (replications), yielding a total of 81,000 individual model runs.

• Step (5)

  We computed the “observed” values of Y in our network effects model by transforming the equation y = ρWy + Xβ + γD + ε to y = (I – ρW)⁻¹(Xβ + γD + ε), and then inserting the simulated W, the three X variables and intercept unit vector as well as their corresponding coefficients (α and three βs), the residuals (ε), and a set of assigned population autocorrelation parameters (ρ), and the population event parameter γ.

• Step (6)

  We returned to the original autocorrelation model (y = ρWy + Xβ + γD + ε) and used this y along with W, X, and D to estimate the model parameters of ρ (and γ). If these estimated parameters are unbiased, then the value of ρ (and γ) computed from these trials should have a sampling distribution with a mean approximately equal to the originally specified population value (Mizruchi & Neuman, 2008).

For step (1) we employed the MATA programming language in STATA to generate the random bipartite graphs conditioned on Poisson outdegree distributions and then exported these matrices to the R environment to perform the remaining steps, using the “lnam” function in the “sna” package program (Butts, 2008) for steps (4) and (5) in a manner similar to (Mizruchi & Neuman, 2008).

7. Results

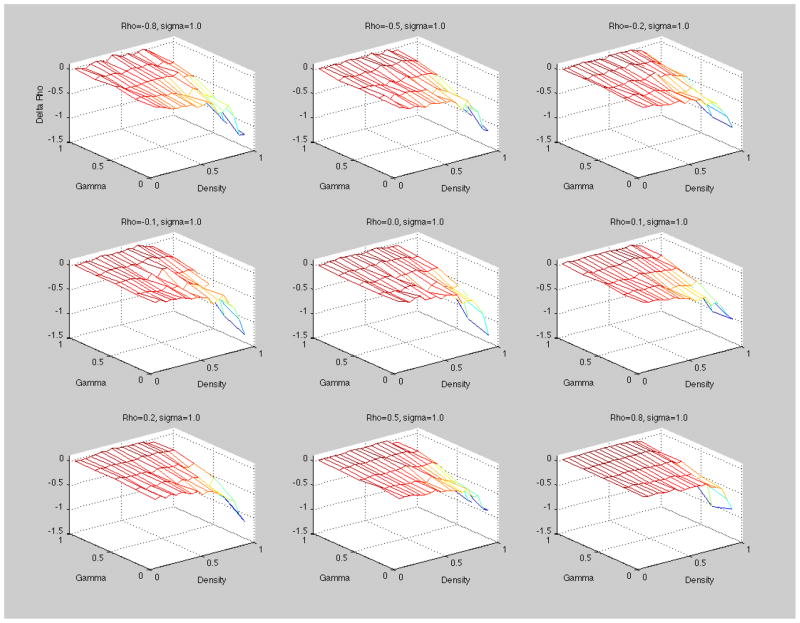
For the first set of results, we report three-dimensional (3D) graphs of the simulation results to observe some overall trends. Figure 2 shows graphs of the mean difference between estimated ρ and the population ρ (= Δρ) as a 3D-surface against the varying density level and population gamma γ values for each population value of ρ (ρ= −0.8, −0.5, −0.2 going from left to right in the upper row, ρ= −0.1, 0.0, 0.1 going from left to right in the middle row and ρ=0.2, 0.5, 0.8 going from left to right in the lower row).

Figure 2.

Three-dimensional graphs of the mean difference between the estimated ρ and the population ρ (Delta Rho (Δρ) = estimated ρ-population ρ) against density and population Gamma (γ) for each population value of ρ (with an overall disturbance specification of σ=1.0)

All of these graphs display a general tendency that the surfaces tilt toward the corner of higher density values and lower values in the population of γ. These results imply that there is a negative bias tendency to the autocorrelation parameter as density increases and as γ population values decrease (approaches zero) for all levels of ρ. The first observation (the density effect) is consistent with a similar observation for the one-mode case as reported by Mizruchi and Neuman (2008). The second observation (i.e., less negative bias for higher values of γ) makes sense since D (which is not as random¹⁴ as the other terms given its relation to W) has a stable underlying structure that helps reduce the final variance in the estimates and thus stabilize the system as a whole. The stabilizing effect of D increases as γ approaches one, and leads to a better fit of the model and reduction in the final variance of the residuals. To explore these results in more detail, we have drawn two-dimensional graphs with both specifications of the standard deviation of error term i.e., σ=1.0 and σ=0.1.

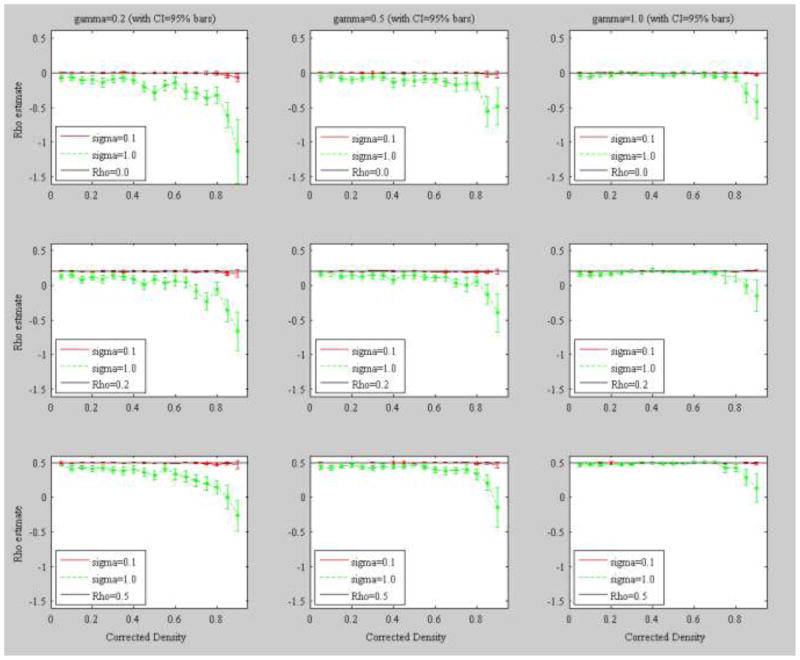
Figure 3 shows the mean plots of the estimated autocorrelation parameter ρ among 100 replications against each level of density in C (Δ_(c)) at each level of population γ. Here we only present the results of three population ρ={0.0, 0.2, 0.5} (moving horizontally from top to bottom in the rows of graphs) and three γ={0.2, 0.5, 1.0} (moving vertically from left to right in the columns of graphs) due to space limitations. Green and red lines represent the sample mean of the estimated ρ with specification of error standard deviation of σ=1.0 and σ=0.1 respectively, and bars represent upper and lower bounds of the 95% confidence interval around the mean. Asterisks indicate that the upper bounds of the 95% confidence interval fall below the given population value of ρ, indicating that the sampling distribution of ρ exhibits a negative bias (Mizruchi & Neuman, 2008). The black line represents a population target value of ρ, but is frequently intertwined with the σ=0.1 (red) curve, which indicates the mean sample estimates for ρ appear to be very close to the values of the specified population parameter at almost all levels of density across each level of population ρ and population γ. When σ=1.0 (green lines) in Figure 3, the results show that negative bias is dependent on the value of γ such that negative bias occurs primarily when the effect of event participation, γ, is small (graphs on the left rather than those on the right). This effect is almost invariant across the levels of ρ.

Figure 3.

Mean plots of the estimated autocorrelation parameter ρ among 100 replications against each level of density in C (Δ_(c)) at each level of population γ. Bars represent upper and lower bounds of the 95% confidence interval around the mean. Asterisks indicate that the upper bound of the 95% confidence interval falls below the given population value of ρ. Event size was specified as 10 (K=10). Δ_(c)={0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90} where the corresponding estimated λ values are {1.80, 2.56, 3.16, 3.65, 4.10, 4.54, 4.93, 5.29, 5.66, 6.03, 6.35, 6.69, 7.07, 7.48, 7.81, 8.18, 8.61, 9.06}.

Table 1 presents fit statistics, means and 95 percent confidence intervals, for the ρ estimates by levels of density and γ. The data show that as γ increases the ρ estimates stabilize across various density levels thus reducing the estimate bias.

Table 1.

For the Disturbance Specification of σ=1.0 and K=10, the Statistics of the Sample Means of the Estimated ρ and Corresponding 95 % Confidence Intervals around the Means for 100 Repetitions are reported.

	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=0.2	0.050	−0.079	−0.125	−0.034	0.050	0.123	0.085	0.161	0.050	0.478	0.454	0.502
	0.100	−0.071	−0.114	−0.027	0.100	0.142	0.100	0.185	0.100	0.417	0.382	0.453
	0.150	−0.113	−0.169	−0.058	0.150	0.072	0.025	0.120	0.150	0.427	0.402	0.451
	0.200	−0.100	−0.159	−0.040	0.200	0.118	0.070	0.167	0.200	0.414	0.373	0.456
	0.250	−0.142	−0.206	−0.077	0.250	0.082	0.024	0.140	0.250	0.421	0.377	0.466
	0.300	−0.091	−0.147	−0.035	0.300	0.132	0.094	0.171	0.300	0.392	0.343	0.441
	0.350	−0.080	−0.129	−0.031	0.350	0.120	0.072	0.168	0.350	0.385	0.328	0.441
	0.400	−0.105	−0.167	−0.043	0.400	0.081	0.022	0.141	0.400	0.402	0.350	0.454
	0.450	−0.209	−0.285	−0.134	0.450	0.009	−0.067	0.084	0.450	0.362	0.306	0.419
	0.500	−0.295	−0.392	−0.197	0.500	0.077	0.019	0.135	0.500	0.315	0.250	0.380
	0.550	−0.185	−0.260	−0.109	0.550	0.024	−0.055	0.103	0.550	0.414	0.365	0.464
	0.600	−0.145	−0.231	−0.059	0.600	0.066	−0.020	0.152	0.600	0.333	0.253	0.413
	0.650	−0.272	−0.380	−0.165	0.650	0.041	−0.038	0.119	0.650	0.296	0.214	0.378
	0.700	−0.292	−0.376	−0.208	0.700	−0.092	−0.193	0.009	0.700	0.241	0.154	0.328
	0.750	−0.363	−0.462	−0.264	0.750	−0.236	−0.360	−0.112	0.750	0.197	0.096	0.298
	0.800	−0.328	−0.445	−0.210	0.800	−0.053	−0.147	0.041	0.800	0.140	0.043	0.237
	0.850	−0.608	−0.791	−0.424	0.850	−0.367	−0.524	−0.210	0.850	0.007	−0.169	0.182
	0.900	−1.073	−1.39	−0.755	0.900	−0.524	−0.717	−0.332	0.900	−0.281	−0.465	−0.097
	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=0.5	0.050	−0.083	−0.122	−0.045	0.050	0.156	0.122	0.189	0.050	0.436	0.406	0.465
	0.100	−0.038	−0.077	0.001	0.100	0.166	0.129	0.202	0.100	0.427	0.396	0.459
	0.150	−0.087	−0.127	−0.048	0.150	0.129	0.091	0.167	0.150	0.446	0.420	0.471
	0.200	−0.104	−0.154	−0.055	0.200	0.133	0.097	0.169	0.200	0.461	0.434	0.488
	0.250	−0.081	−0.119	−0.043	0.250	0.126	0.079	0.173	0.250	0.435	0.406	0.465
	0.300	−0.057	−0.096	−0.018	0.300	0.135	0.090	0.180	0.300	0.423	0.393	0.453
	0.350	−0.065	−0.115	−0.016	0.350	0.132	0.085	0.180	0.350	0.440	0.397	0.483
	0.400	−0.147	−0.216	−0.078	0.400	0.075	0.012	0.138	0.400	0.438	0.407	0.469
	0.450	−0.101	−0.182	−0.020	0.450	0.140	0.094	0.186	0.450	0.448	0.411	0.485
	0.500	−0.120	−0.194	−0.047	0.500	0.134	0.092	0.176	0.500	0.477	0.453	0.501
	0.550	−0.091	−0.140	−0.042	0.550	0.113	0.066	0.160	0.550	0.432	0.400	0.465
	0.600	−0.086	−0.141	−0.032	0.600	0.100	0.061	0.138	0.600	0.402	0.356	0.448
	0.650	−0.133	−0.194	−0.073	0.650	0.117	0.057	0.176	0.650	0.381	0.325	0.437
	0.700	−0.176	−0.275	−0.078	0.700	0.034	−0.030	0.097	0.700	0.389	0.341	0.437
	0.750	−0.152	−0.253	−0.050	0.750	0.001	−0.098	0.101	0.750	0.406	0.342	0.470
	0.800	−0.151	−0.254	−0.049	0.800	0.055	−0.018	0.127	0.800	0.336	0.253	0.418
	0.850	−0.557	−0.772	−0.343	0.850	−0.128	−0.268	0.012	0.850	0.212	0.099	0.326
	0.900	−0.550	−0.747	−0.354	0.900	−0.447	−0.662	−0.231	0.900	−0.161	−0.377	0.055
	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=1.0	0.050	−0.050	−0.088	−0.013	0.050	0.158	0.127	0.189	0.050	0.470	0.449	0.490
	0.100	−0.052	−0.091	−0.014	0.100	0.143	0.112	0.174	0.100	0.476	0.454	0.499
	0.150	−0.023	−0.056	0.009	0.150	0.148	0.122	0.174	0.150	0.471	0.453	0.488
	0.200	−0.037	−0.066	−0.008	0.200	0.160	0.138	0.183	0.200	0.481	0.463	0.500
	0.250	0.000	−0.025	0.025	0.250	0.173	0.150	0.196	0.250	0.476	0.457	0.494
	0.300	−0.015	−0.038	0.009	0.300	0.200	0.176	0.224	0.300	0.477	0.461	0.493
	0.350	−0.021	−0.045	0.002	0.350	0.177	0.153	0.201	0.350	0.499	0.487	0.512
	0.400	−0.022	−0.047	0.003	0.400	0.217	0.192	0.242	0.400	0.497	0.482	0.513
	0.450	−0.047	−0.073	−0.020	0.450	0.187	0.169	0.206	0.450	0.484	0.470	0.498
	0.500	−0.033	−0.061	−0.006	0.500	0.188	0.166	0.209	0.500	0.486	0.472	0.499
	0.550	−0.008	−0.035	0.019	0.550	0.185	0.165	0.204	0.550	0.489	0.477	0.501
	0.600	−0.005	−0.027	0.018	0.600	0.176	0.157	0.195	0.600	0.502	0.488	0.515
	0.650	−0.038	−0.068	−0.008	0.650	0.186	0.164	0.208	0.650	0.503	0.488	0.517
	0.700	−0.055	−0.084	−0.027	0.700	0.170	0.146	0.194	0.700	0.499	0.483	0.516
	0.750	−0.057	−0.095	−0.020	0.750	0.123	0.030	0.217	0.750	0.420	0.358	0.482
	0.800	−0.062	−0.118	−0.005	0.800	0.126	0.050	0.203	0.800	0.419	0.366	0.473
	0.850	−0.289	−0.427	−0.150	0.850	−0.019	−0.120	0.082	0.850	0.286	0.174	0.399
	0.900	−0.437	−0.624	−0.25	0.900	−0.120	−0.267	0.027	0.900	0.115	−0.052	0.282

At the highest ends of the density, across all three levels of population ρ for each value of γ, the degree of negative bias is quite high. For example, densities 0.85 or higher indicate that the average number of co-participated events is greater than 8.61 (the corresponding estimated λ) out of maximum event size K=10. At this level the autocorrelation parameter underestimates affiliation influence significantly.

Regression Analysis

We have also conducted a regression analysis to statistically test the effect of the population γ value on bias in estimated ρ, using our simulation results of K=10 and σ=1.0. We computed the difference between estimated ρ and the population ρ (estimated ρ – population ρ = Δρ) to evaluate the level of bias, and regressed it on density, population γ and population ρ values. Here, we report only the magnitude of the effect size in order to evaluate the bias and do not report significance level since the “statistically significant” results are most likely an artifact of the large sample size (N=81,000). The results show that the standardized coefficient for density effect was −0.23, which indicates that the negative bias in ρ becomes greater as density increased. Findings were consistent with those reported in Neuman & Mizruchi (2010). The standardized coefficient for the γ effect was 0.17, which indicates that the positive bias in ρ becomes greater as the population level of γ increased. These results suggest that increase in negative bias in ρ with higher density level can be offset by the increase in positive bias in ρ with higher values in γ. The stronger the effect of the diagonal, the greater the likelihood that it can cancel out the negative bias in the autocorrelation parameter. Thus the event participation positive bias helps counteract the density negative bias. The effect size for the population effect ρ was 0.05, which indicates the positive bias in ρ becomes greater as the population ρ increases. However, this effect size is very close to zero and hence has a negligible influence. In supplementary analyses, we included an interaction term of density and population effect ρ to statistically test if the negative bias in ρ at higher levels of density increased at increasing levels of population ρ (Mizruchi & Neuman, 2008). The result showed that the standardized coefficient for the interaction effect was 0.02, which indicates virtually no effect. The results were also consistent with those in Neuman and Mizruchi (2010) that did not support the existence of the interaction effect.

Sensitivity Analysis

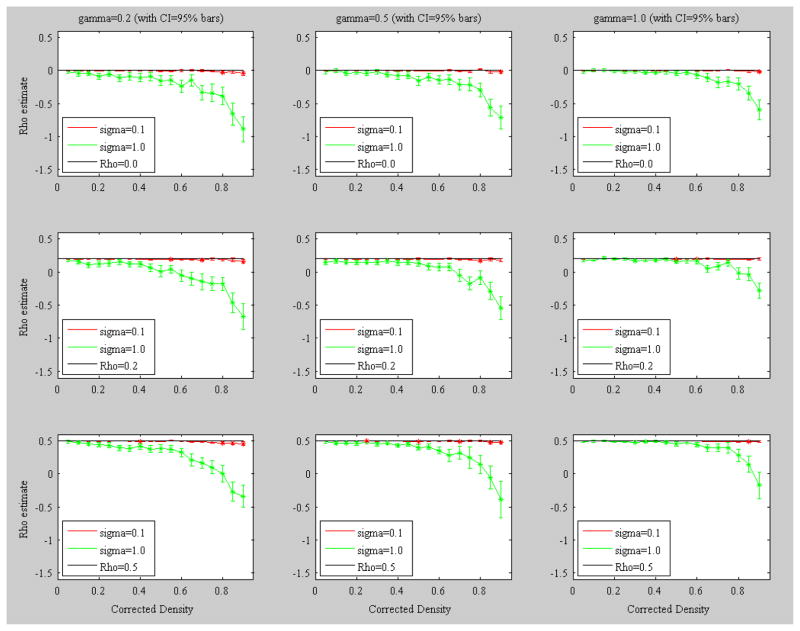
We repeated the simulation analysis for K=20 to compare with the results of the simulation with K=10. For this simulation the A (affiliation) matrix is a 100-actor by 20-events affiliation matrix, and 100 random bipartite graphs were generated for each of the 18 target density levels in C, Δ_(c)={0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90} using the corresponding estimated λ values {3.54, 4.98, 6.08, 7.07, 7.89, 8.66, 9.39, 10.05, 10.64, 11.22, 11.81, 12.43, 12.95, 13.54, 14.08, 14.66, 15.13, 15.71} (refer to Figure 1). We reproduced the baseline model, that is, a model with three X variables plus an intercept term, and specified the standard error of the residuals to be either σ=1.0 or σ=0.1. We selected the same population values for ρ={0.0, 0.2, 0.5} and γ={0.2, 0.5, 1.0} to facilitate comparison with the K=10 case. Figure 4 shows the equivalent graphs for the specification of K=20 case and Table 2 presents the corresponding statistics.

Figure 4.

Mean plots of the estimated autocorrelation parameter ρ among 100 replications against each level of density in C (Δ_(c)) at each level of population γ. Bars represent upper and lower bounds of the 95% confidence interval around the mean. Asterisks indicate that upper bound of the 95% confidence interval fall below the given population value of ρ. Event size was specified as 10 (K=20). Δ_(c)={0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90} where the corresponding estimated λ values are {3.54, 4.98, 6.08, 7.07, 7.89, 8.66, 9.39, 10.05, 10.64, 11.22, 11.81, 12.43, 12.95, 13.54, 14.08, 14.66, 15.13, 15.71}.

Table 2.

For the disturbance specification of σ=1.0 and K=20, the Statistics of the Sample Means of the Estimated ρ and Corresponding 95 % Confidence Intervals around the Means for 100 Repetitions are Reported.

	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=0.2	0.050	−0.020	−0.046	0.006	0.050	0.177	0.152	0.201	0.050	0.487	0.466	0.508
	0.100	−0.045	−0.085	−0.005	0.100	0.152	0.119	0.184	0.100	0.474	0.452	0.495
	0.150	−0.048	−0.079	−0.017	0.150	0.108	0.067	0.149	0.150	0.455	0.429	0.481
	0.200	−0.091	−0.136	−0.046	0.200	0.124	0.079	0.169	0.200	0.442	0.408	0.476
	0.250	−0.050	−0.094	−0.006	0.250	0.129	0.081	0.177	0.250	0.435	0.395	0.475
	0.300	−0.117	−0.166	−0.069	0.300	0.152	0.108	0.196	0.300	0.393	0.352	0.435
	0.350	−0.087	−0.142	−0.032	0.350	0.118	0.077	0.159	0.350	0.385	0.338	0.431
	0.400	−0.111	−0.176	−0.046	0.400	0.120	0.078	0.161	0.400	0.418	0.379	0.457
	0.450	−0.093	−0.155	−0.031	0.450	0.067	0.010	0.124	0.450	0.379	0.330	0.427
	0.500	−0.153	−0.232	−0.073	0.500	0.008	−0.079	0.096	0.500	0.385	0.326	0.443
	0.550	−0.144	−0.214	−0.073	0.550	0.044	−0.015	0.103	0.550	0.380	0.326	0.434
	0.600	−0.241	−0.334	−0.149	0.600	−0.055	−0.139	0.030	0.600	0.322	0.260	0.385
	0.650	−0.150	−0.240	−0.059	0.650	−0.100	−0.198	−0.001	0.650	0.211	0.115	0.307
	0.700	−0.334	−0.444	−0.225	0.700	−0.148	−0.267	−0.030	0.700	0.169	0.088	0.250
	0.750	−0.339	−0.471	−0.208	0.750	−0.180	−0.286	−0.073	0.750	0.101	−0.001	0.203
	0.800	−0.386	−0.517	−0.255	0.800	−0.183	−0.277	−0.088	0.800	0.006	−0.123	0.135
	0.850	−0.660	−0.830	−0.489	0.850	−0.466	−0.621	−0.311	0.850	−0.269	−0.417	−0.122
	0.900	−0.890	−1.084	−0.695	0.900	−0.675	−0.873	−0.477	0.900	−0.343	−0.513	−0.172
	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=0.5	0.050	−0.022	−0.049	0.004	0.050	0.142	0.115	0.170	0.050	0.485	0.467	0.502
	0.100	0.002	−0.026	0.029	0.100	0.163	0.139	0.187	0.100	0.464	0.442	0.485
	0.150	−0.041	−0.078	−0.004	0.150	0.149	0.117	0.182	0.150	0.472	0.454	0.489
	0.200	−0.025	−0.059	0.008	0.200	0.148	0.114	0.183	0.200	0.465	0.437	0.493
	0.250	−0.042	−0.081	−0.004	0.250	0.150	0.121	0.180	0.250	0.479	0.456	0.501
	0.300	−0.015	−0.050	0.020	0.300	0.143	0.113	0.173	0.300	0.452	0.423	0.481
	0.350	−0.065	−0.105	−0.026	0.350	0.168	0.136	0.200	0.350	0.471	0.445	0.498
	0.400	−0.078	−0.132	−0.023	0.400	0.140	0.098	0.182	0.400	0.431	0.405	0.458
	0.450	−0.073	−0.128	−0.019	0.450	0.147	0.109	0.184	0.450	0.453	0.426	0.481
	0.500	−0.158	−0.223	−0.092	0.500	0.129	0.083	0.175	0.500	0.401	0.359	0.444
	0.550	−0.101	−0.157	−0.045	0.550	0.084	0.031	0.137	0.550	0.414	0.374	0.454
	0.600	−0.144	−0.206	−0.082	0.600	0.072	0.012	0.131	0.600	0.352	0.300	0.404
	0.650	−0.139	−0.218	−0.060	0.650	0.077	0.015	0.140	0.650	0.284	0.191	0.377
	0.700	−0.212	−0.294	−0.130	0.700	−0.053	−0.146	0.039	0.700	0.318	0.217	0.418
	0.750	−0.211	−0.310	−0.111	0.750	−0.172	−0.274	−0.071	0.750	0.247	0.077	0.416
	0.800	−0.295	−0.404	−0.186	0.800	−0.086	−0.195	0.022	0.800	0.143	−0.002	0.288
	0.850	−0.561	−0.690	−0.431	0.850	−0.290	−0.426	−0.154	0.850	−0.053	−0.226	0.120
	0.900	−0.715	−0.891	−0.540	0.900	−0.549	−0.721	−0.376	0.900	−0.391	−0.677	−0.105
	ρ=0.0				ρ=0.2				ρ=0.5
	Density	Mean ρ	95%CI		Density	Mean ρ	95%CI		Density	Mean ρ	95%CI
γ=1.0	0.050	−0.022	−0.045	0.002	0.050	0.181	0.161	0.201	0.050	0.490	0.475	0.505
	0.100	0.003	−0.019	0.025	0.100	0.184	0.165	0.202	0.100	0.498	0.484	0.513
	0.150	−0.001	−0.024	0.022	0.150	0.212	0.192	0.232	0.150	0.506	0.494	0.519
	0.200	−0.013	−0.033	0.006	0.200	0.192	0.174	0.209	0.200	0.491	0.478	0.503
	0.250	−0.018	−0.042	0.006	0.250	0.197	0.177	0.217	0.250	0.491	0.477	0.504
	0.300	−0.017	−0.042	0.008	0.300	0.170	0.151	0.189	0.300	0.483	0.467	0.499
	0.350	−0.035	−0.054	−0.015	0.350	0.181	0.157	0.205	0.350	0.487	0.474	0.499
	0.400	−0.027	−0.053	−0.001	0.400	0.176	0.155	0.196	0.400	0.493	0.474	0.512
	0.450	−0.021	−0.050	0.009	0.450	0.190	0.167	0.212	0.450	0.473	0.456	0.490
	0.500	−0.047	−0.084	−0.010	0.500	0.158	0.135	0.181	0.500	0.455	0.421	0.490
	0.550	−0.036	−0.068	−0.005	0.550	0.169	0.137	0.201	0.550	0.479	0.451	0.506
	0.600	−0.069	−0.121	−0.016	0.600	0.162	0.127	0.198	0.600	0.444	0.405	0.484
	0.650	−0.107	−0.168	−0.046	0.650	0.052	0.000	0.104	0.650	0.392	0.341	0.443
	0.700	−0.185	−0.267	−0.103	0.700	0.085	0.030	0.140	0.700	0.399	0.342	0.456
	0.750	−0.170	−0.240	−0.099	0.750	0.142	0.088	0.197	0.750	0.400	0.321	0.479
	0.800	−0.208	−0.303	−0.112	0.800	−0.022	−0.113	0.070	0.800	0.283	0.192	0.374
	0.850	−0.342	−0.445	−0.239	0.850	−0.037	−0.136	0.061	0.850	0.146	0.024	0.269
	0.900	−0.602	−0.754	−0.451	0.900	−0.282	−0.402	−0.161	0.900	−0.172	−0.375	0.032

Figure 3 shows a similar pattern of results produced in the K=10 case. It is interesting to note that the negative bias when σ=1.0 is weaker in the lower densities in the K=20 case than in the K=10 case. This occurs because of the shift in skewness of the Poisson distribution as greater values of λ are employed in the case of K=20,from being left-skewed to being more symmetric around the mean. Additionally, for all levels of γ, strong negative bias starts around a density level of .85 (estimated λ=15.13) for each target ρ value. This negative bias again disappears when the standard deviation of the error term returns to the σ=0.1 scenario. It is also worth noting that the one effect we did not observe in either case but was observed by (Mizruchi & Neuman, 2008) was a dependence on ρ on the magnitude of the bias.

In summary, our results are consistent with the previous Mizruchi and Neuman one-mode simulation¹⁵ in that a significant bias in the estimates for ρ becomes more pronounced as network density increases. However, our results were not consistent with their observation that the negative bias tendency became more pronounced at higher values of population ρ. More specifically (for the σ=1.0 scenario), Mizruchi and Neuman (2008) found that a significant negative bias starts at densities as low as 0.05 for ρ=0.5 but it did not start until the density reached 0.20 for ρ=0.0. One possible explanation for the divergence of findings is that the addition of D (the diagonal count of the number of events) to our regression model adds information that consequently reduces the proportion of disturbance in the model (it increases model fit) since D is essentially the out-degree of the corresponding row the W matrix¹⁶ and thus is a count of the number of disturbance terms. This additional information may reduce variances in the iterative maximum likelihood optimization process of the linear network autocorrelation model, and acts to counter the ρ-dependent bias observed by Mizruchi and Neuman (2008). In other words, the two-mode estimation case provides additional information (D) from the network data thus making network effects estimation more accurate.

8. Conclusion

We have introduced a two-mode version of the network autocorrelation model by developing a new influence model of “Affiliation Exposure,” potentially opening up new network analysis opportunities for datasets which lack traditional friendship network data. In addition to the alternate formulation of W, the two-mode network autocorrelation model is distinguished from its one-mode counterpart by the inclusion of D (the diagonal of the W matrix) and the corresponding estimation of γ in the regression equation. Our simulation analysis based on Poisson outdegree distributions (chosen because of the appearance of this distribution in several real-world datasets) has shown that the two-mode network autocorrelation model has similar statistical properties to the one-mode version (i.e., negative bias in ρ becoming stronger with higher density). However, the degree of this bias, unlike the one-mode case, was independent of the true population value (ρ). Additionally, the simulation results have shown that stronger D terms helped to reduce the observed tendency of the negative estimation bias to increase with density. Combining these results together, the additional structure of D may serve to help stabilize the estimates in the presence of noise as part of the maximum likelihood optimization process, and thus acts to counter the ρ-dependent bias observed by others in single-mode networks, but further research will be needed to confirm this.

Substantively, special attention is needed when the average number of events each actor participated in is high. When our two-mode version of the network autocorrelation model exceeds a Δ_(c) of 0.80 in the co-membership matrix, the autocorrelation parameter tends to be severely underestimated. Consequently, estimating network effects when participation in events is exceedingly high may be biased. For example, when attendance at community events by community leaders is near universal, estimating social influences may be problematic and underestimated. Methodologically, our simulation results were obtained by generating random bipartite graphs based on Poisson outdegree distributions. Future research will be expanded by generating random bipartite graphs with other distributional assumptions, such as such as exponential or power-law distributions, as well as using joint distribution of in-degree and out-degree distributions if they are known. Finally, this simulation study has shown that one of the possible solutions to attenuate the negative bias as a function of density would be to include meaningful information from the social influence weight matrix in a regression model. Including this additional information might mitigate the influence of noise in the model. Our two-mode version of network autocorrelation model has shown the utility of such method by including the diagonal values of the converted matrix in an autocorrelation model. This method may be applied to the one-mode case where the diagonal information of the influence weight matrix is meaningful, but further research is needed to confirm the utility of this approach as well. In conclusion, we find that network influence estimates can be validly obtained from two–mode network data and that the affiliation exposure may become an important method used to understand how co-participation influences social norms, attitudes, and behaviors.

Research highlights.

• Introduces a two-mode version of the network autocorrelation model

• Conduct simulation analysis to explore biasness in autocorrelation parameter

• Affiliation exposure helps attenuating negative bias in autocorrelation parameter