Reconstruction from a Few Projections by ℓ₁-Minimization of the Haar Transform

Abstract

Much recent activity is aimed at reconstructing images from a few projections. Images in any application area are not random samples of all possible images, but have some common attributes. If these attributes are reflected in the smallness of an objective function, then the aim of satisfying the projections can be complemented with the aim of having a small objective value. One widely investigated objective function is total variation (TV), it leads to quite good reconstructions from a few mathematically ideal projections. However, when applied to measured projections that only approximate the mathematical ideal, TV-based reconstructions from a few projections may fail to recover important features in the original images. It has been suggested that this may be due to TV not being the appropriate objective function and that one should use the ℓ₁-norm of the Haar transform instead. The investigation reported in this paper contradicts this. In experiments simulating computerized tomography (CT) data collection of the head, reconstructions whose Haar transform has a small ℓ₁-norm are not more efficacious than reconstructions that have a small TV value. The search for an objective function that provides diagnostically efficacious reconstructions from a few CT projections remains open.

1. Introduction

The aim of image reconstruction from projections is to acquire knowledge of the interior of an object or a body from some physically obtained approximations of line integrals of some spatially varying physical parameter (such as the x-ray attenuation). In practice, measurements are taken for a number of lines. We wish to reconstruct the distribution of the spatially varying physical parameter from the measured data; such a distribution is typically referred to as an image, it is represented by a real-valued function f of two variables of bounded support. The mathematical problem is to reconstruct the function from its (noisy and incomplete) projections [1, 2].

We define a projection in the direction θ ∈ [0, π) as follows. Let (s₁, s₂) denote the coordinates of the point r = (r₁, r₂) ∈ ℝ² in the coordinate system rotated by θ. Then, the projection of f in the direction θ (i.e., the θ-projection of f) is defined as the function [ 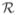f ] (•, θ) of the variable s₁ for which

$$[\mathcal{R}f](s_1,\theta )={\int }_{L_{s_1,\theta }}f(r){ds}_2,$$ (1)

where L_s,θ is the line at the distance s from the origin that makes the angle θ with the r₂-axis. It can be said that the transform 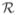defined by (1) gives the θ-projections of f for any θ ∈ [0, π). The transform 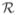is called the Radon transform of f [3].

In practice, we sample θ-projections of f by taking physical measurements for a number of directions θ in a finite nonempty set Θ. Let, for s ∈ ℝ and θ ∈ Θ, g (s, θ) denote the approximation to [ 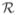f] (s, θ) that we obtain based on our measurements. For any θ ∈ Θ, we use S_θ to denote the finite nonempty set of all s for which we have such a g (s, θ). The reconstruction task consists of finding a “good” approximation f* to the unknown function f from the set

$$\{g(s,\theta )\mid \theta \in \mathrm{\Theta },s\in S_{\theta }\}$$ (2)

of approximations to [ 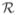f](s, θ).

In many applications, it is desirable (and sometimes necessary) to take the measurements in such a way that the cardinality of Θ is small (i.e., in the order of 100 or less) and then we have the task of trying to find a good reconstruction f* from a few projections. One example of this is electron tomography [4] in which a structure in a biological cell is imaged using an electron microscope. The taking of the measurements for any one θ-projection damages the structure and so only a few (typically 70) θ-projections can be sampled before the resulting structural change is such that further measurements are useless.

The possibility of obtaining good reconstructions from a few projections is based on the fact that images in any application area are not random samples of all possible images, but have some common attributes. For example, in industrial nondestructive testing the object to be reconstructed is known to contain only certain types of materials of known x-ray attenuations and using this the distribution of these materials in the image can often be recovered from very few projections by the methods of discrete tomography [5, 6].

More recently an alternative approach to reconstructing objects from a few projections was proposed. In [7] a mathematically described image that was supposed to be a representation of a cross section of the human head (a head phantom) was “reconstructed exactly” from only 22 projections. The underlying idea was that the common attribute of the previous paragraph should be that the desirable images have a small total variation (TV). (This, and all other concepts mentioned in this section without definition, are defined in the next section.) The number of papers that cite [7] is truly impressive; two examples that specifically concern themselves with reconstructions with small TV are [8, 9].

However, the impression given in [7], namely that one can obtain in practice “exact” reconstructions of head cross sections from only 22 projections using TV minimization, is misleading. From the practical point of view, there are two essential problems in the illustration provided by [7]. First, the head phantom used in there is unrealistically simple, it is piecewise constant with only a few simple features and is therefore particularly (and unrealistically) appropriate for reconstruction by TV minimization. Second, the method by which the projections of the head phantom were obtained in [7] is a mathematical idealization of the physical process of projection taking, resulting in a consistency between the phantom and the projections that is much greater than what can be possibly obtained in any application. This was illustrated in [10], by using a more realistic head phantom. It was shown there that with such a phantom a TV-minimizing reconstruction even from 82 mathematically-ideal projections is not “exact”, although it is quite good. More importantly, it was also shown that a TV-minimizing reconstruction from 82 realistically simulated projections is unacceptable from the medical point of view: it failed to recover a large tumor in the brain. A similar conclusion was drawn in [11] using physically obtained projections of a cadaver head.

It has been suggested recently [12] that the reason for the unacceptable performance of TV-minimizing reconstruction from 82 realistically simulated projections as reported in [10] may be due to using TV as the objective function and that one should use the ℓ₁-norm of the Haar transform instead. The authors of [12] are not alone in considering this a good direction; see, for example, the section on “Intuitive Introduction of Compressed Sensing (CS)” in [13] on the use of the ℓ₁-norm of a sparsifying transform such as the Haar transform. Unfortunately, the investigation reported below does not confirm the superiority over TV of the ℓ₁-norm of the Haar transform. It is demonstrated by experiments simulating the computerized tomography (CT) data collection of the human head (as was done in [10]) that a reconstruction whose Haar transform has a small ℓ₁-norm is not any more useful from the medical diagnostic point of view than the reconstruction that has a small TV value. Thus the search for an objective function that provides diagnostically efficacious reconstructions from a limited number of CT projections remains open.

While our orientation in this paper is strictly toward CT, the ideas that are presented are relevant to related inverse problems; examples are inverse scattering problems from a few angles [14] and the inversion of Radon spherical transform for a few angles [15].

Our paper is organized as follows. The following section discusses the mathematical notions that we use in our work. In Section 3 we show the results of our experiments. In Section 4 we discuss the methods by which these results were obtained. We provide our conclusions in Section 5.

2. Mathematical Background

Since computers store and process images in a digital form, in order to fully understand what goes on in practical image reconstruction from projections, we must make precise the concept of digitization of an image f (which we defined in the previous section as a real-valued function of bounded support on ℝ²). Throughout this paper N denotes a positive integer. An N × N digital image is a function p: [0, N − 1]² → ℝ. For any (t₁, t₂) ∈ [0, N − 1] × [0, N − 1] and for any positive real number d, referred to as the sampling interval, we define a pixel (which is a subset of ℝ²) by

$${\text{pix}}^{N,d}(t_1,t_2)=\left\{(r_1,r_2)\in {\mathbb{R}}^2\mid -\frac{d(N-2t_2)}{2}<r_1\le -\frac{d(N-2-2t_2)}{2}\text{and}\frac{d(N-2-2t_1)}{2}<r_2\le \frac{d(N-2t_1)}{2}\right\}.$$ (3)

Given an image f and a sampling interval d, we define the N × N digitization $p_f^{N,d}$ of f with a sampling interval d by

$$p_f^{N,d}(t_1,t_2)=\frac{1}{d^2}{\int }_{{\text{pix}}^{N,d}(t_1,t_2)}f(r)dr.$$ (4)

Conversely, an N × N digital image p and a d > 0 give rise to an image $f_p^d$ that is defined by

$$f_p^d(r)=\{\begin{array}{ll}p(t_1,t_2),\hfill & \text{if}r\in {\mathit{pix}}^{N,d}(t_1,t_2)\text{for}\text{some}(t_1,t_2)\in [0,N-1]\times [0,N-1],\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

For any image f, positive integer N, and sampling interval d, we refer to the image $f_{\left[p_f^{N,d}\right]}^d$ as the N × N pixelization of f with a sampling interval d. The pixelization is supposed to be an acceptable approximation of f; in order for that to be true it is necessary the Nd be large enough so that the support of f is a subset of the support of $f_{\left[p_f^{N,d}\right]}^d$, but d be small enough so that important details in the image are not lost due to the pixelization. In image reconstruction from projections, we typically first select such an N and d, and then the reconstruction algorithm is supposed to produce an N × N digital image p* that is a “good” approximation of $p_f^{N,d}$ for the image f for which the projection data were collected. Note that this intuitively implies that $f\ast =f_{p\ast }^d$ will be a “good” approximation of f. We now discuss the criteria by which the p* should be chosen.

First, it should be reasonably consistent with the projection data (2). Following [16], we use r(p) to denote a measure of inconsistency of p with the data. There are many ways of defining r, in this paper we use

$$\mathcal{P}r(p)=\sqrt{\sum _{\theta \in \mathrm{\Theta }}\sum _{s\in S_{\theta }}{(g(s,\theta )-[\mathcal{R}{f}_p^d](s,\theta ))}^2}.$$ (6)

Second, we should define an objective function φ, such that φ(p) measures how badly $f_p^d$ violates the desired common attribute of images (for our application). As mentioned previously, one common choice is total variation (TV); see, e.g., [7, 8, 9, 10, 11, 16] and their references. We define it here by

$$TV(p)=\sum _{t_1=0}^{N-2}\sum _{t_2=0}^{N-2}\sqrt{{(p(t_1+1,t_2)-p(t_1,t_2))}^2+{(p(t_1,t_2+1)-p(t_1,t_2))}^2}.$$ (7)

As discussed in the previous section, our paper is concerned with the investigation of the claim that instead of using TV, should use the ℓ₁-norm of the Haar transform as the objective function. The ℓ₁-norm of an N × N digital image p is defined as

$${\left|\right|p\left|\right|}_1=\sum _{t_1=0}^{N-1}\sum _{t_2=0}^{N-1}\mid p(t_1,t_2)\mid .$$ (8)

The definition of the Haar transform is more complicated. We define it only for M × M digital images with M a power of 2. We therefore introduce an auxiliary-operator B that maps any N × N digital image p into an M × M digital image Bp, where M is the smallest power of 2 that is not smaller than N, defined by

$$\mathbf{B}p(t_1,t_2)=\{\begin{array}{ll}p(t_1,t_2),\hfill & \text{if}0\le t_1,t_2<N,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (9)

In our algorithm we will also make use of the inverse of this operator that, for any M × M digital image p, with M ≥ N, produces the N × N digital image B⁻¹p defined by

$${\mathbf{B}}^{-1}p(t_1,t_2)=p(t_1,t_2),\text{for}0\le t_1,t_2<N.$$ (10)

A standard way of defining the Haar transform is done using matrices. For any N × N digital image p, we use p̂ to denote the N × N matrix whose (t₁, t₂)th entry is p (t₁, t₂), for 0 ≤ t₁, t₂ < N. Conversely, for any N × N matrix P with entries p_{t1, t2}, we denote by P̄ the digital image for which P̄ (t₁, t₂) = p_t1t2, for 0 ≤ t₁, t₂ < N. For any positive integer k, we define the 2^k × 2^k Haar matrix K_k recursively by [17]

$$K_{k+1}=\left(\begin{array}{c}{K}_k\otimes (\begin{array}{cc}1& 1\end{array})\\ 2^{k/2}{I}_{2^k}\otimes (\begin{array}{cc}1& -1\end{array})\end{array}\right),$$ (11)

where

$$K_1=\left(\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 1& \hfill -1\end{array}\right),$$ (12)

I_2^k is the 2^k × 2^k identity matrix and the Kronecker product of an N × N matrix P with entries p_t1t21, for 0 ≤ t₁, t₂ < N, and a 1 × 2 matrix Q is defined as the N × 2N matrix [18]

$$P\otimes Q=\left(\begin{array}{ccc}{p}_{0,0}Q& \cdots & p_{N-1,0}Q\\ ⋮& \ddots & ⋮\\ p_{N-1,0}Q& \cdots & p_{N-1,N-1}Q\end{array}\right).$$ (13)

Let p be any M × M digital image with M = 2^k, where k is a positive integer. The Haar transform of p is the M × M digital image

$$\mathbf{H}p=\overline{\frac{1}{M}{K}_k\widehat{p}{K}_k^T}$$ (14)

and the inverse Haar transform of p is the M × M digital image

$${\mathbf{H}}^{-1}p=\overline{\frac{1}{M}{K}_k^T\widehat{p}{K}_k}.$$ (15)

For an arbitrary N × N digital image p, we define the ℓ₁-norm, of its Haar transform (L1H) to be

$$L1H(p)={\left|\right|\mathbf{H}{\mathbf{B}}_p\left|\right|}_1.$$ (16)

Having defined two choices for the objective function φ (namely TV and L1H) we now return to the discussion of the output N × N digital image p* that is supposed to be a “good” approximation of $p_f^{N,d}$ for the image f for which the projection data were collected. The conditions that p* must satisfy in order to be considered to be an acceptable output are that both r (p*) and φ (p*) be “small.” The first of these conditions is made mathematically precise by specifying a positive real number ε and requiring that r (p*) ≤ ε. The choice of ε has to be application dependent: the noisier the data are, the larger the ε ought to be chosen. For noisy projection data, it may happen that for a small choice of ε there is no p* that satisfies the condition and, even when there is one, it may be that it fits the noise in the data more than the noiseless projection measurements [ 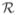f] (s, θ). An intuitively reasonable choice is $\epsilon =\mathcal{P}r\left(p_f^{N,d}\right)$, but in actual practice we do not know what f is (it is the image that we wish to reconstruct from the data) and so such an ε need to be estimated based on prior knowledge regarding the application area. The second of the conditions has a similar mathematical interpretation: it is desired that $\phi (p\ast )\le \phi \left(p_f^{N,d}\right)$. Again, this condition cannot be used in actual practice as a criterion to be satisfied by the output of an algorithm, since f is not known. However, in evaluating algorithms on simulated data we can test whether or not the condition happens to be satisfied by the output. In the next section we report on outputs produced by our algorithms, in all cases they satisfy both conditions. Whatever conclusions we will reach regarding the relative merits of the objective functions TV and L1H based on the outputs of our algorithms will not be essentially dependent of the actual algorithms used: the outputs of the algorithms for TV and L1H will both be such that the value of the inconsistency with the data is just less than ε and $\phi (p\ast )\le \phi \left(p_f^{N,d}\right)$. It is the choice of the objective function φ, rather than the specific algorithm used to obtain a p* that satisfies the stated conditions, that determines the appearance of the p*.

3. Results

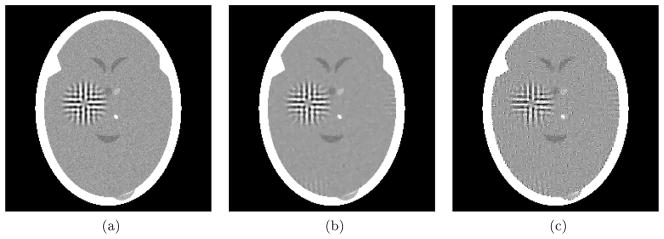
In this section we report on experiments aimed at answering the question: Can one obtain superior reconstructions form a few projections to those reported in [10] by using L1H instead of TV as the objective function? In the first two experiments, in the same way as was reported in [10], we reconstructed a head phantom h (see Figs. 1(a) and 2(a) for renderings of $p_h^{243,d}$ as defined by (4) and d = 0.0752 measured in centimeters) from 82 projections with the geometrical arrangement of the lines for which data were collected as used in that paper. Also as in [10], two modes of data collection were simulated. (We note that all computational work reported in this paper, such as phantom and projection data generation, reconstruction, statistical analysis of the results and the display of digital images, was done within the framework of the software package SNARK09 [19].)

Figure 1.

Experiment using 82 mathematically idealized projections, see (17). (a) Digitized head phantom $p_h^{243,d}$ with tumor and variability. (b) Reconstruction p_TV with a small TV value, see (7). (c) Reconstruction p_L1H with a small L1H value, see (16).

Figure 2.

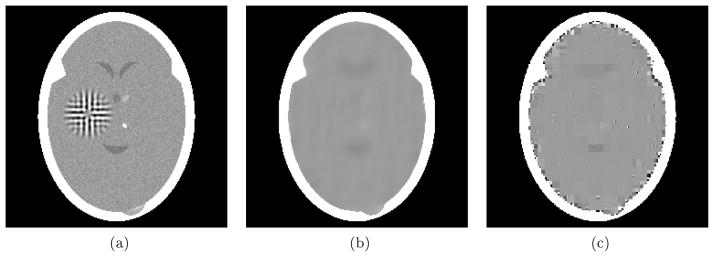
Experiment using 82 realistic projections. (a) Digitized head phantom $p_h^{243,d}$ with tumor and variability. (b) Reconstruction p_TV with a small TV value, see (7). (c) Reconstruction p_L1H with a small L1H value, see (16).

The first mode of data collection is a mathematically idealized one: for each θ ∈ Θ and s ∈ S_θ, we used

$$g(s,\theta )=\left[\mathcal{R}{f}_{p_h^{243,d}}^d\right](s,\theta ),$$ (17)

see (1), (4) and (5) for the notation. In this mathematically idealized case we have that $\mathcal{P}r(p_h^{243,d})=0$; a consistency between the phantom and the data that is not achievable in practical CT. We used two reconstruction methods (discussed in the next section) that produced from these idealized data reconstructions whose inconsistencies (6) are less than 0.05. One of the methods was aimed at producing a reconstruction p_TV, shown in Fig. 1(b), for which TV (p_TV) is relatively small, while the other method was aimed at producing a reconstruction p_L1H, shown in Fig. 1(c), for which L1H(p_L1H) is relatively small: see (7) and (16). The numerical values associated with the phantom and the two reconstructions are reported in Table 1. Note that the reconstructions have the desired properties: both r (p_TV) and r(p_L1H) are less than 0.05, the TV value of p_TV is smaller than that of the digitized phantom $p_h^{243,d}$ and that of p_L1H, and the L1H value of p_L1H is smaller than that of the digitized phantom $p_h^{243,d}$ and that of p_TV. Visual qualities of the reconstructions in Figs. 1(b) and (c) are quite good, but they are by no means exact in the sense of being identical to the phantom in Fig. 1(a). This illustrates yet again the validity of the claim in [10] that for the perfection of the reconstructions in [7] it was necessary to have not only mathematically idealized data (which is the case in this experiment as well), but also unrealistically simple phantoms. The realism of our head phantom from the medical point of view is justified in Chapter 4 of [2].

Table 1.

Comparison of numerical values provided by (6), (7) and (16) for the experiment using 82 mathematically idealized projections of the digitized head phantom $p_h^{243,d}$, the reconstruction p_TV with a small TV value and reconstruction p_L1H with a small L1H value.

Mathematically Idealized Experiment
	$p=p_h^{243,d}$	p = pTV	p = pL1H
r (p)	0.0000000	0.0499954	0.0499997
TV (p)	488.2	441.7	520.6
L1H (p)	866.1	848.9	842.6

The approach just described is an idealization of what really occurs in CT and, in fact, in most real applications of image reconstruction. Among other things, the approach just described does not take into account the phenomenon of scattering, nor the stochastic nature of the imaging process, nor the fact that detectors have a width and in consequence they cannot acquire line integrals. To investigate the likely performance of our algorithms on real CT data we used a second mode of data collection that more realistically simulates that of a CT scanner. For details how the 82 realistically simulated projections were obtained we refer to [10]. An essential difference between this realistic case and the mathematically ideal case is that value of r for the digitized phantom $p_h^{243,d}$ (shown in Fig. 2(a)) is no longer 0, but 1.79088; in other words, the digitized phantom is inconsistent with the projection data used as the input to the reconstruction algorithms. Since the digitized phantom is what an exact reconstruction method should produce, there is no point in insisting that the inconsistency of a reconstruction with the realistic data be much less than $\mathcal{P}r\left(p_h^{243,d}\right)=1.79088$. We again used two reconstruction methods (discussed in the next section) that produced from these realistic data reconstructions whose inconsistencies (6) are less than $\mathcal{P}r\left(p_h^{243,d}\right)$. One of the methods was aimed at producing a reconstruction p_TV, shown in Fig. 2(b), for which TV (p_TV) is relatively small, while the other method was aimed at producing a reconstruction p_L1H, shown in Fig. 2(c), for which L1H (p_L1H) is relatively small. The numerical values associated with the phantom and the two reconstructions are reported in Table 2. Note that the reconstructions have the desired properties: both r (p_TV) and r (p_L1H) are less than $\mathcal{P}r\left(p_h^{243,d}\right)$, the TV value of p_TV is smaller than that of the digitized phantom $p_h^{243,d}$ and that of p_L1H, and the L1H value of p_L1H is smaller than that of the digitized phantom $p_h^{243,d}$ and that of p_TV. Visual qualities of the reconstructions in Figs. 2(b) and (c) are quite unacceptable from the medical point of view: the large tumor in the phantom is totally invisible in both of the reconstructions. This illustrates that the negative result reported in [10] that using TV as the objective function results in not recovering a large tumor from 82 realistic projections cannot be improved upon by replacing TV by L1H as the objective function. In fact, if anything, the reconstruction got worse by such a replacement, as can be seen by comparing Figs. 2(b) and (c).

Table 2.

Comparison of numerical values provided by (6), (7) and (16) for the experiment using 82 realistic projections of the digitized head phantom $p_h^{243,d}$, the reconstruction p_TV with a small TV value and reconstruction p_L1H with a small L1H value.

Realistic Experiment
	$p=p_h^{243,d}$	p = pTV	p = pL1H
r (p)	1.79088	1.78993	1.78996
TV (p)	488.4	422.1	599.4
L1H (p)	866.3	836.9	766.0

The anecdotal experiment with realistic data that is presented in the previous paragraph is not sufficient for a firm conclusion. We therefore designed a third experiment that uses statistical hypothesis testing (SHT) for task-oriented comparison of reconstruction algorithm performance [2, Section 5.2]. Using SHT we are able to assign a numerical statistical significance by which we can reject the null hypothesis that the algorithm that produces a small TV and the one that produces a small L1H are equally efficacious for a task of detecting low contrast tumors in the brain, in favor of the alternative hypothesis that the algorithm that produces a small TV is more efficacious for that task. Details of this methodology can be found, for example, in [2, Section 5.2]. Roughly it consists of the following four steps. (i) Generation of random samples from a (statistically described) ensemble of phantoms. (ii) Generation of realistic projection data sets and reconstructions using the two algorithms on each of the projection data sets. (iii) Assignment of figures of merit (FOMs) to each of the reconstructions. An FOM is supposed to measure the goodness of a reconstruction for a given task. (iv) Computation of the statistical significance (based on the average FOMs of all the reconstructions for all the data sets) by which we can reject the null hypothesis in favor the alternative hypothesis. The statistical significance is measured by the P-value, which is the probability under the null hypothesis of observing a difference between the average FOMs that is as large or larger than what we have actually observed. A small P-value indicates high statistical significance.

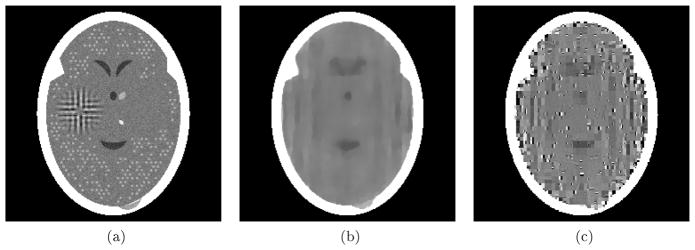
The ensemble of phantoms used for the SHT experiment of this paper is exactly the same ensemble that was used for SHT experiments in [2]; it is specified in Section 5.2 of that book. A random sample from that ensemble is shown in Fig. 3(a). In addition to the features included in the head phantoms of our previous two experiments, it contains a large number of symmetric pairs of potential tumor sites, only one of which contains a tumor; for each pair of sites, the choice is done randomly with equal probability while generating the sample phantom. For each sample phantom, projection data were generated according to the realistic parameters specified in [2. Section 5.8] for the standard projection data, with two exceptions. Since our paper is concerned with reconstruction from a few projections, instead of generating data for 360 projections as in [2, Section 5.8], we generated data for only 60 (equally-spaced) projections. In addition, for this paper, we made the simplifying assumption that data are collected using a monochromatic x-ray source. For each of the reconstructions for each of the samples, two FOMs were calculated: hit ratio (HITR) and image wise region of interest (IROI). The first of these indicates the fraction of all pairs for which the average density in the reconstruction of the tumor site is larger than the average density in the reconstruction for the symmetric non-tumor site. The second is proportional to a signal-to-noise ratio, where the signal is the difference in the reconstruction of the total densities in all tumor sites and all non-tumor sites and noise is the standard deviation in the densities in the reconstruction at the non-tumor sites. For more detailed definitions of these two FOMs. see for example [2, Section 5.2].

Figure 3.

Reconstructions from 60 noisy projections generated with the parameters of the SHT experiment. (a) A random sample from the ensemble of phantoms used in the SHT experiment ( r = 1.07460, TV = 454.0, L1H = 851.1). (b) Reconstruction p_TV with a small TV value ( r = 1.06758, TV = 403.9, L1H = 820.7). (c) Reconstruction p_L1H with a small L1H value ( r = 1.06171, TV = 559.2, L1H = 750.9).

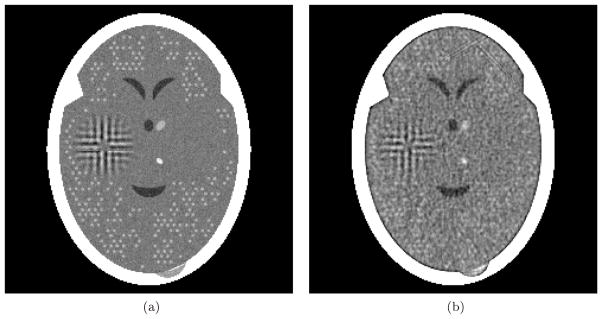
For the SHT experiments we used 30 samples from the ensemble of phantoms. The results, reported in Table 3, are conclusive: the P-values for both of the FOMs were less than 1.3 × 10⁻¹². In other words, we can reject with confidence the null hypothesis that the two algorithms are equally good for detecting low contrast tumors in the brain in favor of the alternative hypothesis that the one that produces low TV is better for the task at hand. Nevertheless, looking at the reconstructions, one cannot possibly agree with the statement that the reconstructions are medically useful. As an illustration, we include in Fig. 3 a sample phantom and its reconstructions by the two algorithms. As can be seen, using only 60 noisy projections, neither p_TV nor p_L1H resolve the individual tumors, however the increased density due to the tumors is slightly better indicated in the small TV reconstruction. However, this is hardly relevant as compared to what one can do by using more projections. To demonstrate that, we picked a sample from our ensemble of phantoms and generated a projection data set using exactly the same parameters that were used for our SHT experiment, except that it contained 360 projections rather only 60. We reconstructed from this data set using a standard algorithm (an algebraic reconstruction technique, ART, using blob basis functions, relaxation parameter 0.05 and 10 cycles through the projection data; see [2, Chapter 11]). The result of this reconstruction is illustrated in Fig. 4. Using 360 projections allows us to visualize the small tumors very well. The values for this reconstruction of HITR and IROI are 0.9569 and 0.3923, respectively; these values are much higher than what we have been able to obtain from 60 projections, even with the help of algorithms that aim at a small value of TV or L1H.

Table 3.

Results of the SHT experiment using reconstructions from 60 noisy projections.

SHT Experiment
	TV	L1H	P-value
Average HITR	0.6790	0.6127	1.3 × 10−12
Average IROI	0.0735	0.0360	7.0 × 10−13

Figure 4.

Reconstructions from 360 noisy projections generated with the parameters of the SHT experiment. (a) A random sample from the ensemble of phantoms used in the SHT experiment. (b) Reconstruction using ART with blob basis functions, relaxation parameter 0.05 and ten cycles through the data.

4. Methods

The method that we used to produce p_TV, for both data collection modes, was the iterative algorithm used for TV-minimization in [10]. The difference between the two applications of that algorithm was that in the case of the mathematical idealized data the process was stopped when the inconsistency got below 0.05, while in the case of the realistic data the process was stopped when the inconsistency got below 1.79. It was pointed out in [10] that the methodology proposed in there is applicable to objective functions φ other than TV and this was formalized and made mathematically rigorous in [16], where it was referred to as the superiorization methodology.

An essential aspect of the superiorization methodology as described in [16] is that at certain points the algorithm attempts to reduce the objective function φ by moving in a direction that is the negative of one of its subgradients. When we were contemplating the nature of the objective function L1H, it seemed to us that there is a more natural way to reduce its value. We now present the variant of the superiorization methodology [16] that we used to obtain the p_L1H in the previous section.

The algorithm makes use of a family of operators W_{β, w}, with 0 < β ≤ 1 and 0 < w, mapping N × N digital images into N × N digital images, defined by

$$[{\mathbf{W}}_{\beta ,w}p](t_1,t_2)=\{\begin{array}{ll}\hfill p(t_1,t_2)-\beta w,& \text{if}p(t_1,t_2)\ge w,\hfill \\ \hfill (1-\beta )p(t_1,t_2),& \text{if}\mid p(t_1,t_2)\mid <w,\hfill \\ \hfill p(t_1,t_2)+\beta w,& \text{if}p(t_1,t_2)\le -w,\hfill \end{array}$$ (18)

for (t₁, t₂) ∈ [0, N − 1]². It is obviously the case that ||W_{β, w}p||₁ < ||p||₁. Such operators have been used in the literature in conjunction with the objective function L1H, compare it for example with equation (10) of [12].

We also make use of another operator P mapping N × N digital images into N × N digital images, whose desired essential property is that r (Pp)< r(p), whenever 0< r(p). In other words, P is supposed to reduce the inconsistency of p with the data. To obtain p_L1H, we used the operator P defined by equations (10) and (11) of [10], which is the same operator that we used in the algorithm to obtain p_TV. To make our paper self-contained, the definition of P is reproduced in the Appendix below. Note that the definition of P depends on the production data (2) in an essential way.

The following pseudocode describes how we obtained p_L1H, given projection data (2). It makes use of the parameter w (which we selected to be 0.0005 in our actual experiment), an initial value β₀ for β (which we selected to be 1), an initial value p₀ of the digital image (which we selected to be the image whose value is zero everywhere), a real number parameter a, 0 < a < 1 (which we selected to be 0.9999) and a positive real number parameter ε (which we selected to be 0.05 for the mathematically idealized data, 1.79 for the realistic data used to produce Fig. 3 and 1.07 for the SHT experiment that involves fewer projections each of which is generated using a larger number of photons).

Algorithm 1.

Algorithm to obtain p_L1H

1:	k = 0
2:	β = β0
3:	pk = p0
4:	WHILE r (pk) > ε DO
5:	q = HBpk
6:	logic = true
7:	WHILE logic
8:	pk+1 = PB−1H−1Wβ.wq
9:	IF r (pk+1) < r (pk) THEN logic=false
10:	β = a × β
11:	k=k+1
12:	pL1H = pk

In this algorithm q is the Haar transform of p^k. The operator W_{β, w} reduces its ℓ₁-norm, and the changing parameter β controls by how much. As β gets smaller, B⁻¹H⁻¹W_β,wq gets to be more similar p^k. From the nature of the operator P (its desired behavior discussed above and its continuity), we expect that as β gets small enough the condition r (p^k+1) < r (p^k) will be satisfied and we get out of the WHILE logic loop and go onto the next iteration. As illustrated in the previous section, our algorithm indeed terminates for the modes of data collection to which it was applied and its output p_L1H indeed has desired mathematical properties: small values of both the inconsistency with the data and of the ℓ₁-norm of the Haar transform.

5. Conclusions

We have presented an algorithm that is designed to deal with the ℓ₁-norm of the Haar transform as the objective function: as illustrated, it terminates for the modes of data collection to which it was applied and its output p_L1H indeed has the desired mathematical property of having small values for both the inconsistency with the data and the ℓ₁-norm of the Haar transform.

However, this does not appear to be of use in the medical application of reconstruction from a few projections: the output on realistic data does not appear to contain diagnostically important information in the object to be reconstructed; if anything it is of worse quality than what is obtained by using total variation as the objective function.

We have no explanation to offer for this behavior of the two objective functions, we leave the discovery of such an explanation to those who advocate them. Our aim here was less ambitious: we wished to see if using the ℓ₁-norm of the Haar transform is superior to using TV, as claimed in the literature; and here we simply report, based on evidence that we found, that this does not appear to be the case.

Appendix

Here we reproduce the definition of the operator P that is specified by equations (10) and (11) of [10], but using the notation of our Sections 1 and 2. In addition we make use of the notation that if p and q are N × N digital images, then p + q is the N × N digital image defined by [p + q] (t₁, t₂) = p (t₁, t₂) + q (t₁, t₂), for (t₁, t₂) ∈ [0, N − 1] × [0, N − 1]. Further, for every θ ∈ Θ and every s ∈ S_θ, we use a^s,θ to denote the N × N digital image such that a^s,θ (t₁, t₂) is the length of the segment of the line L_s,θ that lies in the pixel ${\text{pix}}^{N,d}(t_1^i,t_2^i)$.

We first define, for every θ ∈ Θ, an operator P_θ mapping N × N digital images into N × N digital images by (this corresponds to equation (10) of [10])

$${\mathbf{P}}_{\theta }p=p+\frac{1}{\mid S_{\theta }\mid }\sum _{s\in S_{\theta }}\frac{g(s,\theta )-[\mathcal{R}{f}_p^d](s,\theta )}{{\sum }_{t_1=0}^{N-1}{\sum }_{t_2=0}^{N-1}{(a^{s,\theta }(t_1,t_2))}^2}{a}^{s,\theta },$$ (19)

where |S_θ| is the cardinality of S_θ and p is an arbitrary N × N digital image.

For the definition of P we need to order the projection directions as in Θ = {θ₁, θ₂, …, θ_T}. In practice we use the so-called efficient ordering (see, for example, p. 209 of [2]). We define the operator P mapping N × N digital images into N × N digital images by (this corresponds to equation (11) of [10])

$$\mathbf{P}p={\mathbf{P}}_{{\theta }_T\cdots }{\mathbf{P}}_{{\theta }_2}{\mathbf{P}}_{{\theta }_1}p,$$ (20)

where p is an arbitrary N × N digital image.