Slice-timing effects and their correction in functional MRI

Abstract

Exact timing is essential for functional MRI data analysis. Datasets are commonly measured using repeated 2D imaging methods, resulting in a temporal offset between slices. To compensate for this timing difference, slice-timing correction (i.e. temporal data interpolation) has been used as an fMRI pre-processing step for more than fifteen years. However, there has been an ongoing debate about the effectiveness and applicability of this method. This paper presents the first elaborated analysis of the impact of the slice-timing effect on simulated data for different fMRI paradigms and measurement parameters, taking into account data noise and smoothing effects. Here we show, depending on repetition time and paradigm design, slice-timing effects can significantly impair fMRI results and slice-timing correction methods can successfully compensate for these effects and therefore increase the robustness of the data analysis. In addition, our results from simulated data were supported by empirical in vivo datasets. Our findings suggest that slice-timing correction should be included in the fMRI pre-processing pipeline.

Highlights

► Slice acquisition delays can degrade sensitivity of fMRI data analysis. ► Slice-timing correction during pre-processing suppresses estimator bias. ► Our findings based on extensive simulations are supported by in vivo data.

Introduction

Functional magnetic resonance imaging (fMRI) data sets are generally acquired using sequential 2D imaging techniques like single-shot echo planar imaging sequences (Stehling et al., 1991; Turner et al., 1998). Since fMRI data analysis is essentially a time course analysis, exact timing with respect to the stimulus presentation paradigm is crucial.

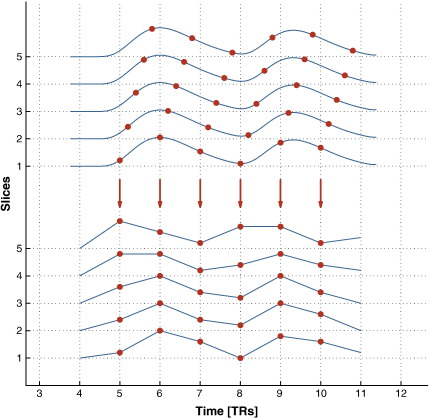
Single-shot EPI sequences allow for single-slice acquisition times in the range of 50–150 ms. Whole-brain coverage is achieved by sequentially repeated image acquisition for a stack of individual slices. Depending on brain coverage and slice thickness, a whole volume can be acquired within typical repetition times (TRs) ranging from hundreds of milliseconds to several seconds. This causes slice acquisition delays between individual slices which may add up to significant temporal shifts over the full 3D volume between the expected and actually measured hemodynamic response (Fig. 1). As a consequence, the reliability and power of time series analysis may be compromised, resulting in degraded sensitivity to detect activations.

Fig. 1.

Illustration of the slice-timing problem. The hemodynamic responses of the individual slices are acquired at different points in time (top), yielding an aberration in the scanned data (bottom). The observed time courses of a hemodynamic response reach their maximum amplitude earlier in slices acquired later. Without adequate compensation this leads to biased estimators in fMRI analysis.

To compensate for slice acquisition delays slice-timing correction (STC) has been proposed as a pre-processing step (Calhoun et al., 2000; Henson et al., 1999) and is currently included in all major fMRI software packages (such as SPM, AFNI, BrainVoyager or FSL). In STC, the individual slice is temporally realigned to a reference slice based on its relative timing using an appropriate resampling method. Different data interpolation methods have been proposed for STC including linear, sinc and cubic spline interpolation (Goebel, 2010).

A more elegant way would be to model known nuisance factors during analysis rather than changing the data. Accordingly, it has also been suggested to account for slice-timing differences via adjustments in the analysis procedure, in particular the model setup, by using (a) additional regressors based on the temporal derivatives of the expected hemodynamic response function in the general linear model (GLM), or (b) slice-dependent regressors time-shifted according to their acquisition lag (Henson et al., 1999).

Adding temporal derivatives might be advisable to compensate for non-linear neural and vascular effects resulting in time-shifted and time-dispersed BOLD responses in different regions, a crucial issue particularly for event-related fMRI (Calhoun et al., 2004; Friston et al., 1998; Worsley and Taylor, 2006). However, it has not been shown yet, whether including temporal derivatives into the GLM can fully compensate for slice acquisition delays.

The second strategy to counter slice-timing effects is based on constructing slice-specific time-shifted regressors (Henson et al., 1999). This strategy, however, is problematic with spatially smoothed data sets. In many fMRI processing pipelines spatial smoothing is considered a mandatory pre-processing step; it not only allows for random-field approximation based corrections for multiple comparisons, but also for group analyses in standard space (and also to increase image signal-to-noise ratios) (Hopfinger et al., 2000). Usually 6 − 10 mm³ isotropic Gaussian kernels are used for smoothing, leading to considerable signal dispersion across adjacent slices. Whereas this is not a serious concern for sequentially acquired volumes, it may cause significant estimator bias for interleaved acquisition, because neighboring slices are typically about a half TR apart in time.

So far, no extensive study has been published on the effectiveness and robustness of STC and potential unwanted effects on data quality. Henson et al. (1999) showed a better detection rate of neural activity for slice-timing corrected data for a particular event-related design. Since then, the applicability of STC, and whether to perform it or not, has been discussed vigorously (if informally) within the neuroimaging community. The main contention has been whether slice-timing correction removes artefactual variance components when there is a long interval between scans (e.g. TR > 2 s). This is the situation in which STC would be most effective but it is also the situation, which presents the greatest problems for STC interpolation schemes. This paper is an attempt to treat slice-timing effects formally and assess whether their correction can improve fMRI data analyses.

Here we assess the influence of slice acquisition delays (slice-timing effects) using simulated data sets varying acquisition parameters, paradigm designs and noise levels. Herein we compare the results from GLM analyses of uncorrected and slice-timing corrected data (as implemented in SPM8) in order to quantify the efficacy of STC methods. To further assess the interaction between STC and the inclusion of temporal derivatives in the GLM, we compared STC to no STC, with and without temporal derivatives. This resulted in a comparison of four schemes or methods corresponding to the cells of a 2 × 2 factorial design. To validate the conclusion from simulated data, we also show the results of a study in human subjects using a paradigm, which was specifically designed to investigate slice-timing effects in real fMRI studies.

Methods

Slice-timing correction approaches

Different methods of temporal interpolation can be used for slice-timing correction. While linear interpolation (Eq. (1)) is easily implemented and fast, it may introduce undesired temporal smoothing and more sophisticated interpolation schemes are preferred, such as sinc interpolation as used by default within SPM8. Assuming an acquired time series y of slice number n at time point t(n), linear interpolation to the slice-time of a reference slice t(r) can formally be expressed as:

$$y_n^{\left(r\right)}=\frac{\left(t\left(r\right)-t\left(n-1\right)\right)y_n+\left(t\left(n\right)-t\left(r\right)\right)y_{n-1}}{t\left(n\right)-t\left(n-1\right)}$$ (1)

An efficient implementation of the sinc interpolation (Eq. (2)) entails applying a phase shift (i.e. adding a constant value) in the frequency domain of the signal, obtained by fast Fourier transformation. This method is used in SPM, using an implementation to compensate for interpolation and wrap-around effects (Calhoun et al., 2000).

$$y_n^{\left(r\right)}=\sum _{i=-\infty }^{\infty }{x}_i\text{sinc}\left(\frac{\pi }{\text{TR}}\left(r-i\text{TR}\right)\right)$$ (2)

Cubic spline interpolation is the default interpolation method in BrainVoyager (Goebel, 2010).

The effects of slice-timing correction were studied based on extensive simulations covering a wide range of blocked and event-related design paradigms, varying inter-stimulus intervals, contrast-to-noise ratios (CNRs), slice acquisition orders and TRs. In addition, fMRI data from a specifically designed group study were analyzed in order to validate the findings in simulated data. Slice-timing corrections were performed using the spm_slice_timing.m function as implemented in SPM8 (Wellcome Trust Centre for Neuroimaging, UCL, UK) and results were analyzed using MathWorks MATLAB R2009a (Natick, MA, USA).

Simulated data

A set of 4-dimensional matrices were created to simulate a series of MRI scans with 20 slices, a resolution of 32 × 32 px² and 300 seconds run duration. Voxel size was set to 1.5 × 1.5 × 3 mm³. The time courses of each set were based on different blocked and event-related designs convolved with the canonical hemodynamic response function included in SPM8.

The length of on and off blocks in blocked designs was set to 10, 15, 20, 25, and 30 s. Event-related designs were single events with an average stimulus onset asynchrony (SOA, i.e. the time between the onset of one stimulus and the consecutive stimulus) of 4, 6, 8, 10, and 12 s; SOAs were jittered according to a uniform distribution within $\pm 50\raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$ SOA. Although very short SOAs are known to furnish low detection sensitivity, they were included in our test set as an extreme example.

This raw data with high temporal resolution (f = 20Hz) were sampled to temporal resolutions of TR = 1, 2, 3, and 4 seconds, including slice-dependent acquisition time differences by shifting the response function by $TR-\frac{TR}{numberofslices}$ between the first and the last scanned slice. Sequential and interleaved scanning orders were simulated.

Different levels of white noise were added to time courses of each voxel yielding simulated contrast-to-noise ratios (CNR) of 1.7, 2.5, 5, and infinite (i.e. noise-free), respectively.

After 3-dimensional spatial smoothing of 6 mm FWHM (isotropic Gaussian kernel), GLM analysis was performed with stimulus onsets aligned to the acquisition time of the middle slice. This caused a TR-dependent slice-timing difference of approximately up to ± 0.5, 1, 1.5, and 2s, respectively, between slices. In separate analyses, the temporal derivative of the response function was also modeled in the GLM to allow some flexibility in the signal onsets and to evaluate its capabilities in compensating slice acquisition delays (Friston et al., 1998).

Finally, four datasets were evaluated: uncorrected (original) and STC (STC) data, each analyzed with and without temporal derivatives (original + TD, STC + TD) in the GLM.

Human fMRI data

Subjects

13 healthy subjects (8 male, 5 female; age: 25.4 ± 3.3 years) participated in this study, which was approved by the ethics committee of the Medical University of Vienna, Austria, and gave written informed consent prior to the experiment. Subjects were clinically assessed and free of current or past psychiatric or neurological conditions. Negative drug screening was mandatory. Nicotine or caffeine intake was not allowed on the day of the measurement.

Data acquisition and fMRI paradigm

The participants were instructed to do bimanual finger tapping during the display of an animated checkerboard, changing black and white tiles with a frequency of 8Hz, in a blocked paradigm, consisting of six blocks of 10s resting and 10s finger-tapping periods (130s total). This design is known to robustly trigger neural activation in visual areas (occipital lobe) and motor areas (precentral gyrus, supplementary motor area, basal ganglia). Finger movements were self-paced and none of the subjects reported difficulties with this task.

75 volumes were acquired on a TIM TRIO 3T full-body MR scanner (SIEMENS Medical, Germany) using single-shot 2D EPI with the following parameters: 20 axial slices of 3mm thickness (2.1mm slice gap) aligned to the connecting line between anterior and posterior commissure with a matrix size of 128 × 128px², TE = 40 ms, TR = 1800 ms and a field of view of 192 × 192 mm² (1.5 × 1.5 × 3 mm³ voxel size). Slices were acquired interleaved along the z-axis in feet-to-head direction starting with even-numbered slices (i.e. 2, 4,…, 20, 1, 3,…, 19).

Pre-processing and analysis

Slice-timing correction as implemented in SPM8 was applied to all 13 empirical datasets. All other standard pre-processing steps were similarly performed on both the uncorrected original data and the STC data, including realignment to compensate for bulk head movements, normalization to MNI space and spatial smoothing with a Gaussian kernel of 8 × 8 × 8 mm³ FWHM. Each data set was masked with the SPM8 brainmask template.

GLM analysis was performed using regressors generated by convolving the time course of the visual stimulation onsets and duration with the SPM8 canonical hemodynamic response function. Motion parameters obtained from realignment were included in the GLM. All other analysis steps were identical to those described for simulated data, yielding four datasets of uncorrected and slice-timing corrected data, each with and without temporal derivatives. The single-subject parameter estimate maps from the canonical regressors were used for second level group analyses.

We assessed the effect of slice-timing correction and temporal derivative modeling in two ways. First, we quantified the bias in parameter estimation, associated with temporal correction and modeling, by examining the parameter estimates relative to the estimates from noiseless data. To assess sensitivity, we analyzed all combinations of treated data to test for activations at the group level in the empirical study, using statistical parametric maps based upon T-statistics.

Results

Simulated data

Our results clearly showed a reduction of parameter estimates (β-values) with increased estimator bias, depending on the measurement and paradigm parameters. In general, this bias was reduced by the STC procedure.

As expected, the reduction of parameter estimates due to slice-delay effects were more pronounced for long TRs, event-related designs and designs with shorter SOA. We found a maximum decrease of parameter estimates of 63% (event-related design, average SOA = 4s, TR = 4s). In blocked designs we observed a reduction of 12% (block length 10s, TR = 4 s). Note that in our simulations the paradigm regressors and slice-timing correction are temporally aligned to the middle slice of the 3D volume. Therefore, a TR of e.g. 4 s in this simulation is comparable to a dataset with a TR of 2s when the first (or last) slice acquired are used as a reference slice. This can be a reasonable practice, if the region of interest and putative activations are located near the first (or last) slice because it suppresses temporal interpolation effects in these areas.

Compared to uncorrected data an increase of parameter estimates was found for all tested paradigms, TRs and CNRs in slice-timing corrected data. Importantly, STC did not cause a decrease in average or minimum parameter estimates in any of our datasets (Fig. 2B). One simulation set (event-related design, average SOA = 4s, TR = 4s; Fig. 2B, lower panel, 1st box, 4th column) showed a decrease by 4% in maximum parameter estimates. This, however, is attributable to aliasing artifacts caused by noncritical sampling, which can occur when the average SOA is shorter or equal to the TR.

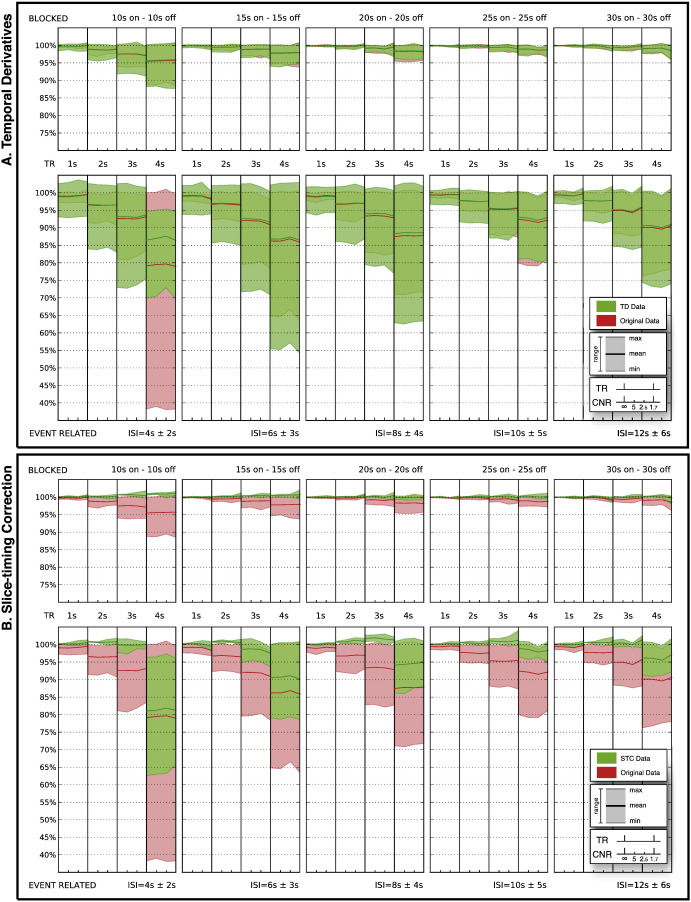
Fig. 2.

Effects of including temporal derivatives (TD) [A] or performing slice-timing correction (STC) [B] on simulated data. The figure shows a comparison of parameter estimates for uncorrected (red) and corrected (green) data for blocked and event-related designs (upper and lower boxes respectively), varying TRs (columns) and CNRs (sub-columns within TR columns). Values are shown relative to the maximum parameter estimate of the uncorrected, noise-free data. Bold lines indicate the mean across all slices. Shaded areas show the range from highest to lowest estimate. It can be seen that parameter estimates of the slice-timing corrected datasets [B] are, in general (higher mean and smaller range), higher than the uncorrected datasets and therefore closer to the unbiased estimates with optimal temporal alignment (i.e. 100%). Also for lower contrast-to-noise ratios (CNRs) higher parameter estimates were consistently gained for slice-timing corrected data sets.

Omitting STC and compensating for slice-timing effects by including the temporal derivatives into the model yielded no increase in mean parameter estimates (Fig. 2A).

While higher levels of Gaussian noise caused higher residual values in the result of the GLM analysis, it had little impact on the parameter estimates. We found no noise-related changes in the performance efficiency of slice-timing correction.

To better assess the consequences of slice-timing correction we further analyzed its effect on the parameter estimates in individual slices. Fig. 3 shows a comparison of typical event-related designs. It can be seen that in all presented cases slice-timing correction led to an increase of parameter estimates and a reduction of residuals. We found this for all tested designs and image parameters, with the exception of designs with subcritical sampling. It should be noted, however, that this decrease in parameter estimates was not due to a failure of the slice-timing correction algorithm but due to aliasing artifacts because of noncritical sampling of the data.

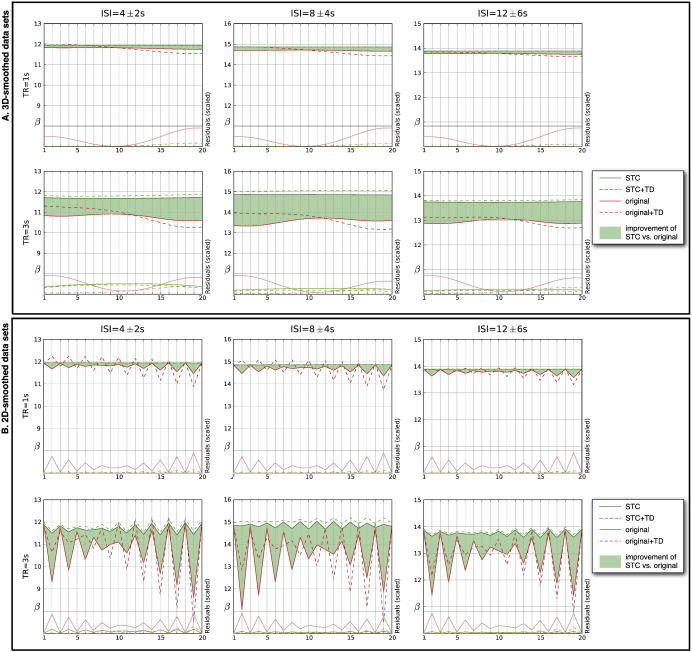
Fig. 3.

Slice-dependent changes in a selection of typical event-related designs. The top part of each graph shows a comparison of parameter estimates from uncorrected (red) and slice-timing corrected (green) data sets. Dashed lines represent the parameter estimates of models where temporal derivatives were included. Residuals of the models are plotted at the bottom part of the graphs. To visualize the impact of spatial smoothing on the temporal alignment the same data is presented 3D (panel A) and 2D (panel B) smoothed.

Three-dimensional smoothing may conceal the effects of STC on the individual slices. Therefore we also analyzed simulated images that were only smoothed in-plane. For our tested datasets slice-timing correction yielded robust and profound improvements of parameter estimates for all individual slices. There was a significant decrease of parameter estimates and increase of residuals in the uncorrected datasets in slices with larger temporal offset (Fig. 3).

Human fMRI data

As expected, the paradigm stimulated brain activation changes in the motor areas (M1, SMA, z = 56 mm [MNI]), the visual cortex (V1, z = − 4 mm [MNI]) and the cerebellum (culmen, V1, z = − 24 mm [MNI]) (Fig. 4, left table, original).

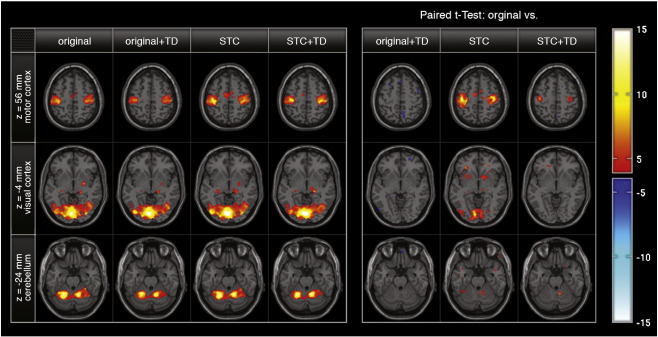
Fig. 4.

Comparison of in vivo fMRI data. Group SPMs of a visual-motor task versus rest condition (left table) and paired t-test comparisons of compensation strategies for slice-timing effects. Threshold was set to p < 0.001. The positive effects of slice-timing correction on the parameter estimates (STC, left table, third column) are present particularly in the motor network (first row). Due to our measurement parameters (feet-to-head acquisition order) slice-timing effects were expected to be most prominent in this dorsal section. Comparison of the uncorrected and STC data revealed significant increase of t-values in group statistics.

Comparing slice-timing corrected and uncorrected data using paired T-tests (Fig. 4, right table, orig. vs STC) revealed significant (p < 0.001) activation differences. This particularly affected dorsal regions, i.e. regions with higher temporal offset due to the acquisition direction, where the slice-timing effect was expected to be most dominant. Importantly, robust SMA activation was detected in the STC data sets only. Differences were less prominent in ventral brain regions, where slice-timing effects were expected to be lower.

For uncorrected data, adding temporal derivative regressors in the design matrix caused a reduction in sensitivity, particularly in the motor network (M1 and SMA) (Fig. 4, left table, TD, and right table, xtitoriginal vs TD).

Including the temporal derivatives in the GLM analysis of the slice-timing corrected data yielded higher parameter estimates in the focal point of M1 activation (Fig. 4, left table, STC+TD, and right table, original vs STC+TD). However, we found no activation in the SMA.

Discussion

Our results clearly show a benefit of slice-timing correction for parameter estimation on single-subject level, which, in turn, could significantly improve sensitivity in group statistical analysis. This is particularly true for event-related designs and blocked designs with short block length. Analysis of in vivo fMRI images supported our findings from simulated data.

No adverse effects of STC with respect to parameter estimate bias were found for realistic paradigm designs. Higher noise levels had no impact on estimates or the efficiency of the applied STC algorithm. Further, no adverse effects were found in in vivo datasets with non-Gaussian noise due to physiological and motion artifacts.

While beneficial effects were found for STC, adding temporal derivatives to the model did not suppress bias (shrinkage) in parameter estimates to the same extent. Clearly, the shrinkage of parameter estimates does not necessarily decrease sensitivity, provided the between subject variability in parameter estimates decreases in proportion. However, our empirical example suggests that slice-timing correction increased sensitivity to group effects in a way that was subverted by including temporal derivatives. It has been shown previously that using TD in whole-brain analyses can diminish power depending on the response latency (Della-Maggiore et al., 2002). This finding is consistent with our findings.

Furthermore, we know that temporal derivatives can explain variance due to temporal delays of about ± 1s (Henson et al., 2002). This upper bound on the delays that temporal derivatives can handle reflects the failure of the first-order Taylor expansion implicit in their use, which is determined quantitatively by the characteristic time constants of the HRF. This bound means that, even under the assumption of an optimal model (i.e. regressors time-locked to the middle of one TR), derivatives will not model adequately slice-timing effects caused by TRs greater than 2s. Our simulations corroborate this fact and additionally showed no consistent improvements even for shorter TRs. This is expected as the canonical HRF and its derivative can lose their orthogonality when convolved with a stimulus function. Therefore, a part of the variance explained by the canonical HRF regressor may be modeled by its derivative. In general, including the temporal derivatives will thus lead to a decrease in residuals, possibly increasing statistical significance on the single-subject level, but it will also reduce the parameter estimates of the canonical regressor. This may reduce sensitivity, as only the latter usually enter ordinary least squares random-effects group analysis. In principle, the problem of non-orthogonality can be addressed by specifying (F) contrasts at the second level over both the canonical and temporal derivative parameter estimates. However, this depends upon their being a consistent group effect on both, which may not be guaranteed if slice-timing effects are artefactual (Calhoun et al., 2004; Henson et al., 1999; Steffener et al., 2010).

The question of whether to include temporal derivatives or not is really an issue of model selection. Generally speaking, their inclusion will explain away early or late hemodynamic responses, which could reduce sensitivity. On the other hand, it is at least theoretically possible that modeling real or artifactual latency differences will increase the precision of parameter estimates. The overall impact on sensitivity to canonical hemodynamic responses is clearly difficult to generalize about. However, the procedure described in this paper provides a simple protocol for assessing the impact of temporal derivatives, with or without slice-timing correction (see Fig. 4).

The results in this paper are based on SPM8's implementation of the STC algorithm. Nevertheless, our findings should be transferable to the implementations in other fMRI applications, as cubic spline interpolation and sinc interpolation have been shown to provide almost identical results (Goebel, 2010).

A sometimes-neglected issue is the interaction of the slice-timing effect and motion. Subject movement along the z-axis or head tilts around the x-axis will introduce not only spatial but also temporal artifacts. This is a concern particularly for clinical applications where patients might not be able to fully suppress their movements while in the scanner. Given the nature of typical serial fMRI pre-processing pipelines one could consider performing slice-timing correction before realignment if subject movement is moderate. In the presence of pronounced inter-slice movements it might be preferable to realign before STC. Clearly, serial correction approaches like these are suboptimal and cannot compensate for the interactions between time shifts and movement (Bannister et al., 2007), and a combined method of motion and timing correction might thus be indicated (Bannister et al., 2004). However, this is not yet implemented in the major fMRI analysis packages.

A non-beneficial side effect of all resampling methods is the possible introduction of aliasing effects for signals at frequencies above the Nyquist sampling limit of $f=\frac{1}{2\times TR}$. Given a typical TR of 2 s (f = 0.25 Hz) a minimal inter-stimulus interval (ISI) of more than 4 s is recommended. When using the slice acquired in the middle of the acquisition period (TR) as a reference slice, the signal needs to be shifted by TR / 2, therefore reducing the suggested minimal ISI to 2 s. When choosing the mid-slice as the target less temporal interpolation is needed. This might decrease the risk of interpolation artifacts. Note that all regressors in the GLM also need to be adjusted for this shift in time by TR / 2.

Finally, Holmes et al. (1997) had shown that no physiologically induced signal change was present at frequencies over 0.25 Hz. As a consequence fMRI data can be assumed band-limited, which means that potential aliasing effects by STC only affect signal components originating from noise.

In conclusion, slice-timing correction has been shown to suppress bias in quantitative parameter estimates at the single-subject level and, empirically, to increase sensitivity in group-level statistical inferences.