Investigation of Design Space for Freeze-Drying: Use of Modeling for Primary Drying Segment of a Freeze-Drying Cycle

Abstract

In this work, we explore the idea of using mathematical models to build design space for the primary drying portion of freeze-drying process. We start by defining design space for freeze-drying, followed by defining critical quality attributes and critical process parameters. Then using mathematical model, we build an insilico design space. Input parameters to the model (heat transfer coefficient and mass transfer resistance) were obtained from separate experimental runs. Two lyophilization runs are conducted to verify the model predictions. This confirmation of the model predictions with experimental results added to the confidence in the insilico design space. This simple step-by-step approach allowed us to minimize the number of experimental runs (preliminary runs to calculate heat transfer coefficient and mass transfer resistance plus two additional experimental runs to verify model predictions) required to define the design space. The established design space can then be used to understand the influence of critical process parameters on the critical quality attributes for all future cycles.

INTRODUCTION

Quality by design (QbD) is gaining wide acceptance within the industry to help pharmaceutical manufacturing move into the twenty first century with enhanced process understanding and process capability. The primary aim of a QbD approach is to assure that product quality is built into the product by design. This applies to both formulation and manufacturing processes. Design space is a key part of QbD paradigm. Design space is representation of multidimensional interaction of input variables such as process parameters and/or material attributes which affect the quality of the product. Several reports in literature address design space as it relates to formulation development (1–3). To date, articles reporting design space and its applications in the area of freeze-drying process are few (4–6).

Primary drying is usually the longest part of the freeze-drying cycle during which period the ice is sublimed. Effectively defining the design space for primary drying will enable defining an operating window of critical process parameters to get an optimal product. Successful presentation of primary drying cycle conditions in this format will allow operational freedom and also regulatory freedom for unforeseen excursions in process parameters.

Recently, Nail and Searles presented an approach to define design space for primary drying (4). The suggested approach comprised of identifying boundaries of shelf temperature and chamber pressure that will result in product temperatures below collapse temperature and sublimation rates below a threshold that will avoid choked flow conditions in the freeze dryer. Design space for primary drying was described in another article although "design space" term was not used in that paper (7). Investigation of the freeze-drying design space would require multiple experimental runs and can be very expensive especially if the experiments involve full-scale freeze dryers, although the process is conceptually straightforward. To reduce cost associated with a thorough investigation of the design space, we propose the use of freeze-drying models. Modeling primary drying during freeze-drying in a vial is a fairly well-understood area. Broadly, the models can be classified into steady state and nonsteady-state models. In steady-state modeling approach, pseudo steady-state approximation is used to obtain a solution of the heat and mass transfer equations at several stages during the primary drying phase, thus evaluating product temperature profile as a function of time (8). Several researchers have developed nonsteady-state models of sublimation and desorption. Some advantages of nonsteady-state models include residual moisture prediction as a function of time and describing the nonsteady-state parts of primary drying (immediately after a change in shelf temperature; 9–11). Success in obtaining good predictions using these models hinges on the quality of input data to the model. Inputting accurate heat transfer coefficient and mass transfer resistance is essential for the model to predict accurate product temperatures and drying times. This means user has to spend time and additional resources to perform specific experiments to determine heat transfer coefficient and mass transfer resistance.

The primary objective of this study was to explore the application of modeling to investigate design space concepts for primary drying. Critical quality attributes (CQAs) are physical, chemical, biological, or microbiological properties of the drug product that define the product quality (12). Some of the CQAs that are relevant to freeze-dried product are potency and purity of the product, reconstitution time, and residual moisture levels. In addition, appearance of the freeze-dried cake can be considered an important attribute to meet aesthetic requirements. Product temperature should be maintained below critical product temperature to get the desired cake appearance and to ensure quality product. Also, the set point of primary drying time should allow sublimation to be completed before ramping the temperature into secondary drying. Neither product temperature nor sublimation endpoint is directly controlled by the operator. They are indirectly controlled by shelf temperature and chamber pressure. To ensure that the CQAs are acceptable, it is essential that the product temperature during primary drying and duration of primary drying meet prespecified constraints, i.e., critical product temperature and complete sublimation before ramping to secondary drying.

Critical process parameters (CPPs) are those which can be controlled and affect the critical quality attributes. Shelf temperature, chamber pressure and the duration for primary drying set point are critical process parameters that influence the product temperature during primary drying. Therefore in this work, we consider the shelf temperature and the chamber pressure during primary drying as critical process parameters and establish the functional dependence of product temperature during drying and sublimation end point on the shelf temperature and chamber pressure (CPPs), i.e., establish design space for primary drying portion of freeze-drying process.

Once the design space is established, using model predictions, two experiments were conducted to verify the model predictions. The confirmed design space can then be used for commercial manufacturing for the given product. This simple step by step by approach to defining and confirming design space for the primary drying will allow us to minimize the number of experimental runs resulting in significant time and financial savings.

MATERIALS AND METHODS

Pfizer A, a small molecule is utilized as a model compound to implement the design space concepts for primary drying. Formulation details are listed in Table I. Laboratory and pilot scale freeze-drying experiments were done in Lyostar II and Lyovac GT 20/FAK 3011, Amsco/Finn Aqua (shelf area 1.08 m²), respectively. Stoppering of vials can be done sequentially from the top shelf to the bottom shelf in pilot scale freeze dryer. Commercial scale runs were conducted in Lyomax supplied by IMA Edwards.

Table I.

Details of Pfizer A Formulation

Solids concentration, g/g	0.16
Fill volume, mL	21
Critical product Temperature, °C	−16

Mathematical modeling was performed using commercially available PASSAGE Freeze Drying software by Technalysis Inc. Details of the model equations and assumptions are described elsewhere (9,13). The model describes the heat and mass transfer equations in frozen and dried regions of a single vial. These equations are solved by finite element formulation in 2-D axissymetric space. An arbitrary Lagrangian Eulerian method was used to accurately model the sublimation interface. This model requires several input parameters. These parameters include formulation details such as concentration of solids and fill volume in the vial, vial dimensions, heat transfer coefficient of vial under the process conditions, and mass transfer resistance the dried cake offers to vapor flow due to sublimation of ice. Complete details of the model including assumptions and limitations can be found in the reference (9,13).

Two important parameters for accurate model predictions are the heat transfer coefficient and the mass transfer resistance. Heat transfer coefficient is measured by performing vial sublimation tests. This involves filling the vial of interest with pure water and freeze-drying under the process conditions of interest to result in partial sublimation of the contents of the vials. By weighing the vials before and after sublimation test, we can calculate the overall heat transfer coefficient of the vial. Procedure for inputting this measured heat transfer coefficient into the model is described in literature (9). Sublimation tests in this study were conducted in a commercial-scale dryer. Of the 30-mL vials, 47,000 were filled with 22.6 g of WFI then loaded into the freeze dryer. After freezing the water, the vials were processed using the following conditions during sublimation—+20°C shelf temperature, 15 Pa chamber pressure, and 12 h of drying. Sublimation cooling will ensure that the frozen ice will not melt even though the shelf temperature during primary drying is higher than the equilibrium melting point of ice. Vials were then stoppered, unloaded, and samples were removed to determine the water loss by sublimation. Knowing the amount of ice sublimed and heat of sublimation of the ice, the heat transfer coefficient can be calculated. Details of these calculations are provided in the Appendix.

Mass transfer resistance of the dried cake is measured by conducting a gravimetric test. During the freeze-drying process, few vials were completely stoppered at regular time intervals thus stopping sublimation in those vials from that point forward. By noting the weight of water that sublimed and knowing the heat of sublimation of ice, product resistance can be calculated. Pfizer A formulation was freeze-dried in pilot freeze dryer (Lyovac GT/20). About ten vials on each shelf were stoppered after 11, 19, 33, and 40 h after initiation of primary drying. The vials were weighed before and after drying. The average weight loss was plotted versus time and product resistance is then calculated. Details of these calculations are given in the Appendix. The product resistance measured has to be input into the model as Knudsen flow coefficient, the details of which are explained elsewhere (9).

Utilizing model predictions, a set of primary drying conditions, i.e., shelf temperatures and chamber pressures were explored to obtain product temperature and primary drying time. The primary drying time is then converted to average sublimation rate during primary drying as we know the amount of water that is removed during primary drying. Once the model predictions are confirmed with few experimental data points (two experimental runs were conducted at pilot scale to confirm model predictions), boundaries for product temperature, drying time, and average sublimation rate are drawn on the contour plots based on critical quality attributes. Product temperature boundary is defined by the critical product temperature (−16°C) to avoid collapse. The critical product temperature was determined in separate freeze-drying experiments by visually inspecting the vials during and after the freeze-drying cycle. Critical product temperature was identified as the maximum product temperature during primary drying (noted by thermocouple reading) that produces visually acceptable (following standard procedures to release a freeze-dried product where the dried cake is observed for any shrinkage or loss of aesthetic appearance) cake after freeze-drying. Limit on the drying time is defined by the maximum allowable time for one lyophilization run to accommodate the plant’s demands for product supply. Constraint on average sublimation rate is defined by the maximum sublimation rate that the condenser can handle. These constraints on product temperature, sublimation time, and sublimation rate define the boundaries for critical process parameters, i.e., shelf temperature and chamber pressure thus defining the design space for further use. The product can withstand slightly higher product temperatures than −16°C. But having −16°C as the constraint will provide additional comfort level to ensure quality product.

RESULTS AND DISCUSSION

Building/Assembling Model

One of the important inputs to the model is the dry layer resistance of the freeze-dried cake. It is defined as the resistance the dried layer offers to the moisture coming from the subliming layers as the sublimation proceeds from top of the cake to the bottom. Mathematical definition and equation to calculate dry layer resistance can be found in Appendix. Table II shows the dry layer resistance as function of dry layer thickness from gravimetric measurement during a cycle where primary drying shelf temperature was −5°C and chamber pressure was 10 Pa. This lyophilization run was conducted in a pilot scale freeze dryer (Lyovac GT/20) details of which are mentioned in the experimental section. Details of cycle conditions are mentioned in Table III. It was confirmed using differential scanning calorimetry that the physical state of the frozen sample is amorphous.

Table II.

Dry Layer Resistance Calculated from Freeze Drying Run where Shelves are Sequentially Stoppered to Provide Sublimation Rate as a Function of Time

Thickness of dried layer, cm	Rp, cm2 × Torr × h/g
0.86	4.77
1.42	5.72
2.33	7.28
2.85	7.89

This sublimation rate is then used to calculate the dry layer resistance as a function of dry layer thickness

Table III.

Operating Conditions for Cycle Used to Measure Product Resistance

Lowest shelf temperature during freezing, °C	−40
Shelf temperature during primary drying, °C	−5
Chamber pressure during primary drying, Pa	10
Product temperature from thermocouple measurement, °C	−22

Heat transfer coefficient was measured in the commercial scale freeze dryer using water sublimation experiment. This experiment was carried at 15 Pa and shelf temperature of 20°C. The results varied from 0.000384 to 0.000632 cal/cm² sK. This variation can be attributed to the location of the vial in the freeze dryer and is also consistent with the variation reported in literature (14). Edge vials that are close to chamber walls experience higher heat transfer due to radiation than the center vials and hence the heat transfer coefficient of edge vials is higher than the heat transfer coefficient than the center vials. In this work, we therefore use 0.000384 cal/cm² sK as the heat transfer coefficient to determine the primary drying time for the last to dry vial and 0.000632 cal/cm² sK as the heat transfer coefficient to determine the maximum temperature that the product experiences in the edge vials. The following equation shows the functional dependence of heat transfer coefficient on the chamber pressure and is adapted from literature (8,15).

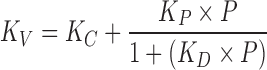where, K_C combines the contact heat transfer and radiative heat transfer, K_P relates free molecular diffusivity of the gas at 0°C and accommodation coefficient, and K_D is another combination of the separation distance between vial bottom and shelf surface, thermal conductivity of gas at ambient pressure, free molecular diffusivity of the gas at 0°C and accommodation coefficient. Complete details of these terms can be found in corresponding references (8,15). In the above equation, K_C depends on the location of the vial in the freeze dryer and P is the chamber pressure in millimetres of mercury. Value of K_C was set at 0.000127 cal/cm² sK for center vial and 0.000376 cal/cm² sK for the edge vial to match the experimentally observed values from the sublimation test conducted at 15 Pa. K_P and K_D are equal to 0.00332 cal/cm² sK mm Hg and 3.97 (mm Hg)⁻¹ as reported in the literature (8,15). Inclusion of the heat transfer coefficient and mass transfer resistance completes the model building activity. The next step is to utilize this model to predict the product temperature and during primary drying and sublimation time to complete the design space.

Design Space by Model

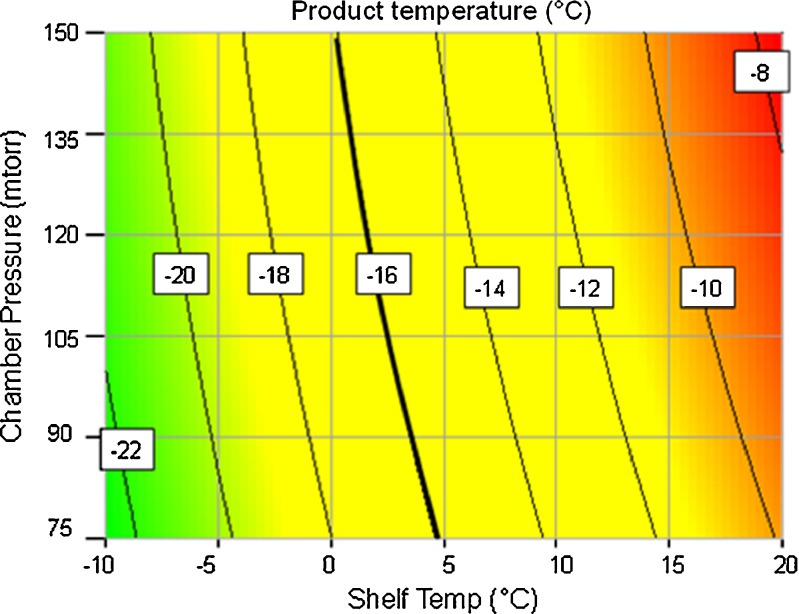
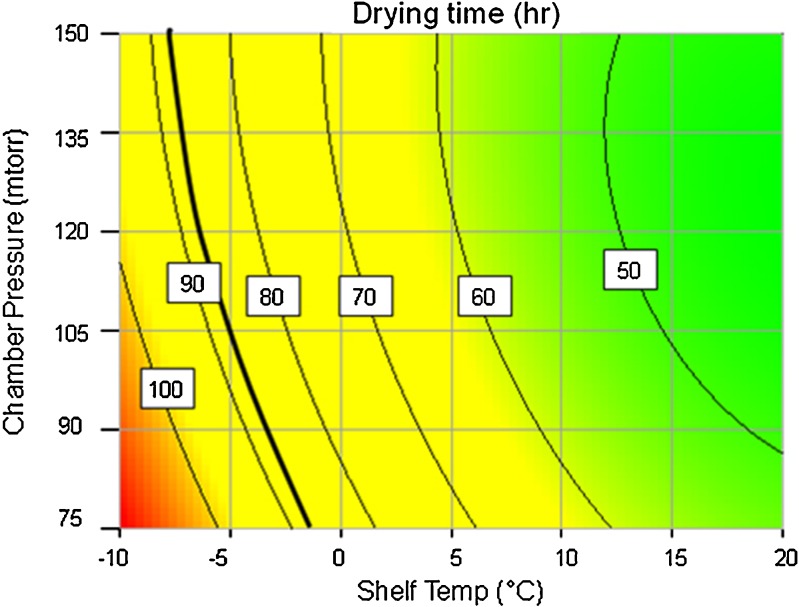
Using the aforementioned heat and mass transfer parameters, model predictions for product temperature and primary drying time and average sublimation rate during primary drying were obtained for multiple primary drying conditions (changes in shelf temperature and chamber pressure). This data is represented in Table IV. The same data is then also presented as contours of product temperature and primary drying time as a function of shelf temperature and chamber pressure in Figs. 1 and 2.

Table IV.

Product Temperature Predicted by PASSAGE Model as a Function of Shelf Temperature and Chamber Pressure during Primary Drying

Shelf temperature, °C	Chamber pressure, Pa	Product temperature, °C	Primary drying time, hr	Sublimation rate in freeze dryer, kg/h
20	10	−10.0	53	19.64
0	10	−18.0	84	12.34
−10	10	−22.7	115	8.98
20	15	−8.5	46	22.62
0	15	−17.0	73	14.03
−10	15	−21.8	100	10.18
20	20	−7.6	48	21.93
0	20	−16.2	67	15.20
−10	20	−21.0	95	10.72

Fig. 1.

Contours of product temperature predicted by PASSAGE model as a function of shelf temperature and chamber pressure during primary drying. Thick line represents the iso line for critical product temperature

Fig. 2.

Contours of primary drying time predicted by PASSAGE model as a function of shelf temperature and chamber pressure during primary drying. Thick line represents the iso line for highest acceptable primary drying time

Also marked in Fig. 1 is a line which represents critical product temperature (−16°C) above which the product is considered collapsed. This presents a constraint on the highest temperature the freeze-dried product can experience during primary drying. In other words, this −16°C line defines the upper boundary of the design space for shelf temperature and chamber pressure to maintain the product temperature within the predetermined value.

In Fig. 2, the solid line represents the contour for primary drying time of 87 h. This is determined by the maximum allowable time for one lyophilization run to accommodate the plant’s demands for product supply. The solid line, then, in Fig. 2 represents the upper boundary of the design space for shelf temperature and chamber pressure to maintain the primary drying time within the predetermined value to avoid partially dried vials entering secondary drying which can result in product melt back or collapse.

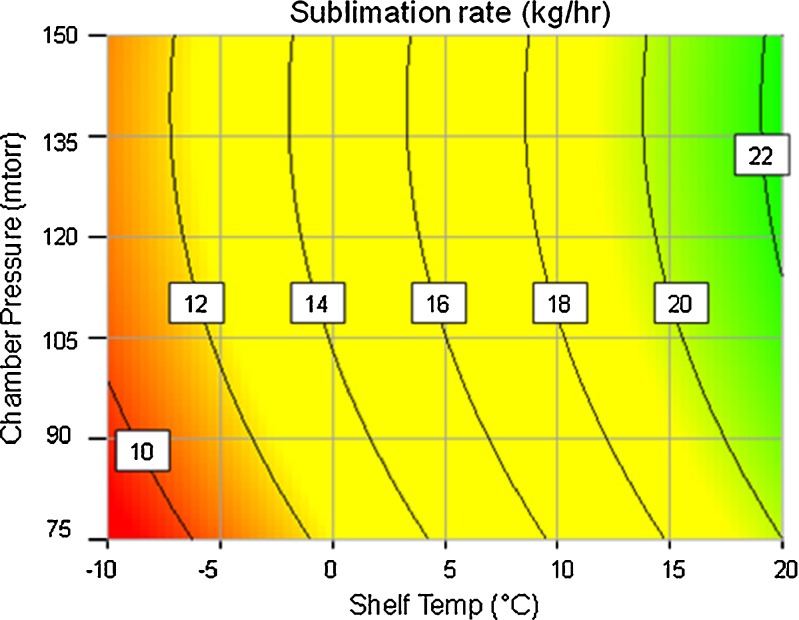
Figure 3 (also presented in Table IV) represent overall mass flow rate from the chamber to the condenser as a function of shelf temperature and chamber pressure. To calculate overall mass flow rate from the main chamber into condenser, we need to know the number of edge vials and number of center vials. Since the heat transfer coefficient of center and edge vials vary by almost a factor of 0.6, the differences in sublimation rates between center and edge vials need to be incorporated into the calculation of overall sublimation rate from the freeze dryer. In this work, we used an estimate of one row of vials as being edge vials that are located at the extreme outer row from historical experience. These vials constitute about 10% of the total load in the freeze dryer (47,000 vials per lot of which about 4,700 vials are along the extreme outer row) and the remaining vials as being center vials. Knowing the percent of edge vials, we can then easily translate the primary drying time of edge and center vials into overall mass flow rate from chamber to condenser. This data is both presented in Table IV and as contour plot (Fig. 3). Average sublimation rate observed during the pure water sublimation test to measure heat transfer coefficient was 36.4 kg/h. This number far exceeds sublimation rates predicted in Table IV or Fig. 3 (12–20 kg/h). Therefore for this work, we safely concluded that freeze dryer condenser can handle the sublimation rates that are experienced during the runs with Pfizer A formulation.

Fig. 3.

Contours of average mass flow rate from chamber to condenser based on primary drying time predicted by PASSAGE model as a function of shelf temperature and chamber pressure during primary drying, Threshold for sublimation rate: <36 kg/h, satisfied throughout the space

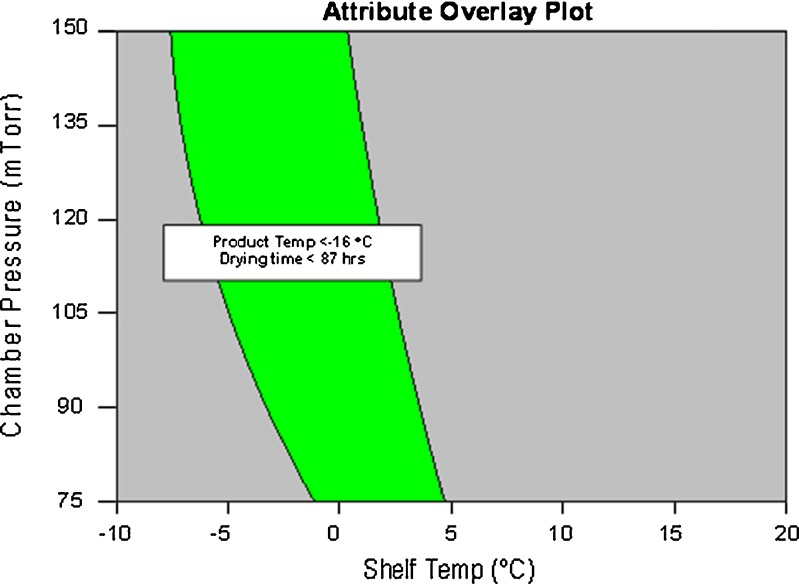
Figures 1, 2, and 3 are combined into Fig. 4. This represents the combined design space for shelf temperature and chamber pressure to maintain the product temperature below target product temperature of −16°C, drying time below 87 h. It is widely accepted fact that maintaining the product temperature below collapse temperature will ensure desired product quality (16). The constraint on sublimation rate has been relaxed because of the fact that the freeze dryer can handle much higher sublimation rates than those are possible during freeze-drying of Pfizer A as was demonstrated by sublimation rates observed in water sublimation tests. This representation of design space clearly defines the boundaries for shelf temperature and chamber pressure that will maintain the critical quality attributes for the product.

Fig. 4.

Overall design space (satisfies sublimation rate, product temperature, and drying time criteria shown on plot) during primary drying of Pfizer A including contours of product temperature, primary drying time, and overall sublimation rate

Verification of the “Design-Space-By-Model” Through Experiment

To gain confidence, the model prediction was verified using two experimental runs at pilot scale. At these values of shelf temperature and chamber pressure, the product temperature and primary drying time were confirmed using experimental runs. The overall mass flow rate is a function of primary drying time and hence need not be evaluated explicitly. Comparison of model predictions to experimental observations is presented in Fig. 5a (shelf temperature of −5 °C and chamber pressure of 10 Pa) and Fig. 5b (shelf temperature of −2 °C and chamber pressure of 11 Pa) at two conditions of chamber pressure and shelf temperature during primary drying. Note that we used the heat transfer coefficient values obtained from sublimation tests conducted on a commercial scale freeze dryer.

Fig. 5.

a Comparison of experimental product temperature profiles during primary drying to model predictions. Product temperature reading 1 is from a vial that is closer to the center of the shelf and product temperature reading 2 is closer to the edge of the shelf although not the absolute edge. Shelf temperature and chamber pressure during primary drying were −5°C and 10 Pa. The two model predictions represent two predictions utilizing two values of heat transfer coefficients representative of center and edge vials in the freeze dryer. b Comparisons of experimental product temperature profiles during primary drying to model predictions. Shelf temperature and chamber pressure during primary drying were −2°C and 11 Pa. The two model predictions represent two predictions utilizing two values of heat transfer coefficients representative of center and edge vials in the freeze dryer

Product temperature is measured during primary drying by placing a thermocouple in the vial during primary drying. There are different notions to determining the end point of primary drying. One technique is to use the product thermocouple reading. The point where the thermocouple reading starts to offset from steady state represented at point A or the point where the thermocouple reading starts to reach the shelf set point represented as point B in Fig. 5 can be used as an indication of completion of primary drying when the temperature at the bottom of the product rose due to absence of sublimation cooling. In this work, we take the conservative approach and consider point B as the end point of primary drying.

Also plotted in Fig. 5a, b are model predictions. Two sets of model predictions are plotted—one representing the temperature profile of the center vial for drying time comparison and the other representing the temperature profile of the edge vial for product temperature comparison. The product temperature noted by the thermocouples is in between the two predicted temperature profiles of the hottest and coldest vials in the freeze dryer. Primary drying time (point B from the thermocouple readings) is also less than the coldest vial drying time predicted by the model. It should be noted that the experimental temperature profiles are not necessarily from the vials that have the lowest or highest heat transfer coefficient. Considering other factors effecting the thermocouple reading (e.g., vials in which thermocouples are present lower the resistance to vapor flow by providing additional pathways for vapor transport from the vial to the chamber and thus result in faster drying and also probably higher ice nucleation temperature in thermocouple vials reduce resistance), the model predictions of product temperature and drying time are quite satisfactory. Utilizing model prediction, we will not risk product temperature above the critical product temperature and drying time that is not sufficient to completely sublime all ice. In this work, we used the commercial scale heat transfer coefficient to simulate cycles at pilot scale. The rationale was that majority of samples in pilot and commercial scale dryers can be considered as center vial, which means that the heat transfer coefficient of the center vials in both the dryers should be close to each other. Regarding the edge vials, the authors decided to use the heat transfer coefficient measured in commercial scale dryer and confirm the accuracy by comparing the model predictions to experimental results. As expected, the primary drying temperature prediction for the hottest vial (i.e., edge vial) is higher than what has been experimentally observed as shown in Fig. 5a, b. This was satisfactory as it suggests that if we use the edge vial heat transfer coefficient that is measured at commercial scale to define pilot scale operating conditions, we will not risk exposing the product to higher than desired temperatures. Similar explanation can be extended to the drying time prediction using the heat transfer coefficient measured at commercial scale.

These comparisons of model predictions and experimental values show successful verification of the design space presented in Fig. 4 and present comprehensive representation of ranges of shelf temperature and chamber pressure to maintain product temperature, drying time, and overall mass flow rate within desired ranges. As a verified design space, this figure can further be used in all future batches to be manufactured to select operating conditions and also to answer quality related questions about the product arising dues to process deviations.

How Accurate is the Model?

Uncertainties in the Input Parameters

Two important parameters that are input into the model are the heat transfer coefficient and mass transfer resistance. Both of these parameters are measured experimentally and independent of each other. Therefore, it is important to understand the effect of uncertainty in these measured parameters on the model predictions. We use parametric approach to understand the effect of uncertainty on model predictions

Effect of uncertainty in heat transfer coefficient has been indirectly tested when different heat transfer coefficient values are assigned to center and edge vials. As discussed in the results above, the heat transfer coefficient has significant impact on the predicted product temperature during primary drying and also on the duration of primary drying. Therefore, measuring the correct heat transfer coefficient is very important for accurate model predictions.

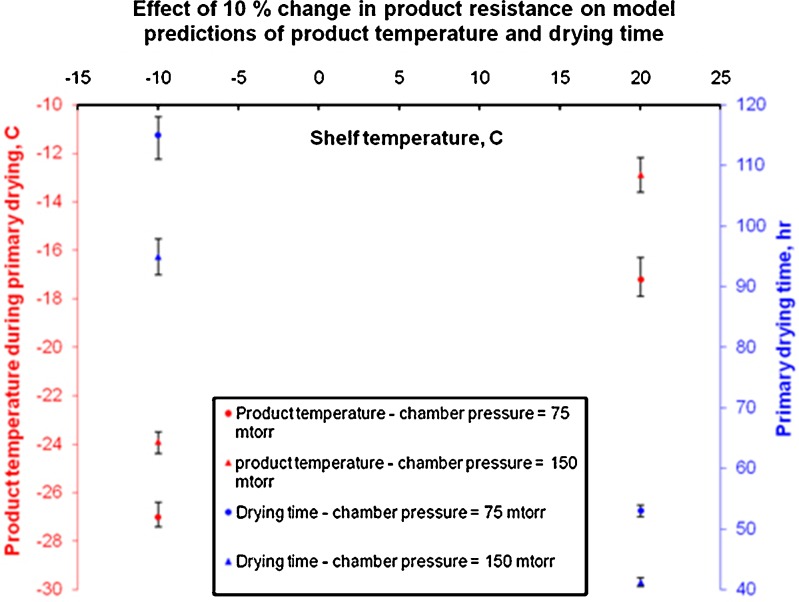
We attempted to quantify the effect of error in measurement of product resistance, Rp. An arbitrary change of ±10% in product resistance values given in Table I has resulted in changes in model predictions of product temperature and drying time. These changes in model predictions are shown in Fig. 6. For the purposes of these simulations, we have chosen extreme operating conditions of design space and also simulated the behavior of center vial as majority of the vials in the batch can be considered as center vials. Effect of change in product resistance on drying time prediction is significant at lower shelf temperatures where a 10% increase in Rp caused approximately 3% increase in drying time at both the chamber pressures tested. Also, the effect of change in product resistance on product temperature prediction during primary drying is significant at higher shelf temperatures where a 10% increase in Rp caused approximately 5% increase in product temperature (temperature expressed in °C). This stronger impact of change in Rp on drying time prediction at lower shelf temperatures can be explained by the fact that at lower shelf temperatures, usually, primary drying time is longer. Therefore, a small increase (decrease) in product resistance can have significant increase (decrease) primary drying time. Similarly, impact of change in Rp is significant on product temperature prediction at higher shelf temperature. This can be expected as the product temperature is higher at higher shelf temperatures and a small increase (decrease) in product resistance can significantly increase (decrease) the product temperature prediction. For ease of understanding, the same data is also presented in Table V. Chamber pressure did not significantly impact the influence of Rp on either product temperature or drying time. This data signifies the importance of measuring the product resistance accurately to obtain accurate model predictions. Actual operating conditions dictate the level of risk involved in wrong estimation of Rp. When operating at conditions that are close to the edge of failure, it becomes even more important that we accurately estimate Rp as a 5% error in prediction (of product temperature or drying time) will put us out of the design space.

Fig. 6.

Plot showing the effect of a 10% error in measurement of Rp on product temperature and drying time predictions during primary drying. Error bars represent changes in primary drying temperature and drying time when product resistance changes by 10%. Primary drying time is plotted on right y-axis and product temperature during drying is plotted on left y-axis

Table V.

Effect of a 10% Change in Product Resistance Measurement on Prediction of Primary Drying Time and Product Temperature during Primary Drying

Shelf temperature, C	Chamber pressure, Pa	Nominal Rp	10% lower Rp	10% higher Rp
		Product temperature, C
−10	10	−27	−27.4	−26.4
20	10	−17.2	−17.9	−16.3
-10	20	−23.9	−24.4	−23.5
20	20	−12.9	−13.6	−12.2
		Drying time, h
−10	10	115	111	118
20	10	53	52	53.9
−10	20	94.9	91.9	97.9
20	20	41.2	40.5	41.96

Model Shortcomings

Even though the model predictions are fairly accurate, there are some noticeable shortcomings in the mathematical modeling approach that we used in this work. Other modeling approaches to incorporate sublimation from all the vials in the freeze dryer (multiscale model) and not base the predictions on calculations performed on a single vial can be advantageous in certain situations to incorporate the scale differences inherent into the model. This approach will be computationally intensive and with limited added advantage when compared to the approach describe in this paper. Our approach of incorporating the scale differences in freeze dyers into the measured heat transfer coefficient does provide a simple alternative and yet reasonably accurate solution. This approach will save computational time when compared to a multiscale model especially on commercial freeze dryers that have upwards of 50,000 vials. Model predictions we obtain from the modeling approach proposed in this paper provide good comparison to experimental values if the input parameters are measured accurately. Hence, we think this approach will give good predictions with limited computational resources.

Estimation of the Project Value: Dollar Savings

To establish design space with experimental runs, we would need to run nine experiments described in Table III. To estimate cost of the experiments, we assumed that it costs $10 to manufacture one vial. This estimate is based on historical cost of goods calculation. With 50,000 vials in a freeze dryer, a total cost of nine experiments is $4.5 M. By using modeling, we can reduce the number of the experimental runs. Depending on the level of confidence in the model, we can run as few as one or two runs at large scale (additional characterization runs such as sublimations tests for heat transfer coefficient measurement and experiments to determine product resistance are required), resulting in savings of $3.5–4 M. Obviously, a higher confidence in the model can result in fewer experimental runs and therefore more significant cost savings.

CONCLUSIONS

In this work, we successfully defined design space as it relates to the primary drying phase of the freeze-drying process relating the critical quality attributes to critical process parameters (shelf temperature and chamber pressure). Further, we explored the applicability of mathematical modeling for a practical application in industrial freeze-drying of Pfizer A. Utilizing the mathematical model, we built the design space without conducting elaborate design of experiments and then verified the model predictions by conducting experiments at few points in the design space. In all, we established a design space for primary drying portion of Pfizer A lyophilization process using mathematical modeling.

Nomenclature

Rp

Dry layer resistance

Pi

Vapor pressure of the subliming ice

Pc

Chamber pressure

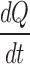
Rate of heat transfer from surroundings to the vial

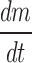
Sublimation rate of ice

∆H_s

Heat of sublimation of ice

T_b

Product temperature at the bottom of the vial

T_i

Temperature at the subliming interface

T_s

Shelf temperature

A_v

Outer cross-sectional area of the vial

K_I

Thermal conductivity of ice

L_ice

Thickness of ice at any given point in time

APPENDIX

Calculation of dry layer resistance from sublimation rate data

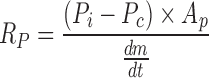
Equation relating mass flow rate to resistance of the dry layer

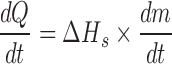
Equation relating heat required to sublime a given amount of ice

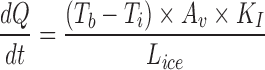
Equation relating heat transport in the frozen ice layer

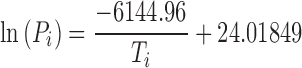
Equation relating vapor pressure of ice to sublimation interface temperature.

Knowing 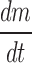from the experimental data and product temperature T_b, from thermocouple measurement above equations can be solved to calculate R_P at given time during the sublimation.

Calculation of heat transfer coefficient from sublimation tests

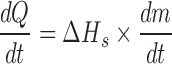Knowing 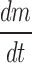and product temperature T_b, from the sublimation tests heat transfer coefficient K_V can be calculate from above equations