Abstract
Automatic processing of irrelevant stimulus dimensions has been demonstrated in a variety of tasks. Previous studies have shown that conflict between relevant and irrelevant dimensions can be reduced when a feature of the irrelevant dimension is repeated. The specific level at which the automatic process is suppressed (e.g., perceptual repetition, response repetition), however, is less understood. In the current experiment we used the numerical Stroop paradigm, in which the processing of irrelevant numerical values of 2 digits interferes with the processing of their physical size, to pinpoint the precise level of the suppression. Using a sequential analysis, we dissociated perceptual repetition from response repetition of the relevant and irrelevant dimension. Our analyses of reaction times, error rates, and diffusion modeling revealed that the congruity effect is significantly reduced or even absent when the response sequence of the irrelevant dimension, rather than the numerical value or the physical size, is repeated. These results suggest that automatic activation of the irrelevant dimension is suppressed at the response level. The current results shed light on the level of interaction between numerical magnitude and physical size as well as the effect of variability of responses and stimuli on automatic processing.
Keywords: automaticity, congruity effect, diffusion modeling, executive control, inhibition
Cognitive control is the ability that comes into play when automatic processes need to be inhibited, by suppressing dominant responses in favor of less accessible but more appropriate ones. One factor that affects cognitive control is the sequence of the presented trials. This was previously demonstrated in the Stroop task, in which subjects are asked to name the ink color of a written word while ignoring its semantic meaning. In this task, color words can be presented in a congruent color (e.g., the word RED presented in red ink) or in an incongruent color (e.g., the word RED presented in blue ink). A common finding is a congruity effect—that is, participants are slower and/or make more mistakes when they have to name the ink color of an incongruent stimulus compared with the ink color of a congruent stimulus. Notebaert and colleagues (Notebaert & Soetens, 2006; Notebaert, Soetens, & Melis, 2001) observed that the Stroop congruity effect was reduced when the same feature of the irrelevant dimension was repeated (e.g., the same word was presented on subsequent trials) and the intertrial interval was kept relatively short. The current work disentangles the perceptual and the motor sequence in order to pinpoint the precise mechanism for the reduced congruity effect after distractor repetition.
Before focusing on the effect of distractor repetitions in more detail, we would like to differentiate this sequence effect from another sequence effect, the Gratton effect. The Gratton effect demonstrates an effect of the congruity condition (i.e., congruent/incongruent) of the previous trial on the congruity effect in the current trial (Gratton, Coles, & Donchin, 1992). More specifically, it shows a smaller congruity effect after an incongruent trial than after a congruent trial. The Gratton effect is considered to reflect increased control after incongruent trials (Botvinick, Braver, Barch, Carter, & Cohen, 2001; Verguts & Notebaert, 2009).
The crucial differences between the Gratton effect and the reduced congruity effect after distractor repetition are threefold. First, the Gratton effect, by definition, depends on the congruity status of the preceding trial (e.g., congruent at trial n − 1 versus incongruent at trial n − 1), whereas the reduced congruity effect after distractor repetition does not (Morein-Zamir, Henik, & Spitzer-Davidson, 2002; Notebaert et al., 2001; Ridderinkhof, 2002). Second, although the reduced congruity effect after distractor repetition depends on the repetition of the distractor, the Gratton effect does not (e.g., Notebaert & Verguts, 2007). Finally, the Gratton effect is not observed at extremely short response–stimulus intervals (e.g., 50 ms; Notebaert, Gevers, Verbruggen, & Liefooghe, 2006), whereas such intervals seem to be a requirement for the reduced congruity effect for distractor repetition (Notebaert & Soetens, 2006). Given these substantial differences it is important to also investigate the mechanisms responsible for the reduced congruity effect when the distractor is repeated, as this is important for understanding how and when irrelevant information is automatically processed.
The reduced congruity effect after distractor repetition has been demonstrated in several congruity effects. For example, Notebaert et al. (2001) used the Simon task to initially demonstrate the effect. The Simon effect is characterized by faster reaction times (RTs) and/or increased accuracy when the stimulus presentation and response occur in the same relative location (congruent condition) compared with a situation when stimulus presentation and response occur in different locations (incongruent condition). The Simon effect is observed even when the stimulus location is task irrelevant. Notebaert et al. found that repetition of the irrelevant location reduced the magnitude of the congruity effect.
As discussed earlier, similar results have been reported for the Stroop task—namely, it has been shown that this congruity effect disappears when the irrelevant word is repeated, whereas the congruity effect is evident when the word changes (Notebaert & Soetens, 2006). Nevertheless, the precise mechanism for the reduced congruity effect after distractor repetition is still unknown (Notebaert, Verbruggen, & Soetens, 2005).
Two explanations of this effect have been put forward: (a) According to the perceptual-attention hypothesis, the distraction caused by irrelevant information is attenuated when it is repeated, compared with when this information changes. This hypothesis received some support from the findings of Morein-Zamir et al. (2002), which demonstrated an absence of the congruity effect when the information of the irrelevant dimension is repeated during a particular block, suggesting that irrelevant information needs to vary for it to be processed automatically. (b) According to the response-suppression hypothesis, the reduction of the congruity effect after irrelevant information repetition is due to sustained suppression of the response that was activated on the basis of irrelevant information. This hypothesis is derived from the activation-suppression hypothesis that describes suppression of irrelevant information after its initial activation (Ridderinkhof, 2002). This suppression mechanism can explain the decrease of congruity effects with increasing RTs (Forstmann, van den Wildenberg, & Ridderinkhof, 2008). It is interesting that both hypotheses explain the reduced congruity effect irrespective of the congruity of the preceding trial. This idea clearly dissociates this effect from the Gratton effect, which entirely depends on the congruity of the preceding trial (Botvinick et al., 2001; Verguts & Notebaert, 2009).
To assess both alternatives, we used a numerical Stroop paradigm to disentangle the sequence of irrelevant perceptual information and the sequence of responses activated by this irrelevant information. In the numerical Stroop paradigm (also called the size congruity paradigm; Schwarz & Ischebeck, 2003; Tzelgov, Meyer, & Henik, 1992), participants are asked to decide which of two digits is physically larger or smaller than a given standard (which appears at a medium size), while ignoring the numerical values of both digit (e.g., 1) and standard (the digit 5). Commonly, participants fail to ignore the numerical value, which leads to interference with the physical judgment. This results in slower responses for incongruent trials—for example,
1 or 6,
than for congruent trials—for example,
1 or 6,
which amounts to the congruity effect.
The specific motivation for using the numerical Stroop paradigm is that this paradigm enables us to dissociate the irrelevant perceptual sequence from the irrelevant response sequence. By using five digits (1, 4, 6, and 9 as targets, and 5 as the standard), the irrelevant numerical value and the irrelevant response activation can be repeated (identical sequence: 1 followed by 1, for instance); the irrelevant numerical value can change while the irrelevant response activation is repeated (same sequence: 1 followed by 4, for instance, as both are smaller than the standard 5), or the irrelevant numerical value and the irrelevant response can change altogether (different sequence: 4 followed by 9, as they are, respectively, smaller and larger than the standard 5). Note that technically, a similar design with a Stroop color-naming task is also possible, but this would require artificially mapping four colors onto two responses. This procedure reduces the direct association between the irrelevant dimension and the responses and as a consequence reduces the Stroop effect (MacLeod, 1991).
Moreover, by dissociating irrelevant perceptual repetition and irrelevant response sequence, we were able also to examine current theories that postulate that automaticity can be reduced or eliminated due to lack of, or small variance in, irrelevant dimensions (Melara & Algom, 2003; Morein-Zamir et al., 2002; Pansky & Algom, 1999). Critically, these studies did not pinpoint whether the crucial factor was variability at the stimulus level or at the response level. By manipulating the variation at the response level and/or the stimulus level on a trial-by-trial basis, the current study has the potential to shed further light on the critical component for obtaining a reliable congruity effect.
The other motivation for employing the current paradigm was the possibility of testing two competing theories in numerical cognition and comparative judgment. According to one set of theories, the numerical congruity effect is due to a conflict between two different magnitudes (e.g., physical size, numerical values, temporal duration) at a preresponse level (e.g., Cohen Kadosh, Cohen Kadosh, & Henik, 2008; Pansky & Algom, 1999; Schwarz & Heinze, 1998; Schwarz & Ischebeck, 2003). Another set of theories have attributed the numerical congruity effect to a conflict between two magnitudes that are processed, at least partly, independently until a response-related stage (Cohen Kadosh et al., 2007; Santens & Verguts, 2011; Szücs, Soltész, & White, 2009). Finding that the size of the congruity effect is modulated by repetition of irrelevant numerical value or response sequence can provide support for each of these theories—namely, results that would provide support for the perceptual-attention hypothesis would be in line with the first set of theories, whereas supportive findings for the response-suppression hypothesis would be in concordance with the latter set of theories.
The predictions of both accounts are clear in this design; both hypotheses predict an interaction between congruity and irrelevant sequence. However, the perceptual-attention and the response-suppression hypotheses predict different types of interaction. Both hypotheses predict reduced or no congruity effects for identical sequence, wherein the irrelevant numerical value is repeated (e.g., 1 followed by 1). Similarly, both hypotheses predict a full-blown congruity effect for different sequence, wherein both the irrelevant number and its associated response change (e.g., 4 to 6). Crucially, the hypotheses diverge in their predictions for the congruity effect for same sequence where the irrelevant number changes but the associated response is repeated (e.g., change from 1 to 4). The perceptual-attention hypothesis predicts that the congruity effect in this case should be intact as the irrelevant numerical value changes. In contrast, the response-suppression hypothesis predicts reduced or no congruity effect, since the irrelevant response sequence is repeated.1
In addition to measuring RT and error rates, we also elaborated on this by using diffusion modeling (Wagenmakers, van der Maas, & Grasman, 2007). This approach is very similar to classical signal detection theory in its aim, scope, and method. Based on accuracy, mean RT, and RT variance, the model yields three different parameters: (a) drift rate, which combines speed and accuracy to quantify subject ability and can be interpreted as an index of the signal-to-noise ratio (the equivalent of d′ in the signal detection theory framework) of the information processing system (Wagenmakers et al., 2007); (b) boundary separation, which indicates response conservativeness (the equivalent of beta in the signal detection theory framework); and (c) mean of nondecision time. Generally speaking, one could argue that the perceptual-attention hypothesis would predict the reduced congruity effect for distractor repetition to be located in the drift rate because the signal quality varies as a function of the distractor sequence, whereas the sustained-suppression hypothesis would predict the effect at the boundary separation as response thresholds vary as a function of irrelevant response sequence, as we can expect more influence of the irrelevant response when the irrelevant response changes.
Method
Participants
Twenty-one students (mean age 23.86 years old, SD = 3.72) participated in the experiment for partial fulfillment of a course requirement. All participants had normal or corrected-to-normal vision and no reading or mathematical deficits.
Stimuli
On each trial a single digit appeared at the center of a black computer screen. The participants sat 55 cm from the screen. The digits were 1, 4, 6, and 9 (Cohen Kadosh, 2008), which could appear in a vertical visual angle of 0.7°, 0.9°, 1.2°, or 1.4°. There were two levels of congruity: congruent and incongruent. Congruent stimuli included digits that were larger (or smaller) both in physical size and numerical value than the standard digit 5, which subtended a vertical visual angle of 1.05°—for example,
9 or 1.
Incongruent stimuli included digits that were smaller (larger) in physical size but larger (smaller) in numerical value than the standard digit 5—for example,
1 or 9.
Each digit, as well as each physical size, was presented an equal number of times as a congruent or as an incongruent stimulus.
Stimuli were arranged in five blocks of trials with each block composed of 288 trials, amounting to a total of 1,440 trials. An equal proportion of responses were made with the left hand and right hand. A block of 32 practice trials, identical to the experimental block, preceded each experimental block. Stimuli in the practice and the experimental blocks appeared in a random order.
Procedure
The participant's task was to decide whether the stimulus in a given display was physically larger or smaller than the standard 5. Participants were asked to respond as quickly as possible but to avoid mistakes and to attend only to the physical size while ignoring the irrelevant numerical dimension. The participants indicated their choices by pressing one of two keys (i.e., P or Q on a QWERTY keyboard). The assignment of the keys to large and small was counterbalanced across participants. The amount of smaller responses was equal to the amount of larger responses.
Each trial began with the standard digit 5 (in yellow ink) presented for 200 ms at the center of a computer screen. At 100 ms after the offset of the standard digit, a target digit (in white ink) appeared and remained in view until the participant pressed a key (but not for more than 3,000 ms). A new trial began 100 ms after the participant's response. After each block, the participants took a break, which was terminated upon their decision.
Design
Three variables were manipulated: congruity (congruent, incongruent), physical size sequence (henceforth relevant sequence), and numerical value sequence (henceforth irrelevant sequence). Relevant sequence had three levels: identical, same, and different. In an identical sequence the physical size was repeated and therefore also the response. In a same sequence the physical size was changed, but the response remained the same (e.g., physical sizes are different but both are smaller than the standard 5). In a different sequence the physical size has been changed together with the response (e.g., one physical size was larger and one physical size was smaller than the standard 5). For the irrelevant sequence we also had three levels: identical, same, and different. In this context identical sequence means the number was repeated (e.g., 1 followed by 1); same sequence means the number changed but the relative magnitude compared with the standard 5 did not (e.g., 1 followed by 4); and finally, different sequence means the number changed together with the relative magnitude (e.g., 1 followed by 6).
Results
Only trials with RTs longer than 150 ms and shorter than 2,000 ms were included in the analyses (99.7% of all correct trials).
First we calculated the mean RT for every participant in each condition, including only those trials in which both the current trial and the preceding trial (trial n − 1) were responded to correctly. These means were subjected to a three-way analysis of variance (ANOVA) with congruity, relevant sequence, and irrelevant sequence as within-subject factors (for details on RT and error rates in each condition, see Table 1).
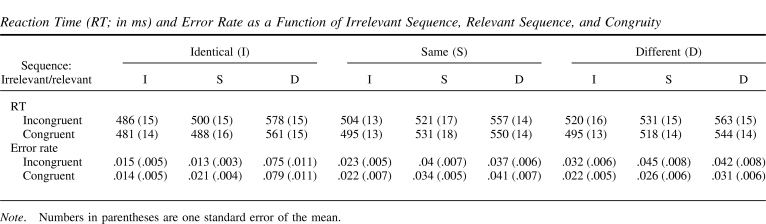
Table 1. Reaction Time (RT; in ms) and Error Rate as a Function of Irrelevant Sequence, Relevant Sequence, and Congruity.
The main effects of congruity, F(1, 20) = 13.88, MSE = 802, p < .001, ηpartial2 = .4; relevant sequence, F(2, 40) = 41.12, MSE = 3,107, p < .001, ηpartial2 = .67; and irrelevant sequence, F(2, 40) = 13.04, MSE = 460, p < .001, ηpartial2 = .39 were significant. The sequence effects point to the advantage of stimulus and response repetition over stimulus and response alternation (Bertelson, 1965). In addition, the two-way interaction between relevant sequence and irrelevant sequence was significant, F(4, 80) = 23.55, MSE = 364, p < .001, ηpartial2 = .54 (see Figure 1). This interaction indicates a feature binding process (Notebaert et al., 2001)—namely, when the relevant sequence was identical or the same (i.e., response was the same as n − 1 trial), RTs were faster when the irrelevant sequence was also identical, compared with same and different irrelevant sequence, F(1, 20) = 15.93, MSE = 691, p < .001, ηpartial2 = .44, and F(1, 20) = 52.66, MSE = 516, p < .001, ηpartial2 = .72, for identical and same relevant sequence, respectively. In contrast, when the relevant sequence was different (i.e., response was alternated), same and different irrelevant sequence yielded faster RTs than the identical irrelevant sequence, F(1, 20) = 19.13, MSE = 358, p < .001, ηpartial2 = .49.
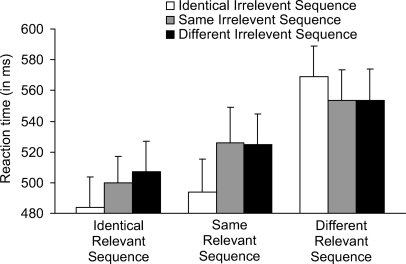
Figure 1. Mean reaction time as a function of relevant sequence and irrelevant sequence. Error bars depict one standard error of the mean.
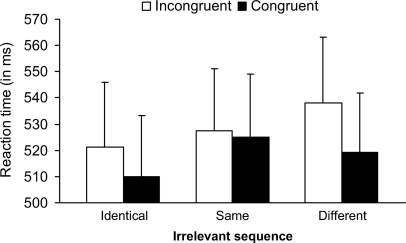
Crucially for the purpose of the current study, the congruity effect was modulated by the irrelevant sequence, F(2, 40) = 4.62, MSE = 491, p < .01, ηpartial2 = .19 (see Figure 2). The three-way interaction between congruity, relevant sequence, and irrelevant sequence was not significant, F(4, 80) = 1.49, MSE = 376, p > .21, ηpartial2 = .07.
Figure 2. Mean reaction time as a function of congruity and irrelevant sequence. Error bars depict one standard error of the mean.
Further simple effects analyses for congruity at each level of irrelevant sequence were conducted (Keppel, 1991). As predicted by both accounts, the simple main effect of congruity was significant for the different sequence—that is, when the numerical value changed together with the triggered “response” by the irrelevant dimension, F(1, 20) = 17.71, MSE = 643, p < .001, ηpartial2 = .47. It is more surprising, however, that the congruity effect was also significant for the identical sequence (same numerical value that triggered response repetition by the irrelevant dimension), F(1, 20) = 7.79, MSE = 531, p < .01, ηpartial2 = .28. In contrast, the congruity effect for the same sequence (different numerical value that triggered response repetition by the irrelevant dimension) was not significant, F(1, 20) = 0.22, MSE = 609, p > .64, ηpartial2 = .01.
Although the small congruity effect for identical sequence challenges both accounts, the lack of a congruity effect for same sequence is in line with the response-suppression hypothesis. The interaction therefore supports the response-suppression hypothesis and challenges the perceptual-attention hypothesis's prediction. The response-suppression hypothesis further predicts a larger congruity effect for the different sequence compared with identical and same sequence. We found that the congruity effect for different sequence was larger compared with identical sequence and same sequence, F(1, 20) = 6.71, MSE = 468, p < .01, ηpartial2 = .25, and explained 69% of the variance of the interaction between congruity and irrelevant sequence.
Error Rates
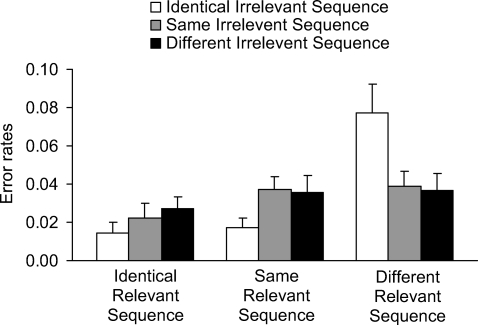
The main effect of relevant sequence was significant, F(1, 20) = 21.41, MSE = 0.001, p < .001, ηpartial2 = .51. As in the RT analysis, the two-way interaction between relevant sequence and irrelevant sequence was significant, F(4, 80) = 23.84, MSE = 0.0005, p < .001, ηpartial2 = .54, and followed the same trend (see Figure 3). In addition, the interaction between congruity and irrelevant sequence was significant, F(2, 40) = 5.07, MSE = 0.0004, p < .01, ηpartial2 = .2 (see Figure 4). The other interactions were not significant, Fs < 1, ηpartial2 ≤ .03.
Figure 3. Error rates as a function of relevant sequence and irrelevant sequence. Error bars depict one standard error of the mean.
Figure 4. Error rates as a function of congruity and irrelevant sequence. Error bars depict one standard error of the mean.
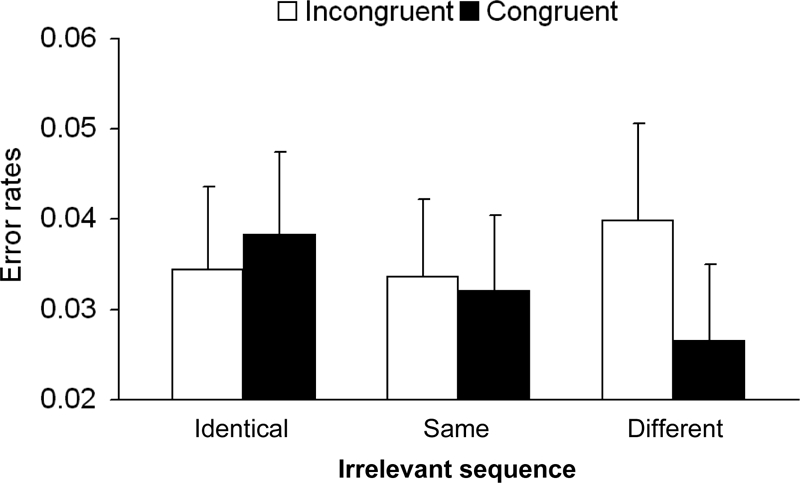
Further simple effects analyses for congruity at each level of irrelevant sequence revealed that only the simple main effect of congruity for the different sequence was significant, F(1, 20) = 7.58, MSE = 0.0007, p < .01, ηpartial2 = .27. In contrast, the congruity effect for same sequence, and identical sequence, which in contrast to the RT data showed the opposite trend, was not significant, both Fs < 1, ηpartial2 ≤ .04. As with the RT analysis, and in line with the response-suppression hypothesis, we found that the congruity effect for different sequence was larger compared with identical same sequence and different same sequence, F(1, 20) = 7.09, MSE = 0.0004, p < .01, ηpartial2 = .26, and explained 91% of the variance of the interaction between congruity and irrelevant sequence.2
Diffusion Modeling
In this analysis we took into account mean RT, its variance, and error rate. According to the perceptual-attention hypothesis the reduced congruity effect for distractor repetition might be due to signal quality variation as a function of the distractor sequence and, therefore, the interaction between congruity and irrelevant sequence should be located in the drift rate. In contrast, we predicted that if the current results are due to response suppression it should affect the boundary separation index, which signals changes at the response level.
We first confirmed that the EZ-diffusion model was not misspecified by conducting EZ checks for the model's misspecification (Wagenmakers et al., 2007).
The interaction between congruity and irrelevant sequence for the drift rate was not significant, F(1, 20) = 1.66, MSE = 0.005, p > .2, ηpartial2 = .07, thus challenging the predictions made by the perceptual-attention hypothesis. However, as predicted by the response-suppression hypothesis, the interaction between congruity and irrelevant sequence was significant for the boundary separation index, F(2, 40) = 3.66, MSE = 0.001, p < .05, ηpartial2 = .15. Further simple effects analyses showed that as expected by the response-suppression hypothesis, the congruity effect was significant only for the different sequence: congruent = 0.155, incongruent = 0.139, t(20) = 2.00, p < .05, one-tailed, p > .92, and p > .49, for identical sequence and same sequence, respectively. Further analysis found that the congruity effect for different sequence yielded a trend toward a larger effect compared with identical and same sequence, F(1, 20) = 3.59, MSE = 0.005, p < .07, ηpartial2 = .15, and explained 62% of the variance of the interaction between congruity and irrelevant sequence. No higher order interactions were observed in any of the diffusion model parameters (all ps > .2). The results from the boundary separation index suggest that the irrelevant information had an effect only in the different sequence condition, a finding that is in accordance with the response-suppression hypothesis. Moreover, the evaporation of a congruity effect in the case of identical and same sequence indicates similar response conservativeness for the congruity conditions, probably due to the suppression of the irrelevant response. In other words, it appears that the sustained suppression of the irrelevant response increases the response threshold for incongruent trials in the identical and same sequence.
Discussion
In the current study we used RT and error rate measures in a sequential analysis, together with the diffusion model, to discern the level at which the conflicting information between numerical value and physical size is reduced.
We found that the congruity effect is reduced (see RTs) and even eliminated (error rates, boundary separation) when the response activated by the irrelevant dimension is repeated (i.e., the identical and same conditions for the irrelevant sequence). Although the findings for the identical irrelevant sequence cannot dissociate the predictions made by the two hypotheses, the consistent evaporation of the congruity effect for the same irrelevant sequence can do so—namely, the perceptual-attention hypothesis predicts that the congruity effect for the same sequence should not be affected by this type of repetition, whereas the response-suppression hypothesis predicts that the congruity effect in this condition should be reduced and even eliminated. Note that this conclusion is based not on a null result but on a significant interaction with a robust congruity effect for the different irrelevant sequence. Moreover, in the diffusion modeling the interaction between congruity and irrelevant sequence was significant for the boundary separation, as would be predicted by the response-suppression hypothesis. However, in contrast to the predictions made by the perceptual-attention hypothesis, the same interaction was not significant for the drift rate.
It is important to stress that this effect is caused by the irrelevant response sequence. Although others have adequately described the effect of the relevant response sequence (e.g., Bertelson, 1965), we were able to show how automatic processing is affected by the suppression of irrelevant information as is described in the response-suppression model (Ridderinkhof, 2002). The results support the idea that the response that was activated on the basis of the irrelevant information is suppressed after its initial activation.
Previous attempts to validate the response-suppression hypothesis have been less successful (Notebaert et al., 2005; Zeischka, Commans, Deroost, Vandenbossche, & Soetens, 2011). For example, Notebaert et al. (2005) used negative priming to examine the response-suppression hypothesis. Negative priming is the observation of increased RT (and decreased accuracy) when the irrelevant information of trial n − 1 becomes the relevant information on trial n. One explanation for this effect is that the irrelevant information (or the response that was activated by it) is suppressed on trial n − 1 and that sustained suppression causes slower responses on trial n. Consequently, it appears that the suppression of irrelevant information results in reduced congruency effects when the irrelevant information is repeated and in slower RTs when the irrelevant information turns relevant. In a first attempt to investigate their relationship, Notebaert et al. failed to find a correlation between the two effects, in the sense that no negative priming was observed in a condition where reduced congruency effects for distractor repetitions were observed.
Before concluding that these results (contrary to the present data) argue against (sustained) response-suppression, we would like to stress that response-suppression is but one of the many explanations for negative priming. According to memory accounts for negative priming (e.g., Neill & Valdes, 1992), for instance, no relation between negative priming and reduced congruency effects for distractor repetitions is predicted. Finally, measuring negative priming is not always as straightforward as it seems. The reason is that it is very hard, if not impossible, to separate it from other sequence effects. In the current task a small 1 followed by a small 1, for instance, is a negative priming transition, but one would hardly expect slow RTs here. Therefore, we believe that the approach described in this article is more suitable for investigating the source of reduced congruity effects after distractor repetition.
The current results also challenge previous theories that attributed the numerical congruity effect to conflict at a preresponse level. For example, a few studies have suggested that the relevant and irrelevant dimensions are converted into a common magnitude representation of similar structure prior to a response-related stage (e.g., response selection; for a review, see Cohen Kadosh, Lammertyn, & Izard, 2008). Our results indicate that the congruity effect is modulated by a repetition of the same response, rather than the same magnitude, thus supporting the idea that both dimensions are processed, at least partly, independently until a response-related stage (Cohen Kadosh et al., 2007; Santens & Verguts, 2011; Szücs et al., 2009).
In addition, previous studies have claimed that automaticity can be reduced or eliminated with little or no variance of the irrelevant dimensions (Melara & Algom, 2003; Morein-Zamir et al., 2002; Pansky & Algom, 1999). Although this is a plausible suggestion, it is important to note that these studies did not dissociate between variability at the stimulus level and the response level. The current results indicate that variation at the response level, rather than the stimulus level, is the critical component for obtaining a reliable congruity effect. This factor has important implications for basic research as well as for applied research, in which researchers would like to maximize the likelihood of receiving an effect or, alternatively, reduce the interference from automatic processes.
In sum, the results of the current study are in support of the response-suppression hypothesis (Ridderinkhof, 2002) by showing that the congruity effect is reduced or eliminated when the irrelevant dimension activates the response of the irrelevant dimension repeatedly. In addition to clarifying the mechanism that reduces congruity effects for irrelevant repetitions, this study also supports the notion of fast online cognitive control in the sense that suppression occurs during the time-course of a trial and not only between trials (e.g., Botvinick et al., 2001).
Acknowledgments
Roi Cohen Kadosh is supported by the Wellcome Trust (WT 88378); Wim Gevers is supported by the Flemish Fund for Scientific Research. We would like to thank Orit Moscovitch and Teresa Iuculano for help with the data collection, and Kathrin Cohen Kadosh and Devin B. Terhune for their helpful comments.
Footnotes
Note that another way to formalize the predictions in the current case is by conducting a trend analysis that will characterize the pattern of the congruity effect according to each hypothesis—namely, for the perceptual-attention account the weights should be −2, 1, and 1, for identical, same, and different irrelevant sequence, respectively, and −1 and 1 for congruent and incongruent. For the response-suppression hypothesis the weights should be −1, −1, and 2, for identical, same, and different irrelevant sequence, respectively, and −1 and 1 for congruent and incongruent. However, we did not base our results on this type of analysis as the contrasts are not independent (i.e., they are not orthogonal) in this case. However, whenever we found support for one account over the other, the analysis was supplemented with a trend analysis.
Whereas the difference between the congruity effect for identical irrelevant sequence and different irrelevant sequence in the RT analysis was not significant, t(20) = 1.4, p > .088, one-tailed, it was significant in the error rates analysis, t(20) = 3.23, p < .002, one-tailed.
References
- Bertelson P. (1965). Serial choice reaction time as a function of response versus signal-and-response repetition. Nature, 206, 217–218. doi:10.1038/206217a0 [DOI] [PubMed] [Google Scholar]
- Botvinick M. M., Braver T. S., Barch D. M., Carter C. S., & Cohen J. D. (2001). Conflict monitoring and cognitive control. Psychological Review, 108, 624–652. doi:10.1037/0033-295X.108.3.624 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R. (2008). Numerical representation: Abstract or nonabstract? Quarterly Journal of Experimental Psychology, 61, 1160–1168. doi:10.1080/17470210801994989 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Cohen Kadosh K., & Henik A. (2008). When brightness counts: The neuronal correlate of numerical-luminance interference. Cerebral Cortex, 18, 337–343. doi:10.1093/cercor/bhm058 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Cohen Kadosh K., Linden D. E. J., Gevers W., Berger A., & Henik A. (2007). The brain locus of interaction between number and size: A combined functional magnetic resonance imaging and event-related potential study. Journal of Cognitive Neuroscience, 19, 957–970. doi:10.1162/jocn.2007.19.6.957 [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Lammertyn J., & Izard V. (2008). Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Progress in Neurobiology, 84, 132–147. doi:10.1016/j.pneurobio.2007.11.001 [DOI] [PubMed] [Google Scholar]
- Forstmann B. U., van den Wildenberg W. P. M., & Ridderinkhof K. R. (2008). Neural mechanisms, temporal dynamics, and individual differences in interference control. Journal of Cognitive Neuroscience, 20, 1854–1865. doi:10.1162/jocn.2008.20122 [DOI] [PubMed] [Google Scholar]
- Gratton G., Coles M. G. H., & Donchin E. (1992). Optimizing the use of information: Strategic control of activation of responses. Journal of Experimental Psychology: General, 121, 480–506. doi:10.1037/0096-3445.121.4.480 [DOI] [PubMed] [Google Scholar]
- Keppel G. (1991). Design and analysis: A researcher's handbook (3rd ed.). Upper Saddle River, NJ: Prentice Hall. [Google Scholar]
- MacLeod C. M. (1991). Half a century of research on the Stroop effect: An integrative review. Psychological Bulletin, 109, 163–203. doi:10.1037/0033-2909.109.2.163 [DOI] [PubMed] [Google Scholar]
- Melara R. D., & Algom D. (2003). Driven by information: A tectonic theory of Stroop effects. Psychological Review, 110, 422–471. doi:10.1037/0033-295X.110.3.422 [DOI] [PubMed] [Google Scholar]
- Morein-Zamir S., Henik A., & Spitzer-Davidson I. (2002). The importance of irrelevant-dimension variability in the Stroop flanker task. Psychonomic Bulletin & Review, 9, 119–125. doi:10.3758/BF03196266 [DOI] [PubMed] [Google Scholar]
- Neill W. T., & Valdes L. A. (1992). Persistence of negative priming: Steady state or decay? Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 565–576. doi:10.1037/0278-7393.18.3.565 [DOI] [PubMed] [Google Scholar]
- Notebaert W., Gevers W., Verbruggen F., & Liefooghe B. (2006). Top-down and bottom-up sequential modulations of congruency effects. Psychonomic Bulletin & Review, 13, 112–117. doi:10.3758/BF03193821 [DOI] [PubMed] [Google Scholar]
- Notebaert W., & Soetens E. (2006). Sustained suppression in congruency tasks. Quarterly Journal of Experimental Psychology, 59, 178–189. doi:10.1080/17470210500151360 [DOI] [PubMed] [Google Scholar]
- Notebaert W., Soetens E., & Melis A. (2001). Sequential analysis of a Simon task. Evidence for an attention-shift account. Psychological Research/Psychologische Forschung, 65, 170–184. doi:10.1007/s004260000054 [DOI] [PubMed] [Google Scholar]
- Notebaert W., Verbruggen F., & Soetens E. (2005). Analysis of relevant and irrelevant stimulus information in the Stroop task. European Journal of Cognitive Psychology, 17, 642–658. doi:10.1080/09541440540000095 [Google Scholar]
- Notebaert W., & Verguts T. (2007). Dissociating conflict adaptation from feature integration: A multiple regression approach. Journal of Experimental Psychology: Human Perception and Performance, 33, 1256–1260. doi:10.1037/0096-1523.33.5.1256 [DOI] [PubMed] [Google Scholar]
- Pansky A., & Algom D. (1999). Stroop and Garner effects in comparative judgment of numerals: The role of attention. Journal of Experimental Psychology: Human Perception and Performance, 25, 39–58. doi:10.1037/0096-1523.25.1.39 [DOI] [PubMed] [Google Scholar]
- Ridderinkhof K. R. (2002). Micro- and macro-adjustments of task set: Activation and suppression in conflict tasks. Psychological Research/Psychologische Forschung, 66, 312–323. doi:10.1007/s00426-002-0104-7 [DOI] [PubMed] [Google Scholar]
- Santens S., & Verguts T. (2011). The size congruity effect: Is bigger always more? Cognition, 118, 97–113. [DOI] [PubMed] [Google Scholar]
- Schwarz W., & Heinze H. J. (1998). On the interaction of numerical and size information in digit comparison: A behavioral and event-related potential study. Neuropsychologia, 36, 1167–1179. doi:10.1016/S0028-3932(98)00001-3 [DOI] [PubMed] [Google Scholar]
- Schwarz W., & Ischebeck A. (2003). On the relative speed account of the number-size interference in comparative judgment of numerals. Journal of Experimental Psychology: Human Perception and Performance, 29, 507–522. doi:10.1037/0096-1523.29.3.507 [DOI] [PubMed] [Google Scholar]
- Szücs D., Soltész F., & White S. (2009). Motor conflict in Stroop tasks: Direct evidence from single-trial electro-myography and electro-encephalography. NeuroImage, 47, 1960–1973. doi:10.1016/j.neuroimage.2009.05.048 [DOI] [PubMed] [Google Scholar]
- Tzelgov J., Meyer J., & Henik A. (1992). Automatic and intentional processing of numerical information. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 166–179. doi:10.1037/0278-7393.18.1.166 [Google Scholar]
- Verguts T., & Notebaert W. (2009). Adaptation by binding: A learning account of cognitive control. Trends in Cognitive Sciences, 13, 252–257. doi:10.1016/j.tics.2009.02.007 [DOI] [PubMed] [Google Scholar]
- Wagenmakers E.-J., van der Maas H. L. J., & Grasman R. P. P. P. (2007). An EZ-diffusion model for response time and accuracy. Psychonomic Bulletin & Review, 14, 3–22. doi:10.3758/BF03194023 [DOI] [PubMed] [Google Scholar]
- Zeischka P., Commans D., Deroost N., Vandenbossche J., & Soetens E. (2011). Target–flanker discriminability affects conflict size but not sustained suppression. Acta Psychologica, 136, 148–156. doi:10.1016/j.actpsy.2010.11.004 [DOI] [PubMed] [Google Scholar]