Remarkable patterns of surface water ordering around polarized buckminsterfullerene

Abstract

Accurate description of water structure affects simulation of protein folding, substrate binding, macromolecular recognition, and complex formation. We study the hydration of buckminsterfullerene, the smallest hydrophobic nanosphere, by molecular dynamics simulations using a state-of-the-art quantum mechanical polarizable force field (QMPFF3), derived from quantum mechanical data at the MP2/aug-cc-pVTZ(-hp) level augmented by CCSD(T). QMPFF3 calculation of the hydrophobic effect is compared to that obtained with empirical force fields. Using a novel and highly sensitive method, we see polarization increases ordered water structure so that the imprint of the hydrophobic surface atoms on the surrounding waters is stronger and extends to long-range. We see less water order for empirical force fields. The greater order seen with QMPFF3 will affect biological processes through a stronger hydrophobic effect.

Buckminsterfullerene (C₆₀), commonly known as the buckyball, has been the focus of many experimental and theoretical studies because of its promise in both biomedicine and nanomaterials (1–8). Carbon nanotubes, a nanomaterial similar to fullerenes, exhibit unique mechanical properties, electrical and heat conductivity; they are often hailed as a twenty-first century material that could revolutionize a number of industries (2). The behavior of fullerenes in water is of special interest for biosensors (9). Moreover, water-soluble buckyball derivatives could potentially be used for a wide variety of medical applications, including HIV protease inhibition, DNA photoclevage, antibacterial activity, and photocytotoxicity for cancer treatment (10).

The interaction of water with hydrophobic surfaces is responsible for many biological processes, such as protein folding, substrate binding and biological self-assembly of micelles, lyotropic mesophases, and lipid membranes. The molecular surface of proteins can have extended hydrophobic patches, so that buckyballs, graphite surfaces, and carbon nanotubes provide model systems for study of water molecules near large hydrophobic surfaces. An accurate description of interactions between water and its surrounding environment is essential for understanding and simulating such processes. Molecular dynamics (MD) simulations are used to study the behavior of water molecules next to hydrophobic surfaces at atomic detail and subpicosecond time resolution. The hydration structure of nonpolar solutes of varying size has been studied extensively in the past (11–22) using empirical force fields. Work from our lab has used empirical potential energy functions with popular water models to model the effect of a single molecule of benzene, cyclohexane (18, 21), methane, and C₆₀ (22) on the structural details of water around these solutes. All these studies used force fields with nonpolarizable fixed point charge water models and analyzed water structure with a low-sensitivity method unable to detect the effect of solute surface “roughness” on water structure.

Polarization, which allows the effective charge on an atom to change in response to surrounding electric fields, has been studied extensively for methane in water (23–27) and has used a variety of different methods to allow charges to change. Recently studied picoseconds-long first-principle MD with electronic structure calculations using density functional theory are only possible for small solutes such as methane (28) and benzene in water (29, 30). Other studies have modeled polarization in carbon nanotubes (31–35). Vernov and Steele (36) considered a charge-induced dipole moment and static quadrupole moments on a graphite surface, whereas Zimmerli et al. (37) included a curvature-induced static dipole in simulations of carbon nanotubes. For large mesoscale solutes, nothing is known about the effect of explicit polarization of all atoms (water and surface) on the hydrophobic effect.

Many have attempted to include polarization in empirical nonpolarizable force fields, such as the polarizable versions of OPLS (38), AMBER (39), and CHARMM (40–42). The AMOEBA force field (43) was constructed to include polarization as multipoles in a self-consistent field. Recently, Donchev et al. introduced a highly transferable ab initio quantum mechanical polarizable force field (QMPFF1 and QMPFF2) fitted solely to high-level quantum mechanical data using the second order of Møller–Plesset perturbation approach (MP2) with the Dunning aug-cc-pVTZ basis set in which the higher polarization functions were removed [MP2/aug-cc-pVTZ(-hp) level] (44, 45). A third generation of the quantum mechanical polarizable force field QMPFF3, which added a coupled-cluster with single and double and perturbative triple excitations [CCSD(T)] correction for higher-accuracy treatment of aromatic carbon atom types, was shown to successfully reproduce experimental data for a large array of chemical compounds in all three phases of matter (46–48).

The insensitivity of water structure around small nonpolar solutes to the particular water model has been shown for empirical force fields (18); this may not be true for large hydrophobic solute like C₆₀. Early studies showed that solvent polarization had a small but significant affect on small nonpolar solutes like methane in water (23, 24, 26), but a fluctuating charge model of methane and water showed the effect of solute and solvent polarization to be negligible (25). More recent studies with polarized methane (27) as well as density functional theory calculations of methane (28) and benzene (29, 30) in water showed polarization to be more significant. The dependence of water structure on surface polarizability is well known for extended nonatomic polarizable surfaces (49–51), whereas the effect of explicit polarization on a polarizable protein in water showed polarization is important only for charged residues (52).

Carbon nanotubes and spheres like C₆₀ consist only of carbon atoms bonded to three other carbon atoms. As such, they do not have any net charges or even any permanent partial charges: All electrostatic interactions must arise from the fluctuating partial charges, dipoles, and quadrupoles that result from polarization. As such, this family of molecules is a particularly good system to test different force fields and models of polarizability.

We used QMPFF3 to model the water structure around C₆₀. The high symmetry of C₆₀ increases the sensitivity of our analysis by using the azimuthal distribution functions (ADFs) to show the water structure in spherical shells. We find QMPFF3 polarization orders water structure significantly: The water oxygen density fluctuations in the first water hydration shell of C₆₀ were more than twice as large as with the nonpolarizable empirical all-atom OPLS force field (OPLS-AA) for C₆₀ (53) and the simple point charge (SPC) (54) or TIP4P (55) models of water. The symmetry of the C₆₀ molecule with its 12 pentagons and 20 hexagons is imprinted on the water; with polarization, this imprinting is much stronger and of longer range than for empirical water models. The ordering of water molecules in a spherical shell is very high with much larger density fluctuations than those seen in the radial direction as defined by the familiar radial distribution function (RDF).

Results

Visualization of Surface Roughness.

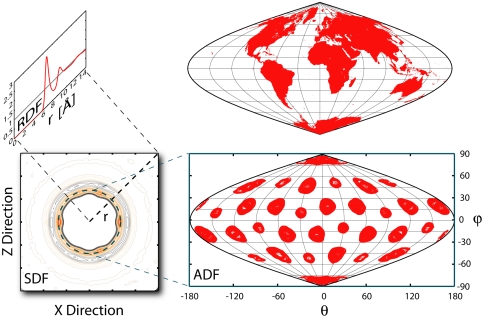
In order to account for the truncated dodecahedron (soccer ball) symmetry of C₆₀ as well as to visualize the O and H density distribution in concentric spherical shells around the C₆₀ spatial distribution function (SDF) (Fig. S1), we calculated the time-averaged ADF as illustrated in Fig. 1 (SI Materials and Methods). This is an improvement over the spatial distribution functions introduced by Kusalik and Svishchev (56), which also maps the three-dimensional density of water, around any arbitrary shaped solute. In the same way that the peaks in the familiar one-dimensional RDF indicate the presence of order in water structure, the ADF shows the ordering of the water O and H atom density over the C₆₀ surface due to the surface roughness resulting from the arrangement of carbon atoms in C₆₀.

Fig. 1.

Different distribution functions of a water molecule. Three different ways to measure the order of water O and H atoms around C₆₀ or indeed any solute. Most obvious is the three-dimensional spatial distribution function (SDF) that shows the density at each volume element centered at every point in space defined by coordinates (x, y, z). It suffers from the severe difficulties associated with viewing and analysis of a general three-dimensional map. Most commonly used is the one-dimensional radial distribution function (RDF) that averages the number of O or H atoms over all volume elements at a distance r from the center of C₆₀, where r² = x² + y² + z². Although such averaging increases the signal-to-noise ratio, the RDF hides many features of the three-dimensional density map. Faced with these limitations, we introduce the azimuthal distribution function (ADF) that calculates density maps in thin spherical shells at a particular r value in terms of spherical polar coordinates (r, θ, φ). The results, which present all salient three-dimensional features of C₆₀, are easily viewed on paper using the Sanson–Flamsteed projection (69) used by early cartographers.

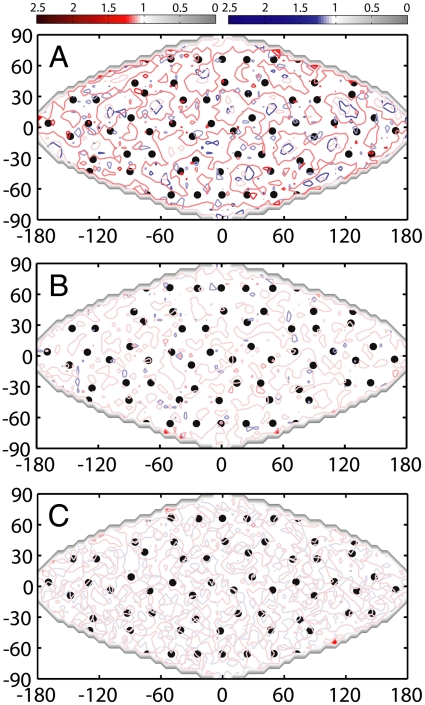
In our previous studies of water structure around a C₆₀ solute using empirical force fields, we assumed C₆₀ to be a smooth sphere and averaged over all azimuthal angles to get a very accurate RDF (22). Little did we expect the dramatic ordering of water structure in spherical shells as shown by the ADFs averaged over 100 ns of MD simulation (Figs. 2 and 3). The ADF is shown in Fig. 2 for water O atoms (red contours) and water H atoms (blue contours) of QMPFF3 and OPLS-AA with TIP4P and SPC water. These ADFs for QMPFF3 and OPLS-AA with TIP4P and SPC simulations are shown at two distances from the C₆₀ center (r), 6.55 and 7.35 Å. The average density of O and H atoms over the entire surface is equal to that expected from the one-dimensional RDF at these distances (Fig. 4 A and B). The dramatic variation of the O and H atom density in the shell was not expected. There is a clear imprinting of the 12 pentagons and 20 hexagons of C₆₀ onto the arrangement of water O and H atoms with high water atom density above the centers of each pentagon and hexagon. This gives a characteristic pattern of 32 density peaks that is seen in most of the ADFs in Fig. 2. In fact, the pattern provides a very sensitive way to detect azimuthal ordering, which is clearly apparent for both the O and H density with QMPFF3 at r = 6.55 and 7.35 Å. For the nonpolarizable force fields TIP4P and SPC, there is clear order at r = 6.55 Å but almost none at r = 7.35 Å.

Fig. 2.

Short-range ADFs. The ADF for density of water O atoms (red contours) and H atoms (blue contours) around C₆₀. The 60 carbon atoms of C₆₀ are shown as black dots. The first column shows the ADF for QMPFF3; the second and third columns show OPLS-AA with TIP4P and SPC, respectively. Results are given for water layers 0.1 Å thick. (A–F) At 6.55 Å from the C₆₀ center, the water O and H atom density patterns (ρ_o and ρ_H) are most similar [this value of r corresponds to the maximum (ρ_o, ρ_H) correlation for QMPFF3; see Fig. 4D]. There is always more density over the 20 hexagonal faces of C₆₀ to give an icosahedral pattern of peaks that is most pronounced for QMPFF3. For both empirical force fields, the O atom density over the 12 pentagonal faces of C₆₀ is almost as high as that over the 20 hexagonal faces to give a 32 vertex object known as a Pentakis Dodecahedron. (G–L) At 7.35 Å from the C₆₀ center, the water O and H atom densities are most different [minimum (ρ_o, ρ_H) correlation]. The H density for QMPFF3 at 7.35 Å is similar to that at 6.55 Å; it is less ordered for SPC and TIP4P. The O density is surprising for all force fields with low density depressions (ρ_o ≈ 1.0) over the hexagonal faces and higher density plateaus over the pentagonal faces. The order, so clearly apparent in these contour maps, can be characterized by the ratio of maximum to minimum density taken over the middle quarter of the maps (-π/2 ≤ θ ≤ π/2, -π/4 ≤ φ ≤ π/4). For the O density at 6.55 Å, the density ratio values are 5.12, 1.77, and 1.85 for QMPFF3, TIP4P and SPC, respectively. For the O density at 7.35 Å, the ratios are 1.63, 1.32, and 1.30, respectively. For the H density these ratios are 1.55, 1.47, and 1.29 at 6.55 Å and 1.72, 1.14, and 1.20 at 7.35 Å.

Fig. 3.

Long-range ADFs. The ADF for density of water O atoms (red contours) and H atoms (blue contours) over C₆₀ carbon atoms (black dots) at 9.95 Å from the C₆₀ center. Order is perceived in the ADF for water O atoms for (A) QMPFF3 by reference to the symmetric arrangement of hexagons and pentagons on the C₆₀ surface. No order is perceived in the ADFs for water O and H atoms for (B) TIP4P and (C) SPC. The weak ordering for QMPFF3 is due to solute polarization that gives rise to a long-range induction effect not present in empirical force fields. The ADFs at 9.95 Å are calculated using the method described in Materials and Methods.

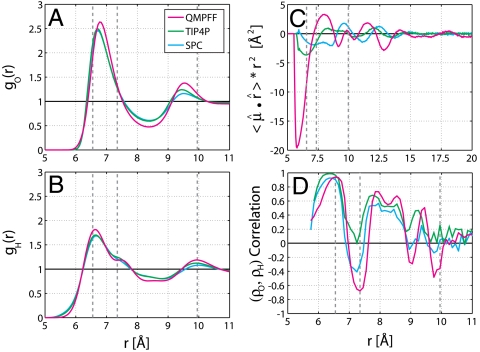
Fig. 4.

One-dimensional radial plots of key water properties. Showing one-dimensional radial plots of key water properties to allow for easy comparison of results from the three different force fields used here. (A and B) The one-dimensional RDF of water O and H atoms hints at more order in QMPFF3 compared to TIP4P and SPC, but these differences are small. (C) The radially normalized and spherically averaged projection of the water dipole moment is much larger for QMPFF3 compared to TIP4P and SPC. The effect for QMPFF3 extends to long-range (20 Å). (D) The correlation coefficient of the O and H density (ρ_o and ρ_H) at the same radius from the C₆₀ center fluctuates greatly. The ADFs for water O and H atoms are positively correlated at many r values (peaks at 6.55, 7.85, 8.55, and 9.45 Å), indicating that both O and H atoms occur at the same location over the C₆₀ surface; this occurs when the water O–H bond lies in the particular azimuthal plane. The ADFs for water O and H atoms are negatively correlated at other r values (valleys at 7.35, 9.05, and 9.75 Å); this occurs due to depressions in O atom density over hexagons as shown in Fig. 2 G–I for r = 7.35 Å.

Polarization Dramatically Increases Ordering Around Large Hydrophobic Solutes.

For QMPFF3, we always see more O and H atom density over each hexagonal face compared to a pentagonal face of C₆₀. A similar but less-pronounced pattern is seen for OPLS-AA with TIP4P and SPC waters (Fig. 2). We calculated the O and H density fluctuations over the entire surface as the ratio of the highest density compared to the lowest density. These values vary dramatically and are much larger than the corresponding peaks in the RDF. The ratio of the number of water molecules closer to a hexagonal face than to a pentagonal face is 3.95 for QMPFF3 and only 1.12 for OPLS-AA with SPC.

At r = 6.55 Å, the O and H densities in the water shell have a positive correlation coefficient in that the O and H density patches occur at the same positions over hexagons and pentagons of C₆₀. This is puzzling, because in liquid water, the O and H atoms cannot occupy the same volume of space at the same time. Because these ADFs are time-averaged over many trajectories, the O and H atom must occur over pentagonal and hexagonal faces at different times. We used a time-dependent correlation study of water positions (see SI Text) to show that this correlated O and H density comes from atoms that are in a water O–H bond moving in the azimuthal plane of the spherical shell at r = 6.55 Å (the O and H atom centers are just 1 Å apart so that their time-averaged density is very similar). A visually similar pattern is seen for the ADF at r = 7.35 Å for QMPFF3, but it is actually inverted with a negative correlation coefficient between O and H water shell density. This comes from high H atom density coinciding in space with low O atom density. The high H atom density comes from a hydrogen atom that is bonded to the O atom at r = 6.55 Å, whereas the low O density at these sites results from repulsive interactions with this same O atom. Clearly, there is much greater surface water ordering for QMPFF3 compared to TIP4P and SPC simulations where the water density is more diffuse over the C₆₀ surface.

Polarization Induces a Long-Range Hydrophobic Effect.

Long-range forces between hydrophobic surfaces may be important for self-assembly in biological macromolecules. It has been suggested (57) that the strength of this long-range force of attraction depends on the polarization field produced by strong coupling of water dipoles at the hydrophobic surfaces. We are able to perceive long-range order in the water O density for a water shell around C₆₀ at r = 9.95 Å (Fig. 3A). This long-range order is much weaker than the order perceived at r = 6.55 Å for QMPFF3 (Fig. 2A). It would be very hard to detect such long-range order at r = 9.95 Å if the symmetrical arrangement of hexagons and pentagons of C₆₀ was not known. No such order in water structure is detected in the ADFs of O and H density for OPLS-AA with TIP4P and SPC waters around C₆₀ at r = 9.95 Å (Fig. 3 B and C).

Water Orientation Function.

The ADFs given above in Fig. 2 show two regions of high water oxygen density: above hexagonal faces and above pentagonal faces. The water molecules in these regions are moving rapidly and can adopt the full range of possible orientations while keeping their oxygen position relatively fixed. The water orientation function is computed for different r values to give the spatial orientation for water molecules closest to the centers of the twelve pentagonal and twenty hexagonal faces of C₆₀ (see Fig. 5 and SI Materials and Methods). We define the roll angle (γ), which is used together with the dipole angle (ω) to completely characterize the three-dimensional spatial orientation of the water molecule (angle definitions in Fig. 5). The water orientation functions are plotted for both short-range (r = 6.7 Å) and long-range (r = 9.5 Å) water structure; this corresponds to the first and second peaks in the one-dimensional RDF of water O atom (see Fig. 4A), also referred to as the first and second hydration shells, respectively. The water orientation functions for QMPFF3 and OPLS-AA with either TIP4P or SPC water share many features, but there are key differences.

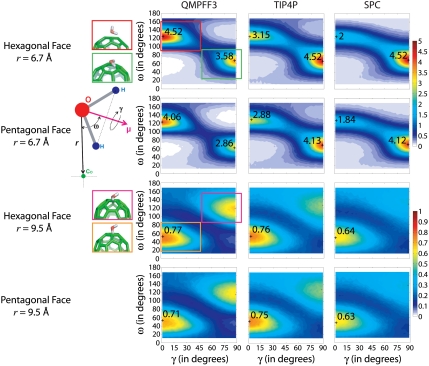
Fig. 5.

Three-dimensional water orientation functions. The complete spatial orientation of the planar water molecule near the pentagonal and hexagonal faces of C₆₀ is defined by roll angle (γ) and dipole angle (ω). The schematic defines γ as the dihedral angle made by the water H–H vector measured about the water dipole vector μ and relative to r, the radial vector from the water oxygen atom to the center of C₆₀. For γ = 0°, the H–O–H molecule lies in a plane that slices the spherical C₆₀ in half (e.g., in the plane of the page). For γ = 90° the H–H vector is perpendicular to the radial vector, r, and the water molecule lies in a plane tangential to the C₆₀ surface. For QMPFF3 at r = 6.7 Å (first hydration shell), most water molecules have (γ,ω) = (0°,125°): One water O–H bond points radially away from the C₆₀ center and the other points toward the surface; the water dipole is at 125° to the radial vector, r (red box). The peak at (γ,ω) = (90°,60°) is weaker: Both water hydrogen atoms point indirectly toward C₆₀ to interact mainly with the hexagonal face; the water dipole is at 60° to the radial vector, r (green box). The first peak is more clearly defined for QMPFF3 than for TIP4P and SPC, especially over pentagons; the reverse occurs for the second peak. For QMPFF3 at r = 9.5 Å (second hydration shell) there are also two preferred (γ,ω) orientations, which are exactly opposite to what is seen for the first hydration shell. Most popular is (γ,ω) = (0°,50°): one water O–H bond points radially toward the C₆₀ center (orange box). The peak at (γ,ω) = (90°,120°) is weaker: Both water hydrogen atoms point indirectly away from C₆₀ (magenta box). This second peak is only seen with QMPFF3.

At r = 6.7 Å, the water orientation functions for QMPFF3 show two water populations that are much more distinct than for OPLS-AA with TIP4P or SPC. These two peaks show: (i) For γ = 0°, water dipoles point away from the pentagonal and hexagonal faces of C₆₀ with one water O–H pointing directly away from the center of C₆₀ and the other water O–H bond oriented toward the C₆₀ surface (red box in Fig. 5); and (ii) for γ = 90°, the water dipoles point toward the pentagonal and hexagonal faces of C₆₀, the water is tangential to the C₆₀ surface, and both water hydrogens are oriented toward C₆₀ (green box in Fig. 5). For OPLS-AA with TIP4P and SPC, there are more tangential water molecules than seen for QMPFF3. These empirical force fields also show very similar distributions over hexagonal and pentagonal faces, whereas QMPFF3 shows less interaction with the pentagonal faces.

At r = 9.5 Å, the water orientation functions for QMPFF3 show two preferred (γ,ω) orientations, whereas there is just one orientation for OPLS-AA with TIP4P or SPC. Most water dipoles are oriented toward the pentagonal and hexagonal faces of C₆₀ with γ = 0° such that one O–H bond points directly into the C₆₀ surface (orange box in Fig. 5) and is hydrogen bonded to the surrounding water molecules (see Fig. S2 D–F at r = 9.5 Å). For QMPFF3, a distinct peak is shown for water dipoles pointing away from C₆₀, and both water hydrogen atoms are oriented away from C₆₀ (magenta box in Fig. 5).

We should point out that the water oxygen density above hexagonal or pentagonal faces (Fig. 2 A–C) is the integral of the water orientation function over all (γ,ω) values. Using the peak height as an indication of oxygen or hydrogen atom density seen in the ADF can be misleading.

Discussion

Dispersion Affects Short-Range Order.

We did not expect to see any azimuthal ordering of water molecules for the nonpolarizable empirical water models. These models used fixed point charges, and for the C₆₀ molecule these charges are located on the atoms. The C₆₀ molecule is made up of 60 identical carbon atoms, and the whole molecule carries no charge so that every C atom must be neutral. This means that all the variation in water density arises solely from van der Waals forces between the C atom of C₆₀ and the O atom of each water molecule (there is no van der Waals interaction between C and the water H atom).

The importance of van der Waals forces in the azimuthal ordering of water in empirical models leads us to believe that dispersion (similar to the attractive van der Waals term in empirical force fields) also causes the highly correlated water shell O and H densities near the solute surface for QMPFF3. Specifically, the extensive ordering in O and H density over the C₆₀ surface seems to come from strong dispersion interactions, which are modeled as attraction between nuclei and short-range electrostatics between induced multipole moments (dipole and quadrupole) of a water molecule and C₆₀ carbon atoms, as well as from the exchange repulsion between oxygen atoms of different water molecules. The much greater ordering seen for QMPFF3 indicates the dispersion is very strong compared to empirical force fields. Others (58) have found that van der Waals interactions are responsible for surface density distributions on carbon nanotubes.

To test this hypothesis, we computed the ADF for water O and H atoms after increasing the attractive part of the van der Waals interaction between C–O by twofold; i.e., 2 ∗ ϵ_(C–O), for OPLS-AA with SPC. We observed increased ordering for ADF of O and H atom densities in the first hydration shell (r ≤ 8.6 Å) over the C₆₀ surface, in that the ADF for QMPFF3 is remarkably similar to that for 2 ∗ ϵ_(C–O) for SPC (Fig. S3). We conclude that the dispersion effect in QMPFF3 is much larger than the attractive van der Waals interaction between the C atom of C₆₀ and water O atom for empirical force fields. The exchange repulsion between electron clouds acting at short distances from the C₆₀ surface is also stronger for QMPFF3 in that the water H atom closest to the C₆₀ surface is at 5.13 Å for QMPFF3, 4.93 Å for TIP4P, and 4.83 Å for SPC. The strong dispersion and exchange effects in QMPFF3 could significantly affect the critical distance of dewetting observed when two large hydrophobic surfaces approach each other (59–61).

The orientation of water dipoles near the C₆₀ surface is strongly affected by dispersion and short-range electrostatics between dipoles and quadrupoles in QMPFF3 (see SI Text and Fig. S4), which gives rise to a large value of the spherically averaged projection of the water dipole moment around C₆₀ when compared to empirical force fields (Fig. 4C). The water molecules in the first hydration shell (r ≤ 8.6 Å) adopt a range of orientations with most water dipoles pointing away and one O–H bond arranged tangentially to the nonpolar solute surface (see Fig. 5 and Fig. S2). Water dipoles pointing tangentially away from a nonpolar solute surface is a well-known result that has also been observed experimentally (62). For QMPFF3, a large number of water dipoles point away from the C₆₀ surface, compared to equal populations of dipole vectors pointing toward and away from the solute surface for SPC (Fig. S2 A–C). Note that one water O–H bond in the tangential plane at r = 6.55 Å and the other H atom of this water further from the C₆₀ surface (at r = 7.35 Å) is exactly what is inferred from the analysis of the ADF correlations in Fig. 2. The strong orientation of water dipoles around C₆₀ for QMPFF3 results in fewer water–water hydrogen bonds (see SI Text and Table S1) due to strong C₆₀–water interactions (11, 63).

Electrostatics and Induction Affect Long-Range Order.

Dispersion is not responsible for the long-range order of the water structure around C₆₀ because no surface order pattern is seen in the O density ADF at r = 9.95 Å for OPLS-AA with doubled van der Waals attraction 2 ∗ ϵ_(C–O) for SPC water (Fig. S5). Electrostatics and induction in QMPFF3 are likely to be the main cause for the increase in long-range order of the water structure around C₆₀. The main source of long-range interactions in QMPFF3 is between the induced and permanent multipoles of C₆₀ and water. No induced multipoles can exist in the nonpolarizable empirical force fields. Both long-range electrostatics and induction in QMPFF3 affect waters orientations near hexagons and pentagons in the second hydration shell of C₆₀ (8.6 Å < r < 12.1 Å) with two preferred water orientations; only one preferred orientation is observed for empirical force fields (see Fig. 5). Similar long-range effects in QMPFF3 are seen in the oscillations of radially normalized and spherically averaged projection of the water dipole that extends beyond 15 Å from the C₆₀ center (Fig. 4C). It seems that this long-range effect is mediated through the water–water interactions around C₆₀ (see “long” contacts in SI Text and Table S1).

Accurate Modeling of C₆₀-Water in QMPFF3.

Could the high surface ordering of water molecules arise from errors in our modeling of the relative motion of water and C₆₀ molecules? To check this, we compare the structure of QMPFF3 water with experiment (Fig. S6) and also calculate the translational diffusion coefficient (D) and rotational diffusion coefficient (D_r) for water and C₆₀ using QMPFF3 and OPLS-AA with TIP4P and SPC (Table S2). For QMPFF3, the translational diffusion constant of pure water, D = 1.55 × 10^-5 cm²/s, is closer to the experimental value of 2.299 × 10^-5 cm²/s at 25 °C (64) than the values of 3.71 × 10^-5 and 4.33 × 10^-5 cm²/s found for TIP4P and SPC, respectively. The experimentally measured water relaxation times, τ₁ and τ₂ (65) are much closer to the relaxation times computed from simulations for QMPFF3 water than for empirical water models (Table S2). The dynamic properties of the C₆₀ solute are also closer to experiment for QMPFF3 (Table S2). The translational diffusion constant of C₆₀ is D = 0.55 × 10^-5 cm²/s for QMPFF3, 0.86 × 10^-5 cm²/s for TIP4P, and 0.99 × 10^-5 cm²/s for SPC. Assuming a sphere radius of 5.125 Å, the Debye–Stokes–Einstein equation (66) gives D = 0.64 × 10^-5 cm²/s, which is close to the QMPFF3 value. NMR has measured the related slow rotational motion of water molecules near C₆₀, compared to waters in bulk (67). Our calculated C₆₀ relaxation times of τ₂ = 11.26 ps for QMPFF3 in water at 298 K is similar to the experimentally determined value of τ₂ = 15.5 ps for C₆₀ dissolved in tetrachloroethane (viscosity similar to water) as well as the solid-state C₆₀ NMR measurements of τ₂ = 6.8–14.9 ps in the temperature range 241–331 K (68).

Conclusions

We have developed a highly sensitive method to measure surface roughness with an ADF that allows us to detect extensive short-range and long-range ordering of water molecules around C₆₀. Dispersion in QMPFF3 is responsible for short-range C₆₀–water interactions in the first hydration shell. This suggests that water–carbon dispersion (van der Waals) should be corrected in the empirical force fields to agree with the quantum result and lead to stronger hydrophobic interactions. Electrostatics and induction are responsible for the long-range interactions in QMPFF3, which affects the water structure in the second hydration shell and beyond. The long-range order is a direct consequence of the strong induction effect in QMPFF3, which is not present in empirical force fields. The dramatic increase in both short-range and long-range ordering for water O and H density around large nonpolar solutes like C₆₀ increases hydrophobic interactions to have a profound effect on key biological processes.

Materials and Methods

Simulation Methodology.

MD simulations are done using two different empirical force fields (OPLS-AA with TIP4P and SPC, respectively) and the quantum mechanical polarizable force field (QMPFF3), each run for a total of 100 ns at constant temperature and pressure (see SI Materials and Methods).

Analysis of Water Structure around C₆₀.

Analysis in one and three dimensions was done using the conventional RDF and SDF (see SI Materials and Methods). In order to account for the surface roughness resulting from the arrangement of carbon atoms in C₆₀, we calculated the time-averaged ADF to visualize the O and H density distribution in concentric spherical shells around the C₆₀ SDF (Fig. S1). The ADF is calculated by peeling off thin layers (0.1 Å) of water in spherical shells around C₆₀ as if we were dealing with layers of an onion. We then use the 350-y-old Sanson–Flamsteed sinusoidal equal-area projection (69) (ca. 1650, but also used by Mercator) to map the water O and H atom density as if we were mapping the earth (see SI Materials and Methods and Fig. 1). In order to eliminate Brownian motion of the C₆₀ solute, each frame of our simulation is reoriented to superimpose the C₆₀ on a standard C₆₀ reference structure. This reorientation is essential because without it all features of the ADF would be smeared.