Measurement and Estimation of Organic-Liquid/Water Interfacial Areas for Several Natural Porous Media

Abstract

The objective of this study was to quantitatively characterize the impact of porous-medium texture on interfacial area between immiscible organic liquid and water residing within natural porous media. Synchrotron X-ray microtomography was used to obtain high-resolution, three-dimensional images of solid and liquid phases in packed columns. The image data were processed to generate quantitative measurements of organic-liquid/water interfacial area and of organic-liquid blob sizes. Ten porous media, comprising a range of median grain sizes, grain-size distributions, and geochemical properties, were used to evaluate the impact of porous-medium texture on interfacial area. The results show that fluid-normalized specific interfacial area (A_f) and maximum specific interfacial area (A_m) correlate very well to inverse median grain diameter. These functionalities were shown to result from a linear relationship between effective organic-liquid blob diameter and median grain diameter. These results provide the basis for a simple method for estimating specific organic-liquid/water interfacial area as a function of fluid saturation for a given porous medium. The availability of a method for which the only parameter needed is the simple-to-measure median grain diameter should be of great utility for a variety of applications.

INTRODUCTION

The critical role of fluid-fluid interfaces in multi-phase flow phenomena and contaminant transport has long been recognized. However, examination of fluid-fluid interfacial phenomena and the potential impact of system properties and conditions has been constrained by a lack of means by which to measure interfacial areas. This in turn has limited the development and testing of methods for estimating interfacial areas. The influence of porous-medium texture on fluid-fluid interfaces is one aspect of interest with respect to both phenomenological behavior and estimation efforts. For example, Costanza and Brusseau (1) used theoretical-model based data reported by Cary (2) to evaluate the influence of porous-medium texture on fluid-fluid interfacial area, and observed larger interfacial areas for the media with smaller grain size and larger specific surface area. They hypothesized that texture effects would be mediated by specific surface area of the porous medium. The recent availability of methods for measuring interfacial area has allowed experiment-based investigation of texture effects, which has been examined in a small number of studies.

Anwar et al. (3) used an aqueous surfactant column method to measure air-water interfacial areas for three glass-bead media and observed interfacial area to be smaller for the larger diameter media. Costanza-Robinson and Brusseau (4) used air-water interfacial area data reported in the literature for several porous media, measured with the aqueous-phase and gas-phase interfacial partitioning tracer test methods, to evaluate the influence of texture. They reported strong, quantitative correlations between maximum specific interfacial area and porous-medium specific surface area for the two sets of data, which could be used to predict maximum interfacial area for a given porous medium. Peng and Brusseau (5) used the gas-phase interfacial tracer test method to measure air-water interfacial areas for eight soils and natural sands. The results showed that interfacial area was strongly dependent upon porous-medium texture, and an equation was developed to predict interfacial area as a function of fluid saturation and porous-medium properties. Cho and Annable (6) used the aqueous-phase interfacial tracer test method to measure organic-liquid/water interfacial areas for five sands. They observed a quantitative correlation between interfacial area and inverse grain diameter. Dobson et al. (7) used the aqueous-phase interfacial tracer test method to measure organic-liquid/water interfacial areas for four sands, and observed a correlation between interfacial area and inverse grain diameter.

The results reported above wherein interfacial area is observed to correlate with specific solid surface area and inverse median grain diameter are consistent with general concepts of fluid configurations at the pore scale. However, the analyses reported above were based on measured data obtained with various interfacial partitioning tracer methods, which provide an indirect, macroscopic measure of interfacial area. Thus, testing hypotheses proposing that the influence of texture on fluid-fluid interfacial area is mediated by pore-scale fluid configuration effects is generally problematic with these methods. Schnaar and Brusseau (8) used the synchrotron X-ray microtomography method to measure fluid configurations and interfacial areas for two sands and a soil for both two-phase and three-phase systems. They observed that the fluid-normalized organic-liquid/water interfacial area correlated with the inverse median grain diameter. Furthermore, by measuring and quantifying the size distributions of the organic-liquid blobs, they showed that the median blob length correlated directly with the median grain diameter, thus explaining the correlation between interfacial area and inverse median grain diameter. Costanza-Robinson et al. (9) used the synchrotron X-ray microtomography method to measure air-water interfacial areas for several glass-bead and sand media. They observed a quantitative correlation between interfacial area and specific surface area of the porous medium. Similar results were reported for a study involving several soils and sands (10). Quantification of fluid body size distributions were not reported in the latter two studies.

The objective of this study was to quantitatively characterize the influence of porous-medium texture on interfacial area between immiscible organic liquid and water residing within natural porous media. Synchrotron X-ray microtomography was used to obtain high-resolution, three-dimensional images of solid and liquid phases in packed columns. The image data were processed to generate quantitative measurements of organic-liquid/water interfacial area and of organic-liquid blob sizes. Ten porous media, comprising a range of median grain sizes, grain-size distributions, and geochemical properties, were used to evaluate the impact of porous-medium texture on interfacial area.

MATERIALS AND METHODS

Materials

Tetrachloroethene was used as the model organic liquid for this study. To enhance image contrast, tetrachloroethene was doped with iodobenzene (8% by volume). Measurements conducted prior to the study indicated minimal impact of the dopant on tetrachloroethene-water interfacial tension and measured interfacial areas (11). All chemicals were reagent grade (Sigma-Aldrich Co.).

A total of ten porous media were used in the study: three soils, five natural, commercially available sands (Accusand and Granusil, Unimin Co.), and two glass-bead media. Relevant physical properties of the porous media are provided in Table 1. The median grain sizes (d₅₀) and the grain-size distributions, as characterized by the uniformity coefficient (U), vary considerably. The organic-carbon contents of the media also vary, from zero for the glass beads, to low values for the sands (~0.02%), to moderate values for the soils (0.08, 0.09, and 0.38% for Hayhook, Vinton, and Eustis, respectively). The porous media are considered to be completely to predominantly water-wetting.

Table 1.

Physical properties of porous media

Porous Medium	Porosity	Bulk Density (g/cm3)	Ua	Median Grain Diameter (d50, mm)	Specific Solid Surface Area(cm−1)b	Snc
Sand- 20/30	0.39	1.63	1.2	0.677	54	0.15
Sand- 45/50	0.34	1.8	1.1	0.35	113	0.16
Sand- 70/100	0.36	1.69	1.8	0.172	222	0.12
Sand- 100/140	0.37	1.66	1.7	0.145	261	0.08
Sand- Mixed	0.28	1.9	3.4	0.279	154	0.15
Hayhook soil	0.38	1.65	16	0.26	144	0.16
Vinton soil	0.42	1.54	2.4	0.234	149	0.23
Eustis soil	0.38	1.65	2.3	0.27	138	0.24
Glass beads-1	0.39	1.52	1.0	0.42	87	0.22
Glass beads-2	0.44	1.28	1.0	1.0	34	0.08

^aU = uniformity coefficient (d₆₀/d₁₀), d_i is the ith percent of grains by mass that are smaller than a a given sieve size.

^bSpecific solid surface area is calculated using the smooth-sphere assumption [=6(1-n)/d₅₀, where n is porosity]

^cS_n is saturation of organic liquid

Experiment Methods

The porous media were dry-packed into thin-walled, X-ray transparent columns constructed of aluminum, with aluminum fittings. The columns were 4.4 cm long, with an outer diameter of 0.635 cm and an inner diameter of 0.58 cm. Polypropylene porous frits (10-µm pores) were placed on both ends of the column to promote uniform flow and retain the porous media. The porosities and bulk densities of the packed columns are reported in Table 1; they are similar to those obtained for larger columns packed with the same media (unpublished data).

After packing, the columns were purged with CO₂ and saturated for several days by pumping de-aired water upward through the column with a single-piston HPLC pump (Acuflow Series II, VWR Inc.). The equivalent of 2.5 pore-volumes of organic liquid was then pumped vertically upward into the column at a Darcy velocity of 4.5 cm/hr using a syringe pump (Sage). An aqueous solution containing tetrachloroethene and iodobenzene at equilibrium concentrations (assuming Raoult’s Law applicability), was then flushed vertically downward at 20 cm/hr to displace the organic liquid. The capillary number for this displacement was 10⁻⁶, which is similar to values typically used to establish a stable, discontinuous distribution (i.e., residual saturation) of non-wetting phase (e.g., 12–15). Once the saturation process was complete, the columns were sealed and imaged as described below. A minimum of two to four and a maximum of 15 image sets were collected for each medium at residual saturation conditions. Analysis showed that the coefficients of variation were less than 10% for each medium. Inspection of the microtomography images revealed no air was present for most columns, indicating that the column preparation procedures produced water-saturated conditions. A very small number of isolated air bubbles were present in a few columns; the interval in which they resided was not used in the characterization of organic-liquid/water interfacial areas.

An additional set of experiments was conducted for three media (glass beads-2, 45/50 sand, and Vinton soil) to examine the relationship between interfacial area and fluid saturation. The columns were packed and saturated as above and transported to the imaging facility. Images were collected between sequential periods of drainage and imbibition (with sufficient time to allow equilibrium conditions to develop). Another set of columns were prepared for these media to measure the specific surface area of the solid phase. These columns were either dry (no water or tetrachloroethene) or saturated with an aqueous solution doped with CsCl to enhance image contrast.

Synchrotron X-Ray Microtomography

The advent of synchrotron X-ray microtomography has provided a method that can quantitatively characterize fluid-fluid interfaces for natural porous media. The majority of the imaging for the current study was conducted at the GeoSoilEnviroCARS (GSECARS) BM-13D beamline at the Advanced Photon Source (APS), Argonne National Laboratory, IL. A small number of columns were imaged using the 8.3.2 beamline at the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory, CA.

Imaging was conducted by directing the monochromatic X-ray beam through the column, perpendicular to the longitudinal axis. The transmitted X-rays were converted to visible light with a single-crystal scintillator, and projected onto a mirror inclined 45° to the incoming beam. A photograph of the image on the mirror was then taken with a high resolution CCD-camera attached to a microscope objective (5×). This image represents a depth-integrated grayscale map of the linear attenuation of the X-ray beam as it passed through the column. After an image was collected, the column was rotated (APS = 0.5°, ALS = 1°), and the image-acquisition process was repeated. A total of 720 (APS) or 360 (ALS) two-dimensional images of each sample were collected in this manner. Additionally, several backfield projections, or images of the beam without any sample present, were collected during each set of scans. The image resolution (pixel size) was approximately 4–11 µm. The length of the imaged zone was approximately 5 mm. The images were collected from the centers of the columns, thus minimizing the potential influence of end effects. Analysis of the data sets indicated that REV requirements were met for image volumes of approximately 30–50 mm³, depending on the porous medium. These results are similar to those reported in prior studies (16,17). The volumes of the imaged zones were larger than the minimum for all data sets.

The synchrotron beam was tuned to specific incident energies to take advantage of the X-ray absorption K-edge of the doping compounds. The K-edge refers to the X-ray energy at which the absorption of the beam by that element increases dramatically. For example, the absorption of the beam by the iodine-doped organic liquid is significantly greater at an energy slightly above the iodine K-edge compared to its absorption below the iodine K-edge. However, the absorption of the beam by other constituents of the matrix (e.g., porous media solids) remains essentially unchanged. Images of the columns were collected sequentially below and above the iodine K-edge (33.0169 and 33.269 keV) to specifically resolve the organic liquid. For selected experiments (noted above), the column was scanned below and above the cesium K-edge (33.269 and 36.085 keV) to resolve the aqueous phase, which in these cases was doped with CsCl.

Image Processing and Analysis

The set of two-dimensional images collected for a given scan were preprocessed and reconstructed with algorithms developed by Rivers (18). Preprocessing of the two-dimensional images removes artifacts and adjusts for the backfield projections. Reconstruction is used to build a single three-dimensional image file from the two-dimensional images. After reconstruction, the data can be visualized as “thin sections”, two-dimensional slices in either the x–y (perpendicular to the longitudinal (rotational) axis of the column) or x–z (parallel to the rotational axis of the column) direction. The reconstructed thin sections show the attenuation (grayscale) of the X-ray beam in a discrete location (voxel), and thus the internal distribution of the attenuation is obtained. Reconstructed three-dimensional images acquired with incident energy below the iodine K-edge were subtracted from the corresponding images obtained from above the iodine K-edge to produce images wherein only voxels comprising the organic liquid display grayscale values different from the background. Use of subtracted image files simplifies data processing, ensures that voxels comprising organic liquid are successfully separated from the surrounding matrix, and eliminates artifacts associated with highly attenuating components of the porous media, such as metal oxides.

Additional image data processing and extraction of quantitative information were conducted with the software package Blob3D, which was specifically developed for high resolution X-ray microtomography data (19). An array of binary images was created wherein voxels considered to be organic liquid were assigned a grayscale of 255 (white) and all others were assigned a grayscale of 0 (black). Contiguous voxels assigned as organic liquid were identified and combined to form three-dimensional units (blobs). Once data processing was complete, quantitative information was generated for each individual organic-liquid blob. Blob volume was calculated as the total volume of all the voxels contained within a blob. The effective resolution with respect to blob volume was approximately 10⁻⁵ mm³. Surface area was calculated from the isosurface connecting the selected grayscale value (e.g., 127) in the binarized image. The methods used have been tested and employed successfully in prior research (8,11,17,20–23).

Fluid-fluid interfacial area is comprised of two components, area associated with capillary domains (e.g., menisci) and area associated with non-wetting fluid in contact with films of wetting fluid. This study will focus on total interfacial area. This is done in part for consistency with the other primary method for measuring interfacial areas, the interfacial partitioning tracer test method, which provides measures of total interfacial area. The total surface area of tetrachloroethene, the non-wetting phase, was used to determine total organic-liquid/water interfacial area. This is based on the assumption that all porous-medium grains are solvated by water. The specific organic-liquid/water interfacial area (A_nw, cm⁻¹) was then calculated by dividing total interfacial area by the volume of porous medium comprising the imaged domain. It is important to note that interfacial areas measured with synchrotron X-ray microtomography do not include area associated with microscopic surface heterogeneities (e.g., surface roughness), as discussed previously (17,22,23). As noted above, the majority of the imaging was conducted at APS, while a small subset was conducted at ALS. The results obtained from the two facilities for a common porous medium were indistinguishable.

RESULTS AND DISCUSSION

Inspection of the image data shows that the three phases, organic liquid, water, and porous-medium grains, were very well differentiated, as has been shown in prior work (8,20). The organic liquid was observed to be evenly distributed throughout the columns, both longitudinally and radially, with no apparent preferential accumulation along the walls or centers of the columns. Organic-liquid blobs in the center and outer sections of the column appeared to have similar morphologies. The blobs varied greatly in both size and shape, ranging from small spheres (≥ 0.03-mm in diameter) to large, amorphous ganglia with mean lengths of a few mm. The general blob morphologies were similar for all of the media with the exception of the two glass-bead media. For the glass beads, the blobs were somewhat smaller and consisted almost entirely of single spheres. The range of blob sizes and shapes is consistent with the results of prior studies employing blob casting and three-dimensional imaging.

Independent sets of images were collected for selected columns that were either dry or water saturated (contained no organic liquid). These data were used to directly measure the specific surface area of the solid phase. The value obtained for the glass beads-2 medium was 35 cm⁻¹, which is essentially identical to the specific solid surface area calculated using the smooth-sphere assumption (Table 1). Given that the glass beads are spherical and of uniform diameter, the specific solid surface area calculated with the smooth-sphere assumption will be a very accurate measure of true surface area in this case. The similarity between the surface area measured with microtomography and the smooth-sphere based value indicates that the image processing procedures were robust. The specific solid surface areas measured with microtomography for the 45/50 sand and the Vinton soil were 95 and 142 cm⁻¹, respectively. These values are relatively similar to the respective surface areas calculated with the smooth-sphere assumption (Table 1).

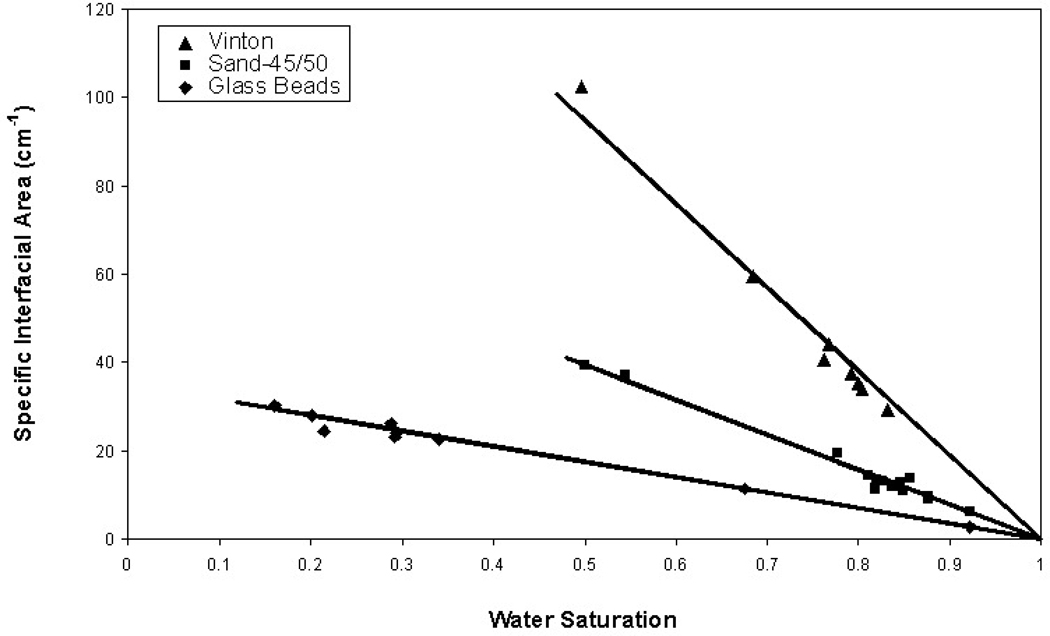
The specific total organic-liquid/water interfacial area (A_nw) was measured as a function of fluid saturation for three porous media, glass beads-2, 45/50 sand, and Vinton soil. The results are presented in Figure 1. The interfacial area is observed to increase linearly with decreasing wetting-phase saturation for all three media over the range investigated. This is consistent with the results of prior theoretical, computational, and experimental studies (e.g., 9,22–26). The linear functions are described with the equation A_nw = A_m (1-S_w), where A_m is the maximum specific interfacial area. The A_m serves as an index for a given system, indicative of the magnitude of interfacial area associated with that system. Inspection of Figure 1 reveals that interfacial areas, and the corresponding A_m values, are smallest for the glass-bead medium and largest for Vinton soil, consistent with the differences in solid surface areas and median grain sizes.

Figure 1.

Specific total organic-liquid/water interfacial area (A_nw) as a function of wetting-phase (water) saturation.

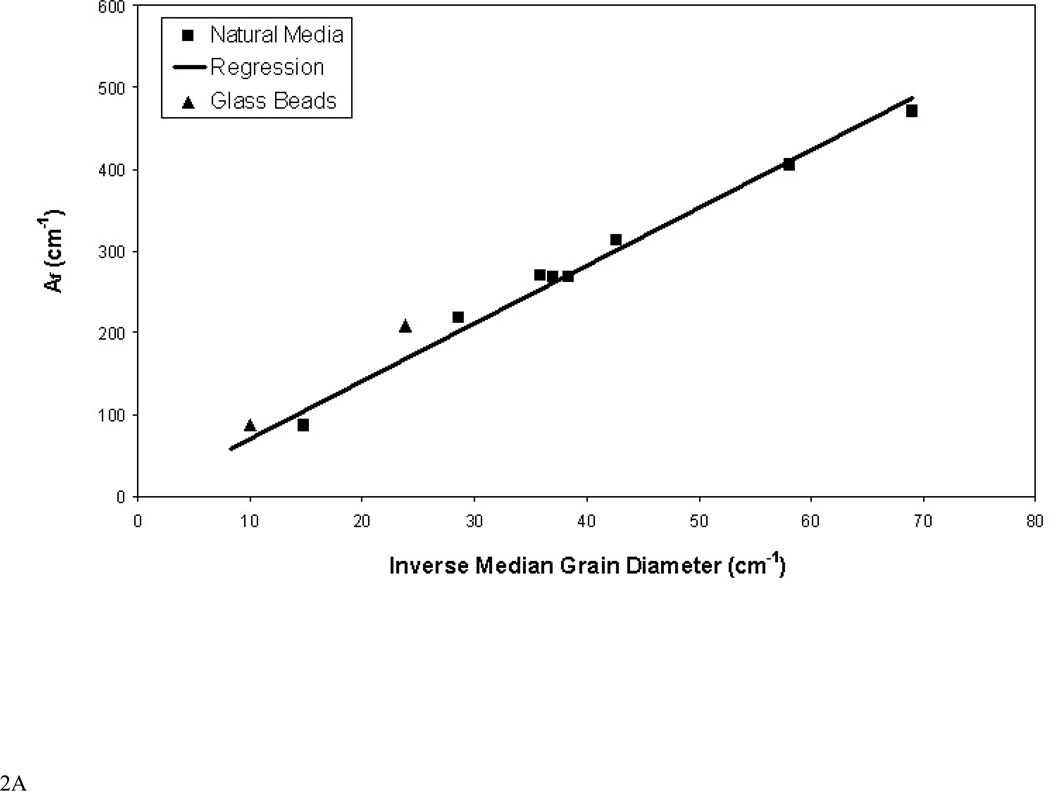
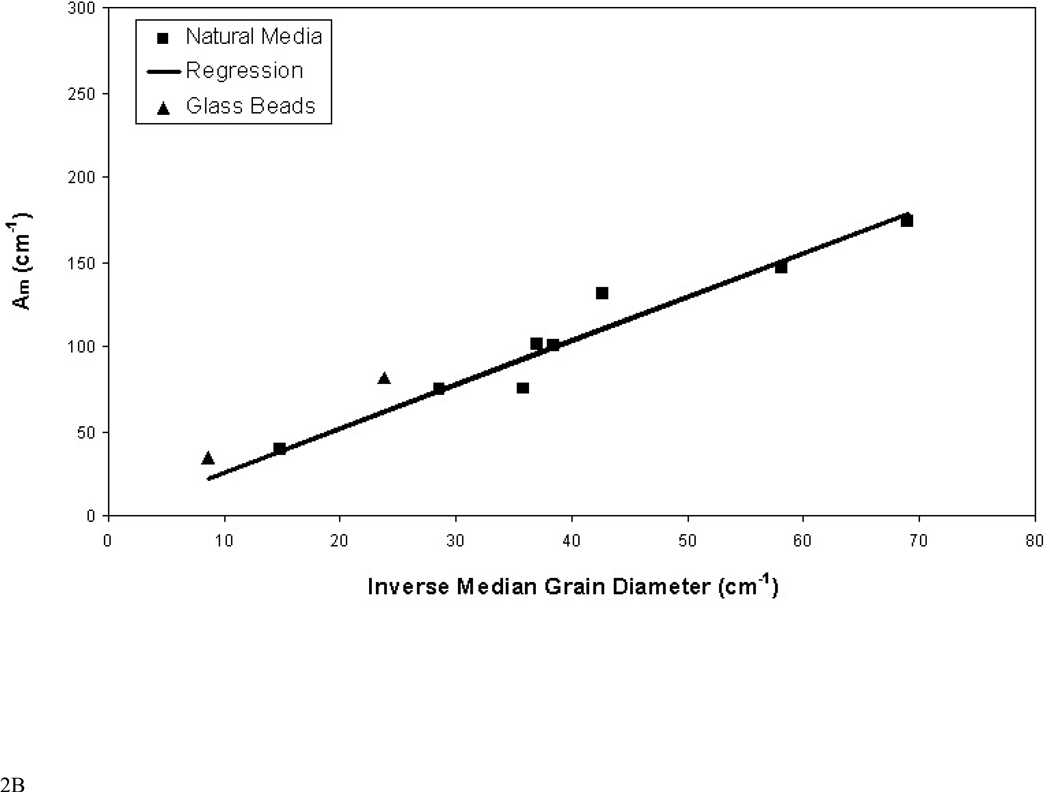
The residual organic-liquid saturations vary from 0.08 to 0.24 for the different media, as shown in Table 1. Comparison of fluid-fluid interfacial areas for systems wherein fluid saturations differ is facilitated by normalizing the measured areas by the volume of non-wetting fluid. These areas, which will be referred to as fluid-normalized specific interfacial area (A_f), are equivalent to the specific surface area of the non-wetting phase (i.e., surface area of non-wetting fluid divided by the volume of non-wetting fluid). The relationship between A_nw and A_f is: A_f = A_nw/θ_n, where θ_n is in this case volumetric organic-liquid content. For systems wherein A_nw is a linear function of S_w, A_f is constant. In these cases, A_f serves as another index of interfacial area for the system. Values of A_f are larger for porous media with smaller median grain diameters (and larger solid surface areas), as illustrated in Figure 2a. The relationship between the fluid-normalized and maximum specific interfacial areas is A_m = A_fn, where n is porosity. A_m values determined in this manner for all media are plotted in Figure 2b, and are observed to vary with median grain diameter.

Figure 2.

A. Relationship between fluid-normalized specific organic-liquid/water interfacial area (A_f) and median grain diameter of the porous media. Regression equation for natural media: A_f = 7.1/d₅₀, r² = 0.998. B. Relationship between maximum specific organic-liquid/water interfacial area (A_m) and median grain diameter of the porous media. Regression equation for natural media: A_m = 2.6/d₅₀, r² = 0.990.

Inspection of Figure 2 reveals that the correlations between fluid-normalized specific organic-liquid/water interfacial area and inverse median grain diameter and between maximum specific organic-liquid/water interfacial area and inverse median grain diameter are excellent. The reason for this correspondence is evident when recognizing that A_f is equivalent to the surface-area-to-volume ratio of the organic-liquid blobs, as noted above. This ratio for a given object is equal to 6/l, where l is a characteristic length (such as diameter for a sphere). Thus, the magnitude of A_f is a function of the representative size of the organic-liquid blobs. The results of prior work have shown that blob size is mediated by pore size, which in turn is mediated by porous-medium grain size. Thus, a correlation between a measure of blob size and porous-medium grain size is in congruence. Analysis of the blob-size distributions for the various media shows that indeed blob size is a direct function of median grain diameter (see Figure 3). Interestingly, the effective blob size for the glass-bead media deviate from the relationship exhibited for the natural media, again indicating that the representative blob size was smaller for the glass-bead media. The slope factor obtained from the regression between median blob diameter and median grain diameter for the natural media (Figure 3), wherein blob diameter was determined by treating the blobs as equivalent spheres, is 0.83. The observation that the representative blob size is similar in magnitude to the median grain size is consistent with the results of prior studies (e.g., 13,20,27).

Figure 3.

Median organic-liquid blob diameter versus median porous-medium grain diameter; both are in units of cm. Regression equation for natural media: Median Blob Diameter = 0.83d₅₀, r² = 0.988. Median blob diameter was calculated treating blobs as equivalent spheres. The dashed line connecting the glass-bead data is used for visualization purposes only.

The magnitude of the surface-area-to-volume ratio is also influenced by the shape of the object. The high degree of correlation obtained between A_f and median grain size (and blob size and grain size) suggests that blob-shape differences had minimal impact, which is consistent with the observation that general blob morphologies were similar for all of the natural media. The smaller representative blob sizes for the glass-bead media should result in comparatively larger A_f values for these media. However, the A_f values measured for the two glass-bead media do not deviate greatly from the relationship obtained for the natural media (Figure 2a). This is likely due in part to the fact that the blobs consisted almost entirely of single spheres for the glass-bead media, for which surface-area-to-volume ratios would be smaller, compensating somewhat for the size effect.

The very strong correlation observed between fluid-normalized and maximum specific interfacial area and inverse median grain diameter suggests that other properties of the porous media had minimal impact on interfacial area for these systems. For example, grain-size distribution appears to have had no measurable impact, given that uniformity coefficients ranged from 1 to 16 for the media employed. In addition, the results obtained for the three soils are consistent with those of the other media, which suggests that any potential changes in organic-liquid morphology and relative interfacial area that may have occurred due to the impact of moderate levels of soil organic matter on surface wettability were insignificant.

The results presented herein show that total specific organic-liquid/water interfacial area (A_nw) is a linear function of fluid saturation. Furthermore, fluid-normalized specific interfacial area (A_f) was shown to correlate to inverse median grain diameter. These two functionalities allow the development of a simple method for estimating total specific organic-liquid/water interfacial area as a function of fluid saturation for a given porous medium:

$${\mathrm{A}}_{\text{nw}}({\mathrm{\theta }}_{\mathrm{n}})=7.1{\mathrm{\theta }}_{\mathrm{n}}/\text{MGD}$$

where median grain diameter (MGD) is in units of cm. An equivalent equation can be developed in terms of A_m (Figure 2b data):

$${\mathrm{A}}_{\text{nw}(\text{Sn})}=2.6{\mathrm{S}}_{\mathrm{n}}/\text{MGD}$$

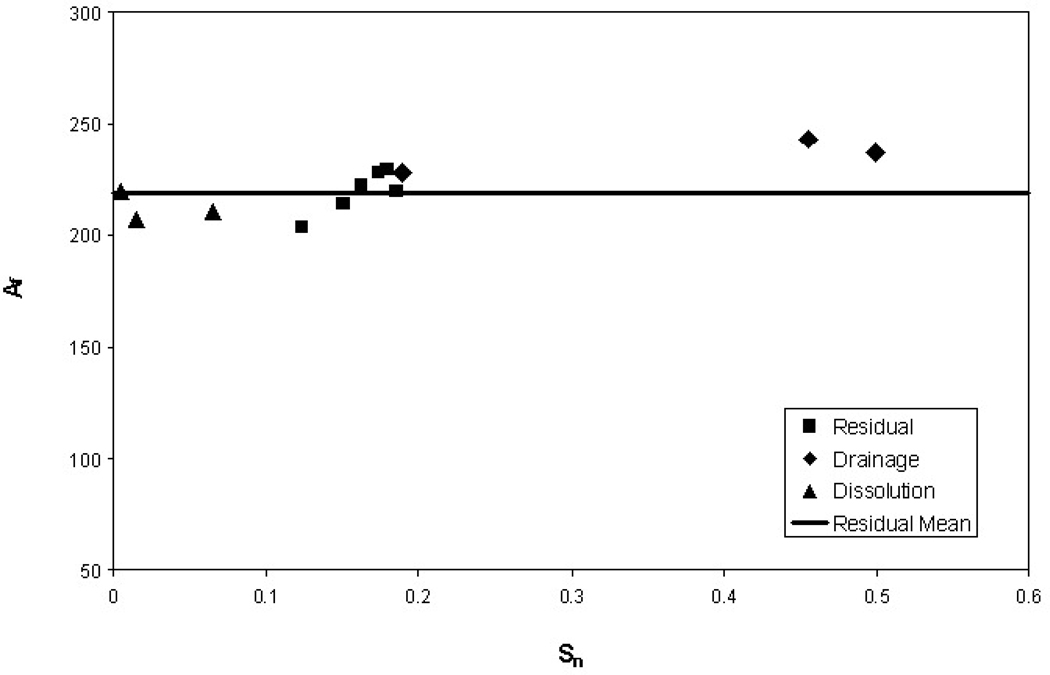
Application of the estimation equation is subject to a few caveats. First, interfacial areas measured with synchrotron X-ray microtomography do not include area associated with microscopic surface heterogeneities (e.g., surface roughness), as noted above. Second, the data used to develop the estimation equations were obtained primarily under conditions associated with residual-saturation formation of the organic (non-wetting phase) liquid (i.e., wetting-phase imbibition). Effective use of the equation for different conditions is depended upon the constancy of A_f as a function of other factors. This issue is evaluated to a limited extent through Figure 4, in which are plotted three sets of A_f vs. S_n data for the 45/50 sand. The data labeled as “drainage” were obtained under water-drainage conditions as opposed to the water-imbibition conditions employed for the “residual” data. The data labeled as “dissolution” were obtained from periodic imaging of a column that was subjected to flushing to remove organic-liquid mass via dissolution. Inspection of the data suggests that A_f is relatively constant for the range of conditions examined.

Figure 4.

Fluid-normalized total specific organic-liquid/water interfacial area (A_f) as a function of system condition; data are for the 45/50 sand. The dissolution data are from Schnaar and Brusseau (21).

Characterizing fluid-fluid interfaces is critical to addressing multiphase flow and contaminant transport issues in a number of fields. This study examined the influence of porous-medium texture on fluid-fluid interfacial area. The results showed interfacial area to be a function of inverse median grain diameter. A simple method for estimating organic-liquid/water interfacial area for a range of natural porous media was developed based on this relationship. The availability of a method for which the only parameter needed is the simple-to-measure median grain diameter should be of great utility for a variety of applications.