Abstract
Localized difference in the cortex is one of the most useful morphometric traits in human and animal brain studies. There are many tools and methods already developed to automatically measure and analyze cortical thickness for the human brain. However, these tools cannot be directly applied to rodent brains due to the different scales; even adult rodent brains are 50 to 100 times smaller than humans. This paper describes an algorithm for automatically measuring the cortical thickness of mouse and rat brains. The algorithm consists of three steps: segmentation, thickness measurement, and statistical analysis among experimental groups. The segmentation step provides the neocortex separation from other brain structures and thus is a preprocessing step for the thickness measurement. In the thickness measurement step, the thickness is computed by solving a Laplacian PDE and a transport equation. The Laplacian PDE first creates streamlines as an analogy of cortical columns; the transport equation computes the length of the streamlines. The result is stored as a thickness map over the neocortex surface. For the statistical analysis, it is important to sample thickness at corresponding points. This is achieved by the particle correspondence algorithm which minimizes entropy between dynamically moving sample points called particles. Since the computational cost of the correspondence algorithm may limit the number of corresponding points, we use thin-plate spline based interpolation to increase the number of corresponding sample points. As a driving application, we measured the thickness difference to assess the effects of adolescent intermittent ethanol exposure that persist into adulthood and performed t-test between the control and exposed rat groups. We found significantly differing regions in both hemispheres.
1. INTRODUCTION
Cortical thickness has been used as a very important morphological trait in many brain studies. For instance, global thinning of the cerebral cortex was reported in middle aged humans.1 Some brain diseases such as Alzheimer are known to cause atrophy in both regional and global cortical regions.2 There have been studies measuring cortical thickness of non-human species as well. Sporns and Zwi3 studied anatomical connection using cortical thickness of cats and macaque monkeys. Marian4 identified removal of rat ovaries at day 1 increased cortical thickness by day 90. Lerch et al.5 found an increase in cortical thickness of the mouse brain in a Huntington’s disease model in a recent study. In our study, we measure and compare the cortical thickness of two groups of rats, ethanol-exposed group and matching controls to assess the effects of adolescent intermittent ethanol exposed rats that persist into adulthood.
Histology and stereology-based techniques are traditional yet powerful methods that directly measure cortical thickness at the cellular level.4 However, wide application of these methods is limited due to their labor-intensive nature. Non-invasive MR technology provides alternatives to traditional thickness measurement methods. MR-based methods first extract the neocortex from volumetric images and then compute thickness based on mathematical definitions rather than anatomical evidence. Even though they cannot perfectly replace traditional methods, these computerized methods are tremendously useful because they are automated and provide dense measurements of the whole brain, which is typically not available through histology.
MR-based cortical thickness measurement methods can be classified as either surface-based methods or voxel-based methods. Surface-based methods construct a polyhedral model of the neocortex and compute distance between inner and outer sides of the cortex.6, 7 These methods are simple and fast for computing the thickness and allow easy control of sampling points. However, the definition of surface distance does not reflect the anatomical structure of cortical columns. Voxel-based methods that count the number of voxels on the path of cortical columns8 can overcome these problems of surface-based methods but have difficulties in comparing local differences. We propose a method that combines these two approaches. We first compute cortical thickness on the image and then sample the thickness measurement on a surface model constructed from the image.
Our method for laboratory rats was adapted from an existing correspondence algorithm for the human brain.9 Adaptation of existing methods have the following advantages: First, the measurement can be directly compared to the findings of cortical thickness studies in humans.10 Second, the smoothness of the rat cortical surface allows a simpler pipeline than is necessary for the convoluted human cortex. In particular, the inflation process to create a smooth surface is not necessary. Finally, since rat brains have smaller variations than humans, more robust results can be expected. For example, the segmentation process used in our method similarly showed stronger results than humans.11
Basically, our pipeline is similar to the one proposed by Lerch et al.5 Both methods are using atlas-based segmentation and Laplacian PDE-based thickness computation. The main difference is the identification of corresponding points, since we use an explicit correspondence algorithm unlike Lerch et al. Explicit correspondence has the advantage of allowing to incorporate additional information during the process. It also allows more flexibility in the choice of segmentation algorithms. Lerch et al method requires atlas-based segmentation for correspondence so that different types of segmentation cannot be used. In addition, the segmentation bias towards the atlas in atlas-based segmentation may introduce errors to the cortical thickness measurement.12
2. METHODS
In this paper, we present an automatic cortical thickness measurement tool for rat brains. The core of this approach lies on Laplacian-PDE based thickness measurement and the use of a correspondence algorithm for statistical analysis. In the Laplacian-PDE based method, the thickness is defined as the length of streamlines crossing cortical layers in perpendicular. Due to the lack of anatomical information, the cortical layers are mathematically derived from Laplacian vector field. Since the vector field is determined by its boundary condition, it is important to define appropriate boundary conditions in order to create analogous to physical layers.
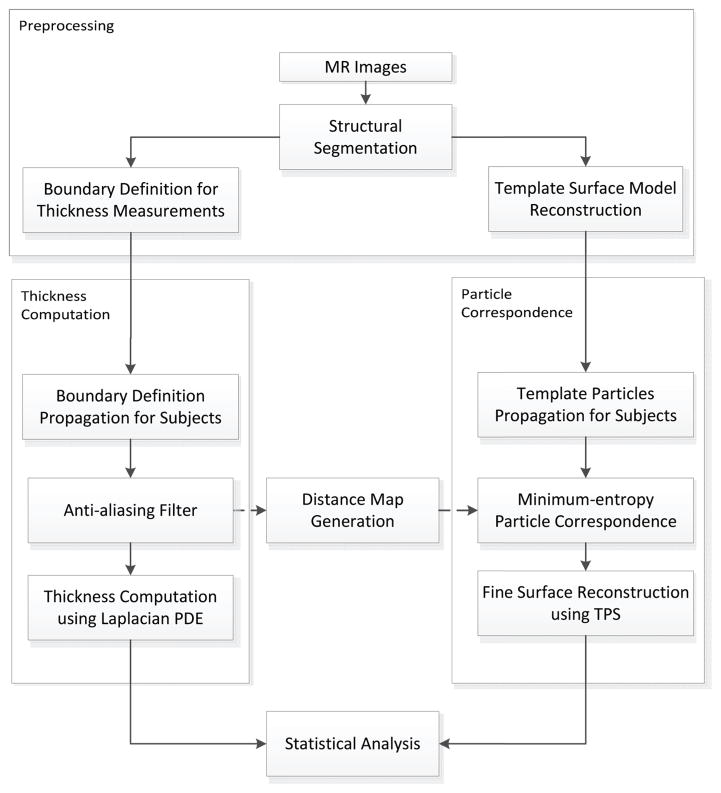
While the thickness is assigned at each voxel of the segmentation of the image, the measurements for statistical analysis are sampled on the reconstructed surface mesh. The vertices of the mesh are used as initial sample points whose correspondence is then optimized to balance a matching criterion of the ensemble and an even distribution of the sample points across each subject. In practice, this optimization is based upon particels that move freely over the surfaces, hence commonly referred to as the particle correspondence algorithm. Combining the above algorithms, our pipeline consists of four steps: preprocessing, thickness measurement, and establishment of correspondence followed by statistical analysis among experimental groups (see Figure 1).
Figure 1.
Pipeline for cortical thickness measurement. The pipeline consists of four steps: preprocessing, thickness measurement, correspondence followed by statistical analysis. Necessary boundary definitions and the template surface model are created from MR images during the preprocessing step. We apply an anti-aliasing filter to the boundary definition for smooth thickness computation. To obtain the sample points, the same neocortex segmentation is used to generate a distance map which provides an implicit surface during the particle correspondence process. We use bspline transformation to propagate initial particles and thin-plate spline for fine surface reconstruction. Statistical analyis is performed on the resulting thickness map using the high number of particles from the reconstruction.
2.1 Preprocessing
In order to prepare data from volumetric images, the segmentation of the neocortex, boundary definition for thickness measurement, and construction of template surface model are performed.
2.1.1 Neocortex Segmentation
As an initial step, the segmentation extracts the neocortex from MR images. Of the variety of available segmentation algorithms, we use atlas-based segmentation algorithm involving nonlinear deformation registration for the following reasons:
Atlas-based segmentation is widely used in brain structure segmentation.
Atlas-based segmentation provides implicit correspondence between groups of subjects, which provides a good initialization for the correspondence optimization step.
Atlas-based segmentation allows the propagation of additional structural information (such as the boundary definitions discussed in the next section) to each subject.
Implicit correspondence is a useful property when comparing features between groups and the availability of automatic propagation reduces the need for tedious manual work that would otherwise be necessary to obtain additional structural information.
2.1.2 Boundary Definition
In addition to the segmentation of the neocortex, the definition of inner and outer cortical surface boundary condition is required in order to define cortical thickness. This boundary definition is provided as a label map assigning different labels to inner and outer boundary voxels. Our thickness measurement algorithm assumes that cortical layers stack up between these two boundaries, which is analogous to cortical columns that develop from inner boundary towards outer boundary.
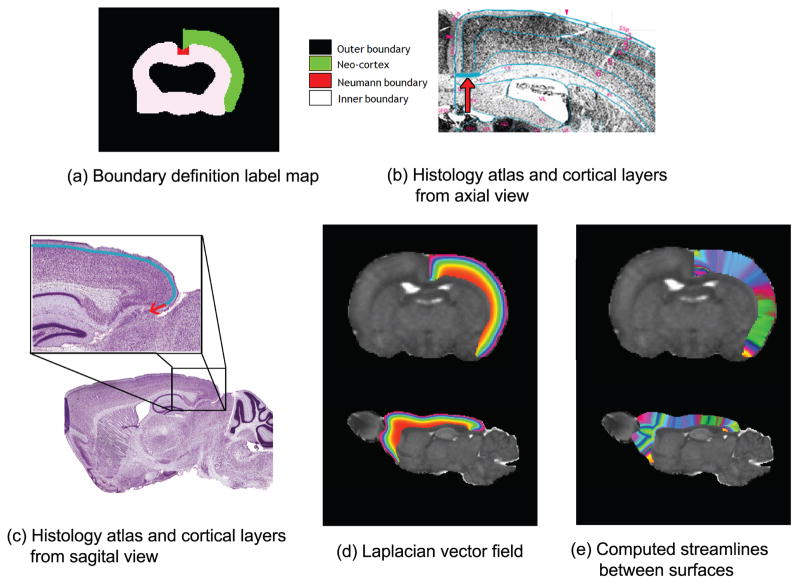
Due to the anatomical character of rodent cortical layers, however, we also need a third type of boundary: the boundary where the layers meet the corpus callosum and the external capsule. In practice, this third boundary can be implemented by applying the Neumann boundary condition, which defines the condition in terms of normal instead of boundary value. Since these boundaries must be defined on every subject, atlas-based segmentation is appropriate to propagate boundaries to avoid manually drawing the boundaries on each subject. The Neumann boundary is not included in the atlas used in our registration step. It is therefore manually added to the atlas (see Figure 2).
Figure 2.
(a) Boundary definitions for thickness measurement. The inner, outer, and Neumann boundaries are defined and the label of the neocortex is used as a solution domain in thickness computation. (b), (c) Histology atlas13, 14 shows a Nissl-stained slice along with anatomical annotations. Note that the six cortical layers stack up from inner boundary towards the outer boundary, and they converge laterally to the Neumann boundary in parallel, which is denoted with the arrow, as shown in (a). (d) Laplacian vector field is shown from axial and sagital view. Note that mathematically derived layers are similar to cortical layers in (c). (e) Thickness map is computed by the boundary definition of (a). Streamlines used to measure cortical thickness are represented as randomly colormapped stripes.
2.1.3 Template Surface Model
In addition to the boundary label map, initial particles on the neocortex surface are required in order to sample thickness measurements at corresponding points. These initial particles are represented as an ordered list of point coordinate tuples in 3D space. In the particle correspondence algorithm, it is possible to create the particles from scratch via a subdivision scheme. However, significant computation time can be saved by providing initial particles. We use the vertices of a template mesh as initial particles for the correspondence algorithm. To create such a template mesh, we use a SPHARM-based algorithm.15 Since SPHARM meshes have uniformly distributed vertices, which saves additional time by allowing a faster convergence of the correspondence algorithm.
2.2 Thickness Measurement
Thickness computation is done on the label map generated from the preprocessing step described in the previous section 2.1.2. The label map consists of four labels: non-interest domain, inner and outer boundary region, the Neumann boundary, and the solution domain where thickness measurements are assigned (Figure 2-a). Thickness is computed in the solution domain by solving two different partial differential equations.
First, a Laplacian vector field is computed from the inner boundary toward the outer boundary. This Laplacian vector field creates mathematical layers between inside and outside boundaries of the cerebral cortex which can be viewed as an analogy to the cortical columns (Figure 2-d). By solving a transport equation on the streamline, each voxel is assigned two values: forward and backward distance. The forward distance is measured between the voxel and source boundary and the backward distance is measured between the voxel and the destination boundary. The thickness is defined as the sum of these two values on boundary voxels (Figure 2-e). Detailed algebra and discussion can be found in Pichon et al.8
2.3 Correspondence Establishment
To compare the thickness between different subjects, corresponding points between subjects need to be identified. This is achieved using the particle correspondence algorithm minimizing entropy between dynamically moving sample points called particles.
Particle correspondence is a non-parameterized method constructing a point-based sampling of the shape ensemble that maximizes both the geometric accuracy and the statistical simplicity of the model at the same time.9, 16, 17 Surface particles are modeled as lists of sample point coordinate tuples moving on a set of implicit surfaces. The location of particles is optimized by gradient descent to minimize an energy function that balances the negative entropy of the particle distribution on each subject with the positive entropy of the ensemble of shapes.
Highly convoluted cortical surfaces in the human brain pose challanges during the optimization process to constrain particles on local tangent planes of implicit surface. On the area where two different surface patches are close, particles may jump between different surface patches and cause inconsistent particle correspondence. Oguz et al. overcome this difficulty by inflating the cortical surface to obtain a smooth, blob-like surface. We can skip this inflation process thanks to the smooth cortical surface in rats. However, flipping of particle location can still happen on the sharp boundary where the inner and outer surfaces meet. To avoid this problem, we include local features such as curvature and normal direction into the ensemble entropy.17
The execution of the algorithm requires initial particles and implicit surfaces for each subject. As described in the preprocessing step, initial particles are generated from SPHARM mesh. SPHARM mesh is a parametric boundary description15 computed from the binary label map; we use its vertices as uniformly distributed particles. Uniform distribution of particles has a near-minimal value of the surface entropy, which helps to save computation time during correspondence optimization. Since the initial particles are not required to have optimal correspondence, we can compute the SPHARM mesh once for the template and then propagate it using non-linear transformation computed in the segmentation step. The segmentation label map is used to compute a distance map which provides an implicit surface for the particles to move freely on. Local features of the implicit surface are computed on the individual subject mesh.
2.4 Statistical Analysis
Once correspondence is established, statistical analysis can be performed by sampling thickness at the established corresponding points. Due to the computational cost, however, it may not be possible to use enough particles to identify the thickness differences between subjects. Therefore, rather than using the particles themselves, we employ a method to reconstruct a fine surface from particles. To this end, we apply thin-plate spline warping to the template SPHARM mesh with a higher degree and subdivision than the one used for particle intiailization. This way, we can generate any number of corresponding points from the established particles.
3. RESULTS
This study was conducted as a prelimary experiment to study the effects of adolescent intermittent ethanol exposure that persist into adulthood. The set of subjects consists of 18 rats – 9 ethanol exposed rats and 9 wild-type rats. We applied our automatic cortical thickness algorithm to the preprocessed images of the subjects and produced a map of 25002 cortical thickness samples per subject. A paired Student’s t-test was used to assess local thickness difference between two groups.
Preprocessing
The subjects of the experiment consist of nine rats exposed to ethanol and nine wild-type rats. Diffusion weighted images of all subjects were acquired along 12 gradient directions and used to estimate diffusion tensors as well as compute mean diffusivity, fractional anistropy, and baseline maps. For the neocortex segmentation, fluid deformation based segmentation algorithm11 was used.
Mean group difference
To study the cortical thickness difference between the groups, we visualized mean thickness measurement in Figure 3. We find that overall thickness distribution is similar to Lerch’s findings.5 Note that, however, our results show more evenly distributed measurements over most regions including ventral regions of the neocortex except the frontal part. This is caused by the difference in the definition of Neumann boundary and highlights the importance of appropriate boundary definition.
Figure 3.
Mean thickness (n = 18) is color-mapped on the template surface with 25,002 corresponding points. Measurements range from 900 μm to 3400 μm. The frontal area connecting to the olfactory bulbs shows the thickest region. Other regions mostly exhibit similar values around 1800 μm.
Localized group difference
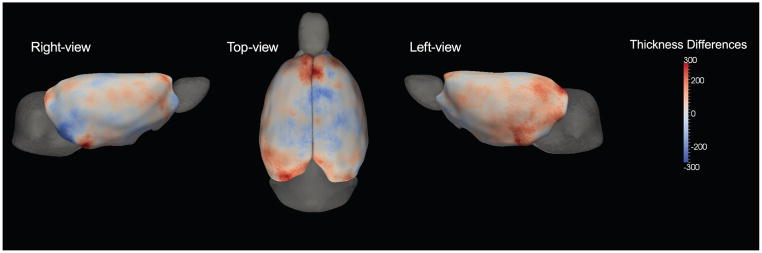
Localized cortical thickness differences can be first identified by the mean difference. In Figure 4, we show the mean difference (μeth − μctl) at each corresponding point. Ethanol-exposed rats are found to be thicker in frontal and cerebra-facing area. There is also asymmetry between left and right hemisphere. The left hemisphere is observed to be thicker than the right.
Figure 4.
Mean thickness difference between ethanol-exposed group and wild-type group is shown. Red shades indicate regions where the ethanol-exposed group is thicker than wild-type, and blue shades indicate regions where the wild-type group is thicker. Standard deviation was 261 μm with a maximum difference of 600 μm.
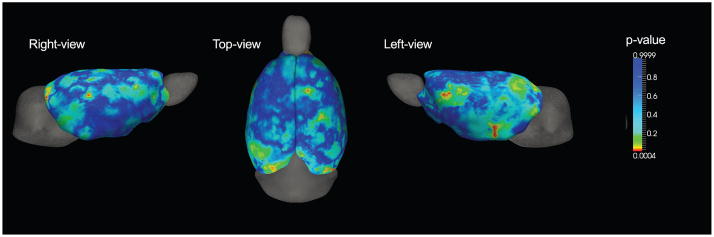
To investigate the statistical significance of these initial findings, we performed a Student’s t-test on each point. As shown in Figure 5, we found significant differences in regions in both hemispheres (p < 0.05). These significantly different areas did not appear to be symmetric. In the left hemisphere, thickness differences were found in the pre-temporal and ventral regions of the neocortex. The right hemisphere showed a smaller significant region compared to the left hemisphere. Outside these regions, the cortical thickness differences was found to be insignificant.
Figure 5.
Significance probability of paired Student’s t-test are mapped on the surface with red color for highly significant regions (p < 0.05) and blue for low (p > 0.2).
4. DISCUSSION
Our experiment was conducted to identify regions different in cortical thickness as a result of ethanol exposure in adolescent rats. Significantly different regions found here will be helpful for the planning of following histology analysis. Once histology analysis is performed, we will be able to validate our pipeline with regard to accuracy and effectiveness in cortical thickness measurement. However, there are aspects in our algorithm that may result in difference from physical measurements.
First, it must be kept in mind that the layer structure used in the thickness computation step is not based on anatomical evidence. Layers computed using Laplacian-PDE based equations are meaningful only in the sense of mathematics. To have a better thickness definition, we need to incorporate additional microstructural information. One promising source of information is diffusion tensor images of the mouse brain in prenatal stages.18 In this early developmental stage, mouse brain has three or more layers inside the cortex that exhibit different principal diffusion directions. By incorporating this information, we may be able to avoid artifically defined layer structures.
The definion of the Neumann boundary is another consideration because it affects the direction of simulated layers and as a result it may lead to different thickness measurements. Such erroneous results can be avoided by careful definition of boundaries. However, manual definition of each boundary is a costly and tedious segmentation task. Automatic propagation via non-linear transformation does not guarantee fully correct boundary definitions. Thus, an improved automatic boundary definition process is necessary for correct thickness computation. Incorporating such boundaries into atlas may be one option.
Finally, correct correspondence is always an important consideration in statistical analysis. Particle correspondence is a very promising correspondence algorithm that enables fully automatic correspondence establishment across subjects. In our experiments, we did not use the lobar parcellation of the neocortex when establishing correspondence. Therefore, the correspondence considered only geometric features such as local curvature, and the results may be improved by incorporating anatomical features as well. The ability to incorporate additional information is one of main advantages of using an explicit correspondence algorithm.
5. CONCLUSION
In this paper, we presented an automatic pipeline for cortical thickness measurement in rat brains. The pipeline was adapted from existing tools for the human brain and modified to provide comparable measurements in rat brains. This versatility is crucial for translational studies. Also, the Laplacian PDE-based thickness measurement has the desirable property of being analogous to the anatomical structure. Use of an explicit correspondence method provides more flexibility compared to registration-based correspondence. As future work, we will use the framework described in this manuscript to investigate the cortical thickness of healthy rats at PND5 and PND14 as well as the effects of prenatal cocaine exposure.
Acknowledgments
We are grateful to Clement Vachet for his insights and technical support. This work was funded by the NADIA U01-AA020022 Scientific Core and the NADIA U01-AA020022 Component 6 as well as the NIH STTR grant R41 NS059095. We would like to further acknowledge the financial support of the National Institute on Drug Abuse grant P01DA022446, the UNC Neurodevelopmental Disorders Research Center HD 03110, the NIH grant RC1AA019211, the UNC Bowles Center for Alcohol Studies as well as the NIH grants AA06059, AA019969.
References
- 1.Salat DH, Buckner RL, Snyder AZ, Greve DN, Desikan RSR, Busa E, Morris JC, Dale AM, Fischl B. Thinning of the cerebral cortex in aging. Cerebral cortex (New York, NY : 1991) 2004 Jul;14:721–30. doi: 10.1093/cercor/bhh032. [DOI] [PubMed] [Google Scholar]
- 2.Querbes O, Aubry F, Pariente J, Lotterie J-A, Démonet J-F, Duret V, Puel M, Berry I, Fort J-C, Celsis P. Early diagnosis of Alzheimer’s disease using cortical thickness: impact of cognitive reserve. Brain : a journal of neurology. 2009 Aug;132:2036–47. doi: 10.1093/brain/awp105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sporns O, Zwi JD. The small world of the cerebral cortex. Neuroinformatics. 2004 Jan;2:145–62. doi: 10.1385/NI:2:2:145. [DOI] [PubMed] [Google Scholar]
- 4.Diamond M, Johnson R, Ehlert J. A comparison of cortical thickness in male and female ratsnormal and gonadectomized, young and adult. Behavioral and Neural Biology. 1979 Aug;26:485–491. doi: 10.1016/s0163-1047(79)91536-x. [DOI] [PubMed] [Google Scholar]
- 5.Lerch JP, Carroll JB, Dorr A, Spring S, Evans AC, Hayden MR, Sled JG, Henkelman RM. Cortical thickness measured from MRI in the YAC128 mouse model of Huntington’s disease. NeuroImage. 2008 Jun;41:243–51. doi: 10.1016/j.neuroimage.2008.02.019. [DOI] [PubMed] [Google Scholar]
- 6.Kim JS, Singh V, Lee JK, Lerch J, Ad-Dab’bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC. Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage. 2005 Aug;27:210–21. doi: 10.1016/j.neuroimage.2005.03.036. [DOI] [PubMed] [Google Scholar]
- 7.Fischl B, Dale aM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the United States of America. 2000 Sep;97:11050–5. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pichon E. A Laplace equation approach for shape comparison. Proceedings of SPIE. 2006;614119:614119–10. [Google Scholar]
- 9.Oguz I, Niethammer M, Cates J, Whitaker R, Fletcher T, Vachet C, Styner M. Cortical correspondence with probabilistic fiber connectivity. Information processing in medical imaging : proceedings of the conference. 2009 Jan;21:651–63. doi: 10.1007/978-3-642-02498-6_54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He Y, Chen ZJ, Evans AC. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cerebral cortex (New York, NY : 1991) 2007 Oct;17:2407–19. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- 11.Lee J, Jomier J, Aylward S, Tyszka M, Moy S, Lauder J, Styner M. Evaluation of atlas based mouse brain segmentation. Proc SPIE. 2009;7259:725943–725949. doi: 10.1117/12.812762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yousefi S, Kehtarnavaz N, Gholipour A, Gopinath K, Briggs R. Comparison of atlas-based segmentation of subcortical structures in magnetic resonance brain images. 2010 IEEE Southwest Symposium on Image Analysis & Interpretation (SSIAI); 2010. pp. 1–4. [Google Scholar]
- 13.Hof P, Young W, Bloom F, Belichenko P, Celio M. Comparative Cytoarchitectonic Atlas of the C57BL/6 and 129/Sv Mouse Brains. Elsevier; 2000. [Google Scholar]
- 14.Franklin KB, Paxinos G. The Mouse Brain in Sterotaxic Coordinates. Academic Press; 1996. [Google Scholar]
- 15.Styner M, Oguz I, Xu S, Brechbühler C, Pantazis D, Gerig G. Framework for the statistical shape analysis of brain structures using spharm-pdm. 2006. [PMC free article] [PubMed] [Google Scholar]
- 16.Cates J, Fletcher P, Styner M, Shenton MR. Shape modeling and analysis with entropy-based particle systems. Processing in Medical. 2007:1–12. doi: 10.1007/978-3-540-73273-0_28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Oguz I, Cates J, Fletcher T, Whitaker R, Cool D, Aylward S, Styner M. Cortical correspondence using entropy-based particle systems and local features. Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium; IEEE; 2008. pp. 1637–1640. [Google Scholar]
- 18.Zhang J, Richards LJ, Miller MI, Yarowsky P, van Zijl P, Mori S. Characterization of mouse brain and its development using diffusion tensor imaging and computational techniques. Conference proceedings : ... Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference; Jan, 2006. pp. 2252–5. [DOI] [PubMed] [Google Scholar]