A Bayesian approach to joint analysis of longitudinal measurements and competing risks failure time data

SUMMARY

In this paper, we develop a Bayesian method for joint analysis of longitudinal measurements and competing risks failure time data. The model allows one to analyze the longitudinal outcome with nonignorable missing data induced by multiple types of events, to analyze survival data with dependent censoring for the key event, and to draw inferences on multiple endpoints simultaneously. Compared with the likelihood approach, the Bayesian method has several advantages. It is computationally more tractable for high-dimensional random effects. It is also convenient to draw inference. Moreover, it provides a means to incorporate prior information that may help to improve estimation accuracy. An illustration is given using a clinical trial data of scleroderma lung disease. The performance of our method is evaluated by simulation studies.

1. INTRODUCTION

In many studies, a response variable (e.g. biomarker) is repeatedly measured during the followup and the occurrence of some key event is monitored for each subject. Often the key event is dependently censored by some events such as disease-related dropout. An example is the Scleroderma Lung Study (SLS) [1]. The objective of this study is to evaluate the effectiveness of oral cyclophosphamide (CYC) versus placebo in the treatment of active, symptomatic lung disease due to scleroderma. The primary lung function outcome is forced vital capacity (FVC, as % predicted) measured longitudinally. The time to treatment failure or death is also recorded. In addition to independent censoring such as moving to another place, there is also dependent censoring by disease-related or treatment-related dropouts, such as those due to worsening disease, or serious adverse events (AEs).

When modeled separately, random effects models [2] and Cox proportional hazards models [3] are often used to evaluate treatment effect on the repeated measures and survival data, respectively. However, joint modeling of both outcomes is often necessary. First of all, for the longitudinal analysis, missing data of the longitudinal response induced by the events might be related to the response itself, making the missing mechanism nonignorable. The separate model without modeling the missing mechanism, such as a linear mixed effects model may give biased inference. For instance, in the SLS study, patients with lower (worse) %FVC may tend to experience failure or drop out from the study earlier than healthier individuals. This leads to fewer measurements of low %FVC, which might result in overestimating the overall %FVC level for the period after the dropouts. Second, some unmeasured variable or latent factor associated with time to events might induce unobserved heterogeneity among subjects. With the help of joint modeling longitudinal measurements, the estimation is expected to be more efficient for parameters in survival endpoint. Third, joint modeling makes it possible to evaluate treatment effects on the two endpoints simultaneously.

Joint modeling has been studied extensively in recent years. Much of the previous work on joint modeling can be classified into three categories: (i) inference for longitudinal measurements with nonignorable missing data due to dropout [4–7]; (ii) inference for time-to-event conditional on the time-dependent covariate [8–12]; and (iii) simultaneous inference for the longitudinal measurements and time-to-event [13, 14]. Most of these joint models assume single failure type with independent censoring. Most recently, Elashoff et al. [15, 16] considered a more general joint model, which incorporates competing risks model for survival endpoint, using a likelihood approach. Their model allows dependent censoring by treating it as a competing risk. Their proposed competing risks models could be a cause-specific model [17] or a mixture sub-model [18], in which the probability of failure type and the conditional hazard rate for each failure type were modeled with the logistic model and the proportional hazards model, respectively. They derived EM-based algorithms to obtain the parameter estimates, and a profile likelihood method was used to estimate the standard errors. However, their EM algorithm involves multi-dimensional integration which can be formidable and computationally expensive for high-dimension random effects problems. The rounding error from numerical integration may also result in inaccurate inference for the parameters. Another problem with the likelihood approach is that variance estimation usually requires asymptotic arguments and can be quite complicated to derive [19]. Moreover, there is always the issue of whether the sample size is large enough for the asymptotic approximation to be valid.

The purpose of this paper is to develop a Bayesian framework for joint modeling of longitudinal measurements and competing risks failure time data. Faucett and Thomas [9], Wang and Taylor [10], and Brown and Ibrahim [11] explored a Bayesian method for a single type of failure with independent censoring. To the best of our knowledge, this paper is the first to apply the Bayesian idea to the more general joint model of Elashoff et al. [16] with multiple types of failures in the failure time data. Under the Bayesian framework, variance estimates and other posterior summaries can be calculated directly from the posterior samples using standard Markov chain Monte Carlo (MCMC) sampling techniques. Unlike the likelihood approach, the Bayesian method can avoid high-dimensional integration and computational implementation is typically not more difficult as the number of random effects grows. For instance, in the SLS study (Section 4, Table I), the cost of computation for the four models are similar even though the last model involves four random effects. The Bayesian method also enables one to incorporate prior information into the current analysis [20] in a natural way. As illustrated in our simulation (Section 5, Table V), for small samples, incorporation of appropriate informative priors may improve the estimation accuracy of some parameters by decreasing the bias or standard error.

Table I.

Results for the different models examined with specification as (7)–(9).

		Latent dependence
Zij	# of RE	Parameter	Inference	DIC
[1]	2	σ u1u	−12.40 (−25.38,−5.41)	5777.1
		ν (2)	0.24 (0.01,0.73)
[timeij]	2	σ u1u	−1.18 (−2.16,−0.62)	4921.1
		ν (2)	0.21 (0.01,0.52)
[1,timeij]	3	σ u1u	−0.84 (−7.20,5.34)	5529.8
		σ u2u	−1.36 (−3.03,−0.58)
		ν (2)	0.27 (0.04,0.64)
[1,timeij,CYCi]	4	σ u1u	−0.65 (−8.21,4.43)	5821.6
		σ u2u	−1.49 (−3.09,−0.64)
		σ u1u	0.67 (−7.46,10.46)
		ν (2)	0.25 (0.04,0.69)

Table V.

Bias, coverage rate of the 95 per cent interval, standard deviation (SD), for the noninformative and informative priors.

		Noninformative priors			Informative prior
n	Parameter	Bias	Coverage	SD	Bias	Coverage	SD
50	β0=10	−0.002	0.945	0.083	−0.001	0.940	0.084
	β1=−1.5	0.024	0.960	0.112	0.007	0.960	0.112
	β2=1	− 0.114	0.890	0.169	− 0.036	0.980	0.094
	σ2=0.25	0.006	0.955	0.028	0.004	0.955	0.027
	${\sigma }_u^2=0.5$	0.005	0.945	0.176	−0.003	0.970	0.148
	${\sigma }_{uv}=0.4$	− 0.155	0.900	0.355	− 0.001	0.975	0.230
	${\sigma }_v^2=0.5$	0.435	0.970	1.231	0.117	0.985	0.365
	${\gamma }_1^{\left(1\right)}=-1$	0.090	0.910	0.635	0.039	0.950	0.517
	${\gamma }_2^{\left(1\right)}=0.8$	0.244	0.935	1.005	0.050	1.000	0.226
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.379	0.905	2.328	−0.340	0.925	2.680
	${\gamma }_2^{\left(2\right)}=0.5$	0.062	0.955	1.202	0.092	0.930	1.096
	ν(2)=1.2	− 1.071	0.925	1.753	− 0.078	0.980	0.493
100	β0=10	−0.003	0.960	0.058	−0.005	0.950	0.057
	β1=−1.5	0.008	0.930	0.078	0.012	0.940	0.076
	β2=1	− 0.039	0.895	0.137	− 0.027	0.965	0.084
	σ2=0.25	0.001	0.965	0.020	0.001	0.945	0.020
	${\sigma }_u^2=0.5$	0.006	0.975	0.117	−0.006	0.980	0.103
	σuv=0.4	− 0.048	0.870	0.266	− 0.001	0.975	0.165
	${\sigma }_v^2=0.5$	0.110	0.920	0.619	0.070	0.970	0.277
	${\gamma }_1^{\left(1\right)}=-1$	0.033	0.945	0.374	−0.006	0.955	0.342
	${\gamma }_2^{\left(1\right)}=0.8$	0.078	0.945	0.626	0.019	0.990	0.252
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.088	0.960	0.434	−0.052	0.960	0.428
	${\gamma }_2^{\left(2\right)}=0.5$	0.064	0.945	0.740	0.046	0.955	0.668
	ν(2)=1.2	0.056	0.890	1.570	0.034	0.985	0.394

Entries in boldface indicate different results from the two analysis methods.

The remainder of the paper is organized as follows. Section 2 gives the formulation of our joint model. Section 3 describes the posterior densities and the sampling procedures. Section 4 presents the analysis of a clinical trial data for Scleroderma lung disease using the developed method. In Section 5, the performance of our joint model is evaluated with simulation studies. We conclude with a discussion in Section 6.

2. THE JOINT MODEL

Our joint model consists of two submodels: a linear mixed effects model and a competing risk model. Suppose there are m subjects in the study. For subject i, the longitudinal response Y_i follows a linear mixed effects model:

$$Y_i=X_i^{\left(1\right)}\beta +Z_i{U}_i+{\epsilon }_i$$ (1)

where Y_i is n_i ×1, $X_i^{\left(1\right)}\left(t\right)$ is an n_i × p design matrix for fixed effects, β is a p×1 parameter vector of regression coefficients, commonly referred to as fixed effects in the model, Z_i is an n_i ×Q matrix of covariates for the Q×1 vector of errors U_i, and ε_i is an n_i It is assumed that ε_i is independent of U_i and is normally distributed N_ni (0,σ² I_ni).

During the followup, each subject may experience one of K distinct types of failure or could be right censored. Occurrence of one type of failure precludes us observing other types of failures. Let C_i =(T_i, D_i) be the competing risks data on subject i, where T_i is the failure time or censoring time, and D_i takes a value from 0,1,…, K, with D_i =0 indicating a censored event and D_i =k, where k =1,…, K, indicating that subject i fails from the kth type of failure. Dependent censoring can be treated as one of the K types of failure. The censoring mechanism other than the considered dependent censoring is assumed to be independent of the survival time. Let $X_i^{\left(2\right)}\left(t\right)$ be a 1×R row vector of covariates potentially related to the competing risks process. A cause-specific hazard model with random effects is assumed for competing risks survival data:

$$\begin{array}{cc}\hfill {\lambda }^{\left(k\right)}(t;X_i^{\left(2\right)},v_i,{\gamma }^{\left(k\right)},{\nu }^{\left(k\right)})& =\underset{h\to 0}{\lim }{h}^{-1}P[t\le T_i<t+h,D_i=k\mid T_i\ge t,X_i^{\left(2\right)}\left(t\right),v_i]\hfill \\ \hfill & ={\lambda }_0^{\left(k\right)}\left(t\right)\text{exp}\{X_i^{\left(2\right)}\left(t\right){\gamma }^{\left(k\right)}+{\nu }^{\left(k\right)}{v}_i\}\hfill \end{array}$$ (2)

where the function ${\lambda }^{\left(k\right)}(t;X_i^{\left(2\right)},v_i,{\gamma }^{\left(k\right)},v^{\left(k\right)})$ gives the instantaneous hazard rate from cause k at time t, given the regression vector $X_i^{\left(2\right)}\left(t\right)$ and the latent unknown factor v_i, in the presence of the other failure types. The regression coefficient ν^(k) represents the effect of the latent variable v_i and γ^(k) represents the effects of the observed covariates in $X_i^{\left(2\right)}\left(t\right)$ to the kth type of failure. Suppose that $X_i^{\left(2\right)}\left(t\right)=[X_i^{\left(21\right)},X_i^{\left(22\right)}\left(t\right)]$, ${\gamma }^{\left(k\right)}=[{\gamma }_1^{\left(k\right)},{\gamma }_2^{\left(k\right)}]$ where $X_i^{\left(21\right)}$ is time-independent and $X_i^{\left(22\right)}\left(t\right)$ is time-dependent. Our model allows both nonignorable monotone missing data caused by death/dropout and ignorable missing data (missing-at-random) at intermittant visit times. It is possible to have two types of missing data for the longitudinal measurements after the event time.

We assume that U_i and v_i jointly have a multivariate normal distribution:

$$\left(\begin{array}{c}\hfill U_i\hfill \\ \hfill v_i\hfill \end{array}\right)~\mathrm{N}\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\Sigma }_u\hfill & \hfill {\Sigma }_{uv}\hfill \\ \hfill {\Sigma }_{uv}^T\hfill & \hfill {\sigma }_v^2\hfill \end{array}\right)\right)$$ (3)

The parameter ν⁽¹⁾ is set to 1 to ensure identifiability. We further assume that the kth baseline hazard is a step function, ${\lambda }_0^{\left(k\right)}\left(t\right)={\lambda }_{0s}^{\left(k\right)}$, for $t_{s-1}^{\left(k\right)}<t\le t_s^{\left(k\right)}$, where $0<t_1^{\left(k\right)}<\cdots <t_{S\left(k\right)}^{\left(k\right)}<\infty$ is a partition of (0, ∞). Here S^(k) is the total number of pieces of the step function for type k failure and s=1,…, S^(k). Note that any hazard function can be approximated by a piecewise step function. More discussion on this issue is given later in the discussion section.

The parameters Σ_uv measure the latent association between the longitudinal measure and time-to-event introduced by U and v. If Σ_uv =0, then the joint model we proposed would reduce to those of separate analysis and the joint model and separate model give identical inference for fixed effects. In addition, recall that dependent censoring can be treated as one of the K competing risks. The magnitude of heterogeneity induced by the unobserved factor v to the first type of event is characterized by ${\sigma }_v^2$. The parameters ν measure the latent association between the competing risks. The parameter ν^(k) measures the latent dependence of the kth type of failure and the first type of failure. For example, in our SLS application, σ_uv<0 would indicate that there is a latent dependence between the longitudinal response %FVC and the survival process. The significance of the coefficient σ⁽²⁾ would indicate that there is a latent association between the two types of events and that the censoring of the key event treatment failure or death is informative. The negative value of σ_uv and the positive value for ν⁽²⁾ would indicate that there is a higher risk of treatment failure and/or disease-related dropout for subjects with more rapidly declining %FVC during the study, which could lead to biased estimation of the time trend and the variance of the random slope.

3. ESTIMATION METHODS

3.1. The likelihood

This section describes our Bayesian estimation procedure. The parameters in the joint model are (U_i, v_i, i = 1,…,m), β, σ², Σ_u, Σ_uv, ${\sigma }_v^2$, γ=(γ⁽¹⁾, γ⁽²⁾,…, γ^(K)), ν=(ν⁽²⁾,…, ν^(K)), and ${\lambda }_0=({\lambda }_{01}^{\left(1\right)},{\lambda }_{02}^{\left(1\right)},\cdots ,{\lambda }_{0S^{\left(K\right)}}^{\left(K\right)})$.

To ease the computation, we reparameterize (3) as

$$v_i={\theta }^{\prime }{U}_i+e_i$$ (4)

where θ is Q vector, e_i~N(0, ${\sigma }_e^2$), and U_i~N(0, Σ_u). It is easy to see that ${\sigma }_v^2$=θ′Σ_uθ+${\sigma }_e^2$ and Σ_uv=Σ_uθ. The reparameterization of (4) provides an attractive alternative for specitfying the noninformative priors for the relationship between two latent factors U_i and v_i. With this reparameterization, one only needs to specify priors for θ and ${\sigma }_e^2$. In contrast, (3) would require specification of noninformative priors for the whole covariance matrix of $(U_i^{\prime },v_i)\prime$ which is notoriously tricky.

Define: Ω=((U_i, e_i, i=1,…,m), β, σ⁽²⁾, Σ_u, γ, ν, λ₀, θ, ${\sigma }_e^2$). Assume that parameters β, σ², Σ_u, γ, ν, λ₀, θ, and ${\sigma }_e^2$ have independent priors. Assume further that for each subject, the longitudinal data are independent of the survival data conditional on Ω, X_i, Z_i, and the latent factors U_i and v_i. Then, the contribution of subject i to the conditional likelihood is:

$$\begin{array}{cc}\hfill f(Y_i,t_i,d_i\mid X_i,Z_i,\Omega )& =f(Y_i\mid X_i^{\left(1\right)},Z_i,\Omega )f(t_i,d_i\mid X_i^{\left(2\right)},\Omega )\hfill \\ \hfill & =f(Y_i\mid X_i^{\left(1\right)},Z_i,\beta ,U_i,{\sigma }^2)f(t_i,d_i\mid X_i^{\left(2\right)},\gamma ,\nu ,{\lambda }_0,\theta ,U_i,e_i)\hfill \\ \hfill & ={\left(2\pi {\sigma }^2\right)}^{-n_i∕2}\text{exp}\{-{(Y_i-X_i^{\left(1\right)}\beta -Z_i{U}_i)}^T(Y_i-X_i^{\left(1\right)}\beta -Z_i{U}_i)∕2{\sigma }^2\}\times \underset{k=1}{\overset{K}{\Pi }}\left({\left({{\lambda }_1}^{\left(k\right)}\left(t_i\right)\right)}^{I(d_i=k)}\text{exp}\{-H^{\left(k\right)}\left(t_i\right)\}\right)\hfill \end{array}$$ (5)

where ${\lambda }_i^{\left(k\right)}\left(t\right)={\lambda }_0^{\left(k\right)}\left(t\right)$ exp $\{X_i^{\left(2\right)}\left(t\right){\gamma }^{\left(k\right)}+(\theta \prime U_i+e_i){\nu }^{\left(k\right)}\}$ and $H^{\left(k\right)}\left(t_i\right)={\int }_0^{t_i}{\lambda }_0^{\left(k\right)}\left(t\right)$ exp $\{X_i^{\left(2\right)}\left(t\right){\gamma }^{\left(k\right)}+(\theta \prime U_i+e_i){\nu }^{\left(k\right)}\}$ dt.

Note that, under the piecewise constant assumption,

$$H^{\left(k\right)}\left(t_i\right)=\text{exp}\{X_i^{\left(21\right)}{\gamma }_1^{\left(k\right)}+({\theta }^{\prime }{U}_i+e_i){\nu }^{\left(k\right)}\}\sum _{s=1}^{S^{\left(k\right)}}{H}_{\mathit{is}}^{\left(k\right)}({\lambda }^{\left(k\right)},{\gamma }^{\left(k\right)},{\nu }^{\left(k\right)})$$ (6)

with $H_{is}^{\left(k\right)}({\lambda }^{\left(k\right)},{\gamma }^{\left(k\right)},{\nu }^{\left(k\right)})=I(t_i>t_{s-1}^{\left(k\right)}){\lambda }_{0s}^{\left(k\right)}{\int }_{t_{s-1}^{\left(k\right)}}^{\min (t_i,t_s^{\left(k\right)})}$ exp $\left\{X_i^{\left(22\right)}\left(t\right){\gamma }_2^{\left(k\right)}\right\}$ dt, s=1,…,S^(k).

3.2. MCMC sampling procedure

Markov chain Monte Carlo (MCMC) methods are used for posterior sampling [21]. Itinvolves sampling directly from the full distribution, Metropolis–Hastings (MH) sampling [22, 23], and adaptive rejection sampling (ARS) [24], as described below.

The full conditional distribution of the parameters is given in the Appendix. For parameters β, σ², Σ_u, ${\sigma }_e^2$, and λ₀ in our joint model, each of the conditional distributions is the product of some standard distribution and the prior. If a conjugate prior is used, drawing random variates from their full conditional distributions is straightforward. For the parameters U_i (i=1,…,m) the full conditional density is the product of a normal density from the longitudinal data and a factor from the survival data. We use the one-step MH algorithm to obtain the update in the sampling sequence, and the normal density from the longitudinal data as the proposal density. The parameter U_i is obtained by first sampling a random variate from the conditional density based on the longitudinal data and then using the conditional likelihood contribution from the survival data to determine the acceptance of the new draw. For the parameter ${\gamma }_r^{\left(k\right)}$ (k=1,…, K, r=1,…, R), in the survival model, we use a Metropolis sampler to update the values of these parameters since the direct sampling is not available. For each of these parameters, we propose a normal density as the proposal density, which has the current parameter value as its mean and its standard deviation set to four times the standard error of a maximum partial likelihood estimate from a standard Cox model [10]. The parameter e_i (i=1,…,m) is obtained by first sampling a random variate from the normal densities as its assumption and then by using the conditional likelihood contribution from the survival data to determine the acceptance of the new draw. Parameters θ and ν^(k) are obtained using ARS.

The initial values of the parameters for sampling are obtained by modeling the longitudinal data and survival data separately. The initial value for ${\lambda }_{0s}^{\left(k\right)}$(s=1,…,S^(k), k=1,…,K) can be obtained by drawing a random variate from the gamma full conditional distribution in the Appendix.

3.3. Inference

We estimate the parameters by the posterior medians. The approximate 95 per cent probability interval is based on the 2.5th percentile and the 97.5th percentile. Standard errors are obtained using the standard deviations of the posterior samples. The procedure has been shown to work well by the application and simulation study in the later sections.

4. APPLICATION

In this section, we apply our method to analyze the SLS data [1] discussed earlier in the Introduction. The SLS is a double-blinded, randomized, placebo-controlled trial on patients with evidence of active alveolitis and scleroderma-related interstitial lung disease. The primary study objective is to determine if oral cyclophosphamide (CYC) compared with placebo can either improve pulmonary function as measured by forced vital capacity (FVC, as % predicted) or reduce the risk of treatment failure or death. Patients received CYC or placebo for 1 year and were followed for an additional year. Initially, patients were given a partial dose, and the dose was gradually increased to the target level within the first 6 months. %FVC was assessed every 3 months. Our analyses use data from 6–21 months from the 140 subjects who completed at least six months of treatment. Baseline covariates such as age and degree of fibrosis in the lung (FIB) were also recorded. It should be noted that the data we use here do not include the measurements of %FVC after the observed treatment failures since the patients might have switched to other treatments after the treatment failures, which differs from the analysis by Elashoff et al. [16].

We observed 16 treatment failures or deaths, 37 disease-related dropouts due to worsening disease or AE, and 12 independent dropouts with no evidence that the dropouts were related to disease. The rest were administratively censored. We consider treatment failure or death as risk 1 and disease-related dropout as risk 2. The average number of visits per patient was 6.0. As discussed earlier in Section 1, both treatment failure or death and disease-related dropout could cause nonignorable missing data for the longitudinal measure %FVC.

We applied the joint model described in Section 2 to the SLS data after adjustment of baseline %FVC, age, and degree of fibrosis in the lung to their means. In the sub-model for %FVC, we fitted the following linear mixed effects model with random effects U_i:

$$FV{C}_{\mathit{ij}}={\beta }_0+{\beta }_1{\text{Age}}_i+{\beta }_2{\text{CYC}}_i+{\beta }_3{\text{FBI}}_i+{\beta }_4{\text{FVC}}_{0i}+{\beta }_5{\text{Age}}_i\times CY{C}_i+{\beta }_6{\text{FBI}}_i\times CY{C}_i+{\beta }_7{\text{FVC}}_{0i}\times CY{C}_i+{\beta }_8{\text{time}}_{\mathit{ij}}+{\beta }_9{\text{time}}_{\mathit{ij}}\times CY{C}_i+Z_{\mathit{ij}}{U}_i+{∊}_{\mathit{ij}}$$ (7)

in which, for subject i, Age_i is the age at baseline, FVC_0i is the baseline %FVC, FIB_i is the degree of fibrosis in the lung, CYC_i is the CYC treatment group indicator, time_ij is the measurement time for visit j in months, U_i represents random effects, and the ε_ij's are mutually independent normal measurement errors with mean 0 and variance σ². Here, Z_ij includes covariates for random effects. We considered multiple choices for Z_ij and selected the model based on the DIC criterion [25]. The results are shown later.

A competing risks sub-model is used to model treatment failure or death (risk 1) and disease-related dropout (risk 2):

$${\lambda }^{\left(1\right)}\left(t\right)={\lambda }_0^{\left(1\right)}\left(t\right)\text{exp}\{{\gamma }_1^{\left(1\right)}{\text{Age}}_i+{\gamma }_2^{\left(1\right)}{\text{CYC}}_i+{\gamma }_3^{\left(1\right)}{\text{FIB}}_i+{\gamma }_4^{\left(1\right)}{\text{FVC}}_{0i}+{\gamma }_5^{\left(1\right)}{\text{Age}}_i\times {\text{CYC}}_i+{\gamma }_6^{\left(1\right)}{\text{FIB}}_i\times {\text{CYC}}_i+{\gamma }_7^{\left(1\right)}{\text{FVC}}_{0i}\times {\text{CYC}}_i+v_i\}$$ (8)

and

$${\lambda }^{\left(2\right)}\left(t\right)={\lambda }_0^{\left(2\right)}\left(t\right)\text{exp}\{{\gamma }_1^{\left(2\right)}{\text{Age}}_i+{\gamma }_2^{\left(2\right)}{\text{CYC}}_i+{\gamma }_3^{\left(2\right)}{\text{FIB}}_{0i}+{\gamma }_4^{\left(2\right)}{\text{FVC}}_{0i}+{\gamma }_5^{\left(2\right)}{\text{Age}}_i\times {\text{CYC}}_i+{\gamma }_6^{\left(2\right)}{\text{FIB}}_i\times {\text{CYC}}_i+{\gamma }_7^{\left(2\right)}{\text{FVC}}_{0i}\times {\text{CYC}}_i+{\nu }^{\left(2\right)}{v}_i\}$$ (9)

in which the latent variables follow a bivariate normal distribution:

$$\left(\begin{array}{c}\hfill U_i\hfill \\ \hfill v_i\hfill \end{array}\right)~\mathrm{N}\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\Sigma }_u\hfill & \hfill {\Sigma }_{\mathit{uv}}\hfill \\ \hfill {\Sigma }_{\mathit{uv}}\hfill & \hfill {\sigma }_v^2\hfill \end{array}\right)\right)$$

in which Σ_uv=[σ_u1v, σ_u1v,…,σ_uQv]^T.

We used a piecewise exponential baseline hazard function with three knots for the event of treatment failure or death and the event disease-related dropout, respectively, and the time points defining the steps are taken to be 3 equally split percentiles of the observed dropout times for the two event types, respectively. We used a combination of weakly informative and standard prior distributions. The corresponding priors for the parameters are given as β₀~ N(70, 400) with other β's β_l~N(0, 400) such that l=1,…,9, σ²~IG(0.001, 0.001), ${\sigma }_u^2$~IG(0.001, 0.001), ${\sigma }_e^2$~IG(0.001, 0.001), θ~N(0, 10¹⁰), ${\lambda }_{0s}^{\left(k\right)}$~Γ(0.1, 0.1) such that s 1,…, S^(k) and k=1, 2; ${\gamma }_r^{\left(k\right)}$~N(0, 20) such that k=1, 2and r=1,…,7, and ν^(k)~N(0, 20) where k=2. Recall that θ is defined in (4). In case θ is a vector, we used an independent element of flat normal prior N(0, 10¹⁰) for each element of θ.

Table I summarizes the results for some models with different structures of random effects Z_ij. The model with a random slope ([Time_ij]) has the smallest DIC, indicating that it provides the best fit for the data among the four models. The inference for Σ_uv indicates that there exists latent dependence between the longitudinal measurements and the survival data since at least one element in Σ_uv is negatively significant in each model. It is worth noting that all the models give a positive significance of ν⁽²⁾, indicating that there is latent association between the two types of failures and censoring for the key event of treatment failure or death by disease-related dropout may be dependent. Subjects with larger latent factor v tend to experience treatment failure and disease-related dropout earlier than those with a lower v.

The results of parameter estimates and 95 per cent confidence intervals based on the selected random slope model with Z_ij as ([Time_ij]) are summarized in Table II, together with those from a separate analysis. In the separate analysis, the longitudinal and survival data are fitted separately using two marginal sub-models, a linear mixed model (7) and a cause-specific competing risks model with a common frailty (8)–(9), respectively.

Table II.

Results from analyzing the SLS data using a random slope model. Entries in boldface indicate different results from the joint and separate analysis.

Factor	Separate analysis Estimate (95 per cent CI)	Joint analysis Estimate (95 per cent CI)
Longitudinal outcome %FVC
Intercept (β0)	66.83 (65.40 68.21)	67.18 (65.87 68.52)
Age (β1)	−0.03 (−0.12 0.06)	−0.03 (−0.11 0.06)
CYC group (β2)	−0.82 (−2.75 1.10)	−0.99 (−2.88 0.90)
Fibrosis (β3)	−1.67 (−2.74 −0.62)	−1.67 (−2.76 −0.58)
Baseline %FVC (β4)	0.91 (0.82 1.00)	0.90 (0.81 1.00)
Age × CYC group (β5)	0.07 (−0.07 0.21)	0.07 (−0.07 0.22)
Fibrosis × CYC group (β6)	1.36 (−0.19 2.94)	1.30 (−0.25 2.89)
Baseline %FVC × CYC group (β7)	0.11 (−0.03 0.25)	0.11 (−0.03 0.25)
Time(month) (β8)	−0.14 (−0.31 0.03)	−0.22 (−0.38 −0.05)
Time (month) × CYC group (β9)	0.21 (−0.03 0.44)	0.25 (0.01 0.48)
σ 2	20.22 (17.91 22.86)	19.79 (17.56 22.38)
${\sigma }_u^2$	0.26 (0.20 0.36)	0.30 (0.22 0.41)
Time to treatment failure or death
Age (${\gamma }_1^{\left(1\right)}$)	0.09 (−0.01 0.45)	0.10 (0.02 0.20)
CYC group (${\gamma }_2^{\left(1\right)}$)	−1.30 (−6.13 1.63)	−1.33 (−3.61 0.61)
Fibrosis (${\gamma }_3^{\left(1\right)}$)	−0.14 (−2.49 1.34)	−0.45 (−1.77 0.68)
Baseline %FVC (${\gamma }_4^{\left(1\right)}$)	0.10 (−0.01 0.55)	0.03 (−0.06 0.13)
Age × CYC group (${\gamma }_5^{\left(1\right)}$)	−0.10 (−0.60 0.10)	−0.13 (−0.30 0.01)
Fibrosis × CYC group (${\gamma }_6^{\left(1\right)}$)	−0.70 (−4.38 2.42)	0.12 (−1.89 2.25)
Baseline %FVC × CYC group (${\gamma }_7^{\left(1\right)}$)	−0.17 (−0.84 0.02)	−0.05 (−0.21 0.12)
Time to disease-related dropout
Age (${\gamma }_1^{\left(2\right)}$)	0.04 (0.00 0.10)	0.05 (0.01 0.09)
CYC group (${\gamma }_2^{\left(2\right)}$)	0.44 (−0.43 1.41)	0.40 (−0.41 1.28)
Fibrosis (${\gamma }_3^{\left(2\right)}$)	0.09 (−0.49 0.68)	0.07 (−0.44 0.58)
Baseline %FVC (${\gamma }_4^{\left(2\right)}$)	−0.07 (−0.14 −0.02)	−0.06 (−0.12 −0.02)
Age × CYC group (${\gamma }_5^{\left(2\right)}$)	−0.01 (−0.09 0.06)	−0.03 (−0.09 0.03)
Fibrosis × CYC group (${\gamma }_6^{\left(2\right)}$)	0.11 (−0.67 0.91)	0.18 (−0.55 0.91)
Baseline %FVC × CYC group (${\gamma }_7^{\left(2\right)}$)	0.10 (0.03 0.19)	0.09 (0.02 0.16)
Random effects for survival endpoint
ν (2)	−0.14 (−5.18 4.52)	0.21 (0.01, 0.52)
${\sigma }_v^2$	13.24 (0.00 142.91)	5.07 (1.52, 18.91)
Covariance of ui and vi
σ uv	—	−1.18 (−2.16, −0.62)

It is seen from Table II, based on our joint model, that the degree of fibrosis in the lung is negatively correlated with %FVC (${\widehat{\beta }}_3=-1.67,95$ per cent CI: (−2.76,−0.58)). The baseline %FVC is highly correlated to %FVC during the followup (${\widehat{\beta }}_4=0.90,95$ per cent CI: (0.81,1.00)). The %FVC for the placebo group declines significantly by a factor of 0.22 each month (95 per cent CI for β₈: (−0.38,−0.05)). This result differs from the analysis by Elashoff et al. [16], who included the measurements of %FVC after the observed treatment failures and found nonsignificant time trend. After carefully examining the available %FVC values after the observed treatment failures, we find that these measurements tend to get greater than those values prior to the treatment failures, which results in a weakened decline time trend in their analysis. The significance of the interaction term between the treatment group and time indicates that the developing trend of %FVC for the CYC group is different from that of the placebo group. During one month, the %FVC decreases for the CYC group is 0.25 (95 per cent CI for β₉: (0.01,0.48)) less than that of the placebo group. In contrast to a declining %FVC in the placebo group, there is an increasing trend for %FVC in the CYC group (${\widehat{\beta }}_8+{\widehat{\beta }}_9=0.03,95$ per cent CI: (−0.14,0.19)).

Our joint analysis for the survival endpoint concludes that older subjects have an increased risk in experiencing treatment failure (${\widehat{\gamma }}_1^{\left(1\right)}=0.10,95$ per cent CI: (0.02,0.20)) and disease-related dropout (${\widehat{\gamma }}_1^{\left(2\right)}=0.05,95$ per cent CI: (0.01,0.09)). Baseline %FVC also affects the risk to experience disease-related dropout (${\widehat{\gamma }}_4^{\left(2\right)}=-0.06,95$ per cent CI: (−0.12,−0.02)), but this effect in the CYC group differs from the placebo group (${\widehat{\gamma }}_7^{\left(2\right)}=0.09,95$ per cent CI:(0.02,0.16)).

The joint and separate analyses give different results on the time trend parameters. Based on our joint model, the %FVC for the placebo group declines significantly (${\widehat{\beta }}_8=-0.22$, 95 per cent CI (−0.38,−0.05)). The interaction term between time trend and the treatment group is significant (${\widehat{\beta }}_9=0.25$, 95 per cent CI: (0.01,0.48)). However, the separate linear mixed effects model analysis fails to detect a significant decline in %FVC for the placebo group (${\widehat{\beta }}_8=-0.14,95$ per cent CI (−0.31,0.03)), and does not reach significance for the difference of developing trends between the placebo and CYC groups (${\widehat{\beta }}_9=0.21$, 95 per cent CI: (−0.03,0.44)). The posterior distribution of β₈ (time trend for the placebo group) and β₈+β₉ (time trend for the CYC group) are noticeably seen different, as shown in Figures 1 and 2.

Figure 1.

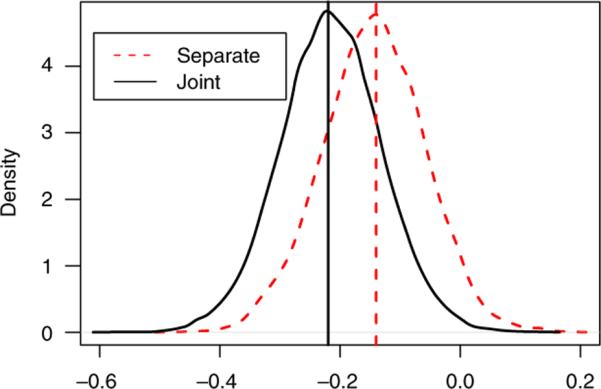
Posterior densities of time trend for the placebo group in the SLS study from the separate models and the proposed joint model. The vertical lines represent the posterior medians. The estimates and CIs for the two methods are: −0.14(−0.31 0.03), −0.22(−0.38−0.05), respectively.

Figure 2.

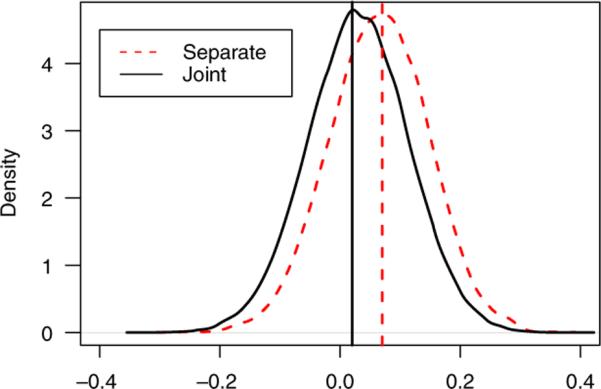
Posterior densities of time trend for the CYC group in the SLS study from the separate models and the proposed joint model. The vertical lines represent the posterior medians. The estimates and CIs for the two methods are: 0.07(−0.10, 0.22), 0.03(−0.14, 0.19), respectively.

Asides from the time trends, the variance of the random slope estimated with the separate analysis (${\widehat{\sigma }}_u^2=0.26$, 95 per cent CI (0.20,0.36)) is smaller than that in joint analysis (${\widehat{\sigma }}_u^2=0.30,95$, per cent CI:(0.22,0.41)). Our simulations in the later section show the underestimation of this parameter with the separate analysis in presence of nonignorable missing data due to the response related events.

We also notice that in the survival submodel the estimates and confidence intervals for some parameters derived with the joint model differ greatly from the separate models. With the help of modeling longitudinal outcomes, the joint model is expected to improve the estimation of the parameters in the survival model.

The differences between the separate and joint analysis might be explained by the negative significance for the covariance σ_uv (estimate −1.18, 95 per cent CI: (−2.16, −0.62)) between the latent variable of the longitudinal model and that of the survival model. This indicates that there is a dependence between the longitudinal response %FVC and the survival process. The significance of the coefficient ν⁽²⁾ (estimate 0.21, 95 per cent CI: (0.01,0.52)) indicates that there is a latent association between the two types of events. The negative value of σ_uv and the positive value for ν⁽²⁾ indicate that there is a higher risk of treatment failure and/or disease-related dropout for subjects with more rapidly declining %FVC during the study, which leads to biased estimation of the time trend and the variance of the random slope.

5. SIMULATION STUDY

First we conducted a simulation to compare the performance of the likelihood and the Bayesian approaches for the joint model we proposed. The longitudinal responses were simulated from a random slope linear mixed model

$$Y\left(t_{\mathit{ij}}\right)={\beta }_0+{\beta }_1{X}_{1i}+{\beta }_2{t}_{\mathit{ij}}+t_{\mathit{ij}}{U}_i+{\epsilon }_{\mathit{ij}}$$ (10)

for j=1,…,n_i, where ε_ij ~N(0,σ²). The covariate X_1i was simulated from a Bernoulli distribution with success probability of 0.5 acting as a treatment group indicator for a 1:1 allocation in randomization trials. The data for longitudinal measurements were generated for every 0.5 unit from 0 to 5. We simulated two competing risks, risk 1 and 2, from the following cause-specific proportional hazards model with the random effects v_i:

$${\lambda }^{\left(1\right)}(t;X_{1i,},X_{2i,},U_i,{\gamma }^{\left(1\right)})={\lambda }_0^{\left(1\right)}\left(t\right)\text{exp}\{{\gamma }_1^{\left(1\right)}{X}_{1i}+{\gamma }_2^{\left(1\right)}{X}_{2i}+v_i\}$$ (11)

$${\lambda }^{\left(2\right)}(t;X_{1i,},X_{2i,},U_i,{\gamma }^{\left(2\right)},{\nu }^{\left(2\right)})={\lambda }_0^{\left(2\right)}\left(t\right)\text{exp}\{{\gamma }_1^{\left(2\right)}{X}_{1i}+{\gamma }_2^{\left(2\right)}{X}_{2i}+{\nu }^{\left(2\right)}{v}_i\}$$ (12)

where X_1i was shared with the longitudinal model and covariate X_2i was simulated from a normal distribution with mean 0 and variance 0.1. We used constant baseline hazards of 0.1 and 0.2 for risk 1 and risk 2, respectively, to generate the event time data. The latent variables were generated from the following bivariate normal distribution:

$$\left(\begin{array}{c}\hfill U_i\hfill \\ \hfill v_i\hfill \end{array}\right)~\mathrm{N}\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_u^2\hfill & \hfill {\sigma }_{\mathit{uv}}\hfill \\ \hfill {\sigma }_{\mathit{uv}}\hfill & \hfill {\sigma }_v^2\hfill \end{array}\right)\right)$$

The censoring time was generated from an exponential distribution with a constant hazard rate of 0.1. The parameters are given in Table III. With this setup, the rate of risk 1 is approximately 0.43, the rate of risk 2 is 0.38, and censoring rate is 0.19. Longitudinal responses are missing after the observed or censored event times. The average number of total longitudinal observations is 3.7 per subject.

Table III.

Bias, coverage rate of the 95 per cent interval, standard deviation (SD), based on the likelihood method and the Bayesian model with noninformative priors.

		Likelihood method			Bayesian method
n	Parameter	Bias	Coverage	SD	Bias	Coverage	SD
100	β0 = 10	0.001	0.965	0.055	−0.003	0.960	0.058
	β1=−1.5	0.001	0.955	0.072	0.008	0.930	0.078
	β2 = 1	−0.027	0.960	0.105	−0.039	0.895	0.137
	σ2 = 0.25	0.001	0.965	0.020	0.001	0.965	0.020
	${\sigma }_u^2=0.5$	−0.020	0.910	0.110	0.006	0.975	0.117
	σuv = 0.4	−0.049	0.915	0.286	−0.048	0.870	0.266
	${\sigma }_v^2=0.5$	0.219	0.990	0.822	0.110	0.920	0.619
	${\gamma }_1^{\left(1\right)}=-1$	−0.059	0.960	0.406	0.033	0.945	0.374
	${\gamma }_2^{\left(1\right)}=0.8$	0.066	0.970	0.604	0.078	0.945	0.626
	${\gamma }_{}^{\left(2\right)}=-1.5$	−0.051	0.965	0.504	−0.088	0.960	0.434
	${\gamma }_2^{\left(2\right)}=0.5$	−0.016	0.960	0.680	0.064	0.945	0.740
	ν(2) = 1.2	0.162	0.930	1.113	0.056	0.890	1.570
200	β0 = 10	0.002	0.970	0.036	0.002	0.945	0.044
	β1=−1.5	−0.002	0.955	0.052	0.002	0.980	0.051
	β2 = 1	−0.019	0.955	0.095	−0.009	0.955	0.087
	σ2 = 0.25	>0.001	0.965	0.014	0.001	0.945	0.014
	${\sigma }_u^2=0.5$	−0.007	0.940	0.078	0.014	0.960	0.084
	σuv = 0.4	−0.013	0.980	0.181	0.002	0.950	0.142
	${\sigma }_v^2=0.5$	0.080	0.980	0.352	0.034	0.975	0.314
	${\gamma }_1^{\left(1\right)}=-1$	−0.029	0.975	0.266	0.007	0.960	0.245
	${\gamma }_2^{\left(1\right)}=0.8$	0.020	0.965	0.384	0.070	0.925	0.422
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.075	0.955	0.395	−0.018	0.950	0.278
	${\gamma }_2^{\left(2\right)}=0.5$	0.013	0.940	0.514	0.022	0.935	0.425
	ν(2) = 1.2	0.118	0.930	0.779	0.051	0.980	0.435
500	β0 = 10	−0.002	0.965	0.027	0.003	0.960	0.026
	β1=−1.5	0.002	0.965	0.038	−0.003	0.970	0.033
	β2 = 1	−0.014	0.965	0.077	0.008	0.950	0.057
	σ2 = 0.25	>0.001	0.965	0.010	>0.001	0.960	0.009
	${\sigma }_u^2=0.5$	−0.007	0.910	0.057	0.013	0.935	0.057
	σuv= 0.4	0.007	0.965	0.118	0.019	0.965	0.090
	${\sigma }_v^2=0.5$	0.067	0.930	0.228	0.024	0.945	0.164
	${\gamma }_1^{\left(1\right)}=-1$	−0.021	0.950	0.162	0.011	0.940	0.156
	${\gamma }_2^{\left(1\right)}=0.8$	0.023	0.980	0.229	0.014	0.965	0.233
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.030	0.950	0.231	<0.001	0.930	0.162
	${\gamma }_2^{\left(2\right)}=0.5$	0.011	0.955	0.289	0.037	0.945	0.259
	ν(2) = 1.2	−0.003	0.925	0.388	−0.008	0.955	0.227

Vague priors were used in the Bayesian model. We used N(0,10¹⁰) priors for β₀, β₁, β₂, ${\gamma }_r^{\left(k\right)}$, ν⁽²⁾, θ, IG(10⁻³,10⁻³) for σ², ${\sigma }_u^2$, ${\sigma }_e^2$, and Γ(10⁻², 10⁻²) for λ_0s. The Jeffreys' [26] priors give similar results and are not shown here. The MCMC sampling in all simulation studies was run using 5 000 iterations, and the estimation results were based on the last 4000 iterations.

For this simulation, sample sizes of 100, 200 and 500 were considered. Table III shows that except for the frailty parameters in the survival submodel, both the Bayesian model with noninformative priors and the likelihood method have small bias and good coverage probabilities in almost all cases. For the frailty parameters, larger samples are needed to get good estimate.

We did another simulation to compare our joint analysis with a separate analysis and a joint analysis that ignores the dependent censoring (i.e. treats the dependent censoring as noninformative censoring). The data were generated same as (10)–(12). We analyzed 200 Monte Carlo data replications with the joint analysis incorporating-dependent censoring (i.e. our joint model treating-dependent censoring as a competing risk), the joint analysis ignoring-dependent censoring and the separate analysis. We compared bias, coverage rate of the 95 per cent intervals and standard deviations of the posterior medians in Table IV. For the separate analysis, a random slope linear mixed model (10) was fitted to the longitudinal outcome and a cause-specific competing risks model (11)–(12) was fitted to the two types of failures separately. In the joint analysis ignoring-dependent censoring, only (10) and (11) were included, with the second type of risk treated as independent censoring. Sample sizes of 200 and 500 were considered in this simulation study.

Table IV.

Bias, coverage rate of the 95 per cent interval, standard deviation (SD), for the separate analysis, the joint analysis ignoring-dependent censoring and the joint analysis incorporating-dependent censoring.

		Separate analysis			Joint analysis ignoring dependent censoring			Joint analysis incorporating dependent censoring
n	Parameter	Bias	Coverage	SD	Bias	Coverage	SD	Bias	Coverage	SD
200	β 0	0.003	0.935	0.043	<0.001	0.9450	0.043	0.002	0.945	0.044
	β1 = −1.5	0.025	0.945	0.052	0.017	0.965	0.052	0.002	0.980	0.051
	β2 = 1	−0.203	0.210	0.070	−0.100	0.780	0.077	−0.009	0.955	0.087
	σ2 = 0.25	0.001	0.960	0.013	0.001	0.960	0.013	0.001	0.945	0.014
	${\sigma }_u^2=0.5$	−0.049	0.935	0.071	−0.011	0.955	0.0140	0.014	0.960	0.084
	σuv=0.4				0.023	0.925	0.169	0.002	0.950	0.142
	${\sigma }_v^2=0.5$	−0.034	0.845	0.690	0.236	0.875	0.400	0.034	0.975	0.314
	${\gamma }_1^{\left(1\right)}=-1$	0.073	0.950	0.256	0.034	0.955	0.257	0.007	0.960	0.245
	${\gamma }_2^{\left(1\right)}=0.8$	0.027	0.950	0.442	0.061	0.955	0.413	0.070	0.925	0.422
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.092	0.930	0.338	—	—	—	−0.018	0.950	0.278
	${\gamma }_2^{\left(2\right)}=0.5$	−0.015	0.935	0.507	—	—	—	0.022	0.935	0.425
	ν(2) = 1.2	0.145	0.935	4.918	—	—	—	0.051	0.980	0.435
500	β0 = 10	0.005	0.950	0.025	0.002	0.975	0.025	0.003	0.960	0.026
	β1 = −1.5	0.019	0.9500	0.033	0.011	0.950	0.033	−0.003	0.970	0.033
	β2 = 1	−0.203	0.005	0.044	−0.093	0.560	0.053	0.008	0.950	0.057
	σ2 = 0.25	<0.001	0.970	0.008	<0.001	0.970	0.008	<0.001	0.960	0.009
	${\sigma }_u^2=0.5$	−0.050	0.810	0.048	−0.013	0.920	0.055	0.013	0.935	0.057
	σuv=0.4				0.022	0.915	0.107	0.019	0.965	0.090
	${\sigma }_v^2=0.5$	−0.029	0.935	0.220	0.200	0.810	0.275	0.024	0.945	0.164
	${\gamma }_1^{\left(1\right)}=-1$	0.012	0.920	0.163	0.033	0.925	0.164	0.011	0.940	0.156
	${\gamma }_2^{\left(1\right)}=0.8$	0.001	0.950	0.250	0.043	0.950	0.250	0.014	0.965	0.233
	${\gamma }_1^{\left(2\right)}=-1.5$	−0.011	0.955	0.173	—	—	—	<0.001	0.930	0.162
	${\gamma }_2^{\left(2\right)}=0.5$	0.034	0.935	0.284	—	—	—	0.037	0.945	0.259
	ν(2) = 1.2	0.108	0.940	1.106	—	—	—	−0.008	0.955	0.227

Entries in boldface indicate different results from the three analysis methods.

We notice from Table IV that the joint analysis incorporating-dependent censoring gives nearly unbiased estimates for all the parameters, and the coverage rates for the 95 per cent confidence intervals are close to the nominal value. In the separate analysis, the time trend β₂ (the time trend for the control group) and the variance of the random slope ${\sigma }_u^2$ are underestimated, even for the larger sample size of 500. This is a consequence of having nonignorable missing data induced by two types of failures. Because the coefficients σ_uv, ν⁽²⁾ are positive, a higher risk of failures is expected for those subjects with greater ascending rates in the longitudinal outcome. This cannot be handled properly by the separate linear mixed effects model. Moreover, the joint analysis incorporating-dependent censoring as a competing risk provides much more accurate estimates than treating it as noninformative censoring. In addition, the standard deviations of the posterior estimates in the separate analysis for the survival data are larger than those in the joint analysis. The accuracy for estimating the frailty and the efficiency for estimating the other parameters in the survival endpoint are improved by incorporating the longitudinal outcome in our proposed joint model. In the joint analysis ignoring the dependent dropout, β₂ (the time trend for the control group) is also biased (underestimated). Because the nonignorable missing values are due to both failure types, considering one failure type may only partially correct this problem. Moreover, the variance of the latent variable in the survival sub-model is overestimated without considering the second type of failure. This shows that the latent variable might not be correctly estimated if dependent censoring is treated as noninformative censoring.

A third simulation was conducted to demonstrate that appropriate informative priors could improve estimation for the parameters, especially for smaller samples. Sample sizes of 50 and 100 were considered. We considered two methods. The first method used the same noninformative priors as in the previous simulations. The second method used informative priors for some parameters, with the prior means set as the true parameter values. We used N(1,0.04) for β₂, N(0.8,0.25) for ${\gamma }_2^{\left(1\right)}$, N(1.2,1) for ν⁽²⁾, N(0.8,4) for θ, IG(5.56,1) for ${\sigma }_e^2$ and the same priors for the other parameters as the previous simulation. We used N(0,4) for β₂, N(0,25) for ${\gamma }_2^{\left(1\right)}$, N(0,4) for ν⁽²⁾, N(0,4) for θ, IG(1,1) for ${\sigma }_e^2$ and the same priors for the other parameters as the previous simulation. The results are summarized in Table V.

It is seen that for the relatively small sample sizes of 50 and 100, some parameters such as β₂, ${\sigma }_v^2$, σ_uv, ${\gamma }_r^{\left(k\right)}$, and ν⁽²⁾ are not well estimated when using noninformative priors. However, with good informative priors, the estimation accuracy is greatly improved. Finally, we note that informative priors should be used with caution since poor prior information may induce additional bias.

Finally, we conducted a simulation using a setup similar to the SLS. The longitudinal response and the competing risks event times were simulated from models (7)–(9) with Z_ij as ([Time_ij]), in which the covariates were generated from distributions similar to those in the SLS. All the parameters for generating the data were set close to the estimated values from the joint analysis for the SLS listed in Table II. Weibull baseline hazard functions were used to produce similar risk rates to those in the SLS since we observed increasing estimated baseline hazard trends for both failure types. The results from the joint analysis and the separate analysis are compared in Table VI using 200 simulated data sets with m equal to 140. We used a piecewise exponential baseline hazard function with three knots for modeling the sample size of 140. The time points defining the intervals are taken to be 33th, 67th, and 100th percentiles of the observed failure times.

Table VI.

Simulation results for SLS data (n=140).

	Separate analysis			Joint analysis incorporating dependent censoring
Factor	Estimate	Coverage	SD	Estimate	Coverage	SD
β0=67	66.911	0.930	0.450	67.022	0.970	0.414
β1=0	0.008	0.965	0.029	0.001	0.930	0.032
β2=−1	−1.016	0.920	0.642	−1.074	0.940	0.599
β3=−1.7	−1.754	0.940	0.362	−1.715	0.940	0.360
β4=1	0.997	0.955	0.032	1.000	0.960	0.033
β5=0	−0.009	0.920	0.047	−0.003	0.925	0.048
β6=1.4	1.469	0.960	0.499	1.407	0.935	0.512
β7=0.1	0.098	0.925	0.048	0.100	0.935	0.048
β8=−0.25	− 0.126	0.710	0.077	−0.249	0.960	0.096
β9=0.25	0.230	0.950	0.118	0.266	0.955	0.123
σ2=20	20.145	0.975	1.141	19.946	0.985	1.146
${\sigma }_u^2=0.3$	0.254	0.860	0.042	0.299	0.945	0.053
${\gamma }_1^{\left(1\right)}=0.1$	0.098	0.875	0.064	0.118	0.960	0.052
${\gamma }_2^{\left(1\right)}=-1.2$	−2.901	0.885	12.066	−1.932	0.875	1.447
${\gamma }_3^{\left(1\right)}=-0.4$	−0.538	0.900	1.505	−0.513	0.910	0.603
${\gamma }_4^{\left(1\right)}=0$	0.001	0.935	0.115	0.005	0.935	0.051
${\gamma }_5^{\left(1\right)}=-0.1$	−0.114	0.880	0.289	−0.114	0.925	0.092
${\gamma }_6^{\left(1\right)}=0.1$	0.107	0.915	4.169	0.048	0.925	1.079
${\gamma }_7^{\left(1\right)}=-0.05$	−0.056	0.915	0.334	−0.070	0.945	0.095
${\gamma }_1^{\left(2\right)}=0.05$	0.071	0.940	0.131	0.051	0.950	0.026
${\gamma }_2^{\left(2\right)}=0.4$	0.415	0.920	1.690	0.446	0.930	0.462
${\gamma }_3^{\left(2\right)}=0.06$	0.305	0.925	1.405	0.107	0.950	0.291
${\gamma }_4^{\left(2\right)}=-0.06$	−0.116	0.875	0.692	−0.046	0.870	0.028
${\gamma }_5^{\left(2\right)}=-0.03$	−0.029	0.945	0.083	−0.028	0.930	0.033
${\gamma }_6^{\left(2\right)}=0.2$	0.392	0.905	1.487	0.196	0.945	0.394
${\gamma }_7^{\left(2\right)}=0.1$	0.380	0.900	2.568	0.080	0.900	0.032
ν(2)=0.2	1.227	0.815	28.930	0.179	0.930	0.156
${\sigma }_v^2=5.2$	16.473	0.475	140.058	9.012	0.935	5.630
σuv=−1.2	—	—	—	−1.399	0.965	0.579

Entries in boldface indicate different results from the two analysis methods.

Table VI shows that joint analysis incorporating-dependent censoring gives good point estimates and coverage rates for the parameters in the longitudinal submodel. The separate analysis produces comparable estimates for most parameters except a biased time trend β₈ and an underestimated variance ${\sigma }_u^2$, which confirms the analysis in Section 4. These biases do not decrease even for the larger sample size of 500 (simulation results are not reported here). The separate competing risks model estimated the random effect parameters (ν⁽²⁾, ${\sigma }_v^2$) and some others (${\gamma }_2^{\left(1\right)}$, ${\gamma }_3^{\left(2\right)}$, ${\gamma }_6^{\left(2\right)}$, ${\gamma }_7^{\left(2\right)}$) poorly. With a small sample size of 140, low event rates (12 per cent for risk 1 and 28 per cent for risk 2) and small number of intervals for the piecewise exponential baseline hazard function, even joint analysis incorporating-dependent censoring may not estimate the random effects v_i well, resulting in poor parameter estimates for the survival data (${\sigma }_v^2$, ${\gamma }_2^{\left(1\right)}$). This can be improved when the sample size increases to 500 and the number of knots increases to 8 (simulation results are not reported here). With more data and more number of knots to allow a better approximation to the true baseline hazard function, the frailty at the survival endpoint is better estimated, along with the other parameters modeling the survival data.

6. DISCUSSION

We proposed a Bayesian method for joint modeling of longitudinal and competing risks survival data. The joint model provides a useful method for analysis of the longitudinal data with nonignorable missing data induced by multiple types of events. The competing risks submodel enables one to handle dependent censoring for the key event by treating it as a competing risk. It also allows simultaneous inference on both longitudinal and survival endpoints. Moreover, by combining the information from the longitudinal data, the joint model improves the accuracy and efficiency of the parameter estimates for the survival endpoint compared with a separate survival analysis. The developed Bayesian method has some appealing features. Computationally, it can easily handle high-dimensional random effects, which is difficult under the frequentist framework (e.g. [15, 27]). In addition, standard errors and confidence intervals can be conveniently obtained from the posterior samples. It also allows incorporation of prior information.

Our method requires a specification of the piecewise baseline hazard in the competing risks submodel (2). In practice, the intervals for the baseline hazard can be defined based on the quantiles of the observed event times. Our simulations with the data generated with the Weibull baseline hazard demonstrated this works well. We also studied the appropriate number of intervals for the function with simulation studies. We observed that an increase in number might decrease the estimation bias for the parameters in the survival submodel with the data generated with a Weibull (nonconstant) baseline hazard rate. We also observed inflated standard errors for these parameters with the data generated with an exponential (constant) baseline hazard rate. The number of intervals has a small effect on the inference for the parameters modeling the longitudinal measurements. In practice, we suggest to first fit the data with a large number of pieces, and then combine the adjacent intervals with similar baseline estimates.

Our model can be extended to handle clustered data. Clustered data arise frequently from multi-site clinical trials in which each site can be viewed as a cluster, from studies with families data, or from studies with recurrent events for each subject. A simple method is to add an additional random effect in our joint model to adjust for heterogeneity across the clusters. Our computational MCMC algorithm can be adopted without much modification.

We assume multivariate normal distribution of random effects in the joint model. Robustness against the departure from the normality assumption has been studied by several authors [19, 28, 29]. These authors have reported similar findings that inference seems generally robust against the normality assumption for the random effects. We also have done some simulation, which is not reported here, and confirm their findings with symmetric distributions. On the other hand, if the underlying distribution is asymmetric, such as exponential, we also observe biased estimation for those parameters directly related to the random effects. To allow more flexibility and robustness for random effects, Brown and Ibrahim [11] proposed a semiparametric Bayesian hierarchical joint model with a single failure type and it can be extended to our situation.

Our limited experience suggests that our method is pretty robust with respect to the normality assumption of measurement errors, even when underlying error distribution is asymmetric, such as exponential or unbalanced normal mixtures. However, our method is observed to be sensitive to outliers. In a sequel, we will develop a robust joint model for longitudinal and survival data.

APPENDIX: FULL CONDITIONAL DENSITIES

We used Gibbs sampling to sample from the joint posterior distribution of the parameters: (U_i, β, σ², Σ_u, ${\gamma }_r^{\left(k\right)}$, ν^(k), ${\lambda }_{0s}^{\left(k\right)}$, e_i, ${\sigma }_e^2$). We use the notation [.] and [.|.] to denote marginal and conditional densities, respectively.

• Sample [σ²|.]∝InvGamma $({\alpha }_{{\sigma }^2},{\beta }_{{\sigma }^2})$[σ²], where ${\alpha }_{{\sigma }^2}={\sum }_{i=1}^m{n}_i∕2-1$, and ${\beta }_{{\sigma }^2}={\sum }_{i=1}^m{(Y_i-X_i^{\left(1\right)}\beta -Z_i{U}_i)}^{\mathrm{T}}(Y_i-X_i^{\left(1\right)}\beta -Z_i{U}_i)∕2$.

• Sample [β|.]∝N((X^T X)⁻¹ X(Y−ZU), (X^T X)⁻¹σ²)[β].

• Sample [Σ_u|.]∝InvWish(m−Q−1, S⁻¹)[Σ_u] where $S={\sum }_{i=1}^m{U}_i{U}_i^{\mathrm{T}}$.

• Sample [U_i|.]∝N $({\mu }_{U_i\mid Y_i},{\Sigma }_{U_i\mid Y_i})\ast {\prod }_{k=1}^K\text{exp}\{({\theta }^{\prime }{U}_i+e_i){\nu }^{\left(k\right)}I(d_i=k)-H^{\left(k\right)}\left(t_i\right)\},i=1,\dots ,m$, i=1,…,m where ${\mu }_{U_i\mid Y_i}={(Z_i^{\mathrm{T}}{Z}_i+{\Sigma }_u^{-1}{\sigma }^2)}^{-1}{Z}_i^{\mathrm{T}}(Y_i-X_i\beta )$ and ${\Sigma }_{U_i\mid Y_i}={(Z_i^{\mathrm{T}}{Z}_i∕{\sigma }^2+{\Sigma }_u^{-1})}^{-1}$ and $H^{\left(k\right)}\left(t_i\right)$ is defined as (6), MH.

• Sample $[{\lambda }_{01}^{\left(k\right)},\cdots ,{\lambda }_{0S^{\left(k\right)}}^{\left(k\right)}\mid .]\propto {\prod }_{s=1}^{S^{\left(k\right)}}\Gamma ({\delta }_s^k,{\beta }_{{\lambda }_{0s}^{\left(k\right)}})[{\lambda }_{01}^{\left(k\right)},\cdots ,{\lambda }_{0S^{\left(k\right)}}^{\left(k\right)}]$, k=1,…,K where ${\delta }_s^k={\sum }_{i=1}^{m}I(d_i=k,t_{s-1}^{\left(k\right)}<t_i\le t_s^{\left(k\right)})+1$ and ${\beta }_{{\lambda }_{0s}^{\left(k\right)}}={\sum }_{i=1}^m\text{exp}\{X_i^{\left(21\right)}{\gamma }_1^{\left(k\right)}+({\theta }^{\prime }{U}_i+e_i){\nu }^{\left(k\right)}\}I(t_i>t_{s-1}^{\left(k\right)}){\int }_{t_{s-1}^{\left(k\right)}}^{\text{min}(t_i,t_s^{\left(k\right)})}\text{exp}\left\{X_i^{\left(22\right)}\left(t\right){\gamma }_2^{\left(k\right)}\right\}$ dt. Here ${\delta }_s^k$ is the number of events occurring in the time interval $(t_{s-1}^{\left(k\right)},t_s^{\left(k\right)}](s=1,\dots ,S^{\left(k\right)})$ for failure type k.

• Sample $[{\gamma }_r^{\left(k\right)}\mid .]\propto \text{exp}\left\{{\gamma }_r^{\left(k\right)}{\sum }_{i=1}^{m}I(d_i=k)X_{\mathit{ir}}^{\left(2\right)}\left(t_i\right)\right\}\left({\prod }_{i=1}^m{S}^{\left(k\right)}\left(t_i\right)\right)\left[{\gamma }_r^{\left(k\right)}\right]$, r=1,…,R k=1,…K where $S^{\left(k\right)}\left(t_i\right)=\text{exp}\{-{\int }_0^{ti}{\lambda }_i^{\left(k\right)}\left(t\right)\mathrm{d}t\}=\text{exp}\{-H^{\left(k\right)}\left(t_i\right)\}$, MH.

• Sample $[{\nu }^{\left(k\right)}\mid .]\propto \text{exp}\left\{{\nu }^{\left(k\right)}{\sum }_{i=1}^{m}I(d_i=k)({\theta }^{\prime }{U}_i+e_i)\right\}\left({\prod }_{i=1}^m{S}^{\left(k\right)}\left(t_i\right)\right)\left[{\nu }^{\left(k\right)}\right]$, k=2,…,K where $S^{\left(k\right)}\left(t_i\right)=\text{exp}\{-{\int }_0^{t_i}{\lambda }_i^{\left(k\right)}\left(t\right)\mathrm{d}t\}=\text{exp}\{-H^{\left(k\right)}\left(t_i\right)\}$, ARS.

• Sample $[{\theta }_q\mid .]\propto {\prod }_{k=1}^K\text{exp}\left\{{\theta }_q{\nu }^{\left(k\right)}{\sum }_{i=1}^{m}I(d_i=k)U_{\mathit{iq}}\right\}\left({\prod }_{i=1}^m{S}^{\left(k\right)}\left(t_i\right)\right)\left[{\theta }_q\right]$, q=1,…,Q where$S^{\left(k\right)}\left(t_i\right)=\text{exp}\{-{\int }_0^{t_i}{\lambda }_i^{\left(k\right)}\left(t\right)\mathrm{d}t\}=\text{exp}\{-H^{\left(k\right)}\left(t_i\right)\}$, ARS.

• Sample $[e_i\mid .]\propto N(0,{\sigma }_e^2)\ast {\prod }_{k=1}^K\text{exp}\{e_i{\nu }^{\left(k\right)}I(d_i=k)-H^{\left(k\right)}\left(t_i\right)\}$, i=1,…,m where $H^{\left(k\right)}\left(t_i\right)$ is defined as (6), MH.

• Sample $[{\sigma }_e^2\mid .]$∝ InvGamma(${\alpha }_{{\sigma }_e^2}$,${\beta }_{{\sigma }_e^2}$) [${\sigma }_e^2$], where ${\alpha }_{{\sigma }_e^2}=m∕2-1$, and ${\beta }_{{\sigma }_e^2}={\sum }_{i=1}^m{e}_i^2∕2$.