Efficiency of reactant site sampling in network-free simulation of rule-based models for biochemical systems

Abstract

Rule-based models, which are typically formulated to represent cell signaling systems, can now be simulated via various network-free simulation methods. In a network-free method, reaction rates are calculated for rules that characterize molecular interactions, and these rule rates, which each correspond to the cumulative rate of all reactions implied by a rule, are used to perform a stochastic simulation of reaction kinetics. Network-free methods, which can be viewed as generalizations of Gillespie’s method, are so named because these methods do not require that a list of individual reactions implied by a set of rules be explicitly generated, which is a requirement of other methods for simulating rule-based models. This requirement is impractical for rule sets that imply large reaction networks (i.e., long lists of individual reactions), as reaction network generation is expensive. Here, we compare the network-free simulation methods implemented in RuleMonkey and NFsim, general-purpose software tools for simulating rule-based models encoded in the BioNetGen language. The method implemented in NFsim uses rejection sampling to correct overestimates of rule rates, which introduces null events (i.e., time steps that do not change the state of the system being simulated). The method implemented in RuleMonkey uses iterative updates to track rule rates exactly, which avoids null events. To ensure a fair comparison of the two methods, we developed implementations of the rejection and rejection-free methods specific to a particular class of kinetic models for multivalent ligand-receptor interactions. These implementations were written with the intention of making them as much alike as possible, minimizing the contribution of irrelevant coding differences to efficiency differences. Simulation results show that performance of the rejection method is equal to or better than that of the rejection-free method over wide parameter ranges. However, when parameter values are such that ligand-induced aggregation of receptors yields a large connected receptor cluster, the rejection-free method is more efficient.

1. Introduction

Protein-protein interactions in cell signaling systems involve domain-based protein interactions and site-specific post-translational modifications [1, 2]. Simulating the dynamics of cell signaling is usually a daunting task because a large (bio)chemical reaction network is typically required to capture protein-protein interactions at the level of site-specific details and submolecular domains [3, 4, 5, 6]. Even though a large-scale biochemical reaction network can be built by either manual or automated construction [7, 8, 9, 10], simulating such models is computationally inefficient because a conventional kinetic Monte Carlo simulation algorithm, for example, has a cost that depends on the size of a network measured by the number of reactions [11] or the number of chemical species [12] in the network.

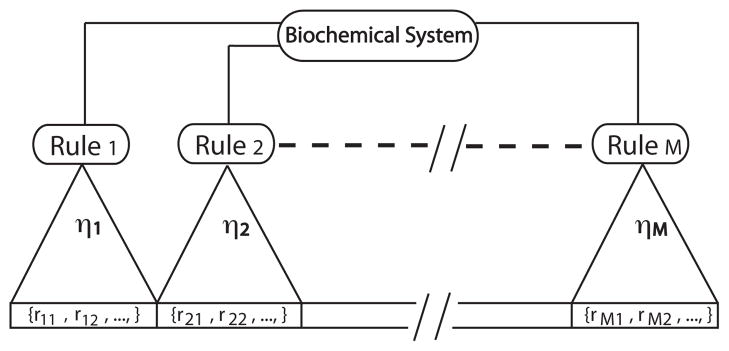
The challenge of simulating protein-protein interactions in cell signaling systems can be addressed with the rule-based modeling approach (see Ref. [4] for a review). Rule-based modeling provides a hierarchical structure to define biochemical reaction systems (Fig. 1). In a rule-based approach, molecules are modeled as structured objects composed of reactive sites, and reaction rules are used to represent interactions [4, 13, 14] (see Fig. 2 for examples of rules for ligand-receptor interactions). In general, a rule specifies local properties of individual sites (e.g., whether a site is free or occupied) in a molecule and application conditions that require checking non-local properties of sites (e.g., whether two sites are members of the same macromolecular aggregate). A rule defines a class of (unidirectional) reactions. Assuming rate laws for elementary reactions, one parameterizes the reactions implied by a rule with a single rate constant. Thus, a rule provides a compact representation of a class of reactions, which are only implicitly defined, at the cost of coarse-graining the representation of the rates of these reactions, which in principle may each be unique.

Figure 1.

Diagrammatic depiction of a biochemical system described by rules and its underlying reaction network. Rules partition the entire reaction list into disjoint subsets which are consolidated by rules into rate processes denoted by {η₁, η₂, …, η_M}. The term r_ij denotes the jth reaction implied by rule. Note that partitions of a reaction network specified by rules are not necessarily of finite size, which is the case for many models of multivalent ligand-receptor interactions (see main text). Rule-based kinetic Monte Carlo samples the rule list (the intermediate layer) to generate reaction events and avoids simulating a system by means of a reaction network (the bottom layer).

Figure 2.

The interactions of a trivalent ligand and a bivalent cell-surface receptor (left). Graphical rules (right) that represent free ligand recruitment to the cell surface (Rule 1), receptor crosslinking by ligand (Rule 2) and ligand-receptor bond dissociation (Rule 3). Rules are parameterized by rate constants k₊₁, k₊₂ and k_off, respectively. An empty (filled) circle inside a container denotes a free (bound) site. A connecting line indicates a ligand-receptor bond. An empty container indicates an arbitrary state (free or bound). An additional assumption is imposed to prohibit reactions defined by R₂ from forming cyclic ligand-receptor aggregates (see main text).

Kinetic Monte Carlo (KMC) methods have been developed for simulating the stochastic dynamics of rule-based models [15, 16, 17]. The methods of Danos et al. [15] and Yang et al. [16] avoid the requirement of specifying a chemical reaction network prior to simulation by directly sampling a rule list to generate reaction events and updating the system state in accordance with reaction rules. The computational cost is essentially independent of network size because a rule list is typically more compact and orders of magnitude smaller than the size of the corresponding reaction network.

The rule-based KMC simulation method of Yang et al. [16] may require checking application conditions for rules and therefore may involve rejection sampling that excludes non-permissible trial sites. After a rule is selected, trial sites with suitable local properties are randomly sampled to potentially undergo the chemical transformation(s) specified by the rule. Trial sites are rejected if they are not compatible with the application conditions of the rule. Random site selection in the rejection sampling steps is a constant-time operation, but efficiency might be significantly compromised in cases where null events become a dominant fraction of all sampled events. This scenario happens when the method is used to simulate multivalent ligand-receptor interactions in a sol-gel region that yields a giant ligand-receptor aggregate at equilibrium, where sampled trial sites are very likely rejected because the vast majority of sites reside in the giant aggregate and are prohibited from binding to each other by an application condition (a model assumption) that prohibits intra-aggregate binding reactions to form cyclic aggregates. The method of Yang et al. [16] has been implemented in software called NFsim [18].

A network-free simulation method that is related to the method of Yang et al. [16] but that is free of null events (i.e., rejection free) has been reported by Colvin et al. [19]. This method has been implemented in software called RuleMonkey [19]. In this method, rates associated with rules are calculated exactly using various formulas for different types of reaction classes that can be defined by rules. The rates are initially calculated as sums but the rates are thereafter iteratively updated as reaction events take place. Exact rule rates are always available and the simulation method is rejection free. Although RuleMonkey and NFsim can be used to simulate benchmark problems and the performance properties of the two software tools can be compared [18], it is not clear that the results obtained in this way represent theoretical performance limits or irrelevant coding differences.

Here, to evaluate the efficiency of rejection and rejection-free site samplings in rule-based KMC simulations, we present problem-specific implementations of the rejection method of NFsim and the rejection-free method of RuleMonkey and we use these implementations to compare the two methods. These implementations are significantly less complicated than the RuleMonkey and NFsim codes, which are each designed to perform simulations of any model that can be encoded in the BioNetGen language (BNGL) [13]. Instead, our implementations are tailored for a single but important class of models: models for multivalent ligand-receptor interactions. In such a model, we consider a population of ligands, each with m equivalent sites, interacting with a population of cell-surface receptors, each with n equivalent sites to generate acyclic ligand-induced receptor aggregates. The class of models for m-valent ligand interaction with n-valent receptor is ideal for evaluating network-free simulation algorithms, because the size of the reaction network encompassing populated chemical species can be tuned from a handful of reactions to very large numbers of reactions [16]. This class of models is also relevant for describing phenomena that are common in cell signaling systems, including of course ligand-induced receptor clustering, which is important for signal initiation in many cell signaling systems [20], and aggregation processes mediated by intracellular signaling proteins [21].

2. Rule-based kinetic Monte Carlo with rejection or rejection-free sampling

In this section, we summarize the rejection and rejection-free KMC methods for simulating rule-based models. In a biomolecular reaction system, particularly in a system involving protein-protein interactions for signal transduction, proteins reversibly bind to one another via their binding sites (e.g., conserved domains and linear motifs). Protein sites (amino acid residues) can also be modified, by phosphorylation, methylation, etc. The state of the system (or a system configuration) is determined by states of individual sites and their connectivities. The temporal dynamics of a biochemical reaction system is the evolution of the system state in time, which can be modeled as a Markov process that is generally described by the Chapman-Kolmogorov equation (or more specifically, the chemical master equation for our case) [22]:

$$\frac{dP(Y,t)}{dt}=\sum _{Y^{\prime }\ne Y}[W(Y\mid Y^{\prime })P(Y^{\prime },t)-P(Y,t)W(Y^{\prime }\mid Y)].$$ (1)

P(Y, t) is the probability that the system is found in state Y, and W(Y′|Y) gives the transition rate from state Y to state Y′. In a conventional chemical reaction system, a state Y is defined by the concentrations of all chemical species. In a rule-based system, a state Y is defined by the site occupancy and connectivity of individual molecules. Analytical solutions to the above master equation are only possible for very simple systems. Direct numerical integration of the above ordinary differential equations is also intractable because the size of the state space is often enormous even for a mildly-complex system that involves interactions among a few protein types. To solve this problem, Monte Carlo simulation is often applied to conduct random walks over the state space and to generate stochastic state trajectories for a system of interest.

Here we consider a biochemical system that is described by a set of reaction rules (see Fig. 1), R = {R₁, …, R_M}. The system evolves in time with corresponding rates η= {η₁, …, η_M} for the rules. Such rate processes can be simulated using the standard kinetic Monte Carlo method [23]. The waiting time τ between two consecutive (reaction) events follows an exponential distribution with a mean waiting time 〈τ〉 = 1/η_tot, where ${\eta }_{\text{tot}}={\sum }_{i=1}^M{\eta }_i$ is the sum of the rule rates. The probability for a rule to be chosen is proportional to its rate. The rule-based kinetic Monte Carlo algorithm requires several additional operations per reaction event following the selections of τ and e: (1) select reactive sites admissible to the rule; (2) excute the chemical transformation defined by rule e; and (3) update rates in the vector η that are affected by the chemical transformation.

To choose reactive sites, we can write the rule-specific probability for a site x in a candidate set X_e to be chosen as:

$$P(x)=P_{a\mid s}(x)P_s(x).$$ (2)

We note that a “site” x denotes a set of interacting protein sites that are defined by the rule. For example, for a bimolecular interaction, x will include two interacting sites. This above equation describes a two-step procedure to find a site x: (a) choose a site x according to the sampling probability P_s(x) and (b) accept the chosen x according to the acceptance probability P_a|s(x). In the rejection method, a convenient sampling distribution P_s(x) of candidate sites, usually a uniform distribution for maximum sampling efficiency, is used to generate trial sites and trial sites may be rejected according to the acceptance probability P_a|s(x) so that the true probability P(x) is recovered. Thus, the rejection method involves the sampling of nonreactive sites and introduces null events or a null process to compensate for the sampling of nonreactive sites. The null process generates a time step without a change in system state, i.e., a null event. The null process is triggered whenever a set of sampled sites is found to be nonreactive after being sampled. The rationale for rejection sampling is to gain efficiency by simplifying the procedure for sampling sites. If a rule has an application condition that is difficult to evaluate, it may be more efficient to sample sites with rejection rather than to explicitly track the sites that satisfy the application condition. We consider an application condition to be difficult to evaluate if satisfaction of the condition depends on a non-local property of a set of sites, such as the indirect connectivity of two sites [16] or the spatial configuration of sites/molecules within molecular complexes [24].

Generally, we can partition the rate of any rule into two parts:

$${\eta }_e={\eta }_{e,a}+{\eta }_{e,n}e=1,\dots ,M,$$ (3)

where η_e,a and η_e,n denote the actual reactive rate and the null process rate of rule e, respectively. Generally, the size of the null fraction of η_e,n depends on the site sampling procedure which also affects the calculation of the rule rate. Operating with the combined rate η_e ignores any application condition by model assumption imposed on this rule in the step of site sampling. The model assumption can however be enforced by a subsequent rejection of the sampled sites that are non-permissible to react. Because the rejection method often can achieve random sampling of reactive sites, the cost per sampling step is constant and the implementation is usually straightforward. Determining whether to accept trial sites for reaction may however incur non-constant cost and complex bookkeeping, which depends on the nature of model assumptions.

The effect of rejection sampling on computational performance can be measured by the rejection ratio given as:

$$\theta =\frac{{\eta }_{\text{tot},\text{n}}}{{\eta }_{\text{tot}}},$$ (4)

where ${\eta }_{\text{tot},\text{n}}={\sum }_{i=1}^M{\eta }_{i,n}$ is the total rate of null processes. It should be noted that the rejection ratio is a function of the time at which rates in Eq. 4 are evaluated. Even at steady state, θ varies with time as a result of stochastic fluctuations in the steady-state rates of reactions. For cases where θ tends to be close to 1, a majority of trial sites will be rejected and the rejection method will be inefficient. For such situations, a method without rejections (or with a substantially reduced number of rejections) is desirable. In contrast, the rejection-free method always accepts a sampled site x. In other words, P_a|s(x) is unity for every trial site x and P(x) is captured at the step of site sampling, i.e., P(x) = P_s(x).

An early rejection-free Monte Carlo simulation method was developed by Bortz, Kalos and Lebowitz (BKL) [25] to simulate Ising spin systems, which overcomes the significant slowing down near the critical temperature by the classic Metropolis method [26]. The BKL algorithm is often called the “n-fold way” method, and it has been widely used to simulate systems with high density and/or at low temperature. Gillespie later developed a stochastic simulation algorithm, equivalent to the BKL algorithm, for simulating coupled chemical reactions in a homogeneous reaction compartment [27]. Below, we describe the rejection-free procedure for simulating rule-based models.

Without loss of generality, we only consider unimolecular and bimolecular reactions. Higher-order reactions can usually be decomposed into these two types of elementary reactions. For a unimolecular reaction (e.g., a single-step site modification or a noncovalent bond dissociation between two proteins) of rule e that involves a single type of protein site A, at a given time, the candidate sites are defined in a set X_e = {a_i|i = 1, …, n_a} that includes all legitimate sites designated by the rule and its application conditions. By the mean-field approximation, sites available according to a rule definition are considered to have equal probability to be chosen. The probability of a site x = a_i to be chosen is

$$P(x=a_i)=P_s(x=a_i)=\frac{w_i}{Z}$$ (5)

where w_i is the reaction propensity for site a_i and Z is a partition function Z = η_e = Σ_Xe w_i. The quantity w_i reflects the biophysical properties that determine the reaction propensity of the site a_i. A rule defines reactions of sites from the same protein types and with identical properties. For this reason and under the law of mass action, we can interpret w_i as the specific rate (or, the rate constant) k_e for the rule. The partition function becomes the total rule rate, Z = k_e|X_e|, where |X_e| denotes the size of the candidate set X_e (i.e., |X_e| = n_a). Effectively, Eq. 5 defines a uniform sampling distribution over X_e. The above analysis can be readily extended to the case of bimolecular reactions. Considering an interaction such as binding between two types of protein sites A and B, we have a candidate set X_e = {a_i, b_j|i = 1, …, n_a, j̇ = 1, …, n_b}. The probability of a pair of sites x = (a_i, b_j) to be chosen to react is

$$P(x=\{a_i,b_j\})=P_s(x=\{a_i,b_j\})=\frac{w_{ij}}{Z}.$$ (6)

Similarly, w_ij can be interpreted as a specific rate k_e that is identical for all site pairs. According to the law of mass action, the partition function Z = Σ_Xe w_ij = k_e|X_e| = k_en_an_b.

Based on the above considerations, we can summarize the rejection-free algorithm as follows.

1. Initialization: assign copy numbers of proteins and specify initial states of individual protein sites, initialize lists of candidate sites for reaction rules, assign rate constants k for rules, and calculate the initial values of η;

2. Sample a waiting time τ from an exponential distribution with a mean waiting time of 1/η_tot. That is, the time step for the next event is calculated as τ = ln(1/ρ₁)/η_tot, where ρ₁ is a random deviate uniformly drawn from the interval (0, 1);

3. Sample a reaction rule e from the reaction rule list. The probability for a rule to be sampled is proportional to the rate of the rule. That is, identify the reaction rule e satisfying ${\sum }_{i=1}^e{r}_i>{\rho }_2{r}_{\text{tot}}$, where ρ₂ is a random deviate uniformly drawn from the interval (0, 1);

   Sample a set of protein sites x based on the true probability distribution P(x) for site x to take part in the sampled reaction rule e. As described in Eq. 6, P(x) is usually a uniform distribution over all candidates.

   Update states of the sampled sites according to the rule specification by executing the chemical transformation defined by the rule;

   Update lists of candidate sites for reaction rules and recalculate the rate vector η for all reaction rules;

   Return to Step (ii), unless a stopping condition is satisfied.

The rejection algorithm [16] is largely the same as the rejection-free algorithm described above. The key differences relate to calculation of η and Step (iv). In the rejection algorithm, rates in η are overestimates of the true rates for those rates associated with rules involving application conditions that depend on non-local site properties (e.g., indirect connectivity or configuration within a molecular complex). Furthermore, Step (iv) is replaced with a step in which sites with local properties of genuine reactive sites are sampled and then evaluated to determine if the sites also have the non-local properties of genuine reactive sites. If the sampled sites are found to lack the non-local properties of genuine reactive sites, then the sites are rejected and a null event occurs, i.e., the procedure bypasses Steps (v) and (vi).

We note that the procedure described above does not include a step for calculating outputs (i.e., functions of the system state) for the sake of simplicity. Specified outputs can be calculated in a manner similar to the calculation of rates. In both rejection and rejection-free simulation, outputs are calculated via iterative updates, which occur upon changes in the state of a system.

In the following section, we apply the rejection-free method to simulate a multivalent ligand-receptor interaction model, and we discuss the implementation details of the rejection-free method within the context of this model.

3. Simulations of multivalent ligand-receptor binding systems

Cell-surface receptor aggregation induced by ligand binding is an important step in many signal transduction pathways [28]. In an earlier study, Goldstein and Perelson developed an equilibrium model to investigate binding interactions between trivalent extracellular ligands and bivalent cell-surface receptors [29]. The Goldstein-Perelson model predicted in theory that for certain parameter values small receptor aggregates and “superaggregates” can coexist at equilibrium. In fact, a sol-gel phase transition can happen in any multivalent ligand-receptor system in which either the ligand or the receptor has more than two binding sites and each ligand and receptor has at least two binding sites.

Recently, Yang et al. [16] developed a rule-based kinetic Monte Carlo method that was used to simulate the stochastic dynamics of a kinetic version of the Goldstein-Perelson model, which has been called the TLBR model, where TLBR represents “trivalent ligand – bivalent receptor.” The gelation processes of ligand-receptor aggregation were observed in simulations, which was consistent with the Goldstein-Perelson theory of sol-gel phase transition. The simulation further revealed the kinetic details about formation of superaggregates. Monine et al. [24] also applied the same method to study steric effects using extended kinetic versions of the Goldstein-Perelson model. The KMC simulation method of Yang et al. [16] includes rejection sampling, which becomes inefficient when a system forms a superaggregate that contains most ligands and receptors. Below, we describe details on how to apply rejection-free sampling to simulate multivalent ligand-receptor aggregation.

3.1. Model of multivalent ligand-receptor binding

We consider a system with N_L ligands and N_R receptors. The ligand and receptor have v_l and v_r identical and independent binding sites, respectively. Three types of reactions are considered: (1) free ligand recruitment to a receptor on the cell surface, (2) crosslinking of two cell-surface receptors by a ligand that is already bound on the cell surface but has at least one free site, and (3) dissociation of a ligand-receptor bond. The rule-based specification of the TLBR model, a kinetic extension of the Goldstein-Perelson model, is illustrated in Fig. 2. The model has three reaction rules (Rules 1–3). To compare results with the Goldstein-Perelson model, we impose the same model assumptions: a) binding sites are equivalent [30], b) a ligand cannot associate with a receptor via more than one bond, and c) a ligand cannot associate with a receptor that is a member of the same aggregate (an aggregate is a ligand-receptor complex that has at least one ligand and one receptor in it). These two model assumptions prevent the formation of cyclic ligand-receptor aggregates and affect the calculation of rule rates, which can be accomplished via rejection or rejection-free sampling procedures for receptor crosslinkings. Using rejection sampling, one randomly samples a ligand-receptor site pair on the cell surface and rejects the trial pair when the ligand and receptor sites reside in the same aggregate.

3.2. Rule rates and site sampling

All rule rates are calculated according to the law of mass action. We first give equations for directly calculating η₁ and η₃. Calculation of η₂ requires non-trivial treatment, and different treatments correspond to different implementations of the simulation algorithm (rejection or rejection-free method). We will explain these issues in detail.

The rate of free ligand recruitment to a cell-surface receptor for Rule 1, η₁, is proportional to the product of the number of free sites on free ligands and the number of free receptor sites on the cell surface,

$${\eta }_1=k_{+1}{v}_l{F}_L(v_r{N}_R-N_B),$$ (7)

where F_L is the number of free ligands and N_B is the number of bonds which increases (decreases) by 1 upon an association (dissociation) event. We note that Rule 1 specifies a class of bimolecular reactions and the rate constant k₊₁ absorbs a volume factor (this also applies to the rate constant k₊₂). The rate of ligand-receptor bond dissociation for Rule 3, η₃, is proportional to the number of ligand-receptor bonds,

$${\eta }_3=k_{\text{off}}{N}_B.$$ (8)

For ligand-mediated receptor cross-linking on the cell surface (an event of Rule 2), to avoid forming cyclic ligand-receptor aggregates, one must ensure that an association event joins either two separate ligand-receptor aggregates or a ligand-receptor aggregate and a free receptor. We note that the probability for a ligand site to be chosen is proportional to the number of free receptor sites to which the ligand site may bind, i.e., the number of free receptor sites excluding ones in the same aggregate with the candidate ligand site. Once a ligand site is chosen, the probability of selecting a binding receptor site is uniform for all free receptor sites that are not in the same aggregate with the selected ligand site. At a given time, if the system has N_A ligand-receptor aggregates on the cell surface (excluding free receptors), the rate η₂ can be given by

$${\eta }_2=k_{+2}\sum _{i=1}^{N_A}{l}_i(v_r{N}_R-N_B-r_i),$$ (9)

where l_i and r_i are the numbers of free ligand and receptor sites in the ith aggregate, respectively. The term (v_rN_R − N_B − r_i) is the total number of free receptor sites that are not in aggregate i. From the above equation, it follows that the probability that an aggregate i contributes a ligand site for a Rule 2 event is

$$P_i=\frac{k_{+2}{l}_i(v_r{N}_R-N_B-r_i)}{{\eta }_2},i=1,\dots ,N_A.$$ (10)

We first sample this distribution to locate an aggregate i that provides a free ligand site and then select a free ligand site in aggregate i. All free ligand sites in aggregate i are equivalent (according to model assumptions) and therefore each of them has an equal probability to be chosen. Then, a free receptor site that is not in aggregate i is chosen to bind with the sampled ligand site. Similarly, all such free receptor sites (either in another aggregate or in the free receptor pool) are equivalent and therefore can be randomly sampled. The number of free ligand and receptor sites, l_i and r_i, can be calculated when the numbers of ligands and receptors in an aggregate are known. In an acyclic aggregate that has n_r receptors and n_l ligands, the number of bonds is given as b = n_r + n_l − 1, and the numbers of free receptor and ligand sites can be calculated as r = v_ln_l − b and l = v_rn_r − b, respectively. The calculation of b is based on a common observation that a connected acyclic graph (equivalent to a tree) has a number of edges one less than the number of nodes [31]. A ligand-receptor aggregate can be represented as a bipartite graph, in which receptors and ligands are nodes and ligand-receptor bonds are edges. The numbers of receptors and ligands can be obtained by a linear-time traversal of the aggregate graph. A better approach is to maintain an aggregate list during simulation. This approach avoids routine traversal of aggregate graphs for each reaction event except for bond dissociation events, in which graph traversals are required to determine the resulting two separate aggregates. Direct calculation of η₂ using Eq. (9) has a linear-time cost scaled by the number of aggregates N_A. To achieve a constant-time cost per event, we update η₂ iteratively by accounting for the change caused by a reaction event. Eq. (9) can be rewritten as follows:

$${\eta }_2=k_{+2}\left([v_l(N_L-F_L)-N_B](v_r{N}_R-N_B)-\sum _{i=1}^{N_A}{l}_i{r}_i\right).$$ (11)

The term [v_l(N_L−F_L)−N_B](v_rN_R−N_B) accounts for all pair combinations of free ligand sites (on the cell surface) and free receptor sites under the law of mass action. We note that, in the method using rejection sampling [16], this quantity is used to calculate rate η₂ and a trial pair of ligand and receptor sites can be randomly chosen but are subject to rejection later if they are found in the same aggregate, which is the only reaction rule in the TLBR model that produces a null process because of rejection sampling. For our rejection-free implementation, the exact rate is obtained by subtracting $u\equiv {\sum }_{i=1}^{N_A}{l}_i{r}_i$, where u is the number of intra-aggregate site-pair combinations, to accommodate the model assumption that prohibits intra-aggregate binding reactions. The first term in Eq. (11) can be easily recalculated with a constant cost after each reaction event. The second term can be updated iteratively by Δu (Table 1). Each reaction event changes the list of aggregates by creating a new one, or modifying or removing existing ones. For instance, a free ligand binding to a receptor may (if the receptor is also free) or may not (if the receptor is already bound to another ligand) create a new aggregate. However, most aggregates do not participate in a reaction event and thus remain unchanged. Therefore, updating Eq. (11) is straightforward by accounting for sites on one or two affected aggregates and it has a constant-time cost. For example, a merge of two aggregates i and j creates one new aggregate k (N_A decreases by 1). In this case, on the newly-formed aggregate, free ligand and receptor sites both decrease by 1 from the sums of those on the two merging aggregates, and it follows that Δu = l_kr_k − l_ir_i − l_jr_j, where l_k = l_i + l_j − 1 and r_k = r_i + r_j − 1. Formulas for all event types are given in Table 1.

Table 1.

Formulas for calculating Δu₂

Rule	Event	Δu2
1	A free ligand binds to a free receptor	(vr − 1)(vl − 1)
	A free ligand binds to aggregate i	(vl − 1)(ri − 1) − li
2	Aggregate i associates with a free receptor	(vr − 1)(li − 1) − ri
	Aggregates i and j associate to form a new aggregate k	lkrk − liri − ljrj
3	An aggregate breaks into a free ligand and a free receptor	− (vr − 1)(vl − 1)
	A ligand dissociates from aggregate i	li − (vl − 1)(ri + 1)
	A receptor dissociates from aggregate i	ri − (vr − 1)(li + 1)
	Aggregate k dissociates into two aggregates i and j	liri + ljrj − lkrk

The rejection method of Yang et al. [16] and the rejection-free method reported here are implemented in the C programming language and provided in the online Supplementary Material. These implementations simulate models for m-valent ligand and n-valent receptor that incorporate model assumptions about site equivalence and acyclic aggregates similar to those of the Goldstein-Perelson model. The rejection and rejection-free codes were written with the intention of making them as much alike as possible, except for the sampling strategies and rule rate calculations, to eliminate irrelevant differences. We note that our implementations of the simulation methods discussed here provide new tools for studying the equilibrium and the kinetics of multivalent ligand-receptor interactions and gelation on cell membranes, topics which have been studied intensely over the years via a variety of approaches [32, 33, 34, 35].

4. Simulation results

In this section, we present results obtained using the rejection and the rejection-free algorithms described above. Parameter values used in simulations were taken from Ref. [16].

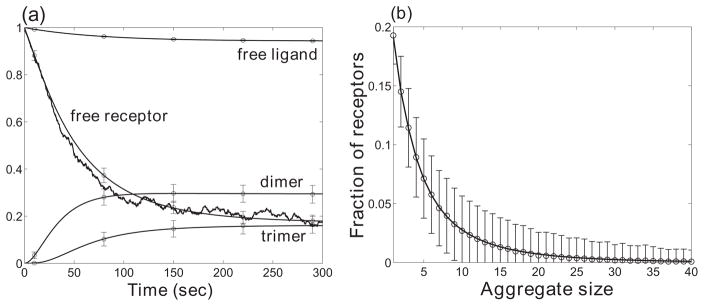
To validate the accuracy of our problem-specific implementation of the rejection-free method, we compare simulation results with those obtained using ordinary differential equations (ODEs). The relaxation kinetics of a bivalent ligand (v_l = 2) – bivalent receptor (v_r = 2) system to equilibrium is shown in Fig. 3(a). The deterministic results were obtained by solving a small number of ODEs as described in Refs. [30, 36]. The stochastic trajectories recapitulate on average the deterministic solutions. In Fig. 3(b), the equilibrium distribution of receptor aggregates in a TLBR system agrees on average with the equilibrium results from the Goldstein-Perelson model. These results demonstrate that our problem-specific rejection-free simulation algorithm produces outcomes consistent with those obtained independently.

Figure 3.

Validation of the rejection-free simulation algorithm for multivalent ligand-receptor interaction systems. (a) Comparison of normalized results to the ODE solutions for the bivalent ligand and bivalent receptor interaction system. The normalization factor is N_R/n, where n is the number of receptors in an aggregate (n = 2 for dimers, n = 3 for trimers, etc.). The means and standard deviations of the simulation results obtained by the simulation method are shown on top of the continuous ODE solutions. One stochastic time trajectory is shown for the free receptor population. (b) Stochastic receptor aggregate distribution for the trivalent ligand and bivalent receptor system. The system reaches equilibrium after 350 seconds and the averages of equilibrium distributions match the results (solid curve) obtained using the model of Goldstein and Perelson [29]. Parameter values: N_R = 300, N_L = 4200, k₊₁ = 6.67×10⁻⁷ s⁻¹, k₊₂ = 100k₊₁, k_off = 0.01 s⁻¹. Initial condition: all simulations start with free ligands and free receptors without bonds.

A phase transition in ligand-receptor clustering at equilibrium is predicted in the Goldstein-Perelson model by varying two dimensionless parameters c_tot = 3k₊₁N_L/k_off and β = k₊₂N_R/k_off, which shows that finite-sized ligand-receptor aggregates can coexist with an infinite-sized polymer-like aggregate in a so-called sol-gel coexistence regime [29]. To investigate the stochastic dynamics of ligand-receptor aggregation and the algorithmic performance at different phase regimes, we use the average receptor aggregate size to measure the degree of ligand-receptor clustering, which can be calculated as

$$\mathrm{\Gamma }=\sum _{n=1}^{N_R}{np}_n=\frac{1}{N_R}\sum _{n=1}^{N_R}{n}^2{x}_n,$$ (12)

where n is the size of a ligand-receptor aggregate measuring the number of receptors in the aggregate and x_n is the number of aggregates of size n. The term p_n = nx_n/N_R is the fraction of receptors in aggregates of size n, which corresponds to the probability of finding an arbitrary receptor in an aggregate of size n. We note that in the above equation the number of aggregates containing single receptors, x₁, accounts for all receptor monomers including free receptors. Therefore, at any given time the average aggregate size Γ takes a value between 1 and N_R. In practice, since the number of aggregates N_A is always much less than N_R (Fig. 4), Γ can be more efficiently calculated as follows:

$$\mathrm{\Gamma }=\frac{F_R}{N_R}+\frac{1}{N_R}\sum _{j=1}^{N_A}{n}_j^2,$$ (13)

where F_R is the number of free receptors and n_j is the number of receptors in aggregate j. Γ can be also calculated iteratively during a simulation by accounting for the changes of aggregation caused by reaction events. To study the effect of the degree of aggregation on algorithmic efficiency by adjusting the parameters c_tot and β, we ran simulations of the TLBR model to equilibrium under a set of different values of the dissociation rate constant k_off in the range between 10⁻⁶ s⁻¹ and 100 s⁻¹, with both N_L and N_R fixed at 5000. Figure 5(a) shows a sigmoid-like relationship between the average aggregate size 〈Γ〉 and the dissociation rate constant k_off. At smaller k_off (sol-gel region), 〈Γ〉 approaches its maximum value N_R, which indicates that a large aggregate containing most receptors exists in the system. At larger k_off (sol region), 〈Γ〉 approaches its minimum value, indicating that the majority of receptors are in the form of free receptors and ligand-bound receptor monomers. The mean aggregate number 〈N_A〉 exhibits a bell-shaped curve with a maximum value of 966 near the phase transition boundary at k_off = 0.17. Figure 5(b) shows the performance comparison between the rejection-free method described in this work and the rejection method of Yang et al. [16] in terms of CPU time per reaction event, for the TLBR model with a typical set of parameters. In most of the sol region (k_off > 1 s⁻¹) and near the sol-gel region (10⁻⁴ s⁻¹ < k_off < 10 s⁻¹), the rejection-free and rejection methods match each other in performance, and the efficiency of both methods deteriorates as 〈Γ〉 increases. The rejection-free method is affected by searching over a near maximum number of aggregates, which is reflected in the increases of CPU time per reaction event near the boundary of the phase transition (10⁻¹ s⁻¹ < k_off < 1 s⁻¹) compared to that of the rejection method. However, the rejection-free method is less sensitive to 〈Γ〉 and outperforms the rejection method in the sol-gel region (k_off < 10⁻⁴), where free intra-aggregate ligand-receptor site pairs are dominant and the rejection method has a rejection ratio θ greater than 99% at equilibrium. As shown in Fig. 5(c), the rejection ratio θ has a log-linear dependence on 〈Γ〉 over a wide range.

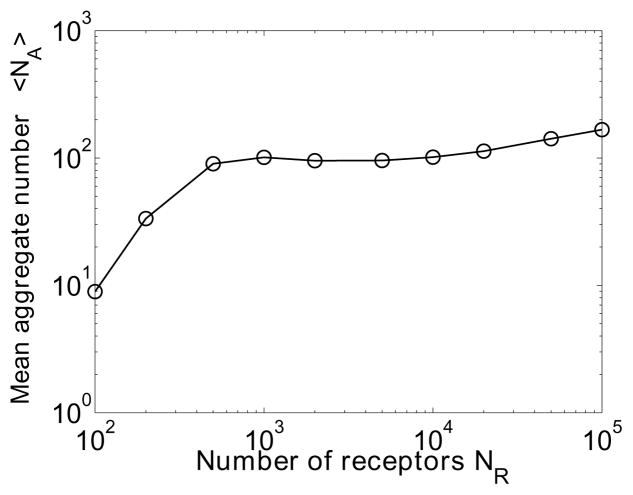
Figure 4.

The relationship between 〈N_A〉 and N_R for the trivalent ligand–bivalent receptor system. The number of ligands N_L is set equal to the number of receptors N_R. 〈N_A〉 is obtained by calculating its mean value from 10⁶ consecutive reaction events after the system reaches equilibrium. Other parameters and initial conditions are identical to the values indicated in Fig. 3.

Figure 5.

Performance comparison of the rejection-free method and the rejection method. (a) The mean average aggregate size 〈Γ〉 (solid line) and the average number of aggregates 〈N_A〉 (dashed line). The results are normalized by the total number of receptors, N_R. Simulation parameters: v_r = 2, v_l = 3, N_R = N_L = 5000. (b) Relationship between CPU time and k_off: rejection-free method (solid line), rejection method of Yang et al. [16] with aggregate bookkeeping (dashed line). (c) The expected rejection ratio 〈θ〉 is plotted as a function of the average aggregate size 〈Γ〉. As can be seen, 〈θ〉 appears to have a log-linear dependence on 〈Γ〉 over a wide range. The quantity 〈θ〉 is calculated as the number of rejection events occurring in a simulation at equilibrium conditions divided by the total number of events required to capture 200,000 reaction events in the simulation. Other quantities reported in this figure, including CPU times per reaction event, 〈Γ〉 and 〈N_A〉, are calculated as averages over the 200,000 reaction events. Unless otherwise indicated, parameter values and initial conditions are the same as those given in the caption of Fig. 3.

To investigate the effect of valence, we varied the number of ligand binding sites v_l and kept receptor valence fixed at v_r = 2 (Fig. 5(b)), which can be accomplished experimentally through synthesis of multivalent ligands [37, 38, 39]. Compared to the rejection method of Yang et al. [16], the rejection-free method has better scaling of CPU time per reaction event with an increase of v_l. Except for the system with bivalent ligands, the rejection-free method is almost insensitive to changes in the number of ligand binding sites, whereas sampling by the rejection method involves large numbers of null events due to increases in intra-aggregate combinations of available ligand and receptor site pairs.

5. Discussion

We have presented problem-specific rejection and rejection-free methods for simulating multivalent ligand-receptor interactions described by reaction rules. Kinetic Monte Carlo procedures are applied to sample the rule list, identify reactant protein sites, and update protein states. In this procedure, all chemical species are formed dynamically. For this reason, the rule-based KMC methods have in general a computational cost independent of reaction network size measured by the numbers of chemical species or reactions. Although our implementations in this study are tailored to multivalent ligand-receptor interactions, general-purpose implementations of the rejection and rejection-free methods considered here are available [18, 19].

The implementation of rejection-free sampling described here in every Monte Carlo step changes the state of the system. Our implementation is closely related to the direct simulation Monte Carlo (DSMC) method developed to simulate coagulation processes where irreversible particle aggregation is considered [40]. The rejection-free method accounts for the exact rates of reaction rules and probability distributions of protein sites. In comparison to the rejection method, implementation of a rejection-free method demands more bookkeeping effort, especially for processing rules that require evaluation of non-local state information. In a more general and straightforward implementation, searching for reactant sites based on the exact probability distributions incurs a linear-time cost per reaction event scaled by the number of sites. In contrast, our rejection-free implementation uses a hierarchical search, which First searches over chemical species that contain candidate sites and after a set of chemical species is selected the algorithm searches for reactant sites in the chemical species. In the multivalent ligand-receptor interaction model, the number of chemical species during a simulation corresponds to the number of ligand-receptor aggregates, N_A. Although the rejection-free method has a higher cost per Monte Carlo step because of searching for candidate sites and the extra bookkeeping required for calculating probabilities for sites, the method outperforms the rejection method when the rejection ratio θ approaches unity.

A comparison between rejection-free and rejection methods was briefly discussed by Yang et al. [16]. The rejection-free algorithm reported by Yang et al. [16] takes a strategy of searching for a ligand-receptor site pair for cross-linking, which is less efficient for simulating formation of large ligand-receptor clusters in comparison to the algorithm presented in this report. This earlier algorithm maintains reaction probabilities of all sites for searching, which has a cost of CPU time per reaction event scaling with the number of molecules. In contrast, the current method searches over an aggregate list that is significantly smaller compared to the full list of molecule sites. For example, as shown in Fig. 5(a), the maximum number of aggregates on average (observed around k_off = 0.1 s⁻¹) was less than one fourth of the total number of receptors (N_R = 5000). At other values of k_off, 〈N_A〉 is much less than N_R (Fig 5(a)). As shown in Fig. 4, at equilibrium 〈N_A〉 has a moderate (sublinear) dependence on the number of molecules.

The rejection and rejection-free methods have similar memory requirements (results not shown). Both require an amount of memory that depends largely on the total number of sites tracked in a simulation. However, the rejection-free method always requires more memory because a list of populated chemical species (i.e., the aggregate list) is tracked in addition to a list of individual sites, as discussed in the preceding paragraph. The extra amount of memory required may only be marginal. As can be seen in Fig. 4, the number of populated chemical species in a system can be orders of magnitude less than the number of molecules or sites.

Implementation of the rejection-free method is more complicated than implementation of the rejection method for at least two reasons. First, updates of rates associated with rules are more complicated. For example, as indicated in Table 1, in our rejection-free simulations, a number of different expressions are used to update the rate associated with Rule 2 in the TLBR model (Fig. 2). In contrast, in rejection simulations, a single expression is always used to obtain the overestimate of the rate associated with this rule [16]. Second, tracking of populated chemical species is an element of the rejection-free method but not the rejection method. As can be seen from inspection of the source codes of NFsim [18] and RuleMonkey [19], a general-purpose implementation of either method is complicated, and it is important not to rely on comparisons of such codes to assess methods. As we have shown here, in a comparison intended to control for irrelevant coding differences, the rejection and rejection-free methods appear to complement each other, with one performing better in one parameter regime and the other performing better in a different parameter regime; also, for many parameter values, the two methods appear to have comparable efficiencies (Fig. 5).

It should be noted that the rejection and rejection-free methods differ only in the handling of rules with application conditions that depend on non-local site properties. In principle, there is no barrier to treating two rules with such application conditions in different ways. Thus, the rejection and rejection-free methods could potentially be combined. A combination of the two methods might be advantageous if one rule among many is responsible for the vast majority of null events in a simulation via the rejection method. In this case, one might consider calculating the rate for this rule exactly, as in the rejection-free method, to reduce the number of null events. Rates for other rules could be determined via rejection sampling, which tends to be more efficient when the rejection ratio, θ, is small (Fig. 5). Monitoring this ratio during a simulation could allow for automatic selection of the best method for calculating each rate in η.

Both rejection and rejection-free methods require explicitly tracking connectivity between sites. This feature erodes the efficiency of simulation, in particular for simulating systems with large aggregates. In simulating multivalent ligand-receptor binding, to process an aggregate dissociation, at least one unweighted traversal of an aggregate subgraph is necessary (with no prior information about which subaggregate is smaller), which presents a major bottleneck to simulating systems in the sol-gel regime because a graph traversal has an order of cost proportional to the size of the aggregate. In the sol-gel regime, most graph traversals will happen on the giant aggregate that has a size close to that of the entire system. Experiments can provide some information about the composition of a protein aggregate but the intra-aggregate (or intra-multiprotein complex) topology usually cannot be resolved. For comparisons of model predictions against certain types of data, it may be sufficient to simulate a system without tracking the aggregate topology. In other words, this approach might be desirable when prediction of connectivity information (e.g., distribution of aggregate topologies for a particular aggregate size) is not of interest. One can refer to our recent algorithm (Q. Chang and J. Yang, arXiv:1010.0339), which improves simulation of models that account for large aggregates, such as a superaggregate [16, 29]. The algorithm avoids tracking connectivity between reaction sites and thus avoids routine graph traversal.

In summary, our results suggest that the rejection method is as efficient or more efficient than the rejection-free method for simulation of models that are not intended to capture the dynamics of large aggregates, which includes many models useful for studying cell signaling. In contrast, the rejection-free method is more efficient than the rejection method for studying the dynamics of large aggregates. Thus, the two methods are complementary.

Figure 6.

Scaling with number of binding sites on the ligand (v_l). For both the rejection-free (squares) and the rejection (circles) simulations, the receptor valence is fixed at v_r = 2 and the copy numbers of receptor and ligand are N_R = N_L = 1000. CPU times per reaction event are calculated by averaging over 200,000 reaction events after simulations reach equilibrium. Other parameters and initial conditions are the same as indicated in Fig. 3.