Mixture Toxicity of S_N2-Reactive Soft Electrophiles: 2—Evaluation of Mixtures Containing Ethyl α-Halogenated Acetates

Abstract

Four ethyl α-halogenated acetates were tested in (1) sham and (2) nonsham combinations and (3) with a nonreactive nonpolar narcotic. Ethyl iodoacetate (EIAC), ethyl bromoacetate (EBAC), ethyl chloroacetate (ECAC), and ethyl fluoroacetate (EFAC), each considered to be an SN2-H-polar soft electrophile, were selected for testing based on their differences in electro(nucleo)philic reactivity and time-dependent toxicity (TDT). Agent reactivity was assessed using the model nucleophile glutathione, with EIAC and EBAC showing rapid reactivity, ECAC being less reactive, and EFAC lacking reactivity at ≤250 mM. The model nonpolar narcotic, 3-methyl-2-butanone (3M2B), was not reactive. Toxicity of the agents alone and in mixture was assessed using the Microtox acute toxicity test at three exposure durations: 15, 30 and 45 min. Two of the agents alone (EIAC and EBAC) had TDT values >100%. In contrast, ECAC (74 to 99%) and EFAC (9 to 12%) had partial TDT, whereas 3M2B completely lacked TDT (<0%). In mixture testing, sham combinations of each agent showed a combined effect consistent with predicted effects for dose-addition at each time point, as judged by EC₅₀ dose-addition quotient values. Mixture toxicity results for nonsham ethyl acetate combinations were variable, with some mixtures being inconsistent with the predicted effects for dose-addition and/or independence. The ethyl acetate–3M2B combinations were somewhat more toxic than predicted for dose-addition, a finding differing from that observed previously for α-halogenated acetonitriles with 3M2B.

In understanding chemical mixture toxicity, it has been suggested that, at least for simple mixtures, the combined effect may be predictable simply by knowing the mode(s) or mechanism(s) of toxic action of the agents (Pöch 1993; Broderius et al. 1995). Two models are often used in such combined effects assessment: dose-addition (e.g., Chen et al. 2001) and independence (Bliss 1939). These are mechanistic models (Pöch et al. 1990, 1996) because the former should occur when the agents are toxic by the same, single mechanism, and the latter should occur when the toxicity of each agent has no effect on the toxicity of the other, thereby implying that the agents have distinct mechanisms of action. A useful discussion of the idea that mixture toxicity may be predictable on a mode or mechanism of action basis has been previously published (Borgert et al. 2004).

The literature holds numerous examples in which a simple mixture shows toxicity that is approximately additive, whether by concentration or by response level (see Calabrese 1991; Rand et al. 1995; Yang 1994). As a result, several investigators have suggested that some toxic chemicals will exert baseline toxicity (i.e., narcosis) at concentrations at or near those that also cause toxicity by another mode of action (McCarty and Mackay 1993; Rand et al. 1995; Hodges et al. 2006). Recent mixture studies using Microtox and soft electrophiles have generated data that supported these conclusions and have noted value in determining time-dependent toxicity (TDT) for interpreting mixture-toxicity results (Gagan et al. 2007; Dawson et al. 2006, 2008).

Based on these works, a series of three studies was initiated to more fully examine the relationship between electro(nucleo)philic reactivity, mode and mechanism of toxic action, TDT, and combined effects. The first study examined three α-halogenated acetonitriles in sham and nonsham combinations and when given with a model nonpolar narcotic (Dawson et al. 2010). In the current study, four ethyl α-halogenated acetates were tested using the same experimental design. The two major differences between this and the first study were that the ethyl α-halogenated acetates are considered to be SN2-H-polar agents (Roberts et al. 2010) and that two, ethyl chloroacetate and ethyl fluoroacetate, had partial TDT (i.e., 0% < TDT < 100%), thereby suggesting two or more modes of toxic action. In the first study, the three α-halo acetonitriles were SN2 reactive, but not H-polar, and all three agents had TDT >100%. Thus, this study was conducted to provide insight into mixture toxicity resulting from SN2 soft electrophiles that have the ability to form strong hydrogen bonds with water.

Materials and Methods

Chemicals

Chemicals tested were (abbreviation, Chemical Abstract Service registry number [purity]): ethyl iodoacetate (EIAC, 623-48-3 [98%]), ethyl bromoacetate (EBAC, 105-36-2 [98%]), ethyl chloroacetate (ECAC, 105-39-5 [99%]), ethyl fluoroacetate (EFAC, 459-72-3 [98%]), and 3-methyl-2-butanone (3M2B, 563-80-4 [99%]). Each agent was purchased from Sigma-Aldrich (Aldrich, Milwaukee, WI) and not further purified. Stock solutions of each were prepared by dissolution in Microtox diluent (a 2% NaCl solution) or in dimethylsulfoxide (maximum concentration in testing 0.1%) with subsequent dilution in diluent. Test solutions were prepared just before testing and held in the dark at 15°C in tightly closed glass vials.

Procedures for In Chemico Reactivity Assessment With GSH

Chemical reactivity was quantified experimentally using the thiol group of the tripeptide glutathione (GSH) (Schultz et al. 2005). During a 2 h incubation period in chemico, in a concentration-response manner, free thiol was quantified spectrophotometrically at 412 nm by its reaction with the chromophore 5,5′-dithio-bis(2)-nitrobenzoic acid. The 50% reactive concentrations (RC₅₀ values in mM, mean of two tests) were determined from nominal concentrations of the toxicants using probit analysis of Statistical Analysis Systems software (SAS, Cary, NC).

Toxicity Assay Procedures

Inhibition of bioluminescence was the end point measured using Microtox (SDIX, Newark, DE). For each chemical combination there was a test of each agent alone (agent A and agent B) and a mixture test (i.e., A:B). Each test had seven duplicated concentrations and a duplicated control treatment. All concentrations were nominal and density corrected. Test concentrations were prepared by serial dilution using 1.867 as the dilution factor. A sham combination of each agent was also tested using the same experimental design. In a sham combination, two stock solutions of a single agent are prepared and tested as if they were two distinct chemicals.

The freeze-dried bacterial reagent (Vibrio fischeri) was reconstituted 15–20 min before test initiation and held at 5°C ± 0.1°C. Initial readings quantified bioluminescence without chemical. Once toxicant solution was added, readings were taken at 15, 30, and 45 min of exposure. Treatment vials were held at 15°C ± 0.2°C during testing.

Procedures for Generating Single-Chemical Concentration-Response Curves

Percent effect data for each agent alone were obtained using Microtox Omni software (SDIX, Newark, DE). Toxicity data were input into custom-made worksheets and program files (SigmaPlot version 11.0; Systat, Chicago, IL). Experimental data points were fit to sigmoid curves using a modified five-parameter logistic function within SigmaPlot, with the minimum-effect parameter removed. Removal of this parameter was necessary because it can unduly influence curve-fitting of single-chemical and mixture curves and therefore affects calculation of theoretical dose-addition and independence curves. By adding an asymmetry parameter to replace minimum effect, curve-fitting remained a four-parameter function, but we have termed it a 5PL–1P (five-parameter logistic minus one parameter) function to indicate that it is not the standard four-parameter logistic (4PL) function found in SigmaPlot. The parameters for the 5PL–1P function were maximum effect, EC₅₀, Hillslope, and s (an asymmetry parameter). Curve-fitting was performed using Eq. 1:

$$\text{y}=max/{(1+{(\text{xb}/\text{x})}^{\wedge }\text{Hillslope})}^{\wedge }\text{s},$$ (1)

in which y = % effect, max = maximum effect, x = concentration, s – asymmetry, and ^ = exponential form (i.e., to the power of). The variable xb was determined from Eq. 2:

$$\text{xb}=\text{EC}50\times {10}^{\wedge }((1/\text{Hillslope})\times log(2^{\wedge }(1/\text{s}-1))).$$ (2)

within SigmaPlot the regressions were run with automatic estimation of the initial parameters. The following constraints were used for fitting the data (1) EC₅₀ >0; (2) 0.1 < s < 10; and (3) max <100. This curve-fitting routine is a modification of the previous approach that used the standard 4PL function within SigmaPlot (e.g., Pöch 1993; Dawson et al. 2006, 1008, 2010; Gagan et al. 2007). Figure 1 shows the differences in curve shape between theoretical curves developed at three values of s when using the 5PL–1P procedure. The more s deviates from 1, the more asymmetric the curves become (not shown). For concentration-response data, the parameter values were calculated for each agent alone at each time point (i.e., 15, 30, and 45 min).

Fig. 1.

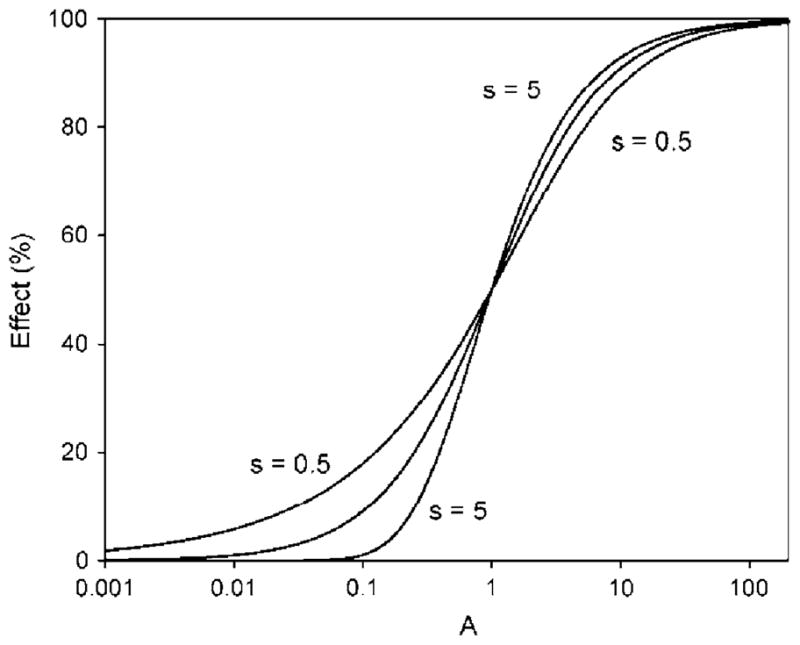
Theoretical concentration-response curves developed for three asymmetry (s) parameter values: 0.5, 1.0 (middle curve), and 5.0. The middle curve is symmetrical, and the others are asymmetrical. Curves with s < 1 show a greater bowing effect at low concentrations; those with s > 1 show bowing at high concentrations

Procedures for Generating Mixture Concentration-Response Curves

Experimental mixtures EC₂₅, EC₅₀, EC₇₅, slope, asymmetry, and maximum-effect values were calculated using the same procedures and equations noted as previously mentioned for single-chemical curves. For mixture data, total chemical concentrations were expressed in terms of concentration equivalents of the more toxic agent (i.e., chemical A). The conversion factor was: [B] = [A]/[B] (Dawson et al. 2010).

Calculation of TDT Values

TDT values were calculated (Gagan et al. 2007) based on the equation E = c × t (c = concentration and t = time). These values were calculated for each single-chemical and mixture concentration-response curve using Eqs. 3 to 5, respectively:

$$\begin{array}{l}15-min{\text{EC}}_{50}-30min{\text{EC}}_{50}=\text{x};\\ 15-min{\text{EC}}_{50}\times 0.5=\text{y},\\ \text{such}\text{that}\text{x}/\text{y}\times 100={\text{TDT}}_{15-30}\end{array}$$ (3)

$$\begin{array}{l}15-min{\text{EC}}_{50}-45min{\text{EC}}_{50}=\text{z};\\ 15-min{\text{EC}}_{50}\times 0.667=\text{w},\\ \text{hence}\text{z}/\text{w}\times 100={\text{TDT}}_{15-45}\end{array}$$ (4)

$$\begin{array}{l}30-min{\text{EC}}_{50}-45min{\text{EC}}_{50}=\text{v};\\ 30-min{\text{EC}}_{50}\times 0.333=\text{u},\\ \text{so}\text{v}/\text{u}\times 100={\text{TDT}}_{30-45}\end{array}$$ (5)

Calculation of Theoretical Dose-Addition and Independence Curves from Single-Chemical Data

Theoretical concentration-response curves for both dose-addition and independence were developed as follows. Conceptually, when agents A and B are dose-additive, the EC₅₀ for a mixture of the two is shifted to the left by a dose-ratio (DR) factor of 2.0 when the agents are equieffective. This is shown below using Eq. 6:

$$\text{Add}50=\text{a}50/\text{DR}50.$$ (6)

Add50 is the EC₅₀ for dose-addition, a50 is EC₅₀ of the more potent agent, and b50 is the EC₅₀ of the less potent agent. The DR50 was determined from Eq. 7:

$$\text{DR}50=1+(\text{a}50/\text{b}50)$$ (7)

When a50 = b50 (i.e., the agents are equieffective) the DR50 = 1 + (1) = 2. As a result, the Add50 = a50/2, giving the EC₅₀ for the theoretical dose-addition curve for the mixture. In a similar manner then, the EC₂₅ and EC₇₅ values for the predicted dose-addition curve can be calculated. Taken together, the predicted dose-addition values for the EC₂₅, EC₅₀, and EC₇₅ and dose-additive maximum effect (y) at max = a50 × 100 (x) allow for the calculation of the theoretical dose-addition curve by applying the same curve-fitting procedure used to generate the single-chemical curves.

Theoretical curves for the independence model of combined effect were also developed using Eq. 8:

$$\text{yA}+(\text{yB}\times (100-\text{yA})/100),$$ (8)

where yA is the percent effect for agent A and yB is the percent effect for agent B.

Calculation of Dose-Additivity and Independence Quotient Values

For a given combination, slope, and EC₂₅, EC₅₀, and EC₇₅ values were calculated at each time point for (1) the agents singly, (2) the mixture, and (3) the predicted dose-addition and independence curves. Then additivity quotient (AQ) values were calculated as AQ = experimental value/predicted value for dose-addition. Likewise, independence quotient (IQ) values were calculated as IQ = experimental value/predicted value for independence.

Determinations of Data Quality

Quality of the concentration-response data was examined in two ways. The first is by calculating correlation coefficients (r²) for each single-chemical and mixture curve. The second approach evaluated test-to-test consistency of each agent alone by calculating coefficient of variation (CV) values for the EC₅₀ and slope parameters at each time point. Use of CV, rather than SE, values is preferred when data result from work performed by multiple operators (Steel and Torrie 1980).

Curve Fit Comparison of 4PL and 5PL Functions

All concentration-response data for this study were also analyzed by the 4PL function, as previously used in this laboratory (Dawson et al. 2008, 2010; Gagan et al. 2007), to compare correlation coefficient (r²) values with those generated using the 5PL–1P function. Mean and median r² values were statistically analyzed within Sigma-Plot for normality (Shapiro-Wilk test) and for statistical significance (Student t test or Mann-Whitney U rank-sum test). Comparisons were made between the 4PL and 5PL–1P functions for single-chemical and mixture curve-fits separately and for all curve-fits combined.

Results

Single-Chemical Data

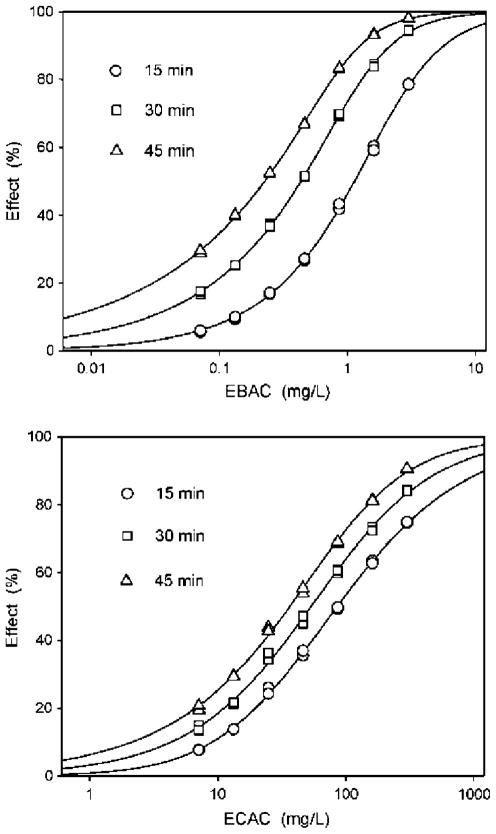
Each single agent tested in the study was evaluated for reactivity with the model nucleophile GSH and for toxicity in Microtox (Table 1). Three ethyl α-halogenated acetates showed reactivity with GSH, with the order of relative reactivity being EIAC > EBAC ≫ ECAC, as consistent with previous work (Hine 1962), whereas EFAC showed no reactivity with GSH at 250 mM (Table 1, column 2). Relative toxicity of these agents showed the same general pattern: EIAC > EBAC ≫ ECAC ≫ EFAC (Table 1, columns 3 to 5).

Table 1.

Mean^a (CV) values for single-chemical reactivity (RC₅₀ [mM]), toxicity (EC₅₀ [mg/L]), dose-response curve slope (slope), and curve asymmetry (s) obtained with Microtox

Agent	RC50b	EC50			Slope			s
		15 min	30 min	45 min	15 min	30 min	45 min	15 min	30 min	45 min
EIAC	0.03	0.31 (19.4)	0.13 (23.9)	0.07 (27.9)	1.42 (5.8)	1.85 (7.3)	2.01 (6.5)	0.68 (21.9)	0.36 (21.1)	0.27 (21.0)
EBAC	0.08	1.09 (4.8)	0.42 (7.8)	0.22 (12.9)	1.56 (6.0)	1.81 (7.1)	2.01 (10.1)	0.52 (13.4)	0.33 (5.2)	0.24 (5.7)
ECAC	3.0	87.9 (7.9)	54.3 (4.7)	35.4 (8.3)	0.81 (8.1)	0.93 (8.1)	1.11 (7.7)	1.63 (28.6)	1.06 (28.2)	0.59 (23.5)
EFAC	–c	1174.3 (9.2)	1077.4 (9.2)	1009.9 (9.3)	0.61 (4.0)	0.79 (10.5)	1.00 (17.8)	3.52 (32.9)	1.10 (34.2)	0.64 (34.1)
3M2B	–d	39.8 (15.3)	42.8 (14.8)	45.5 (16.1)	0.80 (8.1)	0.80 (6.1)	0.83 (6.8)	2.33 (47.1)	2.23 (52.2)	1.90 (47.5)

^aEC₅₀, slope and curve asymmetry values are means for six separate tests of each agent alone

^bReactivity as measured with GSH as the model nucleophile; values are the means of two replicate tests

^cNot reactive with GSH at 250 mM

^dNot reactive with GSH

Slope values for the concentration-response curves of each agent were determined. For EIAC and EBAC, slope values were approximately 1.5 after 15 min of exposure and increased to approximately 1.8 and 2.0 at 30 and 45 min, respectively (Table 1, columns 6 to 8). In contrast, for ECAC and EFAC the slope values were lower at each time point (Table 1, columns 6 to 8). At 15 min, the slope for ECAC (0.79) was similar to that of the nonpolar narcotic (3M2B), with both being greater than that for EFAC (0.61). Over testing time, slope values for ECAC and EFAC increased to at least 1.0 by 45 min. Slope values for 3M2B remained <0.85 at each time point.

TDT was determined for each agent. For both EIAC and EBAC TDT was >100% at each testing interval (Table 2), whereas ECAC showed somewhat lower TDT levels (Fig. 2). For EFAC, although TDT was low (between 9 and 12% at the EC₅₀ for each exposure duration), TDT was actually greater at EC₂₅ (20 to 27%) and EC₇₅ (32 to 40%). The nonpolar narcotic 3M2B lacked reactivity and had toxicity that decreased slightly over time, as reflected by negative TDT values.

Table 2.

Average TDT values (%) for each agent alone in Microtox

Agent	TDT15-30a	TDT15-45b	TDT30-45c	TDT level
EIAC	115	113	126	Full
EBAC	122	118	136	Full
ECAC	74	87	99	High
EFAC	9	12	10	Low
3M2B	−15	−22	−20	Negative

^aTDT between 15 and 30 min

^bTDT between 15 and 45 min

^cTDT between 30 and 45 min

Fig. 2.

Concentration-response curves depicting changes in toxicity with time for EBAC and ECAC. Differences in symmetry are also apparent, with the curves for EBAC being more asymmetrical

Mean values for the asymmetry parameter (s) were always <1.0 for EIAC and EBAC (agents with TDT >100%), with mean s values decreasing as toxicity increased with increased exposure duration (Table 1, columns 9 to 11). For ECAC and EFAC, which both had partial TDT (i.e., 0% < TDT <100%), mean s values were >1.0 at 15 and 30 min and <1.0 at 45 min because toxicity increased with time. In contrast, for 3M2B, mean s values were always >1.0, and toxicity decreased with time.

Mixture Toxicity: Sham Combinations

Five sham combinations were tested as part of the quality-control process for this assay, with EC₅₀-AQ, slope-AQ, EC₅₀-IQ, and slope-IQ values calculated for each exposure duration (sham data in Table 3, rows 1 to 5). For each sham combination, the EC₅₀-AQ values were near 1.0, as expected for dose-addition (Table 3, rows 1 to 5 and columns 2 to 4). Slope-AQ values were also near 1.0 (Table 3, rows 1 to 5 and columns 5 to 7), except for EFAC-EFAC at 15 min. Although it has been suggested that values of 1.0 ± 0.2 are consistent with dose-addition (Broderius et al. 1995; Hodges et al. 2006), in this laboratory AQ values of 1.0 ± 0.1 obtained from dose-response curve analysis of concentration-effect data are used to signify consistency with dose-addition, especially when the slope-AQ values are also in this range. This conclusion is based on extensive experience with two mixture-toxicity assays (Microtox and FETAX [e.g., Dawson et al. 2004]).

Table 3.

AQ and IQ quotients for EC₅₀ and slope for each combination tested in Microtox as classified by the sham, SN2 TDT-level, or SN2:NPN mixture groups

Mixture groupa	EC50-AQ			Slope-AQ			EC50-IQ			Slope-IQ
A:B	15 min	30 min	45 min	15 min	30 min	45 min	15 min	30 min	45 min	15 min	30 min	45 min
Sham
EIAC:EIAC	1.00	0.93	0.90	0.94	0.93	1.02	1.04	1.07	1.15	0.69	0.78	0.92
EBAC:EBAC	1.02	1.05	1.00	0.91	1.02	1.01	1.14	1.31	1.42	0.72	0.89	0.97
ECAC:ECAC	1.01	1.01	0.98	0.90	0.91	0.92	1.29	1.30	1.32	0.70	0.70	0.71
EFAC:EFAC	0.94	1.00	1.02	0.70	0.86	1.01	1.31	1.46	1.56	0.61	0.72	0.83
3M2B:3M2B	0.97	0.98	1.02	1.09	0.95	0.97	1.18	1.22	1.26	0.77	0.70	0.71
Full:full
EIAC:EBAC	1.02	1.01	1.00	0.92	0.94	0.93	1.10	1.22	1.34	0.70	0.84	0.95
Full:high
EIAC:ECAC	1.02	1.07	1.07	1.14	0.90	0.91	1.17	1.32	1.41	0.82	0.69	0.74
EBAC:ECAC	1.07	1.09	1.08	0.84	0.85	0.86	1.26	1.37	1.49	0.64	0.65	0.70
Full:low
EIAC:EFAC	1.12	1.26	1.54	0.81	0.76	0.92	1.42	1.80	2.28	0.64	0.64	0.76
EBAC:EFAC	0.86	0.95	1.13	0.70	0.65	0.84	1.06	1.35	1.77	0.58	0.53	0.54
High:low
ECAC:EFAC	0.82	0.83	0.84	0.69	0.64	0.59	1.06	1.20	1.32	0.57	0.51	0.49
SN2:NPN
EIAC:3M2B	0.90	0.89	0.86	1.09	0.91	0.81	0.97	1.04	1.03	0.77	0.68	0.63
EBAC:3M2B	0.91	0.86	0.87	1.14	0.97	0.87	0.98	1.02	1.08	0.83	0.71	0.65
ECAC:3M2B	0.79	0.78	0.77	0.97	0.95	0.89	0.97	0.96	0.99	0.76	0.71	0.68
EFAC:3M2B	0.87	0.86	0.88	0.81	0.64	0.55	1.07	1.12	1.18	0.57	0.48	0.40

^aMixture group includes sham, SN2 agent TDT level (full, high, low TDT [see Table 2]), and SN2:NPN (nonpolar narcotic) categories, see Table 1 for chemical names. Values shown in bold are within the range of 0.90 to 1.10 and are consistent with dose-addition if AQ values or independence if IQ values

IQ values for each sham mixture were also determined, with an IQ value of 1.0 ± 0.1 being consistent with the predicted response for an independent combined effect. For the sham mixtures all EC₅₀-IQ values were >1.0, with 13 of 15 being ≥1.14 (Table 3, rows 1 to 5 and columns 8 to 10). Slope IQ values for the sham combinations ranged from 0.61 to 0.97, with 13 of 15 being <0.90 (Table 3, rows 1 to 5 and columns 11 to 13). The results suggest that the sham mixtures were not consistent with independence.

Mixture Toxicity: Ethyl α-Halogenated Acetate Combinations

Six combinations of ethyl α-halogenated acetates were tested (Table 3, rows 6 to 11), with the results presented by TDT level of the agents (i.e., EIAC, EBAC = full TDT, ECAC = high TDT, and EFAC = low TDT). The AQ values for EC₅₀ and slope were calculated for these mixtures, with EC₅₀-AQ values for EIAC–EBAC being 1.02, 1.01, and 1.00 at 15, 30, and 45 min, respectively. The respective values were slightly greater for EIAC–ECAC (1.02, 1.07, and 1.07) and EBAC–ECAC (1.07, 1.09, and 1.08). These are consistent with dose-addition. In contrast, EFAC-containing mixtures yielded varied results. For EIAC-EFAC, all EC₅₀-AQ values were ≥1.12, consistent with a less-than-dose-additive combined effect. For EBAC–EFAC the 15-minute EC₅₀-AQ had a greater-than-dose-additive effect (0.86) but consistent with dose-addition at 30 min (0.95) and less-than-dose-additive effect at 45 min (1.13). For ECAC–EFAC the EC₅₀-AQs were always greater-than-dose-additive (0.82–0.84). Slope-AQ values for these mixtures were generally <1.0 at each time point (Table 3).

IQ values for each ethyl acetate combination at each time point were all ≥1.06, with 15 of 18 EC₅₀-IQ values being ≥1.17 (Table 3, rows 6 to 11 and columns 8 to 10). Slope IQ values for these combinations ranged from 0.49 to 0.95, with 17 of the 18 values being <0.85 (Table 3, rows 6 to 11 and columns 11 to 13).

Mixture Toxicity: Ethyl α-Halogenated Acetate–Nonpolar Narcotic Combinations

Each of the ethyl α-halogenated acetates was tested in combination with 3M2B to assess the combined effect of the soft electrophiles with a nonreactive nonpolar narcotic (Table 3, rows 12 to 15). The EC₅₀-AQ values at each time point for each of these mixtures ranged from 0.77 to 0.91 (Table 2, rows 12 to 15 and columns 2 to 4), reflecting toxicity that was somewhat greater than predicted for dose-addition (Fig. 3). Slope-AQ values were variable but always greatest for a given combination at 15 min and lowest at 45 min (Table 3, rows 12 to 1 and columns 5 to 7).

Fig. 3.

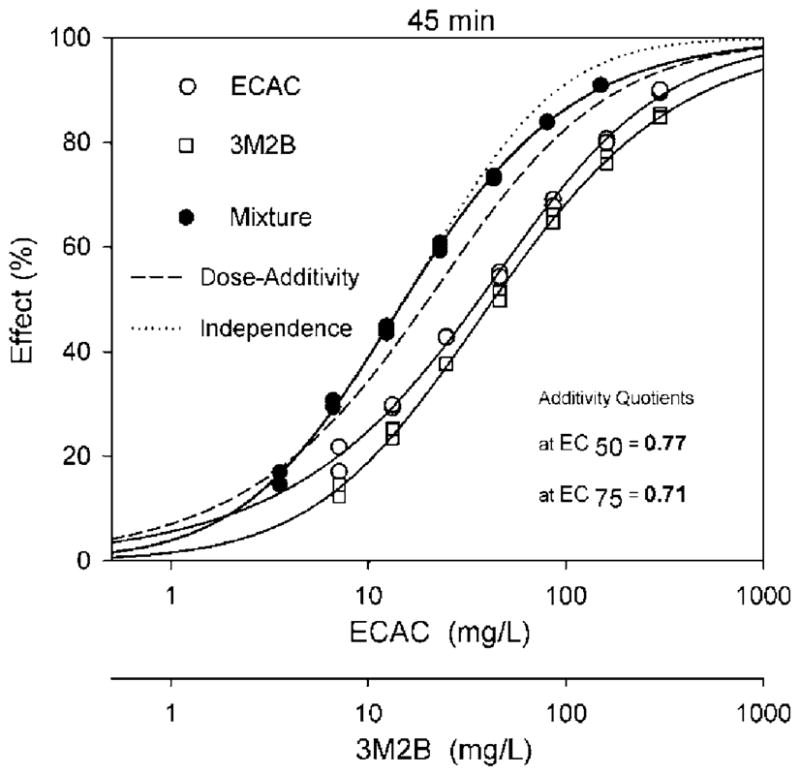
Concentration-response curves for ECAC alone, 3M2B alone, and their mixture after 45 min of exposure along with predicted curves for dose-addition and independence

For independence, EC₅₀ and slope-IQ values for ethyl acetate-3M2B mixtures were determined. For these combinations the EC₅₀-IQ values were fairly close to 1.0 (Table 3, rows 12 to 15 and columns 8 to 10) when 3M2B was given with EIAC, EBAC, and ECAC. The values were somewhat greater for EFAC with 3M2B. Slope IQ values were all well below 1.0 (range 0.63–0.83 [Table 2, rows 12 to 15 and columns 11 to 13]).

Quality and Consistency of Single-Chemical Toxicity Data

The single-chemical test data were subjected to two evaluations of data quality (1) by determining correlation coefficient (r²) values for fit to a sigmoid curve and (2) by calculating CV values for EC₅₀, slope and s values at each time point. For the former, all single-chemical curves (n = 90) had r² values between 0.9861 and 0.9999 (mean 0.9975 ± 0.0029 [Table 4]). This mean was affected by generally lower r² values for EFAC alone (mean 0.9924 ± 0.0028 [Table 4]).

Table 4.

Mean (± SD) and r² values for the 5PL–1P^a and 4PL functions

Function	All curves (n)	Single-agent curves (n)	Mixture curves (n)	EFAC-alone curves (n)	EFAC-mixture curves (n)
Mean
5PL–1P	0.9978 ± 0.0026 (135)	0.9975 ± 0.0029 (90)	0.9984 ± 0.0019 (45)	0.9924 ± 0.0028 (18)	0.9971 ± 0.0028 (15)
4PL	0.9970 ± 0.0027 (135)	0.9966 ± 0.0030 (90)	0.9978 ± 0.0020 (45)	0.9914 ± 0.0027 (18)	0.9964 ± 0.0029 (15)
Median
5PL-1P	0.9988b	0.9987c	0.9989d	0.9924e	0.9983f
4PL	0.9980b	0.9978c	0.9983d	0.9922e	0.9974f

^aMean data were not normally distributed, so Student t test could not be run; thus, median data were evaluated by Mann-Whitney U rank-sum test

^bSignificantly different from each other with P <0.001

^cSignificantly different from each other with P < 0.001

^dSignificantly different from each other with P = 0.002

^eNot significantly different from each other with P = 0.282

^fNot significantly different from each other with P = 0.071

Calculations of test-to-test variation for EC₅₀, slope, and s data, on a chemical-by-chemical basis, resulted in CV values <30.0 at each time point for the EC₅₀ (Table 1) and <20.0 for slope. This suggested good test-to-test consistency because these CVs are similar to those from reported by previous studies (Gagan et al. 2007; Dawson et al. 2006, 2008, 2010). For the asymmetry parameter, CV values were always <55.0. For s, CV values were highest for the nonpolar narcotic 3M2B. Because this is the first time CV values have been calculated for this parameter using this system, it is not yet possible to determine appropriate CV value ranges for s that represent good test-to-test consistency. For 3M2B, there was a decrease in toxicity with time (i.e., negative TDT values), and this may affect curve-fitting such that CV values for s are greater. Further study of this issue is needed.

Quality of Mixture Toxicity Data

Concentration-response data for the mixtures were also examined for quality by determining r² values. All such curves (n = 45) had r² values between 0.9881 and 0.9998 (mean 0.9984 ± 0.0019). Again, EFAC-containing mixtures yielded r² values somewhat lower than mixtures that did not contain EFAC (Table 4).

Comparison of the 4PL and 5PL–1P Curve-Fitting Procedures

Mean r² values for the two curve-fitting functions were calculated for single-agent curves and mixture curves separately and for all curves combined (Table 4). The mean values were not normally distributed, however, so Student t test could not be used for significance determinations. Hence, statistical analyses using median data for r² was conducted using Mann-Whitney U rank-sum test. These analyses showed that the 5PL–1P function yielded significantly better curve fits than the 4PL function.

Discussion

Because the background information, literature, rationale, and need for this type of research have been presented previously (Dawson et al. 2006, 2008, 2010; Gagan et al. 2007), the focus of this section is limited to the specifics of this study.

SN2 and SN2-H-polar Soft Electrophiles and Their Reactivity

The simplest type of substitution reaction in organic chemistry is the S_N2 type, in which one group is directly displaced at a carbon atom by a second group (Jacobs 1997). Some S_N2 electrophiles, such as the ethyl α-halogenated acetates [X–CH₂–CO(=O)–C₂H₅; X = halogen] are considered to be S_N2-H-polar agents (Roberts et al. 2010). “H-polar” is a term that describes compounds that are able to form strong hydrogen bonds with water (Hansch and Leo 1979). Other possible S_N2 electrophiles, such as the α-halogenated acetonitriles [X–CH₂–C≡N; X = halogen], do not have this ability. The presence or absence of strong hydrogen-bonding ability with water for some S_N2 agents offers the opportunity to examine the effect of such bonding ability, if any, on mixture-toxicity outcome.

Reactivity of each agent was tested in this study. The RC₅₀ value for each is the concentration of test compound that produced 50% reaction of the GSH thiol group in 120 min (Schultz et al. 2005). Under standard conditions, RC₅₀ values are mathematically proportional to reciprocal rate constants. Comparison of reactivity for S_N2 electrophiles reveals the ester group to be a stronger activator than the cyano group (e.g., of the α-halogenated acetonitriles). Regardless of the activating group, the reactivity pattern of halide S_N2 electrophiles is consistent with the order I ≈ Br ≫ Cl ≫ F (Roberts et al. 2010).

Inclusion of the Asymmetry Parameter in Curve-Fitting

The use of an asymmetry term for sigmoid or logistic curves has been suggested (Van der Graaf and Schoemaker 1999; Giraldo et al. 2002; Gottschalk and Dunn 2005). Recent mixture-toxicity research with Microtox in this laboratory used a 4PL function with a minimum effect constraint to fit concentration-response data to sigmoid curves (Gagan et al. 2007; Dawson et al. 2006, 2008, 2010). In such research, developing a data analysis procedure that provides for the best curve-fitting across a broad range of industrial organic chemicals is needed to provide the most consistent assessment of mixture toxicity. Initial evaluations of recent data using the 5PL–1P function to develop curve-fits suggested that inclusion of the asymmetry parameter (s) might improve fitting and therefore evaluation of mixture toxicity. The theoretical curves of Fig. 1 (noted previously) showed bowing of concentration-response curves as values of s became >1.0 or <1.0. Analysis of the experimental data collected in this study showed improved curve fits with the 5PL–1P function. This is not surprising when one considers the theoretical 5PL–1P-derived curve having an s value of 0.5 in Fig. 1, for which the EC₅₀ and slope values were 1.0 and the r² was 1. In Fig. 4, x/y data taken from that curve were fit to the 4PL function with and without minimum constraint. Without minimum constraint, the r² value for the curve was 0.9994, with an EC₅₀ of 1.15. With minimum constraint, the r² decreased to 0.9963 and the theoretical EC₅₀ became 0.92. For single-chemical curves, such changes in EC₅₀ values impact prediction of the dose-addition curve, thereby affecting assessment of the combined effect of the mixture.

Fig. 4.

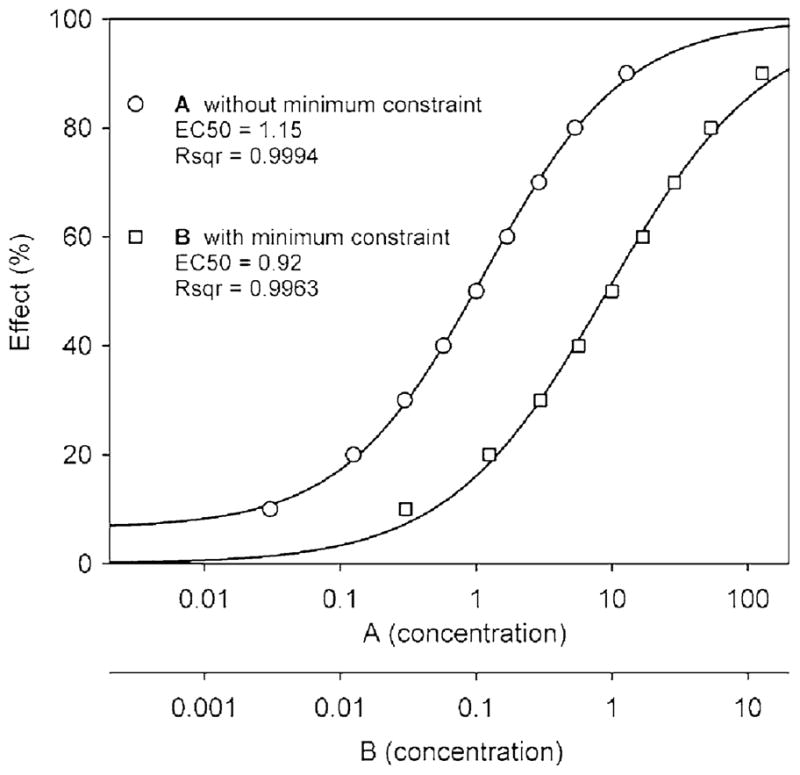
Theoretical concentration-response curves showing comparative fitting of x/y data using the 4PL function without (curve A) and with (curve B) a minimum constraint applied. The x/y data were taken from the theoretical 5PL–1P-derived curve with an s value of 0.5 in Fig. 1. The EC₅₀ and r² values change depending on the function used and whether or not the constraint was applied (5PL–1P curve with s = 0.5 had an EC₅₀ of 1.0, r² = 1.000). Note: For clarity, curves A and B are shown with separate concentration axes so that the curves do not overlap

Another importance of including the asymmetry parameter can be seen in its apparent association with TDT; soft electrophiles with TDT >100%, such as EIAC and EBAC, had s values <1.0 at each time point in testing. In contrast, the nonpolar narcotic 3M2B had negative TDT values but s values >1.0. For ECAC and EFAC, with partial TDT (i.e., 0% < TDT < 100%), s values were >1.0 at 15 and 30 and min but <1.0 at 45 min.

Previous work has shown that many soft electrophiles possess partial TDT, and this had been taken as potential evidence for multiple modes (or mechanisms) of toxic action for such agents (Dawson et al. 2008, 2010; Gagan et al. 2007). The results of this study support this idea, with further support coming from the variability in asymmetry parameter values with respect to differences in TDT. Additionally, statistical analyses showed significantly improved curve-fitting with the 5PL–1P versus 4PL function whether analyzed by single-chemical curve-fits, mixture curve-fits, or both combined Table 4).

The idea that a single agent could possess two or more toxic actions within the same series of concentrations is not new. Rand et al. (1995), in summarizing work from McCarty and Mackay (1993), noted the phenomenon of “approximate additivity” that occurs commonly with organic chemical mixtures. These works suggested the possibility that an agent may induce toxicity at low concentrations by way of narcosis, for example, and at greater concentrations by a second action, such as electro(nucleo)philic reactivity. In such cases, one might expect to see (assuming that enough concentrations have been tested) a biphasic concentration-response curve. Reports of such biphasic curves for a variety of toxic effects are not uncommon in the scientific literature (Celik et al. 2005; Dudek et al. 1991; Hinman 1987).

Assessment of Mixture Toxicity

Individual EC₅₀-AQ and slope AQ-values suggested that mixture toxicity for each sham combination was consistent with dose addition (i.e., AQ = 1.0 ± 0.1). Dose-addition is expected, theoretically, for sham combinations when the agent has a single mechanism of action and presumably when there are multiple mechanisms of action as long as the relative potency ratio is close to 1:1.

It is sometimes useful to also consider AQ values at other points along the concentration-response curves: For example, an EC₅₀-AQ might be 1.00, but the EC₂₅-AQ might be 0.86 and the EC₇₅-AQ 1.22. For each of the five the sham combinations tested in this study, the EC₂₅-AQ, EC₅₀-AQ, and EC₇₅-AQ values were within the range of 0.90 to 1.10, signifying dose-addition 93.3% of the time (42/45 [data not shown]). The three outliers were 0.88 (3M2B-3M2B EC₇₅-AQ at 15 min), 0.88 (EIAC–EIAC EC₂₅-AQ at 30 min), and 0.82 (EIAC–EIAC EC₂₅-AQ at 45 min), yielding one outlier (out of 15 [6.7%]) at each exposure duration.

For independence, sham combinations of ethyl acetates had EC₅₀-IQ values that were mostly >1.10 (13/15 [87%], Table 3) and slope-IQ values that were mostly <0.90 (13/15 [Table 3]). Independence was not expected for sham combinations for the combinations tested in this study, and the results confirmed this expectation.

Individual AQ values for nonsham ethyl acetate combinations were variable (Table 3) depending on the level(s) of TDT of the agents individually. For example, the iodo- and bromo-derivatives showed full TDT, and the EIAC-EBAC mixture produced EC₅₀-AQ (as well as EC₂₅-AQ and EC₇₅-AQ) and slope-AQ values that were consistent with dose-addition at each exposure duration. Taken together, the results suggest that both have the same toxic action in V. fischeri.

Mixtures in which one agent had full TDT and the second had high TDT (e.g., EIAC–ECAC or EBAC–ECAC) also produced results consistent with dose-addition, with EC₅₀-AQ values tending to be closer to 1.1 than 1.0. However, the EC₇₅-AQ values for these two combinations tended to be >1.10 (EIAC–ECAC EC₇₅-AQ = 1.17 at 30 min and 1.15 at 45 min; EBAC–ECAC – EC₇₅-AQ = 1.19 at 15 min, 1.20 at 30 min, and 1.16 at 45 min). Taken together, the results suggests that ECAC produces toxicity much in the same way that EIAC and EBAC do, but they hint at some difference as well. These differences might be due to a low level of toxicity from narcosis with ECAC and/or to inhibition of a variable group of metabolic enzymes between the iodo-, bromo-, and chloro-derivatives due to steric hindrance resulting from the size of the halogen group.

In contrast, EFAC, with low TDT, yielded variable results with each of the other ethyl acetates. For EIAC–EFAC at each exposure duration EC₅₀-AQ values were all >1.10 (as were all EC₂₅-AQ and EC₇₅-AQs [data not shown]). For EBAC–EFAC, the EC₅₀-AQ at 15 min was <0.90 (i.e., greater than dose-additive) but 0.95 at 30 min (i.e., consistent with dose-additive) and 1.13 at 45 min (i.e., less than dose-additive). The EC₂₅-AQ and EC₇₅-AQ values at each of the three exposure durations tended to show the same pattern, so overall mixture toxicity for the EBAC–EFAC combination went from being greater than dose-additive at 15 min to less than dose-additive at 45 min.

The ECAC–EFAC combination, however, gave EC₅₀-AQ values suggesting greater-than-dose-additive toxicity at all three exposure durations. Although the reasons for such variability in results are unclear, examination of features of the concentration response data for EFAC alone suggests that its toxicity differs in one or more ways from that of the other three α-halogenated ethyl acetates.

One such feature is seen with the TDT data. In the study, mean TDT values (Table 1) were calculated based on changes in the EC₅₀ for a given agent with time. However, it is also possible to calculate TDT at other effect levels (e.g., EC₂₅ or EC₇₅). For EFAC, TDT levels at EC₂₅ (mean TDT_15–45 27%) and EC₇₅ (mean TDT_15–45 39%) were actually greater than those at EC₅₀ (mean TDT_15–45 12%), indicating that changes in the toxicity of EFAC with time were greater at lower and greater levels of the concentration-response curves than in the middle of the curves, thus suggesting the possibility of multiple modes of toxic action for EFAC.

The second data feature supporting a different toxic action for EFAC is that lower correlation coefficient values were obtained for EFAC. This may be due to a complex concentration-response relationship curve or to two (or more) superimposed curves. Mean r² values for EFAC alone were lower than those for any of the other agents alone, and mean r² values for mixtures containing EFAC were lower than those for mixtures that did not have EFAC (Table 4).

A third feature suggesting a differing toxic action for EFAC is that EFAC failed to show reactivity with GSH at as much as 250 mM, even though it did have some TDT. The other three ethyl acetates tested showed reactivity with GSH. Although the GSH-reactivity test used herein has proven to be an effective method for assessing reactivity of soft electrophiles (Roberts et al. 2010), it is possible that EFAC reacts with a different subset of biomolecules than do the other three ethyl acetates, which could be expected to give EFAC toxicity a different character.

For independence, nonsham ethyl acetate combinations generally had EC₅₀-IQ values >1.10 and slope-IQ values <0.90. These data suggest that the combined effect for these mixtures is not consistent with independence.

For ethyl acetate-3M2B combinations, EC₅₀-AQ values were typically inconsistent with dose-addition, actually being somewhat more toxic than expected for that model. For independence, EC₅₀-IQ values were often close to 1.0, suggesting an independent combined effect, but the mean slope-IQ values were never consistent with independence (<0.85).

Comparison of Ethyl α-Halogenated Acetate Results With α-Halogenated Acetonitrile Results

In the first study in this series (Dawson et al. 2010), three α-halogenated acetonitriles (the iodo-, bromo-, and chloroforms) were tested in sham combinations, with each other, and with the nonpolar narcotic 3M2B. The α-halo acetonitriles each had TDT values of approximately 100%, and each combination had EC₅₀-AQ values that suggested dose-addition. When tested with 3M2B, however, each α-halo showed mixture toxicity that was less toxic than predicted for dose-addition. The results suggested that toxicity for the α-halo acetonitriles was primarily due to reactivity with endogenous nucleophiles, such as amino acids, whereas 3M2B toxicity was due to membrane effects (Dawson et al. 2010).

In comparison, the results of the present study showed a notable difference. When tested with 3M2B the ethyl α-halogenated acetates had mixture toxicity that was somewhat greater than that predicted for dose-addition. It is suggested that the difference in mixture toxicity between α-halo acetonitrile–3M2B combinations and ethyl α-halogenated acetate–3M2B combinations is due to the difference in the ability of these agents to form strong hydrogen bonds with water. Testing of additional SN2 and SN2-H-polar agents is needed to determine if this is a consistent finding.

The third study in this series will examine combinations of S_N2-H-polar and S_N2 agents. The results of the study will provide additional insight into the effects that agents with a strong ability to form hydrogen bonds with water have in mixture toxicity.

Conclusion

The results of this study add to those that have been designed to assess the relationship between the combined effect obtained and mode or mechanism of action of the toxicants. The main findings were (1) that SN2-H-polar agents, which have the ability to form strong hydrogen bonds with water, produced a combined effect with a nonpolar narcotic that was greater than that observed for SN2 agents, which do not possess such ability (Dawson et al. 2010); (2) that although sham combinations of the α-halogenated ethyl acetates typically showed dose-additive combined effects, nonsham combinations of these agents were less clearly dose-additive, especially when agents with partial TDT (i.e., ECAC and EFAC) were a component of the mixture; and (3) that the new curve-fitting procedure, incorporating an asymmetry parameter, was an improvement compared with the previous approach for assessing mixture toxicity.