Statistical Analysis in Genetic Studies of Mental Illnesses

Abstract

Identifying the risk factors for mental illnesses is of significant public health importance. Diagnosis, stigma associated with mental illnesses, comorbidity, and complex etiologies, among others, make it very challenging to study mental disorders. Genetic studies of mental illnesses date back at least a century ago, beginning with descriptive studies based on Mendelian laws of inheritance. A variety of study designs including twin studies, family studies, linkage analysis, and more recently, genomewide association studies have been employed to study the genetics of mental illnesses, or complex diseases in general. In this paper, I will present the challenges and methods from a statistical perspective and focus on genetic association studies.

1 Introduction

Mental illnesses affect the health and well-being of all popluations and all ages. Schizophrenia–a chronic, severe, and disabling brain disorder–is one of these mental illnesses, affecting about 1.1 percent of the U.S. population age 18 and older in a given year. People with schizophrenia sometimes hear voices others dont hear, believe that others are broadcasting their thoughts to the world, or become convinced that others are plotting to harm them. These experiences can make them fearful and withdrawn and cause difficulties when these people try to have relationships with others (http://www.nimh.nih.gov). Emil Kraepelin (1856-1926) described “Dementia Praecox” as an inherited disorder in his influential “Textbook of Psychiatry” (1899). Dementia Praecox, coined “schizophrenia,” was first used by Arnold Pick (1851-1924)–a professor of psychiatry at the German branch of Charles University in Prague–to describe a patient with a psychotic disorder resembling hebephrenia in 1891.

Nearly a century ago, Cannon and Rosanoff (1911) made an attempt to understand whether there are any forms of nervous and mental diseases that are transmitted from generation to generation in concordance with Mendelian laws. They examined the families of 11 neuropathetic patients, which are now referred to as probands in pedigrees. Using Mendelian laws as their theoretical expectation, they concluded that the neuropathetic make-up is recessive to normal. Although the report was indeed “preliminary,” a few things are noteworthy. First, they noted that “any form of insanity or even all the forms of hereditary insanity do not constitute an independent hereditary character.” This raised an early sign of the complexity associated with studying mental disorders compared to the characterization of the disorders and their comorbidity. Here, comorbidity refers to more than one disease condition in the same patient. Second, they remarked “should larger accumulations of such data in the future give similar results, we shall be able” to confirm their result. The requirement for more samples and replication is another challenge in studies of complex diseases. Lastly, but not the least, while they said “let us test,…, the hypothesis …” they did not mean a statistical test. However, the idea of the χ²-test is evident.

Despite this early work, it wasn’t until 1960s that the researchers began to use scientifically rigorous designs and methods to study the inheritance of mental illnesses. For example, the key idea in adoption studies lies in the belief that any links between an adopted child and the biological parents are attributable to genetics, and any links between that child and adoptive parents can be attributed to environment (Plomin et al., 1997). This enables us to separate the confounding environment (i.e., a family) from genetic contribution. Consequently, there are two strategies in adoption studies. One approach compares the risk of developing schizophrenia in the adopted children of schizophrenic parents to the risk of adopted children whose parents do not have schizophrenia. Several studies including Heston (1966), Rosenthal (1972), and Tienari (1991) used this approach to study schizophrenia. Each study found an elevated risk in adopted-away children of schizophrenic parents, supporting the role of genetics in the transmission of schizophrenia. The origin of this approach is the schizophrenic parents. Another approach backtracks from adopted children who have developed schizophrenia and compares the risks of schizophrenia in their adpotive and biological families. Kety et al. (1978) and others found that the risk was significantly higher in the biological relatives than in the adoptive families, again underscoring the role of genetics as a risk factor.

While these schizophrenia adoption studies are influential in understanding the role of genetics in mental disorders, the majority of the genetic factors associated with mental disorders is based on family and twin studies. By comparing the concordance in the risk between identical (monozygotic) and fraternal (dizygotic) twins, twin studies arguably provide the most compelling results about genetic and environmental effects. For example, the concordance in monozygotic twins for Touretteś syndrome, a complex disorder characterized by repetitive, sudden, and involuntary movements or noises called tics, was reported to be about 50% whereas it is less than 10% in dizygotic twins.

Twin studies are most helpful in demonstrating the magnitude of genetic effect, but they do not provide insight into the inheritance pattern of a condition. Thus, family studies can offer information that twin studies cannot. Thus, Cannon and Rosanoff (1911) employed a small scale, simple family study. Using the Mendelian laws, not only might we find evidence of genetics, but also infer the mode of transmission, as Cannon and Rosanoff (1911) concluded for the heredity of insanity.

Although twin and family studies continue to be useful for understanding the genetics of complex diseases, different studies are needed to locate a specific gene on a chromosome that may underlie the disease. Gene mapping in humans through linkage analysis emerged in 1930s, but it was Morton (1955) that laid the foundation for the methodology. It was only during the 1970s and 1980s, when the Elston-Steward (1971) was developed and implemented (Ott 1974), that the method thrived as a common tool of genetic studies. These initial and subsequent developments allowed for linkage analyses of multiple markers simultaneously. In light of the sheer number of genes and that we do not know which specific gene we are looking for, we typically genotype 300 to 400 “landmarks” that cover the 22 pairs of autosomes and the X chromosome. By inferring the transmission patterns of these markers, then linking them to the disease status, we can obtain information about the most probable region where the gene of interest resides.

While linkage studies have had some successes (e.g., BRCA1), they have generated many more premature excitements. In the late 1980s, two particular studies attracted significant public attention after they reported that bipolar affective disorders were linked to DNA markers on chromosome 11, and that a susceptibility locus for schizophrenia was located on chromosome 5. Unfortunately, these findings were not replicated. Replications in genetic studies of mental disorders do not come easily. For example, Abelson et al. (2005) identified mutations involving the SLITRK1 gene (13q31.1) in a small number of people with Touretteś syndrome. However, most people with Touretteś syndrome do not have a mutation in the SLITRK1 gene. Because the mutations were reported in so few people with this condition, the association of the SLITRK1 gene with this disorder could not be confirmed. In fact, Scharf et al. (2008) reported a lack of the association between SLITRK1var321 and Touretteś syndrome in a large family-based sample.

Various reasons have been suggested to explain the difficulties detouring progress in genetic studies using linkage analysis. A key concept underlying linkage analysis is the recombination fraction, which reflects the distance between any two markers, such as a DNA marker and the disease locus. There may be limited information in the data, however, diminishing the power of the linkage study. Furthermore, complex diseases are polygenic, involving multiple genes (Carter and Chung, 1980). Linkage analyses, however, are generally under the assumption of one major gene. Additionally, heterogeneity in the diagnosis and comorbidity of mental illnesses make linkage analysis considerably more difficult, if even possible at all.

Many investigators have adopted association analyses to take advantage of the advent of high throughput genotyping technologies. Recent efforts have identified genes that contribute to a number of complex human traits using the ultra-dense genetic markers (Arking et al., 2006; Klein et al., 2005; Duerr et al., 2006; Chen et al., 2007). Trios (one affected off-spring and two parents) have been an effective design for association studies, particularly with the development of the elegant transmission/disequilibrium test (TDT) (Spielman, McGinnis and Ewens, 1993). The central idea of this test is that each affected child serves as his or her own matched case and control. This acts to control for all potential confounding issues and examines alleles that both are and are not transmitted from the parents. In the absence of association between the affective status and the gene, the distributions of the transmitted and non-transmitted alleles are expected to be the same. Deviations in distribution as evaluated by a χ²-square test indicate the existence of association. Trios are the simplest example of nuclear family, but when other siblings are available, the trio design is not cost-effective. As a result, family-based association tests (FBAT) including sibships (Spielman and Ewens, 1998; Horvath and Laird, 1998; Knapp, 1999), nuclear families (Weinberg, 1999; Lunetta et al., 2000; Rabinowitz and Laird, 2000), and general pedigrees (Martin, Monks, Warren and Kaplan, 2000) have been developed.

Another restriction in the use of trios is the requirement of defining the affective status of a disease. Consequently, association tests have been proposed for quantitative traits (Allison, 1997; Rabinowitz, 1997), traits with distribution belonging to an exponential family (Liu, Tritchler and Bull, 2002), ordinal traits (Zhang, Wang and Ye, 2006; Wang, Ye and Zhang, 2006), and multiple traits (Lange et al. 2003; Zhang et al. 2010).

Since the early success in identifying the complement factor H polymorphism in age-related macular degeneration (Klein et al., 2005), case-control association studies have intensified, and many genetic variants have been identified and cateloged (Hindorff et al. 2009). Despite the enormous investment, the intense attention to the genetics of diseases, the rapid improvement in technology, and the increasingly large sample sizes in many studies, it remains challenging to identify disease genes, especially those underlying mental illnesses. Some of the common genetic variants that have been identified for complex diseases only account for a small portion of the genetic risk, which may vary across populations (Goldstein 2009). For example, Kopp et al. (2008) and Kao et al. (2008) identified several variations in the MYH9 gene as major contributors to excess risk of kidney disease among African-Americans. They found that 60 percent of African-Americans carry the risk variants as opposed to 4 percent of white Americans.

Technology will continue to improve and the amount of genetic data will increase. The purpose of this article is to review some of the progress from a statistical perspective and discuss some of the potential challenges. Obviously, it would take volumes or series to do justice to all of the work in statistical genetics. Instead of taking on that impossible task, this article is oriented toward the publications directly related to my own recent work.

2 Methods

Since 1952, the American Psychiatric Association has published four editions of the Diagnostic and Statistical Manual of Mental Disorders (DSM) and plans to release its fifth edition in 2013. While widely used, the use and development of the DSM has not gone without controversy and criticism. Unlike diseases for which the diagnoses are well accepted by physicians and patients such as cancer, the diagnosis of mental disorders must reflect biological factors (e.g., gender and racial disparities), non-biological factors such as culture that are not specific to one person, and it also must reflect the natural variation within the same person.

2.1 Ordinal Traits

It is clear from the above discussion that a simple dichotomous diagnosis (e.g., yes or no), or a well-distributed continuous trait is unlikely to characterize the state of mental disorders. In fact, the questions used in the diagnosis of mental disorders, such as DSM-IV, are usually posed in terms of severity or frequency, and hence in an ordinal scale.

Statistical methods for genetic analysis are well established for both quantitative (continuous) and binary traits (see e.g., Blackwelder and Elston 1985; Goldgar 1990; Schork 1993; Amos 1994; Risch and Zhang 1995; Kruglyak et al. 1996; Blangero and Almasy 1997; Ott 1999). While there has been some progress in the analysis of ordinal traits (e.g., Heath et al. 2002; Steinke et al. 2003; Vergne et al. 2003; Zhang et al. 2003; Feng et al. 2004; Zhang et al. 2010), especially in plant science (Rao and Xu 1998; Xu and Xu 2006), not sufficient enough attention has been paid to address the unique challenges of analyzing ordinal traits. Some researchers have recognized that it is difficult to conduct genetic analyses of ordinal traits because such traits cannot be directly characterized by a linear function of genetic and environmental effects (Rao and Xu 1998). To fill in this methodological gap, we have made a systematic effort to develop statistical methods for segregation analysis (Zhang et al. 2003), linkage analysis (Feng et al. 2004), and association analysis (Zhang et al. 2006) of ordinal traits (for family studies and case-control studies).

2.1.1 Analysis of Family Data

Long before the era of genomics, researchers collected data in families, also called pedigrees as illustrated in Figure 1. Although the ascertainment process for families varies, Figure 1 depicts a representative three-generation pedigree. The proband is the first person who enters into the study according to defined inclusion and exclusion criteria: such criteria are related to the disease of interest. Other members of the proband’s family are included and directly or indirectly assessed, depending on the circumstance. The key idea in analyzing family data is that if a gene is a major driving force behind a disease, a trace in the concordance of diseases in family members would reflect the transmission pattern of a gene under the Mendelian laws. This is the fundamental concept that Cannon and Rosanoff (1911) employed. This type of analysis is referred to as segregation analysis.

Figure 1.

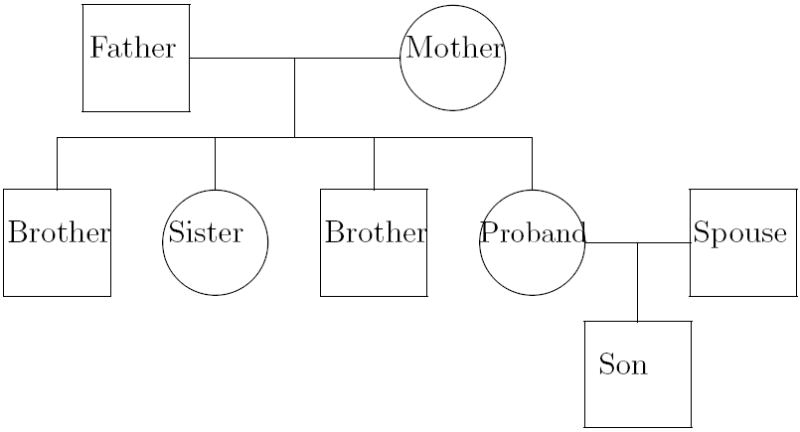
A three-generation pedigree.

The Elston-Stewart (1971) algorithm set up the quintessential framework to analyze data from general pedigrees through a technique called peeling. The main complication in analyzing pedigree data is the complex relationship among family members, making it difficult to express the likelihood function in a easily-computing form. The peeling algorithm makes use of the conditional independence embedded in the pedigree resulting from the Mendelian laws, and so peels off the complete likelihood function into smaller pieces before putting them back together.

Other methods have been relatively recently develop using the concept of latent random variables (Hopper, 1989; Babiker and Cuzick, 1994; Li and Thompson, 1997; Siegmund and McKnight 1998; Zhang and Merikangas, 2000), which are closely related to the classic ousiotype models of Cannings et al. (1978) in pedigree analysis. The basic idea is to use latent variables to represent the contribution of unobserved factors including a major gene, residual genetic factors, and common environmental factors. As discussed by Zhang and Merikangas (2000), the computation involving pedigrees is similar to the peeling algorithm. Advantages of using latent variable based models are that the interactions between underlying genetic effects and the observed covariates (e.g., demographic variables) can be considered. Additionally, more relevant to this article, we can accommodate ordinal traits in the latent-variable framework.

2.1.2 A Latent Variable Model

We follow the notation of Zhang and Merikangas (2000) and Zhang et al. (2003). Consider a trait, Y, that takes an ordinal value of 0, 1, … , K. Let x be a p-vector of covariates that is also available for each study subject. Three types of latent random variables $U_1^i$, $U_2^i$, and $U_3^i$ are introduced within family i to represent, respectively, (a) common, unmeasured environmental factors; (b) genetic susceptibility of the family founders (a founder refers to a subject whose parents are not a part of the observed pedigree, for example, father, mother, and spouse in Figure 1); and (c) the transmission of susceptibility genes from a parent to an offspring.

The concept of latent variables is straightforward, but the interesting and difficult part lies in the specification of their distributions. They need to be interpretable and convenient. The following are the assumptions that we found useful.

• $U_1^i$ follows Bernoulli distributions $P\{U_1^i=1\}=1-P\{U_1^i=0\}={\theta }_1$, where θ₁ is an unknown parameter.

• $U_2^i={(U_{2,1}^i,U_{2,2}^i,\cdots ,U_{2,2n_i-1}^i,U_{2,2n_i}^i)}^{\prime }$, where n_i is the size of pedigree i. Here, $P\{U_{2,2j-1}^i=1\}=1-P\{U_{2,2j}^i=0\}={\theta }_2$ when $U_{2,2j-1}^i$ and $U_{2,2j}^i$ are the $U_2^i$-variables of a founder.

• $U_3^i={(U_{3,1}^i,\cdots ,U_{3,s_i}^i)}^{\prime }$. According to the Mendelian laws, $P\{U_{3,j}^i=1\}=P\{U_{3,j}^i=0\}=\frac{1}{2},j=1,\dots ,s_i$, and s_i is the number of parent-offspring pairs in family i. $U_3^i$ facilitates the transmission of $U_2^i$-variables from the founders to the offspring. For example, if a parent of subject j have $U_2^i$-variables, $U_{2,2k-1}^i$ and $U_{2,2k}^i$, and the $U_3^i$-variable for this parent-offspring pair is $U_{3,l}^i$, then one of subject j’s $U_2^i$-variables is $U_{2,2j-1}^i=U_{2,2k-1}^i{U}_{3,l}^i+U_{2,2k}^i(1-U_{3,l}^i)$.

• All latent variables are independent.

$U_1^i$ is a simple “switch” indicating the presence or absence of a shared environment factor within family i. $U_2^i$ is assigned independently to each of founders who are the source for any gene to enter into a family, and thus mimics the transmission of a single major susceptibility locus with alleles A and a of frequencies θ₂ and 1 − θ₂, respectively.

Conditional on all of the latent variables, denoted by Uⁱ, within family i, the probability distribution for member j is assumed to be

$$P\{Y_j^i\le k|U^i\}=\frac{\exp ({\mathbf{x}}_j^i\beta +{\alpha }_k+{\mathbf{a}}_j^i\gamma )}{1+\exp ({\mathbf{x}}_j^i\beta +{\alpha }_k+{\mathbf{a}}_j^i\gamma )},k=0,\dots ,K-1,$$ (2.1)

where ${\mathbf{a}}_j^i={(U_1^i,U_{2,2j-1}^i+U_{2,2j}^i,U_{2,2j-1}^i{U}_{2,2j}^i)}^T$, and β and γ are p- and 3-vectors of parameters. The α_k is the trait level dependent intercept, k = 0, … , K − 1.

As Zhang et al. (2003) pointed out, the β parameters measure the strength of association between the trait and the covariates, conditional on the latent variables. The γ parameters indicate the familial and genetic contributions to the trait. The mode of inheritance can be inferred from γ. For example, γ₂ = 0 and γ₃ ≠ 0, suggests a recessive effect.

The likelihood function can be derived from (2.1). Due to the presence of latent variables, the EM algorithm (Dempster, Laird, and Rubin, 1977) is the most convenient choice for parameter estimation (Guo and Thompson 1992, Zhang and Merikangas 2000, Zhang et al. 2003). Although Zhang and Merikangas (2000) and Zhang et al. (2003) presented an effective solution (e.g., a modified likelihood), we should note that the lack of concavity in the likelihood function makes it a challenging task to find the maximum likelihood estimates of the model parameters. In addition, the θ’s and γ’s are not fully identifiable. The identifiability issue not only causes computational problems, but also presents theoretical challenges in statistical inference. Another important, yet under-studied, issue is the validation of the assumptions on the distributions of the latent variables.

But, how useful is the latent variable model (2.1)? First, it provides a regression framework to assess familial aggregation and genetic contribution, and possibly interactions between measured covariates and latent factors. Using data from a family study of substance use (Merikangas et al., 1998), Zhang and Merikangas (2000) was able to present extremely significant evidence of familial aggregation p-value < 10⁻⁹ for alcohol dependence. This study additionally demonstrated that transmission does not follow a major locus pattern. In retrospect, their findings predicted the difficulty of identifying major genes associated with alcoholism. In addition, Zhang and Merikangas (2000) presented simulation examples to delineate when the absence of latent variables in (2.1) affects the estimates of the effects by the measured covariates. For example, hypothetically, if the greater presence of females in a family has an impact on the well-being of the family, ignoring the familial latent variables is likely to result in a biased estimate of the sex difference.

Not only is important to include the latent factors, but also it is important to adjust for covariates. To further illustrate this point, Zhang et al. (2003) reported the following simulation. Ten thousand data sets were generated from model (2.1) with θ₁ = 0.3, β chosen from 0, 1, 5, or 10, γ₁ from 0, 1, or 2, α₀ = −1 and α₁ = 1. To focus on the difference of having or not having covariates, they set γ₂ = γ₃ = 0. Each data set consists of 200 families with 7 family members (similar to Figure 1). One covariate x was generated as follows. For family i, $U_1^i$ were generated according to whether a random number r_i1 from the uniform(0,1) was greater than 0.3 or not. For member j in family i, an independent random number r_ij2 from the uniform(0,1) was generated. Then, x_ij = 0.9r_ij2 + 0.2r_i1.

To evaluate the performance of the test statistic, the covariate was deliberately ignored in the test. When β = 0, the covariate played no role in the data generating process. The row corresponding to β = 0 in Table 1 displays the p-value (the column corresponding to γ₁ = 0) and the power for two values of γ₁ (1 or 2).

Table 1.

The probability estimates of rejecting γ₁ = 0 at the significance level of 0.05. The covariate is omitted from the testing despite the fact that its coefficient β may not be zero.

	γ1 = 0	γ1 = 1	γ1 = 2
β = 0	.0494	.9503	1.0
β = 1	.0534	.9843	1.0
β = 5	.1667	.9971	1.0
β = 10	.3828	.9890	1.0

When β ≠ 0, the covariate plays a role in the data generating model. The data in Table 1 reveal the consequence of ignoring the covariate, which is more severe when the the effect of the covariate is greater.

2.1.3 Linkage Analysis

While linkage analysis has a long history, it only became a common practice after the availability of several convenient computing programs (Ott 1974; Kruglyak et al. 1996; Almasy and Blangero 1998). For statisticians, some of the common terminologies in linkage analysis are puzzling, including the so-called LOD-score method and nonparametric method.

Morton (1955) first introduced the term “LOD-score.” LOD stands for “the logarithm (base 10) of odds.” The “odds” is a probability ratio, or likelihood ratio, of the probability under an alternative hypothesis to the probability under the null hypothesis. The LOD-score method is essentially a log-likelihood ratio test with two fundamental differences: (a) the use of the base 10 logarithm versus the natural logarithm; (b) the log-likelihood ratio statistic has a multiplier of 2 conforming to a χ² distribution under certain regularity conditions.

Specifically, the LOD-score is the log(base 10)-ratio of the likelihood when the recombination fraction is less than 1/2 (i.e., two loci are not on the same chromosome, or called unlinked), to the likelihood when the recombination fraction is 1/2 (no linkage). The recombination fraction is the frequency that a chromosomal crossover occurs between two loci (or genes) during meiosis; 1% of combination frequency is termed the distance of one centimorgan (cM) in a genetic linkage map. Because the LOD-score is in base 10, a score of 3 indicates 1000 to 1 odds in favor of the linkage, which is the conventional threshold for declaring the evidence for linkage. If we convert a LOD-score of 3 into the standard log-likelihood ratio statistic, it yields a p-value of 2 × 10⁻⁴ under ${\chi }_1^2$. By Bonnferoni correction, it corresponds a genomewide p-value of 0.05 for 250 markers. This number is in the range for the number of microsatellites used in typical linkage studies.

In order to compute the LOD-score, we first need a number of parameters that determine the likelihood for a given recombination fraction. Then use the maximum likelihood over the recombination fraction for the likelihood under the alternative hypothesis. The parameters that are required include the mode of inheritance, penetrance, and disease allele frequency. These parameters are generally unknown and difficult to estimate for complex diseases including mental illnesses. For example, using segregation analysis (see Section 2.1.1) Pauls and Leckman (1986) examined specific genetic hypotheses about the mode of transmission of Gilles de la Tourette’s syndrome, by performing segregation analyses in 30 nuclear families (two-generation pedigrees). They concluded that Tourette’s syndrome is inherited as an autosomal dominant trait (one copy of the abnormal allele is sufficient to cause the disease). The penetrace (the probability of having the disease for a given genotype) was reported at 0.71 in males and 1.0 in females with at least one abnormal allele. After several decades of research, no major genetic variant has been identified for Tourette’s syndrome, and most likely this syndrome involves multiple genes, interacting with environmental factors. This reality makes it difficult to infer the mode of inheritance, penetrance, and disease allele frequency, and conceptually, this may not make sense for complex diseases (non-Mendelian inheritance).

This difficulty is somewhat alleviated since the LOD-score method has been found to work reasonably well (e.g., Abreu et al. 1999) under various parameter settings. There have been some efforts to improve the robustness of the method (Gastwirth (1966, 1985; Whittemore 1996). See Zheng et al. (2009) for a thorough review. Existing methods do not extend to the case of ordinal traits. The effectiveness of the robust methods remains to be studied. Naturally, non-parametric linkage methods have been developed to avoid specification of the genetic model parameters. In statistics, “nonparametric” methods typically refers to distribution-free methods such as rank-based tests and methods based on the empirical distribution. In linkage analysis, however, “nonparametric” does not mean ”distribution free”, but instead refers to the replacement of true genetic model parameters with the parameters of inheritance of markers, hypothesized to be close to the disease locus. Thus, with nonparametric linkage methods, we still need to compute the likelihood. Two core algorithms are used to compute the likelihood: the Elston-Steward algorithm (1971) and the Lander-Green (1987) algorithm. As previously discussed, the Elston-Steward algorithm (1971) is a peeling algorithm that makes the computation in a large pedigree feasible by splitting it into small pieces. This algorithm was implemented in early versions of linkage analysis programs (e.g., LIPED and LINKAGE); computational time increased linearly in family size, but exponentially with the number of loci. More recent programs (e.g., GENEHUNTER) use the Lander-Green (1987) algorithm that has first order complexity in the number of loci, but unfortunately exponentially in the family size. Although Markov chain Monte-Carlo methods have been used to accommodate linkage analysis of large families and a large number of markers (Guo and Thompson 1992), in practice, one may have to break large pedigrees apart in order to run programs such as GENEHUNTER.

We should note that there had not been a linkage analysis program to handle ordinal traits until the release of LOT (Zhang et al. 2008). Typically, the methods for linkage analysis can be divided into two main steps; only the second step involves the trait (Kruglyak et al. 1996). The first step infers how genetic information travels in a family as represented by the so-called “inheritance vector.”

We will use the pedigree in Figure 1 to illustrate this concept. The two parents and spouse are the founders of the family, meaning that their parents are not in the current pedigree. The four siblings and the child are nonfounders. The inheritance pattern at marker locus t is completely described by an inheritance vector υ(t) = (υ₁, υ₂, υ₃, υ₄, … , υ₉, υ₁₀)′. In other words, we devote two elements for every nonfounder. The founders are not included because they are the sources of the genes in the family and the inheritance vector is conditional on their genes. The paired elements describe the outcomes of the paternal and maternal meioses transmitted to the nonfounders. Specifically, υ_2j−1 = 1 or 2 according to whether the grand paternal or grand maternal allele is transmitted in the paternal meiosis to the jth nonfounder. υ_2j carries the similar information for the corresponding maternal meiosis, namely, υ_2j = 3 or 4 according to whether the grand paternal or grand maternal allele was transmitted in the maternal meiosis to the jth nonfounder.

In practice, the genetic markers do not always allow us to determine the true inheritance vector. In this case, the inheritance distribution is the conditional probability distribution over the possible inheritance vectors that conform with the alleles observed at t, which we denote by p{υ(t) = w} for all inheritance vectors w ∈ V; here V is the set of all possible inheritance vectors. In the absence of any genotypic information, all inheritance vectors are equally likely according to Mendel’s first law; the probability distribution is uniform.

For segregation analysis, we employed latent variables to reflect the “imaginative” genetic effects in (2.1). In linkage analysis, we have genetic markers that flow through the inheritance vector. Thus, we can still use (2.1) for linkage analysis except that ${\mathbf{a}}_j^i$ should be $(U_1^i,U_{2,{\upsilon }_{2j-1}}^i+U_{2,{\upsilon }_{2j}}^i)$. On one hand, we have a reduced number of latent variables. On the other hand, many of the latent variables depend on each other through the inheritance vectors. The computation of the likelihood would be summed over all inheritance vectors w in V, in addition to the probability space of the remaining independent latent variables. Because of this connection and distinction, the challenges in the linkage analysis of ordinal trait are, to a great extent, similar to those in segregation analysis of ordinal traits. For example the asymptotic mixture of χ² distributions and the need to introduce the penalized likelihood (Liang and Rathouz 1999; Zhang et al. 2003).

2.1.4 Association test

As discussed above, linkage analysis focuses on testing the position of a marker, although it has been difficult to replicate findings in linkage studies of mental disorders. An association analysis, however, tests whether a genetic variant, including particular allele or genotype of a marker and a haplotype in several markers, is associated with a trait. Some study cohorts recruited for linkage studies have been re-genotyped for genomewide association analyses. For binary or quantitative traits, many methods have been developed and implemented. Two commonly used programs are PLINK (Purcell et al. 2007) and FBAT (Rabinowitz and Laird 2000). To analyze an ordinal trait, Zhang et al. (2006) introduced the following the proportional odds model,

$$\mathrm{logit}\{P(y_{\mathit{ij}}\le k|G_{\mathit{ij}})\}={\alpha }_k+\beta c_{\mathit{ij}},$$ (2.2)

where α₀, … , α_K−1 are non-descending level parameters, β is the genetic effect. The genetic factor c_ij can be chosen to reflect the underlying mode of inheritance such as the number of the risk allele. Under model (2.2), the null hypothesis is H₀ : β = 0. The score statistic is

$$S=\sum _{i,j}[R^{+}(y_{\mathit{ij}})-R^{-}(y_{\mathit{ij}})]A_{\mathit{ij}},$$ (2.3)

where R⁺(y_ij) and R⁻(y_ij) are the counts of offspring in the entire sample whose trait values are greater or less than y_ij, respectively, and A_ij is the number of copies of transmitted alleles at the marker locus. Thus, Zhang et al. (2006) proposed the following O-TDT test based on the score statistic

$$\frac{{[S-E(S|Y)]}^2}{\mathit{Var}(S|Y)},$$

which follows a ${\chi }_1^2$-distribution asymptotically. For a case-control study, R⁺(y_ij) and R⁻(y_ij) are the numbers of subjects whose trait values are greater or less than y_ij, respectively.

If we rewrite the statistic in (2.3) in a general form as Σ_ij w_ij A_ij, this yields the classic TDT when w_ij = 1 and the QTDT (Rabinowitz 1997) when w_ij = y_ij − ȳ, where ȳ is the average of all y_ij’s. In other words, all of these tests are a weighted function of the number of transmitted alleles at the marker locus, and the choice of the weights depends on the property of the trait. With this observation, after the proper weights are computed, the existing FBAT software can be used to test the association between any trait and alleles at a marker locus.

In the following, we describe a unified method to choose weights for any kind of trait. It is straightforward to categorize a quantitative trait into any reasonable number of categories (such as deciles) and induce an ordinal scaled trait. This would allow the use of the O-TDT for a quantitative trait. In their simulation studies, Zhang et al. (2006) demonstrated that this strategy has comparable power to the QTDT for quantitative traits. This is due to the fact that the number of categories is enough to capture most of the information in the data (e.g. following Cochran’s rule, Cochran 1977). The advantage is that the ordinal scaled test is not affected by the non-normal distribution of a quantitative trait, and so, the unified approach is robust.

One limitation of the test proposed by Zhang et al. (2006) is that it does not adjust for covariates. Environmental factors or covariates, such as gender and age, may confound the association of interest. In a subsequent work, Wang et al. (2006) generalized model (2.2) to include covariates as follows

$$\mathrm{logit}\{P(y_{\mathit{ij}}\le k|G_{\mathit{ij}}),z_{\mathit{ij}}\}={\alpha }_k+\beta c_{\mathit{ij}}+{\delta }^{\prime }{z}_{\mathit{ij}},$$ (2.4)

where z_ij denotes the covariates and δ is the vector of the corresponding coefficients. Consequently, the score statistic becomes

$$S=\sum _{i,j}[\widehat{\gamma }(y_{\mathit{ij}},z_{\mathit{ij}})-\widehat{\gamma }(y_{\mathit{ij}}-1,z_{\mathit{ij}})]A_{\mathit{ij}},$$ (2.5)

where

$$\widehat{\gamma }(k,z)=\frac{\exp ({\widehat{\alpha }}_k+{\widehat{\delta }}^{\prime }{z}_{\mathit{ij}})}{1+\exp ({\widehat{\alpha }}_k+{\widehat{\delta }}^{\prime }{z}_{\mathit{ij}})},$$

which is the estimated probability of having a trait value no greater than k. Thus, the weight function in (2.5) is the difference between the probability of having a trait value greater than y_ij and the probability of having a trait value less than y_ij. Not surprisingly, this is in essence the same as the weight function in (2.3) where we used counts instead of frequency (or probability).

It is important to note that association analysis does not directly equate to a causal relationship. In well-designed genetic association studies, an observed association is expected to result from either a causal functional variant of a gene, or the linkage disequilibrium between the marker and a susceptibility gene. In population based case-control studies, there are typically attempts to match cases and controls by important demographic and/or baseline information. It is not wise to over-match subjects. Alternatively, we can collect potentially important environmental variables and consider them in the association analysis. We can also use principal component analysis on the genotypes to explore whether there are “clusters” in the study cohorts that are not appropriately reflected in the environmental variables. In family based studies, the association tends to be conditional on parental genotypes and all phenotypes.

2.1.5 Unique Challenges in Analyzing Ordinal Traits

Understanding the genetic mechanisms for complex diseases is challenging regardless of whether we analyze binary, ordinal, or continuous traits. Any challenges that exist for analyzing binary and continuous traits remain for ordinal traits. What are the unique challenges in analyzing ordinal traits? The key difference is that there is not a simple distribution function for ordinal traits. For continuous traits, the assumption is that the traits can somehow be treated under normality, by transformation if needed. For binary traits, through a link function (e.g., logit) we only need to deal with a Bernoulli distribution. However, for ordinal traits, the two typical approaches are (a) to assume a reliability variable or a continuous latent variable or (b) to assume a proportional odds model as we presented above. The first challenge is in the estimation. The likelihood function is complicated, and based on the numerical results, it has multiple local maxima. In addition, due to identifiability (or near identifiability), the likelihood function may be relatively flat. Combinations of the EM and other algorithms can provide practical solutions, but finding a more efficient algorithm is an open problem.

The second challenge is in the inference. When latent variables or mixture distributions are used, some of the commonly assumed regularity conditions do not hold. One solution is to use a penalized likelihood function (Zhang et al. 2003) that prevents the parameters from being near the singularity points.

Finally, model diagnostics are difficult. For example, how do we know the latent variable-based model or the proportional odds model provides an adequate fit to the data? Although the models and methods presented above do not address this and other questions, they provide a foundation for further research and improvement.

2.2 Comorbidity

The methods described above only deal with a single trait. However, comorbidity is the rule rather than the exception in studies of mental and behavioral disorders. For example, a patient may suffer from both anxiety and depression (Li and Burmeister, 2009), and the same patient may also be addicted to nicotine, alcohol, or other substances (Merikangas et al., 1998; True et al., 1999). From a data analysis perspective, we need to consider how important it is to accommodate multiple diseases/traits. In a real data example, Chen et al. (2011) analyzed a data set from the Study of Addiction: Genetics and Environment (SAGE). By simply considering addiction to at least two of the six substances (addiction to nicotine, alcohol, marijuana, cocaine, opiates or other drugs), we were available to identify the PKNOX2 gene that reached genomewide significance level among European-origin females. Interestingly, the PKNOX2 gene has been previously identified as one of the cis-regulated genes for alcohol addiction in mice (Mulligan et al. 2006). To further delineate the benefit of considering multivariate traits, Zhu and Zhang (2009) conducted comprehensive simulation studies, considered the correlations of 0.2 and -0.2 among three quantitative traits, and demonstrated that testing correlated traits jointly is more powerful than testing a single trait at a time. Using generalized estimation equation, Lange et al. (2003) developed a family-based association test for multivariate quantitative traits (FBAT-GEE). Recently, Zhang et al. (2010) constructed proposed a nonparametric test based on the generalized Kendall’s tau to accommodate any combination of dichotomous, ordinal, and quantitative traits.

2.2.1 Kendall’s Tau

Kendall’s τ is a rank-based correlation between two variables. It contracts the probability of observing the two variables in the same order in two observations with the probability of observing the two variables in the opposite order. Specifically, for a sample of n observations (X₁, Y₁), ⋯, (X_n, Y_n), two observations (X_i, Y_i) and (X_j, Y_j) are called concordant if (X_i − X_j)(Y_i − Y_j) > 0 and discordant if (X_i − X_j)(Y_i − Y_j) < 0. Then Kendall’s τ is based on the difference between the numbers of concordant pairs and discordant pairs.

We introduce a kernel function,

$$\varphi ((X_i,Y_i),(X_j,Y_j))=\mathrm{sign}\{(X_i-X_j)(Y_i-Y_j)\}=\{\begin{array}{cc}1,& \mathrm{if}(X_i-X_j)(Y_i-Y_j)>0,\\ -1,& \mathrm{if}(X_i-X_j)(Y_i-Y_j)<0,\\ 0,& \mathrm{if}(X_i-X_j)(Y_i-Y_j)=0,\end{array}$$

and define a U-statistic

$$U={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}\varphi ((X_i,Y_i),(X_j,Y_j)).$$ (2.6)

Then, Kendall’s τ is

$$\tau =\frac{U}{\sqrt{{\mathrm{Var}}_0(U)}},$$ (2.7)

where Var₀(U) is the variance of U under the null hypothesis of no correlation between X and Y, and equal to n(n − 1)(2n + 5)/18 if X and Y are continuous variables (Hollander and Wolfe, 1999).

2.2.2 Generalized Kendall’s Tau

To test the association between genetic markers and comorbidity, Zhang et al. (2010) generalized Kendall’s tau as follows. For individuals i and j, let T_i and T_j be their vectors of traits respectively. Then, a trait kernel is defined as

$$F_{\mathit{ij}}={(f_1(T_i^{(1)}-T_j^{(1)}),\dots ,f_p(T_i^{(p)}-T_j^{(p)}))}^{\prime },$$

where function f_k(·) is the identity function for a quantitative or binary trait (Rabinowitz, 1997), or the sign function for an ordinal trait (Zhang et al., 2006).

Also, recall that, as in Section 2.1.4, c is the number of any chosen allele for marker genotype and let C_i refer to the C for the ith subject. Then, Zhang et al. (2010) defined a marker kernel as

$$D_{\mathit{ij}}=c_i-c_j.$$

Their U-statistic is defined as

$$U={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}{D}_{\mathit{ij}}{F}_{\mathit{ij}}.$$ (2.8)

The association test statistic, or generalized Kendall’s tau, is $U^{\prime }{\mathrm{Var}}_0^{-1}(U)U$, where Var₀(U) is the variance of U under the null hypothesis that there is no association between marker alleles and any linked locus that influences the trait T. The test statistic follows an asymptotic χ² distribution under the null hypothesis.

Obviously, the statistic in (2.8) does not incorporate covariate effects. This is relatively straightforward for a single trait as was done in (2.4). Here, the traits can be a hybrid of different traits. An alternative is to impose different weights for each pair of sample in the statistic (2.8) according to the information of their covariates. The weight, denoted by w(z_i, z_j) for the pair (i, j), reflects the relative importance attributed by the covariates when we derive the statistic. Zhu et al. (2010) examined the following weight function. Write z = (z^co, z^ca)′ with z^co = (z⁽¹⁾, … , z^(l₁))′ for the continuous covariates and z^ca = (z^(l₁+1), … , z^(l))′ for the categorical covariates. They defined the weight function w(z_i, z_j) as

$$w(z_i,z_j)=W(\parallel z_i^{\mathit{co}}-z_j^{\mathit{co}}\parallel )I(z_i^{\mathit{ca}}=z_j^{\mathit{ca}}),$$ (2.9)

where W(·) is a positive and decreasing function, e.g., W(u) = exp(−u²/2h²), and I(·) is the indicator function. Then a weighted test statistic is given by

$$S={\left(\begin{array}{c}n\\ 2\end{array}\right)}^{-1}\sum _{i<j}{D}_{\mathit{ij}}{F}_{\mathit{ij}}w(z_i,z_j).$$ (2.10)

Zhang et al. (2010) and Zhu et al. (2010) showed that under the null hypothesis, the test statistic S (weighted or not) has the following asymptotic distribution conditional on all phenotypes and parental genotypes,

$${\mathrm{Var}}_0^{-1/2}(S)[S-E_0(S)]\stackrel{d}{\to }N(0,I_p),$$

where

$$\begin{array}{lll}{E}_0(S)& =& \frac{2}{n-1}\sum _{i=1}^n{\overline{u}}_i{E}_0(C_i|M_i^{\mathit{pa}}),\\ {\mathrm{Var}}_0(S)& =& \frac{4}{{(n-1)}^2}\sum _{i=1}^n\sum _{j=1}^n{\overline{u}}_i{\overline{u}}_j^{\prime }{\mathrm{Cov}}_0(C_i,C_j|M_i^{\mathit{pa}},M_j^{\mathit{pa}}).\end{array}$$

Consequently, the following test statistic

$${\chi }_{\mathit{tau}}^2={[S-E_0(S)]}^{\prime }{\mathrm{Var}}_0^{-1}(S)[S-E_0(S)]$$

converges to ${\chi }_p^2$ in distribution under the null hypothesis provided that Var₀(S) is full rank. In a case-control study, we do not have the markers from parents and hence the conditional expectations are replaced with the unconditional ones. Thus, the key difference in the test statistics between family studies and popluation studies lies in the conditioning on the parental markers. The conditioning on the parental markers gives the family studies a major advantage in removing the effect of popluation admixture, but family studies tend to be more difficult and expensive to carry out.

Under the alternative hypothesis, the test statistic ${\chi }_{\mathit{tau}}^2$ can be written as a weighted sum of noncentral ${\chi }_1^2={\sum }_{i=1}^p{e}_i{\chi }_1^2({\varphi }_i)$, where e₁ ≥ ⋯ ≥ e_p are the non-negative eigenvalues of ${\sum }_1^{1/2}{\sum }_0^{-1}{\sum }_1^{1/2}$. ${\varphi }_i={\mu }_{R_i}^2$ and μ_Ri is the ith component of ${\mathit{\mu }}_R=Q{\sum }_1^{-1/2}\mathit{\mu }$, where Q is an orthonormal matrix such that $Q{\sum }_1^{1/2}{\sum }_0^{-1}{\sum }_1^{1/2}{Q}^{\prime }=\mathrm{diag}(e_1,\dots ,e_p)$. μ is the difference in the means of S under the alternative and null hypotheses. Using the approximation theory of Pearson (1959), Solomon and Stephens (1977), and Liu et al. (2009), we can find a certain degree of freedom l and noncentral parametric υ such that the distribution of ${\chi }_{\mathit{tau}}^2$ can be closely approximated by ${\chi }_l^2(\upsilon )$. Through simulation studies, Zhu et al. confirmed that this approximation is accurate enough for power calculation.

It is noteworthy that the weight function in (2.9) is restrictive with respect to categorical covariates, especially so for ordinal covariates. The use of genomic propensity score can give rise to an alternative weight function. Specifically, a di-allelic marker G (e.g., SNP), the genomic propensity score is the conditional probability p_g(z) = P(G = g∣Z = z). This probability can be fitted by a logistic regression model or proportional odds model depending on whether G is chosen as an allele type or genotype. In the latter choice, the model also depends on the mode of inheritance. In the current genomewide association studies, we usually only have genotypes and cannot distinguish the phases of individual alleles. Thus, we have to construct genomic propensity scores by considering various modes of inheritance. Once the genomic propensity score is estimated, it can be treated as a numerical covariate and then we can use (2.9) again.

2.2.3 Examples

Zhang et al. (2010) re-analyzed a data set from the Collaborative Study on the Genetics of Alcoholism (COGA). The data came from a multi-center (9 sites) consortium that recruited study participants by requiring every proband to meet two alcohol dependence diagnostic criteria based on DSM-IV-R (American Psychiatric Association 1994). The first-degree relatives of the probands were invited into the study. Zhang et al. (2010) included a total of 1614 individuals from 143 families. They considered three phenotypes: (1) alcohol DX-DSM3R+Feighner; (2) maximum number of drinks in a 24 hour period; and (3) the response to “spent so much time drinking, had little time for any thing else.” Using the first phenotype alone, the p-value of the association between a peak marker D7S679 on chromosome 7 and the trait was 0.0019. However, when the three traits are analyzed together, D7S679 remains to be the peak marker, and the p-value is reduced to 0.00055, demonstrating the possibility that the other two phenotypes enhanced the association signal. If the other two phenotypes are analyzed alone, the analysis did not lead to anything worthy of further attention.

In the analysis cited above, the association was assessed without considering covariates. In a follow-up analysis, Jiang et al. (2010) considered two important covariates: age at interview and sex. When these two covariates were controlled for, the p-value of the association between the peak marker D7S679 and the three phenotypes went down further to 0.000313.

3 Discussion

Studying comorbidity is a significant issue in mental and behavioral research, dating back to a century ago (Cannon and Rosanoff 1911). This is challenging due to a lack of statistical methods that accommodate the complexity of comorbidity. While dealing with comorbidity in genetic studies is the focus of this review, it is achieved through gradual development, and accumulation of methods. Various challenges are dealt with along the way.

Although I focused on the analysis of ordinal traits and applications in mental health, the presented methods are closely related to robust and ranked based methods for binary and quantitative traits. Furthermore, ordinal traits arise in studies of diseases besides mental illnesses such as cancer (specifically, different stages).

From the statistical perspective, the methods that are presented here have broad applications beyond genetic association studies. From college admissions, to job searches, to scientific investigations, we make inferences based on multi-dimensional data. It is important and imperative to consider and develop inferential tools for multivariate outcomes, particularly when the outcomes are discrete. There is extensive literature on the statistical analysis of multivariate normal variables as well as on nonparametric tests for a single variable of non-normal distribution. However, few options are available for the inference when we have multiple non-normally distributed variables and potential hybrids of continuous and discrete variables. To overcome this challenge, I presented several useful statistical techniques such as the rank-based U-statistics and the kernel-based weighted statistics to accommodate the mix of continuous and discrete outcomes and the presence of important covariates.