Three-dimensional structure of a sheet crumpled into a ball

Abstract

When a thin sheet is crushed into a small three-dimensional volume, it invariably forms a structure with a low volume fraction but high resistance to further compression. Being a far-from-equilibrium process, forced crumpling is not necessarily amenable to a statistical description in which the parameters of the initially flat sheet and the final confinement fully specify the resulting crumpled state. Instead, the internal geometry and mechanical properties of the crumpled ball may reflect the history of its preparation. Our X-ray microtomography experiments reveal that the internal three-dimensional geometry of a crumpled ball is in many respects isotropic and homogeneous. In these respects, crumpling recapitulates other classic nonequilibrium problems such as turbulence, where a system driven by long-wavelength, low-symmetry, forcing shows only rather subtle fingerprints of the forcing mechanism. However, we find local nematic ordering of the sheet into parallel stacks. The layering proceeds radially inward from the outer surface. The extent of this layering increases with the volume fraction, or degree of compression.

Although the global three-dimensional arrangement of a crumpled object is very complex, a remarkable feature of the geometry is that a large fraction of the surface area is relatively flat. The curvature imposed on an elastic sheet by external confinement or forces is concentrated largely in a network of ridges (1, 2), which meet at vertices known as developable cones (3, 4). For a perfectly elastic sheet, the work done in crumpling is stored in the elastic energy of these focused deformations, which is partitioned in finite fractions of bending and stretching energies (1). For most familiar examples of crumpled sheets such as plastic, paper, or metal foils, the strains at ridges exceed the yield strain and the ridges become irreversibly creased into folds. In the crumpled regime, these focused structures must interact simply because of geometric confinement. Understanding the mechanics of an interacting set of folds is a formidable challenge, and it is crucial to obtain experimental insights into their three-dimensional arrangement.

Some important lessons are learned by studying a lower-dimensional version of the problem, that is, the packing of a one-dimensional elastic curve confined in two dimensions. Experiments on the packing of a wire in a circular cage (5) and of sheets pulled through a circular hole (6) showed a new feature: As a curve is confined, it starts organizing into parallel arcs. Based on a recent lattice simulation of this problem (7), it has been argued that true long-range nematic order can be obtained in the thermodynamic limit. In this lower-dimensional problem, it is possible for the curve to pack without any stretching, and therefore, no focused structures are produced even in the limit of zero thickness. However, two-dimensional sheets confined in a spherical space are subject to greater geometric frustration—they cannot accommodate the constraints presented by confinement in all three directions solely by bending. They are forced to stretch and develop Gaussian curvature by bending in two directions (8). It is thus important to come to terms with the fully three-dimensional problem because there are qualitative differences between these situations.

Two recent sets of numerical simulations of purely elastic (9) and elastoplastic (10) self-avoiding sheets in three dimensions have studied the distribution of elastic energy in ridges and the scaling of compressive forces with confinement. The configurations shown in ref. 10 clearly indicate that layering also occurs in 3D. Although there is no direct spatial quantification of this phenomenon, they find that the energy becomes dominated by self-contacts as the confinement increases.

It is a challenge to experimentally probe the interior geometry of a 3D crumpled object. Ref. 11 studied, by laser profilometry, the statistics of folds and vertices in an unfolded crumpled sheet. However, unfolding the sheet leads to a loss of spatial information about the interactions of the folds and of the sheet’s final crumpled configuration. A recent paper (12) studied, by laser sheet illumination, the early stages of energy focusing in an elastic sheet. X-ray tomography is a tool that is well-suited for providing structural data in the highly crumpled regime. In recent X-ray tomography experiments (13, 14), a 2D analysis of the geometry was performed in terms of tangent vectors to the curves obtained in two-dimensional slices of the crumpled object. This analysis showed parallel orientation of tangent vectors; thus, both simulations and experiment indicate that layering of facets is a geometric element to be considered alongside focused structures such as ridges and vertices. However, a truly three-dimensional experimental characterization of the highly crumpled state remains to be done.

In this article, we present measurements by X-ray microtomography of the location of a crumpled sheet in a 3D volume, along with fully three-dimensional analyses of the curvature, orientation, and layering of the sheet. We concentrate on an analysis of the radial dependence of these metrics of the geometry, in order to identify any possible anisotropy and inhomogeneity imposed on the sheet by the method of crumpling.

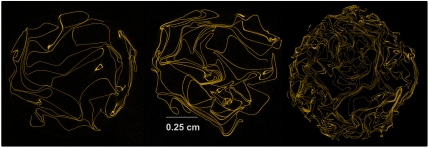
In our experiments, circular aluminum sheets with thickness t = 25.4 μm and initial radius R_i are hand-crumpled into approximately spherical balls with final radius R_o. We have studied balls with average volume fractions of ϕ ≈ 6, 8.5, and 22%. X-ray computerized tomography (CT) is used to image the interior of the crumpled sheet. A CT scanner (Skyscan 1172) images the radiation from a divergent X-ray illumination from a point source. Transmission images are taken after 0.3° rotations of the sample over a total of 180°. These images are reconstructed into a three-dimensional stack of grayscale images with a typical size of approximately 2,000 × 2,000 × 2,000 pixels. The voxels are uniformly distributed in the volume and are cubes with a linear dimension of 8.85 μm ≈ t/3, thus ensuring that the thickness of the sheet is fully resolved. As can be seen in the 2D slices through the crumpled balls shown in Fig. 1, we are now in a position to extract various quantitative measures of the disposition of the sheet in the crumpled volume.

Fig. 1.

Reconstructed slices through an equatorial plane of three crumpled spheres with average volume fractions of ϕ = 6% (R_i ≈ 3.5 cm, R_o ≈ 0.72 cm), 8.5% (R_i ≈ 5 cm, R_o ≈ 0.82 cm) and 22% (R_i ≈ 7 cm, R_o ≈ 0.75 cm), respectively. To remove background noise, all reconstructed images are thresholded before analysis.

Results and Analysis

Mass Distribution.

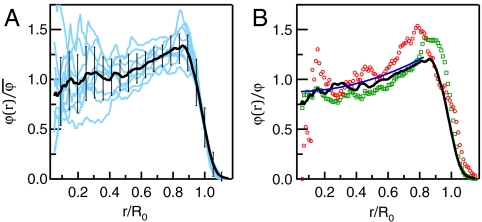
The simplest representation of the geometry of the sheet is the radial dependence of the volume fraction ϕ(r). We ensure, by calibrating with a sample of known geometry, that the mass of film determined from the reconstructed images is not affected by X-ray absorption through the volume of the sphere (see SI Text). As the individual blue curves in Fig. 2A show for nine different crumpled sheets with the same average volume fraction ϕ = 8.5%, there is considerable variation of ϕ(r) from sample to sample. The black curve, which is the average over these samples, more clearly shows a trend of volume fraction increasing from the interior to the exterior of the sphere. Thus, the most elementary analysis reveals a signature of the low-symmetry route to the final crumpled state, where the confining forces are radial and inward. The large variability within any of the individual samples reflects the very heterogenous distribution of void space within the ball. This heterogeneous distribution has often been quantified in terms of a fractal distribution of mass (14–17). However, given that there is an overall radial density gradient, a fractal dimension computed from an average over the volume of the ball is not a useful measure of heterogeneity. The data shown in Fig. 2B compare the radial gradient of volume fraction for three different degrees of confinement. The functional dependence on radial distance does not change significantly with volume fraction over this range of ϕ. This must of course change at extremely low and high (14) confinement where a more homogeneous distribution might be expected.

Fig. 2.

Mass distribution. (A) Radial dependence of volume fraction, ϕ(r), versus r/R_o, the radial distance (r) from the center of mass normalized by the radius of the ball (R_o). The center of the sphere is defined by its center of mass. The data shown are for spheres with a radially averaged volume fraction of ϕ = 8.5%. The volume fractions are normalized by 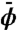, where the overbar represents a further average over samples. The blue curves are for nine separate samples, to give an indication of the sample-to-sample variability. The black curve is the average of these samples. Error bars indicate the standard deviation. The average mass distribution increases approximately 30% from the center of the sphere to the exterior. (B) Normalized volume fraction, ϕ(r)/ϕ, versus the radial distance from the center of mass for spheres with ϕ = 6, 8.5, and 22%. The red open circles and green open squares correspond to spheres with ϕ = 6 and 22%, respectively. The black curve is the average of nine spheres with ϕ = 8.5%. The solid line is a best-fit to the equation 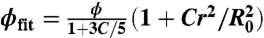, with an adjustable parameter C.

Orientation.

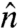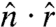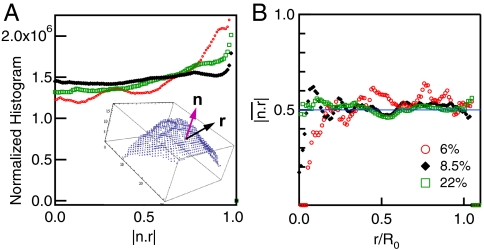
We next move from the location of the sheet to the orientation of sheet within the volume. From the grayscale 3D image, we find the surface normal at all points along the surface. The spatial orientation of the surface normal is quantified by the direction cosine , where 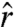is the unit vector from the center of the sphere to the surface point. The distribution of this direction cosine, shown in Fig. 3A, is nearly uniform, thus indicating a near-isotropic distribution of sheet normals. This is a surprising result, given that the crumpling process might be expected to break symmetry between radial and azimuthal directions, and perhaps favor orientation of the sheets parallel to the confining surface, in onion-like fashion. This expectation of alignment by the outer surface is not borne out even as one approaches the surface. In Fig. 3B, we plot the average 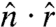as a function of normalized radial position r/R_o. The orientation, 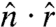, does not deviate from the value expected for random orientation, except perhaps within a small region close to R = R_o. Except for this boundary layer, the orientation of surface normals is both isotropic and homogeneous within the volume, despite the sheet’s route to the crumpled state.

Fig. 3.

Orientation. We quantify local orientation of the sheet by the dot product 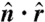of the surface normal and the radial unit vector from the center of the ball, as shown in the 3D patch of sheet in A. We display orientation data from spheres with ϕ = 6, 8.5, and 22% (red open circles, black diamonds, and green open squares, respectively). The 8.5% data are an average of 2 spheres. A (left),Histogram of the sheet orientation, 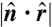. All three volume fractions have a nearly isotropic orientation with only a slight tendency for alignment of the normals with the radial vector. (B) Average orientation versus distance from the center of mass for ϕ = 6, 8.5, and 22%. The solid line displays the average of an isotropic distribution of orientations.

Curvature.

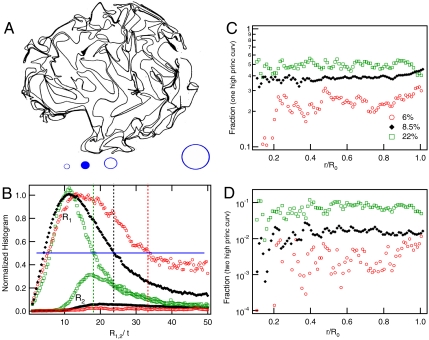
The next higher order in the description of the local geometry of the sheet is the curvature of the sheet. In principle, the curvature can be determined from a complete knowledge of the vector field of surface normals 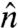(18). However, numerically finding the gradient of this field introduces undesired inaccuracy. We chose to make an independent measurement of the curvature by identifying connected patches of the sheet and fitting ellipsoids to these patches. From the fit parameters, we were able to obtain the two principal radii of curvature, R₁ and R₂( > R₁), at every point on the patch. The unusual geometry of the crumpled state presents a technical challenge here. Although there are many regions of low curvature, the curvature can change sharply at the stress-condensed regions. Thus, the surface has to be fit with rather small patches. It was not possible to infer large radii of curvature with great numerical accuracy by fitting to small patches in space. We therefore focus our analysis on highly curved regions with radii of curvature < 50t, which can be reliably fit. In Fig. 4B, we show, for three volume fractions, the high-curvature part of the histogram of the principal radii of curvature. There is a peak in the histogram at R₁ ≈ 10t, independent of volume fraction. The radii associated with the peak in the histogram, R₁ = 10t, and with the largest fitted radii, R_1,2 = 50t, are indicated by open circles in Fig. 4A. The value of curvature radius at the peak is much higher than that required to introduce plastic folds in the aluminum. The yield stress for Al is 145 MPa (19), and a radius of curvature for yielding of 250t may be inferred from the corresponding yield strain. It thus appears that there is a limiting value of curvature beyond which the crumpling process creates new features, rather than compressing existing folds to sharper dihedral angles. As we discuss below, though, the peak at small radius of curvature does not imply a high level of energy condensation (also see SI Text for further details).

Fig. 4.

Curvature. Displayed are measurements of the high-curvature regions of spheres with ϕ = 6, 8.5, and 22% (red open circles, black diamonds, and green open squares, respectively). The 8.5% data are an average of two spheres. (A). A reconstructed image from a crumpled ball with ϕ = 8.5% is shown to give a sense of scale for the radii of curvature. (B). Normalized histogram of the larger and smaller principal curvature radii R₁ and R₂ in units of t. Radii of curvature between 3t and 50t are shown. There is a peak in the histogram at R₁/t ≈ 10 for all three ϕ. Locations with radius of curvature below a cutoff radius, r_c, are designated as high-curvature regions; r_c is chosen to be the radius at which the normalized histogram falls to half its peak value, and its value is indicated for each volume fraction by the dashed vertical line. From left to right, the three open circles show the radius at the peak in R₁ (10t), r_c for 8.5% (24t), and the upper limit of curvature measurements (50t). (C) The fraction of surface points with at least one high-curvature direction (folds and vertices) versus distance from center of mass. (D) The fraction of surface points with two high-curvature directions (vertices only) versus distance from center of mass. The high-curvature regions are homogeneously distributed.

From the curvatures we have determined, we identify surface points with one and with both radii of curvature below a cutoff radius, and associate these with folds and vertices, respectively. The cutoff radius, r_c, for each ϕ is chosen to be the radius at which the histogram falls to half the value of the peak in the curvature distribution, as shown by the dotted lines in Fig. 4B. The number of high-curvature points identified by applying an arbitrary threshold obviously depends on the value of r_c. With the definition we adopt, we find that the fraction of surface points associated with folds is 37% and with vertices is 4% for the ϕ = 8.5% sample (Fig. 4 C and D). The large fraction of surface points with small radii of curvature indicates that in this regime of confinement, stress condensation is incomplete and that it is not correct to think of the sheet as largely flat. In Fig. 4C, we display the fraction of points with R₁ < r_c (folds and vertices) as a function of radial position. Fig. 4D shows the same quantity for points with R₁ < R₂ < r_c (vertices). It is evident from these data that the high-curvature parts of the sheets are homogeneously distributed through the sphere, and show no evidence of being preferentially generated at the confining walls. A plausible explanation for the radial increase in volume fraction might have been that the exterior part of the sphere allows more gentle curvature, and therefore that it is energetically preferred to have more of the sheet reside in the exterior. In light of the observation of a homogeneous distribution of high-curvature features, and of the isotropic orientation of the sheet normals, this explanation is not tenable. This homogeneous curvature distribution contrasts with crumpling in two dimensions (6), where curvature is different in the bulk and at the boundary, where the object assumes the curvature of the confining wall. Possibly this is due to the fact that the spherical boundary condition imposes a Gaussian curvature on a flat sheet, which, unlike in the 2D analogue, is not possible to accommodate without stretching deformations.

Nematic Ordering.

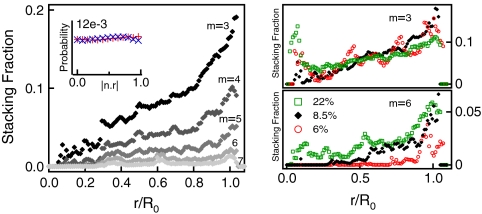
Thus far, we have concentrated entirely on local descriptors of the geometry. We now turn to the stacking of facets that is evident in Fig. 1. As a quantitative measure of this local nematic ordering, we study the correlation of the 3D surface normals along the sheet. From each surface point we search along the normal direction for other surfaces in parallel alignment. We label surfaces stacked together in this way within a chosen search radius, and we count the number of sheets layered together in each stack, m. In Fig. 5A, we show, as a function of radial position, r/R_o, the fraction of surface points that are participating in stacks composed of m = 3 to 7. These data for ϕ = 8.5% reveal a tendency to stack that increases approximately linearly in the radial direction. In Fig. 5B, we show the probability of occurrence of 3-stacks and 6-stacks for different volume fractions. At all three volume fractions we study, the probability of 3-stacks is similar and increases approximately linearly in the radial direction. However, 6-stacks are just beginning to form in the outer layers of the sphere at lower volume fractions and develop more strongly at higher volume fractions. The implication is that stacking is initiated from the outside and progresses inward as crumpling proceeds. Thicker stacks could then be produced by accretion or folding of thinner stacks and are not due to a strong increase in the overall fraction of layered sheet.

Fig. 5.

Stacking. Stacks are identified by starting at all surface points on the sheet, searching in the direction of the normal, 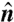, and identifying the number, m, of other surfaces with antiparallel normals within a radius of 16t. For example, m = 1 represents an isolated part of the sheet, and m = 4 represents four closely stacked surfaces. The solid circle in Fig. 4 gives a visual sense of the search radius. (A) Fraction of surface points participating in stacking versus distance from the center of mass for different values of m in one sphere with ϕ = 8.5%. The symbols represent stacks containing m = 3, 4, 5, 6, and 7 facets (darkest to lightest colored diamonds, respectively). The stacking fraction increases with r/R_o for all values of m. (Inset) Histogram of surface orientation, 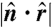, for points on stacked surfaces (i.e., m≥2) only (blue crosses). We also show for comparison the histogram for all surface points (red plus symbols). This shows that the stacked facets are also oriented isotropically. In B and C, we show stacking fraction versus r/R_o for ϕ = 6, 8.5, and 22% (red open circles, black diamonds, and green open squares, respectively) for (B) m = 3 and (C) m = 6. As ϕ increases, stacks become thicker.

As mentioned earlier, the crumpled state spontaneously develops structural rigidity at very low volume fractions without externally imposed design. This rigidity has been attributed to the formation of ridges with high buckling strengths (9, 10). Although there is no direct mechanical verification of either mechanism, the layering shown in Fig. 5 may also be a contributing factor to mechanical rigidity. That is, the structure may be stabilized against external compression by forming multilayered walls rather than pillars. The force threshold to buckle a ridge into smaller ridges (20), or for Euler buckling of a planar region, scales with the bending modulus of the sheet, which grows as t³, the cube of its thickness. If the sheets in an m stack do not slide relative to each other either because of frictional contact or by the ridges that might delimit the edges of the layered region, then the rigidity of such a stack scales as (mt)³. Stacking can thus greatly enhance mechanical rigidity. The relationship between stacking and stress condensation remains to be clarified. It has been suggested in studies of phyllotaxy in cabbages that layered arrangements are nucleated between stiff leaf stems (21). A similar mechanism may be operative here, with the folds playing the role of the stem, and forcing sheets in near-contact to make stacks. Even though the stacks are formed under radial compression, they are also isotropically arranged and potentially strengthen the structure against forces in any direction. This is shown in the Inset to Fig. 5A, where we separately display the distribution of orientation with and without the stacked layers. [A different result was obtained when a 2D determination of orientation was performed (13).] Any arbitrary force applied to the crumpled ball will result in both compression and shear internally. The response of the stack to such a generalized stress state may involve both the self-avoidance of the sheet as well as friction between the sheets.

The detailed geometrical characterization of the crumpled state raises questions that we are currently attempting to address by simultaneous studies of structure and dynamics. However, the principal inference to be drawn from the structural information presented here is that several aspects of the geometry are to a good approximation homogeneous and isotropic, and therefore perhaps amenable to statistical treatment. Despite the low-symmetry path to the crumpled state, it is rather remarkable that from the vantage point of a location in the interior of the ball, no local measurement of geometry points the way to the exterior of the ball.

Materials and Methods

To find the radial distribution of mass, the reconstructed image stack is first thresholded, and then despeckled to remove detector noise. ϕ(r) is determined by counting occupied voxels in spherical shells of thickness Δr = 3.3t. We ensure by measurements on a calibration sample that absorption effects do not affect the measured ϕ(r) (see SI Text). We choose to define the radial distance r from the center of mass of the ball. The exterior hull of the ball is not perfectly spherical, nor is the center of mass necessarily at the geometric center of this hull. However, at these average volume fractions, the differences between these measures is not significant for the results we discuss. The final radius R_o is determined from the steep falloff in ϕ(r) at the exterior of the ball and is chosen to be where ϕ(r) ≈ 0.045ϕ. R_o is consistent with measurement of the caliper radius of the crumpled ball, averaged over orientation.

The orientation of the sheet is determined by applying a 3D canny edge-detector to find the surface normal 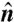at all points. The edges are smoothed by a Gaussian filter. We use a simple threshold to fill in low-intensity surface points.

To measure curvature, the sheet is first thinned by identifying the number of neighbors in a 3 × 3 volume surrounding that point. This procedure reduces both surfaces of the sheet to a one-voxel-thick edge. All detected surface points are only counted once. The entire sheet surface is decomposed into connected patches that are fitted to algebraic functions (see SI Text) from which the local curvatures are determined. Our analysis is optimized toward accurate determinations of the high-curvature features of the sheet.

We identify the number of facets stacked between two parallel surfaces by searching in the direction of the normal at each surface point, 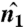, at a radius of up to approximately 16t, (see the solid circle below Fig. 4A for a visual indication of the search radius). We identify all other surface points along this search direction with normal 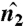that are antiparallel to 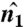as defined by the criterion 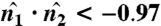. We then return to the raw image to count all occupied voxels between these points with antiparallel normals. m stacks are identified by dividing this count by the sheet thickness measured in pixels. When the sheets are very tightly stacked, the interior surfaces in contact are not resolved in the images. However, our identification of the number of sheets, m, in the stack is not affected by this complication, because we count the entire mass between the two outermost sheets in the stack.