Detection of clustered microcalcifications using spatial point process modeling

Abstract

In this work we propose a spatial point process (SPP) approach to improve the detection accuracy of clustered microcalcifications (MCs) in mammogram images. The conventional approach to MC detection has been to first detect the individual MCs in an image independently, which are subsequently grouped into clusters. Our proposed approach aims to exploit the spatial distribution among the different MCs in a mammogram image (i.e., MCs tend to appear in small clusters) directly during the detection process. We model the MCs by a marked point process (MPP) in which spatially neighboring MCs interact with each other. The MCs are then simultaneously detected through maximum a posteriori (MAP) estimation of the model parameters associated with the MPP process. The proposed approach was evaluated with a dataset of 141 clinical mammograms from 66 cases, and the results show that it could yield improved detection performance compared to a recently proposed SVM detector. In particular, the proposed approach achieved a sensitivity of about 90% with the FP rate at around 0.5 clusters per image, compared to about 83% for the SVM; the performance of the proposed approach was also demonstrated to be more stable over different composition of the test images.

I. Introduction

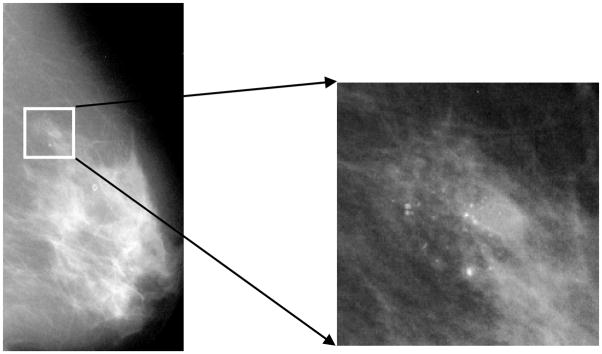
Breast cancer is a common form of cancer diagnosed in women. One of the important early signs of breast cancer in mammograms is the appearance of micro-calcification (MC) clusters, which appear in 30%–50% of mammographically diagnosed cases [1]. MCs are calcium deposits of very small dimension and appear as a group of granular bright spots in a mammogram (shown in Fig. 1). Individual MCs are sometimes difficult to detect because of the surrounding breast tissue, their variation in shape and small dimension. Because of its importance in breast cancer diagnosis, accurate detection of MC clusters is an important problem. In recent years, there has been a great deal of research in development of computerized methods for automatic and accurate detection of MC clusters, which could potentially assist radiologists in diagnosis of breast cancer. A recent review of various MC detection methods reported in the literature can be found, for example, in [2]–[4].

Figure 1.

A mammogram image (left) and a magnified view of a MC cluster (right).

Most of the techniques for MC detection so far typically consist of the following two steps: first, a detection algorithm (a.k.a. pattern classifier) is employed to identify the presence of MCs in a mammogram image; next, the detected individual MCs are subsequently grouped into clusters by a clustering algorithm [5]. For example, in our previous work [6] we developed a supervised-learning approach using support vector machine (SVM) for detection of clustered MCs, which was demonstrated to outperform several well-known algorithms, e.g., the image difference technique (IDT) in [7], and the difference of Gaussian (DoG) method in [8].

In this work we develop a statistical modeling approach to further improve the accuracy of MC detection. Apart from previous reported techniques, in this approach we employ a spatial point process (SPP) to explicitly characterize the spatial clustering property of MCs in a lesion. Indeed, MCs typically appear in tightly distributed clusters when they occur in small lesions in mammograms, which are of significant interests for early cancer detection. Consequently, as explained above, a clustering step is typically employed in an MC detection algorithm in order to reduce spurious detections (false positives). This clustering property was also demonstrated to be beneficial for segmentation of MCs in a pixel-wise Markov random field (MRF) framework [9].

In our proposed approach, the individual MCs are modeled by a spatially interactive process, which are detected simultaneously via stochastic optimization. Specifically, we describe the presence of MCs in a mammogram image by a marked point process (MPP) [10], [11], which is parameterized by the number of present MCs, their spatial locations and amplitudes. We then define a posteriori probability model based on both image data and spatial interaction among individual MCs. The detection is achieved by maximizing this a posteriori probability, for which the technique of reversible jump Markov chain Monte Carlo (RJMCMC) [12], [13] is used in order to accommodate the fact that the number of MCs in a mammogram is not known a priori. Being a statistical sampling procedure, however, RJMCMC can be potentially expensive for numerical implementation. To address this challenge, which is great owing to the large number of pixels in a typical mammogram image, we develop strategies to greatly reduce the search for the possible constellation of the MC locations of the point process. Our results demonstrate that this approach could lead to improved detection performance when compared to the best-performing SVM detector in [6].

We note that in the literature there have been several MPP applications reported for object detection tasks, where MPP is used to characterize the underlying spatial relationship among the objects to be detected. For example, it was used for segmentation and detection of road networks [14] and buildings [15]; in medical imaging applications, it was applied for detection of brain lesions in [16] and leukocytes in [17].

The rest of the paper is organized as follows: A description of the image data model and the spatial point process model for MC cluster detection is given in Section II. Then, the RJMCMC detection algorithm is given in Section III. Issues related to our evaluation study (including mammogram data set, and performance evaluation methods) are described in Section IV. Experiment results and discussions are furnished in Section V. Conclusions and future work are given in Section VI.

II. Spatial point process model for clustered microcalcifications

In this section we begin with a description model of the image data, which consists of a superposition of MC objects in a noisy background. We then characterize the spatial distribution of MCs using a spatial point process (SPP), in which the MCs are modeled as spatially interactive objects. Afterward, we give the formulation of detection of clustered MCs as an estimation problem.

A. Data model

Given a mammogram image defined over domain Ω, we model the image function f(x) as a superposition of a number of microcalcifications (signals) in a noisy background. That is, at pixel location x ∈ Ω, we have

$$f(\mathbf{x})=\sum _{i=1}^N{w}_{i}K(\mathbf{x};{\mathbf{x}}_i)+n(\mathbf{x})$$ (1)

where K(x; x_i) is the signal corresponding to the microcalcification located at x_i, which has strength (or amplitude) w_i, n(x) denotes the background noise, and N is the number of microcalcifications.

To model the microcalcification signal K(x; x_i), we use a truncated Gaussian kernel centered at x_i, i.e.,

$$K(\mathbf{x};{\mathbf{x}}_i)=\{\begin{array}{cc}{e}^{-\frac{{\left|\right|\mathbf{x}-{\mathbf{x}}_i\left|\right|}^2}{2{\sigma }^2}},& \text{if}\left|\right|\mathbf{x}-{\mathbf{x}}_i\left|\right|\le r_0\\ 0,& \text{otherwise}\end{array}$$ (2)

where r₀ is the spatial support of the signal, and σ² is a parameter associated with its effective size. Such a choice is based on the fact that MCs are limited in size and typically appear round in shape.

Given data f(x), our objective is to determine the presence of the individual MCs. Our approach is to estimate the underlying parameters associated with the data model in Eq. (1), which include the number of MC objects N, their locations x_i and amplitude values w_i, i = 1, …, N. For convenience, these parameters are collectively written as:

$$\mathrm{\Theta }=\{N,{\mathbf{x}}_i,w_i,i=1,\dots ,N\}.$$ (3)

B. Spatial point process (SPP) modeling

Spatial point process is a statistical tool for modeling the spatial distribution pattern of a set of points (e.g., object locations). A marked point process (MPP) is a spatial point process in which additional labels (e.g. geometric properties of the objects) are associated with the points. That is, an MPP consists of a set of points together with their property labels {(x_i, m_i), i = 1, …, n}, where x_i denote the point locations and m_i denote their labels (i.e., marks). A detailed description of point process modeling can be found in [11].

We use a point process to model the spatial distribution of MC objects in a mammogram image. For convenience, let each MC object be described by s_i = (x_i, w_i), where x_i denotes its spatial location, and w_i denotes its amplitude. Then a set of MC objects in an image can be described by a spatial point process as s = {s_i, i = 1, …, N}. Our goal is to exploit the spatial clustering properties among the different MC objects so as to improve their detection. For this purpose, we model this process by using a Gibbs point process, for which we define a prior distribution of the following form:

$$p(\mathrm{\Theta })\propto {\beta }^N\prod _{s_i\in \mathbf{s}}{g}_1(s_i)g_2(s_i,\mathbf{s})$$ (4)

in which the role of each term involved is explained as follows. In Eq. (4), the occurrence of MC objects is regulated by a Poisson process, and the density parameter β is used to model the average number of MCs in an image; the term g₁(s_i) is used to characterize the property of individual MC objects (specifically, their amplitude); and the term g₂ (s_i,s) is used to model the spatial interactions between an MC object and its neighboring MCs within a cluster.

Specifically, the term g₁(s_i) in Eq. (4) is defined as a prior distribution on the amplitude w_i of an MC object s_i. We model g₁(s_i) by a Gamma distribution, which is defined as

$$g_1(w_i;k,\theta )=\frac{1}{{\theta }^k\mathrm{\Gamma }(k)}{w}_i^{k-1}{e}^{-\frac{w_i}{\theta }}$$ (5)

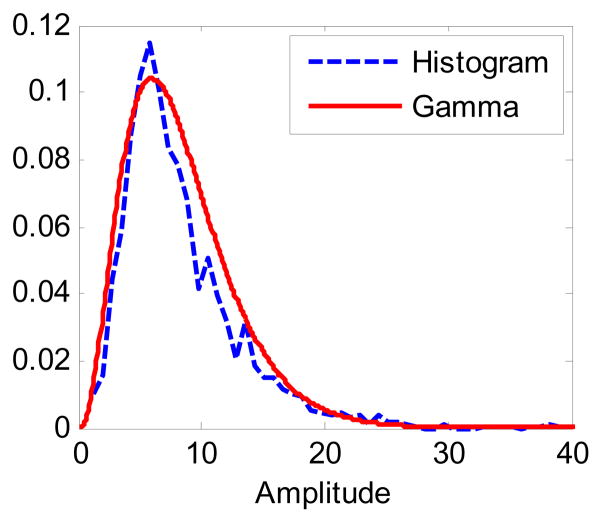
where k and θ are the distribution parameters. To demonstrate this distribution, in Fig. 2 we show a normalized histogram of the amplitude values obtained from a set of training mammograms used in our experiments (Section V.A); a Gamma distribution fitted to this histogram using ML estimation is also shown for comparison (k = 3.59, θ = 2.30). A good agreement between the two can be observed.

Figure 2.

Distribution of MC amplitude values.

Next, the interaction term g₂ (s_i, s) in Eq. (4) is defined as

$$g_2(s_i,\mathbf{s})=g_I(s_i)\prod _{s_i\sim s_j,i<j}h(s_i,s_j)$$ (6)

which consists of two terms: the term g_I (s_i) is used to model whether or not an MC interacts with other objects (1^st order interaction), and the term h (s_i, s_j) is to model its interaction with each of its neighboring MCs (2^nd order interaction). Here, two objects s_i, s_j are considered neighbors (denoted by s_i ~ s_j) if they are within a distance d_n of each other.

The first order interaction function is defined as:

$$g_I(s_i)=\{\begin{array}{ll}\alpha ,\hfill & d_i<d_n\hfill \\ 1,\hfill & \text{otherwise}\hfill \end{array}$$ (7)

where d_i is the distance from object s_i to its nearest neighbor in the point process, d_n is the interaction distance. The parameter 0 < α < 1 is used to assess a penalty when an MC is isolated from any neighboring MC objects. The choice of such an interaction function is motivated by the fact that MC objects of clinical significance typically occur in small clusters. Indeed, in Fig. 3 we show a distribution of the distance between an MC and its nearest neighboring MCs in a cluster, which was obtained for all the MCs in a training set of mammograms (Section V.A). As can be seen, an overwhelmingly majority of the MCs (97.3%) were within 60 pixels from other MCs.

Figure 3.

Distribution of distance between an MC and its nearest neighbor.

The second order interaction function h (s_i, s_j) is defined as

$$h(s_i,s_j)=\{\begin{array}{ll}\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }{d_0},\hfill & \text{if}\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert <d_0\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$$ (8)

In Eq. (8), d₀ is a parameter used to penalize detection of two objects that are too close to each other (e.g., even overlapping). The term h (s_i, s_j) will exert a punitive interaction when the distance between two objects is less than d₀. To illustrate this distribution, in Fig. 4 we show a histogram plot of pair-wise distances among clustered MCs obtained from a set of training mammograms used in our experiments (Section V.A). By observation, the punitive parameter in Eq. (8) was set to d₀ = 10, which yields a good fit between the histogram and the distribution in Eq. (8).

Figure 4.

Distribution of pair-wise distances between MCs in a cluster.

C. Maximum a posteriori (MAP) estimate

We seek a MAP solution for Θ. That is,

$$\widehat{\mathrm{\Theta }}=arg\underset{\mathrm{\Theta }}{max}\left\{L(\mathrm{\Theta })\triangleq p(\mathbf{f}\mid \mathrm{\Theta })p(\mathrm{\Theta })\right\}$$ (9)

where p(f|Θ) denotes the likelihood function of the image data f, a vector representation of the image values at all pixel locations.

We assume a Gaussian noise model with mean μ_b and variance ${\sigma }_b^2$ for the background noise in Eq. (1), i.e., $n(\mathbf{x})\sim N\left({\mu }_b,{\sigma }_b^2\right)$. Then the density function of an image sample can be written as

$$p(f(\mathbf{x})\mid \mathrm{\Theta })={\left(2\pi {\sigma }_b^2\right)}^{-\frac{1}{2}}exp\left\{-\frac{1}{2{\sigma }_b^2}{\left[f(\mathbf{x})-\sum _{i=1}^N{w}_{i}K(\mathbf{x},{\mathbf{x}}_i)-{\mu }_b\right]}^2\right\}.$$ (10)

Note that in the above a stationary noise model is assumed for the image background. This might seem to be overly simplistic, because, as exemplified in Fig. 1, mammogram images can be rather inhomogeneous in intensity owing to many factors such as tissue structures and varying breast densities. To address this issue, in our experiments we first applied a pre-processing procedure (Section IV.B) to equalize the signal-dependent noise, the purpose being to suppress the background structures (and thereby enhancing MC signals) in a mammogram image. In Fig. 5 we show the example mammogram image in Fig. 1 after pre-processing, of which the intensity histogram is shown in Fig. 6. As can be seen, the resulting image is more uniform and amenable to the description model in Eq. (1).

Figure 5.

Mammogram image (Fig. 1) after noise equalization.

Figure 6.

Histogram of the tissue region of the image in Fig. 5.

Substituting both the prior model in Eq. (4) and the data model in Eq. (10) into Eq. (9), and upon algebraic manipulations, we obtain

$$\widehat{\mathrm{\Theta }}=arg\underset{\mathrm{\Theta }}{max}lnL(\mathrm{\Theta })=\left[-\sum _{\mathbf{x}\in \mathrm{\Omega }}\frac{1}{2{\sigma }_b^2}{\left[f(\mathbf{x})-\sum _{i=1}^N{w}_{i}K(\mathbf{x};{\mathbf{x}}_i)-{\mu }_b\right]}^2+\sum _{s_i\in \mathbf{s}}[ln{g}_1(s_i)+ln{g}_2(s_i,\mathbf{s})]+Nln\beta \right].$$ (11)

From Eq. (11) we observe that, for β < 1, the term N lnβ plays the role of assessing a penalty on the number of detected objects. This can avoid the over-fitting of the data by artificially introducing too many candidate objects. In our experiments, we use β to control the level of false-positive (FP) detections. A smaller β would yield a smaller number of detections, which include both true and false detections, and vice versa. By varying β, one can obtain operating points with different FP rates.

To solve the optimization problem in Eq. (11), we use the RJMCMC method, a statistical sampling technique which allows jump between states of different dimensions. This property is useful for this problem because the number of MC objects in an image is not known beforehand. On the other hand, being a statistical sampling procedure, RJMCMC is also known to be computationally expensive. To make the matter even more challenging, a mammogram image (such as those used in our experiments) can have up to tens of millions of pixels. Thus, it becomes computationally prohibitive (and also unnecessary) if one were to sample over all these many pixel locations for the possible constellation of the MC locations in the point process. In the next section we present implementation strategies to make RJMCMC tractable for the optimization of Eq. (11). A good description of RJMCMC methods for optimization can be found in [13].

III. RJMCMC detection algorithm and implementation

In this section we first introduce the RJMCMC sampling procedure for simulating the spatial distribution of MCs in a mammogram image, and describe the sampling steps involved in the procedure. We then present our strategies to facilitate its numerical implementation. The idea is to reduce greatly the sampling space of the parameters, thereby speeding up the numerical solution.

A. RJMCMC sampling for SPP optimization

As described earlier in Section II.A, the spatial distribution of MCs in a mammogram image is modeled by a marked point process, which is characterized by the parameter set Θ in Eq.(3). In our application, the technique of RJMCMC statistical sampling is adopted to simulate this process. At each sampling step, the RJMCMC algorithm updates the parameter set Θ by randomly selecting one among a set of several so-called proposal moves. In our implementation, the following five proposal moves are used: 1) birth of a new candidate object such that it is not necessarily in interaction with any existing ones; 2) death of a candidate object which is not necessarily in interaction with any other existing ones; 3) birth of a new candidate object such that it is in interaction with some existing ones; 4) death of a candidate object which is in interaction with some existing ones; or 5) update the amplitude of an existing candidate object which is selected randomly. At each step, these five moves are selected with equal probability. The initial state for Θ is chosen to be empty, i.e., no candidate objects are included at the start.

During the sampling steps, each of these selected proposal moves is accepted with only a certain acceptance probability. Specifically, let Θ denote the current state, and Θ′ denote the corresponding state after a proposal move. Let also s denote the candidate object to be added or deleted that is associated with the proposal move. Then the acceptance probability of the proposal move is given by r = min{1,R}, where the acceptance ratio R is given in its general form as

$$R=\frac{L({\mathrm{\Theta }}^{\prime })}{L(\mathrm{\Theta })}\times \frac{p({\mathrm{\Theta }}^{\prime }\to \mathrm{\Theta })}{p(\mathrm{\Theta }\to {\mathrm{\Theta }}^{\prime })}\times \left|\frac{\partial {\mathrm{\Theta }}^{\prime }}{\partial (\mathrm{\Theta },s)}\right|$$ (12)

where p(Θ → Θ′), p(Θ′ → Θ) are the probabilities of the forward or its reverse moves, respectively, and $\left|\frac{\partial {\mathrm{\Theta }}^{\prime }}{\partial (\mathrm{\Theta },s)}\right|$ is the Jacobian associated with the move.

Without digression, the details of the acceptance ratio and the probability terms involved in Eq. (12) corresponding to each of the five proposal moves are given in Appendix A.

For optimization of the objective function L(Θ), the RJMCMC sampling is applied in conjunction with a simulated annealing procedure, in which the acceptance ratio in Eq. (12) is modified accordingly as:

$$R={\left(\frac{L({\mathrm{\Theta }}^{\prime })}{L(\mathrm{\Theta })}\right)}^{\frac{1}{T}}\times \frac{p({\mathrm{\Theta }}^{\prime }\to \mathrm{\Theta })}{p(\mathrm{\Theta }\to {\mathrm{\Theta }}^{\prime })}\times \left|\frac{\partial {\mathrm{\Theta }}^{\prime }}{\partial (\mathrm{\Theta },s)}\right|$$ (13)

where T is the temperature parameter. As T → 0, the algorithm converges to the maximum of the objective function. In our experiments, we used an exponential-decaying cooling scheme, in which T was decreased exponentially with the number of iterations (Section V.C).

B. Reduction of search space for the point process

Recall that in the marked point process there are two parameters associated with each MC object s_i = (x_i, w_i), namely its spatial location x_i and amplitude w_i. Based on discussions above, we next describe strategies for speeding up the RJMCMC procedure. First, the search for MC locations will be restricted to only a limited number of most probable candidate locations instead of over the entire image domain. Second, for an MC candidate the search for the amplitude parameter w_i will be restricted to a small neighborhood around its MAP estimate.

Search space reduction for candidate MC locations

Since MC objects are localized in size and are brighter than the background, we can first apply a simple linear detector to select only those most probable locations for further consideration. Specifically, these probable candidate locations are determined as follows:

1. Convolve the image with the MC kernel K(x; 0), then detect the local maxima of the resulting output. This is essentially a template matching detector, where the kernel is used as the template.

2. Among the local maxima detected, select only those with value larger than a threshold T′. These local maxima will serve as the potential candidate locations of the MC objects. In our experiments, the threshold T′ was selected such that only the top 600 candidate locations were kept for further consideration for each image. This number was chosen to be rather conservative in that it is much greater than the actual number of MCs typically seen in a mammogram image.

To further reduce the number of candidate locations, in our experiments we also first applied a pre-scouting step, of which the purpose was to exclude certain regions (such as non-tissue background) in a mammogram image from further consideration. This was based on the fact that, while a whole mammogram image can be very large in size, the spatial extent of clustered MCs is typically limited (less than 1 cm² in area). This pre-scouting step was applied as follows: 1) the local maxima identified in the detector output in the first step above were compared against a threshold which was set to be four times the standard deviation of the detector output of the whole image; once again, the purpose here was to identify potential MC locations; 2) the identified locations were then treated as potential MC objects, and grouped into clusters (the clustering criteria are given in Section IV.C); 3) afterward, a square region (5cm × 5cm) was extracted at the center of gravity of each cluster; 4) for each image up to four such regions (with the most detected locations) were selected for further consideration. Note that, to be conservative, the region size was chosen to be much larger than that of an MC cluster above.

Search space reduction for amplitude parameters

In the general case, the amplitude parameter of a candidate MC object is initially set randomly, and subsequently updated through sampling from its distribution during the RJMCMC procedure. However, in this particular case we can obtain a closed-form estimate for it by using MAP estimation. Specifically, for a new candidate object, we set its initial amplitude parameter by directly maximizing the objective function ln L(Θ) in Eq. (11). Consider candidate object s_i0. Taking the derivative of ln L(Θ) with respect to the amplitude parameter w_i0 and setting it to zero, we obtain

$$\frac{\partial lnL(\mathrm{\Theta })}{\partial w_{i_0}}=\frac{1}{{\sigma }_b^2}\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[K(\text{x};{\text{x}}_{i_0})\left(f(\text{x})-w_{i_0}K(\text{x};{\text{x}}_{i_0})-{\mu }_b\right)\right]+\frac{(k-1)}{w_{i_0}}-\frac{1}{\theta }=0.$$ (14)

Noting that w_i0 > 0, we obtain from above

$$w_{i_0}=\frac{-b+\sqrt{b^2+4a(k-1){\sigma }_b^2}}{2a}$$ (15)

where $a={\displaystyle \sum _{\mathbf{x}\in \mathrm{\Omega }}}{K}^2(\text{x};{\text{x}}_{i_0}),b=\frac{{\sigma }_b^2}{\theta }-{\displaystyle \sum _{\mathbf{x}\in \mathrm{\Omega }}}\left[K(\text{x};{\text{x}}_{i_0})(f(\text{x})-{\mu }_b)\right]$.

Note that in Eq. (14) it is assumed that the new object s_i0 is not in overlap with any other candidate objects. The resulting initial estimate in Eq. (15) is dependent on the current estimate of the background statistics, i.e., μ_b, ${\sigma }_b^2$, and as a consequence is likely not the final optimal solution. To accommodate this, we allow a small perturbation around this estimate for RJMCMC update, i.e., [w_i0 − Δ, w_i0 + Δ]. In our experiments, Δ = 1 was used.

In our experiments, the background statistics, i.e., μ_b, ${\sigma }_b^2$, were estimated from the image data. To suppress their effect, the MC objects detected at the current state were excluded from the image, and the remaining image pixels were used to estimate μ_b and ${\sigma }_b^2$. Since the impact caused by the individual MCs is rather small, the estimate of μ_b and ${\sigma }_b^2$ was updated only for every 1,000 RJMCMC steps.

IV. Performance evaluation

A. Mammogram dataset

In this study, we used a set of 141 mammograms from 66 cases (32 cancer/34 benign) collected by the Department of Radiology at the University of Chicago. Each mammogram had one or more clusters of MCs which were histologically proven. These mammograms were digitized with a spatial resolution of 0.05 mm/pixel and 12-bit grayscale with a dimension of 3,000×5,000 pixels. The MCs in each mammogram were manually identified by a group of experienced radiologists. There were a total of 2,790 MCs in these images. These MCs were used as the ground truth in our evaluation studies.

In our experiments, the dataset was randomly partitioned into two subsets, one for training and the other for testing, each containing 33 cases. It is noted that most of the 66 cases had more than one views (mediolateral oblique view and cranio-caudal view). To avoid any potential bias, the different views of the same case were always assigned together to either the training or the testing subset, but never both.

The subset of training mammograms was used to determine all the necessary parameters associated with the detection algorithm, including the parameters associated with the model distributions introduced in Section II. The subset of testing mammogram was used exclusively for testing the detection performance; at no point was it involved in fine-tuning of the parameters of the algorithm.

B. Pre-processing of mammogram images

To suppress the effect of inhomogeneous background and intensity-dependent noise in mammograms, the images were first pre-processed with a noise equalization procedure as in [18] prior to MC detection. In addition, the non-tissue background of the mammogram excluded by using a thresholding operation on the image gradient (the background area has much lower intensity and smaller gradient amplitude than the tissue area). As an example, Fig. 3 shows the same mammogram image in Fig. 1 after pre-processing.

C. Performance evaluation using FROC and bootstrap sampling

In our experiments, the detection performance was summarized using FROC curves [19]. An FROC curve plots the correct detection rate of MC clusters (i.e., true positive fraction) versus the average number of false-positives (FP) per image over the continuum of the operating range. As explained earlier in Section II.C, in the proposed SPP method the parameter β was varied to control the FP rate; a smaller β value would lead to lower FP but also lower true detections, and vice versa.

For the FROC curves, the detected MC objects were grouped to form MC clusters using a criterion based on recommendations in [4], which was reported to yield more realistic performance than several other alternatives. Specifically, a group of objects is considered to be a cluster if the objects are connected with nearest-neighbor distances (Dnn) less than 0.5 cm and there are at least three objects within a square area of 1 cm². A detected cluster is labeled as a true positive (TP) cluster if: 1) it includes at least two true detected MCs; and 2) its center of gravity is within 1 cm of that of a known true MC cluster. Likewise, a detected cluster is labeled as a false positive (FP) cluster if: 1) it contains no true MCs, or 2) the distance between its center of gravity and that of any known cluster is larger than 1 cm.

In this study we focus primarily on the operating range when the FP rate is no more than 2 FP clusters per image, which is of main interest in clinical practice. To remove the effect of case distributions in the dataset, we conducted an FROC study using a bootstrapping methodology [20]. A total of 2,000 bootstrap sample sets were used, based on which the area under the FROC curve (A_z) was estimated.

The bootstrapping procedure used was as follows: the subset of testing mammograms consisted of 71 images. For each bootstrap step, the same number of images was randomly sampled with replacement from the testing set; the FROC curve was obtained based on the detection performance on this bootstrap sample. By repeating this sampling procedure many times, we obtained a distribution of the bootstrap A_z values. When comparing two detection algorithms, we applied this procedure to obtain a distribution of the bootstrap difference in their performance A_z, based on which statistical inference was drawn.

V. Results and discussions

A. Determination of model parameters from training set

The proposed detection algorithm involves several parameters that need to be determined during the training phase, which include the kernel function K(·; ·) in the data model in Eq. (1) and the various parameters associated with the marked point process model. These parameters were determined as follows in our experiments.

For the MC kernel function K(·; ·), as explained earlier in Sect. II.A., a truncated Gaussian kernel as in Eq. (2) was used. To determine the kernel parameters, i.e., support radius r₀ and effect size σ, we used K(·; ·) as a template, and applied template-matching to detect the MCs in the training mammogram images. The detection results were then summarized using FROC curves, based on which the best setting for r₀ and σ was selected. In our experiments, the following different settings were considered: r₀ =2, 3, 4, and 5, and σ =1, 1.5, 2. In the end, the following setting was selected: r₀ = 3, σ = 1. We note that the detection performance based on the training set was found rather insensitive to these parameter values. For example, σ = 1 would yield very similar performance to σ = 1.5.

For the amplitude prior g₁(s_i) in Eq. (5), the amplitude value w_i was determined for each of the MCs in the training set by using maximum likelihood (ML) estimate, which amounts to least-square fitting given the Gaussian noise assumption. This resulting set of amplitude values from the training MCs was then used to determine the parameters k and θ using ML estimation for the Gamma prior in Eq. (5). The obtained distribution (k = 3.59, θ = 2.30) was shown earlier in Fig. 2.

For the first-order interaction term g_I (s_i) in Eq. (7), we computed the distance from an MC to its nearest neighboring MC in a cluster. Figure 3 shows the histogram of this resulting distance values for all the MCs in the training set. As can be seen, an overwhelmingly majority of the distance values (96.8%) are less than 60 pixels. Based on this observation, the interaction distance d_n in Eq. (8) was set as d_n = 60. The penalty parameter α in Eq. (7) was set to be the same level as β.

In our experiment, the algorithm was tested over a wide range of operating points. When the operating point was at a high FP rate, the presence of potential FP objects render the penalty in g_I (s_i) in Eq. (7) ineffective once they meet the interaction distance d_n. As a safe guard against this, we imposed a requirement that the nearest neighbor should also be large enough in magnitude (w_n > 7.3, the median of the distribution of the magnitude values in Fig. 2).

For the second-order interaction term h (s_i, s_j), we computed the pair-wise distance among MCs within clusters from the training set. A histogram plot of these distance values was shown earlier in Fig. 4. By observation, the punitive parameter in Eq. (8) was set to d₀ = 10.

B. Detection performance

The trained SPP model was evaluated using all the mammograms in the test subset. The detection performance is summarized using FROC results in Fig. 7, where the average FROC curve obtained from the bootstrapping procedure was shown. For comparison, the FROC result was also shown for the SVM detector previously developed in [6], which was demonstrated to have the best performance compared to several representative methods for MC detection reported in the literature.

Figure 7.

Average FROC curves for SVM and SPP obtained from 2,000 bootstrap samples. The most improvement by SPP occurs when the FP is in the range of [0, 1], averaging a net increase of about 8.71% in TP fraction. The smaller variation in the SPP results indicates that the performance of SPP is more stable over the different composition of the test images.

A statistical comparison between the SPP method and SVM detector yields a mean difference of 0.105 in terms of the area under the FROC curve A_z over the FP range of [0, 2] (p-value < 0.002). This corresponds to a net increase of about 5.25% in TP fraction (sensitivity) on average over the FP range of [0, 2]; the most improvement occurs when the FP is in the range of [0, 1], averaging a net increase of about 8.71% in TP fraction. In particular, the SPP achieved a sensitivity of about 90% with the FP rate at around 0.5 clusters per image, compared to about 83% for the SVM.

Furthermore, it is also observed from the FROC results in Fig. 7 that the variation for SPP obtained from bootstrapping is smaller than that of SVM. This indicates that the performance of SPP is also more stable over the different composition of the test images.

It should be noted that the FROC curves are influenced by the criteria used in defining MC clusters. Therefore, caution should be exercised when comparing FROC results reported in the literature when they were derived using various criteria and datasets. As demonstrated in previous study [6], the FROC curves would get higher when the clustering criteria are relaxed; however, the relative ordering of the curves for the different methods were preserved. This is important for comparing different methods.

C. RJMCMC convergence

For the simulated annealing procedure the following exponential-decaying cooling scheme was used: $T_k=T_0{\left(\frac{T_M}{T_0}\right)}^{\frac{k}{M}}$, where k denotes the RJMCMC step index, M is the maximum number of steps allowed, and T_k denotes the temperature at step k. In our experiments, M = 10⁵, T₀ = 50, and T_M = 10⁻⁵ were used. The RJMCMC procedure was terminated when no state change was observed for 1,000 consecutive steps.

As an example, we show in Fig. 8 the evolution of the cooling temperature, the number of candidate objects, and the objective function over 50,000 steps of the RJMCMC procedure in a typical run. In this example, a stable state had been reached in about 30,000 steps.

Figure 8.

The evolution of (a) temperature T, (b) number of detected objects N, and (c) the value of the objective function ln L(Θ) during the RJMCMC steps.

The execution time of SPP depends on the searching space and the simulated annealing procedure. In our experiment, the average runtime was about 51.6 seconds per mammogram image when operated at an FP rate of 0.5 clusters per image. Our implementation was in Matlab on a 2 GHz PC with 2 GB memory.

D. Future work

In this study the size parameter σ² was kept uniform in the kernel function in Eq. (2) for modeling the MCs in a mammogram image. Conceivably, it might be advantageous to allow this parameter to vary so as to accommodate the size variations among different MCs, which could lead to even further improvement in detection. Furthermore, it might also be advantageous to use non-symmetrical kernel functions. This, of course, would increase the search space of the RJMCMC procedure, but is worthy of further investigation.

VI. Conclusion

In this work we developed a spatial point process (SPP) modeling approach for detection of clustered microcalcifications (MCs) in mammogram images. In this approach a marked point process (MPP) was employed to characterize the spatial distribution of clustered MCs in a mammogram image, wherein prior distributions were defined to describe both the amplitude of the MC signals and their spatial interactive patterns. The parameters associated with the prior distributions were determined from a set of training mammogram images. For a given image the detection of MC objects was through determination of the underlying point process using MAP estimation, for which a statistical sampling technique using an RJMCMC procedure was used. We presented several strategies for reducing the computational complexity of RJMCMC in implementation. For performance evaluation, we used a bootstrapping methodology to obtain the detection FROC curves. Compared to a recently reported SVM detector, the proposed SPP approach was demonstrated to achieve a net increase of about 5.25% in sensitivity on average over the FP range between 0 to 2 clusters per image (p-value<0.002). A potential drawback of the proposed approach is the extra computational load associated with the RJMCMC procedure. However, given its benefits on detection performance, it is desirable to investigate additional strategies to further reduce the computation burden of the RJMCMC sampling procedure while maintaining its detection performance.

Appendix A: Acceptance ratios for the different proposal moves in RJMCMC

Below we provide the probability and acceptance ratio terms associated with the five proposal moves in the RJMCMC procedure.

A. Birth or death of a free candidate object

In the proposal birth move, a candidate location x is first selected with equal probability among all those candidate locations in the search space that are not already in the current state Θ; next, an amplitude value w is drawn from a uniform distribution on the interval [w_min, w_max] and assigned to the selected candidate location. With the optimal initial amplitudes, w_min = w_i0 − 1, w_max = w_i0 + 1 and w_max − w_min = 2. This creates a new candidate object s = (x, w). The new state upon the proposal move is Θ′ = Θ ∪ {s}.

The proposal probability term for this forward move is:

$$p(\mathrm{\Theta }\to {\mathrm{\Theta }}^{\prime })=\frac{1}{n_1(w_{max}-w_{min})}$$ (A.1)

where n₁ is the number of candidate locations in the search space that are not already in the current state Θ. On the other hand, the probability for the inverse move is:

$$p({\mathrm{\Theta }}^{\prime }\to \mathrm{\Theta })=\frac{1}{n_2}$$ (A.2)

where n₂ is the number of candidate objects in the state Θ′.

Moreover, the Jacobian $\left|\frac{\partial {\mathrm{\Theta }}^{\prime }}{\partial (\mathrm{\Theta },s)}\right|$ is unity for this move. Hence, the acceptance ratio for the birth move is given by:

$$R_1=\frac{L({\mathrm{\Theta }}^{\prime })}{L(\mathrm{\Theta })}\times \frac{n_1(w_{max}-w_{min})}{n_2}$$ (A.3)

For the death move, a candidate object is randomly selected and removed with equal probability from the current state Θ. The acceptance ratio is the reciprocal of that of the birth move. That is,

$$R_2=\frac{L(\mathrm{\Theta })}{L({\mathrm{\Theta }}^{\prime })}\times \frac{n_2}{n_1(w_{max}-w_{min})}$$ (A.4)

B. Birth or death of an interacting candidate object

Similar to above, here in the proposal birth move a candidate location x is first selected with equal probability among all those candidate locations in the search space that are within the interacting distance d_n from some of the existing candidate objects in the current state Θ; next, an initial amplitude value w is drawn from a uniform distribution on the interval [w_min, w_max] and assigned to the selected candidate location. This creates a new candidate object s = (x, w). The new state upon the proposal move is Θ′ = Θ ∪ {s}.

Similarly, the acceptance ratio for the death move is given by:

$$R_3=\frac{L({\mathrm{\Theta }}^{\prime })}{L(\mathrm{\Theta })}\times \frac{n_3(w_{max}-w_{min})}{n_4}$$ (A.5)

where n₃ is the number of candidate objects in the search space that are within the interacting distance d_n from some of the existing candidate objects in state Θ, and n₄ is the number of candidate objects which are in interaction with some of other candidate objects in state Θ′.

For the death move, the acceptance ratio is the reciprocal of that of the birth move. That is,

$$R_4=\frac{L(\mathrm{\Theta })}{L({\mathrm{\Theta }}^{\prime })}\times \frac{n_4}{n_3(w_{max}-w_{min})}$$ (A.6)

where n₃ is the number of candidate objects in the search space that are within the interacting distance d_n from some of the existing candidate objects in state Θ′, and n₄ is the number of candidate objects which are in interaction with some of other candidate objects in state Θ.

C. Update the parameter of one existing candidate object

In this proposal move, an existing candidate object is randomly chosen among all those in the current state Θ. Then its amplitude value w is replaced with a random number drawn from a uniform distribution on the interval [w_min, w_max]. The acceptance ratio for this move is:

$$R_5=\frac{L({\mathrm{\Theta }}^{\prime })}{L(\mathrm{\Theta })}.$$ (A.7)