Between T = 180 and 240 K, radiation damage progresses on minute timescales when the X-rays are off, suggesting that a fraction of damage at higher temperatures may be outrun using currently available sources and detectors.
Keywords: radiation damage, temperature dependence, glass transition, dark progression, dose rate
Abstract
Can radiation damage to protein crystals be ‘outrun’ by collecting a structural data set before damage is manifested? Recent experiments using ultra-intense pulses from a free-electron laser show that the answer is yes. Here, evidence is presented that significant reductions in global damage at temperatures above 200 K may be possible using conventional X-ray sources and current or soon-to-be available detectors. Specifically, ‘dark progression’ (an increase in damage with time after the X-rays have been turned off) was observed at temperatures between 180 and 240 K and on timescales from 200 to 1200 s. This allowed estimation of the temperature-dependent timescale for damage. The rate of dark progression is consistent with an Arrhenius law with an activation energy of 14 kJ mol−1. This is comparable to the activation energy for the solvent-coupled diffusive damage processes responsible for the rapid increase in radiation sensitivity as crystals are warmed above the glass transition near 200 K. Analysis suggests that at T = 300 K data-collection times of the order of 1 s (and longer at lower temperatures) may allow significant reductions in global radiation damage, facilitating structure solution on crystals with liquid solvent. No dark progression was observed below T = 180 K, indicating that no important damage process is slowed through this timescale window in this temperature range.
1. Introduction
Damage created by the illuminating X-rays is a major factor limiting the amount and quality of structural information that can be obtained from protein crystals. X-rays rapidly damage biomolecular crystals held at room temperature, so that data must often be collected and merged from multiple crystals. Damage is reduced by collecting data at reduced temperatures (Low et al., 1966 ▶; Petsko, 1975 ▶). Cryocrystallographic methods (Hope, 1988 ▶, 1990 ▶; Rodgers, 1994 ▶; Garman & Schneider, 1997 ▶), in which crystals are flash-cooled in liquid nitrogen and data collected at T ≃ 100 K, typically reduce global radiation damage for a given dose by a large factor. We have recently reported this factor to be 35 for thaumatin crystals (Warkentin & Thorne, 2010 ▶) and 48 for lysozyme crystals (Kmetko et al., 2006 ▶, 2011 ▶), although a large range of values (∼10–130) can be inferred from other studies using lysozyme (Blake & Phillips, 1962 ▶; Teng & Moffat, 2002 ▶; Southworth-Davies et al., 2007 ▶; Barker et al., 2009 ▶). Thermal B factors are also reduced, improving the resolution of the data.
Unfortunately, cryocrystallographic procedures have associated costs. To prevent crystalline ice formation, cryoprotectants are added to the growth solution, complicating the search for optimum crystallization conditions, and/or are introduced via post-growth crystal soaks, possibly altering both protein structure and enzymatic function. Flash-cooling invariably degrades crystal mosaicity and may significantly degrade overall order (Juers & Matthews, 2001a ▶,b ▶, 2004 ▶; Kriminski et al., 2002 ▶; Kim et al., 2005 ▶). Cooling-induced mosaic disorder is especially problematic for important targets, including large macromolecular complexes and viruses, because it often leads to excessive diffraction peak overlap, necessitating data collection from unfrozen crystals (Rossmann, 1999 ▶; Fry et al., 1999 ▶; Gilbert et al., 2003 ▶; Duke & Johnson, 2010 ▶).
Perhaps most serious of all, cryocrystallographic procedures severely restrict the kinds of structural and functional information that can be obtained. T = 100 K structures can deviate significantly from the biologically active form (Deacon et al., 1997 ▶; Sandalova et al., 1999 ▶; Scheidig et al., 1999 ▶). Vitrified solvent inhibits large collective motions and prevents the measurement of the protein’s dynamic response to many biologically relevant perturbations. Temperature-dependent structural measurements can provide insight into protein energy landscapes (Frauenfelder et al., 1979 ▶; Chong et al., 2001 ▶). Temperature can be used to control reaction rates in crystallo and allow the trapping of structural intermediates (Bourgeois & Royant, 2005 ▶; Colletier et al., 2008 ▶). For these reasons, the demand for temperature-dependent structural methods, especially at temperatures where the solvent remains liquid, is likely to grow (Hammes-Schiffer & Benkovic, 2006 ▶; Benkovic & Hammes-Schiffer, 2006 ▶; Henzler-Wildman & Kern, 2007 ▶; Ringe & Petsko, 2008 ▶; Weik & Colletier, 2010 ▶; Nashine et al., 2010 ▶). The constraints imposed by radiation damage will then become even more important.
To fully enable temperature-dependent studies, an understanding of the processes involved in radiation damage at temperatures between 100 and 300 K is needed. As a first step, we previously reported the temperature dependence of the global radiation sensitivity of thaumatin crystals (Warkentin & Thorne, 2010 ▶). Here, we discuss the temperature-dependent timescales for important damage processes. We examine what happens when the timescale for X-ray dose delivery and diffraction measurement becomes comparable to or shorter than one or more of these timescales. We discuss the feasibility of collecting full structural data sets on these timescales and estimate the fraction of radiation damage that may be ‘outrun’ in this way.
2. Damage timescales, temperature dependence and dark progression
2.1. Timescales for radiation-damage processes
Radiation damage to protein crystals involves a wide range of processes spanning a wide range of timescales. X-ray–electron and electron–electron interactions occur on femtosecond timescales (Dertinger & Jung, 1970 ▶; Coggle, 1983 ▶) and result in the production of photoelectrons with keV energies and ionizing electrons with energies of 10–100 eV. Reactions involving ionizing electrons produce changes to local electronic structure and create free radicals. These reactions are not diffusion-limited, and should occur on sub-picosecond and at most weakly temperature-dependent timescales. Excitations created by these initial reactions thermally diffuse and cause damage to the protein. At room temperature, this diffusion is very fast, creating bond-scale damage on nanosecond timescales (Anbar & Hart, 1967 ▶; Buxton et al., 1988 ▶) and initiating additional reactions that may proceed, including via cascades, for extended periods. Diffusion slows with decreasing temperature and its timescale diverges near the solvent glass transition (∼190 K for protein-associated water and ∼150 K for bulk-like water in solvent channels; Weik, Kryger et al., 2001 ▶; Weik et al., 2004 ▶, 2005 ▶); at low temperatures damage by processes involving thermal diffusion becomes irrelevant on experimental timescales. Following local (bond-scale) chemical damage protein molecules may undergo a cascade of structural relaxations on many length scales. This begins with conformational changes of side chains and larger elements of molecular structure. For proteins in solution at room temperature, conformational relaxations can occur on timescales from nanoseconds to hours or days (Wolynes et al., 1996 ▶; Socci et al., 1996 ▶; Grabolle et al., 2006 ▶); for proteins in crystals, many of these structural relaxations are slowed or inhibited by lattice constraints. As with damage arising from diffusing free radicals, these solvent-coupled relaxations are diffusive and are slowed on cooling, becoming unimportant below the glass transition.
Finally, changes in molecular packing owing to radiation-induced molecular damage can lead to inhomogeneous lattice stresses, formation of point defects, dislocations and cracks, and plastic failure on timescales that may range from milliseconds to weeks or longer, depending upon radiation dose (which determines the magnitude of lattice stresses), dose non-uniformity across the crystal (which creates stress gradients that facilitate plastic failure), dose rate (which affects how quickly stresses develop), temperature and the presence of defects (cracks, dislocations and impurity-gradient-induced stresses) in the crystal before irradiation which can ‘seed’ additional defect formation, among other factors. Radiation-induced structural (as opposed to chemical) relaxations have a long history of study in the context of, for example, organic and inorganic materials used in nuclear reactors and spacecraft, and in the processing of semiconductors for electronics.
2.2. Global radiation damage versus temperature
The temperature-dependent rates of damage processes determine how protein crystal diffraction properties evolve with temperature. The much smaller radiation sensitivity of protein crystals cooled to T ≃ 100 K has long been attributed to the limited mobility of radicals and protein within the vitrified solvent network (Rodgers, 1994 ▶; Garman & Schneider, 1997 ▶; Garman, 2003 ▶; Nave & Garman, 2005 ▶), as in much earlier work on cryoelectron microscopy. X-ray, neutron and Mossbauer techniques have observed a ‘dynamical transition’ in protein motions near T = 200 K (Parak et al., 1982 ▶; Doster et al., 1989 ▶; Tilton et al., 1992 ▶). This transition is connected to the solvent’s glass transition within the crystal (Weik, Kryger et al., 2001 ▶; Weik, Ravelli et al., 2001 ▶; Weik et al., 2004 ▶, 2005 ▶; Wood et al., 2008 ▶).
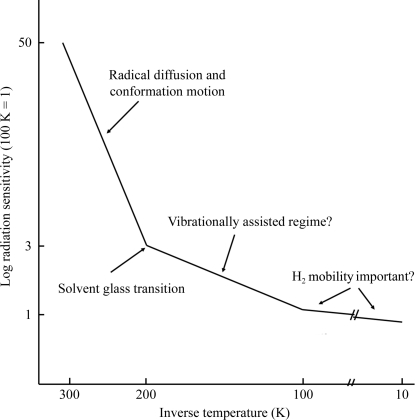
Fig. 1 ▶ schematically illustrates how the rate of global radiation damage to protein crystals varies with temperature, as deduced from our study of thaumatin (Warkentin & Thorne, 2010 ▶) and from other previous experiments (Borek et al., 2007 ▶; Meents et al., 2007 ▶, 2010 ▶; Juers & Weik, 2011 ▶). The measured radiation sensitivity of thaumatin shows a transition in behavior near T = 200 K corresponding to the temperature of the protein–solvent dynamical transition. On warming from T = 200 to 300 K, the radiation sensitivity (damage per dose) increased by a factor of ∼15. The activation energy obtained by fitting to an Arrhenius temperature variation is comparable to that for diffusive motions of protein and solvent and for diffusion-limited reactions of radicals in aqueous solution (Warkentin & Thorne, 2010 ▶).
Figure 1.
Schematic representation of global radiation sensitivity versus inverse temperature for thaumatin crystals. Different damage mechanisms have been suggested to dominate in each of the three distinct temperature regimes.
On cooling from T = 200 to 100 K, the radiation sensitivity decreased by only a factor of 2–3, which is consistent with some previous studies in this temperature range (Borek et al., 2007 ▶; Meents et al., 2010 ▶; Juers & Weik, 2011 ▶) and inconsistent with another, which concluded there was no temperature dependence of global sensitivity between 40 and 150 K (Teng & Moffat, 2002 ▶). The activation energy obtained from Arrhenius fits in this temperature range is comparable to that observed for solvent-free small-molecule organic crystals (Wade, 1984 ▶; Fryer et al., 1992 ▶; Müller et al., 2002 ▶).
Below 100 K the temperature dependence is much weaker, with only a 25% decrease in damage rate on cooling to any temperature below ∼100 K (Teng & Moffat, 2002 ▶; Borek et al., 2007 ▶; Meents et al., 2007 ▶, 2010 ▶), and the corresponding activation energy is near zero. Similar behavior is observed in water-free small-molecule organic crystals, where the global sensitivity becomes essentially temperature-independent below ∼80 K (Wade, 1984 ▶; Fryer et al., 1992 ▶; Müller et al., 2002 ▶).
2.3. Dark progression as a probe of damage timescales
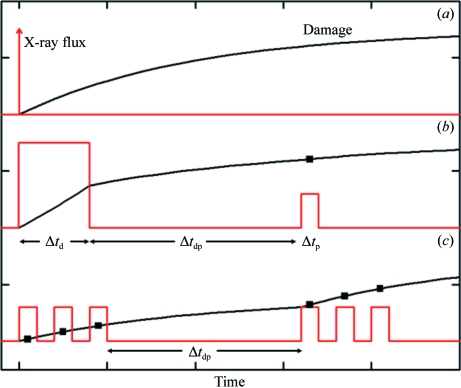
As shown in Fig. 2 ▶(a), an ideal way to probe the timescales of radiation damage is via an ‘impulse-response’ measurement: deliver a very large dose in a time that is short compared with these timescales and then continuously measure damage versus time using much smaller doses. As shown in Fig. 2 ▶(b), in practice a finite time Δt d, determined by the maximum available X-ray flux density, is required to deliver a damaging dose, and a finite dose (which creates additional damage) and therefore time Δt p are required to accurately assess damage. The damage timescales can then be estimated by measuring the amount of damage as a function of the time interval Δt dp when the X-ray beam is off between the initial ‘damaging’ and ‘probe’ pulses. The increase in damage when the X-ray beam is off is called ‘dark progression’.
Figure 2.
Probing damage timescales with X-rays. (a) An ‘impulse-response’ measurement. A very short, very intense pulse delivers a large dose and the evolution of damage is then monitored using short weaker pulses. (b) Maximum available X-ray flux density (dose rate) and minimum doses required to assess damage mean that both the damaging and probe pulses must have finite widths. These widths determine the time resolution of the experiment. (c) Schematic representation of the dosing sequence used in the present experiments.
The duration of the probe pulse Δt p (more generally, the time to acquire diffraction data sufficient to assess damage) limits the shortest damage timescale τ that can be reliably measured. The longest timescale is set by the available experimental time Δt e. If the timescale τ for a damage process is much longer than Δt e or much shorter than Δt p, no dark progression will be measured.
As discussed in §2.1 above, many damage processes are expected to be diffusion-limited. Well below the protein–solvent glass transition the timescales for diffusive processes should be extremely long (i.e. days to years) and well above the transition they should be short. Consequently, there should be a range of temperatures between T = 100 and 300 K where Δt p < τ < Δt e and dark progression is observable on experimentally convenient timescales.
3. Methods
3.1. Crystallization
Tetragonal thaumatin crystals were grown in 24-well trays using the hanging-drop method. The purified protein was obtained from Sigma–Aldrich (St Louis, Missouri, USA). Equal parts protein solution (25 mg ml−1 in 100 mM potassium phosphate buffer pH 6.8) and well solution (1 M sodium potassium tartrate in the same buffer) were dispensed and mixed on siliconized glass cover slips (Hampton Research, Aliso Viejo, California, USA) to form 20 µl hanging drops over 0.5 ml well solution. Crystals appeared overnight and grew to sizes ranging from 100 to 500 µm.
3.2. Crystal mounting
Crystals were harvested from their growth drops and immediately placed under NVH oil (Cargille Labs, Cedar Grove, New Jersey, USA). The surrounding aqueous mother liquor was then thoroughly removed. This protocol allows data collection at all temperatures without ice-crystal formation and without the use of high pressures (Kim et al., 2005 ▶), as described previously (Warkentin & Thorne, 2009 ▶). Crystals were then mounted in MicroMounts (Mitegen, Ithaca, New York, USA), placed on the goniometer and flash-cooled to the desired temperature using a Cryostream 700 cooler (Oxford Cryosystems, Oxford, England) with either liquid nitrogen or liquid helium as the cold gas source.
3.3. X-ray data collection
X-ray diffraction data were collected at the Cornell High Energy Synchrotron Source (CHESS) on MacCHESS station F1 using an X-ray energy of 13.5 keV, a 100 µm collimator and a Quantum 270 CCD detector (ADSC, Poway, California, USA). The flux was measured using a 6 cm nitrogen ionization chamber and was typically ∼1011 photons s−1. The dose (absorbed energy/mass) was calculated using this flux, the beam size, the incident photon energy, the exposure time and the average mass energy-absorption coefficient for the contents of the unit cell. Typical dose rates were ∼8 kGy s−1 and typical maximum doses delivered to each crystal were comparable to the half-dose for loss of diffracted intensity at each temperature, ranging from ∼1 MGy at 300 K to ∼20 MGy at 100 K and below.
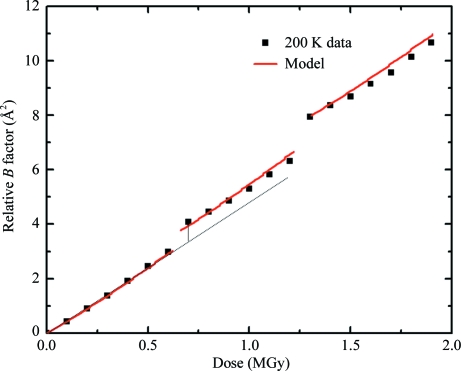
Damage versus dose curves were measured at temperatures of 25, 50, 80, 100, 130, 150, 180, 190, 200, 240, 255 and 300 K following the protocol used in our previous studies (Kmetko et al., 2006 ▶; Warkentin & Thorne, 2010 ▶). Briefly, each damage versus dose data point was obtained from a set of five 1° rotation frames collected over the same 5° range of ϕ, using a typical dose per set of ∼0.1 MGy. This ensured that the irradiated sample volume was at worst only slightly larger than the volume illuminated at fixed ϕ and minimized any tendency for the sample to slip (which can be significant for large rotations). The crystal size roughly matched the 100 µm beam size and the sample position relative to the beam was carefully monitored, including by examining orientation matrices. The beam at the sample, produced using slits smaller than the source size, had a somewhat rounded ‘top-hat’ profile and was assumed in the analysis to be uniform. To quantify dark progression, we used a fixed incident intensity to collect ‘interrupted’ dose curves. Sets of five 1° rotation frames, sufficient to assess global damage, were repeatedly collected and the slope of damage versus accumulated dose was determined. Next, the X-ray beam was turned off for a time Δt dp, the ‘dark interval’, to allow dark progression. Finally, additional sets of diffraction patterns were collected and damage versus dose plotted. As shown in Fig. 3 ▶, the damage offset between fits to the pre-dark-interval and post-dark-interval data points determined the amount of dark progression.
Figure 3.
An interrupted dose curve of relative B factor versus dose acquired at T = 200 K. The time between data points was 40 s. The dark-interval times at each interruption were 240 and 660 s for the first and second interruptions, respectively. The solid line is a fit to the model discussed in §5.3 with α/β = 2 and τ = 240 s. The vertical distance between the dotted line and the data collected immediately after the dark interval determines the amount of dark progression.
3.4. Time resolution
The time Δt p required to collect the five X-ray frames for each point on the dose curve was approximately 40 s. This included five 1 s X-ray exposures, five 3.4 s detector readouts and an ‘overhead’ of 18 s for the experiment to prepare to take another five-frame set. To obtain reliable estimates of dark progression, we used a minimum dark interval Δt dp of 200 s; the maximum time (limited by the available beam time and the number of temperatures to be examined) was 1200 s. Fig. 2 ▶(c) schematically shows the irradiation sequence used in our experiments.
3.5. Determination of relative B factors
To quantify global damage, each set of five frames was independently indexed, refined and integrated using DENZO (Otwinowski & Minor, 1997 ▶) and then scaled using SCALEPACK (Otwinowski & Minor, 1997 ▶). All sets for a given dose curve were then scaled together in another run of SCALEPACK, with the resulting B factors adjusted so that the first set had a B factor of zero. Global radiation damage versus dose D was then evaluated using ΔB = B(D) − B(0). At each temperature, the coefficient of sensitivity s AD = (ΔB/D)/8π2 was determined from the initial slope of ΔB versus dose D (Kmetko et al., 2006 ▶; Warkentin & Thorne, 2010 ▶).
Crystal degradation arising from inadvertent dehydration (important only at T = 300 K, since the vapor pressure of water is negligible below 270 K and too small to produce appreciable dehydration of our oil-coated crystals on our ∼1 h time scales) was detected and controlled for using the measured cell volumes. Radiation damage causes a slight increase in cell volume, while even modest dehydration causes a much larger decrease. Abrupt crystal degradation owing to, for example, plastic failure relieving accumulated stresses was easily detected in the measured mosaicity.
4. Results
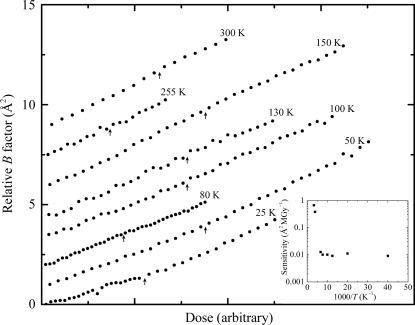
Interrupted dose curves were acquired at T = 25, 50, 80, 100, 130, 150, 180, 190, 200, 240, 255 and 300 K. As shown in Fig. 3 ▶ for T = 200 K, between 180 and 240 K the relative B factor increased while the X-rays were off. As shown in Fig. 4 ▶ (where the data at each temperature have been scaled by dose to give the same slope and have been offset vertically for clarity), no dark progression on timescales between ∼200 and 1200 s was observed at lower or higher temperatures. This indicates that at 255 K and above the timescales for most radiation-related chemical and structural relaxations are much shorter than 200 s. At 150 K and below, the timescales of those relaxations visible between 180 and 240 K have become much longer than 1200 s (or else their overall magnitudes have become much smaller).
Figure 4.
Interrupted dose curves at temperatures between 25 and 300 K where no dark progression was observed. The time between data points was 40 s. The dark-interval times at each interruption (indicated by the arrows) were 840, 1080, 1320, 1320, 1320, 1080, 600 and 600 s at T = 25, 50, 80, 100, 130 150, 255 and 300 K, respectively. At each arrow, a jump in the curve would indicate the presence of dark progression (as in Fig. 3 ▶), so the absence of jumps indicates that no additional damage was manifested during the dark-interval time. Crystal sensitivity to dose and thus the slope of relative B factor versus dose varies strongly with temperature. The doses for each curve in Fig. 4 ▶ have been normalized to give the same slope and the normalization factor (sensitivity) versus temperature is shown in the inset. The curves are also vertically offset for clarity.
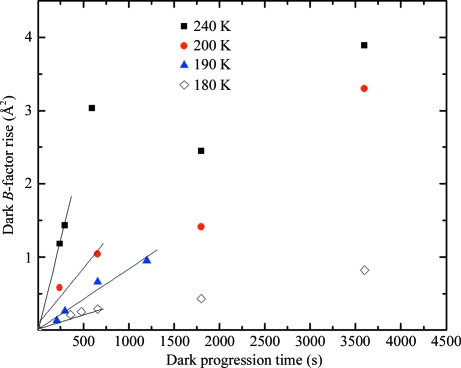
The rate of dark progression (increase in B factor per second) can be estimated from data such as those in Fig. 3 ▶. At each temperature between 180 and 240 K several interrupted dose curves, each with a different dark-interval time, were acquired. Fig. 5 ▶ shows the change in relative B factor versus dark-interval time Δt dp. For long dark-interval times, the magnitude of the B-factor change might be expected to saturate. The data at 240 K show evidence of saturation, but our longest Δt dp was insufficient to convincingly observe this at the other temperatures where we observed measurable progression. The initial rate of dark progression was estimated from the slopes of the linear fits to the data shown in Fig. 5 ▶.
Figure 5.
Dark progression (rise in relative B factor) versus dark-interval time at temperatures between 180 and 240 K obtained from data such as those shown in Fig. 3 ▶. Each time the dose curve was interrupted, the B factor rose by some amount while the X-rays were off, and that rise is shown here as a function of the the dark interval. At each temperature, larger dark intervals produce more damage. Evidence for saturation of damage with dark-interval time is seen at 240 K. The straight lines show linear fits to the initial (<600 s) slope of the data at each temperature; these slopes are shown in Fig. 6 ▶.
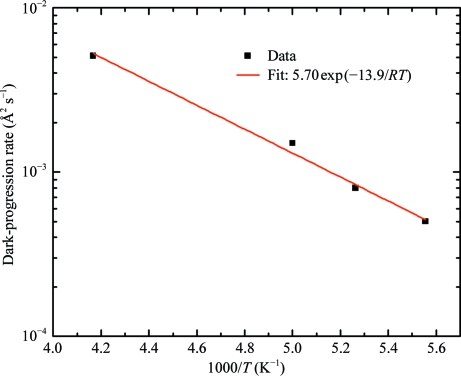
Fig. 6 ▶ shows the temperature dependence (between 180 and 240 K) of the initial dark-progression rate determined in this way. The data can be fitted by an Arrhenius form ΔB/Δt ∝ exp(−E dp/RT) with a single activation energy of E dp = 14 ± 1 kJ mol−1.
Figure 6.
Arrhenius plot of dark-progression rate versus inverse temperature, as determined from the slopes of the linear fits in Fig. 5 ▶. Between 240 and 180 K the data are consistent with a single thermally activated process with an activation energy of 14 ± 1 kJ mol−1, indicated by the solid line fit.
5. Discussion
5.1. Observations of dark progression
Previous experiments by us (Kmetko et al., 2006 ▶, 2011 ▶) and others (Southworth-Davies et al., 2007 ▶) found no evidence for dark progression at either T = 300 K or T = 100 K as assayed by global metrics. Ravelli & McSweeney (2000 ▶) observed increases in R merge during dark periods of ∼10 min and 19 h. In both cases the mosaicity or B factor remained unchanged, suggesting that the R merge increases were a consequence of site-specific rather than global damage effects.
Ample anecdotal information, especially from the early decades of protein crystallography before the broad adoption of cryocrystallographic methods (Blundell & Johnson, 1976 ▶), suggests that crystals can sometimes degrade at room temperature after being taken out of the X-ray beam. However, there is no quantitative report of these effects in the literature. We have observed similar but irreproducible effects with lysozyme crystals. Some crystals with radiation-induced yellow coloring diffracted well after a month or more of storage following initial irradiation, while others exhibited dramatic degradation after only a few hours out of the beam.
Although room-temperature dark progression on timescales of days to months, much longer than the timescales studied here, cannot be ruled out as the cause of at least some prior observations, several ‘artefactual’ mechanisms could also cause observed damage. In the early decades of protein crystallography, data-collection times of days to weeks necessitated by weak X-ray sources, the use of unfrozen capillary-mounted samples and laboratories that were seldom air-conditioned provided ample opportunity for problems to arise. Room-temperature crystals may dry out, suffer osmotic shock, undergo structural transitions and/or fracture if the capillary is not fully sealed, if the liquid plug injected into the capillary is not osmotically matched to the crystal, if changes in atmospheric pressure drive the liquid plug onto the crystal or if changes in laboratory temperature change solubilities and water activity. Radiation damage creates crystal stresses (as indicated by an increase in lattice parameters and mosaicity with dose). Non-uniform irradiation across the crystal must produce non-uniform lattice parameters and inhomogeneous stresses: with a Gaussian beam profile, the lattice parameters of the more intensely irradiated crystal center will want to expand more than those of outer regions. These stresses may be relieved by partial or catastrophic plastic failure of the crystal. In our previous X-ray topography studies of crystal dehydration (Dobrianov et al., 2001 ▶), some tetragonal lysozyme crystals exhibited well ordered diffraction when dehydrated below below 86% relative humidity. Others subjected to nominally identical treatment would at some point abruptly cease diffracting beyond ∼6 Å, develop very large mosaicities and develop complex contrast in X-ray topographs suggestive of a high density of cracks and dislocations, suggesting plastic failure connected with an inhomogeneous lattice transition.
5.2. Dark progression and dose rate effects
X-ray data collection on timescales comparable to or shorter than those for the damage processes that degrade diffraction should also lead to a dose-rate dependence of damage. For a given total dose, diffraction patterns collected using larger dose rates and thus in shorter times should show less damage, so that manifested damage should be inversely related to dose rate. This has been dramatically demonstrated using ultra-intense X-ray pulses tens of femtoseconds long produced by the free-electron laser at the LCLS (Chapman et al., 2011 ▶). Despite receiving a dose of up to 700 MGy per pulse (∼20 times the dose required to severely degrade steady-state diffraction; Henderson, 1990 ▶; Teng & Moffat, 2000 ▶; Owen et al., 2006 ▶), 200 nm to 2 µm crystals yielded indexable diffraction patterns owing to coherent scattering before the molecules disintegrated (Neutze et al., 2000 ▶) and to a lesser extent owing to energetic photoelectrons escaping from these very small crystals, reducing the dose (Finfrock et al., 2010 ▶; Sanishvili et al., 2011 ▶).
Several experiments have found no dose-rate effects on global damage at synchrotron-source intensities (∼2–500 kGy s−1) at both T = 100 K (Sliz et al., 2003 ▶; Leiros et al., 2006 ▶; Kmetko et al., 2006 ▶, 2011 ▶; Shimizu et al., 2007 ▶) and 300 K (Kmetko et al., 2011 ▶), consistent with the absence of dark progression at these temperatures.
An inverse dose-rate effect at T = 300 K, in which the radiation sensitivity of lysozyme crystals decreased by a factor of four when the dose rate was increased by a factor of 1.6, was reported for very low dose rates (6–10 Gy s−1; Southworth-Davies et al., 2007 ▶). No dark progression was observed (over 10 h), so the dose-rate effect cannot be a consequence of outrunning a (very slow) component of global damage, as was concluded by those authors. A subsequent study by the same group (Barker et al., 2009 ▶) using the same protein and similar dose rates showed no evidence of a dose-rate effect and gave half-doses for loss of diffraction intensity comparable to those measured at the kGy s−1 dose rates typical of synchrotrons (Kmetko et al., 2011 ▶).
A recent study of thaumatin and insulin crystals at T = 300 K (Rajendran et al., 2011 ▶) reported a 75% increase in radiation sensitivity as measured by global damage metrics for a roughly sixfold increase in dose rate from 1320 and 8420 Gy s−1. The sign of this effect is opposite to that expected if damage was being outrun. They suggested that the dose-rate effect was either a consequence of temperature-induced sensitization and/or the production of hydrogen in the sample, although no dose-rate effect has been observed at similar dose rates in previous studies.
Note that outrunning a component of radiation damage is not the only possible source of dose-rate effects. They may also arise if the products of individual damage events occur sufficiently close in time and space to interact and produce more or less damage than if their space–time separation was large. Reaction rates depend on concentrations of radiation-induced products and concentrations depend on lifetimes and dose rates, and these complex interactions could yield an overall dose-rate dependence to damage.
5.3. Mechanism of dark progression
Fig. 6 ▶ shows that the temperature-dependence of the dark-progression rate can be described using an Arrhenius form with an activation energy of E dp = 14 ± 1 kJ mol−1. The temperature-dependent radiation sensitivity of thaumatin crystals (illustrated schematically in Fig. 1 ▶) between T = 300 and 100 K has been fitted by
with E a1 = 18 ± 3 kJ mol−1, E a2 = 1.0 ± 0.3 kJ mol−1, A 1 = 513 Å2 MGy−1 and A 2 = 0.043 Å2 MGy−1 (Warkentin & Thorne, 2010 ▶), where the first term dominates above T ≃ 200 K and the second dominates below. The agreement between E dp and E a1 suggests that the observed dark progression and the steep increase in radiation sensitivity above T = 200 K have their origin in similar processes: diffusion and reaction of free radicals and diffusive conformational motions of the protein.
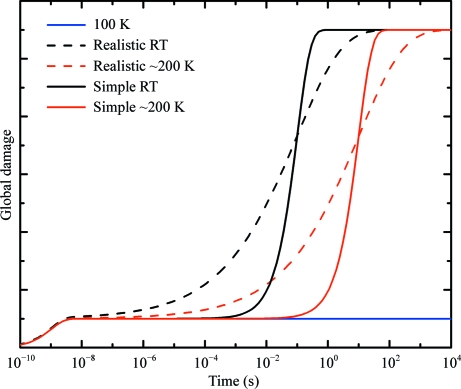
Radiation-sensitivity data (schematically represented in Fig. 1 ▶) show a clear crossover near T = 200 K. The dark-progression data in Fig. 6 ▶ show no such crossover down to 180 K. This suggests that the E a2 damage processes that dominate sensitivity below T = 200 K do not contribute to dark progression, presumably because their timescale is much shorter than that of the subset of E a1 processes that progress on our experimental timescales. Furthermore, the timescales of the E a2 processes remain outside our experimental window all the way down to T = 25 K. This implies that the timescales of the E a1 and E a2 processes are widely separated at all temperatures, as is schematically illustrated in Fig. 7 ▶.
Figure 7.
Schematic illustration of how global radiation damage may evolve with time in response to a very short intense X-ray pulse delivered at t = 0. Solid lines show the damage response assuming two exponential processes: a fast process with a temperature-independent timescale of 1 ns and a slow process whose timescale is temperature-activated. Dashed lines show the damage response assuming that the slow process has a broad distribution of relaxation times characteristic of glassy or disordered systems. The blue (bottom right) line shows the response at T = 100, where the slow temperature-activated processes have frozen out.
Another possible source of dark progression is the mobility of molecular hydrogen gas. Hydrogen gas is generated by irradiation and trapped within crystals and its temperature-dependent diffusion has been suggested to account for the temperature dependence of damage at low (5–100 K) temperatures (Meents et al., 2010 ▶). Generation of molecular hydrogen inside a crystal creates pressure, and crystal properties may change as this pressure is released or redistributed. For example, hydrogen may accumulate at grain boundaries, cracks or voids and drive plastic failure.
The mobility of molecular hydrogen gas on the surface of and inside amorphous ice evolves dramatically with temperature. Desorption from the surface occurs between 16 and 25 K and long-range translational diffusion leading to gas release from the bulk on laboratory timescales occurs between 90 and 140 K (Petrik & Kimmel, 2004 ▶; Zheng et al., 2006 ▶). Hydrogen gas can completely escape a protein crystal at ∼160 K (Meents et al., 2010 ▶), consistent with measurements on amorphous ice. Consequently, if crystal damage owing to the mobility of radiation-induced hydrogen gas is important, there must be some temperature between 90 and 140 K where this damage evolves on the timescale of our experiments. Since we observe no dark progression between T = 25 and 150 K, the mobility of hydrogen appears to be irrelevant to global manifestations of damage in this temperature range.
Consequently, hydrogen appears to behave just like any other damage product inside the crystal. All radiation damage to protein crystals (and to crystals of other organic and inorganic materials) involves the breaking of bonds and creation of defects. These local atomic displacements and electronic rearrangements in turn create internal pressures that cause lattice expansion. In protein crystals, where more than half of the atoms are hydrogen, a significant fraction of the broken bonds will release hydrogen. Hydrogen will thus necessarily contribute significantly both to the internal pressure and to global metrics of radiation damage. However, its special property relative to other radiation damage products, its mobility, does not appear to have major effects on diffraction properties (except, perhaps, when a crystal heavily irradiated at T = 100 K is rapidly warmed to a temperature, e.g. 180 or 300 K, where molecular hydrogen is highly mobile, resulting in violent gas release.)
Spectroscopy of irradiated protein crystals has revealed excitations including trapped solvated electrons and disulfide radicals with lifetimes of tens of seconds at 100, 130 and 160 K (McGeehan et al., 2009 ▶). If these excitations were a dominant cause of global damage (as determined by B factors), we would expect to see dark progression at 100, 130 and 160 K on the same timescales, but no dark progression is observed at these temperatures. This is not surprising. Tiny concentrations of radiation-induced defects can dramatically change the optical absorption spectra of crystals (including diamonds and quartz), yet have no appreciable effect on crystal order as probed by diffraction. Furthermore, spectroscopically active defects typically comprise only a small fraction of total disorder in crystalline solids. However, it would be interesting to explore a possible correlation between the lifetimes of specific excitations and the timescale for any post-irradiation evolution of site-specific damage (as determined by crystallography). This might help explain observed increases in R merge at 100 K and on these timescales (Ravelli & McSweeney, 2000 ▶).
5.4. Modelling dark progression
Motivated by the above discussion, we assume as in Fig. 7 ▶ that global radiation damage, as manifested in relative B factors, has two components: one with a very short timescale, which appears immediately upon irradiation, and one with a timescale comparable to that of the experiment. To model the long-timescale component, we assume that ‘unrelaxed excitations’ (both chemical and structural, including free radicals, broken peptide chains, unstable protein folds etc.) are instantaneously generated by X-rays at a rate γ proportional to the dose rate dD/dt. These excitations then exponentially decay with a lifetime τ. The rate dB/dt at which damage is manifested is assumed to be proportional to the concentration R of unrelaxed excitations at any instant. Thus,
and
where α is the rate at which damage is manifested per unit concentration of excitations and B is the B factor as before.
In steady state, R = γτ and dB/dt = αγτ. When the X-rays are turned off, R decays exponentially with time constant τ. The maximum amount of dark progression possible, determined by integrating to t = ∞, is
and is equal to dB/dt at the steady-state rate in one lifetime τ.
The above assumes that the sample is continuously irradiated during the collection of each data point. However, the actual irradiation in our experiment consisted of a series of five short (1 s) pulses separated by the 3.4 s required for detector readout and followed by 18 s while the goniometer was reset. The data can only be understood in the context of the actual dose sequence. To describe the response to this more complex dosing sequence, we use an impulse-response formulation of the same physical model.
The response of the excitation concentration to an X-ray pulse of width dt delivered at t = t′ is
where θ is the Heaviside step function. This produces a change in B factor
So far, the model only accounts for damage by the long-timescale process in Fig. 7 ▶. If there is also a fast (effectively instantaneous) process, (3) becomes
where β is the sensitivity of the crystal to the fast damage process. (6) then becomes
For a single X-ray pulse beginning at time t = t 0 and ending at time t = t 1, the response is
For a sequence of X-ray pulses, the response is obtained by summing terms such as (9) with appropriate t 0 and t 1 values.
Using the actual experimental dosing sequence, we have calculated fits to relative B factor versus dose data and extracted values of the temperature-dependent ratio α/β and the exponential lifetime τ. Fig. 3 ▶ shows one such fit at T = 200 K with α/β = 2 and τ = 240 s. Despite the long time constant, the fit reproduces the observed linear variation of damage with dose. There is no initial transient increase in slope, as expected if the dose were delivered as an impulse, because of the more complex experimental dosing sequence illustrated in Fig. 2 ▶(c). Similar fits at T = 180 and 190 K give τ ≃ 840 and 580 s, respectively. At T = 240 K, the timescale is too small compared with our ∼200 s resolution to be accurately estimated.
5.5. Can radiation damage above T = 180 K be outrun?
The unambiguous answer from the present data is yes, as can be seen in Fig. 3 ▶. The observation of dark progression on timescales of minutes implies that some damage can be outrun with modest cooling even using ordinary synchrotron dose rates and previous-generation X-ray detectors. For example, at T = 240 K we observe ∼27% less damage (as reflected in the increase in B factor) during a 600 s data collection (just prior to turning off the X-rays) than during a 1200 s collection (just after turning them back on) using the same total dose; in other words, we see a clear reduction in damage with increasing dose rate. Reducing the data-collection time by a factor of 10 (to 60 s) or 100 (to 6 s) may produce larger damage reductions.
The temperature-dependent data-collection time to outrun the ‘dark-progressing’ (as opposed to ‘instantaneous’) component of damage can be crudely estimated from our data at 180–200 K. The factor of ∼3 decrease in τ between 180 and 200 K (from the model in Fig. 3 ▶; see §5.3) is consistent with an activation energy of ∼14 kJ mol−1, comparable to fit values in Fig. 6 ▶ and in (1) and with activation energies for a variety of diffusion-limited processes (diffusion-controlled radical reactions, translational diffusion of hydration water and conformational motions) in proteins (Warkentin & Thorne, 2010 ▶ and references therein). Assuming τ = τ0exp(E a/RT) with E a = 14 kJ mol−1 gives order-of-magnitude estimates of τ ≃ 45, 18 and 9 s at T = 240, 270 and 300 K, respectively. These times are remarkably long compared with those for, e.g., intermolecular diffusion of radicals.
With current data-collection times of a few minutes to tens of minutes (using synchrotron sources) to hours (using laboratory sources), technically speaking some radiation damage is already being outrun. For example, the diffusion-coupled E a1 processes freeze out below the solvent–protein glass transition. By cooling crystals below 180 K, the timescale of these processes becomes much longer than current data-collection times and so they are outrun.
We can estimate how much additional damage might be outrun using much faster data collection from the present results for dark progression. We assume that the timescales for the E a2 damage processes that dominate measurements well below T = 200 K are very short. An upper bound on how much additional damage might be outrun can be estimated using (1) from the fraction of total damage at each temperature that arises from the slower E a1 processes, i.e. from the ratio A 1exp(−E a1/RT)/[A 1exp(−E a1/RT) + A 2exp(−E a2/RT)]. This fraction increases from 12% of the measured damage (at an ∼10 kGy s−1 dose rate) at T = 180 K to 42% at 240 K, 86% at 270 K and 93% at 300 K. If all of the E a1 processes are outrun, the corresponding increase in ‘survivable’ dose is then a factor of ∼3 at 240 K and 14 at 300 K. However, it is likely that the E a1 processes have a distribution of timescales and that the dark progression observed here arises only from those processes with the longest timescales. In that case, the fraction of damage that could be outrun in a given data-collection time may be much smaller.
The importance of the distribution of damage timescales and how it varies with temperature in determining potential damage reductions can be understood by considering the schematic ‘impulse-response’ plots in Fig. 7 ▶. The simple model discussed above assumes a single timescale τ for the E a1 damage processes that dominate above T = 200 K, as shown by the solid lines in Fig. 7 ▶. Provided that data are collected in a time ≃ τ/10, nearly all of this damage component could be outrun, leaving only the small component of damage arising from the fast processes that dominate below 200 K. However, if the E a1 damage processes have a broad distribution of timescales as in glassy relaxation, as shown by the dashed lines in Fig. 7 ▶, then reducing the data-collection times by a factor of ten or 100 might produce only modest increases in survivable doses.
At temperatures above 200 K, damage arises from processes occurring on many length scales, from diffusion and reaction of radicals to solvent-coupled conformational motions to lattice-scale structural relaxations. These processes must involve an extremely broad range of timescales. However, only the timescales for the atomic displacements that dominate in degrading B factors and scale factors are relevant in determining the timescales for global damage in crystallography. If these displacements primarily arise, for example, not from radical-induced bond breaking but from larger-scale collective motions, then the mean of their distribution of timescales may be relatively long. A circumstantial argument in favour of this is as follows. The room-temperature radiation sensitivities of protein crystals having comparable mass energy absorption show large variations from protein to protein. For example, TenA crystals are at least 30 times more sensitive than thaumatin, lysozyme and urease crystals (see, for example, Kmetko et al., 2011 ▶). This large sensitivity variation is unlikely to arise from differences in chemical (bond-scale) damage, but from differences in the extent of structural relaxations.
How much damage can be outrun also depends on the dose required to collect a structural data set, on the maximum achievable or allowable dose rate and on the maximum sample oscillation and diffraction capture rates. The required X-ray dose to achieve a given resolution depends on the molecular weight, solvent content, atomic composition and number of sites in the asymmetric unit, the crystal size and quality and the X-ray energy, and can be estimated using software described by Holton & Frankel (2010 ▶). The dose per irradiated region can be reduced by collecting and merging data from multiple regions within the same crystal or from different crystals.
The maximum allowable dose rate will determine the maximum amount of damage that can be outrun. In steady state, the maximum dose rate is limited by X-ray heating of the crystal (Kriminski et al., 2003 ▶; Mhaisekar et al., 2005 ▶; Snell et al., 2007 ▶). The heated sample volume includes both crystal and surrounding liquid; we assume that the crystals have been mounted with minimal external liquid so that the sample size and crystal size are the same for the purposes of heat transfer.
Heat transfer from smaller samples is more efficient, so for a given dose rate the temperature rise scales with crystal size L as ΔT ∝ L 3/2 (Kriminski et al., 2003 ▶). For an L = 100 µm crystal illuminated with 13 keV X-rays, a dose rate of 200 kGy s−1 (corresponding to a flux density of ∼5 × 1014 photons mm−2 s−1) gives ΔT ≃ 10 K. Larger temperature rises and thus dose rates can be tolerated if the sample is cooled well below T = 100 K, since crystal properties do not evolve significantly with temperature below ∼130 K.
Given heating-imposed limitations on maximum incident fluxes and dose rates, what is the minimum time required to collect a complete data set? Table 1 ▶ gives calculated values for the dose required for a minimally solvable molecular-replacement data set to 2 Å resolution from lysozyme (Holton & Frankel, 2010 ▶), the maximum heating-limited dose rate (conservatively assuming a 10 K rise is acceptable) and the minimum time to collect the data set. In this relatively favorable case, the minimum required data-collection time varies from 0.09 s for a 100 µm crystal to 1.8 s for a 10 µm crystal. X-ray flux densities of up to ∼1015 photons mm−2 s−1 in ∼50 µm beams, corresponding to dose rates of ∼1 MGy s−1, are currently available at third-generation synchrotron sources. X-ray detectors from Dectris (http://www.dectris.ch) and Rayonix (http://www.rayonix.com) allow data collection at frame rates of up to 100 Hz and the next generation of detectors should improve on this by at least a factor of ten. Thus, the required dose and frame rates to achieve these ‘theoretical’ heating-limited data-collection rates are all within reach.
Table 1. Estimates of the dose required for a minimally solvable molecular-replacement data set to 2 Å resolution from lysozyme, the maximum heating-limited dose rate assuming a 10 K rise, the minimum time to collect the data set and the maximum required detector frame rate as a function of crystal size.
The dose required for an MR data set was calculated using the model of Holton & Frankel (2010 ▶) and the program available at http://bl831.als.lbl.gov/xtalsize.html.
| Crystal size (µm) | Dose for MR set (MGy) | Frames | Maximum dose rate (MGy s−1) | Minimum collection time (s) | Maximum frame rate (Hz) |
|---|---|---|---|---|---|
| 10 | 11.8 | 90 | 6.5 | 1.8 | 50 |
| 20 | 1.8 | 90 | 2.3 | 0.78 | 115 |
| 50 | 0.13 | 90 | 0.58 | 0.23 | 400 |
| 100 | 0.018 | 90 | 0.20 | 0.09 | 1000 |
The required dose to obtain a structure at a given resolution and thus the minimum data-collection time increases with increasing molecular weight. Cooling to ∼20 K to allow larger temperature rises should allow dose rates to be increased and bring the collection time back down. De novo structure determination by MAD will also require a means to rapidly change wavelength.
Based upon the above discussion, it appears that significant reductions in radiation damage at temperatures above T = 200 K, including at room temperature, may be possible in the immediate future. Data collection with times ∼τ/10 of 4, 1.5 and 0.7 s may be sufficient to outrun at least some fraction of diffusive global damage at T = 240, 270 and 300 K, respectively. If the distribution of radiation-damage relaxation times is narrow, as indicated by the solid lines in Fig. 7 ▶, at 300 K damage for a given dose may be reduced by as much as a factor of ∼10. Crystals would then be only ∼3 times more radiation sensitive than at T = 100 K, a difference that could be made up by using crystals with linear dimensions only 31/3 = 1.4 times larger. With a T = 100 K dose limit of 30 MGy before diffraction patterns degrade excessively (Teng & Moffat, 2000 ▶; Owen et al., 2006 ▶; Kmetko et al., 2006 ▶), the corresponding limit at 300 K would then be ∼10 MGy (instead of ∼1 MGy for conventional data collection; Blake & Phillips, 1962 ▶; Southworth-Davies et al., 2007 ▶), enabling room-temperature structure determination of modest-size proteins from a single 10 µm crystal. However, in the more likely case that the distribution of radiation-damage relaxation times is broad, as indicated by the dashed lines in Fig. 7 ▶, only much more modest damage reductions for a given dose may be obtained.
6. Conclusions
In this study, we have observed and quantified ‘dark’ progression of global radiation damage to thaumatin crystals on timescales of 200–1200 s using the scaling B factor as a metric. Progression on ∼10 min timescales first becomes visible near the protein–solvent glass transition. The temperature-dependent magnitude and timescale of progression suggest that it arises from diffusion-limited reactions and structural relaxations of the protein and lattice. Dark progression is not observed from 180 K down to 25 K, suggesting that the processes responsible for manifested damage in this temperature range are not thermally activated and occur on short timescales.
Data sets collected in ∼600 s between T = 180 and 240 K show clear reductions in manifested global damage compared with those collected at longer times, indicating that some radiation damage can be outrun. By combining faster data collection with modest cooling, a fraction of damage arising from the diffusive processes important above T = 200 K may be outrun, increasing the amount of data that may be obtained from each crystal. An expansion in the scope of single-crystal diffraction studies, without the need for cryocrystallographic methods or solvent vitrification, may soon be possible.
Acknowledgments
This work was supported by the National Institutes of Health (NIH) under award No. GM065981-05 A1. It is based on research conducted at the Cornell High-Energy Synchrotron Source (CHESS), which is supported by the National Science Foundation (NSF) and the NIH/National Institute of General Medical Sciences under NSF award No. DMR-0225180 using the Macromolecular Diffraction at CHESS (MacCHESS) facility, which is supported by award No. RR-01646 from the NIH, through its National Center for Research Resources.
References
- Anbar, M. & Hart, E. J. (1967). J. Phys. Chem. 71, 3700–3702.
- Barker, A. I., Southworth-Davies, R. J., Paithankar, K. S., Carmichael, I. & Garman, E. F. (2009). J. Synchrotron Rad. 16, 205–216. [DOI] [PubMed]
- Benkovic, S. J. & Hammes-Schiffer, S. (2006). Science, 312, 208–209. [DOI] [PubMed]
- Blake, C. & Phillips, D. C. (1962). Proceedings of the Symposium on the Biological Effects of Ionizing Radiation at the Molecular Level, pp. 183–191. Vienna: International Atomic Energy Agency.
- Blundell, T. & Johnson, L. N. (1976). Protein Crystallography. London: Academic Press.
- Borek, D., Ginell, S. L., Cymborowski, M., Minor, W. & Otwinowski, Z. (2007). J. Synchrotron Rad. 14, 24–33. [DOI] [PubMed]
- Bourgeois, D. & Royant, A. (2005). Curr. Opin. Struct. Biol. 15, 538–547. [DOI] [PubMed]
- Buxton, G. V., Greenstock, C. L., Helman, W. P. & Ross, A. B. (1988). J. Phys. Chem. Ref. Data, 17, 513–886.
- Chapman, H. N. et al. (2011). Nature (London), 470, 73–77.
- Chong, S.-H., Joti, Y., Kidera, A., Go, N., Ostermann, A., Gassmann, A. & Parak, F. (2001). Eur. Biophys. J. 30, 319–329. [DOI] [PubMed]
- Coggle, J. E. (1983). Biological Effects of Radiation, 2nd ed. London: Taylor & Francis.
- Colletier, J.-P., Bourgeois, D., Sanson, B., Fournier, D., Sussman, J. L., Silman, I. & Weik, M. (2008). Proc. Natl Acad. Sci. USA, 105, 11742–11747. [DOI] [PMC free article] [PubMed]
- Deacon, A., Gleichmann, T., Kalb, A. J., Price, H., Raftery, J., Bradbrook, G., Yariv, J. & Helliwell, J. R. (1997). J. Chem. Soc. Faraday Trans. 93, 4305–4312.
- Dertinger, H. & Jung, H. (1970). Molecular Radiation Biology. Berlin: Springer-Verlag.
- Dobrianov, I., Kriminski, S., Caylor, C. L., Lemay, S. G., Kimmer, C., Kisselev, A., Finkelstein, K. D. & Thorne, R. E. (2001). Acta Cryst. D57, 61–68. [DOI] [PubMed]
- Doster, W., Cusack, S. & Petry, W. (1989). Nature (London), 337, 754–756. [DOI] [PubMed]
- Duke, E. M. H. & Johnson, L. N. (2010). Proc. R. Soc. A, 466, 3421–3452.
- Finfrock, Y. Z., Stern, E. A., Yacoby, Y., Alkire, R. W., Evans-Lutterodt, K., Stein, A., Isakovic, A. F., Kas, J. J. & Joachimiak, A. (2010). Acta Cryst. D66, 1287–1294. [DOI] [PubMed]
- Frauenfelder, H., Petsko, G. A. & Tsernoglou, D. (1979). Nature (London), 280, 558–563. [DOI] [PubMed]
- Fry, E. E., Grimes, J. & Stuart, D. I. (1999). Mol. Biotechnol. 12, 13–23. [DOI] [PubMed]
- Fryer, J. R., McConnell, C. H., Zemlin, F. & Dorset, D. L. (1992). Ultramicroscopy, 40, 163–169.
- Garman, E. (2003). Curr. Opin. Struct. Biol. 13, 545–551. [DOI] [PubMed]
- Garman, E. F. & Schneider, T. R. (1997). J. Appl. Cryst. 30, 211–237.
- Gilbert, R. J. C., Grimes, J. M. & Stuart, D. I. (2003). Adv. Protein Chem. 64, 37–91. [DOI] [PubMed]
- Grabolle, M., Haumann, M., Müller, C., Liebisch, P. & Dau, H. (2006). J. Biol. Chem. 281, 4580–4588. [DOI] [PubMed]
- Hammes-Schiffer, S. & Benkovic, S. J. (2006). Annu. Rev. Biochem. 75, 519–541. [DOI] [PubMed]
- Henderson, R. (1990). Proc. R. Soc. Lond. B. Biol. Sci. 241, 6–8.
- Henzler-Wildman, K. & Kern, D. (2007). Nature (London), 450, 964–972. [DOI] [PubMed]
- Holton, J. M. & Frankel, K. A. (2010). Acta Cryst. D66, 393–408. [DOI] [PMC free article] [PubMed]
- Hope, H. (1988). Acta Cryst. B44, 22–26. [DOI] [PubMed]
- Hope, H. (1990). Annu. Rev. Biophys. Biophys. Chem. 19, 107–126. [DOI] [PubMed]
- Juers, D. H. & Matthews, B. W. (2001a). J. Mol. Biol. 311, 851–862. [DOI] [PubMed]
- Juers, D. H. & Matthews, B. W. (2001b). Biophys. J. 80, 60A.
- Juers, D. H. & Matthews, B. W. (2004). Q. Rev. Biophys. 37, 105–119. [DOI] [PubMed]
- Juers, D. H. & Weik, M. (2011). J. Synchrotron Rad. 18, 329–337. [DOI] [PubMed]
- Kim, C. U., Kapfer, R. & Gruner, S. M. (2005). Acta Cryst. D61, 881–890. [DOI] [PubMed]
- Kmetko, J., Husseini, N. S., Naides, M., Kalinin, Y. & Thorne, R. E. (2006). Acta Cryst. D62, 1030–1038. [DOI] [PubMed]
- Kmetko, J., Warkentin, M., Englich, U. & Thorne, R. E. (2011). Submitted. [DOI] [PMC free article] [PubMed]
- Kriminski, S., Caylor, C. L., Nonato, M. C., Finkelstein, K. D. & Thorne, R. E. (2002). Acta Cryst. D58, 459–471. [DOI] [PubMed]
- Kriminski, S., Kazmierczak, M. & Thorne, R. E. (2003). Acta Cryst. D59, 697–708. [DOI] [PubMed]
- Leiros, H.-K. S., Timmins, J., Ravelli, R. B. G. & McSweeney, S. M. (2006). Acta Cryst. D62, 125–132. [DOI] [PubMed]
- Low, B. W., Chen, C. C. H., Berger, J. E., Singman, L. & Pletcher, J. F. (1966). Proc. Natl Acad. Sci. USA, 56, 1746–1750. [DOI] [PMC free article] [PubMed]
- McGeehan, J., Ravelli, R. B. G., Murray, J. W., Owen, R. L., Cipriani, F., McSweeney, S., Weik, M. & Garman, E. F. (2009). J. Synchrotron Rad. 16, 163–172. [DOI] [PMC free article] [PubMed]
- Meents, A., Gutmann, S., Wagner, A. & Schulze-Briese, C. (2010). Proc. Natl Acad. Sci. USA, 107, 1094–1099. [DOI] [PMC free article] [PubMed]
- Meents, A., Wagner, A., Schneider, R., Pradervand, C., Pohl, E. & Schulze-Briese, C. (2007). Acta Cryst. D63, 302–309. [DOI] [PubMed]
- Mhaisekar, A., Kazmierczak, M. J. & Banerjee, R. (2005). J. Synchrotron Rad. 12, 318–328. [DOI] [PubMed]
- Müller, R., Weckert, E., Zellner, J. & Drakopoulos, M. (2002). J. Synchrotron Rad. 9, 368–374. [DOI] [PubMed]
- Nashine, V. C., Hammes-Schiffer, S. & Benkovic, S. J. (2010). Curr. Opin. Chem. Biol. 14, 644–651. [DOI] [PMC free article] [PubMed]
- Nave, C. & Garman, E. F. (2005). J. Synchrotron Rad. 12, 257–260. [DOI] [PubMed]
- Neutze, R., Wouts, R., van der Spoel, D., Weckert, E. & Hajdu, J. (2000). Nature (London), 406, 752–757. [DOI] [PubMed]
- Otwinowski, Z. & Minor, W. (1997). Methods Enzymol. 276, 307–326. [DOI] [PubMed]
- Owen, R. L., Rudiño-Piñera, E. & Garman, E. F. (2006). Proc. Natl Acad. Sci. USA, 103, 4912–4917. [DOI] [PMC free article] [PubMed]
- Parak, F., Knapp, E. W. & Kucheida, D. (1982). J. Mol. Biol. 161, 177–194. [DOI] [PubMed]
- Petrik, N. G. & Kimmel, G. A. (2004). J. Chem. Phys. 121, 3736–3744. [DOI] [PubMed]
- Petsko, G. A. (1975). J. Mol. Biol. 96, 381–392. [DOI] [PubMed]
- Rajendran, C., Dworkowski, F. S. N., Wang, M. & Schulze-Briese, C. (2011). J. Synchrotron Rad. 18, 318–328. [DOI] [PMC free article] [PubMed]
- Ravelli, R. B. & McSweeney, S. M. (2000). Structure, 8, 315–328. [DOI] [PubMed]
- Ringe, D. & Petsko, G. A. (2008). Science, 320, 1428–1429. [DOI] [PubMed]
- Rodgers, D. W. (1994). Structure, 2, 1135–1140. [DOI] [PubMed]
- Rossmann, M. G. (1999). J. Synchrotron Rad. 6, 816–821.
- Sandalova, T., Schneider, G., Käck, H. & Lindqvist, Y. (1999). Acta Cryst. D55, 610–624. [DOI] [PubMed]
- Sanishvili, R., Yoder, D. W., Pothineni, S. B., Rosenbaum, G., Xu, S., Vogt, S., Stepanov, S., Makarov, O. A., Corcoran, S., Benn, R., Nagarajan, V., Smith, J. L. & Fischetti, R. F. (2011). Proc. Natl Acad. Sci. USA, 108, 6127–6132. [DOI] [PMC free article] [PubMed]
- Scheidig, A. J., Burmester, C. & Goody, R. S. (1999). Structure, 7, 1311–1324. [DOI] [PubMed]
- Shimizu, N., Hirata, K., Hasegawa, K., Ueno, G. & Yamamoto, M. (2007). J. Synchrotron Rad. 14, 4–10. [DOI] [PubMed]
- Sliz, P., Harrison, S. C. & Rosenbaum, G. (2003). Structure, 11, 13–19. [DOI] [PubMed]
- Snell, E. H., Bellamy, H. D., Rosenbaum, G. & van der Woerd, M. J. (2007). J. Synchrotron Rad. 14, 109–115. [DOI] [PubMed]
- Socci, N. D., Onuchic, J. N. & Wolynes, P. G. (1996). J. Chem. Phys. 104, 5860–5868.
- Southworth-Davies, R. J., Medina, M. A., Carmichael, I. & Garman, E. F. (2007). Structure, 15, 1531–1541. [DOI] [PubMed]
- Teng, T. & Moffat, K. (2000). J. Synchrotron Rad. 7, 313–317. [DOI] [PubMed]
- Teng, T.-Y. & Moffat, K. (2002). J. Synchrotron Rad. 9, 198–201. [DOI] [PubMed]
- Tilton, R. F., Dewan, J. C. & Petsko, G. A. (1992). Biochemistry, 31, 2469–2481. [DOI] [PubMed]
- Wade, R. H. (1984). Ultramicroscopy, 14, 265–270.
- Warkentin, M. & Thorne, R. E. (2009). J. Appl. Cryst. 42, 944–952. [DOI] [PMC free article] [PubMed]
- Warkentin, M. & Thorne, R. E. (2010). Acta Cryst. D66, 1092–1100. [DOI] [PMC free article] [PubMed]
- Weik, M. & Colletier, J.-P. (2010). Acta Cryst. D66, 437–446. [DOI] [PMC free article] [PubMed]
- Weik, M., Kryger, G., Schreurs, A. M. M., Bouma, B., Silman, I., Sussman, J. L., Gros, P. & Kroon, J. (2001). Acta Cryst. D57, 566–573. [DOI] [PubMed]
- Weik, M., Ravelli, R. B. G., Silman, I., Sussman, J. L., Gros, P. & Kroon, J. (2001). Protein Sci. 10, 1953–1961. [DOI] [PMC free article] [PubMed]
- Weik, M., Schreurs, A. M. M., Leiros, H.-K. S., Zaccai, G., Ravelli, R. B. G. & Gros, P. (2005). J. Synchrotron Rad. 12, 310–317. [DOI] [PubMed]
- Weik, M., Vernede, X., Royant, A. & Bourgeois, D. (2004). Biophys. J. 86, 3176–3185. [DOI] [PMC free article] [PubMed]
- Wolynes, P., Luthey-Schulten, Z. & Onuchic, J. (1996). Chem. Biol. 3, 425–432. [DOI] [PubMed]
- Wood, K., Frolich, A., Paciaroni, A., Moulin, M., Hartlein, M., Zaccai, G., Tobias, D. J. & Weik, M. (2008). J. Am. Chem. Soc. 130, 4586–4587. [DOI] [PubMed]
- Zheng, W., Jewitt, D. & Kaiser, R. I. (2006). Astrophys. J. 648, 753–761.